原子数随时间的变化MATLAB代码
matlab cusum算法求变点代码

matlab cusum算法求变点代码【原创版】目录1.MATLAB 与 CUSUM 算法简介2.CUSUM 算法原理3.MATLAB 中实现 CUSUM 算法的方法4.应用 CUSUM 算法求变点的实例5.总结正文【1.MATLAB 与 CUSUM 算法简介】MATLAB 是一种广泛应用于科学计算、数据分析、可视化等领域的编程语言。
CUSUM(Cumulative Sum)算法,即累积和算法,是一种检测时间序列中变点的方法,具有较高的准确性和可靠性。
【2.CUSUM 算法原理】CUSUM 算法的基本思想是对时间序列数据进行平滑处理,然后计算累积和。
当某个时间点的数据发生突变时,累积和会发生较大的变化,从而可以判断该点为变点。
【3.MATLAB 中实现 CUSUM 算法的方法】在 MATLAB 中,可以使用以下步骤实现 CUSUM 算法:1) 导入数据:首先,将时间序列数据导入到 MATLAB 中,通常使用load、readtable 等函数实现。
2) 数据预处理:对原始数据进行平滑处理,常用的平滑方法有移动平均法、指数平滑法等。
3) 计算累积和:对平滑后的数据计算累积和,可以使用 cumsum 函数实现。
4) 检测变点:通过分析累积和的变化,判断变点出现的位置。
【4.应用 CUSUM 算法求变点的实例】假设我们有以下时间序列数据,其中包含两个变点:```data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];```首先,对数据进行指数平滑处理,然后计算累积和:```matlab% 指数平滑处理smoothed_data = exp1(data);% 计算累积和cumulative_sum = cumsum(smoothed_data);```通过观察 cumulative_sum,我们可以发现变点出现的位置。
在本例中,变点分别位于索引 3 和索引 8 处。
【5.总结】MATLAB 中实现 CUSUM 算法求变点,首先需要对时间序列数据进行平滑处理,然后计算累积和。
matlab时变函数

在MATLAB中,你可以创建和操作时变函数。
时变函数是指其输出随时间变化的函数。
以下是一个简单的例子,演示了如何在MATLAB中创建和操作时变函数:1.定义时变函数:你可以定义一个函数,其中包含时间变量。
例如,假设你有一个函数f(t) = t^2,其中t是时间。
2.使用for循环:你可以使用for循环来模拟时间的变化,并计算函数的值。
matlab复制代码t = 0:0.1:10; % 时间向量y = zeros(size(t)); % 初始化输出向量for i = 1:length(t)y(i) = t(i)^2; % 计算函数的值end% 绘制结果plot(t, y);xlabel('Time');ylabel('Output');3.使用匿名函数:你还可以使用匿名函数来表示时变函数。
匿名函数是MATLAB中创建简单函数的快捷方式。
matlab复制代码t = 0:0.1:10; % 时间向量f = @(t) t.^2; % 定义匿名函数表示的时变函数y = arrayfun(f, t); % 应用函数到时间向量上的每个元素plot(t, y);xlabel('Time');ylabel('Output');4.使用符号表达式:你还可以使用符号表达式来表示时变函数,并使用符号计算工具箱进行操作。
matlab复制代码syms t; % 定义符号变量tf = t^2; % 定义符号表达式表示的时变函数t_values = 0:0.1:10; % 时间向量y = zeros(size(t_values)); % 初始化输出向量for i = 1:length(t_values)y(i) = subs(f, t_values(i)); % 计算函数的值end% 绘制结果plot(t_values, y);xlabel('Time');ylabel('Output');这些示例演示了如何在MATLAB中创建和操作时变函数。
matlab求解3能级系统速率方程

matlab求解3能级系统速率方程
3能级系统速率方程是描述三个不同能级之间转换的过程的方程,通常用于描述原子、分子等系统的能级跃迁过程。
在Matlab中,我们可以通过数值求解来获得系统在不同时间点上的能级分布情况。
以下是在Matlab中求解3能级系统速率方程的一般步骤和相关参考内容:
1. 确定系统的能级结构:首先需要明确系统的能级结构,包括能级的能量、跃迁的速率等信息。
2. 建立速率方程:根据系统的能级结构,建立描述能级之间跃迁速率的方程,一般为一组微分方程。
3. 编写Matlab代码:使用Matlab编写代码,将速率方程转化为数值求解的格式。
可以使用ode45等求解微分方程的函数来求解系统的能级分布随时间的变化。
4. 运行代码并分析结果:运行Matlab代码,得到系统在不同时间点上的能级分布情况。
可以通过绘制能级随时间的变化曲线等方式来分析系统的动力学行为。
5. 调整参数进行模拟:可以通过调整系统的参数,如能级能量、跃迁速率等,来模拟不同条件下系统的行为,从而更深入地理解系统的特性。
通过以上步骤,可以在Matlab中求解3能级系统速率方程,获得系统的能级分布随时间的演化情况,进一步研究系统的动力学行为和特性。
在实际应用中,还可以根据具体情况进行进一步的优化和扩展,以更好地解决相关问题。
matlab中表格时间数据进行加减处理的方法

matlab中表格时间数据进行加减处理的方法MATLAB中表格时间数据的加减处理方法1. 引言时间数据在数据分析和处理中非常常见,尤其在MATLAB中。
本文将介绍在MATLAB中对表格时间数据进行加减处理的方法。
2. 方法一:使用datetime函数MATLAB提供了datetime函数,用于创建和处理日期和时间数据。
以下是使用datetime函数进行加减处理的步骤:1.将时间数据转换为datetime格式:timeData = datetime(timeData, 'InputFormat', 'yyyy-MM-dd HH:mm:ss');2.对时间数据进行加减处理:newTimeData = timeData + duration(0, 2, 30); % 在时间数据上加上2小时30分钟3. 方法二:使用datevec和datenum函数另一种处理时间数据的方法是使用datevec和datenum函数。
以下是使用这两个函数进行加减处理的步骤:1.将时间数据转换为datevec格式:timeData = datevec(timeData, 'yyyy-mm-dd HH:MM:SS');2.将datevec格式转换为datenum格式:timeDataNum = datenum(timeData);3.对时间数据进行加减处理:newTimeDataNum = timeDataNum + (2/24 + 30/(60*24)); % 在时间数据上加上2小时30分钟4.将加减处理后的时间数据转换回datevec格式:newTimeData = datevec(newTimeDataNum);4. 方法三:使用table2timetable函数如果你的时间数据是以表格形式存储,可以使用table2timetable函数将表格转换为timetable格式,然后使用timetable的方法进行加减处理。
MATLAB_simulink中的基本模块的参数、含义、应用
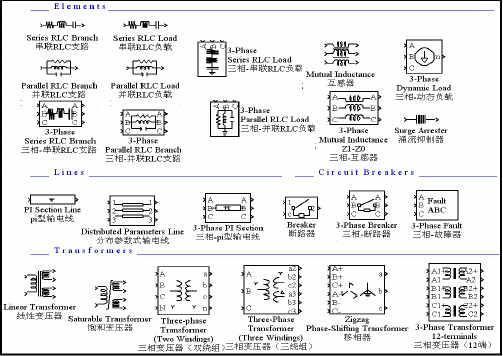
发电机额定值基于定子电阻 Rs 和泄漏电感 LLS 在 PU。 转子[RR',LLR'](PU)
转子电阻 Rr 和漏感 LLR'的,称为定子,在 PU 根据发生器的评分。 磁化电感 Lm(PU)
在 PU 的磁化电感 Lm 上的发电机额定值。 转动惯量,摩擦系数和极对的
组合的发电机和涡轮机的转动惯量 H 在秒,合并的粘性摩擦系数 F 中的普基于在发电 机上的评分和数量的极对数 p。
如果选中,则发送的标记信号的电流测量的。使用从块读取的电流。从块必须跳转到标 签对应的信号标签参数指定的标签。如果没有选择,IABC 可通过功能块输出的电流测量结 果是。 信号标签
指定的标签标记的电流测量。 电流的 PU
如果选中,三相电流测量 PU。否则,他们正在测量安培。 基本功率(VA3 期)
基数的三相电源,伏安(VA),用于将测得的电流 PU。基本功率(VA3 相)参数在对 话框中是不可见的,如果电流在 PU 未被选中。 如果电流如果电流单位。 Three-Phase Mutual Inductance Z1-Z0 三相互感 Z1-Z0
需要注意的是随时间的变化适用于源,除了三个阶段的变化参数的变化。 变异类型
指定的时间变化参数指定的参数被施加不同的变化。选择步骤编程步骤变化。选择斜坡 编程斜坡变化。选择调制方案调制的变化。选择振幅双表编写了一系列的一步变化幅度在特 定时间。 步进幅度 这个参数是唯一可见的,如果变异类型参数设置步骤。 指定的阶跃变化的振幅。指定的振幅的变化在正序振幅的 pu 中。 变化率 这个参数是唯一可见的,如果变异类型参数设置坡道。 指定的变化率,在伏/秒。中指定的电压变化率(pu 中的正序电压)/秒。 Goto 转到
指定的阶跃变化的振幅。指定的振幅的变化在正序振幅的 pu 中。 变化率 这个参数是唯一可见的,如果变异类型参数设置坡道。 指定的变化率,在伏/秒。中指定的电压变化率(pu 中的正序电压)/秒。 振幅调制 这个参数是唯一可见的,如果变化参数的类型被设置为调制。 指定为源的调制参数中指定的时间变化参数的幅度。当不同数量的电压振幅的调制,振幅在 积极序列振幅的 pu 中指定。 的调制频率 这个参数是唯一可见的,如果变化参数的类型被设置为调制。 源参数中指定的时间变化参数指定的频率的调制。 变化的时间(S) 指定的时间,在几秒钟内,在设定的时间变化生效的时间,当它停止。 基本和/或谐波产生 如果选中,可以进行编程,两个谐波叠加在基波电压源。
matlab常用指令简介

1命令行中输入help+工具箱名或函数名,可以显示对应的功能信息。
2 matlab中同样支持复数变量,表示方法为a=m+ni(j)。
当n是表达式时,n与i(j)之间必须要加乘号 b=1+a*i。
另外也可以用complex(x,y)来产生复数。
在循环程序段中一般不把i和j作为变量名称,以免生成数据时发生误解。
3>> i=5;>> a=5+2ia =5.0000 + 2.0000i>> a=5+2*ia =154 first:increment:last表示创建一个从first开始,到last结束,数据元素的增量为increment的等差数组。
冒号表示直接定义数据元素之间的增量,而不是数据元素个数。
若增量为1,上面创建数组的方式可简写为: first:last。
5 linspace通过直接定义数据元素个数,而不是数据元素之间的增量来创建数组。
此函数的调用格式如下:linspace(firstvalue,lastvalue,number)6,与linspace一样,logspace函数也通过直接定义数据元素个数,而不是数据元素之间的增量来创建数组。
logspace函数的调用格式为:logspace(firstvalue,lastvalue,number)此函数表示创建一个从10的firstvalue次幂开始,到10的lastvalue 次幂结束,包含有number个数据元素的等比数组7,数组与标量的四则运算是指数组中的每个元素与标量进行加、减、乘、除运算。
数组的指数运算为exp,以2为底的指数运算为pow2;数组自然对数运算为log,常用对数运算为log10,以2为底的对数运算为log2,开方运算sqrt。
数组与数组之间进行运算时,每个数组必须具有相同的维数,且必须用点乘或点除。
这些运算都是数组中每个元素进行相对应的运算.a=exp([1 2])a =2.7183 7.3891查询x数组的第n个元素,x(n);查询x数组的第2到4个元素,x(2:4);查询x数组的第4到最后1个元素,x(4:end);查询x数组的第3、2、1个元素,x(3:-1:1);查询x数组的小于n元素,x(find(x<n));查询x数组的第4、2、5个元素,x([4 2 5]);将x数组的第n个元素赋值为A,x(n)=A;查询数组A的第2行,第3列的元素,A(2,3);查询数组A的第3行所有的元素,A(3,:);查询数组A的第2列转置后所有的元素,(A(:,2))’。
matlab原子轨道

matlab原子轨道在Matlab中,你可以使用一些函数和工具箱来处理原子轨道的相关问题。
以下是一些可能对原子轨道建模和分析有用的Matlab函数和工具箱:1. MATLAB Quantum Mechanics Toolbox: Quantum Mechanics Toolbox是Matlab的一个工具箱,专门用于量子力学建模和分析。
它包含一些用于处理原子轨道、波函数、哈密顿量等的函数。
请注意,该工具箱可能需要单独购买或安装。
2. MATLAB Symbolic Math Toolbox: Symbolic Math Toolbox 使你能够在Matlab中进行符号计算,这在处理量子力学方程时可能非常有用。
你可以使用符号表达式来表示波函数、哈密顿量等。
3. MATLAB Plotting Functions: 使用Matlab的绘图函数,如plot、surf等,可以可视化原子轨道的形状和特性。
你可以根据波函数的数学表达式绘制原子轨道的图形。
4. Atomic Orbitals (AO) Functions: 如果你已经有了原子轨道的数学描述,你可以使用Matlab中的函数来实现相应的计算和分析。
例如,通过计算和绘制波函数,你可以更好地理解原子轨道的形状和分布。
5. 量子化学软件接口: 如果你使用了专业的量子化学软件(例如Gaussian、GAMESS等),这些软件通常提供了Matlab接口或者输出文件的读取工具,使你能够在Matlab中处理和分析计算结果。
请注意,处理原子轨道问题通常涉及到复杂的量子力学概念和数学,因此了解相关的量子力学理论和Matlab工具是很重要的。
确保查阅Matlab文档和相关工具箱的文档,以获取更详细和具体的信息。
时间转换与星期推算(Matlab版)

时间转换与星期推算(Matlab版)1 概述最近在学习GPS解算算法时需要在GPS时(GPS周和周内秒)和公历⽇期之间进⾏转换,于是就整理了⼀些时间转换的⼩程序。
本⽂介绍了GPS时、公历、儒略⽇(JD)、简化儒略⽇(MJD)之间的转换函数。
gps2cal将GPS周和周内秒转换到公历时间gps2cal1由公历⽇期和GPS周内秒计算公历时间cal2gps将公历GPS时间转换到GPS周和周内秒mjd2cal将简化儒略⽇转换到公历时间cal2mjd将公历时间转换到简化儒略⽇jd2cal从儒略⽇计算公历时间cal2jd将公历时间转换到儒略⽇cal2wd借助MJD,由公历年⽉⽇推算星期⼏,按照格⾥⾼利⼗三世的历法改⾰去掉1582年10⽉5⽇⾄14⽇cal2wd1由公历年⽉⽇推算星期⼏,按照英国⼈的做法去掉1752年9⽉3⽇⾄13⽇cal2wd2不借助MJD,由公历年⽉⽇推算星期⼏,去掉1582年10⽉5⽇⾄14⽇在MJD基础上推算星期是很简单的,我顺带写出了从公历推算星期的函数cal2wd。
不借助MJD也可以推算星期,例如安⽵林同学在《再谈星期的计算》(《程序员》2001年第4期)介绍的⽅法。
本⽂给出了这个⽅法的matlab版本cal2wd1。
cal2wd1按照英国⼈的历法去掉了公历中的公元1752年9⽉3⽇⾄13⽇。
我⼜写了cal2wd2函数,这个函数按照格⾥⾼利⼗三世的做法去掉1582年10⽉5⽇⾄14⽇。
我在2005年写过⼀篇,介绍过⼀些历法的基础知识。
本⽂假设读者了解该⽂介绍的⼀些概念,例如原⼦时标、UTC、闰秒、儒略历、儒略⽇、简化儒略⽇等。
2 GPS周和周内秒GPS时从1980年1⽉6⽇0时开始计时。
GPS时的秒长度与UTC⼀样,采⽤原⼦时标。
但GPS时是连续的,不调整闰秒。
在GPS数据中,GPS时通常被表⽰为GPS周和周内秒。
例如:>> gpst=cal2gps([2009 3 13 22 38 10]) gpst = 1522 513490 >> cal=gps2cal(gpst) cal = 2009 3 13 22 38 10即2009年3⽉13⽇22:38:10对应gps周1522,周内秒513490。
fmcw keystone变换matlab代码

FMCW (Frequency Modulated Continuous Wave)雷达是一种在通信和雷达领域广泛应用的信号形式。
而Keystone变换是用于将接收到的信号从时域转换到频域的一种技术。
以下是一个基本的Keystone变换的MATLAB代码示例:matlab复制代码function[F_out, T_out] = keystone_transform(F_in, T_in,keystone_factor)% Keystone transform function%% Inputs:% F_in: Input frequency vector (Hz)% T_in: Input time vector (s)% keystone_factor: Keystone factor (s/s)%% Outputs:% F_out: Output frequency vector (Hz)% T_out: Output time vector (s)% Check inputsif nargin < 3error('Not enough input arguments');end% Calculate output frequency and time vectorsF_out = F_in * keystone_factor;T_out = T_in / keystone_factor;end此函数接受输入的频率向量(F_in)和时间向量(T_in),以及一个关键因子(keystone_factor),然后返回经过关键变换后的频率向量(F_out)和时间向量(T_out)。
需要注意的是,这只是最基本的关键变换实现,对于复杂的信号处理任务,可能还需要其他类型的信号处理技术,例如FFT(Fast Fourier Transform)等。
anm原子范数最小化 matlab

anm原子范数最小化 matlab(最新版)目录1.介绍 ANM(自适应神经网络)2.ANM 的训练目标:原子范数最小化3.MATLAB 在 ANM 原子范数最小化中的应用4.总结正文1.介绍 ANM(自适应神经网络)自适应神经网络(Adaptive Neural Network,简称 ANN)是一种能够自适应学习输入数据的神经网络。
这种网络可以根据输入数据的变化,自动调整其结构和参数,以达到最佳的性能。
ANN 在处理非线性、非平稳时间序列预测等问题上具有较好的效果。
2.ANM 的训练目标:原子范数最小化ANM(Adaptive Neural Network with Atomic Norm Minimization,自适应神经网络与原子范数最小化)是一种基于原子范数最小化的神经网络。
在 ANM 中,原子范数最小化被用作训练目标,以提高模型的泛化性能。
原子范数是指神经网络中各个参数的范数之和,其作用是防止网络过拟合。
通过最小化原子范数,可以降低神经网络模型的复杂度,从而提高模型的泛化能力。
3.MATLAB 在 ANM 原子范数最小化中的应用MATLAB(Matrix Laboratory,矩阵实验室)是一款广泛应用于科学计算、数据分析、可视化等领域的软件。
在 ANM 原子范数最小化中,MATLAB 可以实现以下功能:(1) 构建 ANM 模型:通过 MATLAB 可以搭建自适应神经网络模型,设定网络结构、激活函数等参数。
(2) 计算梯度:MATLAB 可以计算 ANM 模型的梯度,用于更新网络参数,以实现原子范数的最小化。
(3) 优化算法:MATLAB 提供了多种优化算法,如梯度下降、牛顿法、拟牛顿法等,用于求解原子范数最小化问题。
(4) 训练与验证:MATLAB 可以用于训练 ANM 模型,并在训练过程中进行参数调整,以提高模型性能。
同时,MATLAB 还可以对模型进行验证,评估模型在未知数据上的预测能力。
matlab时变函数

matlab时变函数时变函数是指随着时间变化而改变的函数。
在Matlab中,我们可以使用各种方式来处理和分析时变函数。
本文将介绍在Matlab中处理时变函数的基本方法,包括时域分析和频域分析。
一、时域分析时域分析是指对时变函数在时间轴上进行分析和处理。
在Matlab中,我们可以使用plot函数来绘制时变函数的图像。
以下是一个简单示例:```Matlabt = 0:0.01:10; % 时间范围为0到10,步长为0.01y = sin(t); % 使用sin函数生成时变函数plot(t, y); % 绘制时变函数的图像xlabel('时间'); % 设置x轴标签ylabel('函数值'); % 设置y轴标签title('时变函数示例'); % 设置图像标题```在上面的示例中,我们使用了t = 0:0.01:10来创建一个时间范围为0到10的向量,步长为0.01。
然后,使用sin函数生成了一个以t为自变量的时变函数。
最后,使用plot函数将时变函数的图像绘制出来,并设置了x轴标签、y轴标签和图像标题。
除了绘制时变函数的图像,我们还可以对时变函数进行各种运算和处理。
例如,可以使用diff函数对时变函数进行差分运算,使用int函数对时变函数进行积分运算,使用conv函数对时变函数进行卷积运算等等。
二、频域分析频域分析是指通过将时变函数从时域转换为频域,来分析函数在不同频率上的性质和特征。
在Matlab中,我们可以使用fft函数对时变函数进行傅里叶变换,将其转换为频域表示。
以下是一个简单示例:```Matlabt = 0:0.01:10; % 时间范围为0到10,步长为0.01y = sin(2*pi*5*t) + sin(2*pi*10*t); % 使用两个正弦函数生成时变函数Y = fft(y); % 对时变函数进行傅里叶变换f = 0:length(Y)-1; % 构造频率向量plot(f, abs(Y)); % 绘制频域表示的图像xlabel('频率'); % 设置x轴标签ylabel('幅度'); % 设置y轴标签title('时变函数的频域表示'); % 设置图像标题```在上面的示例中,我们使用了t = 0:0.01:10来创建一个时间范围为0到10的向量,步长为0.01。
单位阶跃函数的z变换matlab

单位阶跃函数的z变换matlab{1t>=0u(t)={0t<0其中,u(t)表示单位阶跃函数,t表示时间。
在MATLAB中,我们可以使用z变换来对单位阶跃函数进行分析和处理。
z变换是一种重要的信号处理工具,它将离散时间域信号转换为复数域频率域信号。
首先,我们需要定义单位阶跃函数的离散表达式。
由于单位阶跃函数是连续函数,我们需要将其离散化,即在一定的时间间隔内对其进行采样。
在MATLAB中,我们可以使用以下代码定义单位阶跃函数的离散表达式:t=-10:0.01:10;%定义时间范围和步长u=t>=0;%根据函数定义生成离散值plot(t, u); % 绘制单位阶跃函数图像title('Unit Step Function'); % 设置图像标题```该代码首先定义了时间范围t,然后使用步长0.01对时间范围进行离散化。
接下来,使用比较符号>=对时间序列t进行判断,得到单位阶跃函数u。
接下来,我们可以对单位阶跃函数进行 z 变换。
在 MATLAB 中,可以使用 `ztrans` 函数进行 z 变换计算。
使用以下代码进行单位阶跃函数的z变换:syms z; % 定义符号变量 zU = ztrans(u, t, z); % 进行 z 变换计算pretty(U); % 输出美观的数学表达式```在上述代码中,首先使用 `syms` 函数定义符号变量 z,然后使用`ztrans` 函数对离散序列 u 进行 z 变换计算。
其中,t 表示时间序列,z 表示 z 变换域。
最后,使用 `pretty` 函数可输出美观的数学表达式。
以上就是使用MATLAB进行单位阶跃函数的z变换的方法。
需要注意的是,上述代码仅仅是一个示例,具体的实现方式可能会因具体的场景和要求而有所变化。
如果你有具体的应用场景和要求,可以提供更多细节,我可以提供更加详细和个性化的解答。
一维粒子扩散过程代码matlab

一维粒子扩散过程代码matlab一维粒子扩散过程是指在一维空间中,粒子由高浓度区域向低浓度区域移动的过程。
这个过程可以用扩散方程进行建模和描述。
在本文中,将介绍如何使用Matlab编写一维粒子扩散过程的代码,并逐步解释每一步。
起初,我们需要定义一维空间的尺寸和时间步长。
在这个例子中,我们假设一维空间的尺寸为L,时间步长为dt。
matlabL = 10; 一维空间尺寸dt = 0.01; 时间步长然后,我们需要定义初始条件和边界条件。
在这个例子中,我们假设初始浓度分布是一个高斯分布,边界条件为周期性边界,即当粒子到达一维空间的边界时会从另一边进入。
matlabN = 100; 粒子数x = linspace(0, L, N); 一维空间均匀分布的点c0 = exp(-(x - L/2).^2); 初始浓度分布为高斯分布c = c0; 当前浓度分布周期性边界条件c(1) = c(end);c(end) = c(1);接下来,我们需要定义扩散系数D,它描述了粒子在单位时间内从高浓度区域向低浓度区域扩散的速率。
在这个例子中,我们假设扩散系数是一个常数。
matlabD = 0.1; 扩散系数然后,我们可以使用扩散方程来模拟粒子扩散的过程。
扩散方程可以写成以下形式:matlabdc = D * (circshift(c,1) - 2*c + circshift(c,-1)) / (dx^2);c = c + dc * dt;在这个方程中,dc表示浓度变化率,circshift函数用于实现周期性边界条件,dx表示一维空间中相邻两个点的间距。
最后,我们需要设置模拟的总时间和输出间隔,并在每一个输出步骤中绘制当前的浓度分布。
matlabtTotal = 10; 总时间tOutput = 0.1; 输出间隔nSteps = round(tTotal / dt); 总步数nOutputSteps = round(tOutput / dt); 输出步数figure;for i = 1:nStepsdc = D * (circshift(c,1) - 2*c + circshift(c,-1)) / (dx^2);c = c + dc * dt;if mod(i,nOutputSteps) == 0plot(x,c);axis([0 L 0 max(c0)]);xlabel('Position');ylabel('Concentration');title(['Diffusion Process at Time = ' num2str(i*dt)]);drawnow;endend通过以上的简单步骤,我们就可以使用Matlab编写一维粒子扩散过程的代码。
激光原理作业——反转粒子数曲线

激光原理作业130212105 曾令辉题目:用Matlab 模拟反转粒子数随时间变化的曲线。
解微分方程⎪⎪⎪⎩⎪⎪⎪⎨⎧<<-+=∆<∆=∆----p t A W p p p t t A p T t e A W W n t n t T e T n t n p p 0]1[)()()()(23211)(2321232 ηηηηηη 符号说明:E4-E3的量子效率η1(对应下面的n1),E3-E2的荧光效率η2(对应下面的n2),第三能级到第二能级的自发辐射跃迁几率A32,泵浦几率Wp ,tp 为泵浦持续时间,n 为粒子总数。
1、探究泵浦持续时间“tp ”的取值对“反转粒子数随时间变化的影响”1.1程序>> clear all>> n1=0.5;n2=0.8;Wp=0.8;A32=0.5;n=1000;>> t=0:0.01:20;>> tp=10;>>y=n*(n1*Wp)*(1-exp((-(n1*n2)*Wp -(A32/n2))*t))/(n1*Wp+(A32/n2)).*(t>=0&t<tp)+n*(n1*Wp )*(1-exp((-(n1*n2)*Wp -(A32/n2))*tp))*exp((-A32/n2)*(t -tp))/(n1*Wp+(A32/n2)).*(t>=tp&t<=20); >> plot(t,y)>> gtext('tp=10')>> title('tp 的取值对“反转粒子数随时间变化曲线的影响”')>> xlabel('时间t')>> ylabel('反转粒子数y')>> hold on>> tp=5;>>y=n*(n1*Wp)*(1-exp((-(n1*n2)*Wp -(A32/n2))*t))/(n1*Wp+(A32/n2)).*(t>=0&t<tp)+n*(n1*Wp )*(1-exp((-(n1*n2)*Wp -(A32/n2))*tp))*exp((-A32/n2)*(t -tp))/(n1*Wp+(A32/n2)).*(t>=tp&t<=20); >> plot(t,y)>> gtext('tp=5')>> hold on>> tp=2;>>y=n*(n1*Wp)*(1-exp((-(n1*n2)*Wp -(A32/n2))*t))/(n1*Wp+(A32/n2)).*(t>=0&t<tp)+n*(n1*Wp )*(1-exp((-(n1*n2)*Wp -(A32/n2))*tp))*exp((-A32/n2)*(t -tp))/(n1*Wp+(A32/n2)).*(t>=tp&t<=20); >> plot(t,y)>> gtext('tp=2')>> hold on>> tp=1;>>y=n*(n1*Wp)*(1-exp((-(n1*n2)*Wp -(A32/n2))*t))/(n1*Wp+(A32/n2)).*(t>=0&t<tp)+n*(n1*Wp )*(1-exp((-(n1*n2)*Wp -(A32/n2))*tp))*exp((-A32/n2)*(t -tp))/(n1*Wp+(A32/n2)).*(t>=tp&t<=20); >> plot(t,y)>> gtext('tp=1')1.2图像1.3结论:在图像变化过程中可看到:(1)当0<tp<2时,曲线快速增大,到达最大值之后迅速衰减;(2)而当tp>2时,曲线先呈快速增大趋势,再趋向于一饱和值(即最大值),最后也快速衰减至无限趋近于0。
matlab实验代码(总)

matlab实验代码(总)% 使⽤两种⽅法,创建⼀稀疏矩阵% 使⽤函数sparse,可以⽤⼀组⾮零元素直接创建⼀个稀疏矩阵。
该函数调⽤格式为:% S=sparse(i,j,s,m,n)% 其中i和j都为⽮量,分别是指矩阵中⾮零元素的⾏号与列号,% s是⼀个全部为⾮零元素⽮量,元素在矩阵中排列的位置为(i,j)% m为输出的稀疏矩阵的⾏数,n为输出的稀疏矩阵的列数。
%⽅法1A9=[0 0 1;0 3 0;2 4 0]B9=sparse(A9)C9=full(B9)%⽅法2A10=sparse([1 3 2 4],[2 3 1 4],[1 2 3 4],4,4)C10=full(A10)A11=[1 2 3];B11=[4 5 6];C11=3.^A11D11=A11.^B11%使⽤函数,实现矩阵左旋90°或右旋90°的功能。
A=[ 1 2 3 ; 4 5 6 ; 7 8 9 ]B=rot90(A,1)C=rot90(A,-1)%求S=2^0+2^1+2^2+2^3+2^4+……+2^10的值(提⽰:利⽤求和函数与累乘积函数。
)A=2*ones(1,10)%10个2B=cumprod(A)%平⽅C=sum(B)+1%加上2^0%建⽴⼀个字符串向量,删除其中的⼤写字母(提⽰:利⽤find函数和空矩阵。
)str='AAAbCcd'b=find(str>='A' & str<='Z');str(b)=[];% 输⼊⼀个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90分~100分为A,80分~89分为B,70分~79为C,60分~69分为D,60分以下为E。
switch(score)case num2cell(90:0.5:100)disp(['成绩等级为:A']);case num2cell(80:0.5:89.5)disp(['成绩等级为:B']);case num2cell(70:0.5:79.5)disp(['成绩等级为:C']);case num2cell(60:0.5:69.5)disp(['成绩等级为:D']);case num2cell(0:0.5:59.5)disp(['成绩等级为:E']);otherwisedisp(['输⼊成绩不合理!']);end%设计程序,完成两位数的加、减、乘、除四则运算,%即产⽣两个两位随机整数,再输⼊⼀个运算符号,做相应的运算,显⽰相应的结果,并要求结果显⽰类似于“a=x+y=34”。
matlab的日期与时间命令

matlab的日期与时间命令日期和时间:Matlab提供三种日期格式:日期字符串如‘1996-10-02’,日期序列数如729300(0000年1月1日为1)以及日期向量如1996 10 2 0 0 0,依次为年月日时分秒。
Matlab用三种格式来表示日期与时间(1)双精度型日期数字:一个日期型数字代表从公元0年到某一日期的的天数,例如,2008年8月26日夜时0点钟被表示为733646,而这同一天的中午12点就被表示为733646.5,也就是说任何一个时刻都可以用一个双精度型数字表示。
(2)不同形式的日期字符串:Matlab定义了28种标准日期格式的字符串。
(3)数值型的日期向量:用一个6元数组来表示一个日期时间,例如,[2008 8 26 12 5 0]表示2008年8月26日12点05分0秒;用一个3元数组来表示一个日期,例如,[2008 8 26]表示2008年8月26日。
用日期数字表示日期使计算机更容易计算,但是不直观,因此Matlab提供了许多函数来实现三种日期格式之间的转化。
(1)datestr:实现将日期数字和日期向量转化为日期字符串,可以在Matlab命令窗口中输入help datestr来查看关于datestr的用法。
(2)datenum:实现将日期字符串和日期向量转化为日期数字,可以在Matlab命令窗口中输入help datenum来查看关于datenum的用法。
(3)datevec:实现将日期数字和日期字符串转化为日期向量,可以在Matlab命令窗口中输入来help datevec查看关于datevec的用法。
(6)calendar:对用户要求的任何一个月生一个日历并显示在命令窗口中,或将其放在一个6×7的矩阵中。
(7)tic,toc:函数tic和toc被用来对一组Matlab运算进行计时。
Tic启动一个秒表,toc 停止这个秒表并计算出所经历的时间。
(8)cputime:函数cputime返回用秒表示的、自从当前的Matlab周期启动之后Matlab 所占用的CPU时间。
vmd算法matlab代码

vmd算法matlab代码以下是一个简单的VMD算法的Matlab实现示例:matlab.function [U, omega] = VMD(x, alpha, tau, K, DC)。
% x: 输入信号。
% alpha: 平滑参数。
% tau: 时频局部化参数。
% K: 原子数。
% DC: 是否包括直流分量。
% 初始化。
U = zeros(K, length(x));omega = zeros(K, length(x));u = x;% 迭代优化。
for k = 1:K.% 求解优化问题。
[u, omega(k, :)] = opti(U(k, :), u, alpha, tau); U(k, :) = u;% 更新残差。
u = x sum(U, 1);end.% 去除直流分量。
if ~DC.U = U(2:end, :);omega = omega(2:end, :);end.end.function [u, omega] = opti(U, u, alpha, tau)。
% 求解优化问题。
maxIter = 200;tol = 1e-6;eta = 1;lambda = 1;for iter = 1:maxIter.% 更新u.u_pre = u;u = softThresh(u + eta (U u), alpha); % 更新omega.omega = exp(-tau sum((u U).^2, 2)); % 更新eta.eta = lambda eta;% 判断收敛。
if norm(u u_pre) < tol.break;end.end.end.function y = softThresh(x, alpha)。
% 软阈值函数。
y = sign(x) . max(abs(x) alpha, 0);end.这是一个简单的VMD算法的Matlab实现示例,其中包括主函数VMD和两个辅助函数opti和softThresh。
matlab求解3能级系统速率方程

【摘要】本文主要介绍了利用Matlab求解三能级系统速率方程的方法。
首先对三能级系统的基本理论进行了介绍,然后详细介绍了利用Matlab编程求解三能级系统速率方程的步骤。
最后通过实例进行了具体的说明,展示了Matlab求解三能级系统速率方程的应用。
【关键词】Matlab;三能级系统;速率方程;编程1. 介绍三能级系统是物理学中常见的一个模型,它广泛应用于原子、分子和固体物理领域。
在研究三能级系统的过程中,我们通常会关注其能级之间的跃迁过程,而速率方程则是描述这些跃迁过程的重要方程之一。
利用速率方程,我们可以求解出三能级系统中各个能级的占据数随时间的变化规律,这对于理论研究和实际应用具有重要意义。
2. 三能级系统速率方程的基本理论假设一个三能级系统包含一个基态和两个激发态,分别用|1〉、|2〉和|3〉表示。
假设该系统在没有外界干扰的情况下,各个能级之间的跃迁过程可以用以下速率方程描述:$\frac{dn1}{dt} = -A_1n_1 + B_{21}n_2 + B_{31}n_3$$\frac{dn2}{dt} = A_1n_1 - (B_{21} + A_2)n_2 + B_{32}n_3$$\frac{dn3}{dt} = A_2n_2 - B_{31}n_1 - B_{32}n_2$其中,$n_1$、$n_2$、$n_3$分别表示基态、第一个激发态和第二个激发态的占据数,$A_1$、$A_2$表示基态到激发态的跃迁速率,$B_{ij}$表示第i个能级到第j个能级的受激辐射速率。
3. 利用Matlab求解三能级系统速率方程的步骤(1)定义速率方程我们需要将上述速率方程用Matlab代码进行定义。
可以使用Matlab 中的ODE函数(ordinary differential equation)来描述速率方程。
代码如下:function dn = rate_equations(t,n)参数定义A1 = 1.0;A2 = 2.0;B21 = 0.5;B31 = 0.6;B32 = 0.7;速率方程dn(1,1) = -A1*n(1) + B21*n(2) + B31*n(3);dn(2,1) = A1*n(1) - (B21 + A2)*n(2) + B32*n(3);dn(3,1) = A2*n(2) - B31*n(1) - B32*n(2);(2)求解速率方程接下来,我们使用Matlab中的ode45函数对定义的速率方程进行求解。
anm原子范数最小化 matlab

anm原子范数最小化matlab摘要:I.引言- 介绍anm 原子范数最小化- 说明其在matlab 中的实现方法II.anm 原子范数最小化概述- 原子范数最小化的定义- anm 方法的基本原理- 为什么需要使用anm 原子范数最小化III.matlab 实现anm 原子范数最小化- 安装并配置matlab 环境- 使用matlab 实现anm 原子范数最小化的步骤- 常用函数和命令介绍IV.anm 原子范数最小化应用案例- 实际应用场景- 具体操作步骤和结果展示V.总结- 概括anm 原子范数最小化在matlab 中的实现- 展望其在未来可能的发展和应用正文:I.引言anm 原子范数最小化,即原子范数最小化的一种方法,主要用于解决信号处理、图像处理等领域中的问题。
通过matlab 提供的强大功能,我们可以方便地实现这一方法。
本文将详细介绍anm 原子范数最小化的相关知识和在matlab 中的具体实现。
II.anm 原子范数最小化概述原子范数最小化是一种求解信号或图像稀疏表示的方法。
给定一个信号或图像,我们希望找到一组基函数,使得这些基函数的线性组合能够表示这个信号或图像,同时使得原子范数(即基函数系数的绝对值之和)最小。
这种表示方法能够帮助我们提取信号或图像的主要特征,从而降低数据维度,提高后续处理的速度和效果。
anm(Atomic Norm Minimization)方法是一种求解原子范数最小化的算法。
它通过引入惩罚项,将原问题转化为一个凸优化问题。
anm 方法的基本原理是,在原子范数的基础上,增加一个凸惩罚项,使得优化问题更容易求解。
这一方法在实际应用中具有较好的性能。
III.matlab 实现anm 原子范数最小化在matlab 中实现anm 原子范数最小化,首先需要确保安装了适当的工具箱和库。
接下来,按照以下步骤进行操作:1.准备数据:输入信号或图像。
2.选择基函数:根据实际需求选择适当的基函数。
