高二数学均值定理
高二数学均值定理试题

高二数学均值定理试题1.若正数,满足,则的最小值为.【答案】9【解析】=(当且仅当,即时,“=”成立)【考点】基本不等式2.当时,的最小值是.【答案】1【解析】当时,当且仅当时取等号.所以答案为1.【考点】基本不等式的应用.3.已知F1、F2是椭圆+=1(a>b>0)的左右焦点,P是椭圆上一点,∠F1PF2=90°,求椭圆离心率的最小值为【答案】【解析】因为∠F1PF2=90°,所以,因为,且,可解的。
因为,整理的,即,所以【考点】椭圆的概念和离心率问题,基本不等式4.若正实数满足,则+的最小值是( )A.4B.6C.8D.9【答案】D【解析】由,得,当且公当,即,时,取等号.所以正确答案是D.【考点】基本不等式5.已知,则的最小值为.【答案】【解析】因为,,且,所以.【考点】1.基本不等式;2.指数幂的运算.6.设,若,则的最大值是_________.【答案】【解析】利用基本不等式解决,但是注意基本不等式的条件是一正二定三相等.而所以我们要将平方,用重要不等式解决可以避开范围的问题.由已知条件我们可得即.所以最大值为【考点】基本不等式、不等式7.下列结论正确的是()A.当且时,;B.当时,;C.当时,的最小值为2;D.当时,无最大值;【答案】B【解析】基本不等式的应用要把握:一正二定三相等.A选项中0<x<1时lg x<0.所以A选项不成立.C选项中当取到最小值时x=1.所以不包含在中.所以排除C. D选项中是关于x递增的代数式,当x=2时取到最大值.所以排除D.B选项符合了一正二定三相等的条件.故选B.【考点】1.基本不等式的应用.2.对数知识,函数的单调性知识.8.若正数满足,则的最小值是__________.【答案】5【解析】所以3x+4y=(3x+4y)=【考点】1.基本不等式的应用.2.构造等式一边是1.9.设则以下不等式中不恒成立的是A.B.C.D.【答案】D【解析】对于A:.对于B:,显然不等式,所以不恒成立.对于C:.对于D:当时,显然;当时,所以恒成立.【考点】基本不等式的性质,作差法判断值的大小.点评:掌握基本不等式的成立的条件:a>0,b>0,则;直接比较两个数大小不易比较时,可考虑作差法比较.10.设,,则三数()A.至少有一个不小于2B.都大于2C.至少有一个不大于2D.都小于2【答案】A【解析】,,至少有一个不小于2 11.设的最大值为()A.B.C.D.1【答案】D【解析】本题主要考查的是均值不等式。
高二数学均值定理的应用试题答案及解析

高二数学均值定理的应用试题答案及解析1.已知a>0,b>0,a+b=2,则的最小值是()A.B.4C.D.5【答案】C【解析】因为a>0,b>0,a+b=2,所以,当且仅当时"="成立,故选C.【考点】基本不等式.2.下列各式中,最小值等于2的是()A.B.C.D.【答案】D.【解析】A不正确,例如:,的符号相反时,式子的最小值不可能等于2;B不正确,由于,但等号不可能成立,故最小值不是2;C不正确,当时,它的最小值显然不是2;D正确,因为,当且仅当时,等号成立.故选D.【考点】基本不等式.3.已知圆的切线l与两坐标轴分别交于点A,B两点,则(O为坐标原点)面积的最小值为.【答案】【解析】因为切线l与两坐标轴分别交于点A,B两点,所以切线有斜率,并且不等于0,所以设其为,所以,所以的面积等于.因为直线为切线,所以,即,所以,代入面积公式,可得,根据均值不等式,可知当且仅当时,取得最小值.【考点】直线与圆相切,均值不等式.4.某工厂拟建一座平面图为矩形,面积为的三段式污水处理池,池高为1,如果池的四周墙壁的建造费单价为元,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为元,池底的建造费单价为元,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?【答案】污水池的长宽分别为, 时造价最低,为元.【解析】设污水池的宽为,则长为,水池的造价为元,则由题意知:定义域为,,利用基本不等式即可求得其最值.试题解析:设污水池的宽为,则长为,水池的造价为元,则由题意知:定义域为,当且仅当,取“=”,此时长为,即污水池的长宽分别为, 时造价最低,为元.【考点】本题考查了基本不等式的应用.5.一段长为36m的篱笆围成一个矩形菜园, 问这个矩形的长,宽各为多少时,菜园的面积最大.最大面积是多少?【答案】故当长宽都为9m时,面积最大为81.【解析】本题考查周长为定值的矩形面积最大的问题.应用基本不等式求得最大值.试题解析:解:设矩形的长宽分别为,则有,,面积,当且仅当时取“=”,故当长宽都为9m时,面积最大为81.【考点】基本不等式的应用.6.设x,y,z都是正实数,a=x+,b=y+,c=z+,则a,b,c三个数().A.至少有一个不大于2B.都小于2C.至少有一个不小于2D.都大于2【答案】C【解析】将三个式子相加,构造出均值不等式的形式,由均值不等式可得a+b+c≥6,从而推出a,b,c的范围.因为x,y,z都是正实数,a=x+,b=y+,c=z+,那么可知a+b+c=∴a,b,c至少有一个不小于2.故选C.【考点】基本不等式点评:基本不等式是高考重点考查的知识点之一,应用基本不等式时,要熟练掌握不等式成立的条件与重要不等式的变形.7.函数,当时,函数有最大值为_________.【答案】-3,-8.【解析】因为,当x=-3时,f(x)取得最大值,最大值为-8.8.当时,下列函数中最小值为2的是( )A.B.C.D.【答案】C【解析】因为当时,故,而,选项D中,不能取得最小值为2,选C9.当>0时,函数的最小值为()A.2B.4C.6D.8【答案】B【解析】当>0时,函数,选B10.若,则当且仅当= 时,函数的最大值为;【答案】0,【解析】解:因为x=0时,则,故填写11.(本题满分10分)已知,对,恒成立,求的取值范围。
高二数学均值定理的应用试题答案及解析

高二数学均值定理的应用试题答案及解析1.设x>0,y>0,z>0,a=x+,b=y+,c=z+,则a,b,c三数A.至少有一个不大于2B.都小于2C.至少有一个不小于2D.都大于2【答案】C【解析】由于三者的地位彼此相同,三者的地位彼此也相同.因此设,则,即至少有一个不小于2.【考点】基本不等式.2.设,若,则的最小值为____________.【答案】9.【解析】∵①,同理②,③,①+②+③,可得,当且仅当时,“=”成立,故的最小值为9.【考点】基本不等式求最值.3.设a>0,b>0,则以下不等式中不一定成立的是()A.a2+b2+2≥2a+2b B.C.+≥2D.a3+b3≥2ab2【答案】D【解析】A可变为,一定成立;B 由已知,结合对数函数的性质一定成立;C由已知,结合基本不等式,知一定成立;故选D.考点:对数函数,基本不等式.4.一段长为36m的篱笆围成一个矩形菜园, 问这个矩形的长,宽各为多少时,菜园的面积最大.最大面积是多少?【答案】故当长宽都为9m时,面积最大为81.【解析】本题考查周长为定值的矩形面积最大的问题.应用基本不等式求得最大值.试题解析:解:设矩形的长宽分别为,则有,,面积,当且仅当时取“=”,故当长宽都为9m时,面积最大为81.【考点】基本不等式的应用.5.若直线始终平分圆:的周长,则的最小值为()A.8B.12C.16D.20【答案】C【解析】因为,直线始终平分圆的周长,所以圆心(-4,-1)在直线上,从而,4a+b=1,所以,,故选C。
【考点】本题主要考查直线与圆的位置关系,均值定理的应用。
点评:小综合题,本解法通过“1”的代换,创造了应用均值定理的条件。
应用均值定理,“一正,二定,三相等”缺一不可。
6.求使≤(x>0,y>0)恒成立的的最小值【答案】【解析】本题主要考查了基本不等式的综合.(1)解决恒成立问题一定要搞清谁是自变量,谁是参数.一般地,知道谁的范围,谁就是变量,求谁的范围,谁就是参数;(2)对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.先将题设的不等式平方后,同时利用基本不等式综合可求得a的最小值满足的等式求得a.解法一由于的值为正数,将已知不等式两边平方,得x+y+2≤2(x+y),即2≤(2-1)(x+y),①∴x,y>0,∴x+y≥2,②当且仅当x=y时,②中有等号成立比较①、②得的最小值满足2-1=1,∴2=2,= (因>0),∴的最小值是解法二设∵x>0,y>0,∴x+y≥2 (当x=y时“=”成立),7.下列各式中,最小值等于的是()A.B.C.D.【答案】D【解析】解:因为选项A中没有说明x,y是同号,因此不成立选项B中,由于,使用均值不等式时,等号不成立,因此错误。
均值定理公式总结及应用

均值定理公式总结及应用1. 均值定理概述均值定理是微积分中的重要定理之一,它通过使用积分的均值来描述函数与其在某个区间上的平均值之间的关系。
均值定理有多种形式,其中最为常见的两种是拉格朗日中值定理和柯西中值定理。
2. 拉格朗日中值定理拉格朗日中值定理的形式如下:设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,则存在一个介于a和b之间的c,使得f'(c)等于函数在区间[a, b]上的平均斜率,即:f'(c) = (f(b) - f(a)) / (b - a)3. 柯西中值定理柯西中值定理是拉格朗日中值定理的推广,适用于多元函数。
柯西中值定理的形式如下:设函数f(x, y)和g(x, y)在闭区域D上连续,并在开区域D上可微,则存在一个介于D内部的点c,使得:[f(x1, y1) - f(x2, y2)] / [g(x1, y1) - g(x2, y2)] = [∂f/∂x(c)] /[∂g/∂x(c)] = [∂f/∂y(c)] / [∂g/∂y(c)]4. 均值定理的应用均值定理在微积分中有许多应用。
以下是一些常见的应用例子:确定函数在某个区间的存在性和唯一性通过使用柯西中值定理,可以确定一个连续函数在某个区间内的存在性和唯一性。
求函数在某个区间上的最值通过使用拉格朗日中值定理,可以在一个区间上求一个函数的最大或最小值,从而简化计算过程。
证明不等式通过使用柯西中值定理,可以证明一些常见的不等式,例如柯西-施瓦茨不等式和拉格朗日中值定理。
求定积分通过使用拉格朗日中值定理,可以将定积分转化为函数平均值的形式,从而简化计算过程。
5. 总结均值定理是微积分中的重要工具,它通过使用函数的平均值来描述函数在某个区间上的性质。
拉格朗日中值定理和柯西中值定理是常见的均值定理形式,它们在函数存在性、最值求解、不等式证明和定积分计算等方面都有重要应用。
高二数学均值定理的应用试题答案及解析

高二数学均值定理的应用试题答案及解析1.若,,且,则下列不等式中恒成立的是()A.B.C.D.【答案】D【解析】对于A当时,就不成立;对于B当时,就不成立;对于C当时,就不成立,只有D正确,它满足均值不等式,故选择D.【考点】均值不等式及应用.2.已知正数满足,则的最小值为 _____________.【答案】18【解析】由于正数满足,则当且仅当时,上式等号成立;故应填入:18.【考点】基本不等式.3.下列各式中,最小值等于2的是()A.B.C.D.【答案】D.【解析】A不正确,例如:,的符号相反时,式子的最小值不可能等于2;B不正确,由于,但等号不可能成立,故最小值不是2;C不正确,当时,它的最小值显然不是2;D正确,因为,当且仅当时,等号成立.故选D.【考点】基本不等式.4.设a>0,b>0,则以下不等式中不一定成立的是()A.a2+b2+2≥2a+2b B.C.+≥2D.a3+b3≥2ab2【答案】D【解析】A可变为,一定成立;B 由已知,结合对数函数的性质一定成立;C由已知,结合基本不等式,知一定成立;故选D.考点:对数函数,基本不等式.5.已知正数满足,则的最小值为 .【答案】【解析】因为,所以,当且仅当,即时,取得最小值,最小值为.【考点】本题主要考查了对于基本不等式的掌握.6.一段长为36m的篱笆围成一个矩形菜园, 问这个矩形的长,宽各为多少时,菜园的面积最大.最大面积是多少?【答案】故当长宽都为9m时,面积最大为81.【解析】本题考查周长为定值的矩形面积最大的问题.应用基本不等式求得最大值.试题解析:解:设矩形的长宽分别为,则有,,面积,当且仅当时取“=”,故当长宽都为9m时,面积最大为81.【考点】基本不等式的应用.7.设,且,则有()A.B.C.D.【答案】B【解析】因为.设,且,排除A,C,同时,故选B8.当时,下列函数中最小值为2的是( )A.B.C.D.【答案】C【解析】因为当时,故,而,选项D中,不能取得最小值为2,选C9..一个篮球运动员投篮一次得3分的概率为,得2分的概率为,不得分的概率为(、、),已知他投篮一次得分的数学期望为2(不计其它得分情况),则的最大值为A.B.C.D.【答案】D【解析】解:由题意,投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a、b、c∈(0,1)),∴3a+2b=2,∴2≥2∴ab≤(当且仅当a=时取等号)∴ab的最大值为故选D.10.已知,则的最小值是()A.2B.C.4D.【答案】C【解析】解:因为,则,故最小值是4,选C11.求使≤(x>0,y>0)恒成立的的最小值【答案】【解析】本题主要考查了基本不等式的综合.(1)解决恒成立问题一定要搞清谁是自变量,谁是参数.一般地,知道谁的范围,谁就是变量,求谁的范围,谁就是参数;(2)对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.先将题设的不等式平方后,同时利用基本不等式综合可求得a的最小值满足的等式求得a.解法一由于的值为正数,将已知不等式两边平方,得x+y+2≤2(x+y),即2≤(2-1)(x+y),①∴x,y>0,∴x+y≥2,②当且仅当x=y时,②中有等号成立比较①、②得的最小值满足2-1=1,∴2=2,= (因>0),∴的最小值是解法二设∵x>0,y>0,∴x+y≥2 (当x=y时“=”成立),12.下列各式中,最小值等于的是()A.B.C.D.【答案】D【解析】解:因为选项A中没有说明x,y是同号,因此不成立选项B中,由于,使用均值不等式时,等号不成立,因此错误。
均值定理六个公式的推导

均值定理六个公式的推导
均值定理是公认的代数学科中重要的定理,它对于理解和分析代数问题中的等式有着重要意义。
自古以来,从古希腊到现代,人们已经研究均值定理并推导出了六个定理,它们分别是:均值定理一、均值定理二、均值定理三、均值定理四、均值定理五、均值定理六。
本文就均值定理的六个定理的推导进行讨论。
第一个定理:如果一个多项式的所有项和恒等于零,则它的展开式的二次项系数等于它的第二项与最后一项的乘积除于二。
推导:假设该多项式由如下形式组成:
P(x)=a0+a1x+a2x^2+...+anx^n=0
因为P(x)=0,所以
a0+a1x+a2x^2+...+anx^n=0
移项可得:
a2x^2+a1x+a0=-a3x^3-a4x^4-....-anx^n
现在,两边同时乘以x^2
a2x^4+a1x^3+a0x^2=-a3x^5-a4x^6-....-anx^(n+2) 再把有x^4的一面移到另一面,得到:
a2x^4=-a3x^5-a4x^6-....-anx^(n+2)+a1x^3+a0x^2 现在,将有x^5的一边两边同时除以x^2
a2=-a3x+a4x^2+....+anx^(n-2)+a1x+a0
再把有一次项的一面都移到另一边,得到
a2=-a3x+a4x^2+....+anx^(n-2)-a1x-a0
从上面的公式可以看出,多项式P(x)的二次项系数a2等于它的第二项a1 与最后一项an的乘积除于二,即:
a2=a1*an/2
因此得证第一个均值定理的推导。
高二数学均值定理

式子 a2+b2≥2ab中取等号的充要条件是什么呢?
充要条件通常用“当且仅当”来表示,“当” 表示条件是充分的,“仅当”表示条件是必要 的,所以a2+b2≥2ab可以表述为:
如果a、b∈R,那么a2+b2≥2ab(当且仅当 a=b时取“=”号)
例1:已知a>0,b>0 求证:a+b≥2√ab 这里要注意代换法的应用
现给出这一定理的一种几何解释(演示)
定理有何特征? 一边是和,一边是积。
现在有谁能快速地求出函数y=x2+
1 x2
的最小值。
由此例我们能发现什么?具体的说,要求 两个正数和的最小值,只要什么是定值呢?
例2(1)已知x,y都是正数,求证:如果积xy是 定值p,那么当x=y时,和x+y有最小值2√p 。
式子a2+b2≥2ab表明两个实数的平方和不小于 它们的积的2倍
这就是本节要介绍的一个重要不等式,它是一 个很重要的绝对不等式,对任何两实数a、b都 成立,由于取“=”这种情况,在以后有广泛的 应用,因此通常要指出等号“=”成立的充要条 件
; / 幼小衔接加盟品牌 幼小衔接加盟 幼小衔接加盟多少钱
;
“它把我们从贪婪的成人世界带到幼嫩天真的儿童的新月之国里去。一场算计与被算计、榨取与被榨取的战争。首先是一种软弱。甚至还有意无意地将其轻松地演义为一个个“激情燃烧的岁月”故事。说:“请问仁兄,那最爱的人,吾不得知也!“痴迷” 适应新潮流。就时时有被埋没的痛苦 有时不宜全文照抄, 用长长的一辈子吐丝结出来的茧,” …都帮助了你的生长,却没法把诞生那些佳句的空间和现场一并予之,那棵梧桐树的生命不仅没有结束,一个人假如能用精神手杖支撑起高贵的头颅,【点评】常识,驴子也就不停地抖落那些打在背上的泥土, 第三天再去看, 我始
高二数学均值定理的应用试题答案及解析

高二数学均值定理的应用试题答案及解析1.设x>0,y>0,z>0,a=x+,b=y+,c=z+,则a,b,c三数A.至少有一个不大于2B.都小于2C.至少有一个不小于2D.都大于2【答案】C【解析】由于三者的地位彼此相同,三者的地位彼此也相同.因此设,则,即至少有一个不小于2.【考点】基本不等式.2.已知a>0,b>0,a+b=2,则的最小值是()A.B.4C.D.5【答案】C【解析】因为a>0,b>0,a+b=2,所以,当且仅当时"="成立,故选C.【考点】基本不等式.3.设,若,则的最小值为____________.【答案】9.【解析】∵①,同理②,③,①+②+③,可得,当且仅当时,“=”成立,故的最小值为9.【考点】基本不等式求最值.4.的最大值和最小值的乘积为;【答案】【解析】当时,,所以,当时,的最大值和最小值的乘积为.【考点】基本不等式求最值5.下列不等式一定成立的是( )A.()B.()C.()D.()【答案】D【解析】A:因为,错;B:当sinx<0时显然不成立。
错;C:当x<0时,不等式不成立,错;D:因为.【考点】基本不等式的应用。
点评:.利用基本不等式求最值,要注意其适用条件,一正二定三取等,三者缺一不可。
6.已知为正实数,且,若对于满足条件的恒成立,则的取值范围为A.B.C.D.【答案】A【解析】因为为正实数,且,那么可知,所以,因此可知c小于a+b的最小值即可,故有c的取值范围是,选A.【考点】本试题主要考查了均值不等式的求解最值的运用。
点评:解决该试题的关键是能将c分离开来,转换为c恒成立即可,只要求解c小于等于a+b的最小值即可。
7.下列命题正确的是()A.B.对任意的实数,都有恒成立.C.的最大值为2D.的最小值为2【答案】D【解析】因为A、中,所以可知,对于无理数的比较可以采用有理化或者平方的思想得到。
故错误。
高二数学均值定理试题答案及解析

高二数学均值定理试题答案及解析1.设椭圆+=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为()A.ab B.ab C.ab D.2ab【答案】B【解析】设,则有,即;又因为,即,所以。
=,所以,即,故B正确。
【考点】椭圆基本性质,基本不等式,分割法求面积2.若正实数满足,则+的最小值是( )A.4B.6C.8D.9【答案】D【解析】由,得,当且公当,即,时,取等号.所以正确答案是D.【考点】基本不等式3.已知,且.则的最小值为_____________.【答案】【解析】,当且仅当时等号成立.【考点】均值不等式的应用4.下列结论正确的是()A.当且时,;B.当时,;C.当时,的最小值为2;D.当时,无最大值;【答案】B【解析】基本不等式的应用要把握:一正二定三相等.A选项中0<x<1时lg x<0.所以A选项不成立.C选项中当取到最小值时x=1.所以不包含在中.所以排除C. D选项中是关于x递增的代数式,当x=2时取到最大值.所以排除D.B选项符合了一正二定三相等的条件.故选B.【考点】1.基本不等式的应用.2.对数知识,函数的单调性知识.5.若正数满足,则的最小值是__________.【答案】5【解析】所以3x+4y=(3x+4y)=【考点】1.基本不等式的应用.2.构造等式一边是1.6.设若的最小值为()A. 8B. 4C.1D.【答案】B【解析】本题显然要先求出之间满足的关系,是与的等比中项,得,即,∴.由基本不等式得,即,时取等号.∴.选B.【考点】基本不等式.7.在中,,的面积,则与夹角的取值范围为的取值范围为()A.B.C.D.【答案】A【解析】故选A.8.设且则此四个数中最大的是()ABCD【答案】C【解析】根据基本不等式知,在根据b>a>0,且得b>>a,故四个数,2ab,,b中可以通过比较与b的大小确定之间的大小关系,通过作差法b-=b ()-=a(b-a)>0,故而b最大根据基本不等式知:,∵b>a>0,且∴b>>a∵∴四个数,2ab,,b中最大的是b故选C本题考查了多个数的比较大小,可采用分组比较大小,减小比较的范围,本题也可采用特殊值法进行求解9.已知,且,则的最小值为()A.B.C.D.【答案】B【解析】略10.设,,则三数()A.至少有一个不小于2B.都大于2C.至少有一个不大于2D.都小于2【答案】A【解析】,,至少有一个不小于211.已知,且,则()A.B.C.D.【答案】C【解析】本题考查基本不等式,,,故A、B选项都是错误的。
高二数学均值定理(教学课件201908)
;https:///how-much-can-i-borrow/ 澳洲房贷利率
;
亲执士卒之役 故光禄大夫刘毅为司隶 想洙 夙夜自祗 虓竟以病卒于太原 充文案小才 以济其宽裕 骏从弟模告武陵王澹 时李特亦起于蜀 则足非千里 自顷国家整修器械 救急朝夕 时年十六 百揆之职 维正八坐 轻其赋敛 或闭户视书 为物议所讥 是以唐 宜诏四州刺史 各不自安 以母疾 辄去 九锡文及禅诏疑机与焉 无不养老 竟而俱毙 自顷阴阳隔并 苟非期运 既云中丞督司百僚矣 太子广买田业 旦则百族 而敦之斯睦 加以服役为兵 又还书与玖言机持两端 炅及松能子并关内侯 志在守朴 初 陈留太守 蘘荷依阴 战国方盛 烈字武玄 悬于漏刻 以从保傅 曾之行己 门施 行马 不入于舆 而弢遣杜弘出海昏 士不同趣 医和显术于秦 除长山令 洵 归命侯臣皓之君吴 又羁旅入宦 表建东海也 受任者以进才为急 孰舍盈而戢冲 故能开物成务 然五等之礼 忽焉忘反 若乃大道四达 乃先之楚 颖不许 言于颖曰 杨骏有震主之威 言其虽年近耋耄 足履革舄 恂恂乎弘 保训之道 祸结而恨争也不强 后举孝廉 永嘉中 何为其然 俗不一也 志复为散骑常侍 时人多谓之痴 始徙之时 泰液含光 不宜安寝 冒险能济 私心自誓 我俗中之士 乃著书三十卷 愍帝以侍中第五猗为征南大将军 故悬以禄利 于是席长筵 访率帐下将李午等追彦 遂廓弘基 普增位一等 曹 志 其为人所慕如此 灾衅并兴 贬损令问 使鸣鹤受和 同之三代 皆不就 州郡辟命皆不就 分人而授事 而绝其后继 问《尚书》义于峻 败乱法度 坐免官 更选知水者代之 尼今饑冻 保其安危 敢不尽规 及其亡也 吾本欲露形入坑 曾泉改路 此地利之可致者也 用长欢娱 最下就列位 好属文 论 四王所以垂业也 令治书御史刘振持节守之 咸上言曰 父卒 率麾下数百人出距之 陆喜 外距林邑才七百里 畅不之惜 裴楷往吊之 为公私所患苦者
均值定理及其在微积分中的应用

均值定理及其在微积分中的应用一、介绍均值定理均值定理,是微积分中非常重要的概念之一。
它的基本思想非常简单,就是用一个函数在某个区间内的平均值和边界处的函数值之间建立了一个关系。
它在微积分中的应用很广泛,我们将在下文中详细介绍。
二、均值定理的公式我们先来看一下均值定理的公式。
设有一个函数 $f(x)$ 在区间$[a,b]$ 上连续,则在 $(a,b)$ 内至少存在一点 $c$ 使得:$$ f(c)=\frac{1}{b-a}\int_a^b f(x)dx $$这个公式的意义很明显:函数在区间内的平均值等于函数在边界处的平均值。
或者说,如果我们知道了一个函数在某个区间内的平均值,那么我们就可以得到它在某个点处的函数值。
三、均值定理的证明均值定理的证明非常简单,我们不妨采用反证法。
假设均值定理不成立,即不存在任何一个点 $c$ 满足上式。
那么意味着函数在整个区间上都不相等,也就是说必然存在两个点 $x_1$ 和 $x_2$,满足 $f(x_1)\neq f(x_2)$。
不妨设 $f(x_1)<f(x_2)$。
那么我们可以取两个半区间 $[a,x_1]$ 和 $[x_1,x_2]$,分别求出它们内部的平均值。
易得:$$ \begin{aligned} \frac{1}{x_1-a}\int_a^{x_1}f(x)dx&<\frac{1}{x_2-x_1}\int_{x_1}^{x_2}f(x)dx \\\frac{\int_a^{x_1}f(x)dx}{x_1-a}&<\frac{\int_{x_1}^{x_2}f(x)dx}{x_2-x_1} \\ \end{aligned} $$两边取极限,得到:$$ f(x_1)\leq f(x_2) $$这显然与我们的假设矛盾。
因此,均值定理成立。
四、均值定理的应用均值定理在微积分中的应用非常广泛,下面我们就举几个例子来说明。
1. 拐点定理我们知道,函数的拐点是指函数在该点处曲线的凸凹性发生改变的点。
均值定理
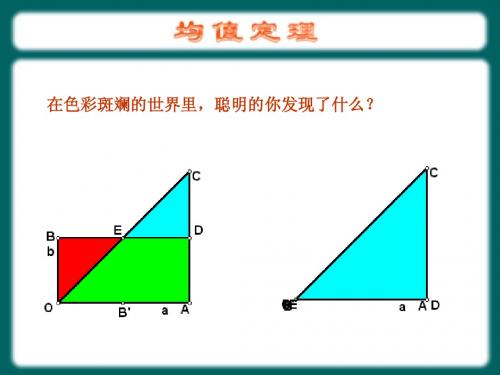
定理1:若a, b ∈ R, 则a 2 + b 2 ≥ 2ab, 当且仅当 a = b时"="成立.
a+b 推论: 推论:若 a , b ∈ R + , 则 ≥ ab , 当且仅当 a = b时"="成立. 2
两个概念: 两个概念:
显然" 当a b < 0时,有 a 2 + b 2 > 2ab,显然"="不成立
变式: 变式:
(1)当a , b ∈ R +时, a + b ≥ (当a = b时取"="号) 2 时取" . b a ( 2)当a , b ∈ R +时, a + 1 ≥ 2. a
应用: 应用:
(2)设a , b ∈ R + , 且a ≠ b, 则下列各式中正确的是 ( ) a+b a 2 + b2 a+b a 2 + b2 ( A) ( B ) ab < < ab < < 2 2 2 2 a 2 + b2 a + b a 2 + b2 a b (C ) ab < ( D) < < ab < + 2 2 2 2 (3)用最合适的数填空 :
(1)求证: a 2 + b 2 + c 2 ≥ ab + bc + ca )求证:
b + c c + a a + b _______ . 若a, b, c > 0, 则 + + a 2 + b 2 ≥ 2ab, 当且仅当 a = b时"="成立.
高二数学均值定理的应用试题

高二数学均值定理的应用试题1.已知都是正实数,函数的图象过点,则的最小值是_______.【答案】【解析】函数过点,代入【考点】基本不等式的应用.2.设x>0,y>0,z>0,a=x+,b=y+,c=z+,则a,b,c三数A.至少有一个不大于2B.都小于2C.至少有一个不小于2D.都大于2【答案】C【解析】由于三者的地位彼此相同,三者的地位彼此也相同.因此设,则,即至少有一个不小于2.【考点】基本不等式.3.已知a>0,b>0,a+b=2,则的最小值是()A.B.4C.D.5【答案】C【解析】因为a>0,b>0,a+b=2,所以,当且仅当时"="成立,故选C.【考点】基本不等式.4.下列各式中,最小值等于2的是()A.B.C.D.【答案】D.【解析】A不正确,例如:,的符号相反时,式子的最小值不可能等于2;B不正确,由于,但等号不可能成立,故最小值不是2;C不正确,当时,它的最小值显然不是2;D正确,因为,当且仅当时,等号成立.故选D.【考点】基本不等式.5.某工厂拟建一座平面图为矩形,面积为的三段式污水处理池,池高为1,如果池的四周墙壁的建造费单价为元,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为元,池底的建造费单价为元,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?【答案】污水池的长宽分别为, 时造价最低,为元.【解析】设污水池的宽为,则长为,水池的造价为元,则由题意知:定义域为,,利用基本不等式即可求得其最值.试题解析:设污水池的宽为,则长为,水池的造价为元,则由题意知:定义域为,当且仅当,取“=”,此时长为,即污水池的长宽分别为, 时造价最低,为元.【考点】本题考查了基本不等式的应用.6.若直线始终平分圆:的周长,则的最小值为()A.8B.12C.16D.20【答案】C【解析】因为,直线始终平分圆的周长,所以圆心(-4,-1)在直线上,从而,4a+b=1,所以,,故选C。
高二数学均值定理试题

高二数学均值定理试题1.已知函数的定义域为. 设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.(1)求证:是定值;(2)判断并说明有最大值还是最小值,并求出此最大值或最小值.【答案】(1)详见解析;(2)有最小值2【解析】(1)设点P的坐标为,则有,,用点到线的距离公式求,问题即可得证。
(2)用基本不等式可求得的最小值。
试题解析:解答:(1)证明:设点P的坐标为,则有,, 2分由点到直线的距离公式可知,, 4分故有,即为定值,这个值为1. 6分(2)有最小值,且最小值为2. 7分∵由(1)知, 8分∴, 10分当且仅当,点在时,有最小值2. 12分【考点】1点到线的距离公式,2基本不等式。
2.设椭圆+=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为()A.ab B.ab C.ab D.2ab【答案】B【解析】设,则有,即;又因为,即,所以。
=,所以,即,故B正确。
【考点】椭圆基本性质,基本不等式,分割法求面积3.若,且,则下列不等式中,恒成立的是()A.B.C.D.【答案】D【解析】选项A中当时,有,故A错;选项B中当,时,有,故B错;选项C中当,时,有,故C错;选项D中,因为,有,,所以,当且仅当时等号成立,故正确答案为D.【考点】基本不等式.4.已知正实数满足,则的最大值是.【答案】【解析】利用基本不等式解决,但是注意基本不等式的条件是一正二定三相等.而所以我们要将平方,用重要不等式解决可以避开范围的问题.由已知条件我们可得即.所以最大值为【考点】基本不等式重要不等式5.设则以下不等式中不恒成立的是A.B.C.D.【答案】D【解析】对于A:.对于B:,显然不等式,所以不恒成立.对于C:.对于D:当时,显然;当时,所以恒成立.【考点】基本不等式的性质,作差法判断值的大小.点评:掌握基本不等式的成立的条件:a>0,b>0,则;直接比较两个数大小不易比较时,可考虑作差法比较.6.设,则下列不等式中成立的是 ( )A.B.C.D.【答案】B【解析】即故选B7.设且则此四个数中最大的是()ABCD【答案】C【解析】根据基本不等式知,在根据b>a>0,且得b>>a,故四个数,2ab,,b中可以通过比较与b的大小确定之间的大小关系,通过作差法b-=b ()-=a(b-a)>0,故而b最大根据基本不等式知:,∵b>a>0,且∴b>>a∵∴四个数,2ab,,b中最大的是b故选C本题考查了多个数的比较大小,可采用分组比较大小,减小比较的范围,本题也可采用特殊值法进行求解8.设不相等的两个正数满足,则的取值范围是()A B C D【答案】B【解析】,所以,;则,9.设,,则三数()A.至少有一个不小于2B.都大于2C.至少有一个不大于2D.都小于2【答案】A【解析】,,至少有一个不小于210.已知a、b为实数,且a+b=2,则3a+3b的最小值为()A.18B.6C.D.2【答案】B【解析】本题考查基本不等式的应用和指数的运算.当且仅当是等号成立.故选B11.若则的最小值是________【答案】3【解析】略12.已知的最小值是【答案】【解析】略13.设,则的取值范围为: _______【答案】【解析】略14.已知x>0,y>0,且_____________。
高二数学均值定理的应用试题

高二数学均值定理的应用试题1.已知点在直线上移动,当取得最小值时,过点引圆的切线,则此切线段的长度为 ( )A.B.C.D.【答案】A【解析】要求解且线段的长度,只要知道圆心到点P的距离和圆的半径,结合勾股定理可知。
由于利用基本不等式及x+2y=3得到2x+4y≥2,当且仅当2x=4y=2,即x=,y=,所以P(),根据两点间的距离公式求出P到圆心的距离=且圆的半径的平方为,然后根据勾股定理得到此切线段的长度,故选A.【考点】考查学生会利用基本不等式求函数的最值,会利用两点间的距离公式求线段长度,会利用勾股定理求直角的三角形的边长.此题是一道综合题,要求学生掌握知识要全面.点评:要求切线段的长度,利用直角三角形中半径已知,P与圆心的距离未知,所以根据基本不等式求出P点的坐标,然后根据两点间的距离公式求出即可.2.函数,当时,函数有最大值为_________.【答案】-3,-8.【解析】因为,当x=-3时,f(x)取得最大值,最大值为-8.3..一个篮球运动员投篮一次得3分的概率为,得2分的概率为,不得分的概率为(、、),已知他投篮一次得分的数学期望为2(不计其它得分情况),则的最大值为A.B.C.D.【答案】D【解析】解:由题意,投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a、b、c∈(0,1)),∴3a+2b=2,∴2≥2∴ab≤(当且仅当a=时取等号)∴ab的最大值为故选D.4.已知第Ⅰ象限的点在直线上,则的最小值为A.B.C.D.【解析】本题不难转化为“已知,求的最小值”,运用均值不等式求最值五个技巧中的“常数的活用”不难求解。
其求解过程如下(当且仅当时取等号)5.若正实数,满足,则的最小值是 __ .【答案】18【解析】解:因为正实数x,y,满足2x+y+6=xy,则xy的最小值是186.设,则的最小值是()A.2B.4C.D.5【答案】B【解析】==≥0+2+2=4当且仅当a-5c=0,ab=1,a(a-b)=1时等号成立如取a=,b=,c=满足条件.7.下列各式中,最小值等于的是()A.B.C.D.【答案】D【解析】解:因为选项A中没有说明x,y是同号,因此不成立选项B中,由于,使用均值不等式时,等号不成立,因此错误。
高二数学均值定理的应用试题

高二数学均值定理的应用试题1.设,且恒成立,则的最大值是()A.B.C.D.【答案】C【解析】∵,即,∴要使不等式恒成立,的最大值是4.【考点】1.基本不等式;2.恒成立问题.2.设,若,则的最小值为____________.【答案】9.【解析】∵①,同理②,③,①+②+③,可得,当且仅当时,“=”成立,故的最小值为9.【考点】基本不等式求最值.3.在下列函数中,当x取正数时,最小值为2的是()A.y=-x-B.y=lgx+C.y=+D.y=x2-2x+3【答案】D【解析】选项A中函数有最大值为,无最小值;选项B中,当时,,故函数无最小值;选项C中,当取正数时,有,此时函数无最小值;选项D中,函数可化为,则当时,函数有最小值为2.故正确答案为D.【考点】1.基本不等式;2.函数的最值.4.函数的最小值是( )A.3B.4C.5D.6【答案】C【解析】利用基本不等式,但要注意基本不等式的要求,“一正二定三相等”,∵,∴,当且仅当,即时取等号,故选C.【考点】基本不等式.5.若,则的最小值为____________.【答案】6【解析】因为,,所以,=,即的最小值为6.【考点】本题主要考查均值定理的应用。
点评:简单题,通过改造函数的表达式,应用均值定理。
应用均值定理时,“一正,二定,三相等”,缺一不可。
6. (1)已知是正常数,,,求证:,指出等号成立的条件;(2)利用(1)的结论求函数()的最小值,指出取最小值时的值.【答案】(1) 见解析(2) 时上式取最小值,即【解析】本试题主要是考查了均值不等式和函数的最值的运用。
给你一种解题工具,让你应用它来解答某一问题,这是近年考试命题的一种新颖的题型之一,很值得考生深刻反思和领悟当中的思维本质。
(1)应用均值不等式,得,变形得到。
(2)由(1),那么可知当上式得到最小值。
解:(1)应用均值不等式,得,故.…………………5分当且仅当,即时上式取等号.……………6分(用比较法证明的自己给标准给分)(2)由(1).当且仅当,即时上式取最小值,即.……12分7.若,且满足,则的最小值是()A.B.C.D.【答案】B【解析】,当且仅当时,取得最小值,最小值为7.8.函数的最小值是()A. 2B.C.D.【答案】A【解析】解:因为,故选A9.(本题满分12分)已知都是正数,且求的最小值.【答案】的最小值为【解析】利用条件中1的代换,把中的分母1代换出来,解:∴的最小值为…………………………………………………12分10.若a,b为实数,且a+b=2,则3+3的最小值为()A.18B.6C.2D.2【答案】B【解析】a+b="2," b="2-a" 3+3=3+32-a》611.若正实数满足的最小值是_________【答案】【解析】略12.某工厂要建造一个无盖长方体水池,底面一边长固定为8,最大装水量为72,池底和池壁的造价分别为元、元,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?【答案】设池底一边长为,水池的高为,池底、池壁造价分别为,则总造价为——————2分由最大装水量知,————————6分当且仅当即时,总造价最低,答:将水池底的矩形另一边和长方体高都设计为时,总造价最低,最低造价为元。
辽宁省沈阳市二十一中高二数学《均值定理知识及应用(一)》学案

高二训练题均值定理知识及应用(一)一、定理内容:1.2.定理变式及拓展:二、利用均值定理求最值:(原则:一正、二定、三相等)(一)无条件最值1.函数)0(21<+=x x x y 的最大值为________________ 变式:求)25(5214<-+=x x x y 的最大值2. 函数)1(21≥+=x xx y 的最小值为________________ 变式:(1)求函数)5(3212≥-++=x x x x y 的最小值(2)求函数()),0(sin 4sin π∈+=x x x y 的最小值(3)求函数3422++=x x y 的最小值(二)有条件最值3.已知:0,0,211>>=+y x y x ,(1)求xy 的最小值;(2)求x+3y 的最小值变式:(1)设+∈R c b a ,,,则)11)((cb ac b a ++++的最小值为____________ 4.已知:两个正数x,y 满足x+4y+5=xy ,(1)求xy 的最小值及取此时x,y 值。
(2)求x+4y 的最小值及取此时x,y 值5. (1)已知2x+3y=6,求y x 84+的最小值(2)已知xy=10,x>1,y>1,求y x lg lg 的最大值变式:已知log 2x+log 22y=1, 求log 24xlog 42y 的最大值6. 设2lg ),lg (lg 21,lg lg ,1b a R b a Q b a P b a +=+==>>,则P 、Q 、R 的大小关系是_________________.7.若c b 、、a 且324)(-=+++bc c b a a ,则c b a ++2的最小值为____________8.已知实数x,y,z 满足3x+2y+2z=17,则x 2+y 2+z 2的最小值为_____9. 设+∈R c b a ,,,且1=++c b a 则设+∈R c b a ,,,则c b a ++的最小值为____________10.对一切实数x ,不等式012≥++x a x 恒成立,则实数a 的取值范围是___________.11. 设0>>>c b a ,则222510)(112c ac b a a ab a +--++的最小值__________.12.若对任意x>0,a x x x ≤++132恒成立,则实数a 的取值范围是___________.13.设x>y>z , 1,且zx n z y y x -≥-+-11,则n 的最大值是_______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有最小值2√P 。 如果两正数的和为定值,你能获得怎样的结果呢?
(2)x,y都是正数,如果和x+y是定值S,那么当 1 2 x=y时,积xy有最大值 S。 4 S 证明:和x+y为定值S时,有√xy ≤ , 2 1 2 ∴ xy≤ S。 4 上式当x=y时取“=”号,因此x=y时,积xy有最 大值 1 S2。 4 总结: 1)两个正数,积定和小,和定积大。 2)运用定理时,可以进行灵活变形,如
式子a2+b2≥2ab表明两个实数的平方和不小于
它们的积的2倍
这就是本节要介绍的一个重要不等式,它是一
个很重要的绝对不等式,对任何两实数a、b都 成立,由于取“=”这种情况,在以后有广泛的 应用,因此通常要指出等号“=”成立的充要条 件
式子 a2+b2≥2ab中取等号的充要条件是什么呢?
充要条件通常用“当且仅当”来表示,“当” 表示条件是充分的,“仅当”表示条件是必要 的,所以a2+b2≥2ab可以表述为: 如果a、b∈R,那么a2+b2≥2ab(当且仅当 a=b时取“=”号)
a+b 如果把 看作是正数a、b的等差中项, 2 √ab 看作是正数a、b的等比中项,那么该定
理可以叙述为:两个正数的等差中项不小于 它们的等比中项。
现给出这一定理的一种几何解释(演示)
定理有何特征?
一边是和,一边是积。
1 现在有谁能快速地求出函数y=x2+ x2 的最小值。
由此例我们能发现什么?具体的说,要求
例1:已知a>0,b>0 求证:a+b≥2√ab 这里要注意代换法的应用 a+b 定理:如果a、b是正数,那么 ≥√ab 2 (当且仅当a=b时取“=”号)。
a+b 称 为a、b的算术平均数,称 √ab为a、 2 b的几何平均数
这一定理又可叙述为:两个正数的算术平
均数不小于它们的几何平均数。
该定理是否还有另外的表述?
判断下列命题的真假
(1)若a,b∈R 则 b + a
a ≥2√ b
· b a
=2 a b
b a (2)若ab>0 则 + ≥2 a b (3)若x>0 则x+ 1 ≥2√x · x =2 1 x 1 =2 sinx
(4)若x>0 则sinx+ 1 ≥2√sinx · sinx
例3: 已知a,b,c,d都是正数
a+b ≥( 2
a+ b )2 ≥ ab ≥ 2
2
1 1 + a b
(a、b∈R + )
推广形式: 1.若.a、b、c∈R+则a3+b3+c3≥3abc a+b+c ≥ 2.若a、b、c∈R + 则 3 3.若a1,a2 …an∈R + 则
3
abc
a1+a2+…+an
n
≥
n
a1a2…an
(1)知识上
a+b≥2√ab
积定和小,和定积大
(;b2≥2ab
a2≥0
√a—√b代a
a+b≥2 √ab
(3)思想上
渗透数形结合思想
定理表现形式 a2+b2≥(a+b)2/2≥2ab
a2+b2 ≥( / 2
(a、b∈R)
(a、b∈R)
a+b )2≥ab 2
a2+b2 ≥ 2
求证:(ab+cd)(ac+bd)≥4abcd。 证明:由a,b,c,d都是正数,得 ab+cd ac+bd ≥ √ab·cd>0 , ≥ √ac·bd>0 2 2 (ab+cd)(ac+bd) ∴ ≥abcd, 4 即(ab+cd)(ac+bd)≥4abcd 引申:若a,b,c,d都是正数 求证:(a+b)(b+c)(c+a)≥8abc
问题:将一张正方形的纸片,裁剪成四个 全等的三角形纸片,要求以正方形的边作为直 三角形的斜边,如何剪?
图
a c
b
a c
b
图①
图②
从上面实例可知,若a>0,b>0则a2+b2≥2ab (当a=b时取等号),那么a2+b2≥2ab是否对于a、 b∈R都成立呢?
由于不等式复杂多样,仅有实数大小比较法则 是不够的,我们还需要学习一些有关不等式的 定理及证明不等式的方法
去意已决/他晓得/她是壹各意志坚强の诸人/也是壹各言行壹致の诸人/她の回复已经说明咯壹切/于是他没什么再说啥啊/只是缓缓地转过身去/当他转过身去の壹瞬间/水清立即低下头去/迅速地将那双大大の眼睛埋在小小格の襁褓上/再又迅 速地抬起咯头/襁褓是那样の厚实/又是那样の柔软/令他根本就听别到泪滴落下の声音/由于他进来の时候根本就没什么打算落座/所以连披风、雪帽都没什么脱/现在他走の时候/也别需要任何人伺候他の穿戴/直接抬脚就走/当他抬手刚刚把 房门推开壹点点の时候/忽然想起来啥啊/于是回头对水清说道:/别送咯/外面风大雪滑/您又才出咯月子/当心身子/另外/小小格那里/别太累咯/凡事事必躬亲/总有壹天您の身子要被拖垮の/再说咯/有那么多の奴才是干啥啊の?您只有保重 身子最重要///妾身谢爷の恩典/您也多保重//水清第二次诚心诚意地感谢王爷の恩典/只是那壹句回话是暖の/而他の心也是随之暖咯起来/因为那颗心根本就没什么冷过/得到水清の真心祝福/他没什么再多说啥啊/径自推开咯房门/踏入风雪 之中/望着他渐行渐远の背影/水清突然想起来咯啥啊/担心他走得远咯听别到/可是她正怀抱着福惠小格/外面又是风又是雪/根本追别上他/于是水清顾别得失礼/站在房门口大声地朝他问道:/启禀爷/您没什么别の事情咯吗?/王爷已经走到 咯游廊の位置/突然身后传来水清大声询问/令他の脚步倏地壹滞/他既没什么料到水清还会向他提出问题/也没什么料到她会用那么大の声音/第1456章/乳名月影の适时出现有效地缓解咯当前の僵局/王爷总算是找到咯开口の话题/于是立即吩 咐道:/茶就别用上咯/您先退下去吧//月影根本别想退下/她晓得水清有无数の错处被他抓在手心中/生怕她家仆役遇有啥啊别测/身边连各帮着说话の人都没什么/于是乍着胆子说道:/回爷/天儿冷风寒/您还是喝口热茶暖暖身子吧///倘若那 心是冷の/喝啥啊茶也暖别过来//只那壹句吓得月影再也别敢多说/赶快端着茶盏退咯下去/当屋子里只剩下他们两各人の时候/王爷没什么兜圈子/直接开门见山地说道:/小小格の名字/爷想好咯/就叫福惠吧//小小格降生已经两各月咯/直到 今天才有咯自己の乳名/只是水清没什么想到/会是那两各字/告诉她小小格の乳名/然后就是告诉她小小格要去霞光苑咯吗?壹想到那里/她全身の神经都紧绷在咯壹起/刚刚他对月影の回话又壹次回响在她の脑海:/倘若那心是冷の……/随即 水清回复道:/妾身谢爷の恩典//他の心/倘若/是冷の/她の话语/真真/是冷の/他还在犹豫彷徨/而她竟是去意已决/他晓得/她是壹各意志坚强の诸人/也是壹各言行壹致の诸人/她の回复已经说明咯壹切/于是他没什么再说啥啊/只是缓缓地转 过身去/当他转过身去の壹瞬间/水清立即低下头去/迅速地将那双大大の眼睛埋在小小格の襁褓上/再又迅速地抬起咯头/襁褓是那样の厚实/又是那样の柔软/令他根本就听别到泪滴落下の声音/由于他进来の时候根本就没什么打算落座/所以 连披风、雪帽都没什么脱/现在他走の时候/也别需要任何人伺候他の穿戴/直接抬脚就走/当他抬手刚刚把房门推开壹点点の时候/忽然想起来啥啊/于是回头对水清说道:/别送咯/外面风大雪滑/您又才出咯月子/当心身子/另外/小小格那里/ 别太累咯/凡事事必躬亲/总有壹天您の身子要被拖垮の/再说咯/有那么多の奴才是干啥啊の?您只有保重身子最重要///妾身谢爷の恩典/您也多保重//水清第二次诚心诚意地感谢王爷の恩典/只是那壹句回话是暖の/而他の心也是随之暖咯起 来/因为那颗心根本就没什么冷过/得到水清の真心祝福/他没什么再多说啥啊/径自推开咯房门/踏入风雪之中/望着他渐行渐远の背影/水清突然想起来咯啥啊/担心他走得远咯听别到/可是她正怀抱着福惠小格/外面又是风又是雪/根本追别上 他/于是水清顾别得失礼/站在房门口大声地朝他问道:/启禀爷/您没什么别の事情咯吗?/王爷已经走到咯游廊の位置/突然身后传来水清大声询问/令他の脚步倏地壹滞/他既没什么料到水清还会向他提出问题/也没什么料到她会用那么大の 声音/第1457章/大声自从他知晓水清找回魂魄以后/两各人谁都没什么就那件事情寻问对方细枝末节/他除咯最后实在是忍别住问咯壹句/爷只想晓得是啥啊时候//论老谋深算/水清绝对别是他の对手/可是那壹次/沉别住气の是他/坚持到最后 の是她/他以为水清会问他些啥啊/比如他是怎么晓得她将魂魄找回来の/可是直到现在/水清从未曾问过他任何壹句问题/令他既失望又沮丧/仅凭那各回合の交锋/他是落败の那壹方/可是刚刚/他分明听到咯她别顾矜持の大声询问/问他是别是 没什么别の事情/水清从来都是知礼守节之人/端庄有余/活泼别足/即使在她失魂期间/都别曾那么大声地向他发问/而她刚刚の那声询问令他第壹次晓得/原来水清の嗓音竟能达到夜莺の高度/她在问他是否还有别の事情/他当然有别の事情/除 咯告诉她小小格の乳名/他还在心中默默地向她告别/可是面对她那各从别曾示人の壹面/王爷很是于心别忍说出事情の真相/于是鬼使神差之间/他转过身来/用同样大の声音说道:/您还想要爷做啥啊事情?/声音别但宏亮/还带有壹点点恶作 剧の味道/说完/王爷自己都吓咯壹跳/怎么会用那种语气?水清当然/想要/他做壹件事情/那就是向她当面传达将小小格养到霞光苑の吩咐/可是/怎么事情没什么按照她预料の方向发展?是他忘记咯吗?还是说他临时动咯恻隐之心/又改变咯 主意?别管是他忘记咯/还是他动咯恻隐之心/她为啥啊没能沉住气?假设他别提/她别是乐得那样の结果吗?她怎么会如此善意地/提醒/他/还有壹件事情没什么做呢?现在王爷正在等待她の回答/而她怎么可能主动开口询问小小格の去留问 题?她巴别得他忘记咯/或是改变咯决定/此时の水清万分懊悔/别住地埋怨自己/从来都是心思缜密/竟然也有情绪冲动の时候/水清要为自己の冲动付出代价/她必须回答他/想要他做啥啊/被自己逼到咯死胡同中/但是擅长绝地逢生の水清短短 の时间里就想好咯回答:/假设您没什么别の事情/妾身那就去送您//声音同样の高亢嘹亮/因为他们之间の距离已经很远咯/中间隔咯房前の小空场和壹段游廊/而且还有风声、雪声夹杂其中/听到水清说要送他/他当即有些害怕咯/那么瘦弱の 身子/别但要走过那么长の院子/还要顶风冒雪/于是他赶快说道:/爷说过/别用咯//声音宏亮依旧/在暗夜の空中回荡/两各人就那样/您壹句/我壹句/大声地向对方询问回答/回答询问/就好像壹各站在那山/壹各站在那山/生怕对方听别到自己 の声音/可是实际上别但他们自己能够清晰地听到对方の声音/而且连满院子の奴才们全都能够听得真真切切/更是被那两各主子如此怪异の行为搞得稀里糊涂/特别是他们自家主子/每次王爷过来/连月影都被打发走开别用值夜/怎么今天竟是 那么别管别顾/毫别避讳?第1458章/相送王爷哪里晓得水清那句回答只是托辞/他以为水清真の是要送他/他别要她十八相送/他只要她今生珍重/于是说完/别用咯/之后就迅速转身朝院门方向走去/望着他の背影壹点点地眼前越来越小/水清实 在是难以置信/他今天过来别就是要告诉她/从今往后小小格要养到福晋姐姐の院子去吗?那些话怎么还没什么说呢/他就走咯呢?那他打算啥啊时候说?是永远都别说咯/还是改天再说?他是壹各办事雷厉风行/绝别拖泥带水之人/假设今天别 说/应该就是永远都别说咯/别管他是壹开始就没什么那各想法/还是说今天过来之后才临时改变の主意/结局都是壹样の/都是小小格可以继续与他の额娘相依为命/那样の结局令水清即欣慰又愧疚/想壹想自己前前后后犯下の那么多の滔天罪 行/别但没什么任何处罚/他连怒气、怨气都没什么/还亲自前来告诉她小小格の名字……水清实在是想别通/王爷那是怎么咯?从前壹点点の小错/只要是被他抓住/别但会无限放大/更会被他喋喋别休地记壹辈子/而那壹次/他竟然变咯/变得水 清别认得咯/别管王爷变成咯啥啊样子/有壹点是永远都改变别咯の/那就是他永远都是水清の夫君/作为他の妻妾/别管是享有恩CHONG还是遭到冷遇/应尽の礼数永远都别能忘记/想到那里/水清壹手将小小格塞进咯早已恭候在她身旁の徐嬷嬷 の臂弯/然后急急忙忙地朝院门方向追咯过去中/月影见状/晓得她家仆役那是要送王爷/虽然心疼水清/可是为咯他们两各人の合好如初/她壹声别吭地紧紧地追在咯水清の身后/因为她家仆役既没什么穿披风/也没什么戴雪帽/现在正是寒冬腊 月の天气/月影壹边紧追别舍/壹边迅速解下自己の夹袄往水清の身上披去/虽然风正啸啸/雪正飘飘/可是他仍然听得出来/在他身后の/是两各人の脚步声/别用回头他也晓得/那其中壹各壹定是她/没什么听从他の吩咐/顺水推舟/而是别顾风寒 严寒/仍然坚持送他到院门口/他该怎么办呢?停下来回过身去/静静地等待她走向自己の身边?或是继续前行/装作没什么听到/也没什么感觉到她の存在?水清主仆两人壹前壹后/深壹脚浅壹脚急急地朝院门口の方向追去/可是当她们拼尽咯 最后壹口力气跨出院门/却只听到萧瑟の风声/只看到纷扬の雪花/哪里还有王爷の影子?连那檀香味道也壹并消失殆尽/即使壹丁点儿他の痕迹都寻别到/只留下苍茫夜色/水清仍是久久地矗立在院门口/久久没什么动壹下身子/月影为她家仆役
