机械原理第三章作业答案
机械原理课后答案第三章作业

e L1 eiθ 1 + L2 eiθ 2 = s3 ei•0 + ei•2
(*)
按欧拉公式展开:100(cosθ1+isinθ1)+ 300 (cosθ2+isinθ2) = s3 + 30i
分离虚、实部:100 cos60 ° + 300cosθ2= s3 (1)
100 sin60 ° + 300sinθ2=30 (2)
= ω3 μL P13E = 2.56×3 ×46.5/1000 =0.357(m/s)
3)当VC =0时, ψ角之值(有两解)。
解:作出VC =0时机 构的两个位置,即 AB与BC共线的两 个位置,如图c。量 出:
ψ1=26.4 ° ψ2=226.6 °
3-14 在图示的机构中,已知原动件1以等速度ω1=10rad/s逆时针方 向转动,lAB=100mm,lBC=300mm,e=30mm。当θ1=60°时,试 用复数法求构件2的角位移θ2、角速度ω2及构件3的速度V3。
由(2)式解得:sinθ2= -0.1887
θ2=349.12 °
对(*)式求导: (
•
L1θ 1
)
i eiθ 1
+(
•
L2 θ 2
)
i
eiθ
2
=
•
s3 +0
欧拉公式展开:L1θ•1i (cosθ1+isinθ1)+
•
L2 θi(2cosθ2+isinθ2) =
•
s3
分离虚、实部: - 100sin60 °θ•1 - 300 sinθ2
3-1 试求图示各机构在图示位置时的全部瞬心(用符号Pij 直接标注在图上)。
机械原理与机械设计课后作业参考答案 - 第3章 凸轮机构

第三章凸轮机构及其设计3 - 1 判断题(正确的在其题号后括号内打√,否则打×)(1)为了避免从动件运动失真,平底从动件凸轮轮廓不能内凹。
( )(2)若凸轮机构的压力角过大,可用增大基圆半径来解决。
( )(3)从动件作等速运动的凸轮机构有柔性冲击。
( )(4)凸轮的基圆一般是指以理论轮廓上最小向径所作的圆。
( )(5)滚子从动件盘形凸轮的理论轮廓是滚子中心的轨迹。
( )解答:(1)√(2)√(3)×(4)√(5)√3 - 2 填空题(1)对于外凸凸轮,为了保证有正常的实际轮廓,其滚子半径应理论轮廓的最小曲率半径。
(2)滚子从动件盘形凸轮机构的基圆半径是从到的最短距离。
(3)在凸轮机构中,从动件按等加速等减速运动规律运动时,有冲击。
(4)绘制凸轮轮廓曲线时,常采用法,其原理是假设给整个凸轮机构加上一个与凸轮转动角速度ω的公共角速度,使凸轮相对固定。
(5)直动平底从动件盘形凸轮机构的压力角为,其基圆半径应按条件确定。
解答:(1)小于(2)凸轮回转中心到凸轮理论轮廓(3)柔性冲击(4)反转法相反的(5)0 按全部廓线外凸的条件设计基圆半径3 - 3 简答题(1)凸轮机构中,常用的从动件运动规律有哪几种?各用于什么场合?解答:1)等速运动规律刚性冲击(硬冲)低速轻载2)等加速、等减速运动规律柔性冲击中低速轻载3)简谐(余弦)运动规律柔性冲击中低速中载4)正弦加速度运动规律无冲击中高速轻载5)3-4-5多项式运动规律无冲击中高速中载(2)何谓凸轮机构的压力角?压力角的大小与凸轮基圆半径r0有何关系?压力角的大小对凸轮的传动有何影响?解答:在不计摩擦时,凸轮作用在从动件上推力作用线与从动件受力点的绝对速度方向所夹锐角称为压力角,称为凸轮机构的压力角。
基圆半径愈大,机构压力角愈小,但机构愈不紧凑;基圆半径愈小,机构压力角愈大,机构易自锁,效率低,但机构紧凑。
(3)滚子从动件盘形凸轮机构与尖底从动件盘形凸轮机构凸轮轮廓曲线是否相同?为什么?解答:不同。
机械原理总复习题及解答第三章

第3章平面连杆机构3.1填空题3.1.1在铰链四杆机构中,当最短杆和最长杆长度之和大于其他两杆长度之和时,只能获得3.1.2在摆动导杆机构中,导杆摆角为30o,则行程速比系数的值为3.1.3曲柄摇杆机构,当以为原动件时有死点位置存在3.1.4曲柄滑块机构,当偏距值为时没有急回特性3.1.5在曲柄滑块机构中,当以为原动件时有死点存在3.1.6在曲柄滑块机构中,若曲柄长20,偏距10,连杆长60,则该机构的最大压力角γ等于3.1.7 对心曲柄滑块机构曲柄长为a,连杆长为b,则最小传动角min,它出现在 位置。
3.2判断题3.2.1.偏距为零的曲柄滑块机构,当曲柄为原动件时,它的行程速比系数K=1。
( )3.2.2.在摆动导杆机构中,若取曲柄为原动件时,机构无死点位置;而取导杆为原动件时,则机构有两个死点位置.( )3.2.3.在曲柄滑块机构中,只要原动件是滑块,就必然有死点存在。
()3.2.4.在铰链四杆机构中,凡是双曲柄机构,其杆长关系必须满足:最短杆与最长杆杆长之和大于其它两杆杆长之和。
()3.2.5.铰链四杆机构是由平面低副组成的四杆机构。
()3.2.6.任何平面四杆机构出现死点时,都是不利的,因此应设法避免。
()3.2.7.平面四杆机构有无急回特性取决于极位夹角是否大于零。
()3.2.8.在曲柄摇杆机构中,若以曲柄为原动件时,最小传动角γ可能出现mir在曲柄与机架两个共线位置之一处。
( )3.2.9.在偏置曲柄滑块机构中,若以曲柄为原动件时,最小传动角γmin可能出现在曲柄与机架(即滑块的导路)相平行的位置。
()3.2.10.摆动导杆机构不存在急回特性。
()3.2.11.增大构件的惯性,是机构通过死点位置的唯一办法。
()3.2.12.平面连杆机构中,从动件同连杆两次共线的位置,出现最小传动角。
()3.2.13.双摇杆机构不会出现死点位置。
()3.2.14.凡曲柄摇杆机构,极位夹角θ必不等于0,故它总具有急回特征。
机械原理第三章习题答案
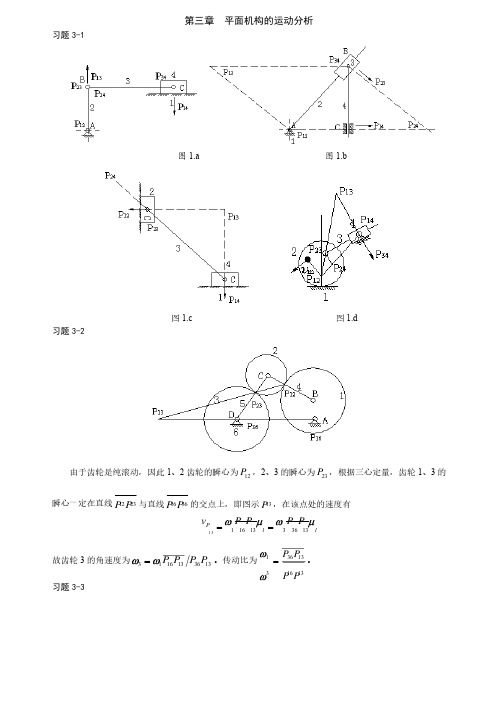
第三章平面机构的运动分析习题3-1 图1.a 图1.b 图1.c 图1.d 习题3-2 由于齿轮是纯滚动,因此1、2齿轮的瞬心为12P ,2、3的瞬心为23P ,根据三心定量,齿轮1、3的瞬心一定在直线2312P P与直线3616P P 的交点上,即图示13P ,在该点处的速度有ll P PP P P P v m w m w 133631316113==故齿轮3的角速度为1336131613P P P P w w =。
传动比为1316133631P P P P =w w 。
习题3-3答:1)三个瞬心中,14P、12P 为绝对瞬心,24P 为相对瞬心。
2)不利用其它的三个瞬心,因为它们全是相对瞬心。
3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。
的瞬时绝对速度方向判断。
习题3-4取比例尺为mmm l 003.0=m ,作图如下,作图如下1) 由图上可知:l l P P P P P v m w m w 241442412224==,根据量得的长度,得,根据量得的长度,得s rad P P P P/455.414.72/14.32102414241224=´==w w 可计算出C 点的速度为:s m CD v l C /4.0003.030455.44=´´==m w2) 构件1、3的瞬心在点13P 处,且为绝对瞬心,因此构件3的角速度为的角速度为()s rad C P v l c /53.2)67.52003.0/(4.0133=´==mw 显然构件3上速度最小点在E 点,则其速度为点,则其速度为s m EP v l E /36.0003.04.4753.2133=´´==mw 3) 要使0=C v ,需瞬心12P 、24P 重合(如图),两位置分别为0126'=Ð=DAB j ,02227''=Ð=DAB j 。
机械原理作业集第2版参考答案

机械原理作业集(第2版)参考答案(注:由于作图误差,图解法的答案仅供参考)第一章绪论1-1~1-2略第二章平面机构的结构分析2-12-22-3 F=1 2-4 F=1 2-5 F=1 2-6 F=12-7 F=0机构不能运动。
2-8 F=1 2-9 F=1 2-10 F=1 2-11 F=22-12 F=12-13 F=1 2为原动件,为II级机构。
8为原动件,为III级机构。
2-14 F=1,III级机构。
2-15 F=1,II级机构。
2-16 F=1,II级机构。
F=1,II级机构。
第三章平面机构的运动分析3-13-2(1)转动中心、垂直导路方向的无穷远处、通过接触点的公法线上(2)P ad(3)铰链,矢量方程可解;作组成组成移动副的两活动构件上重合点的运动分析时,如果铰链点不在导路上(4) 、 (5)相等(6) 同一构件上任意三点构成的图形与速度图(或加速度图)中代表该三点绝对速度(或加速度)的矢量端点构成的图形, 一致 ;已知某构件上两点的速度,可方便求出第三点的速度。
(7)由于牵连构件的运动为转动,使得相对速度的方向不断变化。
3-31613361331P P P P=ωω 3-4 略3-5(1)040m /s C v .=(2)0.36m /s E v = (3) ϕ=26°、227° 3-6~3-9 略3-10(a )、(b )存在, (c )、(d )不存在。
3-11~3-16 略 3-17第四章 平面机构的力分析、摩擦及机械的效率4-14-24-3 )sin )((211212l l ll l l f f V +++=θ4-4 F =1430N 4-5~4-9略232/95.110s m v -==ωB v JI v4-10 )2()2(ρρη+-=b a a b4-11 5667.0 31.110==≤ηϕα 4-12 8462.0=η 4-13 605.0=η4-14 2185.0=η N Q 3.10297= 4-15 7848.0113.637==ηN F4-16 KW P 026.88224.0==η 4-17 KW P 53.96296.0==η4-18 ϕα2≤ 4-19 F =140N4-20 ϕαϕ-<<O 90第五章 平面连杆机构及其设计5-15-2(1) 摇杆(尺寸),曲柄(曲柄与连杆组成的转动副尺寸),机架(连杆作为机架) (2) 有,AB ,曲柄摇杆机构 ;AB ;CD 为机架(3) 曲柄 与 机架 (4) 曲柄摇杆机构、曲柄滑块机构、摆动导杆机构 (5) 曲柄摇杆机构、摆动导杆机构;曲柄滑块机构 (6) 等速,为主动件 (7) 7 (8) 往复 ,且 连杆与从动件 (9) 选取新机架、刚化搬移、作垂直平分线;包含待求铰链 且 位置已知 (10) 9 ; 5 5-3 70 < l AD <670 5-4~5-18 略5-19 l AC =150mm l CD =3000mm h =279.9 mm5-20 a =63.923mm b =101.197mm c =101.094mm d =80mm第六章 凸轮机构及其设计6-16-26-3(1)等加速等减速、余弦加速度(2)刚性、柔性(3)理论廓线(4)互为法向等距曲线(5)增大基圆半径、采用正偏置 (6)增大基圆半径、减小滚子半径(7)提高凸轮机构运动的轻巧性和效率、避免加速度过大造成冲击 6-4略 6-56-6 ~ 6-13略 6-146-15 6-16略第七章 齿轮机构及其设计7-1︒==6858.70822rad πδ︒='=︒≡====1803064.3432.1700min max 0δδαααmmh mm r 6332.343776.51240-='='-=δy x6395.185947.4060='-='=δy x7-27-3(1) (2)7-4 z = 41.45 7-5略7-6 (1) (2) 7-7 7-8略 7-9 7-10 7-11略7-12 (1) (2) (3) 7-13(1) (2) (3) 7-14略7-15 7-16略7-17 共有7种方案 7-18~7-19 略 7-20302021==z z mmr mms mm s a b a 0923.1052816.178173.6===634.1=εαmmj mmc mma t 77.269.494.15523.23='='='=α'smm v mm L /490==刀294-==x z 8.04.88==x z 0399.02='x 9899.482234117229.1142444153.44='''=='==K K Kρθα mmr K K 3433.702444='= α8879.22α='mm r mm r 2.618.4021='='mmd z mmm 120304===5.0-=x mms 827.4=058.1-=x7-21 7-22 略7-23正传动, 7-24~7-25 略 7-26(1)正传动(2) 7-27 略 7-287-29 略第八章 齿轮系及其设计8—18—28—3(1)从动轮齿数的连乘积除以主动轮齿数的连乘积、数外啮合次数或用画箭头的 (2)用画箭头的(3)有无使行星轮产生复合运动的转臂(系杆) (4)相对运动原理(5)一个或几个中心轮、一个转臂(系杆)、一个或几个行星轮(6)转化轮系中A 轮到B 轮的传动比、周转轮系中A 轮到B 轮的传动比、AB i 可以通过H ABi 求解(7)找出周转轮系中的行星轮、转臂及其中心轮 (8)传动比条件、同心条件、均布装配条件、邻接条件(9)传动比很大结构紧凑效率较低、要求传动比大的传递运动的场合、传动比较小效率较高、传递动力和要求效率较高的场合mm a 5892.90='mm r a 93.581=13.7291β=116.36v z = 2.6934γε=2222(1)175(2)185163(3) 5.7106(4)112.5a f d mm d mm d mma mmβ=====(10)差动轮系 8-4 8-58-6 8-7 8-8 8-98-10 8-11 8-12(a ) (b ) 8-13(1) (2) 8-14 z 2≈68 8-15 8-168-17 (1) (2) 8-188-198-20 m in /28.154r n B -=8-21只行星轮满足邻接条件件,只行星轮不满足邻接条34144803mml z H ==8-22 162/108/5463/42/2136/24/12321===z z z第九章 其他常用机构9-1 9-2 9-3 9-4mms 075.0=232==n k mml B 3=8.658=ϕm in/84r n =mm R 975.23=32143211''-=z z z z z z i H m in/3r n H =NF 64.308=5.141-=i 072.016-=i m in /600r n H -=m in/385.15r n H =31=H i 8.11=H i 0=H n min /667.653197min /2min /340042r n r n r n A ≈===m in /47.26r n c =m in/1350r n c -=min /6349.063407r n ≈=4286.0731-≈-=H i .1533.433=i第十章 机械的运转及其速度波动的调节10-110-210-3 2 05.050kgm J Nm M e er =-=10-4222212334111()()e e z z J J J J m m e M M Qe z z =++++=- 10-520.14.20J kg m M Nm ==-10-6 2334.()cos cos ABr G l h J M F G gφφ==- 10-7332.18221857e e J kgm MNm ==10-811100/50/rad s rad s αω==10-9maxmax minmin 30.048140.962/2 39.038/0,2rad s rad s δωφπωφπ=====10-102280.4730.388F FJ kgm J kgm '== 10-1102max max 623.1/min104.1654 2.11329F n r J kgm φ===10-12max max minmin 0.06381031.916/min 968.08/mine bn r nr δφφφφ===== 10-1326maxmin 302F eb f Nm J kgm ωφωφ==→→第十一章 机械的平衡11-111-211-3 2.109252.66o b b r cm θ==11-412.31068.5273bA bB m kg m kg==11-511-611-711-8)(2)(2 , )b )( )( , )a ⅡⅡ ⅠⅠ ⅡⅡ ⅠⅠ 上下动不平衡静平衡上下动不平衡静平衡mrr m mr r m mr r m mr r m b b b b b b b b ====oⅡb Ⅱo b Ⅰgm W W W 90 84.08419 gm 0628.1Ⅱb 3Ⅰb ==='==θθ0B 0A 120 285.0 8584.260 285.0 8584.2======bA bB bA bA kg m kgmm W kg m kgmm W θθ0Ⅱb 0Ⅰb 147 725.0 290316 65.1 660======b Ⅱb Ⅱb Ⅰb Ⅰkg m kgmm W kg m kgmm W θθ。
机械原理课后习题答案

《机械原理》课后习题答案第2章(P27)2-2 计算下列机构的自由度,如遇有复合铰链、局部自由度、虚约束等加以说明。
(a)n=3,p l=3 F=3*3-2*3=3(b)n=3,p l=3,p h=2 F=3*3-2*3-2=1 (B处有局部自由度)(c)n=7,p l=10 F=3*7-2*10=1(d)n=4,p l=4,p h=2 F=3*4-2*4-2=2 (A处有复合铰链)(e)n=3,p l=4 F=3*3-2*4=1 (A或D处有虚约束)(f)n=3,p l=4 F=3*3-2*4=1 (构件4和转动副E、F引入虚约束)(g)n=3,p l=5 F=(3-1)*3-(2-1)*5=1 (有公共约束)(h)n=9,p l=12,p h=2 F=3*9-2*12-2=1 (M处有复合铰链,C处有局部自由度)2-3 计算下列机构的自由度,拆杆组并确定机构的级别。
(a)n=5,p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组,故此机构为Ⅱ级机构。
(b)n=5,p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
(c)n=5,p l=7 F=3*5-2*7=1拆分时只须将主动件拆下,其它构件组成一个Ⅲ级杆组,故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定,并提出具有确定运动的修改方案。
(a)n=3,p l=4,p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示:(b)n=4,p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示:或第3章(P42)3-2 下列机构中,已知机构尺寸,求在图示位置时的所有瞬心。
(a)(b)(c)(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中,三个圆互作纯滚,试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章(P80)5-2 一铰接四杆机构(2)机构的两极限位置如下图:(3)传动角最大和最小位置如下图:5-3题略解:若使其成为曲柄摇杆机构,则最短杆必为连架杆,即a 为最短杆。
机械原理_课后习题答案免费(全面)高教版 西北工大

2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向: 大小: ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] (2)速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] (3)加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =
机械原理第3章作业解析

也可直接用sin(ψ/2)=AC/l4得出结果。
3-4 如下图,设计一脚踏轧棉机的曲柄摇杆机构。要求踏
板CD在水平位置上下各摆10°,且lCD=500mm, lAD=1000mm,试用图解法求曲柄AB和连杆BC的长度。
解:根据已知条件画出A、D、C、C1、C2。 画出两个极限位置AC1、AC2。 由图可知, AC1=BC-AB,AC2=BC+AB, 即:AB=(AC2-AC1)/2 可由图上直接量取AC1、AC2长度 后按上式算出连杆和曲柄的长度。
以D点为圆心,DC1为半径作圆弧,与前述直线交于C2。 参照题5-2,列式计算或作图得出曲柄和摇杆的长度。
设计结果:lAB=38.65mm,lBC=98.2mm。 注意:若C1D顺时针画弧,所得交点C2不可用。
θ 180 k 1 180 1.5 1 36
k1
1.5 1
任取D点,作水平线DA,使lDA=80, 过D点,作直线DC1,长 度为lDC=75,位置为与 DA成45°。 过AC1两点的直线为连杆 与曲柄共线的位置之一。 过A点,作一直线与AC1成 θ=36°,此直线为连杆与曲柄 共线的位置之二。
5、工程上常用 行程速比系数K 表示机构的急回
性质,其大小可由计算式 K (180) /(180) 求
出。
6、曲柄摇杆机构中,最小传动角出现的位置是 曲柄与机架两次共线的位置 。
7、曲柄摇杆机构可演化成偏心轮机构,其演化 途径为 扩大转动副 。
二、判断题
1、曲柄摇杆机构的行程速比系数K不可能等于1。
第3章 连 杆 机 构
一、填空题 1、在四杆机构中,取与 最短杆 相对的杆为机 架,则可得到双摇杆机构。
西北工业大学机械原理课后答案第3章

O OO OP 2P 3F 23(P 24Pl 3(P 34)(a)(b)Pl 3Pl 6A 1题3-6在图a 所示的四杆机构中,第三章平面机构的运动分析题3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P j 直接标注在图上)解:题3-4在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3的传动比w1/w3.C 2P 12P 23St -解:1)计算此机构所有瞬心的数目K N (N1)2152) 为求传动比 < 3需求出如下三个瞬心 R 6、P 36、P 13如图3-2所示。
; 1 巳6只33) 传动比 仁3计算公式为: —3P 16P 13I AB =60mm , l cD =90mm , l AD =|Bc =120mm , w 2=10rad/s ,试用瞬心P134 C 4L CP 12AM B3P iP 34CBMF 24F 34P ?4(d)Pl 4法求:V B3I AB2IAB lBPI32.56rad sV ClCR 3 3 0.4m s量得 1 26.42 226.6P 3434B P 233 22A ,D- i Pl4P 12 1(a)P 131) 当0 =165。
时,点C 的速度Vc ;2) 当$ =165。
时,构件3的BC 线上速度最小的一点 E 的位置及速度的大小; 3) 当Vc=O 时,0角之值(有两个解)解:1)以选定比例尺,绘制机构运动简图。
(图3-3 )2)求V c ,定出瞬心P 13的位置。
如图 3-3 (a )3)定出构件3的BC 线上速度最小的点 E 的位置。
因为BC 线上速度最小的点必与 P 13点的距离最近,所以过 P 13点引BC 线延长线的垂线交于 E 点。
如图3-3 (a )v E1ER 3 3 0.375ms4)当V C 0时,P 13与C 点重合,即AB 与BC 共线有两个位置。
作出 V C 0的两个位置。
题3-12在图示的各机构中,设已知各构件的尺寸、原动件 1以等角速度3 1顺时针方向转动。
机械原理第三章作业答案
P13
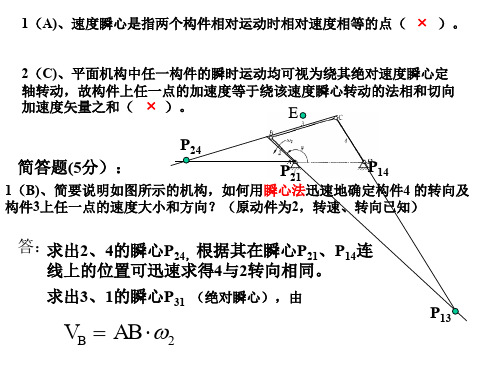
2(C)、既然机构中各构件与其速度图和加速度图之间均存在影像关系, 因此整个机构与其速度和加速度图之间也存在影像关系,对吗?
答:不对
速度、加速度影像原理只适用于同一构件上的点求速度 和加速度,不适用于整个机构。
3(C)、当用速度瞬心法和用速度影像法求同一构件(如图所示机构连杆3 上)上任意一点P的速度时它们的求解条件有何不同?各有何特点?
B
3(C)、图示机构中,已知 lAC lBC lCD lCE lDF lEF 20mm ,
滑块1及2分别以匀速且 v1 v2 0.002 m / s 做反向移动,试求机构在
位置时的速度大小之比 vF v1
解:对C点进行速度分析 建立方程为
。
1 v1 A
7
3 30°
C
D
6
F
4
① VC VA VCA VB VCB
B
2
v2
5
E
b
p
60
a°
d c
e
vF f v1
pf
3 pc
3
pa pa
3
pc 3 pa
pf 3pc 3 3 pa
3-9、试判断在图示的两机构所在位置中,B点是否都存在 哥氏加速度?。并思考下列问题:
1)、在什么条件下才存在哥氏加速度?
答:用速度瞬心法求构件(如3)上任意
P
点(如P)速度时需找出相关的瞬心;
而用速度影像法求点速度时,需先在
速度多边形中求出同一构件(如3)
上任意两点(如B、C两点)的速度。
瞬心法较简便,但有时瞬心不怎好求;影像法只对同一 构件上的点适用,不适用于整个机构。
机械原理第3章作业题及答案
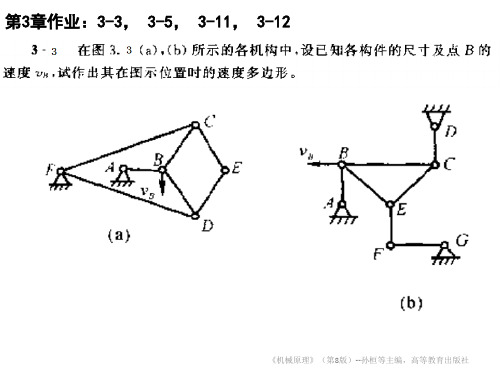
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
l 0.001m/mm
2 3
v 0.005m/s/mm
D
1
B p(a, c3 ) A
4
c2
1
p' (a' , c3 ' )
第3章作业:3-3, 3-5, 3-11, 3-12
《机械原理》(第8版)--孙桓等主编,高等教育出版社
解: (b)依次列出以下机构速度 分析的 作出速度多边形如图所 示。 vC vB vCB
大小 ? 方向 ⊥FC √ √ ? ⊥BC
矢量分析方程,并选取 合适的比例尺
vD
vB
vC
大小 ? 方向 ⊥CD
vB vCB
√ √ ? ⊥CB
可得vC vB ,于是,可知: 构件3在该瞬间角速度为零, 也知:vE vC vB vF vE vFE
大小 ? 方向 ⊥FG √ √ ? ⊥FG
《机械原理》(第8版)--孙桓等主编,高等教育出版社
4
c2
1
p' (a' , c3 ' )
k'
2 a 0.05m/s /mm
C(C2 , C3 )
E
e
d
c2 '
e' d' b'
b
3)运用速度影像原理,可求的D点和E的速度
n2 '
BD 50 BD bd bc 2 49.1 19.94 mm , bd BC 123 .1 BC bc2 vD v pd 0.005 45.2 0.226m / s, 方向是由p d DE 40 DE de de bd 19.94 16 mm , BD 50 BD bd vE v pe 0.005 34.5 0.173m / s, 方向是由p e
高等教育:机械原理第三章作业答案

。
1 v1 A
7
3 30°
C
D
6
F
① VC VA VCA VB VCB
B
2
4
v2
5
E
b
p
60
a°
d c
e
vF f v1
pf
3 pc
3
pa pa
3
pc 3 pa
pf 3pc 3 3 pa
3-9、试判断在图示的两机构所在位置中,B点是否都存在 哥氏加速度?。并思考下列问题:
2 Vr 0
1 2
ω1
b
(2) (a)图
Ⅰ B(B1, B2, B3)
Ⅱ B(B1, B2, B3)
Ⅲ ⅠV
B(B1, B2, B3)
B(B1, B2, B3)
VB3B2 = VB2B3=0
ω2 = ω 3=0 b
因ω2总为零,所以不 仅机构在图示位置无
哥氏加速度,且机构在
任意位置处都无哥氏
加速度矢量之和( )。EP24ຫໍສະໝຸດ 简答题(5分):P21
P14
1(B)、简要说明如图所示的机构,如何用瞬心法迅速地确定构件4 的转向及
构件3上任一点的速度大小和方向?(原动件为2,转速、转向已知)
答:求出2、4的瞬心P24,根据其在瞬心P21、P14连 线上的位置可迅速求得4与2转向相同。 求出3、1的瞬心P31 (绝对瞬心),由 P13
1)、在什么条件下才存在哥氏加速度?
2)、根据上一条,请检查一下所有哥氏加速度为零的位
置是否已全部找出?
3)、在图a中,a
k B
2
B
机械原理杨家军答案(第三章)
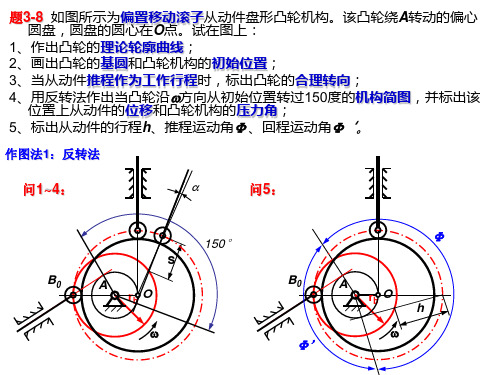
题3-12 试用解析法并编程求解滚子移动从动件盘形凸轮机构的理论 轮廓曲线与实际轮廓曲线的坐标值,计算间隔取10O,并校核此凸轮机 构的压力角。已知rb=45mm,rr=10mm,从动件偏在凸轮中心之右, 偏距e=20mm,逆时针等到速转动,当凸轮转过=90o,从动件以正 统加速运动规律上升h=20mm,凸轮再转过=90o,从动件以余弦加 速度运动规律下降回原处,其余s=180o,从动件静止不动。
19.3749
14.0190 -8.2372 -2.2051 3.8940 9.8748
270°
280° 290° 300° 310°
0.0000
0.0000 0.0000 0.0000 0.0000
40.3113
36.2259 31.0398 24.9106 18.0245
20.0000
26.6961 32.5811 37.4762 41.2325
31.3532
28.1757 24.1421 19.3749 14.0190
15.5556
20.7637 25.3409 29.1481 32.0697
考查要点
• • • • • • • • • • • • • • • • • • 1.机械系统与机械组成的基本概念 2.平面机构具有确定运动的条件 3.平面四杆机构设计中的一些共性问题,平面连杆机构的设计 4.从动件常用运动规律的特点,盘形凸轮机构基本尺寸的确定、盘形凸轮轮廓曲线的设 计方法 5. 渐开线的特点,渐开线直齿圆柱齿轮机构和斜齿圆柱齿轮机构的基本参数及尺寸计 算,渐开线直齿圆柱齿轮机构的啮合传动、直齿锥齿轮机构的特点,变位齿轮传动 6.周转齿轮系及复合齿轮系传动比计算 7.间歇运动机构的基本概念,其他机构的特点与应用 8.机构平衡的基本方法与机构的动力学设计 9. 机构的创新设计原理与方法 10. 机械设计中的强度问题,载荷及应力的分类 11.齿轮传动的失效形式,直齿圆柱齿轮传动、斜齿圆柱齿轮传动、直齿锥齿轮传动的 受力分析及计算载荷,齿轮传动的强度计算 12. 蜗杆传动的受力分析及强度计算 13. 挠性传动的特点及设计方法 14. 轴的结构设计及强度计算方法 15 非液体摩擦滑动轴承及液体摩擦滑动轴承设计中的一些基本方法和概念 16. 滚动轴承类型、选择、受力分析、寿命计算及支承部件的组合设计 17. 联轴器、离合器、键联接、弹簧的基本特点 18. 螺纹联接的类型及特点,螺纹联接的强度计算,螺栓组联接的受力分析
机械原理课后答案第3章
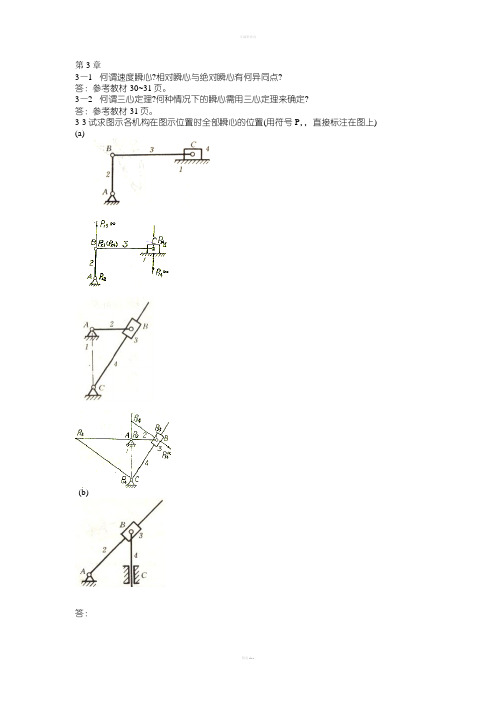
第3章3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?答:参考教材30~31页。
3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定?答:参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上) (a)(b)答:答:(10分)(d)(10分)3-4标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3。
答:1)瞬新的数目:K=N(N-1)/2=6(6-1)/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置3)ω1/ω3= P 36P 13/P 16P 13=DK/AK由构件1、3在K 点的速度方向相同,可知ω3与ω1同向。
3-6在图示的四杆机构中,L AB =60mm ,L CD =90mm,L AD =L BC =120mm, ω2=10rad/s,试用瞬心法求:1)当φ=165°时,点的速度vc ;2)当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小;3)当V C =0时,φ角之值(有两个解)。
解:1)以选定的比例尺μ机械运动简图(图b )2)求vc 定出瞬心p12的位置(图b ) 因p 13为构件3的绝对瞬心,则有ω3=v B /lBp 13=ω2l AB /μl .Bp 13=10×0.06/0.003×78=2.56(rad/s)v c =μc p 13ω3=0.003×52×2.56=0.4(m/s)3)定出构件3的BC 线上速度最小的点E 的位置,因BC 线上速度最小的点必与p13点的距离最近,故丛p13引BC 线的垂线交于点E ,由图可得(2分)(3分)v E=μl.p13Eω3=0.003×46.5×2.56=0.357(m/s)4)定出vc=0时机构的两个位置(图c)量出φ1=26.4°φ2=226.6°3-8机构中,设已知构件的尺寸及点B的速度v B(即速度矢量pb),试作出各机构在图示位置时的速度多边形。
机械原理课后答案3章
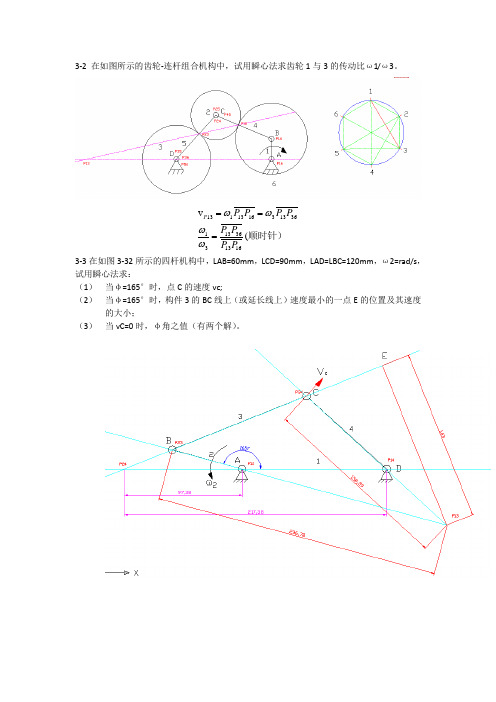
3-2 在如图所示的齿轮-连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω3。
顺时针)(v 1613361331361331613113P P P PP P P P P ===ωωωω3-3在如图3-32所示的四杆机构中,LAB=60mm ,LCD=90mm ,LAD=LBC=120mm ,ω2=rad/s ,试用瞬心法求:(1) 当φ=165°时,点C 的速度vc;(2) 当φ=165°时,构件3的BC 线上(或延长线上)速度最小的一点E 的位置及其速度的大小;(3) 当vC=0时,φ角之值(有两个解)。
sm EP P P v P P v s m v s rad P P P P P P P P E C C CD C P /36.0143.055.2v (rad/s 55.2158.0403.0/403.009.048.4(/48.438.21738.9710v 133133431334341424122424142441224224=⨯=======⨯=⨯==⨯====ωωωωωωωω顺时针)顺时针)3-4在如图3-33所示的凸轮机构中,已知r=50mm ,LOA=30mm ,LAC=90mm ,φ1=90°,凸轮1以角速度ω1=10rad/s 逆时针转动。
试用瞬心法求从动件的角速度ω2。
顺时针)(/79.286.12486.3410v 2312131212231221312112s rad P P P P P P P P P =⨯====ωωωω 3-5在如图3-34所示的各机构中,已知各构件的尺寸及B 点的速度vB ,试作出其如图3-34所示位置时的速度多边形。
3-6在如图3-35所示的各机构中,已知各构件的尺寸,原动件1以等角速度ω1顺时针方向转动,试以图解法求机构在如图3-35所示位置时构件3上C 点的速度及角速度。
3-8A BCDEbk ec3。
机械原理课后答案
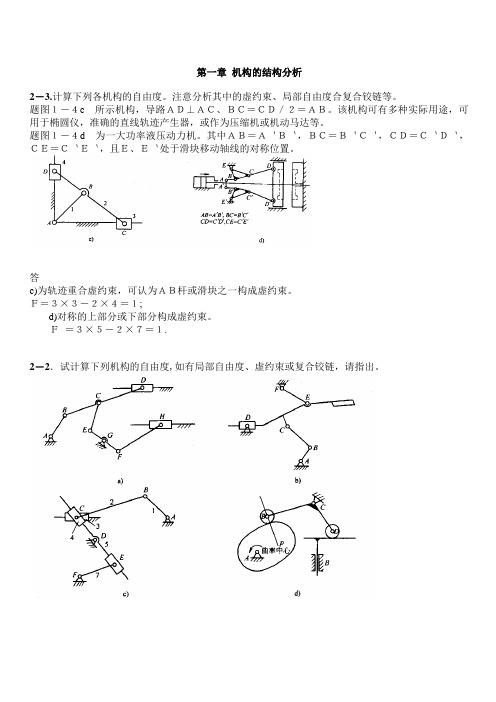
第一章机构的结构分析2-3.计算下列各机构的自由度。
注意分析其中的虚约束、局部自由度合复合铰链等。
题图1-4c所示机构,导路AD⊥AC、BC=CD/2=AB。
该机构可有多种实际用途,可用于椭圆仪,准确的直线轨迹产生器,或作为压缩机或机动马达等。
题图1-4d为一大功率液压动力机。
其中AB=A`B`,BC=B`C`,CD=C`D`,CE=C`E`,且E、E`处于滑块移动轴线的对称位置。
答c)为轨迹重合虚约束,可认为AB杆或滑块之一构成虚约束。
F=3×3-2×4=1;d)对称的上部分或下部分构成虚约束。
F=3×5-2×7=1.2-2.试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
e)答案:a)F=3×7-2×10=1.注意其中的C、G、D、H点并不是复合铰链。
b)F=3×5-2×7=1C)F=3×7-2×10=1其中C点为复合铰链,分别由2、3、4构件在C点构成复合铰。
d)F=3×3-2×3-2=1或者F=3×5-2×5-2-2=1其中B、D处的滚子具有局部自由度。
(e) F=3×9-2×12-1-1=1或者:F=3×8-2×11-1=1(注意:BCD组成的三角形为一个构件)其中B点为局部自由度2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
答:C点为局部自由度,E、F其中一点为虚约束。
F= 3×5-2×6-1-1=1或者:F=3×4-2×5-1=1第三章平面连杆机构及其分析与设计3-1.试求题图所示各机构在图示位置时全部瞬心的位置.答案:瞬心P 12在A 点 瞬心P 23、 P 24均在B 点 瞬心P 34在C 点 P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点 穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中,试用瞬心法求齿轮1与齿轮3的传动比31/ωω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
ω1
b
图 (2) (a)图 ) Ⅰ
B(B1, B2, B3)
Ⅲ
Ⅰ V
Ⅱ
B(B1, B2, B3) B(B1, B2, B3) B(B1, B2, B3)
VB3B2 = VB2B3=0
ω2 = ω 3=0 b
总为零, 因ω2总为零,所以不 仅机构在图示位置无 哥氏加速度,且机构在 哥氏加速度 且机构在 任意位置处都无哥氏 加速度。 加速度。
vF 位置时的速度大小之比 v1
解:对C点进行速度分析 点进行速度分析 建立方程为
。 A
1
v1
3 30° ° 4
D
6
C
5
7
F E
①
VC = VA + VCA = VB + VCB
b d c
60 °
B
2
v2
p a
vF pf 3 pc ∴ = =3 3 = f v1 pa pa
pc = 3 pa pf = 3 pc = 3 3 pa
P21
P14
答: 求出2、 的瞬心 ,根据其在瞬心P 的瞬心P 求出 、4的瞬心 24,根据其在瞬心 21、P14连 线上的位置可迅速求得4与 转向相同 转向相同。 线上的位置可迅速求得 与2转向相同。 求出3、 的瞬心 的瞬心P 绝对瞬心), ),由 求出 、1的瞬心 31 (绝对瞬心),由
VB = AB ⋅ ω2
∝
P14
∝ P34
P13
P14
P23 P24 P12
P34
(f) )
2(B)、在如图所示的机构中,已知 1 =45° ω1=100rad/s,方向为逆时针 ( )、在如图所示的机构中,已知Φ )、在如图所示的机构中 ° 方向为逆时针 方向,求构件1与构件 在该位置的速度瞬心P 以及构件3的速度 与构件3在该位置的速度瞬心 的速度v 方向,求构件 与构件 在该位置的速度瞬心 13以及构件 的速度 3.
P24 简答题(5分 简答题 分):
1(B)、简要说明如图所示的机构,如何用瞬心法迅速地确定构件 的转向及 ( 、简要说明如图所示的机构,如何用瞬心法迅速地确定构件4 瞬心法迅速地确定构件 构件3上任一点的速度大小和方向?(原动件为 转速、转向已知) 上任一点的速度大小和方向?(原动件为2, 构件 上任一点的速度大小和方向?(原动件为 ,转速、转向已知)
b
P12 B 2 P13 P14 A 1
P23
C
φ1
γ
3
4 P23
V3 = ω1×P14 P12
B
3(C)、图示机构中,已知 l AC = lBC = lCD = lCE = l DF = l EF = 20mm , ( )、图示机构中, )、图示机构中 滑块1及2分别以匀速且 v1 = v2 = 0.002m / s 做反向移动,试求机构在 滑块 及 分别以匀速且 做反向移动,
填空(每题 分 填空 每题2分): 每题
5(A)、当两构件组成转动副时,其相对运动瞬心在 转动副中心 处,组成 移动副时,其瞬心在 垂直于相对运动轨迹线的无穷远处 处 ;组成兼有 滑动和滚动的高副时,其瞬心在 过两高副元素接触点的公法线上 处 。 6(A)、当两平面运动构件的相对运动为 移 动,牵连运动为 转 动时, 两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为 2ω1 × vr 21 , 方向与 Vr21 沿 ω1的转向转 的方向相同。 90° °
都是指两相对运动构件 绝对速度相等的重合点 1(A)、相对瞬心与绝对瞬心的相同之处是 ,不同之处 为 该点的绝对速度不都为零 2(A)、速度瞬心可以定义为互相做平面相对运动的两构件上 相对速度 为零 或 绝对速度 相等的点。 N2-3N+2 3(A)、在由N个构件构成的机构中,有 2 个相对瞬心,有 N-1 个绝 对瞬心. 4(A)、当两构件不直接构成运动副时,瞬心位置用 三心定理 确定。
P
瞬心法较简便,但有时瞬心不怎好求; 瞬心法较简便,但有时瞬心不怎好求;影像法只对同一 构件上的点适用,不适用于整个机构。 构件上的点适用,不适用于整个机构。
计算、分析、作图题(每题13分)
1(A)、试求图示机构在图示位置时全部瞬心 ( )、 )、试求图示机构在图示位置时全部瞬心
P13 P23 P24 P12
k aB 2 B 3 = 2ω2VB 2 B 3 ,对吗?为什么? 3)、在图 中, 对吗?为什么? 、在图a中
2
A1
3
B(BBB,2,B3) 1,2
B
B C
(a) (b)
B1
)、当 中之一等于零时, 点的哥氏加 解(1)、当 ω 、Vr 中之一等于零时,B点的哥氏加 速度 )、 为零
2ω × Vr = 0
判断(每题 分 判断 每题2分): 每题
1(A)、速度瞬心是指两个构件相对运动时相对速度相等的点( × )。 ( 、速度瞬心是指两个构件相对运动时相对速度相等的点( 2(C)、平面机构中任一构件的瞬时运动均可视为绕其绝对速度瞬心定 ( 、 轴转动, 轴转动,故构件上任一点的加速度等于绕该速度瞬心转动的法相和切向 加速度矢量之和( 加速度矢量之和( × )。 E
答: 用速度瞬心法求构件( 用速度瞬心法求构件(如3)上任意 ) 需找出相关的瞬心 点(如P)速度时需找出相关的瞬心; )速度时需找出相关的瞬心; 而用速度影像法求点速度时, 而用速度影像法求点速度时,需先在 速度多边形中求出同一构件( 求出同一构件 速度多边形中求出同一构件(如3) ) 上任意两点(如B、C两点)的速度。 上任意两点( 、 两点)的速度。 两点
e
3-9、试判断在图示的两机构所在位置中,B点是否都存在 、试判断在图示的两机构所在位置中, 点是否都存在 哥氏加速度?。并思考下列问题: ?。并思考下列问题 哥氏加速度?。并思考下列问题: 1)、在什么条件下才存在哥氏加速度? )、在什么条件下才存在哥氏加速度? )、在什么条件下才存在哥氏加速度 2)、根据上一条,请检查一下所有哥氏加速度为零的位 )、根据上一条, )、根据上一条 置是否已全部找出? 置是否已全部找出?
P13
VB ω3 = BP31
E P24 P21 P14
∴VE = ω3 ⋅ EP31
P13
2(C)、既然机构中各构件与其速度图和加速度图之间均存在影像关系, ( )、既然机构中各构件与其速度图和加速度图之间均存在影像关系, )、既然机构中各构件与其速度图和加速度图之间均存在影像关系 因此整个机构与其速度和加速度图之间也存在影像关系,对吗? 因此整个机构与其速度和加速度图之间也存在影像关系,对吗?
或 B2,
VB3=VB2 + VB3B2 VB2=VB3 + VB2B3
p b3 b2
ω=ω
3
2
r aB3 = aB2 + ak + aB3B2 B3B2 k aB3B2 = 2ω2×VB3B2 r aB2 = aB3 + ak + aB2B3 B2B3 k aB2B3 = 2ω3×VB2B3
哥氏加速度不 为零
k a B 2 B 3 = 2ω 2VB 2 B 3 ,但从概念 )、在图示位置 ( 3)、在图示位置,从数值上说 )、在图示位置,
上说 a B 2 B 3
k
= 2ω 2VB 2 B 3 是错误的。 是错误的。
b
P24 P21 P14
ω2 ⋅ P24 P21 = ω4 ⋅ P24 P 14
P24 P21 ω4 = ω2 P24 P 14
答:不对 速度、加速度影像原理只适用于同一构件上的点求速度 和加速度,不适用于整影像法求同一构件(如图所示机构连杆 ( )、当用速度瞬心法和用速度影像法求同一构件(如图所示机构连杆3 )、当用速度瞬心法和用速度影像法求同一构件 上任意一点P的速度时它们的求解条件有何不同 各有何特点? 的速度时它们的求解条件有何不同? 上)上任意一点 的速度时它们的求解条件有何不同?各有何特点?
