机械原理课后习题答案(朱理)
机械原理 课后习题答案

⎛ ⎜ ⎝
m / s2 mm
⎞ ⎟ ⎠
作加速度图
C
2
3
D
B
p(d) 4
(c3)
b2 (b1) (b3)
题3-8 c) 解(续2)
[解]
(3)加速度分析 aB 2 (= aB1) → aB3 → aC 3
1) 求aB2
A 1 ω1
2) 求aB3
aB3
=
an B3D
+
at B3D
=
aB
2
+
ak B3B2
得d点
p(c3)
E
vD = μv pd = 0.005 × 44.6 = 0.223 (m / s)
作 de ⊥ bc2
并使
de = DE = lDE = 40 bd BD lBD 50
得e点
vE = μv pe = 0.005 × 32.0 = 0.16 (m / s)
3) 求ω2
ω2
=
vC 2B lBC
p' = 2p'l + p'h − 3n' = 2 × 3 + 0 − 3× 2 = 0
p' = 2p'l + p'h − 3n' = 2 ×10 + 0 − 3×6 = 2
F = 3n − (2pl + ph − p') − F' = 3 × 11 − (2 × 17 + 0 − 2) − 0 =1
P24
B P23
3
2A
P12
1
4
D
P14
vE
=
vB
P13 E P13B
机械原理课后习题答案(朱理)

机械原理作业(部分答案)第一章结构分析作业1.2 解:F = 3n-2P L-P H = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2P L-P H = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s r a d l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ? ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mme 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
机械原理_朱龙英主编_习题解答(全)

《机械原理》习题解答机械工程学院第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征?机器通常由哪三部分组成?各部分的功能是什么?2)、机器与机构有什么异同点?3)、什么叫构件?什么叫零件?什么叫通用零件和专用零件?试各举二个实例。
4)、设计机器时应满足哪些基本要求?试选取一台机器,分析设计时应满足的基本要求。
2、填空题1)、机器或机构,都是由组合而成的。
2)、机器或机构的之间,具有确定的相对运动。
3)、机器可以用来人的劳动,完成有用的。
4)、组成机构、并且相互间能作的物体,叫做构件。
5)、从运动的角度看,机构的主要功用在于运动或运动的形式。
6)、构件是机器的单元。
零件是机器的单元。
7)、机器的工作部分须完成机器的动作,且处于整个传动的。
8)、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9)、构件之间具有的相对运动,并能完成的机械功或实现能量转换的的组合,叫机器。
3、判断题1)、构件都是可动的。
()2)、机器的传动部分都是机构。
()3)、互相之间能作相对运动的物件是构件。
()4)、只从运动方面讲,机构是具有确定相对运动构件的组合。
()5)、机构的作用,只是传递或转换运动的形式。
()6)、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()7)、机构中的主动件和被动件,都是构件。
()2 填空题答案1)、构件2)、构件3)、代替机械功4)、相对运动5)、传递转换6)、运动制造7)、预定终端8)、中间环节9)、确定有用构件3判断题答案1)、√2)、√3)、√4)、√5)、×6)、√7)、√第二章机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
解:a)平面高副b)空间低副c)平面高副2-8将图2-27中机构的结构图绘制成机构运动简图,标出原动件和机架,并计算其自由度。
解:b)n=3,P=4 ,H P=0,F=3×3-2×4=1Lc) n=3,P=4 ,PH=0,F=3×3-2×4=1L2-9试判断图2-28中所示各“机构”能否成为机构,并说明理由。
机械原理课后习题答案

机械原理课后习题答案1. 两个质量分别为m1和m2的物体,它们分别靠在光滑水平面上的两个弹簧上,两个弹簧的弹性系数分别为k1和k2。
求当两个物体分别受到的外力分别为F1和F2时,两个物体的加速度分别是多少?答,根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
根据这个公式,可以得出两个物体的加速度分别为a1=F1/m1,a2=F2/m2。
2. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,物体的加速度是多少?答,同样根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
根据这个公式,可以得出物体的加速度为a=F/m。
3. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的位移是多少?答,根据胡克定律,弹簧的位移与受到的外力成正比,即F=kx,其中x为弹簧的位移。
解出x=F/k,即弹簧的位移与外力成反比。
4. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的振动周期是多少?答,根据弹簧的振动周期公式T=2π√(m/k),可以得出弹簧的振动周期与物体的质量和弹簧的弹性系数有关,与受到的外力无关。
5. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的振幅是多少?答,根据弹簧振动的公式x=Acos(ωt+φ),可以得出弹簧的振幅与受到的外力无关,只与弹簧的弹性系数和物体的质量有关。
求当物体受到外力F时,弹簧的振动频率是多少?答,根据弹簧振动的公式f=1/2π√(k/m),可以得出弹簧的振动频率与受到的外力无关,只与弹簧的弹性系数和物体的质量有关。
7. 一个半径为r的圆盘,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当圆盘受到外力F时,圆盘的加速度是多少?答,根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
朱理版--机械原理课后作业全部答案.

习题解答
2.1 试求图示各机构在图示位置时全部瞬心。
2.2 在图示机构中,已知各构件尺寸为lAB =180mm , lBC =180mm , lBD =180mm , lCD =180mm , lAE =120mm , φ=30º, 构件AB上点E的速度为 vE =150 mm /s ,试求该位置时C、D 两点的速度及连杆2的角速度ω2 。
a5 aD4 a pd4 0.2214.94 3.287rad / s2
aC aB aCnB aCt B
大小
? ω12lAB ω22lBC ?
方向 水平 B→A C→B ⊥CB
aB 12 lAB 102 0.05 5m / s2
a
5/
作业
作业
1.2 1.3(高副低代,拆杆组) 1.4 (a) (b) (c) (d) 1.5
a) F=3x4-2x5-1=1 b) F=3x5-2x6-2=1
F=3x7-2x8-2-2=1 c) F=3x9-2x13=1
d) F=3x6-2x8-1=1 e) F=3x6-2x8=2
作业 2-1 2-2 2-3 2-4
本章考点
①.绘制平面连杆机构运动简图,并确定该机构类型;
②.根据机构中给定的各杆长度(或尺寸范围)来确定属于何种 铰链四杆机构;
③.根据机构中给定的各杆长度判定机构有无急回特性和死点 位置,确定行程速比系数K和最小传动角;
④.已知活动铰链中心的位置设计四杆机构,以实现二个(或 三个)预定的连杆位置;
解:C点速度vC 0 ( P24即C点为绝对瞬心)
vD vp13 1lAp13
vE lAE
l Ap13
机械原理课后习题答案

第四章课后习题4—12图示为一曲柄滑块机构的三个位置,F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆,试决定在此三个位置时作用在连杆AB上的作用力的真实方向(构件重量及惯性力略去不计)。
解:上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故FR12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA在逐渐增大,相对角速度ω23也沿顺时针方向,故FR32应切于摩擦圆的上方。
R32解:上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故F R12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿逆时针方向,F R32应切于摩擦圆的下方。
解:上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大,故相对角速度ω21沿顺时针方向,又因2受拉力,故FR12应切于摩擦圆的上方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿顺时针方向,FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构,凸轮1沿逆时针方向回转,F为作用在推杆2上的外载荷,试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位(不考虑构件的重量及惯性力,解:经受力分析,FR12的方向如上图所示。
在FR12的作用下,2相对于3顺时针转动,故FR32应切于摩擦圆的左侧。
补充题1 如图所示,楔块机构中,已知γ=β=60°,Q =1000N 格接触面摩擦系数f =0.15,如Q 为有效阻力,试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1,R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=))o o ① 对楔块2,同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=))o o ②sin(602sin(602F Q ϕϕ+=⋅-))o o且有2112R R F F = ,8.53arctgf ϕ==o ③联立以上三式,求解得F =1430.65N2 如图示斜面机构,已知:f (滑块1、2与导槽3相互之间摩擦系数)、λ(滑块1的倾斜角)、Q (工作阻力,沿水平方向),设不计两滑块质量,试确定该机构等速运动时所需的铅重方向的驱动力F 。
机械原理课后习题答案

《机械原理》课后习题答案第2章(P27)2-2 计算下列机构的自由度,如遇有复合铰链、局部自由度、虚约束等加以说明。
(a)n=3,p l=3 F=3*3-2*3=3(b)n=3,p l=3,p h=2 F=3*3-2*3-2=1 (B处有局部自由度)(c)n=7,p l=10 F=3*7-2*10=1(d)n=4,p l=4,p h=2 F=3*4-2*4-2=2 (A处有复合铰链)(e)n=3,p l=4 F=3*3-2*4=1 (A或D处有虚约束)(f)n=3,p l=4 F=3*3-2*4=1 (构件4和转动副E、F引入虚约束)(g)n=3,p l=5 F=(3-1)*3-(2-1)*5=1 (有公共约束)(h)n=9,p l=12,p h=2 F=3*9-2*12-2=1 (M处有复合铰链,C处有局部自由度)2-3 计算下列机构的自由度,拆杆组并确定机构的级别。
(a)n=5,p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组,故此机构为Ⅱ级机构。
(b)n=5,p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
(c)n=5,p l=7 F=3*5-2*7=1拆分时只须将主动件拆下,其它构件组成一个Ⅲ级杆组,故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定,并提出具有确定运动的修改方案。
(a)n=3,p l=4,p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示:(b)n=4,p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示:或第3章(P42)3-2 下列机构中,已知机构尺寸,求在图示位置时的所有瞬心。
(a)(b)(c)(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中,三个圆互作纯滚,试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章(P80)5-2 一铰接四杆机构(2)机构的两极限位置如下图:(3)传动角最大和最小位置如下图:5-3题略解:若使其成为曲柄摇杆机构,则最短杆必为连架杆,即a 为最短杆。
机械原理课后全部习题解答

机械原理课后全部习题解答文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2)、机器与机构有什么异同点3)、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。
4)、设计机器时应满足哪些基本要求试选取一台机器,分析设计时应满足的基本要求。
2、填空题1)、机器或机构,都是由组合而成的。
2)、机器或机构的之间,具有确定的相对运动。
3)、机器可以用来人的劳动,完成有用的。
4)、组成机构、并且相互间能作的物体,叫做构件。
5)、从运动的角度看,机构的主要功用在于运动或运动的形式。
6)、构件是机器的单元。
零件是机器的单元。
7)、机器的工作部分须完成机器的动作,且处于整个传动的。
8)、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9)、构件之间具有的相对运动,并能完成的机械功或实现能量转换的的组合,叫机器。
3、判断题1)、构件都是可动的。
()2)、机器的传动部分都是机构。
()3)、互相之间能作相对运动的物件是构件。
()4)、只从运动方面讲,机构是具有确定相对运动构件的组合。
()5)、机构的作用,只是传递或转换运动的形式。
()6)、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()7)、机构中的主动件和被动件,都是构件。
()2 填空题答案1)、构件 2)、构件 3)、代替机械功 4)、相对运动 5)、传递转换6)、运动制造 7)、预定终端 8)、中间环节 9)、确定有用构件3判断题答案1)、√ 2)、√ 3)、√ 4)、√ 5)、× 6)、√ 7)、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
朱理机械原理课后作业全部答案

VS
机械是一种能够完成多种任务的通 用设备,例如将电能转化为机械能 、将液体或气体从一个地方输送到 另一个地方、将物料从一个位置移 动到另一个位置等。
机械的发展史
古代机械
中世纪机械
古代人类已经发明了许多简单的机械,如杠 杆、滑轮、斜面等,用于帮助完成各种任务 。
在中世纪,人们开始使用更复杂的机械,如 钟表、纺织机、水车等,这些机械的出现促 进了手工业的发展。
01
机械阻抗是指机械系统对力的阻抗能力,其大小取决于系统的 刚度、阻尼等因素。
02
机械阻抗与系统的质量、惯量、摩擦、弹性等因素有关。
机械阻抗的概念在机械动力学中非常重要,它可以帮助我们理
03
解系统的稳定性和响应特性。
机械阻抗与动力学方程
动力学方程是描述系统运动状态变化 的数学方程,通常包括牛顿第二定律 、动量定理等。
气压传动的原理
基于帕斯卡原理,即密闭容器内压力处处相等,当外界大气压高 于容器内压力时,压力差推动活塞运动,从而实现动力传递。
气压传动的应用
气压传动广泛应用于各种机械设备的动力传递系统中,如汽车刹 车系统、工业自动化生产线等。
气压元件及其特性
气源的特性
气源是气压传动的基础,其特 性包括供气压力、供气量、气 体纯净度等。
机械制造的分类
根据不同的标准,机械制造可以分为多种类型,如传统机械制造和现代机械制造、单一零件加工和整 体构件加工等。
机械制造的特点
机械制造具有精度高、复杂度高、生产效率快等特点,同时随着技术的发展,机械制造也逐渐向自动 化、智能化、绿色化方向发展。
机械制造工艺过程
机械制造工艺过程概述
机械制造工艺过程是指将原材料通过一定 的加工方法转化为成品的过程,包括多个 环节如材料准备、毛坯制造、零件加工、 热处理、装配调试等。
机械原理习题及课后答案(图文并茂)

2
1 5
解答:原机构自由度 F=33- 2 4-1 = 0,不合理 , 改为以下几种结构均可:
2-3 图 2-39 所示为一小型压力机,其中,1 为滚子;2 为摆杆;3 为滑块;4 为滑杆;5 为齿轮及凸轮;6 为连杆;7 为齿轮及偏心轮;8 为机架;9 为压头。试绘制 其机构运动简图,并计算其自由度。
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料1荷试试下卷卷高问总中题体资2配2料,置试而时卷且,调可需控保要试障在验各最;类大对管限设路度备习内进题来行到确调位保整。机使在组其管高在路中正敷资常设料工过试况程卷下中安与,全过要,度加并工强且作看尽下护可都关能可于地以管缩正路小常高故工中障作资高;料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高,核中或对资者定料对值试某,卷些审弯异核扁常与度高校固中对定资图盒料纸位试,置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高,技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术,、以术来管及避架系免等统不多启必项动要方方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
机械原理课后习题答案

机械原理课后习题答案1. 机械原理是机械工程专业的重要基础课程,通过学习机械原理,可以帮助我们更好地理解和应用机械知识。
下面是一些机械原理课后习题的答案,希望对大家的学习有所帮助。
2. 习题一,已知一个力为200N的物体沿水平方向移动了5m,求所做的功。
答案,功的计算公式为W=Fs,其中W为功,F为力,s为位移。
根据题目,力F为200N,位移s为5m,代入公式计算得W=200N5m=1000J。
所做的功为1000焦耳。
习题二,一个质量为2kg的物体,受到一个力为10N的水平拉力,求物体的加速度。
答案,根据牛顿第二定律F=ma,其中F为力,m为质量,a为加速度。
代入题目数据,10N=2kga,解得a=5m/s²。
物体的加速度为5米每秒平方。
习题三,一个质量为5kg的物体,从静止开始受到一个力为20N的水平拉力,求物体移动2秒后的速度。
答案,根据牛顿第二定律F=ma和速度公式v=at,首先求加速度a=20N/5kg=4m/s²,然后代入速度公式v=4m/s²2s=8m/s。
物体移动2秒后的速度为8米每秒。
3. 通过以上习题的答案,我们可以看到机械原理课程中涉及到了力、功、加速度等重要概念的计算和应用。
这些知识对于我们理解和分析机械运动、设计机械系统等具有重要意义。
希望大家在学习机械原理课程时,能够认真对待课后习题,加强对知识点的理解和掌握,为将来的学习和工作打下坚实的基础。
4. 总之,机械原理课后习题的答案是我们学习和掌握知识的重要参考,希望大家在学习过程中能够认真对待,勤加练习,提高自己的理论水平和实际能力。
祝大家学习进步,取得优异成绩!。
朱理、机械原理部分习题答案
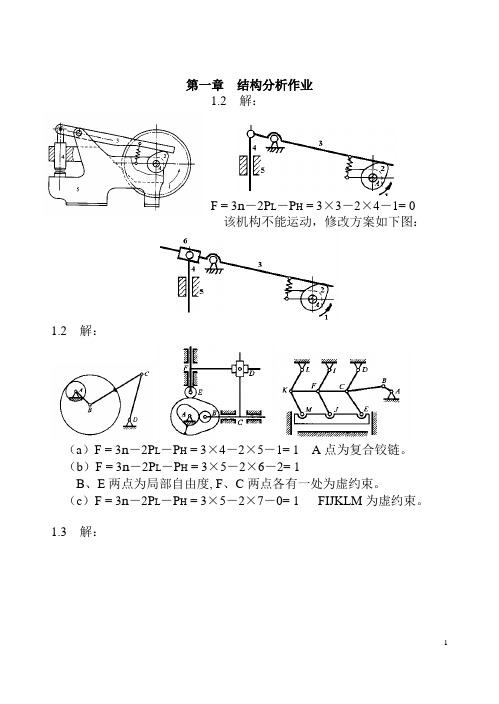
第一章结构分析作业1.2 解:F = 3n-2P L-P H = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2P L-P H = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s r a d l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3srad l V BC B /2.212327033===ω5. 求nB a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ? ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mme 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
机械原理课后题答案

机械原理课后题答案1. 列举并解释一下机械原理中的三大支配因素。
- 动力:指施加在机构元件上的力或力矩,用来驱动机构执行运动或产生工作效果。
- 运动:指机构元件相对运动的方式、路径和速度。
- 连结:指机构元件之间的连接方式,包括直接和间接连接两种形式。
2. 解释一下机械原理中的三大运动副类型。
- 滑动副:两个机构元件之间只能沿着一条确定的直线运动,如推拉杆、滑块等。
- 旋转副:两个机构元件之间只能绕一条确定的轴线旋转运动,如轴承、齿轮等。
- 滚动副:两个机构元件之间存在滚动运动,如滚子轴承、滚珠丝杠等。
3. 什么是机械原理中的受力分析方法?受力分析方法是指通过分析机构元件之间的力和力矩关系,找出各个元件的受力情况,以解决机构设计和运动性能分析的方法。
常用的受力分析方法包括力平衡法、力矩平衡法、虚功原理等。
4. 什么是力平衡法?力平衡法是一种受力分析方法,通过分析机构元件之间的力平衡关系,得到各个元件所受力的大小和方向。
它基于牛顿第一定律,即所有物体受力之和为零,可用来解决机构中受力平衡问题,确定力的大小和方向。
5. 解释一下力矩平衡法。
力矩平衡法是一种受力分析方法,通过分析机构元件之间的力矩平衡关系,得到各个元件所受力的大小和方向。
在机械原理中,力矩平衡法常被用于解决转动副运动问题,根据力矩平衡条件,求解未知力矩和力矩的方向。
6. 什么是虚功原理?虚功原理是一种受力分析方法,通过分析机构元件之间的虚功平衡关系,得到各个元件所受力的大小和方向。
虚功原理是基于功率平衡的原理,即虚功平衡原理,在机械原理中常用于分析运动副的受力情况和功率传递效率。
7. 介绍一下机械原理中的摩擦现象。
摩擦是指两个物体相对运动时由接触面之间的相互作用力导致的阻碍运动的力。
在机械运动中,正常情况下不可避免地存在摩擦力,摩擦力会导致机械能的损失、能量的消耗和部件的磨损。
因此在机械原理中需要对摩擦进行充分的考虑和分析。
机械原理课后题答案

选择填空:(1)当机构的原动件数目小于或大于其自由度数时,该机构将( B )确定运动。
A.有;B.没有;C.不一定;(2)在机构中,某些不影响机构运动传递的重复部分所带入的约束为( A )。
A.虚约束;B.局部自由度;C.复合铰链;(3)机构具有确定运动的条件是(B )。
A.机构自由度数小于原动件数;机构自由度数大于原动件数;B.机构自由度数等于原动件数;(4)用一个平面低副联二个做平面运动的构件所形成的运动链共有( B )个自由度。
A.3;B.4;C.5;D.6;(5)杆组是自由度等于( A )的运动链。
A.0;B.1;C.原动件数。
(6)平面运动副所提供的约束为( D )。
A.1;B.2;C.3;D.1或2;(7)某机构为Ⅲ级机构,那么该机构应满足的必要充分条件是( D )。
A.含有一个原动件组;B.原动件;C.至少含有一个Ⅱ级杆组;D.至少含有一个Ⅲ级杆组;(8)机构中只有一个(D )。
A.闭式运动链;B.原动件;C.从动件;D.机架。
(9)具有确定运动的差动轮系中其原动件数目( C )。
A.至少应有2个;B.最多有2个;C.只有2个;D. 不受限制。
(10)在加速度多边形中,连接极点至任一点的矢量,代表构件上相应点的____B__加速度;而其它任意两点间矢量,则代表构件上相应两点间的______加速度。
A.法向; 切向B.绝对; 相对C.法向; 相对D.合成; 切向(11)在速度多边形中,极点代表该构件上_____A_为零的点。
A.绝对速度B.加速度C.相对速度D.哥氏加速度(12)机械出现自锁是由于( A )。
A. 机械效率小于零;B. 驱动力太小;C. 阻力太大;D. 约束反力太大;(13)当四杆机构处于死点位置时,机构的压力角_B _。
A. 为00;B. 为090;C. 与构件尺寸有关;(14)四杆机构的急回特性是针对主动件_D _而言的。
D. 等速运动;E. 等速移动;F. 变速转动或变速移动;(15)对于双摇杆机构,最短构件与最长构件之和_H _大于其余两构件长度之和。
机械原理第二版朱理作业答案

机械原理第二版(朱理)作业答案机械原理作业第一章结构分析作业1.2解:F = 3n —2P L —P H = 3X 3-2X 4- 1=P H = 3X 4 —2X 5—1= 1 A点为复合铰1.2解:(b) F = 3n —2P L—P H = 3X 5—2X 6—2= 1B、E两点为局部自由度,F、C两点各有一处为虚约束。
(c) F = 3n —2P L—P H = 3X 5 —2X 7—0= 1 FIJKLM 为虚约束1.3解:F = 3n — 2P L — P H = 3X 7 — 2X 10— 0= 1 1) 以构件2为原动件,则结构由 成,故机构为H 级机构(图a )。
2) 以构件4为原动件,则结构由 成,故机构为H 级机构(图b )。
3) 以构件8为原动件,则结构由 个H 级杆组组成,8-7、6-5、4-3三个H 级杆组组 8-7、6-5、2-3三个H 级杆组组 2-3-4-5 一个皿级杆组和6- 7第二章运动分析作业2.1解:机构的瞬心如图所示- “ 气=5 mm/mm ,, t ,,八卄~一2.2解:取1作机构位置图如下图所示8%mm2.3解:取7 " mm/mm作机构位置图如下图a 所示1.求B 2点的速度V B 2V B 2 = 3 1 x L AB =10 x 30= 300 mm/s 2.求B 3点的速度V B 3V B3 =V B2 + VB3B2大小 ? 3 1 x LAB ?方向丄BC 丄AB // BC10 mm/s 取v mm 作速度多边形如下图b 所示,由图量得:阪=22 mm 所以 V B 3 二 沃% = 27X0 = 270 mm/sl BC = BC 和=1231 二 123由图a 量得:BC=123 mm ,贝SBC lV D _ AE 24而 2.求 V E P 14P1325,所以V D =V E ^24 =150 24=144 mm/sDE252531V E1501.25120 rad / s 3.求GD 2P 12P 14 38P 12P2498,所以十 38 =1.25 38=0.46 rad /s2198 984.求C 点的速度 V CV c = 2 P 24C 泊丄I= 0.46 44 5 =101.2 mm/s利用速度影像在速度多边形,过 p 点作丄CE ,过b 3点作丄BE ,得到epd 15 mm pe = 17 mm点;过e 点作丄pb 3,得到d 点,由图量得: , ,”、'V D = pd X »v = 15 汉 10 = 150 mm/ s所以 ,V E 二 pe "v =17 10 = 170 mm/sVB 3B 24•求©二b 2b 3 "v =17 10 = 170 mm/sV B3 270 厂 3 B32.2 rad/s 3I BC 123n5.求aB2a^2「f l AB =102 30 = 3000 mm/s2=50mm/ s 2/mm作速度多边形如上图 c 所示,由图量得:a B3 lBC1000123 2 =8.13 rad /s 26.求aB3a B3 =aB3n+ a B3f=a B2 + aB3B2 * + a B3B2大小 3 3 L BC ? 231 AB23 3V B3B2? 方向 B f C 丄BC B f A 丄BC // BCa n 一 a 一 3 l BC 二 2.22 123 = 595 2 mm/sa $3B2 = 2 3 V B3B 2 = 2 2.2 27° = 1188 mm/s2b'3 =23 mm n 3b'3 =20 mm, ,所以2a B3 二/b'3 笃=23 50 = 1150 mm/s 2a B 3 =n 3b'3"a =20 50 = 1000 mm/s 27.求〉38•求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作 <:b'3esP BE ,即 b'3 _ 二e _ b'3 eCB _C^ ■'BE ,得到e 点;过e 点作丄化,得到d 点,由图量得:「:e = 16 mm 「d =13 mm十「 a D x 4a =13^50 = 650 mm/s 2所以,a E = 2 "a =16 50 = 800 mm/s 2。
机械原理朱如鹏课后题答案

机械原理朱如鹏课后题答案
1.定义机械原理?
机械原理是指利用物理定律、机械学(动力学)的规律和机械设备的性能特点,分析和解决机械系统与其外部环境相互作用中的力学问题的一门学科。
2.概述机械系统的基本要素?
机械系统的基本要素包括动力源、机械系统的构型、机械元件、运动学分析和控制系统。
3.机械系统中动力源的种类?
动力源包括电力驱动源、化学能驱动源、液压传动源、气动传动源和机械传动源等。
4.什么是动力传动?
动力传动是指把一个特定动力源转化成一定的力和动能,并将其传递给机械系统的过程。
5.怎样理解“运动学分析”?
运动学分析指的是对机械系统运行过程中位置、速度、加速度及其变化的研究,用于揭示和求解机械系统动力学性能的过程。
6.怎样理解“控制系统”?
控制系统是指把机械系统的运行参数及机械系统的性能指标调节到期望状态的系统,是机械系统的一个重要分支。
7.运动学分析的基本方法?
运动学分析的基本方法有:分析法、运动结构方程法、动力学模型方法、数值计算方法和虚拟仿真方法等。
8.什么是数值计算方法?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理部分课后答案第一章结构分析作业1.2 解:F = 3n-2P L-P H = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2P L-P H = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mme 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
2.7 解:取mmmm l /2=μ作机构位置图如下图a 所示。
一、用相对运动图解法进行分析 1. 求B 2点的速度V B2V B2 =ω1×L AB =20×0.1 = 2 m/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ?方向 水平 ⊥AB ∥BD 取mms m v /05.0=μ作速度多边形如下图b 所示,由图量得:mm pb 203= ,所以 sm pb V v B /105.02033=⨯=⨯=μ而V D = V B3= 1 m/s3.求n B a 222212/401.020s m l a ABn B =⨯=⨯=ω4. 求3B aa B3 = a B2n + a B3B2τ大小 ω12L AB ?方向 水平 B →A ∥BD取mms m a 2/1=μ作速度多边形如上图c 所示,由图量得:mmb 35'3=π ,所以 233/35135's m b a a B =⨯=⨯=μπ。
二、用解析法进行分析sm l V V AB B D /130sin 1.020sin sin 11123=︒⨯⨯=⨯⨯=⨯=φωφ2212123/6.3430cos 1.020cos cos 1s m l a a AB B D =︒⨯⨯=⨯⨯=⨯=φωφ第三章 动力分析作业3.1 解:根据相对运动方向分别画出滑块1、2所受全反力的方向如图a 所示,图b 中三角形①、②分别为滑块2、1的力多边形,根据滑块2的力多边形①得:ϕϕϕcos )90sin()260sin(1212R R r F F F =+︒=-︒ ,)260sin(cos 12ϕϕ-︒=r R F F由滑块1的力多边形②得:ϕϕϕcos )90sin()260sin(2121R R dF F F =-︒=+︒ ,)260sin()260sin()260sin(cos )260sin(cos cos )260sin(21ϕϕϕϕϕϕϕϕ-︒+︒=-︒+︒=+︒=r r R d F F F F而 ︒===--53.8)15.0(11tg f tg ϕ所以 N F F rd 7.1430)53.8260sin()53.8260sin(1000)260sin()260sin(=︒⨯-︒︒⨯+︒=-︒+︒=ϕϕ 3.2 解:取mm mm l /5=μ作机构运动简图,机构受力如图a)所示;取mm N F /50=μ作机构力多边形,得:N F R 3000506065=⨯= ,N F R 3350506745=⨯=,NF F F F R R R R 335043345445====,NF R 1750503523=⨯=,N F R 2500505063=⨯=,N F F F F R R R R 175021123223==== m N mm N l F M AB R b -=-=⨯==1751750001001750213.2 解:机构受力如图a)所示由图b)中力多边形可得:N tg F tg F R 10001000455465=⨯︒==ϕ N F F F R R 2.141445sin 1000sin 454345=︒===ϕ︒=︒=︒4.18sin 45sin 6.116sin 236343R R R F F F N F F R R 4.11182.14146.116sin 45sin 6.116sin 45sin 4363=⨯︒︒=︒︒=N F F R R 5002.14146.116sin 4.18sin 6.116sin 4.18sin 4323=⨯︒︒=︒︒=所以 N F F F R R R 500612321===m N mm N l F M AB R b -=-=⨯==5050000100500213.3 解:机构受力如图所示由图可得:对于构件3而言则:02343=++R R d F F F ,故可求得 23R F 对于构件2而言则:1232R R F F =对于构件1而言则:02141=++R R b F F F ,故可求得 b F3.7 解:1. 根据相对运动方向分别画出滑块1所受全反力的方向如图a 所示,图b 为滑块1的力多边形,正行程时F d 为驱动力,则根据滑块1的力多边形得:[])cos()(90sin )2sin(2121ϕαϕαϕα+=+-︒=+R R d F F F ,)2sin()cos(21ϕαϕα++=d R F F则夹紧力为:)2sin(cos )cos(cos 21ϕαϕϕαϕ++==d R F F Fr2. 反行程时ϕ取负值,21'R F 为驱动力,而d F '为阻力,故)2sin()cos(''21ϕαϕα--=d R F F ,而理想驱动力为:αααtg F F F ddR 'sin cos ''021== 所以其反行程效率为:)cos()2sin()2sin()cos('''''21210ϕααϕαϕαϕααη--=--==tg F tg F F F ddR R 当要求其自锁时则,0)cos()2sin('≤--=ϕααϕαηtg , 故 0)2sin(≤-ϕα ,所以自锁条件为:ϕα2≤3.10 解:1.机组串联部分效率为:821.095.098.09.0'21223=⨯⨯==ηηηη 2. 机组并联部分效率为: 688.095.098.0327.038.02''32=⨯⨯+⨯+⨯=⨯++=ηηηηηB A B B A A P P P P3. 机组总效率为:%5.56565.0688.0821.0'''==⨯==ηηη 4. 电动机的功率输出功率:kw P P N B A r 532=+=+= 电动机的功率:kw N N rd 85.8565.05===η第四章 平面连杆机构作业4.1 解:1. ① d 为最大,则 c b d a +≤+ 故mma cb d 520120360280=-+=-+≤② d 为中间,则 d b c a +≤+故mmb c a d 200280360120=-+=-+≥所以d 的取值范围为:mmd mm 520200≤≤ 2. ① d 为最大,则 c b d a ++ 故mma cb d 520120360280=-+=-+② d 为中间,则 d b c a ++ 故mmb c a d 200280360120=-+=-+③ d 为最小,则 a b d c ++ 故mmc a bd 40360120280=-+=-+④ d 为三杆之和,则 mmc a bd 760360120280=++=++≤所以d 的取值范围为:mmd mm 20040 和mm d mm 760520≤3. ① d 为最小,则 a b d c +≤+ 故mmc a bd 40360120280=-+=-+≤4.3 解:机构运动简图如图所示,其为曲柄滑块机构。
