MATLAB QPSK调制与解调

合集下载

四相移相键控(QPSK)调制及解调实验

通信对抗原理实验报告实验名称:四相移相键控（QPSK）调制及解调实验学生姓名：学生学号：学生班级:所学专业：实验日期：1. 实验目的1. 掌握QPSK 调制解调原理及特性.2。

. 熟悉Matlab 仿真软件的使用。

2. 实验内容1、编写Matlab 程序仿真QPSK 调制及相干解调。

2、观察IQ 两路基带信号的特征及与输入NRZ 码的关系。

3、观察IQ 调制解调过程中各信号变化。

4、观察功率谱的变化。

5、分析仿真中观察的数据，撰写实验报告。

3. 实验原理1、QPSK 调制原理QPSK 又叫四相绝对相移调制,它是一种正交相移键控。

QPSK 利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，因此，对于输入的二进制数字序列应该先进行分组，将每两个比特编为一组,然后用四种不同的载波相位来表征。

我们把组成双比特码元的前一信息比特用a 代表,后一信息比特用b 代表。

双比特码元中两个信息比特ab 通常是按格雷码排列的,它与载波相位的关系如表1-1所示，矢量关系如图1—1所示。

图1-1（a)表示A 方式时QPSK 信号矢量图,图1—1（b)表示B 方式时QPSK 信号的矢量图。

由于正弦和余弦的互补特性,对于载波相位的四种取值,在A 方式中：45°、135°、225°、315°，则数据k I、k Q 通过处理后输出的成形波形幅度有两种取值±2/2;B 方式中:0°、90°、180°、270°,则数据k I、k Q 通过处理后输出的成形波形幅度有三种取值±1、0。

表(0,1)(1,1)(0,0)参考相位参考相位(a)(b)图1-1 QPSK 信号的矢量图下面以A 方式的QPSK 为例说明QPSK 信号相位的合成方法。

串/并变换器将输入的二进制序列依次分为两个并行序列,然后通过基带成形得到的双极性序列(从D/A 转换器输出，幅度为±2/2）。

通信原理的MATLAB实验 QPSK的调制解调报告

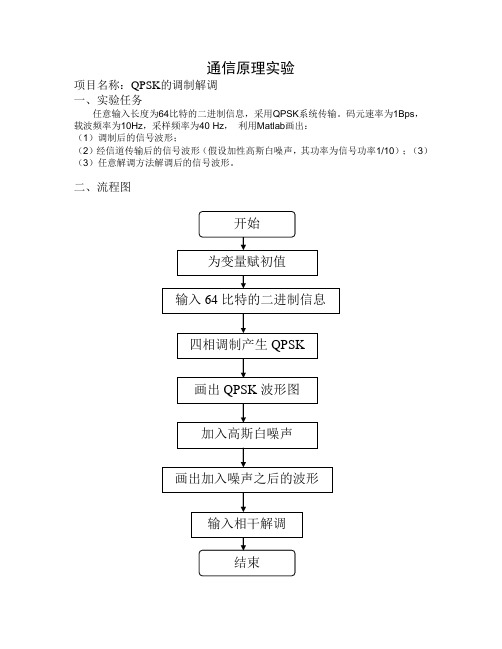
通信原理实验项目名称：QPSK的调制解调一、实验任务任意输入长度为64比特的二进制信息，采用QPSK系统传输。

码元速率为1Bps，载波频率为10Hz，采样频率为40 Hz，利用Matlab画出：（1）调制后的信号波形；（2）经信道传输后的信号波形（假设加性高斯白噪声，其功率为信号功率1/10）；（3）（3）任意解调方法解调后的信号波形。

二、流程图三、完整程序Fd=1; %码元速率Fc=10; %载波频率Fs=40; %采样频率N=Fs/Fd;df=10;x=[ 1 1 0 1 1 0];%任意输入64比特的二进制信息M=2; %进制数SNRpBit=10;%加性高斯白噪声，其功率为信号功率的1/10，即信噪比为10 SNR=SNRpBit/log2(M); %转换为码元速率seed=[12345 54321];numPlot=length(x);figure(1)%画出输入二进制序列subplot(211);stem([0:numPlot-1],x(1:numPlot),'bx');title('输入波形’)%调制y=dmod(x,Fc,Fd,Fs,'fsk',M,df);numModPlot=numPlot*Fs;t=[0:numModPlot-1]./Fs;subplot(212);%画出调制后的信号plot(t,y(1:length(t)),'b-');axis([min(t) max(t) -1.5 1.5]);title('调制后的信号')%在已调信号中加入高斯白噪声randn('state',seed(2));y=awgn(y,SNR-10*log10(0.5)-10*log10(N),'measured',[],'dB');%相干解调figure(2)subplot(211);plot(t,y(1:length(t)),'b-');%画出经过信道的实际信号axis([min(t) max(t) -1.5 1.5]);title('加入高斯白噪声后的已调信号')%带输出波形的相干M元频移键控解调subplot(212);stem([0:numPlot-1],x(1:numPlot),'bx');hold on;stem([0:numPlot-1],z1(1:numPlot),'ro');hold off;axis([0 numPlot -0.5 1.5]);title('相干解调后的信号')四、波形。

BPSK和QPSK调制解调原理及MATLAB程序

2.1 PSK调制方式PSK原理介绍（以2-PSK为例）移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。

绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。

二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。

2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。

在二进制数字调制中，当正弦载波的相位随二进制数字基带信号离散变化时，则产生二进制移相键控(2PSK)信号。

通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。

二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同，在2PSK调制中，an应选择双极性。

1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时，则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出，当发送二进制符号1时，已调信号e2PSK(t)取0°相位，发送二进制符号0时，e2PSK(t)取180°相位。

若用φn表示第n个符号的绝对相位，则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊，所以2PSK信号的相干解调存在随机的“倒π”现象，从而使得2PSK 方式在实际中很少采用。

为了解决2PSK 信号解调过程的反向工作问题，提出了二进制差分相位键控(2DPSK)，这里不再详述。

基于Matlab的QPSK调制解调仿真设计与研究设计说明书

天津理工大学计算机与通信工程学院通信工程专业设计说明书基于Matlab/Simulink的QPSK调制解调仿真设计与研究目录摘要 (2)第一章前言 (2)1.1 专业设计任务及要求 (2)1.2 Matlab简介 (2)1.3 Matlab下的simulink简介 (3)1.4 通信系统模型 (3)第二章QPSK调制 (4)2.1 QPSK介绍 (4)2.2 QPSK调制原理 (4)2.2.1 相乘法 (4)2.2.2 选择法 (5)2.3 QPSK调制原理框图 (6)2.4 QPSK调制方式的Matlab仿真 (6)2.5 QPSK调制方式Matlab-simulink仿真 (7)2.5.1 simulink调制建模 (7)2.5.2 simulink调制仿真结果 (8)第三章QPSK解调 (14)3.1 QPSK解调原理 (14)3.2 QPSK解调原理框图 (14)3.3 QPSK解调方式Matlab仿真 (14)3.4 QPSK解调方式的Matlab-simulink仿真 (15)3.4.1 QPSK解调建模 (15)3.4.2 传输信道 (17)3.4.3仿真结果 (17)3.5 仿真结果分析 (20)第四章QPSK通信系统性能分析 (20)第五章结论 (20)参考文献 (21)附录 (21)摘要正交相移键控（QPSK），是一种数字调制方式。

QPSK技术具有抗干扰能力好、误码率低、频谱利用效率高等一系列优点。

论文主要介绍了正交相移键控(QPSK)的概况，以及正交相移键控QPSK的调制解调概念和原理，利用Matlab中M文件和Simulink模块对QPSK的调制解调系统进行了仿真，对QPSK在高斯白噪声信道中的性能进行了，分析了解Simulink中涉及到QPSK的各种模块的功能。

【关键词】Matlab QPSK Simulnk 仿真第一章前言1.1专业设计任务及要求1了解并掌握QPSK调制与解调的基本原理；2在通信原理课程的基础上设计与分析简单的通信系统；3学会利用MATLAB7.0编写程序进行仿真，根据实验结果能分析所设计系统的性能。

MATLAB-QPSK调制与解调

MATLAB仿真QPSK调制与解调2011-06-22 20:16:45| 分类：学习| 标签：qpsk matlab |字号大中小订阅注意B方式的4PSK用的比较多。

I 路信号是用余弦载波，由2进制数据流的奇数序列组成；Q路信号用正弦载波，由2进制数据流的偶数序列组成。

下面的a是Idata，b就是Qdata，它们分布与各自的载波相乘分别输出I 路信号和Q 路信号。

I 路信号加上Q路信号就是QPSK输出信号。

当I 路载波信号是0相位时为1，是180°相位时为0；当Q路载波信号是0相位时为1，是180°相位时为0。

比如下图的‘11’数据cos(theta) + sin(theta) =sqrt(2)*sin(theta + 45°)是相位超前sin(theta) 45°QPSK即四进制移向键控（Quaternary Phase Shift Keying），它利用载波的四种不同相位来表示数字信息，由于每一种载波相位代表两个比特信息，因此每个四进制码元可以用两个二进制码元的组合来表示。

两个二进制码元中的前一个码元用a表示，后一个码元用b表示。

% QPSK调相法基本原理解释clear allclose all% x1是类似[1 1 -1 -1 -1 -1 1 1]的分布,作用是控制相位的180°反转。

%由于仿真中载波的频率是f=1Hz，所以1s的间隔内有一个完整周期的正弦波t=[-1:0.01:7-0.01]; % t共800个数据，-1~7st1 = [0:0.01:8-0.01]; %t1也是800个数据点，0 ~8stt=length(t); % tt=800x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt2 = 0:0.01:7-0.01; %t2是700个数据点，是QPSK_rc绘图的下标t3 = -1:0.01:7.1-0.01; %t3有810个数据点，是i_rc的时间变量t4 = 0:0.01:8.1-0.01; %t4有810个数据点，是q_rc的时间变量%x2是类似于[1 1 -1 -1 1 1 1 1]的分布,作用是控制相位的180°反转tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f); %xrc是一个低通特性的传输函数y1=conv(x1,xrc)/5.5; %y1和x1 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带y2=conv(x2,xrc)/5.5; % y2和x2 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t); % x1就是I dataq=x2.*sin(2*pi*f1*t1); %x2就是Q dataI=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3); % y1就是I data，i_rc可能是贴近实际的波形,i则是理想波形q_rc=y2.*sin(2*pi*f1*t4); %y2就是Q data，q_rc可能是贴近实际的波形,q则是理想波形I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');上图解释：合成序列表示的数据：11 01 00 00 01 11 11相对于sin(theta)合成序列相位: Pi/4, 3/4Pi[即sin(theta-45)=sin(theta-45+180)], -3/4Pi[即-sin(theta+45)], -3/4Pi[即-sin(theta+45)] , 3/4Pi, Pi/4, Pi/4。

QPSK调制与解调在MATLAB平台上的实现(word文档良心出品)

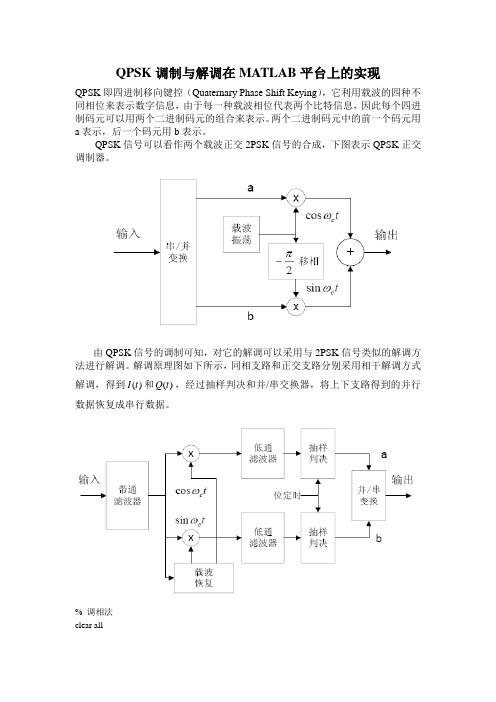
QPSK调制与解调在MATLAB平台上的实现QPSK即四进制移向键控（Quaternary Phase Shift Keying），它利用载波的四种不同相位来表示数字信息，由于每一种载波相位代表两个比特信息，因此每个四进制码元可以用两个二进制码元的组合来表示。

两个二进制码元中的前一个码元用a表示，后一个码元用b表示。

QPSK信号可以看作两个载波正交2PSK信号的合成，下图表示QPSK正交调制器。

由QPSK信号的调制可知，对它的解调可以采用与2PSK信号类似的解调方法进行解调。

解调原理图如下所示，同相支路和正交支路分别采用相干解调方式解调，得到()Q t，经过抽样判决和并/串交换器，将上下支路得到的并行I t和()数据恢复成串行数据。

% 调相法clear allclose allt=[-1:0.01:7-0.01];tt=length(t);x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt1=[0:0.01:8-0.01];t2=0:0.01:7-0.01;t3=-1:0.01:7.1-0.01;t4=0:0.01:8.1-0.01;tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f);y1=conv(x1,xrc)/5.5;y2=conv(x2,xrc)/5.5;n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t);q=x2.*sin(2*pi*f1*t1);I=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3);q_rc=y2.*sin(2*pi*f1*t4);I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列'); subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');效果图：% 设定T=1,加入高斯噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列'); 效果图：% 设定T=1, 不加噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;t=0:0.1:1e3-0.1;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);% 解调I_demo=QPSK_rc.*cos(2*pi*f1*t1);Q_demo=QPSK_rc.*sin(2*pi*f1*t1);I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)]; end;ddd = -2*bit_in+1;ddd1=repmat(ddd',10,1);for i=1:1e4ddd2(i)=ddd1(i);endfigure(1)subplot(4,1,1);plot(t3,I);axis([0 20 -6 6]);subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]);subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]); subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]);效果图：% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);效果图：11。

在matlab上的的QPSK调制与解调仿真

QPSK的调制与解调电路的MATLAB实现摘要本课程设计主要讨论了QPSK的调制解调原理，分析了它们的调制解调实现过程的程序设计。

在课程设计中，系统开发平台为Windows 2000，程序运行平台为MATLAB集成环境下的Simulink仿真平台。

用Simulink构建QPSK调制与解调电路仿真模型，得到调制、解调信号，绘制调制前后频谱图，分析QPSK在各种噪声信道中的性能。

程序运行初步实现了QPSK的调制解调，其所得结果基本与理论结果一致。

关键词Simulink；调制解调；QPSK；目录1.前言 (1)1.1QPSK系统的应用背景简介 (1)1.2 QPSK实验仿真的意义 (1)1.3 实验平台和实验内容 (2)1.3.1实验平台 (2)1.3.2实验内容 (2)2系统实现框图和分析 (3)2.1、QPSK调制部分 (3)2.2、QPSK解调部分 (4)3实验结果及分析 (6)3.1、理想信道下的仿真 (6)3.2、高斯信道下的仿真 (7)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (8)4致谢 (9)参考文献 (10)附录 (11)1.前言1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称，意为正交相移键控，是一种数字调制方式。

在19世纪80年代初期,人们选用恒定包络数字调制。

这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。

19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。

1.2 QPSK实验仿真的意义通过完成设计内容，复习QPSK调制解调的基本原理，同时也要复习通信系统的主要组成部分，了解调制解调方式中最基础的方法。

MATLAB实现QPSK信号的调制解调以及计算误码率BER

MATLAB实现QPSK信号的调制解调以及计算误码率BER QPSK（Quadrature Phase Shift Keying）是一种基于调制的数字通信方法，它能够提高频谱利用率并减小误码率。

在QPSK调制中，每个符号由两个正交的载波信号之一进行相位调制，共有四种可能的相位状态。

本文将介绍如何使用MATLAB实现QPSK信号的调制、解调，并计算误码率BER（Bit Error Rate）。

首先，我们将使用MATLAB生成一个随机的二进制数列作为待传输的数字数据。

假设数据位数为N。

```matlabN=1000;%数据位数data = randi([0, 1], 1, N); % 生成随机二进制数据```接下来，我们将二进制数据转换为QPSK调制所需的两个IQ通道数据。

其中，I通道代表实部，Q通道代表虚部。

我们将0和1分别映射为QPSK调制的四个相位状态（例如：00映射为相位0°，01映射为相位90°，10映射为相位180°，11映射为相位270°）。

```matlabqpsk_data = reshape(data, 2, N/2); % 转换为2*N/2矩阵qpsk_data = 2*qpsk_data - 1; % 转换为-1和1之间的数值I = qpsk_data(1, :);Q = qpsk_data(2, :);```现在，我们得到了I和Q两个IQ通道的数据。

接下来，我们将对这两个通道的数据进行调制。

在QPSK调制中，我们使用两个不同相位的正弦信号。

```matlabfs = 1000; % 采样率fc = 10; % 载波频率t = 0:1/fs:N/fc-1/fs; % 时间序列I_modulated = real(sqrt(2/T).*I.*cos(2*pi*t*fc)); % I通道调制Q_modulated = real(sqrt(2/T).*Q.*sin(2*pi*t*fc)); % Q通道调制QPSK_signal = I_modulated + Q_modulated; % QPSK信号```现在，我们得到了QPSK信号。

QPSK调制与解调在MATLAB平台上的实现

QPSK调制与解调在MATLAB平台上的实现QPSK（Quadrature Phase Shift Keying）是一种常用的调制解调技术，常用于数字通信中。

在QPSK调制中，每个符号代表两个比特，通过将这两个比特与正交信号载波进行调制，实现高效的数据传输。

在这篇文章中，我们将介绍如何在MATLAB平台上实现QPSK调制和解调。

1.QPSK调制首先，我们需要生成待发送的二进制比特序列。

我们可以使用randi 函数生成0和1之间的随机整数序列。

```matlabbits = randi([0,1],1,N);```N表示待发送的比特数。

接下来，我们需要将这个二进制序列转换为QPSK调制符号。

在QPSK 调制中，我们将每两个比特映射到一个复数符号。

将0映射为1+j，将1映射为1-j。

```matlabfor i = 1:2:Nif bits(i) == 0 && bits(i+1) == 0symbols((i+1)/2) = 1 + 1i;elseif bits(i) == 0 && bits(i+1) == 1symbols((i+1)/2) = 1 - 1i;elseif bits(i) == 1 && bits(i+1) == 0symbols((i+1)/2) = -1 + 1i;elseif bits(i) == 1 && bits(i+1) == 1symbols((i+1)/2) = -1 - 1i;endend```最终得到的symbols变量即为QPSK调制后的复数符号序列。

2.QPSK解调首先，我们需要接收到的QPSK信号进行解调，得到复数符号序列。

```matlabsymbols_received = received_signal./carrier; % 将接收到的信号除以载波得到复数符号序列```其中received_signal为接收到的QPSK信号，carrier为发送端使用的载波。

基于matlab的oqpsk调制解调

基于matlab的oqpsk调制解调在MATLAB 中进行OQPSK（Offset Quadrature Phase Shift Keying）调制和解调可以使用Communications Toolbox 提供的功能。

下面分别给出 OQPSK 调制和解调的示例代码：OQPSK 调制：% 参数设置Fs = 1000; % 采样率Ts = 1/Fs; % 采样间隔fc = 100; % 载波频率data = randi([0, 1], 1, 100); % 随机生成二进制数据% OQPSK 调制modulatedSignal = oqpskmod(data, fc, Fs, 'InputType', 'bit', 'PhaseOffset', pi/4);% 显示调制后的信号t = (0:length(modulatedSignal)-1) * Ts;figure;plot(t, real(modulatedSignal), t, imag(modulatedSignal));title('OQPSK Modulated Signal');xlabel('Time (s)');legend('I Channel', 'Q Channel');OQPSK 解调：% OQPSK 解调demodulatedData = oqpskdemod(modulatedSignal, fc, Fs, 'OutputType', 'bit', 'PhaseOffset', pi/4);% 显示解调后的数据figure;stem(data, 'r', 'DisplayName', 'Original Data');hold on;stem(demodulatedData, 'b', 'DisplayName', 'Demodulated Data');title('OQPSK Demodulation Result');xlabel('Bit Index');ylabel('Bit Value');legend('Original Data', 'Demodulated Data');这里使用了Communications Toolbox 中的oqpskmod 和oqpskdemod 函数，其中oqpskmod 用于OQPSK 调制，oqpskdemod 用于OQPSK 解调。

QPSK调制与解调(Matlab仿真)

QPSK调制与解调（Matlab仿真）1. 一般在仿真的时候，大家都喜欢直接做等效基带仿真（类似于星座点的仿真）。

但实际要传，还是要传频带的波形信号。

2. 为了模拟真实的环境，先把基带信号经过一个自定义的信道，然后再做脉冲成型，上变频，加一点噪声AWGN进去。

3. 为了模拟同步，应该用专用的同步算法。

但是这里的重点不在同步。

所以用了很简单粗暴的办法。

假装直接同步上了。

4. 为了造出不同步的结果，可以这样写 x_未同步 = [x(300:end); x; x]; 相当于循环发送，循环接收。

这是仿真。

Main%%% 单载波QPSK 接收端% 2017年5月17日18:02:56clear;close all;clcrand_seed = 0;rand('seed',rand_seed);randn('seed',rand_seed);%%% Set up parameters and signals.M = 4; % Alphabet size for modulationbaud_rate = 100; % Baud ratef_carrier1 = 75; % Carrier frequencyNsym = 10000; % Number of symbolsmsg = randi([0 M-1],Nsym,1); % Random messagehMod = comm.RectangularQAMModulator(M);modmsg = step(hMod,msg); % Modulate using QAM. % 映射后的基带信号trainlen = 1000; % Length of training sequencerolloff = .3; % 滚降因子span = 20 ; % 截断长度sps = 10; % Samples per symbolrrcFilter=rcosdesign(rolloff,span,sps,'sqrt'); %根升余弦滚降滤波器，‘sqrt’均方根升余弦；‘normal’升余弦fs = baud_rate*sps; % 时间采样率,时间采样间隔为1/fs 秒Tsymbol=1/baud_rate;% 2. 脉冲成型% txSig = upfirdn(modmsg, rrcFilter, sps); % 发送端的基带复波形信号% chan = [1; .001];chan = [.986; .845; .237; .123+.31i]; % Channel coefficients% chan = [1 0.45 0.3+0.2i]; % Channel coefficientsfiltmsg = filter(chan,1,modmsg); % Introduce channel distortion.（已经经过信道的畸变的基带复信号，星座点）txSig = upfirdn(filtmsg, rrcFilter, sps); % 发送端的基带复波形信号txSig = awgn(txSig,20,'measured'); % Add AWGNt = (0:1/fs:((length(txSig)-1)/fs)).';T = t(end)+1/fs;df = 1/T;freq = -fs/2:df:fs/2-df;cos1 = cos(2*pi*f_carrier1 * t);sin1 = sin(2*pi*f_carrier1 * t);x_upconv = real(txSig).* cos1 + imag(txSig) .* sin1;%% === 接收端x_training_wave = x_upconv;x_training_msg = msg;rxSig = [x_upconv(300:end) ; x_upconv];% 1. 同步x_resampled = resample(rxSig,1,1);x_sync = sync_two_signals( x_resampled,x_training_wave,0);figure(2);plot(freq,20*log10(abs(fftshift(fft(x_sync))/max(abs(fftshift(fft(x_sync)))))));ylim([-100,10])xlim([0,freq(end)])grid on;xlabel('频率(Hz)');title('接收信号');% 2. 下变频+ 匹配滤波xi_dnconv = x_sync .* cos1;xq_dnconv = x_sync .* sin1;x_filtered = xi_dnconv + 1j * xq_dnconv;rxFilt = upfirdn(x_filtered, rrcFilter, 1, sps);rxFilt = rxFilt(span+1:end-span); % 这是接收端匹配滤波后的信号% 3. 均衡% eq1 = lineareq(6, lms(0.01)); % LMSeq1 = lineareq(30, rls(0.99,0.01)); % Create an equalizer object. % 40 taps，RLS算法，步长0.99，自相关矩阵逆矩阵的初值InvCorrInit对角线上的元素eq1.SigConst = step(hMod,(0:M-1)')'; % Set signal constellation. % 标准星座图[symbolest,~] = equalize(eq1,rxFilt,x_training_msg(1:trainlen)); % Equalize. % 均衡器obj，需要均衡的信号，训练序列symbolest = symbolest ./ mean(abs(symbolest)) .* mean(abs(eq1.SigConst));% Plot signals.h = scatterplot(rxFilt,1,trainlen,'bx'); hold on;scatterplot(symbolest,1,trainlen,'r.',h);scatterplot(eq1.SigConst,1,0,'k*',h);legend('Filtered signal','Equalized signal',...'Ideal signal constellation');hold off;% Compute error rates with equalization.hDemod = comm.RectangularQAMDemodulator(M);demodmsg = step(hDemod,symbolest); % Demodulate detected signal from equalizer.% Create ErrorRate Calculator System objectserVec = step(comm.ErrorRate,msg(trainlen+1:end),demodmsg(trainlen+1:end));srate = serVec(1)snum = serVec(2)% Convert integers to bitshIntToBit = comm.IntegerToBit(log2(M));Tx_bit = step(hIntToBit, msg(trainlen+1:end));Rx_bit = step(hIntToBit, demodmsg(trainlen+1:end));% Calculate BERberVec = step(comm.ErrorRate,Rx_bit,Tx_bit);brate = berVec(1)bnum = berVec(2)同步的代码function x_sync = sync_two_signals( x_resampled,x_training_wave,idx )% sync_two_signals( x_resampled,x_training_wave,idx )% x_resampled：收到的信号% x_training_wave：用发送的信号% idx：要找同步上的第几段。

QPSK调制与解调在MATLAB平台上的实现

QPSK调制与解调在MATLAB平台上的实现QPSK（Quadrature Phase Shift Keying）是一种常见的数字调制技术，主要用于数字通信领域中的高速数据传输。

QPSK调制与解调的实现可以利用MATLAB平台，并结合数字信号处理工具箱中的相关函数来完成。

在本文中，将详细介绍QPSK调制和解调的MATLAB实现步骤，并给出相关代码示例。

1. 生成一个二进制序列作为调制数据。

可以使用MATLAB中的randi函数生成0和1构成的随机序列。

```matlabdata = randi([0 1], 1, N); % N表示数据长度```2. 将二进制序列转换为QPSK调制符号。

由于QPSK调制中每个调制符号代表2个比特，所以需要将二进制序列分成两部分，并将每一部分映射到相应的星座点上。

可以使用MATLAB中的bi2de函数将二进制序列转换为十进制数，并按照星座点的排列顺序进行映射。

示例代码如下：```matlabI_data = bi2de(data(1:2:end), 'left-msb');Q_data = bi2de(data(2:2:end), 'left-msb');```3. 根据映射的结果，使用复数运算来生成QPSK调制信号。

可将实部和虚部分别设置为I_data和Q_data，形成一个复数信号。

示例代码如下：```matlabmodulated_signal = I_data + 1i*Q_data;```4. 将调制信号进行归一化并添加高斯白噪声（可选）。

调制信号一般需要归一化为特定的信号功率，可以使用MATLAB中的awgn函数向调制信号添加高斯白噪声。

示例代码如下：```matlabnormalized_signal = modulated_signal / sqrt(2); % 归一化信号功率noisy_signal = awgn(normalized_signal, SNR); % 向信号添加高斯白噪声，SNR表示信噪比```QPSK解调的实现步骤如下：1.接收到带有噪声的QPSK信号。

matlab qpsk解调算法

在MATLAB中，QPSK解调算法的实现通常包括以下几个步骤：1. 载波恢复：首先，需要从接收到的信号中恢复出载波。

这通常是通过相乘或相除的方式完成的，即通过将接收到的信号与恢复的载波相乘或相除来去除载波。

2. 符号解调：在恢复载波之后，需要进行符号解调。

这通常是通过比较接收到的信号与参考信号的相位差来实现的。

根据比较结果，可以确定接收到的符号是0还是1。

3. 解调后的信号处理：在解调之后，通常需要对解调后的信号进行一些处理，例如去除直流分量、低通滤波等。

下面是一个简单的MATLAB代码示例，演示了如何实现QPSK解调：生成QPSK信号M = 4; % QPSK的调制阶数data = randi([0 M-1], 1000, 1); % 生成1000个随机数据modData = qammod(data, M); % QPSK调制加入高斯白噪声SNR = 10; % 信噪比noise = sqrt(1/2)*(randn(size(modData)) + 1i*randn(size(modData))); % 生成高斯白噪声receivedSignal = modData + noise; % 加入噪声QPSK解调demodData = qamdemod(receivedSignal, M, 'Peak'); % QPSK解调计算误码率errors = sum(abs(data - demodData)) / length(data); % 计算误码率fprintf('误码率为: %f\n', errors);请注意，这只是一个简单的示例代码，实际应用中可能需要更复杂的处理和优化。

此外，上述代码中使用的`qammod`和`qamdemod`函数是MATLAB中提供的QAM调制和解调函数，对于QPSK来说，它们可以正常工作。

基于Matlab的QPSK调制与解调系统仿真

一、多进制调制带通二进制键控系统中，每个码元只能传输1b信息，其频带利用率不高。

为了提高频带利用率，最有效的办法是使一个码元传输多个比特的信息。

这就是多进制键控体制。

多进制数字调制是利用多进制数字基带信号去调制载波的振幅，频率或相位。

因此，相应地有多进制数字振幅调制（MASK)，多进制数字频率调制（MPSK)以及多进制数字相位调制（MPSK)等。

多进制数字调制是利用多进制数字基带信号去调制载波的振幅、频率或相位。

由于多进制数字调制信号的被调参数在一个码元宽度内有多个可能的取值，因此与二进制数字调制相比，具有以下两个特点：(1)在相同的信道码元传输速率下，L进制系统的信息传输速率是二进制系统的log L倍；2(2)在相同的系统传信率下，多进制信道的符号速率可以低于二进制的符号速率，因而所需信道带宽减小。

因此，多进制调制方式获得了广泛的应用，成为提高通信效率的主要手段。

二、QPSK的原理QPSK（4PSK，正交相移键控）又叫四相绝对相移调制，是最常用的MPSK，分为π/2系统和π/4系统两种。

它是利用载波的四种不同相位来表征数字信息。

由于每一种载波相位代表两个比特信息，故每个四进制码元又被称为双比特码元。

QPSK系统在用正交调制部分需要进行串/并变换，其中串/并变换电路将QPSK调制的两位编码按比特分开，走上下两路，分成的两路序列速率减半，电平发生器分别产生双极性二电平信号I(t)和Q(t),然后各自去调制相互正交的正弦波，再进行矢量合成，即得到QPSK信号。

图1 QPSK调制电路在解调部分可以用两个正交的载波信号实现相干解调。

正交路和同相路分别设置两个相关器，得到I(t)和Q(t)，经电平判决和并/串变换即可恢复原始信息。

图2 QPSK解调电路三、详细设计步骤1 根据QPSK的调制及解调原理及原理框图，MATLAB程序来仿真这个系统应遵循以下几个步骤：调制部分：（1）串/并变换（2）极性转换（3）电平产生（4）两分路分别与载波相乘（5）合并两路信号信道部分：加入高斯白噪声解调部分：（1）接收到的信号分别乘以正弦信号及余弦信号（2）两路信号分别进行抽样判决（3）并/串变换2 用MATLAB 程序来实现QPSK 调制与解调系统仿真四、设计结果及分析0100200300400500600700800-2-1.5-1-0.50.511.52产生的二进制波形图1 产生的随机二进制序列050100150200250300350400-2-112二进制信息050100150200250300350400-2-112余弦分路信号图2 基数位的二进制序列及调制后的波形050100150200250300350400-2-112二进制信息050100150200250300350400-2-112正弦分路信号图3偶数位的二进制序列及调制后的波形050100150200250300350400-1-0.50.51加性高斯白噪声时域波形050100150200250300350400051015加性高斯白噪声频谱图4 加性高斯白噪声的时域波形及频谱050100150200250300350400-55接收端信号的时域图050100150200250300350400-202接收端正弦分路信号050100150200250300350400-22接收端余弦分路信号图5接收端信号的时域图及正余弦两路信号的波形0510********35404550-29.5-29-28.5-28-27.5-27-26.5-26-25.5-25-24.5Frequency (Hz)P o w e r /f r e q u e n c y (d B /H z )加性高斯白噪声功率谱密度图6 加性高斯白噪声的功率谱密度0100200300400500600700800-2-1.5-1-0.50.511.52解调出的波形图7 接收端最终解调后的二进制序列五、总结在现代通信中，提高频谱利用率一直是人们关注的焦点之一。

QPSK调制与解调系统的MATLAB实现

QPSK调制与解调系统的MATLAB实现和性能分析摘要：QPSK是英文QuadraturePhaseShiftKeying的缩略语简称，意为正交相移键控，是一种数字调制方式。

四相相移键控信号简称“QPSK”。

在现代通信系统中，调制与解调是必不可少的重要手段。

所谓调制，就是把信号转换成适合在信道中传输的形式的一种过程。

解调则是调制的相反过程，而从已调制信号中恢复出原信号。

本课程设计主要介绍通过进行QPSK调制解调的基带仿真，对实现中影响该系统性能的几个重要问题进行了研究。

针对QPSK的特点，调制前后发生的变化，加上噪声后波形出现的各种变化，通过星座图、眼图、波形图等来观察。

程序设计与仿真均采用MATLAB集成环境下的Simulink仿真平台，最后仿真详单与理论分析一致。

1 引言本课程设计主要是学会运用MATLAB中的Simulink来实现数字基带信号的模拟传输。

在知道其传输原理的情况下，将仿真电路到Simulink之中。

并且对正交振幅调制、解调过程的频谱和波形的分析，同时在无噪声和有噪声的进行分析，加入高斯白噪声，瑞利噪声，莱斯噪声分析调制解调后的频谱、波形，观察其误码率。

1.1课程设计的目的通过本课程的学习我们不仅能加深理解和巩固理论课上所学的有关QPSK调制与解调的基本概念、基本理论和基本方法，而且能锻炼我们分析问题和解决问题的能力；同时对我们独立工作的习惯和科学素质进行培养，为今后参加科学工作打下良好的基础。

1.2课程设计的内容利用MATLAB集成环境下的Simulink仿真平台,设计一个QPSK调制与解调系统.用示波器观察调制前后的信号波形;用频谱分析模块观察调制前后信号频谱的变化;加上各种噪声源,用误码测试模块测量误码率;最后根据运行结果和波形来分析该系统性能。

1.3课程设计的要求1）熟悉MATLAB环境下的Simulink仿真平台，熟悉QPSK系统的调制解调原理，构建QPSK调制解调电路图.2）用示波器观察调制前后的信号波形，用频谱分析模块观察调制前后信号的频谱的变化。

MATLAB_QPSK调制与解调

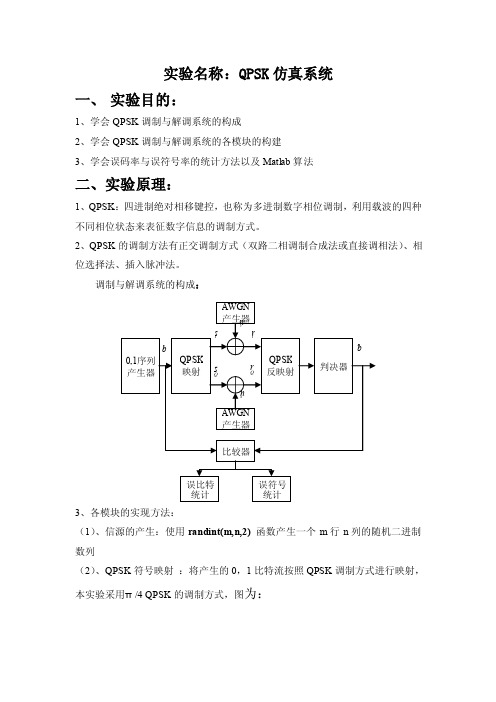
实验名称：QPSK仿真系统一、实验目的：1、学会QPSK调制与解调系统的构成2、学会QPSK调制与解调系统的各模块的构建3、学会误码率与误符号率的统计方法以及Matlab算法二、实验原理：1、QPSK：四进制绝对相移键控，也称为多进制数字相位调制，利用载波的四种不同相位状态来表征数字信息的调制方式。

2、QPSK的调制方法有正交调制方式（双路二相调制合成法或直接调相法）、相位选择法、插入脉冲法。

调制与解调系统的构成：3、各模块的实现方法：（1）、信源的产生：使用randint(m,n,2)函数产生一个m行n列的随机二进制数列（2）、QPSK符号映射：将产生的0，1比特流按照QPSK调制方式进行映射，本实验采用π/4 QPSK的调制方式，图为：（3）、AWGN 信号产生：AWGN 产生器就是产生满足均值为0，方差为1的高斯白噪声。

实验中使用randn(m,n)函数产生一个m 行n 列的高斯噪声序列。

（4）、信号幅度控制：根据AWGN 信道模型，接收信号可以分别表示为α就是当噪声功率归一化为1（0均值，方差为1）时，根据信噪比关系而计算出来的信号平均幅度（5）、QPSK 反映射及判决：对接收到的信号在4种可能的四种信号向量[(1,0), (0,1), (-1,0), (0,-1)]上投影(即进行点积)。

投影最大的值所对应的信号向量就是所发送信号的符号值，然后恢复出比特流（6）、误码率及误符号率统计：误码率：将检测出来的比特流和发送的原始比特流进行比较，统计出出现错误的比特数误符号率：将检测出来的比特流变成两组，构成符号，和发送端符号映射后的符号流进行比较，只要符号中任错一bit ，就算该符号出错。

统计出现错误的符号数三、实验内容：1、调制与解调I I Ir s n α=+Q Q Q r s n α=+22210log 10^10s s n n v SNR SNR v sqrt v v ⎛⎫⎛⎫⎛⎫=⇒=* ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭s v α=clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列');2、误码率仿真% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);3、QPSK在A WGN信道下的仿真close allclcclear allSNR_DB=[0:1:12];sum=1000000;data= randsrc(sum,2,[0 1]);[a1,b1]=find(data(:,1)==0&data(:,2)==0);message(a1)=-1-j;[a2,b2]=find(data(:,1)==0&data(:,2)==1);message(a2)=-1+j;[a3,b3]=find(data(:,1)==1&data(:,2)==0);message(a3)=1-j;[a4,b4]=find(data(:,1)==1&data(:,2)==1);message(a4)=1+j;scatterplot(message)title('B点信号的星座图')A=1;Tb=1;Eb=A*A*Tb;P_signal=Eb/Tb;NO=Eb./(10.^(SNR_DB/10));P_noise=P_signal*NO;sigma=sqrt(P_noise);for Eb_NO_id=1:length(sigma)noise1=sigma(Eb_NO_id)*randn(1,sum);noise2=sigma(Eb_NO_id)*randn(1,sum);receive=message+noise1+noise2*j;resum=0;total=0;m1=find(angle(receive)<=pi/2&angle(receive)>0);remessage(1,m1)=1+j;redata(m1,1)=1;redata(m1,2)=1;m2= find( angle(receive)>pi/2&angle(receive)<=pi);remessage(1,m2)=-1+j;redata(m2,1)=0;redata(m2,2)=1;m3=find( angle(receive)>-pi&angle(receive)<=-pi/2);remessage(1,m3)=-1-j;redata(m3,1)=0;redata(m3,2)=0;m4=find( angle(receive)>-pi/2&angle(receive)<=0);remessage(1,m4)=1-j;redata(m4,1)=1;redata(m4,2)=0;[resum,ratio1]=symerr(data,redata);pbit(Eb_NO_id)=resum/(sum*2);[total,ratio2]=symerr(message,remessage);pe(Eb_NO_id)=total/sum;endscatterplot(receive)title('C点信号的星座图')Pe=1-(1-1/2*erfc(sqrt(10.^(SNR_DB/10)/2))).^2;Pbit=1/2*erfc(sqrt(10.^(SNR_DB/10)/2));figure(3)semilogy(SNR_DB,pe,':s',SNR_DB,Pe,'-*',SNR_DB,pbit,'-o',SNR_DB,Pbit,':+')legend('QPSK仿真误码率','QPSK理论误码率','QPSK仿真误比特率','QPSK理论误比特率',1) xlabel('信噪比/dB')ylabel('概率P')gird on结果：4、QPSK在A WGN信道下的性能检测clear all;%对随机序列产生的方法初始化s = RandStream('mt19937ar','Seed', 5489);RandStream.setDefaultStream(s);s = RandStream('mcg16807', 'Seed',0);RandStream.setDefaultStream(s);N = 10^5; %码元数Eb_N0 = -4:20; %Eb/N0比特信噪比s_data = zeros(1,N);ErrorCount=zeros(1,length(Eb_N0)); %预先分配内存，用于记录错误的码元数for j = 1:length(Eb_N0)p = (2*(rand(1,N)>0.5)-1) + 1i*(2*(rand(1,N)>0.5)-1);s = (1/sqrt(2))*p; %归一化n = 10^(-Eb_N0(j)/40)*1/sqrt(2)*(randn(1,N) + 1i*randn(1,N)); %加性高斯白噪声r = s + n;%解调r_re = real(r); %实部r_im = imag(r); %虚部s_data(r_re < 0 & r_im < 0) = -1 + -1*1i;s_data(r_re >= 0 & r_im > 0) = 1 + 1*1i;s_data(r_re < 0 & r_im >= 0) = -1 + 1*1i;s_data(r_re >= 0 & r_im < 0) = 1 - 1*1i;ErrorCount(j) = size(find(p- s_data),2); %错误的码元数endsim_QPSK = ErrorCount/N;theory_QPSK = erfc(sqrt(0.5*(10.^(Eb_N0/20)))) -(1/4)*(erfc(sqrt(0.5*(10.^(Eb_N0/20))))).^2;close allfiguresemilogy(Eb_N0,theory_QPSK,'b.-');hold onsemilogy(Eb_N0,sim_QPSK,'mx-');axis([-4 20 10^-3 1])grid on总黄酮生物总黄酮是指黄酮类化合物，是一大类天然产物，广泛存在于植物界，是许多中草药的有效成分。

matlab qpsk调制解调代码

一、介绍Matlab是一种专门用于科学计算和数据可视化的强大工具，QPSK调制解调是数字通信领域中常用的调制解调技术。

本文将介绍如何使用Matlab编写QPSK调制解调的代码。

二、QPSK调制原理QPSK是Quadrature Phase Shift Keying的缩写，即正交相移键控。

在QPSK调制中，将输入的数字比特流分成两路，分别用正弦波和余弦波进行调制。

通过将正弦波和余弦波的相位进行调整，可以将数字比特流转换为模拟信号进行传输。

三、QPSK调制过程1.将输入的数字比特流分为两路，分别表示为I路和Q路。

2.将I路比特流进行调制，使用正弦波作为载波信号，调整相位进行调制。

3.将Q路比特流进行调制，使用余弦波作为载波信号，调整相位进行调制。

4.将调制后的信号进行合并，得到QPSK调制信号。

四、QPSK解调过程1.接收到QPSK调制信号后，将信号分为I路和Q路。

2.将I路信号与正弦波进行乘积运算并积分，得到解调后的I路比特流。

3.将Q路信号与余弦波进行乘积运算并积分，得到解调后的Q路比特流。

五、Matlab QPSK调制解调代码实现```matlab生成随机QPSK调制信号data = randi([0, 1], 1, 1000); 生成随机比特流I = data(1:2:end); 取偶数位作为I路数据Q = data(2:2:end); 取奇数位作为Q路数据symbols = 2*I-1 + 1i*(2*Q-1); 将I路和Q路数据映射为QPSK符号显示QPSK调制信号scatterplot(symbols); 显示QPSK调制信号的星座图QPSK解调data_est = zeros(1, length(data));data_est(1:2:end) = real(symbols) > 0; 解调I路数据data_est(2:2:end) = imag(symbols) > 0; 解调Q路数据```六、总结本文介绍了QPSK调制解调的原理和过程，并给出了使用Matlab实现QPSK调制解调的代码。

利用MATLAB实现QPSK调制及解调

郑州轻工业学院课程设计说明书题目：利用MATLAB实现QPSK调制及解调成绩：郑州轻工业学院课程设计任务书题目利用MATLAB实现QPSK调制及解调主要内容、基本要求、主要参考资料等：主要内容：已知数字信号1011000101101011，码元速率为2400波特，载波频率为1200Hz，利用MATLAB画出QPSK调制波形，并画出调制信号经过高斯信道传输后解调波形及接收误码率，将其与理论值进行比较。

基本要求：1、通过本课程设计，巩固通信原理QPSK调制的有关知识；2、熟悉QPSK产生原理；3、熟悉高斯信道的建模及QPSK解调原理；4、熟悉误码率的蒙特卡罗仿真；5、学会用MATLAB来进行通信系统仿真。

主要参考资料：主要参考资料：1、王秉钧等. 通信原理[M].北京：清华大学出版社，2006.112、陈怀琛.数字信号处理教程----MATLAB释义与实现[M].北京：电子工业出版社,2004.目录一前言 (4)1.1QPSK系统的应用背景简介 (4)1.2 QPSK实验仿真的意义 (4)1.3 实验平台和实验内容 (5)1.3.1实验平台 (5)1.3.2实验内容 (5)二、系统实现框图和分析 (5)2.1、QPSK调制部分， (5)2.2、QPSK解调部分 (7)三、实验结果及分析 (7)3.1、理想信道下的仿真 (7)3.2、高斯信道下的仿真 (8)3.3、先通过瑞利衰落信道再通过高斯信道的仿真 (9)参考文献： (11)附录 (12)基于MATLAB的QPSK仿真设计与实现一前言1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称，意为正交相移键控，是一种数字调制方式。

在19世纪80年代初期,人们选用恒定包络数字调制。

这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。

BPSK和QPSK调制解调原理及MATLAB程序

2.1 PSK调制方式PSK原理介绍（以2-PSK为例）移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。

绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。

二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。

在二进制数字调制中，当正弦载波的相位随二进制数字基带信号离散变化时，则产生二进制移相键控(2PSK)信号。

通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。

二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同，在2PSK调制中，an应选择双极性。

为了解决2PSK 信号解调过程的反向工作问题，提出了二进制差分相位键控(2DPSK)，这里不再详述。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验名称：QPSK调制与解调
一、实验目的：
1、学会QPSK调制与解调系统的构成
2、学会QPSK调制与解调系统的各模块的构建
3、学会误码率与误符号率的统计方法以及Matlab算法
二、实验原理：
1、QPSK：四进制绝对相移键控，也称为多进制数字相位调制，利用载波的四种不同相位状态来表征数字信息的调制方式。

2、QPSK的调制方法有正交调制方式（双路二相调制合成法或直接调相法）、相位选择法、插入脉冲法。

调制与解调系统的构成：
3、各模块的实现方法：
（1）、信源的产生：使用randint(m,n,2) 函数产生一个m 行n 列的随机二进制数列
（2）、QPSK 符号映射：将产生的0，1比特流按照QPSK 调制方式进行映射，本实验采用π/4 QPSK 的调制方式，图为：
（3）、AWGN 信号产生：AWGN 产生器就是产生满足均值为0，方差为1的高斯白噪声。

实验中使用randn(m,n)函数产生一个m 行n 列的高斯噪声序列。

（4）、信号幅度控制：根据AWGN 信道模型，接收信号可以分别表示为
α就是当噪声功率归一化为1（0均值，方差为1）时，根据信噪比关系而计算出来的信号平均幅度
I I I r s n α=+Q Q Q
r s n α=+22210log 10^10s s n n v SNR SNR v sqrt v v ⎛⎫⎛⎫⎛⎫=⇒=* ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭
（5）、QPSK 反映射及判决：对接收到的信号在4种可能的四种信号向量[(1,0), (0,1), (-1,0), (0,-1)]上投影(即进行点积)。

投影最大的值所对应的信号向量就是所发送信号的符号值，然后恢复出比特流
（6）、误码率及误符号率统计：
误码率：将检测出来的比特流和发送的原始比特流进行比较，统计出出现错误的比特数
误符号率：将检测出来的比特流变成两组，构成符号，和发送端符号映射后的符号流进行比较，只要符号中任错一bit ，就算该符号出错。

统计出现错误的符号数
三、实验内容：
1、建立QPSK 的Matlab 仿真模型
2、对仿真模型中各个组成部分进行函数设计和功能仿真 randn('seed',10);mark=randn(1,LENGTH);
subplot(2,2,1);plot(mark);title('watermarc:Gaussian noise');
3、成型滤波器的设计
4、带限信道中的QPSK 调制解调
四、实验步骤：
1、开机，设置好本次仿真目录
2、进入matlab 环境，设置工作路径和目录
3、按照实验方法，一步步进行QPSK 各个模块的设计
s
v α=
（1）、Bit流产生：
global p p=0.5;产生随机二进制序列
（2）、QPSK符号映射：
[m_qpsk1,m_qpsk2]=qpsk_modulation(s_qpsk);
figure(2)，判断所在的相限。

（3）、AWGN噪声产生：
编写实部部信号和虚部信号的幅值语句。

（4）、产生QPSK调制后+AWGN的符号流：
通过平方根升余弦滤波器滤波得到QPSK实部输出信号的10个周期。

（5）、反映射和判决：
plot(10*log10(abs(power_qpsk(1:(length(power_qpsk)+1)/ 2)))-max(10*log10(abs(power_qpsk(1:(length(power_qpsk)+1)/ 2)))))
（6）、SER和BER统计，曲线绘制，分析：
把数据通过循环控制分别求出错误的bit数和符号数，与总的bit数和符号数相比，得出BER和SER，再与理论值比较。

五、出现问题及解决方案
qpsk_modulation函数调用出现错误，修改后没有问题。

六、实验心得
通过研究对QPSK的调制和解调原理，以及利用
MATLAB对其调制和解调进行了编程和编译仿真，得到的结论和理论上是一致的。