空间群符号
230种晶体学空间群

230种晶体学空间群230 种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups晶系(Crystal system)点群(Point group)空间群(Space group) 国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1 C1 P1C i P单斜晶系2 P2 P21 C2m Pm Pc Cm Cc2/m P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222 P222 P2221 P21212P212121 C2221 C222 F222 I222 I212121 mm2Pmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2Fdd2 Imm2 Iba2 Ima2mmmPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方晶系4 P4 P41 P42 P43 I4 I41P I4/m P4/m P42/m P4/n P42/n I4/m I41/a422P422 P4212P4122P41212P4222P42212P4322P43212I422I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mmI4cm I41md I41cd2mP 2m P2c P 21m P21c P m2Pc2P b2 P n2Im2I c2 I 2m I 2d4/mmm P4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmc P42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcm不同晶系的晶格类型Lattice Types of Different Crystal Systems简单立方体心立方面心立方三斜三斜晶系立方晶系简单单斜底心单斜简单四方体心四方单斜晶系四方晶系简单正交底心正交交体正交面心正交正交晶系六方三方六方晶系三方晶系32 种晶体学点群的记号Symbols of the 32 Crystallographic Point Groups序号(No. )晶系(Crystalsystem)点群(Point group)轴向对称要素的方向和数目(Orientation and number ofaxial symmetry factor)劳埃群(Lauegroup)国际符号(HM)圣佛利斯符号(Schfl.)1 三斜晶系1 C1C i2 单斜晶系2 C22/m m C32/m C2h3 正交晶系222 D2mmm mm2 D2vmmm D2h4 四方晶系c a [110]4 C4 44/m S44/m C4h422 D4 4 2(2) 2(2)4/mmm 4mm C4v 4 m(2) m(2)2m D2d 2(2) m(2)4/mmm D4h5 三方晶系c a3 C3 3C3i32 D3 3 2(2)m 3m C3v 3 m(3)m D3d6 六方晶系 c a [210]6 C6 6 6/mC3h6/mC 6h622 D 6 6 2(3) 2(3) 6/mmm6mmC 6v 6m(3) m(3) m2D 3hm(3)2(3)6/mmmD 6h7立方晶系c[111] [110]23T2(3) 3(4)mmT h(4)432 O 4(3) 3(4) 2(6) mm3mT d 3(3)3(4)m(6)mmO h(4)点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
点群空间群
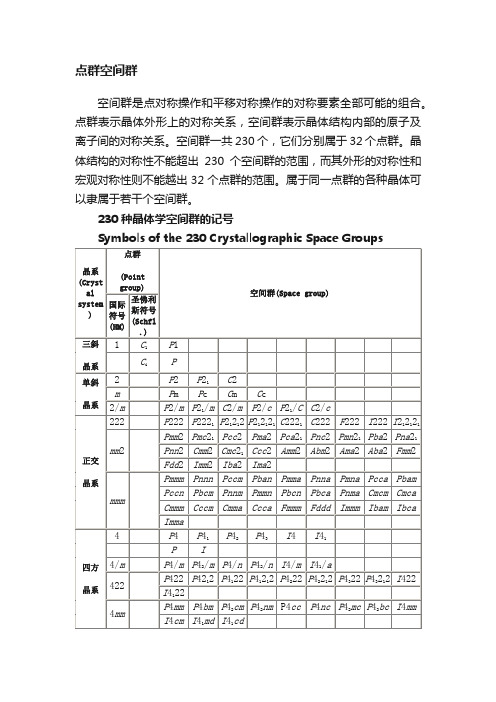
Symbols of the 230 Crystallographic Space Groups
晶系(Crystal system)
点群
(Point group)
空间群(Space group)
国际符号(HM)
圣佛利斯符号(Schfl.)
三斜
晶系
1
C1
P1
Ci
P
单斜
晶系
2
P2
Imma
四方
晶系
4
P4
P41
P42
P43
I4
I41
P
I
4/m
P4/m
P42/m
P4/n
P42/n
I4/m
I41/a
422
P422
P4212
P4122
P41212
P4222
P42212
P4322
P43212
I422
I4122
4mm
P4mm
P4bm
P42cm
P42nm
P4cc
P4nc
P42mc
P42bc
I4mm
I4cm
I41md
I41cd
2m
P2m
P2c
P21m
P21c
Pm2
Pc2
Pb2
Pn2
Im2
Ic2
I2m
I2d
4/mmm
P4/mmm
P4/mcc
P4/nbm
P4/nnc
P4/mbm
P4/mnc
P4/nmm
P4/ncc
P42/mmc
P42/mcm
P42/nbc
P42/nnm
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
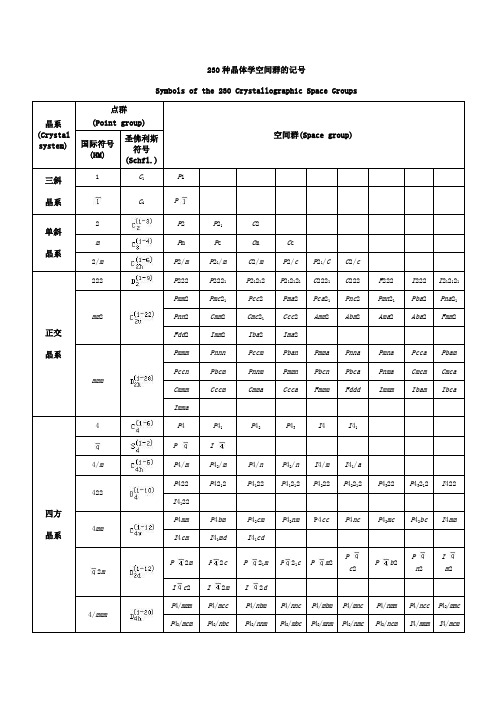
230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups2m 2P P 2m bI c22m 11m P R m c m2m c23m 33I P3Im m n Pm Pn Fm Fm Fd mFdm d空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
菱方是不标准的说法,应该是三方,菱面体是三方的R点阵中的一种,7个晶系分别是立方cubic(a=b=c,α=β=γ=90o,只有一个晶胞参数a)四方tetragonal(a=b≠c,α=β=γ=90o,有2个晶胞参数a和b)六方hexagonal(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c)正交orthorhombic(a≠b≠c,α=γ=90o,有3个晶胞参数a,b和c)单斜monoclinic(a≠b≠c,α=γ= 90o,β≠90o,有4个晶胞参数a,b,c和β)三斜triclinic(a≠b≠c,α≠β≠γ,有6个晶胞参数a,b,c,α,β和γ)三方(a=b≠c,α=β=90o,γ=120o,有2个晶胞参数a和c) rhombohedral对于三方这个问题,很多书上都是错误的,三方跟六方绝对不能混为一谈F is face-centered;P is Primitive; I is body-centered;不同晶系的晶格类型32种晶体学点群的记号2mm mm2m(4)3m 3(3)mm (4)点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
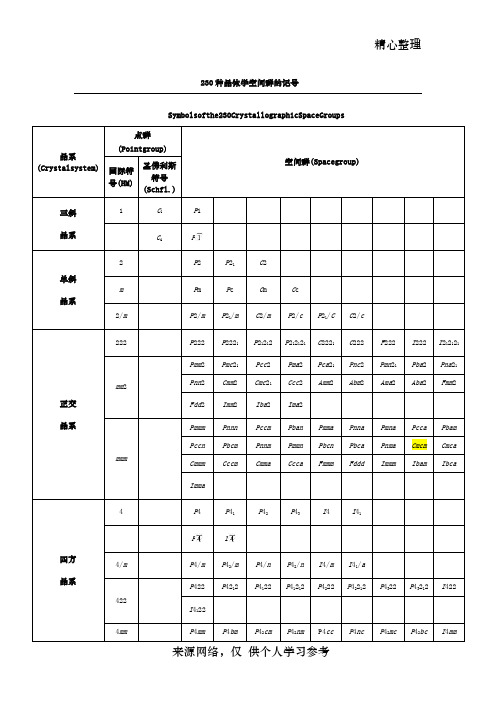
P42/nmc
P42/ncm
I4/mmm
I4/mcm
I41/amd
I41/acd
三方
晶系
3
P3
P31
P32
R3
P
R
32
P312
P321
P3112
P3121
P3212
P3221
R32
3m
P3m1
P31m
P3c1
P31c
R3m
R3c
m
P 1m
P 1c
P m1
P c1
R m
R c
六方
晶系
6
P6
m
Pm3
Pn3
Fm3
Fd3
Im3
Pa3
Ia3
432
P432
P4232
F432
F4132
I432
P4332
P4132
I4132
3m
P 3m
F 3m
I 3m
P 3n
F 3c
I 3d
m m
Pm m
Pn n
Pm n
Pn m
Fm m
Fm c
Fd m
Fd c
Im m
Ia d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。空间群一共230个,它们分别属于32个点群。晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。属于同一点群的各种晶体可以隶属于若干个空间群。
230种晶体学空间群的记号
Symbolsofthe230CrystallographicSpaceGroups
种晶体学空间群的记号及常见矿石的名称分子式与所属晶系
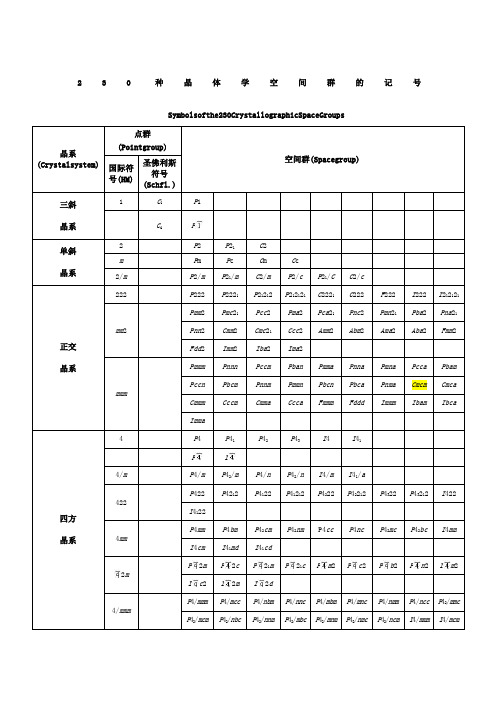
230种晶体学空间群的记号Symbolsofthe230CrystallographicSpaceGroups晶系(Crystalsystem)点群(Pointgroup)空间群(Spacegroup)国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1C1P1C i P单斜晶系2P2P21C2m P m P c C m C c2/m P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222P222P2221P21212P212121C2221C222F222I222I212121 mm2Pmm2Pmc21Pcc2Pma2Pca21Pnc2Pmn21Pba2Pna21Pnn2Cmm2Cmc21Ccc2Amm2Abm2Ama2Aba2Fmm2Fdd2Imm2Iba2Ima2mmmPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方晶系4P4P41P42P43I4I41P I4/m P4/m P42/m P4/n P42/n I4/m I41/a422P422P4212P4122P41212P4222P42212P4322P43212I422I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mmI4cm I41md I41cd2mP2m P2c P21m P21c P m2P c2P b2P n2I m2I c2I2m I2d4/mmmP4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmcP42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcmI41/amd I41/acd三方晶系3P3P31P32R3P R32P312P321P3112P3121P3212P3221R32 3m P3m1P31m P3c1P31c R3m R3cm P1m P1c P m1P c1R m R c六方晶系6P6P61P65P62P64P63P6/m P6/m P63/m622P622P6122P6522P6222P6422P6322 6mm P6mm P6cc P63cm P63mcm2P m2P c2P2m P2c6/mmm P6/mmm P6/mcc P63/mcm P63/mmc立方晶系23P23F23I23P213I213m Pm3Pn3Fm3Fd3Im3Pa3Ia3432P432P4232F432F4132I432P4332P4132I41323m P3m F3m I3m P3n F3c I3dm mPm m Pn n Pm n Pn m Fm m Fm c Fd m Fd c Im mIa d晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
230种晶体学空间群熊夫符号

深入探讨230种晶体学空间群熊夫符号一、引言在晶体学领域中,晶体结构的描述和分类要依赖于空间群。
空间群是对晶格进行平移、旋转和镜面反射操作的一组对称操作的集合。
而熊夫符号则是对这些对称操作进行简洁表示的一种形式。
全球晶体学家们经过长期的努力,总结出了230种不同的晶体学空间群熊夫符号,这些符号有着极其丰富的内涵和深刻的科学意义。
在本文中,我们将深入探讨230种晶体学空间群熊夫符号的分类、特点和应用,并共享对这一主题的个人观点和理解。
二、230种晶体学空间群熊夫符号的分类230种晶体学空间群熊夫符号根据其对称性和操作特征可以分为七大类,分别是三维空间群、菱形系空间群、四方系空间群、正交系空间群、单斜系空间群、三斜系空间群和五维空间群。
每一类空间群都有其独特的特点和应用范围,对于晶体学研究和应用具有重要意义。
1. 三维空间群三维空间群是最基本的一类空间群,共有73种不同的熊夫符号代表着它们各自的对称操作特点。
在晶体学研究中,三维空间群被广泛应用于描述和分类各种晶体结构,为我们理解晶体的对称性和性质提供了重要的参考。
2. 菱形系空间群菱形系空间群共有16种不同的熊夫符号,它们具有特殊的对称性和操作特点,在一些特定的晶体结构中发挥着重要的作用。
研究人员对菱形系空间群进行了深入的探讨和分析,为我们理解和应用这些空间群提供了重要的理论基础。
3. 四方系空间群四方系空间群包括各种四方晶系中的空间群,共有22种不同的熊夫符号。
这些空间群在研究四方晶体结构和性质方面发挥着重要的作用,对于高温超导材料等功能材料的研究具有重要意义。
4. 正交系空间群正交系空间群是描述和分类正交晶系中的空间群,共有59种不同的熊夫符号代表着它们丰富的对称性和操作特点。
研究人员对正交系空间群进行了深入研究,为我们理解和应用这些空间群提供了重要的理论指导。
5. 单斜系空间群单斜系空间群包括各种单斜晶系中的空间群,共有13种不同的熊夫符号。
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系
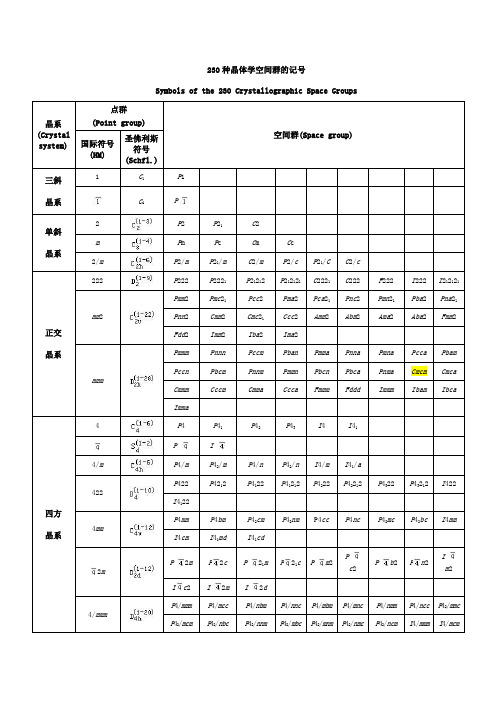
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R m c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m
m (4)
点群不存在平移操作,所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
有这4个对称要素组合出32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。
正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。
230种空间群
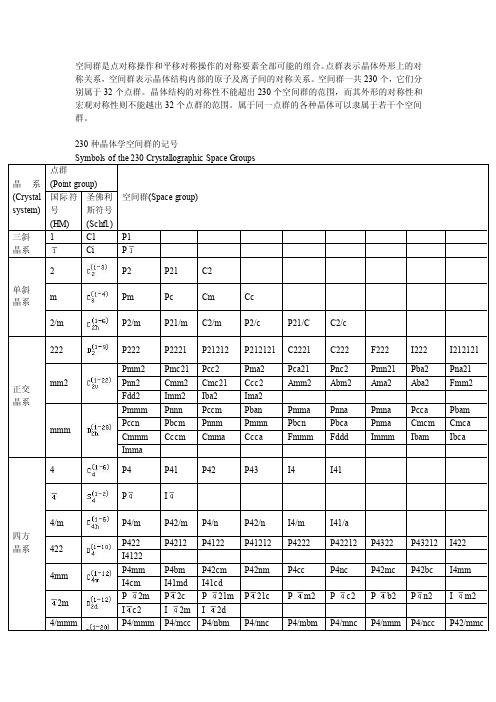
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
230种晶体学空间群的记号
Ci
I
2m
2m P P P I
m 1m P
m2 m2
m
3m 3m I P
Pm Im m
1 三斜晶系
2 单斜晶系
3 斜方晶系
4 四方晶系
为2,
为⊥m,5 三方晶系
6 六方晶系
(191) P6/mmm 7 等轴晶系。
晶体结构空间群点群

(二)点群、单形及空间群点群:晶体可能存在的对称类型。
通过宏观对称要素在一点上组合运用而得到。
只能有32种对称类型,称32种点群表1- 3 32种点群及所属晶系*2/m表示其对称面与二次轴相垂直,/表示垂直的意思。
其余类推同一晶系晶体可为不同点群的原因:阵点上原子组合情况不同。
如错误!未找到引用源。
,对称性降低,平行于六面体面的对称面不存在,4次对称轴也不存在。
理想晶体的形态―单形和聚形:单形:由对称要素联系起来的一组同形等大晶面的组合。
32种对称型总共可以导出47种单形,如错误!书签自引用无效。
,错误!书签自引用无效。
,错误!书签自引用无效。
所示聚形:属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。
大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体,如单形四方柱与平行双面形成了四方柱体的真实晶体形态空间群:描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。
属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群,空间群有230种,见教材中表1- 4国际通用的空间群符号及其所代表的意义为:P:代表原始格子以及六方底心格子(六方底心格子为三方晶系和六方晶系所共有)。
F:代表面心格子。
I:代表体心格子。
C:代表(001)底心格子(即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
A:代表(100)底心格子(即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
R:代表三方原始格子。
其它符号:意义与前述相同表1- 4 晶体的空间群、点群、晶系、晶族一览表续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4/k/174/stu/content/1.1.3.2.htm。
230种空间群符号例题

230种空间群符号例题
空间群是描述晶体结构的一种方法,它包括点群操作和平移操作。
空间群共有230种不同的类型,每一种类型都有其特定的空间
群符号。
这些符号通常由字母、数字和下标组成,用来表示空间群
的对称性质和操作特征。
举例来说,空间群P1的符号表示为"P1",其中P表示
primitive(基本的),1表示空间群的编号。
另外,空间群C2/m
的符号表示为"C2/m",其中C表示有一个反演中心,2表示有二重
旋转轴,m表示有镜面反射。
其他的空间群符号包括但不限于,P2₁/c、P4₂/mnm、I4/mmm、Fm-3m等。
每个符号代表着不同的对称性质和操作特征,这些符号
在晶体学和固体物理研究中具有重要的意义。
总的来说,空间群符号是一种用来描述晶体结构对称性和操作
特征的标记,它们的多样性和复杂性反映了晶体结构的多样性和复
杂性。
230种晶体学空间群的记号和常见矿石的名称、分子式与所属晶系
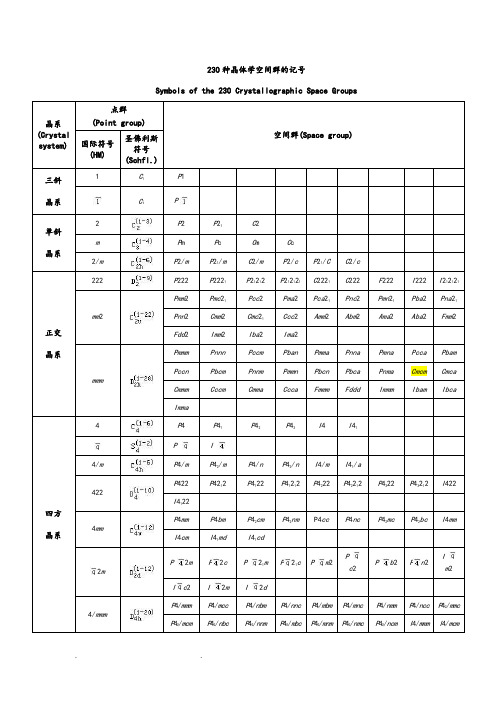
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R m c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系.空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个.它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围.而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m
m (4)
点群不存在平移操作.所有的对称要素都集中在一个共同的点上。
对称要素包括旋转、反映、反伸(对称中心)与旋转反伸。
有这4个对称要素组合出32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。
正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。
230种空间群符号及含义

空间群(Space group)是一种描述晶体结构的数学工具,它把晶体中的所有原子看作点,并使用符号(由数字和符号组成)来表示这些点的几何排列。
空间群的种类非常多,通常在几千种以上,但常用的只有几十种。
以下是一些常用的空间群符号及其含义:
1. 225型空间群(P22_1_5):这种空间群表示具有两套相互垂直的近正方形的简单晶体结构,每个原子都在一个平面上,通过角顶相互连接。
2. 432型空间群(P4_3_2):这种空间群表示具有四套相互垂直的矩形排列的简单晶体结构,每个原子都在一个平面上,通过角顶相互连接。
3. 62型空间群(I6_2):这种空间群表示具有六套相互垂直的六边形排列的复杂晶体结构,每个原子都在一个平面上,通过角顶相互连接。
4. 61型空间群(P6_1):这种空间群表示具有六套相互垂直的六边形排列的简单晶体结构,每个原子都在一个六边形的顶点上。
5. 31型空间群(P3_1):这种空间群表示具有三套相互垂直的平面排列的简单晶体结构,每个原子都在一个平面上。
需要注意的是,空间群的种类非常多,不同文献和教科书可能会对同一晶体的空间群描述有所不同。
因此,在进行晶体结构分析时,需要参考具体的文献或教科书来确定具体的空间群符号和含义。
此外,不同的晶体结构也可能需要不同的计算参数和方法,因此在应用空间群进行晶体结构分析时需要选择适当的软件和算法。
目前常用的晶体结构分析软件如VESTA、Pymatgen等都提供了对空间群的详细解释和使用方法。
以上就是部分常见的空间群符号及含义,如果您需要了解更多空间群的符号及含义,建议您查阅相关的专业书籍或咨询专业人士。
空间群

国际符号international symbol 采用国际符号,不仅可以表示出各种晶类中有那些对称元素,而且还能表示出这些对称元素在空间的方向。
国际符号根据各种晶类的对称性可以是三项、或二项、或一项符号组成,它分别表示晶体某三个、或二个、或一个方向上的对称元素。
如果在某一个方向上,同时具有对称轴和垂直于此轴的对称面,则写成分数形式。
熊夫利斯(Sch öenfles )符号C n :字母表示旋转的意思,组标n 表示旋转的次数,n=1、2、3、4、6。
例如C 2代表二次旋转轴。
C nh :表示除了n 次旋转轴外,还包括一个与此轴垂直的对称面。
C nv :表示除了n 次旋转轴外,还包括一个与此轴重合(即平行)的对称面。
C ni :表示除了n 次旋转轴外,还包括一个对称中心。
C i:表示有一个对称中心。
S4:表示有一个四次旋转倒反轴。
D n:表示除了n次主旋转轴外,还包括n 个与之轴垂直的二次旋转轴。
D nh:表示除了D n的对称性外,还包括一个与主旋转轴垂直的对称面,和n个与二次旋转轴重合(即平行)的对称面。
D nd:表示除了D n的对称性外,还包括n个T:除了四个三次旋转轴外,还包括三个正交的二次旋转轴。
T h:除了T的对称性外,还包括与二次旋转轴垂直的三个对称面。
T d:除了T的对称性外,还包括六个平分两个二次旋转轴夹角的对称面。
O:包括三个互相垂直的四次旋转轴,六个二次旋转轴,和四个三次旋转轴。
O h:除了O的对称性外,还包括T d与T h的对国际符号与熊氏符号对比国际符号熊氏符号1C 12C 23C 34C 46C 6m C sC i ,S 2S 14其它注意事项由于分子没有无限周期性的限制,所以分子点群的数目要多于晶体中的点群数目32个; 自然界对称性很多,例如:五度对称性,足球,富勒烯C 60,buckministerfullerence ,碳管小结summary密勒指数(Miller indices)对称元素和对称操作晶体的三十二个点群对称性和点群对于压电铁电体非常重要! 只有晶体才会有压电铁电性,不存在非晶压电铁电体。
种空间群记号
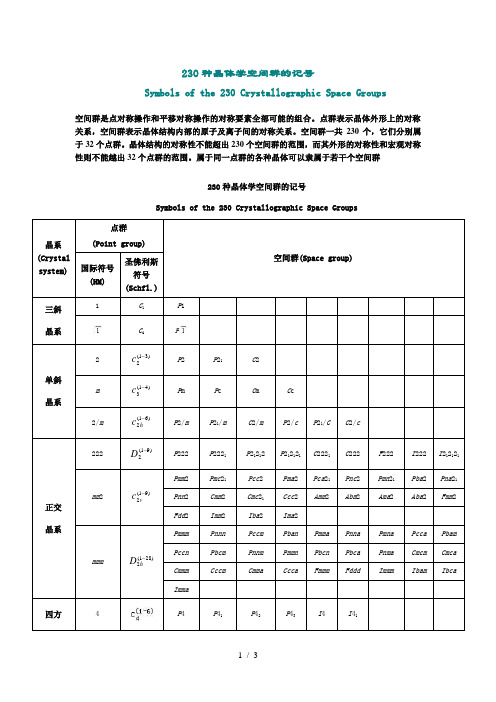
230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups晶系(Crystal system)点群(Point group)空间群(Space group) 国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1 C1P1C i P单斜晶系2 )31(2-c P2 P21 C2m )41(3-c P m P c C m C c2/m )61(2-hc P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222 )91(2-D P222 P2221 P21212 P212121 C2221 C222 F222 I222 I212121 mm2 )91(2-vcPmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2Fdd2 Imm2 Iba2 Ima2mmm )281(2-hDPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方 4 P4 P41 P42P43 I4 I414/m P4/m P42/m P4/n P42/n I4/m I41/a422P422 P4212 P4122 P41212 P4222 P42212 P4322 P43212 I422I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mmI4cm I41md I41cd2mP2m P2c P21m P21c P m2 P c2 P b2 P n2 I m2I c2 I2m I2d4/mmmP4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmcP42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcmI41/amd I41/acd三方晶系3 P3 P31P32R3P R32 P312 P321 P3112 P3121 P3212 P3221 R323m P3m1 P31m P3c1 P31c R3m R3cm P1m P1c P m1 P c1 R m R c六方晶系6 P6 P61P65P62P64P63P6/m P6/m P63/m622 )61(6-D P622 P6122 P6522 P6222 P6422 P63226mm)41(6-vc P6mm P6cc P63cm P63mcm2)41(3-hD P m2 P c2 P2m P2c6/mmm )41(6-hD P6/mmm P6/mcc P63/mcm P63/mmc立方晶系23)51(-TP23 F23 I23 P213 I213m)71(-hT Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3432)81(-OP432 P4232 F432 F4132 I432 P4332 P4132 I4132 3m )61(-dT P3m F3m I3m P3n F3c I3dM3m )61(-hOPm m Pn n Pm n Pn m Fm m Fm c Fd m Fd c Im mIa d。
空间群符号

空间群符号230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups晶系(Crystal system)点群(Point group)空间群(Space group) 国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1 C1P1C i P单斜晶系2 P2 P21 C2m P m P c C m C c2/m P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222 P222 P2221 P21212 P212121 C2221 C222 F222 I222 I212121 mm2Pmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2Fdd2 Imm2 Iba2 Ima2mmmPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方 4 P4 P41 P42P43 I4 I41晶系P I4/m P4/m P42/m P4/n P42/n I4/m I41/a422P422 P4212 P4122 P41212 P4222 P42212 P4322 P43212 I422 I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mm I4cm I41md I41cd2mP2m P2c P21m P21c P m2 P c2 P b2 P n2 I m2I c2 I2m I2d4/mmm P4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmc P42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcm I41/amd I41/acd 三方晶系3 P3 P31P32R3P R32 P312 P321 P3112 P3121 P3212 P3221 R32 3m P3m1 P31m P3c1 P31c R3m R3cm P1m P1c P m1 P c1 R m R c六方晶系6 P6 P61P65P62P64P63P6/m P6/m P63/m622 P622 P6122 P6522 P6222 P6422 P6322 6mm P6mm P6cc P63cm P63mcm2P m2 P c2 P2m P2c6/mmm P6/mmm P6/mcc P63/mcm P63/mmc立方晶系23 P23 F23 I23 P213 I213m Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3432 P432 P4232 F432 F4132 I432 P4332 P4132 I41323m P3m F3m I3m P3n F3c I3dm mPm m Pn n Pm n Pn m Fm m Fm c Fd m Fd c Im mIa d。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。
点群表示晶体外形上的对称关系,空间群表示晶体结构内部的原子及离子间的对称关系。
空间群一共230个,它们分别属于32个点群。
晶体结构的对称性不能超出230个空间群的范围,而其外形的对称性和宏观对称性则不能越出32个点群的范围。
属于同一点群的各种晶体可以隶属于若干个空间群。
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
晶系(Crystal system)
点群
(Point group)
空间群(Space group) 国际符号
(HM)
圣佛利斯
符号
(Schfl.)
三斜晶系1 C1P1
C i P
单斜晶系
2 P2 P21 C2
m P m P c C m C c
2/m P2/m P21/m C2/m P2/c P21/C C2/c
正交晶系222 P222 P2221 P21212 P212121 C2221 C222 F222 I222 I212121 mm2
Pmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21
Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2
Fdd2 Imm2 Iba2 Ima2
mmm
Pmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca Pbam
Pccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm Cmca
Cmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam Ibca
Imma
四方 4 P4 P41 P42P43 I4 I41
晶系P I
4/m P4/m P42/m P4/n P42/n I4/m I41/a
422
P422 P4212 P4122 P41212 P4222 P42212 P4322 P43212 I422
I4122
4mm
P4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mm
I4cm I41md I41cd
2m
P2m P2c P21m P21c P m2 P c2 P b2 P n2 I m2
I c2 I2m I2d
4/mmm P4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmc P42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcm I41/amd I41/acd
三方晶系3 P3 P31P32R3
P R
32 P312 P321 P3112 P3121 P3212 P3221 R32 3m P3m1 P31m P3c1 P31c R3m R3c
m P1m P1c P m1 P c1 R m R c
六方晶系
6 P6 P61P65P62P64P63
P
6/m P6/m P63/m
622 P622 P6122 P6522 P6222 P6422 P6322 6mm P6mm P6cc P63cm P63mc
m2P m2 P c2 P2m P2c
6/mmm P6/mmm P6/mcc P63/mcm P63/mmc
立方晶系
23 P23 F23 I23 P213 I213
m Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3
432 P432 P4232 F432 F4132 I432 P4332 P4132 I4132
3m P3m F3m I3m P3n F3c I3d
m m
Pm m Pn n Pm n Pn m Fm m Fm c Fd m Fd c Im m
Ia d。
