热学玻尔兹曼分布.ppt
《物理化学第4版》第六章6.4 玻尔兹曼分布ppt课件

能量零点的选择对玻尔 兹曼分布有无影响 ?
ni
N
gq0 qe0 kT
形式完全相同!
ni
N q
g i e i
kT
N q0 eε 0
kT
g e
ε
0 i
ε
0
kT
i
N q0
g eε
0 i
i
kT
结论:对玻尔兹曼分布中任一能级上粒子的分布
4. 能量零点的选择对配分函数的影响
设粒子的能级为ε0,ε1,ε2,…,则
q
g i e i
kT
g 0 e 0
kT
g e1 / kT 1
i
通常选择粒子的基态能级作为能量的零点(任何能级的
能量不为负),各能级的能量为 i0 i 0
q0
g ei0 i
kT
g eε
0 0
0
kT
g1eε
0 1
/ kT
数 ni 没有影响。
结论:选择不同的能量零点会影响配分函数的
值,但对计算玻尔兹曼分布中任一能级上粒子 的分布数 ni 没有影响。
注意:
由基态能级的能位为零的粒子 配分函数q0,计算所得系统系
U
nii
ni
(
0 i
0)
统的热力学函数U、H、A、G
i
i
,与由绝对能量对应的粒子配
ni
0 i
N 0
kT
i
振动配分函数
qv
g e v,i v ,i
kT
i
电子配分函数
qe
g ee ,i e ,i
kT
i
热力学统计 第七章玻尔兹曼统计

al !
al lal ln ln N ! N ln N al ln al ! l l l x 1 ln x ! x ln x x S k ln S
0
设=1时,S=0 S0=0
ln Z S Nk (ln Z )
2.内能U与广义力Y的统计表达式
2.1 内能U的统计表达式
N N l U al l ll e Z Z l l N Z ln Z N Z
e l l
N al l e l Z Z l e l
配分函数Z :
l
Z l e l
l
分布在能级l 的粒子数:
N al l e l Z
已知(l, l),可求Z——并不容易!
经典粒子: 配分函数Z :
Z l e l
l
Z e
( q . p )
dqdp e D( )d r h
积分因子:
如果 X ( x, y )dx Y ( x, y )dy 不是全微分,但存在函数 ( x, y ) ,使得
( x, y ) X ( x, y )dx ( x, y )Y ( x, y )dy 为全微分, 即
( x, y ) X ( x, y )dx ( x, y )Y ( x, y )dy ds ( x, y )
S k ln
满足经典极限的非定域系统:
ln
l
la
l
al !
al S k N ln N al ln l l
S0
lal al ln ln N ln N al ln ln N ! l l al ! l
玻尔兹曼速度分布律

分子平均动能与温度的关系
分子平均动能是气体分子动能的平均值,与温度T有关。根据 玻尔兹曼速度分布律,分子平均动能随着温度的升高而增大 。这是因为高温下气体分子运动速度更快,具有更高的动能 。
分子平均动能与温度的关系可以用公式E=3/2kT表示,其中E 是分子平均动能,k是玻尔兹曼常数,T是绝对温度。这个公 式反映了气体分子平均动能与温度的正比关系。
高温高压下的适用性
当温度和压力较高时,玻尔兹曼速度分布律可能不再适用。这是因为高温和高压条件下,气体分子间 的相互作用以及分子与容器壁之间的相互作用变得更加复杂,需要考虑量子效应和相对论效应的影响 。
在高温高压条件下,可能需要采用其他理论模型,如量子统计力学或相对论统计力学,来描述气体分 子的速度分布。
适用范围
玻尔兹曼速度分布律适用于稀薄气体,即在分子数密度较低的情况 下,气体分子的运动行为可以用该定律来描述。
02 玻尔兹曼速度分布律的数 学表达式
表达式概述
玻尔兹曼速度分布律是描述气体分子在平衡态下速度分布的统计规律,其数学表达 式为:f(v) = (m/2πkT)^(3/2) * 4πv^2 * e^(-mv^2/2kT),其中m是分子质量,k 是玻尔兹曼常数,T是绝对温度。
玻尔兹曼速度分布律
目录
CONTENTS
• 引言 • 玻尔兹曼速度分布律的数学表达式 • 玻尔兹曼速度分布律的物理意义 • 玻尔兹曼速度分布律的应用 • 玻尔兹曼速度分布律的局限性 • 玻尔兹曼速度分布律的发展与展望
01 引言
背景介绍
气体分子运动论
气体分子运动论是物理学的一个重要 分支,主要研究气体分子在空间中的 运动规律和相互作用。
气体分子运动论和热力学基础之玻尔兹曼分布律

kT
)dvx
dvy
dvz
dxdydz
在温度一定时,分子的平均动能是一定的, 所以,分子优先占据势能较低的位置。
如果对坐标 进行积分
N0 n0
V
exp( p )dxdydz
kT
上式就演化为麦克 斯韦速率分布律。
由于对速率的积
分是归一化的
(m 2πkT
)3/ 2
exp(
k kT
)dvxdvydvz
/
2
exp(
kT
)dvx
dvy
dvz
dxdydz
分布律,exp(-ε/kT) 称为概率因子。
其中n0表示εp = 0处单位体积内各种速度的总分子数。
在一定的速度和坐标范围内,在一定的温度下的 平衡状态中,分子的能量越低,分子数就越多态。
{范例8.6} 玻尔兹曼分布律
dN
n0
(
m 2πkT
)3
/
2
exp(
[解析](2)在重力场中,气体分子的密度 随高度的分布可用点的密集程度表示。
不论什么 分子,由 于重力的 作用,分 子数密度 在低空比 较大,在 高空比较 小。
氖气的分 子量比较 小,分子 数密度减 小得比较 慢,在同 样的高度 内,点数 相对比较 均匀。
氧气的 分子量 比较大, 分子数 密度减 小得比 较快, 在高空 比较稀 薄。
由于势能与位置有关,因此分子在空间的分布是不均匀的。
玻尔兹曼认为:气体在一定的温度下处于平衡状态时,在速
度间隔vx~vx + dvx、vy~vy + dvy、vz~vz + dvz和坐标间隔x~x + dx 、
y~ y + dy、z~z + dz中的分子数为
11-3最可几分布、平衡分布、玻尔兹曼分布及配分函数定义

Physical Chemistry(下册)物理化学(下册)第七章电化学第九章化学动力学第八章界面现象第十章胶体化学第十一章统计热力学物理化学(下)绪论第十一章统计热力学Chapter 11 Statistical thermodynamics§11-!本章基本要求§11-1统计热力学基本概念及术语§11-2能级分布的微态数及系统的总微态数§11-3最可几分布、平衡分布、玻尔兹曼分布及配分函数定义§11-4粒子配分函数的计算§11-5系统内能热容与配分函数的关系§11-6系统熵与配分函数的关系§11-7其它热力学函数与配分函数的关系§11-8理想气体反应标准平衡常数与配分函数的关系§11-$本章小结与学习指导一、概率二、等概率定理三、最概然分布四、最概然分布与平衡分布五、最概然分布推导六、粒子配分函数定义七、玻尔兹曼分布§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义1.概率若一个事件有多种可能则称为复合事件,各种可能出现的事件称为可能事件,或偶然事件。
复合事件重演m 次偶然事件A 出现n 次,当m趋于无穷大时,n/m 为定值,定义为事件A 出现的概率或称概然率,用PA表示。
一、概率§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义一、概率§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义在统计热力学中,系统的粒子数量级一般为1024左右,且粒子在不停的运动,碰撞频率极高,使系统微态不断变化。
在很短的时间内粒子经历的微态已足以反映出各种微态出现几率的稳定性。
即出现各微态的可能性与数学几率相符。
等概率定理:在(N、U、V)确定情况下,系统各微态出现的概率相等。
P=1/二、等概率定理§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义1.分布概率在(N、U、V)确定时粒子的各种分布D的微态数ωD不同,所以各种分布出现的几率不同。
玻尔兹曼分布

玻尔兹曼分布玻尔兹曼分布律是一种覆盖系统各种状态的概率分布、概率测量或者频率分布。
当有保守外力(如重力场、电场等)作用时,气体分子的空间位置就不再均匀分布了,不同位置处分子数密度不同。
玻尔兹曼分布律是描述理想气体在受保守外力作用、或保守外力场的作用不可忽略时,处于热平衡态下的气体分子按能量的分布规律玻尔兹曼(L.E.Boltzmann)将麦克斯韦分布律推广到有外力场作用的情况。
在等宽的区间内,若E1>E2,则能量大的粒子数dN1小于能量小的粒子数dN2,状态即粒子优先占据能量小的,这是玻尔兹曼分布律的一个重要结果。
经过将近一个世纪的传播,物理学界、化学界渐渐接受了道尔顿的“原子—分子模型”,但原子、分子的确凿证据迟迟没有找到。
恰恰此时,一股更强大的科学成就——热力学第一、第二定律出现了。
热力学原则上解决了一切化学平衡的问题。
1892年,物理化学家奥斯特瓦尔德试图在此基础上证明,将物理学和化学问题还原为原子或分子之间的力学关系是多余的。
他试图将“能量”赋以实物一样的地位,甚至要把物质还原为能量。
他提出“世界上的一切现象仅仅是由于处于空间和时间中的能量变化构成的”。
在统计学中,麦克斯韦- 玻尔兹曼分布是一种特殊的概率分布,以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。
它一开始在物理中定义并使用是为了描述(特别是统计力学中描述理想气体)在理想气体中粒子自由移动的在一个固定容器内与其它粒子无相互作用的粒子速度,除了它们相互或与它们的热环境交换能量与动量所产生的非常短暂的碰撞。
在这种情况下粒子指的是气态粒子(原子或分子),并且粒子系统被假定达到热力学平衡。
在这种分布最初从麦斯威尔1960年的启发性的基础上衍生出来时,玻尔兹曼之后对这种分布的物理起源进行了大量重要调查粒子速度概率分布指出哪一种速度更具有可能性:粒子将具有从分布中随机选择的速度,并且比其它选择方法更可能在速度范围内。
玻尔兹曼分布

玻尔兹曼分布定律是覆盖系统各种状态的概率分布,概率测量或频率分布。
当存在保守的外力(例如重力场,电场等)时,气体分子的空间位置不再均匀分布,并且在不同位置分子数密度也不同。
玻尔兹曼分布定律描述了在保守外力或保守外力场的作用下处于热平衡状态的理想气体分子的能量分布。
L. E. Boltzmann将麦克斯韦分布定律扩展到外力场的情况。
在相同的宽度范围内,如果E1> E2,则能量DN1大的粒子的数量少于能量DN2小的粒子的数量,并且状态是粒子优先占据较小的能量,这是玻尔兹曼的重要结果分配法。
经过近一个世纪的传播,物理和化学界逐渐接受道尔顿的“原子分子模型”,但是原子和分子的确凿证据尚未得到发现。
这时,出现了更强大的科学成就,即热力学的第一定律和第二定律。
热力学原则上解决了化学平衡的所有问题。
1892年,物理化学家奥斯特瓦尔德(Ostwald)试图证明没有必要将物理和化学问题减少到原子或分子之间的机械关系。
他试图赋予“能量”与物质对象相同的状态,甚至使物质恢复能量。
他提出“世界上所有现象都仅由时空的能量变化构成”。
在统计中,麦克斯韦·玻尔兹曼分布是一种特殊的概率分布,以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。
它首先被定义并在物理学中用于描述(特别是在统计力学中)粒子在理想气体中自由移动而不与固定容器中的其他粒子相互作用的速度,除了粒子与其热环境之间的非常短时间的碰撞之外通过交换能量和动力。
在这种情况下,粒子是指气态粒子(原子或分子),并且假定粒子系统达到了热力学平衡。
当这种分布最初是从1960年的麦克斯韦启蒙运动中获得的时,玻尔兹曼对这种分布的物理起源进行了许多重要的研究。
粒子速度的概率分布表明哪个速度更有可能:粒子具有从分布中随机选择的速度,并且比其他选择方法更有可能处于速度范围内。
分布取决于系统温度和颗粒质量。
Maxwell Boltzmann分布适用于经典理想气体,这是理想的真实气体。
第七章节-玻尔兹曼统计

在准静态过程中,系统从外界所吸收的热量等于 粒子在各能级重新分布所增加的内能. 根据热力学第二定律
dQ不是全微分,与过程有关,有一积分因子, 除以T后得全微分dS,dS是全微分
BEIJING NORMAL UNIVERSITY
BEIJING NORMAL UNIVERSITY
积分因子
熵的统计表达式
3 U = NkT 2
BEIJING NORMAL UNIVERSITY
麦克斯韦速度分布律
讨论气体分子作无规热运动时,气体分子质心的平移 运动速度所表现出来的统计分布规律。 一、麦克斯韦速度分布律 1859年,麦克斯韦在研究分子相互碰撞作无规则运 动时,得到了气体分子按其质心速度分布的统计规律 麦克斯韦速度分布律
物态方程
∂ ln Z 注:也可直接利用公式 p = NkT 计算 ∂V
⎛ ∂F ⎞ S = −⎜ ⎟ ⎝ ∂T ⎠V
2πmk 3 3 3 = Nk ln V + Nk ln 2 + Nk ln T + Nk 2 h 2 2
3 = Nk ln V + Nk ln T + S 0 2
BEIJING NORMAL UNIVERSITY
熵的统计表达式,Boltzmann 关系
BEIJING NORMAL UNIVERSITY
由于
特性函数,自由能
量子情况下,粒子不可分辨性带来的差别
BEIJING NORMAL UNIVERSITY
计算单原子分子理想气体的熵:
3 3 2πmkT S = Nk + Nk ln V + Nk ln( ) 2 2 2 h
(ⅰ)系统在热力学过程中的规律 (ⅱ)系统的基本热力学函数
§9.4 玻尔兹曼分布

玻耳兹曼(Boltzmann)对独立子系统的平衡分布 做了定量描述:
在系统的N个粒子中,能量为j 的某一量子态 j 上的粒子分布数nj 正比于它的玻尔兹曼因子
nj λ e-ε j /kT
其中: 为比例系数,k 为玻耳兹曼常数,T
为热力学温度。
1
若能级i的简并度为gi ,说明有gi 个量子态具 有同一种能量i ,在系统的N个粒子中,能量为i 的能级 i 上的粒子分布数ni正比于它的玻尔兹曼因 子与统计权重gi的乘积。
既然玻耳兹曼分布即是平衡分布,也是最概然分
布。所以对于N、U、V 确定的系统,微观状态数WD 值
取极大的分布即是玻耳兹曼分布。在9.2节中,已经
得出离域子与定域子在某一套能级分布数 ni 下的WD
的求法,以下只要一eε j /kT
N g eεi /kT
i
j
i
定义以上两式的分母为粒子的配分函数,以 q 表示:
q
def
e
ε
j
/kT
def
gi
eεi /kT
j
i
9.4.4
所以得到玻耳兹曼分布的数学表达式
n
j
N q
eε j /kT
(9.4.5a)
ni
N
q
g eεi /kT
i
(9.4.5b)
g e εi /kT i
ni ginj λ gi eεi /kT
由于系统的总粒子数 N 既是各量子态分布数之和
,也是各能级分布数之和,所以有:
按状态分布加和:
N nj e j /kT
j
j
按能级分布加和:
N
ni
g ei /kT i
热力学统计物理玻耳兹曼统计
义
粒子处在该
能级的几率
有效状 态数
al
N Z1
l
e
l
al
el l
N
Z1
el l el l
玻耳兹
曼因子 粒子总是优先占据较低能级;温度升高,占 据该能级的几率增大。
Z1——有效状态和 一个粒子所有可能达到的有效状态的总和。
热统 西华大学 理化学院
6
f e s
l 能量为εl的一个量子态s上的平均粒子数
p
3.粒子配分函数的经典表达式
处元于内能层的l 粒l内子,数运为动:状态处于相体积
al
l
h0r
fs
l h0r
e l
N Z1
l
h0r
el
l x
Z1
l
el l
h0r
al
N Z1
l
h0r
el
取 l 足够小,求和可化为积分:
Z1
el d
h0r
e ( p,q) dq1dq2 dqr dp1dp2 dpr h0r
l l
FD l l! BE
l
l
l
e l
ln
l l
l
对于满足非兼并条件的处
于平衡态(最可几分布) lnFD lnBE l ln l lnl !
的非定域(玻色、费米) 系统,通过对所对应的系 统微观状态数目取对数, 得到了微观状态数目的对 数ln与系统包含的粒子数
l
l
l ln l l ln l 1
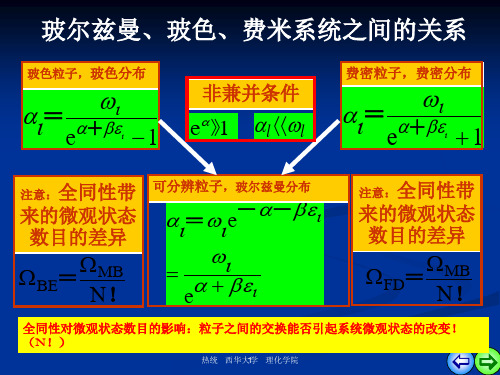
玻尔兹曼、玻色、费米系统之间的关系
玻色粒子,玻色分布
=
e+
1
非兼并条件
e》1 l l
费密粒子,费密分布
热辐射 玻尔兹曼分布 玻色爱因斯坦

热辐射的研究可追溯至19世纪初,当时物理学家试图解释物体发出的热能。
其中,玻尔兹曼分布和玻色爱因斯坦模型在描述热辐射的能量分布和粒子行为方面发挥了重要作用。
1. 玻尔兹曼分布玻尔兹曼分布是描述理想气体中粒子速度分布的统计分布。
该分布表明,在平衡状态下,粒子的速度在不同方向上呈现高度的随机性和均匀性,这一主题在统计物理学和热力学中一直备受关注。
2. 玻色爱因斯坦模型玻色爱因斯坦模型则是描述玻色子(一类基本粒子)的行为模型,特别是在低温下的行为。
根据玻色爱因斯坦的统计推导,玻色子在低温下将呈现出玻色-爱因斯坦凝聚,形成所谓的Bose-Einstein凝聚态。
在探究这些概念的过程中,我们必须深入理解热辐射的性质和行为。
热辐射是指由物体散发的热量和光辐射,其性质由物体的温度和材料决定。
在低温下,热辐射的性质更倾向于玻色爱因斯坦模型所描述的玻色子行为,在高温下,将更符合玻尔兹曼分布的特性。
通过深入研究热辐射的性质和粒子行为,我们可以更好地理解热辐射的能量分布、粒子属性和统计规律。
这不仅有助于我们在物理学和热力学领域的研究,还对光子学、能源理论和材料科学等领域具有潜在的应用和发展前景。
在总结本文时,我们可以得出结论:热辐射是一个复杂而丰富的研究领域,涉及到物体的能量释放、粒子行为的统计规律等多个方面。
玻尔兹曼分布和玻色爱因斯坦模型为我们提供了对热辐射行为的重要理论支持,促使我们更深入地理解热辐射的本质和规律。
在个人观点方面,我认为热辐射的研究不仅有助于我们更好地理解自然界的现象,也为技术和应用的发展提供了重要的理论基础。
通过探索玻尔兹曼分布和玻色爱因斯坦模型,我们可以不断拓展对热辐射的认识,并在实践中应用这些理论,推动科学和技术的进步,创造更多的创新和发展机遇。
通过本文的阐述,我们深入探讨了热辐射、玻尔兹曼分布和玻色爱因斯坦模型等相关内容,希望能为您对这些主题的理解提供一定的启发和帮助。
在现代物理学领域,热辐射的研究一直是一个备受关注的话题。
10.2麦克斯韦-玻尔兹曼分布律

dN ) v f (vmv N m dv
2 2 kT RT v 2
§10.2
麦克斯韦-玻尔兹曼分布律
f (v )
平均速率
O
v
v
§10.2 麦克斯韦-玻尔兹曼分布律
(3)方均根速率: 气体分子速率平方的平均值的平方根。
v
2
v
2
N dN f ( v ) m 1. 73 f (v ) 4 N e dv 2kT
§10.2 麦克斯韦-玻尔兹曼分布律
1.分子热运动的基本特征 分子热运动的基本特征是永恒的运动与频繁 的相互碰撞。它与机械运动有本质的区别,故不 能简单应用力学定律来解决分子热运动问题。
(1)无序性 某个分子的运动,是杂乱无章的,无序的; 各个分子之间的运动也不相同,即无序性;这正 是热运动与机械运动的本质区别。
§10.2
麦克斯韦-玻尔兹曼分布律
统计方法: 气体动理论中,求出大量分子的某些微观量 的统计平均值,用它来解释实验中测的宏观量, 故可从实测的宏观量了解个别分子的真实性质。
统计方法同时伴随着起伏现象。 如对气体中某体积内的质量密度的多次 测量,各次测量对平均值都有微小的偏差。当气 体分子数很大时,起伏极微小,完全可忽略;当 气体分子数较小时,起伏将与平均值可比拟,不 可忽略。故统计规律只适用于大量分子的整体。
3 2
mv
2 2 kT v 2
§10.2 麦克斯韦-玻尔兹曼分布律
f (v )
最 概 然 速 率
O
vp
v
§10.2 麦克斯韦-玻尔兹曼分布律
(2)平均速率:气体分子速率的算术平均值。
v
N
0
高二物理竞赛麦克斯韦-玻尔兹曼能量分布律PPT(课件)

16
理想气体内能
内能:气体内所有分子的动能、分子内的势能与分子间的 相互作用势能的总和。
理想气体内能: • 对理想气体,分子间的势能为0; • 对刚性分子,分子内的势能为0。
k R 波尔兹曼常数
NA
理想气体内能是其所有分子的平均动能之和。
刚性分子:无内部相对运动。
• 单原子分子: (He氦、Ne氖、…)
i t 3
• 双原子分子: (O2、H2、CO…)
• t=3 • r=2 • 绕轴转动自由度无意义
i tr 5
• 多原子分子: (H2O 水蒸气、CO2、…)
i tr 6
14
能量均分定理(按自由度)
在温度为T 的平衡态下,气体分子
每个自由度所对应的平均动能都等于
双原子分子: (O2、H2、CO…)
1 kT 2
1. 平动情况: 重力场中粒子按高度的分布
6* 麦克斯韦-玻尔兹曼能量分布律
重力场中粒子按高度的分布
1 3 6* 麦克斯韦-玻尔兹曼能量分布律
由平均平动动能: mv kT 重力场中粒子按高度的分布
2 2 对刚性分子,分子内的势能为0。
2 k
9* 真实气体 范德瓦耳斯方程
统计物理学的奠基人之一.
每个平动自由度的平均平动动能:
经典名著:《气体理论讲义》 dN /(N ·dv):某 v 处单位速率间隔内分子数与总数N之比。
重力场中粒子按高度的分布
玻耳兹曼
1844年~1906年
5. 气体动理论
5.1 热运动的描述 理想气体模型和状态方程 5.2 分子热运动和统计规律 5.3 气体动理论的压强和温度公式 5.4 能量均分定理 理想气体的内能 5.5 麦克斯韦速率分布律 5.6* 麦克斯韦-玻尔兹曼能量分布律
气体分子运动论和热力学基础之玻尔兹曼分布律

此外,可以结合量子力学和经典力学理论,深入研究气体分子在不同 尺度下的运动规律和相互作用机制。
04
通过这些研究,有望进一步揭示气体分子行为的奥秘,为相关领域的 发展提供新的思路和方法。
THANKS FOR WATCHING
感谢您的观看
该理论在统计物理学、热力学 、化学反应动力学等领域有着 广泛的应用,对于理解气体分 子行为的本质和规律具有重要 意义。
对未来研究的展望
01
随着实验技术和计算机模拟方法的不断发展,对气体分子运动和热力 学性质的研究将更加深入。
02
未来研究可以进一步探索玻尔兹曼分布律在不同条件下的适用范围和 局限性,例如极端温度、高压等极端条件下的气体分子行为。
02 气体分子运动论基础
分子运动论的基本概念
1 2
分子
物质的最小单位,具有热运动和相互碰撞的性质。
分子的热运动
分子在不停地做无规则的热运动,温度越高,热 运动越剧烈。
3
分子的碰撞
分子之间会发生碰撞,碰撞过程中会传递能量和 动量。
分子动理论的基本假设
分子无规则热运动的假设
分子在空间中的运动是无规则的,即每个分子的运动方向和速度 都是随机的。
该定律基于微观分子运动和宏观热力 学性质之间的关系,为理解气体性质 和热力学过程提供了基础。
玻尔兹曼分布律的重要性
玻尔兹曼分布律是热力学统计物理学的基石之一,对于理解气体分子在平 衡态下的行为至关重要。
该定律有助于解释和预测气体在不同温度和压力下的性质,如密度、压强、 内能等。
玻尔兹曼分布律在物理学、化学、生物学等领域都有广泛的应用,对于理 解物质的宏观性质和微观机制具有重要意义。
分子之间相互碰撞的假设
GL.普物I-热学Ch.3-2 玻尔兹曼分布

GL.普物I-热学CH.3
14
(2)粒子在外势场中的分布律
回顾在大气系统等温(等 g) 假设下,大气内微粒子在重力场中 按海拔高度,或按微粒子重力势能的分布律为
p mg n( z ) n(0)exp( z ), n( p ) n(0)exp( ) kT kT
推广: 位于
r 处或 (x, y, z)处的粒子,势能为
k p m 32 f M.B. ( r , v ) n( r ) f M. (v ) n(0)( ) exp( ) 2 kT kT m 32 f M.B. ( r , v ) n(0)( ) exp( ) f M.B. ( ) 2 kT kT
式中, n(0) 是 粒子势能为零时的粒子数密度
GL.普物I-热学CH.3 18
1 m 3 2 n1 n( 1 ) n(0)( ) exp( ) 2 kT kT 两式相比,可得 3 2 m 2 n2 n( 2 ) n(0)( ) exp( ) 2 kT kT
n2 n1 exp(
2 1
kT
)
该式表明了在温度为 T 的平衡态, 系统中粒子处于不同能量 状态下的概率分布情况 可见,系统在平衡态时 系统中粒子处于 ε 较小的低能量状态的概率大,对应较稳定态 系统中粒子处于 ε 较大的能量状态的概率小,对应不太稳定态
在一定温度下,当重力和微粒子热运动两种作用达到平衡时,气体 微粒子在空间按其重力势能的大小( εp=mgz ) 呈现稳定,但不均 匀的分布
mgz n( z ) n(0)exp( ) kT
GL.普物I-热学CH.3
10
显然,在一定温度下,当重力和微粒子热运动两种作用达到平衡时,
大气压强按其海拔高度呈现稳定,但不均匀的分布 mg p( z ) p(0)exp( z) kT
热力学与统计物理 第七章 玻尔兹曼统计

e Z1 r dq1 dqr dp1 dpr h0
粒子自由度为3
e Z1 3 dxdydzdpx dp y dpz h0
15
Z1
V Z1 3 h0
方法一:
e
2 2 px p2 y pz
2m
h
3 0
dxdydzdp x dp y dp z
ln Z1 S Nk ln Z1
7
ln Z1 S Nk ln Z1 ln Z1 Nk ln Z1 T Nk ln Z1 自由能 F U TS N kT F NkT ln Z1
l l Z1 r e h0
体积元 l 取得足够小时,
l d dq1 dqr dp1 dpr
l l Z1 r e h0
Z1
e
h
r 0
dq1 dqr dp1 dpr
14
§7.2
理想气体的物态方程
N ln Z1 p V
Z1 l e l
Z1 l ln Z1 U N
l e l
l l e l l
2
三、广义力
Y 广义力
dW pdV
y
外参量
dW Ydy
Y l作用在该粒子上 当某个粒子处在 l 能级上,若有一“外力”
e
2 2 px p2 y pz
2m
dp x dp y dp z
V Z1 3 h0
4V Z1 3 h0
则
1 e t t 2 dt
玻尔兹曼分布

在统计力学和数学中,玻尔兹曼分布(或吉布斯分布)是处于各种可能的微观量子状态下的粒子的概率分布,概率测度或频率分布。
具有以下形式,其中,量子态能量(随各个量子态而变化)和(对于玻尔兹曼分布是常数)是玻尔兹曼常数与热力学温度的乘积。
概率分布可以表示为,其中,量子态I的概率,量子态I的能量,玻尔兹曼常数,系统温度以及系统具有的量子态数。
对于两个状态的玻尔兹曼分布的比率,获得了玻尔兹曼因子。
可以看出,这仅与量子态之间的能量差有关。
玻尔兹曼分布取材于路德维希·博尔兹曼,他在1868年研究热平衡气体的统计力学时首次提出了这种分布。
然后在1902年,约西亚·威拉德·吉布斯提出了更为一般化的玻尔兹曼分布形式。
应特别注意Boltzmann分布与Maxwell-Boltzmann分布之间的差异。
前者给出了每个量子态中粒子的分布概率,而后者则用来描述理想气体中粒子的速度分布。
该表达在光谱学中具有重要的应用。
光谱中光谱线的位置表示粒子的量子态转移能量。
为了使谱线强度足够,必须有足够的处于高量子态的粒子。
因此,可以通过上述表达式确定颗粒分布与系统温度和能级差之间的关系,并且可以获得适当的系统参数。
统计力学的应用:玻尔兹曼分布可以应用于具有热平衡的隔离(或近似隔离)系统。
最常见的情况是常规合奏的概率分布,但在某些特殊情况下(源自常规合奏)也有相关应用。
数学的应用:在数学上,玻尔兹曼函数的广义形式是吉布斯测度。
在统计和机器学习中也称为对数线性模型。
MaxwellBoltzmann分布律.ppt

费米系统
离域子、粒子不可分辨、处在同一个量子态上的粒子数只限一个; 讨论能级εi 上ni个粒子放在ωi个量子态上的排列数 第1个粒子有 ωi 第2个粒子有 ωi-1 …… 第ni个粒子有 ωi-(ni-1) 种放法: 进一步考虑粒子不可分辨性,排列数为 则分布{ni}拥有的微 观状态数为: 宏观状态(N,V,E) 总的微观状态数 种放法: 种放法:
Lagrange不定乘数α,β由守恒条件确定
i N n e i i i i
( 8)
i E n e ii i i i i
e
N i e i
i
( 8)
β的数值现阶段还无法直接求解,以后我们会证明
由于δni受到守恒条件(4)(5)式的限制,应用Lagrange不定乘数法,分别用α、 β乘以(4)(5)两式,并减去(6)式
n i n ( i 1 , 2 , . . . ) i
7/2h
5/2h
3/2h
A: B: C:
1/2h
状态1 A: n=0 B: n=0 C: n=4
状态2 A: n=0 B: n=4 C: n=0
状态3 A: n=4 B: n=0 C: n=0
状态4 A: n=0 B: n=3 C: n=1
状态5 A: n=0
状态6 A: n=3 B: n=0 C: n=1
F D i i i i i n i i M B i i i i i i i i
玻色子分布与费米子分布在非简并条件趋向相同,都趋向 于麦-玻分布,显然N!是粒子不可分辨性代入的校正因子
从前面讨论可以看出:微观状态数Ω是宏观状态的状态函数,可以表示为 Ω(N,V,E),事实上Ω是以N,V,E为特征变量的特性函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n(z) n(0) exp( m*gz ), RT
其中m* m(1 0 )
1908年法国科学家 Perrin首次观测到,1926年 获得诺贝尔物理奖。
旋转体中悬浮粒子径向分布: ω
l
r dr
h
超速离心技术与同位素分离:
台风、飓风和龙卷风:
四、玻尔兹曼分布
设n1和n2分别表示在温度T的系统中,处于粒子能 量为ε 1的某一状态与ε 2的另一状态的粒子数密度。
例4 气体分子的自由度
将每个原子看作质点 所以分子是 质点系
单原子分子
t 3
双原子分子 多原子分子
t 3 r 2 s 1
t 3 r 3 s 3N 6
刚性分子 单原子分子 双原子分子 多原子分子
s0
t 3
t3 r2
t3 r3
i t r
i 3 i 5 i 6
n1
n2
exp(
1 2
kT
)
玻尔兹曼分布
对于处于平衡态的气体中的原子、分子、布朗粒子, 以及液体、固体中的很多粒子,一般都可应用玻尔兹曼 分布,只要粒子之间相互作用很小而可予忽略。
T
1 2
k ln( n1 )
n2
它表示处于平衡态的系统,在(无 相互作用)粒子的两个不同能量的状态 上的粒子数的比值与系统的温度及能量 之差有确定 的关系。
若受到限制自由度降低 平面上 2个 平动自由度 t=2 直线上 1个 平动自由度 t=1
例2 自由运动的刚体 (如大家熟悉的手榴弹)自由度? 首先应明确刚体的振动自由度 s = 0 按基本运动分解:平动 + 转动 整体随某点(通常选质心)平动
cc
cc
c
6个自由度 t+ r = 3 + 3 = 6
定质心位置 需3个平动自由度
§2.7 能量均分定理
§2.7.1 理想气体的热容
定义热容:
c lim Q dQ T 0 T dT
C=νCm, C=mc
Cm为摩尔热容,c为比热
理想气体的内能: 对单原子理想气体
3
3
Um NA 2 kT 2 RT
理想气体的热容:
3 CV ,m 2 R
1 2
mvx2
n(z) n(0) exp( Mmgz ) RT
p+dp
系统 ρg
z+dz
z p
二、等温大气标高
定义大气标高:
kT RT H
mg M m g
大气标高是粒子按高度分布的特征量,它反映
了气体分子热运动与分子受重力场作用这一对矛盾。
三、悬浮微粒按高度的分布
设每一个微粒的质量为m,体积为V,微粒的密度为ρ 。
P101,2.24 1
小球可以看作质点 杆的直径可以忽略
小球可以看作质点
(1)
2 杆的直径不可以忽略
3
小球可以不看作质点
杆的直径可以忽略
(2)
2+1+1=4
1+1 2+1 1+1+1
§2.7.3能量均分定理
能量按自由度均分定理(简称能量均分定理)---处于温度为T的平衡态的气体中,分子热运动动 能平均分配到每一个分子的每一个自由度上,每 一个分子的每一个自由度的平均动能都是kT/2。
1 2
mv
2 y
1 2
mvz2
1 2
kT
每一个方向的平均平动动 能都均分 kT/2
§2.7.2 自由度与自由度数
描述一个物体在空间的位置所需的独立坐标称为 该物体的自由度。而决定一个物体在空间的位置所需 的独立坐标数称为自由度数。
1)平动
质点
任一直线形成一组平行线
2)转动
3)振动
例1 自由运动的质点 (三维空间) 3 个 平动自由度 记作 t = 3
复习、提问
最概然速度=? 思考题2.14
§2.6 玻尔兹曼分布
一、等温大气压强公式
该系统达到平衡的条件为:
p A ( p dp) A gAdz, dp gdz
p dp
z mg dz
0p
0 kT
p(z) p(0) exp( M m gz ) RT
每一点绕过c 点的轴转动 共有 3个转动自由度
可以理解成物体系 对三个轴的旋转
例3 由 N 个独立的粒子组成的
质点系的自由度 (一般性讨论)
● 每个独立的粒子各有3个自度
系统最多有3N个自由度
●基本形式 平动 + 转动 + 振动
t
r
s
随某点平动 t = 3
过该点轴的转动
r=3
其余为振动
s = 3N-6
§2.7.6能量均分定理的局限 自由度的冻结
1、能量均分定理的局限
2、自由度的冻结
CV,m / R
7/2
振动 5/2
转动 3/2
平动
0 25 100 500 1000 5000 T / K 氢气CV,m---T曲线
课后作业
2.7.1 2.7.3
每一个分子的总的平均能量为: (t r 2v) kT 1 ikT,
22
注意
i t r 2v
1)、各种振动、转动自由度都应是确实对能量均分定理作全部贡献的自由度。 2)、只有在平衡态下才成立。 3)、它是对大量分子统计平均所得结果。 4)、它不仅适用于理想气体,而且也适用于液体和固体。 5)、气体:靠分子间大量无规则的碰撞来实现;液体、固体:分子间强相 互作用来实现
