EXCEL单因素方差分析
EXCEL在方差分析中的运用

EXCEL在方差分析中的运用一、单因素方差分析在Excel中,可以使用[方差分析:单因素方差分析]工具来完成单因素方差分析。
【例6-4】本章例6-1的Excel统计分析步骤如下。
1.输入数据。
如图6-3所示。
图6-32.调出[方差分析:单因素方差分析]对话框,其主要选项含义如下。
输入区域:在此输入待分析数据区域的单元格引用。
该引用必须由两个或两个以上按列或行组织的相邻数据区域组成。
本例为“$B$1:$D$6”。
分组方式:如果需要指出输入区域中的数据是按行还是按列排列,请单击[行]或[列]。
本例分组方式为“列”。
标志位于第一行/列:如果输入区域的第一行中包含标志项,请选中[标志位于第一行]复选框;如果输入区域的第一列中包含标志项,请选中[标志位于第一列]复选框;如果输入区域没有标志项,则该复选框不会被选中,Excel将在输出表中生成适宜的数据标志。
α:在此输入计算F 统计临界值的置信度。
本例为0.05。
本例对话框的填写如图6-3所示。
图中分组方式为“列”方式,因为三家分店的日营业额是按列排列的,即分别排在B、C、D列。
3.单击[确定]按钮,可得方差分析表(结果已在本章第二节的表6-3中给出)。
二、无交互作用下的双因素方差分析该项工作可利用[方差分析:无重复双因素方差分析]工具来完成。
【例6-5】本章例6-2的Excel统计分析步骤如下。
1.输入数据。
如图6-4所示。
2.调出[方差分析:无重复双因素分析]对话框,填写如图6-4所示。
该工具对话框设置与单因素方差分析类似。
要注意,本例中[标志]复选框被选中,输入区域必须包括A因素与B因素的水平标志(如“工人一”、“工人四”、“设备B”等)所在的单元格区域,也即输入区域为“$M$1:$R$4”,而不是只包括数据的单元格区域“$N$2:$R$4”。
图6-43.单击[确定]按钮。
得到方差分析表。
(结果已在本章第三节表6-6中给出)。
三、有交互作用的双因素方差分析该项工作可以使用[方差分析:可重复双因素方差分析]工具来完成。
Excel数据管理与图表分析 单因素方差分析

Excel 数据管理与图表分析 单因素方差分析单因素方差分析不考虑个体差异的影响,仅涉及一个处理因素,但可以有两个或多个水平。
主要用于多个样本均数间的比较,其统计原理是推断各样本所代表的各总体均数是否相等。
例如,某军区总医院欲研究A 、B 、C 三种降血脂药物,对家兔ACE (血清肾素血管紧张素转化酶)的影响,将26只家兔随机分为4组,均喂以高脂饮食,其中三个试验组,分别给予不同的降血脂药物,而对照组不给药。
一段时间后测定家兔血清ACE 浓度(u/ml ),问4组家兔血清ACE 浓度是否相同?下面来运用单因素方差分析的方法来分析4组家兔血清ACE 浓度是否相同。
在使用单因素方差分析功能之前,应首先通过【加载宏】来加载【分析工具库】工具。
单击Office 按钮,并且单击【Excel 选项】按钮。
在弹出的【Excel 选项】对话框中,选择【加载项】选项卡,并单击【转到】按钮。
然后,在弹出的【加载宏】对话框中,启用【分析工具库】复选框,如图13-1所示。
图13-1 加载【分析工具库】提 示单击【加载宏】对话框中的【确定】按钮后,用户将发现在【数据】选项卡的【分析】组中添加了一个【数据分析】按钮。
接下来进行数据的单因素方差分析。
在一张空白的工作表中,创建“对照组及各实验组家兔血清ACE 浓度(u/ml)”表格,如图13-2所示。
图13-2 创建表格 图13-3 选择方差分析项选择【数据】选项卡,单击【分析】组中的【数据分析】按钮。
在弹出的【数据分析】对话框中,选择【分析工具】栏中的【方差分析:单因素方差分析】选项,如图13-3所示。
在弹出的【方差分析:单因素方差分析】对话框中,设置【输入区域】为$B$3:$E$10;并启用【标志位于第一行】复选框,如图13-4所示。
选择单击创建 单击单击设置图13-4 设置方差分析参数其中,在该对话框中,主要包含以下几项内容,其功能如下:●输入区域选择分析数据所在区域(针对表中数据进行分析时选取),还可以选择水平标志。
实验四用EXCEL实现方差分析

《田间试验设计与统计》实验
例4.3 将A1、 A2 、 A3 、 A4 四 种 生 长 素 , 并 用 B1 、 B2 、 B3 三 种 时 间 浸渍菜用大豆品 种 种 子 , 45 天 后 测得各处理的平 均 单 株 干 物 重 (g) 于 表 4.3 , 试 作 分 析。
用EXCEL实现方差分析
对于多重比较的EXCEL方法请参考前述有关内容, 在此不再赘述;而其它试验设计方法所获得的试验结 果的方差分析方法,请大家参考其它有关书籍自行学 习掌握。
而不同的试验设计方法所产生的变异来源不同完全随机设计可分为处理间变异和误差变异两部分随机区组设计则可分为处理间变异区组间变异和误差变异三部分而拉丁方设计则可以分为处理间变异横向区组间变异纵向区组间变异以及误差变异四个部分
《田间试验设计与统计》实验
用EXCEL实现方差分析
实验四 用EXCEL进行方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=IF(E35>=D$32,FIXED(E35,1)&”**”,IF(E35>=D$31,FIXED(E 35,1)&”*”,FIXED(E35,1)))”,并按住填充柄向左填充
第十步: 将梯形表中右 下角的无用数 据清除后,再 复制一次梯形 表,在第二个 梯形表中删除 所有差数,并 编制公式进行 填充,以获得 差异显著性。
《田间试验设计与统计》实验
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
▼注意修正公式中的单元 格引用,使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(D36>=D$32,FIXED(D36,1)&”**”,IF(D36>=D$31,FIXED(D 1)&”*”,FIXED(D36,1)))”,同理按住填充柄向左填充
EXCEL中方差分析
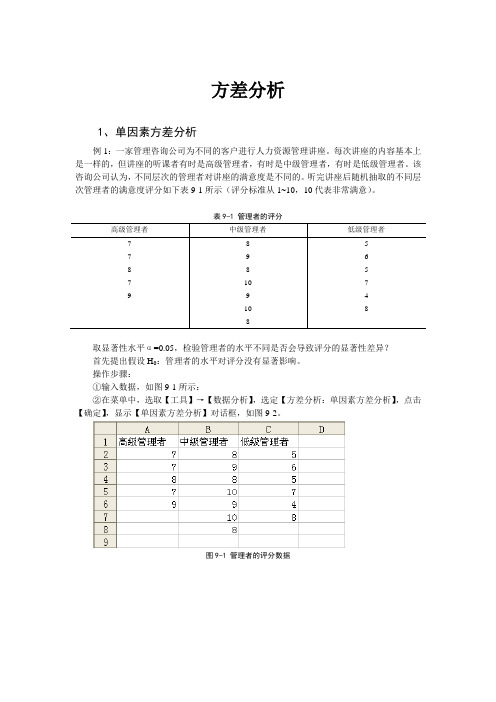
方差分析1、单因素方差分析例1:一家管理咨询公司为不同的客户进行人力资源管理讲座。
每次讲座的内容基本上是一样的,但讲座的听课者有时是高级管理者,有时是中级管理者,有时是低级管理者。
该咨询公司认为,不同层次的管理者对讲座的满意度是不同的。
听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1所示(评分标准从1~10,10代表非常满意)。
表9-1 管理者的评分高级管理者中级管理者低级管理者7 8 57 9 68 8 57 10 79 9 410 88取显著性水平α=0.05,检验管理者的水平不同是否会导致评分的显著性差异?首先提出假设H0:管理者的水平对评分没有显著影响。
操作步骤:①输入数据,如图9-1所示:②在菜单中,选取【工具】→【数据分析】,选定【方差分析:单因素方差分析】,点击【确定】,显示【单因素方差分析】对话框,如图9-2。
图9-1 管理者的评分数据图9-2 单因素方差分析对话框③在“输入区域”框输入数据矩阵(首坐标:尾坐标),可选为“A1:C8”,点选“标志位于第一行”,在“分组方式”框选定“列”,指定显著水平α=0.05,输出选项的输出区域可为工作表的任何位置,本例选择在I4处。
④点击【确定】,则得输出结果,如下图9-3所示。
图9-3 单因素方差分析结果图9-3是一个单因素方差分析结果的报告。
第一个表是有关各样本的一些描述统计量,它可以作为方差分析的参考信息。
第二个表是方差分析结果。
其中SS 表示平方和,df 为自由度,MS 表示均方,F 为检验的统计量,P-value 为用于检验的P 值,F crit 为给定α水平下的临界值。
从方差分析表可以看到,由于68232.375573.11=>=αF F ,所以拒绝原假设,即管理者的水平对评分的影响是显著的。
在进行决策时,可以直接利用方差分析表中的P 值与显著性水平α的值进行比较,若 P <α,则拒绝原假设;若P >α,则不能拒绝原假设。
excel单因素方差分析默认置信度

excel单因素方差分析默认置信度excel单因素方差分析默认置信度为0.05
1、选择单因素方差分析工具。
在Excel 2007中切换到“数据”选项卡,单击“分析”区域的“数据分析”按钮。
2、弹出“数据分析”对话框,在该对话框的列表框区域选择“方差分析:单因素方差分析”选项。
3、设置单因素方差分析相关参数。
单击“确定”按钮,弹出“方差分析:单因素方差分析”对话框。
单击“输入区域”文本框右边的“压缩对话框”按钮,选择输入数据区域选项。
4、选择完成后单击对话框右下角的“展开对话框”按钮,再单击“分组方式”选项中“列”前面的单选框,并勾选“标志位于第一行”前面的复选框,将置信度参数α设为默认值0.05。
在“输出选项”选区中,单击“输出区域”前面的单选按钮并选定输出区域。
α为置信度参数,表示输入区域中数据有多大的可信度。
α=0.05表示数据有95%的可信度。
Excel进行单因素方差分析的步骤

Excel进行单因素方差分析的步骤Excel是一种功能强大的电子表格软件,可以用于进行各种数据分析,包括单因素方差分析。
单因素方差分析是一种常用的统计方法,用于比较不同组之间的均值是否存在显著差异。
下面是在Excel中进行单因素方差分析的步骤:步骤1:准备数据首先,需要准备好用于分析的数据。
假设我们有一个实验,分为三个组,每个组有若干个观测值。
我们需要将这些观测值依次输入到Excel的一些工作表中。
步骤2:计算各组的均值和总均值在Excel中,可以使用平均值函数(AVERAGE)计算每个组的均值。
将这些均值记录在另一列或另一个工作表中。
然后,使用平均值函数计算所有组的总均值。
步骤3:计算组内平方和和组间平方和使用Excel的平方和函数(SUMSQ)来计算每个组的组内平方和。
组内平方和可以通过将每个观测值与其对应组的均值之差的平方相加来计算。
然后,使用平方和函数计算组间平方和。
组间平方和可以通过将每个组的均值与总均值之差的平方乘以该组的观测数量相加来计算。
步骤4:计算均方计算组内平方和和组间平方和的均方,即将组内平方和除以自由度(观测数量减去组数)得到组内均方,将组间平方和除以组数减1得到组间均方。
步骤5:计算F值使用Excel的F分布函数(FDIST)来计算F值。
F值可以通过将组间均方除以组内均方来计算。
步骤6:确定显著性水平和临界值根据实验设计和显著性水平的设置,确定F分布的临界值。
在Excel 中,可以使用F分布的临界值函数(FINV)来计算临界值。
步骤7:进行假设检验根据F值和临界值的比较结果,进行假设检验。
如果F值大于临界值,则可以拒绝原假设,即组均值存在显著差异。
如果F值小于等于临界值,则不能拒绝原假设,即组均值没有显著差异。
步骤8:进行事后比较(可选)如果在步骤7中发现组均值存在显著差异,可以使用Excel的多重比较方法,如Bonferroni校正、Tukey HSD等,进行事后比较。
Excel中的单因素方差分析
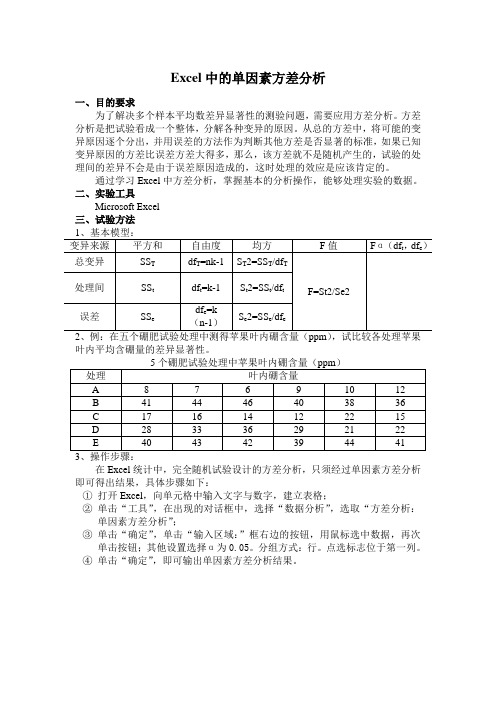
Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题,需要应用方差分析。
方差分析是把试验看成一个整体,分解各种变异的原因。
从总的方差中,将可能的变异原因逐个分出,并用误差的方法作为判断其他方差是否显著的标准,如果已知变异原因的方差比误差方差大得多,那么,该方差就不是随机产生的,试验的处理间的差异不会是由于误差原因造成的,这时处理的效应是应该肯定的。
通过学习Excel中方差分析,掌握基本的分析操作,能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法叶内平均含硼量的差异显著性。
在Excel统计中,完全随机试验设计的方差分析,只须经过单因素方差分析即可得出结果,具体步骤如下:①打开Excel,向单元格中输入文字与数字,建立表格;②单击“工具”,在出现的对话框中,选择“数据分析”,选取“方差分析:单因素方差分析”;③单击“确定”,单击“输入区域:”框右边的按钮,用鼠标选中数据,再次单击按钮;其他设置选择α为0.05。
分组方式:行。
点选标志位于第一列。
④单击“确定”,即可输出单因素方差分析结果。
4、方差分析输出结果:SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.5差异源SS df MS F P-value F crit 组间5160.467 4 1290.117 94.1691 1.07E-14 2.75871 组内342.5 25 13.7总计5502.967 295、多重比较:由方差分析的结果,采用新复极差测验法,再稍加计算比较处理,即可得出:60.05显著,并可知除E与B二处理间无极显著差异外,其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析,是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题,如各组之间有显著差异,说明这个因素(分类变量)对因变量是有显著影响的,因素的不同水平会影响到因变量的取值。
Excel 财务应用 单因素方差分析

Excel 财务应用 单因素方差分析单因素方差分析用于完全随机设计的多个样本均数间的比较,其统计推断是推断各样本所代表的各总体均数是否相等。
1.创建数据模型设有三部机器A 、B 、C 制造同一种产品,对每一部机器观察4天的日产量,记录如图7-3所示。
问在产量上,各机器之间是否有显著差别?图7-3 数据模型可以把每部机器生产的日产量看作是一个总体,问题是检验三种产品总体的均值是否相等,因此,可以采用单因素方差分析法。
现在假设3台机器之间在产量上是没有差异的,要检验这个假设能否成立,我们可以根据上面模型介绍中,通过人工计算方差分析表来实现。
在计算样本均值时,需要使用到Excel 的均值函数AVERAGE ,其功能是返回参数的平均值(算术平均值)。
其语法为:AVERAGE(number1,number2,…)其中,number1,number2,…为需要计算平均值的30个参数。
需要说明的是,参数可以是数字,或者是包含数字的名称、数组或引用。
如果数组或引用参数包含文本、逻辑值或空白单元格,则这些值将被忽略,但包含零值的单元格将计算在内。
例如,选择第1天所对应的样本均值所在的单元格(B7单元格),并选择【公式】选项卡,在【函数库】组中,单击【自动求和】按钮,执行【平均值】命令,按Enter 键即可求出第1天的样本均值,如图7-4所示。
图7-4 计算样本均值提 示选择B7所在的单元格,将鼠标置于该单元格的填充柄上,向右拖动至该行的其他单元格中,即可计算出其他单元格的“样本均值”。
接下来可以对总体均值进行计算。
选择“总体均值”所对应的单元格(B8单元格),单击【函数库】组中的【插入函数】按钮,在弹出的【插入函数】对话框中,选择函数AVERAEGA 函数,如图7-5所示。
创建表格 执行图7-5 选择函数 图7-6 计算“总体均值”单击【确定】按钮后,将弹出【函数参数】对话框,设置函数的参数,即可求出“总体均值”,结果如图7-6所示。
excel单因素方差分析

excel单因素方差分析Excel的单因素方差分析(One-WayAnalysisofVariance,ANOVA)是一种统计技术,可以帮助我们检验某个变量在不同分组或组之间的差异。
它主要通过检验有效性的F检验,来分析两个或多个数据组之间的平均值是否具有统计学意义。
此外,Excel中的单因素方差分析技术还可以用来测量和比较不同因素对总体中样本值的影响程度,从而更好地判断因素之间的关联性。
Excel中的单因素方差分析是一种重要的统计分析工具,在许多研究领域中都得到了广泛应用,如市场营销研究中对用户满意度的比较,社会科学研究中对实验组和对照组的分析等。
它可以有效地帮助我们判断因素之间的关联性,从而更好地进行决策分析。
Excel中的单因素方差分析首先要准备数据,准备之前要注意几个问题:数据要符合正态分布,变量要是独立的,没有多重共线性等。
接下来,将准备好的数据输入Excel中。
进入数据分析对话框后,选择单因素方差分析,根据自己的分析需求,可以设置分析参数,比如比较的组别或因子,按照不同实验设置设定P值和alpha值等参数,最后点击确定,Excel就会根据我们的分析需求自动生成报告,包括F-检验和P-值等参数。
Excel中的单因素方差分析技术也具有一定的局限性要注意,它只能用于定量数据的分析,不能用于定性数据的分析,而且它不能用于多维数据分析,只能用于单维数据的分析。
此外,由于它的统计假设比较严格,不能适用于所有数据分析情形。
总之,Excel单因素方差分析是一种有效且易于使用的分析工具,能够用于在数据分析中帮助我们检验某个变量在不同分组或组之间的差异,比较实验组和对照组的差异,并用于测量和比较不同因素对总体样本值的影响程度,从而更好地判断因素之间的关联性。
但是,它也有一些局限性,在使用之前要仔细考虑,以确保最终的分析结果的准确性。
实验四 单因素方差分析

实验四单因素方差分析
一、实验目的
学会用Excel进行方差分析。
二、实验要求
会用Excel进行单因素方差分析。
三、实验内容
由于是随机抽样,有一些地区的样本容量较多,而有些地区样本容量较少。
试以α=0.01的显著性水平检验各地区平均每天交通事故的次数是否相等。
实验步骤:
第1步:在Excel中将数据输入到A2到C11中;
第2步:选择“工具”下拉菜单;
第3步:选择“数据分析”选项;
第4步:在分析工具中选择“单因素方差分析”;
第5步:当出现对话框后,在“数据区域”方框内键入A2:C11;在α方框内输入0.01;在“输出选项”中选择输出区域A9;选择“确定”。
输出结果如表2。
Excel数据处理之三 方差分析
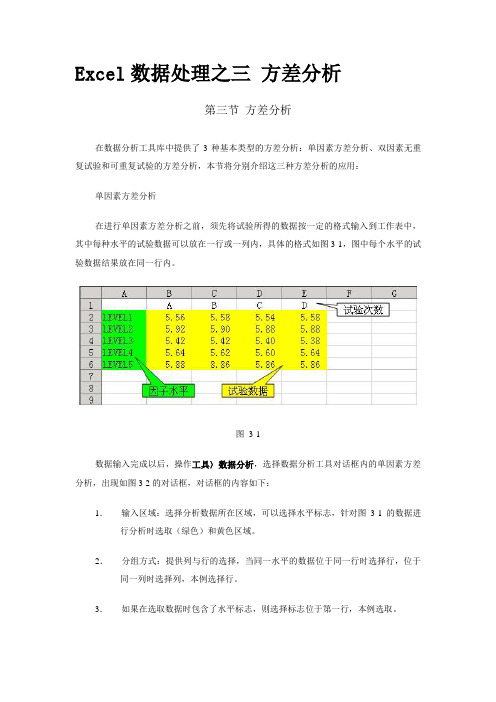
第三节方差分析
在数据分析工具库中提供了3种基本类型的方差分析:单因素方差分析、双因素无重复试验和可重复试验的方差分析,本节将分别介绍这三种方差分析的应用:
单因素方差分析
在进行单因素方差分析之前,须先将试验所得的数据按一定的格式输入到工作表中,其中每种水平的试验数据可以放在一行或一列内,具体的格式如图3-1,图中每个水平的试验数据结果放在同一行内。
图3-4
数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因素无重复方差分析,出现如图3-5的对话框,对话框的内容如下:
1.输入区域:选择数据所在区域,可以包含因素水平标志。
2.果数据输入时选择了因素水平标志,请选择标志按钮。
3.显著性水平α:根据实际情况输入,一般选择0.05。
4.输出选项:按需要选择分析结果存储的位置。
1.输入区域:选取图4-1数据表中的绿色和黄色区域,表示标志与数据。
2.分组方式:根据数据输入的方式选择逐行或逐列,此例选择逐列。
3.由于数据选择时包含了标志,所以要勾选标志位于第一行。
4.根据需要选择输出的位置。
图4-2
将信息按图4-2输入对话框后,选择确定,输出结果如图4-3所示。
图4-3
协方差分析
图3-5
分析图3-4中的数据,对话框如图3-5输入,分析结果输出如图3-6:
图3-6
双因素可重复方差分析
双因素可重复方差分析与双因素无重复方差分析数据输入的区别在于对重复试验数据的处理,如图3-7所示,就是将重复试验的数据叠加起来。
图3-7
数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因素可重复方差分析,出现如图3-8的对话框,对话框的内容基本与双因素无重复方差分析相同,区别在于每一样本的行数选项,在此输入重复试验的次数即可。
实验三 用Excel进行方差分析实验报告

3种课程训练平均销售记录多重比较表
课程 B课程 A课程 C课程
平均数 x i 2928 2228.8 1951.6
x i 1951 6 . 976.4 277.2
x i 2228.8 699.2
因为MSe 3992323, n 5, 所以标准误 x 为 . s
的提高无显著影响,不 同改革方
q0.01 6.93 5.95 5.41
LSR0.05 1.6996 1.5288 1.4280
LSR0.01 3.0356 2.6063 2.3698
进一步对改革方案各水 平平均经
3.多重比较
品种小麦收获量极显著高于B4品种,但B1、B2和B3品
方案
B2 B3
B1
式为
F值 1.61 20.49**
自由度df 均方MS 4 3.5245 3 44.8818 12 2.1902 19
SS B
1 1 x2j C 3 2 (20 an
2415655 2411208 444
SSAB SSAB SSA SSB 469
因为MSe 3992323, n 5, 所以标准误 x 为 . s
s x MSe / n 3992323 / 5 282.5712 .
q值与LSR值
dfe
12
秩次距 2 3
q0.05 3.08 3.77
q0.01 4.32 5.05
LSR0.05 870.3193 1065.2934
A2
单个观测值试验资料。A因素有5个水平,即a=5
b=5× 4=20个观测值。方差分析如下:
EXCEL单因素方差分析

E X C E L单因素方差分析Prepared on 21 November 2021用Excel进行数据分析:单因素方差分析什么是方差分析什么又是单因素方差分析方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”或“F检验”,是R.A.Fister发明的,用于两个及两个以上样本均数差别的显着性检验。
一个复杂的事物,其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显着影响的因素,各因素之间的交互作用,以及显着影响因素的最佳水平等。
方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
单因素方差分析,顾名思义,就是基于一个因素分组研究,比较该因素的效应。
一、应用场景基本思想:通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
下面我们用一个简单的例子来说明方差分析的基本思想:如某克山病区测得11例克山病患者和13名健康人的血磷值(mmol/L)如下:|患者:0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11健康人:0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87问该地克山病患者与健康人的血磷值是否不同?二、操作步骤1、选中数据,点击功能区数据—>数据分析—>方差分析:单因素方差分析注:本操作需要使用Excel扩展功能,如果您的Excel尚未安装数据分析,可以参考该专题文章的第一篇《》。
2、在弹出的选项框里面,进行如下设置3、点击确认,得到如下结果从以上资料可以看出,24个患者与健康人的血磷值各不相同,如果用离均差平方和(SS)描述其围绕总均数的变异情况,则总变异有以下两个来源:组内变异,即由于随机误差的原因使得各组内部的血磷值各不相等;组间变异,即由于克山病的影响使得患者与健康人组的血磷值均数大小不等。
单因素方差分析-excel教程

检验假设:
H0 : 1 2 ... r
r
考察统计量 SST
ni
2
Xij X
总离差平方和
i1 j1
经恒等变形,可分解为: SST SSA SSE
其中
r ni
2
SSA
Xi X
i1 j1
组间平方和(系
如果H0 成立,则SSA 较小。 统离差平方和)
反映的是各水平平均值偏离总平均值的偏离程度。
观测值
消费者对四个行业的投诉次数
行业
零售业
旅游业
航空公司
家电制造业
1
57
68
31
44
2
66
39
49
51
3
49
29
21
65
4
40
45
34
77
5
34
56
40
58
6
53
51
7
44
1. 分析四个行业之间的服务质量是否有显著差 异,作出这种判断需要检验这四个行业被投 诉次数的均值是否相等
2. 如果它们的均值相等,就意味着“行业”对 投诉次数是没有影响的,即它们之间的服务 质量没有显著差异;
i1 j1
▪ 前例的计算结果:SSE = 2708
构造检验的统计量
(三个平方和的关系)
▪ 总离差平方和(SST)、误差项离差平方和
(SSE)、水平项离差平方和 (SSA) 之间的关 系
k ni
k
k ni
xij x 2 ni xi x2
xij xi 2
i1 j1
i1
i1 j1
SST = SSA + SSE ▪ 前例的计算结果:
实验 利用EXCEL软件进行方差分析(一)
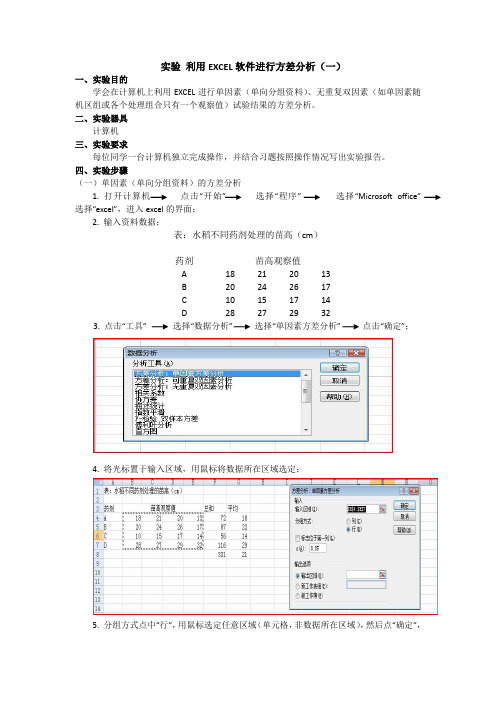
实验利用EXCEL软件进行方差分析(一)一、实验目的学会在计算机上利用EXCEL进行单因素(单向分组资料)、无重复双因素(如单因素随机区组或各个处理组合只有一个观察值)试验结果的方差分析。
二、实验器具计算机三、实验要求每位同学一台计算机独立完成操作,并结合习题按照操作情况写出实验报告。
四、实验步骤(一)单因素(单向分组资料)的方差分析1. 打开计算机点击“开始” 选择“程序” 选择“Microsoft office” 选择“excel”,进入excel的界面;2. 输入资料数据;表:水稻不同药剂处理的苗高(cm)药剂苗高观察值A 18 21 20 13B 20 24 26 17C 10 15 17 14D 28 27 29 323. 点击“工具” 选择“数据分析” 选择“单因素方差分析” 点击“确定”;4. 将光标置于输入区域,用鼠标将数据所在区域选定;5. 分组方式点中“行”,用鼠标选定任意区域(单元格,非数据所在区域),然后点“确定”,即可得到结果。
(二)无重复双因素(如单因素随机区组或各个处理组合只有一个观察值)试验结果的方差分析1. 打开计算机点击“开始” 选择“程序” 选择“Microsoft office” 选择“excel”,进入excel的界面;2. 输入资料数据,例如;表:小麦品比试验(随机区组)的产量结果(kg)品种区组T t ⅠⅡⅢA 10.9 9.1 12.2 32.2B 10.8 12.3 14.0 37.1C 11.1 12.5 10.5 34.1D 9.1 10.7 10.1 29.9E 11.8 13.9 16.8 42.5F 10.1 10.6 11.8 32.5G 10.0 11.5 14.1 35.6H 9.3 10.4 14.4 34.13. 点击“工具” 选择“数据分析” 选择“无重复双因素方差分析” 点击“确定”;4. 将光标置于输入区域,用鼠标将数据所在区域选定;5. 将光标置于输出区域,用鼠标选定任意区域(单元格,非数据所在区域),然后点“确定”,即可得到结果。
Excel中的数据分析工具假设检验和方差分析

Excel中的数据分析工具假设检验和方差分析Excel中的数据分析工具——假设检验和方差分析数据分析在现代社会中扮演着重要的角色,而Excel作为一款常用的办公软件,在数据分析方面具有强大的功能和工具。
本文将重点介绍Excel中的数据分析工具——假设检验和方差分析。
一、假设检验假设检验是一种统计方法,用于确定一个样本是否代表着整个总体的特征。
它通过对样本数据进行分析,来推断和判断总体的参数。
Excel提供了多种假设检验的方法,常用的有t检验和z检验。
1. t检验t检验用于对一个总体或两个总体的均值是否存在显著差异进行判断。
在Excel中,可以通过T.TEST()函数进行t检验的计算。
该函数的语法为:T.TEST(array1, array2, tails, type)。
其中,array1和array2分别表示两个样本的数据范围,tails表示尾部情况(单尾或双尾),type表示两个样本是否具有相等的方差。
2. z检验z检验用于判断一个样本均值和总体均值的显著性差异。
在Excel 中,可以通过Z.TEST()函数进行z检验的计算。
该函数的语法为:Z.TEST(array, x, sigma)。
其中,array表示样本数据范围,x表示总体均值的猜测值,sigma表示总体标准差。
二、方差分析方差分析是一种用于分析多个样本之间差异性的统计方法。
它可以用于判断一个因素是否对样本产生了显著影响。
Excel中提供了ANOVA()函数来进行方差分析的计算。
方差分析可以分为单因素方差分析和双因素方差分析两种情况。
1. 单因素方差分析单因素方差分析用于对一个因素(变量)的多个水平(组别)之间的差异进行比较。
在Excel中,可以通过使用ANOVA()函数进行单因素方差分析的计算。
该函数的语法为:ANOVA(data, group)。
其中,data表示包含多个组别数据的范围,group表示包含组别标识的范围。
2. 双因素方差分析双因素方差分析用于分析两个因素(变量)对样本数据的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E X C E L单因素方差分析Prepared on 21 November 2021
用Excel进行数据分析:单因素方差分析
什么是方差分析什么又是单因素方差分析
方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”或“F检验”,是R.A.Fister发明的,用于两个及两个以上样本均数差别的显着性检验。
一个复杂的事物,其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显着影响的因素,各因素之间的交互作用,以及显着影响因素的最佳水平等。
方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
单因素方差分析,顾名思义,就是基于一个因素分组研究,比较该因素的效应。
一、应用场景
基本思想:通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
下面我们用一个简单的例子来说明方差分析的基本思想:
如某克山病区测得11例克山病患者和13名健康人的血磷值(mmol/L)如下:
|患者:0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11
健康人:0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87
问该地克山病患者与健康人的血磷值是否不同?
二、操作步骤
1、选中数据,点击功能区数据—>数据分析—>方差分析:单因素方差分析
注:本操作需要使用Excel扩展功能,如果您的Excel尚未安装数据分析,可以参考该专题文章的第一篇《》。
2、在弹出的选项框里面,进行如下设置
3、点击确认,得到如下结果
从以上资料可以看出,24个患者与健康人的血磷值各不相同,如果用离均差平方和(SS)描述其围绕总均数的变异情况,则总变异有以下两个来源:
组内变异,即由于随机误差的原因使得各组内部的血磷值各不相等;
组间变异,即由于克山病的影响使得患者与健康人组的血磷值均数大小不等。
而且:SS总=SS组间+SS组内 v总=v组间+v组内
如果用均方(即自由度v去除离均差平方和的商)代替离均差平方和以消除各组样本数不同的影响,则方差分析就是用组内均方去除组间均方的商(即F值)与1相比较,若F值接近1,则说明各组均数间的差异没有统计学意义,若F值远大于1,则说明各组均数间的差异有统计学意义。
实际应用中检验假设成立条件下F值大于特定值的概率可通过查阅F界值表(方差分析用)获得。
