二年级奥数数阵图带答案

二年级奥数：巧妙填数数阵图练习题含答案

第二讲：数字游戏—填图与拆数【有话要说】填数是一种既有趣，又能锻炼头脑、发展智力的趣味活动。

它不仅可以提高你的运算能力，而且能促使你积极地去思考问题，解决问题。

填数这类题目的题型比较多，解答时除了口算要熟练外，更重要的是要会分析、推理。

有的题目答案不止一种，要多尝试，要尽量运用发散思维、求异思维，把各种可能的答案想出来。

【经典例题】例1：把1、3、5、7、9、11、13七个数填入右图中的七个圆圈内，使每条直线上三个数的和都等于21.思路导航：这道题可以这样想：1+3+5+7+9+11+13=49,21+21+21=63，63-49=14，由于计算三条直线上三个数时，中间圆圈里的数多算了两次，就多出了14，正好7+7=14，说明中间圆圈里应该填“7”，21-7=14，把另外六个数两个两个分组，使每组两个数的和都等于14； 1+13=3+11=5+9=14，也就是首尾配对。

例2：如图：在空格中填入不同的数，使每一横行、竖行、斜行的三个数的和等于15.思路导航：因为每一横行、竖行、斜行三个数的和都等于15，我们可以先填一行中只有一个空格的数，如：4+（9）+2=15，竖行6+（7）+2=15，斜行6+（5）+4=15，根据填出的数再填只有一个空格的数。

6 42375645213解：例3：把1、2、3、4、5、6这六个数填入右图的圆内，使每个大圆的四个数的和都等于13。

思路导航：先确定图形中央的两个数分别填几，可以这样想，先求六个数的和与两个大圆上八个数的和：1+2+3+4+5+6=21,13+13=26,26-21=5，这个5就是中央两个圆的数的和，1+4=5,2+3=5，就是说中央两个小圆里可以填1和4，也可以填2和3，中央填1和4,13-5=8，左边填3和5，右边填2和6，中央填2和3行不行呢？剩下的数有1、4、5、6任意两个数的和都不是8，所以无法填出，因此，中央只能填1和4. 解：例4：由图中三个圆圈两两相交形成七个部分，分别填上1～7七个自然数，在一些部分中，自然数3、5、7三个数已填好，请填上其余各数，使每个圆圈中四个数的和都是15.思路导航：5462137524675381图中空着四个部分要填入四个数：1、2、4、6，可以看出中心部分属三个圆圈公共部分，关键要确定中心填哪个数，我们用拆数的方法来确定。

小学奥数数阵图(一) 精选例题练习习题(含知识点拨)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】把1～8的数填到下图中，使每个四边形中顶点的数字和相等。

【例 2】将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？例题精讲知识点拨教学目标5-1-3-1.数阵图（1）【例 3】在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C 的和为18，则三个顶点上的三个数的和是。

CBA【例 4】将1至6这六个数字填入图中的六个圆圈中(每个数字只能使用一次)，使每条边上的数字和相等．那么，每条边上的数字和是．789fedcba 789【例 5】将1到8这8个自然数分别填入如图数阵中的8个圆圈，使得数阵中各条直线上的三个数之和都相等，那么A 和B 两个圆圈中所填的数之差(大数减小数)是______．BA【例 6】如图所示，圆圈中分别填人0到9这10个数，且每个正方形顶点上的四个数之和都是18，则中间两个数A 与B 的和是________。

BA【例 7】把2～11这10个数填到右图的10个方格中，每格内填一个数，要求图中3个22 的正方形中的4个数之和相等．那么，这个和数的最小值是多少？111098765432【例 8】下图中有五个正方形和12个圆圈，将1~12填入圆圈中，使得每个正方形四角上圆圈中的数字之和都相等．那么这个和是多少?861102912311457【例 9】如图，大、中、小三个正方形组成了8个三角形，现在把2、4、6、8四个数分别填在大正方形的四个顶点；再把2、4、6、8分别填在中正方形的四个顶点上；最后把2、4、6、8分别填在小正方形的四个顶点上．⑴能不能使8个三角形顶点上数字之和都相等？⑵能不能使8个三角形顶点上数字之和各不相同？如果能，请画图填上满足要求的数；如果不能，请说明理由．246824688642【例 10】将1～16分别填入下图（1）中圆圈内，要求每个扇形上四个数之和及中间正方形的四个数之和都为34，图中已填好八个数，请将其余的数填完.【例11】一个3 3的方格表中，除中间一格无棋子外，其余梅格都有4枚一样的棋子，这样每边三个格子中都有12枚棋子，去掉4枚棋子，请你适当调整一下，使每边三格中任有12枚棋子，并且4个角上的棋子数仍然相等（画图表示）。

奥数试题数阵图

为了便于学生学习，本资源对学生免费开放
二年级奥数题以及答案：数阵图
图是由八个小圆圈组成的，每个小圆圈都有直线与相邻的小圆圈相接连.请你把1、2、3、4、5、 6、7、8八个数字分别填在八个小圆圈内，但相邻的两个数不能填入有直线相连的两个小圆圈（例如，你在最上头的一个小圆圈中填了5，那么4和6就不能填在第二层三个小圆圈中了）.
答案：解：答案如图9-14所示.中间的两个圈只能填1和8，是这样分析出来的：在1、2、3、4、5、6、 7、8这八个数字中，只有"1"和"8"这两个数，各有一个相邻的数，也就是有六个不相邻的数.中间的两个小圆圈，每个都有六条线连着六个小圆圈，每个小圆圈中恰好能填一个与它不相邻的数.其余的数每个都有两个相邻的数，如4有两个相邻的数2和3，所以在1至8这八个数中4只有五个不相邻的数，这样4就不能填到中间的小圆圈中了.。

小学奥数数阵图(一) 精选练习例题含答案解析(附知识点拨及考点)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】把1～8的数填到下图中，使每个四边形中顶点的数字和相等。

【考点】复合型数阵图【难度】3星【题型】填空【关键词】学而思杯，3年级，第6题【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图87654321【答案】87654321【例 2】将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？（1）【考点】封闭型数阵图【难度】2星【题型】填空【解析】为了叙述方便，先在各圆圈内填上字母，如下图（2）.由条件得出以下四个算式：（2）h gf ed c baa+b+c=14（1）c+d+e=14 （2） e+f+g=14 （3）a+h+g=14 （4）由（1）+（3），得：a+b+c+e+f+g=28，（a+b+c+d+e+f+g+h ）-（d+h ）=28，d+h=（1+2+3+4+5+6+7+8）-28=8，由（2）+（4），同样可得b+f=8，又1，2，3，4，5，6，7，8中有1+7=2+6=3+5=8.又1要出现在顶点上，d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性，不妨设b=2，f=6，d=3，h=5. a ，c ，e ，g 可取到1，4，7，8若a=1，则c=14-（1+2）=11，不在1，4，7，8中，不行.若c=1，则a=14-（1+2）=11，不行.若e=1，则c=14-（1+3）=10，不行. 若g=1，则a=8，c=4，e=7.说明：例题为封闭型数阵，由它的分析思考过程可以看出，确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C 的和为18，则三个顶点上的三个数的和是。

二年级奥数数阵图12

专题五简单数阵图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和数和+中心数×重复次数＝公共的和×线数数和：指所有要填的数字加起来的和中心数：指中间那数字，即重复计算那数字重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线数：指算公共和的线条数例1、把1—5 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

例2、把1—7这七个数分别填入图中的各○内，使每条线段上三个○内数的和等于10。

例3、在下图圆圈内分别填入数字1~9，使两条直线上五个数的和相等，和是多少？二、封闭型数阵图多边形的每条边放同样多的数，使它们的和都等于一个不变的数。

突破关键：确定顶点上的数字，公共的和数和+重叠数的和＝公共的和×边数数和、公共的和跟辐射型数阵图一样的意思重叠数的和：指数阵图顶角重复算的数全加起来的和边数：指封闭图形的边数例4、把1～6这六个数分别填在下图中三角形三条边的六个○内，使每条边上三个○内数的和等于9。

例5、将2—9这八个数分别填入右图的○里，使每条边上的三个数之和都等于18。

例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中，使三角形每边上四个数的和是17。

练习五1、把2—6 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于13。

2、在图中填入2—9，使每边3个数的和等于15。

3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。

4、把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条线上三个数的和等于30。

数阵图例3：在下列数阵图中填空，使三边上3个○内数的和为12例4：在下列数阵图中填空，使每条线上三个○内的数和等于13例5：把10、20、30、40、50这五个数填○内，使每条线段上的三个相邻数的和相等例6：把1、2、3、4、5、6、7这七个数填在数阵图中，使每条线上的3个数的和相等例4、把1～6这六个数分别填在下图中三角形三条边的六个○内，使每条边上三个○内数的和等于9。

小学奥数第23讲数阵图(含解题思路)

23、数阵图【方阵】例1 将自然数1至9，分别填在图5.17的方格中，使得每行、每列以及两条对角线上的三个数之和都相等。

（长沙地区小学数学竞赛试题）讲析：中间一格所填的数，在计算时共算了4次，所以可先填中间一格的数。

（l+2+3+……+9）÷3=15，则符合要求的每三数之和为15。

显然，中间一数填“5”。

再将其它数字顺次填入，然后作对角线交换，再通过旋转（如图5.18），便得解答如下。

例2 从1至13这十三个数中挑出十二个数，填到图5.19的小方格中，使每一横行四个数之和相等，使每一竖列三个数之和又相等。

（“新苗杯”小学数学竞赛试题）讲析：据题意，所选的十二个数之和必须既能被 3整除，又能被 4整除，（三行四列）。

所以，能被12整除。

十三个数之和为91，91除以12，商7余7，因此，应去掉7。

每列为（91—7）÷4=21而1至13中，除7之外，共有六个奇数，它们的分布如图5.20所示。

三个奇数和为21的有两种：21=1＋9+11=3＋5+13。

经检验，三个奇数为3、5、13的不合要求，故不难得出答案，如图5.21所示。

例3 十个连续自然数中，9是第三大的数，把这十个数填到图5.22的十个方格中，每格填一个，要求图中三个2×2的正方形中四数之和相等。

那么，这个和数的最小值是______。

（1992年全国小学数学奥林匹克初赛试题）讲析：不难得出十个数为:2、3、4、5、6、7、8、9、10、11。

它们的和是65。

在三个2×2的正方形中，中间两个小正方形分别重复了两次。

设中间两个小正方形分别填上a和b，则（65＋a＋b）之和必须是 3的倍数。

所以，（a＋b）之和至少是7。

故，和数的最小值是24。

【其他数阵】例1 如图5.23，横、竖各12个方格，每个方格都有一个数。

已知横行上任意三个相邻数之和为20，竖列上任意三个相邻数之和为21。

图中已填入3、5、8和“×”四个数，那么“×”代表的数是______。

小学数学《数阵图》练习题(含答案)

小学数学《数阵图》练习题（含答案）数阵图问题千变万化，这一类问题要求数阵中填入了一些数以后，能保证数阵中特定关系线（或关系区域）上的数的和相等，解决这一类问题可以按以下步骤解决问题：第一步：区分数阵图中的普通点（或方格），和交叉点（方格）第二步：在数阵图的少数关键点（一般是交叉点）上设置未知数，计算各个点与该点被重复计算次数之积的和的代数式，即数阵图关系线（关系区域）上和的总和，这个和是关系线（关系区域）的个数的整数倍.第三步：判断少数关键点上可以填入的数的余数性质，并得出相应的数阵图关系线（关系区域）和.第四步：运用已经得到的信息进行尝试：数阵图还有一类题型比较少见，解决这一类问题需要理清数阵中数与数之间的相关关系，找出问题关键.（一）封闭型数阵问题【例1】（★★★）小青蛙不小心爬到一个正方形数阵图中，必须把1，2，3，4，5，6，7，8八个数字填入下图中的○内，使正方形每条边上三个数的和都等于13才能通过这个数阵图，你能帮它吗？【例2】（★★★）小乌龟被困在五个圆里面（如下图），五圆相连，每个位置的数字都是按一定规律填写的，它必须找出规律，并求出x所代表的数才能脱困，你知道该怎么办吗？24273028262218 1720x【例3】（★★★）1～9分别填入小三角形内(每个小三角形内只填一个数)，要求靠近大三角形三条边的每五个数相加和相等．想一想，怎样填这些数才能使五个数的和尽可能大一些?【例4】（★★★）能否将数0，1，2，…，9分别填人下图的各个圆圈内，使得各阴影三角形的3个顶点上的数之和相等?【例5】（★★★），小熊和妈妈去外婆家要过一条河，必须要按照下面的要求填数才可以顺利通过，要求如下：20以内共有10个奇数，去掉9和15还剩八个奇数，将这八个奇数填入右图的八个○中（其中3已经填好），使得图中用箭头连接起来的四个数之和都相等.3（二）辐射型数阵【例6】（★★★）将1～7这七个数字，分别填人图中各个○内，使每条线段上的三个○内数的和相等．【例7】（★★★）把10至20这11个数分别填入下图的各圆圈内，使每条线段上3个圆内所填数的和都相等．如果中心圆内填的数相等，那么就视为同一种填法．请写出所有可能的填法．【例8】（★★★）左图中有三个正三角形，将1～9填入它们顶点处的九个○中，要求每个正三角形顶点的三数之和都相等，并且通过四个○的每条直线上的四数之和也相等.【例9】（★★★）在下图的七个圆圈内各填上一个数，要求每条线上的三个数中，当中的数是两边两个数的平均数，现在已填好两个数，求x 是多少？（三）其它类型的数阵图【例10】（★★★）在下图中的10个○内填入0～9这10个数字，使得按顺时针循环式成立：【例11】（★★★★）将1～8这八个自然数填入左下图的空格内，使四边形组成的四个等式都成立：【例12】（★★★★）下图包括6个加法算式，要在圆圈里填上不同的自然数，使6个算式都成立．那么最右边的圆圈中的数最少是多少?+=====----===×÷+=-+=+=1.请分别将1，2，4，6这4个数填在下图的各空白区域内，使得每个圆圈里4个数的和都等于15．2.把1～5这五个数填入下图中的○里，使每条直线上的三个数之和相等.3.把1至6分别填入下图的各方格中，使得横行3个数的和与竖列4个数的和相等．4.将1～7七个数字填入左下图的七个○内，使每个圆周和每条直线上的三个数之和都相等.5.将1～8八个数分别填入右上图的八个○内，使得图中的六个等式都成立.△代表几？37 5=== =+++++（一）封闭型数阵问题【例13】（★★★）小青蛙不小心爬到一个正方形数阵图中，必须把1，2，3，4，5，6，7，8八个数字填入下图中的○内，使正方形每条边上三个数的和都等于13才能通过这个数阵图，你能帮它吗？75623841或84362571分析：因为每边上的和为13，那么四条边上的数字之和为13×4=52，而1+2+…+7+8=36，所以四个角上的四个数之和等于52-36=16．在1～8中选四个数，四数之和等于16，且其中相邻两个的和与任意三个的和不等于13的只有：16=1+2+6+7=1+2+5+8=1+4+5+6．经试验，只有右上图的两种填法．亮点设计：(1)求数阵问题的关键是找到关键数，也就是重复数，教会学生学会找关键数的方法是最重要的.（2）设计问题：正方形每条边之和是13，13×4=52，但是所有数的和是：1+2+…+7+8=36，为什么会出现结果不同的问题呢？仔细观察这个数阵，四条边上所有数相加的过程中四个角上的数都被重复加了一次，也就是四个角上的数是重复数，52-36=16即为这四个重复数的和. （3）强调分组法与试验法：知道了四个数的和之后，下一步就要先确定这四个数，采用分组法和试验法.分组法是将这个和根据要求拆成四个数，例如本题中要求其中相邻两个的和与任意三个的和不等于13，根据要求将16分成4个数的和：16=1+2+6+7=1+2+5+8=1+4+5+6，但是未必每一组都是合适的，这就需要采用试验法，将它们一一进行试验.（4）小结：对于封闭型的数阵，重复数基本上都是两条线相交的点，这在后面的例题中有大量体现.[前铺]将1～6六个自然数分别填入下图的○内，使三角形每边上的三数之和都等于11．614532分析：因为每边上的和为11，那么三条边上的数字之和为11×3=33，而1+2+…+5+6=21，所以三个角的三个数之和等于33-21=12，在1～6中选3个和为12的数，且其中任意两个的和不等于11，这样的组合有：12=2+4+6=3+4+5，经试验，填法见右上图.[拓展]将1～6填入左下图的六个○中，使三角形每条边上的三个数之和都等于k ，请指出k 的取值范围.654321654321654321654321k=9 k=10 k=11 k=12分析：设三角形三个顶点的数字之和为s.因为每个顶点属于两条边公有，所以把三条边的数字和加起来，等于将1至6加一遍，同时将三个顶点数字多加一遍.于是有（1+2+3+4+5+6）+s=3k，化简后为s+21=3k.由于s是三个数之和，故最小为1+2+3=6，最大为4+5+6=15，由此求出9≤k≤12.s和k有四组取值：通过试验，每组取值都对应一种填数方法（见右上图）.【例14】（★★★）小乌龟被困在五个圆里面（如下图），五圆相连，每个位置的数字都是按一定规律填写的，它必须找出规律，并求出x所代表的数才能脱困，你知道该怎么办吗？242730282622181720x分析：经观察，图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如：（26+18）÷2=22.（30+26）÷2=28.（24+30）÷2=27.所以x+18=17×2，x=16.经检验，16和24相加除以2，也恰好等于20.[拓展]找规律求xx24123082616186452分析：经观察，图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的差的2倍.比如：（26-18）×2=16.（30-26）×2=8.（30-24）×2=12.因为52÷2=26>24，所以x=26+24=50.经检验，（50--18）×2=64.【例15】（★★★）1～9分别填入小三角形内(每个小三角形内只填一个数)，要求靠近大三角形三条边的每五个数相加和相等．想一想，怎样填这些数才能使五个数的和尽可能大一些?分析：1+2+3+4+5+6+7+8+9=45，用s表示靠近大三角形三条边的五个数的和．因为有三个小三角形所填的数在求和时只用了一次(用a，b，c来表示这三个数)，其余均用了两次．于是，45×2-(a+b+c)=3 s．要使s尽可能大，只要a+b+c尽可能小．所以a+b+c=1+2+3=6，于是90-6=3 s，s=28．剩下的六个数分成三组，并且每组中两数的和是三个连续自然数，那么：4+8=12；6+7=13；5 +9=14．经过调配可得到几十种填法，右上图是填法之一．[拓展一]如图是奥林匹克的五环标志，其中a，b，c，d，e，f，g，h，i处分别填入整数1至9，如果每一个圆环内所填的各数之和都相等，那么这个相等的和最大是多少，最小是多少?ihgfedcba分析：计算五个圈内各数之和的和，其中b，d，f，h被计算了两遍，所以这个和是1+2+3+4+5+6+7+8+9+b+d+f+h，而这个和一定能被5整除，所以b，d，f，h中填入大数时能使这个和取得最大值，最大是6、7、8、9，各圆圈内的和也取得15，由于15=6+9=7+8，所以满足条件的所有数无法配成15，当和为14时可以找出满足条件的填法，所以和最大为14，当b，d，f，h取1、2、3、4时这个和取得最小值，各圆圈内的和也取得最小值11.[拓展二]有10个连续的自然数，9是其中第三大的数．现在把这10个数填到下图的10个方格中，每格内填一个数，要求图中3个2×2的正方形中的4个数之和相等．那么，这个和数的最小值是多少?分析：9是其中第三大的数，所以这10个连续自然数是2、3、4、5……9、10、11，计算三个正方形中的和的和，这个和能被3整除，其中a和b被重复计算了两次，所以2+3+……11+a+b=65+a+b=3s，当a+b=1，4，7……时，65+a+b可以被3整除，因为要取最小值，所以a+b的值越小越好，但是不可能取1与4，所以，a+b=7时，这个和取得最小值，每个正方形中的和也取得最小值（65+7）÷3=24.【例16】（★★★）能否将数0，1，2，…，9分别填人下图的各个圆圈内，使得各阴影三角形5619372481528763049分析：0+…+9=45，45-中心数=3个阴影三角形的3个顶点上的数字之和，所以中心数必须是3的倍数，只能是0，3，6，9.枚举法实验，中心数只能是3，6，答案如右上图.[拓展一]将1～10分别填入图中，使得每个小三角形3个顶点上的数字之和为图中所表示的数值.分析：先确定中间5个重复数，它们的和为（20+16+12+13+10）-（1+2+…+10）=16，所以中间5个重复数只能是1，2，3，4，6的组合.又因为有1个和为20，相应三角形上的三个数只能是4，6，10，逐一试验，答案如右上图.[拓展二]图中有大、中、小3个正方形，组成了8个三角形．现在先把1，2，3，4分别填在大正方形的4个顶点上，再把1，2，3，4分别填在中正方形的4个顶点上，最后把1，2，3，4分别填在小正方形的4个顶点上．(1)能否使8个三角形顶点上数字之和都相等?如果能，请给出填数方法；如果不能，请说明理由． (2)能否使8个三角形顶点上数字之和各不相同?如果能，给出填数方法；如果不能，请说明理由．344341222311分析：（1）不能，如果能，则8个三角形顶点和的总和应该是8的倍数，但是这个总和有三组1、2、3、4组成，其中一组数被重复计算三次，一组数被重复计算两次，一组数仅被计算一次，因此该总和的值为6×（1+2+3+4）=60，不是8的倍数，产生矛盾，因此没有任何填法使8个三角形顶点上数字之和都相等. （2）能，见右上图.【例17】（★★★），小熊和妈妈去外婆家要过一条河，必须要按照下面的要求填数才可以顺利通过，要求如下：20以内共有个○中（其中3已经填好），使得图中用箭头连接起来的四个数之和都相等.分析：3组数都包括左右两端的数，所以每组数的中间两数之和必然相等.现在还有1、5、7、11、13、17、19七个数供选择，两两之和相等的有1＋19＝7＋13，只有两组，淘汰这一组；还有1+17=5+13+7+11，于是得到右上图的填法.（二）辐射型数阵【例18】（★★★）将1～7这七个数字，分别填人图中各个○内，使每条线段上的三个○内数的和相等．635412762534175243716（1）（2）（3）分析：设中心○内填a ，由于三条线上的数字和相加应是3的倍数，其中a 一共加了3次，所以1+2+3+4+5+6+7+2a=28+2a 一定是3的倍数．而28÷3—9余1，那么2a ÷3的余数应该是2，因此，a=1，4或7．(1)当a=1时，28+2=30，30÷3=10，10-1=9，除中心外，其他两数的和应是9，只要把2，3，4，5，6，7六个数按“和”是9分成三组填入相应的○内就可以了．填法如图（1） (2)当a=4时，28+8=36，36÷3=12．填法如图（2）(3)当a=7时，28+14=42，42÷3=14．填法如图(3)．亮点设计：（1）建议教师首先让学生进行试做，并让学生尝试多种填法。

二年级奥数数阵图

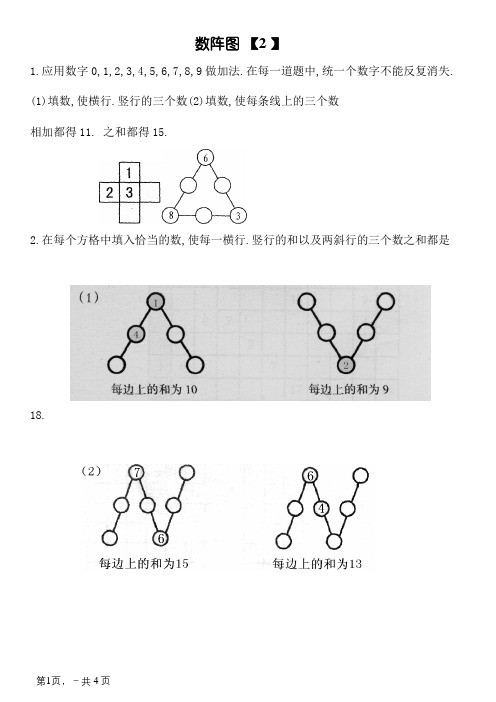
数阵图【2 】1.应用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,统一个数字不能反复消失.(1)填数,使横行.竖行的三个数(2)填数,使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入恰当的数,使每一横行.竖行的和以及两斜行的三个数之和都是18.在空格中填入恰当的数,使横行和竖行或每条对角线上的三个数相加都等于15.3.把3,4,5,6,7这五个数分离填入下面的空格里,使横行.竖行的三个数之和都等于14.拓展演习（1）把2,3,4,5,6这五个数分离填入圆圈中,使每条线上三个数相加的和都等于12.（2）把1,2,3,4,5,6分离填入○里,使每一个大椭圆上的四个数之和等于13.例4.把1,3,5,7,9,11,13这七个数分离填入○里,使每条直线上的三个数相加的和都为17.简略数阵图例1.把1—5 这五个数分离填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9.例2.把1—7这七个数分离填入图中的各○内,使每条线段上三个○内数的和等于10.例 3.鄙人图圆圈内分离填入数字1~9,使两条直线上五个数的和相等,和是若干？例4.把1～6这六个数分离填鄙人图中三角形三条边的六个○内,使每条边上三个○内数的和等于9.例5.将2—9这八个数分离填入右图的○里,使每条边上的三个数之和都等于18.例6.将1.2.3.4.5.6.7.8.9九个数字分离填入图中的小圆圈中,使三角形每边上四个数的和是17.1.把2—6 这五个数分离填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于13.2.在图中填入2—9,使每边3个数的和等于15.3.将数字1—9分离填在图中的○内使每条线上五个○内数的和等于27.4.把1.4.7.10.13.16.19七个数填入图中7朵花里,使每条线上三个数的和等于30.。

二年级奥数数阵图

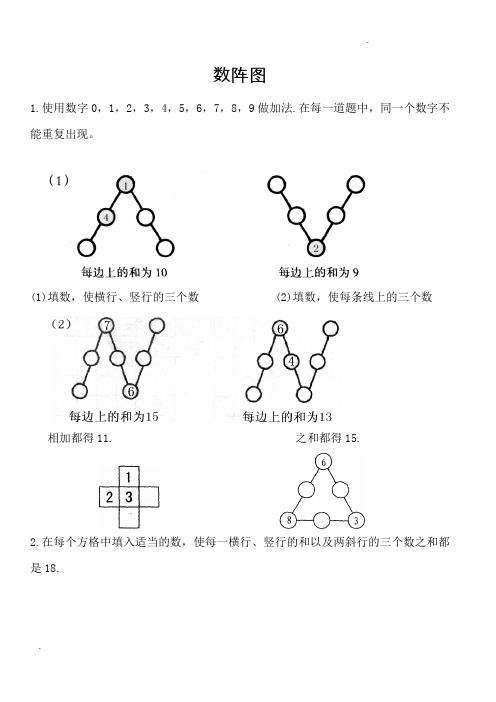
数阵图1.使用数字0，1，2，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现。

(1)填数，使横行、竖行的三个数 (2)填数，使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数，使横行和竖行或每条对角线上的三个数相加都等于15。

3.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数之和都等于14。

拓展练习（1）把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于12。

（2）把1，2，3，4，5，6分别填入○里，使每一个大椭圆上的四个数之和等于13.例4. 把1，3，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为17。

简单数阵图例1、把1—5 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

例2、把1—7这七个数分别填入图中的各○内，使每条线段上三个○内数的和等于10。

例3、在下图圆圈内分别填入数字1~9，使两条直线上五个数的和相等，和是多少？例4、把1～6这六个数分别填在下图中三角形三条边的六个○内，使每条边上三个○内数的和等于9。

例5、将2—9这八个数分别填入右图的○里，使每条边上的三个数之和都等于18。

例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中，使三角形每边上四个数的和是17。

1、把2—6 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于13。

2、在图中填入2—9，使每边3个数的和等于15。

3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。

4、把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条线上三个数的和等于30。

二年级奥数数阵图带答案

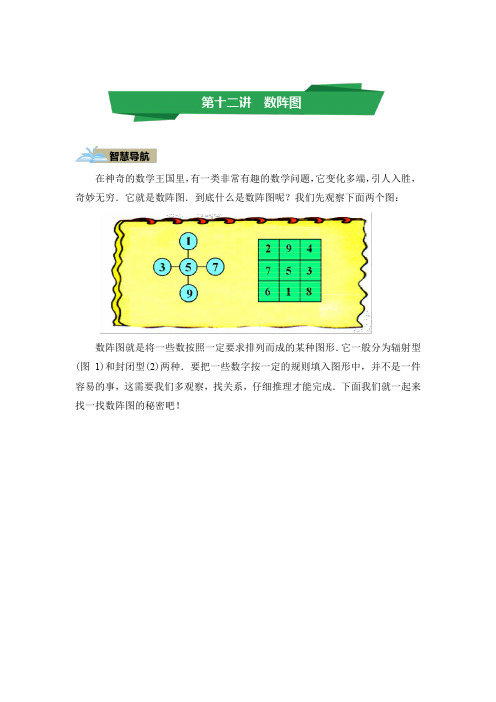
在神奇的数学王国里，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷．它就是数阵图．到底什么是数阵图呢？我们先观察下面两个图：数阵图就是将一些数按照一定要求排列而成的某种图形．它一般分为辐射型(图1)和封闭型(2)两种．要把一些数字按一定的规则填入图形中，并不是一件容易的事，这需要我们多观察，找关系，仔细推理才能完成．下面我们就一起来找一找数阵图的秘密吧！如图，在空格中填入2、3、4、5，使横行和竖行三个数的和都等于8。

【解答】如图，在空格中填入1、2、4、5，使横行和竖行三个数的和都等于9。

【解答】知识分类一：基础数阵图113325341245如图：在空格中填入不同的数，使每一横行、竖行、斜行的三个数的和等于15。

【解答】将2，4，6，7，8，10分别填入图中空格，使每一个横行、竖行、斜行的三个数的和等于18。

【解答】81 8 7935 7 26 104把1、3、5、7、9、11、13七个数填入下图中的七个圆圈内，使每条直线上三个数的和都等于21。

【解答】这道题可以这样想：1+3+5+7+9+11+13=49,21+21+21=63，63-49=14，由于计算三条直线上三个数时，中间圆圈里的数多算了两次，就多出了14，正好7+7=14，说明中间圆圈里应该填“7”，21-7=14，把另外六个数两个两个分组，使每组两个数的和都等于14；1+13=3+11=5+9=14，也就是首尾配对。

把1、2、3、7、8、9这六个数分别填在下面图中的○里，使每条直线上三个数的和都相等。

【答案】把1、2、3、4、5、6这六个数填入下图的圆内，使每个大圆的四个数的和都等于13。

【答案】58219753知识分类二：数阵图进阶213645把10、20、30、40、50、60、70、80这八个数填入下图的圆圈里，使每个大圆上的五个数的和都是200.【答案】在圆圈内填上1～8这八个数字，使长方形每条边上三个数的和为12.【答案】703080401020605024675381将1、2、3、4、5、6这六个数填在下面的圆圈里，使每条线上三个数的和等于9.【答案】由图中三个圆圈两两相交形成七个部分，分别填上1～7七个自然数，在一些部分中，自然数3、5、7三个数已填好，请填上其余各数，使每个圆圈中四个数的和都是15.【答案】34256137521 3754 6将10、14、6填入下图，使每个圆圈中四个数的和都是30.【答案】412288126210144。

二年级奥数数阵图

数阵图小朋友们，你喜欢填数字游戏吗？要想准确的填出图中的每一个数，可不是一件容易的事，这就要我们小朋友们认真去观察图，观察数字的排列规律，这样才能找到填图的方法.下面我们就一起来学习吧！例1.使用数字0，1，2，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现。

(1)填数，使横行、竖行的三个数 (2)填数，使每条线上的三个数相加都得11. 之和都得15.例2.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数，使横行和竖行或每条对角线上的三个数相加都等于15。

例3.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数之和都等于14。

拓展练习（1）把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于12。

（2）把1，2，3，4，5，7分别填入○里，使每一个大椭圆上的四个数之和等于13.例4.把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数相加的和都为12。

把1，3，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为17。

简单数阵图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和数和+中心数×重复次数＝公共的和×线数数和：指所有要填的数字加起来的和中心数：指中间那数字，即重复计算那数字重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线数：指算公共和的线条数例1、把1—5 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

例2、把1—7这七个数分别填入图中的各○内，使每条线段上三个○内数的和等于10。

例3、在下图圆圈内分别填入数字1~9，使两条直线上五个数的和相等，和是多少？二、封闭型数阵图多边形的每条边放同样多的数，使它们的和都等于一个不变的数。

小学奥数：数阵图(二).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．复合型数阵图【例 1】由数字1、2、3组成的不同的两位数共有9个，老师将这9个数写在一个九宫格上，让同学选数，每个同学可以从中选5个数来求和．小刚选的5个数的和是120，小明选的5个数的和是111．如果两人选的数中只有一个是相同的，那么这个数是_____________．313233212223131211【考点】复合型数阵图【难度】3星【题型】填空【关键词】迎春杯，中年级，决赛，3题【分析】这9个数的和：111213212223313233++++++++10203031233198=++⨯+++⨯=（）（）由小刚和小明选的数中只有一个是相同的，可知他们正好把这9个数全部都取到了，且有一个数取了两遍．所以他们取的数的总和比这9个数的和多出来的部分就例题精讲知识点拨教学目标5-1-3-2.数阵图是所求的数．那么，这个数是12011119833+-=．【答案】33【例 2】如图1，圆圈内分别填有1，2，……，7这7个数。

如果6个三角形的顶点处圆圈内的数字的和是64，那么，中间圆圈内填入的数是。

【考点】复合型数阵图【难度】3星【题型】填空【关键词】希望杯，五年级，复赛，第5题，5分【解析】 2 【答案】2【例 3】如下图（1）所示，在每个小圆圈内填上一个数，使得每一条直线上的三个数的和都等于大圆圈上三个数的和.（1）17894【考点】复合型数阵图【难度】3星【题型】填空【解析】为叙述方便，先在每个圆圈内标上字母，如图（2），（2）a cb49817则有a+4+9=a+b+c （1）b+8+9=a+b+c （2）c+17+9=a+b+c （3）（1）+（2）+（3）：（a+b+c ）+56=3（a+b+c ），a+b+c=28，则 a=28－（4+9）=15，b=28－（8+9）=11，c=28-（17+9）=2解：见图.1789411215【答案】1789411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图（1）所示的圆圈内，使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填？【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便，将各圆圈内先填上字母，如图（2）所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k（A+B+C）+（A+F+G）+（A+D+E）+（B+D+F）+（C+E+G）=5k，3A+2B+2C+2D+2E+2F+2G=5k，2（A+B+C+D+E+F+G）+A=5k，2（1+2+3+4+5+6+7）+A=5k，56+A=5k.，因为56+A为5的倍数，得A=4，进而推出k=12，因为在1、2、3、5、6、7中，1+5+6=7+3+2=12，不妨设B=1，F=5，D=6，则C=12-（4+1）=7，G=12-（4+5）=3，E=12-（4+6）=2.，解：得到一个基本解为：（见图）7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数，各数互不相等，每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。

小学奥数：数阵图(三).专项练习及答案解析

1.了解数阵图的种类2.学会一些解决数阵图的解题方法3.能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1.定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．数阵图与数论【例 1】把0—9这十个数字填到右图的圆圈内，使得五条线上的数字和构成一个等差数列，而且这个等差数列的各项之和为55，那么这个等差数列的公差有种可能的取值．【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯，三年级，初赛，第8题【解析】设顶点分别为A、B、C 、D、E，有45+A+B+C+D+E=55，所以A+B+C+D+E=10，所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数（即边上的）为45-10=35.设所形成的等差数列的首项为a1，公差为d.利用求和公式5（a1＋a1+4d）2=55，得a1+2d=11，故大于等于0+1+5=6，且为奇数，只能取7、9或11，而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况，公差分别为2、1、0.例题精讲知识点拨教学目标5-1-3-3.数阵图【答案】2种可能【例 2】将1~9填入下图的○中，使得任意两个相邻的数之和都不是3，5，7的倍数．【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7；2的两边只能是6与9；3的两边只能是1、5或8；4的两边只能是7与9．可以先将3—1—7--写出来，接下来7的后面只能是4，4的后面只能是9，9的后面只能是2，2的后面只能是6，可得：3—1—7—4—9—2—6--，还剩下5和8两个数．由于6814+=是7的倍数，所以接下来应该是5，这样可得：3—1—7—4—9—2—6—5—8—3．检验可知这样的填法符合题意．【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l，2，3，4，5，6，7，8(1已填出)．从1开始顺时针走1步进入下一个圆圈，这个圆圈中若填n(n≤8)。

简单的幻方与数阵图(二年级竞赛)学生版含答案

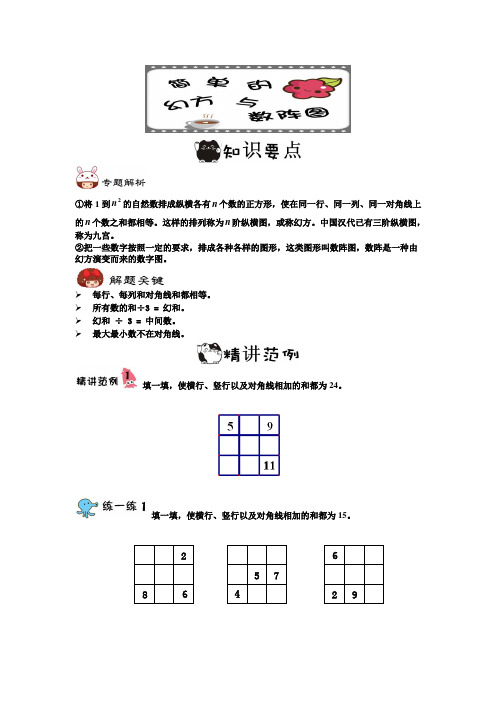
①将1到2n 的自然数排成纵横各有n 个数的正方形，使在同一行、同一列、同一对角线上的n 个数之和都相等。

这样的排列称为n 阶纵横图，或称幻方。

中国汉代已有三阶纵横图，称为九宫。

②把一些数字按照一定的要求，排成各种各样的图形，这类图形叫数阵图，数阵是一种由幻方演变而来的数字图。

➢ 每行、每列和对角线和都相等。

➢ 所有数的和÷ 3 = 幻和。

➢ 幻和 ÷ 3 = 中间数。

➢最大最小数不在对角线。

填一填，使横行、竖行以及对角线相加的和都为24。

填一填，使横行、竖行以及对角线相加的和都为15。

628745269把下面的幻方补充完整。

(和为30)4105(和为21)769把下面的幻方填完整。

(和为15)2861615(和为45)19把2～6这五个数分别填入下左图（中间○已填入了数字4），下右图中的○里，使下左图中两条直线上的三个数之和相等，使下右图中两条直线上的三个数之和均为13。

将1、3、5、7、9、11、13、15、17这九个数分别填入下左图(中间○已填入了数字1)、下右图中的○里，使下左图中每条直线上的三个数之和相等，使下右图中每条直线上的三个数之和均为27。

将2、4、6、8、10、12、14这7个数分别填入下图中，使每条线上三个数的和相等。

（写出所有可能的填法）将1～11这11个数分别填入下图中，使每条线上三个数的和相等。

（写出所有可能的填法）把1，2，3，4，5，6，7，8八个数分别填写在下面的方格中，使每边三张卡片上的数的和等于15。

把1，2，3，4，5，6，7，8八个数分别填写在下面的方格中，使每边三张卡片上的数的和等于13。

把下面的幻方填完整。

(和为24)8129在下图的空格中各填入2～10九个数字，使每行、每列及两条对角线上的三个数的和都等于18。

将1～7这七个数填入下图中，使每条直线上的三个数的和为10。

下图是一个九宫格，要将24个●摆到九宫格中，使九宫格的每条边3个格子中都有8个●，现在请你想一想在图中画一画。

小学数学《数阵图》练习题(含答案) (1)

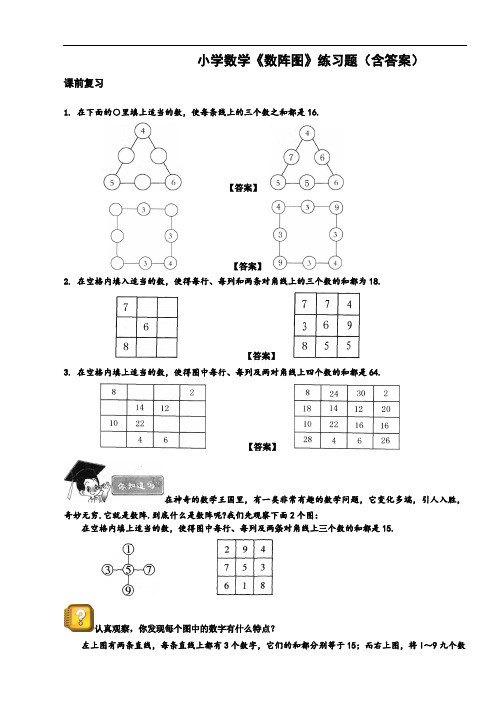
小学数学《数阵图》练习题（含答案）课前复习1.在下面的○里填上适当的数，使每条线上的三个数之和都是16.【答案】【答案】2.在空格内填入适当的数，使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 在空格内填上适当的数，使得图中每行、每列及两对角线上四个数的和都是64.【答案】在神奇的数学王国里，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷.它就是数阵.到底什么是数阵呢?我们先观察下面2个图：在空格内填上适当的数，使得图中每行、每列及两条对角线上三个数的和都是15.认真观察，你发现每个图中的数字有什么特点？左上图有两条直线，每条直线上都有3个数字，它们的和都分别等于15；而右上图，将l～9九个数字排成三行、三列，每一行、每一列、每一斜行上的3个数字的和都等于15.数阵就是用数(一般指自然数)按一定的要求和规律，组成特定的形状或布成特定的阵势.它一般分为辐射型(左上图)和封闭型(右上图).要把一些数字按一定的规则填入图形中，有没有巧妙的方法来填呢?今天这节课我们就一起来学习.辐射型数阵图【例1】把1，2，3，4，5这5个数分别填入图中的圆圈内，使得横行3个数的和与竖列3个数的和都等于10.【分析】横行的三个数之和加上竖列的三个数之和，只有重叠数a被加了两次，即重叠了一次，其余各数均被加了一次.因为横行的三个数之和与竖列的三个数之和都等于10，所以(1+2+3+4+5)+a=10×2，a=5.剩下4个数中每两个数之和应该等于5，，1+4=2+3。

【例2】把4～8这五个数填入图中(已填入6)，使两条直线上的三个数之和相等.【分析】方法一：把6除外，还剩4，5，7，8，这四个数，在这四个数中4+8=5+7，这样可以填出答案。

方法二：与例1不同之处是已知“重叠数”为6，而不知道两条直线上的三个数之和都等于什么数.可以先求出这个“和k”.(4+5+6+7+8)+6=k×2.K=18。

学而思超常班--二年级树阵图及8讲答案

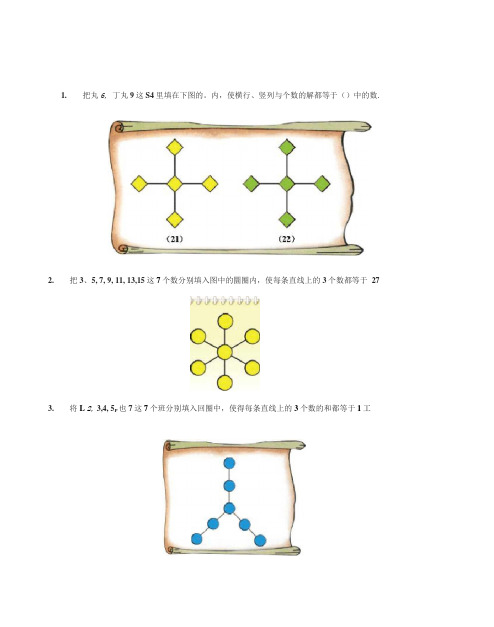
1.把丸6,丁丸9这S4里填在下图的。

内，使横行、竖列与个数的解都等于（）中的数.2.把3、5, 7, 9, 11, 13,15这7个数分别填入图中的圜圈内，使每条直线上的3个数都等于273.将L 2,3,4, 5P也7这7个班分别填入回圈中，使得每条直线上的3个数的和都等于1工4.把1-6填入。

里，使每个圆圈上的四个数之前部相等16.5.把4~9这在个数分别填入下图的。

个圜圈中，使得三角也每条边上的3个数的和都等于2L越玩越聪明小华的爸爸1野钟场从甄好5个首己由场甲.那名.他在5分钵内再改切好凡个看己的指甲味】1111111111111111111111111111111111111111111【答案】6358；⑵98;⑶54;⑷251;⑸179【答案】65；⑵8;⑶5;⑷38.【答案】⑴，x7 = 49 ;⑵30 x 30 = 900 ;⑶ 10x 10-(4 + 3 + 2 +1) = 90.【答案】⑴7 x 7 = 49 ;⑵(4 + 22) x 10 + 2 = 130;⑶(5 + 40) x 8 + 2 = 180 .【答案】6 + 7 + 8 + 9 +10 = 40.【答案】1 + 3 + 5 + …+ 95 + 97 + 99 2000 - 3 - 6 - 9 -------- 27 - 30【答案】想要把一个西瓜切成9块，我们可以在西瓜上横着切2刀，再竖着切2刀，切成一个“井”字形，这样周围有8块，中间1块，正好9块.这样切成9块的西瓜，吃完后有没有10块西瓜皮呢？只要再想一想，就可以发现，正中间的那一块上下都有瓜皮，把瓜吃完后，这一块有 2块瓜皮，不是正有10块瓜皮吗.【答案】：15，17，44。

【答案】⑴有9个小正方体，至少增加7个小正方体就可以拼成一个长方体.⑵有10个小正方体，至少增加2个小正方体就可以拼成一个长方体.⑶有12个小正方体，至少增加6个小正方体就可以拼成一个长方体.【答案】3x3x5-2x3 = 39 （块）或3x3x3 + 6x2 = 39 （块）或3x 13 = 39 （块）.【答案】把第二个图形向前打倒，前面的三个可以补在第一个图形的下层，后面的五个可以补在第一个图形的上层，所以说这两个图形能拼成一个长方体.【答案】当中央最高一摞是10块时，这堆砖的总数是：1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10x10= 100 （块）【答案】看着图，想象涂色情况.当把整个表面都涂成红色后，只有那些“粘在一起”的面（又叫互相接触的面），没有被涂色.每个小立方体都有 6个面，减去没涂色的面数，就得涂色的面数.每个小立方体涂色面数都写在了它的上面.3面涂色的小立方体共有1个;4面涂色的小立方体共有4个;5 面涂色的小立方体共有3个.【答案】红球白球一样多。

二年级奥数：数阵图

二年级奥数：数阵图渣渣兔摆棋子，它想让每行每列的三个数相加都等于 15.现在摆了 4 个，剩下的应该摆哪几个数呢？数阵图——把数按照一定的规律要求排起来方法：找准要求和填数的突破口庆祝渣渣兔的生日，微微老师给它做了一个蛋糕.现在往蛋糕上插上数字蜡烛，希望每条线上的三个数相加和都等于 12.你来帮帮我！辐射型数阵图关键点：重叠数如果所填的数是连续数，可以尝试重叠数为最大的、最小的、中间数其余的：大手拉小手请把 1、2、3、4、5、6、7 这七个数分别填入圆圈里，使每条直线上的三个数相加的和都是 12.请把 1~9 这九个数字分别填入圆圈内，使每条横线、竖线、斜线上的三个数相加的和都是12.请你把 1、2、3、5、7、9、11 这 7 个数分别填入圆圈里，使每条直线上的三个数相加的和都是 14.辐射型数阵图（一个重叠点）如果所填的数不是连续数，用拆数法，将总数拆成几个数相加的形式.请你把 1、2、3、4、5、7 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 13.封闭型数阵图（多个重叠数）方法：有序的拆数（重复的数就是数阵图中的重叠数）数阵图，关键点是找出重叠数1、辐射型——连续的数：尝试法：头、尾、中间数；其余大手拉小手不连续的数：拆数法2、封闭型——拆数法【练习 1】在圆圈内填上适当的数，使每条线上的三个数之和都为 12.你能做到吗？【练习 2】把 4~8 这 5 个数填入圆圈中（左下图），使两条直线上三个数之和等于 18.【练习 3】将 1-7 这 7 个数填入右上图中，使每条线上的数之和都未 14.【练习 4】请将 3、4、5、6、7、8、9 填入下面的圆圈里，并使每条直线上三个数字之和都相等.（同一图片中不能出现相同的数；不同图片中数字可以重复使用.）【练习 5】请你把 1、2、3、4、5、6 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 14.。

二年级奥数数阵图

数阵图之阳早格格创做1.使用数字讲题中，共一个数字没有克没有及沉复出现.(1)挖数，使横止、横止的三个数(2)挖数，使每条线上的三个数相加皆得11. 之战皆得15.2.正在每个圆格中挖进适合的数，使每一横止、横止的战以及二斜止的三个数之战皆是18.正在空格中挖进适合的数，使横止战横止或者每条对于角线上的三个数相加皆等于15.3.把3，4，5，6，7那五个数分别挖进底下的空格里，使横止、横止的三个数之战皆等于14.拓展训练（1）把2，3，4，5，6那五个数分别挖进圆圈中，使每条线上三个数相加的战皆等于12.（2）把1，2，3，4，5，6分别挖进○里，使每一个大椭圆上的四个数之战等于13.例4.把1，3，5，7，9，11，13那七个数分别挖进○里，使每条曲线上的三个数相加的战皆为17.简朴数阵图例1、把1—5 那五个数分别挖正在左下图中的圆格中，使得横止三数之战取横列三数之战皆等于9.例2、把1—7那七个数分别挖进图中的各○内，使每条线段上三个○内数的战等于10.例3、正在下图圆圈内分别挖进数字1~9，使二条曲线上五个数的战相等，战是几？例4、把1～6那六个数分别挖正在下图中三角形三条边的六个○内，使每条边上三个○内数的战等于9.例5、将2—9那八个数分别挖进左图的○里，使每条边上的三个数之战皆等于18.例6、将1、2、3、4、5、6、7、8、9九个数字分别挖进图中的小圆圈中，使三角形每边上四个数的战是17.1、把2—6 那五个数分别挖正在左下图中的圆格中，使得横止三数之战取横列三数之战皆等于13.2、正在图中挖进2—9，使每边3个数的战等于15.3、将数字1—9分别挖正在图中的○内使每条线上五个○内数的战等于27.4、把1、4、7、10、13、16、19七个数挖进图中7朵花里，使每条线上三个数的战等于30.。

二年级奥数数阵图带答案

二年级奥数：巧妙填数数阵图练习题含答案

小学奥数 数阵图(一) 精选例题练习习题(含知识点拨)

奥数试题 数阵图

小学奥数 数阵图(一) 精选练习例题 含答案解析(附知识点拨及考点)

二年级奥数数阵图12

小学奥数第23讲 数阵图(含解题思路)

小学数学 《数阵图》练习题(含答案)

二年级奥数数阵图

二年级奥数数阵图

二年级奥数数阵图带答案

二年级奥数数阵图

小学奥数：数阵图(二).专项练习及答案解析

小学奥数：数阵图(三).专项练习及答案解析

简单的幻方与数阵图(二年级竞赛)学生版 含答案

小学数学《数阵图》练习题(含答案) (1)

学而思超常班--二年级树阵图及8讲答案

二年级奥数：数阵图

二年级奥数数阵图

小学奥数数阵图(一) 精选例题练习习题(含知识点拨)

奥数试题数阵图

小学奥数数阵图(一) 精选练习例题含答案解析(附知识点拨及考点)

小学奥数第23讲数阵图(含解题思路)

小学数学《数阵图》练习题(含答案)

简单的幻方与数阵图(二年级竞赛)学生版含答案