1.静电场习题课
静电场习题优秀课件

设经过S1、S2旳电场强度通量分别为1、2,经过整个
球面旳电场强度通量为3,则
[]
(A)1>2,3=q/0 (B)1<2,3=2q/0 (C)1=2,3=q/0; (D)1<2,3=q/0;
q
o
S2
图1-4
2q
o
X
S12a
答:[ D ]
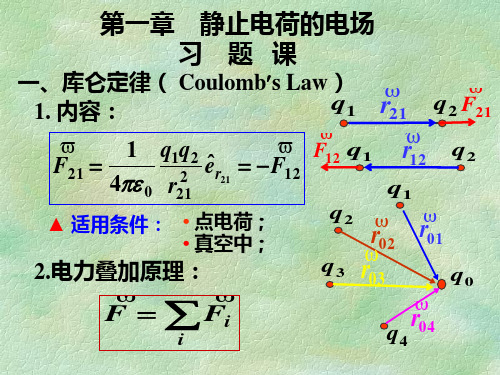
1-14(a) 点电荷q位于边长为a旳正立方体旳中心,经 过此立方体旳每一面旳电通量各是多少?
(b) 若电荷移至正方体旳一种顶点上,则经过每个面 旳电通量又各是多少?
解: (a) 因为6个全等旳正方形构成一种封闭
面, 所以 q 6 0
(b) 该顶点可视为边长等于2a 旳大立方 q
体旳中心, 经过每个大面旳电通量为 每个小立方体中不经过该顶点旳
6 0
三个小面上旳电通量为
q
24 0
而经过该顶点旳另三个 小面旳电通量为0.
s
E
dS
4r
2E
q内
0
(1) E1 = 0
(2)E2
q1
4 0r22
9
109
1.0 108 (0.2)2
q1 q2
2.25 103 v / m
(3)
E3
q1 q2
4 0r32
9
109
(1.0
1.5) (0.5)2
108
9 102 v / m
E不是r旳连续函数, 在两个球面处有跃变.
1-16 (1)设地球表面附近旳场强约为200v·m-1,方向指向 地球中心,试求地球所带旳总电量。 (2) 在离地面 1400m高处,场强降为20v·m-1,方向仍指向地球中心, 试计算在1400m下大气层里旳平均电荷密度.
静电场习题课

2
(2)两离子初速度分别为 v、v/,则
L 2v L qE n m
L 2v l′ + qE = v m
L 2m Δt=t-t′ = (v v ) vv qE
L 2m 0 要使 Δt=0,则须 vv qE 2mvv 所以:E= qL
7.如图所示,同一竖直平面内固定着两水平绝缘细杆 AB、CD,长 均为 L,两杆间竖直距离为 h,BD 两端以光滑绝缘的半圆形细杆 相连,半圆形细杆与 AB、CD 在同一竖直面内,且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线,O 为 AD、BC 连线的交点,在 O 点 固定一电量为 Q 的正点电荷.质量为 m 的小球 P 带正电荷,电量 为 q,穿在细杆上,从 A 以一定初速度出发,沿杆滑动,最后可 到达 C 点.已知小球与两水平杆之间动摩擦因数为μ ,小球所受 库仑力始终小于小球重力.求: (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值; (2) P 从 A 点出发时初速度的最小值.
1 2 -mgh-2mg·2L=0- 2 mv0 ,
得 v0= 2 gh(h 2L) .
8.一个质量为m,带有电荷-q的小物体,可在倾角 为θ 的绝缘斜面上运动,斜面底端有一与斜面垂 直的固定绝缘挡板,斜面顶端距底端的高度为h, 整个斜面置于匀强电场中,场强大小为E,方向水 平向右,如图所示.小物体与斜面的动摩擦因数 为μ ,且小物体与档板碰撞时不损失机械能。求: (1) 为使小物体能从静止开始沿斜面下滑,μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m,如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB, 可测得离子飞越 AB 所用时间 t1。改进以上方法,如图 2,让离子飞越 AB 后进入场强为 E(方向如图)的匀强电场区域 BC,在电场的作用下 离子返回 B 端,此时,测得离子从 A 出发后飞行的总时间 t2, (不计离 子重力) ⑴忽略离子源中离子的初速度, ①用 t1 计算荷质比; ②用 t2 计算荷质比。
第6章 静电场习题课(1)

x dx
P
O
a
x
l
细杆的电荷线密度l=q / (l),在x处取电荷元dq = ldx=qdx /l, 它在P点产生的电势为
dq
dx
dU P 4 0 l a x 4 0 l a x
整个杆上电荷在P点产生的电势
q lnl a x l
8 0l
l
q ln1 l
4 0l a
(2)U P
在半径为r的球面内包含的总电荷为:
qin
dV
V
r 4Ar 3 d r Ar 4
0
(r≤R)
Q
E1 4r 2
qin
0
Ar 4 / 0
E
得到: E1 Ar 2 /4 0 , (r≤R)
方向沿径向,A>0时向外,A<0时向里.
在球体外作一半径为r的同心高斯球面,按高斯定理有
E2 4r 2 qin / 0 qin ?
在半径为r的球面内包含的总电荷为:
qin
dV
V
r 4Ar 3 d r Ar 4
0
(r≤R)
qin AR4
Q
得到:E2 AR 4 / 4 0r 2 , (r >R)
方向沿径向,A>0时向外,A<0时向里.
E
6.如图所示,在电荷体密度为的均匀带电球体中,存
在一个球形空腔,若将带电球心O指向空腔球心O’的矢
R2
R1<r<R2时,
E 2rl 1 l E l
0
2r 0
R1
R1>r 或 r>R2时, E 2rl 0 E 0 L
r
10.三个互相平行的均匀无限大带电平面,面电荷密度为
静电场习题课

e ES cos
闭合曲面外法线方向(自内向外)为正
s
穿进闭合面的电场线对该闭合面提供负通量; 穿出闭合面的电场线对该闭合面提供正通量 C.有时利用高斯定理求电通量非常方便
利用高斯定理求电通量 例1: 点电荷q位于正立方体中 q 心,则通过侧面abcd的电通量 e 6
4 0
(A)
0
(B)
(C)
(D)
8 0
2. 如图所示,两个“无限长”的共轴圆柱面, 半径分别为R1和R2,其上均匀带电,沿轴线 方向单位长度上所带电荷分别为1和2 ,则 在两圆柱面之间、距离轴线为r的P点处的场 [ A ] 强大小E为: 1 1 1 2 2 (A) 2 π r (B) (C) 2 R r (D) 2 0 r R1 0 2 2 0 r 0
UP
i
E
3、 先求 V,再求 E 。 E gradV
V V V gradV x i y j z k
4 0 r 带电体
dq
2
r
0
4 0 ri
dq 4 0 r
qi
U
带电体
先求 E 再求 U 。
pe q
q2 F q 2 0 2 0 s
Sd S
•电偶极子在均匀外电场中所受到的力和力矩 =p e e E F=0 M •力偶矩 力图使电偶极子的偶极矩 转到与外电场
一致方向上来
八、电势、电势差与电势能 零电势点 1. 电势: U E dl ( = E dl ) a
底
2 E DS d DS / 0
静电场习题课一

(1)若将放在电场中某点的电荷q改为-q,则该点的电场强度 大小不变,方向与原来相反。 (2)若取走放在电场中某点的电荷,则该点的电场强度变为零。 (3)沿电场线方向,场强一定越来越小。 (4)若电荷q在A处受到的电场力比B点时大,则A点电场强度比 B点的大。 (5)电场中某点电场线的方向,就是放在该点的电荷所受电场 力的方向。 (6)在电场中,电场强度越大的地方电势越高。 (7)原静止的点电荷在只受电场力时,一定从电势高处向电势 低处运动。 (8)电荷沿电场线方向移动时,其电势能一定减小。 (9)检验电荷在电场中某点所受的电场力很大时,它在该点具 有的电势能也一定大。 (10)把两个异号电荷靠近时,电荷电势能增电场中相邻的四个 等势面,一个电子垂直经过等势面D时动能为 20eV,经过等势面C时的电势能为-10eV,到达等 势面B时速度恰好为零,已知相邻等势面间距离为 5cm,则下列说法正确的是( )
A.A等势面的电势为-10V
B.匀强电场的场强为200V/m
选ABD
C.电子再次经过D等势面时, 动能为l0eV
D.电子的运动是匀变速直线 运动
• 练习:A、B是一条电场线上的两个点,一带 负电的微粒仅在电场力作用下以一定初速度 从A点沿电场线运动到B点,其速度—时间图 象如图1-15所示.则这一电场可能是
A
例1:如图,倾角 的光滑绝缘斜面处于水平向右的匀强 场中,电场强度 ,有一个质量为 的带电小球,以速度 沿斜面匀速下滑,求: (1)小球带何种电荷?电荷量为多少? (2)在小球匀速下滑的某一时刻突然撤去斜面,此后经 内小球的位移是多大?( 取 )
小球必带正电,
重力场、电场叠加而成的复合场
等效重力场 等效重力 等效重力加速度
重力、电场力的合力
习题课第1章 静电场的基本规律

第1章 静电场的基本规律(习题课)一、 本章内容提要要求:理解和掌握各种物理量(概念)的定义和物理含义,掌握各种物理定理(律)的成立条件和运用方法。
1. 两种电荷、电荷守恒和电荷量子化2. 库仑定律 rr q q F ˆ412210⋅=πε 3. 电场强度 0q FE=4. 场强叠加原理 ∑=i E E5. 点电荷电场 r rqE ˆ4120⋅=πε 6. 电荷连续分布的带电体 三种电荷分布 ⎪⎩⎪⎨⎧===dl dq dS dq dVdq λσρ r r dq E d E 2041⋅==⎰⎰πε 计算电场分布的第一种方法(如何计算矢量积分?)7. 电场线及其性质发自正电荷(无穷远),终止于负电荷(无穷远),不在没有电荷处中断。
在静电场中,电场线不构成闭合曲线。
两条电场线不相交。
8. 高斯定理 电场的通量ε∑⎰⎰=⋅isqS d E(积分形式)ερ=⋅∇E (微分形式)电场的散度 E⋅∇=Ed i v , 有源场和无源场 高斯定理的意义——反映一般电场性质的规律。
哈密顿算符 z k y j x i ∂∂+∂∂+∂∂=∇ˆˆˆ,θϕθθϕ∂∂+∂∂⋅+∂∂=∇r e r e r er 1ˆsin 1ˆˆ计算电场分布的第二种方法(有条件的)9. 静电场的环路定理 电场的环量0l d =⋅⎰E L(积分形式)0=⨯∇E(微分形式)电场的旋度 E⨯∇=Er o t ,有旋场和无旋场 反映静电场性质的规律。
静电力是保守力,静电场是有势场。
10. 静电势能 l d 0⋅==-⎰QPPQ Q P E q A W W代表0q 与场源电荷之间的相互作用能 11. 电势差和电势l d 0⋅==-=-=⎰QPPQ QP Q P PQ E q A q W W U U Ul d ⋅=-=⎰o Po P p E U U U电势U 和静电势能W 参考零点的选择:(A )场源电荷分布于有限空间内,无穷远;(B )地面、金属外壳。
大学物理-静电场习题课PPT课件

★场强E是高斯面上任一点的电场强度。当高斯面内无电荷时,高斯面上的场
强并不一定处处为零;当高斯面上的场强处处为零时,高斯面内一定无电荷或代 数和为零。
★高斯面可任意选取,但解题中应充分利用对称性。
★适用于任何静电场,也适用于变化的电场,是电磁场的基本定理之一。
4
第10章 恒定磁场
常见应用高斯定理求解的问题
补偿法:均匀带点球+小面元(视为点电荷)
点 电 荷u q 4πε0r
带 电 球 面u(R) Q 4πε0 R
Q 4πR 2
q S Q S
4πR2
1
Q
S
E 4πε0R (Q q) 4πε0R (1 4R2 )
13
第10章 恒定磁场
个人观点供参考,欢迎讨论
高斯定理:
1
s
E
• ds
0
qi
静电场是有源场
3
第10章 恒定磁场
高斯定理:通过任意闭合曲面的电通量等于这个闭合曲面(高斯面)所包围的电
荷的代数和除以 0 ,而与闭合曲面外的电荷无关。
真空中
1
e s E • ds 0
qi
q1 S
注意:
q3
q2
★过曲面的通量由曲面内的电荷决定
★高斯面上的场强 E 是由全部电荷(面内外电荷)共同产生
5 如图所示,在边长为的正方形平面的中垂线上, 距中心O点a/2处,
有一电量为q的正电荷,则通过 该平面的电场强度通量为______________
a
a/2 q
a/2q
a
由高斯定理 q 0
a
q 60
9
第10章 恒定磁场
P30 计算题1.一半径为R的带电球体,其电荷体密度分布为 ρ =A r (r≤R) , ρ =0 (r>R) A为一常量.试求球体内外的场强分布.
静电场的基础知识课后习题(仅供参考)

4.4解:如图所示建立坐标系,在半圆 环上取一小段圆弧,其长度为θRd则其带电量为θλ=Rd q d此段圆弧在环心O 点产生的电场强度为R4d R 4dq dE 020πεθλ=πε=由半圆环的对称性可知0点的场强E沿y 轴负向,所以有R4d sin sin dE dE 0y πεθθλ=θ=故环心处的电场强度大小R2R 4d sin dE E E 000y y πελ=πεθθλ===⎰⎰π所以 j R2E 0πελ-=4.5解:(1)两电荷同号时,在其连线外侧电场强度方向相同,内侧电场强度方向相反,故电场强度为零的点在两电荷连线内侧,设该点与q 1距离为r 1 ,(r 1>0),由场强叠加原理有0)(4421022101=--r d q rq πεπε 可得2111q q d q r +=(2)两电荷异号时,在其连线内侧电场强度方向相同,外侧电场强度方向相反。
故电场强度为零的点在两电荷连线外侧,又由于q 2>q 1 ,所以电场强度为零的点在q 1的外侧,设该点与q 1的距离为2r ,由场强叠加原理得0)r d (4q r 4q 22022201=+πε-πε可得 1212q q d q r -=4.7 解:建立如图所示的坐标系。
将带电 线分成两部分半圆环和两条半无 限长直线进行考虑。
设带电线线电荷密度为λ,分析半圆环部分:在半圆环上取一小段圆弧,其长度为dl ,则其带电量为 θλ=λ=d R dl dq 此段圆弧在环心0点产生的电场强度为: 20Rd R 41E d θλπε=电场分布关于x 轴对称:0=y E ,θθλπε=θ=sin R d R 41sin dE dE 20x所以R2d sin R 4sin R rd 41sin E E 000020πελ=θθπελ=θθλπε=θ=⎰⎰⎰ππ 方向沿x 轴正方向 分析两个半无限长直线:建立如图所示的坐标系,在带电直线上取电荷元dx dq λ=,它在O 点产生的电场强度大小为O ′)(4422020R x dxr dq dE +==πελπε 由带电线的对称性可知O 点的电场强度E沿x 轴负方向,所以有2/322022220)(4)(4cos R x xdxRx x R x dxdE dE x +=++==πελπελθ所以剩下部分在O 点产生的场强大小RR x xdxdE E E x x 002/32202)(4πελπελ=+===⎰⎰∞方向水平向左。
静电场中的导体与电介质习题课.ppt

S2
代入上面式子,可求得:
E1
1
r1 0
E2 2 r20
1 S2 E1
- S1 2 E2
D2
D、E 方向均向右。
D1
A d1
d2
B
静电场中的导体和介质习题课
(2)正负两极板A、B的电势差为:
U A U B E1d1 E2d2
d1
1
d2
2
q S
d1
1
d2
2
按电容的定义式:C
q UA UB
d1
S
d2
1 2
上面结果可推广到多层介质的情况。
静电场中的导体和介质习题课
【例题】平行板电容器的极板是边长为 a的正方形,间
距为 d,两板带电±Q。如图所示,把厚度为d、相对介
电常量为εr的电介质板插入一半。试求电介质板所受
电场力的大小及方向。
解:选取坐标系
OX,如图所示。 当介质极插入x 距离时,电容器 的电容为
功等于电容器储能的增量,有
F
W (x) x
( r 20a[a
1)Q2d
(r 1)x]2
静电场中的导体和介质习题课
插入一半时,x=a/2 ,则
F( a ) 2( r 1)Q2d 2 0a3 ( r 1)2
F(a/2)的方向沿图中X轴的正方向。
注释:由结果可知,εr>1,电场力F是指向电容器内 部的,这是由于在电场中电介质被极化,其表面上产 生束缚电荷。在平行极电容器的边缘,由于边缘效应 ,电场是不均匀的,场强E 对电介质中正负电荷的作 用力都有一个沿板面向右的分量,因此电介质将受到 一个向右的合力,所以电介质板是被吸入的。
E E0
r
05静电场——习题课
1.14(1)点电荷 位于边长为 的正立方体的中心, ( )点电荷q位于边长为 的正立方体的中心, 位于边长为a 通过此立方体的每一面的电通量各是多少? 通过此立方体的每一面的电通量各是多少? (2)若电荷移至正方体的一个顶点上,那么通过每 )若电荷移至正方体的一个顶点上, 个面的电通量又各是多少? 个面的电通量又各是多少? q 解: 1)由于立方体的 6 个侧面对于其 ( ) ● 中心对称, 则由Gauss定理知,通过各 定理知, 中心对称, 则由 定理知 个面的电通量都相等。 个面的电通量都相等。且等于整个闭合 q ● 高斯面电能量的六分之一, 高斯面电能量的六分之一,所以每个面 通过的电通量应为 q / (6ε0)。 。 填空题1039 (本题 分)在边长为 的正 本题3分 在边长为a的正 填空题 a 方形平面的中垂线上,距中心o点 方形平面的中垂线上,距中心 点a/2 处 q 有一电量q的正电荷,则通过该平面的电 有一电量 的正电荷, 的正电荷 ● a a/2 场强度通量为 q / (6ε0) 。 为边长作一个正六面体。 解:以a 为边长作一个正六面体。
ε0
E = 0 (r < a ) r > a , q int = 2π al σ , E 在筒外, 在筒外, δa (r ≥ a ) E = ε 0r o E-r 曲线如图。 曲线如图。
E∝1 r
a
r
1.18 两个无限长同轴圆筒半径分别为R1和R2,单位长 两个无限长同轴圆筒半径分别为 度带电量分别为+λ和 。求内筒内、 度带电量分别为 和-λ。求内筒内、两筒间及外筒外的 电场分布。 电场分布。 根据电场分布的轴对称性, 解:根据电场分布的轴对称性,可以选与圆筒同轴的圆 柱面(上下封顶 作高斯面。再根据高斯定律即可得出: 上下封顶)作高斯面 柱面 上下封顶 作高斯面。再根据高斯定律即可得出: 在筒内, 在筒内,r < R1 : E = 0 在筒间, 在筒间, R1 < r < R2 :
静电习题课

xdq dE 2 2 3/ 2 4 0 ( r x )
哈尔滨工程大学理学院
静电场习题课
y
dl R r O x R x R x
y
r
O dE
r R sin ,
x R cos ,
dl Rd
E
/2
0
2R 3 sin cos d 3 4 0 40 R
哈尔滨工程大学理学院
静电场习题课 2. 一锥顶角为θ的圆台,上下底面半径分别为R1和R2 , 在它的侧面上均匀带电,电荷面密度σ,求:顶角O的 电势。(以无穷远处电势为零点)
R1
R2
哈尔滨工程大学理学院
静电场习题课 1、判断带电体类型(均匀的连续面分布) 2、选坐标 3、找微元
dq ds
4 r q U 4 r
i 1 0
i
连续分布的带电体 场无对称性
U
dq 4 r
0
场有对称性
哈尔滨工程大学理学院
U P E dl
P
静电场习题课
F
定理
D ds q
0
qq ˆ r 4 r 1
1 2 2
i
有源场
s
静 电 学
方向沿x正方向
电荷元在球面电荷电场中具有电势能: dW = (qdx) / (40 x) 整个线电荷在电场中具有电势能:
q W 4 0
哈尔滨工程大学理学院
r0 l r0
r0 l dx q ln x 4 0 r0
静电场习题课 8.一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半 径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量 为r 的各向同性、均匀电介质.电容器接在电压U = 32 V 的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点 的电场强度和A点与外筒间的电势差.
静电场习题课

Q2 Q2 C2 , W2 , W1:W2 2: 1 ; 串:W1 2C1 2C 2 C1
1 1 C1 2 2 1: 2; 并:W1 C1U , W2 C 2U , W1:W2 2 2 C2
12. 若把电子想象为一个相 对介电常数 r 1 的球体, 它的电荷 e 在球体内部均匀分布, 假设电子的静电能 量 m0 c 2 时,求电子的半径R。
②电势
UP
P(零点) 0
P
W PP0 E dl = q0
是从带电体在电场力作用下移动时,电场力对 它做功而引入的描述电场本身性质的又一物理量。
q 1 点电荷 U , 点电荷系 U= 4 0 r 4 0 1 dq 电荷连续分布 U 4 0 r 1 qi i ri
q q 定义:C , C , U U1 U 2 孤立导体球C 4 0 R, 平行板电容器 C
0S
d
,
4 0 R1 R2 2 0 L 球形电容器C , 圆柱形电容器 C R2 R1 ln R2 / R1
⑤电极化强度矢量
P
pe
V
⑥电位移矢量 D o E P, 对各向同性介质 D 0 r E E
q v0
x
O
2 rdr
4 0 r 2 x 2
b
R rdr 2 2 U ( x R x) 2 2 0 2 0 2 0 r x
R 当 x 0, U 0 。 当 x b, U b ( b 2 R 2 b) 2 0 2 0
静电场习题课
一、小结 1.基本概念:①电场强度矢量
F E q0
最新静电场习题课(北邮版08级用[1].)
![最新静电场习题课(北邮版08级用[1].)](https://img.taocdn.com/s3/m/97411f3caeaad1f347933f61.png)
A.导体是个等势体,导体表面是个等势面。
B. 导体内部各点(宏观点)净余电荷为零;电荷只 能分布在表面。
C. 导体表面附近一点的总电场强度方向
D. 与导体表面垂直;场强大小与导体 E. 表面对应点的电荷面密度成正比。
E
0
1 2 3 4
例:设静电平衡后E,va金lu属ati板on各on面ly.所带
ea电•te当荷d w两面it板密hCA带度ospp等之yors量i间ge.h异S的tl2i号关d0e0电s系4f-荷o2r0 时.11 N1 :EA T4 s1p3 ,o.5 s4= e2 C0 P l,it ey n2L3 ttP dr.o3file 5.2.0
23. 接地线的存在意味着: A.导体的电势为零;
B.接地线只提供导体与地交换电荷的通道,并不 保证导体腔外壁上的电荷在任何情况下都为零。
例:如图,两导体板分别带qa和
2 3
qb当一导体接地时,求两板之间
的场强。E 2 qa
S
ea222t564e...d电w有D i孤位t介h C立移A质o0 s导矢ppr 时yE o体量r si的ge= 0的.hD S高tl的电2EiE 斯d 0v引容e0a0s定4sl入uf-o理2art0i.1CoN1n EAoe Tqns pl3yo..5sS D eCPlditS eyn Lqt atPidr.q oq0 fiible 5.2.0
(当电荷分布具有一定的对称性时,用高斯定理很容易求
出场强分布,这种情况下用该式求电势较方便) 外
例: 半径为R,带电量为 q 的均
内
匀带电球面的电场中的电势分布。
R
eateUd外 with4CAoq spp外 yorrsige.hStl2Eid0ve0Uas4l内uf-o=2art0i.1o4N1nqEAoT外nsRpl3yo..5seCPliteynLt tPdr.ofile 5.2.0
静电场习题课

O
原电荷
P点E 1
2 0
R
圆孔
P点
E220(1
x) x2R2
x EE1E22 x2R2
E
PX
三.“无限”带电体零电势点的选取
1.求无限长均匀带电直线的电势分布
场强分布 E
2 0r
由定义
uPEdr r 20rdr
PQ
r
发散
R
选有限远为电势零点( Q )
uPR rEd 2 r0rd r20ln R r
2
二.补偿法求场强
d
1.带电圆弧 已知: R50 cm
Eo
d2cm q3.12109C
求: Eo
o
R
解:圆弧
q 2 R
带电园环
园弧上电荷
空隙
o处的 E1 0
o 点电荷
处的 E24q0 R240 d R2
d Eo E2 40R2
2. 球体内挖一空腔
已知: R r d
求: Eo
Eo
❖证明空腔内为均匀电场
解:
0处
原电荷
E1 0
R Eo r
0
0
d
空腔
0 处
dq 4r3
sE2dsE24d2s0
3
0
E2
4r3
3
40d2
r3 30d2
r3 Eo E2 30d2
O 点场强的计算
0 处
空腔
原电荷
dq 4d3
sE1dsE14d2s0
3
0
0 处
E2 0
E1
4d3
3
4 0d2
d 30
R
0
Eo
dy
静电场习题课1

2.两条无限长平行直导线相距为 0,均匀带有等量异号电荷,电 两条无限长平行直导线相距为r 均匀带有等量异号电荷, 两条无限长平行直导线相距为 .(1) 荷线密度为λ.( )求两导线构成的平面上任一点的电场强度 设该点到其中一线的垂直距离为x);( );(2) (设该点到其中一线的垂直距离为 );( )求每一根导线上 单位长度导线受到另一根导线上电荷作用的电场力. 单位长度导线受到另一根导线上电荷作用的电场力. 分析: 分析 : ( 1 ) 在两导线构成的平面上 任一点的电场强度为两导线单独在 此所激发的电场的叠加. 此所激发的电场的叠加. (2)由F = qE,单位长度导线所受 , 的电场力等于另一根导线在该导线 o 处的电场强度来乘以单位长度导线 所带电的量, 应该注意: 所带电的量,即:F = λE应该注意: 应该注意 式中的电场强度E是除去自身电荷 式中的电场强度 是除去自身电荷 外其它电荷的合电场强度. 外其它电荷的合电场强度.
= r0 λ i 2πε 0 x ( r0 x )
λ
E
E+
λ
p
o
分别表示正, (2)设F+,F-分别表示正,负带电 导线单位长度所受的电场力, 导线单位长度所受的电场力,则有
x
x
r0
λ2 F+ = λE = i 2πε0r0
λ2 F = λE+ = i 2πε0r0
相互作用力大小相等, 相互作用力大小相等,方向相 两导线相互吸引. 反,两导线相互吸引.
b2 x =0 2
2
x=
b , ( 0 ≤ x ≤ b) 2
6
6.在一半径为 的金属球A外面套有一个同心的金属球壳 6.在一半径为R1 =6.0 cm的金属球 外面套有一个同心的金属球壳 在一半径为 的金属球 B.已知球壳 的内,外半径分别为 2 =8.0 cm,R3 =10.0 cm.设 的内, .已知球壳B的内 外半径分别为R , . 带有总电荷Q 球壳B带有总电荷 带有总电荷Q 球A带有总电荷 A= 3.0×10-8C ,球壳 带有总电荷 B= 2.0×10-8C. 带有总电荷 × × . 和球壳B的电势 (l)求球壳 内,外表面上所带的电荷以及球 和球壳 的电势; )求球壳B内 外表面上所带的电荷以及球A和球壳 的电势; 接地然后断开, 接地, 和球壳B (2)将球壳 接地然后断开,再把金属球 接地,求球 和球壳 )将球壳B接地然后断开 再把金属球A接地 求球A和球壳 外表面上所带的电荷以及球A和球壳 的电势. 和球壳B的电势 内,外表面上所带的电荷以及球 和球壳 的电势. 分析:( )根据静电感应和静电平衡 分析:(1) :( 时导体表面电荷分布的规律,电荷Q 时导体表面电荷分布的规律,电荷 A 均匀分布在球A表面 球壳B内表面带 表面, 均匀分布在球 表面,球壳 内表面带 电荷电荷-QA ,
习题课(静电场中的导体和电介质)

习题课(静电场中的导体和电介质)1、半径为R 1的导体球带正电Q 1其内外半径分别为R 2和R 3,球壳带正电Q 2(1)此带电系统的场强分布;(2)球的电势U 1和球壳的电势U 2; (3)球与球壳的电势差;(4)若用导线将球和球壳相连,U 1和U 2解:(1)电量均匀分布在球面上,即R 1球面电量为Q 1,R 2球面电量为-Q 1,R 3球面电量为Q 1+Q 2 ,利用均匀带电球面在空间任一点场强的结果和场强叠加原理,可求得场强分布为: r < R 1: E 1 = 0; R 1 < r <R 2 : E 2 = Q 1/4πε0r 2; R 2 < r < R 3 : E 3 = 0 r > R 3: E 4 = (Q 1+Q 2)/4πε0r 2(2) 30214243R Q Q dr E U Rπε+==⎰∞dr E dr E dr E U R R R R R ⎰⎰⎰∞++=332214321302121014)11(4R Q Q R R Q πεπε++-=(3) )11(421012112R R Q U U U -=-=πε (4) 3021214R Q Q U U πε+== 2、如图,在半径为a 的金属球外有一层外半径为b 的均匀电介质球壳,电介质的相对电容率为εr (1)介质层内外的场强大小;(2)介质层内外的电势; (3)金属球的电势;(4)电场的总能量; (5)解:(1)电量Q 均匀分布在半径为a r的球面为高斯面,利用高斯定理可求得场强分布 r < a : E 1 = 0; a < r < b : 2024rQ E r επε=; r > b : rQ E 034πε=(2) r > b : rQ dr E U r0334πε==⎰∞a < r <b : b Q b r Q dr E dr E U r bb r 003224)11(4πεεπε+-=+=⎰⎰∞r < a : b Q b a Q dr E dr E dr E U r bb a a r 0032114)11(4πεεπε+-=++=⎰⎰⎰∞(3)金属球的电势等于U 1(4)abb a a Q dV E dV E W r r b r baεπεεεεε022302208)(2121+-=+=⎰⎰∞ (5)ba a ab U Q C r r +-==εεπε014 3、在半径为R 的导体球壳薄壁附近与球心相距为d(d >R)的P 点处,放一点电荷q ,求:(1)球壳表面感应电荷在的球心O 处产生电势和场强; (2)空腔内任一点的电势和场强; (3)若将球壳接地,计算球壳表面感应电荷的总电量。
第1章 静电场基本规律 课后习题

dq=dx
Ex 40
l l x dx
1 l d l x2
0
(l
x)2 a2 3/2
4 0
( ) 2
0
(l
x)2 a2 3/2
8 0
l d[l x2 a2 ]
0 (l x)2 a2 3/2
l
[ l x 2 a2 ]1/2
[ l x 2 a2 ]1/2 l
a 4 0
2(
3 2
1)a 2
lx
l x2
a2
31 2
2 3 3 2
2( 3 1)a2 2
l
dx
0
l
x2
1
a
2
2
l
lx
l
q
4 0
a
lx
2
a
2
1/
2
0
4 0
a
l2 a2
1/2 4 0a
l2 a2
1/ 2
9.0
109
2.0 10-7 1 (22 12 )1/
1
0
(S)
qi
可得立方体内的电荷为: q 0 1.058.851012 9.291012 (C)
v 总 E 通量的三个无关:
(3) 当R>>L时,该点的场强为:
E y 2 0 R
2 0 R2
L 4R2 L2
L 42 (L / r)2
L
Q
4 0 R 4 0 R
可近似看做点电荷
dE θ
y
M
R
O dx
x
1-11、(附加)电荷以线密度λ均匀分布在长为L的直线段 上。求在棒的延长线,且离棒中心为r 处的电场强度。
(三)静电场习题课

答:(1)第①式和第②式中的电荷q的意义不同。第① 式中q是置于静电场中并受到电场力F的点电荷;第② 式中电荷q是产生场E的场源电荷。
(2)它们适用的范围怎样?
①式普遍适用,它是电场的定义式;②式只适用于 点电荷;③式当A、B两点间距为l时适用于均匀场。
16.一个孤立导体球壳B带电量为Q,当另一个带电体A 移近球壳B时:
(1)B的引入不改变A表面附近的场强。
能够做到的。如B是和A同心的球壳,但B的半径较 大,就可不改变A表面附近的场。
(2)B的引入不改变A表面的电势。
这是不可能的。电势由整个空间总电场确定的,随 着另一带电体的引入,总电场的分布必将改变。
23.(1)电容器的电容与其带电量有关吗?与哪些物理量有
关? 无关
(2) 若将球 A接地, A、B 上的电荷如何分布 ?
A球接地仅意味着电势为零!
Q
UA
q
4 0R1
q
4 0R2
Q q
4 0R3
0
解出q既可.
B
R1
A q
R2
R3
(3) 若在距球心O为r 处(r > R3)放一电荷q,则A、B 两导体的 电势是否改变? A、B 的电势差是否改变?
答:若在距球心O为r 处(r>R3)放一电荷q , r <R3 空间的电场强度不变则 A、B 的电势差不改变。而
势升高。
(4)带电体A是否在球壳内产生电场?壳内场强是否还是零?
答:带电体A在球壳内产生电场,当静电平衡时 和B球壳上的感应电荷所产生的电场抵消,即B
壳内场强为零。
(5) 如果在球壳内放一个点电荷,它是否受到壳外带电体A
的静电力作用?静电屏蔽如何体现?
答:如果在球壳内放一个点电荷,它将受到壳外带电
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点电荷的电场强度: 点电荷的电场强度:E =
q0
q
2
r0
3. 电场强度的叠加原理: 电场强度的叠加原理: • 多个点电荷的场强叠加: 多个点电荷的场强叠加:
电场中任何一点的总场强等于每个点电荷 单独存在时在该点所产生的场强的矢量和.
∑Q E= 2 4πε 0 r
σ E = 2ε 0
的均匀带电无限长圆柱型分布: ③ 电荷线密度为 λ 的均匀带电无限长圆柱型分布: ∑ λ ∑ λ :过场点所做同轴圆柱面包围的电荷 E= 线密度代数和。 2πε 0 r 线密度代数和。 λ λ 柱面: 柱面: E = 柱体: 柱体: E 外 = 外 2πε 0 r 2πε 0 r λr E内 = E内 = 0 2
Q
L
19. 场强与电势梯度的关系: = − dU en 场强与电势梯度的关系: E
dn
场强沿任意方向的分量等于电势沿该方向空间 变化率的负值。 变化率的负值。 ∂U ∂U ∂U ; Ez = − ∴Ex = − ; Ey = − ∂y ∂x ∂z
• 场强和电势不能点点对应。 场强和电势不能点点对应。 20. 导体的静电平衡条件:导体内部电场强度处 导体的静电平衡条件: 处为零。即:内 部 合 = 0 处为零。 E 21. 导体处于静电平衡状态时的性质: 导体处于静电平衡状态时的性质:
dE = 4πε 0 ( L + d − x )
λ dx
2
∴E = ∫
L
0
Q 轴正方向) (沿X轴正方向) 轴正方向 dE = 4πε 0d ( d + L )
4. 带电量为 的均匀带电圆环轴线上一点 P 的电 带电量为q 场强度。 场强度。E = q cos θ P 2
4πε 0 ℓ
方向:沿轴线,正电荷背离; 方向:沿轴线,正电荷背离;负电荷指向 5. 电偶极矩 电偶极矩:
13. 电势:U = 电势: a ∫
零电势点
a
E ⋅ dl = ∫ E ⋅ dl ) (
a
∞
当电荷只分布在有限区域 有限区域时 当电荷只分布在有限区域时,电势零点通常选在 无穷远处。 无穷远处。 b 14. 电势差:U ab = Ua − Ub = a E ⋅ dl 电势差:
∫
• 两点之间的电势差与电势零点的选取无关。 两点之间的电势差与电势零点的选取无关 零点的选取无关。 15. 点电荷 在电场中的电势能:Wa= qUa 点电荷q 在电场中的电势能: • 点电荷 1和 q2之间的相互作用能(即电势能): 点电荷q 之间的相互作用能(即电势能): q2 W = q1U = q1 4πε 0 r 16. 电场力的功等于电势能的减少。 电场力的功等于电势能的减少 减少。 即:A电场力 = Wa - Wb= qUa- qUb 电场力ab
为中心以r为半径的球面 解:做一个以q为中心以 为半径的球面 做一个以 为中心以
q 2π r(r − h) q h Φe = ⋅ S球冠 = ⋅ = (1 − ) 2 S球面 4π r 2ε0 ε0 R2 + h 2
q
O
h
P q
ε0
10. 能用高斯定理求电场强度的几个对称性分布 的特例: 的特例: 均匀带电的球型分布 包括球体和球壳) 带电的球型分布( ① 均匀带电的球型分布(包括球体和球壳):
• 外力的功等于电势能的增量:A外力 = qUb- qUa 外力的功等于电势能的增量: 外力ab 的功等于电势能的增量 17. 电势的计算: 电势的计算: [1] 用点电荷电势公式加电势叠加原理: 用点电荷电势公式加电势叠加原理: q (1) 点电荷的电势公式: = 点电荷的电势公式: (选U∞ = 0) U 4πε 0 r (2) 电势的叠加原理: 电势的叠加原理: 一个电荷系的电场中, 一个电荷系的电场中,任一点的电势等于每一个 带电体单独存在时在该点所产生电势的代数和。 带电体单独存在时在该点所产生电势的代数和。 qi 点电荷系的电场中, 点电荷系的电场中,U = ∑ πε0r i 4 i dq 电荷连续分布的电场中, 电荷连续分布的电场中,U = ∫ 4πε 0 r 带电体
在非均匀外电场中, 在非均匀外ห้องสมุดไป่ตู้场中,电偶极子 ①一方面受到力
矩的作用,使电偶极矩力图转到与外电场一致 矩的作用, 的方向;②另一方面其中心还要受到合力的作 的方向; 用:通常对于稳定平衡位置,其方向指向场强 通常对于稳定平衡位置, 对于稳定平衡位置 数值增大的方向;对于非稳定平衡位置,合力 数值增大的方向;对于非稳定平衡位置, 增大的方向 非稳定平衡位置 方向指向场强数值减小的方向。 方向指向场强数值减小的方向。 减小的方向
2πε 0 R 11. 有关电场强度及电场力在真空中的所有公式,当充 有关电场强度及电场力在真空中的所有公式, 满均匀电介质(或分层均匀充满) 满均匀电介质(或分层均匀充满)时,只要将公式 中的ε 0改为场点处电介质的电容率 ε 即可.
12. 静电场的环流定理:∫LE ⋅ dl = 0 静电场的环流定理: 静电场的积分与路径无关, 即:静电场的积分与路径无关,只取决于始末位 故静电场是保守场。 置,故静电场是保守场。
1 2
3
4
静电平衡后, 例:静电平衡后,金属板各面所带电 荷面密度之间的关系: 荷面密度之间的关系:σ1 = σ4 , σ2 = −σ3 • 当两板带等量异号电荷时 σ1 =σ4 = 0 , σ2 =−σ3 当两板带等量异号电荷时: 等量异号电荷时 • 当两板带等量同号电荷时 σ1 = σ 4 , σ 2 = −σ3 = 0 当两板带等量同号电荷时: 等量同号电荷时 22. 静电平衡下空腔导体的性质: 静电平衡下空腔导体的性质: 若金属空腔内部无带电体, ①若金属空腔内部无带电体,则空腔内表面不带
电 学 总 结
1. 库仑定律 大小: = 库仑定律: 大小: F
1 4 πε
0
q1q 2 r2
方向:沿两电荷的联线,且同性相斥, 方向:沿两电荷的联线,且同性相斥, 异性相吸。 异性相吸。 • 适用条件:两个静止的点电荷 之间的相互 适用条件: 作用力 F 2. 电场强度的定义: = 电场强度的定义: E
带电体
2 pe = 3 4πε 0 r
dqE
是指排除所考虑的受力带电体以外 E是指排除所考虑的受力带电体以外 空间其它 处产生的合场强。 所有电荷在 dq 处产生的合场强。 q -q σ q2 S S d 例:两板之间的相互作用力:F = q ⋅ = 两板之间的相互作用力: 2ε0 2ε0s 7.电偶极子在均匀外电场中所受到的力和力矩: 电偶极子在均匀外电场中所受到的力和力矩: 电偶极子在均匀外电场中所受到的力和力矩 Me = pe × E F=0 •力偶矩 Me 力图使电偶极子的偶极矩 pe转到与外 电场 E 一致方向上来。 一致方向上来。
任何电荷,空腔内部任一点场强为零。 任何电荷,空腔内部任一点场强为零。
②若金属空腔内部有带电体,则空腔内表面有等 若金属空腔内部有带电体,
量异号感应电荷。 量异号感应电荷。
③外界无电荷,且导体接地,则外壁上电荷处处 外界无电荷,且导体接地,
为零,外部空间任一点场强为零。 为零,外部空间任一点场强为零。 腔内电荷(包括内壁上的电荷) ④腔内电荷(包括内壁上的电荷)对内壁以外空间 任何一点的合场强为零;腔外电荷(包括外壁上的 任何一点的合场强为零;腔外电荷( 电荷)对外壁以内空间任何一点的合场强也为零。 电荷)对外壁以内空间任何一点的合场强也为零。
[2] 用电势定义式:U a = 用电势定义式:
∫
∞
a
E ⋅ dl
ε外
(当电荷分布具有一定的对称性时,用高斯定理很容易 当电荷分布具有一定的对称性时, 求出场强分布,这种情况下用该式求电势较方便) 求出场强分布,这种情况下用该式求电势较方便)
例:半径为R,带电量为 的均匀带电 半径为 ,带电量为q的均匀带电 ε内 球面的电场中的电势分布。 球面的电场中的电势分布。 R q q U内 = U外 = 4π ε 外 R 4πε 外 r [3] 利用已知电势结果加电势叠加原理: 利用已知电势结果加电势叠加原理: 18. 等势面的性质: 等势面的性质: U= 4πε 0 L Q •电力线与等势面正交 电力线与等势面正交; 电力线与等势面正交 •沿着电力线的方向电势降低 沿着电力线的方向电势降低; 沿着电力线的方向电势降低 •等势面较密集的地方,场强较大。 等势面较密集的地方, 等势面较密集的地方 场强较大。
A 有时利用高斯定理求电通量非常方便。 ③ 有时利用高斯定理求电通量非常方便。 位于正立方体中心, 例1:点电荷 位于正立方体中心, :点电荷q位于正立方体中心 q 则通过侧面abcd的电通量:Φ e = 的电通量: 则通过侧面 的电通量
6ε 0
b q d c
a
若将点电荷q位于正立方体的 角上 若将点电荷 位于正立方体的A角上 位于正立方体的 角上, q 则通过侧面abcd的电通量:Φe = 的电通量: 则通过侧面 的电通量
24ε 0 的圆平面。 例2: 真空中有一半径为 的圆平面。在通过圆心 与平 : 真空中有一半径为R的圆平面 在通过圆心O与平 面垂直的轴线上一点P处 有一电量为q的点电荷 的点电荷。 、 面垂直的轴线上一点 处,有一电量为 的点电荷。O、P r 间距离为h,试求通过该圆平面的电通量。 h,试求通过该圆平面的电通量 间距离为h,试求通过该圆平面的电通量。
8. 电场中通过任一曲面 的电通量: 电场中通过任一曲面S的电通量: 的电通量
Φ e = ∫ E ⋅ dS = ∫ EdS cos θ
S S
匀强电场中 通过平面 S 的电场强度通量: 的电场强度通量:
Φ e = ES cosθ
通过任一闭合曲面S的电场强度通量: 通过任一闭合曲面 的电场强度通量: e = ∫ E ⋅ dS 的电场强度通量 Φ 外法线方向(自内向外)为正方向。 闭合曲面外法线方向(自内向外)为正方向。 S 穿进闭合面的电场线对该闭合面提供 负通量; 通量。 穿出闭合面的电场线对该闭合面提供 正通量。 1 9. 静电场的高斯定理: E ⋅ dS = ∑ qi 静电场的高斯定理: ∫
