模拟电磁波衰减的matlab程序

利用MATLAB图形技术实现电磁波的可视化

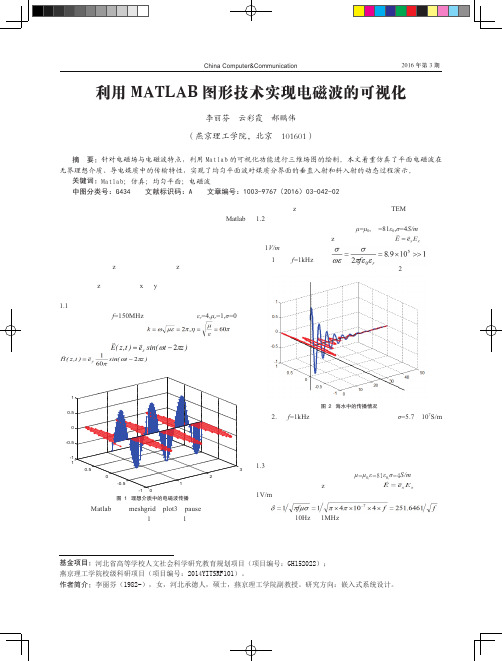
，电
场的表达式为，伴随的磁场。

，振幅水是良导体，电磁波在海水中的传播情况如图2所示。

图２　海水中的传播情况
2.当f=1kHz的均匀平面波在电参数为σ=5.7×107
的铜中传输时，电磁波的传输距离，仅为海水中的万分之一。

所以，电磁波在良导体中衰减极快；电导率越大，传输距离越短。

因此，良导体中的电磁波局限于导体表面附近的区域。

当为理想导体时，电磁波不能进入导体内部。

　同一媒质中不同频率波的仿真
以均匀平面波在电参数为μ=μ0,ε=81ε0,σ=4S/m的海水中传输为例，已知波沿z轴正方向传播，设，振幅为
1V/m。

趋肤深度为：
频率从10Hz到1MHz范围内，海水中趋肤深度随着频率的增加，电磁波在海水中衰减得很快。

因此，要保持低衰减，电磁波的频率必须很低。

，参数为ε1、的半空间为导电媒质、σ2。

因此，媒质1中为合成波。

综上所述，当均匀平面电磁波从一种导电媒质入射到另一种导电媒质中时，波数
　对理想导体分界面的垂直入射
已知入射波电场为
无限大理想导电平面上，则反射系数Γ
被反射形成反向传播的反射波。

合成波为驻波，不发生能量传输过程，仅在两个波节间进行电场能量和磁场能的交换。

所以，垂直极化波的入射波会发生全反射，波的传播情况如图
到z=0的理想导体平面上为
，因此反射的电场为。

入
所示，图中左侧为入射波形，右。

基于MATLAB电磁波传播的可视化仿真

基于MATLAB电磁波传播的可视化仿真余建立;刘双兵【摘要】The course of electromagnetic field and electromagnetic wave has the characteristics of complex theory, complete structure and abstract concept. The propagation of the electromagnetic wave is simulated visually with MATLAB language. The simulation results can display the distribution of electromagnetic waves dynamically in the free space and the dielectric interface. The simulation results are in agreement with the theory. The application of simulation animation in classroom teaching can deepen students' learning and understanding of concepts and improve classroom teaching effect.%针对电磁场与电磁波课程具有理论复杂、结构完整和概念抽象等特点, 利用MATLAB语言编程对电磁波的传播进行了可视化仿真.仿真结果能够形象动态地演示电磁波在自由空间和媒质分界面上电磁场的分布, 将仿真动画用于课堂教学中, 能够加深学生对概念的学习和理解, 可提高课堂教学效果.【期刊名称】《宜春学院学报》【年(卷),期】2018(040)012【总页数】6页(P50-55)【关键词】电磁场与电磁波;MATLAB;可视化【作者】余建立;刘双兵【作者单位】安徽省巢湖学院机械与电子工程学院,安徽巢湖 238000;安徽省巢湖学院机械与电子工程学院,安徽巢湖 238000【正文语种】中文【中图分类】G642.0“电磁场与电磁波”是电子信息工程、通信工程等专业的一门重要的必修基础课，该课程具有结构严谨、理论性强、数学公式复杂及概念抽象等特点，学生在学习过程中普遍存在理解和数学运算等方面的困难。

应用MATLAB设计电磁场与电磁波模拟仿真实验

第39卷第9期高师理科学刊 Vol. 39 No.9 2019年 9月 Journal of Science of Teachers′College and University Sep. 2019文章编号：1007-9831（2019）09-0052-04应用MATLAB设计电磁场与电磁波模拟仿真实验凌滨，郭也，刘文川（东北林业大学机电工程学院，黑龙江哈尔滨 150040）摘要：由于电磁场与电磁波课程在电磁波传播部分授课中的理论和概念抽象，难以理解．利用MATLAB语言编程技术，针对电磁场和电磁波传播2个方面，设计2个模拟仿真实验：均匀平面波在无界空间中的传播和设定各参数实验数据获得分界面上波形的变化．2个具体仿真实验形象地再现了均匀平面电磁波在自由空间传播状态和在2个媒介边界上的变化特征，通过实验有助于学生对电磁场和电磁波基本规律的掌握．关键词：电磁场与电磁波；MATLAB；仿真实验；均匀平面波中图分类号：O441.4 文献标识码：A doi：10.3969/j.issn.1007-9831.2019.09.014Application of MATLAB to design electromagnetic field andelectromagnetic wave simulation experimentLING Bin，GUO Ye，LIU Wen-chuan（School of Mechanical and Electrical Engineering，Northeast Forestry University，Harbin 150040，China）Abstract：The theoretical and conceptual abstraction of the electromagnetic field and electromagnetic wave course in the teaching of electromagnetic wave propagation is difficult to understand．Using MATLAB language programming technology，two simulation experiments were designed for electromagnetic field and electromagnetic wave propagation，the propagation of uniform plane wave in unbounded space and setting experimental data of each parameter to obtain the waveform change on the interface．Two specific simulation experiments vividly reproduced the variation characteristics of uniform plane electromagnetic waves in free space and the boundary of two media．The experiment helps students master the basic laws of electromagnetic fields and electromagnetic waves．Key words：electromagnetic field and electromagnetic wave；MATLAB；simulation experiment；uniform plane wave电磁场与电磁波作为电子信息和通信工程的专业基础课之一，通过实验课程的环节来加深对电磁场理论知识的理解，并且可以将课堂上所学到的理论知识在实验课中进行验证，加深理解[1-2]．由于目前教学过程中受到实验室的硬件环境的限制，在实验教学环节中以仿真验证为主，利用MATLAB软件对所学的理论知识进行实验，通过理论知识来指导实践．将两者相结合，可以达到提高学生发现并分析问题，利用所学知识解决问题能力的目的，进一步将所学的理论知识完善巩固，更加全面地了解电磁场与电磁波的概念[3-5]．MATLAB仿真软件的数据分析和数据计算的能力十分强大，将实验数据以图形的形式进行展示，提供了一个数据可视化的平台[6]．本文在电磁场与电磁波的实验教学中，利用MATLAB模拟了2种情况下的仿收稿日期：2019-04-10基金项目：东北林业大学教育教学研究课题项目（JG2016008）作者简介：凌滨（1962-），男，黑龙江哈尔滨人，副教授，硕士，从事电磁场与电磁波研究．E-mail：756595015@第9期凌滨，等：应用MATLAB 设计电磁场与电磁波模拟仿真实验 53真实验，分别是自由空间和媒质空间中均匀平面电磁波传播波形的变化以及2种介质分界面上电磁波波形的变化．1 均匀平面波在真空和媒质中的传播仿真实验由麦克斯韦方程组可知，变化的电场和磁场相互作用下，产生的电磁波以光速在真空中传播；电磁波在理想介质中是横波，电场和磁场的方向与波的传播方向相互垂直，另外，电场方向与磁场方向也相互垂直[7]．理想介质中均匀平面电磁波的波动方程可以由麦克斯韦方程组推理得到220022200200E E tH H t e m e m ì¶Ñ-=ïï¶í¶ïÑ-=ï¶îu vu v uu v uu v （1）若电场为线极化方式，且电磁波沿x 轴方向，可以得到22000022(()E H H Ex t t x x tm m e m ¶¶¶¶¶¶=-=-=¶¶¶¶¶¶ （2）同理220022H Hx te m ¶¶=¶¶，这２个公式都属于波动方程．电场与磁场的传播速度，也就是电磁波在真空中的传播速度，即81/310m/s c =»´．由此可见，电磁波的传播速度（在真空中）与光速等值，理论数据和实验数据一致，这为光的电磁波理论提供了一个重要的理论依据．由波动方程 220022220022E E x tH H x t e m e m ì¶¶=ïï¶¶í¶¶ï=ï¶¶î （3）在真空中当平面电磁波的电场强度和磁场强度的频率和相位相同时，２个波动方程的瞬时表达式为m (,)cos()x x E z t e E t z w b =-r r（4）m (,)cos()x y E H z t e t z w b h=-r r （5）其中：m x E 是电场强度振幅；w 是电磁波的圆频率；b 是相位常数；h 是本征阻抗．设计的仿真均匀平面波形波动见图 1．均匀平面波在导电媒质中具有传播特性：电媒质的典型特征是电导率 0s ¹；电磁波在导电媒质中传播时，由于传导电流J E s =的存在，同时还伴随着电磁能量的损耗；电磁波的传播特性与非导电介质中的传播特性有所不同[8-10]．电场E 、磁场H 瞬时值形式m (,)e cos()z x x E z t e E t z a w b -=-v r（6） m (,)e cos()z x y cEH z t e t z a w b j h -=--r r （7）在导电媒质中衰减常数a 、相位常数b 和本征阻抗c h分别为a = （8）b = （9）54 高师理科学刊第39卷1arctg 2e j c c s weh h === （10）通过改变介电参数e 、磁导率m 、电导率s 和波的频率w ，电磁波在传播中是不断变化的，设计的仿真实验波形变化见图2．应用仿真实验可以形象直观地看到均匀平面波的传播特征，并通过改变介质各参数来观察电磁波的波形变化特性．2 均匀平面波的传播、反射及透射的仿真实验电磁波在入射到不同媒质分界面上时，一部分波会在分界面上进行反射，一部分波会透过分界面．入射波（已知）＋反射波（未知）= 透射波（未知）（1） 0z <中，导电媒质1的参数为111s e m ，，；（2） 0z >中，导电媒质2的参数为222s e m ，，．沿x 方向极化的均匀平面波从媒质1 垂直入射到与导电媒质2 的分界平面上，电场和磁场的变化见图3．媒质1中的入射波 1i im ()e zx E z e E g -=r r （11）1im i 1()e z y cEH z e g h -=r r （12）媒质1中的反射波1r rm ()e z x E z e E g -=r r（13） 1rm r 1()e z y cEH z e g h -=r r （14）媒质1中的合成波11im rm 1i r 12()()()e e z z y y c cE E H z H z H z e e g g h h --=+=-r r r r r H （15）111i r im rm ()()+()e e z z x x E z E z E z e E e E g g --==+r r r r r（16）其中传播常数1g 和波阻抗1c h为11211)j j s g we =- （17）11211c j s h we -==- （18）媒质2中的透射波第9期凌滨，等：应用MATLAB 设计电磁场与电磁波模拟仿真实验 5522tm t tm t 2()e ,()e zz x y cE E z e E H z e g g h --==r r r r （19）其中：传播常数2g 和波阻抗2c h为12222)j j s g we =- （20）12222c j s h we -=- （21）改变各参数的数值，介质1，2为不同媒质时，设计的仿真实验波形见图4．改变各参数的数值，介质1为非导电媒质、2为导电媒质时，设计的仿真实验波形见图5．改变各参数的数值，介质1，2为相同电媒质时，设计的仿真实验波形见图6．通过该仿真实验系统操作，设定各参数实验数据，即获得分界面上波形的变化特征．对实验结果进行分析和解释，得到合理有效的结论．3 结束语本文提出了利用MATLAB 来完成电磁场与电磁波的仿真实验，通过仿真实验将理论教学有效地运用到实践教学中，能够使学生更加有效地理解所学的理论知识．电磁场与电磁波的仿真实验练习可以让学生对自己所学的知识有更深地理解，可以用更加灵活的方式掌握专业技能，并对所学专业的应用领域和前景有进一步的了解．在鼓励学生自己利用所学知识解决实际问题的同时，将书本知识与工程实践相结合，将复杂的电磁波问题简化，可以有效地提高授课效果．参考文献：[1] 谢处方，饶克谨．电磁场与电磁波[M]．北京：高等教育出版社，2006[2] 刘亮元，贺达江．电磁场与电磁波仿真实验教学[J]．实验室研究与探索，2010，29（5）：30-32[3] 王明军．MATLAB 在电磁场与电磁波课程教学中的应用[J]．咸阳师范学院学报，2009，24（2）：89-91 [4] 郭瑜，虞致国．电磁场与电磁波仿真实验教学研究[J]．无锡职业技术学院学报，2018，17（2）：28-31[5] 杨明珊，谭凤杰，李志中，等．电磁场与电磁波实验仿真系统[J]．郑州大学学报：理学版， 2013，45（2）：64-67 [6] 乔世坤．Matlab 在通信课程中的仿真应用[M]．哈尔滨：东北林业大学出版社，2017 [7] 马冰然．电磁场与微波技术[M]．广州：华南理工大学出版社，1999[8] William Hayt，John Buck．Engineering Electromagnetics[M]．Beijing：Tsinghua University Press，2011[9] 万棣，范懿．电磁场与电磁波虚拟仿真系统的设计与开发[J]．电气电子教学，2017，39（4）：141-144[10]邓红涛，刘巧，田敏．利用仿真软件优化电磁场与电磁波教学[J]．电脑知识与技术，2014，10（4）：792-794。

matlab瑞利信道函数

matlab瑞利信道函数一、瑞利信道简介在无线通信系统中，信号传输过程中会受到多种干扰和衰落，其中最常见的是多径效应。

在多径传输中，信号经过不同路径的传播，到达接收端时会产生相位差异，导致信号衰落和失真。

瑞利信道就是一种常见的多径衰落模型。

二、瑞利信道模型瑞利信道模型是一种统计学模型，它描述了在自由空间中没有直线障碍物的情况下，电磁波经过多个随机反射后到达接收端的情况。

由于反射路径的不确定性和随机性，每个接收器都会得到不同的电场强度值。

三、瑞利信道函数瑞利信道函数是用来描述瑞利衰落特性的数学函数。

它通常用来计算在给定频率下接收到的电场强度分布，并且可以用于预测无线通信系统中数据传输速率和误码率等参数。

在Matlab中可以使用rayleighchan函数生成瑞利衰落模拟数据。

四、rayleighchan函数rayleighchan函数是Matlab中用于生成瑞利衰落模拟数据的函数。

它可以生成瑞利信道的实部和虚部，以及相位信息。

使用该函数可以模拟无线通信系统中的多路径传输效应，帮助我们更好地了解无线通信系统中的信号传输特性。

五、rayleighchan函数语法rayleighchan函数的语法如下：h = rayleighchan(Ts,fd)其中，Ts是采样时间，fd是最大多普勒频移。

函数返回一个瑞利信道对象h。

六、使用rayleighchan函数生成瑞利衰落数据在Matlab中使用rayleighchan函数可以生成瑞利衰落数据。

下面是一个简单的示例代码：Ts = 1/1000; %采样时间fd = 30; %最大多普勒频移h = rayleighchan(Ts, fd); %生成瑞利信道对象x = randn(10000, 1); %随机输入序列y = filter(h, x); %经过瑞利信道后的输出序列七、总结本文介绍了瑞利信道模型和瑞利信道函数，在Matlab中使用rayleighchan函数可以生成瑞利衰落模拟数据。

电磁场中matlab仿真实现工具箱

实验六：使用偏微分方程工具箱对电磁场的仿真一、实验目的与要求1.掌握微分方程工具箱的使用方法；2.掌握使用偏微分方程工具箱分析电磁场。

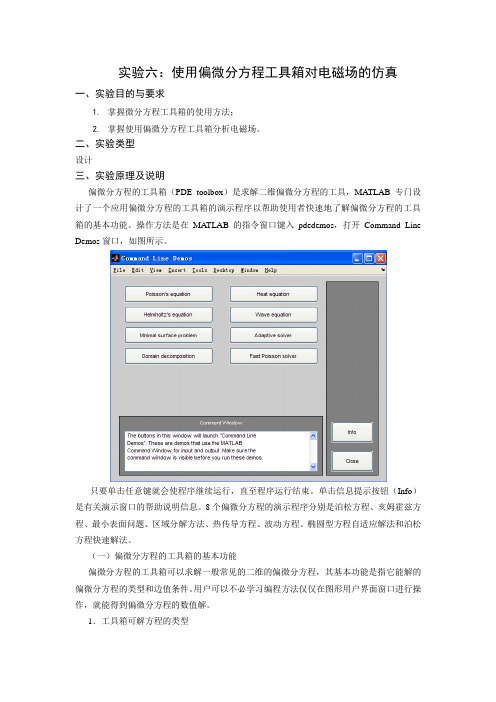
二、实验类型设计三、实验原理及说明偏微分方程的工具箱（PDE toolbox）是求解二维偏微分方程的工具，MA TLAB专门设计了一个应用偏微分方程的工具箱的演示程序以帮助使用者快速地了解偏微分方程的工具箱的基本功能。

操作方法是在MA TLAB的指令窗口键入pdedemos，打开Command Line Demos窗口，如图所示。

只要单击任意键就会使程序继续运行，直至程序运行结束。

单击信息提示按钮（Info）是有关演示窗口的帮助说明信息。

8个偏微分方程的演示程序分别是泊松方程、亥姆霍兹方程、最小表面问题、区域分解方法、热传导方程、波动方程、椭圆型方程自适应解法和泊松方程快速解法。

（一）偏微分方程的工具箱的基本功能偏微分方程的工具箱可以求解一般常见的二维的偏微分方程，其基本功能是指它能解的偏微分方程的类型和边值条件。

用户可以不必学习编程方法仅仅在图形用户界面窗口进行操作，就能得到偏微分方程的数值解。

1．工具箱可解方程的类型定义在二维有界区域Ω上的下列形式的偏微分方程，可以用偏微分方程工具箱求解：椭圆型()f au u c =+∇∙∇- 抛物型()f au u c tu d =+∇∙∇-∂∂ 双曲型()f au u c tu d =+∇∙∇-∂∂22 本征值方程()du au u c λ=+∇∙∇-式中，u 是偏微分方程的解；c 、a 、d 、f 是标量复函数形式的系数，在抛物型和双曲型方程中，它们也可以是t 的函数，λ是待求的本征值。

当c 、a 、f 是u 的函数时，称之为非线性方程，形式为()()()()u f u u a u u c =+∇∙∇-也可以用偏微分方程工具箱求解。

2．工具箱可解方程的边值条件解偏微分方程需要的边值条件一般为下面两种之一：狄里赫利(Diriclet)边值条件 hu=r广义诺曼(Generalized Neumann)边值条件 ()g qu u c n =+∇∙式中，n为边界外法向单位向量；h 、q 、r 、g 是在边界上定义的复函数。

Matlab中的电磁场模拟和电磁波传播

Matlab中的电磁场模拟和电磁波传播1. 引言电磁场模拟和电磁波传播在现代科学和工程中起着至关重要的作用。

借助计算机仿真和数值模拟工具，我们可以预测和分析电磁场中的各种现象，包括场强分布、能量传输、辐射特性等。

Matlab作为一种功能强大的数值计算软件，为电磁场模拟和电磁波传播提供了便捷而高效的工具。

本文将围绕Matlab中的电磁场模拟和电磁波传播展开深入探讨。

2. 电磁场模拟方法在电磁场模拟中，最常用的方法之一就是有限元分析（Finite Element Analysis，简称FEA）。

Matlab中提供了丰富的有限元分析工具箱，如Partial Differential Equation Toolbox和RF Toolbox等。

利用这些工具箱，我们可以建立各种复杂的电磁场模型，并进行精确的分析和计算。

FEA方法相对于其他方法具有较高的准确性和灵活性，能够适应不同场景中的电磁问题。

除了有限元分析，Matlab还支持其他一些电磁场模拟方法，如有限差分法（Finite Difference Method，简称FDM）、时域有限差分法（Finite Difference Time Domain，简称FDTD）和边界元法（Boundary Element Method，简称BEM）。

这些方法在不同场景和应用中有着各自的优势，可以根据具体情况选择使用。

3. 电磁波传播特性的模拟与分析电磁波传播是电磁场模拟中一个重要的研究方向。

Matlab提供了用于电磁波传播分析的各种工具函数和库，我们可以利用这些工具函数和库模拟电磁波在不同环境中的传播特性。

在电磁波传播分析中，波束传播（Beam Propagation）是常用的方法之一。

Matlab中的光纤传输工具箱（Optical Fiber Toolbox）提供了一系列用于光波束传播分析的函数和类，可以模拟光波在光纤中的传播特性，并分析波束的衍射、色散等效应。

此外，Matlab还提供了用于天线设计和分析的工具箱，如Antenna Toolbox。

《电磁场与电磁波》仿真实验

年《电磁场与电磁波》仿真实验————————————————————————————————作者：————————————————————————————————日期：《电磁场与电磁波》仿真实验2016年11月《电磁场与电磁波》仿真实验介绍《电磁场与电磁波》课程属于电子信息工程专业基础课之一，仿真实验主要目的在于使学生更加深刻的理解电磁场理论的基本数学分析过程，通过仿真环节将课程中所学习到的理论加以应用。

受目前实验室设备条件的限制，目前主要利用MATLAB 仿真软件进行，通过仿真将理论分析与实际编程仿真相结合，以理论指导实践，提高学生的分析问题、解决问题等能力以及通过有目的的选择完成实验或示教项目，使学生进一步巩固理论基本知识，建立电磁场与电磁波理论完整的概念。

本课程仿真实验包含五个内容：一、电磁场仿真软件——Matlab的使用入门二、单电荷的场分布三、点电荷电场线的图像四、线电荷产生的电位五、有限差分法处理电磁场问题目录一、电磁场仿真软件——Matlab的使用入门 (4)二、单电荷的场分布 (10)三、点电荷电场线的图像 (12)四、线电荷产生的电位 (14)五、有限差分法处理电磁场问题 (17)实验一电磁场仿真软件——Matlab的使用入门一、实验目的1. 掌握Matlab仿真的基本流程与步骤；2. 掌握Matlab中帮助命令的使用。

二、实验原理（一）MATLAB运算1.算术运算(1)．基本算术运算MATLAB的基本算术运算有：＋(加)、－(减)、*(乘)、/(右除)、\(左除)、^(乘方)。

注意，运算是在矩阵意义下进行的，单个数据的算术运算只是一种特例。

(2)．点运算在MATLAB中，有一种特殊的运算，因为其运算符是在有关算术运算符前面加点，所以叫点运算。

点运算符有.*、./、.\和.^。

两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维参数相同。

例1：用简短命令计算并绘制在0≤x≦6范围内的sin(2x)、sinx2、sin2x。

电磁波在理想介质中的传播 matlab程序

电磁波在理想介质中的传播 matlab程序电磁波在理想介质中的传播1. 介绍电磁波是一种能量传播的波动现象，广泛应用于通讯、雷达、无线电等领域。

在理想介质中，电磁波的传播具有一定的特性和规律。

为了更好地理解和研究电磁波在理想介质中的传播，我们可以借助matlab程序进行模拟和分析。

2. 理论基础在讨论电磁波在理想介质中的传播前，首先需要了解电磁场的基本原理和Maxwell方程组。

Maxwell方程组描述了电磁波在空间中的传播规律，而在理想介质中，电磁波的传播可以通过Maxwell方程组的求解来进行模拟和分析。

3. matlab程序模拟通过编写matlab程序，我们可以模拟电磁波在理想介质中的传播过程。

我们需要定义介质的特性参数，如介电常数和磁导率。

可以通过数值方法求解Maxwell方程组，得到电磁波在介质中的传播模式和传播特性。

在程序模拟过程中，可以考虑不同频率和波长下的电磁波传播情况，以及介质界面、反射和折射等现象。

4. 结果分析通过matlab程序模拟得到的结果，可以分析电磁波在理想介质中的传播特性。

通过分析传播模式、能量传输、反射损耗等参数，可以深入理解电磁波在理想介质中的行为规律和物理特性。

这些分析结果有助于优化电磁波设备和系统的设计，提高传输效率和性能。

5. 个人观点电磁波在理想介质中的传播是一个复杂而又充满挑战的研究课题。

借助matlab程序的模拟分析，可以更好地理解和探索电磁波在介质中的传播规律，为电磁波技术的发展提供有力支持。

我认为电磁波在理想介质中的传播研究还有待深入，需要更多的理论和实验研究来支持和完善。

总结电磁波在理想介质中的传播是一个重要的研究课题，对于电磁波技术和应用具有重要意义。

通过matlab程序的模拟分析，可以更好地理解和研究电磁波在理想介质中的传播规律，为相关领域的研究和应用提供有力支持。

希望未来能够有更多的科研人员投入到这一领域，共同推动电磁波技术的发展和进步。

matlab仿真电磁波的极化实验

电磁场与电磁波实验实验四电磁波的极化实验学院：电子工程班级：姓名：秦婷学号：理论课教师：实验课教师：同做者：实验日期：2020 年 5 月20 日请务必填写清楚姓名、学号、班级及理论课任课老师。

实验四电磁波的极化实验一、实验目的：1. 通过虚拟仿真观察并理解电磁波极化的概念2. 学习电磁波极化的测量方法3. 学会判读线极化波，圆极化波的方法二、实验装置实验装置如图1所示。

图中：①为微波源；②为隔离器；③为负载；④为可变衰减器；⑤为T 型接头；⑥和⑦为发射天线；⑧为可变相移器；⑨为接收天线；⑩为检波器；⑪为指示电流表。

①②⑤③④⑧⑥⑦⑨⑩⑪图1 电磁波极化实验系统T 型接头用以将传来的微波功率分成等强度的两束波。

衰减器用于调节支路中的功率强弱。

相移器用以调节支路中的初相位φ，从而产生相位的变化。

三、实验原理：平面电磁波沿轴线前进没有z E 分量，一般情况下，存在x E 分量和y E 分量，如果y E 分量为零，只有x E 分量我们称其为X 方向线极化。

如果只有y E 分量而没有x E 分量我们称其为Y 方向线极化。

在一般情况下，x E 和y E 都存在，在接收此电磁波时，将得到包含水平与垂直两个分量的电磁波。

如果此两个分量的电磁波的振幅和相位不同时，可以得到各种不同极化形式的电磁波。

1. 如果电磁波场强的X 和Y 分量为：()1cos x xm E E t kz ωϕ=+− (1)()2cos y ym E E t kz ωϕ=+−(2)其中1ϕ、2ϕ为初相位，2k πλ=。

若1ϕ等于2ϕ，或1ϕ与2ϕ相位差为2n π时，其合成电场为线极化波，其幅度为：()1E t kz ωϕ==−+(3)电场分量与X 轴的夹角为：arctanarctany ym xxmE E E E α===常数 (4)2. 如果1ϕ与2ϕ相位差90°或270°，则：()1cos x xm E E t kz ωϕ=−+ (5)()2cos y ym E E t kz ωϕ=−+(6)合成电磁场为：E ===常数(7)它的方向是：()1tan tan y xE t kz E αωϕ==−+(8)1t kz αωϕ=−+(9)表示合成场振幅不随时间变化，其方向是随时间而旋转的圆极化波。

电磁场与电磁波【matlab】实验三平面电磁波的反射和干涉实验

电磁场与电磁波实验实验三平面电磁波的反射和干涉实验成绩：请务必填写清楚姓名、学号、班级及理论课任课老师。

实验三平面电磁波的反射和干涉实验一、实验目的：1.通过虚拟仿真观察并理解平面电磁波的传输特性。

2.利用平面线极化电磁波投射到介质板上产生反射波和透射波的干涉现象来了解平面电磁波传播的一些基本特性。

3.利用干涉条纹（即空间驻波）的分布学习一种测量微波波长的方法，观察在介质中电磁波的传播从而测量其相对介电常数。

二、实验装置：实验装置如图1所示，微波源与各透射板、反射板有足够的距离以保证近似为平面波。

分束板应与入射电磁波成45°，与两反射板也成45°，A、B两反射板互相垂直。

图1微波干涉仪三、实验原理：1.平面电磁波的传播、反射及透射电磁波在传播过程中遇到两种不同波阻抗的介质分界面时，在介质分界面上将有一部分电磁能量被反射回来，形成反射波；另一部分电磁能量可能透过分界面继续传播，形成透射波。

设分界面为无限大平面，位于z=0处。

入射波的电场和磁场分别依次为：10ˆjk z i x i E aE e -= 1011ˆjk z i y i H a E e η-= 其中，0i E 是z=0处入射波的振幅，k 1和η1为介质1的相位常数和波阻抗，且有：1k =，1η=(1)当平面电磁波向理想导体垂直入射时如图2所示，因为介质2为理想导体，其中的电场和磁场均为零，即：20E = ，20H = 。

因此，介质2中没有透射波，电磁波不能透过理想导体表面，而是被分界面全部反射，在介质1中形成反射波r E 和r H。

图2平面电磁波向理想导体垂直入射则反射波的电场和磁场为：0r x r 1011ˆjk z r y r H a E e η=- 其中，0r E 为z=0处反射波的振幅，负号表示磁场方向发生了变化。

在分界面两侧，电场强度E 的切向分量连续，即：001r i E E Γ==-在z<0区域，也就是区域I 中，复振幅表示的合成电场和磁场分别为：()111001ˆˆ()2sin jk z jk z x i x i E aE e e a jE k z -=-=- ()110101111ˆˆ()2cos jk z jk z i y i y E H a E e e a k z ηη-=+= (2)当平面电磁波向理想介质垂直入射时如图3所示，均匀平面电磁波向理想介质的垂直入射时，因介质参数不同，到达分界面上的一部分入射波被分界面反射，另一部分入射波透过分界面进入区域II 传播。

水下光子传播matlab仿真程序 -回复

水下光子传播matlab仿真程序-回复水下光子传播是研究光在水下传播过程中的特性与行为的重要课题之一。

光在水中的传播具有许多特殊性质，如衰减、散射和吸收等，对于水下光通信、水下影像等应用具有重要意义。

为了更好地理解水下光子传播的特性，并对相关应用进行优化和设计，研究人员利用Matlab仿真程序，对水下光子传播进行模拟和分析。

首先，我们需要了解水下光子传播的基本原理。

光在水中的传播过程可以通过Maxwell方程和光衰减方程来描述。

Maxwell方程组是描述电磁波传播的基本方程组，可以通过数值方法求解得到光在水中的传播路径和强度分布。

光衰减方程则用于描述在传播过程中，光强度随着距离的增加而衰减的情况。

在Matlab中，我们可以利用光线追迹（ray tracing）方法和蒙特卡洛方法来模拟水下光子传播。

光线追踪是一种光学仿真技术，可以通过跟踪单个光线的路径和相互作用来模拟光在水中的传播。

蒙特卡洛方法则是一种随机模拟方法，通过随机生成光的路径和跃迁过程，来模拟光在水中的传播。

在进行水下光子传播的仿真前，我们首先需要设定一些参数，如入射光的强度、波长以及水的折射率等。

这些参数的设置将直接影响仿真结果的准确性和可靠性。

接下来，我们可以利用Matlab的光线追踪函数来模拟光在水中的传播路径。

通过设定入射点和入射角度，我们可以追踪光线在水中的传播过程，并计算出光在不同位置的强度分布。

在蒙特卡洛方法中，我们可以随机生成光线的路径和相互作用过程。

通过在每个传输步骤中考虑散射、折射和吸收等因素，我们可以模拟出光在水中的传播路径和强度分布。

通过对仿真结果进行分析，我们可以得到光在水中的传播特性，如光强度的衰减情况、传播路径的弯曲程度以及散射角度的分布等。

这些结果对于水下光通信、水下成像等应用的优化和设计具有重要意义。

同时，在进行仿真的过程中，我们还可以通过设置不同的参数和条件，来研究光在水中的传播特性对于不同因素的响应情况。

电磁波仿真实验

电磁波仿真实验实验内容1．本次实验介绍了matlab的安装过程2．初步对于MATLAB有了基本的认识与了解3．熟悉MATLAB软件的基本操作有时，为了使图形具有可读性，需要在所绘制的图形中，加上一些网格线来反映信号的幅度大小。

在MATLAB中使用grid函数可实现在图形中加网格线。

gridon%在图形中加网格线gridoff%取消图形中的网格线holdon%图形显示窗口原来的图像保持holdoff%关闭图形保持功能figure%打开新的显示窗口MATLAB的工作环境主要由工具栏、文件路径，当前文件夹，命令窗口以及工作变量区构成（由于设置不同，软件中也会显示历史窗口，记录的是在命令窗口的历史输入），如图1所示。

工具栏也就是如下图所示的部分，它是用来对软件进行一系列操作的区域。

命令窗口是进行一系列命令输入的地方，当有指令输入并按下Enter 键时，软件会自动执行该条指令，并执行出该命令的结果。

文件路径是当前文件夹的地址，在该区域可以实现文件路径的切换。

当前文件夹是显示当前文件路径下所有文件的窗口，可以在此双击打开所需要的.m等不同格式的文件。

工作变量区是存放所执行程序中涉及到的所有变量值的空间，可以在该区域双击某变量查看该变量具体表示情况。

MATLAB使用中的部分注意事项如下：1、变量不需要先定义，随时用随时起名字即可；2、用文本编辑器编写的程序、函数的文件扩展名均为“.m”；3、程序文件在起名字时要注意不能用数字和中文作为文件名；4、函数文件在保存时会自动以定义的函数名作为其文件名，不允许修改，否则函数无法运行；5、变量和常量的标识符中的第一个字符必须是英文字符；6、MATLAB变量区分大小写；7、如果不想在命令行窗口输出运行结果，只需在代码后面加上分号即可；8、plot是绘图的意思，ub是子的意思。

ubplot(m,n,p)表示生成m某n个子图，当前激活第p个子图；9、程序某=input(‘Typeinignal某(t)incloedform:’)，表示接收键盘输入值并赋值给某。

电磁场相关的matlab程序

一、概述电磁场是物理学中一个重要的研究领域，对于电磁场的研究不仅在理论方面有重要意义，也在工程应用中起着关键作用。

MATLAB作为一种强大的科学计算软件，可以被广泛应用于电磁场的数值模拟和分析。

本文将介绍与电磁场相关的MATLAB程序的编写和应用，希望能够对相关领域的研究者和工程师有所帮助。

二、电场计算程序1. 电场的数值计算是电磁场研究的重要内容之一。

在MATLAB中，可以通过使用有限差分法（finite difference method）来进行电场的数值模拟。

需要定义空间网格和边界条件，然后利用差分格式来离散化Maxwell方程组，最后通过迭代计算来求解电场分布。

这样的程序可以用于分析不同几何形状的电场分布和电场中的电势等情况。

2. 电场在介质中的传播也是电磁场研究的重要内容。

可以通过编写MATLAB程序来模拟介质中电场的传播情况。

对于各向同性介质，可以利用Maxwell方程组在介质中的形式来推导出传播方程，然后通过数值方法求解得到电场的传播情况。

这样的程序可以用于分析不同介质中电场的传播特性，并且可以进一步扩展到非各向同性介质的情况。

三、磁场计算程序1. 磁场的数值计算同样是电磁场研究的重要内容之一。

在MATLAB中，可以通过使用有限元法（finite element method）来进行磁场的数值模拟。

需要定义空间网格和边界条件，然后利用有限元方法来离散化Maxwell方程组，最后通过迭代计算来求解磁场分布。

这样的程序可以用于分析不同几何形状的磁场分布和磁场中的磁感应强度等情况。

2. 磁场在介质中的传播也是电磁场研究的重要内容。

可以通过编写MATLAB程序来模拟介质中磁场的传播情况。

同样可以利用Maxwell 方程组在介质中的形式来推导出传播方程，然后通过数值方法求解得到磁场的传播情况。

这样的程序可以用于分析不同介质中磁场的传播特性，并且可以进一步扩展到非线性介质的情况。

四、电磁场耦合计算程序1. 在实际应用中，电磁场的耦合效应也是一个重要的研究内容。

电磁场与电磁波Matlab仿真

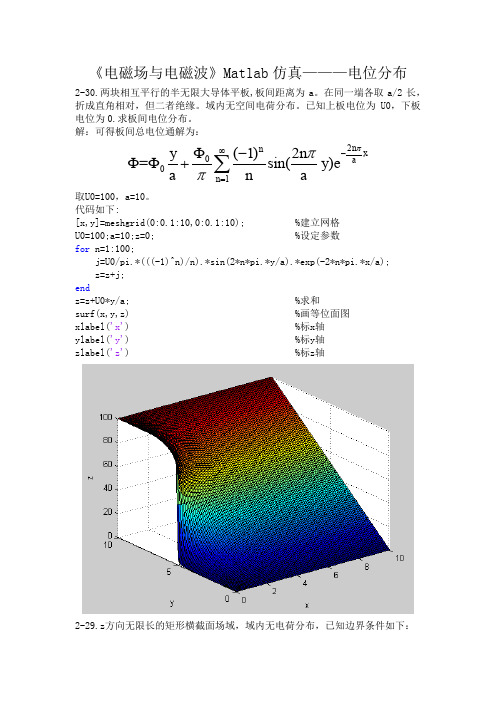
2-28.两无限大平行导体平面，相距为 a，上下极板电位均为 0.它们之间有一与
z 轴平行的线电荷（C/m），位于（0，d）处。求板间电位分布。
解:得到最后得电位解为：
0
取 a= =10;
n | x| 1 n n sin( d )sin( y )e a a a n 1 n
《电磁场与电磁波》Matlab 仿真———电位分布
2-30.两块相互平行的半无限大导体平板,板间距离为 a。在同一端各取 a/2 长，折成直角相对，但二者绝缘。域内无空间电荷分布。已知上板电位为 U0，下板电位为 0.求板间电位分布。解：可得板间总电位通解为：
2 n x y 0 (1) n 2n a = 0 sin( y ) e a n1 n a
cosh(
n n x)sin( y) b b
取U0=100，a=10,b=10。代码如下: [x,y]=meshgrid(0:0.1:10,0:0.1:10); %建立网格 U0=100;a=10;b=10;z=0; %设定参数 for i=1:100; n=2*i-1; j=4*U0/pi*(1/(n*cosh(n*pi*a/b)).*(cosh(n*pi*x/b)).*(sin(n*pi*y/b))); z=z+j; end %求和 surf(x,y,z) %画等位面图 xlabel('x') %标x坐标 ylabel('y') %标y坐标 zlabel('z') %标z坐标
2-29.z方向无限长的矩形横截面场域，域内无电荷分布，已知边界条件如下：
| y 0 | y b 0 ，
|x 0 0 ， |x a ：

电磁场与电磁波【matlab】实验一带电粒子在电磁场中的受力与运动特性研究实验

电磁场与电磁波实验实验一带电粒子在电磁场中的受力与运动特性研究实验成绩：请务必填写清楚姓名、学号、班级及理论课任课老师。

一带电粒子在电磁场中的受力与运动特性研究实验一、实验目的：1.通过虚拟仿真，观察带电粒子在电磁场中的运动行为。

2.学习运用Matlab 对电磁场进行数值模拟的方法。

二、实验原理带电粒子在磁场中运动会受到磁场力的作用，且随着初始运动方向和磁场分布的不同，其运动轨迹会发生不同的变化。

设带电粒子电量为q，以速度v 运动，则受到外磁场的作用力为：F qv B=⨯ 该公式表明：(1)磁场作用力同时垂直于磁感应强度和粒子运动速度；(2)磁场作用力只作用于运动的带电粒子，且永远不对带电粒子做功，只改变其运动方向。

若带电量为q 的运动电荷所在空间同时存在电场和磁场，则它所受的电场力和磁场力的综合即为洛伦兹力：()F q E v B =+⨯ 若不考虑粒子所受重力的作用，上式综合牛顿运动定律就可以精确确定带电粒子在电磁场中的运动轨迹。

设带电粒子质量为m，电量为q，进入电场E 与磁场B 方向正交的叠加电磁场中。

以电磁场中某点为原点，以电场E 为OY 方向，以磁感应强度B 为OZ 方向建立直角坐标系O-XYZ，则电场E 只有Y 分量，磁感应强度B 只有Z 分量，带电粒子在该电磁场中的运动微分方程为：22()d r m q E v B dt=+⨯ 上式可以在直角坐标系中展开为如下形式：2222220d x qB dy dtm dt d y qE qB dx dtm m dt d z dt⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩令1w x =，2dx w dt =，3w y =，4dy w dt =，5w z =，6dz w dt =，则上式可以化简为如下一阶微分线性方程组：12243442566dw w dt dw qB w dt m dw w dt dw qE qB w dt m m dw w dt dw dt ⎧=⎪⎪⎪=⎪⎪⎪=⎪⎨⎪=-⎪⎪⎪=⎪⎪=⎪⎩通过Matlab 编写程序，即可求解上述微分方程组。

matlab中cpml代码

matlab中cpml代码MATLAB是一种面对科学、工程、统计数据分析等领域的高级编程语言。

这种编程语言在数值计算、可视化和编程环境等方面都有着很高的应用价值。

其中，CPML是MATLAB中一种代码实现方法，它通常应用于数值模拟中，本文将围绕“MATLAB中CPML代码”展开讲述。

1. CPML是什么？CPML(Conductive Perfectly Matched Layer)是一种计算电磁波或弹性波时常用的人工边界条件。

在一些有限差分方法中，为了能够处理完整的问题域，需要将问题域扩展一些距离作为计算边界。

由于边界条件与介质的物理性质不一致，从而导致介质反射和折射以及波的驻留。

CPML正是为了避免这些问题而有所发明的。

2. CPML的应用CPML主要应用在电磁波和弹性波两个领域。

在电磁波计算中，CPML已经广泛应用于各种频谱范围内的计算，如微波、毫米波和红外等等。

在弹性波计算中，CPML也是一个常用的计算边界条件。

3. MATLAB中CPML的实现MATLAB中编写CPML可以采用不同的方法。

下面我们以一种较为常见的例子为例，展开详细讲述MATLAB中CPML的实现步骤。

3.1 声波方程的形式给定声速$c$和胶粘剂阻尼系数 $a(x,y)$，声波方程可以用如下的形式来描述：$$\frac{\partial u}{\partialt}=c\sqrt{1+i2\eta}{\scriptstyle\left[-\frac{\partialu}{\partial x}-\frac{\partial v}{\partial y}\right]}-a(x,y)u $$其中，$u(x,y,t)$和$v(x,y,t)$分别表示$x$方向和$y$方向的位移，$c$表示声速，$\eta$表示传播方向的相对介电常数，$a(x,y)$表示$x$和$y$的位置相关的阻尼系数。

3.2 CPML的建立为了进行CPML近似，可以构造一个虚拟场$v_{cp-}=v+v_f$使其等于总场$v_{tot}$，但在影响总场之前，对其进行吸收。

matlab中衰减函数

MATLAB中的衰减函数1. 起步在MATLAB中，衰减函数是常用的数学工具之一，用于描述随着时间或者空间的推移而变弱的现象。

衰减函数在信号处理、滤波和通信系统等领域中具有广泛的应用。

本文将探讨MATLAB中衰减函数的基本概念、数学表示、应用实例以及如何在MATLAB中进行实现。

2. 衰减函数的概念与分类2.1 衰减函数的定义衰减函数是指具有指数减小特性的函数。

通常情况下，衰减函数可以通过指数函数或者幂函数来表示。

衰减函数在实际应用中往往是时间或者空间的函数，可以表示随着时间或者空间的推移而逐渐减小的现象。

2.2 衰减函数的分类根据衰减函数的性质和表示方式，可以将衰减函数分为以下几种类型：1.指数衰减函数：指数衰减函数是一种按指数规律递减的函数，常用形式为f(t)=e−αt，其中t表示时间，α表示衰减的速率。

2.幂函数衰减：幂函数衰减是指以幂函数的形式表示衰减，常用形式为f(t)=t−α，其中t表示时间，α表示衰减的速率。

3.高斯函数衰减：高斯函数衰减是指以高斯函数的形式表示衰减，常用形式为f(t)=e−12(tσ)2，其中t表示时间，σ表示高斯函数的标准差。

3. 衰减函数的数学表示3.1 指数衰减函数的数学表示指数衰减函数可以用指数函数来表示，常用形式为f(t)=e−αt。

其中，t表示时间，α表示衰减的速率。

3.2 幂函数衰减的数学表示幂函数衰减可以用幂函数来表示，常用形式为f(t)=t−α。