六大基本初等函数图像及其性质
基本初等函数的图像与性质

在数学的发展过程中,形成了最简单最常用的六类函数,即 常数函数 、 幂函数、 指数函数 、 对数函数 、 三角函数 与 反三角函数 ,这六类函数称为 基本初等函数。
一、常数函数y = c 或 f ( x ) = c , x ∈ R ,其中 c 是常数。
它的图像是通过点 (0,c),且平行 x轴的直线,如下图所示:常数函数的图像常数函数的性质:1、常数函数是有界函数,周期函数(没有最小的正周期)、偶函数;2、常数函数既是单调增加函数又是单调减少函数,特别的当 c = 0 时,它还是奇函数。
二、幂函数1、形如 y = x^a 的函数是幂函数,其中 a 是实数 。
幂函数图(1)2、常见幂函数的图像:幂函数图(2)注:画幂函数图像时,先画第一象限的部分,在根据函数奇偶性完成整个图像。
3、幂函数的性质:① 幂函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点 。
② 所有幂函数在 (0,+∞)上都有定义,并且图像都经过点 (1,1)。
③ 若 a > 0 , 幂函数图像都经过点 (0,0)和(1,1),在第一象限内递增;若 a三、指数函数1、一般地,函数 y = a^x (a > 0 且 a ≠ 1)叫做 指数函数 ,自变量 x 叫做 指数 ,a 叫做 底数 ,函数的定义域是 R 。
2、指数函数的图像:指数函数图象3、指数函数的性质:① 指数函数 y = a^x (a > 0 且 a ≠ 1)的函数值恒大于零 ,定义域为 R ,值域为(0,+∞);② 指数函数 y = a^x (a > 0 且 a ≠ 1)的图像经过点 (0,1);③ 指数函数 y = a^x (a > 1)在 R 上递增 ,指数函数 y = a^x (0四、对数函数1、对数及其运算:一般地,如果 a (a > 0 , a ≠ 1)的 b 次幂等于 N ,即 a^b = N,那么 b 叫做以 a 为底N 的 对数 ;记作: log aN = b , 其中 a 叫做对数的 底数 , N 叫做 真数 。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 α1.2.幂函数的性质;21xy1)当α为正整数时,函数的定义域为区间为∈x,他们的图形都经过原点,并当α>1时在原点-∞(+∞,)处与x轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数;m时,n为偶数时函数的定义3)当α为正有理数n域为(0, +∞),n为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时,还跟y轴对称;m,n均为奇数时,跟原点对称;5)当α为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1)当1>a 时函数为单调增,当10<<a 时函数为单调减;2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ; 1xa.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式); a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4) ()n n nb a ab =b.根式的性质; (1)()a a nn= ; (2)当n为奇数时,a a nn =当n 为偶数时,f x xxx g ⎪⎫⎛=1)(⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a an m nm (2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 Nab=,那么数b 叫做以a 为底N 的对数,记作bN a=log,其中a 叫做对数的底数,N 叫做真数,式子N alog 叫做对数式。
六大基本初等函数图像及其性质
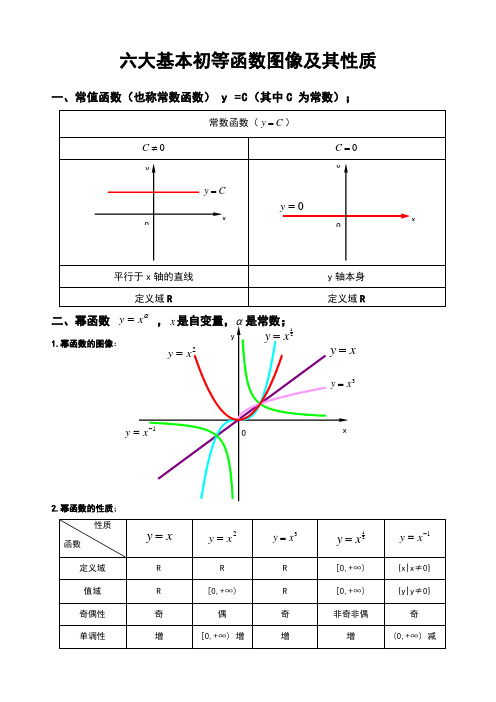
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质(总12页)

六大基本初等函数图像及其性质(总12页)抛物线函数 y = x^2- 图像为开口朝上的抛物线,顶点在原点(0,0)- 奇函数,即f(-x) = -f(x)- 定义域为全体实数,值域为[0, +∞)- 极值点为顶点(0,0),不存在最大值和最小值- 函数单调递增且无拐点反比例函数 y = 1/x-tu.grid正比例函数 y = x- 图像为平面直线,通过原点(0,0)- 定义域为全体实数,值域为全体实数- 函数单调递增,无拐点- 斜率代表变化率,斜率越大表示变化速度越快,斜率为正则表示函数单调增加,斜率为负则表示函数单调减少指数函数 y = a^x (a>0且a≠1)- 图像为上凸曲线,通过点(0,1)- 定义域为全体实数,值域为(0,+∞)- 当a>1时,函数单调递增;当0<a<1时,函数单调递减- 随着自变量x的增大,函数值加速增大或减小对数函数y = logₐ(x) (a>0且a≠1)- 反指数函数,图像和指数函数的图像呈镜像关系- 定义域为(0,+∞),值域为全体实数- 当a>1时,函数单调递增;当0<a<1时,函数单调递减- 随着自变量x的增大,函数值增长速度逐渐变慢三角函数 y = sin(x), y = cos(x), y = tan(x)- 正弦函数图像为周期性上下波动的连续曲线,取值范围[-1, 1] - 余弦函数图像为周期性波动的连续曲线,取值范围[-1, 1]- 正弦函数、余弦函数的定义域为全体实数,值域为[-1, 1]- 正弦函数、余弦函数是周期性函数,周期为2π- 正切函数图像为周期性波动的连续曲线,定义域为实数集合-{(2n + 1)π/2 | n∈Z},值域为全体实数这些基本初等函数的图像和性质对数学的学习和应用有着重要的作用,掌握这些函数的图像及其性质,有助于理解数学问题的规律,并能够在实际问题中进行分析和求解。
六大基本初等函数图像及其性质
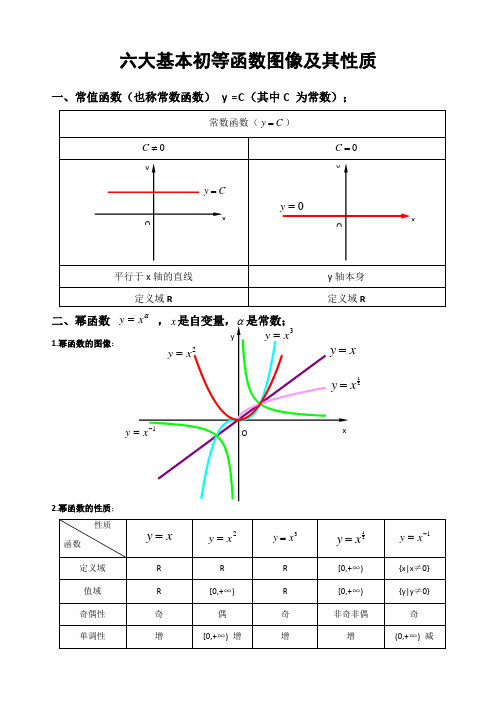
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;21xy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1)n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnmaaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质
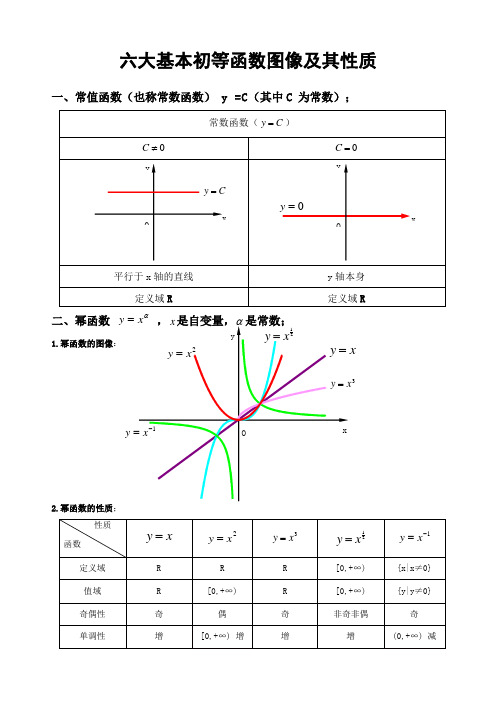
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性 在),(∞+∞-是增函数在),(∞+∞-是减函数1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
(完整版)六大基本初等函数图像与性质
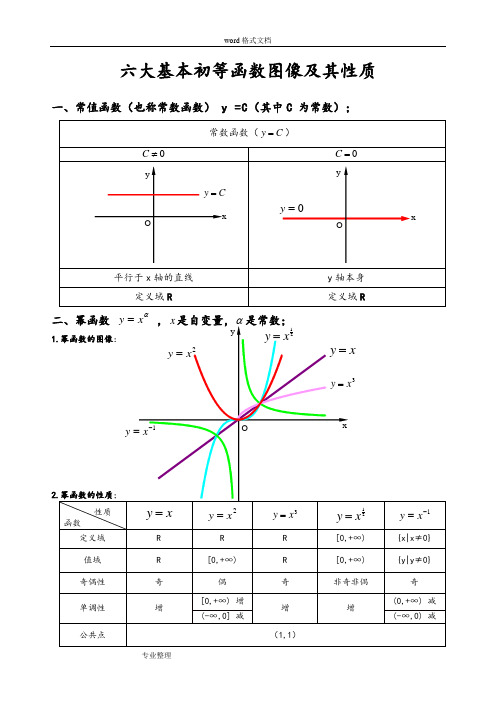
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及性质

WORD 格式整理版六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C (其中 C 为常数);常数函数( y C )C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x ,x是自变量,是常数;y 11. 幂函数的图像:y x2y x2y x1O2.幂函数的性质;性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点( 1,1)C 0yOy轴本身定义域 Ry xy x3x1y x2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减WORD 格式整理版1)当 α 为正整数时,函数的定义域为区间为x ( ,),他们的图形都经过原点,并当α >1 时在原点处与 x 轴相切。
且 α为奇数时,图形关于原点对称;α 为偶数时图形关于 y 轴对称;2)当 α 为负整数时。
函数的定义域为除去 x=0 的所有实数;3)当 α 为正有理数m时, n 为偶数时函数的定义域为(0, +∞), n 为奇数时函数的定义域为( -n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)如果 m>n 图形于 x 轴相切,如果m<n,图形于 y 轴相切,且 m 为偶数时,还跟y 轴对称; m , n均为奇数时,跟原点对称;5)当 α 为负有理数时, n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除 x=0 以外的一切实数。
三、指数函数 ya x ( x 是自变量 , a 是常数且 a0 , a 1) ,定义域是 R ;[ 无界函数 ]1. 指数函数的图象 :ya xyyya x(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质 ;性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x0 时, y 1单调性 在( ,)是增函数在(, )是减函数1 ) 当 a 1时 函 数 为 单 调 增 , 当 0 a 1时函数为单调减;2 ) 不 论 x 为 何 值 , y 总 是 正 的 , 图 形 在 x 轴 上 方 ;3 ) 当 x0 时 , y1,所以它的图形通过(0,1) 点。
六大基本初等函数图像及其性质
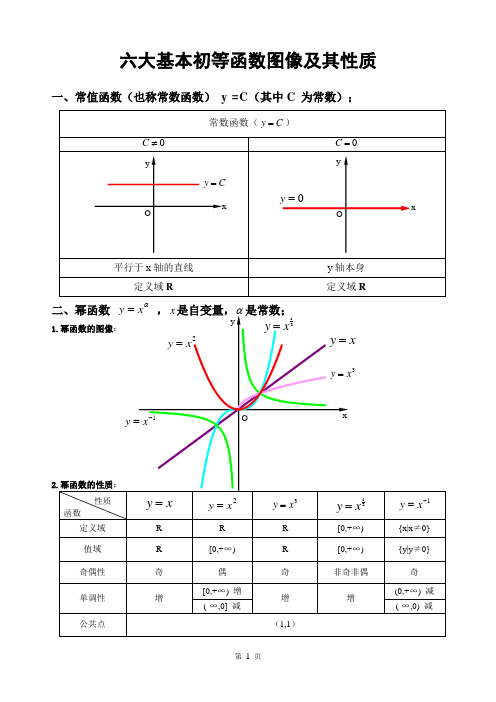
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性 在),(∞+∞-是增函数在),(∞+∞-是减函数1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质
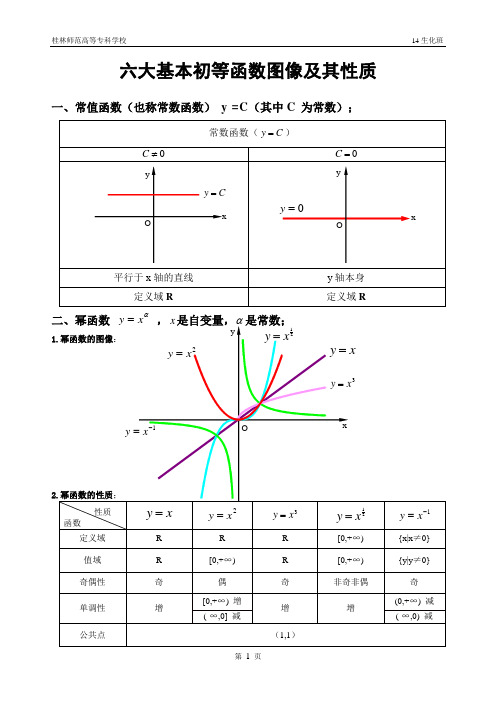
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。
x4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2) n m n ma a a -=÷(3)()()mn nmn m aaa ==(4) ()n n nb a ab =b.根式的性质;(1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b =,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质
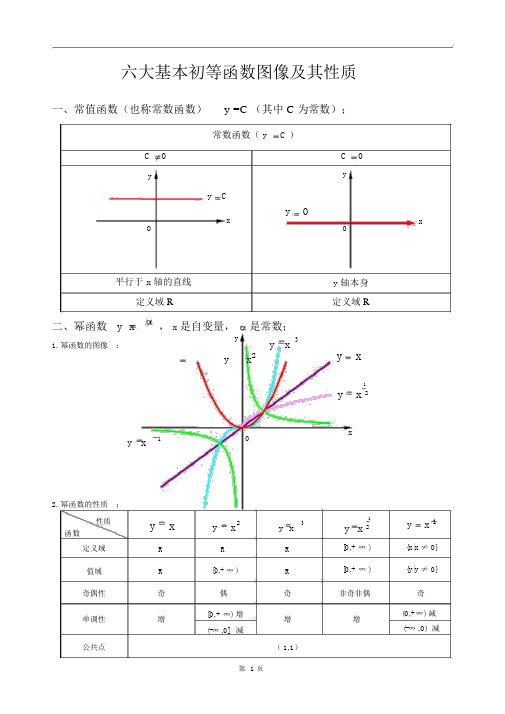
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C (其中 C 为常数);常数函数( y C )C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x, x 是自变量,是常数;1. 幂函数的图像:y y x3y x2y x1O2.幂函数的性质;性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点( 1,1)C 0yOy轴本身定义域 Ry x1y x 2x1y x 2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减第 1 页1)当 α 为正整数时,函数的定义域为区间为x ( ,),他们的图形都经过原点,并当α >1 时在原点处与 x 轴相切。
且 α为奇数时,图形关于原点对称;α 为偶数时图形关于 y 轴对称;2)当 α 为负整数时。
函数的定义域为除去 x=0 的所有实数;3)当 α 为正有理数m时, n 为偶数时函数的定义域为(0, +∞), n 为奇数时函数的定义域为( -n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)如果 m>n 图形于 x 轴相切,如果m<n,图形于 y 轴相切,且 m 为偶数时,还跟y 轴对称; m , n均为奇数时,跟原点对称;5)当 α 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数ya x(x 是自变量,a 是常数且a0 , a1 ),定义域是R ;[ 无界函数 ]1. 指数函数的图象 :yaxyyy ax(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质 ;性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x 0 时, y1单调性 在(, )是增函数 (, )在是减函数1 ) 当 a1时 函 数 为 单 调 增 , 当 0 a 1时函数为单调减;2 ) 不 论 x 为 何 值 , y 总 是 正 的 , 图 形 在 x 轴 上 方 ;3 ) 当 x 0 时 , y1,所以它的图形通过(0,1)点 。
六大基本初等函数图像及其性质
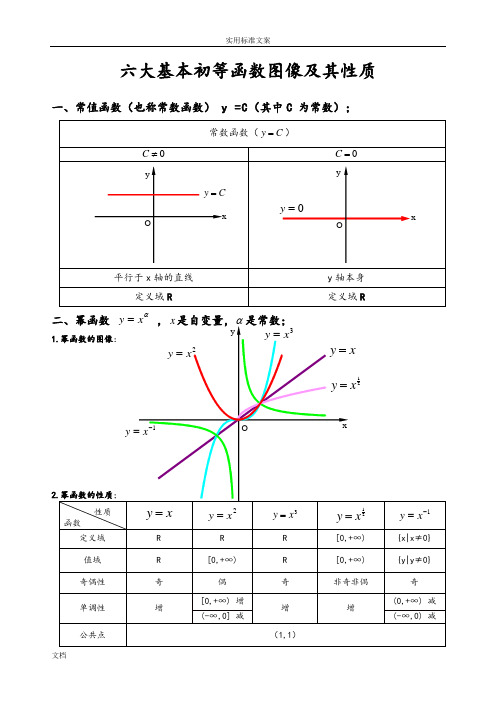
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
基本初等函数图像及性质

基本初等函数图像及性质
在数学的发展过程中,形成了最简单最常用的六类函数,即常数函数、幂函数、指数函数、对数函数、三角函数与反三角函数,这六类函数称为基本初等函数。
基本初等函数图像(常数函数)。
y=c或f(x)=c,x∈R,其中c是常数。
它的图像是通过点(0,c),且平行x轴的直线,如下图所示:
常数函数的图像。
基本初等函数的(常数函数)性质:
1、常数函数是有界函数,周期函数(没有最小的正周期)、偶函数。
2、常数函数既是单调增加函数又是单调减少函数,特别的当c=0时,它还是奇函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m aa a +=⋅(2)nm nmaa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
对数函数x y a log =与指数函数x a y =互为反函数,所以x y a log =的图象与x a y =的图象关于直线x y =对称。
2.常用对数:N 10log 的对数叫做常用对数,为了简便,N 的常用对数记作N lg 。
3.自然对数:使用以无理数7182.2=e 为底的对数叫做自然对数,为了简便,N 的自然对数N e log 简记作N ln 。
4.对数函数的图象:5.对数函数的性质;1)对数函数的图形为于y 轴的右方,并过点(1,0);2)当1>a 时,在区间(0,1),y 的值为负,图形位于x 的下方;在区间(1, +∞),y 值为正,图形位于x 轴上方,在定义域是单调增函数。
1<a 在实际中很少用到。
x a )1(>a)10(<<a6.(选,补充)对数函数值的大小比较*N ∈a ;a.底数互为倒数的两个对数函数x y a log =,x y a1log =的函数图像关于x 轴对称。
b.1. 当1>a 时,a 值越大,x x f a log )(=的图像越靠近x 轴;b.2. 当)10(<<a 时,a 值越大,x x f a log )(=的图像越远离x 轴。
7.对数的运算法则(公式);a.如果a >0,a ≠1,M >0,N >0,那么: ()N M MN a a a log log log +=N M NMa a alog log log -= Mn M a n a log log =b.对数恒等式:N a N a =log )010(>≠>N a a ,且c.换底公式: (1)bNN a a b log log log =(1,0≠>a a ,一般常常换为e 或10为底的对数,即b NN b ln ln log =或bNN b lg lg log =)(2)由公式和运算性质推倒的结论:bmnb a na n log log =d.对数运算性质(1)1的对数是零,即01log =a ;同理01ln =或01lg = (2)底数的对数等于1,即1log =a a ;同理1ln =e 或110lg =xa x a1x2xx 3log )(=x 21x x 31log )(=五、三角函数1.正弦函数xy sin=,有界函数,定义域),(+∞-∞∈x,值域]1,1[+-∈y图象:五点作图法:0,2π,π,23π,π22.余弦函数xy cos=,有界函数,定义域),(+∞-∞∈x,值域]1,1[+-∈y图象:五点作图法:0,2π,π,23π,π23.正、余弦函数的性质;性质函数xy sin=)(Zk∈xy cos=)(Zk∈定义域R值域[-1,1] [-1,1]奇偶性奇函数偶函数周期性π2=Tπ2=T 对称中心)0,(πk)0,2(ππk对称轴2ππ+=kx)0,2(ππ+k单调性在⎥⎦⎤⎢⎣⎡+-∈22,22ππππkkx上是增函数在⎥⎦⎤⎢⎣⎡++∈232,22ππππkkx上是减函数在[]πππkkx2,2-∈上是增函数在[]πππ+∈kkx2,2上是减函数最值22ππ+=kx时,1max=y22ππ+=kx时,1min-=yπkx2=时,1max=yππ+=kx2时,1min-=yx y tan =的图像x y cot =的图像6.正、余切函数的性质;8.余割函数xx y sin 1csc ==,无界函数,定义域{})(,Z k k x x ∈≠π,值域1csc ≥x9.正、余割函数的性质;x y sec =的图像x y csc =的图像续表:六、反三角函数1.反正弦函数x y arcsin =,无界函数,定义域[-1,1],值域],0[πA.反正弦函数的概念:正弦函数x y sin =在区间⎥⎦⎤⎢⎣⎡-2,2ππ上的反函数称为反正弦函数,记为x y arcsin =2.反余弦弦函数x y arccos =,无界函数,定义域[-1,1],值域],0[πB.反余弦函数的概念:余弦函数x y cos =在区间π,0上的反函数称为反余弦函数,记为y =x y arcsin =的图像 x y arccos =的图像3.反正、余弦函数的性质;4.反正切函数x y arctan =,有界函数,定义域),(+∞-∞∈x ,值域⎪⎭⎫⎝⎛-2,2ππC.反正切函数的概念:正切函数x y tan =在区间⎪⎭⎫⎝⎛-2,2ππ上的反函数称为反正切函数,记为x y arctan =5.反余切函数x arc y cot =,有界函数,定义域),(+∞-∞∈x ,值域()π,0D.反余切函数的概念:余切函数x y cot =在区间()π,0上的反函数称为反余切函数,记为x arc y cot =xy arctan =的图像 x arc y cot =的图像6.反正、余弦函数的性质;三角函数公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=。
正弦:ry=αsin 余弦:r x =αcos正切:xy=αtan 余切:y x =αcot正割:xr=αsec 余割:y r =αcsc二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα商数关系:αααcos sin tan =,αααsin cos cot =平方关系:1cos sin22=+αα,αα22sec tan 1=+,αα22csc cot 1=+三、诱导公式x 轴上的角,口诀:函数名不变,符号看象限;y 轴上的角,口诀:函数名改变,符号看象限。
四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+βαβαβαtan tan 1tan tan )tan(⋅+-=-五、二倍角公式αααcos sin 22sin =ααα2tan 1tan 22tan -=ααααα2222sin 211cos 2sin cos 2cos -=-=-=二倍角的余弦公式常用变形:(规律:降幂扩角,升幂缩角)αα2cos 22cos 1=+ αα2sin 22cos 1=- 2)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=-22cos 1cos 2αα+=,22sin 1sin 2αα+=,ααααα2cos 12sin 2sin 2cos 1tan +=-=六、三倍角公式)3sin()3sin(sin 4sin 4sin 33sin 3απαπααα+-=-=)3cos()3cos(cos 4cos 3cos 43cos 3απαπααα+-=-=)3tan()3tan(tan tan 31tan tan 33tan 23απαπααααα+-=--= 七、和差化积公式2cos 2sin2sin sin βαβαβα-+=+ 2sin2cos2sin sin βαβαβα-+=-2cos2cos2cos cos βαβαβα-+=+ 2sin2sin2cos cos βαβαβα-+-=-八、辅助角公式)sin(cos sin 22ϕ++=+x b a x b x a其中:角ϕ的终边所在的象限与点),(b a 所在的象限相同,22sin b a b +=ϕ,22cos b a a +=ϕ,ab=ϕtan 九、三角函数的周期公式函数)sin(ϕω+=x A y ,R x ∈及函数)cos(ϕω+=x A y ,R x ∈(A,ϕω,,为常数,且0,0>≠ωA )周期: ωπ2=T函数)tan(ϕω+=x A y ,Z k k x ∈+≠,2ππ(A,ϕω,,为常数,且0,0>≠ωA )周期: ωπ=T 十、正弦定理R C cB b A a 2sin sin sin ===(R 为ABC ∆外接圆半径) 十一、余弦定理A bc c b a cos 2222⋅-+=B ac c a b cos 2222⋅-+=C ab b a c cos 2222⋅-+=。
