清表面积计算
如何确定清如何确定公路的清表面积

如何确定清如何确定公路的清表面积?清表面积的计算规则:清表面积=E (路基设计宽度+填(挖)高度(深度)幼坡坡率X2)澗面长度;一般在路基设计表或者设计文件中早已给出。
图纸上给的有这个量,我们这边刚做过这个,就是你清表的公里数*清表宽度,这个宽度需要跟监理协商确定,有的是按60m,或者90m,假设你是按90m清表的,但是计量只按60m那也就是60m 呵呵 ........... 根据[公路工程国内招标文件范本]的要求(P3 8),即公路工程的统一标准,在合同中没有另外规定的,按照以下方法计量:1、施工场地清理的计量应按监理工程师书面指定的范围进行验收后现场实地测量,按投影平面面积以平方米计量。
现场清理包括路基范围内的所有垃圾、灌木、竹林及胸径小于150mm 的树木、石头、废料、表土(腐殖土)、草皮的铲除与开挖。
2、砍伐树木仅计胸径(即离地面 1.3m处的直径)大于150mm 的树木,以棵计量。
3、所有场地清理、拆除与挖掘工作的一切挖方、回填、压实,以及适用材料的移运、堆放、废料的移运处理等作业均不另行计量。
我这里是按平方米计量的,清场是按设计清场20cm 厚。
清场不一定是30 厘米,按设计图。
按投影面积计算。
我们这里计算投影面积是:挖方计算至顶边坡,填方至坡脚线,两侧为路肩墙的,只计算路肩墙内侧与地面线接触之间的投影面积。
清表回填的土方是要计量的,关键就看设计挖填方数量中是否包含了清表的开挖和回填,如果设计挖方中包含了清表挖方,则挖方工程量中要扣减清表挖方;如果设计填方中未包含清表的填方,则在填方工程量中要加上清表回填的土方。
一般设计的断面方中是不包含清表的,你可以核查一下路基横断面。
我们这清表是30CM ,其实就按照设计的清表厚度计算清表量就行了。
标高是肯定要测的,因为你要比较下清表后高程和按理论的清表高程那个划算,当然高程高的对自己有利了。
至于原地面-设计高程,这个设计高程是什么高程?原地面?还是道路设计高程?实际清表高程= 实测原地面高程(业主认可后方有效)-清表后高程;理论清表高程=设计图纸上的原地面高程-设计清表厚度我原来在过的公路项目,对清除表土也是这样处理的(清单挖土方中扣除在填方中给相应的量),这也是主要参考《公路工程工程量清单计量规则》zhulong corr造价的人应对施工工序及管理有所了解才行,其实在承包人进场后,首先应对原地表进行复测,这叫定位.然后才进行清表施工,不管填挖地段均应进行清表,填方段清表后需要进行碾压,然后对填前地表标高进行复测(联测),这个是承包人填方量计算的基础,多翻翻技术规范多个章节的土石方计算规则,你就明了了.比较模糊的是挖方段的清表与挖方量的计算,应该是这个原则,同样的部位只能计量一次.1\如果你的挖方是以原地面复测为基础来计算的,则不应再计量清表数量.2\如果挖方地段的清表量已单独计量,则计算挖方应以清表后复测的标高为基础计算.3\两种方法,不一定对哪方有利,可以协商解决.没有硬性规楼上有很多网友说,清表后回填至原地面线的填方已计算填方单价中,这是根据概算有关说明中来的,与技术规范中的计量规则不相附.应将该部分工程量列入填方量内计量,也不能作为换填来计量,因为换填是针对填方地段,地表以下的非适用土而言的,也就是当清表达到30公以上,还存在非适用土的情况下,才适用这个.如果清单中的换填量,等于清表土的体各量,只能说明那个编制招标清单的人,水平太低了,没有实际经验.。
公路的清表面积计算

如何确定公路的清表面积?清表面积的计算规则:清表面积=刀(路基设计宽度+填(挖)高度(深度)X边坡坡率x 2)x断面长度:一般在路基设计表或者设计文件中早已给出。
图纸上给的有这个量,就是你清表的公里数* 清表宽度,这个宽度需要跟监理协商确定,有的是按60m,或者90m,假设你是按90m 清表的,但是计量只按60m 那也就是60m..根据[公路工程国内招标文件范本]的要求(P38),即公路工程的统一标准,在合同中没有另外规定的,按照以下方法计量:1、施工场地清理的计量应按监理工程师指定的范围进行验收后现场实地测量,按投影平面面积以平方米计量。
现场清理包括路基范围内的所有垃圾、灌木、竹林及胸径小于150mm 的数目、石头、废料、表土(腐殖土)、草皮的铲除与开挖。
2、砍伐树木仅计胸径(即离地面1.3处得直径)大于150mm 的树木,以颗计量。
3、所有场地清理、拆除与挖掘工作的一切挖方、回填、压实, 以适用材料的移运、堆放、废料的移运处理等均不另行计量。
这里是按平方米计量的,清场是按设计清场20cm 厚。
清场不一定是30 厘米,按设计图。
按投影面积计算。
计算投影面积是:挖方计算至顶边坡,填方至坡脚线,两侧为路肩墙的,只计算路肩墙内侧与地面线接触之间的投影面积。
清表回填的土方时要计量的,关键就看设计挖填方数量是否包含了清表的开挖和回填方,如果设计挖方中包含了清表挖方,则挖方工程量中要扣减清表挖方;如果设计填方中未包含清表的填方,则在填方工程量中要加上清表回填的土方。
一般设计的断面方中是不包含清表的,你可以核查一下路基横断面。
这清表是30cm,其实就是按照设计的清表厚度计算清表量就行了。
标高是肯定要测的,因为你要比较一下清表后高程和按理论的清表高程那个哪个划算,当然高程高的对自己有利了。
至于原地面-设计高程,这个设计高程是什么高程?原地面?还是道路设计高程?实际清表高程=实测原地面高程(业主认可后方有效)-清表后高程:理论清表高程=设计图纸上的原地面高程设计清表厚度-设计清表厚度造价的人应对施工工序及管理有所了解才行,其实在承包人进场后,首先应对原地表进行复测,这叫定位,然后才进行清表施工,不管填挖地段均应进行清表,填方段清表后需要进行碾压,然后对填前地表标高进行复测(联测),这个是承包人填方量计算的基础。
土石方工程量计算培训ppt课件

B
•土石方工程量计算培训
土石方定额工程量计算
6. 基槽基坑土石方计算: 2) 一般基槽基坑土石方计算:
外墙按
沟槽长度
内墙按
外墙槽底中心线L外中 内墙槽底净长线L内净
挖基槽 平面图
槽底宽
内墙槽底 净长
外墙中心线长度
•土石方工程量计算培训
土石方定额工程量计算
6. 基槽基坑土石方计算: 2) 一般基槽基坑土石方计算:
土石方定额工程量计算
➢ 土壤和岩石分类 ➢ 土石方施工及计算内容 ➢ 土石方施工方式 ➢ 土石方工程量计算需准备资料 ➢ 土石方定额工程量计算规则和方法
➢
•土石方工程量计算培训
土石方定额工程量计算
一、土壤和岩石分类
土壤分类
土壤名称性状 砂 砂壤土 腐殖土 泥炭
开挖方法及工具 用尖锹开挖
一、二类 土壤
其土方量凡有施工图注明的,按施工图计算;无施工图的,一般按沟深0.9m、沟 宽按最外边的保护管两侧边缘外各增加0.3m工作面计算。另电缆管的埋设深度不应小 于0.7m(如过路加钢套管则同人行道);在人行道下面敷设时,不应小于0.5m。
则: V挖=(S挖1+S挖2+√s挖1*s挖2)/3*L
注:其计算的重点在于截面的绘制
•土石方工程量计算培训
土石方定额工程量计算
四、土石方定额工程量计算规则及方法
6. 基槽基坑土石方计算: 2) 一般基槽基坑土石方计算: 沟槽:—般按沟槽的横截面面积×槽长以m3计算。 (注意:挖沟槽——适用于设计图纸中采用带型混凝土基础或带型垫层。)
•土石方工程量计算培训
土石方定额工程量计算
岩石分类
岩石名称性状
开挖方法及工具
高中数学必修二 19-20 第8章 8 3 2 第1课时圆柱、圆锥、圆台的表面积和体积

8.3.2圆柱、圆锥、圆台、球的表面积和体积第1课时圆柱、圆锥、圆台的表面积和体积学习目标核心素养1.通过对圆柱、圆锥、圆台的研究,掌握圆柱、圆锥、圆台的表面积与体积的求法.(重点)2.会求与圆柱、圆锥、圆台有关的组合体的表面积与体积.(难点、易错点)1.借助圆柱、圆锥、圆台的表面积、体积的计算,培养数学运算素养.2.通过对圆柱、圆锥、圆台的体积的探究,提升逻辑推理的素养.1.圆柱、圆锥、圆台的表面积圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πrl+2πr2圆锥底面积:S底=πr2侧面积:S侧=πrl表面积:S=πrl+πr2圆台上底面面积:S上底=πr′2下底面面积:S下底=πr2侧面积:S侧=πl(r+r′)表面积:S=π(r′2+r2+r′l+rl)2.圆柱、圆锥、圆台的体积公式 V 圆柱=πr 2h (r 是底面半径,h 是高), V 圆锥=13πr 2h (r 是底面半径,h 是高),V 圆台=13πh (r ′2+r ′r +r 2)(r ′、r 分别是上、下底面半径,h 是高).1.判断正误(1)圆柱的表面积就是侧面积.( )(2)在一个圆锥中,母线长度不一定相同.( ) (3)圆台是用平行于底面的平面截圆锥得到的.( ) [答案] (1)× (2)× (3)√2.圆柱的侧面展开图是长12 cm ,宽8 cm 的矩形,则这个圆柱的体积为( ) A.288π cm 3 B.192π cm 3 C.288π cm 3或192π cm 3D .192π cm 3C [圆柱的高为8 cm 时,V =π×⎝ ⎛⎭⎪⎫122π2×8=288π cm 3,当圆柱的高为12 cm时,V =π×⎝ ⎛⎭⎪⎫82π2×12=192π cm 3.]3.圆台的上、下底面半径分别为3和4,母线长为6,则其表面积等于( ) A .72 B .42π C .67πD .72πC [表面积S =π(3+4)×6+π×32+π×42=67π.]圆柱、圆锥、圆台的表面积【例面积的比是( )A.1+2π2πB.1+4π4πC.1+2ππD.1+4π2π(2)已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和. ①求圆台的母线长. ②求圆台的表面积.(1)A [设圆柱底面半径为r ,则高为2πr , 表面积∶侧面积=[(2πr )2+2πr 2]∶(2πr )2=1+2π2π.](2)[解] ①设圆台的母线长为l ,则由题意得 π(2+6)l =π×22+π×62, ∴8πl =40π,∴l =5, ∴该圆台的母线长为5. ②由①可得圆台的表面积为 S =π×(2+6)×5+π·22+π×62 =40π+4π+36π =80π.圆柱、圆锥、圆台的表面积的求解步骤解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助于平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:(1)得到空间几何体的平面展开图. (2)依次求出各个平面图形的面积. (3)将各平面图形的面积相加.1.轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( )A .4倍B .3倍C .2倍D .2倍D [由已知得l =2r ,S 侧S 底=πrl πr 2=lr =2,故选D.]圆柱、圆锥、圆台的体积【例2】 圆锥的过高的中点且与底面平行的截面把圆锥分成两部分的体积之比是( )A .1∶1B .1∶6C .1∶7D .1∶8C [如图,设圆锥底半径OB =R ,高PO =h , ∵O ′为PO 中点,∴PO ′=h2, ∵O ′A OB =PO ′PO =12,∴O ′A =R 2, ∴V 圆锥PO ′=13π·⎝ ⎛⎭⎪⎫R 22·h2=124πR 2h .V 圆台O ′O =π3·⎝ ⎛⎭⎪⎪⎫⎝ ⎛⎭⎪⎫R 22+R 2+R 2·R ·h 2=724πR 2h . ∴V 圆锥PO ′V 圆台O ′O=17,故选C.]求几何体体积的常用方法2.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是()A.233π B.2 3 C.736π D.733πD[S1=π,S2=4π,∴r=1,R=2,S侧=6π=π(r+R)l,∴l=2,∴h= 3.∴V=13π(1+4+2)×3=733π.故选D.]组合体的表面积与体积【例3】如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内过点C作l⊥CB,以l为轴旋转一周.求旋转体的表面积和体积.[解]如题图,在梯形ABCD中,∠ABC=90°,AD∥BC,AD=a,BC=2a,∠DCB=60°,∴CD=BC-ADcos 60°=2a,AB=CD sin 60°=3a,∴DD′=AA′-2AD=2BC-2AD=2a,∴DO=12DD′=a.由于以l为轴将梯形ABCD旋转一周后形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥.由上述计算知,圆柱母线长3a,底面半径2a,圆锥的母线长2a,底面半径a.∴圆柱的侧面积S1=2π·2a·3a=43πa2,圆锥的侧面积S2=π·a·2a=2πa2,圆柱的底面积S3=π(2a)2=4πa2,圆锥的底面积S4=πa2,∴组合体上底面积S5=S3-S4=3πa2,∴旋转体的表面积S=S1+S2+S3+S5=(43+9)πa2.又由题意知形成的几何体的体积为一个圆柱的体积减去一个圆锥的体积.V 柱=Sh=π·(2a)2·3a=43πa3,V锥=13S′h=13·π·a2·3a=33πa3,∴V=V柱-V锥=43πa3-33πa3=1133πa3.如果将例题的梯形绕着BC边所在直线旋转一周,如何求旋转体的表面积和体积?表面积和体积又分别为多少?[解]如图所示旋转体为一个圆锥和与它同底的一个圆柱组成,由条件可得:AD=BO=OC=a,DO=AB=3a,DC=2a,所以该旋转体的表面积为:S=S圆柱底+S圆柱侧+S圆锥侧=π·(3a)2+2π3a·a+π·3a·2a=3πa2+23πa2+23πa2=(3+43)πa2,该旋转体的体积为V=V圆锥+V圆柱=12·a+π(3a)2a3π(3a)=4πa3.求组合体的表面积和体积,首先要认清组合体是由哪些简单几何体构成的.组合体的表面积是可见的围成组合体的所有面的面积之和,但不一定是组成组合体的几个简单几何体的表面积之和;组合体的体积是构成组合体的几个简单组合体的体积之和(差).1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的面积,因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系,是掌握它们的侧面积公式及解有关问题的关键.2.计算柱体、锥体和台体的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面及旋转体的轴截面,将空间问题转化为平面问题.1.若圆锥的高等于底面直径,则它的底面积与侧面积之比为()A.1∶2B.1∶ 3C .1∶ 5 D.3∶2C [设圆锥底面半径为r ,则高h =2r ,∴其母线长l =5r .∴S 侧=πrl =5πr 2,S 底=πr 2.则S 底∶S 侧=1∶ 5.]2.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D .3A [设圆台较小底面半径为r ,则另一底面半径为3r .由S =π(r +3r )·3=84π,解得r =7.]3.已知圆台上、下底面半径分别为1,2,高为3,则圆台体积为 . 7π [由已知圆台上、下底面积分别为 S 上=π,S 下=4π.则V 圆台=13·(π+π·4π+4π)·3=7π.]4.一个高为2的圆柱,底面周长为2π,该圆柱的表面积为 . 6π [由底面周长为2π可得底面半径为1.S 底=2πr 2=2π,S 侧=2πr ·h =4π,所以S 表=S 底+S 侧=6π.]5.已知圆锥的底面半径为2,高为5,求这个圆锥的体积. [解] 由题意V 锥体=13Sh =13πr 2·h =20π3.。
型材表面积计算

型材表面积计算一、型材表面积计算的重要性型材在我们的生活和工程中可是相当常见的呢,像建筑里的钢梁啊,还有一些家具的框架之类的。
那为啥要计算型材的表面积呢?这可关系到好多方面呢。
比如说,如果我们要给型材涂漆,就必须知道表面积才能算出需要多少油漆,不然买多了浪费,买少了又不够。
再比如说,如果要给型材包裹一层保护膜之类的东西,也得清楚表面积是多少呀。
二、不同形状型材表面积计算方法1. 矩形型材对于简单的矩形型材,它的表面积计算就比较直观啦。
假如这个矩形型材的长是a,宽是b,高是c。
那它的表面积S = 2(ab + ac+ bc)。
就像是把这个矩形型材展开,它有六个面,相对的面面积是一样的,所以这样计算就可以得到它的总表面积啦。
比如说,有一个矩形型材长是3米,宽是0.5米,高是0.3米。
那按照公式来算,S = 2×(3×0.5+3×0.3 + 0.5×0.3)=2×(1.5 + 0.9+0.15)=2×2.55 = 5.1平方米。
2. 圆形型材如果是圆形型材,这里指的是那种圆柱形状的型材哦。
假设它的底面半径是r,高是h。
那它的表面积S = 2πr²+ 2πrh。
这里的2πr²是两个底面圆的面积,2πrh是侧面展开长方形的面积。
举个例子,如果一个圆柱型材底面半径是0.2米,高是2米。
那S= 2×3.14×0.2²+2×3.14×0.2×2 = 2×3.14×0.04 + 2×3.14×0.4 = 0.2512+2.512 = 2.7632平方米。
3. 三角形型材对于三角形型材,如果这个三角形的底边长是a,高是h,型材的长是l。
那它的侧面积就是三角形的周长乘以型材的长,假设三角形三边分别是a、b、c,那侧面积S侧=(a + b + c)l。
公路清表面积计算

公路清表面积计算1.清表面积的计算规则:清表面积=∑(路基设计宽度+填(挖)高度(深度)X边坡坡率x 2)x断面长度:一般在路基设计表或者设计文件中早已给出。
图纸上给的有这个量,就是你清表的公里数* 清表宽度,这个宽度需要跟监理协商确定,有的是按60m,或者90m,假设你是按90m 清表的,但是计量只按60m 那也就是60m.. 根据[公路工程国内招标文件范本]的要求(P38),即公路工程的统一标准,在合同中没有另外规定的,按照以下方法计量:1、施工场地清理的计量应按监理工程师指定的范围进行验收后现场实地测量,按投影平面面积以平方米计量。
现场清理包括路基范围内的所有垃圾、灌木、竹林及胸径小于150mm 的数目、石头、废料、表土(腐殖土)、草皮的铲除与开挖。
2、砍伐树木仅计胸径(即离地面1.3处得直径)大于150mm 的树木,以颗计量。
3、所有场地清理、拆除与挖掘工作的一切挖方、回填、压实, 以适用材料的移运、堆放、废料的移运处理等均不另行计量。
这里是按平方米计量的,清场是按设计清场20cm 厚。
清场不一定是30 厘米,按设计图。
按投影面积计算。
计算投影面积是:挖方计算至顶边坡,填方至坡脚线,两侧为路肩墙的,只计算路肩墙内侧与地面线接触之间的投影面积清表回填的土方时要计量的,关键就看设计挖填方数量是否包含了清表的开挖和回填方,如果设计挖方中包含了清表挖方,则挖方工程量中要扣减清表挖方: 如果设计填方中未包含清表的填方,则在填方工程量中要加上清表回填的土方。
一般设计的断面方中是不包含清表的,你可以核查一下路基横断面。
这清表是 30cm,其实就是按照设计的清表厚度计算清表量就行了。
标高是肯定要测的,因为你要比较一下清表后高程和按理论的清表高程那个哪个划算,当然高程高的对白己有利了至于原地面-设计高程,这个设计高程是什么高程?原地面?还是道路设计高程?实际清表高程=实测原地面高程(业主认可后方有效)-清表后高程:理论清表高程-设计图纸上的原地面高程设计清表厚度-设计清表厚度。
圆柱体表面积公式字母

圆柱体表面积公式字母圆柱面积的公式:S=2πr²+2πhr,其中,S为圆柱的表面积,r为圆柱的底面半径,h为圆柱的高。
圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体。
圆柱(cylinder)是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体。
直圆柱也叫正圆柱、圆柱,就是底面和顶面是同样半径(r)的圆,并且两圆圆心的连线和顶面、底面的互相垂直,并且我们可以得知,圆柱侧面展开图是长方形。
假设圆柱体底面半径为r,高度为h,则:底面积为:πr²侧面积为:2πrh表面积为:2底面积+侧面积=2πr²+2πrh=2πr(r+h)圆柱的侧面积、表面积和体积计算公式用字母表示为:S侧=______;S表=______;V圆柱=______圆柱的侧面积、表面积和体积计算公式用字母表示为:S侧=2πrh,S表=2πr²+2πrh,V圆柱=πr²h。
h表示圆柱的高,r表示底面圆的半径。
圆柱的侧面积=底面的周长×高。
圆柱的表面积=侧面积+两个底面积(S表=S侧+2S底)圆柱所占空间的大小,叫做这个圆柱体的体积。
求圆柱的体积跟求长方体、正方体一样,都是底面积×高。
圆柱的两个完全相同的圆面叫做底面(又分上底和下底);圆柱有一个曲面,叫做侧面;两个底面的对应点之间的距离叫做高(高有无数条)。
特征:1、圆柱的底面都是圆,并且大小一样。
2、圆柱两个面之间的垂直距离叫做高,把圆柱的侧面打开,得到一个矩形,这个矩形的一条边就是圆柱的底面周长。
圆柱的表面积计算公式用字母怎样表示圆柱的表面积公式S=Ch+2πr^2=2πr(r+h)圆柱体是由两个底面和一个侧面组成的,所以表面积等于两个底面的面积加上侧面的面积。
1.圆柱的两个圆面叫底面,周围的面叫侧面,一个圆柱体是由两个底面和一个侧面组成的。
第二节 简单几何体的表面积和体积(知识梳理)
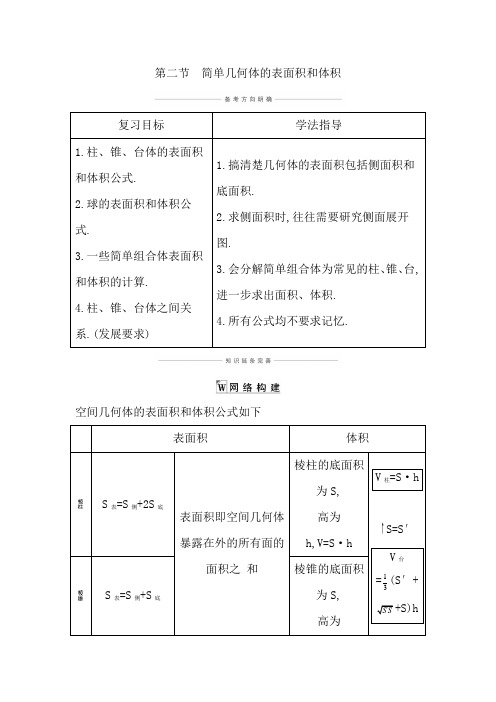
第二节简单几何体的表面积和体积复习目标学法指导1.柱、锥、台体的表面积和体积公式.2.球的表面积和体积公式.3.一些简单组合体表面积和体积的计算.4.柱、锥、台体之间关系.(发展要求)1.搞清楚几何体的表面积包括侧面积和底面积.2.求侧面积时,往往需要研究侧面展开图.3.会分解简单组合体为常见的柱、锥、台,进一步求出面积、体积.4.所有公式均不要求记忆.空间几何体的表面积和体积公式如下表面积体积S表=S侧+2S底表面积即空间几何体暴露在外的所有面的面积之和棱柱的底面积为S,高为h,V=S·hV柱=S·hS=S′V台=13(S′+S S +S)h S表=S侧+S底棱锥的底面积为S,高为h,V=13S ·h S ′=0 V 锥=13S ·hS 表=S 侧+ S 上底+S 下底棱台的上、下底面 面积分别为S ′,S,高为h, V=13(S ′+ S S+S)h圆柱的底面半径和母线长分别为r,lS 表=2πr 2+2πrl 圆柱的高为h,V=πr 2h圆锥的底面半径和母线长分别为r,l S 表=πr 2+πrl 圆锥的高为h,V=13πr 2h圆台的上、下底面半 径和母线长分圆台的高为h,V=13π(r ′2+别为r,r′,l,S表=π(r′2+r2+r′l+rl)r′r+r2)h球球半径为R,S球=4πR2V球=43πR31.概念理解(1)表面积应为侧面积和底面积的和,要注意组合体中哪些部分暴露或遮挡.(2)求空间几何体体积的常用方法①公式法:直接根据相关的体积公式计算.②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.2.求面积或体积中相关联的结论几个与球有关的切、接常用结论(1)正方体的棱长为a,球的半径为R,①正方体的外接球,则3②正方体的内切球,则2R=a;③球与正方体的各棱相切,则2(2)长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=222a b c ++.(3)正四面体的外接球与内切球的半径之比为3∶1.1.圆柱的底面积为S,侧面展开图是一个正方形,那么圆柱的侧面积是( A )(A)4πS (B)2πS (C)πS (D)23πS 解析:由πr 2=S 得圆柱的底面半径是πS , 故侧面展开图的边长为2π·πS =2πS,所以圆柱的侧面积是4πS.故选A.2.正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为3,D为BC 的中点,则三棱锥A-B 1DC 1的体积为 . 解析:如图,在正三棱柱ABC-A 1B 1C 1中, 因为AD ⊥BC,AD ⊥BB 1, BB 1∩BC=B,所以AD ⊥平面B 1DC 1. 所以11A B DC V-=1113B DC S ∆·AD=13×12×233=1. 答案:13.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 cm 3,表面积为 cm 2.解析:由三视图可得该几何体为二分之一圆锥, 圆锥的底面半径为1,高为2,所以可得该几何体的体积为12×13×π×12×2=π3, 该几何体的表面积为12×π×12+12π×114++12×2×2=)51π2+2.答案: π3)51π2+24.已知正四棱锥O-ABCD 32,3,则以O 为球心,OA 为半径的球的表面积是 . 解析:设O 到底面的距离为h,则13×3×32,解得32()()2233+62262h ⎛⎫+ ⎪ ⎪⎝⎭6故球的表面积为4π×62=24π.答案:24π5.(2019·浙江宁波模拟)已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为,该三棱锥的外接球体积为.解析:由三视图得几何体的直观图如图.所以S表=2×12×2×2+12×3512×3 1153如图,作DE⊥DB,以D为原点,DB所在直线为x轴,DE所在直线为y 轴,DA所在直线为z轴,建立空间直角坐标系,则3设球心坐标为(x,y,z),因为(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)23)2+z2=x2+y2+z2,③所以x=1,y=3,z=1,所以球心的坐标是(1,3,1), 所以球的半径是()222131++=5.所以球的体积是43π×(5)3=2053π.答案:4+15+32053π考点一几何体的表面积[例1] (1)(2018·金丽衢十二校联考)某四面体的三视图如图所示,正视图、侧视图都是腰长为2的等腰直角三角形,俯视图是边长为2的正方形,则此四面体的最大面的面积是( )(A)2 23(D)4(2)(2019·湖州模拟)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )(A)4π3(B)5π3(C)4π3(D)5π3(3)若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为;(4)四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若四棱锥S-ABCD的体积取值范围为4383],则该四棱锥外接球表面积的取值范围是.解析:(1)因为几何体为一个四面体,六条棱长分别为2223所以四面体的四个面的面积分别为12×2×2=2,12×2×2212×2×221 2×22sin π33因此四面体的最大面的面积是3.故选C.(2)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.(3)设圆锥底面半径为r,母线长为l,母线与轴夹角为θ, 则=22π122rl r l r⋅-2π,r l=3,即sin θ=3,θ=π3. 解析:(4)四棱锥S-ABCD 中,可得AD ⊥SA,AD ⊥AB ⇒AD ⊥平面SAB ⇒平面SAB ⊥平面ABCD,过S 作SO ⊥AB 于O,则SO ⊥平面ABCD, 设∠SAB=θ, 故S ABCDV-=13S 四边形ABCD ·SO=83sin θ, 所以sin θ∈[3,1]⇒θ∈[π3,2π3]⇒-12≤cos θ≤12, 在△SAB 中,SA=AB=2, 则有SB=221cos θ-,所以△SAB 的外接圆半径r=2sin SBθ=21cos θ-,将该四棱锥补成一个以SAB 为一个底面的直三棱柱,得外接球的半径R=21r +⇒S=4πR2=4π(21cos θ++1), 所以S ∈[28π3,20π]. 答案:(1)C (2)D (3)π3答案:(4)[28π3,20π] (1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.1.(2019·浙江十校联盟)如图所示,已知某几何体的三视图及其尺寸(单位:cm),则该几何体的表面积为( C )(A)15π cm2(B)21π cm2(C)24π cm2(D)33π cm2解析:由三视图可知,则该几何体是一个圆锥,圆锥的底面半径为3,母线长为5,故该几何体的表面积为S表=πr2+πrl=π×32+π×3×5=24π(cm2).故选C.2.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )(A)81π4(B)16π(C)9π(D)27π4解析:易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+(2)2=R2, 解得R=94,所以球的表面积为4π×(94)2=814π.故选A.考点二几何体的体积[例2] (1)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )(A)12cm3(B)1 cm3(C)16 cm3 (D)13cm3(2)(2018·天津卷)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H, M(如图),则四棱锥M-EFGH的体积为.解析:(1)由题意,根据给定的三视图可知,该几何体表示一个底面为腰长为1的等腰直角三角形,高为1的三棱锥, 如图所示,所以该三棱锥的体积为V=13×12×1×1×1=16(cm 3),故选C.解析:(2)依题意,易知四棱锥M-EFGH 是一个正四棱锥,且底面边长为2,高为12. 故M EFGHV=13×(2)2×12=112. 答案:(1)C 答案:(2)112(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解,其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.某三棱锥的三视图如图所示,则该三棱锥的体积为( D )(A)60 (B)30 (C)20 (D)10解析:如图,把三棱锥A-BCD 放到长方体中,长方体的长、宽、高分别为5,3,4,△BCD 为直角三角形,直角边分别为5和3,三棱锥A-BCD 的高为4,故该三棱锥的体积V=13×12×5×3×4=10.故选D.考点三 与面积、体积相关的综合问题[例3] (1)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则12S S = ;(2)将边长为a 的正方形ABCD 沿对角线AC 折起,点A,B,C,D 折叠后对应点为A ′,B ′,C ′,D ′,使B ′D ′=a,则三棱锥D ′-A ′B ′C ′的体积为 .解析:(1)设正四面体棱长为a,则正四面体的表面积为 S 1=43a 23a2,正四面体的高2233a a ⎛⎫- ⎪ ⎪⎝⎭6a,由13r ·S 1=1332·h 知r=146a. 因此内切球的表面积为S 2=4πr 2=2π6a,则12S S 2236a a 63.解析:(2)如图所示,正方形ABCD 及折叠后的直观图.易知在直观图中,A ′B ′=B ′C ′=C ′D ′=D ′A ′=a, 且A ′D ′⊥D ′C ′,A ′B ′⊥B ′C ′, 取A ′C ′的中点E,连接D ′E,B ′E, 则D ′E ⊥A ′C ′,D ′E=EB ′=2a,所以D ′E ⊥EB ′,所以D ′E ⊥平面A ′B ′C ′. D ′E 即为三棱锥D ′-A ′B ′C ′的高. 故D A B C V''''-=13S △A ′B ′C ′·D ′E =13×12×a ×a ×2a=2a 3.答案:(1)63 答案:(2)2a 3(1)①解决与球有关问题的关键是球心及球的半径,在球中球心与截面圆圆心的连线、截面圆圆心与截面圆周上一点、该点与球心的连线构成一个直角三角形.②解决多面体(或旋转体)的外接球、内切球问题的关键是确定球心在多面体(或旋转体)中的位置,找到球半径(或直径)与几何体相关元素之间的关系.有时将多面体补形为正(长)方体再求解.(2)求几何体表面上两点间的最短距离的常用方法是选择恰当的母线或棱将几何体展开,转化为求平面上两点间的最短距离.1.已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( C ) (A)3172 (B)210(C)132(D)310解析:如图,由球心作平面ABC 的垂线, 则垂足为BC 的中点M.又AM=12BC=52,OM=12AA 1=6, 所以球O 的半径 R=OA=22562⎛⎫+ ⎪⎝⎭=132. 故选C.2.已知某几何体的三视图如图所示,则该几何体的表面积是 ,体积是 .解析:本题考查空间几何体的三视图、体积和表面积的计算.由三视图得该几何体为底面是以上底为1,下底为3,高为3的直角梯形,高为3的直四棱柱,则其表面积为2×3×1+32+3×3+1×3+3×3+3×13=33+313,体积为3×3×1+32=18.答案:33+31318考点四易错辨析[例4] (2019·浙江绍兴模拟)如图是由半球和圆柱组合而成的几何体的三视图,则该几何体的体积为( )(A)5π3 (B)8π3(C)10π3(D)12+2π3解析:由题得,几何体是水平放置的一个圆柱和半个球,所以该几何体的体积为V=43π×13×12+π×12×2=83π,故选B.正确解决此类问题应注意确认几何体的形状时,要紧扣三视图,不能凭感觉去确定.已知直三棱柱ABC-A1B1C1的侧棱长为4,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( C ) 2(B)3 3(D)4解析:如图,不妨设N在B处,AM=h,CQ=m,则有MB2=h2+4,BQ2=m2+4,MQ2=(h-m)2+4,由MB2=BQ2+MQ2,得m2-hm+2=0.则Δ=h2-8≥0,即h2≥8,所以该直角三角形的斜边MB≥23.故选C.类型一几何体的表面积1.如图是一个封闭几何体的三视图,则该几何体的表面积为( C )(A)7π cm2(B)8π cm2(C)9π cm2(D)11π cm2解析:依题意,题中的几何体是从一个圆柱中挖去一个半球后所剩余的部分,其中圆柱的底面半径是1 cm、高是 3 cm,球的半径是1 cm,因此该几何体表面积等于12×(4π×12)+π×12+2π×1×3=9π(cm2).故选C.2.某三棱锥的三视图如图所示,该三棱锥的表面积是( B )(A)28+65(B)30+65(C)56+125(D)60+125解析:根据三棱锥的三视图可还原此几何体的直观图如图,此几何体为一个底面为直角三角形,高为4的三棱锥,因此表面积为S=12×(2+3)×4+12×4×5+12×4×(2+3)+12×5415 5故选B.类型二几何体的体积3.某几何体的三视图如图所示,它的体积为( C )(A)72π(B)48π(C)30π(D)24π解析:由三视图知该几何体是由一个半球和一个圆锥构成的组合体,所以其体积为V=12×43π×33+13π×32×4=30π.故选C.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A)π2(B)1+π2(C)1+π(D)2+π解析:由三视图可得,该几何体是一个长方体和半个圆柱的组合体,则该几何体的体积为V=12×2+12×π×12×2=2+π,故选D.5.(2018·全国Ⅲ卷)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为3则三棱锥D-ABC体积的最大值为( B )3333解析:由等边△ABC的面积为3323,所以AB=6,所以等边△ABC的外接圆的半径为r=33AB=23.设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则d=22R r-=1612-=2.所以三棱锥D-ABC高的最大值为2+4=6,所以三棱锥D-ABC体积的最大值为13×93×6=183.故选B.6.(2019·名校协作体模拟)某几何体的三视图(单位:mm)如图所示,则它的体积是cm3,表面积是cm2.解析:由三视图得该几何体底面是一个以上底为2,下底为4,高为3的直角梯形,高为33的四棱锥,则其体积为13×33×2+42×3=93(cm3),表面积为1 2×3×33+2+42×3+12×3×2+12×3×4+12×5×33=(18+63)(cm2).答案:93(18+63)7.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.解析:由题意知所给的几何体是棱长均为2的八面体,它是由两个有公共底面的正四棱锥组合而成的,正四棱锥的高为1,所以这个八面体的体积为2V 正四棱锥=2×13×(2)2×1=43.答案:43类型三 面积、体积综合问题8.(2018·浙江绍兴质量调测)已知一个几何体的三视图如图所示,则该几何体的体积是( A )(A)83 (B)8 (C)203(D)6 解析:如图所示,在棱长为2的正方体中,题中的三视图对应的几何体为四棱锥P-ADC 1B 1,其中P 为棱A 1D 1的中点,则该几何体的体积11P ADC B V -=211P DB C V -=211D PB C V-=2×13×11PB C S∆×DD 1=83. 故选A.9.已知球的直径SC=4,A,B是该球球面上的两点,AB=3,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( C )(A)33(B)23(C)3 (D)1解析:由题意知,如图所示,在棱锥S-ABC中,△SAC,△SBC都是有一个角为30°的直角三角形,且3,SC=4,所以3作BD⊥3×3)2×3. SC于D点,连接AD,易证SC⊥平面ABD,因此V=13故选C.。
如何计算圆柱体的表面积

如何计算圆柱体的表面积在我们的日常生活和学习中,经常会遇到各种各样的几何图形,圆柱体就是其中一种常见的形状。
比如我们喝的饮料罐、使用的铅笔、家里的柱子等等,很多都是圆柱体。
那你有没有想过,如何计算圆柱体的表面积呢?今天,咱们就一起来研究研究这个问题。
要计算圆柱体的表面积,首先得搞清楚圆柱体的构成。
圆柱体是由两个底面和一个侧面组成的。
底面是两个完全相同的圆,侧面则是一个曲面。
我们先来看看圆柱体的底面积怎么算。
圆的面积公式大家应该都很熟悉,那就是 S =πr² ,其中 S 表示面积,π 通常取 314 左右,r 表示圆的半径。
因为圆柱体有两个底面,所以圆柱体的两个底面积之和就是2πr² 。
接下来,就是圆柱体侧面的面积计算啦。
圆柱体的侧面展开后是一个长方形,这个长方形的长等于底面圆的周长,宽等于圆柱体的高。
底面圆的周长公式是 C =2πr ,所以侧面长方形的面积就是底面圆的周长乘以圆柱体的高,即2πrh 。
那么,圆柱体的表面积就等于两个底面积加上侧面积,用公式表示就是:S =2πr² +2πrh 。
为了让大家更清楚地理解这个公式,咱们来举个例子。
假设一个圆柱体的底面半径是 3 厘米,高是 10 厘米。
先算底面积:π 取 314 ,一个底面的面积就是 314×3²= 2826 平方厘米,两个底面的面积就是 2×2826 = 5652 平方厘米。
再算侧面积:底面圆的周长是 2×314×3 = 1884 厘米,侧面积就是1884×10 = 1884 平方厘米。
最后算表面积:表面积就是 5652 + 1884 = 24492 平方厘米。
在实际计算中,一定要注意单位的统一。
如果半径和高的单位不一致,要先把单位换算成相同的,再进行计算。
另外,还有一些特殊情况需要注意。
比如,如果圆柱体是无盖的,那么表面积就只需要计算一个底面积加上侧面积;如果圆柱体只有上盖或者只有下盖,那就要相应地调整计算的部分。
立体图形的表面积和体积计算“一点研究”错例分析及其解决策略

立体图形的表面积和体积计算“一点研究”错例分析及其解决策略平时我们强调数学教学要与现实生活相联系,要从学生的已有生活经验出发,引导学生通过观察、猜想、探讨等一系列学习活动,学习新知。
很可惜,由于学生的生活经验不足、空间想象能力差、老师讲解不清等因素的影响,造成学生在学习立体图形的表面积时总是出现种种错误。
实践表明,学生对形体特征掌握得精确与否,求表面积计算正确与否,很大程度上依赖于空间观念的积累水平。
下面笔者结合自己近期对长方体、正方体、圆柱体的表面积和体积计算的“一点研究”中遇到的错例及其解决策略,进行阐述。
一、概念不清晰,计算公式混淆小学阶段立体图形的表面积和体积的计算,由于学生审题不认真、空间观念不强等因素的影响,造成学生在计算时经常用错公式。
错例如:一台压路机的滚筒宽5米,直径1.8米。
如果它滚动20周,压路的面积是多少?1.8÷2=0.9(米)S=πr h=3.14×0.9×5=3.14×0.81×5=15.7×0.81=12.617(平方米)12.617×20=252.34(平方米)答:压路的面积是252。
34平方米。
学生访谈:师:这道题是求什么的?生:侧面积。
师:侧面积怎样算?生:底面周长乘高。
师:底面周长怎样算?错因分析:很明显学生对表面积和体积的意义理解不清。
长方体和正方体、圆柱体是一类最简单的立体图形,小学阶段有关长方体和正方体、圆柱体的题多数是体积、表面积的计算题,表面积和体积不仅含义不同,计量的单位也不同。
学生如果对表面积和体积的含义理解不深,计算起来很容易相互混淆。
另一方面由于学生生活经验较缺乏,也给理解题意带来一定的困难。
两个案例中都是把侧面积当成体积算了,反映了学生对物体表面积和体积概念的含义理解不清晰,造成计算公式混乱,而导致这些错误的内在原因还是学生空间观念没有真正建立起来。
解决策略:(一)动手制作,使学生分清图形的表面积和体积教授完表面积和体积后不妨多上一节图形的表面积和体积对比课。
清表面积计算

根据[公路工程国内招标文件范本]的要求(P38),即公路工程的统一标准,在合同中没有另外规定的,按照以下方法计量: 1、施工场地清理的计量应按监理工程师书面指定的范围进行验收后现场实地测量,按投影平面面积以平方米计量。
现场清理包括路基范围内的所有垃圾、灌木、竹林及胸径小于150mm的树木、石头、废料、表土(腐殖土)、草皮的铲除与开挖。
2、砍伐树木仅计胸径(即离地面处的直径)大于150mm的树木,以棵计量。
3、所有场地清理、拆除与挖掘工作的一切挖方、回填、压实,以及适用材料的移运、堆放、废料的移运处理等作业均不另行计量。
我这里是按平方米计量的,清场是按设计清场20cm厚。
清场不一定是30厘米,按设计图。
按投影面积计算。
我们这里计算投影面积是:挖方计算至顶边坡,填方至坡脚线,两侧为路肩墙的,只计算路肩墙内侧与地面线接触之间的投影面积。
清表回填的土方是要计量的,关键就看设计挖填方数量中是否包含了清表的开挖和回填,如果设计挖方中包含了清表挖方,则挖方工程量中要扣减清表挖方;如果设计填方中未包含清表的填方,则在填方工程量中要加上清表回填的土方。
一般设计的断面方中是不包含清表的,你可以核查一下路基横断面。
我们这清表是30CM,其实就按照设计的清表厚度计算清表量就行了。
标高是肯定要测的,因为你要比较下清表后高程和按理论的清表高程那个划算,当然高程高的对自己有利了。
至于原地面-设计高程,这个设计高程是什么高程原地面还是道路设计高程实际清表高程=实测原地面高程(业主认可后方有效)-清表后高程;理论清表高程=设计图纸上的原地面高程-设计清表厚度我原来在过的公路项目,对清除表土也是这样处理的(清单挖土方中扣除在填方中给相应的量),这也是主要参考《公路工程工程量清单计量规则》造价的人应对施工工序及管理有所了解才行,其实在承包人进场后,首先应对原地表进行复测,这叫定位.然后才进行清表施工,不管填挖地段均应进行清表,填方段清表后需要进行碾压,然后对填前地表标高进行复测(联测),这个是承包人填方量计算的基础,多翻翻技术规范多个章节的土石方计算规则,你就明了了.比较模糊的是挖方段的清表与挖方量的计算,应该是这个原则,同样的部位只能计量一次.1\如果你的挖方是以原地面复测为基础来计算的,则不应再计量清表数量.2\如果挖方地段的清表量已单独计量,则计算挖方应以清表后复测的标高为基础计算.3\两种方法,不一定对哪方有利,可以协商解决.没有硬性规定.楼上有很多网友说,清表后回填至原地面线的填方已计算填方单价中,这是根据概算有关说明中来的,与技术规范中的计量规则不相附.应将该部分工程量列入填方量内计量,也不能作为换填来计量,因为换填是针对填方地段,地表以下的非适用土而言的,也就是当清表达到30公以上,还存在非适用土的情况下,才适用这个.如果清单中的换填量,等于清表土的体各量,只能说明那个编制招标清单的人,水平太低了,没有实际经验.。
小学六年级【小升初】数学《立体图形的表面积专题课程》含答案

25. 立体图形的表面积知识要点梳理一、立体图形的切割1.立体图形每切割一次,增加两个面的面积。
2.立体图形每拼一次,减少两个面的面积。
二、表面积表面积:物体表面面积的总和叫做物体的表面积。
表面积通常用 S 表示,常用面积单位有平方千米、公顷、平方米、平方分米、平方厘米。
1.长方体、正方体的表面积为 6 个面的面积和。
2.圆柱的表面积=侧面积+2 个底面面积。
3.圆锥的表面积=侧面积+底面积三、立体图形的表面积计算公式考点精讲分析典例精讲考点1 长方体与正方体的表面积【例 1 】一个长 40 厘米,截面是正方形的长方体,如果长增加 5 厘米,表面积就增加80 平方厘米,原来长方体的表面积是多少?【精析】根据题意可知,一个长方体如果长增加 5 厘米,增加的80 平方厘米是 4个同样的长方形的面积和。
【答案】 80÷4÷5=4(厘米)0×4×4+4×4×2=672(平方厘米)答:原来长方体的表面积是672 平方厘米。
【归纳总结】根据长方体增加的面积,计算出长方体的宽和高,然后根据长方体的表面积计算公式解答即可。
【例2】学校新建一个游泳池,长50 米,宽 20 米,深 2 米。
这个游泳池占地面积有多大?如果游泳池的四壁和底面都要贴上瓷砖,一共需要贴多少平方米的瓷砖?【精析】此题主要考查长方体底面积及表面积的计算方法在实际生活中的应用。
解答时要清楚长方体游泳池的占地面积是指长方体的底面积。
贴瓷砖的面积,就等于游泳池的表面积减去上面的面积。
【答案】占地面积:50× 20= 1000(平方米)贴瓷砖的面积:( 50× 2+ 20× 2)×2+50× 20= 1280(平方米)答:这个游泳池占地面积有1000 平方米,共需要贴1280 平方米的瓷砖。
【归纳总结】这类题目解答时一般遵循下列步骤:①识别形体;②搞清问题(求表面积还是求体积、容积、求表面积涉及几个面);③回忆公式;④正确列式;⑤计算解答。
如何计算圆锥体的表面积

如何计算圆锥体的表面积在我们的日常生活和学习中,经常会遇到各种几何图形,圆锥体就是其中一种。
学会计算圆锥体的表面积,不仅能帮助我们解决数学问题,在实际生活中也有很多用处,比如制作圆锥形的帽子、灯罩等。
那么,到底如何计算圆锥体的表面积呢?下面就来详细说一说。
首先,我们要明确圆锥体的表面积是由两部分组成的,分别是侧面积和底面积。
圆锥体的底面积很好理解,就是一个圆的面积。
圆的面积公式我们都很熟悉,就是π乘以半径的平方。
如果圆锥体底面的半径用 r 表示,那么底面积 S 底就可以表示为 S 底=πr² 。
接下来,重点说一说圆锥体的侧面积。
圆锥体的侧面展开图是一个扇形。
要计算这个扇形的面积,我们需要先了解一些相关的概念和公式。
扇形的面积与它的圆心角和半径有关。
对于圆锥体侧面展开的扇形,其半径就是圆锥体的母线长度,我们用 l 来表示。
而扇形的圆心角的度数与圆锥体底面圆的周长和扇形的弧长有关。
我们先来说说圆锥体底面圆的周长。
圆的周长公式是2πr ,这里的r 还是底面圆的半径。
圆锥体侧面展开扇形的弧长就等于底面圆的周长,即2πr 。
那么,扇形的面积公式是 1/2 ×弧长 ×半径。
对于圆锥体侧面展开的扇形,其面积 S 侧就可以表示为1/2 × 2πr × l =πrl 。
现在,我们已经知道了圆锥体的底面积 S 底=πr² ,侧面积 S 侧=πrl ,那么圆锥体的表面积 S 表就等于底面积加上侧面积,即 S 表= S 底+ S 侧=πr² +πrl 。
这里要注意,母线 l 的长度可以通过圆锥体的高 h 和底面半径 r ,利用勾股定理计算得出。
假设圆锥体的高为 h ,母线 l 、高 h 和底面半径 r 构成一个直角三角形,根据勾股定理,l =√(r²+ h²) 。
为了让大家更清楚地理解如何计算圆锥体的表面积,我们来举个例子。
假设一个圆锥体,底面半径 r 为 3 厘米,高 h 为 4 厘米。
高速公路路基路面桥梁项目台账编制

0#台账编制基础(二)
• 按照分部分项工程单元划分迚行编制。
0#台账编制基础(二)
0#台账编制基础-工程量清单
0#台账编制
• 根据清单量 复核图纸量 确定 0#台账量 • 在做好了以上准备工作后,就可以建立excel
电子表栺来作为合同工程计量的电子台账WBS。在此表栺中,不合同文件中工程量清 单第100章~第700章中的各个清单编号、清 单项目完全一致。 • 编制好的0#台账如下:
路基填筑之路床掺灰
• 清单编号:204-1-d,204-1-e;单位:m3 • 设计图纸:
路基填筑之路床掺灰
• 设计图纸:
路基填筑之路床掺灰
• 204-1-d工程量计算: 每米路床掺灰处理上层面积=13.42*1=13.42 m2 每米路床掺灰处理下层面积=13.72*1=13.72 m2 灰土处理长度:1356m 路床掺灰处理工程量:1356*(13.42+13.72)*0.2=7360 m3 204-1-e低填下挖路段处理,工程量计算参照上述方法。 204-1-g锥坡及台前溜坡填土,一般采用设计图纸工程量。
软基处理之浆喷桩
软基处理之水泥土垫层
• 清单编号:205-1-h,单位:m3 • 相关设计图纸:
• 工程量拆分: • 205-1-h: 13598.2
软基处理之强夯
• 清单编号:205-1-o、p、q,单位:m2 • 相关设计图纸:
软基处理之强夯
• 相关设计图纸:
软基处理之强夯
• 工程量清单拆分:
(6)土土合成材料的计量、支付按第205节规定执行。 (7)渗井、检查井、雨水井的计量、支付按第314节规定执行。
排水工程之排水沟
• 清单编号:207-3、4,单位:m • 相关图纸:
zdm软件命令

fgdgx 网格划分
bgbz 标注设计标高地块编号
caltw 计算区域局部挖填方量
addbp 方格区挖填方量汇总
addtw 填挖方量累加
chbg 修改设计标高地块编号
chsx 修改挖填数字属性
tjtw 分类汇总挖填方量
chtw 修改设计高程重算挖填方量
addh 增、减纵断面表格行
zdmgl 曲线与曲线名称文字关联
getzdmbg 增加修改纵断面表格中标注
outzdm 表格文字输出到文本文件
zdmkw 按纵断面计算挖、填量
[数据文件生成横断面]
hddmz 给剖切线加高程点
whddm 获取剖切线断面数据文件
trandm 数据文件格式转换
ejl 墙线恢复
swin 边开窗门
mwin 中开窗门
awin 开弧窗
lwin1 二门铝合金窗
lwin2 三门铝合金窗
door1 单开门
door2 双开门
door3 卷廉门
sdt 平面梯、立面梯
[钢筋图]
gj1 画线钢筋
gj 线变钢筋
ofgj 偏移绘钢筋
wggj 网状布筋
zdmkw 按纵断面计算挖、填量
ppedit 减少、增加、移动线路特征点
cbh 移动编号位置
tran3dp 平面线路转三维线路
stls 断面沿线路拉伸实体
[渠道开挖]
inkwdm 插入设计断面块
qdkw1 梯形渠道开挖面积长度计算
qdqj 清表土面积计算
qdkw 给定梯形渠道尺寸计算开挖
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据[公路工程国内招标文件范本]的要求(P38),即公路工程的统一标准,在合同中没有另外规定的,按照以下方法计量:1、施工场地清理的计量应按监理工程师书面指定的范围进行验收后现场实地测量,按投影平面面积以平方米计量。
现场清理包括路基范围内的所有垃圾、灌木、竹林及胸径小于150mm的树木、石头、废料、表土(腐殖土)、草皮的铲除与开挖。
2、砍伐树木仅计胸径(即离地面1.3m处的直径)大于150mm的树木,以棵计量。
3、所有场地清理、拆除与挖掘工作的一切挖方、回填、压实,以及适用材料的移运、堆放、废料的移运处理等作业均不另行计量。
我这里是按平方米计量的,清场是按设计清场20cm厚。
清场不一定是30厘米,按设计图。
按投影面积计算。
我们这里计算投影面积是:挖方计算至顶边坡,填方至坡脚线,两侧为路肩墙的,只计算路肩墙内侧与地面线接触之间的投影面积。
清表回填的土方是要计量的,关键就看设计挖填方数量中是否包含了清表的开挖和回填,如果设计挖方中包含了清表挖方,则挖方工程量中要扣减清表挖方;如果设计填方中未包含清表的填方,则在填方工程量中要加上清表回填的土方。
一般设计的断面方中是不包含清表的,你可以核查一下路基横断面。
我们这清表是30CM,其实就按照设计的清表厚度计算清表量就行了。
标高是肯定要测的,因为你要比较下清表后高程和按理论的清表高程那个划算,当然高程高的对自己有利了。
至于原地面-设计高程,这个设计高程是什么高程?原地面?还是道路设计高程?实际清表高程=实测原地面高程(业主认可后方有效)-清表后高程;理论清
表高程=设计图纸上的原地面高程-设计清表厚度我原来在过的公路项目,对清除表土也是这样处理的(清单挖土方中扣除在填方中给相应的量),这也是主要参考《公路工程工程量清单计量规则》
造价的人应对施工工序及管理有所了解才行,其实在承包人进场后,首先应对原地表进行复测,这叫定位.然后才进行清表施工,不管填挖地段均应进行清表,填方段清表后需要进行碾压,然后对填前地表标高进行复测(联测),这个是承包人填方量计算的基础,多翻翻技术规范多个章节的土石方计算规则,你就明了了.比较模糊
的是挖方段的清表与挖方量的计算,应该是这个原则,同样的部位只能计量一次.1\如果你的挖方是以原地面复测为基础来计算的,则不应再计量清表数量.2\如果挖方地段的清表量已单独计量,则计算挖方应以清表后复测的标高为基础计算.3\两种方法,不一定对哪方有利,可以协商解决.没有硬性规定.楼上有很多网友说,清表后回填至原地面线的填方已计算填方单价中,这是根据概算有关说明中来的,与技术规范中的计量规则不相附.应将该部分工程量列入填方量内计量,也不能作为换填来计量,因为换填是针对填方地段,地表以下的非适用土而言的,也就是当清表达到30公以上,还存在非适用土的情况下,才适用这个.如果清单中的换填量,等于清表土的体各量,只能说明那个编制招标清单的人,水平太低了,没有实际经验.。
