变速恒频风力发电机组的无功功率极限
风力发电中的变速恒频技术综述

风力发电中的变速恒频技术综述1引言风力发电技术是一种利用风能驱动风机浆叶。
进而带动发电机组发电的能源技术。
由于风能储量丰富、用之不竭、无污染等特点,被各国广泛重视,纷纷投入大量的人力物力财力来发展风力发电技术。
第一次世界大战后,丹麦首开先河,制造了仿螺旋桨高速风力发电机组。
随后美国、法国、前西德等国先后制造出了风力发电机组并投入运行。
前西德在风机桨叶制造上首次使用了质地轻、强度高的复合材料。
到20世纪60年代,由于石油廉价和内燃机的广泛运用,风力发电成本高的问题显得突出,和以内燃机为动力的发电技术相比失去竞争力,发展几近停止。
但1973年全世界的石油危机以及燃料发电带来的环境污染问题,使得风力发电技术重新受到重视。
风力发电又进入迅速发展阶段。
先后有美国研制的1000kW大型风力发电机、前西德的3000kW大型风力发电机、英国加拿大的3800kW大型风力发电机投入运行,自动控制技术日益成熟,并形成了能并网运行的风力发电机群(见图1)。
2002年,世界各国风电装机总量达到近40000MW,并且每年增长率达20%,发展势头强劲。
我国现代风力发电技术始于20世纪70年代。
2002年底,我国风力发电装机容量达473MW,遍布新疆、内蒙古、广东、辽宁、浙江等地[1]。
图1风力发电机群最近世界风力发电技术的发展取得很大进步,主要表现为以下几点:(1)风力发电机单机容量稳步变大。
现在单机容量已达到兆瓦级;(2)变桨距调节成为气动功率调节的主流方式。
目前,绝大多数的风力发电机采用这种技术;(3)变速恒频发电系统迅速取代恒速恒频发电系统,风能利用更加有效;(4)无齿轮箱风力发电系统市场份额增长迅速。
这主要是由于没有齿轮箱系统效率显著提高[2]。
2 风力发电机的气动功率调节方式气动功率调节是风力发电的关键技术之一。
风力发电机组在超过额定风速以后,由于桨叶、塔架等的机械强度、发电机变频器等的容量限制,必须降低风机吸收功率,使其在接近额定功率下运行,同时减少桨叶承受的载荷冲击,使其不致受到损坏。
变速恒频风电机组额定风速以上恒功率控制

用的是 315 - 2DP) 系列可编程控制器作为整个电控 系统的控制核心 。S7 —300 控制器内部自带有连续 PID 控制器功能“CONT- C”,实际使用中我们只需要调 用“CONT- C”,并为其设定相关参数即可 。
系统程序的流程图如图 4 所示 。
图 4 程序流程图
6 结论
区域修改控制器的增益值 。
仿真用机组参数 :
角β↓。
风轮半径 :30. 325m ;额定风速 :11m/ s ;发电机额
(3) 风机叶片瞬时吸收的功率 Pmech和风能利用系
定功率 :1000kW ;风轮额定转速 :21. 5r ;发电机额定转 数 Cp 变化趋势显示了桨距角β的变化限制了叶片瞬
速 :1500r ;桨距角控制精度 :0. 2°。
2002 2 程静 ,王维庆 ,岳雷. 变速恒频风力发电机组的模糊控
制 ,新疆大学学报 ,2004 ,21 (1) :56 - 59 3 E. Muljadi , C. P. Butterfield. Pitch - controlled Variable -
speed Wind Turbine Generation. NREL ,2002
(5) 发电机转速 n 的波动受 ( Pmech - Pe ) 和机组的
惯性影响 。
(下转第 49 页)132005年第 Nhomakorabea3
变速恒频风力发电机空载并网控制

变速恒频风力发电机空载并网控制随着环境保护和可持续发展的重要性日益凸显,风力发电作为一种清洁、可再生的能源,得到了广泛应用。
在风力发电机组中,变速恒频风力发电机是一种常见的类型。
本文将重点探讨变速恒频风力发电机空载并网控制的原理、优缺点及应用。
变速恒频风力发电机组是一种通过风轮捕捉风能,并将其转换为电能的技术。
与恒速恒频风力发电机相比,变速恒频风力发电机具有更高的风能利用率和更宽的转速范围。
其工作原理是,通过调整风轮转速,以适应风速的变化,从而保持发电机输出频率的稳定。
空载并网控制是指风力发电机在不带负载的情况下与电网连接。
实现空载并网的关键在于控制风轮转速和发电机电流,以确保发电机与电网的同步。
常见的空载并网控制策略包括以下两种:直接并网法:在风速达到额定值后,风轮直接驱动发电机进入同步状态,然后进行并网。
此种方法简单直接,但并网瞬间会产生较大的冲击电流。
软并网法:通过控制风轮和发电机的转速,缓慢地将发电机接入电网,从而避免冲击电流的产生。
这种方法需要更多的控制环节和算法,但其并网效果较直接并网法更为平稳。
优点: a.由于能够适应风速的变化,所以具有较高的风能利用率; b.通过调整转速,可以减轻风轮和发电机的机械应力,提高设备的寿命;c.与恒速恒频风力发电机相比,其启动和停止更为灵活。
缺点: a.控制系统的设计较为复杂,需要精确的转速和电流控制; b.并网过程中可能产生较大的冲击电流,对电网造成一定的影响; c.需要采取措施来应对电网的波动,以保证系统的稳定运行。
变速恒频风力发电机空载并网控制在现代风力发电场中得到了广泛应用。
例如,根据某风力发电场的数据,采用变速恒频风力发电机空载并网控制后,该风电场的年发电量增加了30%,同时设备维护成本降低了20%。
这充分证明了变速恒频风力发电机空载并网控制在提高发电效率和降低运行成本方面的优势。
变速恒频风力发电机空载并网控制是风力发电技术中的重要一环。
通过控制风轮转速以适应风速的变化,保持发电机输出频率的稳定,可以实现高效的电能转换。
FD-1500-III风机介绍

风电机组推力曲线
FD-77/1500-IIIA Ct曲线
1.4 1.2
推力系数-Ct [.]
1 0.8 0.6 0.4 0.2 0
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
风速 [m/s]
偏航系统技术数据
偏航轴承
四点接触回转球支撑
上段35t 中段52t 下段74t
• 72m(轮毂高度74m)----仍在设计之中
• 66m(轮毂高度68m)
材质:Q345c~e
总重90t
上段23t 中段25t 下段42t
主要部件制造商
叶片 轮毂 主轴 底架 齿轮箱 发电机
新誉风电公司 无锡一汽 重庆齿轮厂 无锡一汽
变流器 德国阿尔斯通 主控制器 德国艾斯贝 变桨系统 德国艾斯贝 主要轴承 FAG LYC以及
跳闸温度 储存温度 海拔高度 冷却方式 功率因数 外形尺寸 设备供应
>85℃
-25~+65℃ 2000m以下 强制空冷 cap0.9~1~ind0.9 2606*605*2205
德国CONVERTEAM
电气主回路原理图
风电机组功率-效率曲线
FD-77/1500-IIIA功率-效率Cp曲线
1600 1400 1200
75m/s 80m/s 7.0 84m² 6.5t
原型及模具 设计及工艺
德国EUROS
德国EUROS
发电机技术数据
电机形式 4极双馈 异步发电机 额定功率 1560kW 工作电压 690V 定子电流 1088A 转子电流 388A 转速范围 1000~2000rpm 额定转速 1810rpm 额定扭矩 8207Nm 绝缘等级 安装方式 冷却方式 防护登记 接线方式 转子绕组 功率因数 电机效率 电机质量 F IMB3 IC616 IP54 定子Δ、转子Y 开路电压1924V 1左右 cap0.95~ind0.95 92.7~97.1% 7.7t
变速恒频双馈风力发电机的主要优点和基本原理

变速恒频双馈风力发电机的原理和优点研究摘要随着地球能源的日益紧缺,环境污染的日益加重,风能作为可再生绿色能源越来越被人们重视,风力发电技术成为世界各国研究的重点。
变速恒频发电技术是一种新型风力发电技术,其主要优点在于风轮以变速运行。
通过调节发电机转子电流的大小、频率和相位,从而实现转速的调节,可在很宽的风速范围内保持近乎恒定的最佳叶尖速比,进而实现追求风能最大转换效率;同时又可以采用一定的控制策略灵活调节系统的有功、无功功率,抑制谐波,减少损耗,提高系统效率。
而其与双馈发电机构成的风力发电系统的研究已经成为目前国际上风力发电的必然趋势。
关键词:风能,,风力发电,变速恒频,双馈发电机1 国内外风力发电现状风力发电作为一种无污染的清洁能源,日益受到各个国家的重视。
由于近年来电力电子技术发展的势头突飞猛进,尤其是计算机与控制技术的飞速发展,各国看到了风能的潜力,都在风能的开发利用上投入了大量的人力物力精力,风力发电的技术得到长足的进步和飞速发展。
机械、空气动力、计算机、自动控制、电力电子技术的发展和新领域的利用,促进了很多当初制约风力发电发展的一些技术难关的攻克,并且在各国政府的大力支持下,风电的时代已经来临。
预计到2020年,世界风电的装机容量将达到1231000MW,发电量约为30000亿KWh,风力发电将占世界发电总量的12%。
“风力12%”的蓝图,展示出风力发电已经成为解决世界能源问题的不可缺的重要力量。
风力发电不再是一种可有可无的补充能源,已经成为最具有商业化发展前景的成熟技术和新兴产业,有可能成为世界未来最重要的替代能源。
在欧洲,德国一直引领着世界风电市场的发展,他们制定了一个新的风电发展规划,到2025年风电至少占总用电量的25%。
丹麦、西班牙和法国的风电也在高速发展,其中西班牙和法国的风电装机容量以每年60%的速度增长,丹麦已成功用风电来满足国内18%的电力需求,是世界上风电贡献率最高的国家。
变速恒频风力发电技术综述

变速恒频风力发电技术综述摘要:随着世界经济的深入发展和国际工业化进程的加快,世界各国对能源的需求日益增加,能源消耗速度不断增长,煤炭、石油等常规能源逐渐枯竭。
为了缓解能源危机,人类越来越重视可再生能源的利用,而风能作为一种取之不尽、用之不竭、清洁无污染、具有大规模开发利用前景的能源,是可再生能源中最廉价、最具潜力的“绿色能源”。
风力发电是利用风能的一种有效形式,它通过风力发电机的旋转将风能转化为可以方便利用的电能。
利用风能发电由于其“环保节能”的特点,已经引起了许多国家的关注。
关键词:风力发电;风力机;变速恒频;发展趋势;风力发电正在以前所未有的速度发展,变速恒频风力发电是一门新技术。
介绍了风力发电机的组成和分类。
通过和恒速恒频风力发电机进行比较,分析了变速恒频风力发电技术的优点。
展望了风力发电的前景。
一、变速恒频风力发电技术的优点风力发电机主要由风力机、发电机和其他辅助部件组成。
大中型风力发电机组大多采用异步发电机,因为它制造简单,并网容易,励磁功率可直接从电网中获得。
风力机组主要有两种类型:定桨距失速型风力机和变桨距风力机。
定桨距失速型风力机利用风轮叶片翼型的气动失速特性来限制叶片吸收过大的风能,功率调节由风轮叶片来完成,对发电机的控制要求比较简单。
这种风力机的叶片结构复杂,成型工艺难度较大。
而变桨距风力机则是通过风轮叶片的变桨距调节机构控制风力机的输出功率。
由于采用的是异步发电机,无论是定桨距还是变桨距风力发电机,并网后发电机磁场旋转速度由电网频率所固定,异步发电机转子的转速变化范围很小,转差率一般为3%~5%,故属于恒速恒频风力发电机。
恒速恒频风力发电机的主要缺点有以下几点:一是风力机转速不能随风速而变,从而降低了对风能的利用率;二是当风速突变时,巨大的风能变化将通过风力机传递给主轴、齿轮箱和发电机等部件,在这些部件上产生很大的机械应力;三是并网时可能产生较大的冲击电流。
变速恒频风力发电技术是目前国内外风力发电技术的最优化方案,这是20世纪70年代发展起来的一种新型发电方式,它将电力电子技术、矢量变换控制技术和微机信息处理技术引入发电机控制之中,获得了一种全新的、高品质的电能获取方式。
变速恒频风电机组运行控制

ωref 根据电网给定发电功率由以下方程求解 :
Pref = ω Topt ref = f (ωref )ωref = h (ωref )
(5)
为避免求解方程 ,实际运行时 ,可将曲线 Pref =
h (ωref ) 存储在控制器中 。根据给定 Pref 反查曲线得
到ωref ,从而确定式 (4) 中的 g (ωr ) ,根据当前转速控
Tref = g (ωr ) = Pref ωr
ωr > ωref
(4)
式中 : Tref 为控制器输出电磁转矩参考值 ; g (ωr ) 为控
制函数 ; Topt 为最优运行电磁转矩 ; Pref 为指定发电
功率 ;ωr 为转子转速 ; Topt = f (ωr ) 为最优运行曲线 ;
ωref 为参考功率对应的最优转速 。
·绿色电力自动化 · 舒 进 ,等 变速恒频风电机组运行控制
态下风机捕获功率 。若该矩形为 Cmec8 上所有点中 面积最大者 ,则 B 点为风速 8 m/ s 的最优运行点 , 相应 ω2 为最优转速 。对于某一确定的风速仅有唯 一最佳运行点 。若使 D FIG 运行于各风速下最优运
变速恒频风力发电系统运行与控制研究

变速恒频风力发电系统运行与控制研究一、本文概述随着全球对可再生能源需求的不断增长,风力发电作为一种清洁、可再生的能源形式,在全球范围内得到了广泛的关注和应用。
变速恒频风力发电系统作为风力发电的一种重要形式,其运行与控制策略的研究对于提高风力发电的效率和稳定性具有重要意义。
本文旨在深入研究变速恒频风力发电系统的运行与控制技术,探讨其在实际应用中的性能表现和优化策略。
文章首先介绍了变速恒频风力发电系统的基本原理和组成结构,包括风力发电机组、变速恒频控制器、并网逆变器等关键部分。
然后,文章重点分析了变速恒频风力发电系统的运行特性,包括风速变化对系统运行的影响、最大功率跟踪策略的实现等。
在控制策略方面,文章详细探讨了变速恒频风力发电系统的控制技术,包括变速恒频控制、最大功率跟踪控制、并网控制等。
文章还分析了现有控制策略的优缺点,并在此基础上提出了一种优化的控制策略,以提高系统的运行效率和稳定性。
文章通过仿真实验和现场测试验证了所提控制策略的有效性和可行性,为变速恒频风力发电系统的实际应用提供了理论支持和技术指导。
本文的研究对于推动风力发电技术的发展,提高风力发电系统的运行效率和稳定性具有重要意义。
二、变速恒频风力发电系统基本原理变速恒频风力发电系统(Variable Speed Constant Frequency Wind Power Generation System, VSCF-WPGS)是一种新型的风力发电技术,其核心在于通过变速运行的风力发电机组,实现电网频率的恒定输出。
这一系统相较于传统的恒速恒频风力发电系统,具有更高的风能利用率和更好的电网适应性。
VSCF-WPGS的基本原理主要基于风力机、发电机以及控制系统的相互作用。
风力机通过风轮捕获风能,并将其转换为机械能。
由于风速的自然变化,风轮的转速也会相应变化,这就是所谓的“变速”特性。
接着,这种变化的机械能传递给发电机,通过电磁转换过程,将机械能进一步转换为电能。
浅谈变速恒频风力发电系统的运行和控制

浅谈变速恒频风力发电系统的运行和控制风力发电作为清洁能源发电,具有很大的发展潜力,能够在未来的电力行业中占据一席之地。
但是风力发电并入电网存在一定的技术难点,需要通过变速恒频实现风电系统和电网的高效互联,进一步提升风电系统的发展空间和能力。
一、风力发电系统变速恒频运行的技术基础探析风力发电系统在变速恒频运行模式下,随着外界风速的变化,风力机的转速也会随之对应出现变化,需要通过一定的控制手段,实现电能传输恒定,就是变速恒频的实质所在。
风力机功率的影响因素主要包括了三个,即叶尖转速比、桨叶节距角和风速。
根据相关资料可知,风力机功率的计算式为:;;;上述三个计算式中:为空气密度;R为风力机的风轮半径;为风轮的角速度;为风能利用系数。
可以看出,桨叶节距角以及叶尖转速比都可对风能利用系数产生较大的影响。
在桨叶节距角处于一个固定值时,就只有叶尖转速比对风能利用系数产生影响了。
对于风力机来说,其具有一个风能利用系数上限,也就是最大利用值,该值下对应的叶尖转速比是最佳值。
在变速恒频技术中,风力机在不同风速下具有不同的运转速度,可以有效切换运转速度追求风能最大转换。
风电系统变速恒频的运行方式非常适用,具有下面几个优点。
第一,变速恒频运行可以有效减少风力机受到阵风冲击的机械应力影响,可以在风速升高时把阵风余量转化为风力机的转动惯量;当外界风速出现下降的时候,又可以把转动惯量重新释放,通过一定的控制手段使其转为电能。
第二,电网和风电机组可以在变速恒频运行模式下进行柔性连接,有效削弱电网和风电系统之间存在的差异,切实降低并网后冲击电流引发的问题,保障电网运行安全。
除此之外,变速恒频的实现比较容易,是进行风电并网的不二选择。
第三,风力机在低风速条件下会产生噪音,但是变速恒频技术可以有效缓解这一问题。
在低风速情况下,风力机可以把存储的动能释放保证风力机的稳定运行,这就避免了风速较低情况下恒速运行产生的噪音。
总之,变速恒频运行已经得到国内外风电行业的一致认可,并且开始使用变速恒频取代恒速恒频,在提高发电效率和捕获风能等方面进行着深入研究。
1[1].5MW变速恒频控制技术
![1[1].5MW变速恒频控制技术](https://img.taocdn.com/s3/m/9653f822a21614791711289b.png)
一. 交流励磁发电机变速恒频运行原理1.风力机最大风能捕获运行机理风力是一种取之不尽,用之不竭的可再生能源,但又是一种具有随机性﹑爆发性﹑不稳定性特征的动力源,因而存在一个如何使用风力机实现风能的高效采集﹑高效利用的问题。
由空气动力学原理,通过叶轮旋转面的风能只能被风力机吸收一部分,可用风能利用系数C p 来描述: C p =P m / P w (Ⅰ—1)其中:P m 为风力机吸收且输出的机械功率;P w 为通过浆叶输入风力机的功率。
故系数C p 反映了风力机吸收利用风能的效率。
风力机的风能利用系数C p 与风力机的一个重要运行参数叶尖速比λ密切相关,如图Ⅰ—1所示。
叶尖速比即叶轮的叶尖线速度与风速之比,即λ=R Ω/V=R2πn/(60V) (Ⅰ—2)式中R 为叶轮的半径,Ω为叶轮旋转的角速度,n 为叶轮的转速,V 为风速。
风力机的风能利用系数C p 与叶尖速比密切相关,风能利用系数与叶尖速比的关系曲线如图Ⅰ—1所示。
从图中可以看出只有在一个特定的叶尖速比λm 下,风能利用系数才能达最大值C pmax ,即获得最大风能利用(捕获)。
风力机从风能中吸收的功率,即风力机的输出功率为:p m C SV P 321ρ= (Ⅰ—3) 式中ρ为空气密度,S 为风力机叶轮的扫掠面积, V 为风速。
对于一个确定的风力机,从不同的风速和转速查得对应的C p 值,计算出不同风速下的输出功率,获得不同风速下风力机输出功率和风力机轴转速之间的关系曲线,如图Ⅰ—2所示。
可以看出,不同风速下风力机输出机械功率随叶轮转速而变化,每一个风速下存在一个最大输出功率点P max ,对应于图Ⅰ—1的最大风能利用系数C pmax 。
将各个风速下的最大功率点连接成线,即可得到最佳功率曲线P opt ,运行在这条曲线上,风力机将会获得最大风能捕获,有最大功率输出P max式中n 为风力机轴转速,ωm 为风力机机械角速度。
由此可见,实现最大风能捕获的关键是控制风力机转速。
变速恒频风力发电机最大功率

!B!C!!
(S)
4D!CE!
(")
! D!C4B!C/
(T)
因为定子绕组接于无穷大电网,所以 E! 恒定
不 变 。 F!!C/,!!CE! G &!C常 数 。 可 以 得 出 方 程 :
6
B!C
!! 83
O
8B 83
6
B.
(!/)
<5BCO7I
8B 83
!!6 @.
(!!)
由此可知,只要控制了 6D.,6B. 就可以控制定
摘 要:分析了风能的特性,对双馈电机数学模型进行了分析与研究,在试验的基础上,基于最佳叶尖速比控 制(即风能最大利用率)和机械功率最大转化效率控制?提出了兆瓦级变 速 恒 频 双 馈 风 力 发 电 机 组 双 闭 环 的 一 种控制策略方案,并用 @’A)’( 软件进行系统仿真,证明该方案是可行的。 关键词:变速恒频;双馈电机;最佳叶尖速比 中图分类号:A@"!B 文献标识码:’ 文章编号:!"C!D0.>.(.//0)/.D//!"D/B
图 ! 发电机的不同风速下的运行方式
在这里我们假设采用双馈电机同步转速为
! $$$ 6 ) *78,调速范围为(9+%:),额定功率为 ;$$
’<。23 段为风力机并网后在额定风速以下的运行
情况,此时保持最佳叶尖速比 #=.>,即保证最大风能 利用率系数 -.*45,转速沿着 -.*45 曲线随着风速的增 大而增大,直到 3 点(此时电机转速大约为 ! #%$
6 ) *78)。从 3 点开始,风力机组的变桨系统开始运
行工作,一是为保证在旋转部件的机械强度范围之
内而留出一定的裕度,二是在变桨时,可以随高频
变速恒频双馈风力发电机的功率控制

3. 2 神经网络控制器的设计 双馈风力发电机采用的神经网络控制器是具有
两个输入和两个输出的单层结构 ,其结构见图 4.
3 基于模糊神经网络的功率解耦控制
图 4 神经网络控制器结构图
本文基于模糊神经网络的双馈风力发电机实现 有功功率和无功功率解耦控制的基本思路是 :通过
82
湖 北 工 业 大 学 学 报
2011 年第 3 期
目前引用最广泛的 B T 算法对双馈发电机的有功和
无功电流分量实现线性逼近 , 而要找到神经网络单
元的最优权值 ,就需要训练有功误差量和无功误差
量的目标函数最小项 , 然后对神经网络的控制器输
入量与最有权值进行线性组合 , 最终得到转子电压
81
1) 定 、转子电压方程 : ums = - Rs i ms - DΨms + Ψtsω1 , uts = - Rs i ts - DΨts - Ψmsω1 , umr = R r i mr + DΨmr - Ψtrωs , utr = R r i tr + DΨtr + Ψ ω mr s .
2) 定 、转子磁链方程 : Ψms = L s i ms - L m i mr , Ψts = L s i ts - L m i tr , Ψmr = L r i mr - L m i ms , Ψtr = L r i tr - L m i ts .
3) 转矩方程 :
Tem
=
3 2
N pL m
its i mr -
ims i tr
.
以上各式中 , ums , uts , umr , utr 分别为定 、转子电压的
m 、t 轴分量 ; ims , its , imr , itr 分别为定 、转子电流的 m 、t
变速恒频风力发电技术优势及应用探索

变速恒频风力发电技术优势及应用探索摘要:随着科学技术的进步以及工业生产的规模扩大,可供人类使用的能源日益减少,能源呈现出短缺紧张的现象。
所以借助先进的技术开发清洁能源、绿色能源、高效能源成为重点。
在能源开发过程中,变速恒频风力发电技术可在一定程度上降低研发成本,提高风力发电的效率及电能质量,研究价值极为突出。
关键词:变速恒频;风力发电技术;优势;应用前言随着社会的不断发展,对于电能需求量是越来越更多,为了更好的满足人们对于电能需求,加大了对风力发电开发。
风力发电具有无污染和使用周期长的特点,可以更好的对环境进行保护。
在风力发电中,电力发电机组安全运行在不断扩大,对于电能使用容量也是越来越大,通过变速恒频风力发电技术应用,可以更好的保证风力发电系统安全稳定运行,从而更好的促进我国风力发电的发展。
1风力发电技术的发展现状随着社会的不断发展,对于风力发电越来越重视。
风力发电很好的体现了人们对于自然资源有效利用,可以很好的通过机械能转化为电能。
在全球范围内风能源有很大潜力,但是我国对于风能利用还处于发展阶段。
级数比较大的风会对人们生活造成很大影响,如果通过先进技术可以对风能进行合理利用,可以更好的促进经济的发展。
在我国风能的利用中,在改革开放之前就开始了对风能利用的研究,在现阶段我国西北地区在风能利用已经取得了很大进步。
2变速恒频风力发电技术发展的重要性在风力发电中,风力发电机组要对风力发电的布局进行承担,承担着风力发电机组容量增大负荷,所以风力发电机组系统在风力发电中具有重要作用。
在风力发电系统中,机组容量在不断增加,风力发电机组配置中存在一些问题,所以对于风力发电机组设计优化具有重要意义,通过风力发电机组优化,可以提高风力发电机组性能,保证风力发电系统正常运行。
在风力发电中,通过变速恒频风力发电技术应用,可以保证风力发电机组安全稳定运行,对风力发电中转动系统具有重要作用。
3变速恒频风力发电技术重要性及其优势3.1变速恒频风力发电技术的重要性风力发电机组包括风轮与发电机,在发电工作中需要承担相应的负荷。
风电场详细信息参数表-双馈机型

2024年教师德能勤绩廉个人工作小结8篇篇1光阴似箭,日月如梭,转眼间,2024年已经过去,即将迎来充满希望的2024年。
回顾过去的一年,我在工作中认真履行职责,积极进取,努力提高自身素质,不断开拓创新。
为了更好地做好今后的工作,现将一年的工作总结如下:一、德作为一名教师,我深知师德的重要性。
在工作中,我始终以高尚的师德要求自己,遵守学校的各项规章制度,严于律己,以身作则,为人师表。
我热爱教育事业,热爱学生,尊重学生的人格和个性发展,注重培养学生的学习兴趣和创新能力。
我注重自身素质的提升,不断学习新知识,新技能,以适应教育教学的需要。
二、能在教学工作中,我始终以提高教学质量为目标,积极钻研教材教法,认真备课上课。
我注重培养学生的自主学习能力,注重激发学生的学习兴趣和积极性。
在教学方法上,我注重运用启发式、讨论式等教学方法,激发学生的学习兴趣和积极性。
同时,我不断探索新的教学方法和手段,如多媒体教学法、小组合作探究法等,以提高课堂效果和教学质量。
三、勤我深知教育工作的重要性和责任性。
在工作中,我始终以勤奋的态度对待工作,认真履行职责。
我注重与学生的交流和沟通,关注学生的成长和发展。
同时,我不断学习新知识、新技能,以适应教育教学的需要。
我积极参与学校组织的各项活动,为学校的发展贡献自己的力量。
四、绩在过去的一年中,我取得了显著的教学成果。
我所教班级的学生在各项考试中取得了优异的成绩,同时,我也获得了学校和家长的认可和好评。
此外,我还积极参与了学校的教育科研工作,取得了不错的成果。
五、廉作为一名教师,我深知廉洁自律的重要性。
在工作中,我始终保持清正廉洁的作风,严格遵守教师的职业道德和行为规范。
我注重自身形象的建设和维护,时刻保持清醒的头脑和坚定的立场。
同时,我也积极配合学校的反腐败工作,为学校的廉政建设贡献自己的力量。
总之,在过去的一年中,我取得了不错的成绩和收获。
在今后的工作中,我将继续努力提高自身素质和能力水平;继续探索新的教学方法和手段;注重与学生的交流和沟通;加强团队合作意识;为学校的发展贡献自己的力量。
变速恒频风力发电系统的运行与控制

变速恒频风力发电系统的运行与控制摘要:变速恒频风力发电系统在当今是发电系统中较为优良的一种发展方向。
本文针对当今在风力发电系统方面进行了一系列的讨论。
文章首先对风力发电系统的发展进行了简单的介绍说明,并对当今较为常见的风力发电系统进行了分析,阐述了不同种类风力发电系统的特点。
文章后半部分则对较为主要的变速恒频风力发电系统进行了分析讨论,对如何提高风力发电系统的运行与控制水平进行了讨论,对风力发电系统运行与控制工作的改进提供了一定的参考。
关键词:变速恒频;风力发电系统;运行控制前言:随着人们越发重视环保,在进行能源开发生产利用时,愈发倾向采用清洁能源,而风能便是当今具有良好发展前景的一种清洁能源,而且风能具有较多的开发手段,风能在我国西北部等地区储量较多,在进行开发利用时能够根据当地情况选择合适的利用方法其中利用风能进行发电是最为高效的一种能源生产措施。
不同结构的风力发电系统其发电水平以及具体的电力应用也会存在着一定的差异,其中变速恒频风力发电产生的电能较为稳定,对其运行控制进行研究分析有助于对变速恒频风力发电系统的应用进行推广。
1.风力发电系统概述1.1风力发电系统发展概况风力发电系统在当今是较为受关注的一个领域,主要是由于该领域的发展能够帮助人们进行更加高质量的能源开发,人们的生活已经离不开电力,如何进行电力的生产是较为重要的讨论内容。
传统的电力生产工作大多采用煤炭等各种化学能源产生相应的热能之后进行多次能量转换形成电能。
地球上的气体一直在流动,而流动的气体形成风之后也具有能量,在过去化学物质能源较为充足的时候,很少有人考虑进行风能的利用,相较于实体能源,风能无法直观的观察,因此比较容易受到人们的忽视,一直到上世纪西方一些发达国家出现能源危机后,指导化学能源有限不能永久使用,便开始进行新型能源的开发。
在进行新型能源开发时,也着重解决过去化学能源利用时常见的问题,包括污染以及对气候的影响等,因此在进行新型能源开发时大多从自然界中没有污染的方向获取能源,在对自然界进行勘察后,发现了水能太阳能和风能等一系列无污染可以利用能源,而如何进行利用便成了各国讨论的话题。
风力发电相关技术参数
风力发电相关技术参数链接:/tech/9080.html风力发电相关技术参数1、变速恒频系统可用于风力发电的变速恒频系统有多种:如交一直一交变频系统,交流励磁发电机系统,无刷双馈电机系统,开关磁阻发电机系统,磁场调制发电机系统,同步异步变速恒频发电机系统等。
这种变速恒频系统有的是通过改造发电机本身结构而实现变速恒频的;有的则是发电机与电力电子装置、微机控制系统相结合而实现变速恒频的。
它们各有其特点,适用场合也不一样。
为了充分利用不同风速时的风能,应该对各种变速恒频技术做深入的研究,尽快开发出实用的,适合于风力发电的变速恒频技术。
2、四级变速风力发电机原理多级变速风力发电机主要由2台发电机(发电机1和发电机2)、控制系统和变速机3部分组成,其技术原理如图所示。
大功率的发电机2的定子绕组与电网连接,向电网输送频率为ft的工频电流,转子绕组经控制系统与小功率的发电机1的定子绕组相连。
大功率的发电机2只有在风速较大(风机输入功率较大)时才和变速机联接运行。
发电机2输出的电流频率不仅和转子的机械转速有关,还和输入转子绕组的电流频率有关,具有将转子的机械旋转频率和转子绕组电路的电流频率“相加”的功能,其定子绕组输出“频率相加”后的电流,这一特点简称为“合频”特性。
四级变速风力发电技术利用改变发电机极对数及大小2个发电机的相互配合,达到在4个风速点都能实现风能最大利用,根据统计如果变速恒频风力发电在整个工作风速范围内风能利用量为1个单位,则四级变速风力发电风能利用量能达到80%左右,恒速恒频风力发电风能利用量约为40%。
3、双馈电机的控制双馈电机的结构类似于绕线式感应电机,定子绕组也由具有固定频率的对称三相电源激励,所不同的是转子绕组具有可调节频率的三相电源激励,一般采用交-交变频器或交-直-交变频器供以低频电流。
任何一个风力发电机组都包括作为原动机的风力机和将机械能转变为电能的发电机。
其中,作为原动机的风力机,其效率在很大程度上决定了整个风力发电机组的效率,而风力机的效率又在很大程度上取决于其负荷是否处于最佳状态。
变速恒频双馈风力发电机组控制技术

定义与特点
变速恒频双馈风力发电机组是一 种通过调节发电机转速来实现恒 频输出的风力发电系统,具有风 能利用率高、运行范围广等优点
。
工作原理
风力机将风能转化为机械能,通 过变速装置驱动双馈发电机运行 ,发电机输出的电能经过电力电
子装置调节后并入电网。
技术优势
变速恒频双馈风力发电机组具有 较宽的运行范围,能够适应不同 风速条件下的高效发电,提高风
06
结论与展望
研究结论与创新点总结
结论一
控制策略优化提升效率。通过对变速恒频双馈风力发电机 组的控制策略进行优化,可以显著提高机组的运行效率, 并降低能耗。
结论二
多变量控制实现稳定运行。引入多变量控制技术,有效应 对风力发电过程中的不确定性,提高机组的稳定性。
创新点
自适应控制算法。研发自适应控制算法,使机组能够根据 不同环境条件自动调整运行参数,提升发电效率。
控制参数调整:根据最大功率点的位 置,动态调整发电机的转速、励磁电 流等参数,以实现最大功率捕获。
功率曲线拟合:根据历史数据拟合风 速-功率曲线,确定当前风速下的最 大功率点。
这些控制策略在变速恒频双馈风力发 电机组中具有重要作用,能够提高风 力发电效率、保障电力系统稳定运行 ,并降低对环境的影响。
前景分析
随着全球对可再生能源需求的增长,变速恒频双馈风力发电机组控制技术将迎来更广阔的 发展空间。同时,政策的支持和市场的驱动将为该技术的发展提供有力保障。
THANKS
感谢观看
变速恒频双馈风 力发电机组控制 技术
汇报人:
2023-11-22
目录
• 引言 • 双馈风力发电机组的数学模型与
控制策略 • 变速恒频双馈风力发电机组的控
变速恒频风力发电机组输出特性分析

Journal
of
华北电力大学学报 Nort h China Electric Power
U niversity
Vol135 ,
J ul1 ,
No14 2008
变速恒频风力发电机组输出特性分析
胡冬良 , 赵成勇
(华北电力大学 电力系统保护与动态安全监控教育部重点实验室 , 河北 保定 071003) 摘要 : 以变速恒频风力发电系统为研究对象 , 依据发电机数学模型和交流电机矢量变换控制原理 , 设计了交 流励磁变速恒频 (VSCF) 发电机定子磁链定向的矢量变换控制系统 , 对转子侧变换器建立了外环定功率控制 内环定电流控制的双闭环控制结构 , 实现双馈发电机定子有功 P 和无功 Q 的解耦控制 , 从而获得最大风能捕 获的高效发电运行 。并在 PSCAD/ EM TDC 仿真环境下建立了变速恒频风力发电机组的整体动态数学模型 。以 渐变风和阵风为例 , 对由 5 台单机容量为 2 MVA 双馈感应电机 (DFIG) 组成的风电场并网前后的运行特性 进行仿真研究 , 通过仿真分析 , 揭示了风电场并网运行的动态特性 , 并验证了数学模型和控制策略的正确性 和有效性 。 关键词 : 变速恒频发电机组 ; 双馈感应电机 ; 矢量变换控制 ; 最大风能捕捉 中图分类号 : TM614 ; TP391 文献标识码 : A 文章编号 : 1007 - 2691 (2008) 04 - 0001 - 06
Abstract : The system of variable speed constant frequency (VSCF) wind power generation is taken as study object in t his paper. According to t he generator mat hematical models and t he control principle of vector2oriented , t he control system of AC excitation VSCF generator is designed based on stator flux orientation. The rotor converter adopts double locked loops control structure. Namely , t he external2loop is controlled by constant power and t he inner2loop is con2 trolled by constant current , which implement t he decoupling control of active power P and reactive power Q to t he stator. Consequently , t he maximal energy capture is obtained to operate wit h high2active power generation. Moreover , a whole dynamic model of double fed induction generator (DFIG) is presented using PSCAD/ EM TDC. Then t he ramp change of wind speed and gust are taken for example. The operation characteristic of wind farm interconnected net2 work , which is composed by five DFIG wit h 2 MVA capacity , is simulated. The interconnecting dynamic performance of wind farm is validated by simulation experiment . The results also show t he mat hematic model and control strategy is exact and effective. Key words : variable speed constant frequency ( VSCF) ; double fed induction generator (DFIG) ; vector transform control ; maximal energy capture
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变速恒频风力发电机组的无功功率极限申洪,王伟胜,戴慧珠(中国电力科学研究院,北京100085)摘 要:根据变速恒频风电机组的工作原理,建立了变速恒频风电机组的稳态数学模型,该模型考虑了风力机、双馈电机及其转速控制的稳态特性。
在此模型的基础上,提出了计算变速恒频风电机组无功功率极限的方法,并对一变速恒频风电机组进行了计算分析,验证了所提方法的可行性。
关键词:变速恒频风电机;双馈电机;无功功率极限1 引言近年来世界风力发电发展迅速,风电装机容量平均每年以高于20%的速度增长。
截止到2002年底,全世界风力发电装机容量约为31128MW,其中我国风电装机容量达468.42MW。
目前,兆瓦级风力发电机组已逐渐取代600kW级的机组,成为国际上风力发电机市场的主力机型,风电机组正向着大型化、变桨距和变速恒频的方向不断发展和完善。
虽然变速恒频风电机组与固定转速的风电机组相比在性能上有较大改善,但由于风速变化的随机性,变速恒频风电机组的并网运行对电力系统而言仍然是一种波动的冲击功率,因而必须对这种风电机组的并网运行特性进行研究。
变速恒频风电机组的发电机采用双馈感应电机,文献[1]~[3]对它的稳态模型进行了研究,建立了基于与定子磁场同步旋转的dq坐标系的数学模型。
因为双馈发电机的转速和定子侧的无功功率都可以调节,所以转速控制规律和无功功率控制规律对变速恒频风电机组的稳态特性也有很大的影响。
文献[1]、[2]介绍了转速控制和无功功率控制的基本思想,其中转速控制的目标是使风力机的功率系数最优,而无功功率控制则根据其接入的电力系统的实际运行方式可以设定为功率因数恒定或端电压恒定两种控制方式。
风电机组发出的有功功率主要取决于风速的大小,而无功功率则取决于风电机组的无功控制方案。
一般风电场位于偏远地区,电网结构薄弱,当无功功率控制的设定值达到风电机组的无功功率极限时,一方面转子绕组发热将导致风电机组停机,另一方面由于不能向系统中提供或吸收足够的无功功率,将导致端电压降低或升高,严重时将导致系统电压失稳。
因而研究变速恒频风电机组的无功功率极限是很有必要的。
文献[4]对此问题进行了一定的研究,但它只讨论了发电机定子绕组中有功功率和无功功率的稳态运行域问题,并没有解决整个风电机组注入系统的有功功率和无功功率的稳态运行域问题。
另外,该文献没有考虑转速控制规律的影响。
本文建立了变速恒频风电机组的稳态数学模型,在此模型基础上提出了计算无功功率极限的方法,该方法解决了风电机组注入系统的有功功率和无功功率稳态运行域问题,并且考虑了转速控制的影响。
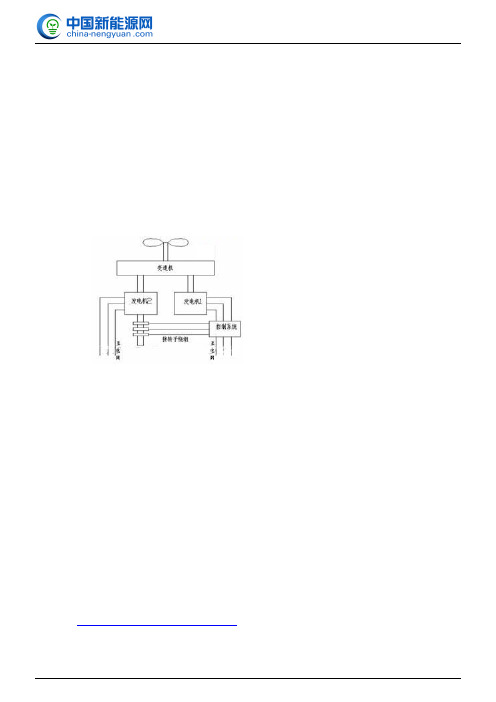
2 变速恒频风电机组的数学模型2.1 风力机的机械功率变速恒频风电机组采用双馈感应电机,与固定转速风电机组相比,增加了定子绕组与转子绕组之间的变频装置,其基本结构如图1所示。
风力机的机械功率PM 可以表示为式中Cp 是功率系数,它描述的是流过风力机的空气动能中转换的机械能所占的比例,是桨距角和叶尖速比λ 的函数(R 是叶片半径,W 是风力机转速);A 为叶片扫风面积;ρ为空气密度;v 为风速。
2.2 发电机模型双馈感应电机的稳态等值电路如图2所示[5]。
据图2可列出双馈感应电机的稳态数学模型采用在空间以同步转速旋转的dq坐标系统,在电机定子磁场定向矢量控制下[5],忽略定子电阻时有变流器在电机定子侧产生的无功功率可以通过调节触发角使功率因数约等于1。
由于变流器传输的有功功率比较小,变流器从系统中消耗的无功功率可以忽略不计,所以,风电机组注入系统的有功功率Pe为定子侧和转子侧有功功率的代数和,注入系统的无功功率Qe则主要由定子绕组的无功功率决定,即在稳态运行时,风电机组注入系统的有功功率Pe等于风力机的机械功率PM。
当风速一定时,Pe可通过式(1)求得。
2.3 转速控制规律模型变速恒频风电机组的转子转速控制规律是指风电机的转速与风力机的机械功率或机械转矩的对应关系。
不同变速恒频风电机组生产厂商设计和采用的转速控制规律有所区别,其中通常采用的转速控制规律如图3所示。
该风力机转速控制规律可用分段函数表示为(7)式中Prating为额定功率;功率P1、P2、P3是由风力机参数决定的;kopt 是由风力机叶片参数决定的系数[6],它可以保持风力机功率系数最优;wmin为风力机转速下限;wmax为风力机转速上限;wr为发电机同步速对应的风力机转速。
3 变速恒频风电机组的无功功率范围风电机组注入系统的有功功率为定子绕组的有功功率和转子绕组的有功功率之和。
在次同步速运行方式下,转子绕组吸收有功;超同步速运行方式下,转子绕组发出有功。
转子绕组的有功功率可以由式(8)求得[5]。
定子侧有功功率和无功功率运行范围受定子绕组、转子绕组和变流器转子侧的电流限制影响,但其中起主要作用的是变流器转子侧的电流限制[4],可以表示为式中Irmax 为变流器电流限制值,一般为变流器额定电流的150 % [6]。
将式(6)分别代入式(8)和式(9),可得式(10)为一空间曲面方程,其在Pe -Qe 平面的投影就是变速恒频风电机组的无功功率限制范围。
当风电机组的有功功率Pe 在0~Prating 之间变化时,相应的无功功率极限可以由式(10)求得。
4 算例分析选取额定功率为800kW的变速恒频风电机组,感应电机的参数为:rs=4.52mΩ;xs=74.3mΩ;rr=4.34mΩ;xs=53.6mΩ;xm=1.09mΩ;机端电压为690V;额定功率因数为-0.98。
它的风功率特性示于表1。
发电机调速范围为-30%至+22%。
其转速控制规律如图3所示,其中wmin=0.7wr;wmax=1.22wr;kopt=0.75;Prating=800kW;P1=198kW;P2=576kW;P3=656kW。
风电机组注入系统有功功率变化时,其无功功率极限变化曲线如图4所示。
可以看出,该曲线不是规则曲线,这是因为当风电机组注入系统有功功率Pe变化时,转差率s将按照图3所示的控制规律变化,则式(10)中第1个方程式中的参数将随之变化,导致曲线发生不规则变化。
图中,位于上半平面的曲线表示风电机组发出无功功率的极限,下半平面的曲线表示吸收无功功率的极限。
当风电机组端电压变化时,它的无功功率极限也随之变化。
机端电压越高,它发出的无功功率极限越低,可以吸收的无功功率极限越大。
从式(10)的第2式可以看出,当变流器电流限制一定时,风电机组的无功功率极限取决于定子绕组有功功率。
图5所示为风电机组定子侧有功功率随风电机组注入系统有功功率变化情况。
当风电机组注入系统有功功率达到一定值时,定子绕组有功功率将维持恒定,因而此时图4中风电机组的无功功率极限也将维持恒定。
5 结论根据变速恒频风电机组的结构和工作原理,本文建立了变速恒频风电机组的稳态数学模型,并提出了一种计算变速恒频风电机组的无功功率极限的方法,该方法能够计算出风电机组注入系统的有功功率和无功功率运行范围。
应用本文提出的方法对一台800kW的变速恒频风电机组进行了计算分析,计算结果表明:(1)变速恒频风电机组定子侧无功功率可以在一定范围内进行调节,其调节范围随定子侧有功功率而变化,并受风电机组转子转速和转子侧功率变化情况的影响;(2)在考虑了风电机组的转速控制以后,其稳态功率运行范围边界是一簇随机端电压变化的不规则曲线。
该方法可用于确定变速恒频风电机组的无功功率控制整定值。
另外,在电力系统潮流计算中,可以将变速恒频风电机组处理为PV 节点,应用该方法能确定变速恒频风电机组的无功功率极限。
当风电机组发出的无功功率超过无功功率极限时,其节点属性将从PV 节点转换为PQ 节点。
参考文献[1] Muljadi E,Butterfield C P.Pitch-controlled variable speed wind turbinegeneration[R].IEEE Industry Applications Society,Annual Meeting,Phonenix,Arizona,1999.[2] Refoufi L,Al Zahawi B A T,Jack A G.Analysis and modeling of the steady state behavior of static kramer induction generator[J]. IEEE Transactions on Energy Conversion,1999,14(3):333-339.[3] 邱培基,汤宁平,叶文键,等(Qiu Peiji,Tang Ningping,Ye Wenjian et al).变速交流励磁感应发电机的稳态分析(Steady-state analysis of variable-speed ac-excited induction generator)[J].电工技术学报(Transactions of China Electrotechnical Society),1998,13(5):16-20.[4] Tapia A,Tapia G,Ostolaza X et al.Modeling and dynamic regulation of a wind farm[R].Power Electronics Congress,2000,CIEP 2000.VII IEEE International,2000.[5] 高景德,王祥珩,李发海.交流电机及其系统的分析[M].北京:清华大学出版社,1993.[6] Pena R,Clare J C,Asher G M.A doubly fed induction generator usingback-to-back PWM converters supplying an isolated load from a variable speed wind turbine[J].IEE Proc-Electr Power Appl,1996,143(5):380-387.[7] 现代机械设备设计手册(2)——机电系统与控制[M].北京:机械工业出版社,1996.电网技术。
