理论力学题库第五章
理论力学课后答案第五章(周衍柏)上课讲义

理论力学课后答案第五章(周衍柏)第五章思考题5.1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5.3广义动量a p 和广义速度a q 是不是只相差一个乘数m ?为什么a p 比a q 更富有意义?5.4既然a q T ∂∂是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d 是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了aq T ∂∂项?你能说出它的物理意义和所代表的物理量吗?5.5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5.6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个是独立的?5.7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5.8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动和无阻尼时有何不同?能否列出它们的微分方程?5.9 dL 和L d 有何区别?a q L ∂∂和aq L ∂∂有何区别? 5.10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5.11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5.12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5.13哈密顿原理是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5.14正则变换的目的及功用何在?又正则变换的关键何在?5.15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5.17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动定律相比较,并加以评价.第五章思考题解答5.1 答:作.用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的.即时位置变更,故虚功也是假想的、符合约束的、无限小的.且与过程无关的功,它与真实的功完全是两回事.从∑⋅=iii r F W δδ可知:虚功与选用的坐标系无关,这正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分.在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力,这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2 答 因拉格朗日方程是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标,它不一定是长度,可以是角度或其他物理量,如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11 知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度,则αθ一定是力,若αθ是力矩,则αq 一定是角度,若αq 是体积,则αθ一定是压强等.5.3 答 αp 与αq 不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
理论力学题库第五章

C拉格朗日函数与哈密顿函数得变量不同;
D拉格朗日方程与哈密顿正则方程就是分析力学中两个基本得方程,不能相互推演。
5-4、 分析力学得特点中,正确得有:【C】
A分析力学就是对力学体系得分析过程得理论;
B分析力学中系统得广义坐标一定与系统得空间坐标有关;
10、如果质点系质心在某轴上得坐标保持不变,则D
(A)作用在质点系上所有外力得矢量与必恒等于零;
(B)开始时各质点得初速度均必须为零;
(C)开始时质点系质心得初速度必须为零;
(D)作用在质点系上所有外力在该轴上投影得代数与必恒等于零,但开始时质点系质心得初速度并不一定等于零。
11、图示三个均质圆盘A、B、C得重量均为P,半径均为R,它们得角速度得大小、转向都相同。A盘绕其质心转动,B盘绕其边缘上O轴转动,C盘在水平面上向右滚动而无滑动。在图示位置时,A、B、C三个圆盘得动量分别用KA、KB、KC表示,则C
A广义速度可以就是线速度,也可以就是其她得物理量;
B广义动量就就是动量;
C 广义动量等于系统得广义速度乘以系统得质量;
D 广义动量得增量等于力对时间得冲量。
5-8、 关于虚功指得就是【B】
A 当质点发生位移时力所作得功;
B 质点在约束可能范围内发生虚位移时力所作得功 ;
C 虚力在质点发生位移时所作得功;
5-5、虚位移就就是假想得、符合约束条件得、无限小得、即时得位置变更。
5-6、稳定约束情况下某点得虚位移必在该点曲面得切平面上。
5-7、理想、完整、稳定约束体系平衡得充要条件就是主动力虚功之与为零、
5-8、有效力(主动力 + 惯性力)得总虚功等于零。
北航理论力学第五章习题解答
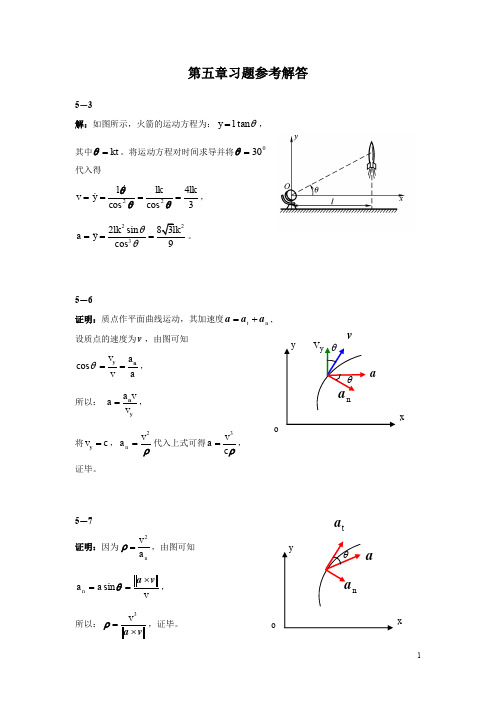
l x2 l 2
x
2
2 2 v0 l 0 。将其代入直角坐标形式的 , y x3
运动微分方程可得: F m( g
2 2 v0 l l ) 1 。 3 x x
5-11
vB
O A
x
(a)
B O r
x
vA
A
(b)
2
解:假设绳子与圆盘的切点为 B,绳子相对圆盘无滑动,故 vB r 。如图(b)所示,绳 子始终处于拉直状态,因此绳上 A、B 两点的速度在 A、B 两点连线上的投影相等,即
ve
va
vr
va ve vr
如图(a)所示。将上式在垂直于 O1A 杆的轴上, 以及在 O1C 轴上投影得 (a)
va cos 30 0 ve cos 30 0 , va cos300 vr cos300
ve va R , va vr R , 1
根据加速度合成定理有
aC 2vr 8r 2 。根据加速度合成定理 aa ae ar aC
ae M
O
ar B
aC
A (b)
aa
x'
将上式在 x ' 轴上投影,可得: aa cos ae cos aC
,
由此求得: aa 14r 2 。
5-21 解:求汽车 B 相对汽车 A 的速度是指以汽车 A 为参考 系观察汽车 B 的速度。 动点:汽车 B; 动系:汽车 A( Ox' y' ) ; 定系:路面。 运动分析 绝对运动:圆周运动; 相对运动:圆周运动; 牵连运动:定轴转动(汽车 A 绕 O 作定轴转动) 。 求相对速度 根据速度合成定理
理论力学题库

2014级理论力学期末考试试题题库理论力学试题第一章物系受力分析画图题1、2、3、4、5、第二章平面汇交力系计算题1、2、4、6、第三章平面任意力系计算题1、2、6、7、8、第四章空间力系计算题1、2、3、4、5、6、第五章静力学综合填空题1、作用在刚体上某点的力,可以沿着其作用线移动到刚体上任意一点,并不改变它对刚体的作用效果。
2、光滑面约束反力方向沿接触面公法线指向被约束物体。
3、光滑铰链、中间铰链有1个方向无法确定的约束反力,通常简化为方向确定的 2 个反力。
4、只受两个力作用而处于平衡的刚体,叫二力构件,反力方向沿二力作用点连线。
5、约束力的方向与该约束所能阻碍的位移方向相反 .6、柔软绳索约束反力方向沿绳索 ,指向背离被约束物体.7、在平面内只要保持力偶矩和转动方向不变,可以同时改变力偶中力的大小和力臂的长短,则力偶对刚体的作用效果不变。
8、力偶的两个力在任一坐标轴上投影的代数和等于零,它对平面内的任一点的矩等于力偶矩,力偶矩与矩心的位置无关。
9、同一平面内的两个力偶,只要力偶矩相等,则两力偶彼此等效.10、平面汇交力系可简化为一合力 ,其大小和方向等于各个力的矢量和,作用线通过汇交点.11、平面汇交力系是指力作用线在同一平面内 ,且汇交与一点的力系.12、空间平行力系共有 3 个独立的平衡方程.13、空间力偶对刚体的作用效果决定于力偶矩大小、力偶作用面方位、力偶的转向三个因素。
14、空间任意力系有 6 个独立的平衡方程.15、空间汇交力系的合力等于各分力的矢量和,合力的作用线通过汇交点 .第五章静力学综合摩擦填空题1、当作用在物体上的全部主动力的合力作用线与接触面法线间的夹角小于摩擦角时,不论该合力大小如何,物体总是处于平衡状态,这种现象称为自锁现象.2、答案:50N3、答案:φm/24、静摩擦力Fs的方向与接触面间相对滑动趋势的方向相反,其值满足__0<=F S<=F MAX摩擦现象分为滑动摩擦和__滚动摩阻__两类。
2021年新版理论力学题库

理论力学题库一一第五章一、填空题1.限制力学体系中各质点自由运动条件称为________________ 。
质点始终不能脱离约束称为___________ 约束,若质点被约束在某一曲面上,但在某一方向上可以脱离,这种约束称为 _____________ 约束。
2.受有抱负约束力学体系平衡充要条件是__________________ ,此即_______ 原理。
3.基本形式拉格朗日方程为 ___________________________ ,保守力系拉格朗日方程为_________________________-4.若作用在力学体系上所有约束力在任意虚位移中所作虚功之和为零,则这种约束称为__________ 约束。
5.哈密顿正则方程详细形式是 ________________ 和 ______________ 05-1.力个质点构成系统如有个约束,则只有3n _ k个坐标是独立.5-2.可积分运动约朿与几何约朿在物理实质上没有区别,合称为完整约束.5-3自由度可泄义为:系统广义坐标独立变分数目,即可以独立变化坐标变更数5-4. r义坐标就是拟泄力学体系空间位置一组独立址标。
5-5.虚位移就是假想、符合约束条件、无限小、W_位程变更。
5-6.稳定约束状况下某点虚位移必在该点曲面切平而I:。
5-7.抱负、完整、稳泄约束体系平衡充要条件是积极力虚功Z和为零•5-8.有效力(积极力+惯性力)总虚功等于壬。
5-9. r义动量时间变化率等于广义力(或:枳极力+拉氏力)。
5-10.简正坐标可以使系统动能和势能分別用广义速度和广义坐标平方项表达。
5-11 •勒让徳变换就是将一组独立变数变为另一组独立变数变换。
5-12•勒让徳变换可表述为:新函数等于不要变量乘以原函数对该变量偏微商和,再减去原函数。
5-13. r义能量积分就是_t_为循环坐标时循环积分。
5T4.泊松定理可表述为:若卩(Gp,f)=C],0g,p,/) = C2是止则方程初积分,则[卩,#] = °3也是正则方程初积分.5-15•哈密顿正则方程泊松括号表达为:p a=[p a,H] : q a=[q a,H]。
理论力学(周衍柏)的习题集答案,第五章.doc

第五章习题解答5.1解如题5.1.1图杆受理想约束,在满足题意的约束条件下杆的位置可由杆与水平方向夹角所唯一确定。
杆的自由度为1,由平衡条件:即mg y =0①变换方程y=2rcos sin-= rsin2②故③代回①式即因在约束下是任意的,要使上式成立必须有:rcos2-=0④又由于cos=故cos2=代回④式得5.2解如题5.2.1图三球受理想约束,球的位置可以由确定,自由度数为1,故。
得由虚功原理故①因在约束条件下是任意的,要使上式成立,必须故②又由得:③由②③可得5.3解如题5.3.1图,在相距2a的两钉处约束反力垂直于虚位移,为理想约束。
去掉绳代之以力T,且视为主动力后采用虚功原理,一确定便可确定ABCD的位置。
因此自由度数为1。
选为广义坐。
由虚功原理:w①又取变分得代入①式得:化简得②设因在约束条件下任意,欲使上式成立,须有:由此得5.4解自由度,质点位置为。
由①由已知得故②约束方程③联立②③可求得或又由于故或5.5解如题5.5.1图按题意仅重力作用,为保守系。
因为已知,故可认为自由度为1.选广义坐标,在球面坐标系中,质点的动能:由于所以又由于故取Ox为零势,体系势能为:故力学体系的拉氏函数为:5.6解如题5.6.1图.平面运动,一个自由度.选广义坐标为,广义速度因未定体系受力类型,由一般形式的拉格朗日方程①在广义力代入①得:②在极坐标系下:③故将以上各式代入②式得5.7解如题5.7.1图又由于所以①取坐标原点为零势面②拉氏函数③代入保守系拉格朗日方程得代入保守系拉格朗日方程得5.8解:如图5.8.1图.(1)由于细管以匀角速转动,因此=可以认为质点的自由度为1.(2)取广义坐标.(3)根据极坐标系中的动能取初始水平面为零势能面,势能:拉氏函数①(4),代入拉氏方程得:(5)先求齐次方程的解.②特解为故①式的通解为③在时:④⑤联立④⑤得将代回式③可得方程的解为:5.9解如题5.9.1图.(1)按题意为保守力系,质点被约束在圆锥面内运动,故自有度数为2. (2)选广义坐标,.(3)在柱坐标系中:以面为零势能面,则:拉氏函数-①(4)因为不显含,所以为循环坐标,即常数②对另一广义坐标代入保守系拉氏方程③有得④所以此质点的运动微分方程为(为常数)所以5.10解如题5.10.1图.(1)体系自由度数为2.(2)选广义坐标(3)质点的速度劈的速度故体系动能以面为零势面,体系势能:其中为劈势能.拉氏函数①(4)代入拉格郎日方程得:②代入拉格郎日方程得③联立②,③得5.11 解如题5.11.1图(1)本系统内虽有摩擦力,但不做功,故仍是保守系中有约束的平面平行运动,自由度(2)选取广义坐标(3)根据刚体力学其中绕质心转动惯量选为零势面,体系势能:其中C为常数.拉氏函数(4)代入保守系拉氏方程得:对于物体,有5.12解如题5.12.1图.(1)棒作平面运动,一个约束,故自由度. (2)选广义坐标(3)力学体系的动能根据运动合成又故设为绕质心的回转半径,代入①得动能②(4)由③(其中)则④因为、在约束条件下任意且独立,要使上式成立,必须:⑤(5)代入一般形式的拉氏方程得:⑥又代入一般形式的拉氏方程得:⑦⑥、⑦两式为运动微分方程(6)若摆动角很小,则,代入式得:,代入⑥⑦式得:⑧又故代入⑧式得:(因为角很小,故可略去项)5.13解如题5.13.1图(1)由于曲柄长度固定,自由度.(2)选广义坐标,受一力矩,重力忽略,故可利用基本形式拉格朗日方程:①(3)系统动能②(4)由定义式③(5)代入①得:得5.14.解如题5.14.1图.(1)因体系作平面平行运动,一个约束方程:(2)体系自由度,选广义坐标.虽有摩擦,但不做功,为保守体系(3)体系动能:轮平动动能轮质心转动动能轮质心动能轮绕质心转动动能.①以地面为零势面,体系势能则保守系的拉氏函数②(1)因为不显含,得知为循环坐标.故=常数③开始时:则代入得又时,所以5.15解如题5.15.1图(1)本系统作平面平行运动,干限制在球壳内运动,自由度;选广义坐标,体系摩擦力不做功,为保守力系,故可用保守系拉氏方程证明①(2)体系动能=球壳质心动能+球壳转动动能+杆质心动能+杆绕中心转动动能②其中代入②得以地面为零势面,则势能:(其中为常数)(3)因为是循环坐标,故常熟③而代入①式得④联立③、④可得(先由③式两边求导,再与④式联立)⑤⑤试乘并积分得:又由于当5.16解如题图5.16.1.(1)由已知条件可得系统自由度.(2)取广义坐标.(3)根据刚体力学,体系动能:①又将以上各式代入①式得:设原点为零势能点,所以体系势能体系的拉氏函数②(1)因为体系只有重力势能做工,因而为保守系,故可采用③代入③式得即(5)解方程得5.17解如题5.17.1图(1)由题设知系统动能①取轴为势能零点,系统势能拉氏函数②(2)体系只有重力做功,为保守系,故可采用保守系拉氏方程.代入拉氏方程得:又代入上式得即③同理又代入上式得④令代入③④式得:欲使有非零解,则须有解得周期5.18解如题5.18.1图(1)系统自由度(2)取广义坐标广义速度(3)因为是微震动,体系动能:以为势能零点,体系势能拉氏函数(4)即①同理②同理③设代入①②③式得欲使有非零解,必须解之又故可得周期5.19解如题5.19.1图(1)体系自由度(2)取广义坐标广义速度(3)体系动能体系势能体系的拉氏函数(4)体系中只有弹力做功,体系为保守系,可用①将以上各式代入①式得:②先求齐次方程③设代入③式得要使有非零,必须即又故通解为:其中又存在特解有②③式可得式中及为积分常数。
理论力学第五章
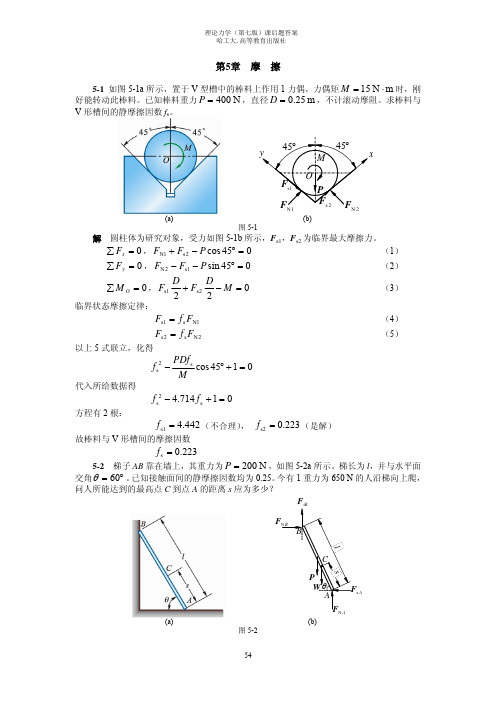
∑ Fx = 0 , F = FsE + FsA , FsE = f s FNE , FsA = f s FNA FsE = FsA , F = 2 FsA 2h ∑ME = 0,F − FsA h − FNA ⋅ bmin = 0 3
综上化得
b 4h − h − min = 0 3 fs
56
理论力学(第七版)课后题答案 哈工大.高等教育出版社
2 R = O1O2 = KD = CD = O1 A = KL = O2 L = 0.5 m , O1 B = 0.75 m ,AC = O1 D = 1 m , ED = 0.25 m ,求作用于鼓轮上的制动力矩。
′ FEK K FN 2 FO2 x
θ
FEK θ ′ FDx FOy FOx
E FDy
5-5 门高为 h 。 若在门上 不计自重的拉门与上下滑道之间的静摩擦因数均为 f s ,
2 h处 3
用水平力 F 拉门而不会卡住,求门宽 b 的最小值。问门的自重对不被卡住的门宽最小值是 否有影 (b)
E
Fs E FN E
解 (1)不计自重时受力如图 5-5b 所示 ∑ Fy = 0 , FNE = FNA
F 较大时,滑块 B 滑动趋势与图 c 相反,即摩擦力 Fs 与图 c 所示相反,则此时式(1) , (4) 不变,式(2)变为
' FAB sin θ − F cos β + Fs = 0
式(1) , (4)代入上式,得
M M sin θ − F cos β + f s + f s F sin β ) = 0 l cosθ l M (tan θ + f s ) = F (cos β − f s sin β ) l M (tan θ + f s ) F= l (cos β − f s sin β ) 同样令 f s = tan ϕ ,则 M sin(θ + ϕ ) F= l cosθ cos( β + ϕ ) M sin(θ − ϕ ) M sin(θ + ϕ ) ≤F≤ l cos θ cos( β − ϕ ) l cos θ cos( β + ϕ ) 5-7 轧压机由两轮构成,两轮的直径均为 d = 500 mm ,轮间的间隙为 a = 5 mm ,两 轮反向转动,如图 5-7a 上箭头所示。已知烧红的铁板与铸铁轮间的摩擦因数 f s = 0.1 ,问
理论力学简明教程第五章答案

第五张 刚体力学平动中见彼此,转动中见分高低.运动美会让你感受到制造的乐趣.走过这遭,或许会有曾经沧海难为水的感叹.别忘了,坐标变换将为你迷津救渡,同时亦会略显身手.【要点分析与总结】1 刚体的运动(1)刚体内的任一点的速度、加速度(A 为基点)A r υυω'=+⨯()()A d r a a r dtωωω'⨯'=++⨯⨯ (2)刚体内的瞬心S :()21s A A r r ωυω=+⨯〈析〉ω为基点转动的矢量和,12ωωω=++A r r r '=+dr dtυ=*A A A dr dr d r r r dt dt dt υωυω''''=+=++⨯=+⨯ ()A d r d d a dt dt dtωυυ'⨯==++()r ωω'⨯⨯ 值得注意的是:有转动时r '与r ω'⨯的微分,引入了r ω'⨯与()r ωω'⨯⨯项。
2 刚体的动量,角动量,动能 (1)动量:c P m υ=(2)角动量: x x xx xy xz i i i y yxyy yz y zx zyzz z z L J J J L r m L J J J J J J J L ωυωωω⎛⎫⎛⎫⎛⎫-- ⎪ ⎪⎪=⨯===-- ⎪ ⎪ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭∑式中:转动惯量()()()222222xx yy zz J y z dmJ z x dm J x y dm ⎧=+⎪⎪=+⎨⎪=+⎪⎩⎰⎰⎰惯量积xx yy zz J xydm J yzdm J zxdm ⎧=⎪⎪=⎨⎪=⎪⎩⎰⎰⎰且c c cL r m L υ'=⨯+* l e 方向(以l 为轴)的转动惯量:(),,l l J e J e J ααβγβγ⎛⎫ ⎪== ⎪ ⎪⎝⎭222222xx yy zz yz zx xy J J J J J J αβγβγγααβ=++---(,,αβγ别离为l e 与,,x y z 轴夹角的余弦) * 惯量主轴惯量主轴能够是对称轴或对称面的法线若X 轴为惯量主轴,那么含X 的惯量积为0,即: 0==xy xz J J 若,,x y z 轴均为惯量主轴,那么:xx yy zz L J i J j J k =++ 〈析〉成立的坐标轴轴应尽可能的是惯量主轴,如此会降低解题繁度。
理论力学第五章习题答案
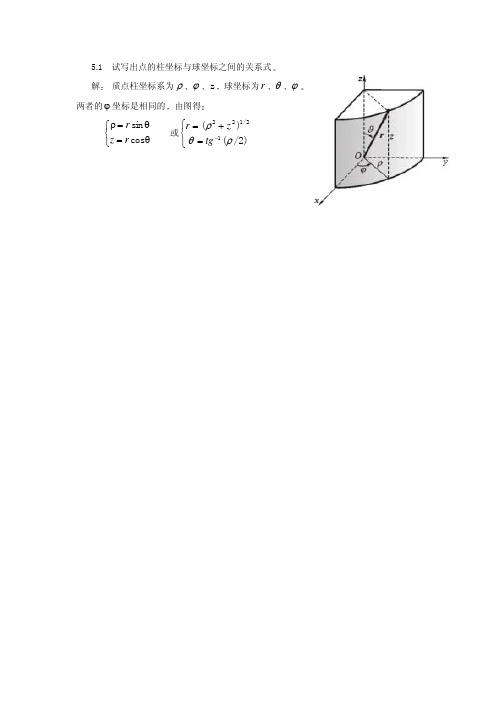
& = ak sin kt y
得
积分得 s = 4a (1 − cos
kt ) 2
5.3
根据下列点在极坐标系中的轨迹方程
试写出点的直角坐标轨迹方程
式中 p
e 均为正的常数
1
ρ=
p 1 + e cos ϕ p 1 − e cos ϕ p 1 − cos ϕ
e <1
2
ρ=
e >1
3 解
ρ=
直角坐标与极坐标有以下关系:
与 前 题 相 比 仅
e 差 一 符 号
→ (1 − e 2 ) x 2 + y 2 − 2 pex − p 2 = 0
3
ρ=பைடு நூலகம்
p 1 − cos ϕ
与 前 题 相 比
只 要 令 前 题 中 e =1 即 可
→ y 2 − 2 px − p 2 = 0
5.4 加速度 解
试以直角坐标及其导数表示 x = a ( kt − sin kt ) 切向加速度 法向加速度以及轨迹的曲率半径
sin γ = Rω / v
则由式 (**) 得 ρ = v / Rω = R / sin γ
2
2
2
5.8
如图所示
飞机 P 在任一时刻的经度为 ψ (t )
纬度为 λ (t )
高度为 h(t )
其在
地心坐标系中的球坐标运动方程为
r = R + h(t )
其中 R 是地球半径
θ = π / 2 − λ (t )
5.1 解
试写出点的柱坐标与球坐标之间的关系式 质点柱坐标系为 ρ
ϕ
z 球坐标为 r θ
ϕ
两者的 ϕ 坐标是相同的
理论力学课后答案第五章

第五章思考题5、1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点与缺点? 5、2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5、3广义动量a p 与广义速度a q &就是不就是只相差一个乘数m ?为什么a p 比a q &更富有意义?5、4既然aq T &∂∂就是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d &就是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了a q T ∂∂项?您能说出它的物理意义与所代表的物理量不?5、5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5、6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个就是独立的?5、7什么叫简正坐标?怎样去找?它的数目与力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5、8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动与无阻尼时有何不同?能否列出它们的微分方程?5、9 dL 与L d 有何区别?a q L ∂∂与aq L ∂∂有何区别? 5、10哈密顿正则方程能适用于不完整系不?为什么?能适用于非保守系不?为什么? 5、11哈密顿函数在什么情况下就是整数?在什么情况下就是总能量?试祥加讨论,有无就是总能量而不为常数的情况?5、12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5、13哈密顿原理就是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5、14正则变换的目的及功用何在?又正则变换的关键何在?5、15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤、5、16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5、17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5、18分析力学学完后,请把本章中的方程与原理与牛顿运动定律相比较,并加以评价、第五章思考题解答5、1 答:作、用于质点上的力在任意虚位移中做的功即为虚功,而虚位移就是假想的、符合约束的、无限小的、即时位置变更,故虚功也就是假想的、符合约束的、无限小的、且与过程无关的功,它与真实的功完全就是两回事、从∑⋅=ii i r F W ρρδδ可知:虚功与选用的坐标系无关,这正就是虚功与过程无关的反映;虚功对各虚位移中的功就是线性迭加,虚功对应于虚位移的一次变分、在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这就是虚位移无限小性的结果、虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这就是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标与广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性、由于虚功方程中不含约束反力、故不能求出约束反力,这就是虚功原理的缺点、但利用虚功原理并不就是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件与约束反力、5.2 答 因拉格朗日方程就是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程就是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力、这里讨论的就是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正、广义坐标市确定质点或质点系完整的独立坐标,它不一定就是长度,可以就是角度或其她物理量,如面积、体积、电极化强度、磁化强度等、显然广义坐标不一定就是长度的量纲、在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以就是力也可以就是力矩或其她物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11ρρ知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲、若αq 就是长度,则αθ一定就是力,若αθ就是力矩,则αq 一定就是角度,若αq 就是体积,则αθ一定就是压强等、5.3 答 αp 与αq &不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
《理论力学》第五章-桁架与摩擦试题及答案
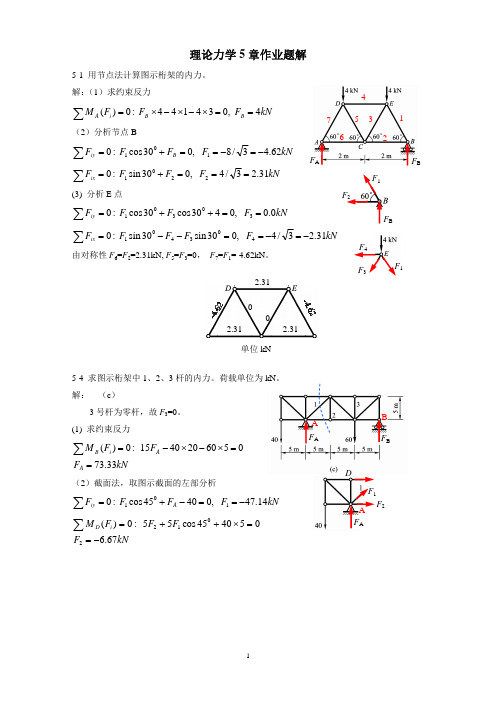
5-1 用节点法计算图示桁架的内力。
解:(1)求约束反力
r
å M A (Fi ) = 0 : FB ´ 4 - 4´1- 4´ 3 = 0, FB = 4kN
(2)分析节点 B
å Fiy = 0 : F1 cos300 + FB = 0, F1 = -8 / 3 = -4.62kN
F4 F3 F2 F1
δ δδδ FN4 FN3 FN2 FN1
附图(a)
FN4 δ F4
取脱离体钢管,示力图为(b),仅给出 4 号管的示力图。
r
å M D (Fi ) = 0 : FN 4 ´ 2d - F4 ´ 2r = 0 ⑶
同理对 3、2、1 号管可有:
FN3 ´ 2d - F3 ´ 2r = 0 ⑷ FN 2 ´ 2d - F2 ´ 2r = 0 ⑸ FN1 ´ 2d - F1 ´ 2r = 0 ⑹ 联合求得:W ´ 2d - F ´ 2r = 0 , F = 0.1kN 。
å Fix = 0 : F1 sin 300 + F2 = 0, F2 = 4 / 3 = 2.31kN
4
7
53
1
6
2
FA
FB
F1
(3) 分析 E 点
F2
å Fiy = 0 : F1 cos300 + F3 cos300 + 4 = 0, F3 = 0.0kN
FB
å Fix = 0 : F1 sin 300 - F4 - F3 sin 300 = 0, F4 = -4 / 3 = -2.31kN
木箱所需的水平力 F 。若不用钢管而使木箱直接在木板上移动,已知木箱与木板的摩擦因数
《理论力学》第5-9章习题参考解答
《理论力学》第7章-习题解答
D
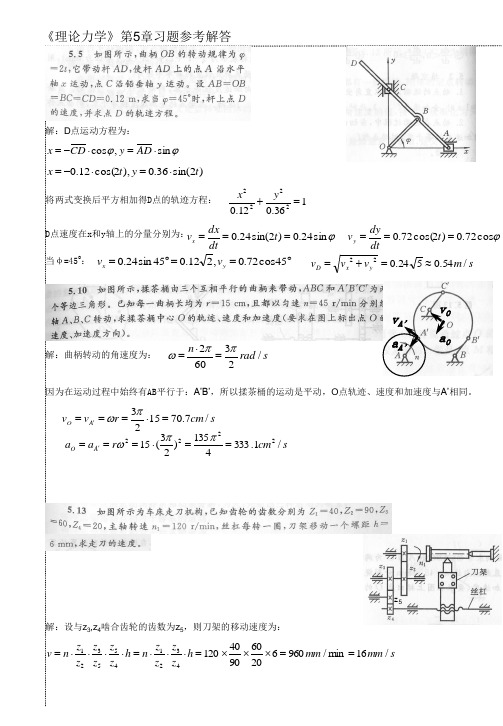
dϕ π 解:OA转动的角速度为 ω = = (rad / s ), v A = OA ⋅ ω = 0.05π (m / s ) dt 3 7π π 当s=7s时: ϕ = = 2π + , OB = OA = 0.15(m) 3 3 2 2 BD = OB tan ϕ = 0.15 3 (m), O1 B = O1O + OB = 0.25(m) BD v A = 0.05 3π (m / s ) 根据vA和vB可以确定AB的速度瞬心在D点: vB = OA
r F
a
r F
a
FN
图a
r G
FN
图b
r G
解:①当加速度较小时,物块A会有向下滑的趋势,受力图如图a,动力学方程为:
G 2 2 a = FN −F (1) g 2 2 2 2 0=F + FN − G (2) 2 2 1− f 联立(1)(2)(3)求得: a≥ g 1+ f
其中:
F ≤ FN f
ωOC
解:设杆AB上的A点为动点,摇杆OC为动系,则由速度合成定理得:
r r r v A = vr + ve
其中:
vA = v
r ac
r aA r ar rτ ae
r ve
α OC
r vA
r vr
将矢量方程分别在ve 和vr方向投影得:
Hale Waihona Puke r aenvr = v A sin ϕ = v sin 45°, ve = v A cos ϕ = v cos 45° v v cos 45° v 所以摇杆OC的角速度为: ωOC = e = = (方向如图所示) L OA 2L cos 45° r rτ r n r r 由加速度合成定理得:a A = ae + ae + ar + ac L v 2 v2 v 2v 2 2 n 其中: a A = 0, ae = OA ⋅ ωOC = ( ) = , ac = 2ωOC vr = 2 v sin 45° = cos 45° 2 L 2L 2L 2 2L rτ 2v 2 将矢量方程在 ae 方向投影得: τ 2 a 2L = v 2 α 所以OA的角加速度为: OC = e = 2v τ L OA 2 L2 0 = aτ − ac , ae = ac = e 2L cos 45°
北师大理论力学习题答案5第五章思考题

图s5.4 第五章 非惯性系中的质点力学思5.1答:这种说法不正确。
于某时将质点与S'系就地固连(就地固连是指若在另一时刻,质点相对S'系的位置将发生变化,质点就需固连于S'系中另一位置),由于S'系的运动而引起的质点相对于S 系的运动称为牵连运动。
思5.2答:'υ对S '系确有一定的依赖关系,因为若没有S'系,就不存在质点相对于S'系的速度。
但这种依赖关系并不意味着,对于除S'系以为的其它参考系(如S 系)'υ就不存在。
在选定两个参考系(S 和S'系)后,'υ这个客观存在的矢量既可以向S'系(O'x'y'z')投影,也可以向S 系(Oxyz )投影;随着时间的推移,'υ相对于S'系会发生改变,相对于S 系也会发生改变;因此当然可以求相对速度'υ的绝对变率。
思5.3答:这种说法不对。
应注意t υ和t a 的存在,并不说明质点真的被S'系带着以这个速度和加速度运动,它是假设质点与S'系就地固连后产生的对S 系的速度和加速度。
思5.4答: ω为P 点相对S'绕O 点作圆周运动的角速度,而不是S'系的角速度,ω是相对变率,当然对于ω,其相对变率与绝对变率总是相等的。
0a 为牵连加速度,()''⨯+⨯⨯ωr ωωr 为相对加速度 Oxyz 为平动坐标系 0∴=ω P 点相对S'系的速度''=⨯υωr ω是P 点相对S'绕O 点作圆周运动的角速度 t c '∴=++a a a a ()*0d 2d ''t=++⨯⨯υa ωωr 0''=⨯+⨯+ωr ωr a()0''=⨯+⨯⨯+ωr ωωr a思5.5答:若选择与圆盘固连的O'x'y'z'为S'系,则P 点相对S'的相对速率为0'=υ,S 系的角速度为ω()0''∴=+⨯+⨯⨯a a ωr ωωr其中ω为S'系的角速度的相对变率,ω为S'系的角速度。
理论力学试题题目含参考答案

理论力学部分第一章 静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
( )2.两端用光滑铰链连接的构件是二力构件。
( )3.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
( )4.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
( )5.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
( )6.约束反力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
( )二、选择题1.若作用在A 点的两个大小不等的力1F 和2F ,沿同一直线但方向相反。
则其合力可以表示为 。
① 1F -2F ;② 2F -1F ;③ 1F +2F ;2.三力平衡定理是 。
① 共面不平行的三个力互相平衡必汇交于一点;② 共面三力若平衡,必汇交于一点;③ 三力汇交于一点,则这三个力必互相平衡。
3.在下述原理、法则、定理中,只适用于刚体的有 。
① 二力平衡原理; ② 力的平行四边形法则;③ 加减平衡力系原理; ④ 力的可传性原理;⑤ 作用与反作用定理。
4.图示系统只受F 作用而平衡。
欲使A 支座约束力的作用线与AB 成30︒角,则斜面的倾角应为________。
① 0︒; ② 30︒;③ 45︒; ④ 60︒。
5.二力A F 、B F 作用在刚体上且0=+B A F F ,则此刚体________。
①一定平衡; ② 一定不平衡;③ 平衡与否不能判断。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
3.作用在刚体上的两个力等效的条件是。
4.在平面约束中,由约束本身的性质就可以确定约束力方位的约束有,可以确定约束力方向的约束有,方向不能确定的约束有(各写出两种约束)。
理论力学课后习题参考答案第5章
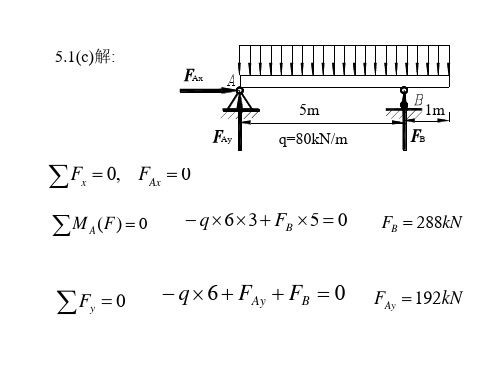
40kNm D 2m
FD
F
y
0
FA FB FD Q2 0 FA 15kN
5.24a解: 对于BC梁:
M
B
(F ) 0
q 6 3 FC 4 0
FC 18kN
整体:
FAx 0
y
F
M
0
(F ) 0
FAy FC q 6 0
M F 0 :
x
FA AD Q ED Gl cos 0
1 FA a sin 60 100 a sin 60 30 3.5cos 30 0 3 FA 12.3kN
M
y
(F) 0
FB BD FC CD G l sin 0
a a FB FC 30 3.5sin 30 0 2 2
(a)
F
z
0, FB FC FA Q G 0
FB FC 12.3 100 30 0 (b)
联立求解(a)(b)两式得:
FB 48.3kN FC 69.4kN
5.23(b) 题解:
5.16解
z
,, z
5 cm 0
M
M
z
(F ) 0
F2 0
z,
0m 0c 1
z, y ,4 5 y 6 x , 3
(F ) 0
1
2
F4 0
x
M
z ,,
(F ) 0
F6 0
z
,, z
5 cm 0
M
x,
(F ) 0
F 50 F1 50 0
胡汉才编著《理论力学》课后习题答案第5章习题解答

5-1 凸轮以匀角速度ω绕O 轴转动,杆AB 的A 端搁在凸轮上。
图示瞬时AB 杆处于水平位置,OA 为铅直。
试求该瞬时AB 杆的角速度的大小及转向。
解: r e a v v v += 其中,22e r v e -=ωe v v e a ωφ==tg所以 le l v a AB ωω==(逆时针)5-2. 平底顶杆凸轮机构如图所示,顶杆AB 可沿导轨上下移动,偏心圆盘绕轴O 转动,轴O 位于顶杆轴线上。
工作时顶杆的平底始终接触凸轮表面。
该凸轮半径为R ,偏心距e OC =,凸轮绕轴O 转动的角速度为ω,OC 与水平线成夹角ϕ。
求当︒=0ϕ时,顶杆的速度。
(1)运动分析轮心C 为动点,动系固结于AB ;牵连运动为上下直线平移,相对运动为与平底平行直线,绝对运动为绕O 圆周运动。
(2)速度分析,如图b 所示5-3. 曲柄CE 在图示瞬时以ω0绕轴E 转动,并带动直角曲杆ABD 在图示平面内运动。
若d 为已知,试求曲杆ABD 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e av v v +=0a 2ωl v =;0e a 2ωl v v ==01e1ωω==AO v BC O (顺时针) 5-4. 在图示平面机构中,已知:AB OO =1,cm 31===r B O OA ,摇杆D O 2在D 点与套在AE 杆上的套筒铰接。
OA 以匀角速度rad/s 20=ω转动,cm 332==l D O 。
试求:当︒=30ϕ时,D O 2的角速度和角加速度。
解:取套筒D 为动点,动系固连于AE 上,牵连运动为平动 (1)由r e a v v v += ① 得D 点速度合成如图(a ) 得 ϕtg e a v v =, 而r v e 0ω= 因为 r v a 0331ω⨯=,所以 rad/s 67.02==lv aD O ω 方向如图(a)所示(2)由r e na a a a a a +=+τ ②得D 点加速度分析如图(b ) 将②式向DY 轴投影得θϕϕτsin sin cos e n a a a a a -=-错了 而r a la e D O n a 2022ωω==θϕsin sin r l =所以ϕθϕτcos sin sin e na a a a a -=2rad/s 05.2cos sin sin 2-=-==ϕθϕετl a a l a e n a a DO 什么东西?,方向与图(b)所示相反。
理论力学参考答案第5章

理论力学参考答案第5章第5章摩擦· ·47· 47·第5章摩擦一、是非题正确的在括号内打“√”、错误的打“×” 1静滑动摩擦力与最大静滑动摩擦力是相等的。
× 2最大静摩擦力的方向总是与相对滑动趋势的方向相反。
√ 3摩擦定律中的正压力即法向约束反力是指接触面处物体的重力。
× 4当物体静止在支撑面上时支撑面全约束反力与法线间的偏角不小于摩擦角。
× 5斜面自锁的条件是斜面的倾角小于斜面间的摩擦角。
√ 二、填空题1当物体处于平衡时静滑动摩擦力增大是有一定限度的它只能在0≤Fs≤Fsmax范围内变化而动摩擦力应该是不改变的。
2静滑动摩擦力等于最大静滑动摩擦力时物体的平衡状态称为临界平衡状态。
3对于作用于物体上的主动力若其合力的作用线在摩擦角以内则不论这个力有多大物体一定保持平衡这种现象称为自锁现象。
4当摩擦力达到最大值时支撑面全约束反力与法线间的夹角为摩擦角。
5重量为G的均质细杆AB与墙面的摩擦系数为0.6f如图5.12所示则摩擦力为0。
6物块B重2kNP物块A重5kNQ在B上作用一水平力F如图5.13所示。
当系A之绳与水平成30角B与水平面间的静滑动摩擦系数s102f.物块A与B之间的静滑动摩擦系数s2025f.要将物块B拉出时所需水平力F的最小值为2.37kN。
A CB G A B F 图5.12 图5.13 ·48·理论力学·48·三、选择题1如图5.14所示重量为P的物块静止在倾角为的斜面上已知摩擦系数为sfsF为摩擦力则sF的表达式为B 临界时sF的表达式为 A 。
A sscosFfP B ssinFP C sscosFfP D ssinFP NF P sF 图5.14 2重量为G的物块放置在粗糙的水平面上物块与水平面间的静摩擦系数为sf今在物块上作用水平推力P 后物块仍处于静止状态如图5.15所示那么水平面的全约束反力大小为C 。
理论力学题库第五章

理论力学题库——第五章一、填空题1. 限制力学体系中各质点自由运动的条件称为 。
质点始终不能脱离的约束称为 约束,若质点被约束在某一曲面上,但在某一方向上可以脱离,这种约束称为 约束。
2. 受有理想约束的力学体系平衡的充要条件是 ,此即 原理。
3. 基本形式的拉格朗日方程为 ,保守力系的拉格朗日方程为 。
4. 若作用在力学体系上的所有约束力在任意虚位移中所作的虚功之和为零,则这种约束称为 约束。
5. 哈密顿正则方程的具体形式是 和 。
5-1. n 个质点组成的系统如有k 个约束,则只有 3n - k 个坐标是独立的. 5-2.可积分的运动约束与几何约束在物理实质上没有区别,合称为 完整约束 .5-3自由度可定义为:系统广义坐标的独立 变分数目 ,即可以独立变化的 坐标变更数 . 5-4.广义坐标就是确定力学体系空间位置的一组 独立坐标 。
5-5.虚位移就是 假想的 、符合约束条件的、无限小的、 即时的 位置变更。
5-6.稳定约束情况下某点的虚位移必在该点曲面的 切平面上 。
5-7.理想、完整、稳定约束体系平衡的充要条件是 主动力虚功之和为零 . 5-8.有效力(主动力 + 惯性力)的总虚功等于 零 。
5-9.广义动量的时间变化率等于 广义力 (或:主动力+拉氏力)。
5-10.简正坐标能够使系统的动能和势能分别用 广义速度 和 广义坐标 的平方项表示。
5-11.勒让德变换就是将一组 独立 变数变为另一组 独立 变数的变换。
5-12.勒让德变换可表述为:新函数等于 不要的变量 乘以原函数对该变量的偏微商的 和 ,再减去原函数。
5-13.广义能量积分就是 t 为循环坐标时的循环积分。
5-14. 泊松定理可表述为:若是正则方程21),,(,),,(c t p q c t p q ==ψϕ的初积分,则[]3c ,=ψϕ 也是正则方程的初积分.5-15.哈密顿正则方程的泊松括号表示为: ],[H p pαα= ; ],[H q q αα= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学题库——第五章一、填空题1.限制力学体系中各质点自由运动的条件称为。
质点始终不能脱离的约束称为约束,若质点被约束在某一曲面上,但在某一方向上可以脱离,这种约束称为约束。
2.受有理想约束的力学体系平衡的充要条件是,此即原理。
3.基本形式的拉格朗日方程为,保守力系的拉格朗日方程为。
4.若作用在力学体系上的所有约束力在任意虚位移中所作的虚功之和为零,则这种约束称为约束。
5.哈密顿正则方程的具体形式是和。
5-1. n个质点组成的系统如有k个约束,则只有3n - k个坐标是独立的.5-2.可积分的运动约束与几何约束在物理实质上没有区别,合称为完整约束.5-3自由度可定义为:系统广义坐标的独立变分数目,即可以独立变化的坐标变更数. 5-4.广义坐标就是确定力学体系空间位置的一组独立坐标。
5-5.虚位移就是假想的、符合约束条件的、无限小的、即时的位置变更。
5-6.稳定约束情况下某点的虚位移必在该点曲面的切平面上。
5-7.理想、完整、稳定约束体系平衡的充要条件是主动力虚功之和为零.5-8.有效力(主动力+ 惯性力)的总虚功等于零。
5-9.广义动量的时间变化率等于广义力(或:主动力+拉氏力)。
5-10.简正坐标能够使系统的动能和势能分别用 广义速度 和 广义坐标 的平方项表示。
5-11.勒让德变换就是将一组 独立 变数变为另一组 独立 变数的变换。
5-12.勒让德变换可表述为:新函数等于 不要的变量 乘以原函数对该变量的偏微商的 和 ,再减去原函数。
5-13.广义能量积分就是 t 为循环坐标时的循环积分。
5-14. 泊松定理可表述为:若21),,(,),,(c t p q c t p q ==ψϕ是正则方程的初积分,则[]3c ,=ψϕ 也是正则方程的初积分.5-15.哈密顿正则方程的泊松括号表示为: ],[H p pαα= ; ],[H q q αα= 。
5-16.哈密顿原理可表述为:在相同 始终 位置和 等时 变分条件下,保守、完整力系所可能做的真实运动是 主函数 取极值.5-17.正则变换就是 使正则方程 形式不变的广义坐标的变换。
5-18.正则变换目的就是通过正则变换,使新的H * 中有更多的 循环坐标 。
5-19. 哈密顿正则方程为:ααp H q∂∂= ;ααq H p ∂∂-= 。
5-20. 哈密顿正则变换的数学表达式为:∑-∂∂=sL q Lqt q p H 1),,(αα 。
二、选择题5-1. 关于广义坐标的理解,下列说法正确的是:【B 】A 广义坐标就是一般的坐标;B 广义坐标可以是线量,也可以是角量;C 一个系统的广义坐标数是不确定的;D 系统广义坐标的数目一定就是系统的自由度数5-2. 关于自由度数目的理解,下列说法正确的是:【B 】A 系统的自由度数目就是系统的独立的一般坐标的数目;B系统的自由度数目与系统的广义坐标的独立变更数目一定相同;C 一个系统的自由度数目是不确定的,与系统广义坐标的选取有关;D系统的自由度数目一定与系统的广义坐标的数目相同。
5-3. 关于分析力学中的概念,找出错误的说法:【D】A 拉格朗日方程是S个二阶常微分方程组成的方程组;B 哈密顿正则方程是2S个一阶常微分方程组成的方程组;C 拉格朗日函数和哈密顿函数的变量不同;D 拉格朗日方程和哈密顿正则方程是分析力学中两个基本的方程,不能相互推演。
5-4. 分析力学的特点中,正确的有:【C】A 分析力学是对力学体系的分析过程的理论;B分析力学中系统的广义坐标一定与系统的空间坐标有关;C分析力学的研究方法是通过选定系统的广义坐标从而确定系统的运动规律;D 分析力学的研究方法只对力学体系有效5-5. 关于系统约束的分类,错误的描述有:【D】A 系统约束可分为几何约束和运动约束;B 系统约束可分为稳定约束和不稳定约束;C 约束就是对物体运动的位置或速度进行限定;D运动约束就是完整约束。
5-6. 分析力学中的循环坐标,下列描述中错误的有:【D】A 循环坐标是指拉格朗日函数中或哈密顿函数中不显含的广义坐标;B 循环坐标能使拉格朗日方程或哈密顿正则方程求解简单;C 循环坐标可以是线坐标,也可以是其它物理量;D 系统确定,循环坐标数目就一定确定5-7. 关于广义动量和广义速度,下列说法正确的有:【A 】A 广义速度可以是线速度,也可以是其他的物理量;B 广义动量就是动量;C 广义动量等于系统的广义速度乘以系统的质量;D 广义动量的增量等于力对时间的冲量。
5-8. 关于虚功指的是【B 】A 当质点发生位移时力所作的功;B 质点在约束可能范围内发生虚位移时力所作的功 ;C 虚力在质点发生位移时所作的功;D 虚力和虚位移所作的功。
9. 设A 、B 两质点的质量分别为m A 、m B ,它们在某瞬时的速度大小分别为v A 、v B ,则C(A) 当v A =v B ,且m A =m B 时,该两质点的动量必定相等; (B) 当v A =v B ,而m A m B 时,该两质点的动量也可能相等; (C) 当v A v B ,且m A m B 时,该两质点的动量有可能相等; (D) 当v A v B ,且m A m B 时,该两质点的动量必不相等; 12-2. 设刚体的动量为K ,其质心的速度为v C ,质量为M ,则B(A) K =M v C 式只有当刚体作平移时才成立; (B) 刚体作任意运动时,式K =M v C 恒成立;(C) K =M v C 式表明:刚体作任何运动时,其上各质点动量的合成的最后结果必为一通过质心的合动量,其大小等于刚体质量与质心速度的乘积;(D) 刚体作任何运动时,其上各质点动量合成的最后结果,均不可能为一通过质心的合动量。
10. 如果质点系质心在某轴上的坐标保持不变,则D(A) 作用在质点系上所有外力的矢量和必恒等于零; (B) 开始时各质点的初速度均必须为零; (C) 开始时质点系质心的初速度必须为零;(D) 作用在质点系上所有外力在该轴上投影的代数和必恒等于零,但开始时质点系质心的初速度并不一定等于零。
11. 图示三个均质圆盘A 、B 、C 的重量均为P ,半径均为R ,它们的角速度的大小、转向都相同。
A 盘绕其质心转动,B 盘绕其边缘上O 轴转动,C 盘在水平面上向右滚动而无滑动。
在图示位置时,A 、B 、C 三个圆盘的动量分别用K A 、K B 、K C 表示,则CωRAωR C ω RB(A)K A =K B =K C ;(B)K A K B K C ; (C)K A K B =K C ;(D)K A =K B K C ;12. 图a 所示机构中,O 1A O 2B ,且O 1A=O 2B=10cm ,曲柄O 1A 以匀角速度=2rad/s绕O 1轴朝逆时针向转动,O 1、O 2位于同一水平线上。
图b 所示CD 杆的C 端沿水平面向右滑动,其速度大小v C =20cm/s ,D 端沿铅直墙滑动。
图c 所示EF 杆在倾角为45的导槽内滑动,契块以匀速u=20cm/s 沿水平面向左移动。
设AB 、CD 、EF 三均质杆的重量相等,在图示位置时,它们的动量矢量分别用K 、K 、K 表示,则B(A)K AB CDEF AB EF CD AB CDEF AB CD = K EF .13. 图示均质杆AB 重W ,其A 端置于水平光滑面上,B 端用绳悬挂。
取图示坐标系oxy ,此时该杆质心C 的坐标x C =0。
若将绳剪断,则C(A) 杆倒向地面的过程中,其质心C 运动的轨迹为圆弧; (B) 杆倒至地面后,x C >0; (C) 杆倒至地面后,x C =0; (D) 杆倒至地面后,x C <0。
14. 一圆盘置于光滑水平面上,开始处于静止。
当它受图示力偶(F ,F ')作用后A(A) 其质心C 将仍然保持静止;(B) 其质心C 将沿图示轴方向作直线运动; (C) 其质心C 将沿某一方向作直线运动; (D)其质心C 将作曲线运动。
15. 试判断以下四种说法中,哪一个是正确的?B(A) 质点系的动量必大于其中单个质点的动量;(B) 质点系内各质点的动量均为零,则质点系的动量必为零;o y xFF' c BA o W C yx (b)45︒ v CCD (c)45︒45︒uEF45︒ω O 2O 1B A (a)(C) 质点系内各质点的动量皆不为零,则质点系的动量必不为零; (D) 质点系的动量的大小等于其各个质点的动量的大小之和。
16. 图示三物体在地面附近某一同样的高度分别以不同的质心初速v a 、v b 、v c (v a >v b >v c )抛出,它们的质量均为M 。
若不计空气阻力,它们的质心加速度分别以a a 、a b 、a c 表示。
以下四种说法中,哪一个是正确的?A(A) a a =a b =a c ;(B) a a <a b <a c ;(C) a a >a b >a c ;(D) a a >a b <a c 。
17.图示三物体在地面附近某一同样的高度分别以不同的质心初速v a 、v b 、v c (v a >v b >v c )抛出,它们的质量均为M 。
若不计空气阻力,它们的速度在坐标轴上的投影,有以下四种说法,其中哪些是正确的?AD(A) v ax =常量,v bx =常量,v cx =常量; (B) v ax 常量,v bx =常量,v cx =常量; (C) v ay 常量,v by =常量,v cy 常量; (D) v ay 常量,v by 常量,v cy 常量。
18.图示均质方块质量为m ,A 、B 两处装有两个大小忽略不计的圆轮,并可在光滑水平面上滑动,开始时方块处于静止状态,若突然撤去B 端的滑轮支撑,在刚撤去滑轮B 的瞬(A) 在刚撤滑轮B 的支撑时,方块的质心加速度a c AC 向下; (B) 只有在刚撤滑轮B 的支撑时,方块的质心加速度a c 铅直向下; (C) 滑轮B 的支撑撤去后,方块质心加速度a c 始终铅直向下; (D) 只有在刚撤滑轮B 的支撑时,方块质心速度v c 铅直向下;(E) 滑轮B 的支撑撤去后,方块质心速度v c 在x 轴上的投影始终为零; (F)滑轮B 的支撑撤去后,方块质心的x 坐标x c 始终保持不变。
(b)v b(c)v cv a(a)v a(a)(b)v b(c)v cCAB19. 图示一均质圆盘以匀角速度绕其边缘上的O 轴转动,已知圆盘的质量为m ,半径为R ,则它对O 轴的动量矩G O 大小为A(A) G O =3mR 2/2 (B) G O =mR 2 (C) G O =mR 2/2 (D) G O =mR 2/320.图示一均质圆盘的质量为m ,半径为R ,沿倾角为的斜面滚动而无滑动。
