初中计算题练习题汇总
初一数学计算题及答案50题

初一数学计算题及答案50题1、计算题: 48×3+27=()答案: 1652、计算题: 90÷( 30-24)=()答案: 153、计算题: 10×[48÷(16-8)]=()答案: 804、计算题: [40-(8+2)]×9=()答案: 2705、计算题: (12-4)×3+9=()答案: 336、计算题: 12÷[( 41-34)×2]=()答案: 37、计算题: 3×[28-(13+7)]=()答案: 488、计算题: 18÷(3-1)+6=()答案: 129、计算题: 17-8÷(4-2)=()答案: 910、计算题: (9-5)×(7-2)=()答案: 28以上只是初一数学计算题及答案的一部分,希望对大家有所帮助。
初一数学找规律题及答案找规律是数学学习中一个重要的部分,它能帮助学生发展逻辑思维和解决问题的能力。
下面,我将展示一些初一数学找规律的问题,并附上相应的答案,以便帮助学生理解并解决类似的问题。
问题1:观察下列数字序列,找出规律,并预测下一个数字。
1,2,3,5,8,13,21,34,55,89...答案:这个数字序列是著名的斐波那契数列。
它的规律是每个数字是前两个数字的和。
因此,下一个数字应该是34 + 55 = 89。
问题2:观察下列图形序列,找出规律,并预测下一个图形。
图1:△图2:□△图3:△□□图4:□△□□图5:△□□□答案:这个图形序列的规律是每个图形都是由一个或多个三角形和一个正方形组成。
每个图形中的三角形数量比前一个图形多一个,而正方形数量与前一个图形相同。
因此,下一个图形应该是□△□□□。
问题3:观察下列等式序列,找出规律,并预测下一个等式。
a +b = cb +c = dc +d = ed +e = f答案:这个等式序列的规律是每个等式都是前两个等式的和。
(精品)七年级数学计算题大全

七年级数学计算题大全第一部分:数的运算一、加法1. 基础加法:计算 23 + 45 = ?2. 进位加法:计算 57 + 48 = ?3. 多位数加法:计算 123 + 456 = ?二、减法1. 基础减法:计算 56 23 = ?2. 借位减法:计算 87 45 = ?3. 多位数减法:计算 123 456 = ?三、乘法1. 基础乘法:计算7 × 8 = ?2. 两位数乘法:计算23 × 45 = ?3. 多位数乘法:计算123 × 456 = ?四、除法1. 基础除法:计算56 ÷ 7 = ?2. 两位数除法:计算456 ÷ 23 = ?3. 多位数除法:计算5 ÷ 456 = ?五、分数的运算1. 分数加法:计算 1/2 + 3/4 = ?2. 分数减法:计算 3/4 1/2 = ?3. 分数乘法:计算1/2 × 3/4 = ?4. 分数除法:计算3/4 ÷ 1/2 = ?六、小数的运算1. 小数加法:计算 1.23 + 4.56 = ?2. 小数减法:计算 5.67 2.34 = ?3. 小数乘法:计算1.23 ×4.56 = ?4. 小数除法:计算5.67 ÷ 2.34 = ?七、整数与分数、小数的混合运算1. 整数加分数:计算 3 + 1/2 = ?2. 整数减分数:计算 5 3/4 = ?3. 整数乘分数:计算2 × 3/4 = ?4. 整数除分数:计算4 ÷ 3/2 = ?5. 分数加小数:计算 1/2 + 0.25 = ?6. 分数减小数:计算 3/4 0.5 = ?7. 分数乘小数:计算1/2 × 0.5 = ?8. 分数除小数:计算1/2 ÷ 0.5 = ?七年级数学计算题大全第一部分:数的运算一、加法1. 基础加法:计算 23 + 45 = ?2. 进位加法:计算 57 + 48 = ?3. 多位数加法:计算 123 + 456 = ?二、减法1. 基础减法:计算 56 23 = ?2. 借位减法:计算 87 45 = ?3. 多位数减法:计算 123 456 = ?三、乘法1. 基础乘法:计算7 × 8 = ?2. 两位数乘法:计算23 × 45 = ?3. 多位数乘法:计算123 × 456 = ?四、除法1. 基础除法:计算56 ÷ 7 = ?2. 两位数除法:计算456 ÷ 23 = ?3. 多位数除法:计算5 ÷ 456 = ?五、分数的运算1. 分数加法:计算 1/2 + 3/4 = ?2. 分数减法:计算 3/4 1/2 = ?3. 分数乘法:计算1/2 × 3/4 = ?4. 分数除法:计算3/4 ÷ 1/2 = ?六、小数的运算1. 小数加法:计算 1.23 + 4.56 = ?2. 小数减法:计算 5.67 2.34 = ?3. 小数乘法:计算1.23 ×4.56 = ?4. 小数除法:计算5.67 ÷ 2.34 = ?七、整数与分数、小数的混合运算1. 整数加分数:计算 3 + 1/2 = ?2. 整数减分数:计算 5 3/4 = ?3. 整数乘分数:计算2 × 3/4 = ?4. 整数除分数:计算4 ÷ 3/2 = ?5. 分数加小数:计算 1/2 + 0.25 = ?6. 分数减小数:计算 3/4 0.5 = ?7. 分数乘小数:计算1/2 × 0.5 = ?8. 分数除小数:计算1/2 ÷ 0.5 = ?八、应用题1. 求解问题:小华有 3 个苹果,小明有 5 个苹果,他们一共有多少个苹果?2. 面积问题:一个长方形的长是 8 厘米,宽是 5 厘米,求这个长方形的面积。
初一代数式计算题50道

初一代数式计算题50道一、整式的加减1.化简:3x + 2x - 5x。
2.化简:4y - 3y + 2y。
3.化简:2a + 3b - a + 2b。
4.化简:5m - 3n - 2m + 4n。
5.化简:3(x + 2y) - 2(x - y)。
6.化简:2(3a - 2b) + 3(2a + b)。
7.化简:-(2x - 3y) + 4(3x - 2y)。
8.化简:5(a - b) - 2(a + 3b)。
9.化简:3x² + 2x² - 4x²。
10.化简:4y² - 3y² + 2y²。
二、整式的乘法11.计算:2x·3x。
12.计算:-3a·2a²。
13.计算:4m·(-2m²n)。
14.计算:5xy·(-3x²y)。
15.计算:(2a²b)·(-3ab³)。
16.计算:(-3x²y³)·2xy²。
17.计算:(4m²n)·(-2m³n²)。
18.计算:(-5a²b³)·(3a³b²)。
19.计算:(2x + 3)(x - 1)。
20.计算:(3x - 2)(2x + 1)。
三、整式的除法21.计算:6x²÷2x。
22.计算:-12a³b²÷(-3ab²)。
23.计算:24m³n²÷(-8m²n)。
24.计算:30x³y²÷(-5x²y)。
25.计算:(15a³b⁴c)÷(-5a²b²c)。
26.计算:(-24x⁴y⁵z²)÷(-8x²y³z)。
初一上册计算题精选集

初一上册计算题精选集初一的学习是为整个初中阶段打下坚实基础的重要时期,而数学中的计算题更是锻炼思维和提升能力的关键。
下面为大家精选了一些初一上册常见的计算题,通过练习和掌握这些题目,相信能帮助同学们更好地理解和运用所学知识。
一、有理数的运算1、计算:(-5) + 3这道题考查有理数的加法。
异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
在这道题中,|-5|>|3|,所以结果为负,用 5 3 = 2,最终答案为-2 。
2、计算:(-8) (-5)这是有理数的减法运算,减去一个数等于加上这个数的相反数。
所以原式可转化为-8 + 5 =-3 。
3、计算:(-2)×(-3)有理数乘法,同号得正,异号得负。
所以这道题的结果为 6 。
4、计算:(-12)÷(-3)两数相除,同号得正,异号得负。
所以答案为 4 。
二、整式的运算1、化简:3x + 2x同类项合并,系数相加,字母和指数不变。
所以结果为 5x 。
2、化简:(2x²+ 3x 5) (x² 2x + 1)去括号,然后合并同类项。
原式= 2x²+ 3x 5 x²+ 2x 1 = x²+5x 6 。
3、计算:2x(3x 1)使用乘法分配律,原式= 2x×3x 2x×1 = 6x² 2x 。
三、一元一次方程1、解方程:2x + 3 = 7首先,将 3 移到等号右边得到 2x = 7 3 ,即 2x = 4 ,然后两边同时除以 2 ,解得 x = 2 。
2、解方程:3(x 1) = 2x + 1先去括号得到 3x 3 = 2x + 1 ,然后将 2x 移到左边,-3 移到右边,得到 3x 2x = 1 + 3 ,解得 x = 4 。
四、综合计算题1、计算:(-2)³ ×(-4) 6 ÷(-3)先计算指数运算,(-2)³=-8 ,然后计算乘法-8×(-4) = 32 ,再计算减法 32 6 = 26 ,最后除以-3 ,得到-26/3 。
七年级上册数学计算题专练

七年级上册数学计算题专练一、有理数运算类。
1. 计算:(-3)+5 - (-2)- 解析:- 根据有理数加减法法则,减去一个数等于加上这个数的相反数。
- 所以(-3)+5 - (-2)=(-3)+5 + 2。
- 先计算(-3)+5 = 2,再计算2+2 = 4。
2. 计算:-2×(-3)÷(1)/(2)- 解析:- 根据有理数乘除法法则,先算乘法-2×(-3)=6。
- 再算除法6÷(1)/(2)=6×2 = 12。
3. 计算:(-2)^3+(-3)×[(-4)^2 - 2]- 解析:- 先计算指数运算,(-2)^3=-8,(-4)^2 = 16。
- 然后计算括号内的式子(-4)^2-2 = 16 - 2=14。
- 接着计算乘法-3×14=-42。
- 最后计算加法-8+(-42)=-8 - 42=-50。
二、整式加减类。
4. 化简:3a + 2b-5a - b- 解析:- 合并同类项,对于a的同类项3a-5a=(3 - 5)a=-2a。
- 对于b的同类项2b - b=(2 - 1)b = b。
- 所以化简结果为-2a + b。
5. 计算:(2x^2 - 3x + 1)-(3x^2 - 5x - 2)- 解析:- 去括号,得到2x^2-3x + 1-3x^2 + 5x+2。
- 合并同类项,2x^2-3x^2=(2 - 3)x^2=-x^2,-3x+5x=( - 3+5)x = 2x,1 + 2=3。
- 所以结果为-x^2+2x + 3。
三、一元一次方程类。
6. 解方程:2x+3 = 5x - 1- 解析:- 移项,将含x的项移到一边,常数项移到另一边,得到2x-5x=-1 - 3。
- 合并同类项-3x=-4。
- 系数化为1,x=(4)/(3)。
7. 解方程:(x+1)/(2)-(2x - 1)/(3)=1- 解析:- 先去分母,等式两边同时乘以6,得到3(x + 1)-2(2x - 1)=6。
120个计算题和120个解方程及答案 初一

初一(上)解方程、有理数计算综合一、计算题(本大题共90小题,共540.0分)1.解方程(1)4x−35−1=7x−23;(2)x−40.2−x−30.5=1.2.解方程(1)2−3(x+1)=8(2)5x+34−x−13=−23.解下列方程.(1)2(x+4)=3x−8(2)2x+13−x−56=14.解下列方程:(1)x+3x=−16;(2)16y−2.5y−7.5y=5;(3)3x+5=4x+1;(4)9−3y=5y+5.5.解方程:(1)4x−3=2x+5;(2)20−5x=3x−9−15.6.解下列方程:(1)5x−2x+x=12;(2)12x−32x=6;(3)−3y−7y=10.7.解方程:7+2x=12−2x.8.解方程:x+40.2−x−30.5=2.9.解方程(1)3y+14=2−2y−13(2)x−12+2x+16−x−13=2.10.解下列方程:(1)2x−(x+10)=5x+2(x−1);(2)3x−7(x−1)=3−2(x+3).11.解方程:x−x−22=1+2x−1312.解方程:(1)2(x−4)=5x−6(2)x+34−2x−43=213.解方程:(1)4−3(8−x)=5(x−2)(2)y+24−2y−16=114.解方程:(1)4x−3(20−x)=3;(2)3x−14−1=5x−76。
15.解方程:1−3(8+x)=x−2(15−2x).16.解方程:(1)5x+2=3x−18;(2)2x+12−x−13=1.17.利用等式的性质解下列方程并检验:(1)x−5=6;(2)0.3x=45;(3)5x+4=0;(4)2−14x=3.18.利用等式的性质解方程,并检验:(1)−2x+4=2;(2)5x+2=2x+5.19.解方程(1)3x−5(x−2)=2;(2)2x+13−x−24=1.20.解方程:(1)3x+7=27−2x;(2)1−x3−x−26=1.21.解方程:(1)4(2x−1)−3(x−2)=12;(2)3x+12−2x−23=2x−1.22.(对应目标5)解下列方程:(1)−3(x+3)=24.(2)4x−3=2(x−1).(3)5−(2x−1)=x.(4)5(x−6)=−4x−3.23.解方程:3x+12−2=3x−210−2x+35.24.解方程:x−73−1+x2=1.25.解下列方程:(1)2x−19=7x+6;(2)x−2=13x+43;(3)2.5m+10m−15=6m−21.5;(4)43+112y=3+8y.26.(对应目标4)解下列方程:(1)−3x+3=1−x−4x;(2)5x−3x+7=1−3x;(3)−4x+6=5x−3;(4)−2x−7x+5=3x−x−6.27.解下列方程:(1)3(x+3)=5x−1(2)1−x3=2−x+2528.解方程:x+13+1=x−x−12.29.解方程:(1)x+5(2x−1)=3−2(−x−5)(2)x+32−2=−2x−2530.解下列方程:(1)x+12−1=2+2−x4;(2)3x+x−12=3−2x−13.31.解下列方程:(1)x+325=x−32;(2)3y−14−1=5y−76.32.解下列方程:(1)y+24−1=2y−16;(2)x+74−x−13=x+1.33.解下列方程:(1)3(2x+1)=5−4(x−2);(2)2(2−x)−5(2−x)=9.34.(对应目标6)解方程:(1)4−2(x+4)=2(x−1);(2)13(x+7)=25−12(x−5);(3)0.3x−0.40.2+2=0.5x−0.20.3.35.解方程:(1)2x+13−5x−16=1;(2)1−x+23=x−12.36.解方程:3x+5=30−2x.37.解下列方程:(1)6x−7=4x−5;(2)12x−6=34x.38.解方程:x−12=2+3x4.39.解方程:(1)4y−3(20−y)=6y−7(11−y);(2)2(x+1)3=5(x+1)6−1.40.解方程:(1)3x−2=−6+5x;(2)3x+22−x−53=1.41.(对应目标5,6)解方程:(1)2−3x=0.5(14−2x);(2)x+24−1=3−2x6.42.解方程:x−3=−12x−4.43.解下列方程:(1)6(x−5)=−24;(2)−2x+9=3(x−2);(3)7y+(3y−5)=y−2(7−3y);(4)3x−2(x−1)=2−3(5−2x).44.解方程(1)3(x+1)−x=13−(2x−1)(2)y+12−1=2+2−y445.解方程:0.5x−0.7=6.5−1.3x.46.解下列一元一次方程:(1)4−2x=3(2−x);(2)4x+3(2−x)=12−(x−4);(3)(y−2)+1=5−2(2y−1).47.解下列方程:(1)2x−13=x−34;(2)1+x−12=x+26;(3)y−y+12=2−y+25;(4)3x+x−12=2−2x−13;(5)3x−14−5x−76=1;(6)1−0.1x1.2−x−0.12.4=1.48.解方程:(1)2x−20=−3x;(2)2x+2.5x=−6−1.5x;(3)2x−5=15−3x;(4)−3+y=1.2y−5.49.解方程:12[x−12(x−1)]=23(x−1);50.解方程:2(x−1)=3(x+1);51.解方程3x+22−1=2x−14−2x+1552.解下列方程:(1)19100x=21100(x−2);(2)x+12−2=x4;(3)5x−14=3x+12−2−x3;(4)3x+22−1=2x−14−2x+15.53.解下列方程:(1)43−8x=3−112x;(2)0.5x−0.7=6.5−1.3x;(3)16(3x−6)=25x−3;(4)1−2x3=3x+17−3.54.解下列方程:(1)3x+52=2x−13;(2)x−3−5=3x+415;(3)3y−14−1=5y−76; (4)5y+43+y−14=2−5y−512.55. (人教七上P23练习T1变式2)计算:(1)5−9; (2)(+6)−(−4); (3)(−8)−(−2); (4)0−(−7); (5)(−3.5)−7.5; (6)2.1−(−2.9).56. (人教七上P25习题T4变式2)计算:(1)(+15)−(−45); (2)(−27)−(−57); (3)15−17; (4)(−13)−13; (5)−12−(−56); (6)0−(−35);(7)(−2)−(+14); (8)(−1235)−(−835)−(+25).57. (人教七上P25习题T3变式1)计算:(1)(−6)−6; (2)(−5)−(−5); (3)5−(−5); (4)9−9; (5)0−7; (6)0−(−3); (7)17−37; (8)24−(−54); (9)(−7.8)−(+7); (10)(−7.9)−(−6.9).58. (人教七上P20练习T1变式1)计算:(1)21+(−17)+8+(−23); (2)(−5)+3+1+(−2)+5+(−3).59.计算题:(1)|−12|−(−18)+(−7)+6;(2)−12−(−32)×(34−212+158);(3)16×[1−(−3)2]÷(−13).60.(人教七上P23练习T1变式1)计算:(1)6−8;(2)(+4)−(−9);(3)(−4)−(−10);(4)0−(−9);(5)(−5.5)−9.5;(6)1.9−(−2.9).61.(人教七上P20练习T1变式2)计算:(1)12.4+(−20.4)+37.6+(−6.6);(2)(−4)+2+1+(−5)+2+(−6).62.计算(1)(−79+56−34)×(−36);(2)−14−(1−0.5)×13×|1−(−5)2|.63.(人教七上P25习题T3变式2)计算:(1)(−10)−10;(2)(−7)−(−7);(3)7−(−17);(4)0−0;(5)0−8;(6)0−(−9);(7)18−48;(8)39−(−61);(9)(−9.8)−(+7.8);(10)(−6.9)−(−9.9).64.(人教七上P24习题T2变式2)计算(1)(−18)+20+2+(−4);(2)9+(−6)+4+9+(−4)+(−9);(3)(−2.8)+1.2+(−1.4)+(−2.1)+2.8+3.5; (4)15+(−27)+45+(−12)+(−27).65. 计算:(1)(−1)3−14×[2−(−3)2]; (2)(14+16−12)×12+(−2)3÷(−4).66. (人教七上P24习题T1变式1)计算:(1) 1−4+3−0.5; (2) −2.4+3.5−4.6+3.5; (3) (−7)−(+5)+(−4)−(−10);(4)34−12+(−13)−(−23).67. (人教七上P24习题T2变式1)计算:(1)(−8)+8+2+(−2);(2)6+(−6)+4+9+(−4)+(−9);(3)(−0.18)+1.4+(−0.7)+(−1.4)+0.18+3.7;(4)13+(−15)+45+(−23)+(−35).68. (人教七上P19练习T3变式1)计算:(1)18+(−28); (2)(−21)+(−9); (3)(−1.8)+1.2; (4)13+(−12).69. 计算:(1)−5+(−6)−(−9); (2)(−83)×(−58)÷19;(3)−32−(−2)3÷32; (4)(−43+56−78)×(−24).70. (人教七上P25习题T4变式1)计算:(1)(+27)−(−57); (2)(−23)−(−13); (3)14−13; (4)(−14)−13; (5)−25−(−15); (6)0−(−35); (7)(−2)−(+27); (8)(−1235)−(−1045)−(+115).71. (人教七上P24习题T1变式2)计算:(1)(−10)+(+10); (2)(+12)+(−22); (3)(−17)+(−13); (4)(+16)+(−10); (5)(−1.2)+(−2.8); (6)0.67+(−2.87); (7)(−313)+23; (8)(−215)+(−145). .72. (人教七上P24习题T1变式1)计算:(1)(−8)+(+6); (2)(+3)+(−4); (3)(−5)+(−5); (4)(+7)+(−7); (5)(−0.9)+(−2.1); (6)27+(−37);(7)(−15)+45; (8)(−315)+(−1110).73. (人教七上P24习题T1变式2)计算:(1)3−5+2−3.5; (2)−4.4+2.5−5.6+7.5; (3)(−10)−(+4)+(−5)−(−8); (4)37−74+(−14)−(−47)−1.74.计算(1)2×(−3)3−4×(−3)+15(2)(−2)3+(−3)×[(−4)2+2]−(−3)2÷(−2) 75.(教材P33练习变式1)(1)−85×(−0.25)×(−4)(2)−(222022)×16×10112023(3)(79−38)×36(4)713×(−23)+73×71376.(教材P38习题T7变式1)计算:(1)−12×13×(−14);(2)−16×(−15)×(−17);(3)254×12.5×8;(4)0.2÷(−0.001)÷(−10);(5)23×(−114)÷23;(6)−6×(−0.5)×532;(7)(−9)×(−12)×0÷(−2022);(8)−15×(−14)÷6÷(−2).77.(教材P36练习变式2)(1)12×(−3)+(−152)÷(112)(2)(−14)×2÷13−12(3)6+23−(−12)÷1378.(对应目标4、6)合并同类项:(1)−3x2y+5xy2−6xy2+4−7x2y−9;(2)a3−a2b+ab2+a2b−ab2+b3.79.计算:(1)−7x2+(8x2+3xy)−(2y2−xy+x2);(2)(3x2−xy−2y2)−2(x2+xy−2y2).80.若(a+3)2+|b−2|=0,求3ab2−{2a2b−[5ab2−(6ab2−2a2b)]}的值.81.计算:(1)(3a2+2a+1)−(2a2+3a−5);(2)(−x2+2xy−y2)−2(xy−3x2)+3(2y2−xy).82.化简:(1)4a2+3b2+2ab−4a2−4b2;(2)2(x2+xy−5)−4(2x2−xy).83.计算:(1)x2y−3x2y;(2)10y2+0.5y2;(3)−12a2bc+12cba2;(4)14mn−13mn+7;(5)7ab−3a2b2+7+8ab2+3a2b2−3−7ab;(6)3x3−3x2−y2+5y+x2−5y+y2.84.计算:(1)x2y−3x2y;(2)10y2+0.5y2;(3)−12a2bc+12cba2;(4)14mn−13mn+7;(5)7ab−3a2b2+7+8ab2+3a2b2−3−7ab;(6)3x3−3x2−y2+5y+x2−5y+y2.85.计算:(1)(4a3b−10b3)+(−3a2b2+10b3);(2)(4x2y−5xy2)−(3x2y−4xy2);(3)5a2−[a2+(5a2−2a)−2(a2−3a)];(4)15+3(1−a)−(1−a−a2)+(1−a+a2−a3);(5)(4a2b−3ab)+(−5a2b+2ab);(6)(6m2−4m−3)+(2m2−4m+1);(7)(5a2+2a−1)−4(3−8a+2a2);(8)3x2−[5x−(12x−3)+2x2].86.计算:(1)12x−20x;(2)x+7x−5x;(3)−5a+0.3a−2.7a;(4)13y−23y+2y;(5)−6ab+ba+8ab;(6)10y2−0.5y2.87.计算:(1)(9x−6y)−(5x−4y);(2)3−(1−x)+(1−x+x2);(3)2(x2−y2+1)−2(x2+y2)+xy;(4)(3x−2y)−[−4x+(z+3y)].88.计算:(1)3−2x2+3x+3x2−5x−x2−7(2)−3(2a2−ab)+4(a2+ab−6)89.化简:(1)x−2x.(2)−12(4x−6).(3)2(a2−ab)−3(23a2−ab).90.先化简,再求值.(1)(3x2+y2−5xy)+(−4xy−y2+7x2),其中x=2,y=32.(2)−8m2+[7m2−2m−(3m2−4m)],其中m=−12.答案和解析1.【答案】解:(1)4x−35−1=7x−23去分母得:3(4x−3)−15=5(7x−2),去括号得:12x−9−15=35x−10,移项得:12x−35x=−10+9+15,合并同类项得:−23x=14,系数化为1得:x=−1423;(2)x−40.2−x−30.5=1整理得:5x−20−2x+6=1,移项得:5x−2x=1+20−6,合并同类项得:3x=15,系数化为1得:x=5.【解析】(1)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解;(2)方程整理后,去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握一元一次方程的解法是解本题的关键.2.【答案】解:(1)去括号得:2−3x−3=8,移项合并得:−3x=9,系数化为1得:x=−3;(2)去分母得:3(5x+3)−4(x−1)=−24,去括号得:15x+9−4x+4=−24,移项合并得:11x=−37,系数化为1得:x=−3711.【解析】(1)方程去括号,移项合并同类项,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并同类项,把x系数化为1,即可求出解.此题考查解一元一次方程,熟练掌握运算法则是解本题的关键.3.【答案】解:(1)去括号,得:2x+8=3x−8,移项,得:2x−3x=−8−8,合并同类项,得:−x=−16,系数化为1得:x=16.(2)去分母,得:2(2x+1)−(x−5)=6,去括号,得:4x+2−x+5=6,移项,得:4x−x=6−2−5,合并同类项,得:3x=−1,系数化为1得:x=−1.3【解析】本题主要考查了一元一次方程的解法.(1)去括号,移项,合并同类项,系数化为1即可得到答案;(2)去分母,去括号,移项,合并同类项,系数化为1即可得到答案.4.【答案】解:(1)合并同类项,得4x=−16.系数化为1,得x=−4.(2)合并同类项,得6y=5..系数化为1,得y=56(3)移项,得3x−4x=1−5.合并同类项,得−x=−4.系数化为1,得x=4.(4)移项,得−3y−5y=5−9.合并同类项,得−8y=−4..系数化为1,得y=12【解析】见答案5.【答案】解:(1)4x−3=2x+5移项,得4x−2x=3+5,合并同类项,得2x=8,系数化为1,得x=4.(2)20−5x=3x−9−15移项,得−5x−3x=−9−15−20,合并同类项,得−8x=−44,系数化为1,得x=5.5.【解析】见答案.6.【答案】解:(1)5x−2x+x=124x=12x=3;(2)12x−32x=6−x=6x=−6;(3)−3y−7y=10−10y=10y=−1.【解析】本题考查的是一元一次方程的解法.(1)按照一元一次方程的解法先合并同类项,再系数化为1即可;(2)按照一元一次方程的解法先合并同类项,再系数化为1即可;(3)按照一元一次方程的解法先合并同类项,再系数化为1即可.7.【答案】解:移项,得:2x+2x=12−7,合并同类项,得:4x=5,系数化为1,得:x=54.【解析】根据等式的基本性质依次移项、合并同类项、系数化为1可得.本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的一般步骤.8.【答案】解:去分母,得5(x+4)−2(x−3)=2,去括号,得5x+20−2x+6=2,移项,得5x−2x=2−20−6,合并同类项,得3x=−24,系数化为1,得x=−8.【解析】本题考查的是一元一次方程的解法,首先对该方程去分母,然后去括号,移项,合并同类项,最后系数化为1即可.9.【答案】解:(1)去分母得:3(3y+1)=24−4(2y−1),去括号得:9y+3=24−8y+4,移项、合并同类项可得:17y=25,;系数化为1,得:y=2517(2)去分母,得:3(x−1)+2x+1−2(x−1)=12,去括号得:3x−3+2x+1−2x+2=12,移项、合并同类项得:3x=12,系数化为1,得:x=4.【解析】(1)依次去分母、去括号、移项、合并同类项、系数化为1可得;(2)依次去分母、去括号、移项、合并同类项、系数化为1可得.本题主要考查解一元一次方程的能力,熟练掌握解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,是解题的关键.10.【答案】解:(1)2x−(x+10)=5x+2(x−1)去括号,得2x−x−10=5x+2x−2,移项,得2x−x−5x−2x=−2+10,合并同类项,得−6x=8,.系数化为1,得x=−43(2)3x−7(x−1)=3−2(x+3)去括号,得3x−7x+7=3−2x−6,移项,得3x−7x+2x=3−6−7,合并同类项,得−2x=−10,系数化为1,得x=5.【解析】本题考查的是解一元一次方程,熟练掌握解一元一次方程的一般步骤是解答此题的关键.(1)先去括号,然后移项,再合并同类项,把x的系数化为1即可;(2)先去括号,再移项,合并同类项,把x的系数化为1即可.11.【答案】解:x−x−22=1+2x−13去分母,得:6x−3(x−2)=6+2(2x−1)去括号,得:6x−3x+6=6+4x−2移项,得:6x−3x−4x=6−6−2合并同类项,得:−x=−2系数化为1,得:x=2【解析】本题主要考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解答本题的关键.根据解一元一次方程的步骤解答即可.12.【答案】解:(1)去括号得:2x−8=5x−6,移项得:2x−5x=−6+8,合并得:−3x=2,解得:x=−23;(2)去分母得:3(x+3)−4(2x−4)=24,去括号得:3x+9−8x+16=24,移项得:3x−8x=24−9−16,合并得:−5x=−1,解得:x=15.【解析】(1)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.此题考查了解一元一次方程,其步骤为:去分母,去括号,移项,合并同类项,把未知数系数化为1.13.【答案】解:(1)去括号得:4−24+3x=5x−10,移项合并同类项得:−2x=10,化系数为1得:x=−5;(2)去分母得:3(y+2)−2(2y−1)=1×12,去括号得:3y+6−4y+2=12移项合并同类项得:−y=4,化系数为1得:y=−4.【解析】本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.(1)根据一元一次方程的解法,去括号、移项、合并同类项、系数化为1即可得解;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项、化系数为1,从而得到方程的解.14.【答案】解:(1)4x−3(20−x)=3去括号得,4x−60+3x=3,移项得,4x+3x=3+60,合并同类项得,7x=63,系数化成1得,x=9;(2)3x−14−1=5x−76去分母得,3(3x−1)−12=2(5x−7),去括号得,9x−3−12=10x−14,移项得,9x−10x=−14+3+12,合并同类项得,−x=1,系数化成1得,x=−1.【解析】本题主要考查了一元一次方程的解法,关键是熟练掌握一元一次方程的解法步骤.(1)先去括号,然后移项,合并同类项,最后系数化成1可得结果;(2)先去分母,然后去括号,移项,合并同类项,最后系数化成1可得结果.15.【答案】解:1−3(8+x)=x−2(15−2x)去括号,得1−24−3x=x−30+4x,移项,得−3x−x−4x=−30−1+24,合并同类项,得−8x=−7,.系数化为1,得x=78【解析】本题主要考查一元一次方程的解法.解一元一次方程的步骤为去分母、去括号、移项、合并同类项、系数化为1.按照解一元一次方程的步骤解答即可.16.【答案】解:(1)移项,得5x−3x=−18−2,合并同类项,得2x=−20,系数化为1,得x=−10;(2)去分母,得3(2x+1)−2(x−1)=6,去括号,得6x+3−2x+2=6,移项,得6x−2x=6−2−3,合并同类项,得4x=1,.系数化为1,得x=14【解析】本题考查一元一次方程的解法,掌握解一元一次方程的基本步骤是解答本题的关键.(1)移项,合并同类项,系数化为1即可;(2)方程去分母,去括号,移项,合并同类项,系数化为1即可.17.【答案】解:(1)方程两边加5,得x=11.检验:将x=11代入方程x−5=6的左边,得11−5=6.方程的左右两边相等,所以x=11是方程的解.(2)方程两边除以0.3,得x =150.检验:将x =150代入方程0.3x =45的左边,得0.3×150=45. 方程的左右两边相等,所以x =150是方程的解. (3)方程两边减4,得5x =−4. 两边除以5,得x =−45.检验:将x =−45代入方程5x +4=0的左边, 得5×(−45)+4=0.方程的左右两边相等,所以x =−45是方程的解. (4)方程两边减2,得−14x =1. 两边除以−14,得x =−4.检验:将x =−4代入方程2−14x =3的左边,得2−14×(−4)=3. 方程的左右两边相等,所以x =−4是方程的解.【解析】见答案18.【答案】解:(1)方程两边同时减去4得−2x =−2, 两边同时除以−2,得x =1,当x =1时,左边=−2×1+4=2,右边=2, 左边=右边,故x =1是方程的解. (2)方程两边同时减去(2x +2)得3x =3, 两边同时除以3得x =1,当x =1时,左边=5×1+2=7,右边=2×1+5=7, 左边=右边,故x =1是方程的解.【解析】见答案.19.【答案】解:(1)去括号得:3x −5x +10=2,移项合并得:−2x =−8, 解得:x =4;(2)去分母得:8x +4−3x +6=12,移项合并得:5x=2,解得:x=25.【解析】(1)方程去括号,移项合并同类项,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并同类项,把x系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.20.【答案】解:(1)3x+7=27−2x,移项,得3x+2x=27−7,合并同类项,得5x=20,系数化1,得x=4;(2)1−x3−x−26=1,去分母,得2(1−x)−(x−2)=6,去括号,得2−2x−x+2=6,移项,得−2x−x=6−2−2,合并同类项,得−3x=2,系数化1,得x=−23.【解析】本题考查了解一元一次方程,解一元一次方程的步骤是:去分母(含有分母的一元一次方程),去括号,移项,合并同类项,系数化1.(1)方程移项,合并同类项,系数化1即可;(2)方程去分母,去括号,移项,合并同类项,系数化1即可.21.【答案】解:(1)4(2x−1)−3(x−2)=12,去括号得:8x−4−3x+6=12,移项得:8x−3x=12−6+4,合并同类项得:5x=10,化系数得:x=2;(2)3x+12−2x−23=2x−1,去分母得:3(3x+1)−2(2x−2)=6(2x−1),去括号得:9x+3−4x+4=12x−6,移项得:9x−4x−12x=−6−3−4,合并同类项得:−7x=−13,化系数得:x=13.7【解析】(1)根据一元一次方程的解法步骤:去括号、移项、合并同类项、系数化为1,即可求解;(2)根据一元一次方程的解法步骤:去分母、去括号、移项、合并同类项、系数化为1,即可求解.本题考查一元一次方程的解法,熟练掌握一元一次方程的解法是解题的关键.22.【答案】解:(1)−3(x+3)=24,去括号得:−3x−9=24,移项,合并同类项得:−3x=33,系数化1得:x=−11.(2)4x−3=2(x−1),去括号得:4x−3=2x−2,移项,合并同类项得:2x=1,.系数化1得:x=12(3)5−(2x−1)=x,去括号得:5−2x+1=x,移项,合并同类项得:−3x=−6,系数化1得:x=2.(4)5(x−6)=−4x−3,去括号得:5x−30=−4x−3,移项,合并同类项得,9x=27,系数化1得:x=3.【解析】见答案23.【答案】解:去分母得,5(3x+1)−20=(3x−2)−2(2x+3),去括号得,15x+5−20=3x−2−4x−6,移项得,15x−3x+4x=−2−6−5+20,合并同类项得,16x=7,系数化为1得,x=716.【解析】本题主要考查了解一元一次方程.先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.24.【答案】解:去分母,得2(x−7)−3(1+x)=6,去括号,得2x−14−3−3x=6,移项,得2x−3x=6+14+3,合并同类项,得−x=23,系数化为1,得x=−23.【解析】方程去分母、去括号、移项、合并同类项、把x系数化为1,即可求出方程的解.此题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解本题的关键.25.【答案】解:(1)2x−19=7x+62x−7x=6+19−5x=25x=−5;(2)x−2=13x+43x−13x=2+4323x=10 3x=5;(3)2.5m+10m−15=6m−21.5 2.5m+10m−6m=15−21.5 6.5m=−6.5m=−1;(4)43+112y=3+8y112y−8y=3−4 3−52y=53y=−23.【解析】本题考查的是一元一次方程的解法.(1)(2)(3)(4)按照一元一次方程的解法先移项,再合并同类项,系数化为1即可.26.【答案】解:(1)−3x+x+4x=1−32x=−2x=−1(2)5x−3x+3x=1−75x=−6x=−65(3)−4x−5x=−3−6 −9x=−9x=1(4)−2x−7x−3x+x=−6−5−11x=−11 x=1【解析】见答案27.【答案】解:(1)3(x+3)=5x−1,去括号得:3x+9=5x−1,移项得:2x=10,系数化为1得:x=5;(2)1−x3=2−x+25去分母得:5×(1−x)=2×15−3×(x+2),去括号得:5−5x=30−3x−6,移项合并同类项得:2x=−19,.系数化为1得:x=−192【解析】本题主要考查了解一元一次方程,其步骤为:去分母,去括号,移项合并同类项,将未知数系数化为1,即可求出解.28.【答案】解:去分母得:2(x+1)+6=6x−3(x−1),去括号得:2x+2+6=6x−3x+3,移项合并得:−x=−5,解得:x=5.【解析】方程去分母,去括号,移项合并同类项,把x系数化为1,即可求出解.此题考查了解一元一次方程,解方程去分母时注意两边都乘各分母的最小公倍数.29.【答案】解:(1)去括号,得:x+10x−5=3+2x+10,移项,得:x+10x−2x=3+10+5,合并同类项,得:9x=18,系数化为1,得:x=2;(2)去分母,得:5(x+3)−20=−2(2x−2),去括号,得:5x+15−20=−4x+4,移项,得:5x+4x=4−15+20,合并同类项,得:9x=9,系数化为1,得:x=1.【解析】(1)根据解一元一次方程的步骤依次:去括号、移项、合并同类项、系数化为1即可得;(2)根据解一元一次方程的步骤依次:去分母、去括号、移项、合并同类项、系数化为1即可得.本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.30.【答案】解:(1)方程两边同时乘以4得2x+2−4=8+2−x,移项,合并同类项得3x=12,解得x=4;(2)方程两边同时乘以6得18x+3x−3=18−4x+2,移项,合并同类项得25x=23,解得x=2325.【解析】本题主要考查的是一元一次方程的解法的有关知识.(1)先去分母,然后移项,合并同类项,最后将系数化为1求解即可;(2)先去分母,然后移项,合并同类项,最后将系数化为1求解即可.31.【答案】解:(1)去分母得:2(x+3)=25(x−3)去括号得:2x+6=25x−75,移项、合并同类项得:−23x=−81,系数化为1,得:x=8123;(2)去分母得:3(3y−1)−12=2(5y−7),去括号得:9y−3−12=10y−14,移项、合并同类项,得−y=1,系数化为1,得:y=−1.【解析】本题主要考查了一元一次方程的求解,去分母、去括号、移项、合并同类项、化系数为1是常用的解方程方法.(1)先去分母,再去括号,移项、合并同列项,系数化为1,从而得到方程的解;(2)先去分母,再去括号,最后移项,系数化为1,从而得到方程的解.32.【答案】解:(1)y+24−1=2y−16,3(y+2)−12=2(2y−1),3y+6−12=4y−2,3y−4y=−2−6+12,−y=4,y=−4;(2)x+74−x−13=x+1,3(x+7)−4(x−1)=12x+12,3x+21−4x+4=12x+12,3x−4x−12x=12−21−4,−13x=−13,x=1.【解析】本题主要考查一元一次方程的解法.(1)先去分母,再去括号,移项,合并同类项,系数化为1即可;(2)先去分母,再去括号,移项,合并同类项,系数化为1即可.33.【答案】解:(1)3(2x+1)=5−4(x−2)6x+3=5−4x+810x=10x=1(2)2(2−x)−5(2−x)=94−2x−10+5x=93x=15x=5【解析】本题主要考查一元一次方程的解法.(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去括号,移项合并,把x系数化为1,即可求出解.34.【答案】(1)解:4−2(x+4)=2(x−1)去括号得:4−2x−8=2x−2,移项得:−2x−2x=−2−4+8,合并得:−4x=2,解得x=−0.5;(2)解:13(x+7)=25−12(x−5)去分母得:10(x+7)=12−15(x−5),去括号得:10x+70=12−15x+75,移项得:10x+15x=12+75−70,合并得:25x=17,解得x=1725;(3)解:0.3x−0.40.2+2=0.5x−0.20.3整理得3x−42+2=5x−23去分母得:3(3x−4)+12=2(5x−2),去括号得:9x−12+12=10x−4,移项得:9x−10x=−4+12−12,合并得:−x=−4,解得x=4.【解析】见答案35.【答案】解:(1)2x+13−5x−16=1,2(2x+1)−(5x−1)=6,4x+2−5x+1=6,−x+3=6,x=−3.(2)1−x+23=x−12,6−2(x+2)=3(x−1),6−2x−4=3x−3,−2x+2=3x−3,−5x=−5,x=1.【解析】【分析】本题考查一元一次方程的解法,解题的关键是熟练掌握解方程的方法和步骤.(1)根据一元一次方程的解法即可求出答案.(2)根据一元一次方程的解法即可求出答案.36.【答案】解:3x+5=30−2x,3x+2x=30−5,5x=25,解得:x=5.【解析】此题主要考查了解一元一次方程,掌握解方程的方法和步骤是解题关键.直接移项、合并同类项、系数化为1解方程得出答案.37.【答案】解:(1)移项,得6x−4x=−5+7.合并同类项,得2x=2.系数化为1,得x=1.(2)移项,得12x−34x=6,合并同类项.得−14x=6.系数化为1,得x=−24.【解析】见答案38.【答案】解:x−12=2+3x42(x−1)=8+3x 2x−2=8+3x 2x−3x=8+2−x=10x=−10.【解析】本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.按照解一元一次方程的步骤进行计算即可.39.【答案】解:(1)去括号,得4y−60+3y=6y−77+7y,移项,得4y+3y−6y−7y=−77+60,合并同类项,得−6y=−17,.系数化为1,得y=176(2)去分母,得4(x+1)=5(x+1)−6,去括号,得4x+4=5x+5−6,移项,得4x−5x=5−6−4,合并同类项,得−x=−5,系数化为1,得x=5.【解析】见答案.40.【答案】解:(1)移项,3x−5x=−6+2,合并同类项,可得:−2x=−4,系数化为1,可得:x=2.(2)去分母,可得:3(3x+2)−2(x−5)=6,去括号,可得:9x+6−2x+10=6,移项,合并同类项,可得:7x=−10,.系数化为1,可得:x=−107【解析】此题主要考查了解一元一次方程的方法,要熟练掌握,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.(1)移项、合并同类项、系数化为1,即可求出方程的解.(2)去分母、去括号、移项、合并同类项、系数化为1,即可求出方程的解.41.【答案】解:(1)去括号得:2−3x=1−x,8移项得:3x−x=2−1,8合并得:2x=15,8解得:x=15;4(2)去分母得:3(x+2)−12=2(3−2x),去括号得:3x+6−12=6−4x,移项得:3x+4x=12,合并得:7x=12,.解得:x=127【解析】见答案.42.【答案】解:移项,得x+1x=−4+3.2合并同类项,得3x=−1.2.系数化为1,得x=−23【解析】此题考查了解一元一次方程,掌握解方程的步骤是解题的关键.方程移项,合并同类项,将x系数化为1,即可求出解.43.【答案】解:(1)去括号得6x−30=−24移项得6x=−24+30合并同类项得6x=6系数化成1得x=1;(2)去括号得−2x+9=3x−6移项得−2x−3x=−6−9合并同类项得−5x=−15系数化成1得x=3;(3)去括号得7y+3y−5=y−14+6y移项得7y+3y−y−6y=5−14合并同类项得3y=−9系数化成1得y=−3,(4)去括号得3x−2x+2=2−15+6x移项得3x−2x−6x=2−15−2合并同类项得−5x=−15系数化成1得x=3【解析】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.(1)方程去括号,移项合并,将x系数化为1,即可求出解;(2)方程去括号,移项合并,将x系数化为1,即可求出解;(3)方程去括号,移项合并,将x系数化为1,即可求出解;(4)方程去括号,移项合并,将x系数化为1,即可求出解.44.【答案】解:(1)3x+3−x=13−2x+13x−x+2x=13+1−34x=11x=11 4(2)2(y+1)−4=8+2−y2y+2−4=8+2−y2y+y=8+2−2+43y=12y=4.【解析】见答案.45.【答案】解:移项得:1.3x+0.5x=0.7+6.5,整理得:1.8x=7.2,解得:x=4.【解析】此题考查了一元一次方程的解法.此题比较简单,解题的关键是掌握解一元一次方程的步骤:去分母,去括号、移项、合并同类项以及系数化为1等.根据解一元一次方程的步骤:移项合并同类项,再把系数化为1,即可求得答案;46.【答案】解:(1)4−2x=3(2−x)去括号,得4−2x=6−3x,移项,得3x−2x=6−4,合并同类项,得x=2;(2)4x+3(2−x)=12−(x−4)去括号,得4x+6−3x=12−x+4,移项,得4x−3x+x=12−6+4,合并同类项,得2x=10,系数化为1,得x=5;(3)(y−2)+1=5−2(2y−1)去括号,得y−2+1=5−4y+2,移项,得y+4y=5+2+2−1,合并同类项,得5y=8,.系数化为1,得y=85【解析】本题主要考查了一元一次方程的解法,根据等式的基本性质和解一元一次方程的步骤求解即可.(1)可先去括号,然后移项,合并同类项即可求解;(2)可先去括号,然后移项,合并同类项,系数化为1即可求解;(3)可先去括号,然后移项,合并同类项,系数化为1即可求解.47.【答案】解:(1)去分母得:4(2x−1)=3(x−3),去括号得:8x−4=3x−9,移项得:8x−3x=−9+4,合并同类项得:5x=−5,系数化为1得:x=−1;(2)去分母得:6+3(x−1)=x+2,去括号得:6+3x−3=x+2,移项得:3x−x=2−6+3,合并同类项得:2x=−1,系数化为1得:x=−0.5;(3)去分母得:10y−5(y+1)=20−2(y+2),去括号得:10y−5y−5=20−2y−4,移项得:10y−5y+2y=20−4+5,合并同类项得:7y=21,系数化为1得:y=3;(4)去分母得:18x+3(x−1)=12−2(2x−1),去括号得:18x+3x−3=12−4x+2,移项得:18x+3x+4x=12+2+3,合并同类项得:25x=17,系数化为1得:x=17;25(5)去分母得:3(3x−1)−2(5x−7)=12,去括号得:9x−3−10x+14=12,移项得:9x−10x=12−14+3,合并同类项得:−x=1,系数化为1得:x=−1;(6)去分母得:2(1−0.1x)−(x−0.1)=2.4,去括号得:2−0.2x−x+0.1=2.4,移项得:−0.2x−x=2.4−2−0.1,合并同类项得:−1.2x=0.3,系数化为1得:x=−1.4【解析】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.(1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(5)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.48.【答案】解:(1)移项,得2x+3x=20合并同类项,得5x=20系数化成1,得x=4;(2)移项,得2x+2.5x+1.5x=−6合并同类项,得6x=−6系数化成1,得x=−1;(3)移项,得2x+3x=15+5合并同类项,得5x=20系数化成1,得x=4;(4)移项,得y−1.2y=−5+3合并同类项,得−0.2y=−2,系数化成1,得y=10.【解析】本题主要考查一元一次方程的解法.其步骤为:去分母,去括号,移项,合并同类项,系数化成1,可得解.(1)方程移项,合并同类项,最后把未知数的系数化成1即可得解;(2)方程移项,合并同类项,最后把未知数的系数化成1即可得解;(3)方程移项,合并同类项,最后把未知数的系数化成1即可得解;(4)方程移项,合并同类项,最后把未知数的系数化成1即可得解.49.【答案】解:原方程可化为12[(x−1)+1−12(x−1)]=23(x−1),去中括号,得12(x−1)+12−14(x−1)=23(x−1),解得x=115.【解析】本题考查解一元一次方程,将原方程可化为12[(x−1)+1−12(x−1)]=23(x−1),再去中括号、移项、合并同类项即可求解.50.【答案】解:去括号得:2x−2=3x+3,移项得:2x−3x=3+2合并得−x=5系数化1得:x=−5.【解析】此题考查了解一元一次方程有关知识.方程去括号,移项,合并同类项,把x系数化为1,即可求出解.51.【答案】解:去分母得:10(3x+2)−20=5(2x−1)−4(2x+1),去括号得:30x+20−20=10x−5−8x−4移项得:30x−10x+8x=−5−4,合并同类项得:28x=−9,系数化1得:x=−928.【解析】此题考查解一元一次方程的解法,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.52.【答案】解:(1)去分母(方程两边乘100),得19x=21(x−2).去括号,得19x=21x−42.移项,得19x−21x=−42.合并同类项,得−2x=−42.系数化为1,得x=21.(2)去分母(方程两边乘4),得2(x+1)−8=x.去括号,得2x+2−8=x.移项,得2x−x=8−2.合并同类项,得x=6.(3)去分母,得3(5x−1)=6(3x+1)−4(2−x).去括号,得15x−3=18x+6−8+4x.移项,得15x−18x−4x=6−8+3.合并同类项,得−7x=1..系数化为1,得x=−17(4)去分母,得10(3x+2)−20=5(2x−1)−4(2x+1).去括号,得30x+20−20=10x−5−8x−4.移项,得30x−10x+8x=−5−4−20+20.合并同类项,得28x=−9..系数化为1,得x=−928【解析】见答案53.【答案】解:(1)去分母,得8−48x=18−33x.移项,得−48x+33x=18−8.合并同类项,得−15x=10..系数化为1,得x=−23(2)移项,得0.5x+1.3x=6.5+0.7.合并同类项,得1.8x=7.2.系数化为1,得x=4.(3)去括号,得12x−1=25x−3.移项,得12x−25x=−3+1.合并同类项,得110x=−2.系数化为1,得x=−20.(4)去分母,得7(1−2x)=3(3x+1)−63.去括号,得7−14x=9x+3−63.移项、合并同类项,得−23x=−67.系数化为1,得x=6723.【解析】见答案54.【答案】解:(1)去分母,得3(3x+5)=2(2x−1).去括号,得9x+15=4x−2.移项,得9x−4x=−2−15.合并同类项,得5x=−17.系数化为1,得x=−175.(2)去分母,得−3(x−3)=3x+4.去括号,得−3x+9=3x+4.移项、合并同类项,得−6x=−5.系数化为1,得x=56.(3)去分母,得3(3y−1)−12=2(5y−7).去括号,得9y−3−12=10y−14.移项、合并同类项,得−y=1.系数化为1,得y=−1.(4)去分母,得4(5y+4)+3(y−1)=24−(5y−5).去括号,得20y+16+3y−3=24−5y+5.移项、合并同类项,得28y =16. 系数化为1,得y =47.【解析】见答案55.【答案】解:(1)−4;(2)10;(3)−6;(4)7;(5)−11;(6)5.【解析】见答案56.【答案】解:(1)1;(2)37;(3)235;(4)−23;(5)13;(6)35;(7)−94;(8)−425.【解析】见答案57.【答案】解:(1)−12;(2)0;(3)10,(4)0;(5)−7;(6)3;(7)−20;(8)78;(9)−14.8;(10)−1. 【解析】见答案58.【答案】解:(1)−11;(2)−1.【解析】见答案59.【答案】解:(1)|−12|−(−18)+(−7)+6=12+18+(−7)+6 =30+(−7)+6 =23+6=29;(2)−12−(−32)×(34−212+158) =−1+32×(34−52+138) =−1+32×34−32×52+32×138=−1+24−80+52=−5;(3)16×[1−(−3)2]÷(−13)=16×(1−9)×(−3)=16×(−8)×(−3)=4.【解析】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.(1)根据有理数的加减运算法则即可解答本题;(2)根据有理数的乘方和乘法分配律即可解答本题;(3)根据有理数的乘方、有理数的乘除法和减法的运算法则可以解答本题.60.【答案】解:(1)−2;(2)13;(3)6;(4)9;(5)−15;(6)4.8.【解析】见答案61.【答案】解:(1)23;(2)−10.【解析】见答案62.【答案】解:(1)(−79+56−34)×(−36)原式=−79×(−36)+56×(−36)−34×(−36)=28+(−30)+27=25;(2)−14−(1−0.5)×13×|1−(−5)2|原式=−1−12×13×|1−25|=−1−12×13×24=−1−4=−5.【解析】(1)根据乘法分配律计算即可;(2)先算乘方和括号内的式子、再算乘法、最后算减法即可.本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序.63.【答案】解:(1)−20;(2)0;(3)24;(4)0;(5)−8;(6)9;(7)−30;(8)100;(9)−17.6;(10)3.【解析】见答案64.【答案】解:(1)0;(2)3;(3)1.2;(4)−114.【解析】见答案65.【答案】解:(1)原式=−1−14×(2−9)=−1−14×(−7)=−1+7 4=34;(2)原式=14×12+16×12−12×12+(−8)÷(−4)=3+2−6+2=1.【解析】(1)先算乘方,再算乘法,最后算减法;如果有括号,要先做括号内的运算;(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算,注意运用乘法分配律简便计算.本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.66.【答案】解:(1)−0.5;(2)0;(3)−6;(4)712.【解析】见答案67.【答案】解:(1)0;(2)0;(3)3;(4)−13.【解析】见答案68.【答案】解:(1)−10;(2)−30;(3)−0.6;(4)−16.【解析】见答案69.【答案】解:(1)−5+(−6)−(−9)=−5−6+9=−2;(2)(−83)×(−58)÷19=(−83)×(−58)×9=15;(3)−32−(−2)3÷3 2=−9−(−8)×2 3=−9+16 3=−113;(4)(−43+56−78)×(−24)=−43×(−24)+56×(−24)−78×(−24)=32−20+21=33.【解析】此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.(1)先将减法转化为加法,再根据有理数加法法则计算即可;(2)先将除法转化为乘法,再根据有理数乘法法则计算即可;(3)先算乘方,再算除法,最后算减法即可;(4)利用乘法分配律计算即可.70.【答案】解:(1)1;(2)−13;(3)−112;(4)−712;(5)−15;(6)35;(7)−167;(8)−3.【解析】见答案71.【答案】解:(1)0;(2)−10;(3)−30;(4)6;(5)−4;(6)−2.2;(7)−83;(8)−4.【解析】见答案72.【答案】解:(1)−2;(2)−1;(3)−10;(4)0;(5)−3;(6)−17;(7)35;(8)−4310.【解析】见答案73.【答案】(1)−3.5;(2)0;(3)−11;(4)−2.【解析】见答案74.【答案】解:(1)原式=2×(−27)+12+15=−54+12+15=−27;(2)原式=−8+(−3)×(16+2)−9÷(−2)=−8+(−3)×18+4.5 =−8−54+4.5=−57.5.【解析】本题考查的是有理数的混合运算,掌握有理数混合运算的顺序是解题关键. (1)根据有理数的运算顺序:首先计算乘方,再算乘除,最后算加减进行计算即可; (2)先算乘方,再算乘除,最后算加减,有括号先算括号里面的即可.75.【答案】解:(1)原式=−85(2)原式=−(40462022)×16×10112023=−16(3)原式=(79−38)×36=28−272=292(4)原式=713×(−23)+73×713=713×(−23+73)=3539【解析】见答案.76.【答案】解:(1)2184(2)−4080(3)625(4)20(5)−54(6)1532(7)0(8)−352【解析】见答案.77.【答案】解:(1)原式=−41(2)原式=−272(3)原式=1283【解析】见答案.78.【答案】解:(1)−3x2y+5xy2−6xy2+4−7x2y−9=−3x2y−7x2y+5xy2−6xy2+4−9=(−3−7)x2y+(5−6)xy2+(4−9)=−10x2y−xy2−5(2)a3−a2b+ab2+a2b−ab2+b3=a3−a2b+a2b+ab2−ab2+b3=a3+(−a2b+a2b)+(ab2−ab2)+b3 =a3+b3【解析】先判断同类项,再根据合并法则进行合并即可.79.【答案】解:(1)原式=−2y2+4xy.(2)原式=x2−3xy+2y2.【解析】见答案。
(完整)100道初一数学计算题(11页)

100道初一数学计算题(11页)一、整数的运算1. 计算:3 + 7 5 + 42. 计算:(2³) × (4)3. 计算:(5)² 3²4. 计算:24 ÷ (3) × 25. 计算:(8) ÷ 2 (3) ÷ 2二、分数的运算6. 计算:1/2 + 1/3 1/67. 计算:2/5 × 3/48. 计算:5/8 ÷ 2/39. 计算:1 3/4 + 1/210. 计算:3/5 + 2/3 1/6三、小数的运算11. 计算:0.3 × 0.412. 计算:0.8 ÷ 0.213. 计算:0.5 + 0.7 0.314. 计算:1.2 × 0.515. 计算:2.4 ÷ 0.6四、混合运算16. 计算:2/3 + 0.4 × 517. 计算:3² ÷ 2/518. 计算:1/4 × (0.8 0.5)19. 计算:2/3 + 3/4 × 220. 计算:1.2 ÷ (0.3 + 0.2)五、简便计算21. 计算:99 + 98 + 97 + 9622. 计算:1001 × 1002 × 100323. 计算:1.25 × 824. 计算:0.125 × 825. 计算:4.5 × 2/3六、平方与立方运算26. 计算:7²27. 计算:(4)³28. 计算:10² 5²29. 计算:2³ + 3³30. 计算:(1/2)²七、根式运算31. 计算:√3632. 计算:√(49/81)33. 计算:3√2734. 计算:√(2/3) × √(3/2)35. 计算:√(16 + 9)八、百分数运算36. 计算:50% × 8037. 计算:120 ÷ 40%38. 计算:75% 25%39. 计算:150% + 50%40. 计算:20% of 500九、比例运算41. 如果 a : b = 3 : 4,且 a = 9,求 b 的值。
七年级计算题500道

七年级计算题500道一、有理数运算类。
1. 计算:(-3)+5- 解析:异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
|5| = 5,| - 3|=3,5>3,所以(-3)+5 = 2。
2. 计算:4 - (-2)- 解析:减去一个数等于加上这个数的相反数,所以4-(-2)=4 + 2=6。
3. 计算:(-2)×(-3)- 解析:两数相乘,同号得正,异号得负,并把绝对值相乘。
所以(-2)×(-3)=6。
4. 计算:-4÷2- 解析:两数相除,异号得负,并把绝对值相除。
所以-4÷2=-2。
5. 计算:(-2)^3- 解析:(-2)^3=(-2)×(-2)×(-2)= - 8。
二、整式加减类。
6. 化简:3a + 2b - 5a - b- 解析:- 合并同类项,同类项是指所含字母相同,并且相同字母的指数也相同的项。
- 对于a的同类项3a和-5a,3a-5a=-2a。
- 对于b的同类项2b和-b,2b - b=b。
- 所以,3a + 2b - 5a - b=-2a + b。
7. 化简:(2x^2 - 3x + 1)-(x^2+2x - 3)- 解析:- 去括号法则:括号前是正号,把括号和它前面的正号去掉后,原括号里各项的符号都不改变;括号前是负号,把括号和它前面的负号去掉后,原括号里各项的符号都要改变。
- 所以(2x^2 - 3x + 1)-(x^2+2x - 3)=2x^2-3x + 1 - x^2 - 2x+3。
- 然后合并同类项,2x^2-x^2=x^2,-3x-2x=-5x,1 + 3=4。
- 最终结果为x^2-5x + 4。
三、一元一次方程类。
8. 解方程:2x+3 = 7- 解析:- 首先进行移项,把常数项移到等号右边,2x=7 - 3。
- 然后计算7-3 = 4,得到2x=4。
- 最后系数化为1,两边同时除以2,x = 2。
初中数学计算题(200道)

初中数学计算题(200道) 实用文档1.5乘以-9减去12除以-456除以-7减去2除以5加0.43.57乘以29除以-45.6除以-2.8减去-50除以29.6减去7.3)乘以(-5减去-7)12.3除以(5.6减去1.2)75.6除以(1/4加1/5)9.5乘以-9.5除以1/295.77除以-2减去-34.651.88除以2减去-5乘以241.25乘以-3加70乘以-5加5乘以-3加25 9999乘以3加101乘以11乘以(101减去92) 23/4减去3/4)乘以(3乘以6加2)3/7乘以49/9减4/38/9乘以15/36加1/2712乘以5/6减2/9乘以38乘以5/4加1/46除以3/8减去3/8除以64/7乘以5/9加3/7乘以5/9 5/2减去(3/2加4/5)7/8加(1/8加1/9)9乘以5/6加5/63/4乘以8/9减1/37乘以5/49加3/146乘以(1/2加2/3)8乘以4/5加8乘以11/5 31乘以5/6减5/69/7减去(2/7减去10/21)5/9乘以18减14乘以2/74/5乘以25/16加2/3乘以3/4 14乘以8/7减5/6乘以12/15 17/32减去3/4乘以9/243乘以2/9加1/35/7乘以3/25加3/73/14乘以2/3加1/61/5乘以2/3加5/69/22加1/11除以1/25/3乘以11/5加4/345乘以2/3加1/3乘以157/19加12/19乘以5/61/4加3/4除以2/38/7乘以21/16加1/2101乘以1/5减1/5乘以2150加160除以40120减144除以18加35347加45乘以2减4160除以5237乘以(58加37)除以(64减去9乘以5)已做95除以(64减去45)178减去145除以5乘以6加42812减去700除以(9加31乘以11) 85加14乘以(14加208除以26) 120减去36乘以4除以18加35 58加37)除以(64减去9乘以5) 6.8减去6.8乘以0.55)除以8.5标准文案实用文档1.5乘以-9减去12除以-456除以-7减去2除以5加0.43.57乘以29除以-45.6除以-2.8减去-50除以29.6减去7.3)乘以(-5减去-7)12.3除以(5.6减去1.2)75.6除以(1/4加1/5)9.5乘以-9.5除以1/295.77除以-2减去-34.651.88除以2减去-5乘以241.25乘以-3加70乘以-5加5乘以-3加25 9999乘以3加101乘以11乘以(101减去92) 23/4减去3/4)乘以(3乘以6加2)3/7乘以49/9减4/38/9乘以15/36加1/2712乘以5/6减2/9乘以3 8乘以5/4加1/46除以3/8减去3/8除以6 4/7乘以5/9加3/7乘以5/9 5/2减去(3/2加4/5)7/8加(1/8加1/9)9乘以5/6加5/63/4乘以8/9减1/37乘以5/49加3/146乘以(1/2加2/3)8乘以4/5加8乘以11/531乘以5/6减5/69/7减去(2/7减去10/21)5/9乘以18减14乘以2/74/5乘以25/16加2/3乘以3/4 14乘以8/7减5/6乘以12/15 17/32减去3/4乘以9/243乘以2/9加1/35/7乘以3/25加3/73/14乘以2/3加1/61/5乘以2/3加5/69/22加1/11除以1/25/3乘以11/5加4/345乘以2/3加1/3乘以15 7/19加12/19乘以5/61/4加3/4除以2/38/7乘以21/16加1/2101乘以1/5减1/5乘以2150加160除以40120减144除以18加35347加45乘以2减4160除以5237乘以(58加37)除以(64减去9乘以5)已做95除以(64减去45)178减去145除以5乘以6加42812减去700除以(9加31乘以11)85加14乘以(14加208除以26)120减去36乘以4除以18加3558加37)除以(64减去9乘以5)6.8减去6.8乘以0.55)除以8.5标准文案18.1 + (3 - 0.299 ÷ 0.23) × 1 6.8 - 6.8 × 0.55) ÷ 8.50.12 × 4.8 ÷ 0.12 × 4.83.2 × 6 + (1.5 + 2.5) ÷ 1.60.68 × 1.9 + 0.32 × 1.910.15 - 10.75 × 0.4 - 5.75.8 × (3.87 - 0.13) + 4.2 × 3.74 32.52 - (6 + 9.728 ÷ 3.2) × 2.5 7.1 - 5.6) × 0.9 - 1.15] ÷ 2.5 5.4 ÷ [2.6 × (3.7 - 2.9) + 0.62] 12 × 6 ÷ (12 - 7.2) - 612 × 6 ÷ 7.2 - 633.02 - (148.4 - 90.85) ÷ 2.576.25% - 695% - 12%) × 3677 ÷ 4 × 3 ÷ 5 + 3 ÷ 4 × 2 ÷ 5 81/36 + 2/211/10 × 9/53/4 ÷ 9/10 - 1/61/3 + 1/2) ÷ 5/6 - 1/3 ÷ 1/7 3/5 + 3/10 + 3/42 - 2/3 ÷ 1/2) × 2/5 5268.32 - 256986.3 + 456 - 52 × 85% + 3/7 × 49/9 - 4/39 × 5/12 + 1/272 × 5/6 - 2/9 × 33 × 5/4 + 1/494 ÷ 3/8 - 3/8 ÷ 65/9 + 3/96/2 - (3/2 + 4/5)8 + (1/8 + 1/9)8 × 5/6 + 5/6 = 8 5/61/4 × 8/9- 1/3 = 1/910 × 5/49 + 3/14 = 13/98 1.5×(1/2 + 2/3)= 2.252/9×4/5 + 8×11/5 = 94/45 3.1 × 5/6 –5/6 = 2.354/7 -(2/7–10/21)= 4/2119 × 18 –14 × 2/7 = 332 4/75 × 25/16 + 2/3 × 3/4 = 27/44 × 8/7 –5/6 × 12/15 = 46/217/32–3/4 × 9/24 = -67/1922/3÷1/2-1/4×2/5 = 5/62-6/13÷9/26-2/3 = -2 79/338 2/9+1/2÷4/5+3/8 = 67/9010÷5/9+1/6×4 = 46/31/2×2/5+9/10÷9/20 = 1/25/9×3/10+2/7÷2/5 = 31/1261/2+1/4×4/5-1/8 = 5/83/4×5/7×4/3-1/2 = 5/1423-8/9×1/27÷1/27 = 238×5/6+2/5÷4 = 33/101/2+3/4×5/12×4/5 = 11/208/9×3/4-3/8÷3/4 = 11/245/8÷5/4+3/23÷9/11 = 1/21.2×2.5+0.8×2.5 =3.58.9×1.25-0.9×1.25 = 1012.5×7.4×0.8 = 749.9×6.4-(2.5+0.24)= 60.16 27)6.5×9.5+6.5×0.5 = 1794.5 0.35×1.6+0.35×3.4 = 0.9450.25×8.6×4 = 8.66.72-3.28-1.72 = 1.720.45+6.37+4.55 = 11.375.4+6.9×3-(25-2.5)= 16.22×-620-380 =4.8×46+4.8×54 = 5040.8+0.8×2.5 = 21.25×3.6×8×2.5-12.5×2.4 = 71.5 28×12.5-12.5×20 = 25023.65-(3.07+3.65)= 16.934+0.4×0.25)8×7×1.25 = 70 1.65×99+1.65 = 163.3527.85-(7.85+3.4)= 16.648×1.25+50×1.25×0.2×8 = 170 7.8×9.9+0.78 = 77.221010+309+4+681+6)×12 =3×9146×782×6×854 = 1.4×10^115.15×7/8+6.1-0. = 10.3/7 × 49/9- 4/3 = -11/218/9 × 15/36 + 1/27 = 7/5412× 5/6 –2/9 ×3 = 19 7/188× 5/4 + 1/4 = 116÷ 3/8 –3/8 ÷6 = 5 5/84/7 × 5/9 + 3/7× 5/9 = 1/25/2 -(3/2 + 4/5)= 9/107/8 +(1/8 + 1/9)= 29/369.9 × 5/6 + 5/6 = 10.453/4 × 8/9- 1/3 = 1/91.(-2)+2-(-52)×(-1) ×5+87÷(-3)×(-1)改写为:计算表达式:(-2)+2-(-52)×(-1) ×5+87÷(-3)×(-1)2.5.6×0.258×(20-1.25)改写为:计算表达式:5.6×0.258×(20-1.25)3.(-7.1)×〔(-3)×(-5)〕÷2改写为:计算表达式:(-7.1)×〔(-3)×(-5)〕÷24.-2.5×(-4.8)×(0.09)÷(-0.27)改写为:计算表达式:-2.5×(-4.8)×(0.09)÷(-0.27)5.127+352+73+44×(-2)改写为:计算表达式:127+352+73+44×(-2)6.89×276+(-135)-33改写为:计算表达式:89×276+(-135)-337.25×71+75÷29-88÷(-2)改写为:计算表达式:25×71+75÷29-88÷(-2)8.243+89+111+57改写为:计算表达式:243+89+111+579.9405-2940÷28×21改写为:计算表达式:9405-2940÷28×2110.920-1680÷40÷7改写为:计算表达式:920-1680÷40÷711.690+47×52-398改写为:计算表达式:690+47×52-39812.148+3328÷64-75改写为:计算表达式:148+3328÷64-7513.360×24÷32+730改写为:计算表达式:360×24÷32+73014.2100-94+48×54改写为:计算表达式:2100-94+48×5415.51+(2304-2042)×23改写为:计算表达式:51+(2304-2042)×2316.4215+(4361-716)÷81改写为:计算表达式:4215+(4361-716)÷8117.(247+18)×27÷25改写为:计算表达式:(247+18)×27÷2518.36-720÷(360÷18)改写为:计算表达式:36-720÷(360÷18)19.1080÷(63-54)×80改写为:计算表达式:1080÷(63-54)×8020.(528+912)×5-6178改写为:计算表达式:(528+912)×5-617821.8528÷41×38-904改写为:计算表达式:8528÷41×38-90422.264+318-8280÷69改写为:计算表达式:264+318-8280÷69 23.796-5040÷(630÷7)改写为:计算表达式:796-5040÷(630÷7)24.285+(3000-372)÷36改写为:计算表达式:285+(3000-372)÷3625.1+5/6-19/12改写为:计算表达式:1+5/6-19/1226.3x(-9)+7x(-9)改写为:计算表达式:3x(-9)+7x(-9)27.(-54)x1/6x(-1/3)改写为:计算表达式:(-54)x1/6x(-1/3)28.1.18.1+(3-0.299÷0.23)×1改写为:计算表达式:1.18.1+(3-0.299÷0.23)×129.2.(6.8-6.8×0.55)÷8.5改写为:计算表达式:2.(6.8-6.8×0.55)÷8.530.0.12× 4.8÷0.12×4.84改写为:计算表达式:0.12× 4.8÷0.12×4.8431.3.2×1.5+2.5÷(-1.6)改写为:计算表达式:3.2×1.5+2.5÷(-1.6)32.(-2)×3.2×(1.5+2.5)÷1.6改写为:计算表达式:(-2)×3.2×(1.5+2.5)÷1.633.5.6-1.6÷4+(6.8-9)改写为:计算表达式:5.6-1.6÷4+(6.8-9)34.5.38+7.85-5.37÷89改写为:计算表达式:5.38+7.85-5.37÷8935.6.7.2÷0.8-1.2×5改写为:计算表达式:6.7.2÷0.8-1.2×536.6-1.19×3-0.43改写为:计算表达式:6-1.19×3-0.4337.6.5×(4.8-1.2×4)改写为:计算表达式:6.5×(4.8-1.2×4)38.0.68×1.9+0.32×1.9改写为:计算表达式:0.68×1.9+0.32×1.939.10.15-10.75×0.4-5.7改写为:计算表达式:10.15-10.75×0.4-5.740.5.8×(3.87-0.13)改写为:计算表达式:5.8×(3.87-0.13)41.(-8.01)+4.2×3.74改写为:计算表达式:(-8.01)+4.2×3.7442.32.52-(6+9.728÷3.2)×2.5改写为:计算表达式:32.52-(6+9.728÷3.2)×2.5 43.[(7.1-5.6)×0.9-1.15]÷2.5改写为:计算表达式:[(7.1-5.6)×0.9-1.15]÷2.544.5.4÷[2.6×(3.7-2.9)+0.62]改写为:计算表达式:5.4÷[2.6×(3.7-2.9)+0.62]45.12×6÷(12-7.2)-6改写为:计算表达式:12×6÷(12-7.2)-646.12×6÷7.2-6改写为:计算表达式:12×6÷7.2-647.33.02-(148.4-90.85)÷2.5改写为:计算表达式:33.02-(148.4-90.85)÷2.548.(-5)-252×(-78)改写为:计算表达式:(-5)-252×(-78)6)×(-2)+3÷(5+50) = 12 + 3/557-7+3-6-(-90) = 778)(-3)×(-8)×25 = 48007+13)÷(-616)÷(-28) = 1/8+14-100-27)÷4 = -26/4 = -13/2 15)÷(-1)-101÷10 = 15-10.1 = 4.916÷0.21×(-8)×(4.1+5.9) = -54410)×(-2)×4÷{-9÷[6+(-5.67)]} = 320/3 18)(-4)2×[8.01×(-3.14)] = 7257.129-32{-890-[79+8.1]×9} = -20)-23+(-9)×9.42 = -113.9824)3.4×104÷(-5)×200.96 = .298|+76+(-87)]×23/[56+(-75)-(7)]-(8+4+3)×5+21×8/2-6-59 = -3768/21-8-11×8+61 = -5/212/9-7/9-56 = -559/814.6-(-3/4+1.6-4-3/4) = 12.11/2+3+5/6-7/12 = 3 1/42/3-4-1/4*(-0.4)]/1/3+2 = -7/622+(-4)+(-2)+4×3 = 282×8-8×1/2+8/1/8 = -19.52/3+1/2)/(-1/12)×(-12) = -1128)/(-6+4)+(-1)+√9 = -22/(-2)+0/7-(-8)×(-2) = -301/4-5/6+1/3+2/3)/1/2 = 1/1218-6/(-3)×(-2)×2^7 = 38645+3/8×8/30)/(-2)-√36 = -5/1284)/2×(-3)/(-6) = 211/2×(-4/15)/2/3 = -1/251+2+3+4+。
(完整版)初中精选数学计算题200道

(完整版)初中精选数学计算题200道4. x2-5x=05. x2-x-1=06. 化简3寸反+6、^言-2x7. 因式分解 x 4-8x2y2+16y 42 1 _ 5 8. 2x+1 +2x-1 =4x2-1 9. 因式分解(2x+y) 2 -(x+2y) 2 10. 因式分解-8a2b+2a3+8ab2 11. 因式分解a 4-161 14. ( -V3 )o- I -3 I +(-1)2015+(2 )-1计算题1.2. 5x+2 3 x2+x ~x+13.会+工=1 x-4 4-x 1* *12.因式分解3ax2-6axy+8ab213.先化简,再带入求值(x+2)x2-2x+1(x-1)-,x= 33 ,,118. (-3-1) X (- 2 )2-2-1 + (- 2 )320. (x+1) 2-(x+2)(x-2) — 1』21. sin60 - I 1-V 3 I + (2 ) -1 22.(-5) 16x (-2)15(结果以幕的形式表示)23. 若 n 为正整数且(m n ) 2 =9,求(1 m 3n ) 3 (m2)2n3 24. 因式分解 a2+ac-ab-bc 25. 因式分解 x2-5x+6 26. 因式分解(x+2)(x+3)+x 2-4 27. 因式分解(a2+1) 2-4a2 128. -12016+18 + (-3) X I -2 I17. 2x-1 (x+1 x-2 -x+1)/ x2+2x+1 19.1 2x-1 34x 2、一 134.计算(-1) 2 - 4 X [2- (-3) 2]35. 解二元一次方程组x-2y=136. 解二元一次方程组37. 解二元一次方程组38.39.40. 虹x+3y=6 2(x-y)3匚5y-x=3x+2y=6 I 3x-2y=2解不等式 3 (x-1) >2x+23x+1 7x-3 解不等式飞3x+y4122(x-2)5 v 20化简a(a-1) 2-(a+1)(a2-a+1)a 41. (a-b_b_+ b-a)1a+b一 - 142.当m*,求代数式1 m+一m143. (2 ) -1-(也-1) o + -3 Itan45o-cos60o+ cos30o tan60山x2-5x+6 44.先化简再求值总寂3.(1奇2)(1+x-3 ),其中x^/345-先化简再求值悬’其中x =-1,y =246. 解方程 x2-3x=047. 6-」(-2)2 - 2-1+ (-3.14) o+拒 +cos245148.计算(A /3 ) 2+4X (- 2 ) -2349.先化简,再求值(a+b) (a-b)+b(b-2),其中 a 淄 ,b=-1a b2 a+b52. 化间 [a-b +a(b-a) ] 无53. 计算-22+(3-3.14) o+3sin30 54.计算(1 ) -1+ (2006-兀)o - V3 tan60 355. 计算 2013-(兀-3.14) o+l-3 I + (-1) 56.157. 计算:-2斗1-3.14|+ (-洞2X 表)颂、3七、「苹 tan 疗 111-Vsl-(5兀+2013)。
初中数学精选计算题练习大全
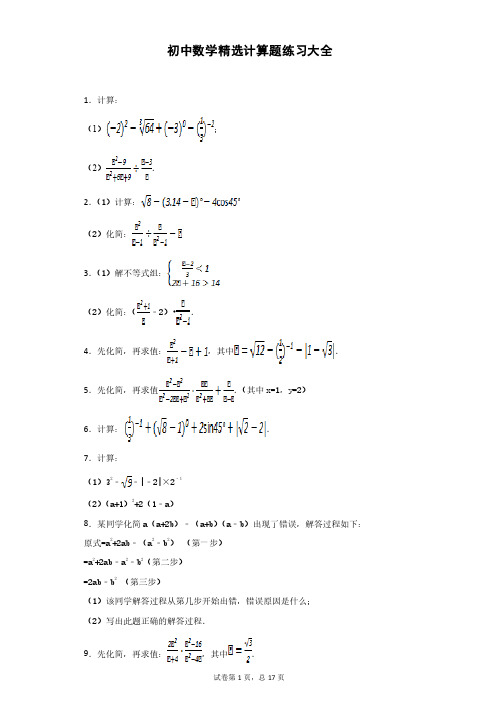
初中数学精选计算题练习大全1.计算:.计算: (1);(2).2.(1)计算:(2)化简:3.(1)解不等式组:(2)化简:(﹣2)•.4.先化简,再求值:,其中.5.先化简,再求值.(其中x=1x=1,,y=2y=2))6.计算:.7.计算:.计算: (1)32﹣﹣|﹣2|×2﹣1(2)(a+1a+1))2+2+2((1﹣a )8.某同学化简a (a+2b a+2b)﹣()﹣()﹣(a+b a+b a+b))(a ﹣b )出现了错误,解答过程如下:)出现了错误,解答过程如下: 原式原式=a =a 2+2ab +2ab﹣(﹣(﹣(a a 2﹣b 2) (第一步)(第一步) =a 2+2ab +2ab﹣﹣a 2﹣b 2(第二步)(第二步) =2ab =2ab﹣﹣b 2(第三步)(第三步)(1)该同学解答过程从第几步开始出错,错误原因是什么;)该同学解答过程从第几步开始出错,错误原因是什么; (2)写出此题正确的解答过程.)写出此题正确的解答过程.9.先化简,再求值:,其中.10.计算:.11.先化简,再求值:;其中,.12.计算:(﹣1)2﹣2sin45°2sin45°++(π﹣2018)0+||.13.计算:.14.计算:15.(1)计算:;(2)分解因式:6(a-b)2+3(a-b).16.计算:.17.计算:2﹣1sin60°+|1|.sin60°+|118.已知T.(1)化简T;的值.(2)若正方形ABCD的边长为a,且它的面积为9,求T的值.19.化简分式(+)÷,并在2,3,4,5这四个数中取一个合适的数作为a 的值代入求值.的值代入求值.20.2﹣1+|1﹣|+(﹣2)00﹣cos60°21.计算:.22.先化简,再求值:,其中23.计算化简(本小题满分10分)分)(1)(2)24.(2011?舟山)计算:.25.先化简,再求值:,其中a2﹣4=0.26..27.(本小题满分5分)分)先化简,再求值:(1-)÷,其中=sin60°=sin60°. . 28.计算:.29.先化简,再求值:,其中x=2x=2..30.计算:31.已知a2=19=19,求,求的值.的值.32.计算:|2﹣|+2sin45°﹣()0.33.先化简,再求值:,其中m=+1.34.计算:35.先化简,再求值:.先化简,再求值:36.计算:37.先化简,再求值:,其中a是方程a2+a﹣6=0的解.的解.38.化简:39.计算:(-3-3))2+2017- ×sin45°.×sin45°.40.化简:.41.计算:.42.化简:(y+2)(y﹣2)﹣(y﹣1)(y+5)43.(1)计算:︱-)计算:︱-22︱+( + 1)0-()-1+tan60°+tan60°(2)解分式方程:+ 1)解分式方程: =+ 144.(题文)先化简,再求值:(a﹣)÷,其中a=,b=1.45.计算:46.先化简,再求值:,其中x=2,y=3.47.Ⅰ.解不等式组,并把解集在数轴上表示出来.,并把解集在数轴上表示出来.Ⅱ.计算:(π﹣3)0+﹣2sin45°﹣()﹣1.48.(1)实数x取哪些整数时,不等式2x﹣1>x+1与x﹣1≤7﹣x都成立?都成立?中选取合适的整数代入求值. (2)化简:()÷,并从0≤x≤4中选取合适的整数代入求值.49.先化简,再求值:,其中.50.算:51.先化简,再求值:,其中.52.计算:53.先化简,再求值:,其中x=﹣.54.计算:+(﹣)﹣1+|1﹣|﹣4sin45°.55.化简:56.计算:57.先化简,再求值:,其中a=+1.58.(1)计算:2﹣11+(2018﹣π)00﹣sin30°;(2)化简:(a+1)22﹣a(a+1)﹣1.59.计算:.计算:(1)(2)2﹣|﹣4|+3﹣1×6+20;(2).60.已知=2,请先化简÷,再求该式子的值.,再求该式子的值.61.先化简,再求值(﹣)÷,其中a,b满足a+b﹣=0.62.计算﹣(﹣2)+(π﹣3.14)0++(﹣)﹣163.解不等式组,并求出它的整数解,再化简代数式•(﹣),从上述整数解中选择一个合适的数,求此代数式的值.从上述整数解中选择一个合适的数,求此代数式的值.64.计算:﹣25÷23+|﹣1|×1|×55﹣(π﹣3.14)065.计算:.计算:);(1)(x+2y)2﹣(x+y)(x﹣y);(2)(a﹣1﹣)÷66.先化简,再求值:(1﹣x+)÷,其中x=tan45°x=tan45°++()﹣1.67.(1)求不等式组的整数解;的整数解;(2)先化简,后求值(1﹣)÷,其中a=+1.68.计算:(﹣1)2018+|﹣|﹣(﹣π)0﹣2sin60°.69.(1)计算:()﹣2+﹣2cos45°;(2)先化简,再求值:÷(1+),其中a=2.70.计算.计算 (1)计算:)计算:22﹣2+(3)÷﹣3sin45°;(2)解方程:+1=. 71.化简:72.计算:|﹣|﹣2﹣1+73.先化简,再求值:(﹣)÷,其中a=3﹣1+2sin30°.74.计算:(+2)22﹣+2﹣275.先化简,再求值:(2m+1)(2m ﹣1)﹣(m ﹣1)2+(2m )3÷(﹣8m ),其中m 是方程x 2+x ﹣2=0的根的根76.计算:4cos45°4cos45°++(π﹣2018)0﹣77.计算:2tan45°﹣|﹣3|+()﹣2﹣(4﹣π)0.78.先化简,再求值:(1﹣)÷,其中a=2+.79.先化简,再求值:÷(a ﹣1﹣),并从﹣1,0,1,2四个数中,选一个合适的数代入求值数代入求值80.计算:()﹣2+|﹣2|﹣+6cos30°+6cos30°++(π﹣3.14)0.81.先化简(1﹣)÷,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.的解代入求值.82.计算:﹣|4﹣|﹣(π﹣3.14)0+(1﹣cos30°)×()﹣2.2cos45°++()﹣1﹣(π﹣1)083.计算:﹣2cos45°84.(1)计算:+|﹣2|;(2)化简:(a+3)(a﹣2)﹣a(a﹣1).85.先化简,再求值:(﹣1)÷,其中x=+1.86.如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形,拿掉边长的小正方形纸板后,将剩下的三块拼成新的矩形.为n的小正方形纸板后,将剩下的三块拼成新的矩形.的代数式表示拼成矩形的周长;(1)用含m或n的代数式表示拼成矩形的周长;,求拼成矩形的面积.(2)m=7,n=4,求拼成矩形的面积.87.先化简,再求值:÷(﹣a),其中a=﹣1,b=1.88.先化简,再求值:(1﹣)÷,其中a=sin30°.89.(1)计算:|3﹣5|﹣(π﹣3.14)0+(﹣2)﹣1+sin30°;(2)解分式方程:+1=.90.(题文)已知:x2﹣y2=12,x+y=3,求2x2﹣2xy的值.的值.91.求值:(﹣1)2018+|1﹣|﹣92.先化简再求值:(a﹣)÷,其中a=1+,b=1﹣.93.计算:|2﹣|+(π﹣1)0+﹣()﹣1194.(1)计算:﹣4cos60°﹣(π﹣3.14)0﹣()﹣1(2)先化简,再求值:(1﹣)÷,其中x=2.95.计算:2sin30°﹣(π﹣)0+|﹣1|+()﹣196.先化简,再求值:(﹣)÷,其中a=.97.先化简,再求值:,其中x=﹣1.98.先化简,再求值:(a+b )2+b (a ﹣b )﹣4ab ,其中a=2,b=﹣.99.计算:(﹣1)2018﹣+(π﹣3)0+4cos45°100.计算:+(π﹣2018)0﹣2tan45°101.计算|1﹣|﹣2sin45°2sin45°+2+2﹣1﹣(﹣1)2018.102.(1)计算:|2﹣|+(+1)0﹣3tan30°3tan30°++(﹣1)2018﹣()﹣1; (2)解不等式组:并判断﹣1,这两个数是否为该不等式组的解.103.先化简,再求值:(+1)÷,其中a=tan60°﹣|﹣1|.104.先化简,再求代数式(1﹣)÷的值,其中a=4cos30°a=4cos30°+3tan45°+3tan45°. 105.计算:|﹣4|+3tan60°﹣﹣()﹣1106.计算:|﹣2|+(﹣1)×(﹣3)107.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.,且任意相邻四个台阶上数的和都相等. 尝试尝试 (1)求前4个台阶上数的和是多少?个台阶上数的和是多少?(2)求第5个台阶上的数x 是多少?是多少? 应用应用 求从下到上前31个台阶上数的和.个台阶上数的和.发现发现 试用含k (k 为正整数)的式子表示出数“1”所在的台阶数.所在的台阶数.108.嘉淇准备完成题目:化简:,发现系数“”印刷不清楚.清楚.(1)他把“”猜成3,请你化简:(3x 2+6x +8)–(6x +5x 2+2););(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?是几? 109.已知x=+1,求x 2﹣2x ﹣3的值.的值.110.计算:(﹣1)2008+π0﹣()﹣1+.111.先化简,再求值:,其中.112.先化简,再求值:(x+2+)÷,其中x=2.113.计算.114.化简代数式:,再从不等式组的解集中取一个合适的整数值代入,求出代数式的值.合适的整数值代入,求出代数式的值.115.先化简,再求值:(a ﹣2b )(a+2b )﹣(a ﹣2b )2+8b 2,其中a=﹣2,b=.116.计算:(﹣1)2+(π﹣3.14)0﹣|﹣2| 117.先化简,再求值:,其中x 为整数且满足不等式组.118.先化简,再求值:(1+)÷,其中x 满足x 2﹣2x ﹣5=0.119.计算:(1)(﹣2)2×|﹣3|﹣()00;(2)(x+1)22﹣(x 22﹣x )120.先化简,再求值:a (a +2b )﹣(a +1)2+2a ,其中.121.先化简,再求值:(1﹣)÷,其中a=﹣3.122.(1)计算:|﹣2|﹣2cos60°2cos60°++()﹣1﹣(2018﹣)0(2)先化简(1﹣)•,再在1、2、3中选取一个适当的数代入求值.中选取一个适当的数代入求值.123.计算:.124.(1)化简÷(x ﹣).(2)解方程:=3.125.先化简,再求值:.其中x=sin60°.126.计算:()﹣2+(π2﹣π)0+cos60°+cos60°+|+|﹣2|127.先化简,再求值:,其中,其中.128.计算:129.先化简,再求值:(x+y )(x ﹣y )+y (x+2y )﹣(x ﹣y )2,其中x=2+,y=2﹣.130.计算:﹣|﹣|+(﹣2)2﹣(π﹣3.14)0×()﹣2.131.对于三个数、、,用表示这三个数的中位数,用表示这三个数中最大数,例如:,,.解决问题:解决问题:(1)填空:,如果,如果,则的取值范围为的取值范围为 ;; (2)如果,求的值;的值; (3)如果,求的值的值..132.计算:133.阅读下列题目的解题过程:.阅读下列题目的解题过程:已知a 、b 、c 为△ABC 的三边,且满足a 2c 2﹣b 2c 2=a 4﹣b 4,试判断△ABC 的形状.的形状. 解:∵a 2c 2﹣b 2c 2=a 4﹣b 4 (A )∴c 2(a 2﹣b 2)=(a 2+b 2)(a 2﹣b 2) (B ) ∴c 2=a 2+b 2 (C ) ∴△∴△ABC ABC 是直角三角形是直角三角形问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ; (2)错误的原因为:)错误的原因为: ; (3)本题正确的结论为:)本题正确的结论为: .134.先化简,再求值:,其中x=2﹣1.135.先化简,再求值:x (x+1)+(2+x )(2﹣x ),其中x=﹣4.136.+-+137.先化简,再求值:(+1)÷,其中x 是方程x 2+3x=0的根.的根.138.计算:﹣2sin45°2sin45°++()﹣1﹣|2﹣|.139.先化简,再求值:.先化简,再求值:,其中.140.先化简,再求值:,其中x 满足x 2-2x -2=0.141.计算:(π-2)°-2)°+4cos30°+4cos30°--(-)-2.142.先化简,再求值:,其中.143.计算:.144.先化简,再求值:(1+)÷.其中x =3.145.计算:|﹣5|+(﹣1)2﹣()﹣1﹣.146.先化简,再求值:,其中,.147.计算:.148.计算:(﹣6)2×(﹣).).149.(1)计算:π0+2cos30°﹣|2﹣|﹣()﹣2;(2)化简:(2﹣)÷.150.化简:151.计算:(-)×)×((-)+|-1|+(5-2π)0152.先化简,再求值:其中153.计算:154.计算:.计算:155.计算:(﹣2)2+20180﹣156.(1)计算:;(2)化简:(m+2)2 +4(2-m)157.先化简,再求值:,其中.158.计算:.159.我们常用的数是十进制数,如,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中等于十进制的数6,等于十进制的数53.那么等于十进制中的哪个数?二进制中的数101011等于十进制中的哪个数?160.(1).(2)化简161.先化简,再求值:,其中.162.计算:.sin30°++(2018﹣)0﹣2﹣1+|﹣4|;163.(1)计算:sin30°(2)化简:(1﹣)÷.164.(1)计算:;(2)解不等式:165.先化简,再求值:(xy2+x2y)×,其中x=π0﹣()﹣1,y=2sin45°﹣.166.对于任意实数、,定义关于“”的一种运算如下:.例如.的值;(1)求的值;(2)若,且,求的值.167.计算或化简.(1);(2).168.如图,在数轴上,点、分别表示数、(1)求的取值范围.的点应落在( )(2)数轴上表示数的点应落在(A.点的左边的右边的左边 B.线段上C.点的右边169.计算.170.先化简,再求值: ,其中171.计算: .172.(1)计算:;(2)化简并求值:,其中,.173.先化简,再求值:,其中是不等式组的整数解.174.(1)计算:.(2)解方程:.175.观察以下等式:.观察以下等式:第1个等式:,第2个等式:,第3个等式:,第4个等式:,第5个等式:,……按照以上规律,解决下列问题:按照以上规律,解决下列问题:个等式: ;(1)写出第6个等式:个等式: (用含n的等式表示),并证明(2)写出你猜想的第n个等式:176.计算:177.先化简,再求值:,其中.178.有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:木工师傅设计了如图所示的三种方案:小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,对于方案一,小明是这样验证的:证的:a2+ab+ab+b2=a2+2ab+b2=(a+b)2请你根据方案二、方案三,写出公式的验证过程.请你根据方案二、方案三,写出公式的验证过程.方案二:方案二:方案三:方案三:179.计算:|﹣2|﹣+23﹣(1﹣π)0.180.(题文)对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”.的倍数,请说明理由; (1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;(2)如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数.若四位数m为“极数”,记D(m)=,求满足D(m)是完全平方数的所有m.181.计算:.计算:))计算:;)计算:..=.先化简,再求值:,其中a=..计算: ()()20212017323p -æö--+---ç÷èø..先化简,再求值: 221x y x y x yæö-¸ç÷--èø,其中=32-,=112-æöç÷èø.211--=1321-- 4312--=3…再求值: 22214244a a a a a a a a +--æö+¸ç÷--+èø,=()10132p -æö-+ç÷èø.(221x x -++)÷21x x x -+ (12)191.先化简,再求值:(m+2m+2﹣﹣52m -)• 243m m --,其中m=m=﹣﹣12. 192.(1)计算:)计算:||﹣4|4|﹣(﹣﹣(﹣﹣(﹣22)2+9﹣(12)0(2)解不等式组32{ 1213x x xx -³+>-.193.计算:.计算:(1)2(1)2-1+sin30°+sin30°-|-2|-|-2|-|-2|;; (2)(2)((-1-1))0-|3-π|+()23p -.。
七年级计算题满分训练

七年级计算题满分训练一、有理数运算。
1. 计算:(-2)+3-(-5)- 解析:- 去括号法则为:括号前是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前是“ - ”,把括号和它前面的“ - ”去掉后,原括号里各项的符号都要改变。
- 所以-(-5)=5,则原式=-2 + 3+5。
- 接着按照从左到右的顺序计算,-2+3 = 1,1 + 5=6。
2. 计算:4×(-3)÷(-6)- 解析:- 根据有理数的乘除法运算顺序,从左到右依次计算。
- 先计算4×(-3)=-12,再计算-12÷(-6)。
- 两数相除,同号得正,异号得负,并把绝对值相除,所以-12÷(-6)=2。
3. 计算:(-2)^3+(-3)×[(-4)^2 - 2]- 解析:- 先计算指数运算。
(-2)^3=-8,(-4)^2 = 16。
- 然后计算括号内的式子:(-4)^2-2=16 - 2=14。
- 接着计算乘法:(-3)×14=-42。
- 最后计算加法:-8+(-42)=-8-42=-50。
4. 计算:(1)/(2)-<=ft(-(1)/(3))+<=ft(-(1)/(4))- 解析:- 去括号得(1)/(2)+(1)/(3)-(1)/(4)。
- 先通分,分母2、3、4的最小公倍数是12。
- 则(1)/(2)=(6)/(12),(1)/(3)=(4)/(12),(1)/(4)=(3)/(12)。
- 所以原式=(6 + 4-3)/(12)=(7)/(12)。
5. 计算:-1^4-(1 - 0.5)×(1)/(3)×[2-(-3)^2]- 解析:- 先计算指数运算,-1^4=-1,(-3)^2 = 9。
- 然后计算括号内的式子:1-0.5 = 0.5=(1)/(2),2-(-3)^2=2 - 9=-7。
- 接着计算乘法:(1)/(2)×(1)/(3)×(-7)=-(7)/(6)。
初中数学计算题库

初中数学计算题库一、有理数运算1. 加法运算- 题目:计算(+3)+( - 5)。
- 解析:这就像是在数轴上玩游戏,正数是向右走,负数是向左走。
先向右走3步,再向左走5步,那最后就到了 - 2这个位置啦,所以(+3)+( - 5)= - 2。
- 题目:( - 2)+( - 3)。
- 解析:两个负数相加,就像两个倒霉蛋凑一块儿了。
向左走2步,再向左走3步,总共向左走了5步,所以( - 2)+( - 3)= - 5。
2. 减法运算- 题目:计算5-(+3)。
- 解析:减一个正数呢,就相当于加上它的相反数。
所以5-(+3)=5+( - 3),在数轴上就是从5这个位置向左走3步,结果就是2啦。
- 题目:( - 3)-(-5)。
- 解析:减一个负数就相当于加上它的正数哦。
那( - 3)-(-5)=(-3)+5,从 - 3这个点向右走5步,就到了2这个位置,所以结果是2。
3. 乘法运算- 题目:计算( - 2)×3。
- 解析:正数乘以负数,结果是负数。
就像你有3个负债2元的账单,那总共就负债6元啦,所以( - 2)×3=-6。
- 题目:( - 2)×(-3)。
- 解析:两个负数相乘就变成正数啦。
可以想象成欠了2次 - 3元,那就是得到了6元,所以( - 2)×(-3)=6。
4. 除法运算- 题目:计算( - 6)÷3。
- 解析:除法和乘法是反着来的。
负数除以正数结果是负数,就像把 - 6元平均分给3个人,每人负债2元,所以( - 6)÷3=-2。
- 题目:( - 8)÷(-2)。
- 解析:两个负数相除结果是正数。
把 - 8元的债务平均分给 - 2个人,那每人就得到4元啦,所以( - 8)÷(-2)=4。
二、整式运算1. 合并同类项- 题目:化简3x + 2x。
- 解析:这就好比3个苹果加上2个苹果,那就是5个苹果啦。
这里x就像苹果,所以3x+2x = 5x。
