高数积分公式大全(2)

高数积分公式

高数积分公式积分是高数学中一个重要的概念，是计算不同函数的累积结果的工具。

在高数学中，积分公式尤其重要，因为它可以用来计算许多不同函数的积分，从而推导出更加复杂的数学公式。

在这篇文章中，我们将介绍一些常见的高数积分公式，以及它们的应用。

高数积分公式大体可以分为几类：一、常见的几何积分公式1、曲线积分：对于不同的曲线，积分的公式也不尽相同，比如：一次函数曲线的积分，可以用如下公式表示：∫ax+b dx = (ax+b)^2/2 + c二次函数曲线的积分，可以用如下公式表示：∫ax^2+bx+c dx = (ax^3/3 + bx^2/2 + cx) + c此外，还有三次函数曲线、指数函数曲线和对数函数曲线的积分公式。

2、多项式积分：多项式积分是一种常见的积分形式，其公式为：∫ax^n+bx^(n-1)++c dx=(ax^(n+1)+bx^n++cx + c其中，n是自然数，a、b、c为常数。

二、椭圆变换的积分公式椭圆变换是一种用于计算不同函数的增量的方法，其积分公式可以表示为：∫f(x) dx = (1/b)∫f((a/b)cosθ + (1/b)sinθ)dθ其中，f(x)为函数，a、b为常数，θ为变量。

三、反幂函数积分公式反幂函数指的是形式形如：y=ax^(-b)的函数，它的积分公式可以表示为：∫ax^(-b) dx = (ax^(1-b))/ (1-b) + c四、指数函数积分公式指数函数指的是形式形如：y=e^(ax)的函数，它的积分公式可以表示为：∫e^(ax) dx = (1/a)e^(ax) + c以上就是我们介绍的一些常见的高数积分公式，其中，每一个公式都有其独特的应用，在高等数学中都可以找到。

因此，认真学习这些公式，能够有效地提升我们的学习效率，更好地理解高等数学中的概念。

高数微积分公式大全(考试必考)

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、基本初等函数的n 阶导数公式（1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan x dx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =+十、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高等数学积分公式大全

高等数学积分公式大全高等数学是一门非常重要的学科，在很多领域都有应用。

其中，积分学是高等数学中的一个重要章节。

积分可以理解为求解曲线图形下面的面积，不同类型的积分公式有着不同的概念和应用，下面，就为大家整理了一份高等数学积分公式大全，让大家对这个知识点有一个更全面的认识。

1. 常数积分公式$$\int kdx=kx+C$$2. 幂函数积分公式$$\int x^ndx=\frac{x^{n+1}}{n+1}+C$$3. 指数函数积分公式$$\int e^xdx=e^x+C$$4. 对数函数积分公式$$\int \frac{1}{x}dx=\ln|x|+C$$5. 三角函数积分公式$$\int \sin xdx=-\cos x+C$$$$\int \cos xdx=\sin x+C$$6. 反三角函数积分公式$$\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x+C$$$$\int \frac{1}{1+x^2}dx=\arctan x+C$$$$\int \frac{1}{\sqrt{x^2-1}}dx=\ln|x+\sqrt{x^2-1}|+C$$7. 换元法积分公式$$\int f(u)du=\int f(u(x))\frac{du}{dx}dx$$8. 分部积分公式$$\int u(x)v'(x)dx=u(x)v(x)-\int v(x)u'(x)dx$$9. 定积分公式$$\int_a^bf(x)dx=F(b)-F(a)$$10. 积分中值定理$$\int_a^bf(x)dx=f(c)(b-a)$$这便是几种高等数学积分公式的介绍，这些公式是数学中不可或缺的知识点，掌握这些公式不仅有助于学生学好数学，还对应用数学的工作有相当多的帮助。

除了这些基本的积分公式之外，高等数学还涉及到一些比较复杂的积分公式，如多重积分、线性代数积分、微积分方程等等。

1. 多重积分公式多重积分是指对多元函数的积分，通常被用于几何问题、概率论问题和物理学问题中。

高等数学积分公式大全

高等数学积分公式大全在高等数学中，积分是求解不定积分、定积分和定积分的一种重要方法。

积分公式是指一些常见函数的积分表达式，熟悉和掌握这些公式可以加快求解积分的速度。

下面是一些常见的高等数学积分公式：一、不定积分公式：1. ∫kdx = kx + C （常数函数的积分）2. ∫x^n dx = (x^(n+1))/(n+1) + C （幂函数的积分）其中n不等于-1，C为常数。

3. ∫1/x dx = ln，x， + C （自然对数函数的积分）4. ∫e^x dx = e^x + C （指数函数的积分）5. ∫sinxdx = -cosx + C （正弦函数的积分）6. ∫cosxdx = sinx + C （余弦函数的积分）7. ∫sec^2xdx = tanx + C （正割函数的积分）8. ∫csc^2xdx = -cotx + C （余割函数的积分）9. ∫secxtanxdx = secx + C （正割函数与正切函数的积分）10. ∫cscxcotxdx = -cscx + C （余割函数与余切函数的积分）二、定积分公式：1. ∫[a,b]kdx = k(b-a) （常数函数的定积分）2. ∫[a,b]xdx = (b^2 - a^2)/2 （幂函数的定积分）3. ∫[a,b]1/x dx = ln，b/a，（自然对数函数的定积分）三、定积分计算方法与公式：1.分部积分法∫u(x)v'(x)dx = u(x)v(x) - ∫v(x)u'(x)dx2.代换法（换元积分法）∫f(g(x))*g'(x)dx = ∫f(g(x))d(g(x))3.增广方法当函数的导数是其本身的倍数，例如dy/dx = ky时，可以使用增广方法进行求解，具体公式为∫d(y)e^(-kx) = e^(-kx)y4.牛顿-莱布尼茨公式若F(x)为f(x)的一个原函数，则∫[a,b]f(x)dx = F(b) - F(a)5.分式积分对于形如∫(P(x)/Q(x))dx的分式积分，其中P(x)和Q(x)是多项式函数，可以使用部分分式法进行分解，然后再分别求积分。

高数微积分公式大全(总结的比较好)---精品管理资料

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x xμμμ-= ⑶()sin cos x x '=⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅⑼()xxee'= ⑽()ln xxaaa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arccot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则 (1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式 (1）()()!n nxn = （2)()()n ax b n ax b e a e ++=⋅ （3)()()ln n x x n a a a =（4）()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ （5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7） ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则 ⑴()0d c = ⑵()1d xxdx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅ ⑼()xxd ee dx = ⑽()ln xxd a aadx = ⑾()1ln d x dx x=⑿()1log ln xad dx x a= ⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arccot 1d x dx x =-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰ ⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式2211arctan xdx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsinxc a=+ ln x c =+九、下列常用凑微分公式十、分部积分法公式⑴形如n ax x e dx ⎰,令nu x =，axdv e dx =形如sin n x xdx ⎰令nu x =,sin dv xdx =形如cos n x xdx ⎰令nu x =,cos dv xdx = ⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可.十一、第二换元积分法中的三角换元公式(1 sin x a t = (2） tan x a t = sec x a t =【特殊角的三角函数值】（1）sin 00= (2）1sin62π=(3）sin 32π= (4)sin 12π=) (5）sin 0π=（1）cos01= （2）cos62π=（3）1cos 32π= (4）cos 02π=）（5）cos 1π=-（1)tan 00= （2）tan63π=（3)tan 3π=(4）tan 2π不存在（5）tan 0π=（1）cot 0不存在（2)cot 6π=（3)cot3π=(4)cot 02π=（5）cot π不存在十二、重要公式（1）0sin lim1x xx→= （2）()10lim 1x x x e →+= (3))1n a o >=（4）1n = (5)limarctan 2x x π→∞=（6)lim tan 2x arc x π→-∞=-（7）limarccot 0x x →∞= （8）lim arccot x x π→-∞= （9）lim 0xx e →-∞=（10)lim x x e →+∞=∞ （11）0lim 1xx x +→= (12）0101101lim0n n n m m x m a n mb a x a x a n m b x b x b n m--→∞⎧=⎪⎪+++⎪=<⎨+++⎪∞>⎪⎪⎩（系数不为0的情况）十三、下列常用等价无穷小关系（0x →）sin x x tan x x arcsin x x arctan xx 211cos 2xx - ()ln 1x x + 1x e x - 1ln x a x a - ()11x x ∂+-∂十四、三角函数公式 1.两角和公式sin()sin cos cos sin A B A B A B +=+ sin()sin cos cos sin A B A B A B -=- cos()cos cos sin sin A B A B A B +=- cos()cos cos sin sin A B A B A B -=+tan tan tan()1tan tan A B A B A B ++=- tan tan tan()1tan tan A BA B A B --=+cot cot 1cot()cot cot A B A B B A ⋅-+=+ cot cot 1cot()cot cot A B A B B A ⋅+-=- 2.二倍角公式sin 22sin cos A A A = 2222cos 2cos sin 12sin 2cos 1A A A A A =-=-=-22tan tan 21tan AA A=-3。

高数积分公式大全

常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +⎰＝1ln ax b C a++ 2．()d ax b x μ+⎰＝11()(1)ax b C a μμ++++（1μ≠-）3．d x x ax b +⎰＝21(ln )ax b b ax b C a+-++ 4．2d x x ax b +⎰＝22311()2()ln 2ax b b ax b b ax b C a ⎡⎤+-++++⎢⎥⎣⎦5．d ()xx ax b +⎰＝1lnax b C b x +-+ 6．2d ()xx ax b +⎰＝21ln a ax b C bx b x +-++ 7．2d ()x x ax b +⎰＝21(ln )b ax b C a ax b++++ 8．22d ()x x ax b +⎰＝231(2ln )b ax b b ax b C a ax b+-+-++ 9．2d ()xx ax b +⎰＝211ln ()ax b C b ax b b x +-++的积分10．x C +11．x ⎰＝22(3215ax b C a -+12．x x ⎰＝22232(15128105a x abx b C a-++13．x＝22(23ax b C a -14．2x＝22232(34815a x abx b C a -++15．＝(0)(0)C b C b ⎧+><16．2a b - 17．x＝b +18．x＝2a x -+ （三）含有22x a ±的积分 19．22d x x a +⎰=1arctan x C a a+ 20．22d ()n x x a +⎰=2221222123d 2(1)()2(1)()n n x n xn a x a n a x a ---+-+-+⎰21．22d xx a -⎰=1ln 2x a C a x a-++ （四）含有2(0)ax b a +>的积分22．2d x ax b +⎰＝(0)(0)C b C b ⎧+>+<23．2d x x ax b +⎰＝21ln 2ax b C a++ 24．22d x x ax b +⎰＝2d x b x a a ax b -+⎰25．2d ()x x ax b +⎰＝221ln 2x C b ax b++ 26．22d ()x x ax b +⎰＝21d a xbx b ax b--+⎰27．32d ()x x ax b +⎰＝22221ln 22ax b a C b x bx +-+28．22d ()x ax b +⎰＝221d 2()2x xb ax b b ax b+++⎰ （五）含有2ax bx c ++(0)a >的积分29．2d x ax bx c ++⎰＝22(4)(4)C b ac Cb ac +<+>30．2d x x ax bx c ++⎰＝221d ln 22b x ax bx c a a ax bx c++-++⎰(0)a >的积分 31．＝1arsh xC a+＝ln(x C + 32．C +33．xC34．x＝C +35．2x2ln(2a x C ++ 36．2x＝ln(x C +++37．1ln aC a x -+ 38．C + 39．x2ln(2a x C ++40．x ＝2243(25ln(88x x a a x C ++++41．x ⎰C42．x x ⎰＝422(2ln(88x a x a x C +++43．d x x ⎰ln a a C x ++44．2d x x ⎰＝ln(x C x-+++(0)a >的积分45．＝1arch x xC x a+=ln x C ++ 46．C +47．x C +48．x ＝C +49．2x 2ln 2a x C ++50．2x ＝ln x C +++51．1arccosaC ax+52．C +53．x 2ln 2a x C ++54．x ＝2243(25ln 88x x a a x C -++55．x ⎰C56．x x ⎰＝422(2ln 88x a x a x C -++57．d x x⎰arccos a a C x +58．2d x x ⎰＝ln x C x-+++(0)a >的积分 59．＝arcsin xC a+ 60．C +61．x ＝C62．x C +63．2x ＝2arcsin 2a x C a + 64．2x arcsinxC a-+65．1ln a C a x +66．C +67．x 2arcsin 2a x C a+68．x ＝2243(52arcsin 88x x a x a C a-+69．x ⎰＝C +70．x x ⎰＝422(2arcsin 88x a x x a C a-+71．x a C ++72．x ＝arcsin xC a-+(0)a >的积分73．2ax b C +++74．x75．x 76．＝C +77．x 2C ++78．x ＝C +79．x ＝((x b b a C --++80．x ＝((x b b a C --81．C ()a b <82．x 2()4b a C -++ （十一）含有三角函数的积分83．sin d x x ⎰＝cos x C -+ 84．cos d x x ⎰＝sin x C + 85．tan d x x ⎰＝ln cos x C -+ 86．cot d x x ⎰＝ln sin x C +87．sec d x x ⎰＝ln tan()42x C π++＝ln sec tan x x C ++ 88．csc d x x ⎰＝ln tan2xC +＝ln csc cot x x C -+ 89．2sec d x x ⎰＝tan x C + 90．2csc d x x ⎰＝cot x C -+ 91．sec tan d x x x ⎰＝sec x C + 92．csc cot d x x x ⎰＝csc x C -+93．2sin d x x ⎰＝1sin 224x x C -+94．2cos d x x ⎰＝1sin 224x x C ++95．sin d n x x ⎰＝1211sin cos sin d n n n x x x x n n----+⎰ 96．cos d n x x ⎰＝1211cos sin cos d n n n x x x x n n ---+⎰97．d sin n x x ⎰＝121cos 2d 1sin 1sin n n x n xn x n x ----⋅+--⎰ 98．d cos n x x ⎰＝121sin 2d 1cos 1cos n n x n xn x n x---⋅+--⎰ 99．cos sin d m n x x x ⎰＝11211cos sin cos sin d m n m nm x x x x x m n m n -+--+++⎰＝11211cos sin cos sin d m n m n n x x x x x m n m n+----+++⎰ 100．sin cos d ax bx x ⎰＝11cos()cos()2()2()a b x a b x C a b a b -+--++-101．sin sin d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b -++-++-102．cos cos d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b ++-++-103．d sin xa b x +⎰tanxa b C ++22()a b >104．d sin x a b x +⎰C +22()a b <105．d cos xa b x+⎰)2x C +22()a b >106．d cos x a b x +⎰C +22()a b <107．2222d cos sin x a x b x +⎰＝1arctan(tan )bx C ab a+ 108．2222d cos sin xa xb x-⎰＝1tan ln 2tan b x a C ab b x a ++- 109．sin d x ax x ⎰＝211sin cos ax x ax C a a -+ 110．2sin d x ax x ⎰＝223122cos sin cos x ax x ax ax C a a a -+++111．cos d x ax x ⎰＝211cos sin ax x ax C a a ++112．2cos d x ax x ⎰＝223122sin cos sin x ax x ax ax C a a a+-+（十二）含有反三角函数的积分（其中0a >） 113．arcsin d xx a ⎰＝arcsin x x C a+114．arcsin d xx x a ⎰＝22()arcsin 24x a x C a -+115．2arcsin d xx x a⎰＝3221arcsin (239x x x a C a +++116．arccos d x x a ⎰＝arccos x x C a117．arccos d xx x a ⎰＝22()arccos 24x a x C a --+118．2arccos d xx x a⎰＝3221arccos (239x x x a C a -++119．arctan d xx a ⎰＝22arctan ln()2x a x a x C a -++ 120．arctan d x x x a ⎰＝221()arctan 22x a a x x C a +-+121．2arctan d xx x a⎰＝33222arctan ln()366x x a a x a x C a -+++（十三）含有指数函数的积分122．d x a x ⎰＝1ln xa C a + 123．e d ax x ⎰＝1e ax C a +124．e d ax x x ⎰＝21(1)e ax ax C a -+125．e d n ax x x ⎰＝11e e d n ax n ax nx x x a a--⎰126．d x xa x ⎰＝21ln (ln )x xx a a C a a -+ 127．d n x x a x ⎰＝11d ln ln n x n xn x a x a x a a --⎰ 128．e sin d ax bx x ⎰＝221e (sin cos )ax a bx b bx C a b -++129．e cos d ax bx x ⎰＝221e (sin cos )ax b bx a bx C a b+++130．e sin d ax n bx x ⎰＝12221e sin (sin cos )ax n bx a bx nb bx a b n--+131．e cos d ax n bx x ⎰＝12221e cos (cos sin )ax n bx a bx nb bx a b n-++（十四）含有对数函数的积分 132．ln d x x ⎰＝ln x x x C -+133．d ln xx x⎰＝ln ln x C + 134．ln d n x x x ⎰＝111(ln )11n x x C n n +-+++135．(ln )d n x x ⎰＝1(ln )(ln )d n n x x n x x --⎰ 136．(ln )d m n x x x ⎰＝111(ln )(ln )d 11m n m n nx x x x x m m +--++⎰ （十五）含有双曲函数的积分 137．sh d x x ⎰＝ch x C + 138．ch d x x ⎰＝sh x C + 139．th d x x ⎰＝lnch x C + 140．2sh d x x ⎰＝1sh224xx C -++ 141．2ch d x x ⎰＝1sh224x x C ++ （十六）定积分142．cos d nx x π-π⎰＝sin d nx x π-π⎰＝0 143．cos sin d mx nx x π-π⎰＝0144．cos cos d mx nx x π-π⎰＝0,,m nm n ≠⎧⎨π=⎩145．sin sin d mx nx x π-π⎰＝0,,m nm n≠⎧⎨π=⎩146．0sin sin d mx nx x π⎰＝0cos cos d mx nx x π⎰＝0,,2m n m n ≠⎧⎪⎨π=⎪⎩147． n I ＝20sin d nx x π⎰＝20cos d n x x π⎰n I ＝21n n I n-- 1342253n n n I n n --=⋅⋅⋅⋅-L （n 为大于1的正奇数），1I ＝1 13312422n n n I n n --π=⋅⋅⋅⋅⋅-L （n 为正偶数），0I ＝2π。

高数微积分公式

高数微积分公式以下是一些高数微积分中常用的公式：1. 极限求导公式：- $\\displaystyle \\frac{d}{dx}(x^{n})=nx^{n-1}$- $\\displaystyle \\frac{d}{dx}(\\sin x)=\\cos x$- $\\displaystyle \\frac{d}{dx}(\\cos x)=-\\sin x$- $\\displaystyle \\frac{d}{dx}(\\ln x)=\\frac{1}{x}$ - $\\displaystyle \\frac{d}{dx}(e^{x})=e^{x}$2. 基本导数法则：- $\\displaystyle \\frac{d}{dx}(cf(x))=cf'(x)$ （常数的导数）- $\\displaystyle \\frac{d}{dx}(f(x)\\pmg(x))=f'(x)\\pm g'(x)$ （和差法则）- $\\displaystyle\\frac{d}{dx}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)$ （乘积法则）- $\\displaystyle\\frac{d}{dx}\\left(\\frac{f(x)}{g(x)}\\right)=\\frac{f'(x)g( x)-f(x)g'(x)}{g^{2}(x)}$ （商法则）- $\\displaystyle \\frac{d}{dx}(f(g(x)))=f'(g(x))\\cdot g'(x)$ （链式法则）3. 积分公式：- $\\displaystyle \\intx^{n}dx=\\frac{1}{n+1}x^{n+1}+C$- $\\displaystyle \\int \\sin xdx=-\\cos x+C$- $\\displaystyle \\int \\cos xdx=\\sin x+C$- $\\displaystyle \\int \\frac{1}{x}dx=\\ln |x|+C$- $\\displaystyle \\int e^{x}dx=e^{x}+C$这些只是一些常用的公式，高数微积分中还有更多的公式和定理。

高数微积分基本公式大全

高数微积分基本公式大全1.导数的基本公式：-基本导数：(常数)' = 0, (x^n)' = nx^(n-1), (e^x)' = e^x, (a^x)' = a^xln(a), (ln(x))' = 1/x, (sin(x))' = cos(x),(cos(x))' = -sin(x), (tan(x))' = sec^2(x), (cot(x))' = -csc^2(x), (sec(x))' = sec(x)tan(x), (csc(x))' = -csc(x)cot(x).-乘法法则：(uv)' = u'v + uv'.-除法法则：(u/v)' = (u'v - uv') / v^2.-链式法则：(f(g(x)))' = f'(g(x)) * g'(x).2.不定积分的基本公式：-基本积分：∫(k) dx = kx + C, ∫(x^n) dx =(1/(n+1))x^(n+1) + C, ∫(e^x) dx = e^x + C, ∫(1/x) dx =ln(|x|) + C, ∫(sin(x)) dx = -cos(x) + C, ∫(cos(x)) dx =sin(x) + C.-分部积分：∫(uv') dx = uv - ∫(u'v) dx.-特殊积分：∫(1/(1+x^2)) dx = arctan(x) + C,∫(1/(sqrt(1-x^2))) dx = arcsin(x) + C.3.微分方程的基本公式：-一阶线性微分方程：dy/dx + P(x)y = Q(x),解为y = e^(-∫P(x)dx) * (∫Q(x)e^(∫P(x)dx)dx + C).-齐次方程：dy/dx = f(y/x),令v = y/x，化为可分离变量的形式求解.-常系数线性齐次微分方程：ay'' + by' + cy = 0，其特征方程为ar^2 + br + c = 0，解为y = C1e^(r1x) + C2e^(r2x)。

【精品】高数微积分公式大全96065

高等数学微积分公式大全一、基本导数公式⑴()0c '=⑵1x x μμμ-=⑶()sin cos x x '=⑷()cos sin x x '=-⑸()2tan sec x x '=⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅⑻()csc csc cot x x x '=-⋅⑼()x x e e '=⑽()ln x x a a a '=⑾()1ln x x'=⑿()1log ln x a x a '=⒀()arcsin x '=⒁()arccos x '=⒂()21arctan 1x x '=+⒃()21arccot 1x x'=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=±()uv u v uv '''=+2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦（2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式（1）()()!n n x n =（2）()()n ax b n ax b e a e ++=⋅(3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭(5)()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+(7)()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c =⑵()1d x x dx μμμ-=⑶()sin cos d x xdx =⑷()cos sin d x xdx =-⑸()2tan sec d x xdx =⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅⑻()csc csc cot d x x xdx =-⋅ ⑼()xxd ee dx =⑽()ln xxd a aadx =⑾()1ln d x dx x=⑿()1logln x a d dx x a =⒀()arcsin d x =⒁()arccos d x dx = ⒂()21arctan 1d x dx x =+⒃()21arccot 1d x dx x =-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰⑵11x x dx c μμμ+=++⎰⑶ln dxx c x=+⎰ ⑷ln xxa a dx c a=+⎰⑸x x e dx e c =+⎰⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰cot ln sin xdx x c =+⎰sec ln sec tan xdx x x c =++⎰csc ln csc cot xdx x x c =-+⎰2211arctan xdx c a x a a=++⎰2211ln 2x a dx c x a a x a -=+-+⎰arcsinxc a=+ln x c =++⎰十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx = ⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数积分公式大全

高数积分公式大全高数积分公式大全在高等数学中，积分是一个重要的概念和工具。

积分公式是进行积分运算时的基本工具，掌握这些公式对于解题和推导都至关重要。

下面是一些常见的高数积分公式大全，希望对学习者有所帮助。

一、基本积分公式1. ∫xn dx = (1/n+1) xn+1 + C (n≠-1)2. ∫(1/x) dx = ln|x| + C3. ∫e^x dx = e^x + C4. ∫a^x dx = (1/ln(a)) a^x + C (a>0, a≠1)5. ∫sin(x) dx = -cos(x) + C6) ∫cos(x) dx = sin(x) + C7. ∫sec^2(x) dx = tan(x) + C8. ∫csc^2(x) dx = -cot(x) + C9. ∫sec(x)tan(x) dx = sec(x) + C10. ∫csc(x)cot(x) dx = -csc(x) + C11. ∫sec(x) dx = ln|sec(x) + tan(x)| + C12. ∫csc(x) dx = ln|csc(x) - cot(x)| + C13. ∫tan(x) dx = -ln|cos(x)| + C14. ∫cot(x) dx = ln|sin(x)| + C15. ∫cot^2(x) dx = -cot(x) - x + C二、一些特殊函数的积分公式1. ∫e^ax sin(bx) dx = (1/(a^2 + b^2))e^ax (a sin(bx)- b cos(bx)) + C2. ∫e^ax cos(bx) dx = (1/(a^2 + b^2))e^ax (a cos(bx) + b sin(bx)) + C3. ∫si n^2(x) dx = (1/2)(x - sin(x)cos(x)) + C4. ∫cos^2(x) dx = (1/2)(x + sin(x)cos(x)) + C5. ∫sin^3(x) dx = -(1/3)cos^3(x) + (1/3)cos(x) + C6. ∫cos^3(x) dx = (1/3)sin^3(x) + (1/3)sin(x) + C三、三角替换公式1. ∫√(a^2 - x^2) dx = (1/2)(x√(a^2 - x^2) +a^2arcsin(x/a)) + C2. ∫√(x^2 + a^2) dx = (1/2)(x√(x^2 + a^2) + a^2ln|x + √(x^2 + a^2)|) + C3. ∫√(x^2 - a^2) dx = (1/2)(x√(x^2 - a^2) - a^2ln|x + √(x^2 - a^2)|) + C四、分部积分公式1. ∫u dv = uv - ∫v du，其中u和v是可微的函数。

高等数学积分公式大全

高等数学积分公式大全在高等数学的学习中，积分是一个非常重要的概念和工具。

积分公式就像是一把把钥匙，能够帮助我们打开解决各种数学问题的大门。

接下来，让我们一起走进这个丰富多彩的积分公式世界。

一、基本积分公式1、常数的积分∫k dx ＝ kx ＋ C （其中 k 为常数，C 为积分常数）这个公式很好理解，对一个常数进行积分，结果就是这个常数乘以自变量再加上积分常数。

2、幂函数的积分∫x^n dx ＝（1/（n ＋ 1)）x^（n ＋ 1) ＋ C （其中n ≠ －1）当 n 为正整数时，这个公式告诉我们幂函数积分后，指数加 1，然后除以新的指数再加积分常数。

3、指数函数的积分∫e^x dx ＝ e^x ＋ C∫a^x dx ＝（1 ／ ln a)a^x ＋ C （其中 a ＞ 0 且a ≠ 1）指数函数的积分依然是它本身，只是要加上积分常数。

4、对数函数的积分∫ln x dx ＝ x ln x x ＋ C这是一个比较特殊的公式，需要记住。

5、三角函数的积分∫sin x dx ＝ cos x ＋ C∫cos x dx ＝ sin x ＋ C∫ta n x dx ＝ ln ｜cos x| ＋ C∫cot x dx ＝ ln ｜sin x| ＋ C三角函数的积分在解决与周期性和波动性相关的问题中经常用到。

二、换元积分法相关公式1、第一类换元法（凑微分法）如果∫f(u) du ＝ F(u) ＋ C，且 u ＝φ(x) 可导，则∫f(φ(x)）φ'（x) dx ＝F(φ(x)）＋ C通过巧妙地凑出合适的微分形式，将复杂的积分转化为已知的积分形式。

2、第二类换元法设 x ＝φ(t) 是单调的、可导的函数，并且φ'（t) ≠ 0，又设f(φ(t)）φ'（t) 具有原函数，则有∫f(x) dx ＝∫f(φ(t)）φ'（t) dt常见的有三角代换、根式代换等。

三、分部积分法公式∫u dv ＝uv ∫v du这个公式常用于两个函数相乘的积分，通过合理地选择 u 和 dv，将积分转化为更容易求解的形式。

高数微积分公式大全(总结的比较好)

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫=⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、基本初等函数的n 阶导数公式（1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭(6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a= ⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x =-+六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫=⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰ ⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan xdx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =++九、下列常用凑微分公式十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，ax dv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos axe xdx ⎰令,sin ,cos ax u e x x =均可。

高数微积分公式大全

2 3 4 n 3 5 7 n 2 n +1 n +1
∑i
i =1 n
2
=
ln (1+x) = xtan-1 x = x-
∑i
i =1
3
= [½n (n+1)]2
x-1 -t 2x-1 − t ∫ t e dt = 2 ∫ t e dt =
2
x x x ( −1) x + - +…+ +… 3 5 7 ( 2n + 1)
-1
∫ sin x dx = -cos x + C ∫ cos x dx = sin x + C ∫ tan x dx = ln |sec x | + C ∫ cot x dx = ln |sin x | + C ∫ sec x dx = ln |sec x + tan x | + C ∫ csc x dx = ln |csc x – cot x | + C ∫ sin-1 x dx = x sin-1 x+ 1 − x 2 +C ∫ cos-1 x dx = x cos-1 x- 1 − x 2 +C ∫ tan x dx = x tan x-½ln (1+x )+C ∫ cot-1 x dx = x cot-1 x+½ln (1+x2)+C ∫ sec-1 x dx = x sec-1 x- ln |x+ x 2 − 1 |+C
sinh x =
∫ sech-1 x dx = x sech-1 x- sin-1 x + C x coth-1( )= a ∫ csch-1 x dx = x csch-1 x+ sinh-1 x + C x −a γ sech-1( )= 2 2 a a x a −x R b

高数微积分公式大全

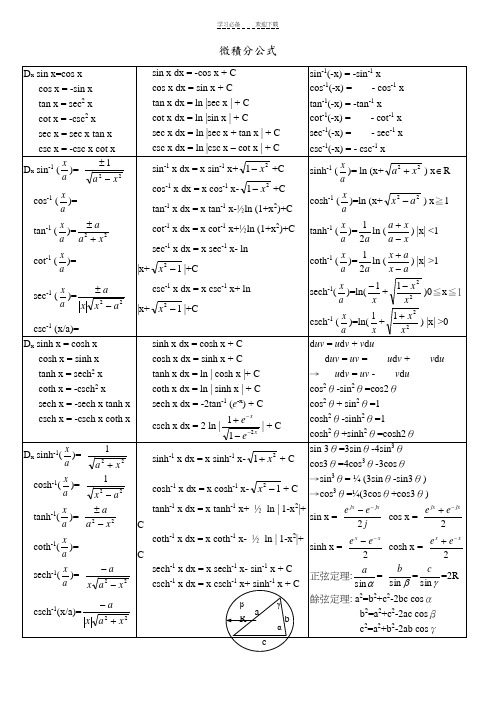
微積分公式sin x dx = -cos x + C cos x dx = sin x + C tan x dx = ln |sec x | + C cot x dx = ln |sin x | + Csec x dx = ln |sec x + tan x | + C csc x dx = ln |csc x – cot x | + C sin -1(-x) = -sin -1 xcos -1(-x) = - cos -1 x tan -1(-x) = -tan -1 x cot -1(-x) = - cot -1 x sec -1(-x) = - sec -1 x csc -1(-x) = - csc -1 xsin -1 x dx = x sin -1 x+21x -+C cos -1 x dx = x cos -1 x-21x -+C tan -1 x dx = x tan -1 x-½ln (1+x 2)+C cot -1 x dx = x cot -1 x+½ln (1+x 2)+C sec -1 x dx = x sec -1 x- ln |x+12-x |+Ccsc -1 x dx = x csc -1 x+ ln |x+12-x |+Csinh x dx = cosh x + C cosh x dx = sinh x + C tanh x dx = ln | cosh x |+ C coth x dx = ln | sinh x | + C sech x dx = -2tan -1 (e -x ) + C csch x dx = 2 ln |xx ee 211---+| + Cd uv = u d v + v d ud uv = uv = u d v + v d u→ u d v = uv - v d u cos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1 cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θsinh -1 x dx = x sinh -1 x-21x ++ Ccosh -1 x dx = x cosh -1 x-12-x + C tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ Ccoth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C sech -1 x dx = x sech -1 x- sin -1 x + C csch -1 x dx = x csch -1 x+ sinh -1 x + Ca bcαβγ R希腊字母 (Greek Alphabets)倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; 顺位高d 顺位低 ;0*=∞1 * =∞∞ = 0*01 = 00 00 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y重点在三方面：一、函数与反函数的关系：(Function and Inverse Function)以前我们学过的相反运算有：加<------->减；乘<------->除；平方<----->开方；指数<----->对数；三角<----->反三角。

自考高等数学一(微积分)常用公式表[2]

高数常用公式表常用公式表（一）1、乘法公式（1）（a+b ）²=a 2+2ab+b 2 （2）(a-b)²=a ²-2ab+b ² （3）(a+b)(a-b)=a ²-b ²（4）a ³+b ³=(a+b)(a ²-ab+b ²) （5）a ³-b ³=(a-b)(a ²+ab+b ²) 2、指数公式：（1）a 0=1 （a ≠0）（2）a P -=P a 1（a ≠0）（3）a m n=m n a（4）a m a n =a n m + （5）a m ÷a n =n ma a =a n m - （6）（a m ）n =a mn（7）（ab ）n =a n b n（8）（b a）n =n nb a （9）（a ）2=a（10）2a =|a| 3、指数与对数关系：（1）若a b =N ，则N b a log = （2）若10b=N ，则b=lgN （3）若b e =N ，则b=㏑N 4、对数公式：（1）b a b a =log , ㏑e b=b （2）N a aN =log ，e Nln =N（3）aNN a ln ln log = （4）a b b e a ln = （5）N M MN ln ln ln +=（6）N M N Mln ln ln -= （7）M n M n ln ln = （8）㏑n M =M n ln 1 5、三角恒等式：（1）（Sin α）²+（Cos α）²=1 （2）1+（tan α）²=(sec α)²（3）1+(cot α)²=(csc α)² （4）αααtan cos sin = （5）αααcot sin cos =（6）ααtan 1cot = （7）ααcos 1csc = （8）ααcos 1sec =6、特殊角三角函数值：7.倍角公式：（1）αααcos sin 22sin = （2）ααα2tan 1tan 22tan -=（3）ααααα2222sin 211cos 2sin cos 2cos -=-=-= 8.半角公式（降幂公式）：（1）（2sin α）2=2cos 1a - （2）（2cos α）2=2cos 1a + （3）2tan α=a a sin cos 1+=a acos 1sin +9、三角函数与反三角函数关系：（1）若x=siny ，则y=arcsinx （2）若x=cosy ，则y=arccosx（3）若x=tany ，则y=arctanx （4）若x=coty ，则y=arccotx 10、函数定义域求法：（1）分式中的分母不能为0，（a 1α≠0）（2）负数不能开偶次方，（a α≥0）（3）对数中的真数必须大于0，（N a log N>0）（4）反三角函数中arcsinx ，arccosx 的x 满足：（--1≤x ≤1）（5）上面数种情况同时在某函数出现时，此时应取其交集。

高数二公式大全

高等数学公式导数公式：基本积分表：ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数的有理式积分：222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=，　，　，　一些初等函数：两个重要极限：三角函数公式： ·诱导公式：xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22）双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxxxx x·和差角公式： ·和差化积公式：倍角公式：·半角公式：ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+=·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( αααααααααα23333133cos 3cos 43cos sin 4sin 33sin tg tg tg tg --=-=-=αααααααααααααα222222122212sin cos sin 211cos 22cos cos sin 22sin tg tg tg ctg ctg ctg -=-=-=-=-==高阶导数公式——莱布尼兹（Leibniz ）公式：)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用：拉格朗日中值定理。