高中数学选修2-2综合测试题与答案

合集下载

人教版高中数学选修2-2试题四套(带答案)(整理)

2高中数学选修《2-2》复习试题一、选择题（共8题，每题5分）1.复数(2)z i i =+在复平面内的对应点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2. 一质点做直线运动,由始点经过s t 后的距离为3216323s t t t =-+,则速度为0的时刻是（）A ．4s t= B ．8s t = C ．4s t =与8s t = D ．0s t =与4s t =3。

某射击选手每次射击击中目标的概率是0.8,如果他连续射击5次，则这名射手恰有4次击中目标的概率是（）（A ）40.80.2⨯ （B)445C 0.8⨯ (C ）445C 0.80.2⨯⨯ (D ）45C 0.80.2⨯⨯ 4.已知14a b c =+==则a,b ，c 的大小关系为（） A ．a>b>cB ．c>a 〉bC ．c 〉b 〉aD ．b>c 〉a5.曲线32y x =-+上的任意一点P 处切线的斜率的取值范围是（） A．)+∞B. )+∞C. ()+∞ D 。

[)+∞ 6。

有一段“三段论”推理是这样的：对于可导函数()f x ，如果0()0f x '=,那么0x x =是函数()f x 的极值点,因为函数3()f x x =在0x =处的导数值(0)0f '=，所以，0x =是函数3()f x x =的极值点. 以上推理中（）A ．大前提错误B ．小前提错误C ．推理形式错误D ．结论正确7。

.在复平面内，复数1 + i 与31+i 分别对应向量OA 和OB , 其中O 为坐标原点，=（ ) A 。

2 B 。

2 C 。

10 D. 48、函数2()1x f x x =-( ）A ．在(0,2)上单调递减B ．在(,0)-∞和(2,)+∞上单调递增C ．在(0,2)上单调递增D ．在(,0)-∞和(2,)+∞上单调递减二、填空题（共6题，30分) 9. .观察下列式子 2222221311511171,1,1222332344+<++<+++< , … … ，则可归纳出________________________________10. 复数11z i =-的共轭复数是________。

高中新课标数学选修(2-2)综合测试题(4)

高中新课标数学选修（2-2）综合测试题一、选择题1、函数2x y =在区间]2,1[上的平均变化率为（）（A ）2 （B ）3 （B ）4 （D ）52曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为（）（A ）38 （B ）37 （C ）35（D ）343、已知直线kx y =是x y ln =的切线，则k 的值为（）（A ）e1 （B ）e1-（C ）e2 （D ）e2-4、设ai b bi a ++,,1是一等比数列的连续三项，则b a ,的值分别为（）（A ）21,23±=±=b a （B ）23,21=-=b a（C ）21,23=±=b a （D ）23,21-=-=b a5、方程)(04)4(2R a ai x i x ∈=++++有实根b ，且bi a z +=，则=z （）（A ）i 22- （B ）i 22+（C ）i 22+- （D ）i 22--6、已知三角形的三边分别为c b a ,,，内切圆的半径为r ，则三角形的面积为a s (21=rc b )++；四面体的四个面的面积分别为4321,,,s s s s ，内切球的半径为R 。

类比三角形的面积可得四面体的体积为（）（A ）R s s s s V )(214321+++= （B ）Rs s s s V )(314321+++=（C ）Rs s s s V )(414321+++= （D ）R s s s s V )(4321+++=7、数列 ,4,4,4,4,3,3,3,2,2,1的第50项是（）（A ）8 （B ）9 （C ）10 （D ）118、在证明12)(+=x x f 为增函数的过程中，有下列四个命题：①增函数的定义是大前提；②增函数的定义是小前提；③函数12)(+=x x f 满足增函数的定义是小前提；④函数12)(+=x x f 满足增函数的定义是大前提；其中正确的命题是（）（A ）①② （B ）②④ （C ）①③ （D ）②③9、若R b a ∈,，则复数i b b a a )62()54(22-+-++-表示的点在（）（A ）在第一象限（B ）在第二象限（C ）在第三象限（D ）在第四象限 10、用数学归纳法证明不等式“)2(2413212111>>+++++n nn n ”时的过程中，由k n =到1+=k n 时，不等式的左边（）（A ）增加了一项)1(21+k（B ）增加了两项)1(21121+++k k（C ）增加了两项)1(21121+++k k ，又减少了11+k ；（D ）增加了一项)1(21+k ，又减少了一项11+k ；11、如图是函数d cx bx x x f +++=23)(的大致图象，则2221x x +等于（）（A ）32 （B ）34 （C ）38 （D ）31212、对于函数233)(x x x f -=，给出下列四个命题：①)(x f 是增函数，无极值；②)(x f 是减函数，有极值；③)(x f 在区间]0,(-∞及),2[+∞上是增函数；④)(x f 有极大值为0，极小值4-；其中正确命题的个数为（）（A ）1 （B ）2（C ）3 （D ）4班级：姓名：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题13、函数13)(3+-=x x x f 在闭区间]0,3[-上的最大值与最小值分别为：14、若i z 311-=，i z 862-=，且21111z z z =+，则z 的值为；15、用火柴棒按下图的方法搭三角形：按图示的规律搭下去，则所用火柴棒数n a 与所搭三角形的个数n 之间的关系式可以是 .16、物体A 的运动速度v 与时间t 之间的关系为12-=t v （v 的单位是s m /，t 的单位是s ），物体B 的运动速度v 与时间t 之间的关系为t v 81+=，两个物体在相距为405m 的同一直线上同时相向运动。

(北师大版)上海市高中数学选修2-2第二章《变化率与导数》测试(含答案解析)

一、选择题1．如图，()y f x =是可导函数，直线l ：2y kx =+是曲线()y f x =在3x =处的切线，令2()()g x x f x =，()g x '是()g x 的导函数，则()3g '等于（）A ．3B ．0C ．2D ．42．已知a ，b 为正实数，直线y x a =-与曲线()ln y x b =+相切，则11ab+的最小值是( ) A ．2B ．42C ．4D ．223．若曲线()xf x mx e n =⋅+在点()()1,1f 处的切线方程为y ex =，则m n +的值为（） A ．12e + B ．12e - C ．12D ．2e 4．函数()2221sin cos 622x xf x x =+-的导函数()y f x '=的图象大致是（） A ． B ．C ．D ．5．已知()ln f x x =，217()(0)22g x x mx m =++<，直线l 与函数()f x ，()g x 的图象都相切，且与()f x 图象的切点为(1,(1))f ，则m 的值为( ) A ．2-B ．3-C ．4-D ．1-6．设曲线y ＝x n ＋1(n ∈N *)在(1,1)处的切线与x 轴的交点的横坐标为x n ，则log 2 014x 1＋log 2014x 2＋…＋log 2 014x 2 013的值为()A ．－log 2 0142 013B ．－1C ．(log 2 0142 013)－1D ．17．已知直线:l y m =，若l 与直线23y x =+和曲线ln(2)y x =分别交于A ，B 两点，则||AB 的最小值为A ．1B ．2C ．455D ．2558．设正弦曲线y ＝sin x 上一点P ，以点P 为切点的切线为直线l ，则直线l 的倾斜角的范围是( ) A ．30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭B ．[0，π)C ．3,44ππ⎡⎤⎢⎥⎣⎦ D ．[0，4π]∪[2π，34π]9．函数为R 上的可导函数，其导函数为()f x '，且()3sin cos 6f x f x x π⎛⎫=⋅+⎪⎝⎭'，在ABC ∆中，()()1f A f B ='=，则ABC ∆的形状为 A ．等腰锐角三角形B ．直角三角形C ．等边三角形D ．等腰钝角三角形10．已知函数()f x 为R 上的可导函数，且x R ∀∈，均有()()f x f x '<，则有（） A ．2019(2019)(0)e f f -<，2019(2019)(0)f e f C ．2019(2019)(0)e f f ->，2019(2019)(0)f e f > D ．2019(2019)(0)e f f ->，2019(2019)(0)f e f <11．设函数sin cos y x x x =+的图象上的点()00,x y 处的切线的斜率为k ，记()0k g x =，则函数()k g x =的图象大致为（）A ．B ．C ．D ．12．函数f （x ）=﹣12x 2+12在x=1处的切线的斜率为（） A ．﹣2B ．﹣1C ．0D ．1二、填空题13．设点P 是曲线3233y x x =-+上的任意一点，P 点处的切线倾斜角为σ，则σ的取值范围为____________. 14．已知函数4()ln 2f x x x xλλ=+-≥，，曲线()y f x =上总存在两点M （x 1，y 1），N （x 2，y 2）使曲线()y f x =在M 、N 两点处的切线互相平行，则x 1+x 2的取值范围为_______． 15．在曲线3211333y x x x =-+-的所有切线中，斜率最小的切线方程为______． 16．若直线y kx b =+是曲线ln 3y x =+的切线，也是曲线ln(1)y x =+的切线，则b =______17．函数在处的切线与直线垂直，则a 的值为______．18．若以曲线()y f x =上任意一点(,)M x y 为切点作切线l ，曲线上总存在异于M 的点11(,)N x y ，以点N 为切点作线1l ，且1//l l ，则称曲线()y f x =具有“可平行性”，下列曲线具有可平行性的编号为__________．（写出所有的满足条件的函数的编号） ①1y x=②3y x x =- ③cos y x = ④2(2)ln y x x =-+ 19．设()()()sin 2',''32f x x xf f x f x f ππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭是的导函数，则___________. 20．过点()1,1-与曲线()32f x x x =-相切的直线方程是__________．三、解答题21．已知函数f (x )＝13x 3－2x 2＋3x (x ∈R)的图象为曲线C . (1)求过曲线C 上任意一点切线斜率的取值范围；(2)若在曲线C 上存在两条相互垂直的切线，求其中一条切线与曲线C 的切点的横坐标的取值范围．22．已知函数()mf x mx x=-，()2ln g x x =. （1）当2m =时，求曲线()y f x =在点(1(1))f ，处的切线方程；（2）当1m =时，判断方程()()f x g x =在区间(1)+∞，上有无实根；（3）若(1]x e ∈，时，不等式()()2f x g x -<恒成立，求实数m 的取值范围. 23．求下列函数的导数：（1）()(1sin )(14)f x x x =+-；（2）()21x xf x x =-+. 24．设函数()bf x ax x=-，曲线y =f （x ）在点（2，f （2））处的切线方程为7x -4y -（1）求y =f （x ）的解析式；（2）证明：曲线y =f （x ）上任一点处的切线与直线x =0和直线y =x 所围成的三角形面积为定值，并求此定值．25．（1）函数()(1sin )f x x x =+的导数为()'f x ，求2f π⎛⎫' ⎪⎝⎭；（2）设l 是函数1y x=图象的一条切线，证明：l 与坐标轴所围成的三角形的面积与切点无关．26．已知函数()()1ln 1x f x x++=和()()1ln 1g x x x =--+（1）若()f x '是()f x 的导函数，求(1)f '的值（2）当0x >时，不等式()()0g x f x kx'->恒成立，其中()g x '是()g x 导函数,求正整数k 的最大值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】2y kx =+是曲线()y f x =在3x =处的切线求出=(3)k f ，由图(3)=1f ，对2()()g x x f x =求导取值可得.【详解】2y kx =+是曲线()y f x =在3x =处的切线,所以切点(3,1)代入切线方程得1=(3)=3k f ，又(3)=1f 2()()g x x f x =，2()2()+()g x xf x x f x ''=，(3)6(3)+9(3)=3g f f ''∴=故选：A. 【点睛】本题考查导数的几何意义.根据导数的几何意义求参数值的思路根据导数的几何意义求参数的值时，一般是利用切点00)(P x y ，既在曲线上又在切线上构造方程组求解．2．C【分析】求函数的导数，由已知切线的方程，可得切线的斜率，求得切线的坐标，可得1a b +=，再由乘1法和基本不等式，即可得到所求最小值．【详解】解：()y ln x b =+的导数为1y x b'=+，由切线的方程y x a =-可得切线的斜率为1，可得切点的横坐标为1b -，所以切点为(1,0)b -，代入y x a =-，得1a b +=，a 、b 为正实数，则111()()22241b a b a a b a b a b a b a b+=++=+++=．当且仅当12a b ==时，11a b+取得最小值4．故选：C 【点睛】本题主要考查导数的应用，利用导数的几何意义以及基本不等式是解决本题的关键，属于中档题．3．A解析：A 【分析】求导得到()()'1xf x m x e =+⋅，由已知得()1f e =，()1f e '=，解得答案.【详解】()x f x mx e n =⋅+，则()()'1x f x m x e =+⋅，故()1f e =，()1f e '=，()11me n e m e e +=⎧∴⎨+=⎩，解得122m en ⎧=⎪⎪⎨⎪=⎪⎩，所以12e m n ++=. 故选：A . 【点睛】本题考查了根据切线方程求参数，意在考查学生的计算能力和转化能力.4．C解析：C 【分析】将函数()y f x =的解析式化简，求出其导数()1sin 3f x x x '=+，，然后结合导函数的符号排除错误选项即可确定导函数的图像.因为()222211sin cos cos 6226x x f x x x x =+-=-，()1sin 3f x x x '∴=+. 当03x <≤时，103x >，sin 0x >，则()1sin 03f x x x '=+>；当3x >时，113x >，1sin 1x -≤≤，则()1sin 03f x x x '=+>. 所以，当0x >时，()1sin 03f x x x '=+>，排除ABD 选项，故选：C. 【点睛】本题考查函数图象的识别，给定函数解析式，一般要结合函数的定义域、奇偶性、单调性（导数）、特殊值符号、零点等知识进行逐一排除，考查分析问题和解决问题的能力，属于中等题.5．A解析：A 【分析】先利用导数求切线斜率,再根据点斜式方程得切线方程,最后根据判别式为零得结果. 【详解】 1()f x x'=，直线l 是函数()f x lnx =的图象在点(1,0)处的切线，∴其斜率为k f ='（1）1=， ∴直线l 的方程为1y x =-．又因为直线l 与()g x 的图象相切，∴211722y x y x mx =-⎧⎪⎨=++⎪⎩，消去y ，可得219(1)022x m x +-+=，得△2(1)902(4m m m =--=⇒=-=不合题意，舍去），故选A 【点睛】本题主要考查函数导数的几何意义,考查直线和曲线的位置关系，意在考查学生对这些知识的理解掌握水平和分析推理能力.6．B解析：B 【解析】【分析】由题意，求出y ＝x n ＋1(n ∈N *)在(1,1)处的切线方程，取0y =，求得n x ，再利用对数的运算性质可得答案. 【详解】由y ＝x n ＋1，可得(1)n y n x =+'，即11x y n ='=+即曲线y ＝x n ＋1(n ∈N *)在(1,1)处的切线方程为1(1)(1)y n x -=+-令0y =，得1n n x n =+ log 2 014x 1＋log 2 014x 2＋…＋log 2 014x 2 013=20141220132014122013log ()log ()1232014x x x =⋅=- 故选B 【点睛】本题考查了曲线的切线方程和对数的运算，细心计算是解题的关键，属于中档题.7．B解析：B 【分析】利用导数求出与直线23y x =+平行的曲线的切线的切点，利用点到直线的距离可得. 【详解】1y x '=,令12x =可得12x =，所以切点为1,02⎛⎫ ⎪⎝⎭. 根据题意可知1,02B ⎛⎫ ⎪⎝⎭且0m =，所以3,02A ⎛⎫- ⎪⎝⎭，此时2AB =.故选B. 【点睛】本题主要考查导数的几何意义.已知切线的斜率，结合导数可得切点.8．A解析：A 【解析】由题得cos y x '=，设切线的倾斜角为α，则，3tan cos 1tan 1[0,][,)44k x ππαααπ==∴-≤≤∴∈⋃，故选A.9．D解析：D 【解析】【分析】求函数的导数，先求出'16f π⎛⎫= ⎪⎝⎭，然后利用辅助角公式进行化简，求出A ，B 的大小即可判断三角形的形状．【详解】函数的导数()''cos sin 6f x x x π⎛⎫=- ⎪⎝⎭，则131''cos sin ''666662262f f f ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则11'262f π⎛⎫= ⎪⎝⎭，则'16f π⎛⎫= ⎪⎝⎭，则()'sin 2cos 6f x x x x π⎛⎫=-=+⎪⎝⎭， ()cos 2cos 3f x x x x π⎛⎫=+=- ⎪⎝⎭，()()'1f A f B ==，()'2cos 16f B B π⎛⎫∴=+= ⎪⎝⎭，即1cos 62B π⎛⎫+= ⎪⎝⎭，则63B ππ+=，得6B π=，()2cos 13f A A π⎛⎫=-= ⎪⎝⎭，即1cos 32A π⎛⎫-= ⎪⎝⎭，则33A ππ-=，则23A π=，则2366C ππππ=--=，则B C =，即ABC 是等腰钝角三角形，故选D ．【点睛】本题考查三角形形状的判断，根据导数的运算法则求出函数()f x 和()'f x 的解析式是解决本题的关键．10．B解析：B 【分析】令()()xf xg x e=，x ∈R ．()()()x f x f x g x e '-'=，根据x R ∀∈，均有()()f x f x '<，可得函数()g x 的单调性，进而得出结论．【详解】解：令()()x f x g x e=，x ∈R ．()()()xf x f xg x e '-'=， x R ∀∈，均有()()f x f x '<， ()g x ∴在R 上单调递增，(2019)(0)(2019)g g g ∴-<<，可得：2019(2019)(0)e f f -<，2019(2019)(0)f e f >．故选B ．【点睛】本题考查了利用导数研究函数的单调性、方程与不等式的解法、构造法，考查了推理能力与计算能力，属于中档题．11．A解析：A 【详解】因为sin cos ,sin cos sin cos y x x x y x x x x x x '=+=+-=，则()cos g x x x =，该函数为奇函数，排除B 、C ，当0,2x π⎛⎫∈ ⎪⎝⎭时，()0>g x ，排除D. 故选:A12．B解析：B 【解析】【分析】根据导数的几何意义可知(1)k f '=，求导后计算即可. 【详解】因为()f x x '=-,所以 (1)1k f '==- ，故选B. 【点睛】本题主要考查了导数的几何意义，属于容易题.二、填空题13．【分析】设点根据导数的几何意义求得即可得到答案【详解】设点由函数可得可得即又由所以故答案为：【点睛】本题主要考查了导数的几何意义及其应用其中解答中熟记导数的几何意义准确计算是解答的关键着重考查推理与解析：20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【分析】设点00(,)P x y ，根据导数的几何意义，求得tan σ≥.【详解】设点00(,)P x y，由函数323y x =+，可得23y x '=可得020|3x x y x ='=，即tan σ≥ 又由[)0,σπ∈，所以20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭. 故答案为：20,,23πππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭. 【点睛】本题主要考查了导数的几何意义及其应用，其中解答中熟记导数的几何意义，准确计算是解答的关键，着重考查推理与运算能力.14．【分析】求出导函数根据题意转化为对恒成立即可得解【详解】曲线上总存在两点M （x1y1）N （x2y2）使曲线在MN 两点处的切线互相平行即所以对恒成立所以x1+x2的取值范围为故答案为：【点睛】此题考查解析：()8+∞，【分析】求出导函数24()1f x x x λ'=--，根据题意转化为()()212121244x x x x x x λλ++=<对2λ≥恒成立，即可得解.【详解】4()ln 2f x x x x λλ=+-≥，，24()1f x x xλ'=--，曲线()y f x =上总存在两点M （x 1，y 1），N （x 2，y 2）使曲线()y f x =在M 、N 两点处的切线互相平行，即121212()(),,0,0f x f x x x x x ''=≠>>，2211224411x x x x λλ--=--， 22121244x x x x λλ-=-，()()212121244x x x x x x λλ++=<所以1216x x λ+>对2λ≥恒成立所以x 1+x 2的取值范围为()8+∞，. 故答案为：()8+∞，【点睛】此题考查导数的几何意义，根据导数的几何意义解决切线斜率相等的问题，求切点横坐标之和的取值范围，利用基本不等式构造不等关系求解.15．【解析】【分析】根据导数的几何意义可知在某点处的导数为切线的斜率先求出导函数利用配方法求出导函数的最小值即为切线最小斜率再用点斜式写出化简【详解】曲线时切线最小斜率为2此时切线方程为即故答案为：【点解析：20x y -=【解析】【分析】根据导数的几何意义可知在某点处的导数为切线的斜率，先求出导函数()f x '，利用配方法求出导函数的最小值即为切线最小斜率，再用点斜式写出化简．【详解】曲线3211333y x x x =-+-，223y x x ∴'=-+，1x ∴=时，切线最小斜率为2，此时，32111131233y =⨯-+⨯-=．∴切线方程为22(1)y x -=-，即20x y -=．故答案为：20x y -=．【点睛】本题主要考查了利用导数研究曲线上某点切线方程，以及二次函数的最值等基础题知识，考查运算求解能力，属于基础题．16．【分析】对两条曲线对应的函数求导设出两个切点的横坐标令它们的导数相等求出两条曲线在切点处的切线方程对比系数求得的值【详解】依题意设直线与相切切点的横坐标为即切点为设直线与相切切点的横坐标为即切点为令解析：2ln 3-【分析】对两条曲线对应的函数求导，设出两个切点的横坐标，令它们的导数相等，求出两条曲线在切点处的切线方程，对比系数求得b 的值. 【详解】依题意，()()''11ln 3,ln 11x x x x +=+=⎡⎤⎣⎦+，设直线y kx b =+与ln 3y x =+相切切点的横坐标为0x ，即切点为()00,ln 3x x +，设直线y kx b =+与()ln 1y x =+相切切点的横坐标为1x ，即切点为()()11,ln 1x x +，令01111x x =+，解得101x x =-，故直线y kx b =+与()ln 1y x =+相切切点为()001,ln x x -.由此求出两条切线方程为()()0001ln 3y x x x x -+=-和()0001ln 1y x x x x -=-+；即001ln 2y x x x =++和000111ln y x x x x =-++，故0001ln 21ln x x x +=-++，013x =，故0ln 22ln3b x =+=-.【点睛】本小题主要考查两条曲线共切线方程的问题，考查切线方程的求法，考查导数的运算，属于中档题.17．0【解析】【分析】求函数的导数根据导数的几何意义结合直线垂直时直线斜率的关系建立方程关系进行求解即可得结果【详解】因为函数y=(x+a)ex 在x=0处的切线与直线x+y+1=0垂直所以函数y=(x+ 解析：【解析】【分析】求函数的导数，根据导数的几何意义结合直线垂直时直线斜率的关系建立方程关系进行求解即可得结果. 【详解】因为函数在处的切线与直线垂直，所以函数在处的切线斜率，因为，所以，解得，故答案是0. 【点睛】该题考查的是有关利用导数研究曲线上某点处的切线的问题，涉及到的知识点有两直线垂直的条件，导数的几何意义，以及函数的求导公式，属于中档题目.18．①③【解析】因为；因为不存在异于的点；因为总存在异于的点满足条件；因为不存在异于的点；所以选①③解析：①③ 【解析】因为122111y x x x x x =-=-∴=-'≠取；因为231,0y x x =-='时不存在异于M 的点N ；因为1sin sin y x x =-=-'∴总存在异于M 的点N 满足条件；因为212412(2)x x y x x x ='-+=-+，22x =不存在异于M 的点N ；所以选①③19．-1【解析】∵令可得：解得则解析：-1 【解析】∵()2(),()2()33f x sinx xf f x cosx f ππ=+'∴'=+'，令3x π=,可得：()2()333f cos f πππ'=+' ,解得1()32f π'=- ，则1()2()1222f cosππ'=+⨯-=- 20．或【解析】由题意可得：设曲线上点的坐标为切线的斜率为切线方程为：(*)切线过点则：解得：或将其代入(*)式整理可得切线方程为：或点睛：曲线y ＝f(x)在点P(x0y0)处的切线与过点P(x0y0)的解析：20x y --=或5410x y +-= 【解析】由题意可得：()2'32f x x =-，设曲线上点的坐标为()3000,2x x x -，切线的斜率为2032k x =-，切线方程为：()()()320000232y x x x x x --=--，(*)切线过点()1,1-，则：()()()32012321x x x x ---=--，解得：01x =或012x =-将其代入(*)式整理可得，切线方程为：20x y --=或5410x y +-=.点睛：曲线y ＝f (x )“在点P (x 0，y 0)处的切线”与“过点P (x 0，y 0)的切线”的区别：前者P (x 0，y 0)为切点，而后者P (x 0，y 0)不一定为切点．三、解答题21．（1）[－1，＋∞)；（2）(－∞，2∪(1,3)∪[2∞). 【解析】试题分析：（1）先求导函数，然后根据导函数求出其取值范围，从而可求出曲线C 上任意一点处的切线的斜率的取值范围；（2）根据（1）可知k 与﹣1k的取值范围，从而可求出k 的取值范围，然后解不等式可求出曲线C 的切点的横坐标取值范围. (1)由题意得f ′(x )＝x 2－4x ＋3，则f ′(x )＝(x －2)2－1≥－1，即过曲线C 上任意一点切线斜率的取值范围是[－1，＋∞)．(2)设曲线C 的其中一条切线的斜率为k ，则由(2)中条件并结合(1)中结论可知，111k k≥-⎧⎪⎨-≥-⎪⎩解得－1≤k ＜0或k ≥1，故由－1≤x 2－4x ＋3＜0或x 2－4x ＋3≥1，得x ∈(－∞，2∪(1,3)∪[2∞) 22．(1) 44y x =-；(2) 内无实数根；（3）241e e ⎛⎫-∞ ⎪-⎝⎭，. 【解析】试题分析：（2）把m 的值代入后，求出f （1），求出x=1时函数的导数，由点斜式写出曲线y=f （x ）在点（1，f （1））处的切线方程；（Ⅱ）代入m 的值，把判断方程f （x ）=g （x ）在区间（1，+∞）上有无实根转化为判断函数h （x ）=f （x ）﹣g （x ）在（1，+∞）上有无零点问题，求导后利用函数的单调性即可得到答案；（Ⅲ）把f （x ）和g （x ）的解析式代入不等式，整理变形后把参数m 分离出来，x ∈（1，e]时，不等式f （x ）﹣g （x ）＜2恒成立，转化为实数m 小于一个函数在（1，e]上的最小值，然后利用导数分析函数在（1，e]上的最小值．试题（1）2m =时，()22f x x x =-，()222f x x='+，()14f '=，切点坐标为()10，， ∴切线方程为44y x =-（2）1m =时，令()()()12ln h x f x g x x x x=-=--， ()()22211210x h x x x x-=+-=≥'，∴()h x 在()0+∞，上为增函数，又()10h =，所以()()f x g x =在()1+∞，内无实数根. （3）2ln 2mmx x x--<恒成立，即()2122ln m x x x x -<+恒成立. 又210x ->，则当(]1x e ，∈时，222ln 1x x xm x +<-恒成立，令()222ln 1x x xG x x +=-，只需m 小于()G x 的最小值. ()()()2222ln ln 21x x x G x x-++-'=，∵1x e <≤，∴ln 0x >，∴(]1x e ，∈时，()0G x '<， ∴()G x 在(]1e ，上单调递减，∴()G x 在(]1e ，的最小值为()241eG e e =-，则m 的取值范围是241e e ⎛⎫-∞ ⎪-⎝⎭，. 点睛：导数问题经常会遇见恒成立的问题：（1）根据参变分离，转化为不含参数的函数的最值问题；（2）若()0f x >就可讨论参数不同取值下的函数的单调性和极值以及最值，最终转化为min ()0f x >，若()0f x <恒成立，转化为max ()0f x <;（3）若()()f x g x >恒成立，可转化为min max ()()f x g x >. 23．（1）'()4cos 4sin 4cos f x x x x x ==-+--；（2）21'()2ln 2(1)x f x x =-+. 【分析】(1)利用积的导数和和差的导数法则求导.(2)利用商的导数和积的导数的法则求导. 【详解】(1)f'(x)=(1+sin x)'(1-4x)+(1+sin x)(1-4x)'=cos x(1-4x)-4(1+sin x)=cos x-4xcos x-4-4sin x.(2)f(x)=1x x +-2x =1-11x +-2x ,则f'(x)=21(1)x +-2xln 2. 【点睛】本题主要考查对函数求导，意在考查学生对该知识的掌握水平和分析推理能力. 24．(1)3()f x x x=-；(2)证明见解析. 【解析】解：(1)方程7x －4y －12＝0可化为y ＝74x －3，当x ＝2时，y ＝12．又f′(x)＝a ＋2b x ，于是1222{744b a b a -=+=，解得13a b ==⎧⎨⎩故f(x)＝x －3x． (2)证明：设P(x 0，y 0)为曲线上任一点，由f′(x)＝1＋23x知，曲线在点P(x 0，y 0)处的切线方程为y －y 0＝(1＋203x )·(x －x 0)，即y －(x 0－03x )＝(1＋203x )(x －x 0)．令x ＝0得，y ＝－06x ，从而得切线与直线x ＝0，交点坐标为(0，－06x )．令y ＝x ，得y ＝x ＝2x 0，从而得切线与直线y ＝x 的交点坐标为(2x 0,2x 0)．所以点P(x 0，y 0)处的切线与直线x ＝0，y ＝x 所围成的三角形面积为12|－06x ||2x 0|＝6．曲线y ＝f(x)上任一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形面积为定值，此定值为6．25．（1）2；（2）证明见解析．【分析】（1）求出()cos 1sin f x x x x '=++，即得2f π⎛⎫'⎪⎝⎭的值；（2）设切点为001,x x ⎛⎫⎪⎝⎭，先求出切线l 的方程为：()020011y x x x x -=--，再求出l 与坐标轴所围成的三角形的面积2S =，即得证. 【详解】（1）()(1sin )f x x x =+，则()[(1sin )](1sin )(1sin )cos 1sin f x x x x x x x x x x ''''=+=+++=++，所以cos 1sin 22222f ππππ'⎛⎫=++=⎪⎝⎭；（2）设切点为001,x x ⎛⎫⎪⎝⎭， ∵1y x =，21y x'∴=-，∴切线l 的斜率201k x =-， ∴切线l 的方程为：()020011y x x x x -=--，令0x =，得02y x =，令0y =，得02x x =，所以l 与坐标轴所围成的三角形的面积0012222S x x =⋅⋅=，因此l 与坐标轴所围成的三角形的面积与切点无关．【点睛】本题主要考查导数的运算，考查导数的几何意义，意在考查学生对这些知识的理解掌握水平. 26．（1）1ln 22--；（2）3 【分析】（1）求出导函数，代入x 的值即可得到结果；（2）不等式()()0g x f x k x-'>恒成立等价于[](1)1ln(1)x x k x+++<对于0x >恒成立.【详解】（1）由题意可得()()2ln 111xx x f x x +='--+ ∴()11ln 22f '=--；（2）当0x >时，不等式()()0g x f x k x'->恒成立即[](1)1ln(1)x x k x+++<对于0x >恒成立设[](1)1ln(1)()x x h x x+++=，则21ln(1)()x x h x x --+'=1()1011x g x x x '=-=>++，()1ln(1)g x x x =--+在区间()0,∞+上是增函数，且()0g x =存在唯一实数根a ,满足(2,3)a ∈，即1ln(1)a a =++ 由x a >时，()0,()0g x h x '>>；0x a <<时，()0,()0g x h x '<< 知()(0)h x x >的最小值为[](1)1ln(1)()1(3,4)a a h a a a+++==+∈故正整数k 的最大值为3. 【点睛】本题考查了函数的单调性问题，考查导数的应用以及函数恒成立问题，是一道中档题．。

(必考题)高中数学高中数学选修2-2第四章《定积分》测试(含答案解析)(1)

一、选择题1．给出下列函数：①()()2ln 1f x x x =+-；②()3cos f x x x =；③()xf x e x =+.0a ∃>使得()0aaf x dx -=⎰的函数是（）A ．①②B ．①③C ．②③D ．①②③2．直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为（） A ．22B ．42C ．2D ．43．曲线y ＝sin x ，y ＝cos x 与直线x ＝0，x ＝2π所围成的平面区域的面积为( ) A ．π20⎰(sin x －cos x )d x B ．2π40⎰(sin x －cos x )d x C ．π20⎰(cos x －sin x )d xD ．2π40⎰(cos x －sin x )d x4．三棱锥D ABC -及其正视图和侧视图如图所示，且顶点,,,A B C D 均在球O 的表面上，则球O 的表面积为（）A ．32πB ．36πC ．128πD ．144π5．曲线x y e =，x y e -=和直线1x =围成的图形面积是（） A ．1e e --B ．1e e -+C ．12e e ---D ．12e e -+-6．已知1(1)1x f x x e ++=-+，则函数()f x 在点(0,(0))f 处的切线l 与坐标轴围成的三角形的面积为 A ．14 B ．12C ．1D ．2 7．121(1)x x dx --=⎰（）A ．1π+B ．1π-C ．πD ．2π8．已知幂函数a y x =图像的一部分如下图，且过点(2,4)P ，则图中阴影部分的面积等于（）A ．163B ．83C ．43D ．239．曲线()sin 0πy x x =≤≤与直线12y =围成的封闭图形的面积是 A 3B ．23C ．π23-D π3310．已知函数20()cos 0x f x x x ≥⎧=⎨<⎩,则12()f x dx π-⎰的值等于（）A ．1B ．2C ．3D ．411．20sin xdx π=⎰（）A ．4B ．2C ．-2D ．012．已知11em dx x=⎰，函数()f x 的导数()()()f x a x m x a '=++，若()f x 在x a =-处取得极大值，则a 的取值范围是（） A ．1a 或0a <D ．01a <<或0a <二、填空题13．曲线y=x 2与y=x 所围成的封闭图形的面积为______．14．在平面直角坐标系中，角α的始边落在x 轴的非负半轴，终边上有一点是(3-，若[)0,2απ∈，则cos xdx αα-=⎰______．15．由曲线22y x =+与3y x =，1x =，2x =所围成的平面图形的面积为________________.16．若()()4112ax x -+的展开式中2x 项的系数为4，则21ae dx x=⎰________________ 17．(12021x x dx +-=⎰________18．定积分2sin cos t tdt π=⎰________．19．π4cos xdx =⎰______．20．曲线2y x 和曲线y x =围成一个叶形图（如图所示阴影部分），其面积是________．三、解答题21．设函数()32f x x ax bx =++在点1x =处有极值2-.(1)求常数,a b 的值;(2)求曲线()y f x =与x 轴所围成的图形的面积.22．已知函数31()ln 2f x x ax x =--()a R ∈.（1）若()f x 在(1,2)上存在极值，求(1)f 的取值范围；（2）当0x >时，()0f x <恒成立，比较a e 与232a e+的大小. 23．已知函数()32f x x ax =+图像上一点()1,P b 的切线斜率为3-，()()()3261302t g x x x t x t -=+-++> （Ⅰ）求,a b 的值；（Ⅱ）当[]1,4x ∈-时，求()f x 的值域；（Ⅲ）当[]1,4x ∈时，不等式()()f x g x ≤恒成立，求实数t 的取值范围.24．已知抛物线2:2C y x x =-+，在点(0,0)A ，(2,0)B 分别作抛物线的切线12,l l ．（1）求切线1l 和2l 的方程；（2）求抛物线C 与切线1l 和2l 所围成的面积S ．25．如图，在棱长为1的正方体1111ABCD A BC D -中，E 为AB 的中点.求：（1）异面直线1BD 与CE 所成角的余弦值；（2）点A 到平面1A EC 的距离.26．已知()ln f x x x mx =+，2()3g x x ax =-+-（1）若函数()f x 在(1,)+∞上为单调函数，求实数m 的取值范围；（2）若当0m =时，对任意(0,),2()()x f x g x ∈+∞≥恒成立，求实数a 的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】利用定义判断①②中的函数为奇函数，根据奇函数和定积分的性质，判断①②；利用反证法，结合定积分的性质，判断③. 【详解】对①，()f x 的定义域为R2212()ln(1)ln(1)ln(1)()f x x x x x x x f x --=+=+=-+=-即函数()f x 为奇函数，则0a ∃>使得()0aaf x dx -=⎰对②，()f x 的定义域为R33()cos()cos ()f x x x x x f x -=--=-=-，即函数()f x 为奇函数，则0a ∃>使得()0aaf x dx -=⎰对③，若0a ∃>，使得()0aaf x dx -=⎰成立则()2102aax x a aa a e x dx e x e e ---⎛⎫+=+- ⎪⎝==⎭⎰，解得0a =，与0a >矛盾，则③不满足故选：A 【点睛】本题主要考查了定积分的性质以运用，属于中档题.2．D解析：D 【解析】直线4y x =与曲线3y x =的交点坐标为(0,0)和(2,8)，故直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积23242001(4)2|8444S x x dx x x ⎛⎫=⎰-=-=-= ⎪⎝⎭．故选D ．3．D解析：D 【解析】π40⎰(-sin x +cos x )d x 2π4π+⎰(sin x -cos x )dx=2π40⎰(cos x －sin x )d x ,选D. 点睛：1.求曲边图形面积的方法与步骤 (1)画图，并将图形分割为若干个曲边梯形；(2)对每个曲边梯形确定其存在的范围，从而确定积分的上、下限； (3)确定被积函数；(4)求出各曲边梯形的面积和，即各积分的绝对值的和．2．利用定积分求曲边图形面积时，一定要找准积分上限、下限及被积函数．当图形的边界不同时，要分不同情况讨论．4．A解析：A 【解析】由三视图可得：DC ⊥平面ABC 且底面ABC 为正三角形，如图所示，取AC 中点F ，连BF ，则BF AC ⊥，在Rt BCF 中，2BF =，2CF =，4BC =，在Rt BCD 中，4CD =，所以42BD =ABC 的距离为d ，因为DC ⊥平面ABC ，且底面ABC 为正三角形，所以2d =，因为ABC 的外接圆的半径为2，所以由勾股定理可得22228R d =+=，则该三棱锥外接球的半径22R =，所以三棱锥外接球的表面积是2432R ππ=，故选A ．点睛：本题考查几何体的三视图，线面垂直的定义，以及几何体外接球问题，由三视图正确还原几何体、以及判断几何体位置关系是解题关键；由三视图画出几何体的直观图，由三视图判断出DC ⊥平面ABC 、求出ABC 的外接圆的半径，列出方程求出三棱锥外接球的半径，由球的表面积公式求出答案.5．D解析：D 【解析】试题分析：根据题意画出区域，作图如下，由{x xy e y e-==解得交点为（0，1），∴所求面积为：()()1101|2x x x x S e e dx e e e e --=-=+=+-⎰ 考点：定积分及其应用6．A解析：A 【解析】试题分析：由1(1)1x f x x e++=-+知()2x f x x e =-+，则()1(0)2xf x e f ''=+⇒=，而(0)1f =-，即切点坐标为()0,1-，切线斜率(0=2k f '=），则切线()():12021l y x y x --=-⇒=-，切线l 与坐标轴的交点分别为1,02⎛⎫⎪⎝⎭和()0,1-，则切线l 与坐标轴围成的三角形的面积为1111224S =⋅⋅-= 考点：函数在某点处的切线7．D解析：D 【解析】因1112111111]|2x dx x ----=+=⎰，故设sin ,[,]22x ππθθ=∈-，则12221221cos 21cos sin cos (2)2sin 2|442d d d ππππππππθπθθθθθπθ-----+====⨯+=⎰⎰⎰，应选答案D 。

高中数学选修2-2综合测试试题及答案解析

高中数学选修2-2综合测试试题及答案解析时间120分钟，满分150分．一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．曲线y ＝4x －x 3在点(－1，－3)处的切线方程是导学号 10510897( ) A ．y ＝7x ＋4 B ．y ＝x －4 C ．y ＝7x ＋2D ．y ＝x －22．设x ＝3＋4i ，则复数z ＝x －|x |－(1－i)在复平面上的对应点在导学号 10510898( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限3．若函数f (x )＝x 2＋bx ＋c 的图象的顶点在第四象限，则函数f ′(x )的图象是导学号 10510899( )4．定义复数的一种运算z 1*z 2=|z 1|＋|z 2|2(等式右边为普通运算)，若复数z ＝a ＋b i ，z －为z 的共轭复数，且正实数a ，b 满足a ＋b ＝3，则z *z －的最小值为导学号 10510900( )A.92B.322C.32D ．945．(2016·宜春高二检测)已知函数f (x )＝sin x ＋e x ＋x 2015，令f 1(x )＝f ′(x )，f 2(x )＝f 1′(x )，f 3(x )＝f 2′(x )，…，f n ＋1(x )＝f n ′(x )，则f 2016(x )＝导学号 10510901( )A ．sin x ＋e xB ．cos x ＋e xC ．－sin x ＋e xD ．－cos x ＋e x6．函数f (x )＝3x －4x 3(x ∈[0,1])的最大值是导学号 10510902( ) A.12 B ．－1 C ．0D ．17．(2016·哈尔滨质检)在平面直角坐标系中，横、纵坐标均为整数的点叫做格点．若函数图象恰好经过k 个格点，则称函数为k 阶格点函数．已知函数：①y ＝sin x; ②y ＝cos(x ＋π6)；③y ＝e x －1;④y ＝x 2.其中为一阶格点函数的序号为导学号 10510903( ) A ．①② B ．②③ C ．①③D ．②④8．(2016·淄博高二检测)下列求导运算正确的是导学号 10510904( ) A ．(2x )′＝x ·2x －1 B ．(3e x )′＝3e xC ．(x 2－1x )′＝2x －1x2D ．(xcos x )′＝cos x －x sin x (cos x )29．古希腊人常用小石子在沙滩上摆成各种形状来研究数．比如：他们研究过图1中的1,3,6,10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1,4,9,16，…，这样的数为正方形数．下列数中既是三角形数又是正方形数的是导学号 10510905( )A ．289B ．1024C ．1225D ．137810．若曲线y ＝x －12在点(a ，a －12)处的切线与两个坐标围成的三角形的面积为18，则a ＝导学号 10510906( )A ．64B ．32C ．16D ．811．(2016·全国卷Ⅲ理，12)定义“规范01数列”{a n }如下：{a n }共有2m 项，其中m 项为0，m 项为1，且对任意k ≤2m ，a 1，a 2，…，a k 中0的个数不少于1的个数，若m ＝4，则不同的“规范01数列”共有导学号 10510907( )A ．18个B ．16个C ．14个D ．12个12．当x ∈[－2,1]时，不等式ax 3－x 2＋4x ＋3≥0恒成立，则实数a 的取值范围是导学号 10510908( )A ．[－5，－3]B ．[－6，－98]C ．[－6，－2]D ．[－4，－3]二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．对任意非零实数a 、b ，若a ⊗b 的运算原理如图所示，则2⊗⎠⎛0πsin x d x ＝________.导学号 1051090914．请阅读下列材料：若两个正实数a 1、a 2满足a 21＋a 22＝1，那么a 1＋a 2≤ 2.证明：构造函数f (x )＝(x －a 1)2＋(x －a 2)2＝2x 2－2(a 1＋a 2)x ＋1.因为对一切实数x ，恒有f (x )≥0，所以Δ≤0，从而得4(a 1＋a 2)2－8≤0，所以a 1＋a 2≤ 2.类比上述结论，若n 个正实数满足a 21＋a 22＋…＋a 2n ＝1，你能得到的结论为________.导学号 1051091015．对大于或等于2的自然数m 的n 次方幂有如下分解方式：导学号 10510911 22＝1＋3,32＝1＋3＋5,42＝1＋3＋5＋7； 23＝3＋5,33＝7＋9＋11,43＝13＋15＋17＋19.根据上述分解规律，若n 2＝1＋3＋5＋…＋19，m 3(m ∈N *)的分解中最小的数是21，则m ＋n 的值为________．16．(2016·全国卷Ⅱ理，16)若直线y ＝kx ＋b 是曲线y ＝ln x ＋2的切线，也是曲线y ＝ln(x ＋1)的切线，则b ＝________.导学号 10510912三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．(本题满分10分)(2016·大连高二期中)已知z 1、z 2为复数，i 为虚数单位，z 1·z －1＋3(z 1＋z －1)＋5＝0，z 2＋3z 2－3为纯虚数，z 1、z 2在复平面内对应的点分别为P 、Q .导学号 10510913(1)求点P 的轨迹方程； (2)求点Q 的轨迹方程； (3)写出线段PQ 长的取值范围．18．(本题满分12分)设函数f (x )＝sin x －cos x ＋x ＋1,0<x <2π，求函数f (x )的单调区间与极值.导学号 1051091419．(本题满分12分)已知A n (n ，a n )为函数y 1＝x 2＋1图象上的点，B n (n ，b n )为函数y 2＝x 的图象上的点，设c n ＝a n －b n ，其中n ∈N *.导学号 10510915(1)求证：数列{c n }既不是等差数列也不是等比数列； (2)试比较c n 与c n ＋1的大小．20．(本题满分12分)设函数f (x )＝x ln x .导学号 10510916 (1)求f (x )的单调区间；(2)求f (x )在区间[18，12]上的最大值和最小值．21．(本题满分12分)(2016·贵州高二检测)已知点列A n (x n,0)，n ∈N *，其中x 1＝0，x 2＝a (a >0)，A 3是线段A 1A 2的中点，A 4是线段A 2A 3的中点，…，A n 是线段A n －2A n －1的中点，….导学号 10510917(1)写出x n 与x n －1、x n －2之间的关系式(n ≥3)；(2)设a n ＝x n ＋1－x n ，计算a 1、a 2、a 3，由此推测数列{a n }的通项公式，并加以证明．22．(本题满分12分)(2016·北京文，20)设函数f (x )＝x 3＋ax 2＋bx ＋c .导学号 10510918 (1)求曲线y ＝f (x )在点(0，f (0))处的切线方程；(2)设a ＝b ＝4，若函数f (x )有三个不同零点，求c 的取值范围； (3)求证：a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．高中数学选修2-2综合测试试题答案解析1．[答案] D[解析] y ′|x ＝－1＝(4－3x 2)|x ＝－1＝1， ∴切线方程为y ＋3＝x ＋1，即y ＝x －2.2． [答案] B[解析] ∵x ＝3＋4i ，∴|x |＝32＋42＝5， ∴z ＝3＋4i －5－(1－i)＝(3－5－1)＋(4＋1)i ＝－3＋5i. ∴复数z 在复平面上的对应点在第二象限，故应选B.3． [答案] A[解析] ∵f ′(x )＝2x ＋b 为增函数，∴排除B 、D ；又f (x )的顶点在第四象限，∴－b2>0，∴b <0，排除C ，故选A.4．[答案] B[解析] 由题意可得z *z －＝|a ＋b i|＋|a －b i|2＝a 2＋b 2＋a 2＋(－b )22＝a 2＋b 2，∵正实数a ，b 满足a ＋b ＝3，∴b ＝3－a ，∴a 2＋b 2＝a 2＋(3－a )2＝2a 2－6a ＋9，由二次函数可知当a ＝32时，上式取最小值322.故选B.5．[答案] A[解析] f 1(x )＝f ′(x )＝cos x ＋e x ＋2015x 2014，f 2(x )＝f 1′(x )＝－sin x ＋e x ＋2015× 2014x 2013， f 3(x )＝f 2′(x )＝－cos x ＋e x ＋2015×2014×2013x 2012，…，∴f 2016(x )＝sin x ＋e x .6．[答案] D[解析] 由f ′(x )＝3－12x 2＝0得，x ＝±12，∵x ∈[0,1]，∴x ＝12，∵当x∈[0，12]，f ′(x )>0，当x ∈[12，1]时，f ′(x )<0，∴f (x )在[0，12]上单调递增，在[12，1]上单调递减，故x ＝12时，f (x )取到极大值也是最大值，f (12)＝3×12－4×(12)3＝1，故选D.7． [答案] C[解析] 对于①，注意到y ＝sin x 的值域是[－1,1]；当sin x ＝0时，x ＝k π(k ∈Z )，此时相应的整数x ＝0；当sin x ＝±1时，x ＝k π＋π2(k ∈Z )，此时没有相应的整数x ，因此函数y ＝sin x 仅过唯一的整点(0,0)，该函数是一阶格点函数．同理可知，对于②，函数y ＝cos(x ＋π6)不是一阶格点函数．对于③，令y ＝e x －1＝k (k ∈Z )得e x ＝k ＋1>0，x ＝ln(k ＋1)，仅当k ＝0时，x ＝0∈Z ，因此函数y ＝e x －1是一阶格点函数．对于④，注意到函数y ＝x 2的图象经过多个整点，如点(0,0)，(1,1)，因此函数y ＝x 2不是一阶格点函数．综上所述知选C.8．[答案] B[解析] 对于A ，(2x )′＝2x ln2；对于B ，(3e x )′＝3e x ；对于C ，(x 2－1x)′＝2x ＋1x 2；对于D ，(xcos x )′＝cos x ＋x sin x (cos x )2；综上可知选B.9．[答案] C[解析] 图1中满足a 2－a 1＝2，a 3－a 2＝3，…，a n －a n －1＝n ，以上累加得a n －a 1＝2＋3＋…＋n ，a n ＝1＋2＋3＋…＋n ＝n ·(n ＋1)2，图2中满足b n ＝n 2，一个数若满足三角形数，其必能分解成两个相邻自然数乘积的一半；一个数若满足正方形数，其必为某个自然数的平方． ∵1225＝352＝49×502，∴选C.10．[答案] A[解析] y ′＝－12x －32，∴k ＝－12a －32，切线方程是y －a －12＝－12a －32(x －a )，令x ＝0，y ＝32a －12，令y ＝0，x ＝3a ，∴三角形的面积是S ＝12·3a ·32a －12＝18，解得a ＝64.11． [答案] C[解析] 由题意可得a 1＝0，a 8＝1，a 2，a 3，…，a 7中有3个0、3个1，且满足对任意k ≤8，都有a 1，a 2，…，a k 中0的个数不少于1的个数，利用列举法可得不同的“规范01数列”有00001111,00010111,00011011,00011101,00100111,00101011,00101101,00110011,00110101,01000111,01001011,01001101,01010011,01010101，共14个．12．[答案] C[解析] ax 3≥x 2－4x －3恒成立．当x ＝0时式子恒成立．∴a ∈R ，当x >0时，a ≥1x －4x 2－3x 3恒成立．令1x ＝t ，x ∈(0,1]，∴t ≥1.∴a ≥t －4t 2－3t 3恒成立．令g (t )＝t －4t 2－3t 3，g ′(t )＝1－8t －9t 2＝(t ＋1)(－9t ＋1)， ∴函数g ′(t )在[1，＋∞)上为减函数而且g ′(1)＝－16<0，∴g ′(t )<0在[1，＋∞)上恒成立． ∴g (t )在[1，＋∞)上是减函数， ∴g (t )max ＝g (1)＝－6，∴a ≥－6；当x <0时，a ≤1x －4x 2－3x 3恒成立，∵x ∈[－2,0)，∴t ≤－12，令g ′(t )＝0得，t ＝－1，∴g (t )在(－∞，－1]上为减函数，在(－1，－12]上为增函数，∴g (t )min ＝g (－1)＝－2，∴a ≤－2.综上知－6≤a ≤－2. 13． [答案]22[解析] ∵⎠⎛0πsin x d x ＝－cos x |π0＝2>2， ∴2⊗⎠⎛0πsin x d x ＝2⊗2＝2－12＝22.14．[答案] a 1＋a 2＋…＋a n ≤n (n ∈N *)[解析] 构造函数f (x )＝(x －a 1)2＋(x －a 2)2＋…＋(x －a n )2＝nx 2－2(a 1＋a 2＋…＋a n )x ＋1， ∵f (x )≥0对任意实数x 都成立，∴Δ＝4(a 1＋a 2＋…＋a n )2－4n ≤0， ∵a 1，a 2，…，a n 都是正数，∴a 1＋a 2＋…＋a n ≤n .15． [答案] 15[解析] 依题意得n 2＝10×(1＋19)2＝100，∴n ＝10.易知m 3＝21m ＋m (m －1)2×2，整理得(m －5)(m ＋4)＝0，又m ∈N *，所以m ＝5，即53＝21＋23＋25＋27＋29，所以m ＋n ＝15.16． [答案] 1－ln2[解析] 设y ＝kx ＋b 与y ＝ln x ＋2和y ＝ln(x ＋1)的切点分别为(x 1，ln x 1＋2)和(x 2，ln(x 2＋1))．则切线分别为y －ln x 1－2＝1x 1(x －x 1)，y －ln(x 2＋1)＝1x 2＋1(x －x 2)，化简得y ＝1x 1x ＋ln x 1＋1，y ＝1x 2＋1x －x 2x 2＋1＋ln(x 2＋1)，依题意，⎩⎨⎧1x 1＝1x 2＋1ln x 1＋1＝－x 2x 2＋1＋ln (x 2＋1)，解得x 1＝12，从而b ＝ln x 1＋1＝1－ln2.17． [解析] (1)设z 1＝x ＋y i ，(x 、y ∈R )，由z 1·z －1＋3(z 1＋z －1)＋5＝0得x 2＋y 2＋6x ＋5＝0，整理得(x ＋3)2＋y 2＝4，∴点P 的轨迹方程为(x ＋3)2＋y 2＝4. (2)设z 2＝x ＋y i ，(x 、y ∈R )， z 2＋3z 2－3＝x ＋3＋y i x －3＋y i ＝x 2＋y 2－9－6y i(x －3)2＋y 2， ∵z 2＋3z 2－3为纯虚数，∴x 2＋y 2＝9且y ≠0， ∴点Q 的轨迹方程为x 2＋y 2＝9(y ≠0)． (3)PQ 长的取值范围是[0,8)． ∵两圆相交，∴PQ 长的最小值为0，又两圆圆心距为3，两圆半径分别为2和3，∴PQ 长的最大值为8，但点Q 的轨迹方程中y ≠0，∴|PQ |<8，∴线段PQ 长的取值范围是[0,8)．18． [解析] f ′(x )＝cos x ＋sin x ＋1＝2sin(x ＋π4)＋1 (0<x <2π)，令f ′(x )＝0，即sin(x ＋π4)＝－22，解之得x ＝π或x ＝3π2.x ，f ′(x )以及f (x )变化情况如下表：∴f (x )的单调增区间为(0，π)和(3π2，2π)，单调减区间为(π，3π2)．f 极大(x )＝f (π)＝π＋2，f 极小(x )＝f (3π2)＝3π2.19． [解析] (1)证明：依题意，a n ＝n 2＋1，b n ＝n ，c n ＝n 2＋1－n . 假设{c n }是等差数列，则2c 2＝c 1＋c 3，∴2(5－2)＝2－1＋10－3. ∴25＝2＋10，产生矛盾， ∴{c n }不是等差数列．假设{c n }是等比数列，则c 22＝c 1c 3，即(5－2)2＝(2－1)(10－3)．有6＝65－32－10，产生矛盾， ∴{c n }也不是等比数列．(2)解：∵c n ＋1＝(n ＋1)2＋1－(n ＋1)>0，c n ＝n 2＋1－n >0， ∴c n ＋1c n ＝(n ＋1)2＋1－(n ＋1)n 2＋1－n ＝n 2＋1＋n(n ＋1)2＋1＋(n ＋1)， 0<n 2＋1<(n ＋1)2＋1，又0<n <n ＋1，∴n 2＋1＋n <(n ＋1)2＋1＋n ＋1， ∴0<n 2＋1＋n(n ＋1)2＋1＋(n ＋1)<1，∴c n ＋1c n<1，即c n ＋1<c n . 20． [解析] (1)由题意知，函数的定义域为(0，＋∞)． ∵f (x )＝x ln x ，∴f ′(x )＝ln x ＋1，令f ′(x )＝0，得x ＝1e ，令f ′(x )>0，得x >1e ，令f ′(x )<0，得0<x <1e，∴f (x )的单调递增区间为(1e ，＋∞)，单调递减区间为(0，1e )．(2)∵f (18)＝18ln 18＝38ln 12，f (12)＝12ln 12，f (1e )＝1e ln 1e ＝－1e ，又12ln 12<38ln 12， ∴求f (x )在区间[18，12]的最大值为38ln 12，最小值为－1e .21． [解析] (1)由题意，当n ≥3时，x n ＝12(x n －1＋x n －2)(2)x 1＝0，x 2＝a ，x 3＝12(x 2＋x 1)＝a 2，x 4＝12(x 3＋x 2)＝3a4，∴a 1＝x 2－x 1＝a ，a 2＝x 3－x 2＝－a 2，a 3＝x 4－x 3＝a4，推测a n ＝a(－2)n －1.方法一证明：对于任意n ∈N *，a n ＝x n ＋1－x n ，a n ＋1＝x n ＋2－x n ＋1＝12(x n ＋1＋x n )－x n ＋1＝－12(x n ＋1－x n )＝－12a n ，又∵a 1＝a >0，∴{a n }是以a 为首项，以－12为公比的等比数列．故a n ＝a ·(－12)n －1＝a(－2)n －1. 方法二下面用数学归纳法证明：①当n ＝1时，a 1＝a ＝a ·(－12)1－1，结论a n ＝a (－2)n －1成立． ②假设当n ＝k (k ≥1，k ∈N )时，a n ＝a (－2)n －1成立，即a k＝a ·(－12)k －1，则当n ＝k ＋1时，a k ＋1＝x k ＋2－x k ＋1＝x k ＋x k ＋12－x k ＋1＝x k －x k ＋12＝－12a k ＝(－12)·a ·(－12)k －1＝a ·(－12)(k ＋1)－1，所以n ＝k ＋1时，a n ＝a(－2)n －1成立．由①②可知，数列{a n }的通项公式为a n ＝a ·(－12)n －1，n ∈N *.22． [解析] (1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b . 因为f (0)＝c ，f ′(0)＝b ，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝bx ＋c . (2)当a ＝b ＝4时，f (x )＝x 3＋4x 2＋4x ＋c ，所以f ′(x )＝3x 2＋8x ＋4.令f ′(x )＝0，得3x 2＋8x ＋4＝0，解得x ＝－2或x ＝－23.f (x )与f ′(x )在区间(－∞，＋∞)上的情况如下：所以，当c >0且c －3227<0时，存在x 1∈(－4，－2)，x 2∈(－2，－23)，x 3∈(－23，0)，使得f (x 1)＝f (x 2)＝f (x 3)＝0.由f (x )的单调性知，当且仅当c ∈(0，3227)时，函数f (x )＝x 3＋4x 2＋4x ＋c 有三个不同零点．(3)当Δ＝4a 2－12b <0时，f ′(x )＝3x 2＋2ax ＋b >0，x ∈(－∞，＋∞)，此时函数f (x )在区间(－∞，＋∞)上单调递增，所以f (x )不可能有三个不同零点．当Δ＝4a 2－12b ＝0时， f ′(x )＝3x 2＋2ax ＋b 只有一个零点，记作x 0. 当x ∈(－∞，x 0)时， f ′(x )>0，f (x )在区间(－∞，x 0)上单调递增；当x ∈(x 0，＋∞)时， f ′(x )>0，f (x )在区间(x 0，＋∞)上单调递增；所以f (x )不可能有三个不同零点．综上所述，若函数f (x )有三个不同零点，则必有Δ＝4a 2－12b >0. 故a 2－3b >0是f (x )有三个不同零点的必要条件．当a ＝b ＝4，c ＝0时，a 2－3b >0，f (x )＝x 3＋4x 2＋4x ＝x (x ＋2)2只有两个不同零点，所以a 2－3b >0不是f (x )有三个不同零点的充分条件．因此a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．。

高中数学选修2-2综合测试题(全册含答案)

高中数学选修2-2综合测试题(全册含答案)1.复数就像平面上的点，有实部和虚部。

2.复数就像向量，有大小和方向。

3.复数就像计算机中的复数类型，有实部和虚部。

4.复数就像两个数字的有序对，有序对的第一个数字是实部，第二个数字是虚部。

改写：关于复数的四种类比推理，可以用不同的比喻来描述复数的实部和虚部。

一种比喻是将复数看作平面上的点，实部和虚部分别对应点的横坐标和纵坐标；另一种比喻是将复数看作向量，实部和虚部分别对应向量的大小和方向；还可以将复数看作计算机中的复数类型，实部和虚部分别对应类型中的两个数；最后一种比喻是将复数看作有序对，实部和虚部分别对应有序对的第一个数字和第二个数字。

①复数的加减法运算可以类比多项式的加减法运算法则。

②由向量a的性质|a|²＝a²，可以类比得到复数z的性质：|z|²＝z²。

③方程ax²＋bx＋c＝0 (a，b，c∈R，且a≠0)有两个不同的实数根的条件是b²－4ac>0，类比可得方程ax²＋bx＋c＝0 (a，b，c∈C且a≠0)有两个不同的复数根的条件是b²－4ac>0.④由向量加法的几何意义，可以类比得到复数加法的几何意义。

其中类比得到的结论正确的是：A。

①③B。

②④C。

②③D。

①④2.删除明显有问题的段落。

3.填空题：11.若复数z满足z＋i＝0，则|z|＝1.12.直线y＝kx＋1与曲线y＝x³＋ax＋b相切于点A(1,3)，则2a＋b的值为4.13.第n个正方形数是n²。

14.＋＋＝AA′BB′CC′；＋＋＋＝AA′BB′CC′DD′。

4.解答题：15.1) F(x)的单调区间为(-∞。

0)和(2.+∞)。

2) F(x)在[1,5]上的最小值为-5，最大值为9.16.因为AD⊥BC，所以AB²=AD²+DB²。

又因为AB⊥AC，所以AC²=AD²+DC²。

高中数学选修2-2分章节测试卷(含答案)

第一章综合能力检测一、选择题：本大题共12小题，每小题5分，共60分． 1．函数y ＝sin(π4－x )的导数为( )A ．－cos(π4＋x )B ．cos(π4－x )C ．－sin(π4－x )D ．－sin(x ＋π4)2．(2009·广东三校联考)函数f (x )＝a ln x ＋x 在x ＝1处取得极值，则a 的值为( ) A.12B ．－1C ．0D ．－123．如果f (x )为定义在R 上的偶函数，且导数f ′(x )存在，则f ′(0)的值为( ) A ．2B ．1C ．0D ．－14．(2009·全国卷Ⅰ)已知直线y ＝x ＋1与曲线y ＝ln(x ＋a )相切，则a 的值为( ) A ．1B ．2C ．－1D ．－25．已知f (x )＝(x －1)2＋2，g (x )＝x 2－1，则f [g (x )]( ) A ．在(－2,0)上递增 B ．在(0,2)上递增 C ．在(－2，0)上递增 D ．在(0，2)上递增6．已知三次函数f (x )＝13x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在R 上是增函数，则m 的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．2≤m ≤47．(2009·江西高考)若存在过点(1,0)的直线与曲线y ＝x 3和y ＝ax 2＋154x －9都相切，则a 等于( )A ．－1或－2564B ．－1或214C ．－74或－2564D ．－74或78．若f (x )＝－12x 2＋b ln(x ＋2)在(－1，＋∞)上是减函数，则b 的取值范围是( )A ．[－1，＋∞)B ．(－1，＋∞)C ．(－∞，－1]D ．(－∞，－1) 9．由y ＝sin x ，y ＝cos x ，x ＝0，x ＝π所围成图形的面积可表示为( ) A.⎠⎛0π(sin x －cos x )dxC.⎠⎛0π(cos x －sin x )dx10．已知f (a )＝⎠⎛01(2ax 2－a 2x )dx ，则f (a )的最大值为( )A ．－12B.19C.29D ．不存在11．(2009·青岛模拟)如右图，在一个长为π，宽为2的矩形OABC 内，由曲线y ＝sin x (0≤x ≤π)与x 轴围成如图所示的阴影部分，向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的)，则所投的点落在阴影部分的概率是( )A.1πB.2πC.3πD.π412．f (x )是定义在(0，＋∞)上的非负可导函数，且满足xf ′(x )＋f (x )≤0，对任意正数a ，b ，若a 0，|φ|<π2)的导函数y＝f ′(x )的部分图象如右图所示，且导函数f ′(x )有最小值－2，则ω＝________，φ＝________.15．若函数y ＝a (x 3－x )的单调递减区间为(－33，33)，则a 的取值范围是________． 16．物体A 以速度v ＝3t 2＋1在一直线上运动，在此直线上物体A 出发的同时，物体B 在物体A 的正前方5 m 处以v ＝10t 的速度与A 同向运动，当t ＝________ s 时，两物体相遇，相遇时物体A 走过________m.三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．(本小题满分10分)(2009·浙江高考)已知函数f(x)＝x3＋(1－a)x2－a(a＋2)x＋b(a，b∈R)．(1)若函数f(x)的图象过原点，且在原点处的切线斜率是－3，求a，b的值；(2)若函数f(x)在区间(－1,1)上不单调．．．，求a的取值范围．18．(本小题满分12分)已知F(x)＝⎠⎛x－1t(t－4)dt，x∈(0，＋∞)．(1)求F(x)的单调区间；(2)求函数F(x)在[1,5]上的最值．19．(本小题满分12分)已知f(x)＝ax3＋bx2＋cx(a≠0)在x＝±1时取得极值，且f(1)＝－1.(1)试求常数a，b，c的值；(2)试判断x＝±1是函数的极小值点还是极大值点，并说明理由．20．(本小题满分12分)求函数y＝x3－3ax＋2的极值，并说明方程x3－3ax＋2＝0何时有三个不同的实根？何时有唯一的实根？(其中a>0)21．(本小题满分12分)已知函数f(x)＝13ax3－bx2＋(2－b)x＋1，在x＝x1处取得极大值，在x＝x2处取得极小值，且0<x1<1<x2<2.(1)证明a>0；(2)求z＝a＋2b的取值范围．22．(本小题满分12分)(2009·湖北黄冈模拟)已知函数f(x)＝12x2－a ln x(a∈R)．(1)若f(x)在x＝2时取得极值，求a的值；(2)求f(x)的单调区间；(3)求证：当x>1时，12x2＋ln x<23x3.第二章综合能力检测一、选择题：本大题共12小题，每小题5分，共60分．1．所有自然数都是整数，4是自然数，所以4是整数，以上三段推理( ) A ．正确 B ．推理形式不正确 C ．两个“自然数”概念不一致 D ．两个“整数”概念不一致 2．若a >0，b >0，则有( )A.b 2a >2b －aB.b 2a <2b －aC.b 2a ≥2b －a D.b 2a≤2b －a 3．设S (n )＝1n ＋1n ＋1＋1n ＋2＋1n ＋3＋…＋1n 2，则( )A ．S (n )共有n 项，当n ＝2时，S (2)＝12＋13B ．S (n )共有n ＋1项，当n ＝2时，S (2)＝12＋13＋14C ．S (n )共有n 2－n 项，当n ＝2时，S (2)＝12＋13＋14D ．S (n )共有n 2－n ＋1项，当n ＝2时，S (2)＝12＋13＋144．F (n )是一个关于自然数n 的命题，若F (k )(k ∈N *)真，则F (k ＋1)真，现已知F (7)不真，则有：①F (8)不真；②F (8)真；③F (6)不真；④F (6)真；⑤F (5)不真；⑥F (5)真．其中为真命题的是( )A ．③⑤B ．①②C ．④⑥D ．③④5．若x ，y ∈R ，且2x 2＋y 2＝6x ，则x 2＋y 2＋2x 的最大值为( ) A ．14B ．15C ．16D ．176．设f (x )(x ∈R )为奇函数，f (1)＝12，f (x ＋2)＝f (x )＋f (2)，则f (5)等于( )A ．0B ．1 C.52D ．57．若O 是平面上一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λ(AB →|AB →|＋AC→|AC →|)，λ∈[0，＋∞)，则动点P 的轨迹一定通过△ABC 的( ) A ．外心 B ．内心 C ．重心D ．垂心8．如图所示为某旅游区各景点的分布图，图中一支箭头表示一段有方向的路，试计算顺着箭头方向，从A 到H 有几条不同的旅游路线可走( )A ．15B ．16C ．17D ．189．对于直角坐标平面内的任意两点A (x 1，y 1)、B (x 2，y 2)定义它们之间的一种“距离”：||AB ||＝|x 2－x 1|＋|y 2－y 1|.给出下列三个命题：①若点C 在线段AB 上，则||AC ||＋||CB ||＝||AB ||； ②在△ABC 中，若∠C ＝90°，则||AC ||2＋||CB ||2＝||AB ||2； ③在△ABC 中，||AC ||＋||CB ||>||AB ||. 其中真命题的个数为( ) A ．0B ．1C ．2D ．310．已知a ，b ，c ，d 是正实数，P ＝a a ＋b ＋c ＋b a ＋b ＋d ＋c c ＋d ＋a ＋d c ＋d ＋b ，则有( )A ．0<P <1B ．1<P <2C ．2<P <3D ．3<P <411．一个等差数列{a n }，其中a 10＝0，则有a 1＋a 2＋…＋a n ＝a 1＋a 2＋…＋a 19－n (1≤n ≤19)．一个等比数列{b n }，其中b 15＝1.类比等差数列{a n }有下列结论，正确的是( )A ．b 1b 2…b n ＝b 1b 2…b 29－n (1≤n ≤29，n ∈N *)B ．b 1b 2…b n ＝b 1b 2…b 29－nC ．b 1＋b 2＋…＋b n ＝b 1＋b 2＋…＋b 29－n (1≤n ≤29，n ∈N *)D ．b 1＋b 2＋…＋b n ＝b 1＋b 2＋…＋b 29－n 12．观察数表1 2 3 4 …第一行 2 3 4 5 …第二行 3 4 5 6 …第三行 4 5 6 7 …第四行 … … … …第一列第二列第三列第四列根据数表中所反映的规律，第n 行与第n 列的交叉点上的数应该是( ) A ．2n －1 B ．2n ＋1 C ．n 2－1D ．n 2二、填空题：本大题共4小题，每小题5分，共20分．13．若三角形内切圆的半径为r ，三边长分别为a ，b ，c ，则三角形的面积S ＝12r (a ＋b ＋c )，根据类比推理的方法，若一个四面体的内切球的半径为R ，四个面的面积分别为S 1，S 2，S 3，S 4，则四面体的体积V ＝________.14．若符号“*”表示求实数a 与b 的算术平均数的运算，即a *b ＝a ＋b2，则两边均含有运算符号“*”和“＋”，且对于任意3个实数a 、b 、c 都能成立的一个等式可以是________．15．把数列{2n ＋1}依次按第一个括号一个数，第二个括号两个数，第三个括号三个数，第四个括号四个数，第五个括号一个数……循环下去，如：(3)，(5,7)，(9,11,13)，(15,17,19,21)，…，则第104个括号内各数字之和为________．16．已知n 次多项式P n (x )＝a 0x n ＋a 1x n －1＋…＋a n －2x 2＋a n －1x ＋a n .如果在一种算法中，计算x k 0(k ＝2,3,4，…，n )的值需要k －1次乘法，计算P 3(x 0)的值共需要9次运算(6次乘法，3次加法)，那么计算P n (x 0)的值共需要________次运算．下面给出一种减少运算次数的算法：P 0(x )＝a 0，P k ＋1(x )＝xP k (x )＋a k ＋1(k ＝0,1,2，…，n －1)．利用该算法，计算P 3(x 0)的值共需要6次运算，计算P n (x 0)的值共需要________次运算．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分10分)证明对于任意实数x ，y 都有x 4＋y 4≥12xy (x ＋y )2.18．(本小题满分12分)(2009·江苏高考)如右图，在直三棱柱ABC －A 1B 1C 1中，E ，F 分别是A 1B ，A 1C 的中点，点D 在B 1C 1上，A 1D ⊥B 1C .求证：(1)EF ∥平面ABC ； (2)平面A 1FD ⊥平面BB 1C 1C .19．(本小题满分12分)求证：y ＝ax 2＋2bx ＋c ，y ＝bx 2＋2cx ＋a ，y ＝cx 2＋2ax ＋b (a ，b ，c 是互不相等的实数)这三条抛物线中，至少有一条与x 轴有两个交点．20．(本小题满分12分)已知函数f(n)(n∈N*)，满足条件：①f(2)＝2，②f(xy)＝f(x)·f(y)，③f(n)∈N*，④当x>y时，有f(x)>f(y)．(1)求f(1)，f(3)的值；(2)由f(1)，f(2)，f(3)的值，猜想f(n)的解析式；(3)证明你猜想的f(n)的解析式的正确性．21．(本小题满分12分)已知数列a1，a2，…，a30，其中a1，a2，…，a10是首项为1，公差为1的等差数列；a10，a11，…，a20是公差为d的等差数列；a20，a21，…a30是公差为d2的等差数列(d≠0)．(1)若a20＝40，求d；(2)试写出a30关于d的关系式，并求a30的取值范围；(3)续写已知数列，使得a30，a31，a40是公差为d3的等差数列，…，依次类推，把已知数列推广为无穷数列．提出同(2)类似的问题((2)应当作为特例)，并进行研究，你能得到什么样的结论？22．(本小题满分12分)对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数f(x)＝x2＋abx－c(b，c∈N)有且只有两个不动点0,2，且f(－2)<－12.(1)求函数f(x)的解析式；(2)已知各项均不为零的数列{a n}满足4S n·f(1a n)＝1，求数列的通项a n；(3)如果数列{a n}满足a1＝4，a n＋1＝f(a n)，求证当n≥2时，恒有a n<3成立．第三章综合能力检测一、选择题：本大题共12小题，每小题5分，共60分． 1．一个实数x 与一个虚数y 的和x ＋y 必为( )A ．实数B ．虚数C ．可能实数也可能是虚数D ．纯虚数 2．复数4＋3i1＋2i 的实部是( )A ．－2B ．2C ．3D ．43．复数z ＝m －2i1＋2i (m ∈R ，i 为虚数单位)在复平面上的对应点不可能位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．若复数a ＋3i1＋2i (a ∈R ，i 为虚数单位)是纯虚数，则实数a 的值为( )A ．－2B ．4C ．－6D ．65．若3＋2i 是关于x 的方程2x 2＋px ＋q ＝0(p ，q ∈R )的一个根，则q 的值是( ) A ．26B ．13C ．6D ．56．已知z 1＝2－5i ，z 2＝－3＋i ，z 1，z 2的对应点分别为P 1，P 2，则向量P 2P 1→对应的复数为( ) A ．－5＋6iB ．5－6iC ．5＋6iD ．－1－4i7．已知m1＋i ＝1＋n i ，其中m ，n 是实数，i 是虚数单位，则m ＋n i 的值为( )A ．1＋2iB ．1－2iC ．2＋iD ．2－i8．复数z 满足|3z ＋1|＝|z －i|，则复数z 对应点的轨迹是( ) A ．直线B ．正方形C ．圆D ．椭圆9．“复数z ＝12＋32i ”是“z ＋1z ∈R ”的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件10．复数－35＋2i 2＋35i ＋(21＋i )2008的虚部为( )A ．－1B ．1C ．－iD ．i11．设f (n )＝(1＋i 1－i )n ＋(1－i 1＋i )n(n ∈N *)，则集合{x |x ＝f (n )}中的元素有( )A ．1个B ．2个C ．3个D ．无穷多个12．若复数z ，a ，x 满足x ＝a －z 1－a z，且|z |＝1，则|x |等于( )A ．0B ．1C ．|a |D.12二、填空题：本大题共4小题，每小题5分，共20分．13．已知复数z 0＝3＋2i ，复数z 满足z ·z 0＝3z ＋z 0，则复数z ＝________. 14．复数z 满足|z ＋2＋2i|＝|z |，那么|z －1＋i|的最小值是________． 15．i 是虚数单位，若1＋7i 2－i＝a ＋b i(a ，b ∈R )，则乘积ab ＝________.16．对于n 个复数z 1，z 1，…，z n ，如果存在n 个不全为零的实数k 1，k 2，…，k n ，使得k 1z 1＋k 2z 2＋…＋k n z n ＝0，就称z 1，z 2，…，z n 线性相关．若要说明复数z 1＝1＋2i ，z 2＝1－i ，z 3＝－2线性相关，那么可取{k 1，k 2，k 3}＝________.(只要写出满足条件的一组值即可)三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分10分)(1)设复数z 1＝1＋i ，z 2＝x ＋2i(x ∈R )．若z 1z 2为实数，求实数x ； (2)计算：(4－i 5)(6＋2i 7)＋(7－i 11)(4－3i)．18．(本小题满分12分)在复数范围内解方程|z 2|＋(z ＋z )i ＝3－i2＋i .(i 为虚数单位)19．(本小题满分12分)已知z ＝(－1＋3i)(1－i)－(1＋3i)i ，ω＝z ＋a i(a ∈R )，当|ωz |≤2时，求a的取值范围．20．(本小题满分12分)已知z ∈C ，z －1z ＋1是纯虚数，求|z 2－z ＋2|的最小值．21．(本小题满分12分)设虚数z 满足|2z ＋5|＝|z ＋10|. (1)求|z |的值；(2)若z m ＋mz为实数，求实数m 的值；(3)若(1－2i)z 在复平面上对应的点在第一、三象限的角平分线上，求复数z .22．(本小题满分12分)对任意一个非零复数α，定义M α＝{ω|ω＝α2n －1，n ∈N *}．(1)设α是方程x ＋1x ＝2的一个根，试用列举法表示集合M α.若在M α中任取两个元素，求其和为零的概率P ；(2)若集合M α中只有三个元素，试写出满足条件的一个α值，并说明理由．第一章综合能力检测答案一、选择题：1．解析：y ′＝－cos(π4－x )＝－sin[π2－(π4－x )]＝－sin(π4＋x )．答案：D2．解析：f ′(x )＝ax ＋1，令f ′(x )＝0，得x ＝－a ，由题知当a ＝－1时，原函数在x ＝1处取得极值．答案：B3．解析：偶函数的导数为奇函数，即f ′(x )为奇函数，故f ′(0)＝0. 答案：C4．解析：y ′＝1x ＋a ，设直线y ＝x ＋1与曲线y ＝ln(x ＋a )相切的切点为(x 0，x 0＋1)，则1x 0＋a ＝1，∴x 0＝1－a ，∴ln(1－a ＋a )＝2－a ，∴e 2－a ＝1， ∴a ＝2. 答案：B5．解析：F (x )＝f [g (x )]＝x 4－4x 2＋6，F ′(x )＝4x 3－8x .令F ′(x )>0，得－2<x <0或x >2，∴F (x )在(－2，0)上递增．答案：C6．解析：由题意，得f ′(x )＝x 2－2(4m －1)x ＋(15m 2－2m －7)，由于f ′(x )≥0恒成立，故Δ≤0，解得2≤m ≤4. 答案：D7．解析：设直线与曲线y ＝x 3的切点为P (x 0，y 0)，则⎩⎪⎨⎪⎧y 0＝x 30y 0x 0－1＝3x 20⇒切线斜率k ＝3x 20＝0或k ＝274. 若k ＝0，切线方程为y ＝0. 由⎩⎪⎨⎪⎧y ＝0，y ＝ax 2＋154x －9，消去y ，得ax 2＋154x －9＝0，其判别式Δ＝0⇒a ＝－2564；若k ＝274，切线方程为y ＝274(x －1)，由⎩⎨⎧y ＝274(x －1)，y ＝ax 2＋154x －9消去y ，得ax 2－3x －94＝0，其判别式Δ＝0⇒a ＝－1. 答案：A8．解析：∵f ′(x )＝－x ＋b x ＋2，由题知，f ′(x )<0在(－1，＋∞)上恒成立，即－x ＋bx ＋2<0，∴b <x (x ＋2)＝(x ＋1)2－1. ∴b <－1.又当b ＝－1时，f ′(x )＝－x －1x ＋2＝－x (x ＋2)＋1x ＋2＝－(x ＋1)2x ＋2<0，∴b ≤－1. 答案：C9．解析：由y ＝sin x ，y ＝cos x ，x ＝0，x ＝π所围成的图形，如下图的阴影部分．答案：B10．解析：⎠⎛01(2ax 2－a 2x )dx＝(23ax 3－12a 2x 2)|10＝23a －12a 2，即f (a )＝23a －12a 2＝－12(a 2－43a ＋49)＋29＝－12(a －23)2＋29，∴当a ＝23时，f (a )有最大值29. 答案：C11．解析：根据几何概型的意义，所投的点落在阴影部分的概率是S 阴影S 矩形，由S 阴影＝⎠⎛0πsin xdx ＝(－cos x )|π0＝2，所求概率为S 阴影S 矩形＝22π＝1π. 答案：A 12．解析：设函数F (x )＝xf (x )，∴F ′(x )＝[xf (x )]′＝f (x )＋xf ′(x )≤0，∴F (x )＝xf (x )在(0，＋∞)上单调递减．∵a <b ，∴F (a )≥F (b )，即af (a )≥bf (b )．又∵0<a <b ，f (b )≥0，∴af (a )≤bf (a )，bf (b )≥af (b )．∴bf (a )≥af (b )．答案：A二、填空题：13.解析：⎠⎛02(2x －e x )dx ＝(x 2－e x )|20＝4－e 2＋1＝5－e 2. 答案：5－e 214．解析：f ′(x )＝ωcos(ωx ＋φ)，依题意，得ω＝2,2cos(π3＋φ)＝－1，解得φ＝π3.答案：2 π315．解析：∵y ′＝a (3x 2－1)，令y ′<0，当a >0时，不等式的解集为(－33，33)；当a <0时，不等式的解集为(－∞，－33)∪(33，＋∞)．∵已知函数y ＝a (x 3－x )在(－33，33)上单调递减， ∴a >0. 答案：a >016．解析：设A 追上B 时，所用的时间为t 0，依题意有s A ＝s B ＋5，即10tdt＋5，t 30＋t 0＝5t 20＋5，即t 0(t 20＋1)＝5(t 20＋1)，解得t 0＝5 s ．所以s A ＝5t 20＋5＝130(m)．答案：130三、解答题：17．解：(1)由函数f (x )的图象过原点，得b ＝0，又f ′(x )＝3x 2＋2(1－a )x －a (a ＋2)， f (x )在原点处的切线斜率是－3，则－a (a ＋2)＝－3，所以a ＝－3，或a ＝1.(2)由f ′(x )＝0，得x 1＝a ，x 2＝－a ＋23.又f (x )在(－1,1)上不单调，即⎩⎨⎧－1<a <1，a ≠－a ＋23，或⎩⎪⎨⎪⎧－1<－a ＋23<1，a ≠－a ＋23.解得⎩⎪⎨⎪⎧ －1<a <1，a ≠－12，或⎩⎪⎨⎪⎧－5<a <1，a ≠－12，所以a 的取值范围是(－5，－12)∪(－12，1)．18．解：F (x )＝⎠⎛x －1(t 2－4t )dt ＝(13t 3－2t 2)|x －1＝13x 3－2x 2－(－13－2)＝13x 3－2x 2＋73(x >－1)． (1)F ′(x )＝x 2－4x ，由F ′(x )>0，即x 2－4x >0，得－1<x <0或x >4，由F ′(x )<0，即x 2－4x <0，得0<x <4，∴F (x )的单调递增区间为(－1,0)∪(4，＋∞)，单调递减区间为(0,4)．(2)由(1)知F (x )在[1,4]上递减，[4,5]上递增．又∵F (1)＝13－2＋73＝23，F (4)＝13×43－2×42＋73＝－253，F (5)＝13×53－2×52＋73＝－6，∴F (x )在[1,5]上的最大值为23，最小值为－253. 19．解：(1)f ′(x )＝3ax 2＋2bx ＋c ，因为x ＝±1是函数f (x )的极值点，所以x ＝±1是方程f ′(x )＝0即3ax 2＋2bx ＋c ＝0的两根．由根与系数的关系，得⎩⎨⎧－2b3a ＝0，①c3a ＝－1，②又f (1)＝－1，所以a ＋b＋c ＝－1.③ 由①②③，解得a ＝12，b ＝0，c ＝－32.(2)因为f (x )＝12x 3－32x ，所以f ′(x )＝32x 2－32＝32(x －1)·(x ＋1)．当x <－1或x >1时，f ′(x )>0，当－1<x <1时，f ′(x )<0.所以函数f (x )在(－∞，－1)和(1，＋∞)上是增函数，在(－1,1)上是减函数．所以当x ＝－1时，函数取得极大值f (－1)＝1，当x ＝1时，函数取得极小值f (1)＝－1.20．解：函数的定义域为R ，其导函数为y ′＝3x 2－3a .由y ′＝0，得x＝±a ，列表讨论如下：x (－∞，－a ) －a(－a ，a ) a (a ，＋∞) f ′(x ) ＋0 －0 ＋f (x )极大值极小值由此可得，函数x ＝－a 处取得极大值2＋2a 32；在x ＝a 处取得极小值2－2a 32.根据列表讨论，可作出函数的草图(如右图所示)，因为极大值f (－a )＝2＋2a 32>0，故当极小值f (a )＝2－2a 32<0，即a >1时，方程x 3－3ax ＋2＝0有三个不同的实根；当极小值f (a )＝2－2a 32>0，即0<a <1时，方程x 3－3ax ＋2＝0有唯一的实根．21．解：求函数f (x )的导数得 f ′(x )＝ax 2－2bx ＋2－b .(1)证明：由函数f (x )在x ＝x 1处取得极大值，在x ＝x 2处取得极小值，知x 1，x 2是f ′(x )＝0的两个根．所以f ′(x )＝a (x －x 1)(x －x 2)．当x <x 1时，f ′(x )>0，函数为增函数，由x －x 1<0，x －x 2<0得a >0. (2)在题设下，0<x 1<1<x 2<2等价于⎩⎨⎧f ′(0)>0，f ′(1)<0，f ′(2)>0.即⎩⎪⎨⎪⎧2－b >0，a －2b ＋2－b <0，4a －4b ＋2－b >0.化简得⎩⎪⎨⎪⎧2－b >0，a －3b ＋2<0，4a －5b ＋2>0.此不等式组表示的区域为平面aOb 上三条直线2－b ＝0，a －3b ＋2＝0,4a －5b ＋2＝0所围成的△ABC 的内部，其三个顶点分别为A (47，67)，B (2,2)，C (4,2)．z 在这三点的值依次为167，6,8.所以z 的取值范围为(167，8)．22．解：(1)f ′(x )＝x －ax ，∵x ＝2是一个极值点，∴2－a2＝0.∴a ＝4.此时f ′(x )＝x －4x ＝x 2－4x ＝(x －2)(x ＋2)x.∵f (x )的定义域是{x |x >0}，∴当0<x <2时，f ′(x )<0；当x >2时，f ′(x )>0. ∴当a ＝4时，x ＝2是f (x )的极小值点．∴a ＝4. (2)∵f ′(x )＝x －ax，∴当a ≤0时，f (x )的单调递增区间为(0，＋∞)．当a >0时，f ′(x )＝x －a x ＝x 2－a x ＝(x －a )(x ＋a )x，令f ′(x )>0有x >a ，∴函数f (x )的单调递增区间为(a ，＋∞)；令f ′(x )<0有0<x <a ，∴函数f (x )的单调递减区间为(0，a )． (3)证明：设g (x )＝23x 3－12x 2－ln x ，则g ′(x )＝2x 2－x －1x，∵当x >1时，g ′(x )＝(x －1)(2x 2＋x ＋1)x >0，∴g (x )在(1，＋∞)上是增函数． ∴g (x )>g (1)＝16>0.∴当x >1时，12x 2＋ln x <23x 3.第二章综合能力检测答案一、选择题：1．解析：三段论中的大前提、小前提及推理形式都是正确的．答案：A 2．解析：∵b 2a －(2b －a )＝b 2－2ab ＋a 2a ＝(b －a )2a ≥0，∴b 2a≥2b －a . 答案：C 3．解析：从n 到n 2共有n 2－n ＋1个自然数，即S (n )共有n 2－n ＋1项．故选D. 4．解析：若F (k )真，则F (k ＋1)一定真，其逆否命题为F (k ＋1)不真，则F (k )不真． ∴F (7)不真，则F (6)不真；F (6)不真，则F (5)不真．答案：A5．解析：x 2＋y 2＋2x ＝x 2＋(6x －2x 2)＋2x ＝－x 2＋8x ＝－(x －4)2＋16≤16. 答案：C6．解析：∵f (x ＋2)＝f (x )＋f (2) ∴令x ＝－1则有 f (1)＝f (－1)＋f (2) ∴f (2)＝2f (1)又∵f (1)＝12，∴f (2)＝1∴f (5)＝f (2＋3)＝f (2)＋f (3) ＝f (2)＋f (2)＋f (1) ＝2f (2)＋f (1)＝2＋12＝52. 答案：C7．解析：OP →＝OA →＋λ(AB →|AB →|＋AC →|AC →|)，AP →＝λ(AB →|AB →|＋AC →|AC →|)＝λ(e 1＋e 2)，∴AP 是∠A 的内角平分线．答案：B8．解析：这是图论中的一个问题，如果一条一条的去数，由于道路错综复杂，哪些已算过，哪些没有算过就搞不清了，所以我们换一个思路，用分析法来试试．要到H 点，需从F 、E 、G 走过来，F 、E 、G 各点又可由哪些点走过来，……，这样一步步倒推，最后归结到A ，然后再反推过去得到如下的计算法：A 至B 、C 、D 的路数记在B 、C 、D 圆圈内，B 、C 、D 分别到F 、E 、G 的路数亦记在F 、E 、G 圆圈内，最后F 、E 、G 各个路数之和，即得至H 的总路数如答图1所示．答案：C9．解析：①当点C 在线段AB 上时，可知||AC ||＋||CB ||＝||AB ||，故①是正确的．②取A (0,0)，B (1,1)，C (1,0)，则||AC ||2＝1，||BC ||2＝1，||AB ||2＝(1＋1)2＝4，故②是不正确的．③取A (0,0)，B (1,1)，C (1,0)，证明||AC ||＋||CB ||＝||AB ||，故③不正确．故选B. 10．解析：P ＝a a ＋b ＋c ＋b a ＋b ＋d ＋c c ＋d ＋a ＋dc ＋d ＋b>a a ＋b ＋c ＋d ＋b a ＋b ＋d ＋c ＋c c ＋d ＋a ＋b ＋d c ＋d ＋b ＋a ＝1， P ＝a a ＋b ＋c ＋b a ＋b ＋d ＋c c ＋d ＋a ＋dc ＋d ＋b<a a ＋b ＋b a ＋b ＋c c ＋d ＋d c ＋d ＝2， ∴1<P <2. 答案：B11．解析：在等差数列{a n }中，a 10＝0，知以a 10为等差中项的项和为0，如a 9＋a 11＝a 8＋a 12＝…＝a 2＋a 18＝a 1＋a 19＝0.而在等比数列{b n }中，b 15＝1，类比地有b 1b 29＝b 2b 28＝…＝b 14b 16＝1.从而类似地总结规律应为各项之积．∵等差数列{a n }中a 10＝0，∴a 1＋a 19＝a 2＋a 18＝…＝a 8＋a 12＝a 9＋a 11＝0. 即：a 19－n ＋a n ＋1＝0， a 18－n ＋a n ＋2＝0， a 17－n ＋a n ＋3＝0， …∴a 1＋a 2＋…＋a n ＝a 1＋a 2＋…＋a n ＋a n ＋1＋a n ＋2＋…＋a 19－n . ∵b 15＝1，∴b 1b 29＝b 2b 28＝…＝b 14b 16＝1. 即b 29－n b n ＋1＝b 28－n b n ＋2＝…＝b 14b 16＝1.∴b 1b 2…b n ＝b 1b 2…b 29－n (1≤n ≤29，n ∈N *)．故选A.12．解析：根据数表可知，第1行第1列上的数为1，第2行第2列上的数为3，第3行第3列上的数为5，第4行第4列上的数为7，那么，由此可以推导出第n 行第n 列交叉点上的数应该是2n －1. 答案：A二、填空题：13．解析：由平面图形到空间图形的类比过程中，边长→面积，面积→体积．答案：13R (S 1＋S 2＋S 3＋S 4)14．解析：答案不唯一．因为a ＋(b *c )＝a ＋b ＋c 2＝2a ＋b ＋c 2，又(a ＋b )*(a ＋c )＝(a ＋b )＋(a ＋c )2＝2a ＋b ＋c2，因此答案成立．同时：(a *b )＋c ＝(a *c )＋(b *c )；a *(b ＋c )＝(a ＋b )*c ＝(b ＋c )*a ＝(a ＋c )*b ；(a *b )＋c ＝(b *a )＋c 也符合题意．答案：a ＋(b *c )＝(a ＋b )*(a ＋c )15．解析：前面103个括号中共用了256个数，第104个括号有4个数分别是515,517,519,521，其和为2072. 答案：207216．解析：P n (x 0)＝a 0x n －10＋…＋a n －2x 20＋a n －1x 0＋a n ，共需n 次加法运算，每个小因式中所需乘法运算依次为n ，n －1，…，1.故共需计算次数为n ＋n (n ＋1)2＝12n (n ＋3)．第二种运算中，P 0(x 0)＝a 0，不需要运算，P 1(x 0)＝x 0P 0(x 0)＋a 1，需2次运算．P 2(x 0)＝x 0P 1(x 0)＋a 2，需2＋2次运算，依次往下，P n (x 0)需2n 次运算．答案：12n (n ＋3) 2n三、解答题：17．证明：(分析法)要证x 4＋y 4≥12xy (x ＋y )2，只需证明2(x 4＋y 4)≥xy (x ＋y )2，即证2(x 4＋y 4)≥x 3y ＋xy 3＋2x 2y 2.只需x 4＋y 4≥x 3y ＋xy 3与x 4＋y 4≥2x 2y 2同时成立即可．又知x 4＋y 4－2x 2y 2＝(x 2－y 2)2≥0，即x 4＋y 4≥2x 2y 2成立，只需再有x 4＋y 4≥x 3y ＋xy 3成立即可．由于x 4＋y 4－x 3y －xy 3＝(x －y )(x 3－y 3)， ∵x －y 与x 3－y 3同号，∴(x －y )(x 3－y 3)≥0，即x 4＋y 4≥x 3y ＋xy 3成立．∴对于任意实数x ，y 都有x 4＋y 4≥12xy (x ＋y )2成立．18．证明：(1)因为E 、F 分别是A 1B 、A 1C 的中点，所以EF ∥BC ，EF ⊄面ABC ，BC ⊂面ABC .所以EF ∥平面ABC .(2)因为三棱柱ABC －A 1B 1C 1为直三棱柱，所以BB 1⊥面A 1B 1C 1，BB 1⊥A 1D ，又A 1D ⊥B 1C ，所以A 1D ⊥平面BB 1C 1C ，又A 1D ⊂平面A 1FD ，所以平面A 1FD ⊥平面BB 1C 1C .19．证明：假设三条抛物线均与x 轴无两交点，则Δ1＝4b 2－4ac ≤0，Δ2＝4c 2－4ab ≤0，Δ3＝4a 2－4bc ≤0，∴a 2＋b 2＋c 2－ab －ac －bc ≤0，即12[(a －b )2＋(b －c )2＋(c －a )2]≤0，∴a ＝b ＝c ，与a ，b ，c 是互不相等的实数矛盾．故三条抛物线中，至少有一条与x 轴有两个交点．20．解：(1)∵f (2)＝f (2×1)＝f (2)·f (1)，又f (2)＝2，∴f (1)＝1.又∵f (4)＝f (2·2)＝f (2)·f (2)＝4,2＝f (2)<f (3)<f (4)＝4，且f (3)∈N *.∴f (3)＝3.(2)由f (1)＝1，f (2)＝2，f (3)＝3，猜想f (n )＝n (n ∈N *)．(3)用数学归纳法证明：(ⅰ)当n ＝1时，f (1)＝1，函数解析式成立． (ⅱ)假设n ＝k 时，f (k )＝k ，函数解析式成立．①若k ＋1＝2m (m ∈N *)，f (k ＋1)＝f (2m )＝f (2)·f (m )＝2m ＝k ＋1. ②若k ＋1＝2m ＋1(m ∈N *)，f (2m ＋2)＝f [2(m ＋1)]＝f (2)·f (m ＋1)＝2(m ＋1)＝2m ＋2，2m ＝f (2m )<f (2m ＋1)<f (2m ＋2)＝2m ＋2. ∴f (2m ＋1)＝2m ＋1＝k ＋1.即当n ＝k ＋1时，函数解析式成立．综合(ⅰ)(ⅱ)可知，f (n )＝n (n ∈N *)成立． 21．解：(1)a 10＝10，a 20＝10＋10d ＝40， ∴d ＝3.(2)a 30＝a 20＋10d 2＝10(1＋d ＋d 2)(d ≠0)， a 30＝10[(d ＋12)2＋34]，当d ∈(－∞，0)∪(0，＋∞)时，a 30∈[7.5，＋∞)；(3)所给数列可推广为无穷数列{a n }，其中a 1，a 2，…，a 10是首项为1，公差为1的等差数列，当n ≥1时，数列a 10n ，a 10n ＋1，…，a 10(n ＋1)是公差为d n 的等差数列．研究的问题可以是：试写出a 10(n ＋1)关于d 的关系式，并求a 10(n ＋1)的取值范围研究的结论可以是：由a 40＝a 30＋10d 3＝10(1＋d ＋d 2＋d 3)，依次类推可得a 10(n ＋1)＝10(1＋d ＋…＋d n ) ＝⎩⎪⎨⎪⎧10×1－d n ＋11－d ，d ≠1，10(n ＋1)，d ＝1.当d >0时，a 10(n ＋1)的取值范围为(10，＋∞)． 22．解：(1)依题意有x 2＋a bx －c＝x ，化简为(1－b )x 2＋cx ＋a ＝0，由根与系数的关系得⎩⎪⎨⎪⎧2＋0＝－c 1－b，2·0＝a 1－b，解得⎩⎪⎨⎪⎧a ＝0，b ＝1＋c 2，代入表达式得f (x )＝x 2(1＋c 2)x －c ，由f (－2)＝－21＋c <－12，得c <3.又因为c ∈N ，b ∈N ，若c ＝0，b ＝1，f (x )＝x 不止有两个不动点，若c ＝1，b ＝32，则f (x )＝x只有一个不动点，所以c ＝2，b ＝2，故f (x )＝x 22(x －1)(x ≠1)．(2)由题设得4S n ·(1a n)22(1a n－1)＝1，得2S n ＝a n －a 2n ，(*) 且a n ≠1，把n －1代入得2S n －1＝a n －1－a 2n －1.(**)由(*)与(**)两式相减得2a n ＝(a n －a n －1)－(a 2n －a 2n －1)，即(a n ＋a n －1)(a n －a n －1＋1)＝0，所以a n ＝－a n －1或a n －a n －1＝－1，把n ＝1代入(*)得2a 1＝a 1－a 21，解得a 1＝0(舍去)或a 1＝－1.由a 1＝－1，a n ＝－a n －1，得a 2＝1，这与a n ≠1矛盾，所以a n －a n －1＝－1，即{a n }是以－1为首项，－1为公差的等差数列，所以a n ＝－n .(3)证明：(采用反证法)假设a n ≥3(n ≥2)，则由(1)知a n ＋1＝f (a n )＝a 2n2a n －2，所以a n ＋1a n ＝a n 2(a n －1)＝12·(1＋1a n －1)≤12(1＋12)＝34<1，即a n ＋1<a n (n ≥2，n ∈N )，有a n <a n －1<…<a 2，而当n ＝2时，a 2＝a 212a 1－2＝168－2＝83<3，所以a 2<3.这与假设矛盾，故假设不成立，所以a n <3.第三章综合能力检测答案一、选择题：1．解析：由复数的概念可知x ＋y 仍是虚数．答案：B2．解析：4＋3i 1＋2i ＝(4＋3i)(1－2i)1＋22＝(4＋6)＋(3－8)i5＝2－i. 答案：B3．解析：m －2i 1＋2i ＝(m －2i)(1－2i)(1＋2i)(1－2i)＝(m －4)－2(m ＋1)i5，对于m 的值，不存在m 使m －4>0且m＋1<0，故对应的点不可能在第一象限．答案：A4．解析：∵z ＝(a ＋3i)(1－2i)(1＋2i)(1－2i)＝a ＋65＋(3－2a )i 5.若z 为纯虚数，则⎩⎪⎨⎪⎧a ＋6＝0，3－2a ≠0⇒⎩⎪⎨⎪⎧a ＝－6，a ≠32.答案：C5．解析：由于实系数一元二次方程的虚根成对出现，是互为共轭复数的，故另一根为3－2i ，则(3＋2i)·(3－2i)＝q2＝13.故选A.6．解析：∵P 2P 1→＝OP 1→－OP 2→，∴P 2P 1→对应的复数为z 1－z 2＝(2－5i)－(－3＋i)＝5－6i. 答案：B7．解析：由m1＋i ＝1＋n i 得m ＝(1＋i)(1－n i)＝(1＋n )＋(1－n )i ，∴⎩⎪⎨⎪⎧ m ＝1＋n ，0＝1－n ，∴⎩⎪⎨⎪⎧m ＝2，n ＝1，∴m ＋n i ＝2＋i. 答案：C8．解析：设z ＝x ＋y i ，则|3x ＋3y i ＋1|＝|x ＋y i －i|. ∴(3x ＋1)2＋9y 2＝x 2＋(y －1)2，即4x 2＋4y 2＋3x ＋y ＝0.∴复数z 对应点Z 的轨迹为圆．故选C.9．解析：由z ＝12＋32i 可得，z ＋1z ＝12＋32i ＋12－32i ＝1∈R . ∴z ＝12＋32i 是z ＋1z ∈R 的充分条件．但z ＋1z ∈R ⇒|z |＝1z ＝12＋32i ，所以z ＝12＋32i 是z ＋1z∈R 的充分非必要条件．答案：A10．解析：－35＋2i 2＋35i ＋(21＋i )2008＝i(35i ＋2)2＋35i ＋1i1004＝i ＋1. 答案：B11．解析：f (n )＝(1＋i 1－i )n ＋(1－i1＋i )n ＝i n ＋(－i)n (n ∈N *)，根据i n 取值的周期性，给n 赋值发现集合{x |x ＝f (n )}＝{0，－2,2}，故应选C.12．解析：由|z |＝1，得|z |2＝1，即z ·z ＝1，所以x ＝a －z z z －a z ＝a －zz (z －a )＝－1z＝－z ，所以|x |＝|－z |＝1. 答案：B二、填空题：13．解析：由已知得z ＝z 0z 0－3＝3＋2i 2i ＝1－32i. 答案：1－32i14．解析：设z ＝x ＋y i(x ，y ∈R )，由|z ＋2＋2i|＝|z |得(x ＋2)2＋(y ＋2)2＝x 2＋y 2，即x ＋y ＋2＝0，点(1，－1)到直线x ＋y ＋2＝0的距离为d ＝|1－1＋2|2＝2，∴|z －1＋i|的最小值为 2. 答案： 215．解析：1＋7i 2－i ＝(1＋7i)(2＋i)4＋1＝－1＋3i由－1＋3i ＝a ＋b i 得a ＝－1，b ＝3 ∴ab ＝－3 答案：－316．解析：由k 1z 1＋k 2z 2＋k 3z 3＝0得k 1(1＋2i)＋k 2(1－i)＋k 2·(－2)＝0，即(k 1＋k 2－2k 3)＋(2k 1－k 2)i ＝0，∴⎩⎪⎨⎪⎧k 1＋k 2－2k 3＝0，2k 1－k 2＝0.∴k 1∶k 2∶k 3＝1∶2∶32.(答案不唯一，只需满足1∶2∶32的任何一组都行) 答案：{1,2，32}三、解答题：17．解：(1)z 1z 2＝(1＋i)(x ＋2i)＝x ＋2i ＋x i －2＝(x －2)＋(2＋x )i ，因为z 1z 2是实数，所以x ＋2＝0，所以x ＝－2.(2)原式＝2(4－i)(3－i)＋(7－i)(4－3i)＝2(12－3i －4i 2)＋(28－4i －21i ＋3i 2)＝2(11－7i)＋25(1－i)＝47－39i.18．解：原方程化简为|z |2＋(z ＋z )i ＝1－i ，设z ＝x ＋y i(x 、y ∈R )，代入上述方程；得x 2＋y 2＋2x i ＝1－i ，所以⎩⎪⎨⎪⎧x 2＋y 2＝1，2x ＝－1.解得⎩⎨⎧x ＝－12，y ＝±32.所以原方程的解是z ＝－12±32i.19．解：z ＝2＋4i －(1＋3i)i ＝1＋i i ＝－i(1＋i)＝1－i ，ω＝1＋(a －1)i ，ωz ＝1＋(a －1)i1－i＝[1＋(a －1)i](1＋i)2＝2－a ＋a i 2，由|ωz |≤2，得(2－a 2)2＋(a2)2≤2，解得1－3≤a ≤1＋ 3.故a 的取值范围是[1－3，1＋3]．20．解：设z ＝x ＋y i(x ，y ∈R )，则z －1z ＋1＝(x －1)＋y i (x ＋1)＋y i ＝x 2＋y 2－1＋2y i(x ＋1)2＋y 2是纯虚数，∴x2＋y 2＝1且y ≠0，于是－1<x <1.而|z 2－z ＋2|＝|(x ＋y i)2－(x ＋y i)＋2|＝|(x 2－y 2－x ＋2)＋y (2x －1)i|＝(x 2－y 2－x ＋2)2＋y 2(2x －1)2＝8x 2－6x ＋2＝8(x －38)2＋78，∴当x ＝38时，|z 2－z ＋2|取得最小值144. 21．解：(1)设z ＝x ＋y i(x ，y ∈R ，且y ≠0)，则 (2x ＋5)2＋(2y )2＝(x ＋10)2＋y 2. 化简得x 2＋y 2＝25.∴|z |＝5. (2)∵z m ＋m z ＝x ＋y i m ＋m x ＋y i＝(x m ＋mx x 2＋y 2)＋(y m －myx 2＋y2)i 为实数，∴y m －myx 2＋y 2＝0. 又y ≠0，且x 2＋y 2＝25， ∴1m －m25＝0，解得m ＝±5. (3)(1－2i)z ＝(1－2i)(x ＋y i)＝(x ＋2y )＋(y －2x )i ，依据题意，得x ＋2y ＝y －2x . ∴y ＝－3x .①又∵|z |＝5，即x 2＋y 2＝25.② 由①、②得⎩⎨⎧x ＝102，y ＝－3102或⎩⎨⎧x ＝－102，y ＝3102.∴z ＝102－3102i 或z ＝－102＋3102i. 22．解：(1)解方程x ＋1x ＝2，得x ＝22±22i.当α1＝22＋22i 时，ω＝α2n －11＝(α21)nα1＝[(22＋22i)2]n α1＝in α1.由i n 的周期性知，ω有四个值，n ＝1时，ω＝22＋22i ；n ＝2时，ω＝－22＋22i ；n ＝3时，ω＝－22－22i ；n ＝4是，ω＝22－22i. 当α2＝22－22i 时，ω＝α2n －12＝(α22)n α2＝(－i)nα2.当n ＝1时，ω＝22－22i ；n ＝2时，ω＝－22－22i ；n ＝3时，ω＝－22＋22i ；n ＝4时，ω＝22＋22i.∴不论α＝22＋22i 还是α＝22－22i ，都有 M α＝{22＋22i ，22－22i ，－22＋22i ，－22－22i}，P ＝2C 24＝13. (2)取α＝－12＋32i ，则α3＝1，α5＝－12－32i ，于是M α＝{α，α3，α5}＝{－12＋32i,1，－12－32i}．(或取α＝－12－32i ，则α3＝1，α5＝－12＋32i)。

高中数学选修(2-2)综合测试(一)

高中数学选修（2-2）综合测试（一）一、选择题：每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．演绎推理是（）Ａ．特殊到一般的推理Ｂ．特殊到特殊的推理Ｃ．一般到特殊的推理Ｄ．一般到一般的推理答案：Ｃ2．m ∈R ，复数22(232)(32)i m m m m --+-+表示纯虚数的充要条件是（）Ａ．12m =-或2m = Ｂ．2m = Ｃ．12m =-Ｄ．2m =或1m =答案：Ｃ3．若()f x 在区间[]a b ，上有()0f x '>，且()f a 0≥，则在()a b ，内有（）Ａ．()0f x > Ｂ．()0f x < Ｃ．()0f x =Ｄ．()f x 符号不确定答案：Ａ4．下列各命题中，不正确的是（）Ａ．若()f x 是连续的奇函数，则()0a a f x dx -=⎰Ｂ．若()f x 是连续的偶函数，则0()2()a aaf x dx f x dx -=⎰⎰Ｃ．若()f x 在[]a b ，上连续且恒正，则()0b af x dx >⎰Ｄ．若()f x 在[]a b ，上连续，且()0ba f x dx >⎰，则()f x 在[]ab ，上恒正答案：Ｄ 5．设*211111()()123S n n n n n n n=+++++∈+++N ，当2n =时，(2)S =（）Ａ．12Ｂ．1123+Ｃ．111234++Ｄ．11112345+++答案：Ｃ6．设复数i()z a b a b =+∈R ，对应的点在虚轴的右侧，则（）Ａ．0a >，0b >Ｂ．0a >，0b <Ｃ．0b >，a ∈R Ｄ．0a >，b ∈R答案：Ｄ7．在平面直角坐标系内，方程1x y ab+=表示在x 轴、y 轴上的截距分别为a b ，的直线，拓展到空间，在x 轴、y 轴、z 轴上的截距分别为(0)a b c abc ≠，，的平面方程为（）Ａ．1x y z a b c++=Ｂ．1x y z abbcca++=Ｃ．1xy yz zx ab bc ca++=Ｄ．1ax by cz ++=答案：Ａ8．已知函数32()f x x px qx =--的图象与x 轴切于(10)，点，则()f x 的极大值和极小值分别为（）Ａ．427，0Ｂ．0，427Ｃ．427-，0Ｄ．0，427-答案：Ａ9．设a b c d ∈R ，，，且c d ，不全为零，若i ia b c d +∈+R ，则（）Ａ．0bc ad +≠ Ｂ．0bc ad -≠ Ｃ．0bc ad -=Ｄ．0bc ad +=答案：Ｃ10．设函数()y f x =在区间[02]，上是连续函数，则2()f x dx =⎰（）Ａ．121()()f t dx f t dx +⎰⎰ Ｂ．1200()()f t dt f t dt +⎰⎰Ｃ．121()()f t dt f t dt +⎰⎰Ｄ．12102()()f x dx f x dx +⎰⎰答案：Ｃ11．把数列{}*21()n n +∈N 依次按第一个括号一个数，第二个括号两个数，第三个括号三个数，第四个括号四个数，第五个括号一个数，…循环，分别为：(3)，(57)，，(91113)，，，(15171921)，，，，(23)，(2527)，，(293133)，，，(35373941)，，，，…，则第104个括号内各数之和为（）Ａ．2036 Ｂ．2048 Ｃ．2060 Ｄ．2072答案：Ｄ12．设()f x 在[]a b ，上连续，则()f x 在[]a b ，上的平均值是（）Ａ．()()2f a f b +Ｂ．()baf x dx ⎰Ｃ．1()2b af x dx ⎰Ｄ．1()b af x dx b a-⎰答案：Ｄ二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上． 13．若3()log (1)(1)f x x x =->，则(2)f '= ．答案：1ln 314．观察223sin 20cos 50sin 20cos 504++= ，223sin 15cos 45sin 15cos 454++=，请写出一个与以上两式规律相同的等式：．答案：223sin 10cos 40sin 10sin 404++=15．设222log (33)i log (3)()z m m m m =--+-∈R ，若z 对应的点在直线210x y -+=上，则m 的值是．16．作变速直线运动的物体，初速度为30m /s 时的速度为30 1.5/s v t =--，则该物体停止后，运动的路程为．答案：11500m 81三、解答题：本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题13分）在A B C △中，若90C ∠= ，则22cos cos 1A B +=．在立体几何中，给出四面体类似性质的猜想．解：如图，，在R t ABC △中，2222222cos cos 1a b a b A B c c c +⎛⎫⎛⎫+=+== ⎪ ⎪⎝⎭⎝⎭．于是，把结论类比到四面体，我们猜想：在四面体P A B C -中（如图2），若三个侧面P A B ，PBC ，P C A 两两互相垂直，且分别与底面所成的角为αβγ，，，则222c o s c o s c o s 1αβγ++=．18．（本小题14分）设()y f x =是二次函数，方程()0f x =有两个相等的实根，且()22f x x '=+．（1）求()y f x =的表达式；（2）若直线(01)x t t =-<<把()y f x =的图象与两坐标轴所围成图形的面积二等分，求t 的值．解：（1）设2()(0)f x ax bx c a =++≠，则()2f x ax b '=+．由已知()22f x x '=+，得1a =，2b =．2()2f x x x c ∴=++．又方程220x x c ++=有两个相等的实数根，440c ∴∆=-=，即1c =．故2()21f x x x =++；（2）依题意，得0221(21)(21)ttx x dx x x dx ---++=++⎰⎰，323211133ttx x x x x x ---⎛⎫⎛⎫∴++=++ ⎪ ⎪⎝⎭⎝⎭，整理，得3226610t t t -+-=，即32(1)10t -+=，1t ∴=-19．（本小题14分）已知等腰梯形O A B C 的顶点A B ，在复平面上对应的复数分别为12i +、26i -+，且O 是坐标原点，O A BC ∥．求顶点C 所对应的复数z ．解：设i()z x y x y =+∈R ，．由O A BC ∥，OC AB =，得O A BC k k =，C B A z z z =-，即2612y x -⎧=⎪+=， OA BC ≠ ，3x ∴=-，4y =舍去．5z ∴=-．20．（本小题14分）设x ∈R ，函数2e()(1)2xf x ax a -=++．（1）当1a =-时，求()f x 在[12]-，上的最值；（2）求证：当0a ≥时，()f x 在R 上为减函数．解：（1）当1a =-时，21()e2xf x x -=-，21()e(2)2xf x x x -'=-．由()0f x '=，得0x =或2x =．当10x -<<时，()0f x '>；当02x <<时，()0f x '<．()f x ∴在0x =处取得极大值0．又1(1)e 2f -=-，22(2)ef =-，故在[12]-，上，()f x 的极大值为0，最小值为e 2-；（2）证明：21()e (21)2xf x ax ax a -'=--++．当0a =时，1()e02xf x -'=-<，()f x ∴在R 上为减函数．当0a >时，244(1)40a a a a ∆=-+=-<，2210ax ax a ∴-++>恒成立，则()0f x '<，此时，()f x 在R 上为减函数．故当0a ≥时，()f x 在R 上为减函数．21．（本小题15分）由坐标原点O 向曲线323(0)y x ax bx a =-+≠引切线，切于点O 以外的点111()P x y ，，再由1P 引此曲线的切线，切于1P 以外的点222()P x y ，．如此进行下去，得到点列{}()n n n P x y ，．（1）求n x 与1(2)n x n -≥的关系式；（2）求数列{}n x 的通项公式，并证明．解：（1）2()36f x x ax b '=-+．在点111()P x y ，处的切线为11111:()()(0)l y y f x x x x '-=-≠．1l 过原点，322111111(3)()(36)x ax bx x x ax b ∴--+=--+，解得132x a =．则当2n ≥时，在点()n n n P x y ，处的切线:()()n n n n l y y f x x x '-=-，n l 过点111()n n n P x y ---，， 11()()n n n n n y y f x x x --'∴-=-，整理，得221111[23()]()0n n n n n n n n x x x x a x x x x ----+----=， 211()(23)0n n n n x x x x a --∴-+-=．由1n n x x -≠，得1230n n x x a -+-=，113(2)22n n x x a n -∴=-+≥；（2）由（1）知1131111222x a a a ⎡⎤⎛⎫⎛⎫==+=--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，21131222x a a ⎡⎤⎛⎫=---+ ⎪⎢⎥⎝⎭⎣⎦2112a ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，231131222x a a ⎡⎤⎛⎫=---+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦3112a ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．由此猜想出112nn x a ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．下面用数学归纳法证明： ①当1n =时，已证：②假设当*()n k k =∈N 时，猜想成立，即112kk x a ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，则当1n k =+时，11322k k x x a +=-+1131222ka a ⎡⎤⎛⎫=---+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦1113222k a a a +⎛⎫=---+⎪⎝⎭1111122k k a a a ++⎡⎤⎛⎫⎛⎫=--=--⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦．故当1n k =+时，猜想也成立．由①和②可知，数列{}n x 的通项公式112nn x a ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．。

(典型题)高中数学高中数学选修2-2第三章《导数应用》测试卷(含答案解析)

一、选择题1．已知函数()3f x x ax =-在(1,1)-上单调递减，则实数a 的取值范围为（）A ．()1,+∞B ．[)3,+∞C ．(],1-∞D ．(],3-∞2．已知定义在()1,+∞上的函数()f x ，()f x '为其导函数，满足()()1ln 20f x f x x x x++=′，且()2f e e =-，若不等式()f x ax ≤对任意()1,x ∈+∞恒成立，则实数a 的取值范围是（）A ．[),e +∞B ．()2,2e -C ．(),2e -D ．[),e -+∞3．若函数()22ln 45f x x x bx =+++的图象上的任意一点的切线斜率都大于0，则b 的取值范围是（） A ．(),8-∞- B ．()8,-+∞ C ．(),8-∞D ．()8,+∞4．若曲线21:(0)C y ax a =>与曲线2:x C y e =存在公共切线，则a 的取值范围为（）A ．2[,)8e +∞B ．2(0,]8eC ．2[4e ，)+∞D ．2(0,]4e5．设()f x 在定义域内可导，其图象如图所示，则导函()'f x 的图象可能是（）A ．B ．C ．D ．6．若函数21()ln 2f x kx x x =-在区间(0,]e 上单调递增，则实数k 的取值范围是（） A ．2(,]e -∞B ．(,1]-∞C ．[1,)+∞D ．2[,)e+∞7．在半径为r 的半圆内作一内接梯形，使其底为直径，其他三边为圆的弦，则梯形面积最大时，其梯形的上底为A ．r 2B 3C 3D ．r8．已知函数21()43ln 2f x x x x =-+-在[,1]t t +上不单调，则t 的取值范围是（） A ．(0,1)(2,3)⋃B ．(0,2)C ．(0,3)D ．(0,1][2,3)⋃9．已知函数10()ln ,0x xf x x x x⎧⎪⎪=⎨⎪⎪⎩，＜＞，若()()F x f x kx =-有3个零点，则k 的取值范围为（） A ．(21e -，0) B ．(12e-，0) C ．(0，12e) D ．(0，21e) 10．已知函数21()sin cos 2f x x x x x =++，则不等式(23)(1)0f x f +-<的解集为（） A ．(2,)-+∞B ．(1,)-+∞C ．(2,1)--D ．(,1)-∞-11．若对于任意的120x x a <<<，都有211212ln ln 1x x x x x x ->-，则a 的最大值为（） A ．2eB ．eC ．1D ．1212．设动直线x m =与函数2()f x x =，()ln g x x =的图像分别交于,M N ，则MN 的最小值为（） A ．11ln 222+ B ．11ln 222- C ．1ln2+ D ．ln21-二、填空题13．已知函数()()21,0e ,0x x x f x x ⎧+≤⎪=⎨>⎪⎩，若函数()()g x f x x m =--恰好有2个零点，则实数m 的取值范围为______．14．函数()f x 定义在0,2π⎛⎫⎪⎝⎭上，26f π⎛⎫= ⎪⎝⎭()f x '，且()()cos sinx f x x f x '⋅<⋅恒成立，则不等式()22sinx f x >的解集为_____________.15．已知函数()211020x e x x x ef x lnx x x⎧--+≤⎪⎪=⎨⎪⎪⎩，，＞，若方程f （x ）﹣m =0恰有两个实根，则实数m 的取值范围是_____.16．如图所示，ABCD 是边长为30cm 的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A ，B ，C ，D 四个点重合于图中的点P ，正好形成一个底面是正方形的长方体包装盒，若要包装盒容积3()V cm 最大，则EF 的长为________cm .17．函数()()21xf x x =-的最小值是______.18．已知函数21ln ,0()log ,0xx f x x x x +⎧>⎪=⎨⎪<⎩方程2()2()0()f x mf x m R -=∈有五个不相等的实数根，则实数m 的取值范围是______．19．已知函数()1ln 2f x x x ax ⎛⎫=-⎪⎝⎭有两个极值点，则实数a 的取值范围是_________. 20．若函数()21ln f x x x a x =-++在()0,∞+上单调递增，则实数a 的取值范围是________.三、解答题21．已知函数()212f x x =，()ln g x a x =.设()()()h x f x g x =+ （1）试讨论函数()h x 的单调性. （2）若对任意两个不等的正数12,x x ，都有()()12122h x h x x x ->-恒成立，求实数a 的取值范围；22．在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为v(米/单位时间)，每单位时间的用氧量为＋1(升)，在水底作业10个单位时间，每单位时间用氧量为0.9(升)，返回水面的平均速度为 (米/单位时间)，每单位时间用氧量为1.5(升)，记该潜水员在此次考察活动中的总用氧量为y(升). (1)求y 关于v 的函数关系式；(2)若c≤v≤15(c>0)，求当下潜速度v 取什么值时，总用氧量最少. 23．已知函数()2xf x eax b =-+（0a >，b R ∈，其中e 为自然对数的底数）.（1）求函数()f x 的单调递增区间；（2）若函数()f x 有两个不同的零点12,x x ，当a b =时，求实数a 的取值范围.24．设函数21()2x f x x e =. (1)求f （x ）的单调区间；(2)若当x ∈[－2，2]时，不等式f （x ）>m 恒成立，求实数m 的取值范围.25．一件要在展览馆展出的文物类似于圆柱体，底面直径为0.8米，高1.2米，体积约为0.5立方米，为了保护文物需要设计各面是玻璃平面的正四棱柱形无底保护罩，保护罩底面边长不少于1.2米，高是底面边长的2倍，保护罩内充满保护文物的无色气体，气体每立方米500元，为防止文物发生意外，展览馆向保险公司进行了投保，保险费用和保护罩的占地面积成反比例，当占地面积为1平方米时，保险费用为48000元. （1）若保护罩的底面边长为2.5米，求气体费用和保险费用之和；（2）为使气体费用和保险费用之和最低，保护罩该如何设计？ 26．已知函数2()2ln f x x mx x =-+ （m R ∈）.（1）若()f x 在其定义域内单调递增，求实数m 的取值范围；（2）若45m <<，且()f x 有两个极值点12,x x ，其中12x x <，求12()()f x f x -的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据'()0f x ≤在(1,1)-上恒成立求解．【详解】∵3()f x x ax =-，∴2'()3f x x a =-．又函数()f x 在()1,1-上单调递减，∴2'()30f x x a =-≤在(1,1)-上恒成立，即23a x ≥在(1,1)-上恒成立．∵当(1,1)x ∈-时，3033x ≤<，∴3a ≥．所以实数a 的取值范围是[3,)+∞．故选：B ．【点睛】本题考查根据导函数研究函数的单调性，以及不等式的恒成立问题，注意当'()0()f x x D <∈时，则函数()f x 在区间D 上单调递减；而当函数()f x 在区间D 上单调递减时，则有'()0f x ≤在区间D 上恒成立．解题时要注意不等式是否含有等号，属于中档题．2．D解析：D 【分析】利用导数的运算法则，求出函数()f x 的解析式，然后参数分离，将不等式的恒成立问题转化为ln xa x≥-对任意()1,x ∈+∞恒成立，构造函数，利用导数研究函数的单调性，进而求出函数的最大值，从而得解. 【详解】()()1ln 20f x f x x xx++=′， ()2ln f x x x C ∴+=， ()2ln f e e e C ∴+=，()2f e e =-，∴22e e C -+=，解得0C =，()2ln 0f x x x ∴+=，()2ln x f x x∴=-()1x >，不等式()f x ax ≤对任意()1,x ∈+∞恒成立，∴2ln x ax x-≤对任意()1,x ∈+∞恒成立，即ln xa x≥-对任意()1,x ∈+∞恒成立，令()ln x g x x=-，则()()21ln ln x g x x -=′，令()()21ln 0ln xg x x -==′，解得x e =，∴1x e <<时，()0g x '>，()g x 在()1,e 上单调递增；x e >时，()0g x '<，()g x 在(),e +∞上单调递减， ∴当x e =时，()g x 取得极大值，也是最大值，()()max ln eg x g e e e==-=-， a e ∴≥-，∴实数a 的取值范围是[),e -+∞.故选：D. 【点睛】本题考查利用导数研究不等式的恒成立问题，具体考查导数的运算法则及利用导数研究函数的最值问题，求出函数()f x 的解析式是本题的解题关键，属于中档题.不等式恒成立问题关键在于利用转化思想，常见的有：()f x a >恒成立⇔()min f x a >；()f x a <恒成立⇔()max f x a <；()f x a >有解⇔()max f x a >；()f x a <有解⇔()min f x a <；()f x a >无解⇔()max f x a ≤；()f x a <无解⇔()min f x a ≥. 3．B解析：B 【分析】对函数()f x 求导，得到()f x '，然后根据题意得到()0f x '>恒成立，得到【详解】因为函数()22ln 45f x x x bx =+++，定义域()0,∞+所以()28f x x b x'=++，因为()f x 图象上的任意一点的切线斜率都大于0，所以()280f x x b x'=++>对任意的()0,x ∈+∞恒成立，所以28b x x>--，设()28g x x x=--，则()max b g x > ()228g x x'=- 令()0g x '=，得到12x =，舍去负根，所以当10,2x ⎛⎫∈ ⎪⎝⎭时，()0g x '>，()g x 单调递增，当1,2x ⎛⎫∈+∞⎪⎝⎭时，()0g x '<，()g x 单调递减，所以12x =时，()g x 取最大值，为()max182g x g ⎛⎫==- ⎪⎝⎭，所以8b >-，故选B. 【点睛】本题考查利用导数求函数图像切线的斜率，不等式恒成立，利用导数研究函数的单调性、极值、最值，属于中档题.4．C解析：C 【分析】求出两个函数的导函数，由导函数相等列方程，再由方程有根转化为求最值，求得a 的范围. 【详解】由2(0)y axa =>，得2y ax '=，由xy e =，得x y e '=，曲线21:(0)C y ax a =>与曲线2:x C y e =存在公共切线，则设公切线与曲线1C 切于点211(,)x ax ，与曲线2C 切于点22(,)xx e ，则22211212x x e ax ax e x x -==-，将212x e ax =代入2211212x e ax ax x x -=-，可得2122=+x x ，11212+∴=x e a x ，记12()2+=x e f x x，则122(2)()4xex f x x +-'=，当(0,2)x ∈时，()0f x '<，当(2,)x ∈+∞时，()0f x '>. ∴当2x =时，2()4mine f x =. a ∴的范围是2[,)4e +∞. 故选：C 【点睛】本题主要考查了利用导数研究过曲线上某点处的切线方程，考查了方程有根的条件，意在考查学生对这些知识的理解掌握水平.5．B解析：B 【详解】试题分析：函数的递减区间对应的()0f x '<，函数的递增区间对应()0f x '>，可知B 选项符合题意.考点：函数的单调性与导数的关系.6．C解析：C 【分析】求出函数导数，由题意知()0f x '≥即ln 1x k x+≥在(0,]e 上恒成立，利用导数求出函数ln 1()x g x x+=在(0,]e 上的最大值即可求得k 的范围. 【详解】()ln 1f x kx x '=--，由题意知()0f x '≥在(0,]e 上恒成立，即ln 1x k x +≥在(0,]e 上恒成立，令ln 1()x g x x+=，则2ln ()x g x x -'=，当(0,1)x ∈时，()0g x '>，()g x 单调递增；当(1,]x e ∈时，()0g x '<，()g x 单调递减，所以max ()(1)1g x g ==，故1k .故选C 【点睛】本题考查导数在研究函数中的应用，涉及已知函数的单调区间求参数的取值范围、利用导数求函数的最值，属于基础题.7．D解析：D 【解析】设=COB θ∠，则上底为2cos r θ，高为sin r θ，因此梯形面积为21(2cos 2)sin (1cos )sin 022S r r r r πθθθθθ=+=+∈，（，）因为由22222=(sin cos cos )(1cos 2cos )0S r r θθθθθ'-++=-++=，得1cos 2θ=，根据实际意义得1cos 2θ=时，梯形面积取最大值，此时上底为2cos =r r θ，选D.点睛：利用导数解答函数最值的一般步骤：第一步：利用()0f x '=得可疑最值点；第二步：比较极值同端点值的大小．在应用题中若极值点唯一，则极值点为开区间的最值点.8．A解析：A 【详解】试题分析：此题考查导数的应用；2343(1)(3)()4x x x x f x x x x x-+--=-+-'=-=-，所以当(0,1),(3,)x ∈+∞时，原函数递减，当(1,3)x ∈原函数递增；因为在[],1t t +上不单调，所以在[],1t t +上即有减又有增，所以01{113t t <<<+<或13{31t t <<<+，01t ∴<<或23t <<，故选A.考点：函数的单调性与导数.9．C解析：C 【分析】由函数()()F x f x kx =-在R 上有3个零点，当0x >时，令()0F x =，可得y k =和()2ln x g x x=有两个交点；当0x <时，y k =和()1g x x =有一个交点，求得0k >，即可求解，得到答案. 【详解】由题意，函数10()ln ,0x xf x x x x⎧⎪⎪=⎨⎪⎪⎩，＜＞，要使得函数()()F x f x kx =-在R 上有3个零点，当0x >时，令()()0F x f x kx =-=，可得2ln xk x =，要使得()0F x =有两个实数解，即y k =和()2ln xg x x=有两个交点，又由()312ln xg x x-'=，令12ln 0x -=，可得x =当x ∈时，()0g x '>，则()g x 单调递增；当)x ∈+∞时，()0g x '<，则()g x 单调递减，所以当x =()max 12g x e=，若直线y k =和()2ln xg x x =有两个交点，则1(0,)2k e∈，当0x <时，y k =和()21g x x =有一个交点，则0k >，综上可得，实数k 的取值范围是1(0,)2e. 故选：C. 【点睛】本题主要考查了函数与方程的综合应用，以及利用导数研究函数的单调性与最值的综合应用，着重考查了转化思想以及推理与运算能力.属于中档题.10．C解析：C 【分析】根据条件先判断函数是偶函数，然后求函数的导数，判断函数在[0，)+∞上的单调性，结合函数的奇偶性和单调性的关系进行转化求解即可．【详解】解：2211()sin()cos()sin cos ()22f x x x x x x x x x f x -=--+-+=++=，则()f x 是偶函数，()sin cos sin cos (1cos )f x x x x x x x x x x x '=+-+=+=+，当0x 时，()0f x '，即函数在[0，)+∞上为增函数，则不等式(23)(1)0f x f +-<得()()231f x f +<，即()()|23|1f x f +<，则|23|1x +<，得1231x -<+<，得21x -<<-，即不等式的解集为(2,1)--，故选：C ．【点睛】本题主要考查不等式的求解，结合条件判断函数的奇偶性和单调性，利用函数奇偶性和单调性的关系进行转化是解决本题的关键．属于中档题．11．C解析：C【分析】整理所给的不等式，构造新函数，结合导函数研究函数的单调性，即可求得结果.【详解】解：由已知可得，211212ln ln x x x x x x -<-，两边同时除以12x x ，则121221ln ln 11x x x x x x -<-，化简有1212ln 1ln 1x x x x ++<，而120x x <<，构造函数()ln 1x f x x+=，()2ln x f x x -'=，令()0f x '>，则01x <<；令()0f x '<，则1x > ，所以函数()f x 在()0,1上为增函数，在()1,+∞上为减函数，由1212ln 1ln 1x x x x ++<对于120x x a <<<恒成立，即()f x 在()0,a 为增函数，则01a <≤，故a 的最大值为1.故选：C.【点睛】本题考查导数研究函数的单调性，考查分析问题能力，属于中档题.12．A解析：A【分析】将两个函数作差，得到函数()()y f x g x =-，利用导数再求此函数的最小值，即可得到结论.【详解】设函数()()()2ln 0=-=->y f x g x x x x ， ()212120-'∴=-=>x y x x x x，令0y '<，0x，02∴<<x，函数在2⎛⎫ ⎪⎝⎭上为单调减函数；令0y '>，0x，∴>x，函数在⎫+∞⎪⎪⎝⎭上为单调增函数.2x ∴=时，函数取得极小值，也是最小值为111ln ln 22222-=+. 故所求MN 的最小值即为函数2ln y x x =-的最小值11ln 222+.故选：A.【点睛】本题主要考查利用导数研究函数的最值，属于中档题.二、填空题13．【分析】转化为函数的图象与直线恰有2个交点作出函数的图象利用图象可得结果【详解】因为函数恰好有2个零点所以函数的图象与直线恰有2个交点当时当时所以函数在上为增函数函数的图象如图：由图可知故答案为：【解析：34m > 【分析】转化为函数()y f x x =-的图象与直线y m =恰有2个交点，作出函数的图象，利用图象可得结果.【详解】因为函数()()g x f x x m =--恰好有2个零点，所以函数()y f x x =-的图象与直线y m =恰有2个交点，当0x ≤时，22133()1()244y f x x x x ==++=++≥，当0x >时，()x y f x x e x =-=-，10x y e '=->，所以函数()x y f x x e x =-=-在(0,)+∞上为增函数，函数()y f x x =-的图象如图：由图可知，34m >. 故答案为：34m >【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.14．【分析】构造函数再利用函数的单调性解不等式即可【详解】解：构造函数则当时在单调递增不等式即即故不等式的解集为故答案为：【点睛】关键点点睛：本题解题的关键是根据题目的特点构造一个适当的函数利用它的单调解析：,62ππ⎛⎫ ⎪⎝⎭【分析】构造函数()()sin f x g x x =，再利用函数的单调性解不等式即可. 【详解】解：()()cos sin f x x f x x '<()()sin cos 0f x x x f x '∴->，构造函数()()sin f x g x x =，则()()()2sin cos f x x f x x g x sin x'-'=，当0,2x π⎛⎫∈ ⎪⎝⎭时，()0g x '>， ()g x ∴在0,2π⎛⎫ ⎪⎝⎭单调递增， ∴不等式()f x x >，即()6sin sin 26f f x x ππ⎛⎫ ⎪⎝⎭>== 即()6xg g π⎛>⎫ ⎪⎝⎭， 26x ππ∴<< 故不等式的解集为,62ππ⎛⎫⎪⎝⎭. 故答案为：,62ππ⎛⎫ ⎪⎝⎭. 【点睛】关键点点睛：本题解题的关键是根据题目的特点，构造一个适当的函数，利用它的单调性进行解题.15．【分析】通过求导得出分段函数各段上的单调性从而画出图像若要方程f （x ）﹣m=0恰有两个实根只需y=m 与y=f （x ）恰有两个交点即可从而得出的取值范围【详解】（1）x≤0时f′（x ）=ex ﹣x ﹣1易知解析：(]10e ⎧⎫-∞⋃⎨⎬⎩⎭，【分析】通过求导，得出分段函数各段上的单调性，从而画出图像.若要方程f （x ）﹣m =0恰有两个实根，只需y =m 与y =f （x ）恰有两个交点即可，从而得出m 的取值范围.【详解】（1）x ≤0时，f ′（x ）=e x ﹣x ﹣1，易知f ′（0）=0，而f ″（x ）=e x ﹣1＜0，所以f ′（x ）在（﹣∞，0]上递减，故f ′（x ）≥f ′（0）=0，故f （x ）在（﹣∞，0]上递增，且f （x ）≤f （0）11e=+，当x →﹣∞时，f （x ）→﹣∞. （2）x ＞0时，()21'lnx f x x-=，令f ′（x ）＞0，得0＜x ＜e ；f ′（x ）＜0得x ＞e ；故f （x ）在（0，e ）上递增，在（e ，+∞）递减，故x ＞0时，()1()max f x f e e==；x →0时，f （x ）→﹣∞；x →+∞时，f （x ）→0. 由题意，若方程f （x ）﹣m =0恰有两个实根，只需y =m 与y =f （x ）恰有两个交点，同一坐标系画出它们的图象如下：如图所示，当直线y =m 在图示①，②位置时，与y =f （x ）有两个交点，所以m 的范围是：(]10e ⎧⎫-∞⋃⎨⎬⎩⎭，. 故答案为：(]10e ⎧⎫-∞⋃⎨⎬⎩⎭，. 【点睛】本题考查了方程根的问题转化为函数图像交点问题，以及利用导数求函数单调性.考查了转化思想和数形结合，属于中档题.16．【分析】设cm 根据已知条件求出包装盒的底面边长及高从而求得包装盒体积的关于x 的表达式利用导数研究体积的最大值即可【详解】设cm 则cm 包装盒的高为cm 因为cm 所以包装盒的底面边长为cm 所以包装盒的体积解析：10【分析】设EF x =cm ，根据已知条件求出包装盒的底面边长及高从而求得包装盒体积的关于x 的表达式，利用导数研究体积(x)V 的最大值即可.【详解】设EF x =cm ，则302x AE BF -== cm ，包装盒的高为22GE x = cm ，因为302x AE AH -== cm ，2A π∠=，所以包装盒的底面边长为2=(30)2HE x - cm ，所以包装盒的体积为232222()[(30)](60900)224V x x x x x x =-⋅=-+，030x <<，则22()(3120900)4V x x x '=-+，令()0V x '=解得10x =，当(0,10)x ∈时，()0V x '>，函数(x)V 单调递增；当(10,30)x ∈时，()0V x '<，函数(x)V 单调递减，所以3max 2()(10)(100060009000)10002()4V x V cm ==-+=，即当10EF cm =时包装盒容积3()V cm 取得最大值310002()cm .故答案为：10【点睛】本题考查柱体的体积，利用导数解决面积、体积最大值问题，属于中档题.17．【分析】对求导利用导数即可求得函数单调性和最小值【详解】因为故可得令解得；故当时单调递减；当时单调递增；当时单调递减且当趋近于1时趋近于正无穷；当趋近于正无穷时趋近于零函数图像如下所示：故的最小值为解析：14- 【分析】对()f x 求导，利用导数即可求得函数单调性和最小值,【详解】因为()()21xf xx=-，故可得()()311xf xx---'=，令()0f x'=，解得1x=-；故当(),1x∈-∞-时，()f x单调递减；当()1,1x∈-时，()f x单调递增；当()1,x∈+∞时，()f x单调递减.且()114f-=-，当x趋近于1时()f x趋近于正无穷；当x趋近于正无穷时，()f x趋近于零.函数图像如下所示：故()f x的最小值为14-.故答案为：14-.【点睛】本题考查利用导数研究函数的最值，属综合基础题.18．【分析】作出函数的图象结合图象可求实数的取值范围【详解】当时当时函数为增函数；当时函数为减函数；极大值为且；作出函数的图象如图方程则或由图可知时有2个解所以有五个不相等的实数根只需要即；故答案为：【解析：1(0,)2【分析】作出函数21ln,0()log,0xxf x xx x+⎧>⎪=⎨⎪<⎩的图象，结合图象可求实数m的取值范围.【详解】当0x >时，2ln ()x f x x'=-，当01x <<时，()0f x '>，函数为增函数；当1x >时，()0f x '<，函数为减函数；极大值为(1)1f =，且x →+∞，()0f x →；作出函数21ln ,0()log ,0x x f x x x x +⎧>⎪=⎨⎪<⎩的图象，如图，方程2()2()0()f x mf x m R -=∈，则()0f x =或()2f x m =，由图可知()0f x =时，有2个解，所以2()2()0f x mf x -=有五个不相等的实数根，只需要021m <<，即102m <<；故答案为：1(0,)2.【点睛】本题主要考查导数的应用，利用研究方程根的问题，作出函数的简图是求解的关键，侧重考查数学抽象的核心素养.19．【分析】对函数进行求导得则方程在时有两个根利用导数研究函数的值域即可得答案；【详解】在时有两个根令令当时当时在单调递增在单调递减且当时当时与要有两个交点故答案为：【点睛】本题考查利用导数研究函数的值解析：01a <<【分析】对函数进行求导得()1f x lnx ax '=+-，则方程ln 1x a x +=在0x >时有两个根，利用导数研究函数ln 1()x g x x+=的值域，即可得答案；【详解】 ()1ln 2f x x x ax ⎛⎫=- ⎪⎝⎭，()1f x lnx ax '=+-． ∴ln 1x a x+=在0x >时有两个根，令ln 1()x g x x+=，令()1g x lnx ax =+-，'221(ln 1)ln ()x x x x g x x x ⋅-+==- 当01x <<时，'()0g x >，当1x >时，'()0g x <， ∴()g x 在(0,1)单调递增，在(1,)+∞单调递减，且(1)1g =，当x →+∞时，()0g x →，当0x →时，()g x →-∞，y a =与()y g x =要有两个交点，∴01a <<故答案为：01a <<.【点睛】本题考查利用导数研究函数的值域，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意参变分离法的运用.20．【分析】依题意可得在上恒成立参变分离得到在上恒成立令求出的最大值即可求出参数的取值范围；【详解】解：因为的定义域为且函数在上单调递增在上恒成立即在上恒成立令当时所以即故答案为：【点睛】本题考查利用导解析：18a ≥ 【分析】依题意可得()210a f x x x'=-+≥在()0,x ∈+∞上恒成立，参变分离得到22a x x ≥-在()0,x ∈+∞上恒成立，令()22g x x x =-，求出()g x 的最大值即可求出参数的取值范围；【详解】解：因为()21ln f x x x a x =-++的定义域为()0,x ∈+∞，且函数()21ln f x x x a x =-++在()0,∞+上单调递增，()210a f x x x'∴=-+≥在()0,x ∈+∞上恒成立，即22a x x ≥-在()0,x ∈+∞上恒成立，令()22112248g x x x x ⎛⎫=-=--+ ⎪⎝⎭ 当14x =时()max 18g x = 所以18a ≥即1,8a ⎡⎫∈+∞⎪⎢⎣⎭故答案为：1,8⎡⎫+∞⎪⎢⎣⎭【点睛】本题考查利用导数研究函数的单调性，不等式恒成立问题，属于中档题. 三、解答题21．（1）答案见解析；（2）[)1,+∞.【分析】（1）求导后，分别在0a ≥和0a <两种情况下讨论导函数的正负即可得到结果；（2）将恒成立的不等式转化为()()112222h x x h x x ->-对于任意的12x x >恒成立，从而只需构造函数()()2t x h x x =-，证明()t x 在()0,∞+上单调递增即可，从而将问题进一步转化为()0t x '≥在()0,∞+上恒成立，进而利用分离变量的方法可求得结果.【详解】（1）()()21ln 02h x x a x x =+>，则()()20a x a h x x x x x+'=+=>，当0a ≥时，()0h x '>恒成立，()h x ∴在()0,∞+上单调递增；当0a <时，若(x ∈，()0h x '<；若)x ∈+∞，()0h x '>； ()h x ∴在(上单调递减，在)+∞上单调递增. （2）设12x x >，则()()12122h x h x x x ->-等价于()()112222h x x h x x ->-，即()()112222h x x h x x ->-对于任意的12x x >恒成立. 令()()212ln 22t x h x x x a x x =-=+-，则只需()t x 在()0,∞+上单调递增， ()2a t x x x '=+-，∴只需()0t x '≥在()0,∞+上恒成立即可. 令()200a x x x+-≥>，则()220a x x x ≥-+>，当1x =时，()2max 21x x-+=，1a ∴≥，即实数a 的取值范围为[)1,+∞.【点睛】关键点点睛：本题主要考查导数在函数中的应用，以及不等式的证明，着重考查了转化与化归思想､逻辑推理能力与计算能力，对导数的应用的考查主要从以下几个角度进行：（1）考查导数的几何意义，求解曲线在某点处的切线方程；（2）利用导数求函数的单调区间，判断单调性；已知单调性，求参数；（3）利用导数求函数的最值(极值)，解决函数的恒成立与有解问题，同时注意数形结合思想的应用.22．（1）见解析；（2）若c<3102，则当v ＝3102时，总用氧量最少；若c≥3102，则当v ＝c 时，总用氧量最少．【分析】（1）结合题意可得y 关于v 的函数关系式．（2）由（1）中的函数关系，求导后得到当0<v<3102时，函数单调递减；当v>3102时，函数单调递增．然后再根据c 的取值情况得到所求的速度．【详解】(1)由题意，下潜用时 (单位时间)，用氧量为×＝＋ (升)，水底作业时的用氧量为10×0．9＝9(升)，返回水面用时＝ (单位时间)，用氧量为×1．5＝ (升)，因此总用氧量232409,(0)50v y v v=++>． (2)由（1）得232409,(0)50v y v v=++>， ∴y′＝－＝，令y′＝0得v ＝32当0<v<3102y′<0，函数单调递减；当v>32y′>0，函数单调递增．①若c<32 ，则函数在(c ，32上单调递减，在(310215)上单调递增， ∴ 当v ＝32②若c≥32，则y 在[c ，15]上单调递增，∴ 当v ＝c 时，总用氧量最少．【点睛】（1）在求实际问题中的最大值或最小值时，一般先设自变量、因变量、建立函数关系式，并确定其定义域，利用求函数最值的方法求解，注意结果应与实际情况相符合．（2）用导数求实际问题中的最大(小)值，如果函数在区间内只有一个极值点，那么根据实际意义可知该极值点就是最值点．23．（1）1ln ,22a ⎛⎫+∞⎪⎝⎭（2）32a e > 【分析】（1）直接求出函数的导函数，令()0f x '>，解不等式即可；（2）由题意容易知道2102222a ln a a a f ln e ln a ⎛⎫=-+< ⎪⎝⎭，解出即可求得实数a 的取值范围；【详解】解：（1）因为()2x f x e ax b =-+所以()()220x f x e a a '=->，令()0f x '>，得1ln 22a x >，∴函数()f x 的单调递增区间为1ln ,22a ⎛⎫+∞ ⎪⎝⎭（2）由（1）知，函数()f x 在1,ln 22a ⎛⎫-∞ ⎪⎝⎭递减，在1ln ,22a ⎛⎫+∞ ⎪⎝⎭递增， ∴x →-∞时，()f x →+∞；x →+∞，()f x →+∞，∵函数()f x 有两个零点12,x x ，∴1ln 022a f ⎛⎫< ⎪⎝⎭，又a b =， ∴ln 21ln ln 02222a a a a f e a ⎛⎫=-+< ⎪⎝⎭，即ln 0222a a a a -+< 所以3ln02a -< 所以32a e >【点睛】本题考查利用导数研究函数的单调性及最值问题，考查导数中零点问题，考查转化思想及运算求解能力，属于中档题．24．（1）(,2)(0,)()f x -∞-+∞和为的增区间，(2,0)()f x -为的减区间.（2）m ＜0 ．【详解】解：（1）21()(2)22xxx e f x xe x e x x '=+=+ 令(2)0,02,(,2)(0,)()2xe x x x xf x +>><-∴-∞-+∞或和为的增区间， (2)0,20,(2,0)()2xe x x xf x +<-<<∴-为的减区间. （2）x ∈[－2，2]时，不等式f （x ）>m 恒成立等价于min ()f x >m, 令：21()(2)022xxx e f x xe x e x x =+'=+= ∴x=0和x=－2,由（1）知x=－2是极大值点，x=0为极小值点2222(2),(2)2,(0)0,()[0,2]f f e f f x e e-===∴∈, ∴m ＜0 25．（1）23055元；（2）保护罩为底面边长为2米，高为4米的正四棱柱【分析】（1）根据定义先求保险费用，再计算正四棱柱体积，进而求气体费用，最后求和得结果；（2）先列出气体费用和保险费用之和函数关系式，再利用导数求最值，即得结果.【详解】（1）保险费用为24800076802.5= 正四棱柱体积为22.5(2 2.5)⨯⨯所以气体费用为2500[2.5(2 2.5)0.5]15375⨯⨯⨯-=因此气体费用和保险费用之和为76801537523055+=（元）；（2）设正四棱柱底面边长为a 米，则 1.2a ≥因此气体费用和保险费用之和23224800048000500[(2)0.5]1000250y a a a a a=+⨯⨯-=+- 因为2396000300002y a a a'=-+=∴= 当2a >时，0y '>，当1.22a ≤<时，0y '<，因此当2a =时，y 取最小值，保护罩为底面边长为2米，高为4米的正四棱柱时，气体费用和保险费用之和最低.【点睛】本题考查利用导数求函数最值、列函数解析式，考查基本分析求解能力，属中档题. 26．（1）4m ≤；（2）1504ln 24⎛⎫- ⎪⎝⎭，.【分析】（1）由题意结合导数与函数单调性的关系可转化条件为22m x x ≤+在(0,)+∞上恒成立，利用基本不等式求得22x x+的最小值即可得解；（2）由题意结合函数极值点的概念可得122m x x +=，121x x ⋅=，进而可得1112x <<，转化条件为21211211()()4ln f x f x x x x -=-+，令221()4ln g x x x x =-+（112x <<），利用导数求得函数()g x 的值域即可得解.【详解】（1）()f x 的定义域为(0,)+∞，∵()f x 在(0,)+∞上单调递增， ∴2()20f x x m x '=-+≥在(0,)+∞上恒成立，即22m x x≤+在(0,)+∞上恒成立，又224x x +≥=，当且仅当1x =时等号成立， ∴4m ≤；（2）由题意2222()2x mx f x x m x x-+'=-+=， ∵()f x 有两个极值点12,x x ，∴12,x x 为方程2220x mx -+=的两个不相等的实数根，由韦达定理得122m x x +=，121x x ⋅=， ∵120x x <<，∴1201x x <<<，又121112()2()(4,5)m x x x x =+=+∈，解得1112x <<， ∴()()2212111222()()2ln 2ln f x f x x mx x x mx x -=-+--+ ()()()()22121212122ln ln 2x x x x x x x x =-+--+-()()2221122ln ln x x x x =-+- 2112114ln x x x =-+，设221()4ln g x x x x =-+（112x <<），则4222333242(21)2(1)()20x x x g x x x x x x ---+--=-+='=<， ∴()g x 在1,12⎛⎫ ⎪⎝⎭上为减函数，又1111544ln 4ln 22424g ⎛⎫=-+=- ⎪⎝⎭，(1)1100g =-+=， ∴150()4ln 24g x <<-，即12()()f x f x -的取值范围为1504ln 24⎛⎫- ⎪⎝⎭，.【点睛】本题考查了导数的综合应用，考查了运算求解能力与逻辑推理能力，牢记函数单调性与导数的关系、合理转化条件是解题关键，属于中档题.。

(北师大版)上海市高中数学选修2-2第五章《数系的扩充与复数的引入》测试题(含答案解析)

一、选择题1．设复数z 满足1z =，则1z i -+的最大值为（）A 1B ．2C 1D ．22．若z C ∈且221z i +-=，则12z i --的最小值是（）A ．2B ．3C ．4D ．5 3．复数34i z i -=，|z |＝（）A B ．3 C ．4 D ．5 4．若复数34sin cos 55z i θθ⎛⎫=-+- ⎪⎝⎭是纯虚数，则tan()θ-π的值为( ) A ．34± B ．43 C ．34- D ．43- 5．若复数z 满足(34)25i z i +=，其中i 为虚数单位，则z 的虚部是A ．3iB ．3i -C ．3D ．-3 6．已知复数z 满足z （1﹣i ）＝﹣3+i （期中i 是虚数单位），则z 的共轭复数z 在复平面对应的点是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．已知0)z a a =>且||2z =，则z =( )A．1B ．1C ．2D ．3+ 8．已知复数33i z i --=，则z 的虚部为（） A ．3- B ．3 C ．3i D ．3i -9．复数z 满足(1)35i z i -⋅=+，则||z =A ．2B ．CD 10．已知复数122i z i +=- （i 为虚数单位），则z 的虚部为（） A ．－1 B ．0 C ．1 D ．i11．设i 是虚数单位，则复数734i i ++在复平面内所对应的点位于（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限 12．已知向量OA ＝(2,2)，OB ＝(4,1)，在x 轴上一点P ，使AP ·BP 有最小值，则点P 的坐标为 ( )A ．(－3,0)B ．(2,0)C ．(3,0)D ．(4,0)二、填空题13．设221i z i-=+，则z =_____________． 14．在复数集中分解因式：2364x x -+=________.15．已知复数zi =，i 为虚数单位，则z =____________16．设12,z z 为复数，21z =，则21121z z z z -=-___________. 17．植树节某班20名同学在一段直线公路一侧植树，每人植一棵，相邻两棵树相距10米，开始时需将树苗集中放置在某一树坑旁边，使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小，这个最小值为_____（米）．18．已知复数z 满足21z i i=++，则z 的共轭复数z=__________. 19．已知复数z 满足(1)i z i +=，其中i 为虚数单位，则复数z 的实部为_________． 20．下列四个命题中正确的有_______（填上所有正确命题的序号）①若实数,,a b c 满足3a b c ++=，则,,a b c 中至少有一个不小于1②若z 为复数，且z =1，则z i -的最大值等于2③(0,),sin x x x ∈+∞>任意都有④204π=三、解答题21．已知复数2(1)(24)33Z i m i m i =+-+-+（1）当m 为何值时 , Z 为纯虚数 ?（2）当m 为何值时 , Z 对应的点在y x =上?22．实数m 取什么数值时，复数()2212z m m m i =-+--分别是：（1）实数？（2）虚数？（3）纯虚数？（4）表示复数z 的点在复平面的第四象限？23．已知z 是复数，121z z ==，12z z +=12z z -.24．复数2(21)(1),z a a a i a R =--+-∈.（1）若z 为实数，求a 的值；（2）若z 为纯虚数，求a 的值；（3）若93z i =-，求a 的值.25．方程21(4)02x m x m --+=的两根为α，β，且||||αβ+=m 的值.26．若关于x 的方程22470x zx i -++=有实根，求复数z 的模的最小值和此时z 的值.【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】如图所示，复数满足1z =时轨迹方程为复平面内的单位圆，而()11z i z i -+=--表示z 与复数1i -所对应的点在复平面内的距离，结合圆的性质可知，1z i -+的最大值为()2211121+-+=+.本题选择C 选项. 2．A解析：A 【分析】设z x yi =+，得到()()22221x y ++-=，化简得到()()221212z i x y --=-+-根据其几何意义计算得到答案.【详解】设z x yi =+，则()()()()222222221z i x y i x y +-=++-=++-=，即()()22221x y ++-=，表示圆心为()2,2-，半径为1r =的圆. ()()()()22121212z i x y i x y --=-+-=-+-，表示点(),x y 和()1,2之间的距离，故()()min 12122z i r --=---=.故选：A.【点睛】本题考查了复数的模，与圆相关距离的最值问题，意在考查学生的计算能力和转化能力. 3．D解析：D【分析】根据复数的除法运算先把z 化成(),z a bi a b R =+∈的形式，再根据公式z =求模.【详解】 ()()()2234343443i i i i i z i i i i i----+====----，5z ∴==.故选：D .【点睛】本题考查复数的除法运算和复数的模，属于基础题.4．C解析：C【分析】根据所给的虚数是一个纯虚数，得到虚数的实部等于0，而虚部不等于0，得到角的正弦和余弦值，根据同角三角函数之间的关系，得到结果.【详解】若复数34sin (cos )55z i θθ=-+-是纯虚数，则3sin 05θ-=且4cos 05θ-≠，所以3sin 5θ=，4cos 5θ=-，所以3tan 4θ=-，故tan()θ-π=3tan 4θ=-．故选C ．【点睛】本题主要考查了复数的基本概念，属于基础题．纯虚数是一个易错概念，不能只关注实部为零的要求，而忽略了虚部不能为零的限制，属于易错题.5．C解析：C【分析】本道题目可以设出z a bi =+,然后结合待定系数法,计算参数,即可得出答案.【详解】设z a bi =+,代入原式得到()()()()34343434i z i a bi a b b a i +=++=-++结合待定系数法得到340,3425a b b a -=+=,解得3b =,故选C.【点睛】本道题目考查了待定系数法和复数的四则运算,注意虚部是指i 的系数.6．B解析：B【分析】先化简得到2z i =--，再计算2z i =-+得到答案。

(完整版)数学选修2-2练习题及答案

目录：数学选修2-2第一章导数及其应用 [基础训练A 组] 第一章导数及其应用 [综合训练B 组] 第一章导数及其应用 [提高训练C 组] 第二章推理与证明 [基础训练A 组] 第二章推理与证明 [综合训练B 组]第二章推理与证明 [提高训练C 组] 第三章复数 [基础训练A 组] 第三章复数 [综合训练B 组]第三章复数 [提高训练C 组]（数学选修2-2）第一章导数及其应用[基础训练A 组]一、选择题1．若函数()y f x =在区间(,)a b 内可导，且0(,)x a b ∈则000()()limh f x h f x h h→+--的值为（）A ．'0()f xB ．'02()f xC ．'02()f x - D ．02．一个物体的运动方程为21t t s +-=其中s 的单位是米，t 的单位是秒，那么物体在3秒末的瞬时速度是（） A ．7米/秒 B ．6米/秒 C ．5米/秒 D ．8米/秒 3．函数3yx x 的递增区间是（）A ．),0(+∞B ．)1,(-∞C ．),(+∞-∞D ．),1(+∞4．32()32f x ax x =++,若'(1)4f -=,则a 的值等于（）A ．319 B ．316C ．313 D ．310 5．函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的（）A ．充分条件B ．必要条件C ．充要条件D ．必要非充分条件6．函数344+-=x x y 在区间[]2,3-上的最小值为（）A ．72B ．36C ．12D ．0二、填空题1．若3'0(),()3f x x f x ==，则0x 的值为_________________；2．曲线x x y 43-=在点(1,3)- 处的切线倾斜角为__________； 3．函数sin xy x=的导数为_________________； 4．曲线x y ln =在点(,1)M e 处的切线的斜率是_________，切线的方程为_______________； 5．函数5523--+=x x x y 的单调递增区间是___________________________。

(完整版)高中数学选修2-2综合测试题(附答案)

高二数学选修2-2综合测试题一、选择题：1、i 是虚数单位。

已知复数413(1)3iZ i i+=++-，则复数Z 对应点落在（） A ．第四象限 B ．第三象限 C ．第二象限 D ．第一象限2、在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，…这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形1 3 6 10 15 则第n 个三角形数为（） A ．n B ．2)1(+n n C ．12-n D ．2)1(-n n 3、求由曲线y x =2y x =-+及y 轴所围成的图形的面积错误．．的为（） A.4(2)x x dx -+⎰B.0xdx ⎰C.222(2)y y dy ---⎰ D.022(4)y dy --⎰4、设复数z 的共轭复数是z ,且1z =,又(1,0)A -与(0,1)B 为定点,则函数()f z =(1)z +()z i -︱取最大值时在复平面上以z ,A,B 三点为顶点的图形是A,等边三角形 B,直角三角形 C,等腰直角三角形 D,等腰三角形5、函数f(x)的定义域为R ，f(-1)=2,对任意x R ∈，'()2f x >,则()24f x x >+的解集为(A)(-1，1) (B)(-1，+∞) (c)(-∞，-l) (D)(-∞,+∞)6、用数学归纳法证明412135()n n n +++∈N 能被8整除时，当1n k =+时，对于4(1)12(1)135k k +++++可变形为Ａ．41412156325(35)k k k +++++·Ｂ．441223355k k ++··Ｃ．412135k k +++Ｄ．412125(35)k k +++7、设f (x )，g (x )分别是定义在R 上的奇函数和偶函数,当x <0时，f ′(x )g (x )＋f (x )g ′(x )>0，且(3)0g -=，则不等式f (x )g (x )<0的解集是（） A. (－3，0)∪(3，+∞) B. (－3，0)∪(0，3)C.(－∞，－3)∪(3，+∞)D. (－∞，－3)∪(0，3) 8、已知函数2()f x x bx =+的图象在点(1,(1))A f 处的切线的斜率为3，数列⎭⎬⎫⎩⎨⎧)(1n f的前n 项和为n S ,则2011S 的值为（）20122011.20112010.20102009.20092008.D C B A9、设函数f(x)＝kx 3＋3(k －1)x 22k -＋1在区间（0，4）上是减函数，则k 的取值范围是 ( )A.13k <B.103k <≤C.103k ≤≤D.13k ≤10、函数()y f x =在定义域3(,3)2-内可导，其图象如图所示，记()y f x =的导函数为()y f x '=，则不等式()0f x '≤的解集为（） A ．[)1,12,33⎡⎤-⎢⎥⎣⎦ B ．[]481,2,33⎡⎤-⎢⎥⎣⎦C ．[]31,1,222⎡⎤-⎢⎥⎣⎦D ．3148,1,,32233⎛⎤⎡⎤⎡⎫-- ⎪⎥⎢⎥⎢⎝⎦⎣⎦⎣⎭11、已知函数)(131)(23R b a bx ax x x f ∈+-+=、在区间[-1,3]上是减函数，则b a +的最小值是A.32B.23C.2D. 312、函数32()393,f x x x x =--+若函数()()[2,5]g x f x m x =-∈-在上有3个零点，则m 的取值范围为（） A ．（-24,8） B ．（-24,1]C ．[1,8]D ．[1,8）高二数学选修2-2综合测试题（答题卡）一、选择题（60分）。

人A数学选修2-2 阶段测试 (3)

选修2－2综合测评 (时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分) 1．已知复数z ＝21－i，则z 2－z ·z 等于( ) A ．－2＋2i B ．2i C ．－2－2iD ．－2i解析：∵z ＝21－i ＝2(1＋i )(1－i )(1＋i )＝1＋i ，∴z ＝1－i ，∴z 2－z ·z ＝(1＋i)2－(1＋i)(1－i)＝2i －2＝－2＋2i. 答案：A2．(2019·福建三明高二月考)某演绎推理的“三段”分解如下：①函数f (x )＝13x 是减函数；②指数函数y ＝a x (0<a <1)是减函数；③函数f (x )＝13x 是指数函数，则按照演绎推理的三段论模式，排序正确的是( )A ．①→②→③B ．③→②→①C ．②→①→③D ．②→③→①解析：按照演绎推理的三段论模式可得，已知指数函数y ＝a x (0<a <1)是减函数，因为函数f (x )＝13x ⎝ ⎛⎭⎪⎫0<13<1是指数函数，所以函数f (x )＝13x 是减函数，即排序正确的是②→③→①，故选D.答案：D3．如图，曲线f (x )＝x 2和g (x )＝2x 围成几何图形的面积是( )A.12 B.23C.43D．4解析：由f(x)＝x2与g(x)＝2x得x2＝2x，得x＝0或x＝2，＝4－83＝43，故选C.答案：C4．设z＝(2t2＋5t－3)＋(t2－2t＋2)i，t∈R，则下列命题中正确的是() A．z对应的点Z在第一象限B．z对应的点Z在第四象限C．z不是纯虚数D．z是虚数解析：当t＝12或t＝－3时，2t2＋5t－3＝0，此时z为纯虚数，C不正确；当－3<t<12时，2t2＋5t－3<0，又t2－2t＋2>0，此时z对应的点Z在第二象限，当t<－3或t>12时，2t2＋5t－3>0，又t2－2t＋2>0，此时z对应的点Z在第一象限，A、B不正确；∵t2－2t＋2>0恒成立，∴z是虚数，D正确．故选D.答案：D5．(2019·蚌埠二中高二检测)已知函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则()A．函数f(x)有1个极大值点，1个极小值点B．函数f(x)有2个极大值点，2个极小值点C．函数f(x)有3个极大值点，1个极小值点D．函数f(x)有1个极大值点，3个极小值点解析：根据导函数的图象知，在x2处导函数由大于0变为小于0，此时原函数有极大值，在x3处导函数由小于0变为大于0，此时原函数有极小值，在x1，x4处导函数没有正负变化无极值点，故选A.答案：A6．设函数f(x)＝x cos x＋(a－2)x sin x＋ax.若f(x)为奇函数，则曲线y＝f(x)在点(0,0)处的切线方程为()A．y＝x B．y＝2xC．y＝4x D．y＝3x解析：∵函数f(x)＝x cos x＋(a－2)x sin x＋ax为奇函数，∴a＝2.∴f(x)＝x cos x＋2x，∴f′(x)＝cos x－x sin x＋2，∴f′(0)＝cos 0＋2＝3，∴曲线y＝f(x)在(0,0)处的切线方程为y＝3x.故选D.答案：D7．(2019·南阳一中高二月考)定积分|x|d x＝()A.52B．－52C.32D．－32解析：如图，|x |d x ＝12＋2＝52，故选A.答案：A8．已知函数f (x )＝x 3＋ax 2＋bx ＋a 2在x ＝1处取得极值10，则实数a ＝( ) A ．4或－3 B ．4或－11 C ．4D ．－3解析：∵f (x )＝x 3＋ax 2＋bx ＋a 2， ∴f ′(x )＝3x 2＋2ax ＋b . ∵f (x )在x ＝1处取得极值10，∴⎩⎪⎨⎪⎧ f ′(1)＝0，f (1)＝10，即⎩⎪⎨⎪⎧3＋2a ＋b ＝0，1＋a ＋b ＋a 2＝10，解得⎩⎪⎨⎪⎧a ＝－3，b ＝3或⎩⎪⎨⎪⎧a ＝4，b ＝－11，经检验⎩⎪⎨⎪⎧a ＝－3，b ＝3时函数f (x )在R 上单调递增，无极值，不符合题意，当⎩⎪⎨⎪⎧ a ＝4，b ＝－11时函数f (x )在x ＝1处取得极小值10， ∴⎩⎪⎨⎪⎧a ＝4，b ＝－11，故选C. 答案：C9．设f (x )＝13x 3＋ax 2＋5x ＋6在区间[1,3]上为单调函数，则实数a 的取值范围是()A．[－5，＋∞)B．(－∞，－3]C．(－∞，－3]∪[－5，＋∞)D．[－5，5]解析：f′(x)＝x2＋2ax＋5.由f′(x)≥0在[1,3]上恒成立，或f′(x)≤0在[1,3]上恒成立，得a≥－x2－52x或a≤－x2－52x，设g(x)＝－x2－52x＝－⎝⎛⎭⎪⎫x2＋52x，则g(x) 在[1,3]上的值域为[－3，－5]，∴a≤－3或a≥－ 5.答案：C10．给出下面三个推理：①由“若a、b是实数，则|a＋b|≤|a|＋|b|”推广到复数中，则有“若z1、z2是复数，则|z1＋z2|≤|z1|＋|z2|”；②由“在半径为R的圆内接矩形中，正方形的面积最大”类比推出“在半径为R的球内接长方体中，正方体的体积最大”；③以半径R为自变量，由“圆面积函数的导函数是圆的周长函数”类比推出“球体积函数的导函数是球的表面积函数”．其中，推理得到的结论正确的个数有()A．0个B．1个C．2个D．3个解析：由复数的几何意义知，①正确；设球的内接长方体的长、宽、高分别为a、b、c，则a2＋b2＋c2＝(2R)2，由基本不等式a2＋b2＋c2≥33a2b2c2，即abc ≤，当且仅当a ＝b ＝c 时，等式成立，即正方体的体积最大，②正确；球的体积V ＝43πR 3，则V ′＝4πR 2，③正确，综上所述，三个推理均正确．故选D.答案：D11．(2019·哈尔滨师大附中月考)已知函数f (x )＝x 3－ln(x 2＋1－x )，则对于任意实数a ，b (a ＋b >0)，则f (a )＋f (b )a ＋b的值为( ) A ．恒正 B ．恒等于0 C ．恒负D ．不确定解析：可知函数f (x )＋f (－x )＝x 3－ln(x 2＋1－x )＋(－x )3－ln(x 2＋1＋x )＝0，所以函数为奇函数，同时f ′(x )＝3x 2＋1x 2＋1>0，f (x )是递增函数，f (a )＋f (b )a ＋b ＝f (a )－f (－b )a －(－b )，所以f (a )＋f (b )a ＋b>0，所以选A.答案：A12．(2019·江西赣州十四县(市)期中联考)设f (x )＝e x (x 2＋2x )，令f 1(x )＝f ′(x )，f n ＋1(x )＝f ′n (x )，若f n (x )＝e x (A n x 2＋B n x ＋C n )，则数列⎩⎨⎧⎭⎬⎫1C n 的前n 项和为S n ，当|S n－1|≤12 019时，n 的最小整数值为( )A ．2 017B ．2 018C ．2 019D ．2 020解析：由题意得f 1(x )＝(2x ＋2)e x ＋(x 2＋2x )e x ＝(x 2＋4x ＋2)e x ， f 2(x )＝(2x ＋4)e x ＋(x 2＋4x ＋2)e x ＝(x 2＋6x ＋6)e x ， f 3(x )＝(2x ＋6)e x ＋(x 2＋6x ＋6)e x ＝(x 2＋8x ＋12)e x ，…由此可得C 1＝2，C 2＝6，C 3＝12，故可归纳得C n ＝n (n ＋1)，∴1C n＝1n (n ＋1)＝1n －1n ＋1，∴S n ＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫1n －1n ＋1＝1－1n ＋1，由题意得|S n －1|＝1n ＋1≤12 019，解得n ≥2 018.∴n 的最小整数值为2 018.故选B.答案：B二、填空题(本大题共4小题，每小题5分，共20分) 13．若复数z ＝3－i|2－i|，则|z |＝________. 解析：z ＝3－i |2－i|＝3－i 5，∴|z |＝|3－i|5＝105＝ 2. 答案： 214．对大于或等于2的正整数的幂运算有如下分解方式： 22＝1＋332＝1＋3＋542＝1＋3＋5＋7…23＝3＋533＝7＋9＋1143＝13＋15＋17＋19…根据上述分解规律，若m 2＝1＋3＋5＋…＋11，p 3的分解中最小的正整数是21，则m ＋p ＝______.解析：由所给等式推测m ＝6，p ＝5，∴m ＋p ＝11. 答案：1115．已知z 1＝m 2－(m 2－3m )i ，z 2＝(m 2－4m ＋3)i ＋10(m ∈R )，若z 1<z 2，求实数m 的取值为________．解析：∵z 1<z 2，∴z 1与z 2均为实数，∴⎩⎪⎨⎪⎧m 2－3m ＝0，m 2－4m ＋3＝0，∴m ＝3.答案：316．对于三次函数y ＝ax 3＋bx 2＋cx ＋d (a ≠0)，给出定义：设f ′(x )是函数y ＝f (x )的导数，f ″(x )是f ′(x )的导数，若方程f ″(x )＝0有实数解x 0，则称点(x 0，f (x 0))为函数y ＝f (x )的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心，若f (x )＝13x 3－12x 2＋3x －512，根据这一发现可得：(1)函数f (x )＝13x 3－12x 2＋3x －512的对称中心为________． (2)计算f ⎝ ⎛⎭⎪⎫17＋f ⎝ ⎛⎭⎪⎫27＋f ⎝ ⎛⎭⎪⎫37＋f ⎝ ⎛⎭⎪⎫47＋f ⎝ ⎛⎭⎪⎫57＋f ⎝ ⎛⎭⎪⎫67＝________.解析：(1)依题意，f ′(x )＝x 2－x ＋3， ∴f ″(x )＝2x －1，由2x －1＝0得x ＝12，又f ⎝ ⎛⎭⎪⎫12＝13×18－12×14＋3×12－512＝1，∴函数f (x )的对称中心为⎝ ⎛⎭⎪⎫12，1.(2)由f (x )的对称中心为⎝ ⎛⎭⎪⎫12，1，得f ⎝ ⎛⎭⎪⎫17＋f ⎝ ⎛⎭⎪⎫67＝2，f ⎝ ⎛⎭⎪⎫27＋f ⎝ ⎛⎭⎪⎫57＝2，f ⎝ ⎛⎭⎪⎫37＋f ⎝ ⎛⎭⎪⎫47＝2， ∴f ⎝ ⎛⎭⎪⎫17＋f ⎝ ⎛⎭⎪⎫27＋f ⎝ ⎛⎭⎪⎫37＋f ⎝ ⎛⎭⎪⎫47＋f ⎝ ⎛⎭⎪⎫57＋f ⎝ ⎛⎭⎪⎫67＝6. 答案：(1)⎝ ⎛⎭⎪⎫12，1 (2)6三、解答题(本大题共6小题，共70分)17．(10分)某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：①sin 213°＋cos 217°－sin 13°cos 17°； ②sin 215°＋cos 215°－sin 15°cos 15°； ③sin 218°＋cos 212°－sin 18°cos 12°； ④sin 2(－18°)＋cos 248°－sin(－18°)cos 48°； ⑤sin 2(－25°)＋cos 255°－sin(－25°)cos 55°.(1)试从上述五个式子中选择一个，求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．解：(1)选择②式，计算如下： sin 215°＋cos 215°－sin 15°cos 15° ＝1－12sin 30°＝1－14＝34.(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝34. 证法一：sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos 30°cos α＋sin 30°sin α)2－sin α(cos 30°cos α＋sin 30°sin α)＝sin 2α＋34cos 2α＋32sin αcos α＋14sin 2α－32sin αcos α－12sin 2α＝34sin 2α＋34cos 2α＝34. 证法二：sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝1－cos 2α2＋1＋cos (60°－2α)2－sin α(cos 30°cos α＋sin 30°sin α) ＝12－12cos 2α＋12＋12(cos 60°cos 2α＋sin 60°sin 2α)－32sin αcos α－12sin 2α ＝12－12cos 2α＋12＋14cos 2α＋34sin 2α－34sin 2α－14(1－cos 2α) ＝1－14cos 2α－14＋14cos 2α＝34.18．(12分)(1)已知x 2－y 2＋2xy i ＝2i ，求实数x ，y 的值；(2)关于x 的方程3x 2－a2x －1＝(10－x －2x 2)i 有实根，求实数a 的值．解：(1)∵x 2－y 2＋2xy i ＝2i ，x ，y ∈R ， ∴⎩⎨⎧ x 2－y 2＝0，2xy ＝2，解得⎩⎨⎧ x ＝1，y ＝1或⎩⎨⎧x ＝－1，y ＝－1.(2)∵关于x 的方程3x 2－a2x －1＝(10－x －2x 2)i 有实根，且a ∈R ， ∴⎩⎪⎨⎪⎧3x 2－a 2x －1＝0，10－x －2x 2＝0，解得⎩⎨⎧x ＝2，a ＝11或⎩⎪⎨⎪⎧x ＝－52，a ＝－715.19．(12分)已知数列{a n }的前n 项和为S n ，a 1＝－23，满足S n ＋1S n＋2＝a n (n ≥2)，(1)求S 2，S 3，S 4；(2)根据(1)猜想S n 的表达式，并用数学归纳法证明．解：(1)由a 1＝－23，及S n ＋1S n＋2＝a n (n ≥2)可算得S 1＝－23，S 2＝－34，S 3＝－45，S 4＝－56.(2)由此猜想S n 的表达式是S n ＝－n ＋1n ＋2.下面用数学归纳法证明：①由a 1＝S 1＝－23＝－1＋11＋2知，当n ＝1时，等式成立； ②当n ≥2时，假设n ＝k (k ≥1)时等式成立，即S k ＝－k ＋1k ＋2，那么，当n ＝k ＋1时，由S n ＋1S n ＋2＝a n (n ≥2)得 S k ＋1＋1S k ＋1＋2＝a k ＋1，得－1S k ＋1＝(S k ＋1－a k ＋1)＋2，而S k ＝S k ＋1－a k ＋1，∴－1S k ＋1＝S k ＋2＝－k ＋1k ＋2＋2＝k ＋3k ＋2， ∴S k ＋1＝－k ＋2k ＋3＝－(k ＋1)＋1(k ＋1)＋2. 所以当n ＝k ＋1时，等式成立．综合①②可知，对任意的正整数n ，有S n ＝－n ＋1n ＋2成立． 20．(12分)已知非零实数a ，b ，c 成等差数列，且公差d ≠0，求证：1a ，1b ，1c 不可能是等差数列．证明：假设1a ，1b ，1c 成等差数列，则1a ＋1c ＝2b ，又∵a ，b ，c 成等差数列，∴a ＋c ＝2b ，∴b ＝a ＋c 2，把b ＝a ＋c 2代入1a ＋1c ＝2b ，得(a －c )2＝0，∴a ＝c ，∴c －a ＝2d ＝0，这与公差d ≠0矛盾，∴1a ，1b ，1c 不可能是等差数列．21．(12分)(2019·乾安中学高三模拟)在各项为正的数列{a n }中，数列的前n项和S n 满足S n ＝12⎝ ⎛⎭⎪⎫a n ＋1a n . (1)求a 1，a 2，a 3；(2)由(1)猜想到数列{a n }的通项公式，并用数学归纳法证明你的猜想．解：(1)由S 1＝a 1＝12⎝ ⎛⎭⎪⎫a 1＋1a 1，得a 21＝1，因为a n >0，所以a 1＝1.由S 2＝a 1＋a 2＝12⎝ ⎛⎭⎪⎫a 2＋1a 2，得a 22＋2a 2－1＝0，所以a 2＝2－1，由S 3＝a 1＋a 2＋a 3＝12⎝ ⎛⎭⎪⎫a 3＋1a 3，得a 23＋22a 3－1＝0，所以a 3＝3－ 2.(2)猜想a n ＝n －n －1(n ∈N ＋)．证明：①当n ＝1时，a 1＝1－0＝1，命题成立；②假设n ＝k (k ≥1，k ∈N ＋)时，a k ＝k －k －1成立，则n ＝k ＋1时，a k ＋1＝S k ＋1－S k＝12⎝⎛⎭⎪⎫a k ＋1＋1a k ＋1－12⎝ ⎛⎭⎪⎫a k ＋1a k ，即a k ＋1＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1－12k －k －1＋1k －k －1＝12⎝⎛⎭⎪⎫a k ＋1＋1a k ＋1－k ，所以a 2k ＋1＋2ka k ＋1－1＝0.所以a k ＋1＝k ＋1－k ，则n ＝k ＋1时，命题成立．由①②知，n ∈N ＋，a n ＝n －n －1.22．(12分)(2019·长庆高中高三阶段测试)设函数f (x )＝a e x ln x ＋b e x －1x ，曲线y＝f (x )在点(1，f (1))处的切线方程为y ＝e(x －1)＋2.(1)求a ，b ；(2)证明：f (x )>1.解：(1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝a e x ln x ＋a x e x －b x 2e x －1＋b x e x －1.由题意可得f (1)＝2，f ′(1)＝e.故a ＝1，b ＝2.(2)证明：由(1)知，f (x )＝e x ln x ＋2x e x －1，从而f (x )>1等价于x ln x >x e －x －2e .设函数g (x )＝x ln x ，则g ′(x )＝1＋ln x .所以当x ∈⎝ ⎛⎭⎪⎫0，1e 时，g ′(x )<0；当x ∈⎝ ⎛⎭⎪⎫1e ，＋∞时，g ′(x )>0. 故g (x )在⎝ ⎛⎭⎪⎫0，1e 上单调递减，在⎝ ⎛⎭⎪⎫1e ，＋∞上单调递增，从而g (x )在(0，＋∞)上的最小值为g ⎝ ⎛⎭⎪⎫1e ＝－1e . 设函数h (x )＝x e －x －2e ，则h ′(x )＝e －x (1－x )．所以当x ∈(0,1)时，h ′(x )>0；当x ∈(1，＋∞)时，h ′(x )<0.故h (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，从而h (x )在(0，＋∞)上的最大值为h (1)＝－1e .所以g (x )≥－1e ≥h (x )，又因为等号无法同时取到，所以g (x )>h (x )，即f (x )>1.。

高中数学选修2-2测试卷答案(教师版)

高中数学选修（2-2）第一、三章测试卷一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．函数cos sin y x x x =-的导数为（）（A ）cos x x （B ）sin x x - （C ）sin x x （D ）cos x x -2．下列说法正确的是（）（A ）当0()0f x '=时，0()f x 为()f x 的极大值（B ）当0()0f x '=时，0()f x 为()f x 的极小值（C ）当0()0f x '=时，0()f x 为()f x 的极值（D ）当0()f x 为()f x 的极值时， 0()0f x '=3．如果z 是34i +的共轭复数，则z 对应的向量OA 的模是（）（A ）1 （B （C （D ）54．若函数3()y a x x =-的递减区间为(，则a 的取值范围是（）（A ）(0,)+∞ （B ）(1,0)- （C ）(1,)+∞ （D ）(0,1) 5．(2014·湖北高考文科)i 为虚数单位,错误!未找到引用源。

( ) A.1B.-1C.iD.-i6.下列计算错误的是（）A.ππsin 0xdx -=⎰B.23=⎰C.ππ22π02cos 2cos xdx xdx -=⎰⎰D.π2πsin 0xdx -=⎰7．复数a bi -与c di +的积是实数的充要条件是（）（A ）0ad bc += （B ）0ac bd += （C ）0ad bc -= （D ）0ac bd -= 8．已知函数1sin 2sin 2y x x =+，那么y '是（）（A ）仅有最小值的奇函数（B ）既有最大值又有最小值的偶函数（C ）仅有最大值的偶函数（D ）非奇非偶函数 9．(2014·广东高考理科)已知复数z 满足(3+4i)z=25,则z= ( ) A.-3+4i B.-3-4i C.3+4i D.3-4i10．(2014·陕西高考文科·T3)已知复数z=2-i,则z ·错误!未找到引用源。

(必考题)高中数学高中数学选修2-2第三章《导数应用》测试(含答案解析)

一、选择题1．已知函数()()11332cos 1x x x f x --+=+--，则()()0.52310.5log 9log 2f f f -⎛⎫ ⎪⎝⎭、、的大小关系（） A ．()()0.5231log 9log 0.52f f f -⎛⎫>> ⎪⎝⎭B ．0.5321(log )(0.5)(log 9)2f f f ->>C ．0.5321(0.5)(log )(log 9)2f f f ->>D ．0.5231(log 9)(0.5)(log )2f f f ->>2．已知函数2()1(0)f x ax x a =-+≠，若任意1x ，2[1x ∈，)+∞且12x x ≠都有1212()()1f x f x x x ->-，则实数a 的取值范围（）A ．[1，)+∞B ．(0，1]C ．[2，)+∞D ．(0,)+∞3．已知定义域为R 的偶函数()f x ，其导函数为fx ，对任意[)0,x ∈+∞，均满足：()()2xf x f x >-'．若()()2g x x f x =，则不等式()()21g x g x <-的解集是（）A ．(),1-∞-B ．1,3⎛⎫-∞ ⎪⎝⎭C ．11,3⎛⎫- ⎪⎝⎭D ．()1,1,3⎛⎫-∞-+∞ ⎪⎝⎭4．定义域为R 的连续可导函数()f x 满足()()xf x f x e '-=，且()00f =，若方程()()21016m f x f x ++=⎡⎤⎣⎦有四个根，则m 的取值范围是（） A ．2416e e m -<-D ．2e m >5．直线()0x a a =>分别与曲线21y x =+，ln y x x =+相交于A ，B 两点，则AB的最小值为（） A ．1B ．2C D 6．若函数1()ln f x x a x =-+在区间(1,)e 上存在零点，则常数a 的取值范围为（） A ．01a <--的解集为（）A ．(,0)-∞B ．(,)π-∞-C ．(,)2π-∞-D ．(,)π-∞10．已知f （x ）=-x 3-ax 在（-∞，-1]上递减，且g （x ）=2x-ax在区间（1，2]上既有最大值又有最小值，则a 的取值范围是（） A ．2a >-B ．3a -≤C ．32a -≤<-D ．32a --≤≤11．已知0a >，函数()225,0,2,0,x a x f x x x ⎧+≤⎪=⎨⎪->⎩若关于x 的方程()()2f x a x =-恰有2个互异的实数解，则a 的取值范围为（）A ．14a <<B ．24a <<C ．48a <<D ．28a <<12．已知函数()3242xx f x x x e e=-+-，其中e 是自然对数的底数，若()()2210f a f a +--≤，则实数a 的取值范围为（）A ．1,12⎡⎤-⎢⎥⎣⎦B ．11,2⎡⎤-⎢⎥⎣⎦C ．[]2,1-D ．[]1,2-二、填空题13．已知函数f （x ）是定义在R 上的奇函数，当x ＞0时，f （x ）+xf '（x ）＞0，且f （3）＝0，则不等式xf （x ）＞0的解集是_____．14．若函数()()2212ln 1f x ax a x x =+---只有一个零点，则实数a 的取值范围是______.15．已知函数()f x 是定义在(0,)+∞上的单调函数，()f x '是()f x 的导函数，且对任意的(0,)x ∈+∞都有2(())2f f x x -=，若函数()()2()3F x xf x f x '=--的一个零点0(,1)x m m ∈+，则整数m 的值是__________.16．已知函数()()2ln 2f x x x g x x x a ==-++，，若∀x 1，x 2∈（0，+∞），f （x 1）≥g（x 2）恒成立，则实数a 的取值范围为__________17．已知函数32()1f x x ax x =+++在区间21,33⎛⎫-- ⎪⎝⎭内是减函数，则实数a 的取值范围是________．18．设函数()'f x 是偶函数()(0)f x x ≠的导函数，(1)0f -=，当0x >时，()()0xf x f x '-<，则使得()0f x >成立的x 的取值范围是__________.19．已知函数()1ln f x x a x x=-+，存在不相等的常数m ，n ，使得()()''0f m f n ==，且10,m e ⎛⎤∈ ⎥⎝⎦，则()()f m f n -的最小值为____________.20．设函数()2()1xf x x e =-，当0x ≥时，()1(0)f x ax a ≤+>恒成立，则a 的取值范围是________.三、解答题21．设函数3222ln 11(),()28a x x f x g x x x x +==-+. （1）若曲线()y f x =在点(1,(1))f 处的切线与30x y -+=垂直，求函数()f x 的解析式；（2）如果对于任意的1213,[,]22x x ∈，都有112()()x f x g x ⋅≥成立，试求实数a 的取值范围.22．设函数()ln 1x f x x+=，（1）求曲线()y f x =在点()(),e f e 处的切线方程；（2）当1≥x 时，不等式()()211a x f x x x--≥恒成立，求a 的取值范围． 23．已知函数()2xf x eax b =-+（0a >，b R ∈，其中e 为自然对数的底数）.（1）求函数()f x 的单调递增区间；（2）若函数()f x 有两个不同的零点12,x x ，当a b =时，求实数a 的取值范围.24．已知函数22()ln a f x a x x x=⋅++(0a ≠).（1）若曲线()y f x =在点(1,(1))f 处的切线与直线20x y -=垂直，求实数a 的值；（2）讨论函数()f x 的单调性；（3）当(,0)a ∈-∞时，记函数()f x 的最小值为()g a ，求证：21()2g a e ≤. 25．已知函数321()12f x x x ax =-++. （1）当2a =时，求曲线()y f x =在点(0,(0))f 处的切线方程；（2）若函数()f x 在1x =处有极小值，求函数()f x 在区间32,2⎡⎤-⎢⎥⎣⎦上的最大值.26．已知函数ln xy x=（0x >）. （1）求这个函数的单调区间；（2）求这个函数在区间21,e e⎡⎤⎢⎥⎣⎦的最大值与最小值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】首先设函数()(1)332cos x x g x f x x -=+=+-，判断函数是偶函数，利用导数判断函数的单调性，根据平移关系，可判断函数()y f x =的对称性和单调性，再将2log 9，0.50.5-，以及31log 2转化在同一个单调区间，根据单调性比较大小. 【详解】令()(1)332cos x x g x f x x -=+=+-，()()g x g x -=，所以()g x 是偶函数； ()ln3(33)2sin x x g x x -'=-+，当(0,)x π∈时，()0g x '>，()g x 在(0,)π上是增函数，将()g x 图像向右平移一个单位得到()f x 图像，所以()f x 关于直线1x =对称，且在(1,1)π+单调递增. ∵23log 94<<，0.50.5-=()3312log 2log 22,32-=+∈， ∴0.52314log 92log 0.512->>->>， ∴()()0.5231log 92log 0.52f f f -⎛⎫>-> ⎪⎝⎭，又∵()f x 关于直线1x =对称，∴3311log 2log 22f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，∴()()0.5231log 9log 0.52f f f -⎛⎫>> ⎪⎝⎭. 故选：A【点睛】思路点睛：本题是一道函数单调性，奇偶性，对称性，判断大小的习题，本题所给函数()()11332cos 1x x x f x --+=+--，看似很复杂，但仔细观察就会发现，通过换元后可判断函数()1y f x =+是偶函数，本题的难点是判断函数的单调性，关键点是能利用对称性，转化3311log 2log 22f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭.2．A解析：A 【分析】求出函数的导数，通过讨论a 的范围，得到关于a 的不等式，解出即可．【详解】1212()()1f x f x x x ->-表示函数()f x 在区间[)1,+∞上任意两个不同点连线的斜率都大于1，等价于()'211f x ax =-≥，1x 时恒成立， 0a时，()'0f x <，不合题意，0a >时，只需211ax -，即1ax在[1，)+∞恒成立，故max 1()1a x=，故a 的范围是[1，)+∞，故选：A 【点睛】1212()()1f x f x x x ->-表示函数()f x 在区间[)1,+∞上任意两个不同点连线的斜率都大于1，由此考虑利用导数进行求解.3．C解析：C 【解析】试题分析：[)0,x ∈+∞时()()()()()22(2)0g x xf x x f x x f x xf x =+='+'>'，而()()2g x x f x =也为偶函数，所以()()()()21212121321013g x g x g x g x x x x x x <-⇔<-⇔<-⇔+-<⇔-<<，选C.考点：利用函数性质解不等式【方法点睛】利用导数解抽象函数不等式，实质是利用导数研究对应函数单调性，而对应函数需要构造. 构造辅助函数常根据导数法则进行：如()()f x f x '<构造()()xf xg x e =，()()0f x f x '+<构造()()x g x e f x =，()()xf x f x '<构造()()f x g x x=，()()0xf x f x '+<构造()()g x xf x =等4．A解析：A 【分析】构造函数()()xf x x b e =+，根据()00f =求出0b =，利用导数判断函数的单调性，作出其大致图像，令()t f x =，只需21016mt t ++=两个不同的根1t ，21,0t e ⎛⎫∈- ⎪⎝⎭，利用二次函数根的分布即可求解. 【详解】由()()()()()()()()221x xxxxx x f x e f x e f x f x e e f x e ef x e '-'-=-=⇒'=⇒，则()()()()1xx xf x f x x b x x b e e e f ⎡⎤=⇒=+=+⎢⎥⎣⎦⇒，由()000f b =⇒=，则()xf x e x =⋅.由()()1xf x e x '=+，当()1,x ∈-+∞，()0f x '>，()f x 单调递增；当(),1x ∈-∞-，()0f x '<，()f x 单调递减，当x →-∞，()0f x <，x →+∞，()0f x >，如图所示：令()t f x =，则21016mt t ++=，由已知可得 21016mt t ++=两个不同的根1t ，21,0t e ⎛⎫∈- ⎪⎝⎭，令()2116g t mt t =++，由12121001016t t m m t t m ⎧+=-<⎪⎪⇒>⎨⎪⋅=>⎪⎩，则()21000,41601102g e e g m e em ⎧⎛⎫-> ⎪⎪⎝⎭⎪⎛⎫⎪>⇒∈-⎨⎪∆>⎝⎭⎪⎪-<-<⎪⎩. 故选：A 【点睛】本题考查了构造函数判断函数的单调性、根据方程根的个数求参数的取值范围，考查了二次函数根的分布，此题综合性比较强，属于中档题.5．B解析：B 【分析】设A （a ，2 a+1），B （a ，a+lna ），求出|AB |，利用导数求出|AB |的最小值．【详解】设A （a ，2a+1），B （a ，a+lna ），∴|AB |＝211a a lna a lna +-+=+-（），令y 1x lnx =+-，则y ′=11x-， ∴函数在（0，1）上单调递减，在（1，+∞）上单调递增， ∴x ＝1时，函数y 的最小值为20>，∴|AB |＝2111a a lna a lna a lna +-+=+-=+-（），其最小值为2.故选B ．【点睛】本题考查导数知识的运用，考查学生分析解决问题的能力及转化思想，利用求导得到函数的单调性进而求得最值是关键．6．C解析：C 【分析】先利用导数判断出函数()f x 在区间()1,e 上为增函数，再解不等式(1)ln110f a =-+<，1()ln 0f e e a e=-+>，即得解.【详解】由题得211()0f x x x '=+>在区间()1,e 上恒成立，所以函数1()ln f x x a x=-+在区间()1,e 上为增函数，所以(1)ln110f a =-+<，1()ln 0f e e a e=-+>，可得111a e-<<. 故选：C. 【点睛】本题主要考查利用导数研究函数的单调性和零点，意在考查学生对这些知识的理解掌握水平.7．C解析：C 【解析】y ′＝3x 2＋1>0对于任何实数都恒成立．8．A解析：A 【分析】根据圆柱的高，底面半径以及球半径之间的关系，建立圆柱的高与圆柱体积之间的函数关系，利用导数求体积取得最大值时对应的自变量即可. 【详解】根据题意，设圆柱底面半径为r ，圆柱的高为h ，作出示意图如下所示：显然满足2224h r R =-，故圆柱的体积()23214h r h h R h πππ=⨯=-+，故可得()223,(02)4V h h R h R ππ<'=-+<，令()0V h '>，解得0h <<，故此时()V h 单调递增，令()0V h '<2h R <<，故此时()V h 单调递减.故()maxV h V ⎫=⎪⎪⎝⎭.即当3h R =时，圆柱的体积最大. 故选：A . 【点睛】本题考查圆柱的外接球以及利用导数求体积的最大值，属综合中档题.9．A解析：A 【分析】构造函数()()sin h x f x x =+，根据其单调性，求解目标不等式即可. 【详解】不妨令()()sin h x f x x =+，因为()()cos 0h x f x x =+'<'在[)0,+∞恒成立，即()h x 在[)0,+∞单调递减；又()f x 是奇函数，sin y x =是奇函数，故()h x 是奇函数，且()h x 是R 上的单调减函数.由()3,2f π=-故可得22h π⎛⎫=- ⎪⎝⎭，又()cos 22f x x π+>--，即22h x h ππ⎛⎫⎛⎫+> ⎪ ⎪⎝⎭⎝⎭，故22x ππ+<，则0x <.故选：A . 【点睛】本题考查构造函数法，涉及利用导数研究函数单调性以及利用单调性解不等式，属综合中档题.10．C解析：C 【分析】利用()f x 导数小于等于零恒成立，求出a 的范围，再由()2'2ag x x x =+在(]1,2上有零点，求出a 的范围，综合两种情况可得结果. 【详解】因为函数()3f x x ax =--在(],1-∞-上单调递减，所以()2'30f x x a =--≤对于一切(],1x ∈-∞-恒成立，得23,3x a a -≤∴≥-，又因为()2ag x x x=-在区间(]1,2上既有最大值，又有最小值，所以，可知()2'2ag x x x =+在(]1,2上有零点，也就是极值点，即有解220ax x+=，在(]1,2上解得32a x =-，可得82,32a a -≤<-∴-≤<-，故选C. 【点睛】本题主要考查“分离常数”在解题中的应用以及利用单调性求参数的范围，属于中档题. 利用单调性求参数的范围的常见方法：① 视参数为已知数，依据函数的图象或单调性定义，确定函数的单调区间，与已知单调区间比较求参数需注意若函数在区间[],a b 上是单调的，则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式()'0f x ≤或()'0f x ≥恒成立问题求参数范围. 11．D解析：D 【分析】根据分段函数，看成函数()f x 与直线()2y a x =-的交点问题，分0x =，0x ≤，0x >讨论求解.【详解】当0x =时，()502f a =，对于直线()2y a x =-，2y a =，因为0a >，所以无交点；当0x ≤时，()2f x x '=，令2x a =-，解得 2ax =-，要使方程()()2f x a x =-恰有2个互异的实数解，则252222a a a a ⎛⎫⎛⎫-+<+ ⎪ ⎪⎝⎭⎝⎭，解得 2a >；当0x >时，()2f x x '=-，令2x a -=-，解得 2ax =，因为0x ≤时，方程()()2f x a x =-恰有2个互异的实数解，则0x >时，无交点，则2222a a a ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭，解得 8a <,综上：a 的取值范围为28a <<故选：D 【点睛】关键点点睛：本题关键是由0a >和直线()2y a x =-过定点()2,0，确定方程()()2f x a x =-恰有2个互异的实数解只有一种情况：当0x ≤时，方程恰有2个互异的实数解，当0x >时，方程无实数解.12．A解析：A 【分析】先求得函数()f x 是R 上的奇函数，把不等式转化为()22(1)f a f a ≤+，再利用导数求得函数的单调性，在把不等式转化为221a a ≤+，即可求解. 【详解】由题意，函数32()42xxf x x x e e =-+-的定义域为R ，又由3322()42e (42)()e x xx xf x x x x x e f x e -=-++-=--+-=-，所以()f x 是R 上的奇函数，又因为2222()3423430x x f x x e x x e '=-++≥-+=≥，当且仅当0x =时取等号，所以()f x 在其定义域R 上的单调递增函数，因为()22(1)0f a f a +--≤，可得()22(1)(1)f a f a f a ≤---=+，所以221a a ≤+，解得112a ≤≤，故实数a 的取值范围是1,12⎡⎤-⎢⎥⎣⎦.故选：A 【点睛】利用函数的基本性质求解与函数有关的不等式的方法及策略： 1、求解函数不等式的依据是函数的单调性的定义. 具体步骤：①将函数不等式转化为12()()f x f x >的形式；②根据函数()f x 的单调性去掉对应法则“f ”转化为形如：“12x x >”或“12x x <”的常规不等式，从而得解.2、利用函数的图象研究不等式，当不等式问题不能用代数法求解时，常将不等式问题转化为两函数的图象上、下关系问题，从而利用数形结合求解.二、填空题13．（﹣∞﹣3）∪（3+∞）【分析】令当x ＞0时可得x ∈（0+∞）上函数单调递增由可得由函数是定义在R 上的奇函数可得函数是定义在R 上的偶函数进而得出不等式的解集【详解】解：令当x ＞0时∴x ∈（0+∞）上解析：（﹣∞，﹣3）∪（3，+∞）【分析】令()()g x xf x =，()()()g x f x xf x ''+＝，当x ＞0时，()()0f x xf x '+>，可得x ∈（0，+∞）上，函数()g x 单调递增．由()30f ＝，可得()30g ＝．由函数()f x 是定义在R 上的奇函数，可得函数()g x 是定义在R 上的偶函数．进而得出不等式的解集．【详解】解：令()()g x xf x =，()()()g x f x xf x ''+＝当x ＞0时，()()0f x xf x '+>∴x ∈（0，+∞）上，函数()g x 单调递增．()30f ＝，∴()30g ＝．∵函数()f x 是定义在R 上的奇函数， ∴函数()g x 是定义在R 上的偶函数．由()()03g x g >＝，即()()3g x g ＞， ∴|x |＞3，解得x ＞3，或x ＜﹣3．∴不等式()0xf x ＞的解集是()(),33-，-∞⋃+∞．故答案为：()(),33-，-∞⋃+∞．【点睛】本题考查了利用导数研究函数的单调性、方程与不等式的解法、等价转化方法，考查了推理能力与计算能力，属于中档题．14．或【分析】首先求出函数的导函数当时可得在定义域上单调递减再根据零点存在性定理可得在上存在唯一的零点当时由导数可得函数的单调性及最小值为令利用导数说明的单调性即可求出参数的值；【详解】解：因为定义域为解析：0a ≤或1a = 【分析】首先求出函数的导函数，当0a ≤时，可得()f x 在定义域上单调递减，再根据零点存在性定理可得()f x 在()0,1上存在唯一的零点，当0a >时，由导数可得函数()f x 的单调性及最小值为()min 1112ln f x f a a a ⎛⎫==+-⎪⎝⎭，令()112ln g a a a =+-，()0,a ∈+∞利用导数说明()g a 的单调性，即可求出参数a 的值；【详解】解：因为()()2212ln 1f x ax a x x =+---，定义域为()0,∞+，所以()()()()()222122112221ax a x ax x f x ax a x x x+---+'=+--== 当0a ≤时，()0f x '<恒成立，即()f x 在定义域上单调递减，()()1310f a =-<，当0x +→时，20ax →，()210a x -→，2ln x -→+∞，所以()f x →+∞，所以()f x 在()0,1上存在唯一的零点，满足条件；当0a >时，令()()()2110ax x f x x -+'=>，解得1x a >即函数在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增，令()()()2110ax x f x x-+'=<，解得10x a <<即函数在10,a ⎛⎫⎪⎝⎭上单调递减，则()f x 在1x a =取值极小值即最小值，()min 1112ln f x f a a a ⎛⎫==+- ⎪⎝⎭，令()112ln g a a a =+-，()0,a ∈+∞，则()2221210a g a a a a +'=+=>恒成立，即()112ln g a a a=+-在定义域上单调递增，且()112ln110g =+-=，所以要使函数()()2212ln 1f x ax a x x =+---只有一个零点，则()min 1112ln 0f x f a a a ⎛⎫==+-= ⎪⎝⎭，解得1a =，综上可得0a ≤或1a =；故答案为：0a ≤或1a = 【点睛】本题考查利用导数研究函数的零点问题，考查分类讨论思想，属于中档题.15．2【分析】先通过已知求出得到再利用导数研究得到函数在内没有零点函数的零点在内即得的值【详解】因为函数是定义在上的单调函数且对任意的都有所以是一个定值设所以所以或（舍去）所以所以所以所以函数在是增函数解析：2 【分析】先通过已知求出2()=+1,f x x 得到3()33F x x x =--，再利用导数研究得到函数()F x 在(0,1)内没有零点，函数()F x 的零点在(2,3)内，即得m 的值.【详解】因为函数()f x 是定义在(0,)+∞上的单调函数，且对任意的(0,)x ∈+∞都有2(())2f f x x -=，所以2()f x x -是一个定值，设2()f x x t -=，所以2()=+f x x t ，()2f t =所以2()=+2,1f t t t t =∴=或2t =-（舍去）. 所以2()=+1,()2f x x f x x '=，所以23()(1)22333F x x x x x x =+-⨯-=--，所以2()33=3(1)(1)F x x x x '=-+-，所以函数()F x 在(1,)+∞是增函数，在(0,1)是减函数，因为(0)30,(1)50F F =-<=-<,所以函数()F x 在(0,1)内没有零点.因为(2)86310,(3)2712150F F =--=-<=-=>,函数()F x 在(1,)+∞是增函数，所以函数()F x 的零点在(2,3)内，所以2m =. 故答案为：2 【点睛】本题主要考查函数的单调性的应用，考查利用导数求函数的单调区间，考查利用导数研究零点问题，意在考查学生对这些知识的理解掌握水平和分析推理能力.16．【分析】求导后即可求得根据二次函数的性质可得再由恒成立问题的解决方法可得即可得解【详解】求导得则当时函数单调递减；当时函数单调递增；所以；函数为开口向下对称轴为的二次函数所以当时；由题意可知即故答案解析：11a e≤--【分析】求导后即可求得()()11f x f ee --≥=-，根据二次函数的性质可得()()11g x g a ≤=+，再由恒成立问题的解决方法可得11a e -+≤-，即可得解. 【详解】求导得()ln 1f x x '=+，则当()10,x e -∈时，()0f x '<，函数()f x 单调递减；当()1,x e -∈+∞时，()0f x '>，函数()f x 单调递增；所以()()11f x f e e--≥=-；函数()22g x x x a =-++为开口向下，对称轴为1x =的二次函数，所以当()0,x ∈+∞时，()()11g x g a ≤=+；由题意可知11a e -+≤-即11a e -≤--. 故答案为：11a e -≤--. 【点睛】本题考查了利用导数解决不等式恒成立问题，考查了推理能力，属于中档题.17．【分析】求导得转化条件为在区间内恒成立令求导后求得即可得解【详解】函数在区间内是减函数在区间内恒成立即在区间内恒成立令则当时单调递减；当时单调递增；又故答案为：【点睛】本题考查了导数的综合应用考查了解析：2a ≥【分析】求导得2()321f x x ax '=++，转化条件为1223x x a --≥在区间21,33⎛⎫-- ⎪⎝⎭内恒成立，令()12122333x g x x x ⎛⎫--≤≤-= ⎝-⎪⎭，求导后求得()max 2g x =即可得解. 【详解】32()1f x x ax x =+++，∴2()321f x x ax '=++，函数()f x 在区间21,33⎛⎫-- ⎪⎝⎭内是减函数， ∴()0f x '≤在区间21,33⎛⎫-- ⎪⎝⎭内恒成立，即1223x x a --≥在区间21,33⎛⎫-- ⎪⎝⎭内恒成立，令()12122333x g x x x ⎛⎫--≤≤-= ⎝-⎪⎭，则()2221312232x x x x g -++='=-，∴当2,3x ⎛∈- ⎝⎭时，()0g x '<，()g x 单调递减；当13x ⎛⎫∈- ⎪ ⎪⎝⎭时，()0g x '>，()g x 单调递增；又2734g ⎛⎫-= ⎪⎝⎭，123g ⎛⎫-= ⎪⎝⎭，∴()2g x <，∴2a ≥.故答案为：2a ≥. 【点睛】本题考查了导数的综合应用，考查了运算求解能力与推理能力，属于中档题.18．【分析】构造函数讨论单调性和奇偶性结合特殊值即可求解【详解】设函数是偶函数所以函数是奇函数且当时即当时单调递减所以当时当时是偶函数所以当时当时所以使得成立的的取值范围是故答案为：【点睛】此题考查利用解析：()()1,00,1-⋃【分析】构造函数()()f x F x x=，讨论单调性和奇偶性，结合特殊值即可求解. 【详解】设函数()()f x F x x =，()f x 是偶函数，()()()()f x f x F x F x x x--=-=-=-，所以函数()F x 是奇函数，且()()()()1110,10F f f F ==-=-=，当0x >时，()2()()0xf x f x F x x'-'=<，即当0x >时，()F x 单调递减，()01F =，所以当01x <<时，()()0f x F x x=>，()0f x >，当1x >时，()()0f x F x x=<，()0f x <， ()f x 是偶函数，所以当10x -<<时，()0f x >，当1x <-时，()0f x <，所以使得()0f x >成立的x 的取值范围是()()1,00,1-⋃. 故答案为：()()1,00,1-⋃ 【点睛】此题考查利用导函数讨论函数的单调性解决不等式相关问题，关键在于准确构造函数，需要在平常的学习中多做积累，常见的函数构造方法.19．【分析】求出由已知可得为的两根求出关系并将用表示从而把表示为关于的函数设为利用的单调性即可求解【详解】因为的定义域为令即因为存在使得且即在上有两个不相等的实数根且所以∴令则当时恒成立所以在上单调递减解析：4e【分析】求出()f x '，由已知可得,m n 为()0f x '=的两根，求出,,m n a 关系，并将,n a 用m 表示，从而把()()f m f n -表示为关于m 的函数设为()h m ，利用()h m 的单调性，即可求解. 【详解】因为()1ln f x x a x x=-+的定义域为()0,∞+， ()22211'1a x ax x x xf x ++=++=，令()'0f x =，即210x ax ++=，()0,x ∈+∞，因为存在m ，n ，使得()()''0f m f n ==，且10,m e⎛⎤∈ ⎥⎝⎦，即210x ax ++=在()0,x ∈+∞上有两个不相等的实数根m ，n ，且m n a +=-，1⋅=m n ，所以1n m =，1a m m=--， ∴()()11111ln ln f m f m m m m m m m m m m n ⎛⎫⎛⎫=-+---+--- ⎪ ⎪-⎝⎭⎝⎭ 11l 2n m m m m m ⎡⎤⎛⎫---+ ⎪⎢⎥⎝⎭⎣⎦=，令()112ln h m m m m m m ⎡⎤⎛⎫=--+- ⎪⎢⎥⎝⎭⎣⎦，则()()()22211121ln l 'n m m m m h m m m -+⎛⎫=-=⎪⎝⎭，当10,m e⎛⎤∈ ⎥⎝⎦时，()'0h m <恒成立，所以()h m 在10,m e ⎛⎤∈ ⎥⎝⎦上单调递减，∴()min 14h m h e e ⎛⎫== ⎪⎝⎭，即()()f m f n -的最小值为4e. 故答案为：4e. 【点睛】本题考查最值问题、根与系数关系、函数的单调性，应用导数是解题的关键，意在考查逻辑推理、计算求解能力，属于中档题.20．【分析】求得在处的切线的斜率结合图像求得的取值范围【详解】函数对于一次函数令解得（负根舍去）所以在上递增在上递减画出的图像如下图所示由图可知要使当时恒成立只需大于或等于在处切线的斜率而所以故答案为：解析：[1,)+∞【分析】求得()f x 在0x =处的切线的斜率，结合图像，求得a 的取值范围. 【详解】函数()2()1xf x x e =-，()01f =.对于一次函数()()10g x ax a =+>，()01g =.()()'221,0x f x xx e x =--+⋅≥，令'0f x，解得01x （负根舍去），所以()f x 在()00,x 上递增，在()0,x +∞上递减，画出()f x 的图像如下图所示.由图可知，要使当0x ≥时，()1(0)f x ax a ≤+>恒成立，只需a 大于或等于()f x 在0x =处切线的斜率.而()'01f=，所以1a ≥.故答案为：[1,)+∞【点睛】本小题主要考查利用导数求解不等式恒成立问题，考查数形结合的数学思想方法，属于中档题.三、解答题21．（1）21ln ()x x f x x+=；（2）12a ≥. 【分析】（1）求导3ln 4()x x x a f x x --'=，由已知得(1)1f '=-，求出12a =得解（2）求导2()34g x x x '=-得到()g x 在(12)32，上的最大值为1()12g = 转化11()1,x f x ⋅≥ 得到1112ln a x x x ≥-在113[,]22x ∈恒成立.构造函数1111()ln ,h x x x x =-求得1()h x 的最大值为(1)1h =，得解【详解】（1）3ln 4()x x x af x x --'=，∵曲线()y f x =在点(1,(1))f 处的切线与30x y -+=垂直，∴(1)1f '=-， 12a ∴=.21ln ()x x f x x +∴= （2）2()34g x x x '=-，∴14(,)23x ∈，()0g x '<，43(,)32x ∈，()0g x '>，∴()g x 在14(,)23上递减，在43(,)32上递增， ∴()g x 在14(,)23上的最大值为131()1,()224g g ==较大者，即()1g x ≤， ∵对于任意的113[,]22x ∈，都有112()()x f x g x ⋅≥成立， ∴11()1,x f x ⋅≥ 1112ln 1,a x x x +∴≥ 即对任意的111113(,),2ln 22x a x x x ∈≥-成立. 令1111()ln ,h x x x x =-，11()ln h x x '=-，∴11(,1)2x ∈，1()0h x '>，13(1,)2x ∈，1()0h x '<，∴1()h x 在1(,1)2上递增，在3(1,)2上递减，1()h x 的最大值为(1)1h =， ∴21a ≥，12a ≥. 【点睛】本题考查函数导数几何意义及利用导数研究函数最值及不等式恒成立求参数范围.属于基础题.22．（1）230x e y e +-=（2）(,0]-∞ 【详解】试题分析：（1）先求函数导数，再根据导数几何意义得切线斜率为()'f e ，最后根据点斜式求切线方程（2）构造函数()()2ln 1g x x a x =--，利用导数并按0a ≤，10<2a <，12a ≥进行分类讨论，通过函数的单调性以及最值进行与0比较，可得结果. 试题（1）根据题意可得，()2f e e=， ()2ln 'xf x x -=，所以()22ln 1'e f e e e -==-，即21k e=-，所以在点()(),e f e 处的切线方程为()221y x e e e-=--，即230x e y e +-=．（2）根据题意可得，()()()221ln 110a x x a x f x x x x-----=≥在1≥x 恒成立，令()()2ln 1g x x a x =--，()1x ≥，所以()12g x ax x-'=，当0a ≤时，()0g x '>，所以函数()y g x =在[)1,+∞上是单调递增，所以()()10g x g ≥=，所以不等式()()21a x f x x->成立，即0a ≤符合题意；当0a >时，令120ax x-=，解得x =1=，解得12a =，当10<2a <1，所以()g x '在⎛ ⎝上()0g x '>，在+⎫∞⎪⎪⎭上()0g x '<，所以函数()y g x =在⎛ ⎝上单调递增，在+⎫∞⎪⎪⎭上单调递减，21111ln 1ln g a a a a a a a ⎛⎫⎛⎫⎛⎫=--=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令()1ln h a a a a =--+，()222111'10a a h a a a a-+=-++=>恒成立，则()h a 在10,2⎛⎫ ⎪⎝⎭单调递增所以()1111ln 2ln2202222h a h ⎛⎫<=--+=+-<⎪⎝⎭，所以存在10g a ⎛⎫< ⎪⎝⎭，所以102a <<不符合题意；②当12a ≥1≤ ()0g x '≤在[)1,+∞上恒成立，所以函数()y g x =在[)1,+∞上是单调递减，所以()()10g x g ≤= 显然12a ≥不符合题意；综上所述，a 的取值范围为{}|0a a ≤ 23．（1）1ln ,22a ⎛⎫+∞⎪⎝⎭（2）32a e >【分析】（1）直接求出函数的导函数，令()0f x '>，解不等式即可；（2）由题意容易知道2102222a ln a a a f ln e ln a ⎛⎫=-+< ⎪⎝⎭，解出即可求得实数a 的取值范围；【详解】解：（1）因为()2x f x e ax b =-+所以()()220x f x e a a '=->，令()0f x '>，得1ln 22a x >，∴函数()f x 的单调递增区间为1ln ,22a ⎛⎫+∞ ⎪⎝⎭（2）由（1）知，函数()f x 在1,ln 22a ⎛⎫-∞ ⎪⎝⎭递减，在1ln ,22a ⎛⎫+∞ ⎪⎝⎭递增， ∴x →-∞时，()f x →+∞；x →+∞，()f x →+∞，∵函数()f x 有两个零点12,x x ，∴1ln 022a f ⎛⎫< ⎪⎝⎭，又a b =， ∴ln 21ln ln 02222a a a a f e a ⎛⎫=-+< ⎪⎝⎭，即ln 0222a a a a -+< 所以3ln02a -< 所以32a e >【点睛】本题考查利用导数研究函数的单调性及最值问题，考查导数中零点问题，考查转化思想及运算求解能力，属于中档题．24．（1）1a =-或32a =；（2）答案不唯一，具体见解析；（3）证明见解析. 【分析】（1）利用导数几何意义列方程解得结果；（2）先求导函数，再根据a 的正负分类讨论，对应确定导函数符号，进而确定单调性；（3）根据（2）单调性确定()g a 解析式，再利用导数求()g a 最大值，即证得结果.【详解】（1）()f x 的定义域为(0,)+∞，222()1a a f x x x =-+'，根据题意有(1)2f '=-，则2230a a --=，解得1a =-或32a =；（2）22222222()(2)()1a a x ax a x a x a f x x x x x+--+=-'+==，①当0a >时，∵0x >，由()0f x '>得()(2)0x a x a -+>，解得x a >，由()0f x '<得()(2)0x a x a -+<，解得0x a <<，∴()f x 在(,)a +∞上单调递增，在(0,)a 上单调递减，②当0a <时，∵0x >，由()0f x '>得()(2)0x a x a -+>，解得2x a >-，由()0f x '<得()(2)0x a x a -+<，解得02x a <<-，∴()f x 在(2,)a -+∞上单调递增，在(0,2)a -上单调递减，（3）证明：由（2）知，当(,0)a ∈-∞时()f x 的最小值为(2)-f a ，即22()(2)ln(2)2ln(2)32a g a f a a a a a a a a=-=⋅-+-=⋅---， 2()ln(2)3ln(2)22g a a a a a -=-+⋅=-'---，令()0g a '=，得212a e =-，当21(,)2a e ∈-∞-时()0g a '>，当21(,0)2a e ∈-时()0g a '<，则212a e =-是()g a 在(,0)-∞上的唯一极值点，且是极大值点，从而也是()g a 的最大值点， ∴22222max 11111()()ln[2()]3()22222g a g e e e e e =-=-⋅-⨯--⨯-=， ∴当(,0)a ∈-∞时，21()2g a e ≤恒成立. 【点睛】本题考查导数几何意义、利用导数求单调性、利用导数求函数最值与证不等式，考查综合分析求解与论证能力，属中档题.25．（1）210x y -+=；（2）4927. 【分析】(1）利用导数的几何意义求切线的斜率，再利用点斜式方程即可求出切线方程。

高中数学选修2-2综合测试题与答案.doc

选修 2-2 综合测试题2一、选择题1．在数学归纳法证明“1 a a2an 1 a n 1(a，N ) ”时，验证当 n1时，等式的左1 n1 a边为（）Ａ． 1Ｂ． 1aＣ． 1 aＤ． 1 a22．已知三次函数f ( x)1 x 3 (4 m 1)x 2(15m22m7) x 2 在 x ( ∞ ， ∞ ) 上是增函数，则 m 的3取值范围为（）Ａ． m 2 或 m4Ｂ． 4 m2Ｃ． 2 m 4 Ｄ．以上皆不正确3．设 f ( x)( axb)sin x(cxd )cos x ，若 f ( x) x cosx ，则 a ， b ， c ， d 的值分别为（）Ａ． 1，1，0， 0Ｂ． 1，0，1，0Ｃ． 0，1，0，1Ｄ． 1，0，0，14．已知抛物线 y ax2 bx c 通过点 P(11)，，且在点 Q(2， 1) 处的切线平行于直线 yx 3，则抛物线方程为（）Ａ． y 3x211x 9Ｂ． y3x211x9Ｃ． y 3x211x 9Ｄ． y3x 2 11x92a n ，0≤ a n ≤1，26，则 a 2004 的值为（5．数列 a n满足 a n 11若 a 1）2a ≤ a n，7n，112Ａ．6Ｂ． 5Ｃ．3Ｄ．177776．已知 a ， b 是不相等的正数，x a b， ya b ，则 x ， y 的关系是（）2Ａ． x yＢ． yxＣ． x2 yＤ．不确定7．复数 zm 2i( m R) 不可能在（）1 2iＡ．第一象限Ｂ．第二象限Ｃ．第三象限Ｄ．第四象限8．定义A B，B C， C D， D A 的运算分别对应下图中的（1），（2），（3），（4），那么，图中（Ａ），（Ｂ）可能是下列（）的运算的结果Ａ． B D，A DＢ．B D，A CＣ．B C，A DＤ．C D，A D- 1 -9．用反证法证明命题“a， b N ，如果 ab 可被5整除，那么 a ， b 至少有1个能被5整除．”则假设的内容是（）Ａ． a ， b 都能被5整除Ｂ． a ， b 都不能被 5 整除Ｃ． a 不能被5整除Ｄ． a ， b 有 1 个不能被 5 整除10．下列说法正确的是（）Ａ．函数Ｃ．函数y x 有极大值，但无极小值Ｂ．函数y x 既有极大值又有极小值Ｄ．函数y x 有极小值，但无极大值y x 无极值11．对于两个复数 1 3 i ， 1 3 i，有下列四个结论：① 1 ；② 1 ；③ 1 ；2 2 2 2④33 1）．其中正确的个数为（Ａ． 1 Ｂ． 2 Ｃ． 3 Ｄ． 412．设f ( x)在[ a，b]上连续，则 f ( x)在[ a，b]上的平均值是（）Ａ． f ( a) Ｂ． b Ｃ．1Ｄ．f (b) f (x)dx b f ( x) dx 1 b f ( x)dx2 a 2 a b a a二、填空题13．若复数z log2( x23x 3) i log 2 ( x 3) 为实数，则x 的值为．14．一同学在电脑中打出如下图形（○表示空心圆，●表示实心圆）○●○○●○○○●○○○○●若将此若干个圆依此规律继续下去，得到一系列的圆，那么前2006 年圆中有实心圆的个数为．15．函数f ( x) ax36ax 2b(a0) 在区间 [ 1，2] 上的最大值为，最小值为29 ，则 a ， b 的值分3别为．16．由y2 4 x 与直线 y 2 x 4 所围成图形的面积为．三、解答题n n17．设n N且sin x cos x 1 ，求 sin x cos x 的值．（先观察 n 1，2，3，4 时的值，归纳猜测sin n x cos n x 的值．）18．设关于x的方程x2(tan i ) x (2 i)0 ，（1）若方程有实数根，求锐角和实数根；- 2 -（2）证明：对任意πkπ (k Z ) ，方程无纯虚数根．219．设t0 ，点 P(t，0) 是函数 f (x) x 3ax 与 g( x) bx 2 c 的图象的一个公共点，两函数的图象在点 P 处有相同的切线．（1）用t表示a，b，c；（ 2）若函数y f (x) g ( x)在( 1，3)上单调递减，求 t 的取值范围．20．下列命题是真命题，还是假命题，用分析法证明你的结论．命题：若 a b c，且 a b c0 ，则 b 2 ac3 ．a21．某银行准备新设一种定期存款业务，经预测，存款量与利率的平方成正比，比例系数为k(k0) ，且知当利率为0.012 时，存款量为 1.44 亿；又贷款的利率为 4.8% 时，银行吸收的存款能全部放贷出去；若设存款的利率为x ， x (0 ，0.048) ，则当 x 为多少时，银行可获得最大收益？22．已知函数 f ( x)x，数列 a n 满足 a1 f ( x) ， a n 1f (a n ) ．( x 0)1 x2（1）求a2，a3，a4；（2）猜想数列an的通项，并予以证明．参考答案一、选择题： CCDAC,BABBBD二、填空题： 13、4， 14 、61， 15 、 2,3 16、917、解：当n 1 时， sin x cosx 1 ；当 n 2 时，有 sin 2 x cos 2 x 1 ；当 n 3 时，有 sin 3 x cos 3 x (sin x cos x)(sin 2 x cos 2 x sin xcos x) ，而 sin x cos x 1 ，∴1 2sin x cos x 1 ， sin xcos x 0 ．∴ sin3 x cos 3 x1 ．当 n 4 时，有 sin 4 x cos 4 x (sin 2 x cos2 x) 2 2sin 2 xcos 2 x 1 ．由以上可以猜测，当n N时，可能有sin n x cos n x( 1) n成立．18、解：（ 1）设实数根为a，则a2(tan i )a (2 i ) 0 ，即(a2a tan2) (a1)i 0 ．R ，那么a 2 ，a ， a 1，由于 a ， tan a tan tan 2 0 ．又 0 π，得πa 1 1 tan 1 2 ．4- 3 -（2）若有纯虚数根i(R ) ，使 ( i) 2 (tan)(i ) i (2 ) i 0 ，即 ( 2 2) ( tan 1) i0 ，22 ，由， tan R ，那么，0 由于2 2 0 无实数解．tan 1 0故对任意πZ ) ，方程无纯虚数根kπ (k219、解：（ 1）因为函数 f ( x) ， g (x) 的图象都过点 (t，0) ，所以 f (t ) 0 ，即 t 3 at 0 ．因为 t 0 ，所以 a t 2．g (t ) 0 ，即 bt 2 c 0 ，所以 c ab ．又因为 f ( x) ， g (x) 在点 (t，0) 处有相同的切线，所以 f (t )g (t ) ，而 f ( x) 3x 2 a ， g (x)2bx ，所以 3t 2 a 2bt ．将 a t 2代入上式得 b t ．因此c ab t 3．故a t2， b t ， c t 3．（2）y f (x)g (x) x3t 2 x tx 2t 3， y3x22tx t 2(3 x t )( x t ) ．当 y(3x t )( x t) 0 时，函数 y f ( x) g (x) 单调递减．由 y 0 ，若 t 0 ，则tt ；x3若 t 0 ，则 t x t ．3，t( 1，3) t ，( 13)，由题意，函数 y f ( x) g (x) 在 ( 1，3) 上单调递减，则 3 t或t 3．所以 t ≤9 或 t ≥ 3 ．又当 9 t 3时，函数y f (x) g( x)在( 1，3)上不是单调递减的．所以 t 的取值范围为∞， 9 3，∞．20、解：此命题是真命题．∵ a b c 0 ， a b c ，∴ a0 ， c 0 ．b 2ac 2 2 2 2 2要证a3 成立，只需证bac 3a ，即证 b ac 3a ，也就是证 ( a c) ac 3a ，即证 ( a c)(2 a c) 0 ．∵ a c 0 ， 2a c ( a c)a b a 0 ，∴ (a c)(2 ac) 0 成立，故原不等式成立．21、解：由题意，存款量 f (x) kx2，又当利率为0.012 时，存款量为 1.44 亿，即x 0.012 时，；由2，得，那么 2 ，银行应支付的利息y 1.44 1 . 4 4 k ·(0.012) k 10000 f ( x)1 0 0 0x 0g (x) x·f (x) 10000x 3 ，- 4 -设银行可获收益为 y ，则 y480x 2 10000x 3，由于 y960x 30000x 2，则 y0 ，即 960x30000x20 ，得 x 0 或 x 0.032 ．因为， x(0，0.032) 时， y0 ，此时，函数y480x 2 10000x 3递增；x (0.032 ， 0.048) 时， y 0 ，此时，函数y480x 2 10000x 3递减；故当 x 0.032 时， y 有最大值，其值约为0.164亿．axx22、解：（ 1）由 a 12， f (x) ，得 a 2f (a 1 )1a21 x1 2 x 2 1211xx21x a 3 f (a 2 )a 2 a 21 2 x21221x2x 21xa 3 1 3x2a 4 f (a 3 )a 21231x3x 21x13x 2 x14x2，．（2）猜想： a nxN ) ，(n1 nx2证明：（ 1）当 n 1 时，结论显然成立；（2）假设当 nk 时，结论成立，即 a kx ；kx 21x那么，当 n k 1 时，由 a k 1f (a k )1 kx2x，1x 2 1 (k1)x2kx 21这就是说，当 nk1 时，结论成立；由（ 1），（ 2）可知， a nx 对于一切自然数 n( nN ) 都成立．1 nx 2- 5 -。

湘教版高中数学选修2-2综合检测卷(附答案)

湘教版高中数学选修2-2综合检测卷（附答案）一、单选题1．若复数满足，则在复平面上对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．已知复数（为虚数单位），那么的共轭复数为（）A．B．C．D．3．若曲线在处的切线，也是的切线，则（）A．B．C．D．4．设为虚数单位, ,则复数A ．B．C．D．5．设a为实数，函数的导函数，且是偶函数，则曲线在点处的切线方程为（）A．B．C．D．6．设是奇函数的导函数，当时，，则使得成立的的取值范围是（）A．B．C．D．7．由和围成的封闭图形的面积是（）A． B． C． D．8．下列函数求导运算正确的个数为( )①(3x)′＝3x log3e；①(log2x)′＝；①(e x)′＝e x；①()′＝x；①(x·e x)′＝e x＋1.A．1B．2C．3D．49．已知数列：…依它的前10项的规律，这个数列的第2019项满足（）A ．B．C．D．10．已知，则复数在复平面上对应点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限二、多选题11．定义在的函数，已知是它的极大值点，则以下结论正确的是（）A ．是的一个极大值点B．是的一个极小值点C ．是的一个极大值点D．是的一个极小值点12．已知函数，，则下列说法正确的有（）A．是偶函数B．是周期函数C．在区间上，有且只有一个极值点D．过(0，0)作的切线，有且仅有3条三、填空题13．对于大于1的自然数m，其三次幂可用奇数按一下方式进行“分裂”：对此，若的“分裂数”中有一个是2017，则m=_____. 14．如图，在中，，，，过点作延长线的垂线交延长线于点，过点作延长线的垂线交延长线于点，如此继续下去，设的面积为，的面积为，的面积为，…，以此类推，则_______．。

高中数学模块综合评价(二)(含解析)新人教A版选修2-2-新人教A版高二选修2-2数学试题

模块综合评价(二)(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求)1．(1＋i)16－(1－i)16＝() A ．－256B ．256i C ．0 D ．256解析：(1＋i)16－(1－i)16＝[(1＋i)2]8－[(1－i)2]8＝(2i)8－(－2i)8＝0. 答案：C2．已知函数f (x )＝ln x －x ，则函数f (x )的单调递减区间是() A ．(－∞，1) B ．(0，1)C ．(－∞，0)，(1，＋∞)D ．(1，＋∞)解析：f ′(x )＝1x －1＝1－xx，x >0.令f ′(x )<0，解得x >1.答案：D3．设f (x )＝10x＋lg x ，则f ′(1)等于( ) A ．10 B ．10ln 10＋lg e C.10ln 10＋ln 10 D ．11ln 10解析：f ′(x )＝10x ln 10＋1x ln 10，所以f ′(1)＝10ln 10＋1ln 10＝10ln 10＋lg e. 答案：B4．若函数f (x )满足f (x )＝e xln x ＋3xf ′(1)－1，则f ′(1)＝() A ．－e 2B ．－e3C ．－eD ．e解析：由已知可得f ′(x )＝e xln x ＋exx＋3f ′(1)，令x ＝1，则f ′(1)＝0＋e ＋3f ′(1)，解得f ′(1)＝－e2.答案：A5．用反证法证明命题：“若a ，b ∈N ，ab 能被3整除，那么a ，b 中至少有一个能被3整除”时，假设应为( )A ．a ，b 都能被3整除B ．a ，b 都不能被3整除C ．a ，b 不都能被3整除D ．a 不能被3整除解析：因为“至少有一个”的否定为“一个也没有”．答案：B6．若a ＞0，b ＞0，且函数f (x )＝4x 3－ax 2－2bx ＋2在x ＝1处有极值，则ab 的最大值等于( )A ．2B ．3C ．6D ．9解析：因为f ′(x )＝12x 2－2ax －2b ，又因为在x ＝1处有极值，所以a ＋b ＝6，因为a ＞0，b ＞0，所以ab ≤⎝⎛⎭⎪⎫a ＋b 22＝9，当且仅当a ＝b ＝3时取等号，所以ab 的最大值等于9.答案：D7．观察数列1，2，2，3，3，3，4，4，4，4，…的特点，按此规律，则第100项为( ) A ．10B ．14C ．13D ．100解析：设n ∈N *，则数字n 共有n 个，所以n （n ＋1）2≤100，即n (n ＋1)≤200，又因为n ∈N *，所以n ＝13，到第13个13时共有13×142＝91项，从第92项开始为14，故第100项为14.答案：B8．某工厂要建造一个长方体的无盖箱子，其容积为48 m 3，高为3 m ，如果箱底每平方米的造价为15元，箱侧面每平方米的造价为12元，则箱子的最低总造价为()A ．900元B ．840元C ．818元D ．816元解析：设箱底一边的长度为x m ，箱子的总造价为l 元，根据题意，得l ＝15×483＋12×2⎝ ⎛⎭⎪⎫3x ＋48x ＝240＋72⎝ ⎛⎭⎪⎫x ＋16x (x >0)，l ′＝72⎝ ⎛⎭⎪⎫1－16x 2.令l ′＝0，解得x ＝4或x ＝－4(舍去)．当0<x <4时，l ′<0；当x >4时，l ′>0.故当x ＝4时，l 有最小值816.因此，当箱底是边长为4 m 的正方形时，箱子的总造价最低，最低总造价为816元．故选D.答案：D8．某工厂要建造一个长方体的无盖箱子，其容积为48 m 3，高为3 m ，如果箱底每平方米的造价为15元，箱侧面每平方米的造价为12元，则箱子的最低总造价为()A ．900元B ．840元C ．818元D ．816元解析：设箱底一边的长度为x m ，箱子的总造价为l 元，根据题意，得l ＝15×483＋12×2⎝ ⎛⎭⎪⎫3x ＋48x ＝240＋72⎝ ⎛⎭⎪⎫x ＋16x (x >0)，l ′＝72⎝ ⎛⎭⎪⎫1－16x 2.令l ′＝0，解得x ＝4或x ＝－4(舍去)．当0<x <4时，l ′<0；当x >4时，l ′>0.故当x ＝4时，l 有最小值816.因此，当箱底是边长为4 m 的正方形时，箱子的总造价最低，最低总造价为816元．答案：D10．证明不等式n 2＋n ≤n ＋1(n ∈N *)，某学生的证明过程如下： (1)当n ＝1时，12＋1≤1＋1，不等式成立；(2)假设n ＝k (k ∈N *且k ≥1)时，不等式成立，即 k 2＋k ≤k ＋1，则当n ＝k ＋1时，（k ＋1）2＋（k ＋1）＝ k 2＋3k ＋2≤k 2＋3k ＋2＋（k ＋2）＝（k ＋2）2＝(k ＋1)＋1.所以当n ＝k ＋1时，不等式成立．上述证法( ) A ．过程全都正确 B ．n ＝1时验证不正确 C ．归纳假设不正确D ．从n ＝k 到n ＝k ＋1的推理不正确解析：验证及归纳假设都正确，但从n ＝k 到n ＝k ＋1的推理中没有使用归纳假设，而是通过不等式的放缩法直接证明，不符合数学归纳法的证题要求．故应选D.答案：D11.已知函数f (x )满足f (0)＝0，导函数f ′(x )的图象如图所示，则f (x )的图象与x 轴围成的封闭图形的面积为( )A.13B.43 C ．2D.83解析：由f ′(x )的图象知，f ′(x )＝2x ＋2，设f (x )＝x 2＋2x ＋c ，由f (0)＝0知，c ＝0，所以f (x )＝x 2＋2x ，由x 2＋2x ＝0得x ＝0或x ＝－2. 故所求面积S ＝－∫0－2(x 2＋2x )d x ＝－⎝ ⎛⎭⎪⎫13x 3＋x 2|0－2＝43.答案：B12．已知定义在R 上的奇函数f (x )，设其导数为f ′(x )，当x ∈(－∞，0]时，恒有xf ′(x )<f (－x )，令F (x )＝xf (x )，则满足F (3)>F (2x －1)的实数x 的取值X 围为()A ．(－1，2) B.⎝⎛⎭⎪⎫－1，12C.⎝ ⎛⎭⎪⎫12，2D ．(－2，1) 解析：因为f (x )是奇函数，所以不等式xf ′(x )<f (－x )等价于xf ′(x )<－f (x )，即xf ′(x )＋f (x )<0，即F ′(x )<0.当x ∈(－∞，0]时，函数F (x )单调递减；由于F (x )＝xf (x )为偶函数，所以F (x )在[0，＋∞)上单调递增．所以F (3)>F (2x －1)等价于F (3)>F (|2x －1|)，即3>|2x －1|，解得－1<x <2. 答案：A二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．复数z ＝(1＋2i)(3－i)，其中i 为虚数单位，则z 的实部是________．解析：因为z ＝(1＋2i)(3－i)＝3－i ＋6i －2i 2＝5＋5i ，所以z 的实部是5. 答案：514．在△ABC 中，D 为边BC 的中点，则AO →＝12(AB →＋AC →)．将上述命题类比到四面体中去，得到一个类比命题：_______________．解析：将“△ABC ”类比为“四面体A BCD ”，将“D 为边BC 的中点”类比为“△BCD 的重心”，于是有类比结论：在四面体A BCD 中，G 为△BCD 的重心，则AG →＝12(AB →＋AC →＋AD →)．答案：在四面体A BCD 中，G 为△BCD 的重心，则AG →＝12(AB →＋AC →＋AD →)15．若函数f (x )＝x 2＋ax ＋1在x ＝1处取得极值，则a ＝____________.解析：f ′(x )＝2x （x ＋1）－（x 2＋a ）（x ＋1）2＝x 2＋2x －a （x ＋1）2，令f ′(x )＝0，则x 2＋2x －a ＝0，x ≠－1.又f (x )在x ＝1处取得极值，所以x ＝1是x 2＋2x －a ＝0的根，所以a ＝3.答案：316．下列四个命题中，正确的为________(填上所有正确命题的序号)． ①若实数a ，b ，c 满足a ＋b ＋c ＝3，则a ，b ，c 中至少有一个不小于1； ②若z 为复数，且|z |＝1，则|z －i|的最大值等于2； ③对任意x ∈(0，＋∞)，都有x >sin x ； ④定积分∫π0π－x 2d x ＝π24.解析：①若实数a ，b ，c 满足a ＋b ＋c ＝3，则用反证法证明，假设a ，b ，c 都小于1，则a ＋b ＋c <3，与已知矛盾，故可得a ，b ，c 中至少有一个不小于1，故①正确；②若z 为复数，且|z |＝1，则由|z －i|≤|z |＋|－i|＝2，可得|z －i|的最大值等于2，故②正确；③令y ＝x －sin x ，其导数为y ′＝1－cos x ，y ′≥0，所以y ＝x －sin x 在R 上为增函数，当x ＝0时，x －sin x ＝0，所以对任意x ∈(0，＋∞)，都有x －sin x >0，故③正确．④定积分∫π0π－x 2d x 表示以原点为圆心，π为半径的圆的面积的四分之一，故④正确．答案：①②③④三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知a ∈R，问复数z ＝(a 2－2a ＋4)－(a 2－2a ＋2)i 所对应的点在第几象限？复数z 对应点的轨迹是什么？解：由a 2－2a ＋4＝(a －1)2＋3≥3. －(a 2－2a ＋2)＝－(a －1)2－1≤－1. 知z 的实部为正数，虚部为负数，所以复数z 的对应点在第四象限．设z ＝x ＋y i(x ，y ∈R)，则⎩⎪⎨⎪⎧x ＝a 2－2a ＋4，y ＝－（a 2－2a ＋2），因为a 2－2a ＝(a －1)2－1≥－1，所以x ＝a 2－2a ＋4≥3，消去a 2－2a ，得y ＝－x ＋2(x ≥3)，所以复数z 对应点的轨迹是一条射线，其方程为y ＝－x ＋2(x ≥3)． 18．(本小题满分12分)设函数f (x )＝1x ＋2，a ，b ∈(0，＋∞)． (1)用分析法证明：f ⎝ ⎛⎭⎪⎫a b ＋f ⎝ ⎛⎭⎪⎫b a ≤23；(2)设a ＋b >4，求证：af (b )，bf (a )中至少有一个大于12.证明：(1)要证明f ⎝ ⎛⎭⎪⎫a b ＋f ⎝ ⎛⎭⎪⎫b a ≤23，只需证明1a b＋2＋1b a＋2≤23，只需证明b a ＋2b ＋ab ＋2a ≤23，即证b 2＋4ab ＋a 22a 2＋5ab ＋2b 2≤23，即证(a －b )2≥0，这显然成立，所以f ⎝ ⎛⎭⎪⎫a b ＋f ⎝ ⎛⎭⎪⎫b a ≤23.(2)假设af (b )，bf (a )都小于或等于12，即a b ＋2≤12，b a ＋2≤12，所以2a ≤b ＋2，2b ≤a ＋2，两式相加得a ＋b ≤4，这与a ＋b >4矛盾，所以af (b )，bf (a )中至少有一个大于12.19．(本小题满分12分)已知函数f (x )＝ex ＋2(x 2－3)．(1)求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)求函数y ＝f (x )的极值．解：(1)函数f (x )＝e x ＋2(x 2－3)，则f ′(x )＝ex ＋2(x 2＋2x －3)＝ex ＋2(x ＋3)(x －1)，故f ′(0)＝－3e 2，又f (0)＝－3e 2，故曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＋3e 2＝－3e 2(x －0)，即3e 2x ＋y ＋3e 2＝0.(2)令f ′(x )＝0，可得x ＝1或x ＝－3，如下表：↗↘↗所以当x ＝－3时，函数取极大值，极大值为f (－3)＝e ，当x ＝1时，函数取极小值，极小值为f (1)＝－2e 3.20．(本小题满分12分)已知函数f (x )＝12x 2＋ln x .(1)求函数f (x )在[1，e]上的最大值，最小值；(2)求证：在区间[1，＋∞)上，函数f (x )的图象在函数g (x )＝23x 3图象的下方．解：(1)由f (x )＝12x 2＋ln x 有f ′(x )＝x ＋1x ，当x ∈[1，e]时，f ′(x )>0，所以f (x )max ＝f (e)＝12e 2＋1.f (x )min ＝f (1)＝12.(2)设F (x )＝12x 2＋ln x －23x 3，则F ′(x )＝x ＋1x －2x 2＝（1－x ）（1＋x ＋2x 2）x，当x ∈[1，＋∞)时，F ′(x )<0，且F (1)＝－16<0故x ∈[1，＋∞)时F (x )<0，所以12x 2＋ln x <23x 3，得证．21．(本小题满分12分)已知函数f (x )＝12x 2＋(1－a )x －a ln x .(1)讨论f (x )的单调性；(2)设a >0，证明：当0<x <a 时，f (a ＋x )<f (a －x )； (3)设x 1，x 2是f (x )的两个零点，证明：f ′⎝ ⎛⎭⎪⎫x 1＋x 22>0.解：(1)f (x )的定义域为(0，＋∞)，由已知，得f ′(x )＝x ＋1－a －a x ＝x 2＋（1－a ）x －ax＝（x ＋1）（x －a ）x.若a ≤0，则f ′(x )>0，此时f (x )在(0，＋∞)上单调递增．若a >0，则令f ′(x )＝0，得x ＝a .当0<x <a 时，f ′(x )<0；当x >a 时，f ′(x )>0.此时f (x )在(0，a )上单调递减，在(a ，＋∞)上单调递增．综上，当a ≤0时，f (x )在(0，＋∞)上单调递增；当a >0时，f (x )在(0，a )上单调递减，在(a ，＋∞)上单调递增．(2)令g (x )＝f (a ＋x )－f (a －x )，则g (x )＝12(a ＋x )2＋(1－a )(a ＋x )－a ln(a ＋x )－ [12(a －x )2＋(1－a )(a －x )－a ln(a －x )]＝2x －a ln(a ＋x )＋a ln(a －x )．所以g ′(x )＝2－a a ＋x －aa －x ＝2x2x 2－a 2.当0<x <a 时，g ′(x )<0，所以g (x )在(0，a )上是减函数．而g (0)＝0，所以g (x )<g (0)＝0.故当0<x <a 时，f (a ＋x )<f (a －x )．(3)由(1)可知，当a ≤0时，函数f (x )至多有一个零点，故a >0，从而f (x )的最小值为f (a )，且f (a )<0. 不妨设0<x 1<x 2，则0<x 1<a <x 2，所以0<a －x 1<a . 由(2)得f (2a －x 1)<f (x 1)＝0＝f (x 2)，从而x 2>2a －x 1，于是x 1＋x 22>a .由(1)知，f ′⎝⎛⎭⎪⎫x 1＋x 22>0.22．(本小题满分12分)已知数列{a n }的前n 项和为S n ，且a 1＝1，S n ＝n 2a n (n ∈N *)． (1)试求出S 1，S 2，S 3，S 4，并猜想S n 的表达式； (2)用数学归纳法证明你的猜想，并求出a n 的表达式．解：(1)因为a n ＝S n －S n －1(n ≥2) 所以S n ＝n 2(S n －S n －1)，所以S n ＝n 2n 2－1S n －1(n ≥2) 因为a 1＝1，所以S 1＝a 1＝1. 所以S 2＝43，S 3＝32＝64，S 4＝85，猜想S n ＝2n n ＋1(n ∈N *)． (2)①当n ＝1时，S 1＝1成立．②假设n ＝k (k ≥1，k ∈N *)时，等式成立，即S k ＝2k k ＋1，当n ＝k ＋1时，S k ＋1＝(k ＋1)2·a k ＋1＝a k ＋1＋S k ＝a k ＋1＋2k k ＋1，所以a k ＋1＝2（k ＋2）（k ＋1），所以S k ＋1＝(k ＋1)2·a k ＋1＝2（k ＋1）k ＋2＝2（k ＋1）（k ＋1）＋1.所以n ＝k ＋1时等式也成立，得证．所以根据①、②可知，对于任意n ∈N *，等式均成立．由S n ＝n 2a n ，得2n n ＋1＝n 2a n ，所以a n ＝2n （n ＋1）.。

上海上海第中学高中数学选修2-2第四章《定积分》检测(包含答案解析)

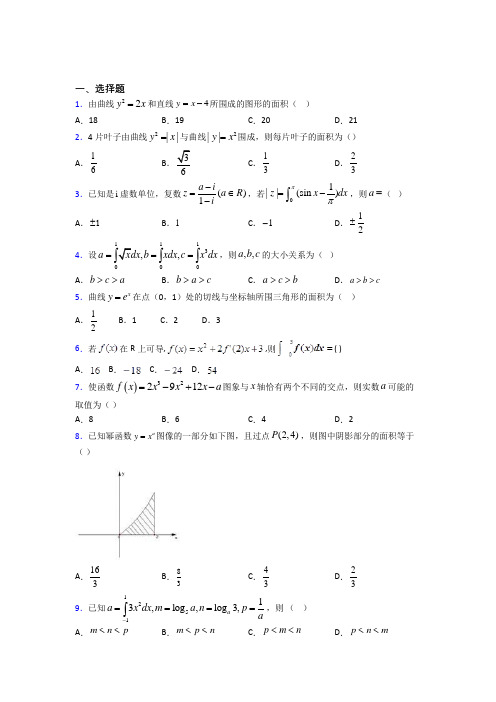
一、选择题1．由曲线22y x =和直线4y x =-所围成的图形的面积（）A ．18B ．19C ．20D ．212．4片叶子由曲线2||y x =与曲线2||y x =围成，则每片叶子的面积为（） A ．16B ．36C ．13D ．233．已知是i 虚数单位，复数()1a i z a R i -=∈-，若01||(sin )z x dx ππ=-⎰，则a =（）A ．±1B ．1C ．1-D ．12±4．设11130,,a xdx b xdx c x dx ===⎰⎰⎰，则,,a b c 的大小关系为（）A ．b c a >>B ．b a c >>C ．a c b >>D ．a b c >>5．曲线x y e =在点（0，1）处的切线与坐标轴所围三角形的面积为（） A ．12B ．1C ．2D ．3 6．若在R 上可导,,则( )A ．B ．C ．D ．7．使函数()322912f x x x x a =-+-图象与x 轴恰有两个不同的交点，则实数a 可能的取值为（） A ．8B ．6C ．4D ．28．已知幂函数a y x =图像的一部分如下图，且过点(2,4)P ，则图中阴影部分的面积等于（）A ．163B ．83C ．43D ．239．已知125113,log ,log 3,a a x dx m a n p a-====⎰，则（） A ．m n p << B ．m p n <<C ．p m n <<D ．p n m <<10．函数()22,04,02x x f x x x -<⎧⎪=⎨-≤≤⎪⎩，则22()f x dx -⎰的值为（）A ．6π+B ．2π-C ．2πD ．811．已知函数()[](]2sin ,,01,0,1x x f x x x π⎧∈-⎪=⎨-∈⎪⎩，则()1f x dx π-=⎰（） A ．2π+B ．2πC ．22π-+D ．24π-12．设21,[0,1]()1,[1,0)x x f x x x ⎧⎪-∈=⎨+∈-⎪⎩，则11()f x dx -⎰等于（）A ．12π+B ．122π+ C ．124π+ D ．14π+二、填空题13．021214edx x dx x-+-=⎰⎰______________.14．计算 121dx x--⎰=_____________． 15．如图所示，直线y kx =分抛物线2y x x 与x 轴所围图形为面积相等的两部分，则k的值为__________．16．已知曲线与直线所围图形的面积______.17．由曲线x y e x =+与直线0,1,0x x y ===所围成图形的面积等于________． 18．(1||214x ex dx --=⎰__________________19．)12111x dx --=⎰__________．20．曲线2y x =与直线230x y --=所围成的平面图形的面积为________.三、解答题21．已知函数()()322,f x x ax bx aa b =+++∈R .（1）若函数()f x 在1x =处有极值为10，求b 的值；（2）若()4,a f x =-在[]0,2x ∈上单调递增，求b 的最小值. 22．已知函数()32f x x ax =+图像上一点()1,P b 的切线斜率为3-，()()()3261302t g x x x t x t -=+-++> （Ⅰ）求,a b 的值；（Ⅱ）当[]1,4x ∈-时，求()f x 的值域；（Ⅲ）当[]1,4x ∈时，不等式()()f x g x ≤恒成立，求实数t 的取值范围.23．已知321()2f x x x ax =+-. （Ⅰ）当4a =时，求()f x 的极值；（Ⅱ）若()f x 在()1,3上不单调，求实数a 的取值范围.24．如图计算由直线y ＝6－x ，曲线8y x =以及x 轴所围图形的面积．25．一物体沿直线以速度()23v t t =-（t 的单位为:秒,v 的单位为:米/秒）的速度作变速直线运动，求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?26．已知函数()xae f x x x=+．（1）若函数()f x 的图象在(1,(1))f 处的切线经过点(0,1)-，求a 的值；（2）是否存在负整数a ，使函数()f x 的极大值为正值？若存在，求出所有负整数a 的值；若不存在，请说明理由；（3）设0a >，求证：函数()f x 既有极大值，又有极小值【参考答案】***试卷处理标记，请不要删除一、选择题1．A 解析：A 【分析】画出两曲线的图像，求得交点坐标，由定积分求得图形的面积即可. 【详解】根据题意，画出量曲线的图像，设其交点为,A B ，如下所示：联立22y x =和4y x =-，解得()()2,2,8,4A B -，根据抛物线的对称性，即可得两曲线围成的面积28222d (24)d S x x x x x =++⎰⎰23022021622d 2233x x x ⎛⎫⎰== ⎪⎝⎭ 82(24)d x x x +⎰83222212432x x x ⎫=-+⎪⎭322212884832⎫=⨯-⨯+⨯⎪⎭322213822242323⎫-⨯-⨯+⨯=⎪⎭故所求面积为28222d (24)d x x x x x ++⎰⎰163833=+18=.故选：A. 【点睛】本题考查由定积分求解曲边梯形的面积，需要注意的是，本题中需要对曲边梯形的面积进行拆分求解，这是本题的难点.2．C解析：C 【分析】先计算图像交点，再利用定积分计算面积. 【详解】如图所示：由2y x y x ⎧=⎪⎨=⎪⎩0,0,x y =⎧⎨=⎩11x y =⎧⎨=⎩，根据图形的对称性，可得每片叶子的面积为)13023210211d 333x x x x x ⎛⎫⎰=-= ⎪⎝⎭.故答案选C 【点睛】本题考查定积分的应用，考查运算求解能力3．A解析：A 【解析】因为11122a i a a z i i -+-==+-，所以222111()()22222a a z a +-=+=+式0011(sin )[cos ]|1x dx x x ππππ-=--=⎰22122112a a +=⇒=，即1a =±，应选答案A 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

选修 2-2 综合测试题 2一、选择题1．在数学归纳法证明“ 1 aa 2a n1 a n 1 (a 1， n N ) ”时，验证当 n 1 时，等式的左1 a边为（）Ａ． 1Ｂ． 1 aＣ． 1 aＤ． 1 a 22．已知三次函数 f ( x) 1 x 3 (4 m 1)x 2(15m 22m 7) x 2在 x ( ∞ ， ∞ ) 上是增函数，则 m 的3取值范围为（）Ａ． m 2 或 m4Ｂ． 4 m2Ｃ． 2 m 4 Ｄ．以上皆不正确3．设 f ( x) ( ax b)sin x (cx d )cos x ，若 f ( x)x cosx ，则 a ， b ， c ， d 的值分别为（）Ａ．1，1，0，0Ｂ． 1，0，1，0Ｃ． 0，1，0，1 Ｄ． 1，0，0，14．已知抛物线 y ax 2 bx c 通过点 P(11)，，且在点 Q(2， 1) 处的切线平行于直线 yx 3 ，则抛物线方程为（）Ａ． y 3x 211x 9Ｂ． y3x 2 11x9Ｃ． y 3x 211x 9Ｄ． y3x 211x9，1，5．数列 a n2a n0≤ a n ≤2若 a 16满足 a n 1，则 a 2004 的值为（）1≤ a n72a n，，112Ａ．6Ｂ．5Ｃ．3Ｄ．177776．已知 a ， b 是不相等的正数， xa2b， ya b ，则 x ， y 的关系是（）Ａ． x yＢ． yxＣ． x2 yＤ．不确定7．复数 zm 2i( m R ) 不可能在（）12iＡ．第一象限Ｂ．第二象限Ｃ．第三象限Ｄ．第四象限8．定义 A B ， B C ， C D ， D A 的运算分别对应下图中的（ 1），（2），（3），（4），那么，图中（Ａ），（Ｂ）可能是下列（）的运算的结果Ａ．B D ，ADＢ．B D ，ACＣ．B C ，ADＤ．C D ，AD9．用反证法证明命题“a， b N ，如果ab可被5整除，那么a，b至少有1个能被5整除．”则假设的内容是（）Ａ． a ， b 都能被5整除Ｂ．a，b都不能被5整除Ｃ． a 不能被5整除Ｄ．a，b有1个不能被5整除10．下列说法正确的是（）Ａ．函数Ｃ．函数y x 有极大值，但无极小值Ｂ．函数y x 既有极大值又有极小值Ｄ．函数y x 有极小值，但无极大值y x 无极值11．对于两个复数13i ，13i ，有下列四个结论：①1；② 1 ；③ 1 ；2222④331．其中正确的个数为（）Ａ． 1Ｂ． 2Ｃ． 3Ｄ． 412．设f ( x)在[ a，b]上连续，则 f ( x)在[ a，b]上的平均值是（）Ａ． f ( a) f (b)Ｂ．bＣ．1bＤ．1bf (x)dx f ( x) dx f ( x)dx2a2a b a a二、填空题13．若复数z log2( x23x3) i log 2 ( x3) 为实数，则 x 的值为．14．一同学在电脑中打出如下图形（○表示空心圆，●表示实心圆）○●○○●○○○●○○○○●若将此若干个圆依此规律继续下去，得到一系列的圆，那么前2006 年圆中有实心圆的个数为．15．函数f ( x) ax36ax2b(a0) 在区间 [1，2] 上的最大值为，最小值为29 ，则 a ， b 的值分3别为．16．由y2 4 x 与直线 y 2 x4所围成图形的面积为．三、解答题17．设n N 且sin x cos x1n x n1，2，3，4时的值，归纳猜测，求 sin cos x 的值．（先观察 nsin n x cos n x 的值．）18．设关于x的方程x2(tan i ) x (2 i)0 ，（1）若方程有实数根，求锐角和实数根；（2）证明：对任意πk π (k Z ) ，方程无纯虚数根．219．设 t 0 ，点 P(t ，0) 是函数 f (x) x 3 ax 与 g( x) bx 2c 的图象的一个公共点，两函数的图象在点 P 处有相同的切线．（ 1）用 t 表示 a ， b ， c ；（2）若函数 y f (x) g ( x) 在 ( 1，3) 上单调递减，求 t 的取值范围．20．下列命题是真命题，还是假命题，用分析法证明你的结论．命题：若 a b c ，且 a b c 0 ，则 b 2ac3 ．a21．某银行准备新设一种定期存款业务，经预测，存款量与利率的平方成正比，比例系数为k(k0) ，且知当利率为 0.012 时，存款量为 1.44 亿；又贷款的利率为 4.8%时，银行吸收的存款能全部放贷出去；若设存款的利率为 x ， x (0，0.048) ，则当 x 为多少时，银行可获得最大收益？22．已知函数 f ( x)x ，数列 a n 满足 a 1 f ( x) ， a n 1 f (a n ) ．( x 0) 1 x 2（1）求 a 2， a 3，a 4 ；（2）猜想数列 a n 的通项，并予以证明．参考答案一、选择题： CCDAC,BABBBD二、填空题： 13、4， 14 、61， 15 、 2,3 16 、 917、解：当 n 1 时， sin x cosx 1 ；当 n 2 时，有 sin 2 x cos 2 x 1 ；当 n 3 时，有 sin 3 x cos 3 x (sin x cos x)(sin 2 x cos 2 x sin xcos x) ，而 sin x cos x1 ，∴1 2sin x cos x 1 ， sin xcos x 0 ．∴ sin 3 x cos 3 x1 ．当 n 4 时，有 sin 4 x cos 4 x (sin 2 x cos 2 x) 2 2sin 2 xcos 2 x 1．由以上可以猜测，当 n N时，可能有 sin n x cos n x ( 1)n 成立．18、解：（ 1）设实数根为 a ，则 a 2 (tani )a (2 i ) 0 ，即 (a 2 a tan2) (a1)i 0 ．2， a ，a1，由于 a ， tanR ，那么 aa tan tan2 又 0π，得tan ．πa 1 112．4（2）若有纯虚数根i(R ) ，使 ( i) 2 (tan)(i ) i (2) i 0，即 (22) ( tan 1) i0 ，2 2，2由， tanR ，那么由于20 无实数解．tan 1，故对任意π Z ) ，方程无纯虚数根k π (k219、解：（ 1）因为函数 f ( x) ， g (x) 的图象都过点 (t ，0) ，所以 f (t ) 0 ，即 t 3 at 0 ．因为 t 0 ，所以 at 2 ． g (t ) 0 ，即 bt 2 c 0 ，所以 c ab ．又因为 f ( x)， g (x) 在点 (t ，0) 处有相同的切线，所以 f (t ) g (t ) ，而 f ( x) 3x 2a ， g (x) 2bx ，所以 3t 2 a 2bt ．将 at 2 代入上式得 b t ．因此 c ab t 3 ．故 at 2 ， b t ， ct 3 ．（2） y f (x) g (x) x 3 t 2 x tx 2 t 3， y 3x 2 2txt 2 (3 x t )( x t ) ．当 y (3x t )( x t) 0 时，函数 yf ( x)g (x) 单调递减．由 y0 ，若 t0 ，则t t ；x3若 t 0 ，则 t xt ．3由题意，函数 yf ( x)g (x) 在 (1，3) 上单调递减，则 ( 1，3)t ， t 或 ( 13)，， t．3t 3所以 t ≤ 9 或 t ≥ 3 ．又当 9t 3 时，函数 y f (x)g( x) 在 ( 1，3) 上不是单调递减的．所以 t 的取值范围为∞ ， 93，∞ ．20、解：此命题是真命题．∵ a b c 0 ， a b c ， ∴ a0 ， c 0 ．要证 b 2 ac3成立，只需证b 2ac3a ，即证 b 2ac 3a 2，也就是证 ( ac) 2 2aac 3a ，即证 ( a c)(2 a c) 0 ．∵ a c 0 ， 2a c ( a c) ab a 0 ，∴ (a c)(2 ac) 0成立，故原不等式成立．21、解：由题意，存款量 f (x)kx 2，又当利率为 0.012 时，存款量为 1.44 亿，即 x 0.012 时，y 1.44；由1 . 4 4 k · 2，得10000，那么f ( x)2，银行应支付的利息(0.012)k1 0 0 0x 0g (x) x ·f (x) 10000x 3，设银行可获收益为 y ，则 y 480x 210000x 3 ，由于 y 960x 30000x 2 ，则 y 0 ，即 960x 30000x 2 0 ，得 x 0 或 x 0.032 ．因为， x(0，0.032) 时， y0 ，此时，函数 y480x 2 10000x 3递增；x (0.032，0.048) 时， y 0 ，此时，函数 y 480x 2 10000x 3 递减；故当 x 0.032 时， y 有最大值，其值约为 0.164亿．x22、解：（ 1）由 a 1f (x) ，得 a 2f (a 1 )a1 x 2x ，11 2 x21 a2x2111x2xa 3f (a 2 )a 2 1 2 x 2x ，1 a 221 3x 2x212x 21xa 4f (a 3 )a 3 1 3x 2x．1 a 221 4x 2x313x 21 （2）猜想： a n x N ) ，(n1 nx 2证明：（1）当 n 1 时，结论显然成立；（2）假设当 nk 时，结论成立，即 a kx ；1 kx 2x那么，当 n k1 时，由 a k 1f (a k )1 kx 2x，1x 21 (k1)x 21 kx2这就是说，当 nk1 时，结论成立；由（ 1），（ 2）可知， a nx对于一切自然数 n( nN ) 都成立．1 nx 2。