9.7组合变形构件的强度
第八章 组合变形 构件的强度计算1

P
D1
=159.4MPa<[ ]
图示矩形截面梁,截面宽度b=90mm,高度h=180mm。 梁在两个互相垂直的平面内分别受有水平力F1和铅垂 力F2 。若已知F1=800N, F2=1650N, L =1m,试 求梁内的最大弯曲正应力并指出其作用点的位置。 M y = F1 L F2 M z = F2 L
或单向压缩),故:
FN M z ,max s max = + A Wz
强度条件
max≤ [ ]
例1
• 最大吊重P=8kN的起重机, AB杆的工字钢,材料为A3 钢,[]=100MPa,选择工 字钢型号。
“M”
“N”
Mmax=12kN· m
N=40kN
先按弯曲正应力选择工字钢型号; 再按组合变形的最大正应力校核强度,必要 时选择大一号或大二号的工字钢; 若剪力较大时,还需校核剪切强度。
-3
2
求内力(作用于截面形心) 取研究对象如图
N=P kN, -2 My =42.5´ 10 P kNm
危险截面 各截面相同 应力分布
危险截面 各截面相同 应力分布
N引起的应力
My引起的应力
N P = MPa σ¢ = A 15
σⅱ t max =
M y zo Iy M y z1 Iy
z
x
F1
L L
σ max =
My Wy
+
Mz Wz
组合变形构件的强度

第八章 组合变形构件的强度8.1概 述到现在为止,我们所研究过的构件,只限于有一种基本变形的情况,例如拉伸(或压缩)、剪切、扭转和弯曲。
而在工程实际中的许多构件,往往存在两种或两种以上的基本变形。
例如图8—1a 中悬臂吊车的横梁AB ,当起吊重物时,不仅产生弯曲,由于拉杆BC 的斜向力作用,而且还有压缩(图8—lb)。
又如图8—2a 所示的齿轮轴,若将啮合力P 向齿轮中心平移、则可简化成如图8—2b 所示的情况。
载荷P 使轴产生弯曲变形;矩为C m 和D m 的两个力偶则使轴产生扭转变形。
这些构件都同时存在两种基本变形,前者是弯曲与压缩的组合;后者则是弯曲与扭转的组合。
在外力作用下,构件若同时产生两种或两种以上基本变形的情况,就称为组合变形。
由于我们所研究的都是小变形构件,可以认为各载荷的作用彼此独立,互不影响,即任一载荷所引起的应力或变形不受其他载荷的影响。
因此,对组合变形构件进行强度计算,可以应用叠加原理,采取先分解而后综合的方法。
其基本步骤是:(1)将作用在构件上的载荷进行分解,得到与原载荷等效的几组载荷,使构件在每组载荷作用下,只产生一种基本变形;(2)分别计算构件在每种基本变形情况下的应力;(3)将各基本变形情况下的应力叠加,然后进行强度计算。
当构件危险点处于单向应力状态时,可将上述应力进行代数相加;若处于复杂应力状态,则需求出其主应力,按强度理论来进行强度计算。
本章将讨论弯曲与拉伸(或压缩)的组合以及弯曲与扭转的组合构件的强度问题。
8.2 弯曲与拉伸 (或压缩) 的组合在外力作用下,构件同时产生弯曲和拉伸(或压缩)变形的情况,称为弯曲与拉伸(或压缩)的组合变形。
图8—1所示悬臂吊的横梁同时受到横向载荷和纵向载荷的作用,这是弯曲与拉伸(或压缩)组合构件的一种受力情况。
在工程实际中,常常还遇到这样一种情况,即载荷与杆件的轴线平行,但不通过横截面的形心,此时,杆件的变形也是弯曲与拉伸(或压缩)的组合,这种情况通常称为偏心拉伸(或压缩)。
组合变形构件的强度计算

eP
Mz
P
z
y
h
b
竖杆的危险点在横截面的 内侧边缘处 ;
4、计算危险点处的正应力
tmax
FN A
Mz Wz
158MPa
tmax [ ]
立柱满足强度条件。
组合变形构件的强度计算
_+
z ++
_+
++
组合变形构件的强度计算
例2 铸铁压力机框架,立柱横截面尺寸如图所示, 材料的许用拉应力[]t=30MPa,许用压应力[]c=
吊斗上方的吊杆AE的各段均是38毫米×38毫米的正
方形截面,A、E两处铰接,且ED=BC=380毫米,
DC=1200毫米,BA=1650毫米。求吊杆AB、BC、
CD各段的最大拉应力。
E
D
B
C
A
组合变形构件的强度计算
7、矩形截面简支梁长度为L=2米,受均布载荷 q=30KN/m与拉力P=500KN的联合作用。求梁内 最大正应力和跨度中央截面处中性轴的位置。
22
min
x
y
2
1 2
x
y
2
4
2 xy
1 2 4 2 0
22
1
2
1 2
2 4 2
2 0
3
2
1 2
2 4 2
强度校核
r3 1 3
2 4 2 105MPa [ ], 安全。
组合变形构件的强度计算
组合变形构件的强度计算
1、在矩形截面杆的中间截面挖去t/2=5mm的槽。 P=10KN, 杆件的许用应力[σ]=160MPa。 校核杆件的强度。
P2 e bh2 6
组合变形时的强度计算

§84弯曲与扭转组合变形
一、单向弯曲与扭转组合变形
1.引例:以钢制摇臂轴为例。
①外力向形心简化(建立计算模型):
②作弯矩、扭矩图(找危险截面):
由弯矩图知:A截面|M|→max;全梁Mn处处相同,
∴A截面为危险截面:
|TMn AP|aPL
③危险截面的危险点:A截面K1、K2点,t、s数值均为最大,
⑤用强度准则进行强度计算
§8-2 两相互垂直平面内的弯曲
平面弯曲:对于横截面具有对称轴的梁,当横向外力或
外力偶作用在梁的纵向对称面内时,梁发生对称弯曲。这时, 梁变形后的轴线是一条位于外力所在平面内的平面曲线。
斜弯曲:双对称截面梁在水平和垂直两纵向对称平面内
同时承受横向外力作用的情况,这时梁分别在水平纵对称面
∴K1、K2点均为危险点:
K1点:
sstmax|M W A z|
tMn W n
K2点:sscmax|M W A z|
tMn W n
y
A d
z
L
Tn
_
PL
M
_
P C
B a x
P Pa
K1
st Pa
K1 A
t s
s K2 t
K2
ss t
s
Байду номын сангаас
④对危险点进行应力分析:(从K1、K2点取单元体,因它们的 s、t数值分别相同,危险程度也相同,不妨取K1点研究):
一、单向弯曲与扭转组合变形
④对危险点进行应力分析(s1≥s2≥s3)
在梁的任意横截面m—m上,由P1和P2引起的弯矩值依次为:
在梁的任意横截面m—m上,由P 和P 引起的弯矩值依次为: 试校核此夹具竖杆的强度。
材料力学复习考点

南通大学建工学院材料力学考点复习(个人自己参考一些资料,总结的复习考点)01 本章小结1.材料力学研究的问题是构件的强度、刚度和稳定性。
2.构成构件的材料是可变形固体。
3.对材料所作的基本假设是:均匀性假设,连续性假设及各向同性假设。
4.材料力学研究的构件主要是杆件,且是小变形杆件。
5.内力是指在外力作用下,物体内部各部分之间的相互作用;显示和确定内力可用截面法;应力是单位面积上的内力。
点应力可用正应力与剪应力表示。
6.对于构件任一点的变形,只有线变形和角变形两种基本变形。
7.杆件的四种基本变形形式是:拉伸(或压缩),剪切,扭转以及弯曲。
02-1 本章小结1.本章主要介绍轴向拉伸和压缩时的重要概念:内力、应力、变形和应变、变形能等。
轴向拉伸和压缩的应力、变形和应变的基本公式是: 正应力公式AN=σ 胡克定律EEAll σε==∆,F 胡克定律是揭示在比例极限内应力和应变的关系,它是材料力学最基本的定律之一。
平面假设:变形前后横截面保持为平面,而且仍垂直于杆件的轴线。
轴向拉伸或压缩的变形能。
2.材料的力学性能的研究是解决强度和刚度问题的一个重要方面。
对于材料力学性能的研究一般是通过实验方法,其中拉伸试验是最主要、最基本的一种试验。
低碳钢的拉伸试验是一个典型的试验。
它可得到如下试验资料和性能指标:拉伸全过程的曲线和试件破坏断口;b s σσ,—材料的强度指标; ψδ,—材料的塑性指标。
其中E —材料抵抗弹性变形能力的指标;某些合金材料的2.0σ—名义屈服极限等测定有专门拉伸试验。
3.工程中一般把材料分为塑性材料和脆性材料。
塑性材料的强度特征是屈服极限 sσ和强度极限 b σ(或 2.0σ),而脆性材料只有一个强度指标,强度极限 b σ。
4.强度计算是材料力学研究的重要问题。
轴向拉伸和压缩时,构件的强度条件:[]σσ≤=AN它是进行强度校核、选定截面尺寸和确定许可载荷的依据。
5.应通过本章初步掌握拉压超静定问题的特点及解法。
材料力学 第7章 组合变形杆的强度-1

材料 力学 Mechanics of Materials
第七章 组合变形杆的强度
材料 第七章 组合变形杆的强度:组合变形和叠加原理 力学 组合变形
构件在载荷的作用下,发生两种或两种以上基本变形
F
材料 第七章 组合变形杆的强度:组合变形和叠加原理 力学
交通路牌立杆——弯、压组合变形
材料 第七章 组合变形杆的强度:组合变形和叠加原理 力学
z z0
F A
1
zF z0
l
2 y
yF y0 lz2
0
得到中性轴方程:1
zF z0
l
2 y
yF y0 lz2
0
结论1:中性轴为不通过形心的直线
其位置不仅与几何形状iy, iz有关
还与载荷位置zF, yF有关
中性轴
中性轴在 y 轴上的截距:
ay iz2 / yF
AB杆为轴向压缩与弯曲的组合变形
材料 第七章 组合变形杆的强度:拉伸(压缩)与弯曲的组合 力学 ������作内力图,确定危险截面
(-) (-) 可知:C的左邻截面为危险截面
材料 第七章 组合变形杆的强度:拉伸(压缩)与弯曲的组合 力学
������选择截面 先不考虑轴力的影响
max
M max Wz
材料 第七章 组合变形杆的强度:拉伸(压缩)与弯曲的组合 力学
φ
载荷分解
Fx F cos 产生沿 x 轴的轴向拉伸 Fy F sin 产生 xy 平面内的平面弯曲
材料 第七章 组合变形杆的强度:拉伸(压缩)与弯曲的组合 力学
应力计算
Fx 单独作用——拉 Fy 单独作用——弯 Fx 和 Fy 同时作用
第八章组合变形构件的强度-

Fx F cos; Fy F sin 2.内力分析
FN Fx F cos FS Fy F sin M z Fy (l x) 上侧受拉
F sin(l x)
m
xm l
z
Fx
x
Fy
F
y
z
FS
FN x
y Mz
§8-2 弯曲与拉伸(或压缩)得组合
一、拉(压)与弯曲组合变形
第八章组合变形构件的强度
第八章 组合变形构件得强度
轴向拉(压)
F
内
FN
力
FN F
扭转
m
x
T
T m
F
应
T
力
FN (x)
A
max
(ρ) T ρ Ip
对称弯曲
FS
M
σ
τ FS
M
My
;
FS
S
z
Iz
bI z
§8-1 概述 一、组合变形
F2
F1
Me
F1 — 轴向拉伸 F2 — 弯曲变形 Me — 扭转变形
F2
2
F1
1
z
FN F1
A bh
x 3
My Wy
F1 b h b2
2 6
3F1 bh
4
l
l
y
Mz Wz
F1 h b h2
2 6
3F1 bh
1
F1 bh
3F1 bh
3F1 bh
F1 bh
3
2
F1 bh
3F1 bh
3F1 bh
7 F1 bh
4
F1 bh
3F1 bh
3F1 bh
工程力学组合受力与变形时的强度计算

FN A
M W
3103
d 2
8 103
d 3
81.1
MPa
81.9
4
32
位置?
例题:图示钢板受集中力P=128KN作用,当板在
一侧切去深4cm的缺口时,求缺口截面的最大正应 力?若在板两侧各切去深4cm的缺口时,缺口截面 的最大正应力为多少?(不考虑应力集中) 10
P
360
求: 1.链环直段部分横截面上 的最大拉应力和最大压应力; 2. 中性轴与截面形心之间 的距离。
解:根据平衡,截面上将
作用有内力分量FNx 和Mz
Fx 0 M C 0
得到 FNx=800 N
Mz= 12 N·m
x FNx
FNx A
4FNx πd 2
π
4 800 122 106
简支梁在中点受力的情
形下,最大弯矩
Mmax=FPl / 4。得到两个 平面弯曲情形下的最大
d
弯矩:
c
M max
FPz
FPx l FPsin l
4
4
M max
(FPy )
FPy l 4
FP
cos l 4
在Mmax(FPy)作用的截面上,截面上边缘的角点 a、b 承受最大压应力;下边缘的角点c、d 承受最 大拉应力。
Pz P cos
以y为中性轴弯曲 M y Pz (l x)
P cos(l x) M cos
M z Py (l x)
P sin(l x) M sin
M z y M y sin M y z M z cos
08第八章 组合变形构件的强度

M z1 17106 125 40(MP a) c Iy 5310 104
t
c
t max t N 242.67 26.7(MPa) [ t ] c max c N 402.67
37.3(MPa) [ c ]
N
∴该立柱安全!
1020 3 [ 102025 2 ] 12
PPLeabharlann 7.27105 mm 4M P zC 500 m N
N 应力分析如图
max
t
M
N M z max A I yc
100 103 500 103 55 800 7.27105
N M
12537.8162.8MPa
My
Mz
-
2 2 2 M M y M z2 2.1 4.2
+
4.7(kNm)
z
y
d
P
m l
P
l
M 2 T 2 r3 W
4.7 2 1.52 10 6 3.14100 3 32
T My Mz
-
50.3MPa
-
安全!
+
[例7] 图示空心圆轴,内径d=24mm,外径D=30mm,轮子
( z P , yP )
,z0)
M y z0 P M z y0 yz x A Iz Iy
P M z y0 M y z0 令: x 0 A Iz Iy
y
中性轴
即
y P y0 z P z 0 P P y P y0 P z P z0 P ( 1 2 2 ) 0 2 2 A iz iy A Aiz Ai y
§8 –3 弯曲与扭转的组合
一级结构注册考试总结

1、受压砌体墙判断是轴心受压还是偏心受压,要看是否受侧向水平荷载产生弯矩,产生弯矩即使传来轴心压力,也是偏心受压,偏心距e=M/N,根据偏心距e和高厚比确定受压承载力影响系数。
2、计算砌体结构挑梁倾覆力矩时,均布荷载倾覆弯矩M=ql*(l/2+x o)(容易计算为M=ql*(l+x o ))/2 后者为错。
3、《地规》3.0.6 对由永久作用控制的基本组合,也可采用简化规则,基本组合的效应设计值Sd可按下式确定:S d=1.35S k.。
4、《钢标》3.3.4 计算冶炼车间或其他类似车间的工作平台结构时,由检修材料所产生的荷载对主梁可乘以0.85,柱及基础可乘以0.75。
5、《钢标》3.4.2 计算结构或构件的变形时,可不考虑螺栓或铆钉孔引起的截面削弱。
6、《钢标》计算下列情况的连接时,表4.4.5 规定的强度设计值应乘以相应的折减系数;几种情况同时存在时,其折减系数应连乘。
1 ) 数施工条件较差的高空安装焊缝乘以系数0.9 ;2 ) 进行无垫板的单面施焊对接焊缝的连接计算应乘折减系数0.857、《钢标》6.2.5 梁的支座处应采取构造措施,以防止梁端截面的扭转。
当简支梁仅腹板与相邻构件相连,钢梁稳定性计算时侧向支承点距离应取实际距离的1.2 倍。
8、《钢标》3.1.7 对于直接承受动力荷载的结构:计算强度和稳定性时,动力荷载设计值应乘以动力系数;计算疲劳和变形时,动力荷载标准值不乘动力系数。
计算吊车梁或吊车桁架及其制动结构的疲劳和挠度时,起重机荷载应按作用在跨间内荷载效应最大的一台起重机确定。
9、T型截面受剪时,腹板承受全部剪力。
10、《钢标》3.1.7 对于直接承受动力荷载的结构:计算强度和稳定性时,动力荷载设计值应乘以动力系数;计算疲劳和变形时,动力荷载标准值不乘动力系数。
计算吊车梁或吊车桁架及其制动结构的疲劳和挠度时,起重机荷载应按作用在跨间内荷载效应最大的一台起重机确定。
11、压弯构件斜截面受剪计算,剪跨比计算框架结构与其他结构计算不同,12、钢结构中计算柱计算长度时,梁线刚度为柱两侧线刚度之和。
构件的强度与刚度讲解汇总.

@ 2005 Nanjing University of Science & Technology . School of Mechanic Engineering . Department of Design Art
杆件的基本变形形式
基本变形
工程实例
P
P P
受力简图
P P
P P
拉伸 压缩
P
剪切
扭转
Nanjing University of Science & Technology
Nanjing University of Science & Technology
强度与刚度
2.3.8 应力集中的概念
P
max
减小应力集中的方法:
P
由于功能与结构的需要,在构件上常存在 切口、孔洞、螺纹、轴肩等结构;实验证 明,在截面形状突变部分,其应力不是均 匀分布,在突变附近的局部范围内,应力 显著增大,这种现象称为应力突变。
Nanjing University of Science & Technology
强度与刚度
2.2
杆件的基本变形形式
• 材料力学的研究对象—杆件 杆件是指一个方向的尺寸远大于另两个方向的尺 寸的构件。 典型的杆件有轴、连杆、梁。 杆件的与其长度方向垂直的截面称为横截面;横 截面形心的连线称为轴线。
强度与刚度
2 构件的强度与刚度
2.1 2.2 2.3 2.4 2.5 2.6 2.7 构件材料的要求与假设 构件的基本变形形式 拉伸与压缩 ★ 剪切与挤压 圆轴的扭转 梁的平面弯曲 组合变形的强度计算
@ 2005 Nanjing University of Science & Technology . School of Mechanic Engineering . Department of Design Art
构件的强度与刚度讲解

1 纵向变形及其规律 L NL EA
强度与刚度
L NL A
2 横向变形及其规律
' d / d
' 或 '
E
式中 为' 横向变形系数;μ为泊松系数或泊松比。
@ 2005 Nanjing University of Science & Technology . School of Mechanic Engineering . Department of Design Art
Nanjing University of Science & Technology
2 构件的强度与刚度
强度与刚度
2.1 构件材料的要求与假设 2.2 构件的基本变形形式 2.3 拉伸与压缩 ★ 2.4 剪切与挤压 2.5 圆轴的扭转 2.6 梁的平面弯曲 2.7 组合变形的强度计算
@ 2005 Nanjing University of Science & Technology . School of Mechanic Engineering . Department of Design Art
Nanjing University of Science & Technology
2.4 剪切与挤压
• 剪切强度计算(实用计算方法)
强度与刚度
Q
A
Q---剪力; A---受剪面积。
P
L
P mn
b
键的受剪面积是多少?
@ 2005 Nanjing University of Science & Technology . School of Mechanic Engineering . Department of Design Art
材料力学 第7章 组合变形杆的强度-2
E1 A1 ydA1 E2 A2 ydA2 0
E1
E2
A1 ydA1
A2 ydA2
A1 y(ndA1)
A2 ydA2 =0
1 M
1 M
M
M
M
E1I1 E2I2
E1I1 E2I2
E2
(
E1 E2
I1
I2)
E2 (nI1 I2 )
My z Iy
Mz Iz
y
F1z=1127 N F2z=1025 N σ
στ
τσ y′
-
σ
+ +
z′
τ
σ
στ
材料 力学
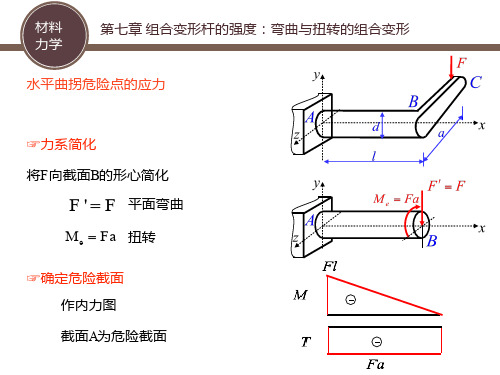
第七章 组合变形杆的强度:弯曲与扭转的组合变形
✓ 确定危险截面
F1y=410 N
F2y=2817 N
F1z=1127 N
F2z=1025 N Me1=Me2=169 N•m
要求熟练掌握的内容: (1)绘制各种简单变形内力图; (2)简单变形时杆件横截面的应力分布规律; (3)应力状态理论; (4)强度理论。
材料 力学
第七章 组合变形杆的强度:本章总结
组合变形杆的强度计算基本步骤
1. 分解: 目标——几种简单变形
2. 分别计算: 内力分析(内力图)—— 确定危险截面 应力分析(应力分布)—— 确定危险点
不发生扭转变形
弯曲中心——横向力作用在杆件的横截面内 使得杆件只发生弯曲变形的特定点 开口薄壁杆件抗扭刚度较小
材料 力学
第七章 组合变形杆的强度:开口薄壁杆件弯曲
二、开口薄壁杆件的弯曲切应力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 弯曲与拉伸或压缩的组合
例:F力作用在杆自由端形心处,作
用线位于xy面内,与x轴夹角为 。
y
·· ·· L
F
x
F力既非轴向力,也非横向力,所以 变形不是基本变形。
1.外力分析
Fy=Fsin y为对称轴,引起平面弯曲 Fx=Fcos 引起轴向拉伸
Fy
F
·· ·· x l
x
Fx
y
2.内力分析
FN=Fx
Mz=Fy(lx)
只有一个方向的 弯矩,就用平面 弯曲的弯矩符号 规定。
Fy
l
Fx
Fx
+
N图
M图
Fyl
3.应力分析
FN对应的应力
FN
A
Mz对应的应力 M z y
Iz
z
y
叠加: FN M z y
A
Iz
由于忽略了剪切应力,横截面上只有正应 力,于是叠加后,横截面上正应力分布规律只 可能为以下三种情况:
C2 y
危险截面上的C1或C2点为危险点。
叠加:C1点
外表面
C1
T Wp M W
横截面
俯视图
C1 外表面
T
Wp
M W
C1 C3
z yC3
C2
y
C3 C1 z
C2 y
4.强度条件
一般轴多采用塑性材料,因而可选第三 或第四强度理论。
第三强度理论:
第四强度理论:
C1
对圆轴弯扭组合变形,危险点C1的应力为:
z C
y
100 10 3 0.08
20 10 3 1.067 10
3
0.2
5 10 3 2.667 10 4
0.1
3.13MPa (压)
Cmax= 6.87MPa
Lmax= 4.37MPa
y
1
F2
2 1m
F1 1m
y z x
b
例:已知矩形截面 木梁上作用有外力, h 水平面内F1=800N, 铅垂面内F2=1650N,
6
y
1
F2
2 1m
z
F1 1m
y
z x
h
b
max ① ②
4800 b3
2475 b3
7275 b3
10106
b 9cm h 2b 18cm
§3 弯曲与扭转的组合
T1 T2 T3 T4 传动轴
传动轴 — 弯扭组合变形
1.外力分析(确定变形种类)
F m z
x
l
y
F: 对称面内的横向力引起平面弯曲。
组合变形构件的强度
§1 概述
摇臂钻--拉(压)弯组合变形
8-1
吊车杆——压弯组合变形
厂房牛腿——偏心压缩
方法:叠加法 范畴:小变形
线弹性
叠加原理
构件在小变形和服从胡克定理的条件下,力的
独立性原理是成立的。即所有载荷作用下的内力、 应力、应变等是各个单独载荷作用下的值的叠加。
解决组合变形的基本方法是将其分解为几种基
[σ]=10MPa,h/b=2, 求截面尺寸。
解:z ①受力分析
②应力分析
Mz F2 1 1650N m My F1 2 1600N m
危险截面在固定端.
Mz Wz
1650 61650 2475 bh2 4b3 b3
6
危险点在①,②点.
My Wy
1600 61600 4800 hb 2 2b3 b3
4.37106 Pa 4.37 MPa (拉)
B
FN A
My Iy
zB
Mz Iz
yB
x D
A
B
a=0.2m
z C
y
100 10 3 0.08
20 10 3 1.067 10 3
0.2
5 10 3 2.667 10 4
0.1
0.63 MPa(拉)
C
FN A
My Iy
zC
Mz Iz
yC
m : 作用平面为横截面的力偶,引起扭转。
2.内力分析(确定危险截面)
略去弯曲剪应力
x M = F(lx)
F m
z
l
y
T = m
危险截面 y
1
T
4
z
x
3
2 Mz
x
Fl M
F m l
T
m=Fa
3.应力分析(确定危险点)
M引起的正应力
C1 C3
M
C2
Wz
y
z yC3
T引起的剪应力 T
Wt
C3 C1 z
x D
A
B
a=0.2m
z C
y
100 10 3 20 10 3
5 10 3
0.08 1.067 10 3 0.2 2.667 10 4 0.1
6.87 MPa(压)
A 4.37MPa B 0.63MPa C 6.87MPa
D
FN A
My Iy
zD
Mz Iz
yD
x D
A
B
a=0.2m
Pk=10kw,两齿轮节圆直径D1= 396 mm,D2 = 168mm,压力
角 20 ,轴的直径d = 50mm,材料为45号钢,许用应许用应
B
a=0.2m
Iz
ba3 12
1 0.4 0.23 12
2.667 10 4 m4
Iy
ab3 12
1 0.2 0.43 12
1.067 10 3 m4
z C
y
A
FN A
My Iy
zA
Mz Iz
yA
x D
A
B
a=0.2m
z C
y
100 103 20 103
5 10 3
0.08 1.067 103 0.2 2.667 104 0.1
N A
Mz Iz
y
Байду номын сангаас
max
例: 图示结构, 求底截面上A,B, C,D四点的正应 力,以及最大拉应 力和最大压应力。
x P=1z00kN 0.05m y
D
C
A
B
a=0.2m
解:① 外力简化 yP=0.05m zP=0.2m P=100kN
My =PzP =1000.2=20kNm
Mz =PyP =1000.05=5kNm
中性轴(零应力线)发生平移。
| FN || M z |
A
Wz
| FN || M z |
A
Wz
| FN || M z |
A
Wz
4. 强度条件
危险点的位置很容易确定,在截面的最上缘或 最下缘。
由于危险点的应力状态为简单应力状态(单向拉 伸或单向压缩),故:
强度条件
max≤ [ ]
max
max
M
W z
而且W
d 3
,
z
32
T
W t
Wt
d3
16
,
C1
W 2W
t
z
代入强度理论:
( M )2 4( T )2 1 M 2 T 2 [ ]
r3
W
WW
z
t
z
( M )2 3( T )2 1 M 2 0.75T 2 [ ]
r4
W
WW
z
t
z
例: 齿轮轴AB如图所示。已知轴的转速n=265r/min,输入功率
x P=1z00kN 0.05m y
D
C
A
B
a=0.2m
② 内力计算 底截面上:
FN = – P = – 100 kN
x
z
D PMy
C
Mz
y
A
B
a=0.2m
My= 20kNm (前拉,后压)
Mz= 5kNm (左拉,右压)
③ 应力计算 x
截面有关几何参数:
D
A=ab=0.20.4=0.08m2
A
