(完整版)全等三角形的判定与性质专题训练
三角形全等的判定方法5种例题+练习全面

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件(5种)1边角边(重点)两边及其夹角分别分别相等的两个三角形全等,可以简写成“边角边”或“SAS”.注:必须是两边及其夹角,不能是两边和其中一边的对角.原因:如图:在A ABC和A ABD中,/ A= / A,AB=AB,BC=BD,显然这两个三角形不全等.A例 1 如图,AC=AD, / CAB= / DAB,求证:A ACB义A ADB.AD例 2 如图,在四边形 ABCD 中,AD〃BC, / ABC= /DCB, AB=DC, AE=DF 求证:BF=CE.例3.(1)如图①,根据“SAS",如果BD=CE, =,那么即可判定4BDC24CEB; (2)如图②,已知BC=EC, NBCE二ACD,要使4ABC2△口£&则应添加的一个条件为例4. 如图,已知AD=AE,N1=N2, BD=CE,则有4ABD2,理由是△ABE义,理由是.例5.如图,在4ABC和4DEF中,如果AB=DE, BC=EF,只要找出N=N 或〃,就可得到4ABC2△DEF.A D例6.如图,已知AB〃DE, AB=DE, BF=CE,求证:4ABC24口£艮例 7.如图,点B 在线段AD 上,BC〃DE, AB=ED, BC=DB. 求证:NA二NE 例8.如图,点E, F 在BC 上,BE=CF, AB=DC, NB=NC.求证: NA=ND.2.角边角两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)例1.如图,在4ABC中,点D是BC的中点,作射线AD,线段AD及其延长线上分别取点E, F,连接CE,BF.添加一个条件,使得4BDF24CDE,你添加的条件是:.(不添加辅助线)例2. 如图,已知人口平分/8人&且N ABD=N ACD,则由“AAS”可直接判定△^A.B例 3.如图,在 RtA ABC 中,N ACB=90°, BC=2cm, CD^AB,在AC 上取一点E,使EC二BC, 过点E作EF^AC交CD的延长线于点F,若EF=5cm,那么AE=cm.例4.如图,AD〃BC,N ABC的角平分线BP与/8人口的角平分线AP相交于点P,作PE L AB于点E.若PE=2,则两平行线AD与BC间的距离为.例 5.如图,已知EC=AC, ZBCE=ZDCA, NA=NE.求证:BC=DC.例6.如图,在4ABC中,D是BC边上的点(不与B, C重合),F, E分别是AD及其延长线上的点,CF〃BE.请你添加一个条件,使4BDE24CDF (不再添加其他线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是:;(2)证明:例7.如图,A在DE上,F在AB上,且BC=DC,N1=N2=N3,则DE的长等于()A. DCB. BCC. ABD. AE+AC【基础训练】1 .如图,已知 AB = DC,NABC=NDCB,则有4ABC2,理由是;且有2 .如图,已知AD=AE,N1 = N2, BD = CE,则有4ABD2,理由是;△ ABF /,理由是.3 .如图,在4ABC 和ABAD 中,因为 AB = BA,NABC=NBAD, =,根 据“SAS”可以得到4ABC2ABAD.4 .如图,要用“SAS”证4ABC2AADE,若AB=AD, AC=AE,则还需条件( ).5 .如图,OA=OB, OC = OD,NO=50°,N D = 35°,则NAEC 等于( ).A. 60°B. 50°C. 45°D. 30°A.NB = ND C.N1 = N2 BNC=NED.N3 = N4(第4皿(第56.如图,如果AE=CF, AD〃BC, AD = CB,那么^ADF和ACBE全等吗?请说明理由.律f题)7.如图,已知AD与BC相交于点O,NCAB = NDBA, AC = BD.求证: (1)NC=ND;(2)AAOC^ABOD.C第T题)8.如图,AACD和4BCE都是等腰直角三角形,NACD=NBCE=90°, AE交DC于F, BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.(第8题)9.如图,在4ABC 中,AB=AC, AD 平分/BAC.求证:NDBC=NDCB.(第KJ题)10.如图,4ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE〃BC.(第门题)角角边两角分别相等且其中一组等角的对边相等的两个三角形全等,可以简写成“角角边”或“AAS”. 例1、如图,在4ABC中,N ABC=45°, H是高AD和高BE的交点,试说明BH=AC.例 2、如图,N ACB=90°, AC二BC, BE±CE, AD±CE 于 D, AD=2.5cm, DE=1.7cm. 求BE的长.例3、如图,在4ABC中,AC±BC, CE±AB于E, AF平分/CAB交CE于点F,过F作FD〃 BC交AB于点D.求证:AC=AD.例 3.如图,AD 平分/BAC, DEXAB 于 E, DFXAC 于 F,且 DB二DC,求证:EB=FC例4.如图,在4ABC中,D是BC的中点,DELAB, DFXAC,垂足分别是E, F, BE=CF. 求证:AD 是4ABC的角平分线.例5.如图,在4ABC中,AB二CB,N ABC=90°, D为AB延长线上的一点,点E在BC 边上,连接 AE, DE, DC, AE二CD.求证:NBAE二NBCD.例6.如图,D是BC上一点,DEL AB, DF±AC, E, F分别为垂足,且AE=AF.(1)AAED与4AFD全等吗?为什么?(2)AD平分/BAC吗?为什么?例 7.如图,已知 ACLBC, BDLAD, BC 与 AD 交于 O, AC=BD.试说明:ZOAB=ZOBA.例8.如图,NACB 和/ADB都是直角,BC二BD, E是AB上任意一点.求证:CE=DE.例 9.如图,已知RtAABC^RtAADE,ZABC=Z ADE=90°, BC 与 DE 相交于点 F, CD, EB.连接(1)图中还有几对全等三角形,请你一一列举;(2)求证:CF=EF.例10.如图,在四边形ABCD中,AC 平分/BAD,并且CB=CD.求/ABC+NADC的度数.例11. (1)如图①,A, E, F, C四点在一条直线上,AE二CF,过点E, F分别作DELAC, 8尸,八0连接BD交AC于点G,若AB二CD,试说明FG=EG.(2)若将4DCE沿AC方向移动变为如图②的图形,(1)中其他条件不变,上述结论是否仍成立?请说明理由.B BD D①. ②课后练习:1.如图,点C在线段AB的延长线上,AD = AE, BD = BE, CD = CE,则图中共有对全等三角形,它们是2.如图,若AB = CD, AC=BD,则可用“SSS”证 23.如图,已知 AB = DC, BE=CF,若要利用“SSS”得到4ABE2△DCF,还需增加的一个条件是.i第3题)(第-I题)4.如图所示是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若想固定其形状不变,需要加钉一根木条,可钉在().A. AE 上B. EF 上C. CF 上D. AC 上5.如图,已知E、C两点在线段BF上,BE=CF, AB=DE, AC=DF.求证:AABC2A DEF.& E C F(第三⑦6.如图,在4ABC和4DCB中,AC与BD相交于点O, AB=DC, AC=BD.(1)求证:4ABC 2ADCB;(2)AOBC的形状是.(直接写出结论,不需证明)<第6题)7、如图,在口ABCD中,点E、F分别是AD、BC的中点,AC 与EF相交于点O.(1)过点B作AC的平行线BG,延长EF交BG于点H;(2)在(1)的图中,找出一个与4BFH全等的三角形,并证明你的结论.8、如图,已知BD±AB, DC,AC,垂足分别为点B、C, CD=BD, AD 平分/BAC吗,为什么?9.如图,四边形ABCD是正方形,点G是BC上的任意一点,DELAG于E, BF#DE,交 AG于F.那NAF与BF+EF相等吗?请说明理由.B G C10.如图,BD、CE分别是4ABC的边AC和边AB上的高,如果BD = CE,试证明AB = AC.11.如图,在RtAABC和RtABAD中,AB为斜边,AC=BD, BC、AD相交于点E (1)请说明AE=BE 的理由;(2)若N AEC=45°, AC = 1,求 CE 的长.12.如图,在4ABC中,D是BC的中点,DELAB, DFLAC,垂足分别是点E、F, BE= CF.(1)图中有几对全等的三角形?请一一列出;(2)选择一对你认为全等的三角形进行证明.4练习21.如图,已知NB = NDEF, AB=DE,要证明△ ABC2△DEF.(1)若以“ASA”为依据,还缺条件;(2)若以“AAS”为依据,还缺条件£(第1期】《第2题)2.如图,已知AD平分/BAC,且NABD=NACD,则由“AAS”可直接判定△2 △.3.如图,已知AB=AC,要根据“ASA”得到以BE2AACD,应增加一个条件是 _______________(第3 (第4(第54.如图,点P是/AOB的平分线OC上的一点,PD±OA, PE LOB,垂足分别为点D、E, 则图中有对全等三角形,它们分别是.5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是().A.带①去B.带②去C.带③去D.带①和②去6.如图,已知AC平分/8八口,/1 = /2, AB与AD相等吗?请说明理由.C£第67.如图,点B、E、F、C在同一直线上,已知NA=ND, 需要补充的一个条件是.(写出一个即可)NB = NC,要使4ABF 2ADCE,8.如图,在4ABC中,N ABC=45°, H是高AD和高BE的交点,试说明BH=AC.A9.如图,已知点A、D、B、E在同一条直线上,且AD=BE,NA=NFDE,则AABC2A DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.10.已知:如图,AB=AE,N1 = N2,NB = NE.求证:BC=ED.21。
(完整版)全等三角形判定综合练习题
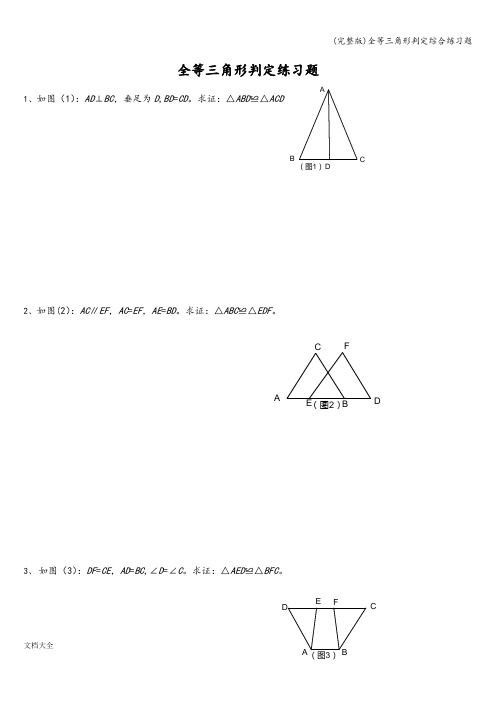
全等三角形判定练习题1、如图(1):AD ⊥BC ,垂足为D ,BD =CD 。
求证:△ABD ≌△ACD2、如图(2):AC ∥EF ,AC =EF ,AE =BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF =CE ,AD =BC ,∠D =∠C 。
求证:△AED ≌△BFC 。
FE (图2)DCBAFEDC(图1)DCBA4、 如图(4):AB =AC ,AD =AE ,AB ⊥AC ,AD ⊥AE .求证:(1)∠B =∠C ,(2)BD =CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE 。
求证:AC ⊥CE 。
E(图4)DCBAE(图5)DCBA6、如图(6):CG =CF ,BC =DC ,AB =ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF =EG ,(2)BF ∥DG .7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN =BC 。
求证:(1)MN 平分∠AMB ,(2)∠A =∠CBM 。
GFE(图6)DC BANM(图7)CBA8、如图(8):A 、B 、C 、D 四点在同一直线上,AC =DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE =CF 。
求证:AM 是△ABC 的中线。
FE(图8)DC B AMFE(图9)CBA10、如图(10)∠BAC =∠DAE ,∠ABD =∠ACE ,BD =CE . 求证:AB =AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA =PD .12、如图(12)AB ∥CD ,OA =OD ,点F 、D 、O 、A 、E 在同一直线上,AE =DF . 求证:EB ∥CF 。
(完整)全等三角形的判定专题

全等三角形的判定证明专题一、全等三角形的性质①全等三角形的对应边相等.②全等三角形的对应角相等。
二、全等三角形的判定定理①角边角公理:有两角和它们的夹边对应相等的两个三角形全等(ASA)。
②边角边公理:有两边和它们的夹角对应相等的两个三角形全等(SAS)。
③边边边公理:有三边对应相等的两个三角形全等(SSS)。
④角角边定理:有两个角和其中一个角的对边对应相等的两个三角形全等(AAS)。
三、一般思考方法1、已知两边对应相等—1。
第三边;2。
夹角;3。
直角2、一角及邻边对应相等—1。
角的另一边;2.边的另一角;3。
边的对角3、一角及对边对应相等—1.另一角4、两角相等-1。
夹边;2。
一已知角的对边第一部分简单证明例题分析例1:已知:如图AC=BD,∠CAB=∠DBA.求证:∠CAD=∠DBC。
例2:已知:AB=CD,AB∥DC,求证:△ABC≌△CDB例3:已知:在△ABC中,AD为BC边上的中线,CE⊥AD,BF⊥AD.求证:CE=BF例4.已知:如图AB=AC,AD=AE,BE和CD相交于G。
求证:AG平分∠BAC.例5:已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连结DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC.求证:△ADE≌△EFC例6:已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC。
求证:△ABG≌△BCH≌△CAD。
自我检测1、已知:△ABC中,AB=AC,D、E分别为AB、AC的中点。
求证:∠ABE=∠ACD.2、已知:AB=DC,AC=BD ,AC 交BD 于E.求证:AE=DE.3、已知:如图,AB=CD ,BE=DF ,AF=EC.求证:BF=DE4、如图,在△ABE 中,AB =AE ,AD =AC ,∠BAD =∠EAC , BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE 。
全等三角形的性质及判定练习题

全等三角形的性质及判定练习题(1)1:下列说法,正确的是( )A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形2:如图1,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD=7cm ,DM=5cm ,∠DAM=39°,则AN =____cm ,NM =____cm ,NAB ∠= .3:如图2,已知ABC ADE ∆≅∆,AB AD =,BC DE =,那么与BAE ∠相等的角是 .4:如图3,ABC ADE ∆≅∆,则AB= ,∠E= _.若∠BAE=120°,∠BAD=40°,则∠BAC= .5:如图,在ABC ∆中,::2:5:11A B ACB ∠∠∠=,若将ACB ∆绕点C 逆时针旋转,使旋转前后的//A B C ∆中的顶点/B 在原三角形的边AC 的延长线上,求/BCA ∠的度数.图4EDCBA图2 图3MDAN BC图1BFADCE6:如图1,,,AE DB BC EF BC ==∥EF .求证:ABC DEF ∆≅∆7:已知.,,AB DF AC DE BE CF ===,求证:AB ∥DF图1ADCFBEAED B8:如图,AC=DF ,AC//DF ,AE=DB ,求证:BC//EF9:如图, AD=EB,AC ∥DF ,BC ∥EF .求证:ABC DEF ∆≅∆10:如图,在△ABC 中, M 在BC 上, D 在AM 上, AB AC =,DB DC =.问BM CM =吗?说明理由.11:如图, △ABC, AD 是它的角平分线,且BD CD =,ED 、DF 分别垂直于AB 、AC ,垂足为E 、F ,请说明BE CF =.12:已知:如图 , CE ∞AB 于E , BF ∞CD 于F , 且BF=CE13:已知:如图,∠A=∠D=90°,AC ,BD 交于O ,AC=BD.求证:OB=OC .14:如图,AB AC =,AD AE =,EAD BAC ∠=∠.求证:△ABD ≌△ACE15:已知如图,AE =AC,AB =AD,∠EAB =∠CAD,试说明:∠B =∠D16:如图,BDA CEA ∠=∠,AE AD =.求证:AB AC =17:如图, △ABC 是等腰三角形,,AD BE 分别是,BAC ABC ∠∠的角平分线, △ABD 和△BAE 全等吗?请说明你的理由.18:已知:如图 , AB=AC , AD=AE , 求证:△OBD ≌△OCE全等三角形的性质及判定练习题(2)第一部分:选择题2.如图,已知AC和BD相交于O,且BO=DO,AO=CO,下列判断正确的是()A.只能证明△AOB≌△COD B.只能证明△AOD≌△COBC.只能证明△AOB≌△COB D.能证明△AOB≌△COD和△AOD≌△COB2题4.如图,已知MB=ND,∠MBA=∠NDC,下列不能判定△ABM≌△CDN的条件是()A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN5.如图,已知0A=OB,OC=0D,下列结论中:①∠A=∠B;②DE=CE;③连OE,则0E平分∠0,正确的是( )A.①② B.②③C.①③D.①②③6.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙第三部分:填空题1.如图,△ABC ≌△AED ,∠BAC=25°,∠B=35°,AB=3cm ,BC=1cm ,则∠E= , ∠ ADE= ;线段DE= cm ,AE= cm .2.已知ABC DEF ∆≅∆,若ABC ∆的周长为32,8AB =,12BC =,则DE = ,DF = . 第四部分:解答题1.如图,已知ABC AED ∆≅∆,AE AB =,AD AC =,20D E ︒∠-∠=,60BAC ︒∠=.求C ∠的度数.2.如图,已知AB=DE ,AF=DC ,BE=CF ,求证:∠A=∠D.3.已知:AB=CD ,AD=BC.试说明∠A=∠C.(公共边)ED CBABEDCAADB EFC DAO4.如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180o,试说明AD=CD.。
2022年《直角三角形全等的判定》专题练习(附答案)

1.3 直角三角形全等的判定一、选择题(本大题共8小题)1. 在以下条件中,不能判定两个直角三角形全等的是( )2. 如下图,AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,那么图中全等的三角形有( )第2题图第5题图第6题图3.以下说法中正确的选项是〔〕A.a,b,c是三角形的三边长,那么a2+b2=c2B.在直角三角形中,两边长和的平方等于第三边长的平方C.在Rt△ABC中,假设∠C=90°,那么三角形对应的三边满足a2+b2=c2D.在Rt△ABC中,假设∠A=90°,那么三角形对应的三边满足a2+b2=c24. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=B′A,那么以下结论中正确的选项是〔〕A. AC=A′C′B.BC=B′C′C.AC=B′C′D.∠A=∠A′5. 如下图,△ABC中,AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点,那么图中全等三角形的对数是〔〕6. 如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,那么△BCE的面积等于〔〕A.10 B.7 C.5 D. 47. 在△ABC和△DEF中,∠A=∠D=90°,那么以下条件中不能判定△ABC和△DEF全等的是( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF8. 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,那么有( )A.DE=DBB.DE=AEC.AE=BED.AE=BD第8题图第9题图二、填空题(本大题共4小题)9. :如图,AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,AB=DC,那么△ABE≌△__________.10. 如图,BD⊥AE于点B,C是BD上一点,且BC=BE,要使Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D或__________或__________或__________.第10题图第11题图11. 如图,△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,假设根据“HL〞判定,还需要加一个条件__________.12. :如图,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,∠D=60°,那么∠A=__________.三、计算题(本大题共4小题)13. :如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE求证:OB=OC.14. :Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE15. 如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:〔1〕CF=EB.〔2〕AB=AF+2EB.16. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)假设CD=2,求AD的长.参考答案:一、选择题(本大题共8小题)1.A2. D3. C4. C5. D6. B7. B8. C二、填空题(本大题共6小题)9.分析:根据直角三角形全等的条件HL判定即可。
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
2024年中考全等三角形的性质与判定专题训练

E B C A DF 2024年中考全等三角形的性质与判定专题训练1.如图,AB =AD ,CB =CD .求证:∠B =∠D .2.如图,点A 、E 、B 、D 在同一条直线上,AE=DB ,AC=DF ,AC ∥DF.请探索BC 与EF 有怎样的位置关系?并说明理由。
3.如图,点B 、D 、C 、F 在同一直线,AB =EF ,∠B =∠F ,BD =CF ,试说明△ABC ≌△EFD .4. 如图,点E ,F 在线段BD 上,已知AF ⊥BD ,CE ⊥BD ,AD=CB ,DE=BF .求证:△AFD ≌△CEB .5.如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.(1)求证:△ABE≌△DCE;(2)当AB=5时,求CD的长.6.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.7.如图,在矩形ABCD中,点E,F在对角线BD上.请添加一个条件,使得结论“AE=CF”成立,并加以证明.8.如图,已知点E在AB上,点C在AD,AB=AC,AD=AE。
求证:BE=CD。
9.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF求证:(1) △ABC≌△DEF(2)AB∥DE9.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:AB=DE.11.如图,已知点B,C,D,E在一条直线上,AB∥FC,AB=FC,BC=DE.求证:AD∥FE.12.如图,∠A =∠D =90°,AC =DB ,AC 、DB 相交于点O .求证:AB =CD .13.已知:如图,AE 和BD 相交于点,,C AC EC BC DC ==;求证:.AB ED =14.已知如图:点C E B F ,,,在同一直线上,∠C=∠F,AC DF =, BF CE =.求证:DEF ABC ∆≅∆。
15.如图,AD∥BC,点E 是CD 的中点,BE 的延长线与AD 的延长线交于点F .则△BCE 和△FDE 全等吗?为什么?A FB EC D16.如图,为一块直角三角板,将CA绕点C顺时针旋转,使得点A落在边AB上的点D处.(1)过点C作于点E,求证:△ACE∽△ABC(2)求BD的长.。
(完整版)全等三角形练习题及答案

全等三角形练习题及答案1、下列判定直角三角形全等的方法,不正确的是()A、两条直角边对应相等。
B、斜边和一锐角对应相等。
C、斜边和一条直角边对应相等。
D、两锐角相等。
2、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C3、下列各条件中,不能作出唯一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ABC与△DEF中,已知AB=DE;∠A=∠D;再加一个条件,却不能判断△ABC与△DEF全等的是().A. BC=EF B.AC=DFC.∠B=∠E D.∠C=∠F5、使两个直角三角形全等的条件是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等6、在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是()A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,还须从下列条件中补选一个,错误的选法是()A、∠ADB=∠ADCB、∠B=∠CC、DB=DCD、AB=AC8、如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为A. 40°B. 80°C.120°D. 不能确定9、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为()A.600 B.700C.750D.85010、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )A. 150°B.40°C.80°D. 90°11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( )A.①③ B.②④ C.②③④ D.①②④12、下列条件中,不能判定两个三角形全等的是()A.三条边对应相等 B.两边和一角对应相等C.两角及其一角的对边对应相等 D.两角和它们的夹边对应相等13、如图,已知,,下列条件中不能判定⊿≌⊿的是()(A)(B)(C)(D)∥14、如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为().A.50° B.30° C.80° D.100°15、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的度数是.16、在△ABC和△中,∠A=44°,∠B=67°,∠=69°,∠=44°,且AC=则这两个三角形全等(填“一定”或“不一定”)17、如图,,,,在同一直线上,,,若要使,则还需要补充一个条件:或.18、(只需填写一个你认为适合的条件)如图,已知∠CAB=∠DBA,要使△ABC≌△BAD,需增加的一个条件是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形判定与性质专题训练
一、全等三角形实际应用问题
1如图,要测量河两岸相对的两点A、B间的距离,先在过B点的AB的垂线L上取两点C、D,使CD=BC,再在过D点的垂线上取点E,使A、C、E在一条直线上,ED=AB这时,测ED的长就得AB得长,判定△ACB≌△ECD的理由是()
A. SAS
B. ASA
C. SSS D .AAS
2.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是()
A.PO B.PQ C.MO D.MQ
3、如图所示,将两根钢条AA′,BB′的中点O连在一起,使A A′,BB′可以绕着点O自由转动,就做成了一个测量工具,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是()A、SSS B、SAS C、ASA D、HL
4、如图:工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是()
A、SSS
B、SAS
C、ASA
D、HL
5、如图,有两个长度相等的滑梯靠在一面墙上.已
知左边滑梯的高度AC与右边滑梯水平方向的长度
DF相等,则这两个滑梯与地面的夹角∠ABC+∠DFE= 度
6、如图,小明把一块三角形的玻璃打碎成了三块,
现在要到玻璃店去配一块完全一样的玻璃,那么最
省事的办法是:( )
A、带①去,
B、带②去
C、带③去
D、①②③都带去
二、证两次全等相关问题
1:如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证: CF=DF
2:如图已知AD∥BC,AB∥CD BF=DE,求证:AE=CF,
3:如图AB⊥AC,AD⊥AE AB=AD,BC=DE,求证AM=AN
三、探索两线段的关系问题
1.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE交CD于点F,试探索线段BE与AD的关系,并证明。
2、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。
试探索线段EC与BF的关系,并证明。
A
E
B M
C
F
3、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。
试探索线段AM与AN的关系,并证明。
B
4、如图,已知:△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
猜想BE与AC的关系并证明。
A
E F
D
B C
四、探索三线段的数量关系问题
1.在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .
(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;
(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
2、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
3.如图,AC平分∠BAD,CM⊥AB于M,∠ADC+∠ABC=180°.
求证:AB+AD=2AM.
五、构造全等三角形问题
1.如图,在△ABC中,BD=DC,∠1=∠2,求证:AD 平分∠BAC.
2·如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由
3如图:AD 为 △ABC 的中线, 求证:21(AB-AC )<AD <2
1(AB+AC )
A
B C D E
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF。
