固体物理课后习题答案
固体物理基础课后1到10题答案

一.本章习题P272习题1.试证理想六方密堆结构中c/a=.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三. 证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'a AB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=οοο633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a ρρρ,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d ρπ2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G ρρρρ++=写出)(321b b b ρρρ与正格子基矢 )(c b a ρρρ的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G ρ。
进而求得此面间距d 。
二、解:c b a ρρρΘ,,互相垂直,可令k c c j b b i a a ρρρρρρ===,,晶胞体积abc c b a v =⨯⋅=)(ρρρ倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b ρρρρρρρρρρρρρρρρρρπππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππρρρρρρρρ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππρ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
固体物理课后习题与答案

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。
《固体物理》课后习题答案

1.1 如果将等体积球分别排列成下列结构,设x 表示钢球所占体积与总体积之比,证明结构x简单立方π/ 6 ≈0.52 体心立方3π/ 8 ≈0.68 面心立方2π/ 6 ≈0.74六方密排2π/ 6 ≈0.74 金刚石3π/16 ≈0.34解:设钢球半径为r ,根据不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,分别为:简单立方:a = 2r金刚石:根据金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比,正是晶格常数为4π/ a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式上的,或者说是倒格子空间中的布拉菲格子。
根据定义,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:根据定义,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义,倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 满足其中a 为立方边长。
解:根据倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢互相正交,因此其大小为则带入前边的关系式,即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。
(参考资料)固体物理习题带答案

D E ( ) ,其中 , 表示沿 x , y , z 轴的分量,我们选取 x , y , z
沿立方晶体的三个立方轴的方向。
显然,一般地讲,如果把电场 E 和晶体同时转动, D 也将做相同转动,我们将以 D' 表示转
动后的矢量。
设 E 沿 y 轴,这时,上面一般表达式将归结为:Dx xyE, Dy yyE, Dz zy E 。现在
偏转一个角度 tg 。(2)当晶体发生体膨胀时,反射线将偏转角度
tg , 为体胀系数
3
解:(1)、布拉格衍射公式为 2d sin ,既然波长改变,则两边同时求导,有
2d cos ,将两式组合,则可得 tg 。
(2)、当晶体发生膨胀时,则为 d 改变,将布拉格衍射公式 2d sin 左右两边同时对 d
考虑把晶体和电场同时绕 y 轴转动 / 2 ,使 z 轴转到 x 轴, x 轴转到 z 轴, D 将做相同
转动,因此
D'x Dz zy E
D'y Dy yyE
D'z Dx xy E 但是,转动是以 E 方向为轴的,所以,实际上电场并未改变,同时,上述转动时立方晶体
的一个对称操作,所以转动前后晶体应没有任何差别,所以电位移矢量实际上应当不变,即
第一章:晶体结构 1. 证明:立方晶体中,晶向[hkl]垂直于晶面(hkl)。
证 明 : 晶 向 [hkl] 为 h1 k2 l3 , 其 倒 格 子 为
b1
2
a1
a2
a3
(a2 a3 )
b2
2
a1
a3 a1 (a2 a3)
b3
2
a1
a1
a2
(a2 a3)
。可以知道其倒格子矢量
固体物理参考答案(前七章)

固体物理习题参考答案(部分)第一章 晶体结构1.氯化钠:复式格子,基元为Na +,Cl -金刚石:复式格子,基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下:原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= , 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解:31A A O ':h:k;l;m==-11:211:11:111:1:-2:1 所以(1 1 2 1) 同样可得1331B B A A :(1 1 2 0); 5522A B B A :(1 1 0 0);654321A A A A A A :(0 0 0 1)3.简立方: 2r=a ,Z=1,()63434r 2r a r 3333πππ===F体心立方:()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ,,则面心立方:()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ,,则 六角密集:2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石:()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ,, 4. 解:'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解:对于(110)面:2a 2a a 2S =⋅=所包含的原子个数为2,所以面密度为22a2a22=对于(111)面:2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2,所以面密度为223a34a 232=8.证明:ABCD 是六角密堆积结构初基晶胞的菱形底面,AD=AB=a 。
固体物理 课后答案

第一章、晶体的结构习题1.以刚性原子球堆积模型,计算以下各结构的致密度分别为:(1)简立方,6π; (2)体心立方, ;83π(3)面心立方,;62π(4)六角密积,;62π(5)金刚石结构,;163π[解答]设想晶体是由刚性原子球堆积而成,一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度,设n为一个晶胞中的刚性原子球数,r表示刚性原子球半径,V表示晶胞体积,则致密度ρ=Vrn334π(1)对简立方晶体,任一个原子有6个最近邻,若原子以刚性球堆积,如图1.2所示,中心在1,2,3,4处的原子球将依次相切,因为,,433aVra==面1.2 简立方晶胞晶胞内包含1个原子,所以ρ=6)(33234ππ=aa(2)对体心立方晶体,任一个原子有8个最近邻,若原子刚性球堆积,如图1.3所示,体心位置O的原子8个角顶位置的原子球相切,因为晶胞空间对角线的长度为,,433aVra==晶胞内包含2个原子,所以ρ=ππ83)(*2334334=aa图1.3 体心立方晶胞(3)对面心立方晶体,任一个原子有12个最近邻,若原子以刚性球堆积,如图 1.4所示,中心位于角顶的原子与相邻的3个面心原子球相切,因为3,42a V r a ==,1个晶胞内包含4个原子,所以ρ=62)(*4334234ππ=a a .(4)对六角密积结构,任一个原子有12个最近邻,若原子以刚性球堆积,如图1。
5所示,中心在1的原子与中心在2,3,4的原子相切,中心在5的原子与中心在6,7,8的原子相切,图 1.5 六角晶胞 图 1.6 正四面体晶胞内的原子O 与中心在1,3,4,5,7,8处的原子相切,即O 点与中心在5,7,8处的原子分布在正四面体的四个顶上,因为四面体的高h =223232c r a == 晶胞体积 V = 222360sin ca ca =, 一个晶胞内包含两个原子,所以ρ=ππ62)(*22233234=ca a .(5)对金刚石结构,任一个原子有4个最近邻,若原子以刚性球堆积,如图1.7所示,中心在空间对角线四分之一处的O原子与中心在1,2,3,4处的原子相切,因为,8 3r a=晶胞体积3aV=,一个晶胞内包含8个原子,所以ρ=163)83(*83334ππ=aa.2.在立方晶胞中,画出(102),(021),(122-),和(201-)晶面。
固体物理习题解答参考答案晶体结构

r
( )
。由 R 所定义的也是一个点阵常数为
r
r r r ( i 2 的 SC 点阵,但相对于上面一个 SC 点阵位移了一个矢量 + j + k ) ,
这个点正好位于体心位置。 上面两个 SC 点阵穿套起来正好是一个 bcc 点阵,故 ni 或全为奇数,或全为偶数所定义的是一个 bcc 点阵。 (2)若
体心立方晶格原胞基矢 a1 = (−i + j + k ) a2 = (i − j + k ) a3 = (i + j − k ) 体心立方晶格原胞体积 倒格子基矢:
r
a 2
r
r
r r
ห้องสมุดไป่ตู้
a r 2
r
r r
a r 2
r
r
同理: 可见由 为基矢构成的格子为面心立方格子。
面心立方格子原胞基矢: 面心立方格子原胞体积: 倒格子基矢: 同理 可见由 为基矢构成的格子为体心立方格子。
(2) 体心立方(书P3,图1-3)
r 取 原 子 球 相 切 时 的 半 径 ( 体 对 角 线 的 1/4 ) , r= 3a / 4 ,n=2, V = a 3 所 以
ρ=
n 4π r 3 3 = 3π / 8 V
(3) 面心立方(书P4,图1-7)
r 取 原 子 球 相 切 时 的 半 径 ( 面 对 角 线 的 1/4 ) r= 2a / 4 ,n=4, V = a 3 , 所 以
则由 ε = AxT ε Ax 得
固体物理习题参考答案

固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。
固体物理课后答案

1.1 如果将等体积球分别排列成下列结构,设x 表示钢球所占体积与总体积之比,证明结构x简单立方π / 6 ≈ 0.52 体心立方 3π / 8 ≈ 0.68 面心立方 2π / 6 ≈ 0.74六方密排 2π / 6 ≈ 0.74 金刚石 3π /16 ≈ 0.34 解:设钢球半径为r ,根据不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,分别为:简单立方:a = 2r金刚石:根据金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比,正是晶格常数为4π/ a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式上的,或者说是倒格子空间中的布拉菲格子。
根据定义,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:根据定义,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义,倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 满足其中a 为立方边长。
解:根据倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢互相正交,因此其大小为则带入前边的关系式,即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。
固体物理(胡安)第二版课后习题答案 Word版 完整版 校核版 精品

Word版完整版校核版第一章 晶体的结构及其对称性1.1石墨层中的碳原子排列成如图所示的六角网状结构,试问它是简单还是复式格子。
为什么?作出这一结构所对应的两维点阵和初基元胞。
解:石墨层中原子排成的六角网状结构是复式格子。
因为如图点A 和点B 的格点在晶格结构中所处的地位不同,并不完全等价,平移A →B,平移后晶格结构不能完全复原所以是复式格子。
1.2在正交直角坐标系中,若矢量k l j l i l R l321++=,错误!未找到引用源。
i ,j ,k为单位向量。
错误!未找到引用源。
为整数。
问下列情况属于什么点阵?(a )当i l为全奇或全偶时; (b )当i l之和为偶数时。
解: 112233123l R l a l a l a l i l j l k=++=++ 错误!未找到引用源。
()...2,1,0,,321±±=l l l当l 为全奇或全偶时为面心立方结构点阵,当321l l l ++错误!未找到引用源。
之和为偶数时是面心立方结构1.3 在上题中若=++321l l l 错误!未找到引用源。
奇数位上有负离子,=++321l l l 错误!未找到引用源。
偶数位上有正离子,问这一离子晶体属于什么结构?解:是离子晶体,属于氯化钠结构。
1.4 (a )分别证明,面心立方(fcc )和体心立方(bcc )点阵的惯用初基元胞三基矢间夹角相等,对fcc 为错误!未找到引用源。
,对bcc 为错误!未找到引用源。
(b )在金刚石结构中,作任意原子与其四个最近邻原子的连线。
证明任意两条线之间夹角θ均为'1c o s109273a r c ⎛⎫-= ⎪⎝⎭'1c o s109273a r c ⎛⎫-= ⎪⎝⎭解:(1)对于面心立方()12a a j k =+ 错误!未找到引用源。
()22a a i k =+ ()32a a i j =+13222a a a a ===()1212121602a a COS a a a a ⋅⋅===()2323231602a a COS a a a a ⋅⋅===()1360COS a a ⋅=(2)对于体心立方()12a a i j k =-++ ()22a a i j k =-+ ()32a a i j k =+-12332a a a a ===()12'12121129273a a COS a a a a ⋅⋅==-=()'1313131129273a a COS a a a a ⋅⋅==-=()'2312927COS a a ⋅=(3)对于金刚石晶胞()134a i j k η=++()234a i j k η=--()2212122122314934a COS a ηηηηηη-⋅⋅===-错误!未找到引用源。
高中物理固体课后习题答案及解析

高中物理固体课后习题答案及解析1.某人为了检验一块薄片物质是否为晶体,做了一个实验。
他以薄片的正中央O为坐标原点,建立Oxy平面直角坐标系,在两个坐标轴上分别取两点x1和y1,使x1和y1到O点的距离相等。
在x1和y1上分别固定一个测温元件,再把一个针状热源放在O点,发现x1点和y1点的温度在缓慢升高,但两点温度的高低没有差异。
于是得出结论:这块薄片是非晶体。
请说明:以上结论科学吗?为什么?解析:实验说明该均匀薄片在x,y两个方向上导热性能相同,但不能因此就确定这块薄片是非晶体,因为晶体有可能在导热性能上表现为各向同性,而在其他性质上表现为各向异性;由于多晶体具有各向同性,该薄片也有可能是多晶体。
2.食盐晶体的结构可以用钠离子和氯离子空间分布的示意图表示(图2.4-8),图中相邻离子的中心用线连起来了,组成了一个个大小相等的立方体。
现在要估算相邻两个钠离子中心的距离,除了知道食盐的密度ρ为2.17×103 kg/m3外,还要知道哪些数据?请用字母表示这些已知数据,推导出相邻两个钠离子中心距离的表达式。
提示:图中最小立方体的个数与离子数目相等。
答案及解析如下:3.内陆盐矿中开采的氯化钠称为岩盐,岩盐的颗粒很大,我们能清楚地看出它的立方体形状。
把大颗粒的岩盐敲碎后,小颗粒的岩盐仍然呈立方体形状。
图2.4-13表示了岩盐晶体的平面结构:粉红点为氯离子,灰点为钠离子,如果把它们用直线连起来,将构成一系列大小相同的正方形,作分界线AA 1,使它平行于正方形的对角线,作分界线BB 1,使它平行于正方形的一边。
在两线的左侧各取一个钠离子M 和N ,为了比较这两个钠离子所受分界线另一侧的离子对它作用力的大小,分别以M 、N 为圆心,作两个相同的扇形,不考虑扇形以外远处离子的作用。
(1)如果F 表示两个相邻离子之间引力的大小,问:M 、N 所受扇形范围内的正负离子对它作用力的合力是F 的多少倍?为使问题简化,设所有离子都是质点,而且它们之间的相互作用遵从“平方反ABB 1A 1 MN 图 2.4-13 岩盐晶体的平面结构比”规律。
固体物理习题解答-完整版
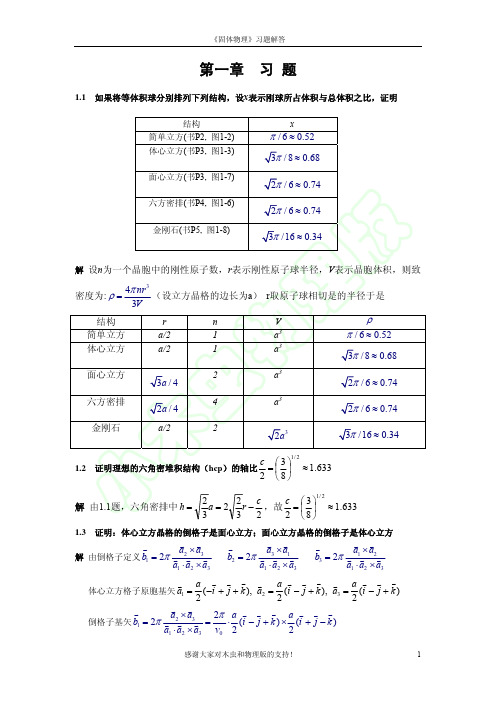
2.3
若一晶体的相互作用能可以表示为 u ( r ) = − 求 1 )平衡间距 r 0
α
r
m
+
β
rn
3 )体弹性模量 4 )若取
2 )结合能 W (单个原子的)
m = 2, n = 10, r0 = 0.3 nm, W = 4 eV ,计算 α , β 值。
解 1)晶体内能 U ( r ) =
N α β (− m + n ) 2 r r
⎛ ε 11 3ε 22 ⎜ + 4 4 0 ⎞ ⎜ ⎟ ⎜ 3ε 11 3ε 22 ε 23 ⎟ = ⎜ − + 4 4 ⎜ ε 33 ⎟ ⎠ ⎜ 3ε 23 − ⎜ 2 ⎝ − 3ε 11 3ε 22 + 4 4 3ε 11 ε 22 + 4 4 − − 3ε 23 ⎞ ⎟ 2 ⎟ ε ⎟ − 23 ⎟ 2 ⎟ ε 33 ⎟ ⎟ ⎠
h k l ( )2 + ( )2 + ( )2 a b c
说明面指数简单的晶面,其面密度较大,容易解理 证 简单正交系 a ⊥ b ⊥ c 倒格子基矢 b1 = 2π
a1 = ai , a2 = bj , a3 = ck b2 = 2π a3 × a1 a1 ⋅ a2 × a3 b3 = 2π a1 × a2 a1 ⋅ a2 × a3
⎛ ε 11 ε 12 ⎜ 假 设 六 角 晶 系 统 的 介 电 常 数 为 ε = ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
⎛ ε 11 ε 12 ⎜ ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
ε 13 ⎞ ⎟ ε 23 ⎟ 则 由 ε = AT ε Ax 得 ε 33 ⎟ ⎠
x
ε 13 ⎞ ⎛ ε 11 − ε 12 − ε 13 ⎞ 0 ⎞ ⎛ ε 11 0 ⎟ ⎟ ⎜ ⎟ ⎜ ε 23 ⎟ = ⎜ − ε 21 ε 22 ε 23 ⎟ 可见 ε = ⎜ 0 ε 22 ε 23 ⎟ 将上式代入 ε = AzT ε Az ⎜ ⎜0 ε ε 33 ⎟ ε 33 ⎟ ε 33 ⎟ 32 ⎠ ⎠ ⎝ ⎠ ⎝ − ε 31 ε 32
固体物理课后习题答案

固体物理课后习题答案固体物理课后习题答案固体物理是物理学中的一个重要分支,研究物质的结构和性质。
它涉及到晶体学、电子结构、磁性、声学等多个方面。
在学习固体物理的过程中,课后习题是巩固知识、提高能力的重要途径。
下面是一些固体物理课后习题的答案,供大家参考。
1. 问题:什么是晶体?晶体的特点是什么?答案:晶体是由周期性排列的原子、离子或分子组成的固体。
晶体的特点包括:- 长程有序性:晶体的原子、离子或分子按照一定的规则排列,形成周期性的结构。
- 均匀性:晶体的结构在宏观和微观尺度上都是均匀的。
- 可预测性:晶体的结构可以通过晶体学方法进行研究和预测。
- 具有特定的物理性质:晶体的结构和周期性排列导致了其特定的物理性质,如光学性质、电学性质等。
2. 问题:什么是晶体的晶格常数?答案:晶体的晶格常数是指晶体中原子、离子或分子排列的周期性重复单位的尺寸。
晶格常数可以用来描述晶体的结构和性质。
在晶体学中,晶格常数通常用晶格常数矢量a、b、c表示,它们分别表示晶格沿着三个坐标轴的长度。
3. 问题:什么是布拉维格子?答案:布拉维格子是指晶体中的离散的点阵结构,用来描述晶体的对称性。
布拉维格子的点阵可以通过晶体的晶格常数和晶体的对称操作得到。
布拉维格子的对称性决定了晶体的物理性质,如晶体的能带结构和声子谱。
4. 问题:什么是声子?声子与固体的性质有什么关系?答案:声子是固体中的一种元激发,它代表了晶格振动的量子。
声子的能量和动量由固体的结构和性质决定。
声子的存在对固体的性质有重要影响,如导热性、电导性等。
声子的研究可以揭示固体的热力学和动力学性质。
5. 问题:什么是费米面?费米面与固体的导电性有什么关系?答案:费米面是描述固体中电子分布的一个表面,它代表了能量最高的占据态和能量最低的未占据态之间的边界。
费米面的形状和位置由固体的电子结构决定。
费米面的性质与固体的导电性密切相关。
在导电体中,费米面与导电性能直接相关,如费米面的形状和移动可以解释固体的电导率和磁性等性质。
固体物理学课后题答案

第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
固体物理学习题解答(完整版)

《固体物理学》部分习题参考解答第一章1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a :对于面心立方,处于面心的原子与顶角原子的距离为:R f=2 a 对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a 那么,Rf Rb31.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:根据题意,由于OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,那么 1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
因为晶面族(hkil )中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ,a 2/k ,a 3/i ,因此123o o o a n hda n kd a n id=== ……… (1) 正方 a=b a ^b=90° 六方 a=b a ^b=120° 矩形 a ≠b a ^b=90° 带心矩形 a=b a ^b=90° 平行四边形 a ≠b a ^b ≠90°由于a 3=–(a 1+ a 2)313()o o a n a a n =-+把(1)式的关系代入,即得()id hd kd =-+ ()i h k =-+根据上面的证明,可以转换晶面族为(001)→(0001),(133)→(1323),(110)→(1100),(323)→(3213),(100)→(1010),(010)→(0110),(213)→(2133)1.5 如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立方:6π(2(3)面心立方:6(4)六方密堆积:6(5)金刚石:。
固体物理学课后题答案

第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(
)
⎞ 2π k⎟= −i + j + k 同理 ⎠ a
(
)
(
)
(
)
2π ⎧ ⎪b1 = a −i + j + k ⎪ 2π ⎪ i− j+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b3 = a i + j − k ⎩
(
)
(
)
(
)
由此可得出面心立方格子的倒格子为一体心立方格子; 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中,晶面常用四个指数(hkil)来表示,如图 所示,前三个指数表示晶面族中最靠近原点的晶面在互成 1200的 共面轴 a1 , a2 , a3 上的截距为
设两法线之间的夹角满足
K 1 i K 2 = K1 i K 2 cos γ
K 1iK 2 cos γ = = K1 i K 2 2π 2π (h1 i + k1 j + l1 k )i (h2 i + k2 j + l2 k ) a a 2π 2π 2π 2π (h1 i + k1 j + l1 k )i (h1 i + k1 j + l1 k ) i (h2 i + k2 j + l2 k )i (h2 i + k2 j + l2 k ) a a a a
a1 a2 a3 , , ,第四个指数表示该晶面 h k i
在六重轴c上的截距为
c 。证明: l
i = −(h + k )
并将下列用(hkl)表示的晶面改用(hkil)表示:
2
第一章 晶体的结构
( 001) , (133) , (110 ) , ( 323) , (100 ) , ( 010 ) , ( 213) .
即 l1k1 + l2 k2 + l3 k3 =
1 p
因为上式左边是整数,而右边是分数,显然是不成立的。要式成立,必须满足 p=1。而此时 h1 , h2 , h3 是互 质的。 1.5 证明:在立方晶系中,面指数为 ( h1k1l1 ) 和 ( h2 k2l3 ) 的两个晶面之间的夹角满足
cos θ =
(
) )
)
1 3 a 4
a 2
(
(
)
2π ⎧ b a 2 × a3 1 = ⎪ Ω ⎪ 2π ⎪ a 3 × a1 ⎨b 2 = Ω ⎪ 2π ⎪ ⎪b3 = Ω a1 × a 2 ⎩
(
) ) )
(
(
Ω = a1 ⋅ a 2 × a 3 =
i a a 2 × a3 = 2 a 2 j 0 a 2
(
k 0 a =i a 2 2 0
5
倒格子矢量为
K h′ = hb1 + kb 2 + lb3 =
第一章 晶体的结构
代表晶面族 ( hkl ) 的法线方向。 晶面族 ( h1k1l1 ) 的法线方向对应倒格矢 K 1 =
2π (h1 i + k1 j + l1 k ) a 2π 晶面族 ( h2 k2l3 ) 的法线方向对应倒格矢 K 2 = (h2 i + k2 j + l2 k ) a
a 2 +j a 0 − 2
a 2
a 2 +k a 0 2
0 a 2
=−
b 1=
a2 a2 a2 i+ j+ k 4 4 4
2π 2π a 2 ⎛ a 2 a2 a2 a 2 × a3 = 3 − i + j + ⎜ a Ω 2 ⎝ 4 4 4 4 2π 2π b 2= i − j + k ,b 3= i+ j−k a a
a2 a3 a1
(1)按基矢 a1 , a2 , a3 在空间作重复平移,就可得到它的布喇菲格子,因为此晶体是简单格子,因此 晶体中原子位置可以认为与格点重合。由右图可见,它是体心立方布喇菲格子,属于立方晶系。
−27 3 (2)原胞体积 Ω = a1 • a2 × a3 = 3i • ⎡3 j ×1.5 i + j + k ⎤ = 13.5 × 10 m
(
)
(
)
2π ⎧ ⎪b1 = a j + k ⎪ 2π ⎪ i+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b 3 = a i + j ⎩
(
) )
(
(
)
1
由此可知,体心立方格子的倒格子为一面心立方格子。
第一章 晶体的结构
我们知面心立方格子的基矢为
a ⎧ a j+k 1 = ⎪ 2 ⎪ a ⎪ ⎨a 2 = i + k 2 ⎪ a ⎪ ⎪a3 = 2 i + j ⎩
A B
a1
C
a2
1 1 1 OA • OB sin ∠AOB + OC • OB sin ∠COB = OA • OC sin ∠AOC 2 2 2 a a a 代入 OA = n, OB = − n, OC = n, 和 ∠AOB = ∠COB = 60 , ∠AOC = 120 ,有 h k i 1a a 1a a 1a a ini(− ) sin 600 + i ni(− ) sin 600 = i ni( ) sin1200 2h k 2i k 2h i 1 1 1 得− − = ,两边同乘(hki)并移项得 hk ik hi
( 001) → ( 0001) , (133) → (1323) , (110 ) → (1100 ) , ( 323) → ( 3213) (100 ) → (1010 ) , ( 010 ) → ( 0110 ) , ( 213) → ( 2133) .
1.3 如将等体积的硬球堆成下列结构,求证能占据的最大体积与总体积之比为: (1)简单立方
3 (i − j + k ) 2 3 (i + j − k ) 2
a3 = a + b − c =
a1 , a2 , a3 对应体心立方结构. a1 , a2 , a3 满足选作基矢的充分条件.可见基矢为, a1 = 3i , a 2 = 3j , a 3 = 1.5(i + j + k ) ,的晶体为体心立方结构.
(
)
⎣
(
)⎦
晶胞体积 V = a • a × a = 3i • 3 j × 3k = 27 × 10
(
)
(
)
−27
m3
因为 Ω =
V ,知该晶体属于立方晶系; 2
参考王矜奉 1.2.6 我们可以构造新的矢量
a1 = c − a =
3 ( −i + j + k ) 2
6
第一章 晶体的结构
a2 = c − b =
1.4 设某一晶面族的面间距为 d,三个基矢 a1 , a2 , a3 的末端
4
第一章 晶体的结构
分别落在离原点距离为 h1d , h2 d , h3 d , 的晶面上,试用反证法证明: h1 , h2 , h3 是互质的。 解:参考王矜奉 1.2.4 设该晶面的单位法向矢量为 n ,由已知条件可得
试求: (1) 此晶体属于什么晶系,属于哪种类型的布喇菲格子? (2) 原胞的体积和晶胞的体积各等于多少? (3) 该晶体的倒格子基矢; (4) 密勒指数为(121)晶面族的面间距; (5) 原子最密集的晶面族的密勒指数是多少? (6) [111]与[111]晶列之间的夹角余弦为多少? 解:参考徐至中 1-5,中南大学 1.17
4 4 6 ⋅ πR 3 6 ⋅ πR 3 3 3 = = α= 2 2 3 (2 R) 3a ⋅c 6 ⋅ (4 6 / 3) R 6 4 4
2π 6
(5)在金刚石的结晶学原胞中,设原子半径为 R ,则原胞的晶体学常数 a = (8 / 3 ) R ,则金刚石的 致密度为:
4 4 8 ⋅ πR 3 8 ⋅ πR 3 3π 3 = = α = 33 3 3 16 a (8 / 3 ) R
2π ⎧ ⎪b1 = Ω a 2 × a 3 ⎪ 2π ⎪ a 3 × a1 ⎨b 2 = Ω ⎪ 2π ⎪ ⎪b3 = Ω a1 × a 2 ⎩
(
) ) )
(
(
Ω = a1 ⋅ a 2 × a 3 =
(
)
1 3 a 2
i a a 2 × a3 = 2 a 2 a2 a2 = j+ k 2 2 b 1=
π
6
; (2)体心立方
3π 2π ; (3)面心立方 8 6
(4)六角密积
2π 3π ; (5)金刚石 6 16
解: 设 N 为一个晶胞中的刚性原子数,R 表示刚性原子的球半径,V 表示晶胞体积,立方晶格的边长为 a, 则致密度为:
3
第一章 晶体的结构
4 N ⋅ π R3 3 α= V
则原胞的晶体学常数 a = 2 R , (1) 在简立方的结晶学原胞中, 设原子半径为 R , 则简立方的致密度(即球可能占据的最大体积与总体积之比)为:
12 12
cos γ =
(h
2 1
+ k12 + l12 ) i( h22 + k22 + l22 )
h1h2 + k1k2 + l1l2
a 2 = 3j , 1.6 有一晶格, 每一晶格上有一个原子, 基矢 (以 nm 为单位) 分别为 a1 = 3i , a 3 = 1.5(i + j + k ) 。
( 3 )在面心立方的结晶学原胞中,设原子半径为 R ,则原胞的晶体学常数
a = 2 2 R ,则面心立方的致密度为:
4 4 4 ⋅ πR 3 2 ⋅ πR 3 3 α = 33 = = a (2 2 R) 3 2π 6
