您的位置：360文档中心› (新)高中数学三角函数知识点及试题总结

(新)高中数学三角函数知识点及试题总结

合集下载

高中数学必修一第五章三角函数知识点归纳总结(精华版)(带答案)

高中数学必修一第五章三角函数知识点归纳总结(精华版)(带答案)

高中数学必修一第五章三角函数知识点归纳总结(精华版)单选题1、若sin (π7+α)=12，则sin (3π14−2α)=（ ） A ．35B ．−12C ．12D ．13答案：C分析：令θ=π7+α可得α=θ−π7，再代入sin (3π14−2α)，结合诱导公式与二倍角公式求解即可令θ=π7+α可得α=θ−π7，故sinθ=12，则sin (3π14−2α)=sin (3π14−2(θ−π7)) =sin (π2−2θ)=cos2θ=1−2sin 2θ=12故选：C2、若sin(π−α)+cos(−α)=15，α∈(0,π)，则tan (32π−α)的值为（ ） A ．−43或−34B ．−43C ．−34D ．34答案：C分析：根据同角三角函数的基本关系及诱导公式求解. 由sin(π−α)+cos(−α)=15可得：sinα+cosα=15，平方得：sin 2α+2sinαcosα+cos 2α=125 所以tan 2α+2tanα+1tan 2α+1=125，解得tanα=−43或tanα=−34， 又sinα+cosα=15，所以|sinα|>|cosα|， 故tanα=−43， 故选：C3、已知函数f(x)=cos 2ωx 2+√32sinωx −12(ω>0,x ∈R)，若函数f(x)在区间(π,2π)内没有零点，则ω的取值范围是（ ）A ．(0,512]B ．(0,56)C ．(0,512]∪[56,1112]D ．(0,512]∪(56,1112] 答案：C分析：先化简函数解析式，由π<x <2π得，求得πω+π6<ωx +π6<2πω+π6，利用正弦函数图象的性质可得2πω+π6≤π或{2πω+π6≤2ππω+π6≥π，求解即可. f(x)=cosωx+12+√32sinωx −12=√32sinωx +12cosωx =sin(ωx +π6)．由π<x <2π得，πω+π6<ωx +π6<2πω+π6， ∵函数f(x)在区间(π,2π)内没有零点，且πω+π6>π6， ∴2πω+π6≤π或{2πω+π6≤2ππω+π6≥π ， 解得0<ω⩽512或56⩽ω⩽1112，则ω的取值范围是(0,512]∪[56,1112].故选：C ．4、已知函数y =√2sin(x +π4)，当y 取得最小值时，tanx 等于（ ）A ．1B ．−1C ．√32D ．−√32答案：A分析：由正弦函数的性质，先求出当y 取得最小值时x 的取值，从而求出tanx . 函数y =√2sin(x +π4)，当y 取得最小值时，有x +π4=2kπ+3π2，故x =2kπ+5π4，k ∈Z ．∴tanx =tan (2kπ+5π4)=tan (π4)=1，k ∈Z ． 故选：A ．5、已知tanθ=2，则sin(π2+θ)−cos(π−θ)cosθ−sin(π−θ)=（ ）A ．2B ．-2C ．0D ．23 答案：B分析：根据tanθ=2，利用诱导公式和商数关系求解. 因为tanθ=2， 所以sin(π2+θ)−cos(π−θ)cosθ−sin(π−θ)，=2cosθcosθ−sinθ， =21−tanθ=−2，故选：B6、要得到函数y =sin (2x +π6)的图象，可以将函数y =cos (2x −π6)的图象（ ） A ．向右平移π12个单位长度B ．向左平移π12个单位长度C ．向右平移π6个单位长度D ．向左平移π6个单位长度 答案：A分析：利用诱导公式将平移前的函数化简得到y =sin (2x +π3)，进而结合平移变换即可求出结果.因为y =cos (2x −π6)=sin (2x −π6+π2)=sin (2x +π3)，而y =sin [2(x −π12)+π3]，故将函数y =cos (2x −π6)的图象向右平移π12个单位长度即可， 故选：A. 7、已知sinα=2√67，cos (α−β)=√105，且0<α<3π4，0<β<3π4，则sinβ=（ ）A ．9√1535B ．11√1035C ．√1535D ．√1035答案：A解析：易知sinβ=sin(α−(α−β))，利用角的范围和同角三角函数关系可求得cosα和sin (α−β)，分别在sin (α−β)=√155和−√155两种情况下，利用两角和差正弦公式求得sinβ，结合β的范围可确定最终结果. ∵sinα=2√67<√22且0<α<3π4，∴0<α<π4，∴cosα=√1−sin 2α=57. 又0<β<3π4，∴−3π4<α−β<π4，∴sin (α−β)=±√1−cos 2(α−β)=±√155. 当sin (α−β)=√155时，sinβ=sin(α−(α−β))=sinαcos (α−β)−cosαsin (α−β) =2√67×√105−57×√155=−√1535， ∵0<β<3π4，∴sinβ>0，∴sinβ=−√1535不合题意，舍去； 当sin (α−β)=−√155，同理可求得sinβ=9√1535，符合题意.综上所述：sinβ=9√1535.故选：A .小提示：易错点睛：本题中求解cosα时，易忽略sinα的值所确定的α的更小的范围，从而误认为cosα的取值也有两种不同的可能性，造成求解错误. 8、若tanθ=2，则sinθ(1−sin2θ)sinθ−cosθ=（ ）A ．25B ．−25C ．65D ．−65 答案：A分析：由二倍角正弦公式和同角关系将sinθ(1−sin2θ)sinθ−cosθ转化为含tanθ的表达式，由此可得其值. sinθ(1−sin2θ)sinθ−cosθ=sinθ(sin 2θ+cos 2θ−sin2θ)sinθ−cosθ=sinθ(sinθ−cosθ)2sinθ−cosθ=sin 2θ−sinθcosθsin 2θ+cos 2θ=tan 2θ−tanθtan 2θ+1=25．故选：A. 多选题9、若α是第二象限的角，则下列各式中成立的是（ ） A ．tanα=−sinαcosαB ．√1−2sinαcosα=sinα−cosαC ．cosα=−√1−sin 2αD ．√1+2sinαcosα=sinα+cosαE ．sinα=−√1−cos 2α 答案：BC解析：利用sin 2α+cos 2α=1,tanα=sinαcosα，结合三角函数在各个象限的符号，代入每个式子进行化简、求值.对A ，由同角三角函数的基本关系式，知tanα=sinαcosα，所以A 错；对B ，C ，D ，E ，因为α是第二象限角，所以sinα>0,cosα<0，所以sinα−cosα>0,sinα+cosα的符号不确定，所以√1−2sinαcosα=√(sinα−cosα)2=sinα−cosα，所以B ，C 正确；D ，E 错． 故选：BC.小提示：本题考查同角三角函数的基本关系、三角函数在各个象限的符号，考查运算求解能力. 10、下列各式中，值为12的是（ ）A ．cos 2π12−sin 2π12B ．tan22.5∘1−tan 222.5∘C ．2sin195°cos195°D ．√1+cos π62答案：BC分析：运用二倍角公式，结合诱导公式和特殊角的三角函数值的求法即可得到答案. 选项A ，cos 2π12−sin 2π12=cos (2×π12)=cos π6=√32，错误； 选项B ，tan22.5°1−tan 222.5°=12⋅2tan22.5°1−tan 222.5°=12tan45°=12，正确；选项C ，2sin195∘cos195∘=sin390∘=sin (360∘+30∘)=sin30∘=12，正确；选项D ，√1+cos π62=√1+√322=√2+√32，错误.故选：BC.11、（多选）已知θ∈(0,π)，sinθ+cosθ=15，则（ ）A ．θ∈(π2,π)B ．cosθ=−35 C ．tanθ=−34D ．sinθ−cosθ=75答案：ABD分析：已知式平方求得sinθcosθ，从而可确定θ的范围，然后求得sinθ−cosθ，再与已知结合求得sinθ,cosθ，由商数关系得tanθ，从而可判断各选项．因为sinθ+cosθ=15①，所以(sinθ+cosθ)2=sin 2θ+2sinθcosθ+cos 2θ=125，所以2sinθcosθ=−2425．又θ∈(0,π)，所以sinθ>0，所以cosθ<0，即θ∈(π2,π)，故A 正确．(sinθ−cosθ)2=1−2sinθcosθ=4925，所以sinθ−cosθ=75②，故D 正确．由①②，得sinθ=45，cosθ=−35，故B 正确．tanθ=sinθcosθ=−43，故C 错误． 故选：ABD ． 填空题12、当θ∈(0,π2)时，若cos (5π6−θ)=−12，则sin (θ+π6)的值为_________．答案：√32##12√3 分析：先由已知条件求出sin (5π6−θ)，然后利用诱导公式可求得结果. ∵θ∈(0,π2)，∴5π6−θ∈(π3,5π6)， ∴sin (5π6−θ)=√1−cos 2(5π6−θ)=√32， ∴sin (θ+π6)=sin [π−(5π6−θ)]=sin (5π6−θ)=√32． 所以答案是：√3213、已知sinα=2cosα，则sin 2α+2sinαcosα=______． 答案：85##1.6分析：根据题意，由同角三角函数关系可得tanα的值，而sin 2α+2sinαcosα1=sin 2α+2sinαcosαsin 2α+cos 2α，最后利用齐次式化成关于tanα的分式即可解.解：由sinα=2cosα，得tanα=sinαcosα=2， 则sin 2α+2sinαcosα1=sin 2α+2sinαcosαsin 2α+cos 2α=tan 2α+2tanαtan 2α+1=22+2×222+1=85.所以答案是：85.14、已知f (x )=sin (ωx +π3)(ω>0)，f (π6)=f (π3)，且f (x )在区间(π6,π3)上有最小值，无最大值，则ω=______.答案：143分析：由题意可得函数的图象关于直线x=π4对称，再根据f(x)在区间(π6,π3)上有最小值，无最大值，可得π4ω+π3=2kπ+3π2(k∈Z)，由此求得ω的值．依题意，当x=π6+π32=π4时，y有最小值，即sin(π4ω+π3)=−1，则π4ω+π3=2kπ+3π2(k∈Z)，所以ω=8k+143(k∈Z).因为f(x)在区间(π6,π3)上有最小值，无最大值，所以π3−π4≤T2=πω，即ω≤12，令k=0，得ω=143.所以答案是：143解答题15、已知函数f(x)=2sinxcosx−2√3sin2x+√3.(1)求函数f(x)的最小正周期及其单调递增区间；(2)当x∈[−π6,π6]，时，a−f(x)≤0恒成立，求a的最大值.答案：(1)最小正周期π，单调递增区间为[kπ−5π12,kπ+π12]，k∈Z(2)最大值为0分析：（1）根据正弦和余弦的二倍角公式以及辅助角公式即可化简f(x)为f(x)=2sin(2x+π3)，然后根据周期公式可求周期，整体代入法求单调增区间,（2）根据x的范围可求2x+π3∈[0,2π3]，进而可求f(x)的值域，故可求a的范围.（1）f(x)=2sinxcosx−2√3sin2x+√3=sin2x+√3cos2x=2sin(2x+π3)故函数f(x)的最小正周期T=2π2=π.由2kπ-π2≤2x+π3≤2kπ+π2得kπ−5π12≤x≤kπ+π12(k∈Z).∴函数f(x)的单调递增区间为[kπ−5π12,kπ+π12]，k∈Z.（2）∵x∈[−π6,π6]，∴2x+π3∈[0,2π3]，∴sin (2x +π3)∈[0,1]，f (x )=2sin (2x +π3)∈[0,2].由a −f (x )≤0恒成立，得a ≤(f (x ))min ，即a ≤0.故a 的最大值为0.。

2024届全国新高考数学精准复习三角函数知识点总结

2024届全国新高考数学精准复习三角函数知识点总结

千里之行，始于足下。

2024届全国新高考数学精准复习三角函数知识点总结2024届全国新高考数学考试中，三角函数是一个重要的知识点。

以下是三角函数的主要内容和考点总结：1. 基本概念：- 弧度与角度的转换：1弧度=180°/π，1度=π/180弧度。

- 正弦、余弦、正切、余切、正割、余割的定义与关系。

2. 三角函数的图像与性质：- 正弦函数和余弦函数的图像特点：周期为2π，在x轴上的零点为kπ，振幅为1。

- 正切函数的图像特点：周期为π，在x轴上的零点为kπ，无振幅。

- 三角函数的奇偶性：正弦函数是奇函数、余弦函数是偶函数、正切函数是奇函数。

- 三角函数的周期性：正弦、余弦函数的周期为2π，正切函数的周期为π。

3. 三角函数的性质与关系：- 三角函数的基本关系：tanx=sinx/cosx，cotx=1/tanx，secx=1/cosx，cscx=1/sinx。

- 三角函数的倒数关系：sinx=1/cscx，cosx=1/secx，tanx=1/cotx。

- 三角函数的平方关系：sin^2x+cos^2x=1，1+tan^2x=sec^2x，1+cot^2x=csc^2x。

4. 三角函数的性质与特殊值：- 正弦函数和余弦函数的取值范围：-1≤sinx≤1，-1≤cosx≤1。

第1页/共2页锲而不舍，金石可镂。

- 正切函数和余切函数的取值范围：tanx属于R，cotx属于R。

- 三角函数的特殊值：sin0=0，cos0=1，sin90°=1，cos90°=0，tan45°=1，cot45°=1。

5. 三角函数的解析式与性质：- sin(x±y)=sinxcosy±cosxsiny。

- cos(x±y)=cosxcosy∓sinxsiny。

- tan(x±y)=(tanx±tany)/(1∓tanxtany)。

((完整版))高中数学三角函数知识点总结和常见题类型归纳,推荐文档

((完整版))高中数学三角函数知识点总结和常见题类型归纳,推荐文档

高中数学三角函数常见习题类型及解法高考试题中出现的三角函数问题，难度相对较低，重点突出。

该类试题集中在第15题的位置，共分为两种考察形式：解三角形和三角函数变换。

因此，在复习过程中既要注重三角知识的基础性，突出三角函数的图象、周期性、单调性、奇偶性、对称性等性质，以及化简、求函数值和最值等重点内容的复习；又要注重三角知识的工具性，突出三角与代数、几何的综合联系，以及三角知识的应用意识。

一、知识整合1．熟练掌握三角变换公式，理解每个公式的含义以及常规使用方法等；熟悉三角变换常用的方法——化弦法，降幂法，角的变换法等；并能灵活应用这些方法进行三角函数的求值、化简；掌握三角变换公式在三角形中应用的特点，并能结合三角形的公式解决一些实际问题。

2．熟练掌握正弦函数、余弦函数、正切函数的性质，并能用它研究复合函数的性质；熟练掌握正弦函数、余弦函数、正切函数的图象特点，会用五点作图法画出函数y=Asin( x+ )的图象；理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化。

3.熟练掌握三角形中的正弦定理和余弦定理，明确两个定理的应用条件。

能够依托题目给的不同已知条件，灵活运用两个定理解决实际问题。

二、高考考点分析近些年北京高考中本部分所占分值大约是13-18分，主要以解答题的形式出现，少数时候会有填空题。

主要考察内容按难度分，我认为有以下两个层次：第一层次：通过对诱导公式和倍角公式等公式的灵活运用，解决有关三角函数基本性质的问题，如判断符号、求值、求周期、判断奇偶性等；通过正弦定理和余弦定理的灵活运用，解决有关三角形的简单问题，如求角、边长等。

第二层次：充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质，解决较复杂的函数问题，如：求复合函数值域。

三、方法技巧（1）常数的代换：特别是：1=cos2θ+sin2θ。

（2）项的分拆与角的配凑。

（3）降幂扩角法和升幂半角法。

部编版高中数学必修一第五章三角函数带答案知识点总结全面整理

部编版高中数学必修一第五章三角函数带答案知识点总结全面整理

(名师选题)部编版高中数学必修一第五章三角函数带答案知识点总结全面整理单选题1、函数f(x)=sin (2x −π3)的一个对称中心的坐标是（ ） A ．(0,0)B ．(0,−√32)C ．(π2,0)D ．(π6,0) 2、已知tanα=−2，则2sinα+cosαcosα−sinα=（ ）A ．−4B ．−12C ．−1D ．−13 3、已知sinαcosα=12，则tanα+1tanα的值为（ ）A ．12B ．−12C ．−2D ．24、已知函数y =√2sin(x +π4)，当y 取得最小值时，tanx 等于（ ） A ．1B ．−1C ．√32D ．−√325、若函数f(x)=sinωx (ω>0)，在区间[0,π3]上单调递增，在区间[π3,π2]上单调递减，则ω=（ ）． A ．1B ．32C ．2D ．36、将函数y =2sin (x +π3)的图象向左平移m (m >0)个单位长度后，所得到的图象关于原点对称，则m 的最小值是（ ） A ．π12B ．π6C ．π3D ．2π37、sin (3π2+α)=（ ）A ．sinαB ．−sinαC ．cosαD ．−cosα8、函数f (x )=2sin (ωx +φ)(ω>0)图像上一点P (s,t )(−2<t <2)向右平移2π个单位，得到的点Q 也在f (x )图像上，线段PQ 与函数f (x )的图像有5个交点，且满足f (π4−x)=f (x )，f (−π2)>f (0)，若y =f (x )，x ∈[0,π2]与y =a 有两个交点，则a 的取值范围为（ ） A ．(−2,−√2]B ．[−2,−√2]C ．[√2,2)D ．[√2,2]多选题9、已知函数f(x)=3sin(ωx +π3)(ω>0)的图象对称轴与对称中心的最小距离为π4，则下列结论正确的是（ ）A ．f(x)的最小正周期为2πB ．f(x)的图象关于(−π6,0)对称 C ．f(x)在(−5π12,π12)上单调递减 D ．f(x)的图象关于直线x =7π12对称 10、下列不等式中成立的是（ ） A ．sin1<sin π3B ．cos2π3>cos2C ．cos (−70∘)>sin18∘D ．sin4π5>sin17π611、已知函数f(x)=sin(3x +φ)(−π2<φ<π2)的图象关于直线x =π4对称，则（ ） A ．函数f (x +π12)为偶函数B ．函数f(x)在[π12,π6]上单调递增C ．若|f (x 1)−f (x 2)|=2，则|x 1−x 2|的最小值为π3D ．将函数f(x)图象上所有点的横坐标缩小为原来的13，得到函数y =sin(x +φ)的图象 填空题12、若sin (θ+π8)=13，则sin (2θ−π4)＝________.13、若cosα=−35, α为第二象限的角，则sin(π−α)=__________．部编版高中数学必修一第五章三角函数带答案(四十二)参考答案1、答案：D分析：解方程2x−π3=kπ,k∈Z即得解.解：令2x−π3=kπ,k∈Z,∴x=12kπ+π6，令k=0,∴x=π6，所以函数f(x)=sin(2x−π3)的一个对称中心的坐标是(π6,0).故选：D2、答案：C分析：利用齐次化可求三角函数式的值.2sinα+cosαcosα−sinα=2tanα+11−tanα=−4+11−(−2)=−1，故选：C．3、答案：D解析：根据题中条件，由切化弦，将所求式子化简整理，即可得出结果.∵sinαcosα=12，∴tanα+1tanα=sinαcosα+cosαsinα=sin2α+cos2αsinαcosα=112=2，故选：D.4、答案：A分析：由正弦函数的性质，先求出当y取得最小值时x的取值，从而求出tanx.函数y=√2sin(x+π4)，当y取得最小值时，有x+π4=2kπ+3π2，故x=2kπ+5π4，k∈Z．∴tanx=tan(2kπ+5π4)=tan(π4)=1，k∈Z．故选：A．5、答案：B分析：根据f(π3)=1以及周期性求得ω.依题意函数f(x)=sinωx (ω>0)，在区间[0,π3]上单调递增，在区间[π3,π2]上单调递减， 则{f (π3)=sin π3ω=1T 2=πω≥π3， 即{π3ω=2kπ+π2,k ∈Z 0<ω≤3 ，解得ω=32.故选：B 6、答案：D分析：由三角函数平移变换可得平移后函数为y =2sin (x +m +π3)，根据对称性得到m +π3=kπ(k ∈Z )，结合m >0可得所求最小值.将y =2sin (x +π3)向左平移m (m >0)个单位长度得：y =2sin (x +m +π3)，∵y =2sin (x +m +π3)图象关于原点对称，∴m +π3=kπ(k ∈Z )，解得：m =−π3+kπ(k ∈Z )，又m >0， ∴当k =1时，m 取得最小值2π3. 故选：D. 7、答案：D分析：利用诱导公式sin (π+α)=−sinα,sin (π2+α)=cos α代入计算． sin (3π2+α)=sin (π+π2+α)=−sin (π2+α)=−cos α． 故选：D ． 8、答案：A分析：首先根据已知条件分析出|PQ |=2π=2T ，可得ω=2，再由f (π4−x)=f (x )可得y =f (x )对称轴为x =π8，利用f (−π2)>f (0)可以求出符合题意的一个φ的值，进而得出f (x )的解析式，再由数形结合的方法求a 的取值范围即可.如图假设P(0,0)，线段PQ与函数f(x)的图像有5个交点，则|PQ|=2π，所以由分析可得|PQ|=2π=2T，所以T=π，可得ω=2πT =2ππ=2，因为f(π4−x)=f(x)所以f[π4−(π8+x)]=f(π8+x)，即f(π8−x)=f(π8+x)，所以x=π8是f(x)的对称轴，所以2×π8+φ=π2+kπ(k∈Z)，即φ=π4+kπ(k∈Z)，f(−π2)=2sin(−π+φ)=−2sinφ>f(0)=2sinφ，所以sinφ<0，可令k=−1得φ=−3π4，所以f(x)=2sin(2x−3π4)，当x∈[0,π2]时，令2x−3π4=t∈[−3π4,π4]，则f(t)=2sint，t∈[−3π4,π4]作f(t)图象如图所示：当t=−3π4即x=0时y=−√2，当t=−π2即x=π8时，y=−2，由图知若y =f (x )，x ∈[0,π2]与y =a 有两个交点，则a 的取值范围为(−2,−√2]， 故选：A小提示：关键点点睛：本题解题的关键是取特殊点P (0,0)便于分体问题，利用已知条件结合三角函数图象的特点，以及三角函数的性质求出f (x )的解析式，再利用数形结合的思想求解a 的取值范围. 9、答案：BD分析：先利用f(x)的图象对称轴与对称中心的最小距离和周期的关系求出ω值，再利用整体思想求其周期、单调性和对称轴.因为f(x)的图象对称轴与对称中心的最小距离为π4，所以T 4=π4，即T =π，即选项A 错误； 由T =2πω=π，得ω=2，即f(x)=3sin(2x +π3)，因为f(−π6)=3sin(−π3+π3)=3sin0=0，所以f(x)的图象关于(−π6,0)对称，即选项B 正确； 当−5π12<x <π12时，则−π2<2x +π3<π2，所以f(x)=3sin(2x +π3)在(−5π12,π12)上单调递增，即选项C 错误；因为f(7π12)=3sin(7π6+π3)=3sin 3π2=−3，所以f(x)的图象关于直线x =7π12对称，即选项D 正确. 故选:BD. 10、答案：ACD分析：结合诱导公式，根据y =sinx 和y =cosx 的单调性依次判断各个选项即可得到结果. 对于A ，∵y =sinx 在(0,π2)上单调递增，又0<1<π3<π2，∴sin1<sin π3，A 正确； 对于B ，∵y =cosx 在(π2,π)上单调递减，又π2<2<2π3<π，∴cos2π3<cos2，B 错误；对于C ，∵cos (−70∘)=cos70∘=sin20∘，又sin20∘>sin18∘，∴cos (−70∘)>sin18∘，C 正确； 对于D ，∵sin4π5=sin (π−π5)=sin π5，sin17π6=sin (3π−π6)=sin π6，又sin π6<sin π5，∴sin 4π5>sin17π6，D 正确.故选：ACD. 11、答案：BC分析：根据函数f(x)=sin(3x +φ)(−π2<φ<π2)的图象关于直线x =π4对称，由3×π4+φ=kπ+π2,k ∈Z 求得函数的解析式，再逐项判断.因为函数f(x)=sin(3x +φ)(−π2<φ<π2)的图象关于直线x =π4对称， 所以3×π4+φ=kπ+π2,k ∈Z ，即φ=kπ−π4,k ∈Z ， 又因为−π2<φ<π2，则φ=−π4， 所以f(x)=sin(3x −π4)，A.函数f (x +π12)=sin(3(x +π12)−π4)=sin3x 为奇函数，故错误；B. 因为x ∈[π12,π6]，则3x −π4∈[0,π4]，又y =sinx 在[0,π4]上递增，所以函数f(x)在[π12,π6]上单调递增，故正确； C. T =2π3因为|f (x 1)−f (x 2)|=2，则f (x 1),f (x 2) 分别为函数的最大值和最小值，则|x 1−x 2|的最小值为T 2=π3，故正确；D.将函数f(x)图象上所有点的横坐标缩小为原来的13，得到函数y =sin(9x −π4)的图象，故错误； 故选：BC 12、答案：−79分析：由题知2(θ+π8)−π2=(2θ−π4)，进而根据诱导公式与二倍角公式求解即可.解：因为2(θ+π8)−(2θ−π4)=π2，所以sin (2θ−π4)=sin [2(θ+π8)−π2]=−cos [2(θ+π8)] =2sin 2(θ+π8)−1=2×(13)2−1=−79． 所以答案是：−7913、答案：45分析：先根据同角三角函数的关系求出sinα，再结合诱导公式即可求出sin(π−α).,α为第二象限的角，∵cosα=−35，∴sinα=√1−cos2α=45∴sin(π−α)=sinα=4.5.所以答案是：45小提示：本题考查同角三角函数的关系以及诱导公式的应用，属于基础题.。

新高考三角函数知识点归纳总结

新高考三角函数知识点归纳总结

新高考三角函数知识点归纳总结三角函数在新高考数学考试中扮演着重要的角色。

掌握三角函数的相关知识点，不仅可以帮助我们解决各类与角度、长度及图形性质相关的问题，还能够为以后的高等数学学习打下坚实的基础。

本文将对新高考中的三角函数知识点进行归纳总结，以帮助同学们更好地复习和应对考试。

一、三角函数的基本概念和性质三角函数包括正弦函数、余弦函数和正切函数，它们都是角的函数，表示角与某一边的长度的比值。

1. 正弦函数（sin）：在直角三角形中，正弦值等于对边与斜边的比值，即sin(A) = a/c。

2. 余弦函数（cos）：在直角三角形中，余弦值等于邻边与斜边的比值，即cos(A) = b/c。

3. 正切函数（tan）：在直角三角形中，正切值等于对边与邻边的比值，即tan(A) = a/b。

此外，我们还需了解三角函数在单位圆上的定义和性质：4. 单位圆的角度：单位圆的半径为1，角度以弧度制表示，其中360°等于2π弧度。

5. 弧度与角度的转换关系：1弧度约等于57.3°，即1弧度≈ 57.3°。

6. 三角函数的周期性：正弦函数和余弦函数的周期为2π，而正切函数的周期为π。

二、三角函数的基本关系及推导1. 三角函数之间的基本关系：根据三角恒等式，我们可以推导出三角函数之间的基本关系。

例如，sin²A + cos²A = 1，tanA = sinA/cosA等。

2. 三角函数的和差化积公式：通过和差化积公式，我们可以将两个三角函数的和差表示为一个三角函数的乘积。

三、三角函数的图像和性质1. 正弦函数的图像和性质：正弦函数的图像是一条连续的波浪线，振幅为1，在0～2π的区间内周期性重复。

2. 余弦函数的图像和性质：余弦函数的图像也是一条连续的波浪线，振幅为1，在0～2π的区间内周期性重复，与正弦函数的图像相位差90°。

3. 正切函数的图像和性质：正切函数的图像有无数个渐近线，它在每个π的整数倍处有一个垂直渐近线，且在每个π/2的整数倍处有一个水平渐近线。

高中数学必修五三角函数知识点+练习题含答案解析(很详细)

高中数学必修五三角函数知识点+练习题含答案解析(很详细)

高中数学必修五三角函数知识点+练习题含答案解析(很详细)第一部分必修五三角函数知识点整理第一章解三角形1、三角形的性质：①.A+B+C=π,? 222A B C π+=-?sin cos 22A B C += ②.在ABC ?中, a b +＞c , a b -＜c ; A ＞B ?sin A ＞sinB ...........................A ＞B ?cosA ＜cosB, a ＞b ? A ＞B③.若ABC ?为锐角?，则A B +＞2π,B+C ＞2π,A+C ＞2π; 22a b +＞2c ，22b c +＞2a ，2a ＋2c ＞2b2、正弦定理与余弦定理：①.(2R 为ABC ?外接圆的直径)2s i n a R A =、2sin b R B =、2sin c R C =sin 2a A R =、 sin 2b B R =、 sin 2c C R= 面积公式：111sin sin sin 222ABC S ab C bc A ac B ?=== ②.余弦定理：2222cos a b c bc A =+-、2222cos b a c ac B =+-、2222cos c a b ab C =+-222cos 2b c a A bc +-=、222cos 2a c b B ac +-=、222cos 2a b c C ab+-= 补充：两角和与差的正弦、余弦和正切公式：⑴()cos cos cos sin sin αβαβαβ-=+；⑵()cos cos cos sin sin αβαβαβ+=-；⑶()sin sin cos cos sin αβαβαβ-=-；⑷()sin sin cos cos sin αβαβαβ+=+；⑸()tan tan tan 1tan tan αβαβαβ --=+ ? （()()tan tan tan 1tan tan αβαβαβ-=-+）；⑹()tan tan tan 1tan tan αβαβαβ++=- ? （()()tan tan tan 1tan tan αβαβαβ+=+-）．二倍角的正弦、余弦和正切公式：⑴sin 22sin cos ααα=．222)cos (sin cos sin 2cos sin 2sin1ααααααα±=±+=±?⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+ ?落幂公式2cos 21cos 2αα+=，21cos 2sin 2αα-=．第二部分必修五练习题含答案解析第一章解三角形1.在△ABC 中，AB ＝5，BC ＝6，AC ＝8，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．非钝角三角形解析：最大边AC 所对角为B ，则cosB ＝52＋62－822×5×6＝－320B>CB ．B>A>C C ．C>B>AD ．C>A>B解析由正弦定理a sinA ＝b sinB ，∴sinB ＝bsinA a ＝32.∵B 为锐角，∴B ＝60°，则C ＝90°，故C>B>A. 答案 C3．在△ABC 中，已知a ＝8，B ＝60°，C ＝75°，则b 等于( )A ．4 2B ．4 3C ．4 6 D.323解:由A ＋B ＋C ＝180°，可求得A ＝45°，由正弦定理，得b ＝asinB sinA ＝8×sin60°sin45°＝8×3222＝4 6. 答案 C4．在△ABC 中，AB ＝5，BC ＝7，AC ＝8，则BA →·BC → 的值为( )A ．5B ．－5C ．15D ．－15解析在△ABC 中，由余弦定理得：cosB ＝AB 2＋BC 2－AC 22AB ·BC ＝25＋49－642×5×7＝17. ∴BA →·BC →＝|BA →|·|BC →|cosB ＝5×7×17＝5. 答案 A5．若三角形三边长之比是1：3：2，则其所对角之比是( )A ．1：2：3B ．1：3：2C ．1：2： 3 D.2：3：2解析设三边长分不为a ，3a,2a ，设最大角为A ，则cosA ＝a 2＋3a 2－2a 22·a ·3a ＝0，∴A ＝90°.设最小角为B ，则cosB ＝2a 2＋3a 2－a 22·2a ·3a ＝32，∴B ＝30°，∴C ＝60°. 所以三角之比为1：2：3. 答案 A6．在△ABC 中，若a ＝6，b ＝9，A ＝45°，则此三角形有( )A ．无解B ．一解C ．两解D ．解的个数别确定解析由b sinB ＝a sinA ，得sinB ＝bsinA a ＝9×226＝3 24>1.∴此三角形无解．答案 A7．已知△ABC 的外接圆半径为R ，且2R(sin 2A －sin 2C)＝(2a －b)sinB(其中a ，b 分不为A ，B 的对边)，这么角C 的大小为( )A ．30°B ．45°C ．60°D ．90°解析依照正弦定理，原式可化为2R ? ??a 24R 2－c 24R 2＝(2a －b)·b 2R ，∴a 2－c 2＝(2a －b)b ，∴a 2＋b 2－c 2＝2ab ，∴cosC ＝a 2＋b 2－c 22ab ＝22，∴C ＝45°. 答案 B8．在△ABC 中，已知sin 2A ＋sin 2B －sinAsinB ＝sin 2C ，且满脚ab ＝4，则该三角形的面积为( )A ．1B ．2 C. 2 D. 3解析由a sinA ＝b sinB ＝c sinC＝2R ，又sin 2A ＋sin 2B －sinAsinB ＝sin 2C ，可得a 2＋b 2－ab ＝c 2.∴c osC ＝a 2＋b 2－c 22ab ＝12，∴C ＝60°，sinC ＝32. ∴S △ABC ＝12absinC ＝ 3. 答案 D9．在△ABC 中，A ＝120°，AB ＝5，BC ＝7，则sinB sinC 的值为( ) A.85 B.58 C.53 D.35解析由余弦定理，得 cosA ＝AB 2＋AC 2－BC 22AB ·AC，解得AC ＝3. 由正弦定理sinB sinC ＝AC AB ＝35. 答案 D10.在三角形ABC 中，AB ＝5，AC ＝3，BC ＝7，则∠BAC 的大小为( )A.2π3B.5π6C.3π4D.π3解析由余弦定理，得cos ∠BAC ＝AB 2＋AC 2－BC 22AB ·AC ＝52＋32－722×5×3＝－12，∴∠BAC ＝2π3. 答案 A11．有一长为1 km 的歪坡，它的倾歪角为20°，现要将倾歪角改为10°，则坡底要加长( )A ．0.5 kmB ．1 kmC ．1.5 km D.32km 解析如图，AC ＝AB ·sin20°＝sin20°，BC ＝AB ·cos20°＝cos20°，DC ＝AC tan10°＝2cos 210°，∴DB ＝DC －BC ＝2cos 210°－cos20°＝1.答案 B12．已知△ABC 中，A ，B ，C 的对边分不为a ，b ，c.若a ＝c ＝6＋2，且A ＝75°，则b 为( )A ．2B ．4＋2 3C ．4－2 3 D.6－ 2解析在△ABC 中，由余弦定理，得a 2＝b 2＋c 2－2bccosA ，∵a ＝c ，∴0＝b 2－2bccosA ＝b 2－2b(6＋2)cos75°，而cos75°＝cos(30°＋45°)＝cos30°cos45°－sin30°sin45°＝22? ????32－12＝14(6－2)，∴b 2－2b(6＋2)cos75°＝b 2－2b(6＋2)·14(6－2)＝b 2－2b ＝0，解得b ＝2，或b ＝0(舍去)．故选A. 答案 A 13．在△ABC 中，A ＝60°，C ＝45°，b ＝4，则此三角形的最小边是____________．解析由A ＋B ＋C ＝180°，得B ＝75°，∴c 为最小边，由正弦定理，知c ＝bsinC sinB ＝4sin45°sin75°＝4(3－1)．答案 4(3－1)14．在△ABC 中，若b ＝2a ，B ＝A ＋60°，则A ＝________.解析由B ＝A ＋60°，得 sinB ＝sin(A ＋60°)＝12sinA ＋32cosA. 又由b ＝2a ，知sinB ＝2sinA.∴2sinA ＝12sinA ＋32cosA. 即32sinA ＝32cosA.∵cosA ≠0，∴tanA ＝33.∵0°<A<180°，∴A ＝30°. 答案30° 15．在△ABC 中，A ＋C ＝2B ，BC ＝5，且△ABC 的面积为103，则B ＝_______，AB ＝_______.解析由A ＋C ＝2B 及A ＋B ＋C ＝180°，得B ＝60°.又S ＝12AB ·BC ·sinB ，∴10 3＝12AB ×5×sin60°，∴AB ＝8. 答案60° 816．在△ABC 中，已知(b ＋c)：(c ＋a)：(a ＋b)＝8：9：10，则sinA ：sinB ：sinC ＝________.解析设b ＋c ＝8k ，c ＋a ＝9k ，a ＋b ＝10k ，可得a ：b ：c ＝11：9：7.∴sinA ：sinB ：sinC ＝11：9：7.答案 11：9：717．在非等腰△ABC 中，角A ，B ，C 所对的边分不为a ，b ，c ，且a 2＝b(b ＋c)．(1)求证：A ＝2B ；(2)若a ＝XXX ，试推断△ABC 的形状．解 (1)证明：在△ABC 中，∵a 2＝b ·(b ＋c)＝b 2＋bc ，由余弦定理，得cosB ＝a 2＋c 2－b 22ac ＝bc ＋c 22ac ＝b ＋c 2a ＝a 2b ＝sinA 2sinB ，∴sinA ＝2sinBcosB ＝sin2B.则A ＝2B 或A ＋2B ＝π.若A ＋2B ＝π，又A ＋B ＋C ＝π，∴B ＝C.这与已知相矛盾，故A ＝2B.(2)∵a ＝XXX ，由a 2＝b(b ＋c)，得XXX 2＝b 2＋bc ，∴c ＝2b.又a 2＋b 2＝4b 2＝c 2.故△ABC 为直角三角形．18．锐角三角形ABC 中，边a ，b 是方程x 2－23x ＋2＝0的两根，角A ，B 满脚2sin(A ＋B)－3＝0.求：(1)角C 的度数；(2)边c 的长度及△ABC 的面积．解 (1)由2sin(A ＋B)－3＝0，得sin(A ＋B)＝32. ∵△ABC 为锐角三角形，∴A ＋B ＝120°，∴∠C ＝60°.(2)∵a ，b 是方程x 2－23x ＋2＝0的两个根，∴a ＋b ＝23，ab ＝2.∴c 2＝a 2＋b 2－2abcosC ＝(a ＋b)2－3ab ＝12－6＝6.∴c ＝ 6.S △ABC ＝12absinC ＝12×2×32＝32. 19.已知△ABC 的角A ，B ，C 所对的边分不是a ，b ，c ，设向量m ＝(a ，b)，n ＝(sinB ，sinA)，p ＝(b －2，a －2)．(1)若m ∥n ，求证：△ABC 为等腰三角形；(2)若m ⊥p ，边长c ＝2，角C ＝π3，求△ABC 的面积．解 (1)证明：∵m ∥n ，∴asinA ＝bsinB.由正弦定得知，sinA ＝a 2R ，sinB ＝b 2R (其中R 为△ABC 外接圆的半径)，代入上式，得a ·a 2R ＝b ·b 2R，∴a ＝b.故△ABC 为等腰三角形．(2)∵m ⊥p ，∴m ·p ＝0，∴a(b －2)＋b(a －2)＝0，∴a ＋b ＝ab.由余弦定理c 2＝a 2＋b 2－2abcosC 得4＝(a＋b)2－3ab，即(ab)2－3ab－4＝0. 解得ab＝4，ab＝－1(舍去)．∴△ABC的面积S＝12absinC＝12×4×sinπ3＝ 3.。

高中数学第五章三角函数重点知识点大全(带答案)

高中数学第五章三角函数重点知识点大全(带答案)

高中数学第五章三角函数重点知识点大全单选题1、若sinα+cosαsinα−cosα=12，则tan (α+π4)的值为（ ） A ．−2B ．2C ．−12D ．12 答案：C分析：利用弦化切和两角和的正切展开式化简计算可得答案. 因为sinα+cosαsinα−cosα=12．所以tanα+1tanα−1=12，解得tanα=−3，于是tan (α+π4)=tanα+tanπ41−tanαtanπ4=−3+11−(−3)=−12．故选：C.2、已知角α的终边经过点P (−3,4)，则sinα−cosα−11+tanα的值为（ ）A ．−65B ．1C ．2D ．3答案：A分析：由三角函数的定义可得sinα=45，cosα=−35，tanα=−43，将其代入即可求解.由√(−3)2+42=5，得sinα=45，cosα=−35，tanα=−43，代入原式得=45−(−35)−11+(−43)=−65．故选：A3、记函数f(x)=sin (ωx +π4)+b(ω>0)的最小正周期为T ．若2π3<T <π，且y =f(x)的图象关于点(3π2,2)中心对称，则f (π2)=（ ） A ．1B ．32C ．52D ．3答案：A分析：由三角函数的图象与性质可求得参数，进而可得函数解析式，代入即可得解. 由函数的最小正周期T 满足2π3<T <π，得2π3<2πω<π，解得2<ω<3，又因为函数图象关于点(3π2,2)对称，所以3π2ω+π4=kπ,k ∈Z ，且b =2，所以ω=−16+23k,k ∈Z ，所以ω=52，f(x)=sin (52x +π4)+2， 所以f (π2)=sin (54π+π4)+2=1. 故选：A4、已知tanα=cosα2−sinα，则sinα=（ ） A ．√154B ．12C ．√32D ．14答案：B分析：利用田家四季歌的基本关系得到sinαcosα=cosα2−sinα，整理可得2sinα=cos 2α+sin 2α，再根据平方关系计算可得；解：由tanα=cosα2−sinα，得sinαcosα=cosα2−sinα，即cos 2α=2sinα−sin 2α，∴2sinα=cos 2α+sin 2α=1， 解得sinα=12， 故选：B.5、已知sinαcosα=−16,π4<α<3π4，则sinα−cosα的值等于（ ）A ．2√33B ．−2√33C ．−√63D ．43答案：A分析：结合同角三角函数的基本关系式，利用平方的方法求得正确结论. 由于sinαcosα=−16,π4<α<3π4，所以sinα>0,cosα<0，故sinα−cosα>0，所以sinα−cosα=√(sinα−cosα)2=√1−2sinαcosα=√1+13=2√33. 故选：A6、√3tan26∘tan34∘+tan26∘+tan34∘= （ ） A ．√33B ．−√3C ．√3D ．−√33答案：C解析：利用两角和的正切公式，特殊角的三角函数值化简已知即可求解．解：√3tan26°tan34°+tan26°+tan34°=√3tan26°tan34°+tan(26°+34°)(1−tan26°tan34°)=√3tan26°tan34°+√3(1−tan26°tan34°) =√3tan26°tan34°+√3−√3tan26°tan34°=√3． 故选：C ．7、已知sinθ+sin (θ+π3)=1，则sin (θ+π6)=（ ） A ．12B ．√33C ．23D ．√22答案：B分析：将所给的三角函数式展开变形，然后再逆用两角和的正弦公式即可求得三角函数式的值. 由题意可得：sinθ+12sinθ+√32cosθ=1，则：32sinθ+√32cosθ=1，√32sinθ+12cosθ=√33， 从而有：sinθcos π6+cosθsin π6=√33， 即sin (θ+π6)=√33. 故选：B.小提示：本题主要考查两角和与差的正余弦公式及其应用，属于中等题.8、将函数y =2sin (x +π3)的图象向左平移m (m >0)个单位长度后，所得到的图象关于原点对称，则m 的最小值是（ ） A ．π12B ．π6C ．π3D ．2π3答案：D分析：由三角函数平移变换可得平移后函数为y =2sin (x +m +π3)，根据对称性得到m +π3=kπ(k ∈Z )，结合m >0可得所求最小值.将y =2sin (x +π3)向左平移m (m >0)个单位长度得：y =2sin (x +m +π3)，∵y=2sin(x+m+π3)图象关于原点对称，∴m+π3=kπ(k∈Z)，解得：m=−π3+kπ(k∈Z)，又m>0，∴当k=1时，m取得最小值2π3.故选：D.多选题9、已知tanθ=2，则下列结论正确的是（）A．tan(π−θ)=−2B．tan(π+θ)=−2C．sinθ−3cosθ2sinθ+3cosθ=−17D．sin2θ=45答案：ACD分析：对于A，B利用诱导公式可求解；对于C，D利用齐次式化简可判断. 对于A选项，tan(π−θ)=−tanθ=−2，故A选项正确；对于B选项，tan(π+θ)=tanθ=2，故B选项错误；对于C选项，sinθ−3cosθ2sinθ+3cosθ=tanθ−32tanθ+3=2−34+3=−17，故C选项正确；对于D选项，sin2θ=2sinθcosθ=2sinθcosθsin2θ+cos2θ=2tanθtan2θ+1=44+1=45，故D选项正确.故选：ACD10、下列选项中，与sin(−330∘)的值相等的是（）A．2cos215∘B．cos18∘cos42∘−sin18∘sin42∘C．2sin15∘sin75∘D．tan30∘+tan15∘+tan30∘tan15∘答案：BC分析：求出sin(−330∘)的值以及各选项中代数式的值，由此可得出合适的选项.sin(−330∘)=sin(360∘−330∘)=sin30∘=12.对于A选项，2cos215∘=2×1+cos30∘2=1+cos30∘=1+√32；对于B选项，cos18∘cos42∘−sin18∘sin42∘=cos(18∘+42∘)=cos60∘=12；对于C选项，2sin15∘sin75∘=2sin15∘sin(90∘−15∘)=2sin15∘cos15∘=sin30∘=12；对于D选项，∵tan45∘=tan(30∘+15∘)=tan30∘+tan15∘1−tan30∘tan15∘=1，化简可得tan30∘+tan15∘+tan30∘tan15∘=1.故选：BC.11、已知tanα=4，tanβ=−14，则（ ）A ．tan(−α)tanβ=1B ．α为锐角C ．tan(β+π4)=35D ．tan2α=tan2β 答案：ACD分析：由诱导公式可判断A ，由正切函数的定义可判断B ，由正切函数的两角和公式可判断C ，由二倍角公式可判断D.对于A ，∵tanα=4，tanβ=−14，∴tan(−α)tanβ=−tanαtanβ=1，故A 正确；对于B ，∵tanα=4>0，∴α为第一象限角或第三象限角，故B 错误； 对于C ，∵tanβ=−14，∴tan(β+π4)=1+tanβ1−tanβ=35，故C 正确；对于D ，∵tanα=4，tanβ=−14，∴tan2α=2tanα1−tan 2α=2×41−42=−815,tan2β=2×(−14)1−(−14)2=−815，故D 正确.故选：ACD12、设α是第三象限角，则α2所在象限是（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限 答案：BD解析：用不等式表示第三象限角α，再利用不等式的性质求出α2满足的不等式，从而确定α2的终边所在的象限．∵α是第三象限角，∴k ⋅360°+180°<α<k ⋅360°+270°，k ∈Z ， 则k ⋅180°+90°<α2<k ⋅180°+135°，k ∈Z ，令k =2n ，n ∈Z 有n ⋅360°+90°<α2<n ⋅360°+135°，n ∈Z ；在二象限；k =2n +1，n ∈z ， 有n ⋅360°+270°<α2<n ⋅360°+315°，n ∈Z ；在四象限；故选：B D ．小提示：本题考查象限角的表示方法，不等式性质的应用，通过角满足的不等式，判断角的终边所在的象限,属于容易题.13、下列化简正确的是A．tan(π+1)=tan1B．sin(−α)tan(360∘−α)=cosαC．sin(π−α)cos(π+α)=tanαD．cos(π−α)tan(−π−α)sin(2π−α)=1答案：AB解析：利用诱导公式，及tanα=sinαcosα，依次分析即得解利用诱导公式，及tanα=sinαcosαA选项：tan(π+1)=tan1，故A正确；B选项：sin(−α)tan(360o−α)=−sinα−tanα=sinαsinαcosα=cosα，故B正确；C选项：sin(π−α)cos(π+α)=sinα−cosα=−tanα，故C不正确；D选项：cos(π−α)tan(−π−α)sin(2π−α)=−cosα⋅(−tanα)−sinα=−cosα⋅sinαcosαsinα=−1，故D不正确故选：AB小提示：本题考查了诱导公式和同角三角函数关系的应用，考查了学生概念理解，转化划归，数学运算能力，属于基础题.填空题14、已知函数f(x)=3sin(ωx+π6)(ω>0)在(0，π12)上单调递增，则ω的最大值是____.答案：4分析：根据正弦型函数的单调性即可求解.由函数f(x)=3sin(ωx+π6)(ω>0)在区间(0，π12)上单调递增，可得ω⋅π12+π6≤π2，求得ω≤4，故ω的最大值为4，所以答案是：415、已知f(x)=2sin(2x+π3)，若∃x1,x2,x3[0,3π2]，使得f(x1)=f(x2)=f(x3)，若x1+x2+x3的最大值为M，最小值为N，则M+N=___________.答案：23π6分析：作出f(x)在[0,3π2]上的图象，x1,x2,x3为f(x)的图象与直线y=m交点的横坐标，利用数形结合思想即可求得M和N﹒作出f(x)=2sin(2x+π3)在[0,3π2]上的图象（如图所示）因为f(0)=2sinπ3=√3，f(3π2)=2sin(π+π3)=−√3，所以当f(x)的图象与直线y=√3相交时，由函数图象可得，设前三个交点横坐标依次为x1、x2、x3，此时和最小为N，由2sin(2x+π3)=√3，得sin(2x+π3)=√32，则x1=0，x2=π6，x3=π，N=7π6；当f(x)的图象与直线y=−√3相交时，设三个交点横坐标依次为x1、x2、x3，此时和最大为M，由2sin(2x+π3)=−√3，得sin(2x+π3)=−√32，则x1+x2=7π6，x3=3π2，M=8π3；所以M+N=23π6.所以答案是：23π6.16、已知角α终边落在直线y=34x上，求值：sinα+1cosα=_______．答案：2或−12解析：由题意利用任意角的三角函数的定义，同角三角函数的基本关系，分类讨论，分别求得sinα和cosα的值，可得要求式子的值．解：当角α终边落在直线y =34x(x ⩾0)上，α为锐角，sinαcosα均为正值，且tanα=sinαcosα=34，再结合sin 2α+cos 2α=1，求得sinα=35，cosα=45， 则sinα+1cosα=35+145=2．当角α终边落在直线y =34x(x <0)上，α∈(π,3π2)，sinαcosα均为负值，且tanα=sinαcosα=34，再结合sin 2α+cos 2α=1，求得sinα=−35，cosα=−45， 则sinα+1cosα=−35+1−45=−12，所以答案是：2或−12．小提示：本题主要考查任意角的三角函数的定义，同角三角函数的基本关系，考查运算能力，属于基础题． 解答题17、已知0<α<π2，cos (α+π4)=13．(1)求sinα的值；(2)若−π2<β<0，cos (β2−π4)=√33，求α−β的值．答案：(1)4−√26(2)α−β=π4分析：（1）利用同角三角函数的基本关系结合两角差的正弦公式可求得sinα的值；（2）利用二倍角的余弦公式可求得sinβ的值，利用同角三角函数的基本关系以及两角差的余弦公式求出cos (α−β)的值，结合角α−β的取值范围可求得结果. （1）解：因为0<α<π2，∴π4<α+π4<3π4，又cos(α+π4)=13，所以sin(α+π4)=√1−(13)2=2√23，所以sinα=sin[(α+π4)−π4]=sin(α+π4)cosπ4−cos(α+π4)cosπ4=√22(2√23−13)=4−√26.（2）解：因为cos(β2−π4)=√33，sinβ=cos(β−π2)=cos[2(β2−π4)]=2cos2(β2−π4)−1=2×13−1=−13，又因为−π2<β<0，所以cosβ=√1−sin2β=2√23，由（1）知，cosα=cos[(α+π4)−π4]=cos(α+π4)cosπ4+sin(α+π4)sinπ4=4+√26，所以cos(α−β)=cosαcosβ+sinαsinβ=4+√26×2√23+4−√26×(−13)=√22．因为0<α<π2，−π2<β<0，则0<α−β<π，所以α−β=π4．18、已知函数f(x)=2sinxsin(π3−x)+2cos2x−12.（1）求函数f(x)的单调增区间；（2）当x∈(−π6,π4)时，函数g(x)=f2(x)−2mf(x)+m2−116有四个零点，求实数m的取值范围.答案：（1）[kπ−5π12,kπ+π12]，k∈Z（2）2√3+14<m<4√3−14分析：（1）化简f(x)的解析式，根据正弦函数的增区间可得结果；（2）转化为ℎ(t)=t2−2mt+m2−116在(√32,√3)内有两个零点，根据二次函数列式可得结果.（1）f(x)=2sinxsin(π3−x)+2cos2x−12=2sinx(sinπ3cosx−cosπ3sinx)+1+cos2x−12 =√3sinxcosx−sin2x+1+cos2x−12=√32sin2x+cos2x+cos2x−12=√32sin2x+1+cos2x2+cos2x−12=√32sin2x+32cos2x=√3sin(2x +π3)，由2kπ−π2≤2x +π3≤2kπ+π2，k ∈Z ， 得kπ−512π≤x ≤kπ+π12，k ∈Z ，所以函数f (x )的单调增区间为[kπ−5π12,kπ+π12]，k ∈Z . （2）当x ∈(−π6,π4)时，2x +π3∈(0,5π6)，f(x)=√3sin(2x +π3)∈(0,√3]，因为函数g (x )=f 2(x )−2mf (x )+m 2−116有四个零点，令t =f(x)，则t ∈(0,√3)且ℎ(t)=t 2−2mt +m 2−116在(√32,√3)内有两个零点， 所以{Δ=4m 2−4(m 2−116)>0√32<m <√3ℎ(√32)>0ℎ(√3)>0，即{ √32<m <√334−√3m +m 2−16>03−2√3m +m 2−16>0，解得{√32<m <√3m 〈2√3−14或m 〉2√3+14m 〈4√3−14或m 〉4√3+14，解得2√3+14<m <4√3−14，所以实数m 的取值范围是2√3+14<m <4√3−14. 小提示：方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.。

(完整版)高中三角函数知识点总结

(完整版)高中三角函数知识点总结

(完整版)高中三角函数知识点总结高中三角函数知识点总结1. 基本三角函数概念- 三角函数是以单位圆为基础的函数，包括正弦函数、余弦函数和正切函数。

- 正弦函数（sin）：在直角三角形中，对于一个锐角，其对边与斜边的比值称为正弦值。

即：sinA = 对边/斜边。

- 余弦函数（cos）：在直角三角形中，对于一个锐角，其邻边与斜边的比值称为余弦值。

即：cosA = 邻边/斜边。

- 正切函数（tan）：在直角三角形中，对于一个锐角，其对边与邻边的比值称为正切值。

即：tanA = 对边/邻边。

2. 基本三角函数性质和公式- 三角函数的周期性：正弦函数和余弦函数的周期都是2π；正切函数的周期是π.- 三角函数的奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。

- 三角函数的同角关系：sinA/cosA = tanA。

- 三角函数的和差化积公式和积化和差公式：具体公式可根据需要进行查阅。

3. 三角函数图像和性质- 正弦函数图像：在0到2π的区间内，正弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于零值。

- 余弦函数图像：在0到2π的区间内，余弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于最大值。

- 正切函数图像：在0到π的区间内，正切函数的图像无法在x=π/2和3π/2时定义，其他点对应的图像为一条连续的射线。

4. 三角函数的应用- 三角函数广泛应用于科学和工程领域中的周期性现象的描述和计算，例如电流的正弦波，声波的波动等。

- 在几何学中，三角函数也应用于测量角度和距离等问题的解决。

以上为高中三角函数的基本知识点总结，更详细的内容和公式可以参考相关教材或资料。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

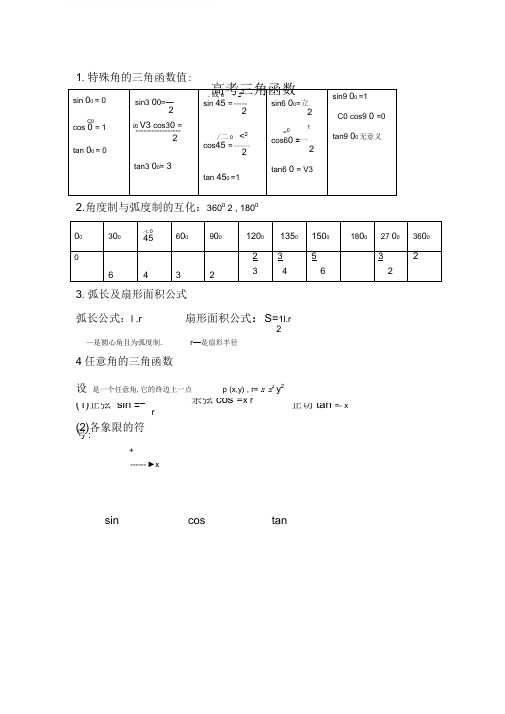
高考三角函数1.特殊角的三角函数值：2．角度制与弧度制的互化：,23600π= ,1800π=3.弧长及扇形面积公式弧长公式：r l .α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。

r-----是扇形半径4.任意角的三角函数设α是一个任意角，它的终边上一点p （x,y ）, r=22y x + (1)正弦sin α=r y 余弦cos α=r x 正切tan α=xy (2)各象限的符号：sin α cos α tan αxy+O— —+x yO — ++— +y O— ++ —5.同角三角函数的基本关系：（1）平方关系：s in 2α+ cos 2α=1。

（2）商数关系：ααcos sin =tan α （z k k ∈+≠,2ππα）6.诱导公式：记忆口诀：2k παα±把的三角函数化为的三角函数，概括为：奇变偶不变，符号看象限。

()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+= ⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭．口诀：正弦与余弦互换，符号看象限．7正弦函数、余弦函数和正切函数的图象与性质降幂公式： 1+cos α=2cos 22α cos 2α22cos 1α+=1-cos α=2sin 22αsin 2α22cos 1α-= 9．正弦定理 ：2sin sin sin a b cR A B C===. 余弦定理：2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-.三角形面积定理.111sin sin sin 222S ab C bc A ca B ===.1．直角三角形中各元素间的关系：如图，在△ABC 中，C ＝90°，AB ＝c ，AC ＝b ，BC ＝a 。

（1）三边之间的关系：a 2＋b 2＝c 2。

（勾股定理）两角和与差的三角函数关系 sin(α±β)=sin α·cos β±cos α·sin β cos(α±β)=cos α·cos β sin α·sin β βαβαβαtan tan 1tan tan )tan(⋅±=±倍角公式 s in2α=2sin α·cos α cos2α=cos 2α-sin 2α=2cos 2α-1 =1-2sin 2αααα2tan 1tan 22tan -=（2）锐角之间的关系：A ＋B ＝90°； （3）边角之间的关系：（锐角三角函数定义） sin A ＝cos B ＝c a ，cos A ＝sin B ＝c b ，tan A ＝ba。

2．斜三角形中各元素间的关系：在△ABC 中，A 、B 、C 为其内角，a 、b 、c 分别表示A 、B 、C 的对边。

（1）三角形内角和：A ＋B ＋C ＝π。

（2）正弦定理：在一个三角形中，各边和它所对角的正弦的比相等R CcB b A a 2sin sin sin ===。

（R 为外接圆半径）（3）余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍a 2＝b 2＋c 2－2bc cos A ；b 2＝c 2＋a 2－2ca cos B ；c 2＝a 2＋b 2－2ab cos C 。

3．三角形的面积公式：（1）△＝21ah a ＝21bh b ＝21ch c （h a 、h b 、h c 分别表示a 、b 、c 上的高）； （2）△＝21ab sin C ＝21bc sin A ＝21ac sin B ；（3）△＝)sin(2sin sin 2C B C B a +＝)sin(2sin sin 2A C A C b +＝)sin(2sin sin 2B A BA c +；（4）△＝2R 2sin A sin B sin C 。

（R 为外接圆半径） （5）△＝Rabc 4； （6）△＝))()((c s b s a s s ---；⎪⎭⎫ ⎝⎛++=)(21c b a s ； （7）△＝r ·s 。

4．解三角形：由三角形的六个元素（即三条边和三个内角）中的三个元素（其中至少有一个是边）求其他未知元素的问题叫做解三角形．广义地，这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等．解三角形的问题一般可分为下面两种情形：若给出的三角形是直角三角形，则称为解直角三角形；若给出的三角形是斜三角形，则称为解斜三角形解斜三角形的主要依据是：设△ABC 的三边为a 、b 、c ，对应的三个角为A 、B 、C 。

（1）角与角关系：A +B +C = π；（2）边与边关系：a + b > c ，b + c > a ，c + a > b ，a －b < c ，b －c < a ，c －a > b ； （3）边与角关系：正弦定理 R CcB b A a 2sin sin sin ===（R 为外接圆半径）； 余弦定理 c 2 = a 2+b 2－2bc cos C ，b 2 = a 2+c 2－2ac cos B ，a 2 = b 2+c 2－2bc cos A ；它们的变形形式有：a = 2R sin A ，baB A =sin sin ，bc a c b A 2cos 222-+=。

5．三角形中的三角变换三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点。

（1）角的变换因为在△ABC 中，A+B+C=π，所以sin(A+B)=sinC ；cos(A+B)=－cosC ；tan(A+B)=－tanC 。

2sin 2cos ,2cos 2sinCB AC B A =+=+； （2）三角形边、角关系定理及面积公式，正弦定理，余弦定理。

r 为三角形内切圆半径，p 为周长之半。

（3）在△ABC 中，熟记并会证明：∠A ，∠B ，∠C 成等差数列的充分必要条件是∠B=60°；△ABC 是正三角形的充分必要条件是∠A ，∠B ，∠C 成等差数列且a ，b ，c 成等比数列。

四．【典例解析】 题型1：正、余弦定理（2009岳阳一中第四次月考）.已知△ABC 中，AB a =，AC b =，0a b ⋅<，154ABC S ∆=， 3,5a b ==，则BAC ∠=（ ）A.． 30 B ．150- C ．0150 D ． 30或0150 答案 C例1．（1）在∆ABC 中，已知032.0=A ，081.8=B ，42.9=a cm ，解三角形；（2）在∆ABC 中，已知20=a cm ，28=b cm ，040=A ，解三角形（角度精确到01，边长精确到1cm ）。

例2．（1）在∆ABC 中，已知23=a 62c 060=B ，求b 及A ； （2）在∆ABC 中，已知134.6=a cm ，87.8=b cm ，161.7=c cm ，解三角形 解析：（1）∵2222cos =+-b a c ac B=22(23)(62)223(62)+-⋅⋅cos 045 =212(62)43(31)+- =8 ∴2 2.=b求A 可以利用余弦定理，也可以利用正弦定理：解法一：∵cos 222222(22)(62)(23)1,22222(62)+-++-==⨯⨯+b c a A bc ∴060.=A （2）由余弦定理的推论得：cos 2222+-=b c a A bc 22287.8161.7134.6287.8161.7+-=⨯⨯0.5543,≈ 05620'≈A ；cos 2222+-=c a b B ca 222134.6161.787.82134.6161.7+-=⨯⨯ 0.8398,≈ 03253'≈B ；0000180()180(56203253)''=-+≈-+C A B 09047.'= 例3．在∆ABC 中，sin cos A A +=22，AC =2，AB =3，求A tan 的值和∆ABC 的面积。

.21)45cos(,22)45cos(2cos sin =-∴=-=+ A A A A又0180<<A , 4560,105.A A ∴-==13tan tan(4560)2313A +∴=+==---,.46260sin 45cos 60cos 45sin )6045sin(105sin sin +=+=+==A S AC AB A ABC ∆=⨯=⨯⨯⨯+=+1212232643426sin ()。

例4．（2009湖南卷文）在锐角ABC ∆中，1,2,BC B A ==则cos ACA的值等于 ， AC 的取值范围为 .答案 2)3,2(解析 设,2.A B θθ∠=⇒=由正弦定理得,1 2.sin 2sin 2cos cos AC BC AC ACθθθθ=∴=⇒=由锐角ABC ∆得0290045θθ<<⇒<<，又01803903060θθ<-<⇒<<，故233045cos 22θθ<<⇒<<， 2cos 2,3).AC θ∴=∈例5．（2009浙江理）（本题满分14分）在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且满足5cos25A =，3AB AC ⋅=．（I ）求ABC ∆的面积； （II ）若6b c +=，求a 的值． 解 （1）因为25cos25A =，234cos 2cos 1,sin 255A A A ∴=-==，又由3AB AC ⋅= 得cos 3,bc A =5bc ∴=，1sin 22ABC S bc A ∆∴== （2）对于5bc =，又6b c +=，5,1b c ∴==或1,5b c ==，由余弦定理得2222cos 20a b c bc A =+-=，25a ∴=例6．（2009全国卷Ⅰ理）在ABC ∆中，内角A 、B 、C 的对边长分别为a 、b 、c ，已知222a c b -=，且sin cos 3cos sin ,A C A C = 求b解法一：在ABC ∆中sin cos 3cos sin ,A C A C =则由正弦定理及余弦定理有:2222223,22a b c b c a ac ab bc+-+-=化简并整理得：2222()a c b -=.又由已知222a c b -=24b b ∴=.解得40(b b ==或舍）.例7．ABC ∆的三个内角为A B C 、、，求当A 为何值时，cos 2cos 2B CA ++取得最大值，并求出这个最大值。

相关文档
最新文档