外啮合圆柱齿轮参数计算教学资料
外啮合圆柱齿轮几何计算公式

求出啮合角α'后,由上式求(x1+x2)值,再进行分配
中心距变动系数y
y=(a'-a)/m
=(z1+z2)(cosα/cosα'-1)/2
yn=(a'-a)/mn
=(z1+z2)(cosαt/cosαt'-1)
/(2cosβ)
yt=ynconβ
外啮合圆柱齿轮几何计算公式
名称及代号
计算公式及说明
直齿轮
斜齿及人字齿轮
由强度计算或结构设计确定,
并取标准值
法向模数mn取标准值。
端面模数:mt=mncosβ
β=0
两轮螺旋角相等,方向相反
α=20°
αn=20°
tanαt=tanαn/cosβ
d=mz
d=mtz
a=(d1+d2)/2
=(z1+z2)m/2
变位后的中心距a'
a'=a+ym=acosα/cosα'
a'=a+ytmt=a+ynmn=acosαt/cosαt'
齿根圆直径df
df=d-2(ha+c-xm)
df=d-2(han+cn-xnmn)
齿顶圆直径da
da1=2a'-df2-2c
da2=2a'-df1-2c
da1=2a'-df2-2cn
da2=2a'-df1-2cn
纵向重合度εβ
εβ=0
εβ=bsinβ/(mnπ)
b——齿轮宽度
总重合度εγ
εγ=εα
εγ=εα+εβ
注:角标n为法面,t为端面;1为小齿轮,2为大齿轮。
a=(d1+d2)/2
齿轮各参数计算公式知识讲解

齿轮各参数计算公式13-1什么是分度圆?标准齿轮的分度圆在什么位置上? 13-2 一渐开线,其基圆半径r b = 40 mm ,试求此渐开线压力角 =20。
处的半径r 和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径 da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4两个标准直齿圆柱齿轮,已测得齿数 z i = 22、z 2 = 98,小齿轮齿顶圆直径d ai = 240 mm ,大 齿轮全齿高h = 22.5 mm ,试判断这两个齿轮能否正确啮合传动 ?名称 代号 计算公式 模数 m m=p/n =d/z=da/(z+2)(d 为分度圆直径齿距 P p= n m=t d/z 齿数 z z=d/m=n d/p 分度圆直径 d d=mz=da-2m齿顶圆直径 da da=m(z+2)=d+2m=p(z+2)/ n 齿根圆直径 df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼 ha ha=m=p/n 齿根高 hf hf=1.25m齿高 h h=2.25m 齿厚 s s=p/2= n m/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数 k k=z/9+0.5公法线长度ww=m[2.9521(k-0.5)+0.014z]模数齿轮计算公式 ,z 为齿数)13-5有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z i = 19、Z2 = 81,模数m= 5 mm,压力角=20°若将其安装成a' = 250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数Z1 = 21、Z2 = 66,模数m =3.5 mm,压力角 =20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
标准圆柱齿轮参数及其几何计算课件

汽车变速箱等部件中大量使用了标准圆柱齿轮,这些齿轮对于汽车的传动和动力输出起着关键作用。
标准圆柱齿轮的制造及检验方法
制造方法
主要包括铸造、锻造、切削加工 等方法,根据不同的材料和尺寸 选择合适的制造方法。
检验方法
主要包括几何测量、力学性能测 试、金相检验等方法,对齿轮的 精度、强度、耐磨性等方面进行 全面检测。
齿高的取值根据齿轮的设计要求来确定,一般齿高 h=2.25~7.5mm。
02
标准圆柱齿轮的主要几何尺寸
齿顶圆直径(diameter of tooth circle)
定义
齿顶圆直径是指圆柱齿轮齿顶部的圆周直径。
计算
齿顶圆直径是齿轮几何参数计算的重要基础,可 以通过查表或公式计算得到。
重要性
齿顶圆直径的大小直接影响到齿轮的啮合性能和 强度。
作用
模数决定着齿轮的强度和 刚度,是设计齿轮的重要 依据。
取值范围
模数的取值通常根据齿轮 的使用要求来确定,一般 模数m=1~6mm。
齿数(number of teeth)
定义
齿数是齿轮上齿的个数, 通常用齿数表示齿轮的基 本参数。
作用
齿数直接影响着齿轮的传 动平稳性和承载能力。
取值范围
齿数的取值根据齿轮的设 计要求来确定,一般齿数 z=17~140。
计算公式
s = m×(ha+c) 其中, m为模数,ha为齿高等 ,c为中心距。
作用
齿厚是决定齿轮传动平 稳性和承载能力的重要 参数。对于标准齿轮来 说,齿厚可以通过查表 或使用公式进行计算。
齿槽宽(slot width)
定义
齿槽宽是指齿轮齿槽的宽度,用字母e表示。
计算公式
外啮合变位圆柱齿轮传动几何尺寸计算

外啮合变位圆柱齿轮传动几何尺寸计算外啮合变位圆柱齿轮传动的几何尺寸计算是指根据给定的齿轮参数,计算其相关的几何尺寸。
这些几何尺寸包括齿轮的齿数、模数、齿顶高、齿根高、齿轮间隙等,这些参数是设计和制造齿轮传动系统的重要依据。
下面将详细介绍外啮合变位圆柱齿轮传动几何尺寸的计算方法。
1.齿数计算:齿数是齿轮传动中的重要参数,它决定了齿轮的大小和转速比。
在外啮合变位圆柱齿轮传动中,齿数的计算一般按照下面的公式进行:N=Z1+Z2=(p1-p2)/m+2,其中,N表示齿数,Z1和Z2分别为两个齿轮的齿数,p1和p2表示两个齿轮的啮合位置,m表示模数。
2.模数计算:模数是齿轮传动中的重要参数,它决定了齿轮的尺寸和载荷能力。
在外啮合变位圆柱齿轮传动中,模数的计算一般按照下面的公式进行:m=(p1-p2)/(Z1+Z2),其中,m表示模数,p1和p2表示两个齿轮的啮合位置,Z1和Z2分别为两个齿轮的齿数。
3.齿顶高计算:齿顶高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿顶高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿顶高,m表示模数。
4.齿根高计算:齿根高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿根高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿根高,m表示模数。
5.齿轮间隙计算:齿轮间隙是齿轮传动中的重要参数,它决定了齿轮的啮合性能和传动精度。
在外啮合变位圆柱齿轮传动中,齿轮间隙的计算一般按照下面的公式进行:C=0.25*m,其中,C表示齿轮间隙,m表示模数。
以上是外啮合变位圆柱齿轮传动几何尺寸的计算方法。
通过这些计算,可以确定齿轮的相关几何参数,为设计和制造齿轮传动系统提供重要的参考依据。
同时,还需要根据具体的传动要求和工作条件,进行更详细的设计和计算。
给定中心距计算外啮合渐开线圆柱齿轮传动编程计算

外啮合渐开线圆柱齿轮传动计算--给定中心距输入数据1 模数: mn=1.752 齿数: z1=16z2=433 螺旋角: helix=19+31/60+33/3600= 19.5258334 基本齿廓齿形角: an=20齿顶高系数: ha_m=1.0径向间隙系数: c_m=0.25齿根圆角半径系数: p_m=0.385 工作中心距: a_work=54.2756 精度等级: pgrade=77 齿宽: gw1=25gw2=208 工作齿宽: gw_work=MIN[gw1,gw2]= 209 当量齿数: zv1=z1/(cos(helix)^3)= 19.111224zv2=z2/(cos(helix)^3)= 51.36141410 传动比: u=z2/z1= 2.6875主要几何参数计算1 分度(标准)中心距: a_bz=(z1+z2)*mn/cos(helix)*0.5= 54.7750652 中心距变动系数: ya=(a_work-a_bz)/mn= -0.2857523 端面齿形角: at=atan(tan(an)/cos(helix))= 21.1155164 端面啮合角: at1=acos[a_bz/a_work*cos(at)]= 19.7033355 变位系数和:x_sum=[(z1+z2)*(inv(at1)-inv(at))/(2*tan(an))]= -0.2767336 补偿变位系数: deta_y=x_sum-ya= 0.0090187 分度圆直径: d1=mn*z1/cos(helix)= 29.708510d2=mn*z2/cos(helix)= 79.8416218 基圆直径: db1=d1*cos(at)= 27.713762db2=d2*cos(at)= 74.4807369 分配变位系数(原则:大小轮的滑动比相等):x1=rote[x1,-1 to 1,(1+u)*(tan(acos(db2/(d2+2*mn*(ha_m+x_sum-x1-deta_y))))-tan(at1 ))/(tan(at1)-u*(tan(acos(db2/(d2+2*mn*(ha_m+x_sum-x1-deta_y))))-ta n(at1)))-(1+u)*(tan(acos(db1/(d1+2*mn*(ha_m+x1-deta_y))))-tan(at1)) /(u*tan(at1)-(tan(acos(db1/(d1+2*mn*(ha_m+x1-deta_y))))-tan(at1)))] = 0.273863也可以自选小轮变位系数: x1=x1= 0.273863x2=x_sum-x1= -0.55059710 节圆直径: d_node1=2*a_work/(u+1)= 29.437288d_node2=2*a_work*u/(u+1)= 79.11271211 齿顶圆直径: da1=d1+2*(ha_m+x1-deta_y)*mn= 34.135468da2=d2+2*(ha_m+x2-deta_y)*mn= 81.382969 12 齿根圆直径: df1=d1-2*(ha_m+c_m-x1)*mn= 26.292031df2=d2-2*(ha_m+c_m-x2)*mn= 73.53953213 齿高: h1=(da1-df1)/2= 3.921718h2=(da2-df2)/2= 3.92171814 法面分度圆齿厚: sn1=[pi/2+2*x1*tan(an)]*mn= 3.097767sn2=[pi/2+2*x2*tan(an)]*mn= 2.04749115 基圆螺旋角: Bb=asin[sin(helix)*cos(an)]= 18.304993齿厚测量尺寸计算1 固定弦齿厚: s_c1=mn*[pi/2*cos(an)^2+x1*sin(2*an)]=2.735397s_c2=mn*[pi/2*cos(an)^2+x2*sin(2*an)]=1.8079802 固定弦齿高: h_c1=0.5*[da1-d1-s_c1*tan(an)]= 1.715677h_c2=0.5*[da2-d2-s_c2*tan(an)]= 0.4416493 分度圆弦齿厚:deta1=tod[pi/2/z1+2*x1*tan(an)/z1]*[cos(helix)^3]= 5.306948deta2=tod[pi/2/z2+2*x2*tan(an)/z2]*[cos(helix)^3]= 1.305177齿厚: s_1=mn*z1*sin(deta1)/[cos(helix)^3]=3.093339s_2=mn*z2*sin(deta2)/[cos(helix)^3]=2.0473144 分度圆弦齿高:ha_1=0.5*{da1-[cos(deta1)-sin(helix)^2]/[cos(helix)^2]*d1}=2.285159ha_2=0.5*{da2-[cos(deta2)-sin(helix)^2]/[cos(helix)^2]*d2}=0.7823345 公法线长度:z'1=z1*inv(at)/inv(an)= 18.940755z'2=z2*inv(at)/inv(an)= 50.903280跨齿数:k1=toint{z'1/180*acos[z'1*cos(an)/(z'1+2*x1)]+0.5}= 3k2=toint{z'2/180*acos[z'2*cos(an)/(z'2+2*x2)]+0.5}= 5w1=mn*cos(an)*[pi*(k1-0.5)+z1*inv(at)+2*x1*tan(an)]=13.707641w2=mn*cos(an)*[pi*(k2-0.5)+z2*inv(at)+2*x2*tan(an)]=23.836556公法线长度可以测量吗?结果为True(真),表示可以测量;结果为False(假),表示不能测量,需要减少跨齿数再计算:CanMeasure1=among[helix>0,w1< gw1/sin(Bb),True]= TrueCanMeasure2=among[helix>0,w2< gw2/sin(Bb),True]= True改变跨齿数,计算公法线:k1_change=among[k1>2,k1-1,k1]= 2k2_change=among[k2>2,k2-1,k2]= 4 w1_change=mn*cos(an)*[pi*(k1_change-0.5)+z1*inv(at)+2*x1*t an(an)]= 8.541411w2_change=mn*cos(an)*[pi*(k2_change-0.5)+z2*inv(at)+2*x2*t an(an)]= 18.670326公法线长度可以测量吗?结果为True(真),表示可以测量;结果为False(假),表示不能测量:CanMeasure1=among[helix>0,w1_change< gw1/sin(Bb),True]= TrueCanMeasure2=among[helix>0,w2_change< gw2/sin(Bb),True]= True6 量棒(球)跨距M值计算:量棒直径: dp=1.728*mn= 3.024或自定直径: dp=dp= 3.024量棒中心所在圆上的压力角:ad1=ainv{dp/[z1*mn*cos(an)]+inv(at)-pi/2/z1+2*x1*tan(an)/z1}= 28.754439ad2=ainv{dp/[z2*mn*cos(an)]+inv(at)-pi/2/z2+2*x2*tan(an)/z2}= 19.848843M1=among[ceil(z1/2) eq z1/2 ,d1*cos(at)/cos(ad1)+dp,d1*cos(at)/cos(ad1)*cos(90/z1)+dp]= 34.635834M2=among[ceil(z2/2) eq z2/2 ,d2*cos(at)/cos(ad2)+dp,d2*cos(at)/cos(ad2)*cos(90/z2)+dp]= 82.1561567 斜齿轮轴向齿距: px=among[helix> 0 , pi*mn/sin(helix),0]= 16.4490238 斜齿轮导程: pz1=among[helix > 0 ,z1*px,0]= 263.184364pz2=among[helix > 0 ,z2*px,0]= 707.307978 传动质量指标计算1 齿顶点压力角: aa1=acos(db1/da1)= 35.720385aa2=acos(db2/da2)= 23.7675272 端面重合度:ea=0.5*/pi*[ z1*tan(aa1)+z2*tan(aa2)-(z1+z2)*tan(at1)]= 1.4822143 斜齿轮纵向重合度: eB=among[helix> 0 ,gw_work/px,0]= 1.2158784 总重合度: er=ea+eB= 2.6980915 斜齿轮齿顶螺旋角: Ba1=atan[da1/d1*tan(helix)]= 22.169422Ba2=atan[da2/d2*tan(helix)]= 19.873512 6 法面齿顶厚:san1=da1*{[0.5*pi+2*x1*tan(an)]/z1+inv(at)-inv(aa1)}*cos(Ba1) = 1.030677san2=da2*{[0.5*pi+2*x2*tan(an)]/z2+inv(at)-inv(aa2)}*cos(Ba2) = 1.477061判断齿顶厚度是否足够?齿面类型(硬或软): Tooth_face="硬齿面"Thickness1_OK=among[Tooth_face eq "硬齿面",san1 >= 0.25*mn, san1 > 0.4*mn]= TrueThickness2_OK=among[Tooth_face eq "硬齿面",san2 >= 0.25*mn, san2 > 0.4*mn]= True7 滑动比:η1=(1+u)*[tan(aa2)-tan(at1)]/[tan(at1)-u*(tan(aa2)-tan(at1))]= 2.213282η2=(1+u)*[tan(aa1)-tan(at1)]/[u*tan(at1)-(tan(aa1)-tan(at1))]= 2.213282 滑动比的绝对值是否小于等于3?η1_Ok=abs(η1) <= 3= Trueη2_Ok=abs(η2) <= 3= True齿轮精度数据计算(GB/T10095-2001):1 齿距累积总公差Fp: Fp1=table[GB10095_2001_Fp,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.029Fp2=table[GB10095_2001_Fp,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0372 齿圈径向跳动公差Fr: F r1=table[GB10095_2001_Fr,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.023Fr2=table[GB10095_2001_Fr,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0293 单个齿距极限偏差±fpt: fpt1=table[GB10095_2001_fpt,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.01fpt2=table[GB10095_2001_fpt,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0114 齿廓总公差Fa: Fa1=table[GB10095_2001_Fa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.01Fa2=table[GB10095_2001_Fa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0125 齿廓形状公差ffa: ffa1=table[GB10095_2001_ffa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.008ffa2=table[GB10095_2001_ffa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0096 齿廓倾斜极限偏差±fHa: fHa1=table[GB10095_2001_fHa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0065fHa2=table[GB10095_2001_fHa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.00757 螺旋线总公差FB: FB1=table[GB10095_2001_FB,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2>= gw1,精度等级 eq pgrade,公差值]/1000= 0.016FB2=table[GB10095_2001_FB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2>= gw2,精度等级 eq pgrade,公差值]/1000= 0.0158 螺旋线形状公差ffB: ffB1=table[GB10095_2001_ffB,分度圆1<d1,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2>= gw1,精度等级eq pgrade,公差值]/1000= 0.012ffB2=table[GB10095_2001_ffB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2 >= gw2,精度等级eq pgrade,公差值]/1000= 0.0119 螺旋线倾斜极限偏差±fHB: fHB1=table[GB10095_2001_fHB,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2 >= gw1,精度等级eqpgrade,公差值]/1000= 0.012fHB2=table[GB10095_2001_fHB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2 >= gw2,精度等级eq pgrade,公差值]/1000= 0.011。
外啮合直齿圆柱齿轮传动
板书设计或授课提纲课堂教学安排整顿纪律,清点人数。
人员安全教育及预防突发情况的准备在课堂开始之前老师想问大家一个问题,汽车的变速器,是通过什么传动来实现换挡的?二、了解齿轮传动的基本知识1.定义齿轮传动是利用齿轮副来传递运动和(或)动力的一种机械传动,可以用来传递空间任意两轴间的运动,而且传动准确可靠,效率高。
老师:齿轮传动有哪些类型呢?请大家阅读课本思考并回答问题。
2.齿轮传动的常用类型(1)两轴平行(2)两轴不平行3.齿轮传动的传动比4.齿轮传动的应用特点优点(1)能保证瞬时传动比恒定,工作可靠性高,传递运动准确(2)传递功率和圆周速度范围较宽,传递功率可高达5×104 kW,圆周速度可达300 m/s(3)结构紧凑,可实现较大的传动比(4)传动效率高,使用寿命长,维护简便缺点(1)运转过程中有振动、冲击和噪声(2)对齿轮的安装要求较高(3)不能实现无级变速(4)不适用于中心距较大的场合二、外啮合直齿圆柱齿轮传动基本知识1.渐开线齿廓(1)齿轮传动对齿廓曲线的基本要求1)传动要平稳2)承载能力要强老师:让我们一起看一下PPT上的图片和动画视频,请大家思考渐开线是如何形成的?小组讨论并回答2.渐开线的形成动直线AB沿一固定圆作纯滚动,此动直线AB上任意一点K的运动轨迹C称为该圆的渐开线。
3.渐开线齿廓的啮合特性(1)能保证瞬时传动比的恒定,保证了传动的平稳性,减小了振动和冲击(2)即使两轮的实际中心距与设计的中心距稍有改变,其瞬时传动比仍能保持不变4.渐开线标准直齿圆柱齿轮各部分名称5.渐开线标准直齿圆柱齿轮的基本参数(1)压力角压力角:齿廓上某点所受正压力方向(即齿廓上该点法向)与速度方向线之间所夹的锐角。
(2)齿数z齿数z:一个齿轮的轮齿总数(3)模数m模数:齿距p除以圆周率T所得的商m=p/Tm的单位为mm(4)齿顶高系数hαha=ham标准齿轮的齿顶高系数h为1(5)顶隙系数c*c=c*m标准齿轮的顶隙系数c*=0.256.外啮合标准直齿圆柱齿轮的几何尺寸计算例一对标准直齿圆柱齿轮,z1=20,z2=32,m=10。
一对外啮合的直齿圆柱标准齿轮,小轮的齿根厚度和大轮的齿根厚度关系;

外啮合的直齿圆柱标准齿轮,小轮的齿根厚度和大轮的齿根厚度关系1. 引言1.1 概述直齿圆柱标准齿轮是一种常见的机械传动元件,广泛应用于各个领域。
在齿轮啮合过程中,齿根厚度是当今研究的一个重要方面,因为它对齿轮的强度和工作性能有着重要的影响。
而在外啮合直齿圆柱标准齿轮中,小轮的齿根厚度与大轮的齿根厚度之间存在着一定的关系。
1.2 文章结构本文将首先介绍外啮合的直齿圆柱标准齿轮的基本概念和特性,包括其定义、特点以及应用领域。
接下来,将详细讨论小轮的齿根厚度与大轮的齿根厚度之间的关系,并分析其中的影响因素。
随后,将介绍相关计算模型及仿真验证方法,以进一步验证前述理论分析结果。
最后,通过总结研究结果提出结论,并展望未来该领域研究可能发展的方向。
1.3 目的本文旨在深入研究外啮合的直齿圆柱标准齿轮中小轮的齿根厚度与大轮的齿根厚度之间的关系,探讨影响因素,并提出相关计算模型和仿真验证方法。
通过该研究,可以为设计者提供有关在不同应用场景中优化选择齿根厚度的参考指导,以提高齿轮传动系统的可靠性和工作效率。
此外,本文也希望培养读者对于直齿圆柱标准齿轮特性及其在机械传动中的应用领域有更全面的了解。
2. 外啮合的直齿圆柱标准齿轮介绍:2.1 定义与特性:外啮合的直齿圆柱标准齿轮是一种常见的机械传动元件, 具有两个相互啮合的齿轮: 大轮和小轮。
它们由金属材料加工而成,具有相对简单的结构。
其中大轮拥有较大的直径,而小轮则比大轮尺寸更小。
这种齿轮常用于各种工业领域,如汽车、机床等,用于实现速度转换、扭矩传递和运动分配。
2.2 齿轮应用领域:外啮合的直齿圆柱标准齿轮广泛应用于许多行业。
在汽车行业中,它们被用作变速箱和传动系统中关键组件,实现不同挡位之间的变速。
此外,在航空航天、能源发电以及其他工程应用中也可以找到这种类型的齿轮。
2.3 标准规范概述:为了确保外啮合的直齿圆柱标准齿轮在各种应用中具有良好的兼容性和互换性,相关机构制定了一系列标准规范。
已知一对外啮合正常齿标准直齿圆柱齿轮3mm-推荐下载

第5章 习题5-1 已知一对外啮合正常齿标准直齿圆柱齿轮=3mm ,z1=19,z2=41,试m 计算这对齿轮的分度圆直径、齿顶高、齿根高、顶隙、中心距、齿顶圆直径、齿根圆直径,基圆直径、齿距、齿厚和齿槽宽。
5-2 已知一正常具标准直齿圆柱的a=20°=mm ,=40,试分别求出分m z 度圆、基圆、齿顶圆上渐开线齿廓的曲率半径和压力角。
5-3 如图5-3所示一渐开线齿轮在半径为A =95mm 处的齿轮的齿廓压力r 角为8°26′49″,齿厚为A =10.088mm 。
试计算齿廓压力角为B =25°处的s a 齿厚B 及半径B 。
s r5-4 在某项技术革新中,需要采用一对齿轮传动,其中心距=144mm ,a 传动比=2。
现在库房中存有四种现成的齿轮,压力角都是20°,这四种齿轮i 的齿数和齿顶圆直径a 分别为:1=24,al =104mm ;2=47,a2=196mm ;z d z d z d 3=48,a3=250mm ;4=48,a4=200mm 。
试分析能否从这四种齿轮中选出z d z d 符合要求的一对齿轮。
5-5 有一个渐开线直齿圆柱齿轮如图5-4所示,用卡尺测量三个齿和两个齿的公法线长度为3=61.84mm ,2=37.56mm ,齿顶圆直径a =208mm ,齿根W W d 圆直径f =172mm ,数得其齿数=24。
试求:d z(1)该齿轮的模数、分度圆压力角、齿顶高系数a *和顶隙系数c *;m a h(2)该齿轮的基圆距P b 和基圆齿厚b 。
s 5-6 一对渐开线外啮合直齿柱齿轮机构,两轮的分度半径分别为r 1=30mm,r 2=54mm ,=20°,试求:a (1)当中心距′=86mm 时,啮合角′是多少?两个齿轮的节圆半径a a 1和2各为多少?r 'r '(2)当中心距变为′=87mm 时,啮合角′和节圆半径1和2又各为a a r 'r '多少?(3)以上两种中心距情况下的两对节圆半径的比值是否相等,为什么?5-7 已知一对渐开线外啮合标准直齿柱齿轮,1=18, 2=41,=4mm ,z z m =20°,a *=1,试求:a h (1)两轮的几何尺寸、b 、f 、a 和标准中心距,以及重合度εa ;r r r r a (2)用长度度比例尺=0.5mm/mm 画出理论啮合线N 1N 2在其上标出实际ul 啮合线B 1B 2,并标出一对啮合区和两对啮合区,以及节点C 的位置。
外啮合圆柱齿轮参数计算

外啮合圆柱齿轮参数计算外啮合圆柱齿轮是一种常见的机械传动装置,广泛应用于各种机械设备中。
要计算外啮合圆柱齿轮的参数,我们需要先确定齿轮的模数、齿数、压力角等参数,然后通过一系列的计算公式来求解。
下面详细介绍一下具体的计算步骤。
1.确定齿轮的基本参数:齿数、模数、压力角、齿轮修形系数等。
这些参数是计算外啮合圆柱齿轮的基础,可以根据具体应用场景和设计要求来确定。
2.根据齿数和模数计算齿轮的分度圆直径和齿顶圆直径。
分度圆直径是齿轮齿槽的理论直径,齿顶圆直径是齿轮齿顶的理论直径。
这两个参数可以用下面的公式计算:-分度圆直径d=齿数/模数- 齿顶圆直径 da = d + 2h其中,h是齿顶高度,可以通过齿高系数和模数计算得到:-齿顶高度h=m*(1+x)-其中,m是模数,x是齿高系数3.计算齿根圆直径和齿根高度。
齿根圆直径是齿轮齿根的理论直径,齿根高度是齿轮齿根的理论高度。
这两个参数可以用下面的公式计算:- 齿根圆直径 df = d - 2h- 齿根高度 hf = m-齿根高度可以根据具体要求进行修正。
4.计算齿轮齿顶圆与分度圆之间的距离并修正齿轮齿顶圆直径。
齿轮齿顶圆与分度圆之间的距离叫齿顶间隙,可以通过下面的公式计算:-齿顶间隙c=0.25*m- 齿顶圆直径 da = d + 2h + 2c5.计算齿轮齿顶圆与齿根圆之间的距离并修正齿轮齿根圆直径。
齿轮齿顶圆与齿根圆之间的距离叫齿根间隙,可以通过下面的公式计算:-齿根间隙b=0.25*m- 齿根圆直径 df = d - 2h - 2b齿根圆直径也可以根据实际要求进行修正。
6.计算齿轮的齿宽。
齿宽是齿轮齿面的理论宽度,可以通过下面的公式计算:-齿宽b=m*z其中,z是齿轮的齿数。
7.根据计算所得的参数,绘制出齿轮的几何图形。
可以采用计算机辅助设计软件进行齿轮的绘制,以便进行后续的工艺设计和加工制造。
通过以上步骤的计算,我们可以得到外啮合圆柱齿轮的各项参数,用于后续的设计和制造。
外 啮 合 角 变 位 圆 柱 齿 轮 几 何 尺 寸 计 算B - (1)
渐开线的特性
1.发生线上的曲率半径的长度与基圆上被滚过的弧长相等。
2.渐开线上任一点的法线恆为基圆的切线。
3.过渐开线上一点的发生线与基圆的切点是渐开线上该点的曲率中心,故渐开线越靠近基圆,其曲率半径越小,反之越大,基圆上的曲率半径为零。
4.同一基圆上任意一条切线与两条渐开线(不论是同向还是反向)的交点间的距离相等。
测跨棒(球)距时量棒(球)直径的予算值
dp′
dp′
式中
〞
〞
〞
〞
〞
外齿 内齿
〞
外齿 内齿
量棒(球)直径的确认值
齿根圆上端面弧齿厚 因 ; 齿根圆上法向弧齿厚
齿顶圆 上弧齿厚
式中 为齿顶圆 上的压力角, 为分度圆 上的压力角.
齿顶圆上端面弧齿厚 = 齿顶圆上法向弧齿厚
基圆 上弧齿厚
因
基圆 上端面弧齿厚 点基圆 上法向弧齿厚
分度圆弦齿厚
式中 和 分别为分圆齿厚和直径
分度圆端面弦齿厚 式中当量齿数 分度圆法向弦齿厚
工作齿高
齿顶隙
C
两基圆 的内公切线长度
齿顶圆的齿形曲率半径
啮合起始圆的齿形曲率半径
啮合起始圆直径
有效啮合齿高度
=
= =
啮合线长度
端面啮合线长度
重合度
端面(齿形)重合度 轴向(纵向)重合度 式中 为有效齿宽, 为端面上螺旋错移量, 为端面齿距.总重合度 因总重合度 = =
四﹑测量尺寸(齿厚)计算
测公法线长度时跨齿数
径向变位系数之和
(由公式 而来)
因 且
中心距变动系数
(由公式 而来)
与 的关系
齿顶高变动系数
齿顶高系数
外啮合齿轮参数计算(完美整理版)
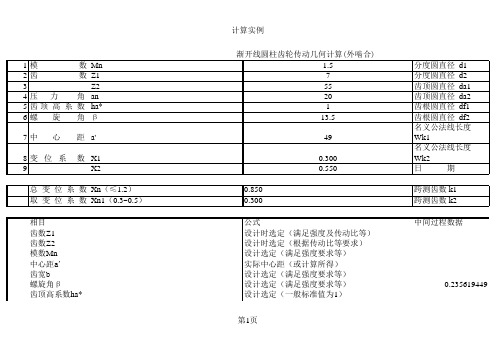
相目公式中间过程数据齿数Z1设计时选定(满足强度及传动比等)齿数Z2设计时选定(根据传动比等要求)模数Mn设计选定(满足强度要求等)中心距a'实际中心距(或计算所得)齿宽b设计选定(满足强度要求等)螺旋角β设计选定(满足强度要求等)0.235619449齿顶高系数ha*设计选定(一般标准值为1)法向压力角αn 设计选定(满足强度要求等)0.34906585顶隙系数cn*设计选定(按标准一般取0.25,0.35,0.4等)1分度圆直径d1d1=Mn*Z1/cosβ10.798359532分度圆直径d2d2=Mn*Z2/cosβ84.844253483未变位时中心距a a=(d1+d2)/2=Mn*(Z1+Z2)/2cosβ47.821306514中心距变动系数Yn Yn=(a'-a)/Mn0.7857956635端面压力角αttan(αt)=tan(αn)/cos β0.374312519αt=arctan(αt)0.3581678116啮合角αwt a'*cos(αwt)=a*cos(αt)0.914012228αwt=arccos(αwt)0.4177299397总变位系数Xninv(αwt)=tan(αwt)-αwt 0.026122587inv(αt)=tan(αt)-αt0.016144708Xn=(Z1+Z2)*(invαwt-invαt)/(2*tanαn)0.8498339558变位系数分配Xn1 Xn2Xn1 取值0.300Xn2=Xn-Xn10.5509齿顶高变动系数ΔYn ΔYn =Xn-Yn0.06410齿顶高ha1 ha2ha1=(ha*+Xn1-ΔYn)*Mn 1.853942562ha2=(ha*+Xn2-ΔYn)*Mn 2.22869349511齿根高hf1 hf2hf1=(ha*+cn*-Xn1)*Mn 1.65hf2=(ha*+cn*-Xn2)*Mn 1.27524906712全齿高 h1 h2h1=ha1+hf1 3.504h2=ha2+hf2 3.50413齿顶圆直径da1 da2da1=d1+2*ha114.50624466da2=d2+2*ha289.3016404714齿根圆直径df1 df2df1=d1-2*hf17.498359533df2=d2-2*hf282.29375534公法线计算Wk1 Wk215当量齿数 Z*1 Z*2Z*1=Z1*invαt/invαn7.582531652Z*2=Z2*invαt/invαn59.57703441 16跨测齿数 k1 k2(1+2*Xn/Z*)*(1+2*Xn/Z*) 1.1645199261.037256527cosan*cosan0.883022222SQRT0.5305635730.392726757k1 1.757262977 k28.142981876 W*1 W*2W*=cos(PI(K-0.5)+Z**invαn) 4.53439459222.9753942217Wk1Wk1=(W*1+2*Xn1*sinαn)*Mn7.109410017 Wk2Wk1=(W*2+2*Xn2*sinαn)*Mn35.02725419变位后的中心距(验算值)a′=a×cos(αt)/cos(αwt)49备注: 1、绿色为输入数据,黄色为结果数据2、根据C12数值选择C13单元参数(一般C12≯1,C13=0.5、或C13=0.5C12)3、C7单元参数输入角度数值4、该程序适用于外啮合齿轮的传动计算外啮合变位圆柱齿轮,已知变位系数,求中心距:1.先算未变位时中心距 a=m(z1+z2)/22.再求变为后的啮合角 invα′=2(x1+x2)×tanα/(z1+z2)+invα3.计算变位后的中心距 a′=a×cosα/cosα′如果是斜齿轮,那么:a=m(z1+z2)/(2cosβ)invαt′=2(xn1+xn2)×tanαn/(z1+z2)+invαta′=a×cosαt/cosαt′invα就是渐开线函数,就是渐开线上那一点的展开角(弧度)。
直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算

外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1,直齿圆柱齿轮变位系数计算:Case1:a,此处例子仅计算用齿条型刀具加工时的情况(插齿刀加工见相关手册公式):小结:由此可知本例选取的齿数在不变位的情况也不会产生根切现象。
b,根据下图选择大小齿轮的变位系数和x∑。
本例在P6-P7区间取值。
即齿根及齿面承载能力较高区,进行选择。
因大小齿轮的齿数和为18+19=37。
所以本例选择的变位系数和x∑=0.8。
本例我们的两个齿轮在工作时属于减速运动,所以按减速运动的变位系数分配线图,进行2个齿轮的变位系数的选择。
先按(z1+z1)/2=18.5,作为横坐标,做一条垂线(图中蓝色的线),再按x∑/2=0.4,作为纵坐标,做一条水平线(图中橙色的线),接着沿着L线的趋势,穿过上面2条线的交点做一条射线(图中红色的线)最后按大小齿轮的齿数做相应的垂线(图中紫色的线),即得到需要的各自变位系数。
最后我们选择的变位系数即为:小齿轮x1=0.42,大齿轮x2=0.38。
【基本保障其和与之前x ∑一致,即可】。
c,验算变位后的齿顶厚度:注:一般要求齿顶厚Sa≥0.25m;对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式(因为当齿轮变位后,齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。
)。
分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结:计算发现变位后的齿轮齿顶厚满足设计需求。
根据上面确定的变位系数,计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。
外啮合圆柱齿轮几何计算公式

外啮合圆柱齿轮几何计算公式齿轮计算公式2010-07-11 18:01:00| 分类:默认分类| 标签:|字号大中小订阅1 齿轮模数:m=p/π齿轮模数m=齿距p 除以3.14测绘时的简易计算m=齿顶圆直径(外径)d 除以(齿数z+2)2 齿轮分度圆直径:d=mz分度圆直径d=模数m 乘以齿数z3 齿轮压力角:标准齿轮的压力角为20度压力角标准为20度其他还有14.5度17.5度15度25度和28度4 齿轮变位系数:用范成法加工齿轮时,刀具中心线不与齿轮的分度圆相切,刀具中心与齿轮的分度圆的距离除以模数所得的商就是齿轮的变位系数。
刀具中心线在齿轮的分度圆之外,为正变位,变位系数为正,反之为负。
注:一般一对齿轮啮合一大一小相差悬殊时,小齿轮要做正变位,大齿轮做负变位,以保证它们的使用寿命比较均衡5 齿轮跨齿数:k=zα/180+0.5跨齿数k=齿数x压力角/180+0.5 (注:必须四舍五入取整数)6 齿轮公法线长度直齿公式Wk=mcosα[(k-0.5)π+zinva]简化为;Wk=m[2.9521*(k-0.5)+0.014z]斜齿公式Wk=mcosα[(k-0.5)π+zinva]+2xtanα α=20时tanα-α=0.01490438其中:α= 压力角标准为20度其他还有14.5度17.5度15度25度和28度K = 跨齿数X=变位系数invα=tan(α)-α7 齿轮齿跳Fr一般为0.025 (表示各齿跳动公差)8 齿轮齿向Fβ一般为0.008 (表示各齿向公差)9 齿轮齿形Ff 一般为0.008 (表示各齿形状大小公差)10 齿轮齿距p=πm m 模数11 齿轮齿顶高ha=ha*m12 齿轮齿根高hf=(ha*+c*)m13 齿轮齿顶圆直径da=(d+2ha) d :分度圆直径ha ;齿顶高14 齿轮齿根圆直径df=d-2hf=(z-2ha-2ca*)m15 中心距a=(d1+d2)/2=(z1+z2)m/2 d1和d2配对的两个齿轮分度圆直径;z1和z2两齿轮齿数。
外啮合圆柱齿轮几何计算公式

外啮合圆柱齿轮几何计算公式计算公式及说明直齿轮斜齿及人字齿轮由强度计算或结构设计确定,法向模数m取标准值。
n并取标准值端面模数:m=mcosβ tnβ=0 两轮螺旋角相等,方向相反名称及代号α=20? nα=20?tanα=tanα/cosβ tnd=mz d=mz ta=(d+d)/2 a=(d+d)/2 1212=(z+z)m/2 =(z+z)m/(2cosβ ) 1212n情况? 已知总变位系数(x+x)时: 12invα,=2(x+x)tanα/(z+z)+invα 1212invα,=2(x+x)tanα/(z+z)+invα tn1n2n12t啮合角α, 求出啮合角α,后,可求出变位后的中心距a,情况? 已知变位后的中心距a,时:cosα,=acosα/a, cosα,=acosα/a, tt求出啮合角α,后,由上式求(x+x)值,再进行分配 12y=(a,-a)/m nny=(a,-a)/m =(z+z)(cosα/cosα,-1) 12tt中心距变动系数y=(z+z)(cosα/cosα,-1)/2 /(2cosβ) 12y=yconβ tn变位后的中心距a, a,=a+ym=acosα/cosα, a,=a+ym=a+ym=acosα/cosα, ttnntt齿根圆直径d d=d-2(h+c-xm) d=d-2(h+c-xm) ffafannnn d=2a,-d-2c d=2a,-d-2c a1f2a1f2n齿顶圆直径d ad=2a,-d-2c d=2a,-d-2c a2f1a2f1n齿顶高h h=(d-d)/2 aaa齿根高h h=(d-d)/2 fff齿高h h=h+h af基圆直径d d=dcosα d=dcosα bbbt节圆直径d, d,=d/cosα, d,=dcosα, bbt分度圆齿距p p=mπ p=mπ ,p=mπ nntt基圆齿距p p=pcosα p=pcosα bbbttt齿顶压力角α α=arccos(d/d) α=arccos(d/d) aabaatba基圆螺旋角tanβ=tanβcosα btβ=0 bβ cosβ=cosβcosα/cosα bbntε=[z(tanα-tanα,)+ ε=[z(tanα-tanα,)+ αα1a11at1t端面重合度ε αz(tanα-tanα,)]/(2π) z(tanα-tanα,)]/(2π) 2a22at2tε=bsinβ/(mπ) βn纵向重合度ε ε=0 ββb——齿轮宽度总重合度ε ε=ε ε=ε+ε γγαγαβ注:角标n为法面,t为端面;1为小齿轮,2为大齿轮。
已知一对外啮合正常齿标准直齿圆柱齿轮3mm

第5章习题5-1 已知一对外啮合正常齿标准直齿圆柱齿轮m=3mm,z1=19,z2=41,试计算这对齿轮的分度圆直径、齿顶高、齿根高、顶隙、中心距、齿顶圆直径、齿根圆直径,基圆直径、齿距、齿厚和齿槽宽。
5-2 已知一正常具标准直齿圆柱的a=20°m=mm,z=40,试分别求出分度圆、基圆、齿顶圆上渐开线齿廓的曲率半径和压力角。
5-3 如图5-3所示一渐开线齿轮在半径为r A=95mm处的齿轮的齿廓压力角为8°26′49″,齿厚为s A=10.088mm。
试计算齿廓压力角为a B=25°处的齿厚s B及半径r B。
5-4 在某项技术革新中,需要采用一对齿轮传动,其中心距a=144mm,传动比i=2。
现在库房中存有四种现成的齿轮,压力角都是20°,这四种齿轮的齿数z和齿顶圆直径d a分别为:z1=24,d al=104mm;z2=47,d a2=196mm;z3=48,d a3=250mm;z4=48,d a4=200mm。
试分析能否从这四种齿轮中选出符合要求的一对齿轮。
5-5 有一个渐开线直齿圆柱齿轮如图5-4所示,用卡尺测量三个齿和两个齿的公法线长度为W3=61.84mm,W2=37.56mm,齿顶圆直径d a=208mm,齿根圆直径d f=172mm,数得其齿数z=24。
试求:(1)该齿轮的模数m、分度圆压力角a、齿顶高系数h a*和顶隙系数c*;(2)该齿轮的基圆距P b和基圆齿厚s b。
5-6 一对渐开线外啮合直齿柱齿轮机构,两轮的分度半径分别为r1=30mm,r2=54mm,a=20°,试求:(1)当中心距a′=86mm时,啮合角a′是多少?两个齿轮的节圆半径r'1和r'2各为多少?(2)当中心距变为a′=87mm时,啮合角a′和节圆半径r'1和r'2又各为多少?(3)以上两种中心距情况下的两对节圆半径的比值是否相等,为什么?5-7 已知一对渐开线外啮合标准直齿柱齿轮,z1=18, z2=41,m=4mm,a=20°,h a*=1,试求:(1)两轮的几何尺寸r、r b、r f、r a和标准中心距a,以及重合度εa;(2)用长度度比例尺ul=0.5mm/mm画出理论啮合线N1N2在其上标出实际啮合线B1B2,并标出一对啮合区和两对啮合区,以及节点C的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相目公式
中间过程数据
齿数Z1设计时选定(满足强度及传动比等)齿数Z2设计时选定(根据传动比等要求)模数Mn 设计选定(满足强度要求等)中心距a'实际中心距(或计算所得)齿宽b 设计选定(满足强度要求等)螺旋角β
设计选定(满足强度要求等)0
齿顶高系数ha*设计选定(一般标准值为1)法向压力角αn 设计选定(满足强度要求等)0.34906585
顶隙系数cn*
设计选定(按标准一般取0.25,0.35,0.4等)
1分度圆直径d1d1=Mn*Z1/cosβ4402分度圆直径d2d2=Mn*Z2/cosβ
13003未变位时中心距a a=(d1+d2)/2=Mn*(Z1+Z2)/(2cosβ)8704中心距变动系数Yn Yn=(a'-a)/Mn
1.6
5端面压力角αt
tan(αt)=tan(αn)/cos β0.363970234αt=arctan(αt)
0.349065856啮合角αwt a'*cos(αwt)=a*cos(αt)
0.90635541αwt=arccos(αwt)
0.4362196137
总变位系数Xn inv(αwt)=tan(αwt)-αwt
0.029950847inv(αt)=tan(αt)-αt
0.014904384Xn=(Z1+Z2)*(invαwt-invαt)/(2*tanαn)
1.798282021
8Xn1 取值0.750Xn2=Xn-Xn1 1.0489齿顶高变动系数ΔYn ΔYn =Xn-Yn 0.19810齿顶高ha1 ha2ha1=(ha*+Xn1-ΔYn)*Mn
31.03435957
ha2=(ha*+Xn2-ΔYn)*Mn
3711齿根高hf1 hf2hf1=(ha*+cn*-Xn1)*Mn
10
hf2=(ha*+cn*-Xn2)*Mn
4.034359574
12全齿高 h1 h2h1=ha1+hf1
41.034h2=ha2+hf2
41.03413齿顶圆直径da1 da2da1=d1+2*ha1
502.0687191
da2=d2+2*ha2
137414
齿根圆直径df1 df2df1=d1-2*hf1
420
df2=d2-2*hf2
1291.931281
变位系数分配Xn1 Xn2(可根据齿数比u(=Z2/Z1)的大小利用手册线图2-7选取)
公法线计算Wk1 Wk2
15当量齿数 Z*1 Z*2Z*1=Z1*invαt/invαn22.00000128
Z*2=Z2*invαt/invαn65.00000378 16跨测齿数 k1 k2(1+2*Xn/Z*)*(1+2*Xn/Z*) 1.141012388
1.065550033
cosan*cosan0.883022222
SQRT0.507927324
0.427232737
k1 4.00704226 k29.598432794 W*1 W*2W*=cosα(PI(K-0.5)+Z**invαn)10.64058189
28.95560869
17Wk1Wk1=(W*1+2*Xn1*sinαn)*Mn223.0722421 Wk2Wk2=(W*2+2*Xn2*sinαn)*Mn593.4535166备注: 1、绿色为输入数据,黄色为结果数据
2、根据C12数值选择C13单元参数(一
般C12≯1,C13=0.5、或C13=0.5C12)
3、C7单元参数输入角度数值
4、该程序适用于外啮合齿轮的传动计
算
5、该程序参照标准《齿轮传动设计手
册》表2-13
最终结果数据
22
65
20
902
330
1
20
0.25
440.000 1300.000 870.000
1.600
0.364 20.000
0.906 24.994
0.030
0.015
1.798
0.750
1.048
0.198 31.034 37.000 10.000
4.034 41.034 41.034 502.069 1374.000 420.000 1291.931
22.000 65.000 1.141 1.066 0.883 0.508 0.427
4
10 10.641 28.956 223.072 593.454。
