因动点产生的面积问题

例21：2011年四川省南充市中考第22题抛物线y=ax2+bx+c与x轴的交点为A（m﹣4，0）和B（m，0），与直线y=﹣x+p相交于点A和点C（2m﹣4，m﹣6）．（1）求抛物线的解析式；（2）若点P在抛物线上，且以点P和A，C以及另一点Q为顶点的平行四边形ACQP面积为12，求点P，Q 的坐标；（3）在（2）条件下，若点M是x轴下方抛物线上的动点，当△PQM的面积最大时，请求出△PQM的最大面积及点M的坐标．解答：解：（1）∵点A（m﹣4，0）和C（2m﹣4，m﹣6）在直线y=﹣x+p上∴，解得：，∴A（﹣1，0），B（3，0），C（2，﹣3），设抛物线y=ax2+bx+c=a（x﹣3）（x+1），∵C（2，﹣3），代入得：﹣3=a（2﹣3）（2+1），∴a=1∴抛物线解析式为：y=x2﹣2x﹣3，答：抛物线解析式为y=x2﹣2x﹣3．（2）解：AC=3，AC所在直线的解析式为：y=﹣x﹣1，∠BAC=45°，∵平行四边形ACQP的面积为12，∴平行四边形ACQP中AC边上的高为=2，过点D作DK⊥AC与PQ所在直线相交于点K，DK=2，∴DN=4，∵ACPQ，PQ所在直线在直线ACD的两侧，可能各有一条，∴PQ的解析式或为y=﹣x+3或y=﹣x﹣5，∴，解得：或，，方程无解，即P1（3，0），P2（﹣2，5），∵ACPQ是平行四边形，A（﹣1，0），C（2，﹣3），∴当P（3，0）时，Q（6，﹣3），当P（﹣2，5）时，Q（1，2），∴满足条件的P，Q点是P1（3，0），Q1（6，﹣3）或P2（﹣2，5），Q2（1，2）答：点P，Q的坐标是P1（3，0），Q1（6，﹣3）或P2（﹣2，5），Q2（1，2）．（3）解：设M（t，t2﹣2t﹣3），（﹣1＜t＜3），过点M作y轴的平行线，交PQ所在直线雨点T，则T（t，﹣t+3），MT=（﹣t+3）﹣（t2﹣2t﹣3）=﹣t2+t+6，过点M作MS⊥PQ所在直线于点S，MS=MT=（﹣t2+t+6）=﹣（t﹣）2+，∴当t=时，M（，﹣），△PQM中PQ边上高的最大值为，答：△PQM 的最大面积是，，点M 的坐标是（，﹣）．点评：本题主要考查对用待定系数法求二次函数的解析式，二次函数的最值，平行四边形的性质，解二元一次方程组等知识点的理解和掌握，综合运用这些性质进行计算是解此题的关键，此题是一个综合性比较强的题目，有一定的难度．例22：2010年广东省湛江市中考第28题如图，在平面直角坐标系中，点B 的坐标为(－3，－4)，线段OB 绕原点逆时针旋转后与x 轴的正半轴重合，点B 的对应点为点A ．(1)直接写出点A 的坐标，并求出经过A 、O 、B 三点的抛物线的解析式；(2)在抛物线的对称轴上是否存在点C ，使BC ＋OC 的值最小？若存在，求出点C 的坐标；若不存在，请说明理由；(3)点P 是抛物线上的一个动点，且在x 轴的上方，当点P 运动到什么位置时，△PAB 的面积最大？求出此时点P 的坐标和△PAB 的最大面积．解：(1)A(5，0) ………1分由抛物线经过点O ，可设抛物线的解析式为bx ax y +=2…2分⎩⎨⎧=-=+4390525b a b a 解得⎪⎪⎩⎪⎪⎨⎧=-=6561b a …………………………4分 ∴抛物线的解析式为x x y 65612+-=…………………………5分 (2)如图，由(1)得抛物线的对称轴是直线25=x ，点O 、A 关于直线25=x 对称，连接AB 交直线25=x 于点C ，则点C 使BC+OC 的值最小………………………6分设直线AB 的解析式为b kx y +=，得⎩⎨⎧-=+-=+4305b k b k ，解得⎪⎪⎩⎪⎪⎨⎧-==2521b k∴直线的解析式为2521-=x y ………………………8分把25=x 代入2521-=x y ，得45-=y ，∴点C 的坐标为)45,25(-………………9分(3)如图，过点P 作y 轴的平行线交AB 于点D ，设点P 的横坐标为x ，得)6561,(2x x x P +-, )2521,(-x x D ………………10分∴PAD PBD PAB S S S ∆∆∆+==)(21B A x x PD -∙＝))((21B A D p x x y y --＝[])3(5)2521()6561(212--⨯⎥⎦⎤⎢⎣⎡--+-x x x ＝1034322++-x x ＝332)1(322+--x ∴当1=x 时，PAB S ∆的最大值为332………………12分把1=x 代入x x y 65612+-=，得32=y ，∴此时点P 的坐标为)32,1(………………13分例23：2012年广东省广州市中考数学模拟第25题平面直角坐标系中，平行四边形ABOC 如图放置，点A 、C 的坐标分别为(0，3)、(1-，0)，将此平行四边形绕点0顺时针旋转90°，得到平行四边形'''A B OC 。

因动点产生的面积问题

80因动点产生的面积问题★林广姗所谓的因动点产生的面积问题就是解决一个会移动的点在坐标系中的位置转变所形成的几何面积问题。

在往年真题中我们可以看到中考命题组特别喜爱动点面积相结合的问题，因动点产生的面积问题大多以函数为背景，充分结合函数、方程、转化及数形结合等思想进行展开，而学生对知识点多且题型复杂的动点问题也是又爱又恨。

在数学教学中，教师可以从哪些方向带着学生不慌不忙延伸拆解每一道题，让学生动脑生趣，不再害怕此类问题。

引言：在中考中，数学要如何和他人拉开距离，保持领先？那么我们就要教会学生破解压轴题，而作我们首要突破的热点压轴题则是动点问题，其中因动点产生的面积问题则是学生们最怕见到的压轴题类型。

如何让学生对动点产生兴趣？高效利用每一道真题，延伸派生，让学生一题多思。

接下来笔者将会对两道中考真题进行思路点拨和延伸，旨在与大家交流研讨。

一、思路建立阶段面积是平面图形中的一个重要的概念，关联着平面图形中的要素边与角，因点的运动而产生的面积问题，是一次函数图象与二次函数图象相结合的形式，经常出现的面积问题有规则图形（如直角三角形、平行四边形、特殊平行四边形的面积）以及不规则图形的面积计算，求解不规则几何图形的面积是中考压轴常考的题型，此类题目运算量较大，要根据不同题目的动点问题思考解的可变性和多可能性。

求解动点相关面积问题经常用到下列与面积有关的方法：平面几何的割与补、等积变形、等比转化等数学思想方法。

解决与面积相关的动点存在性题目，出现频率较高的题型和使用较多的解题策略有两种：一是据图形确定存在性，再列出方程，求解并检验方程的根．二是先认为关系存在，然后列出方程，再据方程的反推假设是否成立．而教师对真题进行延展派生时，可通过以下几个方面进行延展：（1）在原图中加一或多条辅助线，构成新图形，再求解新平面几何图形的面积；（2）改变面积比例求对应点坐标；（3）改变动点活动范围，例如当动点跑出函数外时；（4）求构成特殊图形时特殊点的坐标，例如直角三角形、等腰三角形、等边三角形、平行四边形、特殊的平行四边形等。

因动点产生的面积问题

1
例题 5 如图平面直角坐标系中，O 是坐标原点，抛物线y = �� 2 − 4�� + ��与��轴
交于 A、B 两点（点 A 在点 B 的左侧），与��轴的负半轴交于点 C，且OB = OC。 1) 求该抛物线的解析式及点 B 的坐标； 2) P 是线段 OB 上的一点，过点 P 作PD ⊥ ��轴，与抛物线交于 D 点，直线 BC 能否把∆��分成面积之比为2: 3的两部分？如能，请求出点 P 的坐标；如不能，请说明理由。
��
Hale Waihona Puke 例题 3 如图，已知直线y = 2 ��与双曲线 y = �� （k > 0）交于 A、B 两点，且点 A
的横坐标为 4. 1) 求 K 的值； 2) 若双曲线上的一点 C 的纵坐标为 8，求 AOC 的面积； 3) 过原点 O 的另一条直线交双曲线与 P、Q 两点（P 点在第一象限），若由 A、 B、P、Q 为顶点组成的四边形面积为 24，求点 P 的坐标。
第五篇因动点产生的面积问题例题 1 如图已知一次函数y = ax − a(a ≠ 0)的图像是直线l,点 E 是直线l与y轴的
交点。 1) 证明：当a取不等于 0 的实数时，直线l都经过x轴上的一个定点 P，并求这个定点 P 的坐标； 2) 在x轴上找出点 Q，使 S∆PQE=2S∆OPE ，求出点 Q 的坐标。
例题 2 如图，点 P、点 Q 分别在x轴、y轴上。
1) 已知点 P（3，0），Q（0，4），点 M 在线段 PQ 上，直线 OM 把∆POQ 分成两个三角形，且这两个三角形的面积的比是 2：1，求直线 MO 的函数解析式； 2) 如图，已知 P（m，0），Q（0，n）（m>0,n>0）,反比例函数y = �� 的图像与线段 PQ 交于 C、D 两点，若 S∆POC=S∆COD=S∆DOQ 求 n 的值。

因动点产生的面积问题

因动点产生的面积问题1.如图1, 四边形OABC是矩形, 点A.C的坐标分别为(3,0), (0,1). 点D是线段BC上的动点〔与端点B.C不重合〕, 过点D作直线交折线OAB于点E.〔1〕记△ODE的面积为S, 求S与b的函数关系式；〔2〕当点E在线段OA上时, 假设矩形OABC关于直线DE的对称图形为四边形O1A1B1C1, 试探究四边形O1A1B1C1与矩形OABC的重叠局部的面积是否发生变化？假设不变, 求出重叠局部的面积；假设改变,请说明理由．图12.如图1, 直角梯形OABC的边OA在y轴的正半轴上, OC在x轴的正半轴上, OA＝AB＝2, OC＝3, 过点B作BD⊥BC, 交OA于点D. 将∠DBC绕点B按顺时针方向旋转, 角的两边分别交y轴的正半轴、x轴的正半轴于E和F.〔1〕求经过点A.B.C三点的抛物线的解析式；〔2〕当BE经过〔1〕中抛物线的顶点时, 求CF的长；〔3〕连结EF, 设△BEF与△BFC的面积之差为S, 问当CF为何值时S最小, 并求出最小值．图13.如图1, 在△ABC中, ∠C＝90°, AC＝3, BC＝4, CD是斜边AB上的高, 点E在斜边AB上, 过点E 作直线与△ABC的直角边相交于点F, 设AE＝x, △AEF的面积为y.〔1〕求线段AD的长；〔2〕假设EF⊥AB, 当点E在斜边AB上移动时,①求y与x的函数关系式〔写出自变量x的取值范围〕；②当x取何值时, y有最大值？并求出最大值.〔3〕假设点F在直角边AC上〔点F与A、C不重合〕, 点E在斜边AB上移动, 试问, 是否存在直线EF 将△ABC的周长和面积同时平分？假设存在直线EF, 求出x的值；假设不存在直线EF, 请说明理由．图1 备用图4.如图1, : 抛物线y＝x2＋bx－3与x轴相交于A.B两点, 与y轴相交于点C, 并且O..OC.〔1〕求这条抛物线的解析式；〔2〕过点C作CE // x轴, 交抛物线于点E, 设抛物线的顶点为点D, 试判断△CDE的形状, 并说明理由；〔3〕设点M在抛物线的对称轴l上, 且△MCD的面积等于△CDE的面积, 请写出点M的坐标〔无需写出解题步骤〕．图15.如图1, 在平面直角坐标系xOy中, 直角梯形OABC的顶点O为坐标原点, 顶点A.C分别在x轴、y 轴的正半轴上, CB∥OA, OC＝4, BC＝3, OA＝5, 点D在边OC上, CD＝3, 过点D作DB的垂线DE, 交x 轴于点E.〔1〕求点E的坐标；〔2〕二次函数y＝－x2＋bx＋c的图像经过点B和点E.①求二次函数的解析式和它的对称轴；②如果点M在它的对称轴上且位于x轴上方, 满足S△CEM＝2S△ABM, 求点M的坐标.图16.如图1, 直线l经过点A(1, 0), 且与双曲线(x＞0)交于点B(2, 1). 过点(p＞1)作x轴的平行线分别交曲线(x＞0)和(x＜0)于M、N两点.〔1〕求m的值及直线l的解析式；〔2〕假设点P在直线y＝2上, 求证: △PMB∽△PNA；〔3〕是否存在实数p, 使得S△AMN＝4S△AMP？假设存在, 请求出所有满足条件的p的值；假设不存在,请说明理由．图1因动点产生的面积问题1.〔2021年广州市中考第25题〕如图1, 四边形OABC是矩形, 点A.C的坐标分别为(3,0), (0,1). 点D是线段BC上的动点〔与端点B.C不重合〕, 过点D作直线交折线OAB于点E.〔1〕记△ODE的面积为S, 求S与b的函数关系式；〔2〕当点E在线段OA上时, 假设矩形OABC关于直线DE的对称图形为四边形O1A1B1C1, 试探究四边形O1A1B1C1与矩形OABC的重叠局部的面积是否发生变化？假设不变, 求出重叠局部的面积；假设改变,请说明理由．图1思路点拨1. 数形结合, 用b表示线段OE、CD.AE、BE的长.2．求△ODE的面积, 要分两种情况．当E在OA上时, OE边对应的高等于OC；当E在AB边上时, 要利用割补法求△ODE的面积．3. 第〔2〕题中的重叠局部是邻边相等的平行四边形.4．图形翻折、旋转等运动中, 计算菱形的边长一般用勾股定理．总分值解答(1)①如图2, 当E在OA上时, , 由可知, 点E的坐标为(2b,0), OE＝2b.此时S＝S△ODE＝.②如图3, 当E在AB上时, , 把y＝1代入可知, 点D的坐标为(2b－2,1), CD＝2b－2, BD＝5－2b．把x＝3代入可知, 点E的坐标为, AE＝, BE＝．此时S＝S矩形OABC－S△OAE－S△BDE －S△OCD＝.(2)如图4, 因为四边形O1A1B1C1与矩形OABC关于直线DE对称, 因此DM＝DN,那么重叠局部是邻边相等的平行四边形, 即四边形DMEN是菱形.作DH⊥OA, 垂足为H. 由于CD＝2b－2, OE＝2b, 所以EH＝2.设菱形DMEN的边长为m．在Rt△DNH中, DH＝1, NH＝2－m, DN＝m, 所以12＋(2－m)2＝m2．解得．所以重叠局部菱形DMEN的面积为．图2 图3 图4考点伸展把此题中的矩形OABC绕着它的对称中心旋转, 如果重叠局部的形状是菱形〔如图5〕, 那么这个菱形的最小面积为1, 如图6所示；最大面积为, 如图7所示.图5 图6 图72.2021年湖州市中考第24题如图1, 直角梯形OABC的边OA在y轴的正半轴上, OC在x轴的正半轴上, OA＝AB＝2, OC＝3, 过点B作BD⊥BC, 交OA于点D．将∠DBC绕点B按顺时针方向旋转, 角的两边分别交y轴的正半轴、x 轴的正半轴于E和F．〔1〕求经过点A.B.C三点的抛物线的解析式；〔2〕当BE经过〔1〕中抛物线的顶点时, 求CF的长；〔3〕连结EF, 设△BEF与△BFC的面积之差为S, 问当CF为何值时S最小, 并求出最小值．图1 图2思路点拨1. 过点B向坐标轴作垂线, 图形中就构造出丰富的余角, 从而构造出相似三角形. 此题中因为点B的坐标特殊, 因此构造出全等三角形.2．用CF表示△BEF与△BFC的面积之差, 首先要判断△BEF是等腰直角三角形, 这样△BEF的面积就转化为求BF2的问题．总分值解答(1)根据题意可得A(0,2), B(2,2), C(3,0). 设抛物线的解析式为y＝ax2＋bx＋c,那么解得, , . 所以抛物线的解析式为.(2)由, 得抛物线的顶点G的坐标为〔〕.如图2, 过点B作x轴的垂线, 垂足为M, 过点E作y轴的垂线, 交BM于N.因为∠BEN与∠FBM都是∠EBN的余角, 所以∠BEN＝∠FBM.又因为BM＝EN＝2, 所以△BMF≌△ENB. 因此BE＝BF, BN＝FM.当BE经过抛物线的顶点G时, . 此时.(3)设CF的长为a. 在Rt△BFM中, .因为△BEF是等腰直角三角形, 所以．因此.所以当CF＝2时, S取得最小值, 最小值为.考点伸展：图2是一个典型图, 在这个图形中, △BMC≌△BAD, △BFC≌△BED, △BFM≌△BEA≌△ENB, △BEF与△BDC、△BAM都是等腰直角三角形.如果把此题中的条件“角的两边分别交y轴的正半轴、x轴的正半轴于E和F〞改为“角的两边分别交y 轴、x轴于E和F〞, 那么上述结论依然成立〔如图3, 图4〕．图3 图43.如图1, 在△ABC中, ∠C＝90°, AC＝3, BC＝4, CD是斜边AB上的高, 点E在斜边AB上, 过点E 作直线与△ABC的直角边相交于点F, 设AE＝x, △AEF的面积为y.〔1〕求线段AD的长；〔2〕假设EF⊥AB, 当点E在斜边AB上移动时,①求y与x的函数关系式〔写出自变量x的取值范围〕；②当x取何值时, y有最大值？并求出最大值.〔3〕假设点F 在直角边AC 上〔点F 与A 、C 不重合〕, 点E 在斜边AB 上移动, 试问, 是否存在直线EF 将△ABC 的周长和面积同时平分？假设存在直线EF, 求出x 的值；假设不存在直线EF, 请说明理由．图1 备用图思路点拨1. 第〔1〕题求得的AD 的长, 就是第〔2〕题分类讨论x 的临界点.2. 第〔2〕题要按照点F 的位置分两种情况讨论.3．第〔3〕题的一般策略是：先假定平分周长, 再列关于面积的方程, 根据方程的解的情况作出判断．总分值解答(1) 在Rt △ABC 中, AC ＝3, BC ＝4, 所以AB ＝5. 在Rt △ACD 中, .(2) ①如图2, 当F 在AC 上时, . 在Rt △AEF 中, . 所以 . 如图3, 当F 在BC 上时, . 在Rt △BEF 中, . 所以 . ②当时, 的最大值为；当时, 的最大值为 .因此, 当时, y 的最大值为．图2 图3 图4(3)△ABC 的周长等于12, 面积等于6.先假设EF 平分△ABC 的周长, 那么AE ＝x, AF ＝6－x, x 的变化范围为3＜x ≤5．因此．解方程 , 得．因为在3＜x ≤5范围内〔如图4〕, 因此存在直线EF 将△ABC 的周长和面积同时平分．考点伸展如果把第〔3〕题的条件“点F 在直角边AC 上〞改为“点F 在直角边BC 上〞, 那么就不存在直线EF 将△ABC 的周长和面积同时平分.先假设EF 平分△ABC 的周长, 那么AE ＝x, BE ＝5－x, BF ＝x ＋1．因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---．解方程 . 整理, 得 . 此方程无实数根.4.如图1, : 抛物线y ＝x2＋bx －3与x 轴相交于A.B 两点, 与y 轴相交于点C, 并且OA = OC. 〔1〕求这条抛物线的解析式；〔2〕过点C 作CE // x 轴, 交抛物线于点E, 设抛物线的顶点为点D, 试判断△CDE 的形状, 并说明理由；〔3〕设点M 在抛物线的对称轴l 上, 且△MCD 的面积等于△CDE 的面积, 请写出点M 的坐标〔无需写出解题步骤〕．思路点拨1. 求抛物线的解析式, 关键是求点A 的坐标, 根据条件, 数形结合. 2．判断△CDE 的形状是等腰直角三角形, 可以方便第〔3〕求解点M 的坐标．总分值解答〔1〕因为抛物线y ＝x2＋bx －3与y 轴交于点C(0, －3), OA ＝OC, 所以点A 的坐标为(－3, 0).将A (－3, 0)代入y ＝x2＋bx －3, 解得b ＝2. 因此抛物线的解析式为y ＝x2＋2x －3. 〔2〕由y ＝x2＋2x －3＝(x ＋1) 2－4, 得顶点D 的坐标为(－1, －4) . 因为CE // x 轴所以点C 与点E 关于抛物线的对称轴对称. 因此CE ＝2, DE ＝DC. 由两点间的距离公式, 求得DC ＝ . 于是可得DE2＋DC2＝CE2.所以△CDE 是等腰直角三角形．〔3〕M1〔－1, －2〕, M2〔－1, －6〕．考点伸展第〔3〕题的解题思路是这样的:如图2, 如图3, 因为△MCD 与△CDE 是同底的两个三角形, 如果面积相等, 那么过点E 作CD 的平行线, 与抛物线的对称轴的交点就是要探求的点M ．再根据对称性, 另一个符合条件的点M 在点D 的下方, 这两个点M 关于点D 对称．还有更简单的几何说理方法:因为△CDE 是等腰直角三角形, 对于点D 上方的点M, 四边形CDEM 是正方形, 容易得到点M 的坐标为〔－1, －2〕．再根据对称性, 得到另一个点M 的坐标为〔－1, －6〕．图2 图35.如图1, 在平面直角坐标系xOy 中, 直角梯形OABC 的顶点O 为坐标原点, 顶点A.C 分别在x 轴、y 轴的正半轴上, CB ∥OA, OC ＝4, BC ＝3, OA ＝5, 点D 在边OC 上, CD ＝3, 过点D 作DB 的垂线DE, 交x 轴于点E. 〔1〕求点E 的坐标；〔2〕二次函数y ＝－x2＋bx ＋c 的图像经过点B 和点E. ①求二次函数的解析式和它的对称轴；②如果点M 在它的对称轴上且位于x 轴上方, 满足S △CEM ＝2S △ABM, 求点M 的坐标．图1思路点拨1. 这三道题目步步为赢, 错一道题目, 就要影响下一道的计算.2. 点M 在抛物线的对称轴上且位于x 轴上方, 要分两种情况讨论, 分别为点M 在线段FB 和FB 的延长线上. 因为用点M 的纵坐标表示△ABM 的底边长, 因点M 的位置不同而不同.总分值解答〔1〕因为BC ∥OA, 所以BC ⊥CD. 因为CD ＝CB ＝3, 所以△BCD 是等腰直角三角形. 因此∠BCD ＝45°. 又因为BC ⊥CD, 所以∠ODE ＝45°. 所以△ODE 是等腰直角三角形, OE ＝OD ＝1. 所以点E 的坐标是〔1, 0〕.〔2〕①因为抛物线y ＝－x2＋bx ＋c 经过点B 〔3, 4〕和点E 〔 1, 0〕, 所以解得所以二次函数的解析式为y ＝－x2＋6x －5, 抛物线的对称轴为直线x ＝3.②如图2, 如图3, 设抛物线的对称轴与x 轴交于点F, 点M 的坐标为〔3, t 〕．CEM MEF COE OFMC S S S S ∆∆∆=--梯形111(4)321442222t t t =+⨯-⨯⨯-⨯⨯=+．〔ⅰ〕如图2, 当点M 位于线段BF 上时, .解方程 , 得 . 此时点M 的坐标为〔3, 〕.〔ⅱ〕如图3, 当点M 位于线段FB 延长线上时, .解方程, 得．此时点M的坐标为〔3, 8〕．图2 图3考点伸展对于图2, 还有几个典型结论: 此时, C.M、A三点在同一条直线上；△CEM的周长最小. 可以求得直线AC 的解析式为, 当x＝3时, . 因此点M〔3, 〕在直线AC上. 因为点A.E关于抛物线的对称轴对称, 所以ME＋MC＝MA＋MC. 当A.M、C三点共线时, ME＋MC最小, △CEM的周长最小.6.如图1, 直线l经过点A(1, 0), 且与双曲线(x＞0)交于点B(2, 1). 过点(p＞1)作x轴的平行线分别交曲线(x＞0)和(x＜0)于M、N两点.〔1〕求m的值及直线l的解析式；〔2〕假设点P在直线y＝2上, 求证: △PMB∽△PNA；〔3〕是否存在实数p, 使得S△AMN＝4S△AMP？假设存在, 请求出所有满足条件的p的值；假设不存在,请说明理由．思路点拨1. 第〔2〕题准确画图, 点的位置关系尽在图形中.2. 第〔3〕题把S△AMN＝4S△AMP转化为MN＝4MP, 按照点M与线段NP的位置关系分两种情况讨论.总分值解答〔1〕因为点B(2, 1)在双曲线上, 所以m＝2. 设直线l的解析式为, 代入点A(1, 0)和点B(2, 1), 得解得所以直线l的解析式为.〔2〕由点(p＞1)的坐标可知, 点P在直线上x轴的上方.如图2, 当y＝2时, 点P的坐标为(3, 2). 此时点M的坐标为(1, 2), 点N的坐标为(－1, 2).由P(3, 2)、M(1, 2)、B(2, 1)三点的位置关系, 可知△PMB为等腰直角三角形.由P(3, 2)、N(－1, 2)、A(1, 0)三点的位置关系, 可知△PNA为等腰直角三角形．所以△PMB∽△PNA.图2 图3 图4〔3〕△AMN和△AMP是两个同高的三角形, 底边MN和MP在同一条直线上.当S△AMN＝4S△AMP时, MN＝4MP.①如图3, 当M在NP上时, xM－xN＝4(xP－xM). 因此.解得或〔此时点P在x轴下方, 舍去〕. 此时.②如图4, 当M在NP的延长线上时, xM－xN＝4(xM－xP). 因此.解得或〔此时点P在x轴下方, 舍去〕．此时．考点伸展在此题情景下, △AMN能否成为直角三角形？情形一, 如图5, ∠AMN＝90°, 此时点M的坐标为〔1, 2〕, 点P的坐标为〔3, 2〕.情形二, 如图6, ∠MAN＝90°, 此时斜边MN上的中线等于斜边的一半．不存在∠ANM＝90°的情况.图5 图6。

二次函数--由动点生成面积问题

二次函数--由动点生成面积问题二次函数是数学中重要的一个概念，它描述了一类以二次项为主导的多项式函数。

而这篇文章将重点探讨一个有趣的问题：如何由动点生成二次函数并应用于面积问题。

首先，我们需要了解什么是动点。

动点是平面上一个不固定的点，它的位置随着时间的推移而变化。

在二维平面上，我们通常用坐标系来描述动点的位置，其中x轴和y轴代表两个独立的变量。

考虑以下问题：假设我们有一条规定的直线，上面有两个动点A和B，它们沿着直线运动。

我们假设初始时刻A和B分别位于直线的两个不同的点，运动速度相同且方向相反。

我们还假设直线是垂直于x轴的。

为了简化问题，我们将直线的方程表示为 y = kx + b，其中 k 是直线的斜率，b 是 y 轴的截距。

此外，我们假设 A 和 B 分别运动的距离为 d1 和 d2，而 d1 和 d2 的长度相等。

我们的目标是通过动点A和B的运动来生成一个面积问题，并进一步将其转化为二次函数。

为了实现这一目标，我们需要引入一个新的点C，它是动点A和B的垂直平分线上的一个固定点。

通过仔细观察，我们可以发现三角形ABC的两条边的长度与动点A和B的距离之间存在一定的关系。

假设三角形ABC的高度为h，底边的长度为b，同时A和B分别位于底边的两个端点。

根据数学原理，我们可以通过两个已知长度和一个夹角来计算一个三角形的面积。

那么如何计算三角形ABC的面积呢？首先，我们可以根据两个动点A和B的运动距离d1和d2来计算出三角形底边的长度b。

由于d1和d2的长度相等，我们可以将它们的和除以2来得到b的长度。

即b=(d1+d2)/2接下来，我们需要确定三角形ABC的高度h。

由于点C是动点A和B的垂直平分线上的一个固定点，因此我们可以用坐标系来表示其位置。

假设点C的坐标为(x0,y0)。

由于点C是动点A和B的垂直平分线的交点，因此动点A在以点C为圆心的圆上运动。

同样地，动点B也在以点C为圆心的圆上运动。

我们可以将动点A和B的位置分别表示为(x1,y1)和(x2,y2)。

动点产生的面积问题

例1.已知△ABC 中，AB =4，BC =6，AC ＞AB ，点D 为AC 边上一点，且DC =AB ，E 为BC 边的中点，联结DE ，设AD =x 。

设ABEDCDES y S ∆=四边形，求y 关于x 的函数关系式，并写出定义域。

【解法点拨】：一．寻找题目中的已经条件：1.边：AB =4，BC =6，DC =AB ；2.特殊点：E 为BC 边的中点；3.动点：点D 为AC 边上一动点。

（2）求面积比ABEDCDES S ∆四边形：方法一：用含x 的代数式单独表示四边形ABED 和三角形CDE ∆的面积；方法二：用面积比求解，ABED CDE S S ∆四边形=1ABD BDE ABDCDE CDES S S S S ∆∆∆∆∆+=+；又因为ABD DBC S S ∆∆=24ABD CDE S x S ∆∆=即2ABD CDE S xS ∆∆=，即可求得。

【满分解答】：连BD ，∵点E 为BC 中点，∴BDE CDE S S ∆∆= ∴1ABD BDE ABDCDE CDES S S y S S ∆∆∆∆∆+==+∵4ABD DBC S x S ∆∆=，∴24ABD CDE S x S ∆∆=，即2ABD CDE S x S ∆∆= ∴12xy =+（0＜x ＜6）例2.如图，已知在直角梯形ABCD 中，BD ∥BC ，AB BC ⊥，11AD =，13BC =，12AB =．动点P 、Q 分别在边AD 和BC 上，且2BQ DP =．线段PQ 与BD 相交于点E ，过点E 作EF ∥BC ，交CD 于点F ，射线PF 交BC 的延长线于点G ，设DP x =．（1）求CFDF的值。

（★★★★）（2）当点P 运动时，试探究四边形EFGQ 的面积是否会发生变化？如果发生变化，请用x 的代数式表示四边形EFGQ 的面积S ；如果不发生变化，请求出这个四边形的面积S 。

【参考教法】：可参考以下教法，以问题式引导学生分析题目、解决问题一．寻找题目中的不变条件或特殊条件，让学生找找看。

中考数学复习之因动点产生的面积问题解题策略

因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路：1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路： 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O 顺时针旋转60°，如题图1，连接BC.（1）填空：∠OBC= ;（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN 的面积为y，求当x为何值时y取得最大值？最大值为多少？思路：（1）由旋转的性质可以证明△OBC是等边三角形，从而可得∠OBC的度数；（2）求出△AOC的面积，利用三角形的面积公式计算即可；（3）分三种情形讨论求解即可解决问题：①当0＜x≤83时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E，利用面积公式表示出△OMN的面积（y值）；②当8 3＜x≤4时，M在BC上运动，N在OB上运动．作MH⊥OB于H，利用∠CBO=60°表示出MH，再利用面积公式表示出△OMN的面积（y值）；③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G，易求OG，再利用面积公式表示出△OMN的面积（y值），最后分别求出三种情况下面积最大值，从而求出整个运动过程中y的最大值．例13. 在平面直角坐标系中，抛物线2y ax bx c=++交x轴于A、B两点，交y轴于点C（0，43-），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=34.（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方向以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动为t秒.①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由；②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由.思路：本题是代数几何综合题，以平面直角坐标系为背景，考查了求二次函数解析式，二次函数的性质，，方程组的解法，几何图形面积的表示，相似三角形的判定与性质，分类讨论思想，三角形的面积的最值问题，综合性强，难度大，解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力，还得富有耐心．（1）利用A、B、C三点的坐标确定二次函数的解析式．（2）利用题目的已知条件表示出相关线段的长，①中利用三角函数值探索出∠PAQ=∠ACD，再根据题目中的要求使得△ADC与△PQA相似，进行分类讨论得到对应线段成比例，列出关于t的方程求解即可；②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式，再将所得的二次函数的解析式配方确定最值即可得到答案.。

中考专题3解答(由动点形生成的面积问题)

由动点形生成的面积问题例题1【2010四川宜宾答案】解：（1）由题意知：A （0，6），C （6，0），设经过点A 、B 、C 的抛物线解析式为y=ax 2+bx+c则：⎪⎩⎪⎨⎧++=+-==c b a c b a c 63603906解得：⎪⎪⎩⎪⎪⎨⎧==-=6131c b a∴该抛物线的解析式为6312++-=x x y （2）如图：设点P （x ，0）， ∵PE ∥AB ，∴△CPE ∽△ABC ， ∴2ABC CPE )BCCPS （△△=S又∵S △ABC =21BC ×OA=27 ∴2CPE )9x -627（△=S ∴S △CPE =3)6(2x -=124312+-x xS △ABP ＝21BP ×OA=3x+9设△APE 的面积为S则S= S △ABC —S △ABP —S △CPE =427)23(3163122+--=++-x x x 当x=23时，S 最大值为427 ∴点P 的坐标为（23，0）（3）假设存在点G （x ，y ），使△AGC 的面积与（2）中△APE 的最大面积相等．在（2）中，△APE 的最大面积为427，过点G 做GF 垂直y 轴与点F ． ①当y ＞6时，S △AGC =S 梯形GFOC —S △GFA —S △AOC =21（x+6）y —21x （y-6）—21×6×6=3x+3y-18 即3x+3y-18=427，yxCBOA又∵点G 在抛物线上，6312++-=x x y ， ∴3x+3)631(2++-x x -18=427解得：23,2921==x x ，当x=29时，y=415，当x=23时，y=427．又∵y ＞6，∴ 点G 的坐标为（23，427） ②当y ＜6时，如图： S △AGC =S △GAF +S 梯形GFOC —S △AOC =21x （6—y ）+)6(21+x y -18=3x+3y-18即3x+3y-18=427，又∵点G 在抛物线上，6312++-=x x y ， ∴3x+3)631(2++-x x -18=427解得：23,2921==x x ，当x=29时，y=415，当x=23时，y=427．又因为y ＜6，所以点G 的坐标为（29，415）．综和①②所述，点G 的坐标为（23，427）和（29，415）．（3）解法2：可以向x 轴作垂线，构成了如此下图的图形:则阴影部分的面积等于S △AGC =S △GCF +S 梯形AGFO —S △AOC下面的求解过程略．这样作可以避免了分类讨论．例题2【2010 湖北孝感答案】（1）解：).)2(41(14122-=+-=x y x x y 或（2）证明：设点141)12,(2+-=--x x y m m 在二次函数的图像上，则有：.141122-+=-m m m整理得,0842=+-m m.01684)4(2<-=⨯--=∆∴原方程无解141)12,(2+-=--∴x x y m m 不在二次函数点的图象上说明：由,01)121()12(14122>+---++m m m m 得到从而判断点)12,(--m m 不在二次函数图像上的同样给分。

因动点产生的面积问题

1.6 因动点产生的面积问题例 1 2012年菏泽市中考第21题如图1，在平面直角坐标系中放置一直角三角板，其顶点为A (0, 1)、B (2, 0)、O (0, 0)，将此三角板绕原点O 逆时针旋转90°，得到三角形A ′B ′O ．（1）一抛物线经过点A ′、B ′、B ，求该抛物线的解析式；（2）设点P 是第一象限内抛物线上的一个动点，是否存在点P ，使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形PB ′A ′B 是哪种形状的四边形？并写出它的两条性质．图1思路点拨1．四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍，可以转化为四边形PB ′OB 的面积是 △A ′B ′O 面积的3倍．2．联结PO ，四边形PB ′OB 可以分割为两个三角形．3．过点向x 轴作垂线，四边形PB ′OB 也可以分割为一个直角梯形和一个直角三角形．满分解答（1）△AOB 绕着原点O 逆时针旋转90°，点A ′、B ′的坐标分别为(－1, 0) 、(0, 2)．因为抛物线与x 轴交于A ′(－1, 0)、B (2, 0)，设解析式为y ＝a (x ＋1)(x －2)，代入B ′(0, 2)，得a ＝1．所以该抛物线的解析式为y ＝－(x ＋1)(x －2) ＝－x 2＋x ＋2．（2）S △A ′B ′O ＝1．如果S 四边形PB ′A ′B ＝4 S △A ′B ′O ＝4，那么S 四边形PB ′OB ＝3 S △A ′B ′O ＝3．如图2，作PD ⊥OB ，垂足为D ．设点P 的坐标为 (x ，－x 2＋x ＋2)．232'1111(')(22)22222PB OD S DO B O PD x x x x x x =+=-++=-++梯形．2321113(2)(2)22222PDB S DB PD x x x x x ∆=⨯=--++=-+．所以2'''2+2PDB PB A D PB OD S S S x x ∆=+=-+四边形梯形．解方程－x 2＋2x ＋2＝3，得x 1＝x 2＝1．所以点P 的坐标为(1，2)．图2 图3 图4（3）如图3，四边形PB ′A ′B 是等腰梯形，它的性质有：等腰梯形的对角线相等；等腰梯形同以底上的两个内角相等；等腰梯形是轴对称图形，对称轴是经过两底中点的直线．考点伸展第（2）题求四边形PB ′OB 的面积，也可以如图4那样分割图形，这样运算过程更简单．'11'222PB O P S B O x x x ∆=⋅=⨯=．22112(2)222PBO P S BO y x x x x ∆=⋅=⨯-++=-++．所以2'''2+2PB O PBO PB A D S S S x x ∆∆=+=-+四边形．甚至我们可以更大胆地根据抛物线的对称性直接得到点P ：作△A ′OB ′关于抛物线的对称轴对称的△BOE ，那么点E 的坐标为(1，2)．而矩形EB ′OD 与△A ′OB ′、△BOP 是等底等高的，所以四边形EB ′A ′B 的面积是△A ′B ′O 面积的4倍．因此点E 就是要探求的点P ．例 2 2012年河南省中考第23题如图1，在平面直角坐标系中，直线112y x =+与抛物线y ＝ax 2＋bx －3交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上的一动点（不与点A 、B 重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连结PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，使这两个三角形的面积比为9∶10？若存在，直接写出m 的值；若不存在，请说明理由．图1思路点拨1．第（1）题由于CP //y 轴，把∠ACP 转化为它的同位角．2．第（2）题中，PD ＝PC sin ∠ACP ，第（1）题已经做好了铺垫．3．△PCD 与△PCB 是同底边PC 的两个三角形，面积比等于对应高DN 与BM 的比． 4．两个三角形的面积比为9∶10，要分两种情况讨论．满分解答（1）设直线112y x =+与y 轴交于点E ，那么A (－2,0)，B (4,3)，E (0,1)．在Rt △AEO 中，OA ＝2，OE ＝1，所以AE ．所以sin AEO ∠=．因为PC //EO ，所以∠ACP ＝∠AEO ．因此sin ACP ∠=将A (－2,0)、B (4,3)分别代入y ＝ax 2＋bx －3，得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =，12b =-．（2）由211(,3)22P m m m --，1(,1)2C m m +，得221111(1)(3)42222PC m m m m m =+---=-++．所以221sin 4)1)2PD PC ACP PC m m m =∠==-++=-．所以PD （3）当S △PCD ∶S △PCB ＝9∶10时，52m =；当S △PCD ∶S △PCB ＝10∶9时，329m =．图2考点伸展第（3）题的思路是：△PCD 与△PCB 是同底边PC 的两个三角形，面积比等于对应高DN 与BM 的比．而211cos cos 4)(2)(4)25DN PD PDN PD ACP m m m m =∠=∠-++=-+-，BM ＝4－m ．①当S △PCD ∶S △PCB ＝9∶10时，19(2)(4)(4)510m m m -+-=-．解得52m =．②当S △PCD ∶S △PCB ＝10∶9时，110(2)(4)(4)59m m m -+-=-．解得329m =．例 3 2011年南通市中考第28题如图1，直线l 经过点A (1，0)，且与双曲线my x=(x ＞0)交于点B (2，1)．过点(,1)P p p -(p ＞1)作x 轴的平行线分别交曲线m y x =(x ＞0)和my x=-(x ＜0)于M 、N 两点．（1）求m 的值及直线l 的解析式；（2）若点P 在直线y ＝2上，求证：△PMB ∽△PNA ；（3）是否存在实数p ，使得S △AMN ＝4S △AMP ？若存在，请求出所有满足条件的p 的值；若不存在，请说明理由．图1思路点拨1．第（2）题准确画图，点的位置关系尽在图形中．2．第（3）题把S △AMN ＝4S △AMP 转化为MN ＝4MP ，按照点M 与线段NP 的位置关系分两种情况讨论．满分解答（1）因为点B (2，1)在双曲线my x=上，所以m ＝2．设直线l 的解析式为y kx b =+，代入点A (1，0)和点B (2，1)，得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩所以直线l 的解析式为1y x =-．（2）由点(,1)P p p -(p ＞1)的坐标可知，点P 在直线1y x =-上x 轴的上方．如图2，当y ＝2时，点P 的坐标为(3，2)．此时点M 的坐标为(1，2)，点N 的坐标为(－1，2)．由P (3，2)、M (1，2)、B (2，1)三点的位置关系，可知△PMB 为等腰直角三角形．由P (3，2)、N (－1，2)、A (1，0)三点的位置关系，可知△PNA 为等腰直角三角形．所以△PMB ∽△PNA ．图2 图3 图4（3）△AMN 和△AMP 是两个同高的三角形，底边MN 和MP 在同一条直线上．当S △AMN ＝4S △AMP 时，MN ＝4MP ．①如图3，当M 在NP 上时，x M －x N ＝4(x P －x M )．因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得x 或x =P 在x 轴下方，舍去）．此时p = ②如图4，当M 在NP 的延长线上时，x M －x N ＝4(x M －x P )．因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得x =或x =P 在x 轴下方，舍去）．此时p =考点伸展在本题情景下，△AMN 能否成为直角三角形？情形一，如图5，∠AMN ＝90°，此时点M 的坐标为（1，2），点P 的坐标为（3，2）．情形二，如图6，∠MAN ＝90°，此时斜边MN 上的中线等于斜边的一半．不存在∠ANM ＝90°的情况．图5 图6例4 2011年上海市松江区中考模拟第24题如图1，在平面直角坐标系xOy 中，直角梯形OABC 的顶点O 为坐标原点，顶点A 、C 分别在x 轴、y 轴的正半轴上，CB ∥OA ，OC ＝4，BC ＝3，OA ＝5，点D 在边OC 上，CD ＝3，过点D 作DB 的垂线DE ，交x 轴于点E ．（1）求点E 的坐标；（2）二次函数y ＝－x 2＋bx ＋c 的图象经过点B 和点E ． ①求二次函数的解析式和它的对称轴；②如果点M 在它的对称轴上且位于x 轴上方，满足S △CEM ＝2S △ABM ，求点M 的坐标．图1思路点拨1．这三道题目步步为赢，错一道题目，就要影响下一道的计算．2．点M 在抛物线的对称轴上且位于x 轴上方，要分两种情况讨论，分别为点M 在线段FB 和FB 的延长线上．因为用点M 的纵坐标表示△ABM 的底边长，因点M 的位置不同而不同．满分解答（1）因为BC ∥OA ，所以BC ⊥CD ．因为CD ＝CB ＝3，所以△BCD 是等腰直角三角形．因此∠BCD ＝45°．又因为BC ⊥CD ，所以∠ODE ＝45°．所以△ODE 是等腰直角三角形，OE ＝OD ＝1．所以点E 的坐标是（1，0）．（2）①因为抛物线y ＝－x 2＋bx ＋c 经过点B （3，4）和点E （1，0），所以934,10.b c b c -++=⎧⎨-++=⎩解得6,5.b c =⎧⎨=-⎩所以二次函数的解析式为y ＝－x 2＋6x －5，抛物线的对称轴为直线x ＝3．②如图2，如图3，设抛物线的对称轴与x 轴交于点F ，点M 的坐标为（3，t ）．CEM MEF COE OFMC S S S S ∆∆∆=--梯形111(4)321442222tt t =+⨯-⨯⨯-⨯⨯=+．（ⅰ）如图2，当点M 位于线段BF 上时，t t S ABM -=⨯-=∆42)4(21．解方程)4(242t t -=+，得58=t ．此时点M 的坐标为（3，58）．（ⅱ）如图3，当点M 位于线段FB 延长线上时，42)4(21-=⨯-=∆t t S ABM ．解方程)4(242-=+t t，得8=t ．此时点M 的坐标为（3，8）．图2 图3考点伸展对于图2，还有几个典型结论：此时，C 、M 、A 三点在同一条直线上；△CEM 的周长最小．可以求得直线AC 的解析式为445y x =-+，当x ＝3时，85y =．因此点M （3，58）在直线AC 上．因为点A 、E 关于抛物线的对称轴对称，所以ME ＋MC ＝MA ＋MC ．当A 、M 、C 三点共线时，ME ＋MC 最小，△CEM 的周长最小．例5 2010年广州市中考第25题如图1，四边形OABC 是矩形，点A 、C 的坐标分别为(3,0)，(0,1)．点D 是线段BC 上的动点（与端点B 、C 不重合），过点D 作直线12y x b =-+交折线OAB 于点E ．（1）记△ODE 的面积为S ，求S 与b 的函数关系式；（2）当点E 在线段OA 上时，若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1，试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．图1思路点拨1．数形结合，用b 表示线段OE 、CD 、AE 、BE 的长．2．求△ODE 的面积，要分两种情况．当E 在OA 上时，OE 边对应的高等于OC ；当E在AB 边上时，要利用割补法求△ODE 的面积．3．第（3）题中的重叠部分是邻边相等的平行四边形．4．图形翻着、旋转等运动中，计算菱形的边长一般用勾股定理．满分解答(1)①如图2，当E 在OA 上时，由12y x b =-+可知，点E 的坐标为(2b ,0)，OE ＝2b ．此时S ＝S △ODE ＝112122OE OC b b ⋅=⨯⨯=． ②如图3，当E 在AB 上时，把y ＝1代入12y x b =-+可知，点D 的坐标为(2b －2,1)，CD ＝2b －2，BD ＝5－2b ．把x ＝3代入12y x b =-+可知，点E 的坐标为3(3,)2b -，AE＝32b -，BE ＝52b -．此时S ＝S 矩形OABC －S △OAE － S △BDE －S △OCD ＝1315133()()(52)1(22)22222b b b b -⨯-----⨯⨯- 252b b =-+．(2)如图4，因为四边形O 1A 1B 1C 1与矩形OABC 关于直线DE 对称，因此DM ＝DN ，那么重叠部分是邻边相等的平行四边形，即四边形DMEN 是菱形．作DH ⊥OA ，垂足为H ．由于CD ＝2b －2，OE ＝2b ，所以EH ＝2．设菱形DMEN 的边长为m ．在Rt △DEH 中，DH ＝1，NH ＝2－m ，DN ＝m ，所以12＋(2－m )2＝m 2．解得54m =．所以重叠部分菱形DMEN 的面积为54．图2 图3 图4考点伸展把本题中的矩形OABC 绕着它的对称中心旋转，如果重叠部分的形状是菱形（如图5），那么这个菱形的最小面积为1，如图6所示；最大面积为53，如图7所示．图5 图6 图7例 6 2010年扬州市中考第28题如图1，在△ABC 中，∠C ＝90°，A C ＝3，BC ＝4，CD 是斜边AB 上的高，点E 在斜边AB 上，过点E 作直线与△ABC 的直角边相交于点F ，设AE ＝x ，△AEF 的面积为y ．（1）求线段AD 的长；（2）若EF ⊥AB ，当点E 在斜边AB 上移动时，①求y 与x 的函数关系式（写出自变量x 的取值范围）； ②当x 取何值时，y 有最大值？并求出最大值．（3）若点F 在直角边AC 上（点F 与A 、C 不重合），点E 在斜边AB 上移动，试问，是否存在直线EF 将△ABC 的周长和面积同时平分？若存在直线EF ，求出x 的值；若不存在直线EF ，请说明理由．图1 备用图思路点拨1．第（1）题求得的AD 的长，就是第（2）题分类讨论x 的临界点． 2．第（2）题要按照点F 的位置分两种情况讨论．3．第（3）题的一般策略是：先假定平分周长，再列关于面积的方程，根据方程的解的情况作出判断．满分解答(1) 在Rt △ABC 中， AC ＝3，BC ＝4，所以AB ＝5．在Rt △ACD 中，39cos 355AD AC A ==⨯=．(2) ①如图2，当F 在AC 上时，905x <<．在Rt △AEF 中，4tan 3EF AE A x ==．所以21223y AE EF x =⋅=．如图3，当F 在BC 上时，955x <≤．在Rt △BEF 中，3tan (5)4EF BE B x ==-．所以21315288y AE EF x x =⋅=-+． ②当905x <<时，223y x =的最大值为5425；当955x <≤时，231588y x x =-+23575)8232x =--+(的最大值为7532．因此，当52x =时，y 的最大值为7532．图2 图3 图4(3)△ABC 的周长等于12，面积等于6．先假设EF 平分△ABC 的周长，那么AE ＝x ，AF ＝6－x ，x 的变化范围为3＜x ≤5．因此1142sin (6)(6)2255AEF S AE AF A x x x x ∆=⋅⋅=-⨯=--．解方程2(6)35x x --=，得3x =±因为3x =+3≤x ≤5范围内（如图4），因此存在直线EF 将△ABC 的周长和面积同时平分．考点伸展如果把第（3）题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”，那么就不存在直线EF 将△ABC 的周长和面积同时平分．先假设EF 平分△ABC 的周长，那么AE ＝x ，BE ＝5－x ，BF ＝x ＋1．因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---．解方程23(45)310x x ---=．整理，得2450x x -+=．此方程无实数根．。

函数图象中的存在性问题—因动点产生的面积问题

函数图象中的存在性问题—因动点产生的面积问题函数图像中的存在性问题是函数图像是否存在的研究。

在研究函数图像的存在性时，我们通常会考虑到以下几个问题：函数是否有定义域和值域，函数是否连续，函数是否可导等等。

其中，因动点产生的面积问题是函数图像的一个特殊存在性问题。

考虑一个动点在平面上运动，其轨迹为函数的图像，我们可以通过计算该轨迹所围成的面积来研究函数图像的存在性。

首先，让我们考虑一个较简单的函数图像，例如：y=x。

当动点在平面上矩形区域内运动时，其轨迹就可以看作是函数y=x的图像。

我们可以将矩形区域分成无数个小长方形，并计算每个小长方形所围成的面积的和。

当矩形区域趋近于函数图像所占据的面积时，这个和就可以逼近函数图像所围成的面积。

如果这个和存在且为有限值，则可以认为函数图像所围成的面积存在。

然而，对于一些函数图像，存在动点产生的面积问题可能并不存在。

例如：y=1/x。

当动点运动到x=0的位置时，函数图像与x轴相切，不再围成一个有限的面积。

在这种情况下，我们无法通过动点产生的面积来研究函数图像的存在性。

对于一些较为复杂的函数图像，动点产生的面积问题可能会更加具有挑战性。

例如：y = sin(x)。

当动点在平面上运动时，函数图像会在一些位置出现多个极大值和极小值。

在这种情况下，计算动点产生的面积变得更为复杂，可能需要使用更高级的数学工具来解决。

总之，动点产生的面积问题是函数图像存在性问题的一个特殊情况。

通过计算动点所产生的面积，我们可以研究函数图像的存在性。

然而，对于一些复杂的函数图像，动点产生的面积问题可能并不存在或更加困难。

因此，在研究函数图像的存在性时，我们需要综合考虑多个因素，并使用合适的数学工具来解决。

因动点产生的面积问题

1.6 因动点产生的面积问题例1 2013年苏州市中考第29题如图1，已知抛物线212y x bx c =++（b 、c 是常数，且c ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(－1,0)．（1）b ＝______，点B 的横坐标为_______（上述结果均用含c 的代数式表示）；（2）连结BC ，过点A 作直线AE //BC ，与抛物线交于点E ．点D 是x 轴上一点，坐标为(2,0)，当C 、D 、E 三点在同一直线上时，求抛物线的解析式；（3）在（2）的条件下，点P 是x 轴下方的抛物线上的一动点，连结PB 、PC ．设△PBC 的面积为S ． ①求S 的取值范围；②若△PBC 的面积S 为正整数，则这样的△PBC 共有_____个．图1动感体验请打开几何画板文件名“13苏州29”，拖动点C 在y 轴负半轴上运动，可以体验到，△EHA 与△COB 保持相似．点击按钮“C 、D 、E 三点共线”，此时△EHD ∽△COD ．拖动点P 从A 经过C 到达B ，数一数面积的正整数值共有11个．请打开超级画板文件名“13苏州29”，拖动点C 在y 轴负半轴上运动，可以体验到，△EHA 与△COB 保持相似．点击按钮“C 、D 、E 三点共线”，此时△EHD ∽△COD ．拖动点P 从A 经过C 到达B ，数一数面积的正整数值共有11个．思路点拨1．用c 表示b 以后，把抛物线的一般式改写为两点式，会发现OB ＝2OC ． 2．当C 、D 、E 三点共线时，△EHA ∽△COB ，△EHD ∽△COD ．3．求△PBC 面积的取值范围，要分两种情况计算，P 在BC 上方或下方．4．求得了S 的取值范围，然后罗列P 从A 经过C 运动到B 的过程中，面积的正整数值，再数一数个数．注意排除点A 、C 、B 三个时刻的值．满分解答（1）b ＝12c +，点B 的横坐标为－2c ．（2）由2111()(1)(2)222y x c x c x x c =+++=++，设E 1(,(1)(2))2x x x c ++．过点E 作EH ⊥x 轴于H ．由于OB ＝2OC ，当AE //BC 时，AH ＝2EH ．所以1(1)(2)x x x c +=++．因此12x c =-．所以(12,1)E c c --．当C 、D 、E 三点在同一直线上时，EH CO DH DO =．所以1212c cc --=--．整理，得2c 2＋3c －2＝0．解得c ＝－2或12c =（舍去）．所以抛物线的解析式为213222y x x =--．（3）①当P 在BC 下方时，过点P 作x 轴的垂线交BC 于F ．直线BC 的解析式为122y x =-．设213(,2)22P m m m --，那么1(,2)2F m m -，2122FP m m =-+．所以S △PBC ＝S △PBF ＋S △PCF ＝221()24(2)42B C FP x x FP m m m -==-+=--+．因此当P 在BC 下方时，△PBC 的最大值为4．当P 在BC 上方时，因为S △ABC ＝5，所以S △PBC ＜5．综上所述，0＜S ＜5．②若△PBC 的面积S 为正整数，则这样的△PBC 共有11个．考点伸展点P 沿抛物线从A 经过C 到达B 的过程中，△PBC 的面积为整数，依次为（5），4，3，2，1，（0），1，2，3，4，3，2，1，（0）．当P 在BC 下方，S ＝4时，点P 在BC 的中点的正下方，F 是BC 的中点．例 2 2012年菏泽市中考第21题如图1，在平面直角坐标系中放置一直角三角板，其顶点为A (0, 1)、B (2, 0)、O (0, 0)，将此三角板绕原点O 逆时针旋转90°，得到三角形A ′B ′O ．（1）一抛物线经过点A ′、B ′、B ，求该抛物线的解析式；（2）设点P 是第一象限内抛物线上的一个动点，是否存在点P ，使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）在（2）的条件下，试指出四边形PB ′A ′B 是哪种形状的四边形？并写出它的两条性质．图1动感体验请打开几何画板文件名“12菏泽21”，拖动点P 在第一象限内的抛物线上运动，可以体验到，当四边形PB ′A ′B 是等腰梯形时，四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍．请打开超级画板文件名“12菏泽21”，拖动点P 在第一象限内的抛物线上运动，可以体验到，当四边形PB ′A ′B 是等腰梯形时，四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍．思路点拨1．四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍，可以转化为四边形PB ′OB 的面积是 △A ′B ′O 面积的3倍．2．联结PO ，四边形PB ′OB 可以分割为两个三角形．3．过点向x 轴作垂线，四边形PB ′OB 也可以分割为一个直角梯形和一个直角三角形．满分解答（1）△AOB 绕着原点O 逆时针旋转90°，点A ′、B ′的坐标分别为(－1, 0) 、(0, 2)．因为抛物线与x 轴交于A ′(－1, 0)、B (2, 0)，设解析式为y ＝a (x ＋1)(x －2)，代入B ′(0, 2)，得a ＝1．所以该抛物线的解析式为y ＝－(x ＋1)(x －2) ＝－x 2＋x ＋2．（2）S △A ′B ′O ＝1．如果S 四边形PB ′A ′B ＝4 S △A ′B ′O ＝4，那么S 四边形PB ′OB ＝3 S △A ′B ′O ＝3．如图2，作PD ⊥OB ，垂足为D ．设点P 的坐标为 (x ，－x 2＋x ＋2)．232'1111(')(22)22222PB OD S DO B O PD x x x x x x =+=-++=-++梯形． 2321113(2)(2)22222PDBS DB PD x x x x x ∆=⨯=--++=-+．所以2'''2+2PDB PB A D PB OD S S S x x ∆=+=-+四边形梯形．解方程－x 2＋2x ＋2＝3，得x 1＝x 2＝1．所以点P 的坐标为(1，2)．图2 图3 图4（3）如图3，四边形PB ′A ′B 是等腰梯形，它的性质有：等腰梯形的对角线相等；等腰梯形同以底上的两个内角相等；等腰梯形是轴对称图形，对称轴是经过两底中点的直线．考点伸展第（2）题求四边形PB ′OB 的面积，也可以如图4那样分割图形，这样运算过程更简单．'11'222PB O P S B O x x x ∆=⋅=⨯=． 22112(2)222PBOP S BO y x x x x ∆=⋅=⨯-++=-++．所以2'''2+2PB O PBO PB A D S S S x x ∆∆=+=-+四边形．甚至我们可以更大胆地根据抛物线的对称性直接得到点P ：作△A ′OB ′关于抛物线的对称轴对称的△BOE ，那么点E 的坐标为(1，2)．而矩形EB ′OD 与△A ′OB ′、△BOP 是等底等高的，所以四边形EB ′A ′B 的面积是△A ′B ′O 面积的4倍．因此点E 就是要探求的点P ．例 3 2012年河南省中考第23题如图1，在平面直角坐标系中，直线112y x =+与抛物线y ＝ax 2＋bx －3交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上的一动点（不与点A 、B 重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连结PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，使这两个三角形的面积比为9∶10？若存在，直接写出m 的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“12河南23”，拖动点P 在直线AB 下方的抛物线上运动，可以体验到，PD 随点P 运动的图象是开口向下的抛物线的一部分，当C 是AB 的中点时，PD 达到最大值．观察面积比的度量值，可以体验到，左右两个三角形的面积比可以是9∶10，也可以是10∶9．思路点拨1．第（1）题由于CP //y 轴，把∠ACP 转化为它的同位角．2．第（2）题中，PD ＝PC sin ∠ACP ，第（1）题已经做好了铺垫．3．△PCD 与△PCB 是同底边PC 的两个三角形，面积比等于对应高DN 与BM 的比． 4．两个三角形的面积比为9∶10，要分两种情况讨论．满分解答（1）设直线112y x =+与y 轴交于点E ，那么A (－2,0)，B (4,3)，E (0,1)．在Rt △AEO 中，OA ＝2，OE ＝1，所以5AE =．所以25sin AEO ∠=．因为PC //EO ，所以∠ACP ＝∠AEO ．因此25sin ACP ∠=．将A (－2,0)、B (4,3)分别代入y ＝ax 2＋bx －3，得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =，12b =-．（2）由211(,3)22P m m m --，1(,1)2C m m +，得221111(1)(3)42222PC m m m m m =+---=-++．所以2225251595sin (4)(1)2PD PC ACP PC m m m =∠==-++=--+．所以PD 的最大值为95．（3）当S △PCD ∶S △PCB ＝9∶10时，52m =；当S △PCD ∶S △PCB ＝10∶9时，329m =．图2考点伸展第（3）题的思路是：△PCD 与△PCB 是同底边PC 的两个三角形，面积比等于对应高DN 与BM 的比．而252511cos cos 4)(2)(4)25DN PD PDN PD ACP m m m m =∠=∠=-++=-+-， BM ＝4－m ．①当S △PCD ∶S △PCB ＝9∶10时，19(2)(4)(4)510m m m -+-=-．解得52m =．②当S △PCD ∶S △PCB ＝10∶9时，110(2)(4)(4)59m m m -+-=-．解得329m =．例 4 2011年南通市中考第28题如图1，直线l经过点A(1，0)，且与双曲线myx=(x＞0)交于点B(2，1)．过点(,1)P p p-(p＞1)作x轴的平行线分别交曲线myx=(x＞0)和myx=-(x＜0)于M、N两点．（1）求m的值及直线l的解析式；（2）若点P在直线y＝2上，求证：△PMB∽△PNA；（3）是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11南通28”，拖动点P在射线AB上运动，可以体验到，当直线MN经过（0，2）点时，图形中的三角形都是等腰直角三角形；△AMN和△AMP是两个同高的三角形，MN＝4MP存在两种情况．思路点拨1．第（2）题准确画图，点的位置关系尽在图形中．2．第（3）题把S△AMN＝4S△AMP转化为MN＝4MP，按照点M与线段NP的位置关系分两种情况讨论．满分解答（1）因为点B(2，1)在双曲线myx=上，所以m＝2．设直线l的解析式为y kx b=+，代入点A(1，0)和点B(2，1)，得0,2 1.k bk b+=⎧⎨+=⎩解得1,1.kb=⎧⎨=-⎩所以直线l的解析式为1y x=-．（2）由点(,1)P p p-(p＞1)的坐标可知，点P在直线1y x=-上x轴的上方．如图2，当y＝2时，点P的坐标为(3，2)．此时点M的坐标为(1，2)，点N的坐标为(－1，2)．由P(3，2)、M(1，2)、B(2，1)三点的位置关系，可知△PMB为等腰直角三角形．由P(3，2)、N(－1，2)、A(1，0)三点的位置关系，可知△PNA为等腰直角三角形．所以△PMB∽△PNA．图2 图3 图4（3）△AMN 和△AMP 是两个同高的三角形，底边MN 和MP 在同一条直线上．当S △AMN ＝4S △AMP 时，MN ＝4MP ．①如图3，当M 在NP 上时，x M －x N ＝4(x P －x M )．因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得113x +=或113x -=（此时点P 在x 轴下方，舍去）．此时113p +=． ②如图4，当M 在NP 的延长线上时，x M －x N ＝4(x M －x P )．因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭．解得15x +=或15x -=（此时点P 在x 轴下方，舍去）．此时15p +=．考点伸展在本题情景下，△AMN 能否成为直角三角形？情形一，如图5，∠AMN ＝90°，此时点M 的坐标为（1，2），点P 的坐标为（3，2）．情形二，如图6，∠MAN ＝90°，此时斜边MN 上的中线等于斜边的一半．不存在∠ANM ＝90°的情况．图5 图6例5 2010年广州市中考第25题如图1，四边形OABC是矩形，点A、C的坐标分别为(3,0)，(0,1)．点D是线段BC上的动点（与端点B、C不重合），过点D作直线12y x b=-+交折线OAB于点E．（1）记△ODE的面积为S，求S与b的函数关系式；（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．图1动感体验请打开几何画板文件名“10广州25”，拖动点D由C向B运动，观察S随b变化的函数图象，可以体验到，E在OA上时，S随b的增大而增大；E在AB上时，S随b的增大而减小．双击按钮“第（3）题”，拖动点D由C向B运动，可以观察到，E在OA上时，重叠部分的形状是菱形，面积不变．双击按钮“第（2）题”可以切换．思路点拨1．数形结合，用b表示线段OE、CD、AE、BE的长．2．求△ODE的面积，要分两种情况．当E在OA上时，OE边对应的高等于OC；当E在AB边上时，要利用割补法求△ODE的面积．3．第（3）题中的重叠部分是邻边相等的平行四边形．4．图形翻着、旋转等运动中，计算菱形的边长一般用勾股定理．满分解答(1)①如图2，当E在OA上时，由12y x b=-+可知，点E的坐标为(2b,0)，OE＝2b．此时S＝S△ODE＝112122OE OC b b⋅=⨯⨯=．②如图3，当E在AB上时，把y＝1代入12y x b=-+可知，点D的坐标为(2b－2,1)，CD＝2b－2，BD＝5－2b．把x＝3代入12y x b=-+可知，点E的坐标为3(3,)2b-，AE＝32b-，BE＝52b-．此时S＝S矩形OABC－S△OAE－S△BDE－S△OCD＝1315133()()(52)1(22) 22222b b b b-⨯-----⨯⨯-252b b=-+．(2)如图4，因为四边形O1A1B1C1与矩形OABC关于直线DE对称，因此DM＝DN，那么重叠部分是邻边相等的平行四边形，即四边形DMEN是菱形．作DH⊥OA，垂足为H．由于CD＝2b－2，OE＝2b，所以EH＝2．设菱形DMEN的边长为m．在Rt△DEH中，DH＝1，NH＝2－m，DN＝m，所以12＋(2－m)2＝m2．解得54m=．所以重叠部分菱形DMEN的面积为54．图2 图3 图4考点伸展把本题中的矩形OABC绕着它的对称中心旋转，如果重叠部分的形状是菱形（如图5），那么这个菱形的最小面积为1，如图6所示；最大面积为53，如图7所示．图5 图6 图7例 6 2010年扬州市中考第28题如图1，在△ABC 中，∠C ＝90°，A C ＝3，BC ＝4，CD 是斜边AB 上的高，点E 在斜边AB 上，过点E 作直线与△ABC 的直角边相交于点F ，设AE ＝x ，△AEF 的面积为y ．（1）求线段AD 的长；（2）若EF ⊥AB ，当点E 在斜边AB 上移动时，①求y 与x 的函数关系式（写出自变量x 的取值范围）； ②当x 取何值时，y 有最大值？并求出最大值．（3）若点F 在直角边AC 上（点F 与A 、C 不重合），点E 在斜边AB 上移动，试问，是否存在直线EF 将△ABC 的周长和面积同时平分？若存在直线EF ，求出x 的值；若不存在直线EF ，请说明理由．图1 备用图动感体验请打开几何画板文件名“10扬州28”，拖动点E 在AB 上运动，从y 随x 变化的图象可以体验到，当F 在AC 上时，y 随x 的增大而增大；当F 在BC 上时，y 随x 变化的图象是开口向下的抛物线的一部分，y 的最大值对应抛物线的顶点．双击按钮“第（3）题”，我们已经设定好了EF 平分△ABC 的周长，拖动点E ，观察图象，可以体验到，“面积AEF ”的值可以等于3，也就是说，存在直线EF 将△ABC 的周长和面积同时平分．双击按钮“第（2）题”可以切换。

2019年中考数学复习1.5因动点产生的面积问题

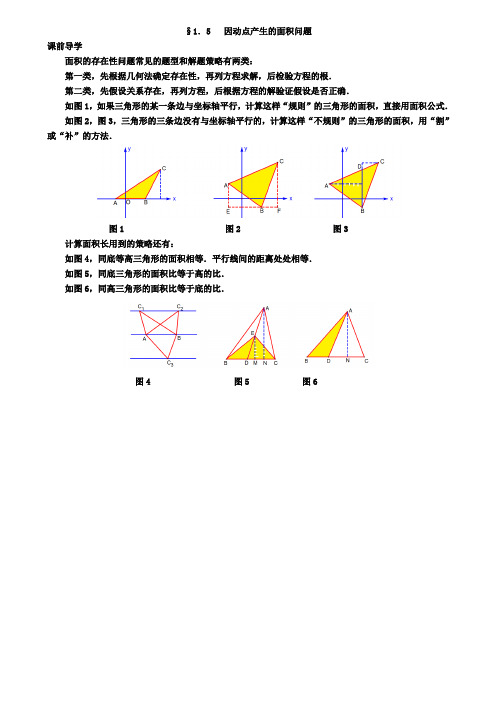
§1．5 因动点产生的面积问题课前导学面积的存在性问题常见的题型和解题策略有两类：第一类，先根据几何法确定存在性，再列方程求解，后检验方程的根．第二类，先假设关系存在，再列方程，后根据方程的解验证假设是否正确．如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．图1 图2 图3计算面积长用到的策略还有：如图4，同底等高三角形的面积相等．平行线间的距离处处相等．如图5，同底三角形的面积比等于高的比．如图6，同高三角形的面积比等于底的比．图4 图5 图6例 32 2019年湖南省常德市中考第25题如图1，已知二次函数的图象过点O(0,0)、A(4，0)、B(2,)，M 是OA 的中点．（1）求此二次函数的解析式；（2）设P 是抛物线上的一点，过P 作x 轴的平行线与抛物线交于另一点Q ，要使四边形PQAM 是菱形，求点P 的坐标；（3）将抛物线在x 轴下方的部分沿x 轴向上翻折，得曲线OB′A（B ′为B 关于x 轴的对称点），在原抛物线x 轴的上方部分取一点C ，连结CM ，CM 与翻折后的曲线OB′A 交于点D ，若△CDA 的面积是△MDA 面积的2倍，这样的点C 是否存在？若存在求出点C 的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14常德25”，拖动点P 在抛物线上运动，可以体验到，当四边形PQAM 是平行四边形时，也恰好是菱形．拖动点C 在抛物线上运动，还可以体验到，△MCA 与△MDA 是同底三角形，它们的面积比等于对应高的比．思路点拨1．设交点式或顶点式求抛物线的解析式都比较简便． 2．先确定四边形PQAM 是平行四边形，再验证它是菱形．3．把△CDA 与△MDA 的面积比，转化为△MCA 与△MDA 的面积比，进而转化为点C 与点D 的纵坐标的比．图文解析（1）因为抛物线与x 轴交于O(0,0)、A(4，0)两点，设y ＝ax(x －4)．代入点B(2,)，得4a =-．解得a ．所以(4)y x -．（2）如图2，由A(4，0)，M 是OA 的中点，可知OA ＝4，MA ＝2，M(2, 0)．如果四边形PQAM 是菱形，已知PQ//OA ，首先要满足PQ ＝2，再必须MP ＝2．因为抛物线的对称轴是直线x ＝2，P 、Q 关于x ＝2对称，所以点P 的横坐标为1，故点P 的坐标为(1,．由M(2, 0)、P (1,，可得MP ＝2．所以当点P 的坐标为(1,时，四边形PQAM 是菱形．（3）如图3，作CE ⊥x 轴于E ，作DF ⊥x 轴于F ．我们把面积进行两次转换：如果△CDA 的面积是△MDA 面积的2倍，那么△MCA 的面积是△MDA 面积的3倍．而△MCA 与△MDA 是同底三角形，所以高的比CE ∶DF ＝3∶1，即y C ∶y D ＝3∶1．因此ME ∶MF ＝3∶1．设MF ＝m ，那么ME ＝3m ．原抛物线的解析式为(4)y x =-，所以翻折后的抛物线的解析式为(4)y x x =-．所以D (2,)(24))m m m +++-，C (233)(234))m m m +++-．根据y C ∶y D ＝3∶13)(234)3)(24)m m m m ⎡⎤++-=++-⎢⎥⎣⎦．整理，得3m2＝4．解得m=．所以232+=±m所以点C的坐标为(2+（如图3），或(2-（如图4）．图2 图3 图4 考点伸展第（1）题可以设抛物线的顶点式：由点O(0,0), A(4，0)，B(2,)的坐标，可知点B是抛物线的顶点．可设2=-O(0,0)，得a(2)y a x例 33 2019年湖南省永州市中考第25题如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴交于A(－1, 0)，B(4, 0)两点，与y 轴交于点C(0, 2)．点M(m, n)是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上．过点M 作x 轴的平行线交y 轴于点Q ，交抛物线于另一点E ，直线BM 交y 轴于点F ．（1）求抛物线的解析式，并写出其顶点坐标；（2）当S △MFQ ∶S △MEB ＝1∶3时，求点M 的坐标．图1动感体验请打开几何画板文件名“14永州25”，拖动点M 在抛物线左半侧上运动，观察面积比的度量值，可以体验到，存在两个时刻，△MEB 的面积等于△MFQ 面积的3倍．思路点拨1．设交点式求抛物线的解析式比较简便．2．把△MFQ 和△MEB 的底边分别看作MQ 和ME ，分别求两个三角形高的比，底边的比（用含m 的式子表示），于是得到关于m 的方程．3．方程有两个解，慎重取舍．解压轴题时，时常有这种“一石二鸟”的现象，列一个方程，得到两个符合条件的解．图文解析（1）因为抛物线与x 轴交于A(－1, 0)，B(4, 0)两点，设y ＝a(x ＋1)(x －4)．代入点C(0, 2)，得2＝－4a ．解得12a =-．所以221131325(1)(4)2()222228y x x x x x =-+-=-++=--+．顶点坐标为325()28，．（2）如图2，已知M(m, n)，作MN ⊥x 轴于N ．由=FQ MNMQ BN，得=4FQ n m m -．所以=4mn FQ m -．因为抛物线的对称轴是直线32x =，所以ME ＝32()322m m -=-．由于S △MFQ ＝12FQ MQ ⋅＝124mnm m⨯⨯-＝2124m n m ⨯-， S △MEB ＝12ME MN ⋅＝1(32)2m n -，所以当S △MFQ ∶S △MEB ＝1∶3时，24m nm-∶(32)m n -＝1∶3．整理，得m 2＋11m －12＝0．解得m ＝1，或m ＝－12．所以点M 的坐标为(1, 3)或(－12,－88)．图2考点伸展第（2）题S △MFQ ∶S △MEB ＝1∶3，何需点M 一定要在抛物线上？从上面的解题过程可以看到，△MFQ 与△MEB 的高的比=4FQ mMN m-与n 无关，两条底边的比=32MQ mME m-也与n 无关．如图3，因此只要点E 与点M 关于直线x ＝32对称，点M 在直线的左侧，且点M 不在坐标轴上，就存在S △MFQ ∶S △MEB ＝1∶3，点M 的横坐标为1（如图3）或－12（如图4）．图3 图42019-2020学年数学中考模拟试卷一、选择题1．如图，A ，B ，C ，D 为⊙O 的四等分点，动点P 从圆心O 出发，沿O ﹣C ﹣D ﹣O 路线作匀速运动，设运动时间为t （s ）．∠APB ＝y （°），则下列图象中表示y 与t 之间函数关系最恰当的是（）A ．B ．C ．D ．2．下列调查中，适合普查的事件是（） A ．调查华为手机的使用寿命v B ．调查市九年级学生的心理健康情况 C ．调查你班学生打网络游戏的情况D ．调查中央电视台《中国舆论场》的节目收视率 3．函数y =x 的取值范围是（） A.4x <B.4x ≠C.4x >D.4x ≤4．下列运算正确的是（） A ．3a 3+a 3＝4a 6B ．（a+b ）2＝a 2+b 2C ．5a ﹣3a ＝2aD ．（﹣a ）2•a 3＝﹣a 65．13的倒数是（） A.13B.3C.3-D.13-6．在2015-2016CBA 常规赛季中，易建联罚球投篮的命中率大约是82.3%，下列说法错误的是（）A ．易建联罚球投篮2次，一定全部命中B ．易建联罚球投篮2次，不一定全部命中C ．易建联罚球投篮1次，命中的可能性较大D ．易建联罚球投篮1次，不命中的可能性较小7．某颗人造地球卫星绕地球运行的速度是7．9×103m／s，那么这颗卫星绕地球运行一年（一年以3．2×107 s计算）走过的路程约是（）A．1.1×1010m B．7.9×1010m C．2.5×1010m D．2.5×1011m8．如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数8yx=，在第二象限的图像经过点E,则正方形AOBC与正方形CDEF的面积之差为（）A.6B.8C.10D.129．如图，点A、B、C、D在⊙O上，CB CD=，∠CAD＝30°，∠ACD＝50°，则∠ADB＝（）A．30°B．50°C．70°D．80°10．如图，是由四个相同的正方体组合而成的两个几何体，则下列表述正确的是（）A．图甲的主视图与图乙的左视图形状相同B．图甲的左视图与图乙的俯视图形状相同C．图甲的俯视图与图乙的俯视图形状相同D．图甲的主视图与图乙的主视图形状相同11．下列各式计算正确的是（）A B．（﹣a2b）3=a6b3C．a3﹒a=a4D．(b﹢2a)(2a﹣b)=b2﹣4a212．如图6, 已知圆锥的高为8，底面圆的直径为12，则此圆锥的侧面积是A.24B.30C.48D.60二、填空题13．如图，直线y＝15x﹣1与x，y轴交于B、A，点M为双曲线ykx=上的一点，若△MAB为等腰直角三角形，则k＝_____．14．如图，已知Rt△ABC中，∠B=90°，∠A=60°，+4，点M、N分别在线段AC、AB上，将△ANM 沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为__．15．不等式组29611x xx k+>+⎧⎨-<⎩的解集为2x<，则k的取值范围为_____．16．已知△ABC的三边长分别为5，7，8，△DEF的三边分别为5，2x，3x﹣5，若两个三角形全等，则x=__．17．如图，已知一次函数y＝kx+b的图象经过点（3，0），则当函数值y小于0时，自变量x的取值范围是_____．18．如图，六边形ABCDEF是正六边形，若l1∥l2，则∠1﹣∠2＝_____．三、解答题19．如图，△ABC是直角三角形，∠ACB＝90°，CD⊥AB于D，E是AC的中点，ED的延长线与CB的延长线交于点F．求证：FD2＝FB•FC．20．为了深入培养学生交通安全意识，加强实践活动，新华中学八年级（1）班和交警队联合举行了“我当一日小交警”活动，利用星期天到交通路口值勤，协助交通警察对行人、车辆及非机动车辆进行纠章．在这次实践活动中，若每一个路口安排5名学生，那么还剩下4人；若每个路口安排6人，那么最后一个路口不足3人，但不少于1人．（1）求新华中学八年级（1）班有多少名学生？（2）在值勤过程中，学生发现每辆汽车驶出路口后有三种方式前行：左转、直行、右转，而且每种前行方式的可能性相同．请通过画树形图或列表的方法，求连续驶出路口的两辆汽车前行路线相同的概率．21．观察下面的变形规律：11=1122-⨯；111=2323-⨯；111=3434-⨯；…．解答下面的问题：（1）若n为正整数，请你猜想1(1)n n+＝；（2）证明你猜想的结论；（3）求和：112⨯+123⨯+134⨯+…+120092010⨯.22．端午节是我国的传统节日，益民食品厂为了解市民对去年销量较好的花生粽子、水果粽子、豆沙粽子、红枣粽子(分别用A、B、C、D表示)这四种不同口味的粽子的喜爱情况，对某居民区的市民进行了抽样调查，并根据调查结果绘制了如下两幅不完整的统计图．(1)本次参加抽样调查的居民有多少人？(2)将两幅统计图补充完整；(3)小明喜欢吃花生粽子和红枣粽子，妈妈为他准备了四种粽子各一个，请用“列表法”或“画树形图”的方法，求出小明同时选中花生粽子和红枣粽子的概率．23．如图，∠A=∠B=30°，P为AB中点，线段MV绕点P旋转，且M为射线AC上（不与点d重合）的任意一点，且N为射线BD上（不与点B重合）的一点，设∠BPN=α．（1）求证：△APM≌△BPN；（2）当MN=2BN时，求α的度数；（3）若AB=4，60°≤α≤90°，直接写出△BPN的外心运动路线的长度。

二次函数--由动点生成面积问题

抛物线与直线型——由动点生成面积问题知识点归纳面积是平面几何中一个重要的概念，关联这平面图形中的重要元素与角。

由动点而生成的面积问题，是抛物线与直线形结合的常见形式。

解这类问题常用到以下与面积相关的知识：（1）图形的割补；（2）等积变形；（3）等比变化。

经典例题【例1】如图，在直角坐标系中，点A 的坐标为（-2，0），连接OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ．（1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由．（昆明市中考题）思路点拨对于（3），抛物线的对称轴是直线1-=x ，当点C 位于的对称轴与线段AB 的交点时，BOC ∆的周长为最小，为此需求出直线AB 的解析式；对于（4）过点p 作y 轴的平行线交AB 解析式；对于（4），过点p 作y 轴的平行线交AB 于D ，则))((21A B P D PBD PAD PAB x x y y S S S --=+=∆∆∆，代入展开整理得关于x 的二次函数。

【例2】如图①，在平面直角坐标系中，点A 的坐标为（1，2），点B 的坐标为（3，1），二次函数2x y =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过A ，B 两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式；（2）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABC ABK S S ∆∆=，求点k 的坐标；（威海市中考题）思路点拨（1）设k 点坐标为),0(h ，通过图形的分割计算，建立h 的方程；（2）K 点必在平行于AB 的直线上，从等积变形入手。

【例3】如图，已知点A （m,6)、B(m,1)为两动点，其中0＜m ＜3，连接OA 、OB ，OA ⊥OB 。

（1）求证：mn=－6；（2）当6-=∆AO B S 时，抛物线经过A ，B 两点且以y 轴为对称轴，求抛物线对应的二次函数的关系式；(3) 在（2）的条件下，设直线AB 交y 轴于点F ，过点F 作直线l 交抛物线于P ，Q 两点，问是否存在直线l ，使？若存在，求出直线l 对应的函数关系式；若不存在，请说明理由。

专题04 因动点产生的面积问题

备战2020中考数学之解密压轴解答题命题规律专题04因动点产生的面积问题【类型综述】面积是平面几何中一个重要的概念，关联着平面图形中的重要元素边与角，由动点而生成的面积问题，是抛物线与直线形结合的觉形式，常见的面积问题有规则的图形的面积（如直角三角形、平行四边形、菱形、矩形的面积计算问题）以及不规则的图形的面积计算，解决不规则的图形的面积问题是中考压轴题常考的题型，此类问题计算量较大。

有时也要根据题目的动点问题产生解的不确定性或多样性。

解决这类问题常用到以下与面积相关的知识：图形的割补、等积变形、等比转化等数学方法.面积的存在性问题常见的题型和解题策略有两类：一是先根据几何法确定存在性，再列方程求解，后检验方程的根．二是先假设关系存在，再列方程，后根据方程的解验证假设是否正确．【方法揭秘】解决动点产生的面积问题，常用到的知识和方法，如下：如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．图1图2图3计算面积长用到的策略还有：如图4，同底等高三角形的面积相等．平行线间的距离处处相等．如图5，同底三角形的面积比等于高的比．如图6，同高三角形的面积比等于底的比．y = - ( x + 1)(x - 4) = - x 2 + x + 2 = - ( x - )2 + ．顶点坐标为 ( ， ) ．图 4图 5 图 6【典例分析】【例 1】如图，抛物线 y ＝ax 2＋bx ＋c （a ≠0）与 x 轴交于 A (－1, 0)，B (4, 0)两点，与 y 轴交于点 C (0, 2)．点M (m , n )是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上．过点 M 作 x 轴的平行线交 y 轴于点 Q ，交抛物线于另一点 E ，直线 BM 交 y 轴于点 F ．（1）求抛物线的解析式，并写出其顶点坐标；（2）当 △S MFQ ∶△S MEB ＝1∶3 时，求点 M 的坐标．思路点拨1．设交点式求抛物线的解析式比较简便．△2．把 MFQ 和△MEB 的底边分别看作 MQ 和 ME ，分别求两个三角形高的比，底边的比（用含 m 的式子表示），于是得到关于 m 的方程．3．方程有两个解，慎重取舍．解压轴题时，时常有这种“一石二鸟”的现象，列一个方程，得到两个符合条件的解．满分解答（1）因为抛物线与 x 轴交于 A(－1, 0)，B(4, 0)两点，设 y ＝a(x ＋1)(x －4)．代入点 C(0, 2)，得 2＝－4a ．解得 a = - 1．所以21 1 3 1 3 252 2 2 2 2 83 252 8与 n 无关，两条底边的比考点伸展第（2）题 △S MFQ ∶△S MEB ＝1∶3，何需点 M 一定要在抛物线上？从上面的解题过程可以看到，△MFQ 与△MEB 的高的比也与 n 无关．FQ m MQ m= =MN 4 - m ME 3 - 2m如图 3，因此只要点 E 与点 M 关于直线 x ＝ 3 2对称，点 M 在直线的左侧，且点 M 不在坐标轴上，就存在 S△MFQ∶△S MEB ＝1∶3，点 M 的横坐标为 1（如图 3）或－12（如图 4）．图 3图 4（t ﹣1）2+ △=3 m 2﹣ m ﹣3）．如图 2，过点 K 作 KE∥y 轴，交 BC 于点 E ．结合已知条件和（2）中的结果．则根据图形得到：S △ CBK =S △CEK +S △=BEK EK•m+ •EK•（4﹣m ），把相关线段的长度代入推知：﹣ m 2+3m= ．易求得 K 1 （1，﹣ ），K 2 （3，﹣）． 27 4⎩16a + 4b - 3 = 0【例 2】如图，在平面直角坐标系中，抛物线 y=ax 2+bx ﹣3（a≠0）与 x 轴交于点 A （﹣2，0）、B （4，0）两点，与 y 轴交于点 C ．（1）求抛物线的解析式；（2）点 P 从 A 点出发，在线段 AB 上以每秒 3 个单位长度的速度向 B 点运动，同时点 Q 从 B 点出发，在线段 BC 上以每秒 1 个单位长度的速度向 C 点运动，其中一个点到达终点时，另一个点也停止运动，当△ PBQ存在时，求运动多少秒使△ PBQ 的面积最大，最大面积是多少？（3△）当 PBQ 的面积最大时，在 BC 下方的抛物线上存在点 K ，使 △S CBK ：△S PBQ =5：2，求 K 点坐标．思路点拨（1）把点 A 、B 的坐标分别代入抛物线解析式，列出关于系数 a 、b 的解析式，通过解方程组求得它们的值；（2）设运动时间为 t 秒．利用三角形的面积公式列出 S △PBQ 与 t 的函数关系式 S PBQ ﹣ 用二次函数的图象性质进行解答；9 9 10 10．利（3）利用待定系数法求得直线 BC 的解析式为 y= 3 4x ﹣3．由二次函数图象上点的坐标特征可设点 K 的坐标为（m ，3 8 4求得 S △CBK = 9 1 1 4 2 23 9 154 8 8满分解答（1）把点 A （﹣2，0）、B （4，0）分别代入 y=ax 2+bx ﹣3（a≠0），得⎧4a - 2b - 3 = 0 ⎨，a=3解得⎨8OC==t5t．∴S△=12（6﹣3t）•32+9S△PBQ最大10．答：运动1△秒使PBQ的面积最大，最大面积是9⎧⎪⎪b=-3⎪⎩4，所以该抛物线的解析式为：y=3x2﹣834x﹣3；（2）设运动时间为t秒，则AP=3t，BQ=t．∴PB=6﹣3t．由题意得，点C的坐标为（0，﹣3）．在Rt△BOC中，BC=32+42=5．如图1，过点Q作QH⊥AB于点H．∴QH∥CO，∴BHQ∽BOC△，∴HB BG HbBC，即35，∴HQ=32PB•HQ=15t=﹣910t2+95t=﹣910（t﹣1）10．当△PBQ存在时，0＜t＜2∴当t=1时，=910；c = -3 ， ⎪k =4 x ﹣3．如图 2，过点 K 作 KE∥y 轴，交 BC 于点 E ．则点 E 的坐标为（m ，34 m ﹣3﹣（ 3 m 2﹣ 4m ﹣3）=﹣ 3 m 2+当△PBQ 的面积最大时，△∵S CBK ：S△=5PBQ：2，S△=9∴S △CBK = 9S △CBK =S △CEK +S △BEK = 12×4•EK4 m 2+3m ． 4 m 2+3m=（3）设直线 BC 的解析式为 y=kx+c （k≠0）．把 B （4，0），C （0，﹣3）代入，得⎧4k + c = 0 ⎨ ⎩⎧解得 ⎨3 4 ， ⎪⎩c = -3∴直线 BC 的解析式为 y=3∵点 K 在抛物线上．∴设点 K的坐标为（m ， 3 m 2﹣ 83 4m ﹣3）．4m ﹣3）．∴EK=38 38 3 2 m ．10．4 ．=12EK•m+12 •EK•（4﹣m ）=2（﹣ 3 m 2+ 83 2m）=﹣ 3即：﹣ 394 ．∴K1（1，﹣27），K2（3，﹣）．将A(－2,0)、B(4,3)分别代入y＝ax2＋bx－3，得⎨解得a=1，b=-．解得m1=1，m2=3．1588【例3】如图，在平面直角坐标系中，直线y=12x+1与抛物线y＝ax2＋bx－3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a、b及sin∠ACP的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为9∶10？若存在，直接写出m的值；若不存在，请说明理由．思路点拨1．第（1）题由于CP//y轴，把∠ACP转化为它的同位角．2．第（2）题中，PD＝PCsin∠ACP，第（1）题已经做好了铺垫．△3．PCD与△PCB是同底边PC的两个三角形，面积比等于对应高DN与BM的比．4．两个三角形的面积比为9∶10，要分两种情况讨论．满分解答（1）设直线y=1x+1与y轴交于点E，那么A(－2,0)，B(4,3)，E(0,1)．2在△Rt AEO中，OA＝2，OE＝1，所以AE=5．所以sin∠AEO=因为PC//EO，所以∠ACP＝∠AEO．因此s in∠ACP=25．5⎧4a-2b-3=0,⎩16a+4b-3=3.122255．⨯ (- m 2+m + 4) = - (m + 2)(m - 4) ，①当 △S PCD ∶△S PCB ＝9∶10 时， - (m + 2)(m - 4) = (4 - m ) ．解得 m = ． ②当 △S PCD ∶△S PCB ＝10∶9 时， - (m + 2)(m - 4) = (4 - m ) ．解得 m = ．考点伸展第（△3）题的思路是： PCD 与△PCB 是同底边 PC 的两个三角形，面积比等于对应高 DN 与 BM 的比．而 DN = PD cos ∠PDN = PD cos ∠ACP = 5 2 5 1 1 5 5 2 5BM ＝4－m ．1 9 5 5 10 21 10 32 5 9 9【例 4】如图，在 △Rt ABC 中，∠C=90°，∠A=30°，AB=4，动点 P 从点 A 出发，沿 AB 以每秒 2 个单位长度的速度向终点 B 运动．过点 P 作 PD ⊥AC 于点 D （点 P 不与点 A 、B 重合），作∠DPQ=60°，边 PQ 交射线 DC 于点 Q ．设点 P 的运动时间为 t 秒．（1）用含 t 的代数式表示线段 DC 的长；（2）当点 Q 与点 C 重合时，求 t 的值；（△3）设 PDQ 与△ABC 重叠部分图形的面积为 S ，求 S 与 t 之间的函数关系式；（4）当线段 PQ 的垂直平分线经过△ABC 一边中点时，直接写出 t 的值．2=3t，思路点拨（1）先求出AC，用三角函数求出AD，即可得出结论；（2）利用AD+DQ=AC，即可得出结论；（3）分两种情况，利用三角形的面积公式和面积差即可得出结论；（4）分三种情况，利用锐角三角函数，即可得出结论．满分解答（1）在△Rt ABC中，∠A=30°，AB=4，∴AC=23，∵PD⊥AC，∴∠ADP=∠CDP=90°，在△Rt ADP中，AP=2t，∴DP=t，AD=AP cosA=2t×3∴CD=AC﹣AD=23﹣3t（0＜t＜2）；（2）在△Rt PDQ中，∵∠DPC=60°，∴∠PQD=30°=∠A，∴P A=PQ，∵PD⊥AC，∴AD=DQ，∵点Q和点C重合，∴AD+DQ=AC，∴2×3t=23，∴t=1；（3）当 0＜t≤1 时，S=S △PDQ = 1DQ×DP=13 =2（t ﹣1）， ∴S=S △PDQ ﹣S △ECQ = 1× 3 t×t ﹣ 13 t 2 (0＜t ≤ 1)∴S= ⎨ 22 PQ= 12 AP=t ，AF= 1 ∴∠PGF=90°，PG= 1 t= 12 AC=3 ，QM= 12 PQ= 1 ∴∠QMN=90°，AN= 1 cos30 ︒ =3 t =23 t ， ∴t= 32 ×3 t×t= 3 2 t 2，当 1＜t ＜2 时，如图 2，CQ=AQ ﹣AC=2AD ﹣AC=2 3 t ﹣2 3 =2 3 （t ﹣1），在 △Rt CEQ 中，∠CQE=30°，∴CE=CQ•tan ∠CQE=2 3 （t ﹣1）× 32 ×23 （t ﹣1）×2（t ﹣1）=﹣3 3 2 t 2+4 3 t ﹣2 3 ，⎧ ⎪ ⎪- 3 3 t 2 + 4 3t - 2 3 (0＜t ＜2 )⎪⎩ 2；（4）当 PQ 的垂直平分线过 AB 的中点 F 时，如图 3，2AB=2，∵∠A=∠AQP=30°，∴∠FPG=60°，∴∠PFG=30°，∴PF=2PG=2t ，∴AP+PF=2t+2t=2，2；当 PQ 的垂直平分线过AC 的中点 M 时，如图 4，2AP=t ，在 △Rt NMQ 中，NQ= MQ∵AN+NQ=AQ ，∴ 3 + 2 32 3 3 t，10∴BF= 1 (x ＞0)和 y = - (x ＜0)于 M 、N 两点．当 PQ 的垂直平分线过 BC 的中点时，如图 5，1BC=1，PE= PQ=t ，∠H=30°，2 2∵∠ABC=60°，∴∠BFH=30°=∠H ，∴BH=BF=1，在 △Rt PEH 中，PH=2PE=2t ，∴AH=AP+PH=AB+BH ，∴2t+2t=5，∴t= 54，即：当线段 PQ 的垂直平分线经过△ABC 一边中点时，t 的值为 123 5秒或秒或秒．4 4【例 5】如图，直线 l 经过点 A (1，0)，且与双曲线 y = m x(x ＞0)交于点 B (2，1)．过点 P( p , p -1) (p ＞1)作 x轴的平行线分别交曲线 y = m mx x（1）求 m 的值及直线 l 的解析式；（2）若点 P 在直线 y ＝2 上，求证：△PMB ∽△PNA ；（3）是否存在实数 p ，使得 △S AMN ＝4△S AMP ？若存在，请求出所有满足条件的 p 的值；若不存在，请说明理由．思路点拨1．第（2）题准确画图，点的位置关系尽在图形中．2．第（3）题把 S △AMN ＝4△S AMP 转化为 MN ＝4MP ，按照点 M 与线段 NP 的位置关系分两种情况讨论．满分解答由P(3，2)、N(－1，2)、A(1，△0)三点的位置关系，可知PNA为等腰直角三角形．所以△PMB∽△PNA．图2图3图4考点伸展在本题情景下，△AMN能否成为直角三角形？情形一，如图5，∠AMN＝90°，此时点M的坐标为（1，2），点P的坐标为（3，2）．情形二，如图6，∠MAN＝90°，此时斜边MN上的中线等于斜边的一半．不存在∠ANM＝90°的情况．图5图6【例6】如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．△Rt CDE中，∠CDE=90°，CD=4，DE=43，直角边CD在y轴上，且点C与点A重合．△Rt CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：（1）如图（2），当△Rt CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．（2）如图（3），在△Rt CDE的运动过程中，当CE经过点B时，求BC的长．（3）在△Rt CDE的运动过程中，设AC=h△，OAB△与CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．思路点拨（1）如图2，由对顶角的定义知，∠BME=∠CMA，要求∠BME的度数，需先求出∠CMA的度数．根据三角形外角的定理进行解答即可；（2）如图3，由已知可知∠OBC=∠DEC=30°，又OB=6，通过解直角△BOC就可求出BC的长度；（3）需要分类讨论：需要分类讨论：①h＜2时，②2≤h＜6-23时，③6-23≤h≤6时，依此即可求解．满分解答（1）如图2，∵在平面直角坐标系中，点A（0，﹣6），点B（6，0）．∴OA=OB，∴∠OAB=45°，∵∠CDE=90°，CD=4，DE=43，∴∠OCE=60°，∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°，∴∠BME=∠CMA=15°；(2)如图3，∵∠CDE=90°，CD=4，DE=43，∴∠OBC=∠DEC=30°，∵OB=6，∴BC=43；（3）①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，∴S=S △EDC ﹣S △EFM =1= S=S △AOB △-S ACM =113 + 13 + 3 S=S △OMC = 1h 2+4h+8(最大值为 15- 3 )；②2≤h ＜6-2 3 时，S=18- h 2（最大值∵CD=4，DE=4 3 ，AC=h ，AN=NM ，∴CN=4﹣FM ，AN =MN =4+h ﹣FM ，∵△CMN ∽△CED ，∴ CN MN = ，CD DE4 - FM 4 + h - FM∴ ，4 4 3解得 FM=4﹣3 + 1h ， 21 3 + 1 3 + 1×4×4 3 ﹣ （4 3 -4﹣h ）×（4﹣ h ）=﹣ 2 2 2 4h 2+4h+8， S=15- 3 ．最大②当 2≤h ＜6-2 3 时，2224×6×6- h （h+ h ）=18-h 2，S=15- 3 ．最大③如图 3，当 6-2 3 ＜h≤6 时，3 OB× 3 OC=（6-h ）2，22S=6 3 ．最大综上所述，①h ＜2 时，S= -3 + 143 + 34为 15- 3 ）；③6-2 3 ≤h≤6 时，S=3 （6-h ）2（最大值为 6 3 ）2【变式训练】1．如图，利用一个直角墙角修建一个梯形储料场 ABCD ，其中∠C ＝120°．若新建墙 BC 与 CD 总长为 12m ，则该梯形储料场 ABCD 的最大面积是（）BC=6-S=11⎛1⎫⎛3⎫3333x+x+6⎪⋅ 63-x⎪=-x2+33x+183=-⎭⎝A．18m2B．183m2C．243m2D．4532m2【答案】C【详解】解：如图，过点C作CE⊥AB于E，则四边形ADCE为矩形，CD=AE=x，∠DCE=∠CEB=90°，则∠BCE=∠BCD-∠DCE=30°，BC=12-x，在△Rt CBE中，∵∠CEB=90°，∴B E=11x 22∴A D=CE=3BE=63-311 x,AB=AE+BE=x+6-x=x+6 222∴梯形ABCD面积(CD+AB)⋅CE=22⎝22⎭888(x-4)2+243∴当x=4时，S最大=243．即CD长为4m时，使梯形储料场ABCD的面积最大为243m2；故选C．2．如图，正方形ABCD的边长为2cm，动点P，Q同时从点A出发，在正方形的边上，分别按A→D→C，A→B→C的方向，都以1cm/s的速度运动，到达点C运动终止，连接PQ，设运动时间为x s，∆APQ 的面积为y cm2，则下列图象中能大致表示y与x的函数关系的是（）=2⨯2-1(4-x)2-⨯2⨯(x-2)-⨯2⨯(x-2)A．B．C．D．【答案】A【详解】①当0≤x≤2时，∵正方形的边长为2cm，∴y=S1 AQ⋅AP=x2；22②当2≤x≤4时，y=S∆APQ=S正方形ABCD -S∆CP'Q'-S∆ABQ'-S∆AP'D112221=-x2+2x，2所以，y与x之间的函数关系可以用两段二次函数图象表示，纵观各选项，只有A选项图象符合，故选A．3．如图，已知直线y=3x-3与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆42D．17上一动点，连结PA、PB△．则PAB面积的最大值是（）A．8【答案】C【详解】解：∵直线y=34B．12C．21x-3与x轴、y轴分别交于A、B两点，2∴A点的坐标为（4，0），B点的坐标为（0，﹣3），3x-4y-12=0，即OA=4，OB=3，由勾股定理得：AB=5，过C作CM⊥AB于M，连接AC，则由三角形面积公式得：∴5×CM=4×1+3×4，111×AB×CM=×O A×OC+×OA×OB，222∴CM=16 5，∴圆C上点到直线y=31621x-3的最大距离是1+=，455 12121∴△PAB面积的最大值是⨯5⨯=，252故选C．4．如图，在等腰直角三角形ABC中，∠ACB=90︒，AB=8cm，C H是AB边上的高，正方形DEFGt = 4 - ⨯ [2 - (4 - t )]2 = - (t - 2)2 + 4 ；t的边 DE 在高 CH 上，F ，G 两点分别在 AC ，AH 上．将正方形 DEFG 以每秒1cm 的速度沿射线 DB 方向匀速运动，当点 G 与点 B 重合时停止运动．设运动时间为 ts ，正方形 DEFG 与 ∆BHC 重叠部分的面积为 Scm 2，则能反映 S 与 t 的函数关系的图象（）A ．B ．C ．D ．【答案】B【详解】由题意得： AH = BH = CH = 4 ， FE = FG = GH = EH = 2 ，（1）当 0剟2 时，如图 1，设 EF 交 CH 于点 K ，则 S = S矩形EDHK= t ⨯ 2 = 2t ；（2） 2 < t … 4 时，如图 2，设 EF 与 BC 交于点 M ， DE 于 BC 交于点 N ，S = S 正方形DEFG - S∆EMN 1 1 2 2（3） 4 < t … 6 时，如图 3，设 GF 交 BC 于点 L ，S = S1⨯ [2 - (t - 4)]2= (t - 6)2 ， 2 2∴当 0剟2 时，函数图象是正比例函数，当2 < t … 4 时，是开口向下的抛物线，当4 < t … 6 时，是开口向上的抛物线，故选： B ．5．如图，点A是直线y=﹣x上的动点，点B是x轴上的动点，若AB=2，则△AOB面积的最大值为（）A．2B．+1C．-1D．2【答案】B【详解】如图所示，作△AOB的外接圆⊙C，连接CB，CA，CO，过C作CD⊥AB于D，则CA=AB，由题可得∠AOB=45°，∴∠ACB=90°，∴CD=AB=1，AC=BC==CO，连接OD，则OD≤OC+CD，+1，∴当O，C，D在同一直线上时，OD的最大值为OC+CD=此时OD⊥AB，∴△AOB的面积最大值为AB×OD=×2（+1）=+1，当点A在第二象限内，点B在x轴负半轴上时，+1，同理可得，△AOB面积的最大值为故选：B．6．如图，已知，以为圆心，长为半径作，是上一个动点，直线交轴于点，则面积的最大值是（）A．B．C．D．【答案】B【详解】当直线AN与⊙B相切时，△AOM面积的最大．连接AB、BN，在△Rt AOB和△Rt ANB中∴△Rt AOB≌△Rt ANB，∴AN=AO=2，设BM=x，∴MN2=（BM-1）（BM+1），∴MN=，∵∠AOM=∠BNM=90°，∠AMO=∠BMN，∴△BNM∽△AOM，∴即，，解得x=，S△AOM=．故选B．7．如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D 是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD面积的最大值为__________【答案】15【详解】∵D是抛物线y=-x2+6x上一点，∴ S V BCD = ⨯ 5 ⨯ (- x 2 + 6 x - 3) = - ( x - 3)2 + 15，Q - < 0，∴设 D( x , - x 2 + 6 x )，∵顶点 C 的坐标为(4,3)，∴OC = 42 + 32 = 5，∵四边形 OABC 是菱形，∴ BC = OC = 5, BC P x 轴，1 52 252∴ S V BCD 有最大值，最大值为 15，故答案为 15.8．如图，线段 AB 的长为 2，C 为 AB 上一个动点，分别以 AC 、BC 为斜边在 AB 的同侧作两个等腰直角三角形△ ACD △和BCE ，那么 DE 长的最小值是______________．【答案】1【详解】设 AC ＝x ，则 BC ＝2－x ，∵△ACD △和 BCE 都是等腰直角三角形，∴∠DCA ＝45°，∠ECB ＝45°，DC ＝ 2 x ，CE ＝ 2 (2－x) .2 2∴∠DCE ＝90°.∴DE 2＝DC 2＋CE 2＝（2 x ）2＋[ 2 (2－x) ]2＝x 2－2x ＋2＝(x －1)2＋1.2 2∴当 x ＝1 时，DE 2 取得最小值，DE 也取得最小值，最小值为 1.9．已知直角梯形OABC在如图所示的平面直角坐标系中，AB∥OC，AB=10，OC=22，BC=15，动点M从A点出发，以每秒一个单位长度的速度沿AB向点B运动，同时动点N从C点出发，以每秒2个单位长度的速度沿CO向O点运动。

2019年中考数学复习1.5因动点产生的面积问题

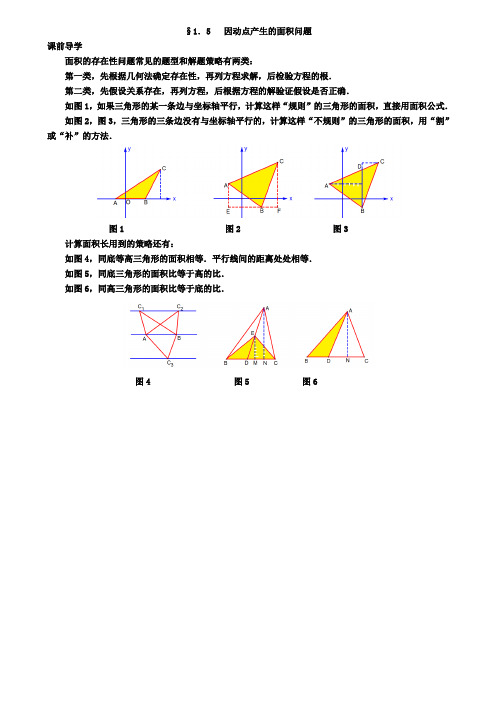
§1．5 因动点产生的面积问题课前导学面积的存在性问题常见的题型和解题策略有两类：第一类，先根据几何法确定存在性，再列方程求解，后检验方程的根．第二类，先假设关系存在，再列方程，后根据方程的解验证假设是否正确．如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．图1 图2 图3计算面积长用到的策略还有：如图4，同底等高三角形的面积相等．平行线间的距离处处相等．如图5，同底三角形的面积比等于高的比．如图6，同高三角形的面积比等于底的比．图4 图5 图6例 32 2019年湖南省常德市中考第25题如图1，已知二次函数的图象过点O(0,0)、A(4，0)、B(2,)，M 是OA 的中点．（1）求此二次函数的解析式；（2）设P 是抛物线上的一点，过P 作x 轴的平行线与抛物线交于另一点Q ，要使四边形PQAM 是菱形，求点P 的坐标；（3）将抛物线在x 轴下方的部分沿x 轴向上翻折，得曲线OB′A（B ′为B 关于x 轴的对称点），在原抛物线x 轴的上方部分取一点C ，连结CM ，CM 与翻折后的曲线OB′A 交于点D ，若△CDA 的面积是△MDA 面积的2倍，这样的点C 是否存在？若存在求出点C 的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14常德25”，拖动点P 在抛物线上运动，可以体验到，当四边形PQAM 是平行四边形时，也恰好是菱形．拖动点C 在抛物线上运动，还可以体验到，△MCA 与△MDA 是同底三角形，它们的面积比等于对应高的比．思路点拨1．设交点式或顶点式求抛物线的解析式都比较简便． 2．先确定四边形PQAM 是平行四边形，再验证它是菱形．3．把△CDA 与△MDA 的面积比，转化为△MCA 与△MDA 的面积比，进而转化为点C 与点D 的纵坐标的比．图文解析（1）因为抛物线与x 轴交于O(0,0)、A(4，0)两点，设y ＝ax(x －4)．代入点B(2,)，得4a =-．解得a ．所以(4)y x -．（2）如图2，由A(4，0)，M 是OA 的中点，可知OA ＝4，MA ＝2，M(2, 0)．如果四边形PQAM 是菱形，已知PQ//OA ，首先要满足PQ ＝2，再必须MP ＝2．因为抛物线的对称轴是直线x ＝2，P 、Q 关于x ＝2对称，所以点P 的横坐标为1，故点P 的坐标为(1,．由M(2, 0)、P (1,，可得MP ＝2．所以当点P 的坐标为(1,时，四边形PQAM 是菱形．（3）如图3，作CE ⊥x 轴于E ，作DF ⊥x 轴于F ．我们把面积进行两次转换：如果△CDA 的面积是△MDA 面积的2倍，那么△MCA 的面积是△MDA 面积的3倍．而△MCA 与△MDA 是同底三角形，所以高的比CE ∶DF ＝3∶1，即y C ∶y D ＝3∶1．因此ME ∶MF ＝3∶1．设MF ＝m ，那么ME ＝3m ．原抛物线的解析式为(4)y x =-，所以翻折后的抛物线的解析式为(4)y x x =-．所以D (2,)(24))m m m +++-，C (233)(234))m m m +++-．根据y C ∶y D ＝3∶13)(234)3)(24)m m m m ⎡⎤++-=++-⎢⎥⎣⎦．整理，得3m2＝4．解得m=．所以232+=±m所以点C的坐标为(2+（如图3），或(2-（如图4）．图2 图3 图4 考点伸展第（1）题可以设抛物线的顶点式：由点O(0,0), A(4，0)，B(2,)的坐标，可知点B是抛物线的顶点．可设2=-O(0,0)，得a(2)y a x例 33 2019年湖南省永州市中考第25题如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴交于A(－1, 0)，B(4, 0)两点，与y 轴交于点C(0, 2)．点M(m, n)是抛物线上一动点，位于对称轴的左侧，并且不在坐标轴上．过点M 作x 轴的平行线交y 轴于点Q ，交抛物线于另一点E ，直线BM 交y 轴于点F ．（1）求抛物线的解析式，并写出其顶点坐标；（2）当S △MFQ ∶S △MEB ＝1∶3时，求点M 的坐标．图1动感体验请打开几何画板文件名“14永州25”，拖动点M 在抛物线左半侧上运动，观察面积比的度量值，可以体验到，存在两个时刻，△MEB 的面积等于△MFQ 面积的3倍．思路点拨1．设交点式求抛物线的解析式比较简便．2．把△MFQ 和△MEB 的底边分别看作MQ 和ME ，分别求两个三角形高的比，底边的比（用含m 的式子表示），于是得到关于m 的方程．3．方程有两个解，慎重取舍．解压轴题时，时常有这种“一石二鸟”的现象，列一个方程，得到两个符合条件的解．图文解析（1）因为抛物线与x 轴交于A(－1, 0)，B(4, 0)两点，设y ＝a(x ＋1)(x －4)．代入点C(0, 2)，得2＝－4a ．解得12a =-．所以221131325(1)(4)2()222228y x x x x x =-+-=-++=--+．顶点坐标为325()28，．（2）如图2，已知M(m, n)，作MN ⊥x 轴于N ．由=FQ MNMQ BN，得=4FQ n m m -．所以=4mn FQ m -．因为抛物线的对称轴是直线32x =，所以ME ＝32()322m m -=-．由于S △MFQ ＝12FQ MQ ⋅＝124mnm m⨯⨯-＝2124m n m ⨯-， S △MEB ＝12ME MN ⋅＝1(32)2m n -，所以当S △MFQ ∶S △MEB ＝1∶3时，24m nm-∶(32)m n -＝1∶3．整理，得m 2＋11m －12＝0．解得m ＝1，或m ＝－12．所以点M 的坐标为(1, 3)或(－12,－88)．图2考点伸展第（2）题S △MFQ ∶S △MEB ＝1∶3，何需点M 一定要在抛物线上？从上面的解题过程可以看到，△MFQ 与△MEB 的高的比=4FQ mMN m-与n 无关，两条底边的比=32MQ mME m-也与n 无关．如图3，因此只要点E 与点M 关于直线x ＝32对称，点M 在直线的左侧，且点M 不在坐标轴上，就存在S △MFQ ∶S △MEB ＝1∶3，点M 的横坐标为1（如图3）或－12（如图4）．图3 图42019-2020学年数学中考模拟试卷一、选择题1．若关于的x 方程230x x a ++=有一个根为1-，则a 的值为（） A ．-4B ．-2C ．2D ．-42．下列运算正确的是（） A ．3a 3+a 3＝4a 6 B ．（a+b ）2＝a 2+b 2 C ．5a ﹣3a ＝2aD ．（﹣a ）2•a 3＝﹣a 63 ） A ．4B ．﹣4C ．2D ．±24．如图，四边形ABCD 内接于⊙O ，已知∠ADC=140°，则∠AOC 的大小是（）A.100B.80C.60D.4052的值在( ) A ．3和4之间B ．4和5之间C ．5和6之间D ．6和7之间6．如图，在矩形ABCD 中，120AOB ∠=︒，3AD =，则AC =（）A ．6B ．C ．5D ．7．下列计算正确（）A ．222a b a b +=+（） B ．235a a a ⋅=C ．822a a a ÷=D ．325a a a +=8．如图，为某校初三男子立定跳远成绩的统计图，从左到右各分数段的人数之比为1：2：5：6：4，第四组的频数是12，对于下面的四种说法 ①一共测试了36名男生的成绩．②立定跳远成绩的中位数分布在1.8～2.0组． ③立定跳远成绩的平均数不超过2.2．④如果立定跳远成绩1.85米以下（不含1.85）为不合格，那么不合格人数为6人．正确的是（）A ．①③B ．①④C ．②③D ．②④9．文艺复兴时期，意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”，可看成圆与正方形的各边均相切，切点分别为,,,A B C D ，BD 所在圆的圆心为点A （或C ）. 若正方形的边长为2，则图中阴影部分的面积为（）AB ．2C ．1π-D ．42π-10．下列四个函数中，自变量的取值范围为x ≥1的是（）A ．y =B ．y =C ．y =D ．y =11．对于一组数据： 4, 3,6, 4, 8,下列说法错误的是（） A ．众数是4B ．平均数是5C ．众数等于中位数D ．中位数是512．已知AB ＝10，C 是射线AB 上一点，且AC ＝3BC ，则BC 的长为（）A.2.5B.103C.2.5或5D.103或5 二、填空题13．如图，在由边长都为1的小正方形组成的网格中，点A ，B ，C 均为格点，点P ，Q 分别为线段AB ，BC 上的动点，且满足AP BQ =．(1)线段AB 的长度等于__________；(2)当线段AQ CP +取得最小值时，请借助无刻度直尺在给定的网格中画出线段AQ 和CP ，并简要说明你是怎么画出点Q ，P 的：_______________________．14．据资料表明：中国已成为全球机器人第二大专利来源国和目标国.机器人几大关键技术领域包括：谐波减速器、RV减速器、电焊钳、3D视觉控制、焊缝跟踪、涂装轨迹规划等，其中涂装轨迹规划的来源国结构（仅计算了中、日、德、美）如图所示，在该扇形统计图中，美国所对应的扇形圆心角是__________度．15．计算432x x⋅的结果等于__________．16．如图，点A1、A2、A3…在直线y＝x上，点C1，C2，C3…在直线y＝2x上，以它们为顶点依次构造第一个正方形A1C1A2B1，第二个正方形A2C2A3B2…，若A2的横坐标是1，则B3的坐标是_____，第n个正方形的面积是_____．17．一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD 水平，BC与水平面的夹角为60°，其中AB=60cm，CD=40cm，BC=40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为____cm．18．在四边形ABCD中，向量、满足=-4，那么线段AB与CD的位置关系是_____．三、解答题19．先化简，再求值：22299(6)3a aaa a-+÷+-，其中a2﹣4a+3＝0．20．2﹣|1|﹣tan45°+（π﹣1978）0．21．如图,在小正方形的边长均为1的方格纸中点A、B、C均在格点上；(1)在图1中画出凸四边形ABCD,使四边形ABCD是轴对称图形,点D在格点上；(2)在图2中画出凸四边形ABCE,点E在格点上,∠AEC=90°,EC>EA，直接写出四边形ABCE的周长_____.22．如图，A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线相交于点D，E是BD的中点，延长AE与CB的延长线相交于点F．（1）求证：AF是⊙O的切线；（2）若BE＝5，BF＝12，求CD的长．23．为如图，已知女排球场的长度OD为18米，位于球场中线处的球网AB的高度2.24米，一队员站在点O处发球，排球从点O的正上方2米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点O的水平距离OE为6米时，到达最高点G，以O为原点建立如图所示的平面直角坐标系．（1）若排球运行的最大高度为2.8米，求排球飞行的高度p（单位：米）与水平距离x（单位：米）之间的函数关系式（不要求写自变量x的取值范围）；（2）在（1）的条件下，这次所发的球能够过网吗？如果能够过网，是否会出界？请说明理由；（3）若李明同学发球要想过网，又使排球不会出界（排球压线属于没出界）求二次函数中二次项系数的最大值．24．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C．（1）求抛物线y=ax 2+2x+c 的解析式:；（2）点D 为抛物线上对称轴右侧、x 轴上方一点，DE ⊥x 轴于点E ，DF ∥AC 交抛物线对称轴于点F ，求DE+DF 的最大值；（3）①在拋物线上是否存在点P ，使以点A ，P ，C 为顶点，AC 为直角边的三角形是直角三角形？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；②点Q 在抛物线对称轴上，其纵坐标为t ，请直接写出△ACQ 为锐角三角形时t 的取值范围．25．如图，在平面直角坐标系中，点O 为坐标原点，点()0,4A 与点B 关于x 轴对称，点(),0C m 为x 轴的正半轴上一动点.以AC 为边作等腰直角三角形ACD ，90ACD ∠=︒，点D 在第一象限内.连接BD ，交x 轴于点F .（Ⅰ）用含m 的式子表示点D 的坐标；（Ⅱ）在点C 运动的过程中，判断OF 的长是否发生变化？若不变求出其值，若变化请说明理由；（Ⅲ）过点C 作CG BD ⊥，垂足为点G ，请直接写出BF DF -与CG 之间的数量关系式.【参考答案】*** 一、选择题二、填空题13．取格点,,,D E F G ．连接,BD EF ，它们相交于点T ，连接,AT CG ，分别交,BC AB 于点,Q P ，则线段AQ 和CP 即为所求． 14．6 15．72x16．(4，2) 22n ﹣4． 17．18．平行三、解答题 19．14. 【解析】【分析】根据分式的运算法则即可求出答案．【详解】原式＝2(3)(3)(3)69a a aa a a a +-⋅-++＝23(3)a a a a +⋅+ ＝13a + ∵a 2﹣4a+3＝0，∴a 1＝1 a 2＝3（舍去） ∴原式＝14【点睛】本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．20．2020-【解析】【分析】直接利用零指数幂的性质以及绝对值的性质和特殊角的三角函数值分别分析得出答案．【详解】解：原式＝20191）﹣1+1＝2020 【点睛】此题主要考查了实数运算，正确化简各数是解题关键．21．（1）如图所示，见解析；（2）如图所示，周长为6+【分析】(1)根据轴对称的性质画出图形即可;(2)画出四边形 ABCDE,再求出其周长即可.【详解】（1）如图所示，（2）如图所示，四边形ABCE的周长为6【点睛】此题考查作图-轴对称变换，掌握作图法则是解题关键22．（1）见解析；（2）【解析】【分析】（1）利用直角三角形斜边中线的性质和等边对等角得到∠EAB＝∠EBA，结合⊙O的切线得出OA⊥AF，从而得出AF是⊙O的切线；（2）先根据勾股定理求得EF的长，再根据切线的性质得出EB＝EA＝5，即可求得AF的长，然后根据切割线定理求得FC，进而得出BC的长，根据E是BD的中点，得出BD的长，最后根据勾股定理即可求得CD 的长．【详解】解：（1）连接AB，OA，∵BC是⊙O的直径，∴∠BAC＝90°，∵DB是⊙O的切线，∴DB⊥BC，∴∠DBO＝90°，在RT△ABD中，E是斜边BD的中线，∴AE＝DE＝BE，∴∠EAB＝∠EBA，∵OA＝OB，∴∠OAB＝∠OBA，∴∠EAB+∠OAB＝∠EBA+∠OBA∴∠EAO＝∠DBO＝90°，∴AF是⊙O的切线；（2）∵在RT△BEF中，BE＝5，BF＝12，∴EF＝13，∵FA、DB是⊙O的切线，∴EA＝EB＝5，∴AF＝EF+EA＝13+5＝18，∵AF2＝FB•FC，∴FC＝22182712AFAB==∴BC＝FC﹣FB＝27﹣12＝15，∵E是BD的中点，∴BD＝2BE＝10，在RT△DBC中，CD==【点睛】本题考查了切线的判定和性质，直角三角形斜边中线的性质，等腰三角形的性质，勾股定理的应用等，正确的作出辅助线是解题的关键．23．（1）p＝145（x﹣6）2+2.8;（2）见解析;（3）154-.【解析】【分析】（1）利用抛物线的顶点坐标为（6，2.8），将点（0，2）代入解析式求出即可（2）利用当x＝9时，x＝18时，分别求出p值即可判断（3）设抛物线的解析式为：p＝a（x﹣6）2+h，将点C代入，此时抛物线的解析式为p＝a（x﹣6）2+2﹣36a，再根据x＝9时，p＞2.24，当x＝18时，p≤0，即可得a的范围，从而取得最大值．【详解】解：（1）由排球运行的最大高度为28米，则顶点的坐标点G为（6，2.8），则设抛物线的解析式为p＝a（x ﹣6）2+2.8∵点C坐标为（0，2），点C在抛物线上∴2＝a（0﹣6）2+2.8解得a＝﹣1 45∴p＝-145（x﹣6）2+2.8则排球飞行的高度p（单位：米）与水平距离x（单位：米）之间的函数关系式：p＝-145（x﹣6）2+2.8（2）当x＝9时，p＝-145（9﹣6）2+2.8＝2.6＞2.24当x＝18时，p＝-145（18﹣6）2+2.8＝﹣0.4＜0故这次发球可以过网且不出边界（3）设抛物线的解析式为：p＝a（x﹣6）2+h，将点C代入得：36a+h＝2，即h＝2﹣36a∴此时抛物线的解析式为p＝a（x﹣6）2+2﹣36a根据题意，不过边界时有：a（18﹣6）2+2﹣36a≤0，解得a≤-1 54要使网球过网：a（9﹣6）2+2﹣36a≥2.24，解得a≤2 225 -故李明同学发球要想过网，又使排球不会出界（排球压线属于没出界）二次函数中二次项系数的最大值为154【点睛】本题考查了二次函数的性质在实际生活中的应用．可根据二次函数的解析式的最值作为临界值来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．24．（1）y=﹣x2+2x+3；（2）DE+DF有最大值为132；（3）①存在，P的坐标为（73，209）或（103，139-）；②23-＜t＜83．【解析】【分析】（1）设抛物线解析式为y=a（x+1）（x﹣3），根据系数的关系，即可解答（2）先求出当x=0时，C的坐标，设直线AC的解析式为y=px+q，把A,C的坐标代入即可求出AC的解析式，过D作DG垂直抛物线对称轴于点G，设D（x，﹣x2+2x+3），得出DE+DF=﹣x2（x-1）=﹣x2+（），即可解答（3）①过点C作AC的垂线交抛物线于另一点P1，求出直线PC的解析式，再结合抛物线的解析式可求出P1，过点A作AC的垂线交抛物线于另一点P2，再利用A的坐标求出P2，即可解答②观察函数图象与△ACQ为锐角三角形时的情况，即可解答【详解】解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；（2）当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3，如答图1，过D作DG垂直抛物线对称轴于点G，设D（x，﹣x2+2x+3），∵DF∥AC，∴∠DFG=∠ACO，易知抛物线对称轴为x=1，∴DG=x-1，（x-1），∴DE+DF=﹣x2+2x+3+x-1）=﹣x2+（），∴当x=1，DE+DF有最大值为132；答图1 答图2（3）①存在；如答图2，过点C作AC的垂线交抛物线于另一点P1，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=13-x+m，把C（0，3）代入得m=3，∴直线P1C的解析式为y=13-x+3，解方程组223133y x xy x⎧=-++⎪⎨=-+⎪⎩，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P1点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P2，直线AP2的解析式可设为y=13-x+n，把A（﹣1，0）代入得n=13-，∴直线PC 的解析式为y=1133x --，解方程组2231133y x x y x ⎧=-++⎪⎨=--⎪⎩，解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩，则此时P 2点坐标为（103，139-），综上所述，符合条件的点P 的坐标为（73，209）或（103，139-）；②23-＜t ＜83．【点睛】此题考查二次函数综合题，解题关键在于把已知点代入解析式求值和作辅助线. 25．(1) G(4+m,m) (2) OF=4，OF 是不变化的 (3) BF DF -是CG 的两倍【解析】【分析】(1)过D 点作x 轴垂线，垂足为G 点，可知△CDG 相似△OAC ，即可求出D 点坐标.(2)利用B,D 两点的坐标给出直线BD 的解析式，然后令解析式的y=0，给出x 的值，如果x 含有参数，则OF 的长是变化的，若x 不含参数，则OF 的长无变化.(3)用含m 的式子表示出BF DF -和CG 的长，结果就出来了，其中BF DF -的长利用△DFG 相似△OBF 可求，CG 的长直接利用勾股定理可求. 【详解】解：(1) 过D 点作x 轴垂线，垂足为H 点， ∵90ACD ∠=︒， ∴=90ACO DCH ∠+∠︒ ∵=90ACO CAO ∠+∠︒, ∴CAO DCH ∠=∠ ，又∵90ACD CHD ∠=∠=︒,AC=CD, ∴在△OAC 和△CDH ，CAO DCHAOC CHD AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ACO CDH∴≌，∴CH=OA,DH=OC=m, ∴OH=4+m ， ∴D(4+m,m).(2)设BD 直线的解析式为：y=kx+b ，将点B(0,-4)与点D(4+m,m)代入方程，()44+m b k b m =-⎧⎨+=⎩ ，解得：11k b =⎧⎨=⎩，BD 的直线解析式为4y x =- ，当y=0时，x=4 ，OF=4，OF 是不变化的；(3)可知△DFH 相似△OBF ，∴::m 4DH OB DF BF ==：，由 B(0,-4)与点D(4+m,m)，可以知道)4m +,∴, DF= ，BF DF -m-4，CG === ∴BF DF -是CG 的两倍. 【点睛】本题是一道综合习题，第一问考查相似与坐标系中点的表示，第二问考查力一次函数，第三问考查力相似与勾股定理，本题第二问关键是给出直线BD 的解析式，第三问的关键是会表示两个线段的长2019-2020学年数学中考模拟试卷一、选择题1．一个数和它的倒数相等，则这个数是（）A．1 B．-1 C．±1D．±1和02．实数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（）A．a＞b B．a＝b＞0 C．ac＞0 D．|a|＞|c|3．二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示，则一次函数y=ax+b与反比例函数y=cx在同一平面直角坐标系中的图象可能是（）A． B．C．D．4．抛物线y＝x2向下平移一个单位，向左平移两个单位，得到的抛物线关系式为（）A．y＝x2+4x+3 B．y＝x2+2x﹣1 C．y＝x2+2x D．y＝x2﹣4x+35．下列运算正确的是（）A.a2×a3＝a6B.a2+a2＝2a4C.a8÷a4＝a4D.（a2）3＝a56．有一张矩形ABCD的纸片（AB＜BC），按如图所示的方式，在A，C两端截去两个矩形AEFG和CE′F′G′，且AE＝CE′，AG＝CG′，再分别过EF，FG，E′F′，F′G′四边的中点，沿平行于原矩形各边的方向剪裁，得到如图的阴影部分，分别记为L1，L2．若L1的周长是矩形ABCD的34，L2的周长是矩形ABCD的35，则AEAG的值为（）A．54B．85C．32D．20971，0( )AB ．﹣1C ．0D 8．某足球生产厂计划生产4800个足球，在生产完1200个后，采用了新技术，工作效率比原计划提高了20%，结果共用了21天完成全部任务．设原计划每天生产x 个足球，根据题意可列方程为（） A ．12004800(120%)x ++＝21 B ．120048001200(120%)x x-++＝21 C ．12004800120020%x x-+＝21 D ．480048001200(120%)x x-++＝21 9．如表是小明同学参加“一分钟汉字听写”训练近6次的成绩：则这组数据的平均数和中位数分别是（） A ．245个、244个 B ．244个、244个 C ．244个、241.5个D ．243个、244个10．如图，在▱ABCD 中，对角线AC ，BD 相交于点O ，AC=6，BD=10，则AD 的长度可以是（）A.2B.7C.8D.1011．一组数1，1，2，3，5，8，13是“斐波那契数列”的一部分，若去掉其中的两个数后这组数的中位数、众数保持不变，则去掉的两个数可能是（） A ．2，5B ．1，5C ．2，3D ．5，812．“定西市乒乓球夏令营”开始在学校报名了，已知甲、乙、丙三个夏令营组人数相等，且每组学生的平均年龄都是14岁，三个组学生年龄的方差分别是2S 甲=17，2S 乙=14.6，2S 丙=19，如果今年暑假你也准备报名参加夏令营活动，但喜欢和年龄相近的同伴相处，那么你应选择( ) A ．甲组 B ．乙组C ．丙组D ．采取抽签方式，随便选一个二、填空题13．如图，点A 是双曲线6y x=-在第二象限分支上的一个动点，连接AO 并延长交另一分支于点B ，以AB 为底作等腰ABC △，且120ACB ∠=︒，点C 在第一象限，随着点A 的运动点C 的位置也不断变化，但点C 始终在双曲线ky x=上运动，则k 的值为________.14．如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，已知CD ＝8，EB ＝2，则⊙O 的半径为_____．15．如图，在△ABO 中，∠ABO ＝90°，点A 的坐标为（3，4）．写出一个反比例函数y ＝kx（k≠0），使它的图象与△ABO 有两个不同的交点，这个函数的表达式为_____．16．如果点（m ，﹣2m ）在双曲线ky x=上，那么双曲线在_____象限． 17．如图，在△ABC 中，DE ∥BC ，AD ：DB=1：2，DE=2，则BC 的长是．18．《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三．问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱：若每人出7钱，还差3钱．则合伙人数为_____人；羊价为_____钱．三、解答题19．如图，在ABC △中，AB AC =，以AB 为直径的⊙O 分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥，垂足为点H ，连接DE ，交AB 于点F .（1）求证：DH是⊙O的切线;=时，求AD的长(结果保留π)；②当sin B=求线段AF （2）若⊙O的半径为4，①当AE FE的长.20．如图，正方形网格中，△ABC为格点三角形（顶点都在格点上）（1）作出△ABC绕点A逆时针旋转90°后的△AB1C1；将△ABC向上平移3格，在向左平移4格得到△A2B2C2；（2）设小正方形的边长为1，求出△ABC旋转到△AB1C1的过程中AB所扫过的面积（结果保留π）21．已知：如图，在平行四边形中，点E在BC边上，连接AE．O为AE中点，连接BO并延长交AD于F．（1）求证：△AOF≌△BOE，（2）判断当AE平分∠BAD时，四边形ABEF是什么特殊四边形，并证明你的结论．22．如图，一种侧面形状为矩形的行李箱，箱盖打开后，盖子的一端靠在墙上，此时BC=10cm，箱底端点E与墙角G的距离为65cm，∠DCG=60°．（1）箱盖绕点A转过的角度为______，点B到墙面的距离为______cm；（2）求箱子的宽EF（结果保留整数，可用科学计算器）．=1.41=1.73）23．如图，某学校甲楼的高度AB是18.6m，在甲楼楼底A处测得乙楼楼顶D处的仰角为40，在甲楼楼顶B 处测得乙楼楼顶D 的仰角为19，求乙楼的高度DC 及甲乙两楼之间的距离AC （结果取整数）.参考数据：cos190.95≈，tan190.34≈，cos400.77≈，tan 400.84≈.24．先化简，再求值222221b a ab a b a b a 2ab b -⎛⎫-÷ ⎪---+⎝⎭，其中a=2sin45°，25．计算：11|2|3-⎛⎫-- ⎪⎝⎭．【参考答案】***一、选择题二、填空题13．214．515．答案不唯一，如：2y x =； 16．二．四；17．18．150三、解答题19．（1）见解析；（2）①AD 的长＝85π；②AF ＝43．【解析】【分析】（1）根据同圆的半径相等和等边对等角证明：∠ODB ＝∠OBD ＝∠ACB ，则DH ⊥OD ，DH 是圆O 的切线；（2）①根据等腰三角形的性质的∠EAF ＝∠EAF ，设∠B ＝∠C ＝α，得到∠EAF ＝∠EFA ＝2α，根据三角形的内角和得到∠B ＝36°，求得∠AOD ＝72°，根据弧长公式即可得到结论；②连接AD ，根据圆周角定理得到∠ADB ＝∠ADC ＝90°，解直角三角形得到AD ＝性质得到AH ＝3，于是得到结论．【详解】（1）连接OD ，如图，∵OB ＝OD ，∴△ODB 是等腰三角形，∠OBD ＝∠ODB ①，在△ABC 中，∵AB ＝AC ，∴∠ABC ＝∠ACB ②，由①②得：∠ODB ＝∠OBD ＝∠ACB ，∴OD ∥AC ，∵DH ⊥AC ，∴DH ⊥OD ，∴DH 是圆O 的切线；（2）①∵AE ＝EF ，∴∠EAF ＝∠EAF ，设∠B ＝∠C ＝α，∴∠EAF ＝∠EFA ＝2α，∵∠E ＝∠B ＝α，∴α+2α+2α＝180°，∴α＝36°，∴∠B ＝36°，∴∠AOD ＝72°，∴AD 的长＝72481805ππ⋅⨯=； ②连接AD ，∵AB 为⊙O 的直径，∴∠ADB ＝∠ADC ＝90°，∵⊙O 的半径为4，∴AB ＝AC ＝8，∵sin 4B =，∴8AD =，∴AD ＝，∵AD⊥BC，DH⊥AC，∴△ADH∽△ACD，∴AH AD AD AC=，8=，∴AH＝3，∴CH＝5，∵∠B＝∠C，∠E＝∠B，∴∠E＝∠C，∴DE＝DC，∵DH⊥AC，∴EH＝CH＝5，∴AE＝2，∵OD∥AC，∴∠EAF＝∠FOD，∠E＝∠FDO，∴△AEF∽△ODF，∴AF AE OF OD=,∴2 44 AFAF=-，∴AF＝43．【点睛】本题考查了等腰三角形的性质和判定、切线的性质和判定、三角形相似的性质和判定、圆周角定理，正确的作出辅助线是解题的关键．20．（1）见解析；（2）254 Sπ=【解析】【分析】（1）根据旋转的性质及平移的性质画出△AB1C1，△A2B2C2即可．（2）利用扇形的面积公式计算即可．【详解】（1）△AB1C1，△A2B2C2如图所示．（2）2905253604S ππ==．【点睛】本题考查作图-旋转变换，平移变换，扇形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21．（1）求证：见解析；（2）四边形ABEF 是菱形，见解析.【解析】【分析】(1)先利用平行四边形的性质得AD ∥BC ，则∠AFB ＝∠CBF ，然后根据“AAS”可判断△AOF ≌△BOE ；(2)利用△AOF ≌△BOE 得到FO ＝BO ，则可根据对角线互相平分可判定四边形ABEF 是平行四边形，根据AE 平分∠BAD ，得∠BAE ＝∠FAE ，又∠FAE ＝∠AEB ，得∠BAE ＝∠AEB ，AB ＝BE ，有一组对边相等的平行四边形是菱形，得四边形ABEF 是菱形．【详解】(1)∵O 为AE 中点，∴AO ＝EO ，∵四边形ABCD 为平行四边形，∴AD ∥BC ，∴∠AFB ＝∠CBF ，在△AOF 和△BOE 中AFO EBO AOF EOB AO EO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOF ≌△BOE ；(2)四边形ABEF 是菱形，理由如下：∵△AOF ≌△BOE ，∴FO ＝BO ，而AO ＝EO ，∴四边形ABEF 是平行四边形，∵AE 平分∠BAD ，∴∠BAE ＝∠FAE ，∵∠FAE ＝∠AEB ，∴∠BAE ＝∠AEB ，∴AB ＝BE ，∴四边形ABEF 是菱形．【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质，菱形的判定等，熟练掌握相关的性质与判定定理是解题的关键.22．（1）150°；5（2）32.4cm【解析】【分析】（1）如图，过点B 作BH ⊥CG 于H ，过点D 作CG 的垂线MN 交AF 于M ，交HG 于N ．利用矩形的性质、直角三角形的性质以及等角的余角相等得到∠MAD=30°，根据周角的定义易求箱盖绕点A 转过的角度；通过解直角△BHC 来求BH 的长度；（2）通过解直角△AMD 得到线段MD 的长度，则DN=65-EF-DM ，利用解直角△DCN 来求CD 的长度，即EF 的长度即可．【详解】（1）如图，过点B 作BH ⊥CG 于H ，过点D 作CG 的垂线MN 交AF 于M ，交HG 于N ．∵∠DCG=60°，∴∠CDN=30°．又∵四边形ABCD 是矩形，∴∠ADC=∠B CD=90°，∴∠MAD=∠CDN=30°（同角的余角相等），∴箱盖绕点A 转过的角度为：360°-90°-30°-90°=150°．在直角△BCH 中，∠BCH=30°，BC=10cm ，则BH=12BC=5cm ．故答案是：150°；5；（2）在直角△AMD 中，AD=BC=10cm ，∠MAD=30°，则MD=AD•sin30°=12×10=5（cm ）． ∵∠CDN=30°，∴cos ∠CDN=cos30°=655DN EF DC EF --=，即655EF EF --= 解得EF=32.4．即箱子的宽EF 是32.4cm ．【点睛】本题考查了解直角三角形的应用．主要是余弦概念及运算，关键把实际问题转化为数学问题加以计算．23．乙楼的高度DC 约为31m ，甲乙两楼之间的距离AC 约为37m.【解析】【分析】过点B 作BE CD ⊥，垂足为点E ，从而判定四边形ABEC 是矩形，得到AB CE =，AC BE =设甲乙两楼之间的距离为x m,在直角三角形BDE 与直角三角形DAC 中，利用三角函数即可用x 表示出DE 与DC ，根据DC DE CE -=，列出方程解之即可．【详解】解：过点B 作BE CD ⊥，垂足为点E ，可知BAC ACE BEC 90∠∠∠===︒.∴四边形ACEB 是矩形.∴AB CE =，AC BE =.设甲乙两楼之间的距离为x m.则BE AC x ==，在Rt DBE 中，DBE 19∠=︒，DE tan DBE BE∠=. ∴DE BE tan DBE x tan19∠=⋅=⋅︒. 在Rt DAC 中，DAC 40∠=︒，DC tan DAC AC∠=. ∴DC AC tan DAC x tan DAC x tan40∠∠=⋅=⋅=⋅︒. ∵DC DE CE -=，∴x tan40x tan1918.6⋅︒-⋅︒=.∴0.84x 0.34x 18.6-≈.解得x 37.2≈.∴AC 37≈.DE x tan4037.2.8431=⋅︒≈⨯≈.答：乙楼的高度DC 约为31m ，甲乙两楼之间的距离AC 约为37m.【点睛】本题考查了解直角三角形的应用，解题的关键是从复杂的实际问题中整理出直角三角形并选择合适的边角关系列出方程．24．6【解析】【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a 与b 的值代入计算即可求出值．【详解】解：原式=()()a b b a b a b +-+-•()2(a b)a a b --=1a b +，当，．【点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．25．5【解析】【分析】原式利用算术平方根定义，负整数指数幂法则，以及绝对值的代数意义计算即可求出值．【详解】原式＝4+3﹣2＝5．【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．。