fluent中多孔介质设置问题和算例
fluent多孔介质孔隙率

fluent多孔介质孔隙率FLUENT多孔介质是一个非常有用的数值模拟工具,因为它可以模拟各种多孔介质的过程。
其中,孔隙率是一个非常重要的参数,因为它可以影响多孔介质的物理和化学性质以及与周围环境的相互作用。
在本文中,我们将探讨FLUENT多孔介质中的孔隙率参数,帮助您更好地理解与其相关的内容。
步骤1:什么是孔隙率?孔隙率是指一个多孔介质中孔隙的总体积与样品总体积的比值。
可以用以下公式表示:φ = Vp / Vt × 100%其中,φ表示孔隙率,Vp表示孔隙的总体积,Vt表示样品的总体积。
步骤2:FLUENT多孔介质中的孔隙率参数在FLUENT中,我们可以使用两种方式来设置孔隙率参数:松散介质模型和实体多孔介质模型。
松散介质模型是一种将多孔介质视为连续介质的模型,其中孔隙率可以通过设置固体和流体的体积分数来确定。
在这种模型中,流体和固体的性质可以根据材料库选择或手动输入来确定。
实体多孔介质模型是一种将真实多孔介质视为离散孔隙和固体组成的模型。
在这种模型中,我们可以通过设置多孔介质的几何形状和孔隙率来模拟多孔介质的过程。
如果知道多孔介质的孔隙率,则可以手动输入。
如果不知道孔隙率,则可以使用体积渗透率来计算它。
步骤3:FLUENT多孔介质模拟中的应用FLUENT多孔介质模拟可以应用于许多领域,如环境保护,油藏开发,地下水资源管理等。
例如,在地下水资源管理中,孔隙率是一个非常重要的参数,因为它可以反映地下水含量和通透性。
使用FLUENT 多孔介质模拟可以确定地下水流量和渗透性,从而更好地管理我们的水资源。
类似的,FLUENT多孔介质也可以在油藏开发中估计原油储藏量和溢油模拟中模拟油污运移等。
总结FLUENT多孔介质模拟是一种非常强大的工具,可以帮助我们更好地理解多孔介质的物理和化学性质,以及与周围环境的相互作用。
孔隙率作为这个模拟过程中的一个重要参数,可以影响多孔介质的特性和FLUENT多孔介质模拟的精度。
fluent中多孔介质模型的设置

fluent中多孔介质模型的设置7.19.6 User Inputs for Porous MediaWhen you are modeling a porous region, the only additional inputs for the problem setup are as follows. Optional inputs are indicated as such.1. Define the porous zone.2. Define the porous velocity formulation. (optional)3. Identify the fluid material flowing through the porous medium.4. Enable reactions for the porous zone, if appropriate, and select the reaction mechanism.5. Enable the Relative Velocity Resistance Formulation. By default, this option is already enabled and takes the moving porous media into consideration (as described in Section 7.19.6).6. Set the viscous resistance coefficients ( in Equation7.19-1,or in Equation 7.19-2) and the inertial resistance coefficients ( in Equation 7.19-1, or in Equation 7.19-2), and define the direction vectors for which they apply. Alternatively, specify the coefficients for the power-law model.7. Specify the porosity of the porous medium.8. Select the material contained in the porous medium (required only for models that include heat transfer). Note that the specific heat capacity, , for the selected material in the porous zone can only be entered as a constant value.9. Set the volumetric heat generation rate in the solid portion of the porous medium (or any other sources, such as mass or momentum). (optional) 10. Set any fixed values for solution variables in the fluid region (optional).11. Suppress the turbulent viscosity in the porous region, if appropriate.12. Specify the rotation axis and/or zone motion, if relevant.Methods for determining the resistance coefficients and/or permeability are presented below. If you choose to use the power-law approximation of the porous-media momentum source term, you will enter thecoefficients and in Equation 7.19-3 instead of the resistance coefficients and flow direction.You will set all parameters for the porous medium inthe Fluid panel (Figure 7.19.1), which is opened from the Boundary Conditions panel (as described in Section 7.1.4).Figure 7.19.1: The Fluid Panel for a Porous Zone Defining the Porous ZoneAs mentioned in Section 7.1, a porous zone is modeled as a special type of fluid zone. To indicate that the fluid zone is a porous region, enablethe Porous Zone option in the Fluid panel. The panel will expand to show the porous media inputs (as shown in Figure7.19.1).Defining the Porous Velocity FormulationThe Solver panel contains a Porous Formulation region where you can instruct FLUENT to use either a superficial or physical velocity in the porous medium simulation. By default, the velocity is set to SuperficialVelocity. For details about using the Physical Velocity formulation, see Section 7.19.7.Defining the Fluid Passing Through the Porous MediumTo define the fluid that passes through the porous medium, select the appropriate fluid in the Material Name drop-down list in the Fluid panel. If you want to check or modify the properties of the selected material, you can click Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel.If you are modeling species transport or multiphase flow,the Material Name list will not appear in the Fluid panel. Forspecies calculations, the mixture material for all fluid/porous zones will be the material you specified in the SpeciesModel panel. For multiphase flows, the materials are specified when you define the phases, as described in Section 23.10.3. Enabling Reactions in a Porous ZoneIf you are modeling species transport with reactions, you can enable reactions in a porous zone by turning on the Reaction option inthe Fluid panel and selecting a mechanism in the ReactionMechanism drop-down list.If your mechanism contains wall surface reactions, you will also need to specify a value for the Surface-to-Volume Ratio. Thisvalue is the surface area of the pore walls per unit volume ( ), and can be thought of as a measure of catalyst loading. With this value, FLUENT can calculate the total surface area on which the reaction takes place in each cell bymultiplying by the volume of the cell. See Section 14.1.4 for detailsabout defining reaction mechanisms. See Section 14.2for details about wall surface reactions.Including the Relative Velocity Resistance FormulationPrior to FLUENT 6.3, cases with moving reference frames used the absolute velocities in the source calculations for inertial and viscous resistance. This approach has been enhanced so that relative velocities are used for the porous source calculations (Section 7.19.2). Using the Relative Velocity Resistance Formulation option (turned on by default) allows you to better predict the source terms for cases involving moving meshes or moving reference frames (MRF). This option works well in cases withnon-moving and moving porous media. Note that FLUENT will use the appropriate velocities (relative or absolute), depending on your case setup. Defining the Viscous and Inertial Resistance CoefficientsThe viscous and inertial resistance coefficients are both defined in the same manner. The basic approach for defining the coefficients using a Cartesian coordinate system is to define one direction vector in 2D or two direction vectors in 3D, and then specify the viscous and/or inertial resistance coefficients in each direction. In 2D, the second direction, which is not explicitly defined, is normal to the plane defined by the specified direction vector and the direction vector. In 3D, the third direction is normal to the plane defined by the two specified direction vectors. For a 3D problem, the second direction must be normal to the first. If you fail to specify two normal directions, the solver will ensure that they are normal by ignoring any component of the second direction that is in the first direction. You should therefore be certain that the first direction is correctly specified. You can also define the viscous and/or inertial resistance coefficients in each direction using a user-defined function (UDF). The user-defined options become available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the coefficients defined in the UDF must utilize the DEFINE_PROFILE macro. For moreinformation on creating and using user-defined function, see the separate UDF Manual.If you are modeling axisymmetric swirling flows, you can specify an additional direction component for the viscous and/or inertial resistance coefficients. This direction component is always tangential to the other two specified directions. This option is available for both density-based and pressure-based solvers.In 3D, it is also possible to define the coefficients using a conical (or cylindrical) coordinate system, as described below.Note that the viscous and inertial resistance coefficients aregenerally based on the superficial velocity of the fluid in the porous media.The procedure for defining resistance coefficients is as follows:1. Define the direction vectors.To use a Cartesian coordinate system, simply specify the Direction-1 Vector and, for 3D, the Direction-2 Vector. The unspecifieddirection will be determined as described above. These directionvectors correspond to the principle axes of the porous media.For some problems in which the principal axes of the porous mediumare not aligned with the coordinate axes of the domain, you may notknow a priori the direction vectors of the porous medium. In suchcases, the plane tool in 3D (or the line tool in 2D) can help you todetermine these direction vectors.(a) "Snap'' the plane tool (or the line tool) onto the boundary of theporous region. (Follow the instructions inSection 27.6.1 or 27.5.1 for initializing the tool to a position on anexisting surface.)(b) Rotate the axes of the tool appropriately until they are alignedwith the porous medium.(c) Once the axes are aligned, click on the Update From PlaneTool or Update From Line Tool button inthe Fluid panel. FLUENT will automatically set the Direction-1Vector to the direction of the red arrow of the tool, and (in 3D)the Direction-2 Vector to the direction of the green arrow.To use a conical coordinate system (e.g., for an annular, conical filter element), follow the steps below. This option is available only in 3D cases.(a) Turn on the Conical option.(b) Specify the Cone Axis Vector and Point on Cone Axis. Thecone axis is specified as being in the direction of the Cone AxisVector (unit vector), and passing through the Point on Cone Axis.The cone axis may or may not pass through the origin of thecoordinate system.(c) Set the Cone Half Angle (the angle between the cone's axis andits surface, shown in Figure 7.19.2). To use a cylindrical coordinate system, set the Cone Half Angle to 0.Figure 7.19.2: Cone Half AngleFor some problems in which the axis of the conical filter element is not aligned with the coordinate axes of the domain, you may notknow a priori the direction vector of the cone axis and coordinates ofa point on the cone axis. In such cases, the plane tool can help you todetermine the cone axis vector and point coordinates. One method is as follows:(a) Select a boundary zone of the conical filter element that isnormal to the cone axis vector in the drop-down list next to the Snap to Zone button.(b) Click on the Snap to Zone button. FLUENT will automatically"snap'' the plane tool onto the boundary. It will also set the Cone Axis Vector and the Point on Cone Axis. (Note that you will still have to set the Cone Half Angle yourself.)An alternate method is as follows:(a) "Snap'' the plane tool onto the boundary of the porous region.(Follow the instructions in Section 27.6.1 for initializing the tool to a position on an existing surface.)(b) Rotate and translate the axes of the tool appropriately until thered arrow of the tool is pointing in the direction of the cone axisvector and the origin of the tool is on the cone axis.(c) Once the axes and origin of the tool are aligned, click onthe Update From Plane Tool button inthe Fluid panel. FLUENT will automatically set the Cone AxisVector and the Point on Cone Axis. (Note that you will still have toset the Cone Half Angle yourself.)2. Under Viscous Resistance, specify the viscous resistancecoefficient in each direction.Under Inertial Resistance, specify the inertial resistance coefficient in each direction. (You will need to scroll down with the scroll bar to view these inputs.)For porous media cases containing highly anisotropic inertial resistances, enable Alternative Formulation under Inertial Resistance.The Alternative Formulation option provides better stability to the calculation when your porous medium is anisotropic. The pressure loss through the medium depends on the magnitude of the velocity vector ofthe i th component in the medium. Using the formulation ofEquation 7.19-6 yields the expression below:(7.19-10) Whether or not you use the Alternative Formulation option depends on how well you can fit your experimentally determined pressure drop data to the FLUENT model. For example, if the flow through the medium is aligned with the grid in your FLUENT model, then it will not make a difference whether or not you use the formulation.For more infomation about simulations involving highly anisotropic porous media, see Section 7.19.8.Note that the alternative formulation is compatible only with the pressure-based solver.If you are using the Conical specification method, Direction-1 is the cone axis direction, Direction-2 is the normal to the cone surface (radial ( )direction for a cylinder), and Direction-3 is the circumferential ( ) direction.In 3D there are three possible categories of coefficients, and in 2D there are two:In the isotropic case, the resistance coefficients in all directions are the same (e.g., a sponge). For an isotropic case, you must explicitlyset the resistance coefficients in each direction to the same value.When (in 3D) the coefficients in two directions are the same and those in the third direction are different or (in 2D) the coefficients inthe two directions are different, you must be careful to specify thecoefficients properly for each direction. For example, if you had aporous region consisting of cylindrical straws with small holes inthem positioned parallel to the flow direction, the flow would passeasily through the straws, but the flow in the other two directions(through the small holes) would be very little. If you had a plane offlat plates perpendicular to the flow direction, the flow would notpass through them at all; it would instead move in the other twodirections.In 3D the third possible case is one in which all three coefficients are different. For example, if the porous region consisted of a plane ofirregularly-spaced objects (e.g., pins), the movement of flow between the blockages would be different in each direction. You wouldtherefore need to specify different coefficients in each direction. Methods for deriving viscous and inertial loss coefficients are described in the sections that follow.Deriving Porous Media Inputs Based on Superficial Velocity, Using a Known Pressure LossWhen you use the porous media model, you must keep in mind that the porous cells in FLUENT are 100% open, and that the values that you specify for and/or must be based on this assumption. Suppose, however, that you know how the pressure drop varies with the velocity through the actual device, which is only partially open to flow. The following exercise is designed to show you how to compute a valuefor which is appropriate for the FLUENT model.Consider a perforated plate which has 25% area open to flow. The pressure drop through the plate is known to be 0.5 times the dynamic head in the plate. The loss factor, , defined as(7.19-11)is therefore 0.5, based on the actual fluid velocity in the plate, i.e., the velocity through the 25% open area. To compute an appropriate valuefor , note that in the FLUENT model:1. The velocity through the perforated plate assumes that the plate is 100% open.2. The loss coefficient must be converted into dynamic head loss per unit length of the porous region.Noting item 1, the first step is to compute an adjusted loss factor, , which would be based on the velocity of a 100% open area:(7.19-12) or, noting that for the same flow rate, ,(7.19-13)The adjusted loss factor has a value of 8. Noting item 2, you must now convert this into a loss coefficient per unit thickness of the perforated plate. Assume that the plate has a thickness of 1.0 mm (10 m). The inertial loss factor would then be(7.19-14)Note that, for anisotropic media, this information must be computed for each of the 2 (or 3) coordinate directions.Using the Ergun Equation to Derive Porous Media Inputs for a Packed BedAs a second example, consider the modeling of a packed bed. In turbulent flows, packed beds are modeled using both a permeability and an inertial loss coefficient. One technique for deriving the appropriate constants involves the use of the Ergun equation [ 98], a semi-empirical correlation applicable over a wide range of Reynolds numbers and for many types of packing:(7.19-15)When modeling laminar flow through a packed bed, the second term in the above equation may be dropped, resulting in the Blake-Kozenyequation [ 98]:(7.19-16) In these equations, is the viscosity, is the mean particlediameter, is the bed depth, and is the void fraction, defined as the volume of voids divided by the volume of the packed bed region. Comparing Equations 7.19-4 and 7.19-6 with 7.19-15, the permeability and inertial loss coefficient in each component direction may be identified as(7.19-17) and(7.19-18) Using an Empirical Equation to Derive Porous Media Inputs for Turbulent Flow Through a Perforated PlateAs a third example we will take the equation of Van Winkle et al. [ 279, 339] and show how porous media inputs can be calculated for pressure loss through a perforated plate with square-edged holes.The expression, which is claimed by the authors to apply for turbulent flow through square-edged holes on an equilateral triangular spacing, is(7.19-19) where= mass flow rate through the plate= the free area or total area of the holes= the area of the plate (solid and holes)= a coefficient that has been tabulated for various Reynolds-numberrangesand for various= the ratio of hole diameter to plate thicknessfor and for the coefficient takes a value of approximately 0.98, where the Reynolds number is based on hole diameter and velocity in the holes.Rearranging Equation 7.19-19, making use of the relationship(7.19-20)and dividing by the plate thickness, , we obtain(7.19-21)where is the superficial velocity (not the velocity in the holes). Comparing with Equation 7.19-6 it is seen that, for the direction normal to the plate, the constant can be calculated from(7.19-22)Using Tabulated Data to Derive Porous Media Inputs for Laminar Flow Through a Fibrous MatConsider the problem of laminar flow through a mat or filter pad which is made up of randomly-oriented fibers of glass wool. As an alternative to the Blake-Kozeny equation (Equation 7.19-16) we might choose to employ tabulated experimental data. Such data is available for many types offiber [ 158].fraction of dimensionless permeability of glass woolwhere and is the fiber diameter. , for use inEquation 7.19-4, is easily computed for a given fiber diameter and volume fraction.Deriving the Porous Coefficients Based on Experimental Pressure and Velocity DataExperimental data that is available in the form of pressure drop against velocity through the porous component, can be extrapolated to determine the coefficients for the porous media. To effect a pressure drop across a porous medium of thickness, , the coefficients of the porous media are determined in the manner described below.If the experimental data is:then an curve can be plotted to create a trendline through these points yielding the following equationwhere is the pressure drop and is the velocity.Note that a simplified version of the momentum equation, relating the pressure drop to the source term, can be expressed as (7.19-24)or(7.19-25)Hence, comparing Equation 7.19-23 to Equation 7.19-2, yields the following curve coefficients:(7.19-26)with kg/m , and a porous media thickness, , assumed to be 1m in this example, the inertial resistance factor, .Likewise,with , the viscous inertial resistancefactor,. Note that this same technique can be applied to the porous jump boundary condition. Similar to the case of the porous media, you have to take into account the thickness of the medium . Yourexperimental data can be plotted in ancurve, yielding an equation that is equivalent to Equation 7.22-1. From there, you can determine the permeability and the pressure jumpcoefficient .Using the Power-Law ModelIf you choose to use the power-law approximation of the porous-media momentum source term (Equation 7.19-3), the only inputs required are the coefficients and . Under Power Law Model in the Fluid panel, enter the values for C0 and C1. Note that the power-law model can be used in conjunction with the Darcy and inertia models.C0 must be in SI units, consistent with the value of C1.Defining PorosityTo define the porosity, scroll down below the resistance inputs inthe Fluid panel, and set the Porosity under Fluid Porosity .You can also define the porosity using a user-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the porosity defined in the UDF must utilize the DEFINE_PROFILE macro. For more information on creating and using user-defined function, see the separate UDF Manual.The porosity, , is the volume fraction of fluid within the porous region (i.e., the open volume fraction of the medium). The porosity is used in the prediction of heat transfer in the medium, as described in Section 7.19.3, and in the time-derivative term in the scalar transport equations for unsteady flow, as described in Section 7.19.5. It also impacts the calculation of reaction source terms and body forces in the medium. These sources will be proportional to the fluid volume in the medium. If you want to represent the medium as completely open (no effect of the solid medium), you should set the porosity equal to 1.0 (the default). When the porosity is equal to 1.0, the solid portion of the medium will have no impact on heat transfer or thermal/reaction source terms in the medium.Defining the Porous MaterialIf you choose to model heat transfer in the porous medium, you must specify the material contained in the porous medium.To define the material contained in the porous medium, scroll down below the resistance inputs in the Fluid panel, and select the appropriate solid in the Solid Material Name drop-down list under Fluid Porosity. If you want to check or modify the properties of the selected material, you canclick Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel. In the Material panel, you can define thenon-isotropic thermal conductivity of the porous material using auser-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the non-isotropic thermal conductivity defined in the UDF must utilize the DEFINE_PROPERTY macro. For more information on creating and using user-defined function, see the separate UDF Manual.Defining SourcesIf you want to include effects of the heat generated by the porous medium in the energy equation, enable the Source Terms option and set anon-zero Energy source. The solver will compute the heat generated by the porous region by multiplying this value by the total volume of the cells comprising the porous zone. You may also define sources of mass, momentum, turbulence, species, or other scalar quantities, as described in Section 7.28.Defining Fixed ValuesIf you want to fix the value of one or more variables in the fluid region of the zone, rather than computing them during the calculation, you can do so by enabling the Fixed Values option. See Section 7.27 for details. Suppressing the Turbulent Viscosity in the Porous RegionAs discussed in Section 7.19.4, turbulence will be computed in the porous region just as in the bulk fluid flow. If you are using one of the turbulence models (with the exception of the Large Eddy Simulation (LES) Model), and you want the turbulence generation to be zero in the porous zone, turn on the Laminar Zone option in the Fluid panel. Refer to Section 7.17.1 for more information about suppressing turbulence generation.Specifying the Rotation Axis and Defining Zone MotionInputs for the rotation axis and zone motion are the same as for a standard fluid zone. See Section 7.17.1 for details.。
ANSYS Fluent多孔介质

ANSYS Fluent多孔介质模型简介
多孔介质是指内部含有众多空隙的固体材料,如土壤、煤炭、木材、过滤器、催化床等。
若采用详细的模型结构及网格划分处理,则会因为过多的网格数目而使计算量非常大,不能满足工程上的实际需求,而多孔介质模型实质上是将多孔介质区域结合了以经验假设为主的流动阻力,即动量源项。
图1、多孔介质模型的应用
ANSYS Fluent中可将所需区域设定为多孔介质模型(见图2),在cell zone conditions中勾选porous zone(通常认为在多孔介质模型内由于阻力原因,流动状况为层流,故而同时勾选laminar zone)。
在其界面中,可设置方向、粘性阻力系数、惯性阻力系数以及孔隙率等参数。
其中粘性阻力系数及惯性阻力系数可通过多种方式确定其具体数值,如试验法(风速及压降的曲线拟合)、Ergun方程法、经验方程法等等。
图2、ANSYS Fluent中多孔介质模型的设置界面通过一个简单的仿真案例进行描述:一个用于汽车尾气净化的催化剂装置,其中类似蜂窝结构的区域可认为是多孔区域模型(见图3)。
在ANSYS Fluent中设置求解器、材料、多孔区域、边界条件等,初始化后进行仿真计算(多孔介质问题的初始化应采用standard initialization,见图4)。
结构后处理中可得到结构内部的速度场、压力场结果(见图5)
图3、汽车尾气净化器流动仿真
图4、ANSYS Fluent初始化界面
图5、不同截面的速度场云图、压力场云图及压力曲线。
fluent多孔介质简单操作
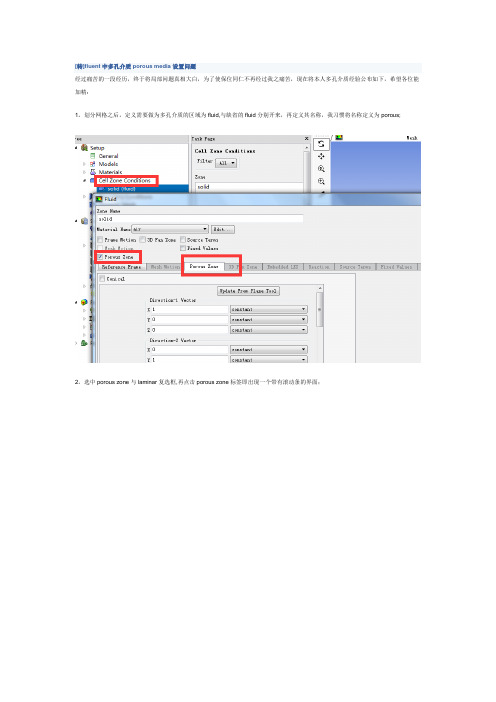
[转]fluent中多孔介质porous media设置问题
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:
1。
划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid分别开来,再定义其名称,我习惯将名称定义为porous;
2。
选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;
3。
porous zone设置方法:
1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;
三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;
(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)
圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:请参看本人上一篇博文“终于搞清fluent中多孔粘性阻力与内部阻力的计算方法”,此处不赘述;
3)如果了定义粘性阻力1/a与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;
4)定义孔隙率porousity,默认值1表示全开放,此值按实验测值填写即可。
完了,其他设置与普通k-e或RSM相同。
总结一下,与君共享!。
Fluent多孔介质设置

1。
Gambit中划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid 分别开来,再定义其名称,我习惯将名称定义为porous;2。
在fluent中定义边界条件define-boundary condition-porous(刚定义的名称),将其设置边界条件为fluid,点击set按钮即弹出与fluid边界条件一样的对话框,选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;3。
porous zone设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:下面是一个例子:通过实验测得速度和压降进行计算:假设实验所得速度和压降的数值如下:通过多孔介质的为空气,密度为1.225kg/m 3粘度为51.789410µ−=× 。
由上面速度与压降的关系可以绘出一个二次由线。
方程如下:20.28296 4.33539p v v ∇=−简化的动量方程所得二次由线与方程相比较,对应的系数相等,可得210.282962i c v v ρ=4.33539n µα∆=− 设厚度为1m,可以解出20.4621242282c α==−依据些方法计算自己所模拟的模型的粘性阻力和惯性阻力。
3)如果了定义粘性阻力1/a 与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity ,默认值1表示全开放,此值按实验测值填写即可。
多孔介质系数计算方法(含模型文件和Excel表格下载)

多孔介质系数的计算方法1.STAR-CCM+中的多孔介质系数(文中所述的Excel文档以及模型源文件均可通过文中图片获取下载地址)在STAR-CCM+中主要需要设置多孔惯性阻力、多孔粘性阻力、孔隙率等参数。
孔隙率为流体在多孔介质中所占的分数,由标量分布法指定,取值介于0-1之间。
通过多孔介质的流量可根据达西定律描述,它基于渗透力度量以使流速与压力梯度相关联。
单相流体压降Δp(压力梯度)指定如下:Δp=−ρ(α|v n|+β)v n式中v n为表面法向速度,官方文档里写的α和β分被为多孔惯性阻力和多孔粘性阻力,但通过量纲分析,在软件参数输入区域α∙ρ为多孔惯性阻力[kg/m4],β∙ρ为多孔粘性阻力[kg/m3·s],ρ为交界面处流体密度。
在软件中,多孔介质需要设定单独的区域,并在类型属性中设定为多孔区域,多孔区域与流体区域通过内部交界面传递数据。
展开多孔区域的物理值菜单,需要输入多孔惯性阻力和多孔粘性阻力,分别表示单位长度的惯性量和粘性量值。
下图以正交各项异性参数为例展示需要输入参数的位置。
多孔惯性阻力和多孔粘性阻力的值通过试验数据的拟合求得,以散热器为例,对散热器芯体进行单体性能试验,得到所通过的气体(密度为1.18415kg/m3)流量和总压降的关系,转化为速度和总压降的关系如下所示。
在Excel中对数据进行拟合,将总压力转换为压力梯度,通过计算可得多孔惯性阻力和多孔粘性阻力。
得到的多孔惯性阻力和多孔粘性阻力是沿流动方向的阻力系数,另外两个方向通常取为比主流方向阻力系数大2-3个数量级的值,以阻止流体在这两个方向上的流动,但取值过大可能会影响收敛性。
下图为计算的Excel文件,填入试验数据即可得两个阻力系数。
下载本文档,将扩展名docx改为rar,得到一个压缩包文件,双击打开,再依次打开word、media文件夹。
然后将media文件夹下的image4.jpg拖拽至桌面或某个文件夹,将其扩展名jpg改为rar,解压缩可得一个包含模型和Excel文件下载地址的txt文本文档download.txt。
Fluent计算多孔介质模型资料

广东省深圳市宝安区沙井辛养社区西部工业园 TEL:+86-755-3366-8888 FAX:+86-755-3366-0612Fluent计算多孔介质模型资料这是一个多孔介质例子,进口速度为0.01m/s,组份为液态水和氧气,其中氧气从多孔介质porous jump 渗透过去,如何看氧气在tissue中扩散的。
porous jump的face permeability1 a=e-8 m_2thickness 设为0.0001pressure jump coefficient为默认porous zone设置如下:direction vector 1, 1,viscous resistance 100 eachinertial resistance 100 eachporosity 0.1边界条件设置如下:Ab – wall - defaultBc – wall – defaultBe – porous jump – face permeability 1e-8, porous medium thickness0.0001Cd – outflow rating – 0.5De – wall – defaultDefault interior – interiorDefault interior001 – interiorDefault interior019 – interiorEf – wall - defaultFg – outflow rating – 1Fluid - porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Gh- wall - defaultHi – wall - defaultHk - porous jump same conditions as otherIj – outflow – 0.5Jk – wall – defaultKl – wall – defaultLa – velocity inlet – 0.01 m/s, temperature 300K, 0.5 mass fraction O2 Lfluid – porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Pipefluid – fluid – default (no porous zone)Models – species transport – water and oxygen mixtureVariations – different boundary conditions at top and bottom (outflow, wall ect)注意,其中porous zone在gambit中设置为fluid,在fluent中设置为porous zone边界条件设置如下:Ab – wall - defaultBc – wall – defaultBe – porous jump – face permeability 1e-8, porous medium thickness0.0001Cd – outflow rating – 0.5De – wall – defaultDefault interior – interiorDefault interior001 – interiorDefault interior019 – interiorEf – wall - defaultFg – outflow rating – 1Fluid - porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Gh- wall - defaultHi – wall - defaultHk - porous jump same conditions as otherIj – outflow – 0.5Jk – wall – defaultKl – wall – defaultLa – velocity inlet – 0.01 m/s, temperature 300K, 0.5 mass fraction O2 Lfluid – porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Pipefluid – fluid – default (no porous zone)Models – species transport – water and oxygen mixtureVariations – different boundary conditions at top and bottom (outflow, wall ect) 注意,其中porous zone在gambit中设置为fluid,在fluent中设置为porous zone。
FLUENT多孔介质数值模拟设置

FLUENT多孔介质数值模拟设置多孔介质条件多孔介质模型可以应用于很多问题,如通过充满介质的流动、通过过滤纸、穿孔圆盘、流量分配器以及管道堆的流动。
当你使用这一模型时,你就定义了一个具有多孔介质的单元区域,而且流动的压力损失由多孔介质的动量方程中所输入的内容来决定。
通过介质的热传导问题也可以得到描述,它服从介质和流体流动之间的热平衡假设,具体内容可以参考多孔介质中能量方程的处理一节。
多孔介质的一维化简模型,被称为多孔跳跃,可用于模拟具有已知速度/压降特征的薄膜。
多孔跳跃模型应用于表面区域而不是单元区域,并且在尽可能的情况下被使用(而不是完全的多孔介质模型),这是因为它具有更好的鲁棒性,并具有更好的收敛性。
详细内容请参阅多孔跳跃边界条件。
多孔介质模型的限制如下面各节所述,多孔介质模型结合模型区域所具有的阻力的经验公式被定义为“多孔”。
事实上多孔介质不过是在动量方程中具有了附加的动量损失而已。
因此,下面模型的限制就可以很容易的理解了。
流体通过介质时不会加速,因为事实上出现的体积的阻塞并没有在模型中出现。
这对于过渡流是有很大的影响的,因为它意味着FLUENT不会正确的描述通过介质的过渡时间。
多孔介质对于湍流的影响只是近似的。
详细内容可以参阅湍流多孔介质的处理一节。
多孔介质的动量方程多孔介质的动量方程具有附加的动量源项。
源项由两部分组成,一部分是粘性损失项 (Darcy),另一个是内部损失项:其中S_i是i向(x, y, or z)动量源项,D和C是规定的矩阵。
在多孔介质单元中,动量损失对于压力梯度有贡献,压降和流体速度(或速度方阵)成比例。
对于简单的均匀多孔介质:其中a是渗透性,C_2时内部阻力因子,简单的指定D和C分别为对角阵1/a 和C_2其它项为零。
FLUENT还允许模拟的源项为速度的幂率:其中C_0和C_1为自定义经验系数。
注意:在幂律模型中,压降是各向同性的,C_0的单位为国际标准单位。
多孔介质的Darcy定律通过多孔介质的层流流动中,压降和速度成比例,常数C_2可以考虑为零。
fluent多孔介质简单操作

[转]fluent中多孔介质porous media设置问题经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:1。
Gambit中划分网格之后,定义需要做为多孔介质的区域为f luid,与缺省的f luid分别开来,再定义其名称,我习惯将名称定义为porous;2。
在f luent中定义边界条件def ine-boundary condition-porous(刚定义的名称),将其设置边界条件为f luid,点击set按钮即弹出与f luid 边界条件一样的对话框,选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;3。
porous zone设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考f luent帮助。
2)定义粘性阻力1/a与内部阻力C2:请参看本人上一篇博文“终于搞清fluent中多孔粘性阻力与内部阻力的计算方法”,此处不赘述;3)如果了定义粘性阻力1/a与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity,默认值1表示全开放,此值按实验测值填写即可。
完了,其他设置与普通k-e或RSM相同。
总结一下,与君共享!。
fluent多孔跳跃模型参数设置

fluent多孔跳跃模型参数设置
【最新版】
目录
1.Fluent 软件简介
2.多孔跳跃模型的定义与设置
3.多孔介质模型的参数设置
4.具体设置步骤
5.模型应用案例
正文
一、Fluent 软件简介
Fluent 是一款国际上流行的商用计算流体动力学(CFD)软件包,广泛应用于航空航天、汽车设计、石油天然气和涡轮机设计等领域。
它具有丰富的物理模型、先进的数值方法和强大的前后处理功能,在美国的市场占有率达到 60%。
二、多孔跳跃模型的定义与设置
多孔跳跃模型是一种描述流体在多孔介质中流动的现象的模型。
在Fluent 中,并不直接支持设置多孔系数,而是通过设置多孔介质模型的相关参数来实现多孔跳跃模型的模拟。
三、多孔介质模型的参数设置
在 Fluent 中设置多孔介质模型,需要定义多孔介质包含的材料属性和多孔性,设定多孔区域的固体部分的体积热生成速度,可选择性地限制多孔区域的湍流粘性,以及指定旋转轴和/或区域运动等。
四、具体设置步骤
1.定义多孔介质包含的材料属性和多孔性。
2.设定多孔区域的固体部分的体积热生成速度(或任何其它源项,如质量、动量)。
3.如果合适的话,限制多孔区域的湍流粘性。
4.如果相关的话,指定旋转轴和/或区域运动。
五、模型应用案例
Fluent 中的多孔跳跃模型在许多实际应用中都有广泛的应用,例如在航空航天、汽车设计、石油天然气和涡轮机设计等领域。
FLUENT多孔介质数值模拟设置

FLUENT多孔介质数值模拟设置多孔介质条件多孔介质模型可以应用于很多问题,如通过充满介质的流动、通过过滤纸、穿孔圆盘、流量分配器以及管道堆的流动。
当你使用这一模型时,你就定义了一个具有多孔介质的单元区域,而且流动的压力损失由多孔介质的动量方程中所输入的内容来决定。
通过介质的热传导问题也可以得到描述,它服从介质和流体流动之间的热平衡假设,具体内容可以参考多孔介质中能量方程的处理一节。
多孔介质的一维化简模型,被称为多孔跳跃,可用于模拟具有已知速度/压降特征的薄膜。
多孔跳跃模型应用于表面区域而不是单元区域,并且在尽可能的情况下被使用(而不是完全的多孔介质模型),这是因为它具有更好的鲁棒性,并具有更好的收敛性。
详细内容请参阅多孔跳跃边界条件。
多孔介质模型的限制如下面各节所述,多孔介质模型结合模型区域所具有的阻力的经验公式被定义为“多孔”。
事实上多孔介质不过是在动量方程中具有了附加的动量损失而已。
因此,下面模型的限制就可以很容易的理解了。
流体通过介质时不会加速,因为事实上出现的体积的阻塞并没有在模型中出现。
这对于过渡流是有很大的影响的,因为它意味着FLUENT不会正确的描述通过介质的过渡时间。
多孔介质对于湍流的影响只是近似的。
详细内容可以参阅湍流多孔介质的处理一节。
多孔介质的动量方程多孔介质的动量方程具有附加的动量源项。
源项由两部分组成,一部分是粘性损失项 (Darcy),另一个是内部损失项:其中S_i是i向(x, y, or z)动量源项,D和C是规定的矩阵。
在多孔介质单元中,动量损失对于压力梯度有贡献,压降和流体速度(或速度方阵)成比例。
对于简单的均匀多孔介质:其中a是渗透性,C_2时内部阻力因子,简单的指定D和C分别为对角阵1/a 和C_2其它项为零。
FLUENT还允许模拟的源项为速度的幂率:其中C_0和C_1为自定义经验系数。
注意:在幂律模型中,压降是各向同性的,C_0的单位为国际标准单位。
多孔介质的Darcy定律通过多孔介质的层流流动中,压降和速度成比例,常数C_2可以考虑为零。
FLUENT中定义多孔介质的方法

FLUENT中定义多孔介质的方法多孔介质计算中需要输入的项目如下:(1)定义多孔介质区域。
(2)定义多孔介质速度函数形式。
(3)定义流过多孔介质区的流体属性。
(4)设定多孔区的化学反应。
(5)设定粘性阻力系数。
(6)设定多孔介质的多孔率。
(7)在计算热交换的过程中选择多孔介质的材料。
(8)设定多孔介质固体部分的体热生成率。
(9)设定流动区域上的任意固定值的流动参数。
(10)需要的话,将多孔区流动设为层流,或取消湍流计算。
(11)定义旋转轴或区域的运动。
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:1。
Gambit中划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid 分别开来,再定义其名称,我习惯将名称定义为porous;2。
在fluent中定义边界条件define-boundary condition-porous(刚定义的名称),将其设置边界条件为fluid,点击set按钮即弹出与fluid边界条件一样的对话框,选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;3。
porous zone设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:见附fluent中多孔粘性阻力系数与惯性阻力系数的方法:对比Darcy 定律v K J =⋅J 为水力坡度,即流经路径长度为L 的水头损失,m/m ;K 为比例系数,也称渗流系数,m/sg p v Kρ∆=- p μνα∆=- 这样可以得到,g K ρμα=,所以1g K ραμ= 其中: 1α为粘性阻力系数,1/m 2; K 为比例系数,也称渗流系数,m/s ;μ为动力粘度,Pa.s ;ρ为流体密度,kg/m 3;g 为重力加速度,m/s 2;采用20℃饱和水的物性参数:密度为998.2kg/m 3 ,运动粘度1.004×10-3Pa.s ;渗流速度取1.0×10-6m/s ,K 取1.0×10-4m/s ,水力坡度约为0.01m/m ; 10461998.29.89.74101.010100410g K ραμ--⨯===⨯⨯⨯⨯ 3)如果了定义粘性阻力1/a 与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity ,默认值1表示全开放,此值按实验测值填写即可。
fluent中多孔介质设置问题和算例
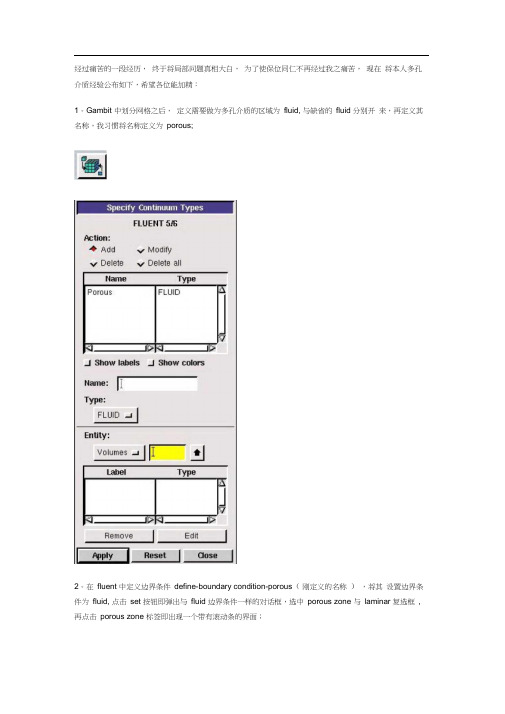
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:1。
Gambit 中划分网格之后,定义需要做为多孔介质的区域为fluid, 与缺省的fluid 分别开来,再定义其名称,我习惯将名称定义为porous;2。
在fluent 中定义边界条件define-boundary condition-porous(刚定义的名称),将其设置边界条件为fluid, 点击set 按钮即弹出与fluid 边界条件一样的对话框,选中porous zone 与laminar 复选框, 再点击porous zone 标签即出现一个带有滚动条的界面;3。
porous zone 设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid 图,看看X,Y,Z 的方向,如果是X 向,矢量为1,0,0, 同理Y 向为0,1,0 ,Z 向为0,0,1, 如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考fluent 帮助。
2)定义粘性阻力1/a 与内部阻力C2:请参看本人上一篇博文“ 终于搞清fluent 中多孔粘性阻力与内部阻力的计算方法”,此处不赘述;3)如果了定义粘性阻力1/a 与内部阻力C2,就不用定义C1 与C0,因为这是两种不同的定义方法,C1与C0 只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity ,默认值1 表示全开放,此值按实验测值填写即可。
完了,其他设置与普通k-e 或RSM相同。
总结一下,与君共享!Tutorial 7. Modeling Flow Through Porous MediaIntroductionMany industrial applications involve the modeling of flow through porous media, such as filters, catalyst beds, and packing. This tutorial illustrates how to set up and solve a problem involving gas flow through porous media.The industrial problem solved here involves gas flow through a catalytic converter. Catalytic converters are commonly used to purify emissions from gasoline and diesel engines by converting environmentally hazardous exhaust emissions to acceptable substances.Examples of such emissions include carbon monoxide (CO), nitrogen oxides (NOx), and unburned hydrocarbon fuels. These exhaust gas emissions are forced through a substrate, which is a ceramic structure coated with a metal catalyst such as platinum or palladium.The nature of the exhaust gas flow is a very important factor in determining the performance of the catalytic converter. Of particular importance is the pressure gradient and velocity distribution through the substrate. Hence CFD analysis is used to design efficient catalytic converters: by modeling the exhaust gas flow, the pressure drop and the uniformity of flow through the substrate can be determined. In this tutorial, FLUENT is used to model the flow of nitrogen gas through a catalytic converter geometry, so that the flow field structure may be analyzed.This tutorial demonstrates how to do the following:_ Set up a porous zone for the substrate with appropriate resistances._ Calculate a solution for gas flow through the catalytic converter using the pressure based solver._ Plot pressure and velocity distribution on specified planes of the geometry._ Determine the pressure drop through the substrate and the degree of non-uniformity of flow through cross sections of the geometry using X-Y plots and numerical reports.Problem DescriptionThe catalytic converter modeled here is shown in Figure 7.1. The nitrogen flows in through the inlet with a uniform velocity of 22.6 m/s, passes through a ceramic monolith substrate with square shaped channels, and then exits through the outlet.While the flow in the inlet and outlet sections is turbulent, the flow through the substrate is laminar and is characterized by inertial and viscous loss coefficients in the flow (X) direction. The substrate is impermeable in other directions, which is modeled using loss coefficients whose values are three orders of magnitude higher than in the X direction.Setup and SolutionStep 1: Grid1. Read the mesh file (catalytic converter.msh).File /Read /Case...2. Check the grid. Grid /CheckFLUENT will perform various checks on the mesh and report the progress in the console. Make sure that the minimum volume reported is a positive number.3. Scale the grid.Grid! Scale...(a) Select mm from the Grid Was Created In drop-down list.(b) Click the Change Length Units button. All dimensions will now be shown in millimeters.(c) Click Scale and close the Scale Grid panel.4. Display the mesh. Display /Grid...(a) Make sure that inlet, outlet, substrate-wall, and wall are selected in the Surfaces selection list.(b) Click Display.(c) Rotate the view and zoom in to get the display shown in Figure 7.2.(d) Close the Grid Display panel.The hex mesh on the geometry contains a total of 34,580 cells.Step 2: Models1. Retain the default solver settings. Define /Models /Solver...2. Select the standard k-ε turbulence model. Define/ Models /Viscous...Step 3: Materials1. Add nitrogen to the list of fluid materials by copying it from the Fluent Database for materials. Define /Materials...(a)Click the Fluent Database... button to open the Fluent Database Materials panel.(a) Select nitrogen from the Material Name drop-down list.(b)Click OK to close the Fluid panel.2. Set the boundary conditions for the substrate (substrate).i. Select nitrogen (n2) from the list of Fluent Fluid Materials.ii. Click Copy to copy the information for nitrogen to your list of fluid materials. iii. Close the Fluent Database Materials panel. (b) Close the Materials panel. Step 4: Boundary Conditions.1. Set the boundary conditions for the fluid (fluid).Define /Boundary Conditions...(a) Select nitrogen from the Material Name drop-down list.(b) Enable the Porous Zone option to activate the porous zone model.(c) Enable the Laminar Zone option to solve the flow in the porous zone without turbulence.(d) Click the Porous Zone tab.i. Make sure that the principal direction vectors are set as shown in Table7.1. Use the scroll bar to access the fields that are not initially visible in the panel.ii. Enter the values in Table 7.2 for the Viscous Resistance and Inertial Resistance. Scroll down to access the fields that are not initially visible in the panel.(e) Click OK to close the Fluid panel.3. Set the velocity and turbulence boundary conditions at the inlet (inlet).(a) Enter 22.6 m/s for the Velocity Magnitude.(b) Select Intensity and Hydraulic Diameter from the Specification Method dropdown list in the Turbulence group box.(c) Retain the default value of 10% for the Turbulent Intensity.(d) Enter 42 mm for the Hydraulic Diameter.(e) Click OK to close the Velocity Inlet panel.4. Set the boundary conditions at the outlet (outlet).(a) Retain the default setting of 0 for Gauge Pressure.(b) Select Intensity and Hydraulic Diameter from the Specification Method dropdown list in the Turbulence group box.(c) Enter 5% for the Backflow Turbulent Intensity.(d) Enter 42 mm for the Backflow Hydraulic Diameter.(e) Click OK to close the Pressure Outlet panel.5. Retain the default boundary conditions for the walls (substrate-wall and wall) and close the Boundary Conditions panel.Step 5: Solution1. Set the solution parameters. Solve /Controls /Solution...(a) Retain the default settings for Under-Relaxation Factors.(b) Select Second Order Upwind from the Momentum drop-down list in the Discretization group box.(c) Click OK to close the Solution Controls panel.2. Enable the plotting of residuals during the calculation. Solve/Monitors /Residual...(a)Enable Plot in the Options group box.(b)Click OK to close the Residual Monitors panel.3.Enable the plotting of the mass flow rate at the outlet.Solve / Monitors /Surface...(a) Set the Surface Monitors to 1.(b) Enable the Plot and Write options for monitor-1, and click the Define... button to open the Define Surface Monitor panel.i. Select Mass Flow Rate from the Report Type drop-down list.ii. Select outlet from the Surfaces selection list.iii. Click OK to close the Define Surface Monitors panel.(c) Click OK to close the Surface Monitors panel.4. Initialize the solution from the inlet. Solve /Initialize /Initialize...(a) Select inlet from the Compute From drop-down list.(b) Click Init and close the Solution Initialization panel.5. Save the case file (catalytic converter.cas). File /Write /Case...6. Run the calculation by requesting 100 iterations. Solve /Iterate...(a) Enter 100 for the Number of Iterations.(b) Click Iterate.The FLUENT calculation will converge in approximately 70 iterations. By this point the mass flow rate monitor has attended out, as seen in Figure 7.3.(c) Close the Iterate panel.7. Save the case and data files (catalytic converter.cas and catalytic converter.dat). File /Write /Case & Data...Note: If you choose a file name that already exists in the current folder, FLUENT will prompt you for confirmation to overwrite the file.Step 6: Post-processing1. Create a surface passing through the centerline for post-processing purposes.Surface/Iso-Surface...(a) Select Grid... and Y-Coordinate from the Surface of Constant drop-down lists.(b) Click Compute to calculate the Min and Max values.(c) Retain the default value of 0 for the Iso-Values.(d) Enter y=0 for the New Surface Name.(e) Click Create.2. Create cross-sectional surfaces at locations on either side of the substrate, as well as at its center.Surface /Iso-Surface...(a) Select Grid... and X-Coordinate from the Surface of Constant drop-down lists.(b) Click Compute to calculate the Min and Max values.(c) Enter 95 for Iso-Values.(d) Enter x=95 for the New Surface Name.(e) Click Create.(f) In a similar manner, create surfaces named x=130 and x=165 with Iso-Values of 130 and 165, respectively. Close the Iso-Surface panel after all the surfaces have been created.3. Create a line surface for the centerline of the porous media.Surface /Line/Rake...(a) Enter the coordinates of the line under End Points, using the starting coordinate of (95, 0, 0) and an ending coordinate of (165, 0, 0), as shown.(b) Enter porous-cl for the New Surface Name.(c) Click Create to create the surface.(d) Close the Line/Rake Surface panel.4. Display the two wall zones (substrate-wall and wall). Display /Grid...(a) Disable the Edges option.(b) Enable the Faces option.(c) Deselect inlet and outlet in the list under Surfaces, and make sure that only substrate-wall and wall are selected.(d) Click Display and close the Grid Display panel.(e) Rotate the view and zoom so that the display is similar to Figure 7.2.5. Set the lighting for the display. Display /Options...(a) Enable the Lights On option in the Lighting Attributes group box.(b) Retain the default selection of Gourand in the Lighting drop-down list.(c) Click Apply and close the Display Options panel.6. Set the transparency parameter for the wall zones (substrate-wall and wall). Display/Scene...(a) Select substrate-wall and wall in the Names selection list.(b) Click the Display... button under Geometry Attributes to open the Display Properties panel.i. Set the Transparency slider to 70.ii. Click Apply and close the Display Properties panel.(c) Click Apply and then close the Scene Description panel.7. Display velocity vectors on the y=0 surface.Display /Vectors...(a) Enable the Draw Grid option. The Grid Display panel will open.i. Make sure that substrate-wall and wall are selected in the list under Surfaces.ii. Click Display and close the Display Grid panel.(b) Enter 5 for the Scale.(c) Set Skip to 1.(d) Select y=0 from the Surfaces selection list.(e) Click Display and close the Vectors panel.The flow pattern shows that the flow enters the catalytic converter as a jet, with recirculation on either side of the jet. As it passes through the porous substrate, it decelerates and straightens out, and exhibits a more uniform velocity distribution.This allows the metal catalyst present in the substrate to be more effective.Figure 7.4: Velocity Vectors on the y=0 Plane8. Display filled contours of static pressure on the y=0 plane.Display /Contours...(a) Enable the Filled option.(b) Enable the Draw Grid option to open the Display Grid panel.i. Make sure that substrate-wall and wall are selected in the list under Surfaces.ii. Click Display and close the Display Grid panel.(c) Make sure that Pressure... and Static Pressure are selected from the Contours of drop-down lists.(d) Select y=0 from the Surfaces selection list.(e) Click Display and close the Contours panel.Figure 7.5: Contours of the Static Pressure on the y=0 planeThe pressure changes rapidly in the middle section, where the fluid velocity changes as it passes through the porous substrate. The pressure drop can be high, due to the inertial and viscous resistance of the porous media. Determining this pressure drop is a goal of CFD analysis. In the next step, you will learn how to plot the pressure drop along the centerline of the substrate.9. Plot the static pressure across the line surface porous-cl.Display /Contours...Plot /XY Plot...(a) Make sure that the Pressure... and Static Pressure are selected from the Y Axis Function drop-down lists.(b) Select porous-cl from the Surfaces selection list.(c)Click Plot and close the Solution XY Plot panel.(a) Disable the Global Range option.Figure 7.6: Plot of the Static Pressure on the porous-cl Line SurfaceIn Figure 7.6, the pressure drop across the porous substrate can be seen to be roughly 300 Pa.10. Display filled contours of the velocity in the X direction on the x=95, x=130 and x=165 surfaces.(b) Select Velocity... and X Velocity from the Contours of drop-down lists.(c) Select x=130, x=165, and x=95 from the Surfaces selection list, and deselect y=0.(d) Click Display and close the Contours panel.The velocity profile becomes more uniform as the fluid passes through the porous media. The velocity is very high at the center (the area in red) just before the nitrogen enters the substrate and then decreases as it passes through and exits the substrate. The area in green, which corresponds to a moderate velocity, increases in extent.Figure 7.7: Contours of the X Velocity on the x=95, x=130, and x=165 Surfaces 11. Use numerical reports to determine the average, minimum, and maximum of the velocity distribution before and after the porous substrate.Report /Surface Integrals...(a) Select Mass-Weighted Average from the Report Type drop-down list.(b) Select Velocity and X Velocity from the Field Variable drop-down lists.(c) Select x=165 and x=95 from the Surfaces selection list.(d) Click Compute.(e) Select Facet Minimum from the Report Type drop-down list and click Compute again.(f) Select Facet Maximum from the Report Type drop-down list and click Compute again.(g) Close the Surface Integrals panel.The numerical report of average, maximum and minimum velocity can be seen in the main FLUENT console, as shown in the following example:The spread between the average, maximum, and minimum values for X velocity gives the degree to which the velocity distribution is non-uniform. You can also use these numbers to calculate the velocity ratio (i.e., the maximum velocity divided by the mean velocity) and the space velocity (i.e., the product of the mean velocity and the substrate length).Custom field functions and UDFs can be also used to calculate more complex measures of non-uniformity, such as the standard deviation and the gamma uniformity index.SummaryIn this tutorial, you learned how to set up and solve a problem involving gas flow through porous media in FLUENT. You also learned how to perform appropriate post-processing to investigate the flow field, determine the pressure drop across the porous media and non-uniformity of the velocity distribution as the fluid goes through the porous media.Further ImprovementsThis tutorial guides you through the steps to reach an initial solution. You may be able to obtain a more accurate solution by using an appropriate higher-order discretization scheme and by adapting the grid. Grid adaption can also ensure that the solution is independent of the grid. These steps are demonstrated in Tutorial 1.。
fluent中多孔介质模型的设置

7.19.6 User Inputs for Porous MediaWhen you are modeling a porous region, the only additional inputs for the problem setup are as follows. Optional inputs are indicated as such.1. Define the porous zone.2. Define the porous velocity formulation. (optional)3. Identify the fluid material flowing through the porous medium.4. Enable reactions for the porous zone, if appropriate, and select the reaction mechanism.5. Enable the Relative Velocity Resistance Formulation. By default, this option is already enabled and takes the moving porous media into consideration (as described in Section 7.19.6).6. Set the viscous resistance coefficients ( in Equation7.19-1,or in Equation 7.19-2) and the inertial resistance coefficients ( in Equation 7.19-1, or in Equation 7.19-2), and define the direction vectors for which they apply. Alternatively, specify the coefficients for the power-law model.7. Specify the porosity of the porous medium.8. Select the material contained in the porous medium (required only for models that include heat transfer). Note that the specific heat capacity, , for the selected material in the porous zone can only be entered as a constant value.9. Set the volumetric heat generation rate in the solid portion of the porous medium (or any other sources, such as mass or momentum). (optional) 10. Set any fixed values for solution variables in the fluid region (optional).11. Suppress the turbulent viscosity in the porous region, if appropriate.12. Specify the rotation axis and/or zone motion, if relevant.Methods for determining the resistance coefficients and/or permeability are presented below. If you choose to use the power-law approximation of the porous-media momentum source term, you will enter thecoefficients and in Equation 7.19-3 instead of the resistance coefficients and flow direction.You will set all parameters for the porous medium inthe Fluid panel (Figure 7.19.1), which is opened from the Boundary Conditions panel (as described in Section 7.1.4).Figure 7.19.1: The Fluid Panel for a Porous Zone Defining the Porous ZoneAs mentioned in Section 7.1, a porous zone is modeled as a special type of fluid zone. To indicate that the fluid zone is a porous region, enablethe Porous Zone option in the Fluid panel. The panel will expand to show the porous media inputs (as shown in Figure 7.19.1).Defining the Porous Velocity FormulationThe Solver panel contains a Porous Formulation region where you can instruct FLUENT to use either a superficial or physical velocity in the porous medium simulation. By default, the velocity is set to SuperficialVelocity. For details about using the Physical Velocity formulation, see Section 7.19.7.Defining the Fluid Passing Through the Porous MediumTo define the fluid that passes through the porous medium, select the appropriate fluid in the Material Name drop-down list in the Fluid panel. If you want to check or modify the properties of the selected material, you can click Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel.If you are modeling species transport or multiphase flow,the Material Name list will not appear in the Fluid panel. Forspecies calculations, the mixture material for all fluid/porous zones will be the material you specified in the SpeciesModel panel. For multiphase flows, the materials are specified when you define the phases, as described in Section 23.10.3.Enabling Reactions in a Porous ZoneIf you are modeling species transport with reactions, you can enable reactions in a porous zone by turning on the Reaction option inthe Fluid panel and selecting a mechanism in the ReactionMechanism drop-down list.If your mechanism contains wall surface reactions, you will also need to specify a value for the Surface-to-Volume Ratio. This value is the surface area of the pore walls per unit volume ( ), and can be thought of as a measure of catalyst loading. With this value, FLUENT can calculate the total surface area on which the reaction takes place in each cell bymultiplying by the volume of the cell. See Section 14.1.4 for detailsabout defining reaction mechanisms. See Section 14.2for details about wall surface reactions.Including the Relative Velocity Resistance FormulationPrior to FLUENT 6.3, cases with moving reference frames used the absolute velocities in the source calculations for inertial and viscous resistance. This approach has been enhanced so that relative velocities are used for the porous source calculations (Section 7.19.2). Using the Relative Velocity Resistance Formulation option (turned on by default) allows you to better predict the source terms for cases involving moving meshes or moving reference frames (MRF). This option works well in cases withnon-moving and moving porous media. Note that FLUENT will use the appropriate velocities (relative or absolute), depending on your case setup. Defining the Viscous and Inertial Resistance CoefficientsThe viscous and inertial resistance coefficients are both defined in the same manner. The basic approach for defining the coefficients using a Cartesian coordinate system is to define one direction vector in 2D or two direction vectors in 3D, and then specify the viscous and/or inertial resistance coefficients in each direction. In 2D, the second direction, which is not explicitly defined, is normal to the plane defined by the specified direction vector and the direction vector. In 3D, the third direction is normal to the plane defined by the two specified direction vectors. For a 3D problem, the second direction must be normal to the first. If you fail to specify two normal directions, the solver will ensure that they are normal by ignoring any component of the second direction that is in the first direction. You should therefore be certain that the first direction is correctly specified. You can also define the viscous and/or inertial resistance coefficients in each direction using a user-defined function (UDF). The user-defined options become available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the coefficients defined in the UDF must utilize the DEFINE_PROFILE macro. For moreinformation on creating and using user-defined function, see the separate UDF Manual.If you are modeling axisymmetric swirling flows, you can specify an additional direction component for the viscous and/or inertial resistance coefficients. This direction component is always tangential to the other two specified directions. This option is available for both density-based and pressure-based solvers.In 3D, it is also possible to define the coefficients using a conical (or cylindrical) coordinate system, as described below.Note that the viscous and inertial resistance coefficients aregenerally based on the superficial velocity of the fluid in the porous media.The procedure for defining resistance coefficients is as follows:1. Define the direction vectors.To use a Cartesian coordinate system, simply specify the Direction-1 Vector and, for 3D, the Direction-2 Vector. The unspecifieddirection will be determined as described above. These directionvectors correspond to the principle axes of the porous media.For some problems in which the principal axes of the porous mediumare not aligned with the coordinate axes of the domain, you may notknow a priori the direction vectors of the porous medium. In suchcases, the plane tool in 3D (or the line tool in 2D) can help you todetermine these direction vectors.(a) "Snap'' the plane tool (or the line tool) onto the boundary of theporous region. (Follow the instructions inSection 27.6.1 or 27.5.1 for initializing the tool to a position on anexisting surface.)(b) Rotate the axes of the tool appropriately until they are alignedwith the porous medium.(c) Once the axes are aligned, click on the Update From PlaneTool or Update From Line Tool button inthe Fluid panel. FLUENT will automatically set the Direction-1Vector to the direction of the red arrow of the tool, and (in 3D)the Direction-2 Vector to the direction of the green arrow.To use a conical coordinate system (e.g., for an annular, conical filter element), follow the steps below. This option is available only in 3D cases.(a) Turn on the Conical option.(b) Specify the Cone Axis Vector and Point on Cone Axis. Thecone axis is specified as being in the direction of the Cone AxisVector (unit vector), and passing through the Point on Cone Axis.The cone axis may or may not pass through the origin of thecoordinate system.(c) Set the Cone Half Angle (the angle between the cone's axis andits surface, shown in Figure 7.19.2). To use a cylindrical coordinate system, set the Cone Half Angle to 0.Figure 7.19.2: Cone Half AngleFor some problems in which the axis of the conical filter element is not aligned with the coordinate axes of the domain, you may notknow a priori the direction vector of the cone axis and coordinates ofa point on the cone axis. In such cases, the plane tool can help you todetermine the cone axis vector and point coordinates. One method is as follows:(a) Select a boundary zone of the conical filter element that isnormal to the cone axis vector in the drop-down list next to the Snap to Zone button.(b) Click on the Snap to Zone button. FLUENT will automatically"snap'' the plane tool onto the boundary. It will also set the Cone Axis Vector and the Point on Cone Axis. (Note that you will still have to set the Cone Half Angle yourself.)An alternate method is as follows:(a) "Snap'' the plane tool onto the boundary of the porous region.(Follow the instructions in Section 27.6.1 for initializing the tool to a position on an existing surface.)(b) Rotate and translate the axes of the tool appropriately until thered arrow of the tool is pointing in the direction of the cone axisvector and the origin of the tool is on the cone axis.(c) Once the axes and origin of the tool are aligned, click onthe Update From Plane Tool button inthe Fluid panel. FLUENT will automatically set the Cone AxisVector and the Point on Cone Axis. (Note that you will still have toset the Cone Half Angle yourself.)2. Under Viscous Resistance, specify the viscous resistancecoefficient in each direction.Under Inertial Resistance, specify the inertial resistance coefficient in each direction. (You will need to scroll down with the scroll bar to view these inputs.)For porous media cases containing highly anisotropic inertial resistances, enable Alternative Formulation under Inertial Resistance.The Alternative Formulation option provides better stability to the calculation when your porous medium is anisotropic. The pressure loss through the medium depends on the magnitude of the velocity vector ofthe i th component in the medium. Using the formulation ofEquation 7.19-6 yields the expression below:(7.19-10) Whether or not you use the Alternative Formulation option depends on how well you can fit your experimentally determined pressure drop data to the FLUENT model. For example, if the flow through the medium is aligned with the grid in your FLUENT model, then it will not make a difference whether or not you use the formulation.For more infomation about simulations involving highly anisotropic porous media, see Section 7.19.8.Note that the alternative formulation is compatible only with the pressure-based solver.If you are using the Conical specification method, Direction-1 is the cone axis direction, Direction-2 is the normal to the cone surface (radial ( )direction for a cylinder), and Direction-3 is the circumferential ( ) direction.In 3D there are three possible categories of coefficients, and in 2D there are two:∙In the isotropic case, the resistance coefficients in all directions are the same (e.g., a sponge). For an isotropic case, you must explicitlyset the resistance coefficients in each direction to the same value.∙When (in 3D) the coefficients in two directions are the same and those in the third direction are different or (in 2D) the coefficients inthe two directions are different, you must be careful to specify thecoefficients properly for each direction. For example, if you had aporous region consisting of cylindrical straws with small holes inthem positioned parallel to the flow direction, the flow would passeasily through the straws, but the flow in the other two directions(through the small holes) would be very little. If you had a plane offlat plates perpendicular to the flow direction, the flow would notpass through them at all; it would instead move in the other twodirections.∙In 3D the third possible case is one in which all three coefficients are different. For example, if the porous region consisted of a plane ofirregularly-spaced objects (e.g., pins), the movement of flow between the blockages would be different in each direction. You wouldtherefore need to specify different coefficients in each direction. Methods for deriving viscous and inertial loss coefficients are described in the sections that follow.Deriving Porous Media Inputs Based on Superficial Velocity, Using a Known Pressure LossWhen you use the porous media model, you must keep in mind that the porous cells in FLUENT are 100% open, and that the values that you specify for and/or must be based on this assumption. Suppose, however, that you know how the pressure drop varies with the velocity through the actual device, which is only partially open to flow. The following exercise is designed to show you how to compute a valuefor which is appropriate for the FLUENT model.Consider a perforated plate which has 25% area open to flow. The pressure drop through the plate is known to be 0.5 times the dynamic head in the plate. The loss factor, , defined as(7.19-11)is therefore 0.5, based on the actual fluid velocity in the plate, i.e., the velocity through the 25% open area. To compute an appropriate valuefor , note that in the FLUENT model:1. The velocity through the perforated plate assumes that the plate is 100% open.2. The loss coefficient must be converted into dynamic head loss per unit length of the porous region.Noting item 1, the first step is to compute an adjusted loss factor, , which would be based on the velocity of a 100% open area:(7.19-12) or, noting that for the same flow rate, ,(7.19-13)The adjusted loss factor has a value of 8. Noting item 2, you must now convert this into a loss coefficient per unit thickness of the perforated plate. Assume that the plate has a thickness of 1.0 mm (10 m). The inertial loss factor would then be(7.19-14)Note that, for anisotropic media, this information must be computed for each of the 2 (or 3) coordinate directions.Using the Ergun Equation to Derive Porous Media Inputs for a Packed BedAs a second example, consider the modeling of a packed bed. In turbulent flows, packed beds are modeled using both a permeability and an inertial loss coefficient. One technique for deriving the appropriate constants involves the use of the Ergun equation [ 98], a semi-empirical correlation applicable over a wide range of Reynolds numbers and for many types of packing:(7.19-15)When modeling laminar flow through a packed bed, the second term in the above equation may be dropped, resulting in the Blake-Kozenyequation [ 98]:(7.19-16) In these equations, is the viscosity, is the mean particlediameter, is the bed depth, and is the void fraction, defined as the volume of voids divided by the volume of the packed bed region. Comparing Equations 7.19-4 and 7.19-6 with 7.19-15, the permeability and inertial loss coefficient in each component direction may be identified as(7.19-17) and(7.19-18) Using an Empirical Equation to Derive Porous Media Inputs for Turbulent Flow Through a Perforated PlateAs a third example we will take the equation of Van Winkle et al. [ 279, 339] and show how porous media inputs can be calculated for pressure loss through a perforated plate with square-edged holes.The expression, which is claimed by the authors to apply for turbulent flow through square-edged holes on an equilateral triangular spacing, is(7.19-19) where= mass flow rate through the plate= the free area or total area of the holes= the area of the plate (solid and holes)= a coefficient that has been tabulated for various Reynolds-numberrangesand for various= the ratio of hole diameter to plate thicknessfor and for the coefficient takes a value of approximately 0.98, where the Reynolds number is based on hole diameter and velocity in the holes.Rearranging Equation 7.19-19, making use of the relationship(7.19-20)and dividing by the plate thickness, , we obtain(7.19-21)where is the superficial velocity (not the velocity in the holes). Comparing with Equation 7.19-6 it is seen that, for the direction normal to the plate, the constant can be calculated from(7.19-22)Using Tabulated Data to Derive Porous Media Inputs for Laminar Flow Through a Fibrous MatConsider the problem of laminar flow through a mat or filter pad which is made up of randomly-oriented fibers of glass wool. As an alternative to the Blake-Kozeny equation (Equation 7.19-16) we might choose to employ tabulated experimental data. Such data is available for many types offiber [ 158].fraction of dimensionless permeability of glass woolwhere and is the fiber diameter. , for use inEquation 7.19-4, is easily computed for a given fiber diameter and volume fraction.Deriving the Porous Coefficients Based on Experimental Pressure and Velocity DataExperimental data that is available in the form of pressure drop against velocity through the porous component, can be extrapolated to determine the coefficients for the porous media. To effect a pressure drop across a porous medium of thickness, , the coefficients of the porous media are determined in the manner described below.If the experimental data is:then an curve can be plotted to create a trendline through these points yielding the following equationwhere is the pressure drop and is the velocity.Note that a simplified version of the momentum equation, relating the pressure drop to the source term, can be expressed as(7.19-24)or(7.19-25)Hence, comparing Equation 7.19-23 to Equation 7.19-2, yields the following curve coefficients:(7.19-26)with kg/m , and a porous media thickness, , assumed to be 1m in this example, the inertial resistance factor, .Likewise,with , the viscous inertial resistancefactor,.Note that this same technique can be applied to the porous jump boundary condition. Similar to the case of the porous media, you have to take into account the thickness of the medium . Your experimental data can be plotted in ancurve, yielding an equation that is equivalent to Equation 7.22-1. From there, you can determine the permeability and the pressure jumpcoefficient.Using the Power-Law ModelIf you choose to use the power-law approximation of the porous-media momentum source term (Equation 7.19-3), the only inputs required are the coefficients and . Under Power Law Model in the Fluid panel, enter the values for C0 and C1. Note that the power-law model can be used in conjunction with the Darcy and inertia models. C0 must be in SI units, consistent with the value of C1.Defining PorosityTo define the porosity, scroll down below the resistance inputs in the Fluid panel, and set the Porosity under Fluid Porosity .You can also define the porosity using a user-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the porosity defined in the UDF must utilize the DEFINE_PROFILE macro. For more information on creating and using user-defined function, see the separate UDF Manual.The porosity, , is the volume fraction of fluid within the porous region (i.e., the open volume fraction of the medium). The porosity is used in the prediction of heat transfer in the medium, as described in Section 7.19.3, and in the time-derivative term in the scalar transport equations for unsteady flow, as described in Section 7.19.5. It also impacts the calculation of reaction source terms and body forces in the medium. These sources will be proportional to the fluid volume in the medium. If you want to represent the medium as completely open (no effect of the solid medium), you should set the porosity equal to 1.0 (the default). When the porosity is equal to 1.0, the solid portion of the medium will have no impact on heat transfer or thermal/reaction source terms in the medium.Defining the Porous MaterialIf you choose to model heat transfer in the porous medium, you must specify the material contained in the porous medium.To define the material contained in the porous medium, scroll down below the resistance inputs in the Fluid panel, and select the appropriate solid in the Solid Material Name drop-down list under Fluid Porosity. If you want to check or modify the properties of the selected material, you canclick Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel. In the Material panel, you can define thenon-isotropic thermal conductivity of the porous material using auser-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the non-isotropic thermal conductivity defined in the UDF must utilize the DEFINE_PROPERTY macro. For more information on creating and using user-defined function, see the separate UDF Manual.Defining SourcesIf you want to include effects of the heat generated by the porous medium in the energy equation, enable the Source Terms option and set anon-zero Energy source. The solver will compute the heat generated by the porous region by multiplying this value by the total volume of the cells comprising the porous zone. You may also define sources of mass, momentum, turbulence, species, or other scalar quantities, as described in Section 7.28.Defining Fixed ValuesIf you want to fix the value of one or more variables in the fluid region of the zone, rather than computing them during the calculation, you can do so by enabling the Fixed Values option. See Section 7.27 for details. Suppressing the Turbulent Viscosity in the Porous RegionAs discussed in Section 7.19.4, turbulence will be computed in the porous region just as in the bulk fluid flow. If you are using one of the turbulence models (with the exception of the Large Eddy Simulation (LES) Model), and you want the turbulence generation to be zero in the porous zone, turn on the Laminar Zone option in the Fluid panel. Refer to Section 7.17.1 for more information about suppressing turbulence generation.Specifying the Rotation Axis and Defining Zone MotionInputs for the rotation axis and zone motion are the same as for a standard fluid zone. See Section 7.17.1 for details.。
Fluent计算多孔介质模型例子

Fluent计算多孔介质模型例子2008-08-27 14:23这是一个多孔介质例子,进口速度为0.01m/s,组份为液态水和氧气,其中氧气从多孔介质porous jump 渗透过去,如何看氧气在tissue中扩散的。
porous jump的face permeability1 a=e-8 m_2thickness 设为0.0001pressure jump coefficient为默认porous zone设置如下:direction vector 1, 1,viscous resistance 100 eachinertial resistance 100 eachporosity 0.1边界条件设置如下:Ab – wall - defaultBc – wall – defaultBe – porous jump – face permeability 1e-8, porous medium thickness0.0001Cd – outflow rating – 0.5De – wall – defaultDefault interior – interiorDefault interior001 – interiorDefault interior019 – interiorEf – wall - defaultFg – outflow rating – 1Fluid - porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Gh- wall - defaultHi – wall - defaultHk - porous jump same conditions as otherIj – outflow – 0.5Jk – wall – defaultKl – wall – defaultLa – velocity inlet – 0.01 m/s, temperature 300K, 0.5 mass fraction O2Lfluid – porous zone - direction vector 1, 1, viscous resistance 100 each,inertial resistance 100 each, porosity 0.1Pipefluid – fluid – default (no porous zone)Models – species transport – water and oxygen mixture Variations – different boundary conditions at top and bottom (outflow, wall ect)注意,其中porous zone在gambit中设置为fluid,在fluent中设置为porous zone2008-08-27 14:36cfx里面的设置1,首先你设置成多孔介质域(porous domain);2,porosity settings里面,就可以设置多孔系数了,如图1所示。
FLUENT帮助里自带的多孔介质算例-经典资料

FLUENT帮助里自带的多孔介质算例-经典资料Tutorial 7. Modeling Flow Through Porous Media IntroductionMany industrial applications involve the modeling of ow through porous media, such as _lters, catalyst beds, and packing. This tutorial illustrates how to set up and solve a problem involving gas ow through porous media.The industrial problem solved here involves gas ow through a catalytic converter. Catalytic converters are commonly used to purify emissions from gasoline and diesel engines by converting environmentally hazardous exhaust emissions to acceptable substances.Examples of such emissions include carbon monoxide (CO), nitrogen oxides (NOx), and unburned hydrocarbon fuels. These exhaust gas emissions are forced through a substrate, which is a ceramic structure coated with a metal catalyst such as platinum or palladium.The nature of the exhaust gas ow is a very important factor in determining the performance of the catalytic converter. Of particular importance is the pressure gradient and velocity distribution through the substrate. Hence CFD analysis is used to designe_cient catalytic converters: by modeling the exhaust gas ow, the pressure drop andthe uniformity of ow through the substrate can be determined. In this tutorial, FLUENTis used to model the ow of nitrogen gas through a catalytic converter geometry, so that the ow _eld structure may be analyzed.This tutorial demonstrates how to do the following:_ Set up a porous zone for the substrate with appropriate resistances._ Calculate a solution for gas ow through the catalytic converter using the pressurebased solver._ Plot pressure and velocity distribution on speci_ed planes of the geometry._ Determine the pressure drop through the substrate and the degree of non-uniformityof ow through cross sections of the geometry using X-Y plots and numerical reports.许多工业应用都涉及通过多孔介质(如过滤器,催化剂床和填料)的流动模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:1。
Gambit中划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid分别开来,再定义其名称,我习惯将名称定义为porous;2。
在fluent中定义边界条件define-boundary condition-porous(刚定义的名称),将其设置边界条件为fluid,点击set按钮即弹出与fluid边界条件一样的对话框,选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;3。
porous zone设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:请参看本人上一篇博文“终于搞清fluent中多孔粘性阻力与内部阻力的计算方法”,此处不赘述;3)如果了定义粘性阻力1/a与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity,默认值1表示全开放,此值按实验测值填写即可。
完了,其他设置与普通k-e或RSM相同。
总结一下,与君共享!Tutorial 7. Modeling Flow Through Porous MediaIntroductionMany industrial applications involve the modeling of flow through porous media, such as filters, catalyst beds, and packing. This tutorial illustrates how to set up and solve a problem involving gas flow through porous media.The industrial problem solved here involves gas flow through a catalytic converter. Catalytic converters are commonly used to purify emissions from gasoline and diesel engines by converting environmentally hazardous exhaust emissions to acceptable substances.Examples of such emissions include carbon monoxide (CO), nitrogen oxides (NOx), and unburned hydrocarbon fuels. These exhaust gas emissions are forced through a substrate, which is a ceramic structure coated with a metal catalyst such as platinum or palladium.The nature of the exhaust gas flow is a very important factor in determining the performance of the catalytic converter. Of particular importance is the pressure gradient and velocity distribution through the substrate. Hence CFD analysis is used to design efficient catalytic converters: by modeling the exhaust gas flow, the pressure drop and the uniformity of flow through the substrate can be determined. In this tutorial, FLUENT is used to model the flow of nitrogen gas through a catalytic converter geometry, so that the flow field structure may be analyzed.This tutorial demonstrates how to do the following:_ Set up a porous zone for the substrate with appropriate resistances._ Calculate a solution for gas flow through the catalytic converter using the pressure based solver. _ Plot pressure and velocity distribution on specified planes of the geometry._ Determine the pressure drop through the substrate and the degree of non-uniformity of flow through cross sections of the geometry using X-Y plots and numerical reports.Problem DescriptionThe catalytic converter modeled here is shown in Figure 7.1. The nitrogen flows in through the inlet with a uniform velocity of 22.6 m/s, passes through a ceramic monolith substrate with square shaped channels, and then exits through the outlet.While the flow in the inlet and outlet sections is turbulent, the flow through the substrate is laminar and is characterized by inertial and viscous loss coefficients in the flow (X) direction. The substrate is impermeable in other directions, which is modeled using loss coefficients whose values are three orders of magnitude higher than in the X direction.Setup and SolutionStep 1: Grid1. Read the mesh file (catalytic converter.msh).File /Read /Case...2. Check the grid. Grid /CheckFLUENT will perform various checks on the mesh and report the progress in the console. Make sure that the minimum volume reported is a positive number.3. Scale the grid.Grid! Scale...(a) Select mm from the Grid Was Created In drop-down list.(b) Click the Change Length Units button. All dimensions will now be shown in millimeters.(c) Click Scale and close the Scale Grid panel.4. Display the mesh. Display /Grid...(a) Make sure that inlet, outlet, substrate-wall, and wall are selected in the Surfaces selection list.(b) Click Display.(c) Rotate the view and zoom in to get the display shown in Figure 7.2.(d) Close the Grid Display panel.The hex mesh on the geometry contains a total of 34,580 cells.Step 2: Models1. Retain the default solver settings. Define /Models /Solver...2. Select the standard k-ε turbulence model. Define/ Models /Viscous...Step 3: Materials1. Add nitrogen to the list of fluid materials by copying it from the Fluent Database for materials.Define /Materials...(a) Click the Fluent Database... button to open the Fluent Database Materials panel.i. Select nitrogen (n2) from the list of Fluent Fluid Materials.ii. Click Copy to copy the information for nitrogen to your list of fluid materials. iii. Close the Fluent Database Materials panel.(b) Close the Materials panel.Step 4: Boundary Conditions. Define /Boundary Conditions...1. Set the boundary conditions for the fluid (fluid).(a) Select nitrogen from the Material Name drop-down list.(b) Click OK to close the Fluid panel.2. Set the boundary conditions for the substrate (substrate).(a) Select nitrogen from the Material Name drop-down list.(b) Enable the Porous Zone option to activate the porous zone model.(c) Enable the Laminar Zone option to solve the flow in the porous zone without turbulence.(d) Click the Porous Zone tab.i. Make sure that the principal direction vectors are set as shown in Table7.1. Use the scroll bar to access the fields that are not initially visible in the panel.ii. Enter the values in Table 7.2 for the Viscous Resistance and Inertial Resistance. Scroll down to access the fields that are not initially visible in the panel.(e) Click OK to close the Fluid panel.3. Set the velocity and turbulence boundary conditions at the inlet (inlet).(a) Enter 22.6 m/s for the Velocity Magnitude.(b) Select Intensity and Hydraulic Diameter from the Specification Method dropdown list in the Turbulence group box.(c) Retain the default value of 10% for the Turbulent Intensity.(d) Enter 42 mm for the Hydraulic Diameter.(e) Click OK to close the Velocity Inlet panel.4. Set the boundary conditions at the outlet (outlet).(a) Retain the default setting of 0 for Gauge Pressure.(b) Select Intensity and Hydraulic Diameter from the Specification Method dropdown list in the Turbulence group box.(c) Enter 5% for the Backflow Turbulent Intensity.(d) Enter 42 mm for the Backflow Hydraulic Diameter.(e) Click OK to close the Pressure Outlet panel.5. Retain the default boundary conditions for the walls (substrate-wall and wall) and close the Boundary Conditions panel.Step 5: Solution1. Set the solution parameters. Solve /Controls /Solution...(a) Retain the default settings for Under-Relaxation Factors.(b) Select Second Order Upwind from the Momentum drop-down list in the Discretization group box.(c) Click OK to close the Solution Controls panel.2. Enable the plotting of residuals during the calculation. Solve/Monitors /Residual...(a) Enable Plot in the Options group box.(b) Click OK to close the Residual Monitors panel.3. Enable the plotting of the mass flow rate at the outlet.Solve / Monitors /Surface...(a) Set the Surface Monitors to 1.(b) Enable the Plot and Write options for monitor-1, and click the Define... button to open the Define Surface Monitor panel.i. Select Mass Flow Rate from the Report Type drop-down list.ii. Select outlet from the Surfaces selection list.iii. Click OK to close the Define Surface Monitors panel.(c) Click OK to close the Surface Monitors panel.4. Initialize the solution from the inlet. Solve /Initialize /Initialize...(a) Select inlet from the Compute From drop-down list.(b) Click Init and close the Solution Initialization panel.5. Save the case file (catalytic converter.cas). File /Write /Case...6. Run the calculation by requesting 100 iterations. Solve /Iterate...(a) Enter 100 for the Number of Iterations.(b) Click Iterate.The FLUENT calculation will converge in approximately 70 iterations. By this point the mass flow rate monitor has attended out, as seen in Figure 7.3.(c) Close the Iterate panel.7. Save the case and data files (catalytic converter.cas and catalytic converter.dat).File /Write /Case & Data...Note: If you choose a file name that already exists in the current folder, FLUENTwill prompt you for confirmation to overwrite the file.Step 6: Post-processing1. Create a surface passing through the centerline for post-processing purposes.Surface/Iso-Surface...(a) Select Grid... and Y-Coordinate from the Surface of Constant drop-down lists.(b) Click Compute to calculate the Min and Max values.(c) Retain the default value of 0 for the Iso-Values.(d) Enter y=0 for the New Surface Name.(e) Click Create.2. Create cross-sectional surfaces at locations on either side of the substrate, as well as at its center.Surface /Iso-Surface...(a) Select Grid... and X-Coordinate from the Surface of Constant drop-down lists.(b) Click Compute to calculate the Min and Max values.(c) Enter 95 for Iso-Values.(d) Enter x=95 for the New Surface Name.(e) Click Create.(f) In a similar manner, create surfaces named x=130 and x=165 with Iso-Values of 130 and 165, respectively. Close the Iso-Surface panel after all the surfaces have been created.3. Create a line surface for the centerline of the porous media.Surface /Line/Rake...(a) Enter the coordinates of the line under End Points, using the starting coordinate of (95, 0, 0) and an ending coordinate of (165, 0, 0), as shown.(b) Enter porous-cl for the New Surface Name.(c) Click Create to create the surface.(d) Close the Line/Rake Surface panel.4. Display the two wall zones (substrate-wall and wall). Display /Grid...(a) Disable the Edges option.(b) Enable the Faces option.(c) Deselect inlet and outlet in the list under Surfaces, and make sure that only substrate-wall and wall are selected.(d) Click Display and close the Grid Display panel.(e) Rotate the view and zoom so that the display is similar to Figure 7.2.5. Set the lighting for the display. Display /Options...(a) Enable the Lights On option in the Lighting Attributes group box.(b) Retain the default selection of Gourand in the Lighting drop-down list.(c) Click Apply and close the Display Options panel.6. Set the transparency parameter for the wall zones (substrate-wall and wall).Display/Scene...(a) Select substrate-wall and wall in the Names selection list.(b) Click the Display... button under Geometry Attributes to open the Display Properties panel.i. Set the Transparency slider to 70.ii. Click Apply and close the Display Properties panel.(c) Click Apply and then close the Scene Description panel.7. Display velocity vectors on the y=0 surface.Display /Vectors...(a) Enable the Draw Grid option. The Grid Display panel will open.i. Make sure that substrate-wall and wall are selected in the list under Surfaces.ii. Click Display and close the Display Grid panel.(b) Enter 5 for the Scale.(c) Set Skip to 1.(d) Select y=0 from the Surfaces selection list.(e) Click Display and close the Vectors panel.The flow pattern shows that the flow enters the catalytic converter as a jet, with recirculation on either side of the jet. As it passes through the porous substrate, it decelerates and straightens out, and exhibits a more uniform velocity distribution.This allows the metal catalyst present in the substrate to be more effective.Figure 7.4: Velocity Vectors on the y=0 Plane8. Display filled contours of static pressure on the y=0 plane.Display /Contours...(a) Enable the Filled option.(b) Enable the Draw Grid option to open the Display Grid panel.i. Make sure that substrate-wall and wall are selected in the list under Surfaces.ii. Click Display and close the Display Grid panel.(c) Make sure that Pressure... and Static Pressure are selected from the Contours of drop-down lists.(d) Select y=0 from the Surfaces selection list.(e) Click Display and close the Contours panel.Figure 7.5: Contours of the Static Pressure on the y=0 planeThe pressure changes rapidly in the middle section, where the fluid velocity changes as it passes through the porous substrate. The pressure drop can be high, due to the inertial and viscous resistance of the porous media. Determining this pressure drop is a goal of CFD analysis. In the next step, you will learn how to plot the pressure drop along the centerline of the substrate.9. Plot the static pressure across the line surface porous-cl.Plot /XY Plot...(a) Make sure that the Pressure... and Static Pressure are selected from the Y Axis Function drop-down lists.(b) Select porous-cl from the Surfaces selection list.(c) Click Plot and close the Solution XY Plot panel.Figure 7.6: Plot of the Static Pressure on the porous-cl Line SurfaceIn Figure 7.6, the pressure drop across the porous substrate can be seen to be roughly 300 Pa.10. Display filled contours of the velocity in the X direction on the x=95, x=130 and x=165 surfaces.Display /Contours...(a) Disable the Global Range option.(b) Select Velocity... and X Velocity from the Contours of drop-down lists.(c) Select x=130, x=165, and x=95 from the Surfaces selection list, and deselect y=0.(d) Click Display and close the Contours panel.The velocity profile becomes more uniform as the fluid passes through the porous media. The velocity is very high at the center (the area in red) just before the nitrogen enters the substrate and then decreases as it passes through and exits the substrate. The area in green, which corresponds to a moderate velocity, increases in extent.Figure 7.7: Contours of the X Velocity on the x=95, x=130, and x=165 Surfaces11. Use numerical reports to determine the average, minimum, and maximum of the velocity distribution before and after the porous substrate.Report /Surface Integrals...(a) Select Mass-Weighted Average from the Report Type drop-down list.(b) Select Velocity and X Velocity from the Field Variable drop-down lists.(c) Select x=165 and x=95 from the Surfaces selection list.(d) Click Compute.(e) Select Facet Minimum from the Report Type drop-down list and click Compute again.(f) Select Facet Maximum from the Report Type drop-down list and click Compute again.(g) Close the Surface Integrals panel.The numerical report of average, maximum and minimum velocity can be seen in the main FLUENT console, as shown in the following example:The spread between the average, maximum, and minimum values for X velocity gives the degree to which the velocity distribution is non-uniform. You can also use these numbers to calculate the velocity ratio (i.e., the maximum velocity divided by the mean velocity) and the space velocity (i.e., the product of the mean velocity and the substrate length).Custom field functions and UDFs can be also used to calculate more complex measures ofnon-uniformity, such as the standard deviation and the gamma uniformity index.SummaryIn this tutorial, you learned how to set up and solve a problem involving gas flow through porous media in FLUENT. You also learned how to perform appropriate post-processing to investigate the flow field, determine the pressure drop across the porous media and non-uniformity of the velocity distribution as the fluid goes through the porous media.Further ImprovementsThis tutorial guides you through the steps to reach an initial solution. You may be able to obtain a more accurate solution by using an appropriate higher-order discretization scheme and by adapting the grid. Grid adaption can also ensure that the solution is independent of the grid. These steps aredemonstrated in Tutorial 1.。
