控制系统的MATLAB仿真和设计课后答案

控制系统仿真实验指导书及解答

实验一 MATLAB 软件操作练习一、实验目的1. 熟悉MATLAB 软件的基本操作；2. 学会利用MATLAB 进行基本数学计算的方法；3. 学会用MATLAB 进行矩阵创建和运算。

二、实验设备计算机一台，MATLAB 软件三、实验内容1. 使用help 命令，查找 sqrt （开方）、roots (求根)等函数的使用方法；2. 用MATLAB 可以识别的格式输入以下矩阵75350083341009103150037193......A ⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦并将A 矩阵的右下角2×3子矩阵赋给D 矩阵。

赋值完成后，调用相应的命令查看MATLAB 工作空间的占用情况。

3. 矩阵运算（1）矩阵的乘法已知A=[1 2;3 4]; B=[5 5;7 8];求A^2*B（2）矩阵除法已知 A=[1 2 3;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];A\B,A/B（3）矩阵的转置及共轭转置已知A=[5+i,2-i,1;6*i,4,9-i];求A.', A'（4）使用冒号选出指定元素已知： A=[3 2 3;2 4 6;6 8 10];求A 中第3列前2个元素；A 中所有列第2，3行的元素；4. 分别用for 和while 循环结构编写程序，求出6323626302122222i i K ===++++++∑并考虑一种避免循环的简洁方法来进行求和。

四、实验步骤1. 熟悉MATLAB 的工作环境，包括各菜单项、工具栏以及指令窗口、工作空间窗口、启动平台窗口、命令历史窗口、图形文件窗口和M 文件窗口；2．在指令窗口中完成实验内容中规定操作并记录相关实验结果；3. 完成实验报告。

实验二 M 文件编程及图形处理一、实验目的1．学会编写MATLAB 的M 文件；2．熟悉MATLAB 程序设计的基本方法；3. 学会利用MATLAB 绘制二维图形。

二、实验设备计算机一台，MATLAB 软件三、实验内容1. 选择合适的步距绘制出下面的图形（1）sin(tan )tan(sin )t t -，其中(,)t ππ∈-（2）-0.5t y=e sin(t-)3π，t ∈[0，20]（3）在同一坐标系中绘制余弦曲线y=cos(t-0.25)和正弦曲线y=sin(t-0.5)， t ∈[0，2π]2.基本绘图控制绘制[0，4π]区间上的x1=10sint 曲线，并要求：（1）线形为点划线、颜色为红色、数据点标记为加号；（2）给横坐标标注’t ’，纵坐标标注‘y(t)‘，3.M 文件程序设计（1）编写程序，计算1+3+5+7+…+(2n+1)的值（用input 语句输入n 值）；（2）编写分段函数⎪⎩⎪⎨⎧≤≤-<≤=其它021210)(x x x x x f的函数文件，存放于文件ff.m 中，计算出)2(f ，)3(-f 的值四、实验要求1. 预习实验内容，按实验要求编写好实验程序；2. 上机调试程序，记录相关实验数据和曲线，3. 完成实验报告。

MATLAB与控制系统仿真练习题及答案 (2)

MATLAB与控制系统仿真练习题1、在同一坐标系内，画出一条正弦曲线和一条余弦曲线，要求正弦曲线用红色实线、数据点用“+”号显示；余弦曲线用黑色点线、数据点用“*”显示。

x=0:1 /10:2*pi;y=sin(x);plot(x,y,'r--+')hold ont=cos(x);plot(x,t,'k-.*')>>2、绘制单位圆。

a=0:1/10:2*pi;x=cos(a);y=sin(a);plot(x,y)axis squaregrid on3、使用极坐标函数绘制)3/ρ=的曲线。

8θsin10(t=0:0.01:2*pi;>> y=8*sin((10*t)/3);>> polar(t,y)4、绘制方程⎪⎩⎪⎨⎧===)cos()sin(t z t y t x 在[]π20，=t 区间的三维曲线。

t=0:pi/50:2*pi;x=t;y=sin(t);z=cos(t);plot3(x,y,z)5、用不同的线型和颜色在同一坐标内绘制曲线x 5.0e 21y -=、)2sin(2y x π=的图形。

x=0:1/10:10;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'r');>> hold onplot(x,y2,'b')6、绘制二维正态分布密度函数)(212221),(y x e y x f +-=π的三维图形。

syms x yz=(1/(2*pi))*exp(-0.5*(x.^2+y.^2));ezsurf(x,y,z)7、选择合适的步长绘制下列函数的图形。

（1）x y cos =，⎥⎦⎤⎢⎣⎡-∈2,2ππx （2）x xe y = x=-2/pi:1/20:2/pi; >> y=sqrt(cos(x)); >> plot(x,y)>> hold on>> y=x.*exp(x);>> plot(x,y)>>8、在同一坐标下绘制函数x 、2x 、3x -、)sin(x x 在()π,0的曲线。

matlab语言与控制系统仿真参考答案第4章

4.5 控制系统的数学模型MATLAB 实训1.练习并掌握TF 模型、ZPK 模型、SS 模型的建立方法。

2.练习并掌握TF 模型、ZPK 模型、SS 模型间的转换方法。

3.练习并掌握求取多个模块串联、并联、反馈后总的模型的方法。

4.练习并掌握模型数据的还原方法。

1.写出以下系统的多项式模型，并将其转换为零极点模型；（1）2153173261552115.35291)(23452341++++++-+-=s s s s s s s s s s G >> n1=[91,-52,3.5,-11,52];d1=[1,15,26,73,31,215];sys1=tf(n1,d1)[z1,p1,k1]=tf2zp(n1,d1)sys1zp=zpk(z1,p1,k1)运行结果如下：Transfer function:91 s^4 - 52 s^3 + 3.5 s^2 - 11 s + 52-------------------------------------------s^5 + 15 s^4 + 26 s^3 + 73 s^2 + 31 s + 215z1 =0.7705 + 0.5468i0.7705 - 0.5468i-0.4848 + 0.6364i-0.4848 - 0.6364ip1 =-13.4656-1.3473 + 1.9525i-1.3473 - 1.9525i0.5801 - 1.5814ik1 =91Zero/pole/gain:91 (s^2 - 1.541s + 0.8927) (s^2 + 0.9697s + 0.6401)--------------------------------------------------------------------------(s+13.47) (s^2 - 1.16s + 2.837) (s^2 + 2.695s + 5.627)（2）21.311395.2251315239.5621.635.711017.38)(23456723452++-+-++++-+-=s s s s s s s s s s s s s G >> n2=[1,-38.7,101,-71.5,63.1,562.39];d2=[1,2,5,-31,51,-22.5,39,311.21];sys2=tf(n2,d2)[z2,p2,k2]=tf2zp(n2,d2)sys2zpkmx=zpk(z2,p2,k2)Transfer function:s^5 - 38.7 s^4 + 101 s^3 - 71.5 s^2 + 63.1 s + 562.4---------------------------------------------------------------------------s^7 + 2 s^6 + 5 s^5 - 31 s^4 + 51 s^3 - 22.5 s^2 + 39 s + 311.2z2 =35.94372.95890.5590 + 1.9214i0.5590 - 1.9214i-1.3206p2 =-2.5015 + 3.1531i-2.5015 - 3.1531i1.9492 + 1.0027i1.9492 - 1.0027i0.2072 - 1.7349i-1.3097k2 =1Zero/pole/gain:(s-35.94) (s-2.959) (s+1.321) (s^2 - 1.118s + 4.004)--------------------------------------------------------------------------------------------------(s+1.31) (s^2 - 3.898s + 4.805) (s^2 - 0.4143s + 3.053) (s^2 + 5.003s + 16.2)2.写出以下系统的零极点模型，并将其转换为多项式模型，并将其展开成为部分分式形式；（1）)11.5)(9.4)(5.3)(6.2)(3.1()02.6)(5.0(36)(1+++++++=s s s s s s s s s G >> z=[-0.5;-6.02];>> p=[0;-1.3;-2.6;-3.5;-4.9;-5.11];>> k=36;>> sys=zpk(z,p,k)Zero/pole/gain:36 (s+0.5) (s+6.02)--------------------------------------------------s (s+1.3) (s+2.6) (s+3.5) (s+4.9) (s+5.11)>> [n,d]=zp2tf(z,p,k)n =0 0 0 0 36.0000 234.7200 108.3600d =1.0000 17.4100 116.1430 367.5889 544.8325 296.2114 0>> systfxs=tf(n,d)Transfer function:36 s^2 + 234.7 s + 108.4-------------------------------------------------------------------------------s^6 + 17.41 s^5 + 116.1 s^4 + 367.6 s^3 + 544.8 s^2 + 296.2 s>> [r,p,k]=residue(n,d);>> [r';p']ans =9.1407 -14.8730 17.4236 -14.7227 2.6656 0.3658-5.1100 -4.9000 -3.5000 -2.6000 -1.3000 0即部分分式分解结果为 s s s s s s s G 3658.03.16656.26.27227.145.34236.179.4873.1411.51407.9)(++++-+++-+=（2）)6)(5)(4)(2()5.3)(3)(1(15.9)(22+-++-++=s s s s s s s s s G >> z=[-1;-3;3.5];>> p=[0;0;-2;-4;5;6];>> k=9.15;>> sys=zpk(z,p,k)Zero/pole/gain:9.15 (s+1) (s+3) (s-3.5)-------------------------------s^2 (s+2) (s+4) (s-5) (s-6)>> [n,d]=zp2tf(z,p,k)n =0 0 0 9.1500 4.5750 -100.6500 -96.0750d =1 -5 -28 92 240 0 0>> systfxs=tf(n,d)Transfer function:9.15 s^3 + 4.575 s^2 - 100.7 s - 96.08---------------------------------------------------s^6 - 5 s^5 - 28 s^4 + 92 s^3 + 240 s^2>> [r,p,k]=residue(n,d);>> [r';p']ans =0.5004 -0.4183 0.0715 0.1123 -0.2659 -0.40036.0000 5.0000 -4.0000 -2.0000 0 0即部分分式分解结果为 24003.02659.021123.040715.054183.065004.0)(s s s s s s s G --++++---= 3.已知系统的状态空间表达式，写出其SS 模型，并求其传递函数矩阵(传递函数模型)，若状态空间表达式为⎩⎨⎧+=+=DuCx y Bu Ax x ，则传递函数矩阵表达式为： D B A sI C s G +-=-1)()(。

控制系统的MATLAB仿真与设计课后答案

控制系统的MATLAB 仿真与设计课后答案第二章1>>x=[15 22 33 94 85 77 60]>>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1 -2 3 -4 2 -3] ;>>n=length(T);>>TT=T';>>for k=n-1:-1:0>>B(:,n-k)=TT.^k;>>end>>B>>test=vander(T)3>>A=zeros(2,5);>>A(:)=-4:5>>L=abs(A)>3>>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为 '; cr='余多项式为 ';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')]) 6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axis equal>>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),grid on;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');grid;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta); >>polar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>hold on>>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1:4))); >>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0]); >>grid on>>hold off第四章1>>for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend2M文件：function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序：[s,p]=fcircle(10)3>>y=0;n=100;for i=1:ny=y+1/i/i;end>>y4 M文件：function f=factor(n)if n<=1f=1;elsef=factor(n-1)*n; end主程序：>>s=0;for i=1:5s=s+factor(i);end>>s5>>sum=0;i=1;while sum<sum=sum+i;i=i+1;end;>>n=i-26for循环M文件：function k=jcsum(n) k=0;for i=0:nk=k+2^i;end主程序：>>jcsum(63)While循环M文件：function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end主程序：>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >>b=[13,-9,6,0]';>>x=A\b2M文件：function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;主程序：[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5]) 3>>X=linspace(0,2*pi,50);。

控制系统仿真matlab第六章习题答案

控制系统仿真第六章课后题作业6.1在图6.1中，已知单位负反馈系统被控对象的传递函数为)1001.0)(11.0()(++=s s s K s G 试编写matlab 程序，设计系统的超前矫正器Gc(s),要求：1）在斜坡信号r （t)=2t 作用下，系统的稳态误差ess<=0.002;2)校正后系统的相位裕度Pm 范围为：45~55；3）绘制系统校正后的bode 图和阶跃响应曲线。

程序：>> s=tf('s');>> G=1000/(s*(0.1*s+1)*(0.001*s+1));>> margin(G) % 绘制校正前的bode 图>> figure(2)>> sys=feedback(G,1);>> step(sys) %绘制校正前的单位阶跃响应曲线>> [Gm,Pm]=margin(G); %该句值计算bode图的增益裕量Gm和相位裕量Pm >> [mag,phase,w]=bode(G); %该句只计算bode图上多个频率点w对应的幅值和相位>> QWPm=50; %取矫正后的相位为50>> FIm=QWPm-Pm+5;>> FIm=FIm*pi/180;>> alfa=(1-sin(FIm))/(1+sin(FIm));>> adb=20*log10(mag);>> am=10*log10(alfa);>> wc=spline(adb,w,am);>> T=1/(wc*sqrt(alfa));>> alfat=alfa*T;>> Gc=tf([T 1],[alfat 1]) %校正器的传递函数Transfer function:0.01794 s + 1-------------0.00179 s + 1>> figure(3)>> margin(Gc*G) % 系统矫正后的bode图>> figure(4)>> step(feedback(Gc*G,1)) % 校正后的单位阶跃响应曲线作业6.2在图6.1中，已知单位负反馈系统被控对象的传递函数为)102.0)(11.0()(++=s s s K s G 试编写matlab 程序，设计系统的滞后校正器Gc （s ）,要求：1) 在斜坡信号r(t)=t 作用下，系统的稳态误差ess 01.0≤；2) 校正后系统的相位裕度Pm 范围为：40~50；3) 绘制系统矫正前后的bode 图和阶跃响应曲线。

MATLAB语言与控制系统仿真-参考答案-第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MA TLAB 绘图的基本知识；2.掌握MA TLAB 子图绘制、图形注释、图形编辑等基本方法；3.学会通过MA TLAB 绘图解决一些实际问题；4.练习二维、三维绘图的多种绘图方式，了解图形的修饰方法；5.学会制作简单的MATLAB 动画。

图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题（1）炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数，可以分解为水平距离)(t x 和垂直距离)(t y 。

)cos()(0αtv t x = %水平方向的行程；205.0)sin()(gt tv t y -=α %垂直方向的行程；其中，0v 是初速度；g 是重力加速度，为9.82m/s ；t 是时间。

（2）炮弹发射程序举例：分析以下程序以及图3-47各个图形的实际意义。

a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos(a);y=t*v0*sin(a)-0.5*g*t.^2;subplot(221);plot(t,x);grid;title(‘时间-水平位移曲线'); subplot(222);plot(t,y);grid;title(‘时间-垂直位移曲线');subplot(223);plot(x,y);grid;title(‘水平位移-垂直位移曲线'); subplot(224);plot(y,x);grid;title(‘垂直位移-水平位移曲线');图3-4745角发射曲线（3）编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹，即发射角90=α，假设初速度分别为[310，290，270]m/s,试绘制时间-垂直位移曲线，编程求取最高射程；绘图要求：◆ 标题设为“炮弹垂直发射问题”； ◆ 在图上通过添加文本的方式表明初速度； ◆ 在x 轴标注“时间”； ◆ 在y 轴上标注“垂直距离”； ◆ 添加网格线； ◆ 将310m/s 的曲线改为线粗为2的红色实线； ◆ 将290m/s 的曲线改为线粗为3的绿色点划线； ◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线；a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos(a);y1=t*v1*sin(a)-0.5*g*t.^2;plot(t,y1);grid; title('炮弹垂直发射问题'); xlabel('时间'); ylabel('垂直距离'); hold on; v2=290;x2=t*v2*cos(a);y2=t*v2*sin(a)-0.5*g*t.^2; plot(t,y2); v3=270;x3=t*v3*cos(a);y3=t*v3*sin(a)-0.5*g*t.^2; plot(t,y3);zgsc=[max(y1); max(y2); max(y3)] %三次发射的最高射程运行结果如下：zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。

Matlab与控制系统仿真部分习题答案

【4.2】程序：num=[5,0];den=conv([1,1],conv([1,2],[1,3])); [numc,denc]=cloop(num,den);[z,p,k]=tf2zp(numc,denc);[A,B,C,D]=tf2ss(numc,denc);g_zp=zpk(z,p,k)g_tf=tf(numc,denc)g_ss=ss(A,B,C,D)运行结果：Zero/pole/gain:5 s----------------------------------(s+0.4432) (s^2 + 5.557s + 13.54)Transfer function:5 s----------------------s^3 + 6 s^2 + 16 s + 6a =x1 x2 x3x1 -6 -16 -6x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 5 0d =u1y1 0【4.3】程序：A=[0 0 0 -1;1 0 0 -2;0 1 0 -3;0 0 1 -4]; B=[0;0;0;1];C=[1 0 0 0];g_ss=ss(A,B,C,D)[num,den]=ss2tf(A,B,C,D);g_tf=tf(num,den)[z,p,k]=ss2zp(A,B,C,D);g_zpk=zpk(z,p,k)运行结果：a =x1 x2 x3 x4x1 0 0 0 -1x2 1 0 0 -2x3 0 1 0 -3x4 0 0 1 -4b =u1x1 0x2 0x3 0x4 1c =x1 x2 x3 x4y1 1 0 0 0d =u1y1 0Continuous-time model.Transfer function:-3.109e-015 s^3 - s^2 - 3.331e-015 s - 4.441e-016 -------------------------------------------------s^4 + 4 s^3 + 3 s^2 + 2 s + 1Zero/pole/gain:- s^2----------------------------------------------(s+0.6724) (s+3.234) (s^2 + 0.0936s + 0.4599)【5.1】（1）程序num=[0,10];den=conv([1,0],[1,7,17]); [numc,denc]=cloop(num,den,-1); G=tf(numc,denc)[y,t]=step(G);plot(t,y,'b-')C=dcgain(G);n=1;while y(n)<0.1*Cn=n+1;endm=1;while y(m)<0.9*Cm=m+1;endrisetime=t(m)-t(n)[Y,k]=max(y); percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettlingtime=t(i)运行结果：Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10risetime =2.7312percentovershoot =-0.4399settlingtime =5.1372图：0123456700.10.20.30.40.50.60.70.80.91（2）程序k=[10,100,1000];t=linspace(1,20,200);num=1;den=conv([1,0],[1,7,17]);for j=1:3;s1=tf(num*k(j),den);sys=feedback(s1,1)y(:,j)=step(sys,t);endplot(t,y(:,1),'r',t,y(:,2),'b',t,y(:,3),'g')gtext('k=10');gtext('k=100');gtext('k=1000') 运行结果：Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10Transfer function:100------------------------s^3 + 7 s^2 + 17 s + 100Transfer function:1000-------------------------s^3 + 7 s^2 + 17 s + 1000图：024681012141618200.20.40.60.811.21.41.61.8图：02468101214161820-3-2-1123422【6.1】程序：（1）num1=[1,1];den1=conv([1,0,0],conv([1,2],[1,4]));sys1=tf(num1,den1)rlocus(sys1)运行结果：-12-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s（2）num2=[1,1];den2=conv([1,0],conv([1,-1],[1,4,16]));sys2=tf(num2,den2)rlocus(sys2)运行结果：-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s（3）num3=[1,8];den3=conv([1,0,0],conv([1,3],conv([1,5],conv([1,7],[1,15])))); sys3=tf(num3,den3)rlocus(sys3)运行结果：-30-25-20-15-10-5051015-20-15-10-505101520Root LocusReal Axis I m a g i n a r y A x i s【6.3】程序：num=[1,2];den=conv([1,0],conv([1,4],conv([1,8],[1,2,5])));sys=tf(num,den)rlocus(sys)[k,poles]=rlocfind(sys)运行结果：Transfer function:s + 2---------------------------------------s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 sSelect a point in the graphics windowselected_point =0.0296 + 2.2826i k =135.8815poles =-7.3248-5.41040.0145 + 2.3021i0.0145 - 2.3021i -1.2939图：-20-15-10-5051015-15-10-551015Root LocusReal Axis I m a g i n a r y A x i s【7.3】程序（1）画波特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)bode(sys)grid图（1）-150-100-50050100M a g n i t u d e (d B)10-210-1100101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)程序（2）画奈奎斯特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)nyquist(sys)grid图（2）-16-14-12-10-8-6-4-20-300-200-100100200300Nyquist DiagramReal Axis I m a g i n a r y A x i s程序（3）画零极点图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)pzmap(sys1)gird图（3）P ole-Zero MapReal Axis I m a g i n a r y A x i s -12-10-8-6-4-20-1.5-1-0.50.511.5程序（4）计算相角裕量和幅值裕量num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)[gm,pm,wcg,wcp]=margin(sys)运行结果Transfer function:50---------------------3 s^3 + 31 s^2 + 10 sTransfer function:50--------------------------3 s^3 + 31 s^2 + 10 s + 50gm =2.0667pm =7.5615wcg =1.8257wcp =1.2645程序（5）绘制阶跃响应曲线num=[50];den=conv([1,0],conv([1,10],[3,1])); sys=tf(num,den)sys1=feedback(sys,1)step(sys1)图（5）00.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d e【7.4】程序如下：num=[300];den=conv([1,0,0],conv([0.2,1],[0.02,1]));sys=tf(num,den)margin(sys)grid波特图如下：-150-100-50050100M a g n i t u d e (d B )10-1100101102103-360-315-270-225-180P h a s e (d e g )Bode DiagramGm = Inf , P m = -78 deg (at 11 rad/sec)Frequency (rad/sec)【9.3】程序：A=[-2 2 -1;0 -2 0;1 -4 0];B=[0;0;1];C=[1,0,0];D=0;M=ctrb(A,B)m=rank(M)if m==3;disp('系统可控')elsedisp('系统不可控')endN=obsv(A,C)n=rank(N)if n==3;disp('系统可观')elsedisp('系统不可观') endsys=ss(A,B,C,D) [num,den]=ss2tf(A,B,C,D) sys1=tf(num,den)[z,p,k]=ss2zp(A,B,C,D)运行结果：M =0 -1 20 0 01 0 -1m =2系统不可控N =1 0 0-2 2 -13 -4 2n =2系统不可观a =x1 x2 x3x1 -2 2 -1x2 0 -2 0x3 1 -4 0b =u1x1 0x2 0x3 1c =x1 x2 x3y1 1 0 0d =u1y1 0 Continuous-time model.0 0 -1 -2den =1 4 5 2Transfer function:-s - 2---------------------s^3 + 4 s^2 + 5 s + 2z =-2p =-1-1-2k = -1【10.1】（1）程序：A=[0,1,0,0;0,5,0,0;0,0,-7,0;0,0,0,-8]; B=[0;1;0;1];C=[1,2,3,4];D=zeros(1,1);G_ss=ss(A,B,C,D)运行结果：a =x1 x2 x3 x4x1 0 1 0 0x2 0 5 0 0x3 0 0 -7 0x4 0 0 0 -8u1x1 0x2 1x3 0x4 1c =x1 x2 x3 x4y1 1 2 3 4d =u1y1 0（2）：程序：[num1,den1]=ss2tf(A,B,C,D); p=roots(den1)i=0;for k=1:1:length(p)if real(p(k))>0i=i+1;endendif i>0disp('系统不稳定');elsedisp('系统稳定');end运行结果：p =5.0000-8.0000-7.0000系统不稳定（3）（4）程序：AA=[0,1,0;0,5,0;0,0,-8];BB=[0;1;1];P=[-1,-2,-8];K=acker(AA,BB,P);i=4;K(4)=0;Kpp=eig(A-B*K)sys1=tf(num1,den1);[y1,t]=step(sys1);plot(t,y1)hold onA_feedback=A-B*K;[num2,den2]=ss2tf(A_feedback,B,C,D); sys2=tf(num2,den2);[y2,t]=step(sys2);plot(t,y2,'r')gridgtext('反馈前')gtext('反馈后')运行结果：K =2 8 0 0pp =-8-2-1-7图形：01234560123456【13.1】程序：A=[0,1;0,0];B=[0;1];C=[1,0];D=zeros(1,1);G_ss=ss(A,B,C,D)M=ctrb(A,B);if rank(M)==2disp('系统完全能控'); elsedisp('系统不完全能控'); endS=[1,0];N=obsv(A,S);if rank(N)==2disp('(A,S)可观测'); elsedisp('(A,S)不可观测'); endR=1;Q=[1,0;0,0];[K,P,E]=Lqr(A,B,Q,R)A_new=A-B*K;G_new=ss(A_new,B,C,D);t=linspace(0,5,100)';y1=step(G_ss,t);y2=step(G_new,t);plot(t,y1,'r:',t,y2,'b-')gridgtext('反馈前')gtext('反馈后')运行结果：a =x1 x2x1 0 1x2 0 0b =u1x1 0x2 1c =x1 x2y1 1 0d =u1y1 0Continuous-time model. 系统完全能控(A,S)可观测K =1.0000 1.4142P =1.4142 1.00001.0000 1.4142E =-0.7071 + 0.7071i-0.7071 - 0.7071i图形：00.51 1.52 2.53 3.54 4.5502468101214。

MATLAB语言与控制系统仿真-参考答案-第8章

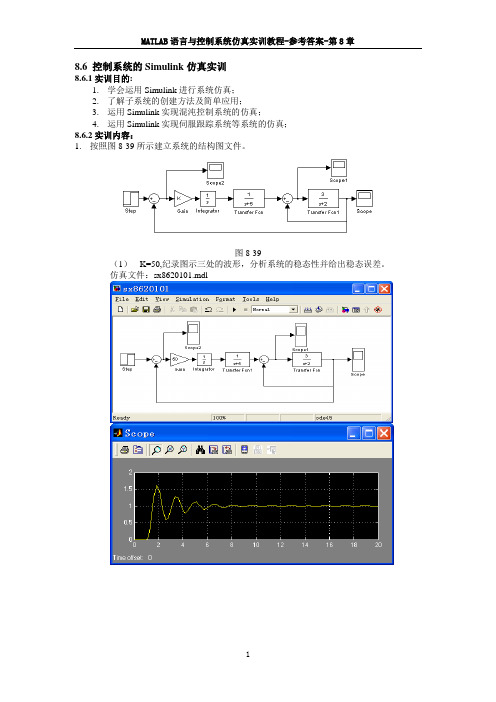
8.6 控制系统的Simulink仿真实训8.6.1实训目的:1.学会运用Simulink进行系统仿真；2.了解子系统的创建方法及简单应用；3.运用Simulink实现混沌控制系统的仿真；4.运用Simulink实现伺服跟踪系统等系统的仿真；8.6.2实训内容：1.按照图8-39所示建立系统的结构图文件。

图8-39（1）K=50,纪录图示三处的波形，分析系统的稳态性并给出稳态误差。

仿真文件：sx8620101.mdl系统稳定，稳态误差为0；（2）K=200,纪录图示三处的波形，根据曲线分析系统的稳定性。

仿真文件：sx8620102.mdl由输出曲线可以看出闭环系统不稳定；（3）编写程序求取K=200时的闭环传递函数，求出系统的闭环极点（特征根），说明系统的稳定性，分析与（2）得出的结论是否一致。

%实训8620103.mn1=3;d1=[1,2];[n2,d2]=cloop(n1,d1);sysa=tf(n2,d2);sysb=tf([200],[1,0])*tf([1],[1,5]);sysc=sysa*sysb/(1+sysa*sysb);[nc,dc]=tfdata(sysc,'v');roots(dc)>> ans =-12.0549 1.0275 + 6.9797i 1.0275 - 6.9797i -5.0000 + 0.0000i -5.0000 - 0.0000i有两个特征根在右半平面，闭环系统不稳定；与（2）得出的稳定性结论一致。

2. 子系统创建实验（1）建立如下系统。

（2）选定范围,创建子系统并定义变量a 。

图8-40(3)利用创建的子系统,分别记录10,8,6,4,2 a 时所示系统的输出波形。

a=2a=4a=6a=8a=103.已知四维混沌系统的运动方程如下，试用Simulink 进行仿真。

⎪⎪⎩⎪⎪⎨⎧+-=+-=-+=+-=321444213343121243212110)(10)(35x x x x xx x x x x x x x x x xx x x x x x （1）四个积分器的初始值自定，建议在（0.01，3.0）范围内随机给出。

MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识；2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法；3.学会通过MATLAB 绘图解决一些实际问题；4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法；5.学会制作简单的MATLAB 动画。

图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。

)cos()(0αtv t x = %水平方向的行程； 205.0)sin()(gt tv t y -=α %垂直方向的行程；其中,0v 是初速度；g 是重力加速度,为9.82m/s ；t 是时间。

〔2炮弹发射程序举例：分析以下程序以及图3-47各个图形的实际意义。

a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程；绘图要求：◆ 标题设为"炮弹垂直发射问题"；◆ 在图上通过添加文本的方式表明初速度； ◆ 在x 轴标注"时间"；◆ 在y 轴上标注"垂直距离"； ◆ 添加网格线；◆ 将310m/s 的曲线改为线粗为2的红色实线； ◆ 将290m/s 的曲线改为线粗为3的绿色点划线；◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线；a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程运行结果如下： zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。

MATLAB与控制系统仿真练习题(含图)及答案

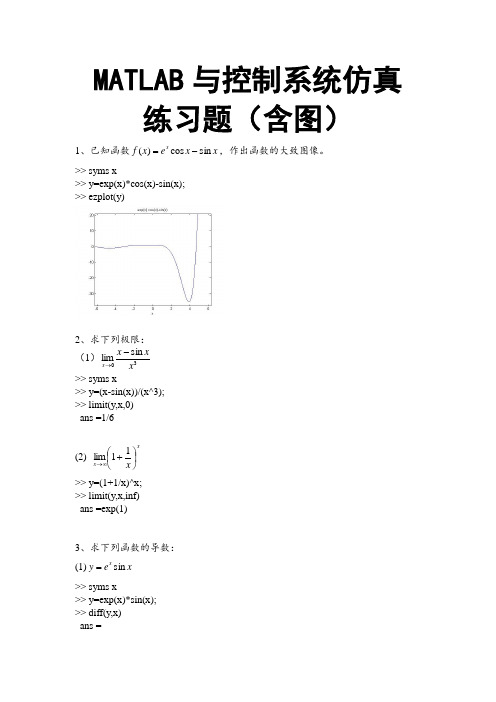
MATLAB 与控制系统仿真练习题（含图）1、已知函数x x e x f x sin cos )(-=，作出函数的大致图像。

>> syms x>> y=exp(x)*cos(x)-sin(x); >> ezplot(y)2、求下列极限：（1）30sin lim xx x x -→ >> syms x>> y=(x-sin(x))/(x^3);>> limit(y,x,0)ans =1/6(2) xx x ⎪⎭⎫ ⎝⎛+∞→11lim >> y=(1+1/x)^x;>> limit(y,x,inf)ans =exp(1)3、求下列函数的导数：(1)x e y x sin =>> syms x>> y=exp(x)*sin(x);>> diff(y,x)ans =exp(x)*sin(x)+exp(x)*cos(x)(2) x e x x y 22sin +=>> syms x>> y=sin(x)+x^2*exp(2*x);>> diff(y,x)ans =cos(x)+2*x*exp(2*x)+2*x^2*exp(2*x)4、求.)1(532⎰-dx x x 和.sin ⎰xdx e x（1）.)1(532⎰-dx x xsyms x>> int(x^2*(1-x^3)^5)ans =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^3（2）.sin ⎰xdx e x>> int(exp(x)*sin(x))ans =-1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x)5、求.)(102⎰-dx x x 和.1102⎰-dx x x (1) .)(102⎰-dx x x>> syms x>> int(x-x^2,0,1)ans =1/6(2) .1102⎰-dx x x>> syms x>> int(x*(1-x^2)^0.5,0,1)ans =1/36、已知二元函数),(cos )sin(2xy xy z +=试求y x z x z y z x z ∂∂∂∂∂∂∂∂∂222,,,。

MATlab 仿真部分习题答案

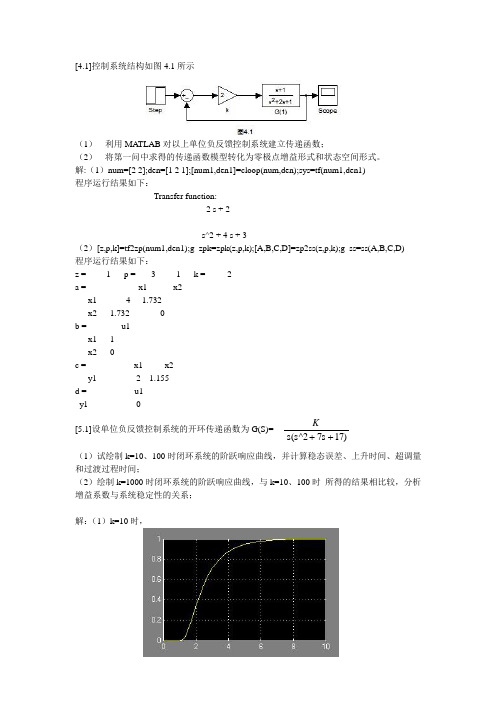
[4.1]控制系统结构如图4.1所示（1）利用MATLAB对以上单位负反馈控制系统建立传递函数；（2）将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。

解:（1）num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下：Transfer function:2 s + 2-------------s^2 + 4 s + 3（2）[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下：z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)（1）试绘制k=10、100时闭环系统的阶跃响应曲线，并计算稳态误差、上升时间、超调量和过渡过程时间；（2）绘制k=1000时闭环系统的阶跃响应曲线，与k=10、100时所得的结果相比较，分析增益系数与系统稳定性的关系；解：（1）k=10时，K=100时，K=10时，利用MA TLAB工作区输入程序：num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10)；c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为：稳定值c=0.5882，响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时，稳定值c=5.882，响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%（3）k=1000时，由其响应曲线可知，增益系数越大，其稳定性越差。

MATLAB语言及控制系统仿真_参考答案解析_第2章

2.12 MATLAB 语言的数值运算-实训2.12.1实训目的1.学会矩阵的建立方法及其矩阵的转置、相乘、求逆等运算；2.识别了解特殊矩阵；3.学会求解方程与方程组；4.学会通过编程解决一些实际问题； 2.12.2实训内容 1.矩阵建立及其运算]4321012345[1-----=A[]0.19.08.07.06.05.04.03.02.01.02=A ]0.19.08.07.06.05.04.03.02.01.0[3=A][40.19.08.07.06.05.04.03.02.01.0e e e e e e e e e e A = ]2222222222[50.19.08.07.06.05.04.03.02.01.0=A求（1）211A A D += （2）232A A D -= （3）4/.13A D = （4）5*.44A A D = （5）5*35A D = （6）)2(.^16A D =>> A1=-5:4;>> A2=0.1:0.1:1.0; >> A3=sqrt(A2); >> A4=exp(A2); >> A5=2.^(A2); >> format bank >> D1=A1+A2 D1 =-4.90 -3.80 -2.70 -1.60 -0.50 0.60 1.70 2.80 3.90 5.00 >> D2=A3-A2 D2 =0.22 0.25 0.25 0.23 0.21 0.17 0.14 0.09 0.05 0 >> D3=1./A4 D3 =0.90 0.82 0.74 0.67 0.61 0.55 0.50 0.45 0.41 0.37 >> D4=A4.*A5D4 =1.18 1.40 1.66 1.972.33 2.763.27 3.874.595.44 >> D5=3*A5 D5 =3.22 3.45 3.69 3.964.24 4.55 4.875.22 5.606.00 >> D6=A1.^2 D6 =25.00 16.00 9.00 4.00 1.00 0 1.00 4.00 9.00 16.002.建立矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=1418712106114231359152345686420B（1）矩阵B 的逆矩阵)(inv B （2）矩阵B 对应的行列式)det(B>> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]B =0 2.00 4.00 6.00 8.00 -6.00 -5.00 -4.00 -3.00 -2.00 15.00 9.00 5.00 13.00 3.00 2.00 4.00 11.00 6.00 10.00 12.00 7.00 8.00 1.00 14.00 >> inv(B) ans =-0.18 0.29 0.11 0.07 0.07 0.31 -0.72 -0.20 -0.23 -0.07 -0.21 0.11 0.03 0.21 -0.02 0.05 0.11 0.08 0.02 -0.04 0.12 0.04 -0.02 -0.06 0.06 >> det(B) ans =-17568.00（3）利用矩阵元素的提取方法建立以下矩阵 ①矩阵b01:矩阵B 的3～4行元素； ②矩阵b02:矩阵B 的2～5列元素；③矩阵b03:由矩阵B 的1～3行2～4列交叉点所对应的元素组成； >> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]; >> b01=B(3:4,:) b01 =15.00 9.00 5.00 13.00 3.002.00 4.00 11.00 6.00 10.00 >> b02=B(:,2:5) b02 =2.00 4.00 6.00 8.00 -5.00 -4.00 -3.00 -2.00 9.00 5.00 13.00 3.004.00 11.00 6.00 10.00 7.00 8.00 1.00 14.00 >> b03=B(1:3,2:4) b03 =2.00 4.00 6.00 -5.00 -4.00 -3.00 9.00 5.00 13.00 3.矩阵的转置与翻转已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=151413121110987654321m ,求取以下矩阵观察并记录。

MATLAB语言与控制系统仿真-参考答案-第1章

1.6 MATLAB操作基础-实训1.6.1实训目的1.熟悉MATLAB语言环境，识别MATLAB桌面和命令窗口，命令历史窗口，工作空间窗口等；2.练习设置变量精度或变量显示方式；3.练习通过MATLAB编程解决一些实际问题；4.通过作图总结自变量增量设置对作图结果的影响；5.学会求解方程、方程组的基本方法；6.练习M文件的建立与执行；7.学会进入工具箱的演示系统，以便于进一步了解和学习感兴趣的知识，为以后的自主学习奠定基础。

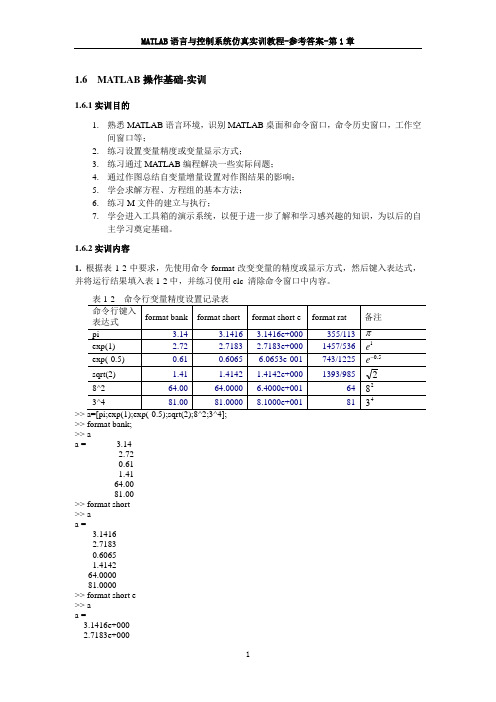
1.6.2实训内容1.根据表1-2中要求，先使用命令format改变变量的精度或显示方式，然后键入表达式，并将运行结果填入表1-2中，并练习使用clc 清除命令窗口中内容。

>> format bank;>> aa = 3.142.720.611.4164.0081.00>> format short>> aa =3.14162.71830.60651.414264.000081.0000>> format short e>> aa =3.1416e+0002.7183e+0006.0653e-001 1.4142e+000 6.4000e+001 8.1000e+001 >> format rat >> a a =355/113 1457/536 743/1225 1393/985 64 812. 编写MA TLAB 程序计算，根据程序运算结果填空（要求保留两位小数）（1）58.135.0+=-ea =（ 4.29 ）；程序为： a=exp(-0.5)+sqrt(13.58)>> format bank;>> a=exp(-0.5)+sqrt(13.58) a =4.29（2）已知两个圆的半径分别为cm 5.31=r ， cm 62=r ，则两个圆的周长分别为=1l （ 21.99 ）cm, =2l （ 37.70 ）cm;面积分别为=1s （ 38.48 ）2cm ，=2s （ 113.10 ）2cm程序：>> format bank; >> r=[3.5 6]; >> [2*pi*r;pi*r.*r]提示：圆的周长计算公式为：r L π2=，圆的面积2r S π=，其中r 为圆的半径。

控制系统的MATLAB仿真和设计课后答案

第二章1>>x=[15 22 33 94 85 77 60]>>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1 -2 3 -4 2 -3] ;>>n=length(T);>>TT=T';>>for k=n-1:-1:0>>B(:,n-k)=TT.^k;>>end>>B>>test=vander(T)3>>A=zeros(2,5);>>A(:)=-4:5>>L=abs(A)>3>>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为'; cr='余多项式为';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')]) 6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axis equal>>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),grid on;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');grid;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta); >>polar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>hold on>>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1:4))); >>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0]); >>grid on>>hold off第四章1>>for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend2M文件：function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序：[s,p]=fcircle(10)3>>y=0;n=100;for i=1:ny=y+1/i/i;end>>y4 M文件：function f=factor(n)if n<=1elsef=factor(n-1)*n; end主程序：>>s=0;for i=1:5s=s+factor(i); end>>s5>>sum=0;i=1; while sum<2000sum=sum+i;i=i+1;end;>>n=i-26for循环M文件：function k=jcsum(n) k=0;for i=0:nk=k+2^i;end>>jcsum(63)While循环M文件：function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end主程序：>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >>b=[13,-9,6,0]';>>x=A\b2M文件：function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])3>>X=linspace(0,2*pi,50);>>Y=sin(X);>>P=polyfit(X,Y,3)>>AX=linspace(0,2*pi,50);>>Y=sin(X);>>Y1=polyval(P,X)>>plot(X,Y,':O',X,Y1,'-*')4>>x=0:2.5:10;>>h=[0:30:60]';>>T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; >>xi=[0:0.5:10];>>hi=[0:10:60]';>>temps=interp2(x,h,T,xi,hi,'cubic');>>mesh(xi,hi,temps);第六章1>>syms x>>y=finverse(1/tan(x))2>>syms x y>>f=1/(1+x^2); g=sin(y);>>fg=compose(f,g)>>g=(exp(x)+x*sin(x))^(1/2);>>dg=diff(g)4>>F=int(int('x*exp(-x*y)','x'),'y')5>>syms x>>F=ztrans(x*exp(-x*10))6>>a=[0 1;-2 -3];>>syms s>>inv(s*eye(2)-a);7>>f=solve('a*x^2+b*x+c')8>>f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')9>>y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') >>ezplot(y),grid on10>>a=maple('simplify(sin(x)^2+cos(x)^2);')11>>f=maple('laplace(exp(-3*t)*sin(t),t,s);')12>>syms t x>>F=sin(x*t+2*t);>>L=laplace(F)第七章1234567第八章1-1>>h=tf([5,0],[1,2,2])1-2>>s = tf('s');>>H = [5/(s^2+2*s+2) ];>>H.inputdelay =21-3>>h=tf([0.5,0],[1,-0.5,0.5],0.1) 2>>num=2*[1,0.5];den=[1,0.2,1.01];>>sys=tf(num,den)>>[z,p,k]=tf2zp(num,den);>>zpk(z,p,k)>>[A,B,C,D]=tf2ss(num,den);>>ss(A,B,C,D)3 >>num=[1,5]; den=[1,6,5,1]; ts=0.1; >>sysc=tf(num,den);>>sysd=c2d(sysc,ts,'tustin')4>>r1=1;r2=2;c1=3;c2=4;>>[A,B,C,D]=linmod('x84');>>[num,den]=ss2tf(A,B,C,D);>>sys=tf(num,den)5>>A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2]; >>n=size(A)>>Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章1>>num=[2,5,1];den=[1,2,3];>>bode(num,den);grid on ;>>figure;>>nyquist(num,den);2>>num=5*[1,5,6];den=[1,6,10,8];>>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;3>>kosi=0.7;wn=6;>>num=wn^2;den=[1,2*kosi*wn,wn^2];>>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;4 M文件：function [rtab,info]=routh(den)info=[];vec1=den(1:2:length(den)); nrT=length(vec1); vec2=den(2:2:length(den)-1);rtab=[vec1; vec2, zeros(1,nrT-length(vec2))];for k=1:length(den)-2,alpha(k)=vec1(1)/vec2(1);for i=1:length(vec2),a3(i)=rtab(k,i+1)-alpha(k)*rtab(k+1,i+1);endif sum(abs(a3))==0a3=polyder(vec2);info=[info,'All elements in row ',...int2str(k+2) ' are zeros;'];elseif abs(a3(1))<epsa3(1)=1e-6;info=[info,'Replaced first element;'];endrtab=[rtab; a3, zeros(1,nrT-length(a3))];vec1=vec2; vec2=a3;end主程序：>>den=[1,2,8,12,20,16,16];>>[rtab,info]=routh(den)>>a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end5>>num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1])); >>[gm,pm,wg,wc]=margin(num,den)第十章1 M文件：function varargout=rg_lead(ng0,dg0,s1)if nargout==1ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=ngv/dgv;thetal=pi-angle(g);zc=real(s1)-imag(s1)/tan(thetal);t=-1/zc;varargout{1}=[t,1];elseif nargout==2ngv=polyval(ng0,s1); dgv=polyval(dg0,s1);g=ngv/dgv; theta=angle(g); phi=angle(s1);if theta>0phi_c=pi-theta;endif theta<0;phi_c=-thetaendtheta_z=(phi+phi_c)/2; theta_p=(phi-phi_c)/2;z_c=real(s1)-imag(s1)/tan(theta_z);p_c=real(s1)-imag(s1)/tan(theta_p);nk=[1 -z_c]; varargout{2}=[1 -p_c]; kc=abs(p_c/z_c);if theta<0kc=-kcendvarargout{1}=kc*nk;elseerror('输出变量数目不正确！');end主程序：>> ng0=[1]; dg0=10000*[1 0 -1.1772];>>g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数>>s=kw2s(0.7,0.5) %期望的闭环主导极点>>ngc=rg_lead(ng0,dg0,s);>>gc=tf(ngc,1)>>g0c=tf(g0*gc);>>rlocus(g0,g0c);>>b1=feedback(g0,1); %未校正系统的闭环传递函数>>b2=feedback(g0c,1); %校正后系统的闭环传递函数>>figure,step(b1,'r--',b2,'b'); grid on%绘2M文件：function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序：>>KK=20;s1=-2+i*sqrt(6);a=1>>ng0=[10];dg0=conv([1,0],[1,4]);>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>gc=tf(ngc,dgc)>>g0c=tf(KK*g0*gc);>>b1=feedback(k*g0,1);>>step(b1,'r--',b2,'b');grid on3M文件：function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序：>>KK=128;s1=-2+i*2*sqrt(3);a=2>>ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>gc=tf(ngc,dgc)>>g0c=tf(KK*g0*gc);>>rlocus(g0,g0c);>>b2=feedback(g0c,1);>>figure,step(b1,'r--',b2,'b');grid on4M文件：function [ngc,dgc]=lead4(ng0,dg0,KK,Pm,w)[mu,pu]=bode(KK*ng0,dg0,w); [gm,pm,wcg,wcp]=margin(mu,pu,w); alf=ceil(Pm-pm+5); phi=(alf)*pi/180;a=(1+sin(phi))/(1-sin(phi)), dbmu=20*log10(mu);mm=-10*log10(a); wgc=spline(dbmu,w,mm), T=1/(wgc*sqrt(a)),ngc=[a*T,1]; dgc=[T,1];主程序：>>ng0=[1];dg0=conv([1,0,0],[1,5]);>>g0=tf(ng0,dg0);>>w=logspace(-3,3);>>KK=1;Pm=50;>>[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);>>gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);>>bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off>>[gm,pm,wcg,wcp]=margin(g0c)>>Kg=20*log10(gm)>>g1=feedback(g0c,1);>>bode(g1),grid on,>>[mag,phase,w]=bode(g1);>>a=find(mag<=0.707*mag(1));>>wb=w(a(1))>>max(mag)>>b=find(mag==max(mag))>>wr=w(b)5M文件：function [ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)[mu,pu]=bode(ng0,dg0,w); %计算原系统的对数频率响应数据[gm,pm,wcg,wcp]=margin(mu,pu,w); %求取原系统的相角裕度和剪切频率alf=ceil(Pm-pm+5); %计算控制器提供的最大超前角度，phi=(alf)*pi/180; %将最大超前角转换为弧度单位a=(1+sin(phi))/(1-sin(phi)); %计算a值dbmu=20*log10(mu); %系统的对数幅值mm=-10*log10(a); %wm处的控制器对数幅值wgc=spline(dbmu,w,mm); %差值求取wm，认为wm＝wc T=1/(wgc*sqrt(a)); %计算Tngc=[a*T,1]; dgc=[T,1];主程序：>>KK=40; Pm=50;>>ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4])); >>g0=tf(ng0,dg0) ;>>w=logspace(-2,4);>>[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)>>gc=tf(ngc,dgc),g0c=tf(g0*gc);>>b1=feedback(g0,1); b2=feedback(g0c,1);>>step(b1,'r--', b2,'b'); grid on>>figure, bode(g0,'r--',g0c,'b',w), grid on,>>[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)。

MATLAB仿真课后习题答案

MATLAB仿真课后习题答案MATLAB仿真课后习题答案第一章1.要求在闭区间[0，2Π]上产生具有10个等间距采样点的一维数组。

试用两种不同的指令实现。

解答：方法1：a=0:2*pi/9:2*pi方法2：a1=linspace(0,2*pi,10)4.任意建立矩阵A，然后找出在[10,20]区间的元素的位置。

解答：A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式：命令文件和函数文件。

命令文件没有输入输出参数，执行时只需在命令窗口中键入文件名回车即可；而函数文件是一条以function语句作为引导。

即文件的第一行为function[返回参数1，返回参数2，…]=函数名(输入参数1，输入参数2，…)。

这一行的有无是区分命令文件与函数文件的重要标志。

函数文件可以接受输入变量，还可以返回输出变量，执行时需在命令窗口中以固定格式调用函数方可。

习题22-1.编写程序，建立向量N=[1,2,3,4,5]，然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答：>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^2 2-2从键盘输入一个3位数的整数，将它反向输出。

如输入639，输出936。

输入一个百分制成绩，要求输出成绩等级A、B、C、D、E。

其中90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下为E。

要求：(1)分别用if语句和switch语句实现。

(2)输入百分制成绩后要判断该成绩的合理性，对不合理的成绩应输出出错信息。

【免费下载】控制系统的MATLAB仿真与设计课后答案

y=y+1/i/i; end >>y
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

控制系统的Matlab仿真与设计课后答案

disp(m)
end
end
4.2[s,p]=fcircle(10)
4.3y=0;n=100;
fori=1:n
y=y+1/i/i;
end
y
4.4s=0;
fori=1:5
s=s+factor(i);
end
s
4.5sum=0;i=1;
whilesum<2000
sum=sum+i;
i=i+1;
end;
n=i-2
y=2*exp(-0.5*x).*sin(2*pi*x);
plot(x,y),grid on;
3.3
t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('X'),ylable('Y'),zlable('Z');grid;
3.4
theta=0:0.01:2*pi;
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho,'k');
3.5
[x,y,z]=sphere(20);
fg=compose(f,g)
6.3symsx
g=(exp(x)+x*sin(x))^(1/2);
Y=sin(X);
P=polyfit(X,Y,3)

MATLAB语言与控制系统仿真-参考答案-第7章

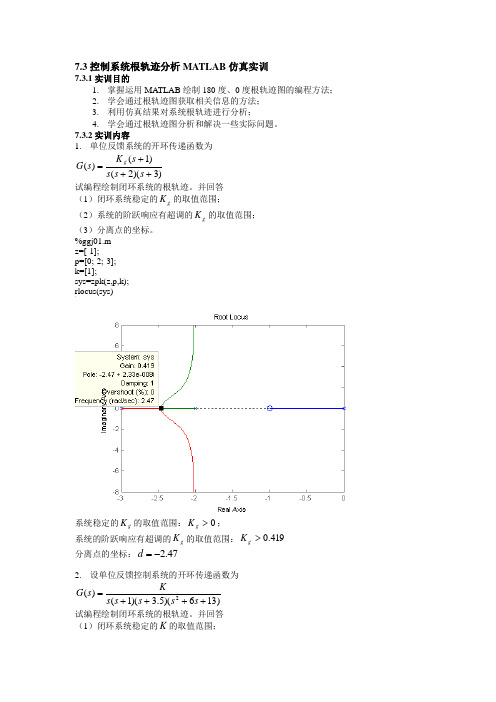
7.3控制系统根轨迹分析MATLAB 仿真实训7.3.1实训目的1. 掌握运用MATLAB 绘制180度、0度根轨迹图的编程方法；2. 学会通过根轨迹图获取相关信息的方法；3. 利用仿真结果对系统根轨迹进行分析；4. 学会通过根轨迹图分析和解决一些实际问题。

7.3.2实训内容1. 单位反馈系统的开环传递函数为)3)(2()1()(+++=s s s s K s G g试编程绘制闭环系统的根轨迹。

并回答（1）闭环系统稳定的g K 的取值范围；（2）系统的阶跃响应有超调的g K 的取值范围；（3）分离点的坐标。

%ggj01.m z=[-1]; p=[0;-2;-3]; k=[1];sys=zpk(z,p,k); rlocus(sys)系统稳定的g K 的取值范围：0>g K ；系统的阶跃响应有超调的g K 的取值范围：419.0>g K 分离点的坐标：47.2-=d2. 设单位反馈控制系统的开环传递函数为)136)(5.3)(1()(2++++=s s s s s Ks G试编程绘制闭环系统的根轨迹。

并回答（1）闭环系统稳定的K 的取值范围；（2）根轨迹与虚轴的交点坐标；（3）分离点的坐标。

ggj02.m%根轨迹仿真实训第2题 n=1;d=conv([1,0],conv([1,1],conv([1,3.5],[1,6,13]))); rlocus(n,d)由图上数据可知：闭环系统稳定的K 的取值范围：9.700<<K ；根轨迹与虚轴的交点坐标：02.1j ±；分离点的坐标：403.0-=d 。

3. 设单位反馈控制系统的开环传递函数为)204)(4()(2+++=s s s s Ks G试编程绘制闭环系统的根轨迹。

并回答（1）闭环系统稳定的K 的取值范围；（2）根轨迹与虚轴的交点坐标；（3）各个分离点的坐标。

%根轨迹仿真实训第3题 n=1;d=conv([1,0],conv([1,4],[1,4,20])); rlocus(n,d)由图上数据可知：闭环系统稳定的K 的取值范围：2620<<K ；根轨迹与虚轴的交点坐标：18.3j ±；分离点的坐标：21-=d ，45.2j 232±-=，d 。