一线三等角模型16927PPT课件
合集下载
中考数学二轮复习《一线三等角模型》知识梳理及典例讲解课件

∠CAD=45°.∴ DE=CD-CE=3.∵ F为AD的中点,∴ AF=
DF= AD=2.∵
∠ADC=90°,∴ ∠EDM=180°-∠ADC=
90°.∵ ∠M=45°,∴
DM=
=3,EM=
=3
.∴ MF=
DF+DM=5.∵ ∠PFE=45°,∴ ∠AFG+∠EFM=180°-
∠PFE=135°.∵ ∠FAG=45°,∴ ∠AFG+∠FGA=180°-
∠FAG=135°.∴ ∠FGA=∠EFM.又∵ ∠FAG=∠M=45°,
∴ △AFG∽△MEF.∴
= ,即 = .∴
AG= .
典例5图答案
强化练习
1. 如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上.
典例4图答案
典例5 如图,正方形ABCD的边长为4,E是边CD上一点,且CE=1,F
是AD的中点,对角线AC交BE于点N,P是线段BE上一点,连接EF,
PF,PF与AC相交于点G.若∠PFE=45°,求AG的长.
解:如图,延长AD至点M,连接EM,使∠M=45°.
∵ 四边形ABCD是正方形,∴ AD=CD=4,∠ADC=90°,
=CE.在Rt△ABC中,BC=
=2
,∴ BD=BC-DC=2 -2.∴ CE
=2 -2.∴ AE=AC-CE=4-2 .③ 当AE=DE时,∠EAD=∠ADE
=45°,∴ ∠AED=90°.∴ DE⊥AC.∵ ∠CAD=∠C=45°,∴ AD=CD.∴
AE= AC=1.综上所述,当△ADE是等腰三角形时,AE的长为2或4-2
DF= AD=2.∵
∠ADC=90°,∴ ∠EDM=180°-∠ADC=
90°.∵ ∠M=45°,∴
DM=
=3,EM=
=3
.∴ MF=
DF+DM=5.∵ ∠PFE=45°,∴ ∠AFG+∠EFM=180°-
∠PFE=135°.∵ ∠FAG=45°,∴ ∠AFG+∠FGA=180°-
∠FAG=135°.∴ ∠FGA=∠EFM.又∵ ∠FAG=∠M=45°,
∴ △AFG∽△MEF.∴
= ,即 = .∴
AG= .
典例5图答案
强化练习
1. 如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上.
典例4图答案
典例5 如图,正方形ABCD的边长为4,E是边CD上一点,且CE=1,F
是AD的中点,对角线AC交BE于点N,P是线段BE上一点,连接EF,
PF,PF与AC相交于点G.若∠PFE=45°,求AG的长.
解:如图,延长AD至点M,连接EM,使∠M=45°.
∵ 四边形ABCD是正方形,∴ AD=CD=4,∠ADC=90°,
=CE.在Rt△ABC中,BC=
=2
,∴ BD=BC-DC=2 -2.∴ CE
=2 -2.∴ AE=AC-CE=4-2 .③ 当AE=DE时,∠EAD=∠ADE
=45°,∴ ∠AED=90°.∴ DE⊥AC.∵ ∠CAD=∠C=45°,∴ AD=CD.∴
AE= AC=1.综上所述,当△ADE是等腰三角形时,AE的长为2或4-2
精品一线三等角相似模型.ppt课件
• (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
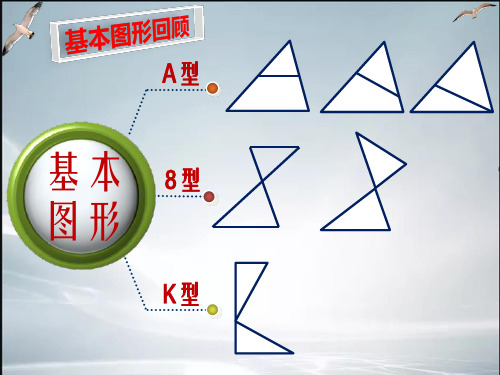
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
CA MBPC5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
CA MBPC5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
相似三角形基本模型一线三等角精品PPT课件

△ABE∽ △ECF ∽ △AEF
A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF
F
((2)1)点点E为E为BBCC上上任任意意一一点点若,∠若B= ∠∠CB==α,∠∠CA=E6F0°= ∠, ∠CA,则EF△=A∠BCE,则与△ EC△FA的B关E与系△还成EC立F吗的?关系还成立吗?
说明理由
B
α
α
B
E
α
C
点拨:要善于运用类比、迁移的数学方法 解决问题。
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E 重合,若AD=10, AB= 8,
则EF=___5___
D
F
C
EE
A
点拨:要善于在复杂图形中寻找基本型。 B
A
E F
B
D
C
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的 中点, 且∠EDF =∠C, (1) 若BE·CF=48,则AB=__8___
(2)在(1)的条件下,若EF=m,
则S△DEF =___3__m__
A EH
F
P
B
D
点拨:联想基本模型,寻找 相关结论。
C
A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF
F
((2)1)点点E为E为BBCC上上任任意意一一点点若,∠若B= ∠∠CB==α,∠∠CA=E6F0°= ∠, ∠CA,则EF△=A∠BCE,则与△ EC△FA的B关E与系△还成EC立F吗的?关系还成立吗?
说明理由
B
α
α
B
E
α
C
点拨:要善于运用类比、迁移的数学方法 解决问题。
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E 重合,若AD=10, AB= 8,
则EF=___5___
D
F
C
EE
A
点拨:要善于在复杂图形中寻找基本型。 B
A
E F
B
D
C
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的 中点, 且∠EDF =∠C, (1) 若BE·CF=48,则AB=__8___
(2)在(1)的条件下,若EF=m,
则S△DEF =___3__m__
A EH
F
P
B
D
点拨:联想基本模型,寻找 相关结论。
C
2024成都中考数学第一轮专题复习之第四章 微专题 一线三等角模型解决全等、相似问题 教学课件

∴∠BCE=∠CAD. ∵△ABC为等腰直角三角形,∴AC=BC.
第1题图
在△BCE和△CAD中,
微专题 一线三等角模型解决全等、相似问题
BEC CDA, BCE CAD, BC CA,
∴△BCE≌△CAD(AAS), ∴CD=BE, ∵DE=2BE, ∴CE=3BE,
∴BC= CE 2 BE 2 3BE 2 BE 2 10BE ,
微专题
一线三等角模型解 决全等、相似问题
微专题 一线三等角模型解决全等、相似问题
一阶 认识模型
模型分析 1. 模型特点: ∠1,∠2,∠3的顶点在同一条直线上,且∠1=∠2=∠3. 基本图形:
一线三等角
一线三垂直
微专题 一线三等角模型解决全等、相似问题 2. 一线三等角模型的结论: (1)△APC和△BDP的关系是_△__A__P_C_∽__△__B__D_P__; (2)若在(1)中的条件下,增加条件_P_C__=__P_D_(_或__A_P_=__B__D_或__A__C_=__B_P_)_,可以 得到△APC≌△BDP.
D G, DAE GEF , AE EF ,
∴△ADE≌△EGF(AAS),
∴AD=EG=4.
∵E为CD的中点,
∴DE=CE=GF=
1 2
CD=2,
∴CG=EG-EC=2,
∴在Rt△CGF中,
CF= CG2 FG2 2 2 .
G
例3题图
微专题 一线三等角模型解决全等、相似问题
例4 如图,在△ABC中,D是BC上一点,连接AD,E是AD上一点,连
例2题图
微专题 一线三等角模型解决全等、相似问题 引入模型
2022成都26题图
微专题 一线三等角模型解决全等、相似问题
《相似三角形的判段——“一线三等角”》公开课教学PPT课件(终稿)

思考
等腰ABC中AB AC,D是BC中点,有MDN B, 请找出图中所有的相似三角形.
上题中,若AB
AC
பைடு நூலகம்10,
BC
12,
SDMN
1 4
SABC ,
求MN长.
思考
变式1.在等腰ABC中,AB AC 10, BC 12, D是BC上任 一点,MDN B,若DM AB,是否有可能使SDNC 4SDMB,如果有可能求BD的长.
问题探究
变式2:在平面直角坐标系中,直线l1:y 2x 4与 x轴y轴分别交于A, B两点.将OAB沿l1翻折. (1) 求O的 对 称 点P的 坐 标.
(2) 直 线l2过 点P, 且 与直 线l1的 夹角 是45, 求 两直 线l1, l2的 交点 坐 标.
回顾反思
1、“一线三等角”模型的特征,以及模型的 提炼、变式和运用 2、从复杂图形中提炼,还原,创设出基本模 型、快速灵活运用基本结论、反思、拓展.
变式2.在等腰ABC中,AB AC 10, BC 12, D是BC上任一 点,MDN B,若BD 4,是否存在这样的位置,使DMN 成为直角三角形, 若存在求BM长.
相似三角形的判断—— “一线三角形”
情景再现
在等边ABC中,D是BC边上的一点,把 ABC折叠,使点 A落
在BC边上的点 D处,折痕为 MN.若 BD 2,请求出 AM 的值.
DC 3
AN
一线三等角
有三个相等角 三个相等角的顶点在一直线上
抽象模型
常见一线三等角图形
点P在线段AB上
点P在线段AB延长线上
问题探究
问题:如图在ABC中,AB AC 5, BC 8,点 D,E分别在BC, AC上,连接AD, DE,使1 B (1)当BD 2,求线段CE的长.
一线三等角模型ppt课件

一线三等角模型
2019
-
1
通俗地讲,一条直线上有三个相等的角一般就会存在相似的三角形!
什么是一线三等角?
如图,等腰△ABC中,AB=AC,∠EDF=∠B,请问图中 是否有相似三角形?
相似三角形判定 定理一: 两角对应相等, 两三角形相似。
注意:对应边千万不要找错,相同的角 标记同一个符号会比较清晰!
2019 2
“一线三等角”模型 教学目标及重、难点
教学目标: 用“一线三等角”基本模型解决相似三角形中的相 关问题; 重点:掌握“一线三等角”基本模型; 难点: “一线三等角”基本图形的提炼、变式和运用。
特别是“一线三直角”辅助线的构造
2019 3
“一线三等角”模型按照角度的分类
锐角形一线三等角
中点型“一线三等角”模型
中点型: 至少有三 对相似三 角形
β
再次提醒:对应边和对应角千万不要找错!
2019
-
7
一线三直角在直角坐标系中的应用
2012年上海中考24题
1 t 2
4 2
t
2
1 t 2
4
2019
-
8
一线三直角巧求点坐标
尝试用上题中你总结的方法解答下题: 2011年宝山一模18题
方法二:两点 距离公式; 方法三:利用 互相垂直的一 次函数(针对 优等生,且此 法适用于任意 三角形翻折)
PD DH CD CH PD AD CD CH DH AD
3 x
2
3 x 2
2
BC 4
3
13
13 2
PD PC AD PD 13 PC BC 2
15
2019
2019
-
1
通俗地讲,一条直线上有三个相等的角一般就会存在相似的三角形!
什么是一线三等角?
如图,等腰△ABC中,AB=AC,∠EDF=∠B,请问图中 是否有相似三角形?
相似三角形判定 定理一: 两角对应相等, 两三角形相似。
注意:对应边千万不要找错,相同的角 标记同一个符号会比较清晰!
2019 2
“一线三等角”模型 教学目标及重、难点
教学目标: 用“一线三等角”基本模型解决相似三角形中的相 关问题; 重点:掌握“一线三等角”基本模型; 难点: “一线三等角”基本图形的提炼、变式和运用。
特别是“一线三直角”辅助线的构造
2019 3
“一线三等角”模型按照角度的分类
锐角形一线三等角
中点型“一线三等角”模型
中点型: 至少有三 对相似三 角形
β
再次提醒:对应边和对应角千万不要找错!
2019
-
7
一线三直角在直角坐标系中的应用
2012年上海中考24题
1 t 2
4 2
t
2
1 t 2
4
2019
-
8
一线三直角巧求点坐标
尝试用上题中你总结的方法解答下题: 2011年宝山一模18题
方法二:两点 距离公式; 方法三:利用 互相垂直的一 次函数(针对 优等生,且此 法适用于任意 三角形翻折)
PD DH CD CH PD AD CD CH DH AD
3 x
2
3 x 2
2
BC 4
3
13
13 2
PD PC AD PD 13 PC BC 2
15
2019
《一线三等角模型》课件

在建筑设计中,一线三 等角模型可防止建筑形 态过于普通化,同时保 证建筑的美学性与功能 性。
一线三等角模型的应用领域
室内设计
可以用于设计会议室、酒店等 场所。
建筑设计
可以用于设计公共建筑、景观 等。
家具设计
可以用于设计桌椅、灯具等家 具。
建模方法
1
建立坐标系
根据设计需求,建立二维坐标系。
2
构造一线三等角模型的形式
《一线三等角模型》PPT 课件
本PPT课件将介绍一线三等角模型的建模方法和应用,以及如何用Python实 现该模型。
什么是一线三等角模型?
1 基本概念
一条长度为1的线段在 平面上,等分成三段, 依次连接首尾得到一个 三角形,这即为一线三 等角模型。
2 特性
3 优点
等边、等角、狭长、占 用空间小、视觉上飘逸、 新颖。
上海环球金融中心 建筑设计
建筑主体外形线条流畅,中 心部分采用一线三等角模型 造型,整个建筑寓意成长、 挑战和超越。
实战演示
1
怎样运用Python实现一线三等角模型
介绍程序员如何使用Python语言进行一线三等角模型的建模和参数化,方便后 续分析应用。
2
ห้องสมุดไป่ตู้
实战演示案例
通过一线三等角模型和Python语言实现的案例,展示该模型方法和应用的可行 性。
总结
一线三等角模型的应用前景
这一模型的美学和实用性优点促进了其在设计领域中的广泛应用,未来发展前景广阔。
未来的研究与发展方向
未来的研究将着重在拓展该模型的应用领域,提高建模准确性和自动化程度。
在坐标系中,通过角平分线和圆心等方法构造出一线三等角模型。
3
最新一线三等角模型的研究教学讲义ppt课件

推广3:如果一个四边形有一组对角相等,那么 我们称它为半对角相等的四边形.如图1中的四 边形ABCD,其中∠B=∠D。解决下列问题:
考题赏析:
2015年第8题
8.在四边形ABCD中,∠A=∠B=∠C,点E在 边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=1/2∠ADC D.∠ADE=1/3∠ADC
•
• 今天,我对自己的过错深感惶恐不安!我辜 负了国家对我的培养,辜负了社会对我的信任,
也辜负了影迷对我的喜爱!在此,我再次向大家
诚恳道歉!请大家原谅!
•
我相信,经过这次整顿,我会讲规矩、遵秩
序、重责任,在把好的作品献给大家的同时,也
要监督公司管理,守法经营,诚实守信,争做富
有文化内涵的好公司【这句浓缩一下就是
“我……争做富有文化内涵的好公司”,主语和
宾语不搭配,最后一句应改为“使公司更加富有
文化内涵”或者“使公司成为富有文化内涵的好
公司”。另外“讲规矩、遵秩序、重责任”三个 动宾短语之间,不用顿号,而用逗号。】
• 再次向社会,向一直支持我的影迷,向关 爱我的朋友家人【“朋友家人”容易产生 歧义,应改为“朋友和家人”】,真诚的 【“的”应为“地”】说一句,对不起!
2.常见类型
3.考题赏析
4.问题推广
• 推广1:如图1,已知四边形ABCD中, ∠B=∠C, AF、DE分别是∠BAD与∠CDA的 平分线。
• 结论:△ABF∽△ECD。
推广2:
已知:已知四边形ABCD中,∠B=∠C, AF、DE 分别是∠BAD与∠CDA的平分线,且E,F重合。
结论:(1)△ABE∽△ECD∽△DEA; (2)BE=CE; (3)BE2=AB×CD。
春季人教版九年级数学下册27.2一线三等角模型的应用(共15张PPT)

13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。21.9.1921.9.1901:37:4701:37:47September 19, 2021 • 14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月19日星期日上午1时37分47秒01:37:4721.9.19 • 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月上午1时37分21.9.1901:37September 19, 2021 • 16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年9月19日星期日1时37分47秒01:37:4719 September 2021 • 17、儿童是中心,教育的措施便围绕他们而组织起来。上午1时37分47秒上午1时37分01:37:4721.9.19
B
C
∴∠BED=∠CDF,
又∵∠CBA=∠ACB
∴△EBD∼△DCF.
问题2:若∠B=∠C=∠EDF=60°,△DBE与△FCD是否相似?
A
E
F
B
C
问题3.当三个角为任意角时,结论还成立吗?
(1)如图1,在△ABC中,AB=AC,E,D,F分别在AB,BC,AC上, 且∠EDF=∠B.这时△DBE与△FCD是否依然相似?
例3.如图,在△ABC中,AB=AC=10,D是边BC上的动点(不
与B、C重合),∠ADE=∠B=α,DE交AC于E,且cosα=4/5.下列
结论:(1)△ADE~△ACD;(2)当BD=6时,△ABD与△DCE全等;
(3)△DCE为直角三角形时,BD为8或12.5;(4)0<CE≤6.4.其中
B
C
∴∠BED=∠CDF,
又∵∠CBA=∠ACB
∴△EBD∼△DCF.
问题2:若∠B=∠C=∠EDF=60°,△DBE与△FCD是否相似?
A
E
F
B
C
问题3.当三个角为任意角时,结论还成立吗?
(1)如图1,在△ABC中,AB=AC,E,D,F分别在AB,BC,AC上, 且∠EDF=∠B.这时△DBE与△FCD是否依然相似?
例3.如图,在△ABC中,AB=AC=10,D是边BC上的动点(不
与B、C重合),∠ADE=∠B=α,DE交AC于E,且cosα=4/5.下列
结论:(1)△ADE~△ACD;(2)当BD=6时,△ABD与△DCE全等;
(3)△DCE为直角三角形时,BD为8或12.5;(4)0<CE≤6.4.其中
一线三等角公开课.ppt

(2)学习几何最重要是学会归纳一些简单 的基本图形,学会从复杂的图形里提 炼基本图形,并将其作为解决问题的 手段和方法。
(3)几何的学习中,要注重图形的运动和 变化,总结和发现图形之间的内在联 系,探求其规律,帮我们解决繁杂问题。
人教版数学九年级下
• 学习目标:
1、熟悉“一线三等角”的基本图形,并能解决相似中 的相关问题.
2、通过抽象模型,图形变换,变式类比等方法提高综 合解题能力.
• 学习重点:
运用“一线三等角”相似型的基本图形解题。
课前回顾
三角形相似的判定定理有哪些?
自主学习
1、如图,已知∠B=∠AEF=∠C=90°,图中有没有相似三角形?并说明理由。
A
D
A
E
E
B1
A 1
E
B
2
F
F
2
G
3C
D 3
G
C
2 1 B
D
A
E
2
1
B
F
3 C
D
3 C
典例解析 综合运用
例1:在等边△ABC中,D为BC边上一点,E为AC边上一点, 且∠ADE=60°, BD=3,CE=2,则△ABC的边长为多少?
A
E
BD
C
典例解析 综合运用
例2、如图,在平面直角坐标系中,o为坐标原点,B点坐标为(5,0) ,梯形OBCD中,CD∥OB,OD=BC=2,DC=3,∠DOB=60°,若点E、F分 别在线段DC、CB上
答:⊿ABE∽ ⊿ECF 理由:∵ ∠B=∠AEF=∠C=90°
A F
∴ ∠A+ ∠1=90°, ∠2+ ∠1=180°- ∠AEF=90 ° ∴ ∠A=∠2
(3)几何的学习中,要注重图形的运动和 变化,总结和发现图形之间的内在联 系,探求其规律,帮我们解决繁杂问题。
人教版数学九年级下
• 学习目标:
1、熟悉“一线三等角”的基本图形,并能解决相似中 的相关问题.
2、通过抽象模型,图形变换,变式类比等方法提高综 合解题能力.
• 学习重点:
运用“一线三等角”相似型的基本图形解题。
课前回顾
三角形相似的判定定理有哪些?
自主学习
1、如图,已知∠B=∠AEF=∠C=90°,图中有没有相似三角形?并说明理由。
A
D
A
E
E
B1
A 1
E
B
2
F
F
2
G
3C
D 3
G
C
2 1 B
D
A
E
2
1
B
F
3 C
D
3 C
典例解析 综合运用
例1:在等边△ABC中,D为BC边上一点,E为AC边上一点, 且∠ADE=60°, BD=3,CE=2,则△ABC的边长为多少?
A
E
BD
C
典例解析 综合运用
例2、如图,在平面直角坐标系中,o为坐标原点,B点坐标为(5,0) ,梯形OBCD中,CD∥OB,OD=BC=2,DC=3,∠DOB=60°,若点E、F分 别在线段DC、CB上
答:⊿ABE∽ ⊿ECF 理由:∵ ∠B=∠AEF=∠C=90°
A F
∴ ∠A+ ∠1=90°, ∠2+ ∠1=180°- ∠AEF=90 ° ∴ ∠A=∠2
初中数学北师大九年级上册图形的相似-相似三角形“一线三等角型”PPT

又ADE C B
△ADE ∽△ABD;
又D为中点
根据三线合一知 ABD为直角三角形
ADE为直角三角形
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(1)证明:AB AC且ADE C ADE B C
DAB ADB 180 B
,求CF的长
证明: ABC 为பைடு நூலகம்边三角形
B C 60
又EDF ABC
EDF B C
在BDE中BED EDB 180 - B
且EDB CDF 180 - EDF
EDB CFD
△BDE ∽△CFD
BD BE CF CD
1 即 1 3
CF 1 CF 1
3
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
ADB CDE 180 ADE
又ADE B
ADB CED △ABD ∽△DCE ;
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(2)解:由(1)可得
y 8
8-y
x
10-x
BD AB CE DC
x 8 8 - y 10 - x
化简得y 1 x2 - 5 x (8 0 x 10) 84
△ADE ∽△ABD;
又D为中点
根据三线合一知 ABD为直角三角形
ADE为直角三角形
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(1)证明:AB AC且ADE C ADE B C
DAB ADB 180 B
,求CF的长
证明: ABC 为பைடு நூலகம்边三角形
B C 60
又EDF ABC
EDF B C
在BDE中BED EDB 180 - B
且EDB CDF 180 - EDF
EDB CFD
△BDE ∽△CFD
BD BE CF CD
1 即 1 3
CF 1 CF 1
3
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
ADB CDE 180 ADE
又ADE B
ADB CED △ABD ∽△DCE ;
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(2)解:由(1)可得
y 8
8-y
x
10-x
BD AB CE DC
x 8 8 - y 10 - x
化简得y 1 x2 - 5 x (8 0 x 10) 84
一线三等角ppt课件

经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
一 找准切入点,初识模型
例1:如图在⊿ABC中,点D,E分别在BC, AC上连接AD,DE,使∠ 1=∠B= ∠C. (1),请写出三个正确结论。
三,增加思维点,研究模型
• 1,强化条件,深化模型
例3,⊿ABC中,AB=AC,点D为BC中点,以D
为顶点作∠MDN=∠B。
(1)
如图,当射线DM经过点A时,DM交AC边于点E,
写出图中所有与⊿ADE相似的三角形。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
• (2)如图,将∠MDN绕点D延逆时针方向 旋转,DM,DN分别交线段AC,AB于E, F(点E与点A不重合),写出图中所有的相 似三角形。并证明你的结论。
⊿BDF∽⊿CED∽⊿DEF
你还能得出其他结论吗?
FD平分∠BFE, ED平分∠FEC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
拓展应用
• (3)如图,D,E是D,A,E三点所在直线 m上的两动点(D,A,E三点互不重合)点 F为∠BAC平分线上的一点,且⊿ABF和 ⊿ACF均为等边三角形,连接BD,CE,若 ∠ BDA=∠AEC= ∠BAC,试判断⊿DEF的形 状。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
一 找准切入点,初识模型
例1:如图在⊿ABC中,点D,E分别在BC, AC上连接AD,DE,使∠ 1=∠B= ∠C. (1),请写出三个正确结论。
三,增加思维点,研究模型
• 1,强化条件,深化模型
例3,⊿ABC中,AB=AC,点D为BC中点,以D
为顶点作∠MDN=∠B。
(1)
如图,当射线DM经过点A时,DM交AC边于点E,
写出图中所有与⊿ADE相似的三角形。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
• (2)如图,将∠MDN绕点D延逆时针方向 旋转,DM,DN分别交线段AC,AB于E, F(点E与点A不重合),写出图中所有的相 似三角形。并证明你的结论。
⊿BDF∽⊿CED∽⊿DEF
你还能得出其他结论吗?
FD平分∠BFE, ED平分∠FEC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
拓展应用
• (3)如图,D,E是D,A,E三点所在直线 m上的两动点(D,A,E三点互不重合)点 F为∠BAC平分线上的一点,且⊿ABF和 ⊿ACF均为等边三角形,连接BD,CE,若 ∠ BDA=∠AEC= ∠BAC,试判断⊿DEF的形 状。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
一线三等角模型 ppt课件

(2)
3x
2
2
x
x2 4
3 x2 4
3
2
3 x 2 3x 2
2
3
13
13 2
方法一:勾股定理; 方法二:证明D是AH中点。
PD DH CD CH PD AD CD CH DH AD
BC 4
PD PC AD PD PC 13 BC
2
2020/9/8
一线三等角模型
15
一线三等角压轴题(共同探讨解题方法和注意事项)
一线三等角模型
2
“一线三等角”模型 教学目标及重、难点
教学目标:
用“一线三等角”基本模型解决相似三角形中的相 关问题;
重点:掌握“一线三等角”基本模型;
难点: “一线三等角”基本图形的提炼、变式和运用。
2020/9/8
特别是“一线三直角”辅助线的构造
一线三等角模型
3
“一线三等角”模型按照角度的分类
锐角形一线三等角
一
线
三
直角形一线三等角
等
角
钝角形一线三等角
一线三等角模型
最特殊 考到概 率最大
4
总结解题规律 一线三角两相似:
60° 60° 60°
60°
60° 60°”基本模型 以等腰三角形(含等边三角形)或等腰梯形为背景的一线三等角
注意:压轴题中出现射线、 直线要分类讨论!
思考:若把
tanBAO
3 3
样?
改t为anBAO
1 2
,解法是否一
2020/9/8
一线三等角模型
10
2a
9 a 9
2
9 2a
9
a
2
八年级全等模型第1讲一线三等角课件

斜边中点定理
中位线定理
证明角度相等方法
④角度的和差关系
⑤证明角所在的三角形全等或类似
⑥四点共圆,对角互补
⑦圆周角定理
⑧等(同)角的余(补)角相等
课堂练习
例1、已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
CD= DE,∠CDE=45°求证:BD= BC.
【解答】已知在等腰Rt△ABC中,∠ACB=90°
∴∠B=45°∵CD= DE,∠CDE=45°
∴∠DCE=
180°−∠
2
= 67.5°
在△DCB中,同理∠CDB=180°-∠DCE-∠B=67.5°
∴∠DCE=∠CDB
∴BD= BC
对应边相等即可,再根据线段的和差关系不难解出答案。
课堂练习
二、等边三角形中的“一线三等角”
例1、如图,△ABC为等边三角形,D,E,F分别AB , BC,AC上的点,∠DEF= 60°, BD=CE.求证:BE= CF.
【解答】
已知△ABC为等边三角形
∴∠B=∠C=60°
∴∠BED+∠BDE=120°
∵∠DEF=60°
∴∠BED+∠FEC=120°
∴∠BDE=∠FEC
在△BED和△FCE中
∠ = ∠ = 60°
∵ ቐ =
∠ = ∠
∴△BED≌△FCE(ASA)
∴BE=CF
【分析】本题关键在于求证△BED≌△FCE(ASA)
一线三等角
中位线定理
证明角度相等方法
④角度的和差关系
⑤证明角所在的三角形全等或类似
⑥四点共圆,对角互补
⑦圆周角定理
⑧等(同)角的余(补)角相等
课堂练习
例1、已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
CD= DE,∠CDE=45°求证:BD= BC.
【解答】已知在等腰Rt△ABC中,∠ACB=90°
∴∠B=45°∵CD= DE,∠CDE=45°
∴∠DCE=
180°−∠
2
= 67.5°
在△DCB中,同理∠CDB=180°-∠DCE-∠B=67.5°
∴∠DCE=∠CDB
∴BD= BC
对应边相等即可,再根据线段的和差关系不难解出答案。
课堂练习
二、等边三角形中的“一线三等角”
例1、如图,△ABC为等边三角形,D,E,F分别AB , BC,AC上的点,∠DEF= 60°, BD=CE.求证:BE= CF.
【解答】
已知△ABC为等边三角形
∴∠B=∠C=60°
∴∠BED+∠BDE=120°
∵∠DEF=60°
∴∠BED+∠FEC=120°
∴∠BDE=∠FEC
在△BED和△FCE中
∠ = ∠ = 60°
∵ ቐ =
∠ = ∠
∴△BED≌△FCE(ASA)
∴BE=CF
【分析】本题关键在于求证△BED≌△FCE(ASA)
一线三等角
一线三等角模型ppt课件

Page 8
3.如图,已知y1=k1x+k1( k1≠0)与反比例函数 (k2≠0)的 图象交于点A、C,其中A点坐标 (1,1). (1)求反比例函数的解析式; (2)根据图象写出在第一象限 内,当取何值时,y1<y2? (3)若一次函数y1=k1x+k1与x 轴交于B点,连接OA,求 △AOB的面积: (4)在(3)的条件下,在坐 标轴上是否存在点P,使△AOP 是等腰三角形?若存在,请写出 P点的坐标;若不存在,请说明 理由.
B
y B
C
D
D O
Page 3
A
x
O
A
E
2013一调22题
C' D C D C' C C
A
B
A' A
B
D
A(A')
B
图1
图2
Page
4
(2)问题探究 如图3,△ABC中, AG⊥BC于点G,以A 为直角顶点,分别以 AB、AC为直角边,向 △ABC外作等腰 Rt△ABE和等腰 Rt△ACF,过点E、F 作射线GA的垂线,垂 足分别为P、Q. 试探究 EP与FQ之间的数量关 系,并证明你ຫໍສະໝຸດ 结论.Page16
已知如图,在梯形ABCD中, AD∥BC,AD=2,BC=4,点M 是AD的中点,△MBC是等边三角 形. (1)求证:梯形ABCD是等腰梯 形; (2)动点P、Q分别在线段BC和 MC上运动,且∠MPQ=60°保持 不变.设PC=x,MQ=y求y与x的 函数关系式. B (3)在(2)中,当取最小值时 ,判断△PQC的形状,并说明理 由.
Page 5
E Q A
P F
B
图3
E
3.如图,已知y1=k1x+k1( k1≠0)与反比例函数 (k2≠0)的 图象交于点A、C,其中A点坐标 (1,1). (1)求反比例函数的解析式; (2)根据图象写出在第一象限 内,当取何值时,y1<y2? (3)若一次函数y1=k1x+k1与x 轴交于B点,连接OA,求 △AOB的面积: (4)在(3)的条件下,在坐 标轴上是否存在点P,使△AOP 是等腰三角形?若存在,请写出 P点的坐标;若不存在,请说明 理由.
B
y B
C
D
D O
Page 3
A
x
O
A
E
2013一调22题
C' D C D C' C C
A
B
A' A
B
D
A(A')
B
图1
图2
Page
4
(2)问题探究 如图3,△ABC中, AG⊥BC于点G,以A 为直角顶点,分别以 AB、AC为直角边,向 △ABC外作等腰 Rt△ABE和等腰 Rt△ACF,过点E、F 作射线GA的垂线,垂 足分别为P、Q. 试探究 EP与FQ之间的数量关 系,并证明你ຫໍສະໝຸດ 结论.Page16
已知如图,在梯形ABCD中, AD∥BC,AD=2,BC=4,点M 是AD的中点,△MBC是等边三角 形. (1)求证:梯形ABCD是等腰梯 形; (2)动点P、Q分别在线段BC和 MC上运动,且∠MPQ=60°保持 不变.设PC=x,MQ=y求y与x的 函数关系式. B (3)在(2)中,当取最小值时 ,判断△PQC的形状,并说明理 由.
Page 5
E Q A
P F
B
图3
E
一线三等角公开课.ppt

(2)学习几何最重要是学会归纳一些简单 的基本图形,学会从复杂的图形里提 炼基本图形,并将其作为解决问题的 手段和方法。
(3)几何的学习中,要注重图形的运动和 变化,总结和发现图形之间的内在联 系,探求其规律,帮我们解决繁杂问题。
答:⊿ABE∽ ⊿ECF 理由:∵ ∠B=∠AEF=∠C=90°
A F
∴ ∠A+ ∠1=90°, ∠2+ ∠1=180°- ∠AEF=90 ° ∴ ∠A=∠2
1
2
B
E
C
∴ ⊿ABE∽ ⊿ECF
图1
2、如图,已知∠B=∠AEF=∠C=60°,图中有没有相似三角形?并说明理由
。
A
F
3、如图,已知∠B=∠AEF=∠C=120°,图中有没有相B 似
人教版数学九年级下
• 学习目标:
1、熟悉“一线三等角”的基本图形,并能解决相似中 的相关问题.
2、通过抽象模型,图形变换,变式类比等方法提高综 合解题能力.
• 学习重点:
运用“一线三等角”相似型的基本图形解题。
课前回顾
三角形相似的判定定理有哪些?
自主学习
1、如图,已知∠B=∠AEF=∠C=90°,图中有没有相似三角形?并说明理由。
三角形?并说明理由。
BA
BA CE
E
C
图2
DFECBiblioteka 抽象模型,揭示实质如图,已知∠A=∠BCD=∠E=α°,图中有没有相似三角形,
并写出证明过程.
结论:
理由:
B
D
A
αα
C
α
E
总结规律
顺口溜: “一线三等角,相似容易找”
运用新知,看图作答
下列每个图形中,∠1=∠2=∠3,请你快速找出“一线三等角”的 基本图形所形成的相似三角形(要求对应的顶点写在对应的位置)
(3)几何的学习中,要注重图形的运动和 变化,总结和发现图形之间的内在联 系,探求其规律,帮我们解决繁杂问题。
答:⊿ABE∽ ⊿ECF 理由:∵ ∠B=∠AEF=∠C=90°
A F
∴ ∠A+ ∠1=90°, ∠2+ ∠1=180°- ∠AEF=90 ° ∴ ∠A=∠2
1
2
B
E
C
∴ ⊿ABE∽ ⊿ECF
图1
2、如图,已知∠B=∠AEF=∠C=60°,图中有没有相似三角形?并说明理由
。
A
F
3、如图,已知∠B=∠AEF=∠C=120°,图中有没有相B 似
人教版数学九年级下
• 学习目标:
1、熟悉“一线三等角”的基本图形,并能解决相似中 的相关问题.
2、通过抽象模型,图形变换,变式类比等方法提高综 合解题能力.
• 学习重点:
运用“一线三等角”相似型的基本图形解题。
课前回顾
三角形相似的判定定理有哪些?
自主学习
1、如图,已知∠B=∠AEF=∠C=90°,图中有没有相似三角形?并说明理由。
三角形?并说明理由。
BA
BA CE
E
C
图2
DFECBiblioteka 抽象模型,揭示实质如图,已知∠A=∠BCD=∠E=α°,图中有没有相似三角形,
并写出证明过程.
结论:
理由:
B
D
A
αα
C
α
E
总结规律
顺口溜: “一线三等角,相似容易找”
运用新知,看图作答
下列每个图形中,∠1=∠2=∠3,请你快速找出“一线三等角”的 基本图形所形成的相似三角形(要求对应的顶点写在对应的位置)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
a
2
9 2
a 9 2
2
9 2a 1
a 27 10
A '( 2 7 , 3 6 ) 55
2020/6/11
.
11
一线三直角在几何综合题中的应用
2012年奉贤二模25题
构造一线三直角可以解决所有问题
.
12
(1)
2 45
3 45
2
45
22
32
3
26
45
1
5
2020/6/11
.
13
(2)
3x
2
2
一线三等角模型
.
1
通俗地讲,一条直线上有三个相等的角一般就会存在相似的三角形!
什么是一线三等角?
如图,等腰△ABC中,AB=AC,∠EDF=∠B,请问图中是 否有相似三角形?
相似三角形判定 定理一: 两角对应相等, 两三角形相似。
2020/6/11
注意:对应边千万不要找错,相同的角 标记同一个符号会比较清晰!
x
x2 4
3
3 x2 4 2
3 x
y 1 x 2 4 3x 2 4 3 x 2 3 (0 x 3 )
2
2
4
2020/6/11
.
14
(2)
3x
2
2
x
x2 4
3 x2 4
3
2
3 x 2 3x 2
2
3
13
13 2
方法一:勾股定理; 方法二:证明D是AH中点。
PD DH CD CH PD AD CD CH DH AD
BC 4
PD PC AD PD PC 13 BC
2
2020/6/11
.
15
一线三等角压轴题(共同探讨解题方法和注意事项)
.
16
一线三等角压轴题(共同探讨解题方法和注意事项)
.
17
肯学肯干 赢在精锐 谢谢!
.
18
a
1
2a
2
2 2a 1 a
2 1
方法一: 一线三直角
注意:点坐标的正负号问题!
.
9
一线三等角在直角坐标系中的应用
2014年宝山一模18题
67
9 2
(9 ,9 3 ) 22
93
9
2
思考:若把
tanBAO
3 3
样?
改t为anBAO
1 2
,解法是否一
2020/6/11
.
10
2a
9 a 9
2
9 2a
.
2
“一线三等角”模型 教学目标及重、难点
教学目标: 用“一线三等角”基本模型解决相似三角形中的相关 问题;
重点:掌握“一线三等角”基本模型;
难点: “一线三等角”基本图形的提炼、变式和运用。
特别是“一线三直角”辅助线的构造
2020/6/11
.
3
“一线三等角”模型按照角度的分类Βιβλιοθήκη 锐角形一线三等角一
至少有三
对相似三
β
角形
2020/6/11
再次提醒:对应边和对应角千万不要找错!
.
7
一线三直角在直角坐标系中的应用
2012年上海中考24题
1t 2
4
2
2
1t
t
2
4
.
8
一线三直角巧求点坐标
尝试用上题中你总结的方法解答下题: 2011年宝山一模18题
方法二:两点 距离公式; 方法三:利用 互相垂直的一 次函数(针对 优等生,且此 法适用于任意 三角形翻折)
线
三
直角形一线三等角
等
角
钝角形一线三等角
.
最特殊 考到概 率最大
4
总结解题规律 一线三角两相似:
60° 60° 60°
60°
60° 60°
.
5
“一线三等角”基本模型 以等腰三角形(含等边三角形)或等腰梯形为背景的一线三等角
注意:压轴题中出现射线、 直线要分类讨论!
.
6
中点型“一线三等角”模型
中点型:
