数据结构实验报告-一元多项式

合集下载

(2023)数据结构利用链表计算一元多项式课程设计实验报告(一)

(2023)数据结构利用链表计算一元多项式课程设计实验报告(一)2023数据结构课程设计实验报告——利用链表计算一元多项式实验背景和目的在本课程设计实验中，我们旨在通过使用链表数据结构，实现对一元多项式的计算功能。

通过本次实验，我们将深入学习和掌握链表的基础知识和应用技能，掌握实现链表操作的代码实现方式，提高编程实践能力和解决问题的能力。

思路和方法首先，我们需要定义链表节点数据结构，包含多项式中的系数和指数两个数据成员。

然后，我们需要实现一元多项式的相加、相减、求导、求值等基本操作。

其中，相加和相减操作需要利用链表遍历的方式，比较两个多项式中的指数，进行对应系数的加减，并将结果存储到新的链表中。

求导操作只需要遍历链表，将每一项的指数减一，系数乘以指数值，再将其插入到新的链表中即可。

求值操作仅需要遍历链表，根据指数和系数计算多项式值即可。

在具体实现过程中，我们需要注意边界条件的判断和处理，如何处理空链表、单项式情况等。

还需要精细设计代码逻辑，避免重复遍历链表，浪费时间和空间资源。

结果分析和展示经过数次测试和调试，我们最终实现了一元多项式的链表计算功能。

我们在终端输入多项式的系数和指数，再根据指令进行相应的操作。

结果能够准确输出，并且经过大量数据测试，程序运行稳定，没有出现崩溃和错误的情况。

总结和反思通过本次实验，我们进一步深入学习了链表数据结构的应用方法和相关算法。

我们学会了如何通过遍历链表实现复杂计算操作，如一元多项式的求导、求值等。

在实现过程中，我们对代码结构和逻辑设计进行反复思考和优化，提高了自己的编程能力和解决问题的能力。

同时，我们也需要进一步加强数据结构的学习，提升自己的算法水平，为后续的专业学习和职业发展打下坚实的基础。

可能的改进和优化方案虽然我们已经实现了一元多项式链表计算功能，但是我们也发现了以下几点可以改进和优化的方案：•异常处理：在用户输入有误或者数据不规范的情况下，程序可能会出现崩溃或者不符合预期的结果。

数据结构综合实验报告_一元多项式

目录1 设计内容和要求 (1)1.1设计要求 (1)1.2设计内容 (1)2 概要设计 (1)2.1程序主要流程 (1)3 详细设计 (3)3.1源程序 (3)4 调试分析 (8)5 总结 (9)6 致谢 (10)参考文献 (11)1 设计内容和要求1.1 设计要求编写一个实现多项式相加和相减的程序。

1、首先，根据键盘输入的一元实系数多项式的系数与指数序列，对多项式进行初始化，并按未知数x的降幂形式输出多项式的合理表示。

2、对于从键盘输入的任意两个一元多项式，正确计算它们的和以及差的多项式，并输出结果。

1.2 设计内容利用单链表表示一元多项式，然后实现各个项的系数和指数的输入，并且进行建立和输出，以及实现各个一元多项式之间的相加和相乘的操作。

2 概要设计实现的方法是先定义多项式结点的结构，该多项式每个结点由三个元素：输入的系数、输入的指数、以及指向下一个结点的指针构成。

该链表采用链式存储结构。

然后通过多次的输入，依次得到两个一元多项式的各个项的系数与指数。

该输入以零结尾。

然后通过对结点的判断是否为零后，进行相加或者终止的操作。

再初始化一个链表LC，将LC的各项系数和指数的指针指向LA+LB所得的结果的值，完成了最后的输出。

2.1程序主要流程建立链表,将多项式的系数与数指数作为链表节点的数据；指示输入两个多项式的数据,分别存在LA与LB中；利用Getlength(PotyNode *L)函数计算出LA与LB的表长；使用循环语句进行两链表的相应数据相加,并将所得到的新链表存放到LC中；打印输出。

如图2－1就是程序主流程图。

在上交资料中请写明：存储结构、多项式相加的基本过程的算法（可以使用程序流程图）、源程序、测试数据和结果、算法的时间复杂度、另外可以提出算法的改进方法。

要求可以按照降指数次序进行排列，结合数据结构中排序的相关知识，运用相应函数实现，实现两个多项式的加减运算。

在此要建立多项式运算的相关规则。

数据结构实验报告-一元多项式

数据结构实验报告-一元多项式
实验目的
1.使用C语言编写一元多项式运算的程序
2.理解和掌握链表的基本概念和操作
3.熟悉链表在实际问题中的应用
实验内容
1.设计一元多项式数据结构，支持多项式的输入、输出、加、减、乘、求导等计算。

2.使用链表来实现多项式数据结构。

3.编写测试程序，测试多项式数据结构的正确性和效率。

实验步骤
1.设计一元多项式数据结构，包括多项式中的每一项所包含的系数和指数，以及链表节点结构体定义。

typedef struct node
{
float coef; // 系数
int expn; // 指数
struct node *next; // 指向下一个节点的指针
} Node, *pNode;
2.按照上述定义的结构体，实现多项式的输入函数。

3.利用链表实现多项式的加法函数。

6.编写测试程序，测试多项式数据结构的正确性和效率。

实验结果
1.输入第一个多项式为 3x^3+2x^2+3 第二个多项式为 2x^3+x^2+4x+1
2.经过程序的处理，两个多项式的加法结果为 5.00x^3+
3.00x^2+
4.00x+4.00
两个多项式的乘法结果为
6.00x^6+10.00x^5+5.00x^4+10.00x^3+14.00x^2+19.00x+3.00
第一个多项式求导结果为 9.00x^2+4.00x
1.链表可以有效地实现多项式数据结构的存储和操作，具有较好的效率和灵活性。

2.通过本次实验，能够更加深入地理解数据结构中链表的应用，有助于提高编程能力和实际问题解决能力。

一元多项式实验报告

数据结构实验报告实验名称：实验一一元多项式学生姓名：叶远锋班级：2010211111班内序号：18学号：10210328日期：2011年11月9日1．实验要求实验目的●熟悉C++语言的基本编程方法，掌握继承编译环境的调试方法；●学习指针、模板类、异常处理的使用；●掌握线性表的操作实现方法；●培养使用线性表解决实际问题的能力。

实验内容利用线性表实现一个一元多项式Polynomial：f（x）=a0+a1X+a2X^2+……+anX^n具体要求如下：①能够实现一元多项式的输入和输出；②能够进行一元多项式相加；③能够进行一元多项式相减；④能够计算一元多项式在x处的值；⑤能够计算一元多项式的导数（选作）；⑥能够进行一元多项式相乘（选作）；⑦编写main（）函数测试算法的正确性。

2. 程序分析2.1 存储结构存储结构：顺序表a[0]a[1]a[2]……a[n].2 关键算法分析1、关键算法：加法、减法、求导、乘法、求值✧加法时间复杂度O（n）输出参数：返回一个新一元多项式c输入参数：两个一元多项式PolyList类对象的引用a、b[1] 从第一项开始，比较a和b 的指数，直到其中一个多项式比较到最后一项[1.1] 如果a对应项的指数小于b对应项的指数，把a的对应项复制给C的对应项，再把a的下一项和b的当前项比较[1.2] 如果a对应项的指数大于b对应项的指数，把b的对应项复制给C的对应项，再把b的下一项和a的当前项比较[1.3] 如果a的对应项指数等于b的对应项指数，则c的对应项的系数等于a的对应项系数和b的对应项系数相加，c的对应项的指数等于a或b的对应项指数，再把a的下一项和b的下一项比较[2] 如果a或b其中有一个没有比较完，就把没有比较的项都复制到c中[3] 返回c✧减法时间复杂度O（n）输出参数：返回一个新一元多项式c输入参数：两个一元多项式PolyList类对象的引用a、b[1] 将多项式b的每一项系数都乘以-1[2] 调用加法，把a+b的值赋给c[3] 返回c✧求导时间复杂度O（n）输出参数：返回一个新一元多项式a输入参数：无[1] 从第一项开始，直到最后一项，如果指数不等于零，则a的对应项系数等于现有项系数乘以现有项指数，a的对应项指数等于现有项指数减一[2] 返回a✧乘法时间复杂度O（mn）输出参数：返回一个新一元多项式 c输入参数：两个一元多项式PolyList类对象的引用a、b[1] 从a的第一项开始，直至最后一项，逐项和b相乘[2] 将每一次相乘得到的多项式相加，并把相加的结果赋给c[3] 返回c✧求值时间复杂度O（n）输出参数：返回一个float型数输入参数：输入一个float型数[1] 从第一项开始，直至最后一项，依次计算每一项的值[2] 将每次计算得到的结果相加，并把相加结果赋给value[3] 返回value3. 程序运行结果1、测试主函数流程：流程图如图所示2、测试条件1)输入项数应少于100项2)输入多项式项数是大于零的整数3)输入多项式时，要从低次项到高次项依次逐项输入，先输入系数，再输入指数4)按屏幕提示输入3、测试结论1)程序可以实现多项式的输入输出操作2)程序可以进行多项式的加减乘及求导和求值运算4. 总结1.调试时出现的问题及解决方法1)问题：main函数中，在定义term结构数组时使用整型n，m变量作为数组的长度遇到系统报错解决方法：为数组申请动态内存2)问题：main函数中，当输入多项式项数小于1时无法报错解决方法：在用户输入完毕后增加if判断语句来实现报错3)问题：用户无法循环输入多项式解决方法：在程序末尾增加按键判断语句，如果用户选择要重新输入多项式则返回程序开头重新执行，否则程序结束2.心得体会1）通过这次编程练习，我加深了对顺序表的理解与运用。

数据结构实验报告实验一题目3一元多项式

数据结构实验报告实验名称：实验一题目3 一元多项式学生姓名：许虎班级：信通20班内序号：10学号：78日期：2012年11月2日1．实验要求实验目的：利用线性表实现一个一元多项式Polynomialf(x) = a0 + a1x + a2x2 + a3x3+ … + a n x n并实现相应功能。

实验内容：使用一元多项式类存储多项式元素，通过定义并实现相关函数完成相应的功能，并通过设计的main函数测试了其正确性。

用户可自行输入正确的多项式进行相关运算，得到相应结果。

相关函数实现的功能：1.能够实现一元多项式的输入和输出2.能够进行一元多项式相加3.能够进行一元多项式相减4.能够计算一元多项式在x处的值5.能够计算一元多项式的导数6.能够进行两个一元多项式相乘2. 程序分析2.1 存储结构存储结构：单链表（带头节点）单链表示意图如下：在本程序中使用结构类型element（赋给模版类型T）数组data储存数据成员，包含coef（系数）和exp（指数）两个成员，但仍为一维数组。

在节点构造类型Node（运用了模版类）中定义了指针域next指向下一个结点，直到链表尾将next置空，front头指针为该链表类私有数据成员，如此得到多项式链表（单链表）。

2.2 关键算法分析1、关键算法：1）一元多项式类求和函数（1）初始化工作指针p_prior(指向A链表头结点),p(p->next)，q(指向B链表第一个结点)。

（2）若p和q都不为空，则循环下列操作：（3）若p->data.exp<q->data.exp，则p_prior=p;p=p->next。

（4）否则，若p->data.exp>q->data.exp，则：将q结点加入到A链表p结点之前，q指向B链表下移个结点。

（5）否则，p->data.coef=p->data.coef+q->data.coef;（6）若p->data.coef==0，删除p结点，p指向下一个结点，删除q结点，q指向下一个结点。

数据结构一元多项式报告

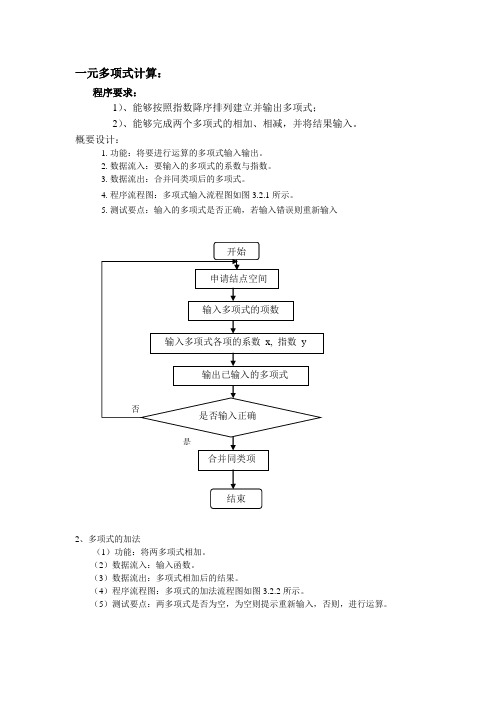
一元多项式计算：程序要求：1）、能够按照指数降序排列建立并输出多项式；2）、能够完成两个多项式的相加、相减，并将结果输入。

概要设计：1.功能：将要进行运算的多项式输入输出。

2.数据流入：要输入的多项式的系数与指数。

3.数据流出：合并同类项后的多项式。

4.程序流程图：多项式输入流程图如图3.2.1所示。

5.测试要点：输入的多项式是否正确，若输入错误则重新输入2、多项式的加法（1）功能：将两多项式相加。

（2）数据流入：输入函数。

（3）数据流出：多项式相加后的结果。

（4）程序流程图：多项式的加法流程图如图3.2.2所示。

（5）测试要点：两多项式是否为空，为空则提示重新输入，否则，进行运算。

3、多项式的减法（1）功能：将两多项式相减。

（2）数据流入：调用输入函数。

（3）数据流出：多项式相减后的结果。

（4）程序流程图：多项式的减法流程图如图3.2.3所示。

（5）测试要点：两多项式是否为空，为空则提示重新输入，否则，进行运算。

详细代码：#include<iostream>#include<conio.h>#include<stdlib.h>using namespace std; struct Node{float coef;//结点类型int exp;};typedef Node polynomial;struct LNode{polynomial data;//链表类型LNode *next;};typedef LNode* Link;void CreateLink(Link &L,int n);void PrintList(Link L);void PolyAdd(Link &pc,Link pa,Link pb);void PolySubstract(Link &pc,Link pa,Link pb); void CopyLink(Link &pc,Link pa);void PolyMultiply(Link &pc,Link pa,Link pb);int JudgeIfExpSame(Link pa,Link e);void DestroyLink(Link &L);int CompareIfNum(int i);void DestroyLink(Link &L){Link p;p=L->next;while(p){L->next=p->next;delete p;p=L->next;}delete L;L=NULL;}//创建含有n个链表类型结点的项，即创建一个n项多项式void CreateLink(Link &L,int n){if(L!=NULL){DestroyLink(L);}Link p,newp;L=new LNode;L->next=NULL;(L->data).exp=-1;//创建头结点p=L;for(int i=1;i<=n;i++){newp=new LNode;cout<<"请输入第"<<i<<"项的系数和指数:"<<endl;cout<<"系数:";cin>>(newp->data).coef;cout<<"指数:";cin>>(newp->data).exp;if(newp->data.exp<0){cout<<"您输入有误，指数不允许为负值!"<<endl;delete newp;i--;continue;}newp->next=NULL;p=L;if(newp->data.coef==0){cout<<"系数为零，重新输入!"<<endl;delete newp;i--;continue;}while((p->next!=NULL)&&((p->next->data).exp<(newp->data).exp)){p=p->next; //p指向指数最小的那一个}if(!JudgeIfExpSame( L, newp)){newp->next=p->next;p->next=newp;}else{cout<<"输入的该项指数与多项式中已存在的某项相同,请重新创建一个正确的多项式"<<endl;delete newp;DestroyLink(L);CreateLink(L,n); //创建多项式没有成功，递归调用重新创建break;}}}/*判断指数是否与多项式中已存在的某项相同*/int JudgeIfExpSame(Link L,Link e){Link p;p=L->next;while(p!=NULL&&(e->data.exp!=p->data.exp))p=p->next;if(p==NULL)return 0;else return 1;}/*输出链表*/void PrintList(Link L){Link p;if(L==NULL||L->next==NULL)cout<<"该一元多项式为空！"<<endl;else{p=L->next;//项的系数大于的种情况if((p->data).coef>0){if((p->data).exp==0)cout<<(p->data).coef;else if((p->data).coef==1&&(p->data).exp==1)cout<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"x^"<<(p->data).exp;else if((p->data).exp==1&&(p->data).coef!=1)cout<<(p->data).coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }//项的系数小于的种情况if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }p=p->next;while(p!=NULL){if((p->data).coef>0){if((p->data).exp==0)cout<<"+"<<(p->data).coef;else if((p->data).exp==1&&(p->data).coef!=1)cout<<"+"<<(p->data).coef<<"x";else if((p->data).exp==1&&(p->data).coef==1)cout<<"+"<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"+"<<"x^"<<(p->data).exp;else cout<<"+"<<(p->data).coef<<"x^"<<(p->data).exp; }if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp;}p=p->next;}}cout<<endl;}/*把一个链表的内容复制给另一个链表*/void CopyLink(Link &pc,Link pa){Link p,q,r;pc=new LNode;pc->next=NULL;r=pc;p=pa;while(p->next!=NULL){q=new LNode;q->data.coef=p->next->data.coef;q->data.exp=p->next->data.exp;r->next=q;q->next=NULL;r=q;p=p->next;}}/*将两个一元多项式相加*/void PolyAdd(Link &pc,Link pa,Link pb){Link p1,p2,p,pd;CopyLink(p1,pa);CopyLink(p2,pb);pc=new LNode;pc->next=NULL;p=pc;p1=p1->next;p2=p2->next;while(p1!=NULL&&p2!=NULL){if(p1->data.exp<p2->data.exp){p->next=p1;p=p->next;p1=p1->next;}else if(p1->data.exp>p2->data.exp){p->next=p2;p=p->next;p2=p2->next;}else{p1->data.coef=p1->data.coef+p2->data.coef;if(p1->data.coef!=0){p->next=p1;p=p->next;p1=p1->next;p2=p2->next;}else{pd=p1;p1=p1->next;p2=p2->next;delete pd;}}}if(p1!=NULL){p->next=p1;}if(p2!=NULL){p->next=p2;}}/*将两个多项式相减*/void PolySubstract(Link &pc,Link pa,Link pb) {Link p,pt;CopyLink(pt,pb);p=pt;while(p!=NULL){(p->data).coef=(-(p->data).coef);p=p->next;}PolyAdd(pc,pa,pt);DestroyLink(pt);}//清屏函数void Clear(){system("pause");system("cls");}/*将两个一元多项式相乘*/void PolyMultiply(Link &pc,Link pa,Link pb) {Link p1,p2,p,pd,newp,t;pc=new LNode;pc->next=NULL;p1=pa->next;p2=pb->next;while(p1!=NULL){pd=new LNode;pd->next=NULL;p=new LNode;p->next=NULL;t=p;while(p2){newp=new LNode;newp->next=NULL;newp->data.coef=p1->data.coef*p2->data.coef;newp->data.exp=p1->data.exp+p2->data.exp;t->next=newp;t=t->next;p2=p2->next;}PolyAdd(pd,pc,p);CopyLink(pc,pd);p1=p1->next;p2=pb->next;DestroyLink(p);DestroyLink(pd);}}//菜单函数void Menu(){cout<<""<<endl;cout<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t\t\t [1] 创建要运算的两个一元多项式\t\t "<<endl; cout<<"\t\t\t [2] 将两个一元多项式相加\t\t\t "<<endl; cout<<"\t\t\t [3] 将两个一元多项式相减\t\t\t "<<endl; cout<<"\t\t\t [4] 将两个一元多项式相乘\t\t\t "<<endl; cout<<"\t\t\t [5] 显示两个一元多项式\t\t\t "<<endl;cout<<"\t\t\t [6] 销毁所创建的二个多项式\t\t "<<endl; cout<<"\t\t\t [7] 退出\t\t\t\t\t "<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<endl;cout<<"\t\t 请选择:";}//判断输入的整数是不是为到的数字int CompareIfNum(int i){if(i>0&&i<8)return 0;else return 1;}void main(){{system("color b");//system("pause");system("color a");//system("pause");}int n;Link L,La=NULL,Lb=NULL;//La,Lb分别为创建的两个多项式int choose;while(1){Menu(); //调用菜单函数cin>>choose;switch(choose){case 1:cout<<"请输入你要运算的第一个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误，请重新输入……"<<endl;Clear();break;}CreateLink(La,n);cout<<"请输入你要运算的第二个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误，请重新输入……"<<endl;Clear();break;}CreateLink(Lb,n);Clear();break;case 2:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolyAdd(L,La,Lb);cout<<""<<endl;cout<<"待相加的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相加后的结果为：";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 3:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolySubstract(L,La,Lb);cout<<"相减的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相减后的结果为：";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 4:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolyMultiply(L,La,Lb);cout<<"相乘的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相乘后的结果为：";PrintList(L);DestroyLink(L);cout<<""<<endl;Clear();break;case 5:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}cout<<"一元多项式A为："<<endl;PrintList(La);cout<<""<<endl;cout<<"一元多项式B为："<<endl;PrintList(Lb);cout<<""<<endl;Clear();break;case 6:if(La&&Lb){DestroyLink(La);DestroyLink(Lb);cout<<"多项式销毁成功！"<<endl;Clear();}else{cout<<"多项式不存在，请重新选择^^^"<<endl;Clear();}break;case 7:exit(0); //exit(0)强制终止程序，返回状态码表示正常结束default:cout<<"您的输入有误，请重新选择操作……"<<endl;Clear();break;}}}。

数据结构实验报告《一、多项式及其运用》

中南大学物理学院数据结构实验报告- - - -一元多项式相加及其运用专业班级：电信0903时间：2010年10月18日数据结构实验报告----一元多项式相加及其运用【问题描述】设计一个一元稀疏多项式简单计算器【基本要求】一元稀疏多项式简单计算器的功能是：（1）输入并建立多项式；（2）输出多项式，输出形式为整数序列：n，c1,e1,c2,e2,………c n,e n,其中n是多项式的项数，c i和e i分别是第i项的系数和指数，序列按指数降序排列；（3）多项式a和b相加，建立多项式a+b；（4）多项式a和b相减，建立多项式a-b。

【运用拓展】（1）计算多项式在x处的值；（2）多项式a和b相乘，建立乘积多项式ab；（3）计算器的仿真友好界面。

【设计思路分析】（1）解决多项式相加，必须要有多项式，所以必须首先建立两个多项式，在这里采用链表的方式存储链表。

（2）运用尾插法建立两条单链表，以单链表polyn p和polyn h分别表示两个一元多项式a和b，a+b的求和运算等同于单链表的插入问题（3）设p、q分别指向单链表polya和polyb的当前项，比较p、q结点的指数项，由此得到下列运算规则：①若p->expn<q->expn，则结点p所指的结点应是“和多项式”中的一项，令指针p后移。

②若p->expn=q->expn，则将两个结点中的系数相加，当和不为0时修改结点p的系数。

③若p->expn>q->expn，则结点q所指的结点应是“和多项式”中的一项，将结点q插入在结点p之前，且令指针q在原来的链表上后移。

【测试数据】多项式a：6x+3x^5-7.1x^11多项式b: 2-5x^5+11x^9若计算a+b则有:(6x+3x^5-7.1x^11)+(2-5x^5+11x^9)=(-7.1x^11+11x^9-2x^5+6x+2)等。

【操作界面显示】1：建立多项式的操作：2：输出多项式及计算x的值3：进行运算操作：4：结束程序：【程序代码】#include<stdio.h> //调用输入输出函数#include<stdlib.h>typedef struct Polynomial //定义一个Polyn结构体{ float coef; int exp; //系数指定为浮点型，指数指定为整型struct Polynomial *next;}*Polyn,Polynomial;void Insert(Polyn p,Polyn h){ //查找位置插入新链节if(p->coef==0) free(p); //p系数为0的话释放结点else{ //否则查找插入位置Polyn q1,q2;q1=h; q2=h->next;while(q2&& p->exp < q2->exp) //指数较大则插前面{ q1=q2; q2=q2->next; }if(q2&& p->exp == q2->exp) //将指数相同相合并{ q2->coef += p->coef;free(p);if(!q2->coef) //系数为0的话释放结点{q1->next=q2->next;free(q2);}}else { p->next=q2; q1->next=p;} //指数为新时将结点插入}//第一个else} //void InsertPolyn CreatePolyn(Polyn head,int m){ //建立一个头指针为head、项数为m的一元多项式int i;Polyn p;p=head=(Polyn)malloc(sizeof(struct Polynomial)); //开辟多项式地址空间head->next=NULL; //指定表尾，然后采用尾插法输入多项式for(i=0;i<m;i++){p=(Polyn)malloc(sizeof(struct Polynomial)); //建立新结点以接收数据printf("请输入第%d项的系数与指数:",i+1);scanf("%f %d",&p->coef,&p->exp);Insert(p,head); //调用Insert函数插入结点}return head;}void PrintPolyn(Polyn P) //输出多项式{ Polyn q=P->next;int flag=1; //项数计数器if(!q){ //若多项式为空，输出0putchar('0');printf("\n");return;} //void ifwhile(q){if(q->coef>0&& flag!=1) putchar('+'); //系数大于0且不是第一项，显示"+"连接if(q->coef!=1&&q->coef!=-1) //系数非1或-1时输出{ printf("%g",q->coef);if(q->exp==1) putchar('X'); //指数为1时，直接输出"X"else if(q->exp) printf("X^%d",q->exp); //指数不为1时，输入"X^"格式}//while if ifelse { if(q->coef==1){ if(!q->exp) putchar('1');else if(q->exp==1) putchar('X');else printf("X^%d",q->exp);}//else ifif(q->coef==-1) //系数为"-1"时，前面加上负号，其他情况与"+1"类似{ if(!q->exp) printf("-1");else if(q->exp==1) printf("-X");else printf("-X^%d",q->exp);}//else if if}//elseq=q->next; flag++;}//whileprintf("\n");}//voidint compare(Polyn a,Polyn b) //两个多项式的判断{ if(a&&b) //若两个多项式都非空{ if(!b||a->exp>b->exp) return 1; //b多项式已空或指数较小，返回1 else if(!a||a->exp<b->exp) return -1; //a多项式已空或指数较小，返回-1else return 0; //a、b两多项式的指数相等，返回0 }//ifelse if(!a&&b) return -1; //a多项式已空，但b多项式非空else return 1; //b多项式已空，但a多项式非空}//comparePolyn AddPolyn(Polyn pa,Polyn pb){ //求解并建立多项式a+b，返回其头指针Polyn qa=pa->next;Polyn qb=pb->next;Polyn headc,hc,qc;hc=(Polyn)malloc(sizeof(struct Polynomial)); //建立头结点hc->next=NULL; //指向结尾，采用尾插法headc=hc;while(qa||qb){ qc=(Polyn)malloc(sizeof(struct Polynomial)); //开辟地址空间switch(compare(qa,qb)) //判断多项式a和b { case 1: { qc->coef=qa->coef; //输入a多项式qc->exp=qa->exp; qa=qa->next; break; }case 0: { qc->coef=qa->coef+qb->coef; //指数相等时系数相加qc->exp=qa->exp; qa=qa->next; qb=qb->next; break; } case -1: { qc->coef=qb->coef; //输入b多项式qc->exp=qb->exp; qb=qb->next; break; }}//switchif(qc->coef!=0) //当相加系数不为0，加入该结点{ qc->next=hc->next; hc->next=qc; hc=qc;}else free(qc); //当相加系数为0时，释放该结点}//whilereturn headc;}Polyn SubtractPolyn(Polyn pa,Polyn pb){ //求解并建立多项式a-b，返回其头指针Polyn h=pb;Polyn p=pb->next;Polyn pd;while(p) { //将pb的系数取反p->coef*=-1; p=p->next;} //whilepd=AddPolyn(pa,h);for(p=h->next;p;p=p->next) //恢复pb的系数p->coef*=-1;return pd;}//SubtractPolynPolyn MultiplyPolyn(Polyn pa,Polyn pb){ //求解并建立多项式a*b，返回其头指针Polyn hf,pf;Polyn qa=pa->next; Polyn qb=pb->next;hf=(Polyn)malloc(sizeof(struct Polynomial)); //建立头结点hf->next=NULL;for(;qa;qa=qa->next){ for(qb=pb->next;qb;qb=qb->next){ pf=(Polyn)malloc(sizeof(struct Polynomial));pf->coef=qa->coef*qb->coef;pf->exp=qa->exp+qb->exp;Insert(pf,hf); //调用Insert函数以合并指数相同的项}//for for}//forreturn hf;}//MultiplyPolynfloat V aluePolyn(Polyn head,int x){ //输入x值，计算并返回多项式的值Polyn p; int i,t; float sum=0;for(p=head->next;p;p=p->next){ t=1; for(i=p->exp;i!=0;){ if(i<0){t/=x;i++;} //指数小于0，进行除法else{t*=x;i--;} //指数大于0，进行乘法}//for forsum+=p->coef*t; //计算求和} //forreturn sum;}//V aluePolynvoid DestroyPolyn(Polyn p) //销毁多项式p{Polyn q1,q2;q1=p->next; q2=q1->next;while(q1->next) //删除q1的元素直至q1为空{ free(q1); q1=q2; q2=q2->next; }}//DestroyPolynvoid main(){ int m,n,a,x;char flag;Polyn pa=0,pb=0,pc;printf(" --------------------------------------------------\n");printf(" 欢迎使用一元多项式及其运用操作程序\n");printf(" --------------------------------------------------\n");printf("请输入多项式a的项数:");scanf("%d",&m);pa=CreatePolyn(pa,m); //建立多项式aprintf("请输入多项式b的项数:");scanf("%d",&n);pb=CreatePolyn(pb,n); //建立多项式b//输出菜单printf(" *****************************************************\n");printf(" * 一元稀疏多项式简单计算器*\n");printf(" * *\n");printf(" * A:输出多项式a B:输出多项式b *\n");printf(" * *\n");printf(" * C:同时输出多项式a和b *\n");printf(" * *\n");printf(" * D:代入x的值计算a E:代入x的值计算b *\n");printf(" * *\n");printf(" * F:代人x的值同时计算a和b *\n");printf(" * *\n");printf(" * G:输出a+b H:输出a-b *\n");printf(" * *\n");printf(" * I:输出a*b J:退出*\n");printf(" * *\n");printf(" *****************************************************\n");while(a){ printf("\n请选择操作："); //提示选择操作scanf(" %c",&flag); //输入选择switch(flag) //输入大小写都可以判断{ case'A':case'a': { printf("\n 多项式a="); //输出多项式aPrintPolyn(pa); //调用输出函数显示break; //跳出}case'B':case'b': { printf("\n 多项式b="); //输出多项式bPrintPolyn(pb);break;}case'C':case'c': { printf("\n 多项式a="); //输出多项式a和bPrintPolyn(pa);printf("\n 多项式b=");PrintPolyn(pb);break;}case'D':case'd': { printf("输入x的值：x="); //输入x值后计算ascanf("%d",&x);printf("\n x=%d时，a=%.3f\n",x,V aluePolyn(pa,x));break;}case'E':case'e': { printf("输入x的值：x="); //输入x值后计算bscanf("%d",&x);printf("\n x=%d时，b=%.3f\n",x,V aluePolyn(pb,x));break;}case'F':case'f': { printf("输入x的值：x="); //输入x值后计算a和bscanf("%d",&x);printf("\n x=%d时，a=%.3f\n",x,V aluePolyn(pa,x));printf("\n x=%d时，b=%.3f\n",x,V aluePolyn(pb,x));break;}case'G':case'g': { pc=AddPolyn(pa,pb); //输出a+b，用新多项式显示printf("\n a+b=");PrintPolyn(pc);break;}case'H':case'h': { pc=SubtractPolyn(pa,pb); //输出a-b，用新多项式显示printf("\n a-b=");PrintPolyn(pc);break;}case'I':case'i': { pc=MultiplyPolyn(pa,pb); //输出a*b，用新多项式显示printf("\n a*b=");PrintPolyn(pc);break;}case'J':case'j': { printf("\n 感谢使用此程序！\n"); //退出该程序DestroyPolyn(pa); //删除多项式aDestroyPolyn(pb); //删除多项式ba=0; //暂停显示界面，用户选择关闭break;}default:printf("\n 您的选择错误，请重新选择!\n");}//swich}//while}//main。

数据结构-实验一-一元多项式相加精品

【关键字】情况、空间、运行、继续、掌握、信心、工程、能力、结构、坚持、巩固、实现、核心、耐心数据结构实验报告实验一：一元多项式相加姓名：周成学号：专业：软件工程任课教师：马慧珠2013年12 月01 日1.实验名称：一元多项式相加2.实验目的:如何使用C语言实现链表的说明、创建以及结点的插入和删除等操作。

3.实验要求：对一元多项式能实现输入、输出，以及两个一元多项式相加及结果显示。

4.实验内容：一元多项式的表示在计算机内用链表来实现，同时为了节省存储空间，只存储其中非零的项，链表中的每个节点存放多项式的系数非零项。

它包含三个域，分别存放多项式的系数，指数，以及指向下一个项的指针。

根据一元多项式相加的运算规则：对于两个一元多项式中所有指数相同的项，对应系数相加，若其和不为零，则构成“和多项式”中的一项，对于两个一元多项式中所有指数不相同的项，则分别复抄到“和多项式”中去。

核心算法PolyAdd是把分别由pa和pb所指的两个多项式相加，结果为pa所指的多项式。

运算规则如下：相加时，首先设两个指针变量qa和qb分别从多项式的首项开始扫描，比较qa和qb所指结点指数域的值，可能出现下列三种情况之一：（1）qa->exp大于qb->exp,则qa继续向后扫描。

（2）qa->exp等于qb->exp,则将其系数相加。

若相加结果不为零，将结果放入qa->coef中，并删除qb所指结点，否则同时删除qa和qb所指结点。

然后qa、qb继续向后扫描。

（3）qa->exp小于qb->exp,则将qb所指结点插入qa所指结点之前，然后qa、qb继续向后扫描。

扫描过程一直进行到qa或qb有一个为空为止，然后将有剩余结点的链表接在结果表上。

所得pa指向的链表即为两个多项式之和。

5.实验程序代码及运行结果：#include"stdafx.h"#include<stdio.h>#include<stdlib.h>#include<malloc.h>#include<stdio.h>#define NULL 0typedef struct NODE{float coef; //系¦Ì数ºyint expn; //指?数ºystruct NODE *next;}NODE;NODE *Creat(int n);void print(NODE *head);NODE *AddPolyn(NODE *head1, NODE *head2);NODE *Delfirst(NODE *head, NODE *q);void InsertBefore(NODE *p1, NODE *p2);int compare(int a, int b);/*创ä¡ä建¡§链¢¡ä表À¨ª*/NODE *Creat(int n){NODE *current, *previous, *head;int i;head = (NODE *)malloc(sizeof(NODE)); /*创ä¡ä建¡§头ª¡¤结¨¢点Ì?*/previous = head;for(i = 0; i < n; i++){current = (NODE *)malloc(sizeof(NODE));printf("请?输º?入¨?系¦Ì数ºy和¨ª指?数ºy : ");scanf("%f%d", &current->coef, &current->expn);previous->next = current;previous = current;}previous->next = NULL;return head;}/*一°?元a多¨¤项?式º?的Ì?想?加¨®，ê?总Á¨¹体¬?考?虑?，ê?可¨¦分¤?qa的Ì?指?数ºy比À¨¨qb小?，ê?或¨°等Ì¨¨于®¨²pb(如¨?果?系¦Ì数ºy相¨¤加¨®等Ì¨¨于®¨²0和¨ª不?等Ì¨¨于®¨²0),或¨°大ä¨®于®¨²pb里¤?面?由®¨¦InsertBefore和¨ªDelfirst两¢?个?小?模¡ê块¨¦组Á¨¦成¨¦一°?部?分¤?*/ NODE *AddPolyn(NODE *head1, NODE *head2){NODE *ha, *hb, *qa, *qb;int a, b;float sum;ha = head1; /*ha和¨ªhb指?向¨°头ª¡¤结¨¢点Ì?*/hb = head2;qa = ha->next; /*qa和¨ªqb指?向¨°头ª¡¤结¨¢点Ì?的Ì?下?一°?个?结¨¢点Ì?*/qb = hb->next;while(qa && qb) /*qa和¨ªqb均¨´非¤?空?*/{a = qa->expn;b = qb->expn;switch(compare(a, b)) {case -1 : /*qa->expn < qb->expn*/ha = qa;qa = qa->next;break;case 0 :sum = qa->coef + qb->coef; /*系¦Ì数ºy的Ì?和¨ª*/if(sum != 0.0) { /*如¨?果?不?是º?0.0*/qa->coef = sum; /*改?变À?系¦Ì数ºy*/ha = qa;}else{free(Delfirst(ha, qa));}free(Delfirst(hb, qb));qa = ha->next;qb = hb->next; /*qb释º¨ª放¤?后¨®要°a重?新?赋3值¦Ì*/ break;case 1 : /*如¨?果?qa-> expn > qb -> expn*/Delfirst(hb, qb);InsertBefore(ha, qb); /*把ã?qb插?入¨?到Ì?ha下?一°?个?结¨¢点Ì?之?前¡ã*/qb = hb->next;ha = ha->next;break;}}if(qb)ha->next = qb; /*插?入¨?剩º¡ê余®¨¤的Ì?pb*/free(head2);return head1;}/*比À¨¨较?*/int compare(int a, int b){if(a < b)return -1;else if(a > b)return 1;elsereturn 0;}/*删¦?除y结¨¢点Ì?q*/NODE *Delfirst(NODE *p1, NODE *q){p1 -> next = q -> next;return (q);}/*插?入¨?结¨¢点Ì?,引°y入¨?结¨¢点Ì?p,可¨¦以°?让¨?p插?入¨?到Ì?p2和¨ªp1之?间?*/ void InsertBefore(NODE *p1, NODE *p2){NODE *p;p = p1->next;p1->next = p2;p2->next = p;}/*打ä¨°印®?,为a了¢?美¨¤观?程¨¬序¨°分¤?开a打ä¨°印®?*/void print(NODE *head){NODE *current;current = head->next;while(current->next != NULL){printf("%0.f * x^%d + ", current->coef, current->expn);current = current -> next;}printf("%0.f * x^%d", current->coef, current->expn);//system（ê¡§"pause");}int main(){NODE *head1, *head2, *head3;int n1, n2;printf("请?输º?入¨?你?需¨¨要°a的Ì?多¨¤项?式º?的Ì?项?数ºy n1 : ");scanf("%d", &n1);head1 = Creat(n1);printf("第Ì¨²一°?个?多¨¤项?式º?的Ì?显?示º? : \n");print(head1);printf("\n请?输º?入¨?你?需¨¨要°a的Ì?多¨¤项?式º?的Ì?项?数ºy n2 : ");scanf("%d", &n2);head2 = Creat(n2);printf("\n第Ì¨²二t个?多¨¤项?式º?的Ì?显?示º? : \n");print(head2);head3 = AddPolyn(head1, head2);printf("\n合?并¡é后¨®的Ì?多¨¤项?式º?的Ì?显?示º? : \n");print(head3);printf("\n");}运行结果：实验数据1如图：输入一个四次二项式X^3+2X^4，一个五次二项式X^4+2X^5，输出如图：实验数据2如图：输入一个五次四项式X^2+X^3+X^4+X^5，还有一个五次五项式1+X+X^3+2X^4+2X^5输出如图所示实验数据3如图：输入一个七次三项式1+2x^5+3X^7，还有一个五次四项式1+2X^2+3X^4+4X^5,输出如图：6.实验总结本来我对编程很没有信心，做这样一个课程设计感觉有点吃力，虽然有些人觉得很简单，但是我还是坚持做下来了，我不断的看书，翻阅资料，询问同学，上网搜索，总算有模有样地把这个程序编的能运行了。

数据结构《一元多项式》

一元多项式相加问题实验报告本实验的目的是进一步熟练掌握应用链表处理实际问题的能力。

一、问题描述通过键盘输入两个形如Po+P₁X¹+P₂X²+…+PX的多项式，经过程序运算后在屏幕上输出它们的相加和。

二、数据结构设计分析任意一元多项式的描述方法可知，一个一元多项式的每一个子项都由“系数-指数”两部份组成，因此可将其抽象为包含系数coef、指数 exp、指针域next 构成的链式线性表。

对多项式中系数为0的子项可以不记录它的指数值，将两个多项式分别存放在两个线性表中，然后经过相加后将所得多项式存放在一个新的线性表中，但是不用再开辟新的存储空间，只依靠结点的挪移来构成新的线性表，期间可以将某些不需要的空间回收。

基于这样的分析，可以采用不带头结点的单链表来表示一个一元多项式。

具体数据类型定义为：struct nodefloat coef;//系数域int exp; //指数域struct node *next;};三、功能函数设计1、输入并建立多项式的功能模块具体函数为node *in f un()此函数的处理较为全面，要求用户按照指数递增的顺序和一定的输入格式输入各个系数不为0的子项，输入一个子项建立一个相关结点，当遇到输入结束标志时住手输入。

关键步骤具体如下：(1)控制用户按照指数递增的顺序输入r=a;while(r!=q->next)if(y<=r->exp)cout<<"请按照指数递增顺序输入，请重新输入";cin>>x>>y;break;r=r->next;从头开始遍历，若遇到目前输入的指数不是最大时，就跳出循环，让用户重新输入。

(2)当输入的系数为零时，不为其分配存储空间存储while(x==0){cin>>x>>y;continue;}即若系数为0,再也不进行动态分配并新建结点，而是重新提取用户输入的下一个子项的系数和指数，利用continue 进入下一次循环。

实验报告-一元多项式

一元多项式实验报告学号：201013131145 姓名：罗启荣1、实验目的1）掌握链表的灵活运用；2）学习链表初始化和建立一个新的链表；3）知道怎样去实现链表删除结点操作与插入结点；4）理解链表的基本操作（包括数据域数据的相加）并能灵活运用。

2、实验内容建立两个链表为稀疏多项式，将他们每项按项相加，最后将得到的链表打印出来。

要求：运用单链表来存储多项式，并且结果链表要用原来的链表空间，空间复杂度为O（1）3、数据结构及算法思想typedef int ElemType;typedef struct CLNode{ElemType coef;ElemType exp;struct CLNode *next;} CLNode, *CLinkList;建立两个单链表，并按要求将结点数据相加，将结果链表存储在C中。

4、模块化分a)主程序；2）初始化单链表；3）建立单链表； 4）相加多项式5、详细设计及运行结果a) 设计思路分析要解决多项式相加，必须要有多项式，所以必须首先建立两个多项式，在这里采用链表的方式存储链表，所以我将结点结构体定义为运用尾插法建立两条单链表，以单链表polya和polyb分别表示两个一元多项式A和B，A+B的求和运算等同于单链表的插入问题（将单链表polyb中的结点插入到单链表polya中），因此“和多项式”中的结点无须另生成。

为了实现处理，设p、q分别指向单链表polya和polyb的当前项，比较p、q结点的指数项，由此得到下列运算规则：①若p->exp>q->exp，则结点p所指的结点应是“和多项式”中的一项，令指针p后移。

②若p->exp=q->exp，则将两个结点中的系数相加，当和不为0时修改结点p 的系数。

③若p->exp<q->exp，则结点q所指的结点应是“和多项式”中的一项，将结点q插入在结点p之前，且令指针q在原来的链表上后移。

数据结构实验报告-一元多项式

数据结构实验报告-一元多项式数据结构课程设计报告课题: 一元多项式姓名：XX学号：201417030218专业班级：XXXX指导教师：XXXX设计时间：2015年12月30日星期三评阅意见：评定成绩：指导老师签名：年月日目录一、任务目标 (3)二、概要设计 (4)三、详细设计 (6)四、调试分析 (8)五、源程序代码 (8)六、程序运行效果图与说明 (15)七、本次实验小结 (16)八、参考文献 (16)一丶任务目标分析 (1) a.能够按照指数降序排列建立并输出多项式b.能够完成两个多项式的相加，相减，并将结果输入要求：程序所能达到的功能：a.实现一元多项式的输入；b.实现一元多项式的输出；c.计算两个一元多项式的和并输出结果；d.计算两个一元多项式的差并输出结果；除任务要求外新增乘法：计算两个一元多项式的乘积并输出结果（2）输入的形式和输入值的范围：输入要求：分行输入，每行输入一项，先输入多项式的指数，再输入多项式的系数，以0 0为结束标志，结束一个多项式的输入。

输入形式：2 3-1 23 01 20 0输入值的范围：系数为int型，指数为float型（3）输出的形式：第一行输出多项式1；第二行输出多项式2；第三行输出多项式1与多项式2相加的结果多项式；第四行输出多项式1与多项式2相减的结果多项式；第五行输出多项式1与多项式2相乘的结果多项式二、概要设计程序实现a. 功能：将要进行运算的二项式输入输出；b. 数据流入：要输入的二项式的系数与指数；c. 数据流出：合并同类项后的二项式；d. 程序流程图：二项式输入流程图；e. 测试要点：输入的二项式是否正确，若输入错误则重新输入。

流程图：三、详细设计（1）：存储结构一元多项式的表示在计算机内可以用链表来表示，为了节省存储空间，只存储多项式中系数非零的项。

链表中的每一个结点存放多项式的一个系数非零项，它包含三个域，分别存放该项的系数、指数以及指向下一个多项式项结点的指针。

数据结构一元多项式求和实验报告

xx大学xxx学院算法与数据结构试验报告设计名称：算法与数据结构设计题目：链表的应用学生学号：xx专业班级：xx学生姓名：xx学生成绩：指导教师（职称）：课题工作时间：2012年4月10日说明：实验课程类别：课程内实验实验课程性质：必修适用专业、年级：2010级计算机工程、计算机网络开课院、系：计算机科学与工程学院计算机工程教研室学时：18编写依据：《算法与数据结构》实验教学大纲修订时间：2012年2月《算法与数据结构》课程实验指导书（以下简称：指导书）是针对计算机学院所开设的对应课程的上机实验而编写的教学文件，供学生上机实验时使用。

上机的工作环境要求：Windows 2000或以上操作系统、VC++ 6.0或者其它高级程序设计语言。

学生应按指导教师的要求独立完成实验，并按要求撰写实验报告。

每一个实验，编程上机调试并且提交电子文档实验报告，以学号姓名作为文件名上传。

报告内容至少包含如下内容：1、学生基本情况：专业班级、学号、姓名2、实验题目、实验内容3、设计分析4、源程序代码5、测试用例（尽量覆盖所有分支）6、实验总结一．实验内容与学时分配一、试验课题链表的应用二、试验内容一元多项式求和。

把任意给定的两个一元多项式P(x),Q(x)输入计算机，计算它们的和并输出计算结果。

三、试验分析系数指数一元多项式链表的结点结构四、源程序代码#include<stdio.h> #include<stdlib.h> /*链表数据类型定义*/ typedef struct LNode {int x,z;struct LNode *next; }LinkList;void OutLinkList(LinkList *L); /*输出函数*/void PutLinkList(LinkList *&L,int n); /*输入函数*/LinkList *AddLinkList(LinkList *a,LinkList *b); /*求和函数*/ void OutXLinkList(LinkList *L); void OutZLinkList(LinkList *L); void main() {int n,m;LinkList *a,*b,*c;printf("\t\t\t本程序可以完成两个一元多项式的加法运算。

一元多项式相加数据结构实验报告

南昌航空大学实验报告课程名称：数据结构实验名称：实验二线性表的链式存储结构班级：080611 学生姓名：学号：08指导教师评定：签名:题目：设计并实现以下算法：给出用单链表存储多项式的结构，利用后接法生成多项式的单链表结构，实现两个多项式相加的运算，并就地逆置相加后的多项式链式。

一、需求分析1.用户可以根据自己的需求分别输入两个一元多项式，并且能够实现输入的一元多项式的显示。

2.能够完成两个一元多项式的相加功能，而且还能显示相加后的逆置的一元多项式。

3.程序执行的命令包括：（1）构造链表A （2）构造链表B （3）两个链表的相加（4）求链表的长度（5）打印（显示）已有的链表（6）将已相加的链表进行逆序排列二、概要设计⒈为实现上述算法，需要线性表的抽象数据类型：ADT Polynomial {数据对象：D={a i:|a i∈TermSet,i=1…n,n≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数} 数据关系：R1={<a i-1,a i>|a i-1,a i∈D,且a i-1中的指数值< a i中的指数值i=2,…n≥0}基本操作:initlink(& L)操作结果：构造一个空的链表L。

Creatlink(&L,n)操作结果：输入n项的系数和指数，建立一个非空的一元多项式L。

LinkLength(L)初始条件：链表L已经存在。

操作结果：返回一元多项式L中的项数。

Displaylink（L）初始条件：链表L已经存在。

操作结果：打印输出一元多项式L。

Addpolyn(A,B,&C)初始条件：一元多项式A和B已存在。

操作结果：完成多项式相加运算，即：C=A+B，并且带回C。

subtracypolyn(&La,&Lb,)初始条件：一元多项式La和Lb已存在。

操作结果：完成多项式的相减运算La=La+Lb，并且销毁多项式Lb。

数据结构实验报告数值转换和一元多项式

编号：江西理工大学数据结构课程设计报告班级：网络112班学号：09姓名：李秀光时间：2012年12月31日~2012年1月11日指导教师：涂燕琼井福荣2013年01月数制转换一、需求分析1、输入的形式和输入值的范围n和f的输入形式均为int型，n和f的输入范围均为1~327672、输出的形式十六进制10-15输出A-E，超过十六进制时按16以上数值按原值输出。

3、程序所能达到的功能把十进制数n转换成任意进制数f（对于输入的任意一个非负十进制整数，输出与其等值的任意进制数（如二，四，八，十六进制）。

4、测试数据n（十进制）f（进制）输出值22 2 10110354 4 112025376 8 1240032767 16 7FFF1、抽象数据类型的定义ADT Stack｛基本操作：InitStack(&S)操作结果：构造一个空栈s。

Push(&S,e)初始条件：栈s已存在。

操作结果：插入元素e为新的栈顶元素。

Pop(SqStack &S)初始操作：栈s已存在且非空。

操作结果：删除s的栈顶元素，并用e返回其值。

StackEmpty(SqStack S)初始条件：栈s已存在。

操作结果：若栈为空则返回1，否则返回0。

｝ADT Stack2、主程序的流程以及各程序模块之间的层次调用关系见（三、详细设计3、流程图）↓1、数据类型// = = = = = ADT Stack 的表示与实现= = = = = //// - - - - - 数制转换- - - - -//#define STACK_INIT_SIZE 100 //存储空间初始分配量#define STACKINCREMENT 10 //存储空间分配增量typedef struct {int *base;int *top;int stacksize;}SqStack;// - - - - - 基本操作的函数原型说明- - - - - //void InitStack(SqStack &S)//构造一个空栈svoid Push(SqStack &S,int e)//插入e为新的栈顶元素int Pop(SqStack &S)//删除s的栈顶元素，并用e返回其值int StackEmpty(SqStack S)//若栈为空则返回1，否则返回0void conversion(int n,int f)//对于输入的任意一个非负十进制整数，打印输出与其等值的八进制数2、伪码算法// - - - - - 基本操作的算法描述 - - - - - //void InitStack(SqStack &S){//构造一个空栈sS.base = (int *)malloc(STACK_INIT_SIZE * sizeof(int));if(!S.base) exit(-2);S.top = S.base;S.stacksize = STACK_INIT_SIZE;}// InitStackvoid Push(SqStack &S,int e){//插入元素e为新的栈顶元素if(S.top- S.base >= S.stacksize){S.base = (int *)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(int));if(!S.base) exit(-2);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;}// Pushint Pop(SqStack &S){//删除s的栈顶元素，并用e返回其值int e;if(S.top == S.base) return 0;e = *--S.top;return e;}//Popint StackEmpty(SqStack S){//若栈为空则返回1，否则返回0if(S.top == S.base) return 1;else return 0;}// StackEmpty//对于输入的任意一个非负十进制整数，打印输出与其等值的八进制数void conversion(int n,int f){InitStack(S);while(n){Push(S,n%f);n = n/f;}while(!StackEmpty(S)){Pop(S,e)printf("%d",e);}}// conversion3、流程图(1)调试过程中遇到的问题和解决方法在调试过程中主要遇到一些符号打错或输出、输出和函数之类的名称打错或漏打，根据第一行提示的错误然后进行修改，修改之后再运行调试，如此循环，直到彻底正常运行，后面就是优化见面的问题了。

一元多项式实验报告

实验二一元多项式相加问题本实验的目的是进一步熟练掌握应用链表处理实际问题的能力。

一、【问题描述】一元多项式相加是通过键盘输入两个形如P0+P1X1+P2X2+…+P n X n 的多项式，经过程序运算后在屏幕上输出他们的相加和。

二、【数据结构设计】分析任意一元多项式的描述方法可知，一个一元多项式的每一个子项都是有“系数－指数”两部分来组成的，所以将它可以抽象成一个由“系数－指数对”构成的线性表，由于对多项式中系数为0的子项可以不记录它的指数值，对于这样的情况就不再付出存储空间来存放它了。

基于这样的分析，我们可以采用一个带有头结点的单链表来表示一个一元多项式。

具体数据类型定义为：typedef struct Polynomial{Float coe; //系数int exp; //指数struct Polynomial *next;}*Polyn,Polynomial; 这三个指针分别作为链表A、B、C的头指针。

三、【功能（函数）设计】1、输入并建立多项式的功能模块：此模块要求按照指数递增的顺序和一定的输入格式输入各个系数不为0的子项的“系数－指数对”，输入一个子项建立一个相关结点，当遇到输入结束标志的时候就停止输入，而转去执行程序下面的部分。

2、多项式相加的功能模块此模块根据在1中建立的两个多项式进行相加的运算，并存放在以C为头指针的一个新链表中。

可以采用如下的方法进行设计：设指针p、q、r分别指向描述多项式的链表A、B、C头部，p指针按照A中结点顺序一个一个的移动，每移动一个结点，就通过q指针的移动来寻找B中是否有与p→exp相同的，（1）如果有，在C中合适的位置（注意多项式存储是按照指数递增有序的）建立新结点，并做如下赋值操作：r→coef=p→coef＋q→coef;r→exp=p→exp;p→flag=1;q→flag=1; /*标志子项已参与过运算*/p=p→next;q=head_b;（2）如果没有，在C中合适的位置（注意多项式存储是按照指数递增有序的）建立新结点，并做如下赋值操作：r→coef=p→coef;r→exp=p→exp;p=p→next;q=head_b;注意：当A、B中可以相加的两项的系数和为0的时候，在C中就不用分配新的空间来进行存储了。

数据结构实验-一元多项式的加法运算

一元多项式加法一、实验目的通过实现多项式加法，对链表有更深入的了解二、实验内容问题描述：设计一个一元稀疏多项式简单的加法计算器实现要求：一元稀疏多项式简单计算器的基本功能是：（1）输入并建立多项式：1785937)(x x x x A +++=；879228)(x x x x B -+=（2）输出多项式（3）多项式A 和B 相加，建立多项式C ＝A ＋B ，并输出相加的结果多项式C（4）选作：多项式A 和B 相减，建立多项式C ＝A －B ，并输出相减的结果多项式D 方法说明：（1）多项式的输入与存储用带表头结点的单链表存储多项式，链表中的每个节点分别存储多项式各项的系数和指数，即每从键盘输入多项式的一对数（系数，指数），可对应建立链表的一个结点。

每个节点的结构为：建立两个链表，其中pa 和pb 分别为它们的头指针：pb结果链表Pa(或者是Pc)Pc（2）多项式数据类型的定义struct tagNode{float coef;int exp;struct tagNode *next;typedef struct tagNode Node;typedef struct tagNode* pNode;（3）主要算法①创建两个链表，分别存放多项式1和多项式2，这两个链表中的节点是按指数降序或者升序排列的②多项式相加，下面给出多项式相加的部分实现/*下面的函数实现两个多项式的相加，要相加的链表分别由pa和pb指向（其中，pa，pb都是分配了空间的头结点）。

相加的结果直接由pa指向的链表保存，即是在pa链表中添加或删除（当系数因为相加为0的情况下）一些结点，构成结果。

相加的链表中指数按从小到大的顺序排列好的，是升序链表。

*/void add_poly(Node *pa,Node *pb){Node *p=pa->pNext;//链表1，将来的结果也放在此Node *q=pb->pNext;//链表2Node *pre=pa;Node *u;//临时用float x;while (p!=NULL && q!=NULL)//当两个链表都不为空{if (p->exp<q->exp)//比较链表1跟链表2当前节点的指数大小，链表1也是存放结果的地方{pre=p;p=p->pNext;//p指向要比较的下一个结点。

一元多项式实验报告

武汉工程大学计算机科学与工程学院__数据结构__课程实验报告专业班级：学号：学生姓名：实验室：指导教师：成绩：日期：_2012_年__5_月_22_日第__十五_周星期_二_节次_9-10_程序运行结果：程序代码：# include <stdio.h># include <malloc.h># include <stdlib.h>typedef struct Polynomial{float coef; //系数int exp; //指数struct Polynomial * next;}S, *ps; //S等价于struct Polynomial，ps等价于struct Polynomial *ps creat(void); //初始化链表S并返回一个头指针void sort(ps S); //链表排序void print(ps p); //输出链表ps PolyAdd(ps pa, ps pb); //求和int main(void){ps p = NULL, q = NULL;printf("一元多项式P(x)：\n");p = creat();printf("排序前：\n");printf("P(x) = ");print(p);printf("排序后：\n");sort(p);printf("P(x) = ");print(p);printf("\n\n");printf("一元多项式Q(x)：\n");q = creat();printf("排序前：\n");printf("Q(x) = ");print(q);printf("排序后：\n");sort(q);printf("Q(x) = ");print(q);printf("\n\n");p = PolyAdd(p, q);printf("P(x) + Q(x) = ");print(p);return 0;}ps creat(void){int len, e;float c;ps head = (ps)malloc(sizeof(S));if(NULL == head){printf("动态内存分配失败\n");exit(-1);}ps tail = head;tail->next = NULL;printf("\t输入该多项式的项数：");scanf("%d", &len);for(int i=0;i<len;i++){ps pNew = (ps)malloc(sizeof(S));printf("\t分别输入第%d项的系数与指数：", i+1);scanf("%f %d", &c, &e);pNew->coef = c;pNew->exp = e;if(NULL == pNew){printf("动态内存分配失败\n");exit(-1);}tail->next = pNew;pNew->next = NULL;tail = pNew;}return head;}void print(ps p) //输出多项式{ps printing;int flag=0;printing=p->next;//正在被打印的链节if(p->next==NULL)//如果函数为空打印0{printf("0\n");return;}while(flag==0){if(printing->coef>0&&p->next!=printing)printf("+");//为正数时打印"+"号if(printing->coef==1);//如果为"1"就不用打印系数了else if(printing->coef==-1)printf("-");//如果为"-1"就打印"-"号就行了elseprintf("%0.2f",printing->coef);//其余情况都得打印if(printing->exp!=0) printf("x^%d",printing->exp);//如果指数为"0"不打印指数项else if((printing->coef==1)||(printing->coef==-1))printf("1");if(printing->next==NULL)flag=1;//如果现在的链节没有下一个就结束elseprinting=printing->next;}printf("\n");}void sort(ps S) //链表排序{ps p = S->next; //p指向第一个结点ps q,r;if(p != NULL) //若原单链表中有一个或一个以上的结点{r = p->next; //r保存*p结点直接后继结点的指针p->next = NULL; //构造只含一个结点的有序表p = r;while(p != NULL){r = p->next;q = S;while(q->next != NULL && q->next->exp < p->exp)q = q->next; //在有序表中找插入*p的直接前驱结点*q的位置p->next = q->next; //将*p插入到*q之后q->next = p;p = r; //扫描原单链表余下的结点}}}ps PolyAdd(ps pa,ps pb) //求和{ps p,q,r,s;float x;p=pa->next;r=pa;q=pb->next;free(pb);while(p!=NULL&&q!=NULL)if(p->exp<q->exp){r=p;p=p->next;}else if(p->exp==q->exp){x = p->coef+q->coef;if(x==0){r->next=p->next;free(p);}else{p->coef=x;r=p;}p=r->next;s=q->next;free(q);q=s;}else{s=q->next;r->next=q;q->next=p;r=q;q=s;}if(q!=NULL)r->next=q;return(pa);}。

实验1-一元多项式实验报告

实验1-一元多项式实验报告数据结构实验报告实验名称：实验1——一元多项式Polynomial学生姓名：孙广东班级：2011211109班内序号：08学号：2011210251日期：2012年11月1日1．实验要求实验目的：1.熟悉C++语言的基本编程方法，掌握集成编译环境的调试方法2.学习指针、异常处理的使用3.掌握单链表的操作的实现方法4.学习使用线性表解决实际问题的能力实验内容：利用线性表实现一个一元多项式Polynomialf(x) = a0 + a1x + a2x2 + a3x3+ … + a n x n要求：1．能够实现一元多项式的输入和输出2．能够进行一元多项式相加3．能够进行一元多项式相减4．能够计算一元多项式在x处的值5．能够计算一元多项式的导数（选作）6．能够进行一元多项式相乘（选作）7．编写测试main()函数测试线性表的正确性2. 程序分析由于多项式是线性结构，故选择线性表来实现，在这个程序中我采用的是带头结点的单链表结构，每个结点代表一个项，多项式的每一项可以用其系数和指数唯一的表示。

如果采用顺序存储，那么对于结点的插入和删除的操作会比较麻烦，程序的时间空间复杂度增加，而且顺序表的结点个数动态增加不便，因为决定采用单链表的方式解决。

本程序完成的主要功能：1.输入和输出：需要输入的信息有多项式的系数和指数，用来向系统动态申请内存；系数和指数用来构造每个结点，形成链表。

在构造链表的时候我添加了出泡排序以及合并同类项的功能，因此输入时没有要求。

输出即是将多项式的内容向屏幕输出。

2.多项式相加与相减：多项式的加减要指数相同即是同类项才能实现，所以在运算时要注意判断指数出现的各种不同的情况，分别考虑可能出现的不同情况。

将每项运算得到的结果都插入到新的链表中，形成结果多项式。

多项式相减可视为加上第二个多项式的相反数。

3.多项式的求导运算：多项式的求导根据数学知识，就是将每项的系数乘以指数，将指数减1即可，将每项得到的结果更新到结果多项式的链表中。

数据结构实验报告-一元多项式

(2023)数据结构利用链表计算一元多项式课程设计实验报告(一)

数据结构综合实验报告_一元多项式

数据结构实验报告-一元多项式

一元多项式实验报告

数据结构实验报告实验一题目3一元多项式

数据结构一元多项式报告

数据结构实验报告《一、多项式及其运用》

数据结构-实验一-一元多项式相加精品

数据结构《一元多项式》

实验报告-一元多项式

数据结构实验报告-一元多项式

数据结构一元多项式求和实验报告

一元多项式相加 数据结构实验报告

数据结构实验报告数值转换和一元多项式

一元多项式实验报告

数据结构实验-一元多项式的加法运算

一元多项式实验报告

实验1-一元多项式实验报告

一元多项式相加数据结构实验报告