测控电路第七章信号细分与辨向电路
测控电路习题详解

测控电路习题详解第一章绪论 (2)第二章信号放大电路 (7)第四章信号分离电路 (14)第五章信号运算电路 (25)第六章信号转换电路 (29)第七章信号细分与辨向电路 (34)第一章绪论1-1为什么说在现代生产中提高产品质量与生产效率都离不开测量与控制技术?为了获得高质量的产品,必须要求机器按照给定的规程运行。
例如,为了加工出所需尺寸、形状的高精度零件,机床的刀架与主轴必须精确地按所要求的轨迹作相对运动。
为了炼出所需规格的钢材,除了严格按配方配料外,还必须严格控制炉温、送风、冶炼时间等运行规程。
为了做到这些,必须对机器的运行状态进行精确检测,当发现它偏离规定要求,或有偏离规定要求的倾向时,控制它,使它按规定的要求运行。
为了保证产品质量,除了对生产过程的检测与控制外,还必须对产品进行检测。
这一方面是为了把好产品质量关,另一方面也是为了检测机器与生产过程的模型是否准确,是否在按正确的模型对机器与生产过程进行控制,进一步完善对生产过程的控制。
生产效率一方面与机器的运行速度有关,另一方面取决于机器或生产系统的自动化程度。
为了使机器能在高速下可靠运行,必须要求机器本身的质量高,其控制系统性能优异。
要做到这两点,还是离不开测量与控制。
产品的质量离不开测量与控制,生产自动化同样一点也离不开测量与控制。
特别是当今时代的自动化已不是本世纪初主要靠凸轮、机械机构实现的刚性自动化,而是以电子、计算机技术为核心的柔性自动化、自适应控制与智能化。
越是柔性的系统就越需要检测。
没有检测,机器和生产系统就不可能按正确的规程自动运行。
自适应控制就是要使机器和系统能自动地去适应变化了的内外部环境与条件,按最佳的方案运行,这里首先需要的是对外部环境条件的检测,检测是控制的基础。
智能化是能在复杂的、变化的环境条件下自行决策的自动化,决策的基础是对内部因素和外部环境条件的掌握,它同样离不开检测。
1-2试从你熟悉的几个例子说明测量与控制技术在生产、生活与各种工作中的广泛应用。
测控电路课后答案(张国雄 第四版)第七章
Uj 滞后 Ud 时(图 7-14c) ,只有 DG2 有可能输出低电平 , Ud′是 Ud 的延时信号,也可起门槛
作用。调节电阻 R 和电容 C 可改变门槛的大小。 7-6 请说明图 7-19 中用 sinAα+cosAαtgBβ代替 sinθd=sin(Aα+Bβ), 用 cosAα-sinAαtgBβ代 替 cosθd=cos(Aα+Bβ),为什么不会带来显著误差? 图 7-19 中把 180 °的相位角先按 α=18 °等分为 10 份,再把 18°按 β=1.8°等分为 10 份, 则 θd= Aα+ Bβ。 A、 B 为 0~9 的整数。可写出 sin θd=sin( Aα+Bβ)=cos Bβ(sin Aα+cos AαtgBβ) cos θd=cos( Aα+Bβ)=cos Bβ(cos Aα-sin AαtgBβ) 因为 Bβ=(0~9)×1.8°=0°~16.2 °,cosBβ=1~0.963。正余弦激磁电压同时增大不影响平 衡位置,故可近似取 sinθd≈sinAα+cos AαtgBβ, cosθd≈cosAα-sin AαtgBβ 。
第七章
7-1
信号细分与辨向电路
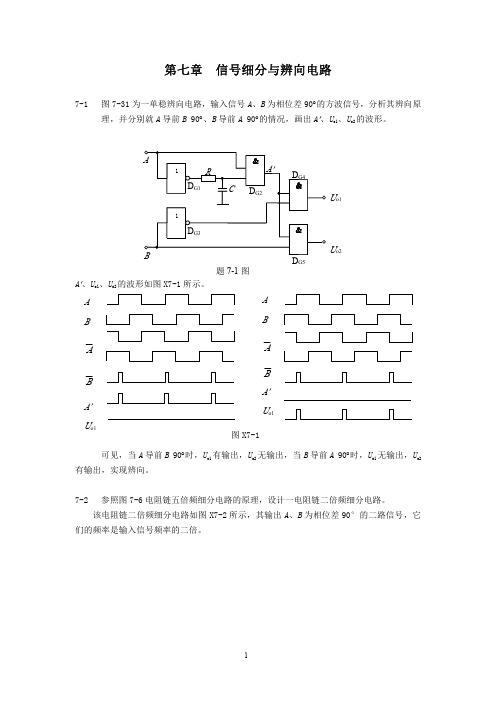
图 7-31 为一单稳辨向电路,输入信号 A、B 为相位差 90°的方波信号,分析其辨向原 理,并分别就 A 导前 B 90°、B 导前 A 90°的情况,画出 A′、Uo1、Uo2 的波形。
A1Biblioteka &RDG1
A′ C
DG2
DG4
&
Uo1
1
DG3
&
B
题 7-1 图
Uo2
DG5
7-7 请比较相位跟踪细分、幅值跟踪细分和脉冲调宽型幅值跟踪细分的优缺点。 相位跟踪细分常用于感应同步器和光栅的细分,由于在一个载波周期仅有一次比 相,因此对测量速度有一定的限制。相位跟踪细分电路较简单。 幅值跟踪细分主要应用于鉴幅型感应同步器仪器。 感应同步器是闭环系统的组成部 分,因而幅值跟踪系统实现了全闭环,而相位跟踪系统只实现半闭环(感应同步器在环 外) , 这使幅值跟踪系统具有更高的精度和更好的抗干扰性能。 电路中函数变压器受温度、 湿度影响小、不易老化,稳定性好,但工艺复杂,技术要求高,体积重量大,也可采用 集成电路的乘法型 D/A 转换器代替函数变压器。 幅值跟踪细分比相位跟踪系统允许更高 的移动速度。但电路较复杂。 脉冲调宽型幅值跟踪细分也是一种幅值跟踪细分系统, 只是用数字式可调脉宽函数发 生器代替上一系统中的函数变压器和切换计数器。因此保留了幅值跟踪系统的优点,系 统有高精度和高抗干扰能力。数字式脉宽函数发生器体积小、重量轻、易于生产,有高 的细分数,且有高的跟踪能力。数字电路可以灵活地根据测速改变跟踪速度。军用的高 速动态测量系统多采用具有高速数字跟踪能力的脉冲调宽方案,它有位置、速度甚至加 速度跟踪能力。当然,电路相当复杂。
第七章 细分电路解读

• 1、原理
–输入信号
• SIN、COS信号
–将SIN、COS信号施加在电阻链两端
• 在电阻链接点上得到不同相位与幅度的信号
–整形
• 在输入信号的一个周期中得到若干计数脉冲信号
u2
R2
uo u1
R1
u2
R2
u2
uo
uo
u1
R1
ER1 R1 R 2
φ u1
a)原理图
ER 2 R1 R 2
b)矢量图
设电阻链由电阻R1和R2串联而成,电阻链两端加有交流电压u1、 u2,其中,u1=Esint,u2=Ecost
uo R2 E sin t /( R1 R2 ) R1 E cost /( R1 R2 )
2 U om E R12 R2 /( R1 R2 )
arct an( R1 / R2 ) uo U om sin(t )
概述
• 信号细分电路概念: 信号细分电路又称插补器,是采用电路的手段对 周期性的测量信号进行插值提高仪器分辨力。 • 信号的共同特点: 信号具有周期性,信号每变化一个周期就对应着空 间上一个固定位移量。 • 电路细分原因: 测量电路通常采用对信号周期进行计数的方法实现 对位移的测量,若单纯对信号的周期进行计数, 则仪器 的分辨力就是一个信号周期所对应的位移量。为了提高 仪器的分辨力,就需要使用细分电路。
第七章
信号细分与辨向电路
功能
• 提高分辨力
• 对周期性测量信 号进行插值
§7.1 直传式细分电路
–四细分辨向电路 –电阻链分相细分 –微型计算机细分 –只读存储器细分
• 识别运动方向
• 识别测量信号的 相位
§7.2 平衡补偿式细分
测控的电路-信号细分和辩向第七章第一部分

细分电路的应用范围?
面向光栅, 感应同步器, 磁栅,容栅和激光干涉仪等 设备输出的周期信号
细分电路的分类?
•按工作原理分:直传式和平衡补偿式细分
•按处理信号分:调制信号和非调制信号细分
2
什么是辨向?为什么要辨向?
辨向:辨别机构的移动方向
A
B C D
E
位移传感器一般允许在正、反两个方向移动;
A'
B'
B'
Uo1 Uo2
Uo1 Uo2
正向运动(A超前B)
反向运动( B超前A ) 8
HCTL-20XX系列四细分辨向电路
• 该系列芯片具有细分与辨向功能; • 具有抗干扰设计; • 将可逆计数器设计在芯片上,芯片的集 成度高; • 简化外围电路的设计。
9
CLK
HCTL-2020具有的功能 CK 细分脉冲 计数方向 U/D 级联脉冲 CNT CAS CNTDECR
54o
= 1
3
33kΩ
24kΩ
18kΩ
56kΩ
72o
13 12
= 1
-Esinω t 144o
11
126o
10
UR
12
3+ 13
11+ 11’
13
电阻链分相细分优缺点
优点: 具有良好的动态特性,应用广泛 缺点: 细分数越高所需的元器件数目也成比例地 增加,使电路变得复杂,因此电阻链细分 主要用于细分数不高的场合。
1 2 3 4 5 6 7 8
19
微机量化细分的优缺点
优点:利用判别卦限和查表实现细分,相对 来说减少了计算机运算时间,若直接算反函 u1 / u2 )或 arc cot(u1 / u2 ) 要化更多的时 数arctan( 间;通过修改程序和正切表,很容易实现高 的细分数。 缺点:需要进行软件查表,细分速度慢,主 要用于输入信号频率不高或静态测量中。
测控电路07_信号细分和辩向电路 共35页

前进B在A 前面 u A
t u B
t 后退A在B 前面
第七章 信号细分与辨向电路
无法根据两路相位差0或180的信号辨向, 相位差90的两路信号最可靠。
第七章 信号细分与辨向电路
7.1 直传式细分电路
直传式细分直接利用位移信号进行细分,称其为直传式 是相对于跟踪式(平衡补偿式)而言的,也因为它可以 由若干细分环节串联而成。
第七章 信号细分与辨向电路
作用:细分电路实现对周期性的测量信号进 行插值,提高仪器的分辨率;辨向电 路实现对周期性信号极性的判断。
7.1 直传式细分电路(★) 7.2 平衡补偿式细分电路
测控电路
1
第七章 信号细分与辨向电路
信号细分电路概念: 信号细分电路又称插补器,是采用电路手段对
周期性的增量码信号进行插值提高仪器分辨力的一 种方法。
第七章 信号细分与辨向电路
什么是辨向:辨别机构的移动方向 为什么要辨向:
由于位移传感器一般允许在正、反两个方向移动,在进 行计数和细分电路的设计时往往要综合考虑辨向的问题。
A B CD E
由A前进至C与由A后退至B信号变化情况相同 由E前进与由D后退信号变化情况相同
难以根据单一信号辨向
第七章 信号细分与辨向电路
输出信号Uo1、Uo2可直接送入标准系列可逆计数集 成电路,实现辨向计数。
测控电路
17
7.1.2 电阻链分相细分
输入信号:相位差90的两路正余弦(正交)模拟信号。 工作原理:将正余弦信号施加在电阻链两端,由于两信号 的叠加作用,在电阻链的接点上得到幅值和相位各不相同 的电信号。这些信号经整形、脉冲形成后,就能在正余弦 信号的一个周期内获得若干计数脉冲,实现细分。 优点:具有良好的动态特性,应用广泛。 缺点:细分数越高所需的元器件数目也成比例地增加,使 电路变得复杂,因此电阻链细分主要用于细分数不高的场 合。
信号细分与辩向电路

u2 R2 uo
E R1 R1 R2
u2
uo
arctan( R1 / R2 )
输出电压的幅值与相位都与R1 u1 和R2的比值有关。
R1
ER2 R1 R 2
u1
不同相的输出电压信号经电压比较器整形为方波,然后经 逻辑电路处理即可实现细分。
测控电路
改变输入信号可改变象限:
Ⅰ: Ⅱ: Ⅲ: Ⅳ: u1=Esin t,u2=Ecos t u1=Ecos t ,u2=-Esin t u1=-Esin t,u2=-Ecos t u1=-Ecos t ,u2=Esin t Ecos t φ=0 ° ~90 ° φ=90 ° ~180 ° φ=180 °~270° φ=270 ° ~360 °
72o
13 12
=
1
11
144o
126o
9 8
=
1
10
UR
图7-6
下一页
返
回
上一页
测控电路
Esint
1 2 3 13 11 13 12 11 3 5 6 4
8
10 9 8 10
五 倍 频 细 分 电 路 的 波 形
4
测控电路
优点: 具有良好的动态特性,应用广泛 缺点: 细分数越高所需的元器件数目也成比例地增加,使电 路变得复杂,因此电阻链细分主要用于细分数不高的场 合。
返
回
上一页
下一页
测控电路
细分的基本原理:
根据周期性测量信号的波形、振幅或者相位的变
化规律,在一个周期内进行插值,从而获得优于
一个信号周期的更高的分辨力。又称插补器。 信号的共同特点:
信号具有周期性,信号每变化一个周期就对应着空间 上一个固定位移量。
测控电路 第7章 信号细分与辨向电路

信号细分与辨向电路
7.1 直传式细分电路 7.2 平衡补偿式细分
信号细分与辨向电路
为什么要细分? 提高分辨力
信号细分电路又称插补器,是采用电路手段对周期性的增量码信号进行插值 提高仪器分辨力的一种方法。细分的基本原理是:根据周期性测量信号的波 形、幅值或者相位的变化规律,在一个周期内进行插补,从而获得优于一个 信号周期的更高的分辨力。 高分辨力是高精度的必要条件。
第7章 信号细分与辨向电路
19
7.2.4频率跟踪细分——锁相倍频细分
锁相式数字频率合成技术:用来实现测量信号的n倍频,以实现n细分
鉴相器 fi
fo/n
环路滤波器 Uc 压控振荡器 fo
n分频器
优点:结构较简单,细分数高的,对信号失真度无严格要求。 缺点:为有差系统,对输入信号的角频率的稳定性要求高,不能辨向。 主要用于电气倍频和回转部件的角度与传动比等的测量,这时比较容易保持fi接近恒定。
i
也可为幅值,相位,频率等
x -x
比较器
iF
K
s
x
F
∫
+
-
N
xo
• xo为系统输出量,是数字代码,代码
F
多是脉冲数
• 计数器具有积分作用
• Ks为前馈环节的灵敏度 • F为反馈环节的灵敏度
细分数为
KF
xo xi
1 F
第7章 信号细分与辨向电路
16
7.2.1 相位跟踪细分
原理
umsin(t+j)
放大 整形
A A B
第7章 信号细分与辨向电路
DG2 &
1
A
AHale Waihona Puke RCDG1
【精品课件】测控电路第七章信号细分与辨向电路

设比较器输出高、低电平电压分别为UOH 和两U个O门L。限电压:U1URR1R 1R2UoLR1R 2R2
U2URR1R 1R2UoH R1R 2R2
滞后电平:
UU 2U 1R 1R 2R 2(U oH U o)L
电阻链5倍频细分电路
从比较器得到的10路方波信号再经过异或门
逻辑组合电路,在3′和4 ′端获得两路相位差 为90° 的五倍频方波信号。注意:该5倍频
-Esinωt
Esinωt
电阻并联桥,在四个象限内依次有一个相位差的 若干输出电压。
~ R 1 相关
R2
每一个臂上都是电位器,可以用来调整相位。
180° ~270° 移相
270° ~360° 移相
-Ecosωt
例:若采用这种移相桥实现12细分,所有的电位器电阻值均为12KΩ,计算第一
象限的各电阻值分阻阻值。
uom~
R1 R2
相关
所以改变R1、R2比值,就能 改变φ、uom,uo是沿u1、u2直 线运动, φ=45°时,uom有最
小值。
这里讲的的是0° ~90° 第一象限的情况。
同理: cosωt
-sinωt
-cosωt
-sinωt
-cosωt
sinωt
90° ~180° 移相
Ecosωt 0° ~90° 移相
信号正好满足上述四细分电路对输入信号的 要求。
参照图7-6电阻链五倍频细分电路的原理,设计一电阻链二倍频细分电路。
Esinω t
12kΩ
12kΩ
0o
∞
-
+
+N
1 =1
A
3
12kΩ
4 5o
∞
测控电路信号细分和辩向电路60页PPT

11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
(完整版)测控电路课后习题答案

第一章绪论1- 1 测控电路在整个测控系统中起着什么样的作用?传感器的输出信号一般很微弱,还可能伴随着各种噪声,需要用测控电路将它放大,剔除噪声、选取有用信号,按照测量与控制功能的要求,进行所需演算、处理与变换,输出能控制执行机构动作的信号。
在整个测控系统中,电路是最灵活的部分,它具有便于放大、便于转换、便于传输、便于适应各种使用要求的特点。
测控电路在整个测控系统中起着十分关键的作用,测控系统、乃至整个机器和生产系统的性能在很大程度是取决于测控电路。
1- 2 影响测控电路精度的主要因素有哪些,而其中哪几个因素又是最基本的,需要特别注意?影响测控电路精度的主要因素有:(1)噪声与干扰;(2)失调与漂移,主要是温漂;(3)线性度与保真度;(4 )输入与输出阻抗的影响。
其中噪声与干扰,失调与漂移(含温漂)是最主要的,需要特别注意。
1- 3 为什么说测控电路是测控系统中最灵活的环节,它体现在哪些方面?为了适应在各种情况下测量与控制的需要,要求测控系统具有选取所需的信号、灵活地进行各种变换和对信号进行各种处理与运算的能力,这些工作通常由测控电路完成。
它包括:(1)模数转换与数模转换;(2)直流与交流、电压与电流信号之间的转换。
幅值、相位、频率与脉宽信号等之间的转换;(3)量程的变换;(4)选取所需的信号的能力,信号与噪声的分离,不同频率信号的分离等;(5)对信号进行处理与运算,如求平均值、差值、峰值、绝对值,求导数、积分等、非线性环节的线性化处理、逻辑判断等。
1- 4 测量电路的输入信号类型对其电路组成有何影响?试述模拟式测量电路与增量码数字式测量电路的基本组成及各组成部分的作用。
随着传感器类型的不同,输入信号的类型也随之而异。
主要可分为模拟式信号与数字式信号。
随着输入信号的不同,测量电路的组成也不同。
图X1-1 是模拟式测量电路的基本组成。
传感器包括它的基本转换电路,如电桥,传感器的输出已是电量(电压或电流)。
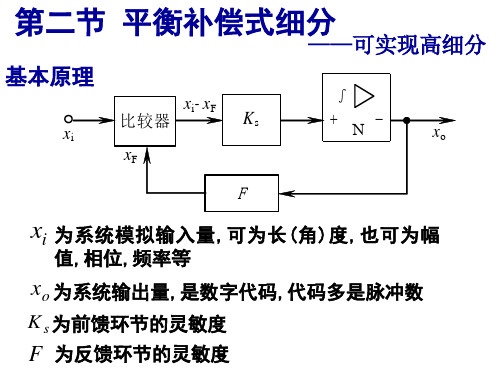
测控的电路-信号细分和辩向II第七章第二部分
Ux f0
2分频
S D
C
R
Q
DF
&
DG1
n/2 分频器
n/4 分频器 相对相位基准
二分频器
N分频,N细分
Ud
&
&
Uc
Fx
Ms
DG2
DG3
去数显电路
Ux
移相脉冲门
W
x N细分数 N移向脉冲数
当U x '0'时,二分频器才起作用 即U j与U d的相位差小于门槛电压
此时Q 1
Ux f0
Fx Ux
Uc
&
Uj
DG2
Ud
&
DG5
FX
Fx
鉴相电路
Ux
&
DG2
&
DG3 移相脉冲门
Uc Ms 去数显电路
谁跟踪谁?谁超前谁?跟踪量是谁?被跟踪量是谁?若有差值, 如何减小这种差值?如何体现细分概念?如何检测这种差值?
1 鉴相电路
Uj
Ud
Uc DG1 Ux Fx
Uj
&
&
Ud
DG1
DG4
FX
Uc
&
UX
DG3
n/2 分频器
S
D
C
&
n/4 分频器
二分频器
R
Q
Ud
DF
DG1 相对相位基准
&
DG2
&
DG3 移相脉冲门
Uc Ms 去数显电路
当U j超前U d时,Fx '1',当U x '1'时,二分频器关闭, DG2门打开,f0
第7章 信号细分与分辨电路

绝对零位
20Ω
sin、cos、-sin三路信号通过电阻链移相产生十路移相信号, 经十路比较器和逻辑电路在O1、O2获得两路正交信号。 绝对零信号经比较器整形后和两路方波信号( 126 、 ) 144 相与,获得标准零脉冲信号。
7.1.3 微型计算机细分
7.1.3.1 与硬件细分相结合的细分技术
缓冲计数器1
光栅 传感器
放大 整形
细分 辨向
缓冲计数器2
微 机 接 口
细分与辨向:由硬件电路完成; 计数、处理和显示:由微机完成; 缓冲计数器:提高系统的响应速度,最高速度为:
v m ax C / ( pN t )
7.1.3 微型计算机细分
7.1.3.2 时钟脉冲细分技术
将光栅一个栅距W内的信号转化为计时的方法实现细分。
7.1.4 只读存储器细分
128
0
128
255 X
7.2 平衡补偿式细分
■
用途:广泛应用于标尺节距大的感应同步器、容栅、 磁栅、光栅等传感器的后续仪器中。 特点:细分数高、分辨率高、精度高,但速度低(带负 反馈的闭环系统)。
前馈回路 xi 比较器 xF F 细分机构,分频数=细分数 x i- x F ∫ Ks + N xo
—— 相位调制信号,作为相位跟踪细分的输入信号。
7.2.1.1 相位跟踪细分原理
Umsin(t+j) 放大整形 鉴相电路
j- d
移 相 脉 冲
移相脉冲门
d
相对相位 基准分频器
显示电路
输入信号:相位差90的两路正余弦(正交)模拟信号。
工作原理:将正余弦信号施加在电阻链两端,由于两信 号的叠加作用,在电阻链的接点上得到幅值和相位各不相 同的电信号。这些信号经整形、脉冲形成后,就能在正余 弦信号的一个周期内获得若干计数脉冲,实现细分。
测控电路课后答案(张国雄_第四版)

第一章绪论1-1为什么说在现代生产中提高产品质量与生产效率都离不开测量与控制技术?为了获得高质量的产品,必须要求机器按照给定的规程运行。
例如,为了加工出所需尺寸、形状的高精度零件,机床的刀架与主轴必须精确地按所要求的轨迹作相对运动。
为了炼出所需规格的钢材,除了严格按配方配料外,还必须严格控制炉温、送风、冶炼时间等运行规程。
为了做到这些,必须对机器的运行状态进行精确检测,当发现它偏离规定要求,或有偏离规定要求的倾向时,控制它,使它按规定的要求运行。
为了保证产品质量,除了对生产过程的检测与控制外,还必须对产品进行检测。
这一方面是为了把好产品质量关,另一方面也是为了检测机器与生产过程的模型是否准确,是否在按正确的模型对机器与生产过程进行控制,进一步完善对生产过程的控制。
生产效率一方面与机器的运行速度有关,另一方面取决于机器或生产系统的自动化程度。
为了使机器能在高速下可靠运行,必须要求机器本身的质量高,其控制系统性能优异。
要做到这两点,还是离不开测量与控制。
产品的质量离不开测量与控制,生产自动化同样一点也离不开测量与控制。
特别是当今时代的自动化已不是本世纪初主要靠凸轮、机械机构实现的刚性自动化,而是以电子、计算机技术为核心的柔性自动化、自适应控制与智能化。
越是柔性的系统就越需要检测。
没有检测,机器和生产系统就不可能按正确的规程自动运行。
自适应控制就是要使机器和系统能自动地去适应变化了的内外部环境与条件,按最佳的方案运行,这里首先需要的是对外部环境条件的检测,检测是控制的基础。
智能化是能在复杂的、变化的环境条件下自行决策的自动化,决策的基础是对内部因素和外部环境条件的掌握,它同样离不开检测。
1-2试从你熟悉的几个例子说明测量与控制技术在生产、生活与各种工作中的广泛应用。
为了加工出所需尺寸、形状的高精度零件,机床的刀架与主轴必须精确地按所要求的轨迹作相对运动。
为了炼出所需规格的钢材,除了严格按配方配料外,还必须严格控制炉温、送风、冶炼时间等运行规程。
07-信号细分和辩向电路解析

2、3、6、7卦限
cot Acos u2 Asin u1
7. 信号细分与辨向电路
7.1 直传式细分电路 〔三〕计算机量化细分
u1 u2
为削减计算机运算时间, 承受软件查表,细分速度 比硬件慢,主要用于静态 测量中。
1 2 34 5 678
200细分
k 100 π
第1卦限, x=k 第3卦限, x=50+k 第5卦限, x=100+k 第7卦限, x=150+k
无法依据两路相位差 0 或 180的信号辨向, 相位差 90的两路信号最牢靠。
7. 信号细分与辨向电路
7.1 直传式细分电路
直传式细分直接利用位移信号进展细分,称其为 直传式是相对于跟踪式〔平衡补偿式〕而言的,也由
于它可以由假设干细分环节串联而成
Dx1
xi
K1
x1
K2
x2
xo Km
系统总的灵敏度Ks为各个环节灵敏度Kj (j=1~m)之积, 假设个别环节灵敏度Kj发生变化,它势必引起系统总的 灵敏度的变化。
2
1+2
3
0o
13
12+13
11
72o
13
144o
12
12+13 11
1ቤተ መጻሕፍቲ ባይዱ+2
3
18o
5
162o
6
5+6
4
90o
8
8+9
10
54o
9
126o
8
8 +9
10
5 +6
4
36o
108o
1+2 0o
12+13 72o 144o
测控电路教程第七章 信号细分与辨向电路

1
11′
144o
126o
9′ = 8′
1
10′
UR
图7-6
电压比较器一般接成施密特触发电路的形式, 电压比较器一般接成施密特触发电路的形式, 使其上升沿和下降沿的触发点具有不同的触发 电平,这个电平差称为回差电压。 电平,这个电平差称为回差电压。让回差电压 大于信号中的噪声幅值, 大于信号中的噪声幅值,可避免比较器在触发 点附近因噪声来回反转,回差电压越大, 点附近因噪声来回反转,回差电压越大,抗干 扰能力越强。 扰能力越强。但回差电压的存在使比较器的触 发点不可避免地偏离理想触发位置,造成误差, 发点不可避免地偏离理想触发位置,造成误差, 因此回差电压的选取应该兼顾抗干扰和精度两 方面的因素。 方面的因素。
式中,V为测量速度;f为载波信号频率;n为细分数;W为 标尺节距。
2π V θ = fW + V
(7-11)
四、频率跟踪细分——锁相倍频细 频率跟踪细分 锁相倍频细
鉴相器 fi fo/n n分频器 环路滤波器 Uc 压控振荡器 fo
图7-29 锁相倍频细分原理图
此系统由四个主要部件——鉴相器、环路滤波器、 压控振荡器和n分频器组成。
3. 相对相位基准和移相脉冲门
a) 时钟脉冲 b) 正常分频 c) 减脉冲 d) 使θd延后 减脉冲 e) 加脉冲 f) 使θd前移 加脉冲
图7-15 加减脉冲改变θd 原理图
n/2分频器 f0 Ux S D C R DF & n/4分频器 相对相位基准 二分频器 Ud DG1
& Fx DG2 Ux
umsin(ωt+θj)
放大 整形
鉴相电路 移 相 脉 冲
θj-θd
移位脉冲门
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 信号细分与辨向电路
计量测试工程学院 朱维斌
信号细分电路概念: 信号细分电路概念: 信号细分电路又称插补器, 信号细分电路又称插补器,是采用电路的手段对周期性的测量信号进行插值 提高仪器分辨力。 提高仪器分辨力。 信号的共同特点: 信号的共同特点: 信号具有周期性,信号每变化一个周期就对应着空间上一个固定位移量。 信号具有周期性,信号每变化一个周期就对应着空间上一个固定位移量。 电路细分原因: 电路细分原因: 测量电路通常采用对信号周期进行计数的方法实现对位移的测量, 测量电路通常采用对信号周期进行计数的方法实现对位移的测量,若单纯对 信号的周期进行计数, 则仪器的分辨力就是一个信号周期所对应的位移量。 信号的周期进行计数, 则仪器的分辨力就是一个信号周期所对应的位移量。为了 提高仪器的分辨力,就需要使用细分电路。 提高仪器的分辨力,就需要使用细分电路。 细分的基本原理: 细分的基本原理: 根据周期性测量信号的波形、振幅或者相位的变化规律, 根据周期性测量信号的波形、振幅或者相位的变化规律,在一个周期内进行插 从而获得优于一个信号周期的更高的分辨力。 值,从而获得优于一个信号周期的更高的分辨力。 辨向: 辨向: 由于位移传感器一般允许在正、反两个方向移动, 由于位移传感器一般允许在正、反两个方向移动,在进行计数和细分电路的 设计时往往要综合考虑辨向的问题。 设计时往往要综合考虑辨向的问题。
阈值电平
稳态 暂态
计量测试工程学院 朱维斌
典型的积分式单稳触发器
正 向 运 动
A′ B′
个过程: 第1个过程: 个过程 A上升沿的时候,A′产生一个窄脉冲。 上升沿的时候, 产生一个窄脉冲 产生一个窄脉冲。 上升沿的时候 B=0,B=1,DG10、DG5为与或非门。Uo1有计数脉 为与或非门。 , , 冲输出, 无输出。 冲输出,Uo2无输出。 A下降沿的时候,A′产生一个窄脉冲。 下降沿的时候, 产生一个窄脉冲 产生一个窄脉冲。 下降沿的时候 有计数脉冲输出, 无输出。 同样, 同样, Uo1有计数脉冲输出,Uo2无输出。 B上升沿的时候,B′产生一个窄脉冲。 上升沿的时候, 产生一个窄脉冲 产生一个窄脉冲。 上升沿的时候 同样, 有计数脉冲输出, 无输出。 同样, Uo1有计数脉冲输出,Uo2无输出。
经电阻链细分后,各相信号仍是模拟信号,为实现数字化, 经电阻链细分后,各相信号仍是模拟信号,为实现数字化,要把它们变换为逻辑 电平, “0”或“1”电平,这项工作由电压比较器完成。 或 电平 这项工作由电压比较器完成。 左半部分是两个区间的细分, 左半部分是两个区间的细分,右边是比 较器(施密特比较器)。 较器(施密特比较器)。
R
R1 + R2 = 12KΩ
180°~270° 180°~270°移相 270°~360° 270°~360°移相 -Ecosωt
R1=4.39 K ,R2=7.61 K
ϕ = arctan 1 = 60o 60°: ° R2
R
R1 + R2 = 12KΩ
R1=7.61 K ,R2=4.39 K
计量测试工程学院 朱维斌
计量测试工程学院 朱维斌
A
1
&
A′ DG4
&
R DG1 C DG2
图为一单稳辨向电路,输入信号A、B为相位差90° 的方波信号,分析其辨向原理,并分别就A导前B 90°、B导前A 90°的情况,画出A′、Uo1、Uo2的波形。
1
Uo1
DG3 B
&
Uo2 DG5
可见,当A导前B 90°时,Uo1有输出,Uo2无输出,当B导前A 90°时,Uo1无输出,Uo2有输出,实现辨向。
360 o = 30 o 12
Ecosωt 90°~180° 90°~180°移相
R2
每个象限内相位差30° 每个象限内相位差 °
0°~90°移相 ~90°
R1
0°: °
ϕ = arctan
R1 = 0o R2
R1 + R2 = 12 KΩ
-Esinωt Esinωt
R1=0 K ,R2=12 K
o 1 30°: ϕ = arctan R = 30 ° 2
计量测试工程学院 朱维斌
7.1 直传式细分
直传式细分 细分电路 平衡补偿式细分:带反馈,可实现高细分数。 平衡补偿式细分:带反馈,可实现高细分数。
∆ x1 xi K1 x1 K2
∆ x2 x2 Km xo
K1、K2、‥ ‥Km为各个环节的灵敏度 中间环节可能是波形变换电路、比较器或 等等。 中间环节可能是波形变换电路、比较器或D/A等等。 等等 ¨¨K ∴总的灵敏度:Ks=K1K2¨¨ m 总的灵敏度: 越靠近输入端,越要做的精细。 越靠近输入端,越要做的精细。 直传式系统抗干扰能力差,精度低于平衡补偿式,但是速度快,简单。 直传式系统抗干扰能力差,精度低于平衡补偿式,但是速度快,简单。
+ N
电阻链二倍频细分电路如图所示,其输出A、B为相位差45°的二路信号,它们的频率是输入 信号频率的二倍
计量测试工程学院 朱维斌
12kΩ Esinωt 12kΩ
0o
-
∞ + 1 3
=1
A
+ N 45o -
Esinωt
∞ + 2 4
=1
B
+ N 12kΩ 12kΩ Ecosωt 12kΩ 135o 90o -
计量测试工程学院 朱维斌
二、电阻链分相细分
要求信号为一对正余弦信号。 要求信号为一对正余弦信号。 一、工作原理 在电阻链两端施加相位差90° 频率相同的相位信号, 在电阻链两端施加相位差 °,频率相同的相位信号,由于两信号的叠加作 在电阻链各接点上,可得幅值和相位都不相同的电信号,这些信号经整形、 用,在电阻链各接点上,可得幅值和相位都不相同的电信号,这些信号经整形、 脉冲形成后,就能获得若干个计数脉冲。 脉冲形成后,就能获得若பைடு நூலகம்个计数脉冲。
设比较器输出高、低电平电压分别为 设比较器输出高、低电平电压分别为UOH 和UOL。 R1 R2
+ U oL R1 + R2 R1 + R2 两个门限电压: 两个门限电压: R1 R2 U2 =UR + U oH R1 + R2 R1 + R2 U1 = U R
滞后电平: 滞后电平:
∆U = U 2 − U 1 =
∴ uo = uom sin(ωt + ϕ )
ϕ ~
uom~
R1 相关 R2
R1 相关 R2
R1 R2
所以改变R 比值, 所以改变 1、R2比值,就能 改变φ、 是沿u 改变 、uom,uo是沿 1、u2直 线运动, 线运动, φ=45°时,uom有 ° 最小值。 最小值。
计量测试工程学院 朱维斌
这里讲的的是0 ~90°第一象限的情况。 这里讲的的是0°~90°第一象限的情况。 同理: 同理: cosωt -sinωt -sinωt -cosωt -cosωt sinωt
1 2 3 4 A B
∞ +
+ N
∞ +
12kΩ -Esinωt UR
+ N
计量测试工程学院 朱维斌
中国计量学院
计量测试工程学院 朱维斌
一、四细分辨向电路
要求:输入两路具有 °相位差的方波信号。 要求:输入两路具有90°相位差的方波信号。
A B
细分的原理:基于两路方波在一个周期内具有两个上升沿和两个下降沿, 细分的原理:基于两路方波在一个周期内具有两个上升沿和两个下降沿,通过 对边沿的处理实现四细分。 对边沿的处理实现四细分。 辨向:根据两路方波相位的相对导前和滞后的关系作为判别依据。 辨向:根据两路方波相位的相对导前和滞后的关系作为判别依据。 原理:利用单稳提取两路方波信号的边沿实现四细分。 原理:利用单稳提取两路方波信号的边沿实现四细分。
180°~270° 180°~270°移相
270°~360° 270°~360°移相 -Ecosωt
计量测试工程学院 朱维斌
细分, 例:若采用这种移相桥实现12细分,所有的电位器电阻值均为 若采用这种移相桥实现 细分 所有的电位器电阻值均为12K ,计算第 一象限的各电阻值分阻阻值。 一象限的各电阻值分阻阻值。
R2 (U oH − U oL ) R1 + R2
计量测试工程学院 朱维斌
电阻链5倍频细分电路 电阻链 倍频细分电路
从比较器得到的10路方波信号再经过异或门 从比较器得到的 路方波信号再经过异或门 逻辑组合电路, 逻辑组合电路,在3′和4 ′端获得两路相位差 的五倍频方波信号。注意: 为90°的五倍频方波信号。注意:该5倍频 倍频 信号正好满足上述四细分电路对输入信号的 要求。 要求。
Ecosωt 90°~180°移相 90°~180° 0°~90°移相 ~90°
电阻并联桥, 电阻并联桥,在四个象限内依次有一个相位差的 若干输出电压。 若干输出电压。
ϕ ~
R1 相关 R2
-Esinωt Esinωt
每一个臂上都是电位器,可以用来调整相位。 每一个臂上都是电位器,可以用来调整相位。
计量测试工程学院 朱维斌
反 向 运 动
反之:反向运动时, 在 的前面 这时在U 中输入了四个为零的计数脉冲, 的前面, 反之:反向运动时,B在A的前面,这时在 o2中输入了四个为零的计数脉冲,Uo1 无输出, 无输出,一直为高电平 ∴DG5 ——Uo1 DG10——Uo2 哪一个输出关系着辨向
根据上述原理,已制成集成电路 根据上述原理,已制成集成电路C5194、C5191 、
单稳四细分辨向电路
B下降沿的时候,B′产生一个窄脉冲。 下降沿的时候, 产生一个窄脉冲 产生一个窄脉冲。 下降沿的时候 同样, 有计数脉冲输出, 无输出。 同样, Uo1有计数脉冲输出,Uo2无输出。
