《计算机图形学基础》第2版(陆枫 何云峰)课后习题答案 电子工业出版社
计算机图形学1_8章习题解答

计算机图形学1_8章习题解答《计算机图形学》1-4章习题解答习题11.计算机图形学的研究内容是什么?答:几何模型构造,图形生成,图形操作与处理,图形信息的存储、检索与交换,人机交互及用户接口,动画,图形输出设备与输出技术,图形标准与图形软件包的研究等。
2.计算机图形学与图像处理有何联系?有何区别?答:计算机图形学与图像处理都是用计算机来处理图形和图像,结合紧密且相互渗透,但其属于两个不同的技术领域。
计算机图形学是通过算法和程序在显示设备上构造图形,是从数据到图像的处理过程;而图像处理是对景物或图像的分析技术,是从图像到图像的处理过程。
3.简述计算机图形学的发展过程。
答:略。
(参考:教材P3)4.简述你所理解的计算机图形学的应用领域。
答:略。
(参考:教材P4~P5)习题21.什么是图像的分辨率?答:在水平和垂直方向上每单位长度所包含的像素点的数目。
2.在CMY 坐标系里找出与RGB 坐标系的颜色(0.2,1,0.5)相同的坐标。
答:1-0.2=0.8,1-1=0, 1-0.5=0.5 坐标为(0.8, 0, 0.5)3.在RGB 坐标系里找出与CMY 坐标系的颜色(0.15,0.75,0)相同的坐标。
答:1-0.15=0.85, 1-0.75=0.25, 1-0=1 坐标为(0.85, 0.25, 1)4.如果使用每种基色占2比特的直接编码方式表示RGB 颜色的值,每一像素有多少种可能的颜色?答:64222222=??5.如果使用每种基色占10比特的直接编码方式表示RGB 颜色的值,每一像素有多少种可能的颜色?答:824107374110242223101010==??6.如果每个像素的红色和蓝色都用5比特表示,绿色用6比特表示,一共用16比特表示,总共可以表示多少种颜色?答:65536222655=??7.解释水平回扫、垂直回扫的概念。
答:水平回扫:电子束从CRT 屏幕右边缘回到屏幕左边缘的动作。
计算机图形学基础教程(第2版)

图书前言
本书是在2005版《计算机图形学基础教程》的基础上修订而成。 《计算机图形学基础教程》是根据作者在清华大学多年教学实践,并参考了国内外最新的相关教材和部分最 新的研究成果编写而成。第2版教材主要修订了以下内容: 1.增加了第1章的1.5节,介绍清华大学近年来的最新研究成果。 2.增加了第3章的3.9节,介绍格表示、简化与细分。 3.增加了第4章的4.1节,介绍图形绘制的基本概念和流程,提高本章整体上的可读性。 4.将第4章4.8节层次细节的内容移入第3章的3.9节,增加有关景物模拟的内容。 5.删除第5章VRML的内容,改写Open GL的内容,增加一些常见的功能,并给出更多的示例。 本教程第1版出版4年来,被国内一大批高等院校采用,相关的老师、同学及读者提出了许多宝贵的建议,在 此表示衷心感谢。徐昆、来煜坤参与了第2版教材的修订,在此也一并表示感谢。
序言
清华大学计算机系列教材已经出版发行了近30种,包括计算机专业的基础数学、专业技术基础和专业等课程 的教材,覆盖了计算机专业大学本科和研究生的主要教学内容。这是一批至今发行数量很大并赢得广大读者赞誉 的书籍,是近年来出版的大学计算机教材中影响比较大的一批精品。
本系列教材的作者都是我熟悉的教授与同事,他们长期在第一线担任相关课程的教学工作,是一批很受大学 生和研究生欢迎的任课教师。编写高质量的大学(研究生)计算机教材,不仅需要作者具备丰富的教学经验和科 研实践,还需要对相关领域科技发展前沿的正确把握和了解。正因为本系列教材的作者们具备了这些条件,才有 了这批高质量优秀教材的出版。可以说,教材是他们长期辛勤工作的结晶。本系列教材出版发行以来,从其发行 的数量、读者的反映、已经获得的许多国家级与省部级的奖励,以及在各个高等院校教学中所发挥的作用上,都 可以看出本系列教材所产生的社会影响与效益。
计算机图形学教程课后习题参考答案.

第一章1、试述计算机图形学研究的基本内容?答:见课本P5-6页的1.1.4节。
2、计算机图形学、图形处理与模式识别本质区别是什么?请各举一例说明。
答:计算机图形学是研究根据给定的描述,用计算机生成相应的图形、图像,且所生成的图形、图像可以显示屏幕上、硬拷贝输出或作为数据集存在计算机中的学科。
计算机图形学研究的是从数据描述到图形生成的过程。
例如计算机动画制作。
图形处理是利用计算机对原来存在物体的映像进行分析处理,然后再现图像。
例如工业中的射线探伤。
模式识别是指计算机对图形信息进行识别和分析描述,是从图形(图像)到描述的表达过程。
例如邮件分捡设备扫描信件上手写的邮政编码,并将编码用图像复原成数字。
3、计算机图形学与CAD、CAM技术关系如何?答:见课本P4-5页的1.1.3节。
4、举3个例子说明计算机图形学的应用。
答:①事务管理中的交互绘图应用图形学最多的领域之一是绘制事务管理中的各种图形。
通过从简明的形式呈现出数据的模型和趋势以增加对复杂现象的理解,并促使决策的制定。
②地理信息系统地理信息系统是建立在地理图形基础上的信息管理系统。
利用计算机图形生成技术可以绘制地理的、地质的以及其它自然现象的高精度勘探、测量图形。
③计算机动画用图形学的方法产生动画片,其形象逼真、生动,轻而易举地解决了人工绘图时难以解决的问题,大大提高了工作效率。
5、计算机绘图有哪些特点?答:见课本P8页的1.3.1节。
6、计算机生成图形的方法有哪些?答:计算机生成图形的方法有两种:矢量法和描点法。
①矢量法:在显示屏上先给定一系列坐标点,然后控制电子束在屏幕上按一定的顺序扫描,逐个“点亮”临近两点间的短矢量,从而得到一条近似的曲线。
尽管显示器产生的只是一些短直线的线段,但当直线段很短时,连成的曲线看起来还是光滑的。
②描点法:把显示屏幕分成有限个可发亮的离散点,每个离散点叫做一个像素,屏幕上由像素点组成的阵列称为光栅,曲线的绘制过程就是将该曲线在光栅上经过的那些像素点串接起来,使它们发亮,所显示的每一曲线都是由一定大小的像素点组成的。
《计算机图形学》1-4章习题解答

光栅扫描显示器的工作原理:将CRT屏幕分成由像素构成的光栅网格,其中像素的灰度和颜色信息保存在帧缓存中。电子束在水平和垂直偏转磁场的作用下从左向右,从上向下扫描荧光屏,产生一幅幅光栅,并由显示内容来控制所扫描的像素点是否发亮,从而形成具有多种彩色及多种明暗度的图像。
相当于:
9.将梁友栋-Barsky线段裁剪算法推广到三维,写出对下述三维观察体所要满足的不等式:
(a)平行规范化观察体;
(b)透视规范化观察体。
答:设 和 是线段的两个端点。线段的参数方程是:
平行规范化观察体是由平面 组成的单位立方体;
透视规范化观察体是由平面 组成的被截断的部分棱锥。
(a)对于平行规范化观察体,内部点满足:
垂直回扫:电子束到达每次刷新周期末尾,从CRT屏幕右下角回到屏幕左上角的动作。
8.为什么很多彩色打印机使用黑色颜料?
答:彩色颜料(青、品红、黄)相对来说较贵,并且在技术上很难通过多种颜色产生高质量的黑色。
9.简述随机扫描显示器和光栅扫描显示器的简单工作原理和各自的特点。
答:随机扫描显示器的工作原理:要显示的图形定义是一组画线命令,存放在刷新缓存中,由显示控制器控制电子束的偏移,周期性地按画线命令依次画出其组成线条,从而在屏幕上产生图形。
(a)绕原点;
(b)绕点P(-1,-1)。
答:三角形矩阵 ,设旋转之后的三角形矩阵为S’
逆时针旋转矩阵
平移矩阵 反平移矩阵
(a) ,得
(b) ,得
。
2.将三角形A(0,0),B(1,1),C(5,2)放大两倍,保持C(5,2)不变。
答:
计算机图形学教程课后习题参考答案.

第一章1、试述计算机图形学研究的基本内容?答:见课本P5-6页的1.1.4节。
2、计算机图形学、图形处理与模式识别本质区别是什么?请各举一例说明。
答:计算机图形学是研究根据给定的描述,用计算机生成相应的图形、图像,且所生成的图形、图像可以显示屏幕上、硬拷贝输出或作为数据集存在计算机中的学科。
计算机图形学研究的是从数据描述到图形生成的过程。
例如计算机动画制作。
图形处理是利用计算机对原来存在物体的映像进行分析处理,然后再现图像。
例如工业中的射线探伤。
模式识别是指计算机对图形信息进行识别和分析描述,是从图形(图像)到描述的表达过程。
例如邮件分捡设备扫描信件上手写的邮政编码,并将编码用图像复原成数字。
3、计算机图形学与CAD、CAM技术关系如何?答:见课本P4-5页的1.1.3节。
4、举3个例子说明计算机图形学的应用。
答:①事务管理中的交互绘图应用图形学最多的领域之一是绘制事务管理中的各种图形。
通过从简明的形式呈现出数据的模型和趋势以增加对复杂现象的理解,并促使决策的制定。
②地理信息系统地理信息系统是建立在地理图形基础上的信息管理系统。
利用计算机图形生成技术可以绘制地理的、地质的以及其它自然现象的高精度勘探、测量图形。
③计算机动画用图形学的方法产生动画片,其形象逼真、生动,轻而易举地解决了人工绘图时难以解决的问题,大大提高了工作效率。
5、计算机绘图有哪些特点?答:见课本P8页的1.3.1节。
6、计算机生成图形的方法有哪些?答:计算机生成图形的方法有两种:矢量法和描点法。
①矢量法:在显示屏上先给定一系列坐标点,然后控制电子束在屏幕上按一定的顺序扫描,逐个“点亮”临近两点间的短矢量,从而得到一条近似的曲线。
尽管显示器产生的只是一些短直线的线段,但当直线段很短时,连成的曲线看起来还是光滑的。
②描点法:把显示屏幕分成有限个可发亮的离散点,每个离散点叫做一个像素,屏幕上由像素点组成的阵列称为光栅,曲线的绘制过程就是将该曲线在光栅上经过的那些像素点串接起来,使它们发亮,所显示的每一曲线都是由一定大小的像素点组成的。
《计算机图形学》习题与解答

《计算机图形学》习题与解答第一章概述1. 试描述你所熟悉的计算机图形系统的硬软件环境。
计算机图形系统是计算机硬件、图形输入输出设备、计算机系统软件和图形软件的集合。
例如:计算机硬件采用PC、操作系统采用windows2000,图形输入设备有键盘、鼠标、光笔、触摸屏等,图形输出设备有CRT、LCD等,安装3D MAX图形软件。
2. 计算机图形系统与一般的计算机系统最主要的差别是什么?3. 图形硬件设备主要包括哪些?请按类别举出典型的物理设备?图形输入设备:鼠标、光笔、触摸屏和坐标数字化仪,以及图形扫描仪等。
图形显示设备:CRT、液晶显示器(LCD)等。
图形绘制设备:打印机、绘图仪等。
图形处理器:GPU(图形处理单元)、图形加速卡等等。
4. 为什么要制定图形软件标准?可分为哪两类?为了提高计算机图形软件、计算机图形的应用软件以及相关软件的编程人员在不同计算机和图形设备之间的可移植性。
图形软件标准通常是指图形系统及其相关应用系统中各界面之间进行数据传送和通信的接口标准,另外还有供图形应用程序调用的子程序功能及其格式标准。
5. 请列举出当前已成为国际标准的几种图形软件标准,并简述其主要功能。
(1)CGI(Computer Graphics Interface),它所提供的主要功能集包括控制功能集、独立于设备的图形对象输出功能集、图段功能集、输入和应答功能集以及产生、修改、检索和显示以像素数据形式存储的光栅功能集。
(2)GKS(Graphcis Kernel System),提供了应用程序和图形输入输出设备之间的接口,包括一系列交互和非交互式图形设备的全部图形处理功能。
主要功能如下:控制功能、输入输出功能、变换功能、图段功能、询问功能等。
6. 试列举计算机图形学的三个应用实例。
(1)CAD/CAM(2)VISC(3)VR.第二章光栅图形学1. 在图形设备上如何输出一个点?为输出一条任意斜率的直线,一般受到哪些因素影响?若图形设备是光栅图形显示器,光栅图形显示器可以看作是一个像素的矩阵,光栅图形显示器上的点是像素点的集合。
计算机图形学课程设计透视投影图三视图

计算机图形学程序课程设计题目:分别在四个视区内显示空间四面体的三视图、透视投影图。
学院:信息科学与技术学院专业:计算机科学与技术姓名:oc学号:oc电话:oc邮箱:oc目录一、设计概述(1)设计题目。
2(2)设计要求。
2(3)设计原理。
2(4)算法设计。
5(5)程序运行结果。
9二、核心算法流程图。
10三、程序源代码。
12四、程序运行结果分析。
24五、设计总结分析。
25六、参考文献。
26一.设计概述•设计题目计算机图形学基础(第二版)陆枫何云峰编著电子工业出版社P228-7.16:利用OpenGL中的多视区,分别在四个视区内显示图7-41所示空间四面体的主视图、俯视图、侧视图、透视投影图。
•设计要求设计内容:1. 掌握主视图、俯视图、侧视图和透视投影变换矩阵;2. 掌握透视投影图、三视图生成原理;功能要求:分别在四个视区内显示P228-图7-41所示空间四面体的主视图、俯视图、侧视图、透视投影图。
•设计原理正投影正投影根据投影面与坐标轴的夹角可分为三视图和正轴测图。
当投影面与某一坐标轴垂直时,得到的投影为三视图,这时投影方向与这个坐标轴的方向一致,否则,得到的投影为正轴测图。
1.主视图(V面投影)将三维物体向XOZ平面作垂直投影,得到主视图。
由投影变换前后三维物体上点到主视图上的点的关系,其变换矩阵为:Tv=Txoz= [1 0 0 0][0 0 0 0][0 0 1 0][0 0 0 1]Tv为主视图的投影变换矩阵。
简称主视图投影变换矩阵。
2.侧视图(W面投影)将三维物体向YOZ平面作垂直投影,得到侧视图。
为使侧视图与主视图在一个平面内,就要使W面绕Z轴正向旋转90°。
同时为了保证侧视图与主视图有一段距离,还要使W面再沿X方向平移一段距离x0,这样即得到侧视图。
变换矩阵为:Tv=Tyoz= [ 0 0 0 0 ][-1 0 0 0 ][ 0 0 1 0 ][-x0 0 0 1]Tv为主视图的投影变换矩阵。
计算机图形学(考前辅导)-2011

限的自相似性。
20
判断例题
1.实体模型的表示中,常用边界表示、构造实体
表示和空间分割表示形式。
(√ )
2.正则形体就是实体模型的描述对象。 (×)
21
单选例题
1. CSG树表示的是( D )的一种。
A. 线框模型 B. 表面模型 C. 物理模型 D. 实体模型
2. 以下哪种情况是正则形体( D )。 A.孤立四边形 B. 孤立点 C. 一条孤立边 D.球
个数为(A),则点B在多边形外部,否则该点在多边形内部。
A. 奇数 B. 无穷大 C.偶数 D. 0
31
简述例题
1.什么是走样?什么是反走样?常用的反走样技术
有哪些?
答:用离散量表示连续量引起的失真,就叫做走样。
用于减少或消除这种效果的技术,称为反走样。常
用的反走样技术有过取样(supersampling,或后 滤波)和区域取样 (area sampling,或前滤波)。
16
单选例题
1.在(B)输入下,立刻进行数据输入,所输入的数据被不断更新。 A. 事件 B. 采样 C. 就绪 D. 请求
2.使用软件采用读命令从键盘上获得数据的输入方式为( D )方式。 A. 事件 B. 就绪 C. 采样 D.请求
3. 在(A )输入下,由输入设备来初始化数据输入、控制数据处理进程。 A. 事件 B. 就绪 C. 采样 D. 请求
桶
p0 p2 p4
p6
7 9 p0p6
5
(c) 边表
p3 p5 1 2 3 4 5 6 7 8 9 10 11 12
x
图5.24 多边形P0P1P2P3P4P5P6
28
填空例题
1.在计算机图形学中常用的字符在计算机内可
02-计算机图形学基础(第二版)-电子工业出版社-(陆枫-何云峰-编著)

1166
第16页,共92页。
阴极射线管(CRT)
电子枪
偏转系统
图2.6 CRT的结构
第17页,共92页。
荧光屏
1177
阴极射线管(CRT)
电子枪:产生一个沿管轴(Z轴)方向前进的高
速的细电子束轰击荧光屏。
具有足够的电流强度。
电流的大小和有无必须是可控的。
1122
第12页,共92页。
图形输入设备
图像扫描仪(Scaner) 图像扫描仪可直接把图纸、图表、照片、
广告画等输入到计算机中,在将它们传过一个 光学扫描机构时,灰度或彩色等级被记录下来, 并按图像方式进行存储。
1133
第13页,共92页。
图形输入设备
声频输入系统 视频输入系统
1144
第14页,共92页。
荫罩吸收大量电子,容易发热变形。
管子的亮度低,要提高管子的亮度,则需提高第二阳极的高压。
2288
第28页,共92页。
彩色阴极射线管——荫罩式
R
G
G
B
R
G
B
R
G
B
R
B
R
图2.15 黑底荫罩管
2299
第29页,共92页。
CRT图形显示器
随机扫描的图形显示器 直视存储管图形显示器 光栅扫描的图形显示器
n 图2.18 光栅扫描原理
第37页,共92页。
垂直回扫(消隐)
3377
工作原理:光栅扫描是控制电子束按某种光栅形状进
行的顺序扫描,而字符、图像是靠Z轴信号控制辉亮
来形成的。
视频信号
z
辉亮放大器
(完整word版)计算机图形学基础教程习题课2(第二版)(孙家广胡事民编著)

习题3-1 参数曲线曲面有几种表示形式? (1) 代数形式一条三次曲线的代数形式是:⎪⎩⎪⎨⎧+++=∈+++=+++=zz z z y y y y x x x x a t a t a t a t z t a t a t a t a t y a t a t a t a t x 012233012233012233)(]1,0[)()((2) 几何形式描述参数曲线的条件有:端点位矢、端点切矢、曲率等。
]1,0[)(11001100∈'+'++=t P G P G P F P F t P上式是三次Hermite (Ferguson )曲线的几何形式,F 0,F 1,G 0,G 1称为调和函数(或混合函数).习题3-2 设有控制顶点为P 0(0,0),P 1(48,96),P 2(120,120),P 3(216,72)的三次B ézier 曲线P (t ),试计算P (0。
4)的(x ,y )坐标,并写出(x (t ),y (t ))的多项式表示。
[][][][][]⎪⎩⎪⎨⎧+-+-+-=+-+-+-==+++=+++=∴+-+-+-==∑=332212033322120333221203332212033,3)1(3)1(3)1()()1(3)1(3)1()(64.8012.69 72216064.0120120288.09648432.000216.0 )4.0()4.0(8.1)6.0(2.1)6.0()4.0()1(3)1(3)1()()(y t y t t y t t y t t y x t x t t x t t x t t x P P P P P P t P t t P t t P t t B P t P i i i习题3—5 设一条三次B ézier 曲线的控制顶点为P 0,P 1,P 2,P 3。
对曲线上一点P (0。
5),及一个给定的目标点T ,给出一种调整B ézier 曲线形状的方法,使得P (0.5)精确通过点T .根据B ézier 曲线的递推算法,构造过程:3P 0习题3—6 计算以(30,0),(60,10),(80,30),(90,60),(90,90)为控制顶点的4次B ézier 曲线在t =1/2处的值,并画出de Casteljau 三角形。
《计算机图形学基础》第2版(陆枫 何云峰)课后习题答案 电子工业出版社

第一章绪论概念:计算机图形学、图形、图像、点阵法、参数法、图形的几何要素、非几何要素、数字图像处理;计算机图形学和计算机视觉的概念及三者之间的关系;计算机图形系统的功能、计算机图形系统的总体结构。
第二章图形设备图形输入设备:有哪些。
图形显示设备:CRT的结构、原理和工作方式。
彩色CRT:结构、原理。
随机扫描和光栅扫描的图形显示器的结构和工作原理。
图形显示子系统:分辨率、像素与帧缓存、颜色查找表等基本概念,分辨率的计算第三章交互式技术什么是输入模式的问题,有哪几种输入模式。
第四章图形的表示与数据结构自学,建议至少阅读一遍第五章基本图形生成算法概念:点阵字符和矢量字符;直线和圆的扫描转换算法;多边形的扫描转换:有效边表算法;区域填充:4/8连通的边界/泛填充算法;内外测试:奇偶规则,非零环绕数规则;反走样:反走样和走样的概念,过取样和区域取样。
5.1.2 中点 Bresenham 算法(P109)5.1.2 改进 Bresenham 算法(P112)习题解答思路岛教育网整理提供习题5(P144)5.3 试用中点Bresenham算法画直线段的原理推导斜率为负且大于1的直线段绘制过程(要求写清原理、误差函数、递推公式及最终画图过程)。
(P111)解: k<=-1 |△y|/|△x|>=1 y为最大位移方向故有构造判别式:推导d各种情况的方法(设理想直线与y=yi+1的交点为Q):所以有: y Q-kx Q-b=0 且y M=y Qd=f(x M-kx M-b-(y Q-kx Q-b)=k(x Q-x M)所以,当k<0,d>0时,M点在Q点右侧(Q在M左),取左点 P l(x i-1,y i+1)。
d<0时,M点在Q点左侧(Q在M右),取右点 Pr(x i,y i+1)。
d=0时,M点与Q点重合(Q在M点),约定取右点 Pr(x i,y i+1) 。
所以有递推公式的推导:d2=f(x i-1.5,y i+2)当d>0时,d2=y i+2-k(x i-1.5)-b 增量为1+k=d1+1+k思路岛决定出路当d<0时,d2=y i+2-k(x i-0.5)-b 增量为1=d1+1当d=0时,5.7 利用中点 Bresenham 画圆算法的原理,推导第一象限y=0到y=x圆弧段的扫描转换算法(要求写清原理、误差函数、递推公式及最终画图过程)。
计算机图形学基础第2版陆枫何云峰课后习题答案电子工业出版社

第一章绪论概念:计算机图形学、图形、图像、点阵法、参数法、图形的几何要素、非几何要素、数字图像处理;计算机图形学和计算机视觉的概念及三者之间的关系;计算机图形系统的功能、计算机图形系统的总体结构。
第二章图形设备图形输入设备:有哪些。
图形显示设备:CRT的结构、原理和工作方式。
彩色CRT:结构、原理。
随机扫描和光栅扫描的图形显示器的结构和工作原理。
图形显示子系统:分辨率、像素与帧缓存、颜色查找表等基本概念,分辨率的计算第三章交互式技术什么是输入模式的问题,有哪几种输入模式。
第四章图形的表示与数据结构自学,建议至少阅读一遍第五章基本图形生成算法概念:点阵字符和矢量字符;直线和圆的扫描转换算法;多边形的扫描转换:有效边表算法;区域填充:4/8连通的边界/泛填充算法;内外测试:奇偶规则,非零环绕数规则;反走样:反走样和走样的概念,过取样和区域取样。
5.1.2 中点 Bresenham 算法(P109)斜率 K 误差项 d 理想点 Q 取下一个点 d 更新<0 在中点上取上点d+2△x-2△y<1>=0 在中点下取下点d-2△y<0 在中点右取右点d-2△x+2△y>1>=0 在中点左取左点d-2△x<0 在中点左取左点d-2△x+2△y<-1>=0 在中点右取右点d-2△x<0 在中点下取下点d+2△x-2△y>-1>=0 在中点上取上点d-2△y5.1.2 改进 Bresenham 算法(P112)斜率 K 改进误差项 e 理想点 Q 取下一个点 e 更新<0 在中点上取上点e-2△x<1>=0 在中点下取下点e+2△y<0 在中点右取右点e-2△y>1>=0 在中点左取左点e+2△x<0 在中点左取左点e-2△y<-1>=0 在中点右取右点e+2△x<0 在中点下取下点e-2△x>-1>=0 在中点上取上点e+2△y习题解答习题5(P144)5.3 试用中点Bresenham算法画直线段的原理推导斜率为负且大于1的直线段绘制过程(要求写清原理、误差函数、递推公式及最终画图过程)。
【精选】计算机图形学考前辅导

环:环是有序、有向边(直线段或曲线段)组成的Байду номын сангаас的封闭边界。环中 的边不能相交,相邻两条边共享一个端点。确定面的最大外边界的环称 之为外环;确定面中内孔或凸台边界的环称之为内环。通常,外环的边 按逆时针方向排序,而内环的边按顺时针方向排序,这样在面上沿一个 环前进,其左侧总是面内,右侧总是面外。
体:体是三维几何元素,由封闭表面围成空间,也是欧氏空间R3中非空、
计算机辅助教学;办公自动化和电子出版技术; 计算机艺术;在工业控制及交通方面的应用; 在医疗卫生方面的应用;图形用户界面。
7
第二章 计算机图形系统及图形硬件
计算机图形系统 图形输入设备 图形显示设备 显示子系统 图形硬拷贝设备 OpenGL图形软件包
8
填空例题
1. 平板显示器的分为为 非发射显示器和 发射显示器 。 2. PC图形显示子系统主要由帧缓冲存储器(帧缓存)、
4-连通区域 常可以看作是8-连通区域,但对边界条件有要求,边界 表示的4-连通区域的外环边界是一个8-连通区域,而边界表示的8连通区域的外环边界是一个4-连通区域。内点表示的4-连通区域也 是8-连通区域,内点表示的8-连通区域则不一定是4-连通区域。
33
3.举例说明奇偶规则和非零环绕树规则进行内外测试时有何不同? 答:奇偶规则和非零环绕树规则是进行多边性内外测试的常用方法,
则集就是正则形体。如果正则形体的表面是二维流形,
即对于实体表面上的任意一点,都可以找到一个围绕着
它的任意小的领域,该领域与平面上的一个圆盘是拓扑
等价 ,那么这个正则形体就是实体。
24
第五章 基本图形生成算法
图形生成的概念 直线段的扫描转换 圆的扫描转换 多边形的扫描转换与区域填充 属性处理 反走样技术 在OpenGL中绘制图形
《计算机图形学》练习册答案
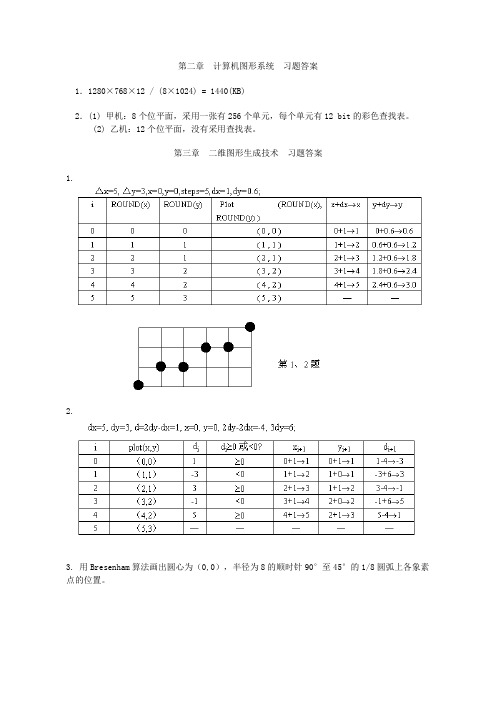
第二章计算机图形系统习题答案1.1280×768×12 / (8×1024) = 1440(KB)2.(1) 甲机:8个位平面,采用一张有256个单元,每个单元有12 bit的彩色查找表。
(2) 乙机:12个位平面,没有采用查找表。
第三章二维图形生成技术习题答案1.2.3. 用Bresenham算法画出圆心为(0,0),半径为8的顺时针90°至45°的1/8圆弧上各象素点的位置。
4.5.6.7. (1) 调用一个点与一条线段的判别算法,以首先排除A在P边界上的情况;(2) 过A向右作一条水平线,去掉P上的水平边;(3) 求出该水平射线与多边形各边的交点;(4) 按"上闭下开"或"下闭上开"的原则处理交点在某些情况下给予计不计数的问题;(5) 按交点数的奇偶性以判别A在P的内或外。
8.9.10.第四章二维图形变换与裁剪习题答案1. vx=0+[0.25-(-0.5)]*(1280-0) / [0.5-(-0.5)] = 960vy=0+(0.75-0) *(1024-0) / (1-0) = 7682.3.4.5.6.7.8.9.10.11.12. 设两条线段为P1P2、P3P4,它们的方程为:第五章曲线与曲面习题答案1.2.3.4.5.6.9.第六章三维图形基础答案1.2.3.4.5.6.(1) V=16,F=14,E=28,R=0,S=1,H=0,左值=2,右值=2,左值=右值,符合欧拉公式。
(2) V=32,F=30,E=60,R=0,S=1,H=0, 左值=2,右值=2,左值=右值,符合欧拉公式。
7.8. 1280*1024*24/(8*1024*1024)=2.75(MB)计算机图形学试题(一)一、写出下列术语的中文含义(共10分)1.CRT/LED/LCD------阴极射线管\发光二极管/液晶显示器2.CAD/CAM/CIMS-----计算机辅助设计\计算机辅助制造\计算机集成制造系统3.GUI/WYSIWYG-----图形化用户界面\所见即所得4.CPU/DPU------中央处理器\显示处理器二、填空题(共20分,每空1分)1.刷新式CRT图形显示器按扫描方式分为随机扫描和光栅扫描两种。
《计算机图形学》习题与解答

《计算机图形学》习题与解答《计算机图形学》习题与解答第一章概述1. 试描述你所熟悉的计算机图形系统的硬软件环境。
计算机图形系统是计算机硬件、图形输入输出设备、计算机系统软件和图形软件的集合。
例如:计算机硬件采用PC、操作系统采用windows2000,图形输入设备有键盘、鼠标、光笔、触摸屏等,图形输出设备有CRT、LCD等,安装3D MAX图形软件。
2. 计算机图形系统与一般的计算机系统最主要的差别是什么?3. 图形硬件设备主要包括哪些?请按类别举出典型的物理设备?图形输入设备:鼠标、光笔、触摸屏和坐标数字化仪,以及图形扫描仪等。
图形显示设备:CRT、液晶显示器(LCD)等。
图形绘制设备:打印机、绘图仪等。
图形处理器:GPU(图形处理单元)、图形加速卡等等。
4. 为什么要制定图形软件标准?可分为哪两类?为了提高计算机图形软件、计算机图形的应用软件以及相关软件的编程人员在不同计算机和图形设备之间的可移植性。
图形软件标准通常是指图形系统及其相关应用系统中各界面之间进行数据传送和通信的接口标准,另外还有供图形应用程序调用的子程序功能及其格式标准。
5. 请列举出当前已成为国际标准的几种图形软件标准,并简述其主要功能。
(1)CGI(Computer Graphics Interface),它所提供的主要功能集包括控制功能集、独立于设备的图形对象输出功能集、图段功能集、输入和应答功能集以及产生、修改、检索和显示以像素数据形式存储的光栅功能集。
(2)GKS(Graphcis Kernel System),提供了应用程序和图形输入输出设备之间的接口,包括一系列交互和非交互式图形设备的全部图形处理功能。
主要功能如下:控制功能、输入输出功能、变换功能、图段功能、询问功能等。
6. 试列举计算机图形学的三个应用实例。
(1)CAD/CAM(2)VISC(3)VR.第二章光栅图形学1. 在图形设备上如何输出一个点?为输出一条任意斜率的直线,一般受到哪些因素影响?若图形设备是光栅图形显示器,光栅图形显示器可以看作是一个像素的矩阵,光栅图形显示器上的点是像素点的集合。
计算机图形学教程课后习题参考答案解析

第一章1、试述计算机图形学研究的基本内容?答:见课本P5-6页的1.1.4节。
2、计算机图形学、图形处理与模式识别本质区别是什么?请各举一例说明。
答:计算机图形学是研究根据给定的描述,用计算机生成相应的图形、图像,且所生成的图形、图像可以显示屏幕上、硬拷贝输出或作为数据集存在计算机中的学科。
计算机图形学研究的是从数据描述到图形生成的过程。
例如计算机动画制作。
图形处理是利用计算机对原来存在物体的映像进行分析处理,然后再现图像。
例如工业中的射线探伤。
模式识别是指计算机对图形信息进行识别和分析描述,是从图形(图像)到描述的表达过程。
例如邮件分捡设备扫描信件上手写的邮政编码,并将编码用图像复原成数字。
3、计算机图形学与CAD、CAM技术关系如何?答:见课本P4-5页的1.1.3节。
4、举3个例子说明计算机图形学的应用。
答:①事务管理中的交互绘图应用图形学最多的领域之一是绘制事务管理中的各种图形。
通过从简明的形式呈现出数据的模型和趋势以增加对复杂现象的理解,并促使决策的制定。
②地理信息系统地理信息系统是建立在地理图形基础上的信息管理系统。
利用计算机图形生成技术可以绘制地理的、地质的以及其它自然现象的高精度勘探、测量图形。
③计算机动画用图形学的方法产生动画片,其形象逼真、生动,轻而易举地解决了人工绘图时难以解决的问题,大大提高了工作效率。
5、计算机绘图有哪些特点?答:见课本P8页的1.3.1节。
6、计算机生成图形的方法有哪些?答:计算机生成图形的方法有两种:矢量法和描点法。
①矢量法:在显示屏上先给定一系列坐标点,然后控制电子束在屏幕上按一定的顺序扫描,逐个“点亮”临近两点间的短矢量,从而得到一条近似的曲线。
尽管显示器产生的只是一些短直线的线段,但当直线段很短时,连成的曲线看起来还是光滑的。
②描点法:把显示屏幕分成有限个可发亮的离散点,每个离散点叫做一个像素,屏幕上由像素点组成的阵列称为光栅,曲线的绘制过程就是将该曲线在光栅上经过的那些像素点串接起来,使它们发亮,所显示的每一曲线都是由一定大小的像素点组成的。
计算机图形学习题参考答案(完整版)

9、使用中点圆算法,绘制圆心为 (0, 0) ,半径 r 10 的圆在第一象限中的部分。 解:
k (x k, yk) (x k ', yk ') pk 0 (0,10) (10, 0) 1r 9 1 (1,10) (10,1) p0 2x 116 2 (2,10) (10, 2) p12x 2 11 3 (3,10) (10, 3) p2 2x 3 2x 4 12y 4 3 5 (5, 9) (9, 5) p4 2x 5 18 6 (6, 8) (8, 6) p5 2x 6 12y6 5 7 (7, 7)
1
度,可以沿着三个方向移动,也可以沿着三个方位旋转,同时还可以建立与其他三维空间的超链接。 因此 VRML 是超空间的。 7、图形的构成要素有哪些? 解: ① 刻画形状的点、线、面、体等几何要素; ② 反映物体表面属性和材质的灰度、颜色等非几何要素。 8、计算机图形学的最高奖以谁的名字命名,获得第一届和第二届该奖的分别是谁? 解: 计算机图形学的最高奖是以 Coons 的名字命名的, 获得第一届和第二届 Coons 奖的是 Ivan Sutherland 和 Pierre Bézier。
2
11、已知: A(0, 0) 、 B(1, 1) 、 C(2, 0) 、 D(1, 2) ,请判断多边形 ABCD 是否是凹多边形。 解: 多 边 形 的 边 向 量 为 AB (1,1, 0) , BC (1, 1, 0) , CD (1, 2, 0) , DA(1, 2, 0) 。 因 为
第 2 章 基本图元的显示
1、假设 RGB 光栅系统的设计采用 810 英寸的屏幕,每个方向的分辨率为每英寸 100 个像素。如果 每个像素 6 位,存放在帧缓冲器中,则帧缓冲器需要多大存储容量(字节数)? 解: 8100101006/8600000 (字节) 。 2、假设计算机字长为 32 位,传输速率为 1 MIP(每秒百万条指令) 。300 DPI(每英寸点数)的激光打 印机,页面大小为 8.511 英寸,要填满帧缓冲器需要多长时间。 解:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论概念:计算机图形学、图形、图像、点阵法、参数法、图形的几何要素、非几何要素、数字图像处理;计算机图形学和计算机视觉的概念及三者之间的关系;计算机图形系统的功能、计算机图形系统的总体结构。
第二章图形设备图形输入设备:有哪些。
图形显示设备:CRT的结构、原理和工作方式。
彩色CRT:结构、原理。
随机扫描和光栅扫描的图形显示器的结构和工作原理。
图形显示子系统:分辨率、像素与帧缓存、颜色查找表等基本概念,分辨率的计算第三章交互式技术什么是输入模式的问题,有哪几种输入模式。
第四章图形的表示与数据结构自学,建议至少阅读一遍第五章基本图形生成算法概念:点阵字符和矢量字符;直线和圆的扫描转换算法;多边形的扫描转换:有效边表算法;区域填充:4/8连通的边界/泛填充算法;内外测试:奇偶规则,非零环绕数规则;反走样:反走样和走样的概念,过取样和区域取样。
5.1.2 中点 Bresenham 算法(P109)斜率 K 误差项 d 理想点 Q 取下一个点 d 更新<0 在中点上取上点d+2△x-2△y<1>=0 在中点下取下点d-2△y<0 在中点右取右点 d-2△x+2△y>1>=0 在中点左取左点d-2△x<0 在中点左取左点 d-2△x+2△y<-1>=0 在中点右取右点d-2△x<0 在中点下取下点d+2△x-2△y>-1>=0 在中点上取上点d-2△y 5.1.2 改进 Bresenham 算法(P112)斜率 K 改进误差项 e 理想点 Q 取下一个点 e 更新<0 在中点上取上点 e-2△x<1>=0 在中点下取下点e+2△y<0 在中点右取右点 e-2△y>1>=0 在中点左取左点e+2△x<0 在中点左取左点e-2△y<-1>=0 在中点右取右点e+2△x<0 在中点下取下点 e-2△x>-1>=0 在中点上取上点e+2△y 习题解答习题5(P144)5.3 试用中点Bresenham算法画直线段的原理推导斜率为负且大于1的直线段绘制过程(要求写清原理、误差函数、递推公式及最终画图过程)。
(P111)解: k<=-1 |△y|/|△x|>=1 y为最大位移方向故有构造判别式:推导d各种情况的方法(设理想直线与y=yi+1的交点为Q):所以有: y Q-kx Q-b=0 且y M=y Qd=f(x M-kx M-b-(y Q-kx Q-b)=k(x Q-x M)所以,当k<0,d>0时,M点在Q点右侧(Q在M左),取左点 P l(x i-1,y i+1)。
d<0时,M点在Q点左侧(Q在M右),取右点 Pr(x i,y i+1)。
d=0时,M点与Q点重合(Q在M点),约定取右点 Pr(x i,y i+1) 。
所以有递推公式的推导:d2=f(x i-1.5,y i+2)当d>0时,d2=y i+2-k(x i-1.5)-b 增量为1+k=d1+1+k当d<0时,d2=y i+2-k(x i-0.5)-b 增量为1=d1+1当d=0时,5.7 利用中点 Bresenham 画圆算法的原理,推导第一象限y=0到y=x圆弧段的扫描转换算法(要求写清原理、误差函数、递推公式及最终画图过程)。
(P115)y坐标圆心角α误差项 d 理想点 Q 取下一个点 d 更新y=0 y=x 0°<=α<=45°<0 在中点右取右点 d+2y+3>=0 在中点左取左点d-2(y-x)+5y=x y=1 45°<=α<=90°<0 在中点上取上点 d+2x+3>=0 在中点下取下点d-2(x-y)+5解:在x=y到y=0的圆弧中,(R,0)点比在圆弧上,算法从该点开始。
最大位移方向为y,由(R,0)点开始,y渐增,x渐减,每次y方向加1,x方向减1或减0。
设P点坐标(xi,yi),下一个候选点为右点Pr(xi,yi+1)和左点Pl(xi-1,yi+1),取Pl和Pr的中点M(xi-0.5,yi+1),设理想圆与y=yi+1的交点Q,构造判别式:d=f(x M,y M)=(x-0.5)2+(y i+1)2+R2当d<0时,M在Q点左方(Q在M右),取右点Pr(xi,yi+1)当d>0时,M在Q点右方(Q在M左),取左点Pl(xi-1,yi+1)当d=0时,M与Q点重合,约定取左点Pl(xi-1,yi+1)所以有:推导判别式:d>=0时,取左点Pl(xi-1,yi+1),下一点为(xi-1,yi+2)和(xi-2,yi+2)d<0时,取右点Pr(xi,yi+1),下一点为(xi,yi+2)和(xi-1,yi+2)d0=f(R-0.,1)=R2-R+0.25+1-R2=1.25-R5.11 如图5-59所示多边形,若采用扫描转换算法(ET边表算法)进行填充,试写出该多边形的边表ET和当扫描线Y=4时的有效边表AET(活性边表)。
(P125)解:1)边表ET表x|ymin ymax 1/k next2)y=4时的有效边表AETx ymax 1/k next注意:水平线不用计算。
5.22 构造两个例子,一个是4-连通图,其边界是8-连通的,另一个是8-连通图,其边界是4-连通的。
(P132)解:4-连通区域 8-连通区域第六章二维变换及二维观察概念:齐次坐标,窗口,视区,二维观察流程,字符裁减的三种策略,外部裁减计算:二维几何变换直线裁减:区域编码法和梁友栋算法多边形裁减:逐边裁减法和双边裁减法6.1.3 二维变换矩阵(P147)3阶二维变换矩阵子矩阵功能a b p c d q l m s abcd 比例旋转 pq 投影变换lm 平移变换 s 整体比例6.2.3 旋转变换(P149)逆时针变换矩阵顺时针变换矩阵cosθ sinθ 0-sinθ cosθ 00 0 1cosθ -sinθ 0sinθ cosθ 00 0 16.2.5 相对任一参考点的二维几何变换(P155) 例如:相对(xf,yf)点的旋转变换平移到坐标原点旋转角度θ反平移回原来位置1 0 0 0 1 0 -xf -yf 1 cosθ sinθ 0-sinθ cosθ 00 0 11 0 00 1 0xf yf 1习题6(P177)6.7 求四边形 ABCD 绕 P(5,4)旋转45度的变换矩阵和端点坐标,画出变换后的图形。
(P147 P148 P155)解:变换的过程包括:1)平移:将点P(5,4)平移至原点(0,0),2)旋转:图形绕原点(0点)旋转45度,3)反平移:将P点移回原处(5,4),4)变换矩阵:平移—旋转—反平移5)变换过程:四边形 ABCD 的规范化齐次坐标(x,y,1) * 3阶二维变换矩阵由旋转后四边形 ABCD 的规范化齐次坐标(x',y',1)可写出顶点坐标:A'(6.4,1.2) B'(7.1,4.7) C'(4.3,8.5) D'(2.2,1.2)6.15 用梁友栋算法裁减线段AB,B点的坐标改为(-2,-1)(P170)解:以A(3,3)为起点,B(-2,-1)为终点所以有x1=3,y1=3,x2=-2,y2=-1,wxl=0,wxr=2,wyb=0,wyt=2构造直线参数方程:x=x1+u(x2-x1)0 x1x x2y A(3,3)3 C(7/4,2)2D(0,3/5) 1-2 -1 0 12 3x B(-2,-1) -1x=x1+u(x2-x1) (0<=u<=1)y=y1+u(y2-y1)把 x1=3,y1=3,x2=-2,y2=-1 代入得x=3-5uy=3-4u计算各个p和q值有:p1=x1-x2=5 q1=x1-wxl=3p2=x2-x1=-5 q2=wxr-x1=-1p3=y1-y2=4 q3=y1-wyb=3p4=y2-y1=-4 q4=wyt-y1=-1根据,u k=q k/p k 算出p k<0时:u2=1/5 u4=1/4p k>0时:u1=3/5 u3=3/4u max=MAX(0,u2,u4)=MAX(0,1/5,1/4)=1/4 (取最大值)u min=MIN(u1,u3,1)=MIN(3/5,3/4,1)=3/5 (取最小值)由于 u max<u min ,故此直线AB有一部分在裁减窗口内,p k<0时,将 u max=1/4 代入直线参数方程x=x1+u(x2-x1)x=3+1/4*(-5)=3-5/4=7/4y=y1+u(y2-y1)y=3+1/4*(-4)=2求出直线在窗口内部分的端点C(7/4,2)p k>0时,将 u min=3/5代入直线参数方程x=x1+u(x2-x1)x=3+3/5*(-5)=0y=y1+u(y2-y1)y=3+3/5*(-4)=3/5求出直线在窗口内部分的端点D(0,3/5)。
所以,直线在窗口内部分的端点为C(7/4,2),D(0,3/5)。
第七章三维变换及三维观察概念:几何变换、投影变换、透视投影、平行投影、灭点平面几何投影的分类以及分类原则计算:三维几何变换、三视图7.2 三维几何变换(P180)4阶三维变换矩阵子矩阵功能a b c pd e f q g h i r l m n s abcdefghi 比例旋转 pqr 透视投影 lmn 平移变换 s 整体比例整体比例变换(P182)s>1 时,整体缩小,如 2 表示2:1缩小。
s<1 时,整体放大,如 1/2 表示1:2放大。
7.3.1 正投影1.主视图 V(P191)4阶三维变换矩阵y轴方向投影1 0 0 00 0 0 00 0 1 00 0 0 12.俯视图 H4阶三维变换矩阵1 0 0 00 0 -1 00 0 0 00 0 -z0 1z轴方向投影绕x轴旋转-90度z轴方向平移-1 1 0 0 00 1 0 00 0 00 0 01 1 0 0 00 cos(-90°) sin(-90°) 00 -sin(-90°) cos(-90°)00 0 0 11 0 00 1 0 00 0 1 00 0 -z0 13.侧视图 W (P192)4阶三维变换矩阵0 0 0 0 -1 0 0 0 0 0 1 0 -x0 0 0 1x 轴方向投影 绕 z 轴旋转90度x 轴方向平移-1 0 0 0 0 0 1 0 0 0 0 1 00 0 0 1 0 cos90° sin90° 0 0 -sin90° cos90° 0 0 0 1 00 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 -x0 0 0 1习题7 (P213)7.5 求空间四面体关于点 P(2,-2,2)整体放大2倍的变换矩阵, 画出变换后的图形。
