计算方法实验一-二分法
计算方法与实习答案1-2

绪论
习题1——10:设 f ( x) = 8 x 5 − 0.4 x 4 + 4 x 3 − 9 x + 1 用秦九韶法求f(3)。 解:
8 − 0.4
24 8 23.6
0
−9
1
x=3
70.8 74.8
224.4 224.4
673.2 664.2
1992.6 1993.6
∴ f(3)=1993.6
第一章 绪论 练习
1.《计算方法》课程主要研究以计算 机为工具的 数值 分析方法 ,并评价 该算法的计算误差。 2.近似值作四则运算后的绝对误差限 公式为 ε ( x1 − x2 ) ≤ ε ( x1 ) + ε ( x2 ) ,近似值 1.0341的相对误差限不大于 1 ×10−2 , 则它至少有三位有效数字。 4
ln(103 ) ∴k ≥ ln(2) ≥ 9.965
2 2 2
∴需二分10次 需二分 次
方程求根——二分法
习题2——2:用二分法求方程2e-x-sinx=0在区 间[0,1]内的1个实根,要求3位有效数字。
解:1)判断是否在该区间有且仅有一个根 f(0)=2>0,f(1)=2/e-sin1≈-0.1<0, f’(x)=-2e-x-cosx,f’=-3,-2/e-cos1<0 2)判断二分次数 由(b-a)/2k+1=1/2k+1≤1/2*10-3,解得k≥3ln10/ln2≥9.965, 所以需要二分10次,才能满足精度要求。
∴ x≈2.981
方程求根
f (xk )(xk − xk −1) xk +1 = xk − f (xk ) − f (xk −1)
习题2——11:用割线法求方程x3-2x-5=0的根,要 求精确到4位有效数字,取x0=2, x1=2.2。
数学计算方法实验报告

数学计算方法实验报告习题二2.估计用二分法求方程f(x)=x3+4x2-10=0在区间[1,2]内根的近似值,为使方程不超过10时所需的二分次数。
f(x k)程序过程:function two (tolerance)a=1;b=2;counter=0;while (abs(b-a)>tolerance)c=(a+b)/2;fa=a^3+4*a^2-10;fb=b^3+4*b^2-10;fc=c^3+4*c^2-10;if ((fa==0|fb==0)) disp(counter);elseif (fa*fc<0)b=c;counter=counter+1;elseif (fb*fc<0)a=c;counter=counter+1;elseif (fb==0)disp(counter);endendsolution=(a+b)/2;disp(solution);disp(counter);实验结果:6.取x0=1.5,用牛顿迭代法求第三中的方程根.f(x)=x3+4x2-10=0的近似值(精确到||x k+1-x k|≦10-5,并将迭代次数与3题比较。
程序过程:function six (g)a=1.5;fa=a^3+4*a^2-10;ga=3*a^2+8*a;b=a-fa/ga;k=1;while(abs(b-a)>g)a=b;fa=a^3+4*a^2-10;ga=3*a^2+8*a;b=a-fa/ga;k=k+1;endformat long;disp(a);disp(k);实验结果:程序结果计算结果8.用弦割法求方程f(x)=x3-3x2-x+9=0在区间[-2,-1]内的一个实根近似值x k,|f(x k)|≦10-5.程序过程:function eight (t)a=-2;b=-1;fa=a^3-3*a^2-a+9;fb=b^3-3*b^2-b+9;c=b-fb*(b-a)/(fb-fa);k=1;while(abs(c-b)>t)a=b;b=c;fa=a^3-3*a^2-a+9;fb=b^3-3*b^2-b+9;c=b-fb*(b-a)/(fb-fa);k=k+1;endformat long;disp(k);disp(b);实验结果: 计算结果9.用艾特肯算法求方程x3+4x2-10=0在区间[1,2]内的根的近似值(取x0=1.5,g(x)=410 x ,精确到|x k+1-x k |≦10-5,并与2,3,6结果比较。
计算方法 实验一 方程求根

实验一方程求根(1)二分法
1、实验程序
实现二分法的MATLAB函数文件agui_bisect.m
2. 在MATLAB命令窗口输入及实验结果及操作界面
(2)迭代法
1、实验程序
实现二分法的MATLAB函数文件agui_iterative.m
2、在MATLAB命令窗口输入及实验结果及操作界面
(3)牛顿法
1、实验程序
实现二分法的MATLAB函数文件agui_newton.m
2、在MATLAB命令窗口输入及实验结果及操作界面
结果分析:
由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果,我们可以得出这样的结论:
二分法要循环k=10次,迭代法要迭代k=4次,牛顿法要迭代k=2次才能达到精度为0.5*10^-3的要求,而且方程0210=-+x e x
的精确解经计算,为0.0905250,由此可知,牛顿法和迭代法的精确度要优越于二分法。
而这三种方法中,牛顿法不仅计算量少,而且精确度高。
从而可知牛顿迭代法收敛速度明显加快,但由所学的内容可知,其收敛性与初值有关,它是局部收敛的。
二分法收敛虽然是速度最慢,但也常用于求精度不高的近似根。
而迭代法是逐次逼近的方法,原理简单,但存在收敛性和收敛速度的问题。
总之各种方法都各有优劣,适用于不同的情况中,须具体情况具体分析。
数值计算方法实验报告

数值计算方法实验报告实验目的:通过实验验证不同数值计算方法在求解数学问题时的精度和效率,并分析其优缺点。
实验原理:实验内容:本实验选取了三个典型的数值计算问题,并分别采用了二分法、牛顿迭代法和梯度下降法进行求解。
具体问题和求解方法如下:1. 问题一:求解方程sin(x)=0的解。
-二分法:利用函数值的符号变化将解空间不断缩小,直到找到满足精度要求的解。
-牛顿迭代法:通过使用函数的斜率来逼近方程的解,并不断逼近真实解。
-梯度下降法:将方程转化为一个极小化问题,并利用梯度下降的方式逼近极小值点,进而找到方程的解。
2.问题二:求解函数f(x)=x^2-3x+2的极小值点。
-二分法:通过确定函数在一个区间内的变化趋势,将极小值所在的区间不断缩小,从而找到极小值点。
-牛顿迭代法:通过使用函数的导数和二阶导数来逼近极小值点,并不断逼近真实解。
-梯度下降法:将函数转化为一个极小化问题,并利用梯度下降的方式逼近极小值点,进而找到函数的极小值点。
3. 问题三:求解微分方程dy/dx = -0.1*y的解。
-二分法:通过离散化微分方程,将微分方程转化为一个差分方程,然后通过迭代计算不同点的函数值,从而得到函数的近似解。
-牛顿迭代法:将微分方程转化为一个积分方程,并通过迭代计算得到不同点的函数值,从而得到函数的近似解。
-梯度下降法:将微分方程转化为一个极小化问题,并利用梯度下降的方式逼近极小值点,从而得到函数的近似解。
实验步骤:1.编写代码实现各个数值计算方法的求解过程。
2.对每个数值计算问题,设置合适的初始值和终止条件。
3.运行程序,记录求解过程中的迭代次数和每次迭代的结果。
4.比较不同数值计算方法的精度和效率,并分析其优缺点。
实验结果:经过实验测试,得到了如下结果:-问题一的二分法迭代次数为10次,求解结果为x=0;牛顿迭代法迭代次数为4次,求解结果为x=0;梯度下降法迭代次数为6次,求解结果为x=0。
-问题二的二分法迭代次数为10次,求解结果为x=1;牛顿迭代法迭代次数为3次,求解结果为x=1;梯度下降法迭代次数为4次,求解结果为x=1-问题三的二分法迭代次数为100次,求解结果为y=e^(-0.1x);牛顿迭代法迭代次数为5次,求解结果为y=e^(-0.1x);梯度下降法迭代次数为10次,求解结果为y=e^(-0.1x)。
MAAB计算方法迭代法牛顿法二分法实验报告

MAAB计算方法迭代法牛顿法二分法实验报告实验目的:比较MAAB计算方法中迭代法、牛顿法和二分法的优缺点,探究它们在求解方程中的应用效果。
实验原理:1、迭代法:将方程转化为x=f(x)的形式,通过不断迭代逼近方程的根。
2、牛顿法:利用函数在特定点的切线逼近根的位置,通过不断迭代找到方程的根。
3、二分法:利用函数值在区间两端的异号性质,通过不断二分缩小区间,最终逼近方程的根。
实验步骤:1、选择一元方程进行求解,并根据方程选择不同的计算方法。
2、在迭代法中,根据给定的初始值和迭代公式,进行迭代计算,直到满足预设的迭代精度要求。
3、在牛顿法中,选择初始点,并根据切线方程进行迭代计算,直到满足预设的迭代精度要求。
4、在二分法中,选择区间,并根据函数值的异号性质进行二分,直到满足预设的迭代精度要求。
5、根据计算结果,比较三种方法的求解效果,包括迭代次数、计算时间、求解精度等指标。
实验结果与分析:通过对多个方程进行测试,得到了以下实验结果:1、迭代法的优点是简单易懂,适用范围广,但当迭代公式不收敛时会导致计算结果不准确。
2、牛顿法的优点是收敛速度较快,但需要计算函数的一阶导数和二阶导数,对于复杂函数较难求解。
3、二分法的优点是收敛性较好,不需要导数信息,但收敛速度较慢。
4、对于线性方程和非线性方程的求解,牛顿法和迭代法通常比二分法更快速收敛。
5、对于多重根的方程,二分法没有明显优势,而牛顿法和迭代法能更好地逼近根的位置。
6、在不同的方程和初值选择下,三种方法的迭代次数和求解精度略有差异。
7、在时间效率方面,二分法在收敛速度较慢的同时,迭代次数较少,牛顿法在收敛速度较快的同时,迭代次数较多,而迭代法对于不同方程有较好的平衡。
结论:1、对于不同类型的方程求解,可以根据具体情况选择合适的计算方法。
2、迭代法、牛顿法和二分法各有优缺点,没有绝对的最优方法,需要权衡各种因素选择最适合的方法。
3、在实际应用中,可以根据方程的特点和精度要求综合考虑不同方法的优劣势,以获得较好的求解效果。
数值分析实验报告——方程求根

《数值分析》实验报告实验一方程求根一、实验目的:掌握二分法、Newton法、不动点迭代法、弦截法求方程的根的各种计算方法、并实施程序调试和运行,学习应用这些算法于实际问题。
二、实验内容:二分法、Newton法、不动点迭代法、弦截法求方程的根、程序的调试和运行,给出实例的计算结果。
观察初值对收敛性的影响。
三、实验步骤:①、二分法:定义:对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
实现方法:首先我们设一方程400*(x^4)-300*(x^3)+200*(x^2)-10*x-1=0,并求其在区间[0.1,1]上的根,误差限为e=10^-4。
PS:本方法应用的软件为matlab。
disp('二分法')a=0.1;b=1;tol=0.0001;n0=100;fa=400*(a.^4)-300*(a.^3)+200*(a.^2)-10*a-1;for i=1:n0 p=(a+b)/2;fp=400*(p.^4)-300*(p.^3)+200*(p.^2)-10*p-1;if fp==0||(abs((b-a)/2)<tol)disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为:')disp(i)break;end;if fa*fp>0 a=p;else b=p;end;end;if i==n0&&~(fp==0||(abs((b-a)/2)<tol)) disp(n0) disp('次二分迭代后没有求出方程的根')end;程序调试:运行结果:用二分法求得方程的根p=0.1108二分迭代次数为:14②Newton法定义:取定初值x0,找到函数对应的点,然后通过该点作函数切线,交x轴,得到新的横坐标值,然后找函数对应的点,做切线,得到新的横坐标值,重复上述步骤,多次迭代,直到收敛到需要的精度。
MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验报告一、引言计算方法是数学的一门重要应用学科,它研究如何用计算机来解决数学问题。
其中,迭代法、牛顿法和二分法是计算方法中常用的数值计算方法。
本实验通过使用MATLAB软件,对这三种方法进行实验研究,比较它们的收敛速度、计算精度等指标,以及它们在不同类型的问题中的适用性。
二、实验方法1.迭代法迭代法是通过不断逼近解的过程来求得方程的根。
在本实验中,我们选择一个一元方程f(x)=0来测试迭代法的效果。
首先,我们对给定的初始近似解x0进行计算,得到新的近似解x1,然后再以x1为初始近似解进行计算,得到新的近似解x2,以此类推。
直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。
本实验将通过对复杂方程的迭代计算来评估迭代法的性能。
2.牛顿法牛顿法通过使用函数的一阶导数来逼近方程的根。
具体而言,对于给定的初始近似解x0,通过将f(x)在x0处展开成泰勒级数,并保留其中一阶导数的项,得到一个近似线性方程。
然后,通过求解这个近似线性方程的解x1,再以x1为初始近似解进行计算,得到新的近似解x2,以此类推,直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。
本实验将通过对不同类型的方程进行牛顿法的求解,评估它的性能。
3.二分法二分法是通过将给定区间不断二分并判断根是否在区间内来求方程的根。
具体而言,对于给定的初始区间[a,b],首先计算区间[a,b]的中点c,并判断f(c)与0的大小关系。
如果f(c)大于0,说明解在区间[a,c]内,将新的区间定义为[a,c],再进行下一轮的计算。
如果f(c)小于0,说明解在区间[c,b]内,将新的区间定义为[c,b],再进行下一轮的计算。
直到新的区间的长度小于规定的误差阈值为止。
本实验将通过对复杂方程的二分计算来评估二分法的性能。
三、实验结果通过对一系列测试函数的计算,我们得到了迭代法、牛顿法和二分法的计算结果,并进行了比较。
数值计算(二分法、简单迭代法、Newton迭代法、弦截法(割线法、双点弦法)).

本科生实验报告实验课程数值计算方法学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名学生学号指导教师实验地址实验成绩二〇一六年五月二〇一六年五月1实验一 非线性方程求根1.1问题描绘实验目的:掌握非线性方程求根的基本步骤及方法, 。
实验内容:试分别用二分法、简单迭代法、Newton 迭代法、弦截法(割线法、双点弦法),求x 5-3x 3+x-1=0在区间[-8,8]上的所有实根,偏差限为10-6。
要求:议论求解的全过程,对所用算法的局部收敛性,优弊端等作剖析及比 较,第2章算法思想2.1二分法思想:在函数的单一有根区间内,将有根区间不停的二分,找寻方程的解。
步骤:1.取中点mid=(x0+x1)/2 2.若f(mid)=0,则mid 为方程的根,不然比较与两头的符号,若与f(x0) 异号,则根在[x0,mid]之间,不然在[mid,x1]之间。
3并重复上述步骤,直抵达到精度要求,则 mid 为方程的近似解。
开始读入a,b,emid=(a+b)/2 F(a)*f(b)<0是 a=mid b=mid no |a-b|<e? yes 输出mid结束22.2简单迭代法思想:迭代法是一种逐次迫近的方法,它是固定公式频频校订跟的近似值,使之逐渐精准,最后获得精度要求的结果。
步骤:1.结构迭代公式f(x),迭代公式一定是收敛的。
2.计算x1,x1=f(x0).3.判断|x1-x0|能否知足精度要求,如不知足则重复上述步骤。
4.输出x1,即为方程的近似解。
开始输入x0,eX1=f(x0)f为迭代函数X1=x0;No|x1-x0|<eyes输出x1结束32.3Newton迭代法思想:设r是的根,选用作为r的初始近似值,过点做曲线的切线L,L的方程为,求出L与x轴交点的横坐标,称x1为r的一次近似值。
过点做曲线的切线,并求该切线与x轴交点的横坐标,称为r的二次近似值。
重复以上过程,得r的近似值序列,此中,称为r的次近似值步骤:1.计算原函数的导数f’(x);结构牛顿迭代公式2.计算,若f’(x0)=0,退出计算,不然持续向下迭代。
计算方法二分法实验
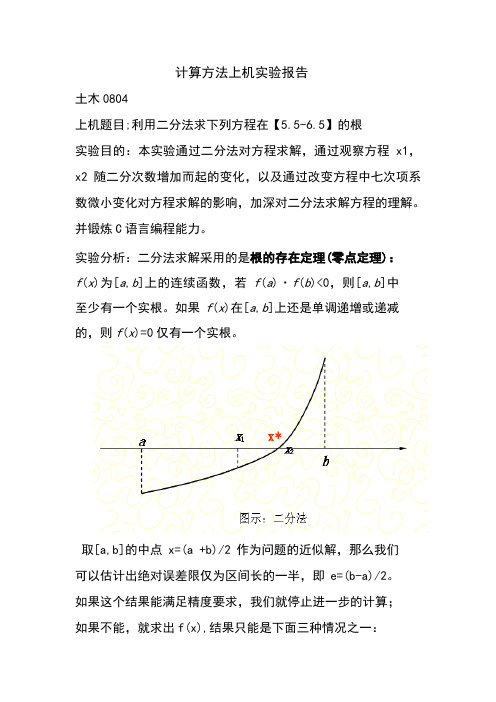
计算方法上机实验报告土木0804上机题目;利用二分法求下列方程在【5.5-6.5】的根实验目的:本实验通过二分法对方程求解,通过观察方程x1,x2随二分次数增加而起的变化,以及通过改变方程中七次项系数微小变化对方程求解的影响,加深对二分法求解方程的理解。
并锻炼C语言编程能力。
实验分析:二分法求解采用的是根的存在定理(零点定理):f(x)为[a,b]上的连续函数,若f(a)·f(b)<0,则[a,b]中至少有一个实根。
如果f(x)在[a,b]上还是单调递增或递减的,则f(x)=0仅有一个实根。
取[a,b]的中点x=(a +b)/2作为问题的近似解,那么我们可以估计出绝对误差限仅为区间长的一半,即e=(b-a)/2。
如果这个结果能满足精度要求,我们就停止进一步的计算;如果不能,就求出f(x),结果只能是下面三种情况之一:(1) f(a)·f(x)<0,此时我们有x*∈[a,x];(2) f(x)·f(b)<0,此时我们有x*∈[x,b];(3) f(x)=0,此时x即为问题的精确解。
在前两种情况下,我们可以用x分别替换原问题中的b或a,从而把求解的区间减小了一半。
这样我们又可以取新区间[a,b]的中点。
经过N次迭代后,剩下的区间长为(b- a)/2N。
这也是结果的绝对误差限。
如此继续下去就达到是有根区间逐步缩小的目的,在这一些相互包含的子区间中构造收敛的数列{}kx来逼近根*x。
实验过程:1;C语言程序# include <stdio.h># include <conio.h># include <math.h># define PRECISION 1e12double f(double c){double m,x,m1,m2,m3;x=c;m1=x*x;m2=m1*x;m3=m1*m1;m=m3*m3-36*m3*m2+546*m2*m3-4536*m3*x+22449*m3-67284*m2+118124*m1-109584*x+40320; return(m);}double Root(float a,float b){ int i;i=0;double x1,x2;x1=a;x2=b;do{printf ("\n i=%d,x1=%f,x2=%f ",i,x1,x2);if(f(x1)*f((x1+x2)/2)<0)x2=(x1+x2)/2;elsex1=(x1+x2)/2;i++;}while (i<=100);return (x1);}void main(){float x1,x2,r;printf ("\n input x1,x2: \n ") ;scanf ("%f %f",&x1,&x2);r=Root(x1,x2);printf ("\n Root x=%f",r);}2.结果分析当a7=-36是,迭代到i=21时,出现x1=x2=6.500000,不再发生变化,出现精确解 x=root=x1=6.500000,收敛速度在数列xn 越靠近根时越慢。
二分法实验报告

二分法实验报告二分法实验报告引言:二分法是一种常用的数值计算方法,广泛应用于求解方程的根、函数的最值等问题。
本实验旨在通过对二分法的实际应用,探讨其原理和优势,并对其在不同场景下的适用性进行分析。
一、二分法原理及步骤二分法,又称折半法,是一种通过不断缩小搜索范围来逼近目标的方法。
其基本原理是将待搜索的区间不断二分,然后根据目标值与中间值的关系,确定下一步搜索的范围,直至找到目标或满足精度要求。
具体步骤如下:1. 确定初始搜索范围[a, b],其中a和b分别为区间的下界和上界。
2. 计算中间值c = (a + b) / 2。
3. 判断目标值与中间值的关系:- 若目标值等于中间值,则找到目标,结束搜索。
- 若目标值小于中间值,则下一步搜索范围为[a, c]。
- 若目标值大于中间值,则下一步搜索范围为[c, b]。
4. 重复步骤2和步骤3,直至找到目标或满足精度要求。
二、实验设计与结果分析为了验证二分法的有效性和适用性,我们选取了两个不同的场景进行实验:求解方程的根和函数的最值。
1. 求解方程的根我们选择了一个简单的一元二次方程作为实验对象:x^2 - 4x + 3 = 0。
根据二分法的原理,我们可以将搜索范围设置为[0, 4],然后通过不断缩小范围来逼近方程的根。
经过多次迭代计算,我们得到了方程的根x ≈ 1和x ≈ 3。
通过与解析解进行对比,我们发现二分法得到的结果非常接近真实值,证明了二分法在求解方程根的问题上的有效性。
2. 求解函数的最值我们选取了一个简单的函数f(x) = x^2 - 2x + 1作为实验对象,目标是找到函数的最小值。
根据二分法的原理,我们可以将搜索范围设置为[0, 2],然后通过不断缩小范围来逼近最小值所在的位置。
经过多次迭代计算,我们得到了函数的最小值f(x) ≈ 0。
通过与解析解进行对比,我们发现二分法得到的结果非常接近真实值,证明了二分法在求解函数最值的问题上的有效性。
MATL新编计算方法迭代法牛顿法二分法实验报告

M A T L新编计算方法迭代法牛顿法二分法实验报告 Prepared on 22 November 2020姓名 实验报告成绩评语:指导教师(签名)年 月 日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理(1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2ab x -=。
否则,继续判断是否0)()(<•x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 软件四、 结果预测 (1)11x = (2)5x = (3)2x =0,09052五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x 的近似根。
数值计算方法实验1
学院(系)名称:)()()()(0101112x x x f x f x f x x ---=附录(源程序及运行结果):一.二分法#include<stdio.h>#include<math.h>double f(double x){return x*x-x-1;}void main(){float a=0,b=0,x=1,m,e;int k;while(f(a)*f(b)>0){printf("请输入区间a,b的值。
以及精度e\n");scanf("%f,%f,%f",&a,&b,&e);}k=0;if(f(a)*f(b)==0){if(f(a)==0)printf("使用二分法输出:a=%f,k=%d\n",a,k);elseprintf("使用二分法输出:b=%f,k=%d\n",b,k);}else{while(f(a)*f(b)!=0){m=(a+b)/2;if(fabs(a-b)/2<e){printf("使用二分法输出:m=%f,k=%d\n",m,k);break;}else {if(f(a)*f(m)>0)a=m;else b=m;k=k+1;}}}}运行结果:二.迭代法与牛顿迭代法#include<stdio.h>#include<math.h>double f(double x){return exp(-x);}double f1(double x){return (x*exp(x)-1);}double ff(double x){return (exp(x)+x*exp(x));}void diedaifa(double x0,double e,int N){double x1;int k=1;while(k!=N){x1=f(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用迭代法输出结果:%lf\n",x1);break;}}}void NDdiedaifa(double x0,double e,int N){int k=1;double x1;while(k!=N){if(ff(x0)==0)printf("公式f(x)奇异!\n");else{x1=x0-f1(x0)/ff(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用牛顿迭代法输出结果:%lf\n",x1);break;}}}}void main(){double x0,e;int N;printf("请输入初值:");scanf("%lf",&x0);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);diedaifa(x0,e,N);NDdiedaifa(x0,e,N);}运行结果:四.双点弦截法#include<stdio.h>#include<math.h>double f(double x){return (x*x*x+3*x*x-x-9);}void main(){double x0,x1,x2,e;int N;int k=1;printf("请输入初值x0和x1:");scanf("%lf,%lf",&x0,&x1);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);while(k!=N){x2=x1-f(x1)*(x1-x0)/(f(x1)-f(x0));if(fabs(f(x2))>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;x1=x2;}else{printf("使用双点弦截法输出结果:%lf\n",x2);break;}}}运行结果:。
计算方法实验五牛顿法,牛顿下山法,切线法,二分法

计算机实现数值积分 实验目的:非线性方程求解 实验内容:1.二分法的 Matlab 实现; 2.牛顿法的 Matlab 实现; 3.牛顿下山法、割线法、艾特金加速法、重根 迭代法、非线性方程组牛顿法中任选其一。 实验要求:1.每种算法要求达到给定的精度,输出近似 解结果及所需迭代次数; 2. P.239、171,或自选题目; 3.每个算法至少实验一个题目。
Therefore,the root is x=1.3571,iteration number is k=2.
6.在 MATLAB 工作窗口输入程序 [k,xk,yk,piancha,xdpiancha]=newtonqx(1,1e-8, 1e-8,100) 7.运行结果 y =16 y =26 y =0.3350 ans =1.0000 1.3846 0.3350 0.6154 0.4444 y =0.3350 y =18.5207 y =-0.0481
-0.0481
0.0181
0.0132
0.0072
0.0026
0.0019
-0.0011
0.0004
0.0003
0.0002
0.0001
0.0000
-0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
-0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
-0.0000
Therefore,the root is x=1.3688,iteration number is k=7.
pare the number of computations for finding the root of
计算方法matlab实验报告

计算方法matlab实验报告计算方法MATLAB实验报告引言:计算方法是一门研究如何用计算机来解决数学问题的学科。
在计算方法的学习过程中,MATLAB作为一种强大的数值计算软件,被广泛应用于科学计算、工程计算、数据分析等领域。
本实验报告将介绍在计算方法课程中使用MATLAB 进行的实验内容和实验结果。
一、二分法求方程根在数值计算中,求解非线性方程是一个常见的问题。
二分法是一种简单而有效的求解非线性方程根的方法。
在MATLAB中,可以通过编写函数和使用循环结构来实现二分法求解方程根。
实验步骤:1. 编写函数f(x),表示待求解的非线性方程。
2. 设定初始区间[a, b],满足f(a) * f(b) < 0。
3. 利用二分法迭代求解方程根,直到满足精度要求或迭代次数达到预设值。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个非线性方程的根。
例如,对于方程f(x) = x^3 - 2x - 5,我们通过二分法迭代了5次,得到了方程的一个根x ≈ 2.0946。
二、高斯消元法解线性方程组线性方程组的求解是计算方法中的重要内容之一。
高斯消元法是一种常用的求解线性方程组的方法,它通过矩阵变换将线性方程组化为上三角矩阵,从而简化求解过程。
在MATLAB中,可以利用矩阵运算和循环结构来实现高斯消元法。
实验步骤:1. 构建线性方程组的系数矩阵A和常数向量b。
2. 利用高斯消元法将系数矩阵A化为上三角矩阵U,并相应地对常数向量b进行变换。
3. 利用回代法求解上三角矩阵U,得到线性方程组的解向量x。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个线性方程组。
例如,对于线性方程组:2x + 3y - z = 13x - 2y + 2z = -3-x + y + 3z = 7经过高斯消元法的计算,我们得到了方程组的解x = 1,y = -2,z = 3。
三、数值积分方法数值积分是计算方法中的重要内容之一,它用于计算函数在给定区间上的定积分。
数值计算方法实验报告(含所有)

本科实验报告课程名称:计算机数值方法实验项目:计算机数值方法实验实验地点:虎峪校区致远楼B401专业班级:软件学院1217班学号:******xxxx 学生姓名:xxx指导教师:xxx2014 年 5 月21 日太原理工大学学生实验报告五、实验结果与分析二分法割线法分析:由程序知,使用二分法和割线法均能计算出方程的根,但利用割线法要比二分法计算的次数少,并且能够较早的达到精度要求。
相比之下,割线法程序代码量较少,精简明了。
六、讨论、心得本次数值计算方法程序设计实验从习题练习中跳脱出来,直接面对实用性较强的程序代码编写。
效果很好,不仅加深对二分法、割线法的理解,还加强了实际用运能力。
将理论知识成功地转化成实践结果。
实验地点虎峪校区致远楼B401指导教师xx太原理工大学学生实验报告l[i][k]=a[i][k];for(r=1;r<k;++r){l[i][k]-=l[i][r]*u[r][k];}l[i][k]/= u[k][k];}l[k][k]=1.0;}for(i=1;i<=n;++i){y[i] = b[i];for(j=1;j<i;++j){y[i]-=l[i][j]*y[j];}}for(i=n;i>0;--i){x[i] = y[i];for(j=i+1;j<=n;++j){x[i]-=u[i][j]*x[j];}x[i]/= u[i][i];}for(i=1;i<=n;++i){printf("%0.2lf\n",x[i]);}return 0;}五、实验结果与分析完全主元素消元法:列主元素消元法:LU分解法:分析:对于两种高斯解方程,完全主元素跟列主元素都是先消元、再回代,由程序段可以发现,始终消去对角线下方的元素。
即,为了节约内存及时效,可以不必计算出主元素下方数据。
列主元素消元法的算法设计上优于完全主元素消元法,它只需依次按列选主元素然后换行使之变到主元素位置,再进行消元即可。
计算方法1-2

e ( x*)
( er ( x ) r )
为
x的相对误差限。
3.有效数字 m 设 x 10 (0.a1 a 2 a n a p ) (a1 0, p ) 1 mn 若 (1.1) x * x 10 2
则说
x 具有n位有效数字,分别是
若
n p ,则称
10 0.04 10 0.1 10 0.00000000004 10
8 9 9
8
3.尽量避免相近数相减 例如,当x很大时,应
,
x1
x
1 x x1
1 1 1 x x 1 x ( x 1) 当x接近于0时,应
1 cos x sin x x 或tg sin x 1 cos x 2
f(x)=0根或f(x)零点,当f(x)复杂时,很难求 (找近似有效简单方法)。
§2.1 区间二分法
理 论 : f(x) ∈ C[a,b],单调, f(a)f(b)<0
f(x)=0在(a,b)有惟一根。
方程求根的步骤:(1)求根的隔离区间;(2)将根精确化 根的隔离区间求法:画草图;多项式函数交点横坐标; 试算。
程序运行 结果:
基本要求:
1.熟悉计算方法在解决实际问题中所处的地位,熟 悉计算方法是以计算机为工具求近似解的数值方 法; 2.熟悉绝对误差(限),相对误差(限)及有效数 字概念; 3.熟悉公式(1.2)--(1.9); 4.熟悉选用算法应遵循的原则;
作业:
第一章 8, 10
第二章 方程求根
§1.2 误差基础知识
一 .误差来源(分类)
1. 模型误差。 2. 观测误差。 3. 截断误差,如
x x sin x x ...... , 3! 5!
数值分析计算方法实验报告

数值分析计算方法实验报告实验报告:数值分析计算方法摘要:数值计算方法是现代科学与工程领域中常用的重要工具。
本实验通过对比分析三种不同的数值计算方法,包括二分法、牛顿迭代法和弦截法的优劣,以及在实际问题中的应用。
实验结果表明,不同的数值计算方法适用于不同的问题,合理选择方法可以提高计算的精度和效率。
一、引言在科学研究和工程实践中,很多问题并不能通过解析方法得到精确解。
数值计算方法可以通过近似计算得到问题的数值解,为科学研究和工程设计提供可靠依据。
本实验主要研究三种常见的数值计算方法,即二分法、牛顿迭代法和弦截法,并通过实例验证其有效性和适用性。
二、方法介绍1.二分法:二分法是一种简单但有效的数值计算方法,适用于通过连续函数的反函数求解根的问题。
其基本思想是将查找区间通过中点划分为两个子区间,根据函数值的符号变化,选择新的查找区间,直到满足精度要求为止。
2.牛顿迭代法:牛顿迭代法是一种基于函数导数的数值计算方法,适用于求解非线性方程的根的问题。
其基本思想是通过对初始值的不断迭代来逼近方程的根,在每次迭代中利用切线的斜率来更新迭代值。
3.弦截法:弦截法是一种近似求解非线性方程根的数值计算方法。
其基本思想是通过初始两个近似解的连线与坐标轴交点的位置,来逼近真实解。
在每次迭代中,通过计算连线与坐标轴的交点来更新迭代值,直到满足精度要求为止。
三、实验内容1.实现二分法、牛顿迭代法和弦截法的数值计算算法;2.通过给定的实例,在同样的精度要求下对三种方法进行比较;3.分析并总结三种方法的优缺点及适用范围。
四、实验结果通过对比实例的计算结果可得到如下结果:1.二分法在给定的实例中,二分法需要进行较多的迭代次数才能达到所要求的精度,计算效率较低,但由于其简单的计算过程和保证收敛性的特点,适用于绝大多数连续函数的求根问题。
2.牛顿迭代法牛顿迭代法的计算速度快且稳定,收敛速度相对较快,但对初始值的选择要求较高。
如果初始值选择不当,可能会导致迭代结果发散。
大学计算实验实验报告

实验名称:数值计算方法实验日期:2021年10月15日实验地点:计算机实验室实验目的:1. 理解数值计算的基本原理和方法。
2. 掌握常用数值计算算法的编程实现。
3. 培养分析和解决实际问题的能力。
实验内容:本次实验主要涉及以下内容:1. 线性方程组的求解2. 函数求值与数值微分3. 函数求根4. 数据插值实验原理:数值计算是计算机科学和工程领域中非常重要的一个分支,它涉及到将数学问题转化为计算机可以处理的数值问题。
本实验主要探讨了以下数值计算方法:1. 高斯消元法:用于求解线性方程组。
2. 牛顿法:用于求解函数的根。
3. 二分法:用于求解函数的根。
4. 拉格朗日插值法:用于数据插值。
实验步骤:1. 线性方程组的求解:- 编写程序实现高斯消元法,用于求解线性方程组。
- 输入方程组的系数和常数项。
- 输出方程组的解。
2. 函数求值与数值微分:- 编写程序实现中点法和辛普森法,用于求函数的近似值。
- 编写程序实现中心差分法,用于求函数的导数近似值。
- 输入函数表达式、求值点和微分点。
- 输出函数的近似值和导数的近似值。
3. 函数求根:- 编写程序实现牛顿法和二分法,用于求解函数的根。
- 输入函数表达式、初始猜测值和误差容忍度。
- 输出函数的根。
4. 数据插值:- 编写程序实现拉格朗日插值法,用于数据插值。
- 输入数据点和待插值点。
- 输出插值结果。
实验结果:1. 线性方程组的求解:- 输入方程组系数和常数项:`2x + 3y = 6`,`x - y = 1`。
- 输出解:`x = 2`,`y = 1`。
2. 函数求值与数值微分:- 输入函数表达式:`f(x) = x^2`,求值点:`x = 2`。
- 输出函数的近似值:`f(2) ≈ 4.000000`。
- 输入微分点:`x = 2`。
- 输出导数的近似值:`f'(2) ≈ 4.000000`。
3. 函数求根:- 输入函数表达式:`f(x) = x^2 - 2`,初始猜测值:`x = 1`,误差容忍度:`10^-6`。
数值计算方法实验报告

数值计算方法实验报告数值计算方法实验报告引言:数值计算方法是一种通过数学模型和计算机算法来解决实际问题的方法。
在科学研究和工程应用中,数值计算方法被广泛应用于求解方程、优化问题、模拟仿真等领域。
本实验报告将介绍数值计算方法的基本原理和实验结果。
一、二分法求根二分法是一种通过不断折半缩小搜索区间来求解方程根的方法。
在实验中,我们选取了一个简单的方程f(x) = x^2 - 4 = 0来进行求根实验。
通过不断将搜索区间进行二分,我们可以逐步逼近方程的根。
实验结果表明,通过二分法,我们可以得到方程的根为x = 2。
二、牛顿迭代法求根牛顿迭代法是一种通过不断逼近方程根的方法。
在实验中,我们同样选取了方程f(x) = x^2 - 4 = 0进行求根实验。
牛顿迭代法的基本思想是通过对方程进行线性近似,求得近似解,并不断迭代逼近方程的根。
实验结果表明,通过牛顿迭代法,我们可以得到方程的根为x = 2。
三、高斯消元法求解线性方程组高斯消元法是一种通过变换线性方程组的系数矩阵,将其化为上三角矩阵的方法。
在实验中,我们选取了一个简单的线性方程组进行求解实验。
通过对系数矩阵进行行变换,我们可以将其化为上三角矩阵,并通过回代求解得到方程组的解。
实验结果表明,通过高斯消元法,我们可以得到线性方程组的解为x = 1,y = 2,z = 3。
四、插值与拟合插值与拟合是一种通过已知数据点来构造函数模型的方法。
在实验中,我们选取了一组数据点进行插值与拟合实验。
通过拉格朗日插值多项式和最小二乘法拟合,我们可以得到数据点之间的函数模型。
实验结果表明,通过插值与拟合,我们可以得到数据点之间的函数关系,并可以通过该函数模型来进行预测和拟合。
结论:数值计算方法是一种通过数学模型和计算机算法来解决实际问题的方法。
通过本次实验,我们学习了二分法求根、牛顿迭代法求根、高斯消元法求解线性方程组以及插值与拟合的基本原理和应用。
这些方法在科学研究和工程应用中具有广泛的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院 长望学院 专业 大气科学实验班 年级 班次 1 姓名 仙女 学号
1. 引言-问题重述
问题一要求对方程3()250f x x x =--=,用二分法,至少找到一个根,并展示一下信息:(a )近似根(b )初始猜测(区间)(c )迭代次数(d )停止准则(3)收敛速度 问题二要求用二分法求出以下两个方程的近似根:
(a )5()10f x x x =--=,
(b )22520x e x -+=.
2. 数学公式-数值方法和参数定义
二分法求根原理为:若[,]f C a b ∈,严格单调,且()()0f a f b <g ,则f 在(,)a b 上有一实根。
其基本思想为:逐步将区间分半,计算中点处的函数值,根据介值定理选择比原区间缩小一半的有根区间,如此继续下去,直到得到满足精度要求,从而求出满足给定精度的根的近似值。
针对问题一,本文根据方程,定义函数f(x)=a*x*x*x+b*x*x+c*x+d=0,其中,,,a b c d 为各项系数;精度16eps e =-;,m n 分别为求根区间的左右端点,即收敛区间[,]m n ;i 为近似根;v 为收敛速度,count 为当前迭代次数。
其中,count 为单精度int 类型,其余均为双精度double 类型。
基于以上参数定义,设置收敛准则为:当根和函数值的精度小于所设置精度时,结束循环,并输出收敛区间、迭代次数、近似根以及收敛速度。
具体表现为:每进行一次循环视近似根i 的相对位置对收敛区间进行修正,同时对迭代次数+1;收敛速度可通过下式计算:
11
n n n n x x v x x +--=-. 针对问题二(a )在问题一的基础上,更改方程f(x)=a*x*x*x+b*x*x+c*x+d=0的系数以及相关项即可求得相应结果。
对于(b )将方程改为:exp(2*x)-5*x*x+20=。
3. 数值实验-讨论和分析数值结果
针对方程3()250f x x x =--=,首先对其求导,判断单调性,再进行需略估算,发现(2)(3)0f f <g ,于是设置初始收敛区间为[2,3],进而通过二分法求得结果如图1。
结果为:迭代次数21次,近似跟* 2.094551x =,收敛速度为0.5.
针对方程5()10f x x x =--=,通过人工求导,判断单调性,粗略估算初始收敛区间为[1,2],同样,通过二分法求解,结果如图2。
结果为:迭代次数21,近似跟* 1.167304x =,收敛速度为0.5.
针对方程22520x e x -+=,通过求导,判断单调性,粗略估算初始收敛区间为[1,0]-,
学院 长望学院 专业 大气科学实验班 年级 班次 1 姓名 仙女 学号 同样,通过二分法求解,结果如图2。
结果为:迭代次数17次,近似跟*0.672398x =-,收敛速度为0.5.
图1 方程3
()250f x x x =--=的求解结果
图2 方程5()10f x x x =--=的求解结果
学院 长望学院 专业 大气科学实验班 年级 班次 1 姓名 仙女 学号
图3 方程22520x e x -+=的求解结果
4. 结论 二分法算法简单,容易理解,且总是收敛的,收敛速度与方程无关,恒为0.5,速度较慢,当精度为16eps e =-时,迭代次数基本在15~25之间。
然而,仅适用于单调函数,当所求函数非单调时,须进行预估;此外,不能求复根、偶数重根等。
5. 程序
#include <stdio.h>
#include <math.h>
const double eps = 0.5*1e-6; //定义我们计算的精度
double a,b,c,d;//假定我们输入的函数是一元三次方程组,a*x*x*x+b*x*x+c*x+d=0 double f(double x) //定义我们的函数
{
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
int count=0;
double m,n,v=0.0;//求根区间[m,n]
double i,j,sum;
printf("请输入一元三次方程组的系数:a,b,c,d:");
scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
学院长望学院专业大气科学实验班年级班次 1 姓名仙女学号
printf("\n请输入初始求根区间[m,n]:");
scanf("%lf%lf",&m,&n);
if(f(m)*f(n)<0)
{
while(fabs(m-n)>eps)
{
i=(m+n)/2.0;
sum=f(i);
printf("第%d次迭代区间为:[%lf,%lf] 近似根:%lf 函数值:%lf\n",count,m,n,i,sum);
if(fabs(sum)<eps)//停止准则
{
break;
}
else if(f(i)*f(m)<0)
{
n=i; //修正区间,将[m,n]换成[m,i],这里的i是中点
}
else if(f(i)*f(n)<0)
{
m=i;//修正区间,将[m,n]换成[i,n],这里的i是中点
}
count++;
}
}
/*else{
printf("请输入正确的初始求根区间") ;
} */
printf("收敛区间:[%lf,%lf]\n迭代次数:%d",m,n,count);
j=(m+n)/2;
v=(m-j)/(n-m);
v=fabs(v);
printf("\n该方程组的近似根:x*=%lf\n收敛速度:%lf\n",j,v);
return 0;
}。
