五年高考真题与解析

合集下载

高考英语五年真题(2019-2023年)专题汇总解析—名词性从句和定语从句

高考英语五年真题（2019-2023年）专题汇总解析—名词性从句和定语从句一、2023年高考真题1.2023新高考全国Ⅱ卷This is ___42___ they need an English trainer.【答案】why【解析】考查表语从句。

句意：这就是他们需要英语培训师的原因。

分析句子结构可知，空处引导表语从句，从句中结构完整，应该用连接副词连接，前文提到需要培训师的原因，此处是表达“这就是他们需要英语培训师的原因”之意，应用why引导表语从句。

故填why。

2.2023全国甲卷...the form of the fable still has values today, ___43___ Rachel Carson says in “A Fable for Tomorrow”【答案】as【解析】考查定语从句。

句意：然而，正如雷切尔·卡森在《明日寓言》中所说，寓言的形式在今天仍然具有价值。

引导非限定性定语从句，且有“正如”之意，用关系代词as引导。

故填as。

3.2023全国甲卷“There was once a town in the heart of America, ___44___ all life seemed to enjoy peaceful existence with is surroundings,”...【答案】where【解析】考查定语从句。

句意：“从前，在美国的中心地带有一个小镇，那里所有的生命似乎都和周围的环境一起享受着和平的生活，”她的寓言是这样开头的，借用了许多古老寓言中的一些熟悉的词。

句中先行词为town，在非限定性定语从句作地点状语，所以用关系副词where引导。

故填where。

4.2023全国乙卷But for all its ancient buildings, Beijing is also a place ____43____ welcomes the fast-paced development of modern life...【答案】which/that【解析】考查定语从句。

解析几何(解答题)--五年(2020-2024)高考数学真题分类汇编(解析版)

专题解析几何(解答题)考点五年考情(2020-2024)命题趋势考点01椭圆及其性质2024Ⅰ甲卷北京卷天津卷2023北京乙卷天津2022乙卷北京卷浙江卷2021北京卷Ⅱ卷2020ⅠⅡ卷新ⅠⅡ卷椭圆轨迹标准方程问题，有关多边形面积问题，定值定点问题，新结构中的新定义问题是高考的一个高频考点考点02双曲线及其性质2024Ⅱ卷2023Ⅱ新课标Ⅱ2022Ⅰ卷2021Ⅰ双曲线离心率问题，轨迹方程有关面积问题，定值定点问题以及斜率有关的证明问题以及新结构中的新定义问题是高考的高频考点考点03抛物线及其性质2023甲卷2022甲卷2021浙江甲卷乙卷2020浙江抛物线有关三角形面积问题，关于定直线问题，有关P 的证明类问题考点01：椭圆及其性质1(2024·全国·高考Ⅰ卷)已知A (0,3)和P 3,32 为椭圆C :x 2a 2+y 2b 2=1(a >b >0)上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ，且△ABP 的面积为9，求l 的方程．【答案】(1)12(2)直线l 的方程为3x -2y -6=0或x -2y =0.【详解】(1)由题意得b =39a 2+94b2=1，解得b 2=9a 2=12 ，所以e =1-b 2a2=1-912=12.(2)法一：k AP =3-320-3=-12，则直线AP 的方程为y =-12x +3，即x +2y -6=0，AP =0-3 2+3-322=352，由(1)知C :x 212+y 29=1，设点B到直线AP的距离为d，则d=2×9352=1255，则将直线AP沿着与AP垂直的方向平移1255单位即可，此时该平行线与椭圆的交点即为点B，设该平行线的方程为：x+2y+C=0，则C+65=1255，解得C=6或C=-18，当C=6时，联立x212+y29=1x+2y+6=0，解得x=0y=-3或x=-3y=-32，即B0,-3或-3,-3 2，当B0,-3时，此时k l=32，直线l的方程为y=32x-3，即3x-2y-6=0，当B-3,-3 2时，此时k l=12，直线l的方程为y=12x，即x-2y=0，当C=-18时，联立x212+y29=1x+2y-18=0得2y2-27y+117=0，Δ=272-4×2×117=-207<0，此时该直线与椭圆无交点.综上直线l的方程为3x-2y-6=0或x-2y=0.法二：同法一得到直线AP的方程为x+2y-6=0，点B到直线AP的距离d=125 5，设B x0,y0，则x0+2y0-65=1255x2012+y209=1，解得x0=-3y0=-32或x0=0y0=-3，即B0,-3或-3,-3 2，以下同法一.法三：同法一得到直线AP的方程为x+2y-6=0，点B到直线AP的距离d=125 5，设B23cosθ,3sinθ，其中θ∈0,2π，则有23cosθ+6sinθ-65=1255，联立cos2θ+sin2θ=1，解得cosθ=-32sinθ=-12或cosθ=0sinθ=-1，即B0,-3或-3,-3 2，以下同法一；法四：当直线AB的斜率不存在时，此时B0,-3，S△PAB=12×6×3=9，符合题意，此时k l=32，直线l的方程为y=32x-3，即3x-2y-6=0，当线AB的斜率存在时，设直线AB的方程为y=kx+3，联立椭圆方程有y =kx +3x 212+y 29=1，则4k 2+3 x 2+24kx =0，其中k ≠k AP ，即k ≠-12，解得x =0或x =-24k 4k 2+3，k ≠0，k ≠-12，令x =-24k 4k 2+3，则y =-12k 2+94k 2+3，则B -24k 4k 2+3,-12k 2+94k 2+3同法一得到直线AP 的方程为x +2y -6=0，点B 到直线AP 的距离d =1255，则-24k4k 2+3+2×-12k 2+94k 2+3-65=1255，解得k =32，此时B -3,-32 ，则得到此时k l =12，直线l 的方程为y =12x ，即x -2y =0，综上直线l 的方程为3x -2y -6=0或x -2y =0.法五：当l 的斜率不存在时，l :x =3,B 3,-32,PB =3,A 到PB 距离d =3，此时S △ABP =12×3×3=92≠9不满足条件.当l 的斜率存在时，设PB :y -32=k (x -3)，令P x 1,y 1 ,B x 2,y 2 ，y =k (x -3)+32x 212+y 29=1 ，消y 可得4k 2+3 x 2-24k 2-12k x +36k 2-36k -27=0，Δ=24k 2-12k 2-44k 2+3 36k 2-36k -27 >0，且k ≠k AP ，即k ≠-12，x 1+x 2=24k 2-12k 4k 2+3x 1x 2=36k 2-36k -274k 2+3,PB =k 2+1x 1+x 2 2-4x 1x 2=43k 2+13k 2+9k +2744k 2+3 ，A 到直线PB 距离d =3k +32k 2+1,S △PAB =12⋅43k 2+13k 2+9k +2744k 2+3⋅3k +32k 2+1=9，∴k =12或32，均满足题意，∴l :y =12x 或y =32x -3，即3x -2y -6=0或x -2y =0.法六：当l 的斜率不存在时，l :x =3,B 3,-32,PB =3,A 到PB 距离d =3，此时S △ABP =12×3×3=92≠9不满足条件.当直线l 斜率存在时，设l :y =k (x -3)+32，设l 与y 轴的交点为Q ，令x =0，则Q 0,-3k +32，联立y =kx -3k +323x 2+4y 2=36，则有3+4k 2 x 2-8k 3k -32x +36k 2-36k -27=0，3+4k2x2-8k3k-3 2x+36k2-36k-27=0，其中Δ=8k23k-3 22-43+4k236k2-36k-27>0，且k≠-1 2，则3x B=36k2-36k-273+4k2,x B=12k2-12k-93+4k2，则S=12AQx P-x B=123k+3212k+183+4k2=9，解的k=12或k=32，经代入判别式验证均满足题意.则直线l为y=12x或y=32x-3，即3x-2y-6=0或x-2y=0.2(2024·全国·高考甲卷)已知椭圆C:x2a2+y2b2=1(a>b>0)的右焦点为F，点M1,32在C上，且MF⊥x轴．(1)求C的方程；(2)过点P4,0的直线交C于A,B两点，N为线段FP的中点，直线NB交直线MF于点Q，证明：AQ⊥y 轴．【答案】(1)x24+y23=1(2)证明见解析【详解】(1)设F c,0，由题设有c=1且b2a=32，故a2-1a=32，故a=2，故b=3，故椭圆方程为x24+y23=1.(2)直线AB的斜率必定存在，设AB:y=k(x-4)，A x1,y1，B x2,y2，由3x2+4y2=12y=k(x-4)可得3+4k2x2-32k2x+64k2-12=0，故Δ=1024k4-43+4k264k2-12>0，故-12<k<12，又x1+x2=32k23+4k2,x1x2=64k2-123+4k2，而N52,0，故直线BN:y=y2x2-52x-52，故y Q=-32y2x2-52=-3y22x2-5，所以y1-y Q=y1+3y22x2-5=y1×2x2-5+3y22x2-5=k x1-4×2x2-5+3k x2-42x2-5=k 2x1x2-5x1+x2+82x2-5=k2×64k2-123+4k2-5×32k23+4k2+82x2-5=k 128k2-24-160k2+24+32k23+4k22x2-5=0，故y1=y Q，即AQ⊥y轴.【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：(1)设直线方程，设交点坐标为x 1,y 1 ,x 2,y 2 ；(2)联立直线与圆锥曲线的方程，得到关于x (或y )的一元二次方程，注意Δ的判断；(3)列出韦达定理；(4)将所求问题或题中的关系转化为x 1+x 2、x 1x 2(或y 1+y 2、y 1y 2)的形式；(5)代入韦达定理求解.3(2024·北京·高考真题)已知椭圆E ：x 2a 2+y 2b 2=1a >b >0 ，以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点0,t t >2 且斜率存在的直线与椭圆E 交于不同的两点A ,B ，过点A 和C 0,1 的直线AC 与椭圆E 的另一个交点为D ．(1)求椭圆E 的方程及离心率；(2)若直线BD 的斜率为0，求t 的值．【答案】(1)x 24+y 22=1,e =22(2)t =2【详解】(1)由题意b =c =22=2，从而a =b 2+c 2=2，所以椭圆方程为x 24+y 22=1，离心率为e =22；(2)直线AB 斜率不为0，否则直线AB 与椭圆无交点，矛盾，从而设AB :y =kx +t ,k ≠0,t >2 ，A x 1,y 1 ,B x 2,y 2 ，联立x 24+y 22=1y =kx +t，化简并整理得1+2k 2 x 2+4ktx +2t 2-4=0，由题意Δ=16k 2t 2-82k 2+1 t 2-2 =84k 2+2-t 2 >0，即k ,t 应满足4k 2+2-t 2>0，所以x 1+x 2=-4kt 1+2k 2,x 1x 2=2t 2-42k 2+1，若直线BD 斜率为0，由椭圆的对称性可设D -x 2,y 2 ，所以AD :y =y 1-y 2x 1+x 2x -x 1 +y 1，在直线AD 方程中令x =0，得y C =x 1y 2+x 2y 1x 1+x 2=x 1kx 2+t +x 2kx 1+t x 1+x 2=2kx 1x 2+t x 1+x 2 x 1+x 2=4k t 2-2 -4kt +t =2t =1，所以t =2，此时k 应满足4k 2+2-t 2=4k 2-2>0k ≠0 ，即k 应满足k <-22或k >22，综上所述，t =2满足题意，此时k <-22或k >22.4(2024·天津·高考真题)已知椭圆x 2a 2+y 2b 2=1(a >b >0)椭圆的离心率e =12．左顶点为A ，下顶点为B ，C 是线段OB 的中点，其中S △ABC =332．(1)求椭圆方程．(2)过点0,-32 的动直线与椭圆有两个交点P ，Q ．在y 轴上是否存在点T 使得TP ⋅TQ ≤0．若存在求出这个T 点纵坐标的取值范围，若不存在请说明理由．【答案】(1)x 212+y 29=1(2)存在T 0,t -3≤t ≤32，使得TP ⋅TQ ≤0恒成立.【详解】(1)因为椭圆的离心率为e =12，故a =2c ，b =3c ，其中c 为半焦距，所以A -2c ,0 ,B 0,-3c ,C 0,-3c 2 ，故S △ABC =12×2c ×32c =332，故c =3，所以a =23，b =3，故椭圆方程为：x 212+y 29=1.(2)若过点0,-32 的动直线的斜率存在，则可设该直线方程为：y =kx -32，设P x 1,y 1 ,Q x 2,y 2 ,T 0,t ，由3x 2+4y 2=36y =kx -32可得3+4k 2 x 2-12kx -27=0，故Δ=144k 2+1083+4k 2 =324+576k 2>0且x 1+x 2=12k 3+4k 2,x 1x 2=-273+4k2,而TP =x 1,y 1-t ,TQ=x 2,y 2-t ，故TP ⋅TQ =x 1x 2+y 1-t y 2-t =x 1x 2+kx 1-32-t kx 2-32-t =1+k 2 x 1x 2-k 32+t x 1+x 2 +32+t 2=1+k 2 ×-273+4k 2-k 32+t ×12k 3+4k 2+32+t 2=-27k 2-27-18k 2-12k 2t +332+t 2+3+2t 2k 23+4k 2=3+2t2-12t -45 k 2+332+t 2-273+4k 2，因为TP ⋅TQ ≤0恒成立，故3+2t 2-12t -45≤0332+t 2-27≤0，解得-3≤t ≤32.若过点0,-32的动直线的斜率不存在，则P 0,3 ,Q 0,-3 或P 0,-3 ,Q 0,3 ，此时需-3≤t ≤3，两者结合可得-3≤t ≤32.综上，存在T 0,t -3≤t ≤32，使得TP ⋅TQ ≤0恒成立.5(2023年全国乙卷理科)已知椭圆C :y 2a 2+x 2b 2=1(a >b >0)的离心率是53，点A -2,0 在C 上．(1)求C方程；(2)过点-2,3 的直线交C 于P ,Q 两点，直线AP ,AQ 与y 轴的交点分别为M ,N ，证明：线段MN 的中点为定点．【答案】(1)y 29+x 24=1(2)证明见详解解析：(1)由题意可得b =2a 2=b 2+c 2e =c a =53，解得a =3b =2c =5，所以椭圆方程为y 29+x 24=1．(2)由题意可知：直线PQ 的斜率存在，设PQ :y =k x +2 +3,P x 1,y 1 ,Q x 2,y 2 ，联立方程y =k x +2 +3y 29+x 24=1，消去y 得：4k 2+9 x 2+8k 2k +3x +16k 2+3k =0，则Δ=64k 22k +3 2-644k 2+9 k 2+3k =-1728k >0，解得k <0，可得x 1+x 2=-8k 2k +34k 2+9,x 1x 2=16k 2+3k 4k 2+9，因为A -2,0 ，则直线AP :y =y 1x 1+2x +2 ，令x =0，解得y =2y 1x 1+2，即M 0,2y 1x 1+2,同理可得N 0,2y 2x 2+2，则2y 1x 1+2+2y2x 2+22=k x 1+2 +3 x 1+2+k x 2+2 +3 x 2+2=kx 1+2k +3 x 2+2 +kx 2+2k +3 x 1+2x 1+2 x 2+2=2kx 1x 2+4k +3 x 1+x 2 +42k +3x 1x 2+2x 1+x 2 +4=32k k 2+3k 4k 2+9-8k 4k +3 2k +34k 2+9+42k +3 16k 2+3k 4k 2+9-16k 2k +34k 2+9+4=10836=3，所以线段MN 的中点是定点0,3 ．6(2020年高考课标Ⅱ)已知椭圆C 1：x 2a 2+y 2b 2=1(a >b >0)右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．(1)求C 1的离心率；(2)设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程．【答案】(1)12；(2)C 1:x 236+y 227=1，C 2:y 2=12x ．解析：(1)∵F c ,0 ，AB ⊥x 轴且与椭圆C 1相交于A 、B 两点，则直线AB 的方程为x =c ，联立x =c x 2a 2+y 2b 2=1a 2=b 2+c 2，解得x =c y =±b 2a，则AB =2b 2a ，抛物线C 2的方程为y 2=4cx ，联立x =cy 2=4cx ，解得x =cy =±2c，∴CD =4c ，∵CD =43AB ，即4c =8b 23a ，2b 2=3ac ，即2c 2+3ac -2a 2=0，即2e 2+3e -2=0，∵0<e <1，解得e =12，因此，椭圆C 1的离心率为12；(2)由(1)知a =2c ，b =3c ，椭圆C 1的方程为x 24c 2+y 23c 2=1，联立y 2=4cxx24c2+y 23c 2=1，消去y 并整理得3x 2+16cx -12c 2=0，解得x =23c 或x =-6c (舍去)，由抛物线的定义可得MF =23c +c =5c3=5，解得c =3．因此，曲线C 1的标准方程为x 236+y 227=1，曲线C 2的标准方程为y 2=12x ．7(2021年新高考全国Ⅱ卷)已知椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0)，右焦点为F (2,0)，且离心率为63．(1)求椭圆C 的方程；(2)设M ，N 是椭圆C 上的两点，直线MN 与曲线x 2+y 2=b 2(x >0)相切．证明：M ，N ，F 三点共线的充要条件是|MN |=3．【答案】解析:(1)由题意，椭圆半焦距c =2且e =c a =63，所以a =3，又b 2=a 2-c 2=1，所以椭圆方程为x 23+y 2=1；(2)由(1)得，曲线为x 2+y 2=1(x >0)，当直线MN 的斜率不存在时，直线MN :x =1，不合题意；当直线MN 的斜率存在时，设M x 1,y 1 ,N x 2,y 2 ，必要性：若M ，N ，F 三点共线，可设直线MN :y =k x -2 即kx -y -2k =0，由直线MN 与曲线x 2+y 2=1(x >0)相切可得2kk 2+1=1，解得k =±1，联立y =±x -2x23+y 2=1 可得4x 2-62x +3=0，所以x 1+x 2=322,x 1⋅x 2=34，所以MN =1+1⋅x 1+x 22-4x 1⋅x 2=3,所以必要性成立；充分性：设直线MN :y =kx +b ,kb <0 即kx -y +b =0，由直线MN 与曲线x 2+y 2=1(x >0)相切可得bk 2+1=1，所以b 2=k 2+1，联立y =kx +bx 23+y 2=1可得1+3k 2 x 2+6kbx +3b 2-3=0，所以x 1+x 2=-6kb 1+3k 2,x 1⋅x 2=3b 2-31+3k 2，所以MN =1+k 2⋅x 1+x 22-4x 1⋅x 2=1+k2-6kb 1+3k22-4⋅3b 2-31+3k 2=1+k 2⋅24k 21+3k 2=3，化简得3k 2-1 2=0，所以k =±1，所以k =1b =-2或k =-1b =2 ，所以直线MN :y =x -2或y =-x +2，所以直线MN 过点F (2,0)，M ，N ，F 三点共线，充分性成立；所以M ，N ，F 三点共线的充要条件是|MN |=3．8(2020年高考课标Ⅰ卷)已知A 、B 分别为椭圆E ：x 2a2+y 2=1(a >1)左、右顶点，G 为E 的上顶点，AG ⋅GB =8，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．(1)求E方程；(2)证明：直线CD 过定点．【答案】(1)x 29+y 2=1；(2)证明详见解析．【解析】(1)依据题意作出如下图象：由椭圆方程E :x 2a2+y 2=1(a >1)可得：A -a ,0 ， B a ,0 ，G 0,1∴AG =a ,1 ，GB =a ,-1 ∴AG ⋅GB =a 2-1=8，∴a 2=9∴椭圆方程为：x 29+y 2=1(2)证明：设P 6,y 0 ，则直线AP 的方程为：y =y 0-06--3x +3 ，即：y =y 09x +3 联立直线AP 的方程与椭圆方程可得：x 29+y 2=1y =y 09x +3 ，整理得：y 02+9 x 2+6y 02x +9y 02-81=0，解得：x =-3或x =-3y 02+27y 02+9将x =-3y 02+27y 02+9代入直线y =y 09x +3 可得：y =6y 0y 02+9所以点C 的坐标为-3y 02+27y 02+9,6y 0y 02+9 ．同理可得：点D 的坐标为3y 02-3y 02+1,-2y 0y 02+1∴直线CD 的方程为：y --2y 0y 02+1=6y 0y 02+9--2y 0y 02+1-3y 02+27y 02+9-3y 02-3y 02+1x -3y 02-3y 02+1，整理可得：y +2y 0y 02+1=8y 0y 02+3 69-y 04x -3y 02-3y 02+1 =8y 063-y 02 x -3y 02-3y 02+1整理得：y =4y 033-y 02 x +2y 0y 02-3=4y 033-y 02x -32故直线CD 过定点32,09(2020年新高考全国Ⅰ卷)已知椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的离心率为22，且过点A (2，1)．(1)求C 的方程：(2)点M ，N 在C 上，且AM ⊥AN ，AD ⊥MN ，D 为垂足．证明：存在定点Q ，使得|DQ |为定值．【答案】(1)x 26+y 23=1；(2)详见解析．解析：(1)由题意可得：c a =324a 2+1b 2=1a 2=b 2+c 2，解得：a 2=6,b 2=c 2=3，故椭圆方程为：x 26+y 23=1．(2)设点M x 1,y 1 ,N x 2,y 2 ．因为AM ⊥AN ，∴AM·AN=0，即x 1-2 x 2-2 +y 1-1 y 2-1 =0,①当直线MN 的斜率存在时，设方程为y =kx +m ,如图1．代入椭圆方程消去y 并整理得：1+2k 2 x 2+4kmx +2m 2-6=0x 1+x 2=-4km 1+2k 2,x 1x 2=2m 2-61+2k 2②,根据y 1=kx 1+m ,y 2=kx 2+m ,代入①整理可得：k 2+1 x 1x 2+km -k -2 x 1+x 2 +m -1 2+4=0将②代入，k 2+1 2m 2-61+2k 2+km -k -2 -4km1+2k2+m -1 2+4=0，整理化简得2k +3m +1 2k +m -1 =0,∵A (2,1)不在直线MN 上，∴2k +m -1≠0，∴2k +3m +1=0，k ≠1，于是MN 的方程为y =k x -23 -13，所以直线过定点直线过定点E 23,-13．当直线MN 的斜率不存在时，可得N x 1,-y 1 ,如图2．代入x 1-2 x 2-2 +y 1-1 y 2-1 =0得x 1-2 2+1-y 22=0,结合x 216+y 213=1,解得x 1=2舍 ,x 1=23,此时直线MN 过点E 23,-13,由于AE 为定值，且△ADE 为直角三角形，AE 为斜边，所以AE 中点Q 满足QD 为定值(AE 长度的一半122-232+1+132=423)．由于A 2,1 ,E 23,-13 ，故由中点坐标公式可得Q 43,13．故存在点Q 43,13，使得|DQ |为定值．10(2022年高考全国乙卷)已知椭圆E 的中心为坐标原点，对称轴为x 轴、y 轴，且过A 0,-2 ,B 32,-1两点．(1)求E 的方程；(2)设过点P 1,-2 的直线交E 于M ，N 两点，过M 且平行于x 轴的直线与线段AB 交于点T ，点H 满足MT =TH．证明：直线HN 过定点．【答案】(1)y 24+x 23=1(2)(0,-2)解析：设椭圆E 的方程为mx 2+ny 2=1，过A 0,-2 ,B 32,-1，则4n =194m +n =1 ，解得m =13，n =14，所以椭圆E 的方程为：y 24+x 23=1．【小问2详解】A (0,-2),B 32,-1，所以AB :y +2=23x ，①若过点P (1,-2)的直线斜率不存在，直线x =1．代入x 23+y 24=1，可得M 1,-263 ，N 1,263 ，代入AB 方程y =23x -2，可得T -6+3,-263 ，由MT =TH 得到H -26+5,-263 ．求得HN 方程：y =2+263x -2，过点(0,-2)．②若过点P (1,-2)的直线斜率存在，设kx -y -(k +2)=0,M (x 1,y 1),N (x 2,y 2)．联立kx -y -(k +2)=0x 23+y 24=1,得(3k 2+4)x 2-6k (2+k )x +3k (k +4)=0，可得x 1+x 2=6k (2+k )3k 2+4x 1x 2=3k (4+k )3k 2+4，y 1+y 2=-8(2+k )3k 2+4y 2y 2=4(4+4k -2k 2)3k 2+4，且x 1y 2+x 2y 1=-24k 3k 2+4(*)联立y =y 1y =23x -2,可得T 3y12+3,y 1 ,H (3y 1+6-x 1,y 1).可求得此时HN :y -y 2=y 1-y 23y 1+6-x 1-x 2(x -x 2)，将(0,-2)，代入整理得2(x 1+x 2)-6(y 1+y 2)+x 1y 2+x 2y 1-3y 1y 2-12=0，将(*)代入，得24k +12k 2+96+48k -24k -48-48k +24k 2-36k 2-48=0,显然成立，综上，可得直线HN 过定点(0,-2).11(2020年新高考全国卷Ⅱ)已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)过点M (2，3),点A 为其左顶点，且AM 的斜率为12，(1)求C 的方程；(2)点N 为椭圆上任意一点，求△AMN 的面积的最大值．【答案】(1)x 216+y 212=1；(2)18．解析：(1)由题意可知直线AM 的方程为：y -3=12(x -2)，即x -2y =-4．当y =0时，解得x =-4，所以a =4，椭圆C :x 2a 2+y 2b 2=1a >b >0 过点M (2，3)，可得416+9b 2=1，解得b 2=12．所以C 的方程：x 216+y 212=1．(2)设与直线AM 平行的直线方程为：x -2y =m ，如图所示，当直线与椭圆相切时，与AM 距离比较远的直线与椭圆的切点为N ，此时△AMN 的面积取得最大值．联立直线方程x -2y =m 与椭圆方程x 216+y 212=1，可得：3m +2y 2+4y 2=48，化简可得：16y 2+12my +3m 2-48=0，所以Δ=144m 2-4×163m 2-48 =0，即m 2=64，解得m =±8，与AM 距离比较远的直线方程：x -2y =8，直线AM 方程为：x -2y =-4，点N 到直线AM 的距离即两平行线之间的距离，利用平行线之间的距离公式可得：d =8+41+4=1255，由两点之间距离公式可得|AM |=(2+4)2+32=35．所以△AMN 的面积的最大值：12×35×1255=18．12(2020年高考课标Ⅲ卷)已知椭圆C :x 225+y 2m 2=1(0<m <5)的离心率为154，A ，B 分别为C 的左、右顶点．(1)求C 的方程；(2)若点P 在C 上，点Q 在直线x =6上，且|BP |=|BQ |，BP ⊥BQ ，求△APQ 的面积．【答案】(1)x 225+16y 225=1；(2)52．解析：(1)∵C :x 225+y 2m 2=1(0<m <5)∴a =5，b =m ，根据离心率e =ca=1-b a2=1-m 5 2=154，解得m =54或m =-54(舍)，∴C 的方程为：x 225+y 2542=1，即x 225+16y 225=1；(2)不妨设P ,Q 在x 轴上方∵点P 在C 上，点Q 在直线x =6上，且|BP |=|BQ |，BP ⊥BQ ，过点P 作x 轴垂线，交点为M ，设x =6与x 轴交点为N 根据题意画出图形，如图∵|BP |=|BQ |，BP ⊥BQ ，∠PMB =∠QNB =90°，又∵∠PBM +∠QBN =90°，∠BQN +∠QBN =90°，∴∠PBM =∠BQN ，根据三角形全等条件“AAS ”，可得：△PMB ≅△BNQ ，∵x 225+16y 225=1，∴B (5,0)，∴PM =BN =6-5=1，设P 点为(x P ,y P )，可得P 点纵坐标为y P =1，将其代入x 225+16y 225=1，可得：x P 225+1625=1，解得：x P =3或x P =-3，∴P 点为(3,1)或(-3,1)，①当P 点为(3,1)时，故MB =5-3=2，∵△PMB ≅△BNQ ，∴|MB |=|NQ |=2，可得：Q 点为(6,2)，画出图象，如图∵A (-5,0),Q (6,2)，可求得直线AQ 的直线方程为：2x -11y +10=0，根据点到直线距离公式可得P 到直线AQ 的距离为：d =2×3-11×1+1022+112=5125=55，根据两点间距离公式可得：AQ =6+52+2-0 2=55，∴△APQ 面积为：12×55×55=52；②当P 点为(-3,1)时，故MB =5+3=8，∵△PMB ≅△BNQ ，∴|MB |=|NQ |=8，可得：Q 点为(6,8)，画出图象，如图∵A (-5,0),Q (6,8)，可求得直线AQ 的直线方程为：8x -11y +40=0，根据点到直线距离公式可得P 到直线AQ 的距离为：d =8×-3 -11×1+4082+112=5185=5185，根据两点间距离公式可得：AQ =6+52+8-0 2=185，∴△APQ 面积为：12×185×5185=52，综上所述，△APQ 面积为：52．1313(2023年北京卷)已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)离心率为53，A 、C 分别是E 的上、下顶点，B ，D 分别是E 的左、右顶点，|AC |=4．(1)求E 的方程；(2)设P 为第一象限内E 上的动点，直线PD 与直线BC 交于点M ，直线PA 与直线y =-2交于点N ．求证：MN ⎳CD ．【答案】(1)x 29+y 24=1(2)证明见解析：(1)依题意，得e =c a =53，则c =53a ，又A ,C 分别为椭圆上下顶点，AC =4，所以2b =4，即b =2，所以a 2-c 2=b 2=4，即a 2-59a 2=49a 2=4，则a 2=9，所以椭圆E 的方程为x 29+y 24=1．(2)因为椭圆E 的方程为x 29+y 24=1，所以A 0,2 ,C 0,-2 ,B -3,0 ,D 3,0 ，因为P 为第一象限E 上的动点，设P m ,n 0<m <3,0<n <2 ，则m 29+n 24=1，易得k BC =0+2-3-0=-23，则直线BC 的方程为y =-23x -2，k PD =n -0m -3=n m -3，则直线PD 的方程为y =n m -3x -3 ，联立y =-23x -2y =n m -3x -3，解得x =33n -2m +63n +2m -6y =-12n 3n +2m -6，即M 33n -2m +6 3n +2m -6,-12n 3n +2m -6，而k PA =n -2m -0=n -2m ，则直线PA 的方程为y =n -2mx +2，令y =-2，则-2=n -2m x +2，解得x =-4m n -2，即N -4mn -2,-2 ，又m 29+n 24=1，则m 2=9-9n 24，8m 2=72-18n 2，所以k MN =-12n3n +2m -6+233n -2m +6 3n +2m -6--4mn-2=-6n +4m -12 n -29n -6m +18 n -2 +4m 3n +2m -6=-6n 2+4mn -8m +249n 2+8m 2+6mn -12m -36=-6n 2+4mn -8m +249n 2+72-18n 2+6mn -12m -36=-6n 2+4mn -8m +24-9n 2+6mn -12m +36=2-3n 2+2mn -4m +12 3-3n 2+2mn -4m +12 =23，又k CD =0+23-0=23，即k MN =k CD ，显然，MN 与CD 不重合，所以MN ⎳CD ．14(2023年天津卷)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左右顶点分别为A 1,A 2，右焦点为F ，已知A 1F =3,A 2F =1．(1)求椭圆方程及其离心率；(2)已知点P 是椭圆上一动点(不与端点重合)，直线A 2P 交y 轴于点Q ，若三角形A 1PQ 的面积是三角形A 2FP 面积的二倍，求直线A 2P 的方程．【答案】(1)椭圆的方程为x 24+y 23=1，离心率为e =12．(2)y =±62x -2 ．解析：(1)如图，由题意得a +c =3a -c =1，解得a =2,c =1，所以b =22-12=3，所以椭圆的方程为x 24+y 23=1，离心率为e =c a =12．(2)由题意得，直线A 2P 斜率存在，由椭圆的方程为x 24+y 23=1可得A 22,0 ，设直线A 2P 的方程为y =k x -2 ，联立方程组x 24+y 23=1y =k x -2，消去y 整理得：3+4k 2 x 2-16k 2x +16k 2-12=0，由韦达定理得x A 2⋅x P =16k 2-123+4k 2，所以x P =8k 2-63+4k 2，所以P 8k 2-63+4k 2,--12k3+4k 2，Q 0,-2k ．所以S △A 2QA 1=12×4×y Q ,S △A 2PF =12×1×y P ,S △A 1A 2P =12×4×y P ，所以S △A 2QA 1=S △A 1PQ +S △A 1A 2P =2S △A 2PF +S △A 1A 2P ，所以2y Q =3y P ，即2-2k =3-12k3+4k 2，解得k =±62，所以直线A 2P 的方程为y =±62x -2 ．15(2022高考北京卷)已知椭圆：E :x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (0,1)，焦距为23．(1)求椭圆E 的方程；(2)过点P (-2,1)作斜率为k 的直线与椭圆E 交于不同的两点B ，C ，直线AB ，AC 分别与x 轴交于点M ，N ，当|MN |=2时，求k 的值．【答案】解析:(1)依题意可得b =1，2c =23，又c 2=a 2-b 2，所以a =2，所以椭圆方程为x 24+y 2=1；(2)解：依题意过点P -2,1 的直线为y -1=k x +2 ，设B x 1,y 1 、C x 2,y 2 ，不妨令-2≤x 1<x 2≤2，由y -1=k x +2x 24+y 2=1，消去y 整理得1+4k 2 x 2+16k 2+8k x +16k 2+16k =0，所以Δ=16k 2+8k 2-41+4k 2 16k 2+16k >0，解得k <0，所以x 1+x 2=-16k 2+8k 1+4k 2，x 1⋅x 2=16k 2+16k1+4k2，直线AB 的方程为y -1=y 1-1x 1x ，令y =0，解得x M =x 11-y 1，直线AC 的方程为y -1=y 2-1x 2x ，令y =0，解得x N =x 21-y 2，所以MN =x N -x M =x 21-y 2-x 11-y 1=x 21-k x 2+2 +1 -x 11-k x 1+2 +1=x 2-k x 2+2 +x 1k x 1+2=x 2+2 x 1-x 2x 1+2k x 2+2 x 1+2=2x 1-x 2k x 2+2 x 1+2=2，所以x 1-x 2 =k x 2+2 x 1+2 ，即x 1+x 22-4x 1x 2=k x 2x 1+2x 2+x 1 +4即-16k 2+8k 1+4k22-4×16k 2+16k 1+4k 2=k 16k 2+16k 1+4k 2+2-16k 2+8k 1+4k2+4 即81+4k 22k 2+k 2-1+4k 2 k 2+k =k1+4k216k2+16k -216k 2+8k +41+4k 2整理得8-k =4k ，解得k =-416(2022年浙江省高考)如图，已知椭圆x 212+y 2=1．设A ，B 是椭圆上异于P (0,1)的两点，且点Q 0,12 在线段AB 上，直线PA ,PB 分别交直线y =-12x +3于C ，D 两点．(1)求点P 到椭圆上点的距离的最大值；(2)求|CD |的最小值．【答案】解析:(1)设Q (23cos θ,sin θ)是椭圆上任意一点,P (0,1),则|PQ |2=12cos 2θ+(1-sin θ)2=13-11sin 2θ-2sin θ=-11sin θ+111 2+14411≤14411，当且仅当sin θ=-111时取等号，故|PQ |的最大值是121111．(2)设直线AB :y =kx +12,直线AB 方程与椭圆x 212+y 2=1联立,可得k 2+112 x 2+kx -34=0,设A x 1,y 1 ,B x 2,y 2 ，所以x 1+x 2=-kk 2+112x 1x 2=-34k 2+112 ，因为直线PA :y =y 1-1x 1x +1与直线y =-12x +3交于C ,则x C=4x 1x 1+2y 1-2=4x 1(2k +1)x 1-1,同理可得,x D =4x 2x 2+2y 2-2=4x 2(2k +1)x 2-1．则|CD |=1+14x C -x D =524x 1(2k +1)x 1-1-4x 2(2k +1)x 2-1=25x 1-x 2(2k +1)x 1-1 (2k +1)x 2-1=25x 1-x 2(2k +1)2x 1x 2-(2k +1)x 1+x 2 +1=352⋅16k 2+13k +1=655⋅16k 2+1916+13k +1≥655×4k ×34+1×123k +1=655，当且仅当k =316时取等号，故CD 的最小值为655．17(2021高考北京)已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)一个顶点A (0,-2)，以椭圆E 的四个顶点为顶点的四边形面积为45．(1)求椭圆E 的方程；(2)过点P (0，-3)的直线l 斜率为k 的直线与椭圆E 交于不同的两点B ，C ，直线AB ，AC 分别与直线交y =-3交于点M ，N ，当|PM |+|PN |≤15时，求k 的取值范围．【答案】(1)x 25+y 24=1；(2)[-3,-1)∪(1,3]．解析：(1)因为椭圆过A 0,-2 ，故b =2，因为四个顶点围成的四边形的面积为45，故12×2a ×2b =45，即a =5，故椭圆的标准方程为：x 25+y 24=1．(2)设B x 1,y 1 ,C x 2,y 2 ，因为直线BC 的斜率存在，故x 1x 2≠0，故直线AB :y =y 1+2x 1x -2，令y =-3，则x M =-x1y 1+2，同理x N =-x 2y 2+2直线BC :y =kx -3，由y =kx -34x 2+5y 2=20可得4+5k 2 x 2-30kx +25=0，故Δ=900k 2-1004+5k 2 >0，解得k <-1或k >1．又x 1+x 2=30k 4+5k 2,x 1x 2=254+5k 2，故x 1x 2>0，所以x M x N >0又PM +PN =x M +x N =x 1y 1+2+x 2y 2+2=x1kx1-1+x2kx2-1=2kx1x2-x1+x2k2x1x2-k x1+x2+1=50k4+5k2-30k4+5k225k24+5k2-30k24+5k2+1=5k故5k ≤15即k ≤3，综上，-3≤k<-1或1<k≤3．考点02双曲线及其性质1(2024·全国·高考Ⅱ)已知双曲线C:x2-y2=m m>0，点P15,4在C上，k为常数，0<k<1．按照如下方式依次构造点P n n=2,3,...：过P n-1作斜率为k的直线与C的左支交于点Q n-1，令P n为Q n-1关于y轴的对称点，记P n的坐标为x n,y n .(1)若k=12，求x2,y2；(2)证明：数列x n-y n是公比为1+k1-k的等比数列；(3)设S n为△P n P n+1P n+2的面积，证明：对任意正整数n，S n=S n+1.【答案】(1)x2=3，y2=0(2)证明见解析(3)证明见解析【详解】(1)由已知有m=52-42=9，故C的方程为x2-y2=9.当k=12时，过P15,4且斜率为12的直线为y=x+32，与x2-y2=9联立得到x2-x+322=9.解得x=-3或x=5，所以该直线与C的不同于P1的交点为Q1-3,0，该点显然在C的左支上.故P23,0，从而x2=3，y2=0.(2)由于过P n x n,y n且斜率为k的直线为y=k x-x n+y n，与x2-y2=9联立，得到方程x2-k x-x n+y n2=9.展开即得1-k2x2-2k y n-kx nx-y n-kx n2-9=0，由于P n x n,y n已经是直线y=k x-x n+y n和x2 -y2=9的公共点，故方程必有一根x=x n.从而根据韦达定理，另一根x=2k y n-kx n1-k2-x n=2ky n-x n-k2x n1-k2，相应的y=k x-x n+y n=y n+k2y n-2kx n1-k2.所以该直线与C 的不同于P n 的交点为Q n2ky n -x n -k 2x n 1-k 2,y n +k 2y n -2kx n1-k 2，而注意到Q n 的横坐标亦可通过韦达定理表示为-y n -kx n 2-91-k 2x n ，故Q n 一定在C 的左支上.所以P n +1x n +k 2x n -2ky n 1-k 2,y n +k 2y n -2kx n1-k 2.这就得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n1-k 2.所以x n +1-y n +1=x n +k 2x n -2ky n 1-k 2-y n +k 2y n -2kx n1-k 2=x n +k 2x n +2kx n 1-k 2-y n +k 2y n +2ky n 1-k 2=1+k 2+2k 1-k2x n -y n =1+k 1-k x n -y n .再由x 21-y 21=9，就知道x 1-y 1≠0，所以数列x n -y n 是公比为1+k 1-k 的等比数列.(3)方法一：先证明一个结论：对平面上三个点U ,V ,W ，若UV =a ,b ，UW=c ,d ，则S △UVW =12ad -bc .(若U ,V ,W 在同一条直线上，约定S △UVW =0)证明：S △UVW =12UV ⋅UW sin UV ,UW =12UV ⋅UW 1-cos 2UV ,UW=12UV⋅UW 1-UV ⋅UWUV ⋅UW 2=12UV 2⋅UW 2-UV ⋅UW 2=12a 2+b 2c 2+d 2-ac +bd2=12a 2c 2+a 2d 2+b 2c 2+b 2d 2-a 2c 2-b 2d 2-2abcd =12a 2d 2+b 2c 2-2abcd =12ad -bc2=12ad -bc .证毕，回到原题.由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n 1-k 2，故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k2x n +y n =1-k1+k x n +y n .再由x 21-y 21=9，就知道x 1+y 1≠0，所以数列x n +y n 是公比为1-k 1+k 的等比数列.所以对任意的正整数m ，都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n=121-k 1+k m -1+k 1-k mx 2n -y 2n=921-k 1+k m -1+k 1-k m .而又有P n +1P n =-x n +1-x n ,-y n +1-y n ，P n +1P n +2=x n +2-x n +1,y n +2-y n +1 ，故利用前面已经证明的结论即得S n =S △P n P n +1P n +2=12-x n +1-x n y n +2-y n +1 +y n +1-y n x n +2-x n +1 =12x n +1-x n y n +2-y n +1 -y n +1-y n x n +2-x n +1 =12x n +1y n +2-y n +1x n +2 +x n y n +1-y n x n +1 -x n y n +2-y n x n +2=12921-k 1+k -1+k 1-k +921-k 1+k -1+k 1-k-921-k 1+k 2-1+k 1-k 2.这就表明S n 的取值是与n 无关的定值，所以S n =S n +1.方法二：由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n 1-k 2，故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k2x n +y n =1-k1+k x n +y n .再由x 21-y 21=9，就知道x 1+y 1≠0，所以数列x n +y n 是公比为1-k 1+k 的等比数列.所以对任意的正整数m ，都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n =921-k 1+k m -1+k 1-k m .这就得到x n +2y n +3-y n +2x n +3=921-k 1+k -1+k1-k=x n y n +1-y n x n +1，以及x n +1y n +3-y n +1x n +3=921-k 1+k 2-1+k 1-k 2=x n y n +2-y n x n +2.两式相减，即得x n +2y n +3-y n +2x n +3 -x n +1y n +3-y n +1x n +3 =x n y n +1-y n x n +1 -x n y n +2-y n x n +2 .移项得到x n +2y n +3-y n x n +2-x n +1y n +3+y n x n +1=y n +2x n +3-x n y n +2-y n +1x n +3+x n y n +1.故y n +3-y n x n +2-x n +1 =y n +2-y n +1 x n +3-x n .而P n P n +3 =x n +3-x n ,y n +3-y n ，P n +1P n +2 =x n +2-x n +1,y n +2-y n +1 .所以P n P n +3 和P n +1P n +2平行，这就得到S △P n P n +1P n +2=S △P n +1P n +2P n +3，即S n =S n +1.【点睛】关键点点睛：本题的关键在于将解析几何和数列知识的结合，需要综合运用多方面知识方可得解.2(2023年新课标全国Ⅱ卷)已知双曲线C 的中心为坐标原点，左焦点为-25,0 ，离心率为5．(1)求C的方程；(2)记C左、右顶点分别为A1，A2，过点-4,0的直线与C的左支交于M，N两点，M在第二象限，直线MA1与NA2交于点P．证明:点P在定直线上．【答案】(1)x24-y216=1(2)证明见解析．解析：(1)设双曲线方程为x2a2-y2b2=1a>0,b>0，由焦点坐标可知c=25，则由e=ca=5可得a=2，b=c2-a2=4，双曲线方程为x24-y216=1．(2)由(1)可得A1-2,0,A22,0，设M x1,y1,N x2,y2，显然直线的斜率不为0，所以设直线MN的方程为x=my-4，且-12<m<12，与x24-y216=1联立可得4m2-1y2-32my+48=0，且Δ=64(4m2+3)>0，则y1+y2=32m4m2-1,y1y2=484m2-1，直线MA1的方程为y=y1x1+2x+2，直线NA2的方程为y=y2x2-2x-2，联立直线MA1与直线NA2的方程可得：x+2 x-2=y2x1+2y1x2-2=y2my1-2y1my2-6=my1y2-2y1+y2+2y1my1y2-6y1=m⋅484m2-1-2⋅32m4m2-1+2y1m×484m2-1-6y1=-16m4m2-1+2y148m4m2-1-6y1=-13，由x+2x-2=-13可得x=-1，即x P=-1，据此可得点P在定直线x=-1上运动．3(2022新高考全国II卷)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的右焦点为F(2,0)，渐近线方程为y=±3x．(1)求C的方程；(2)过F的直线与C的两条渐近线分别交于A，B两点，点P x1,y1,Q x2,y2在C上，且．x1>x2>0,y1>0．过P 且斜率为-3的直线与过Q 且斜率为3的直线交于点M ．从下面①②③中选取两个作为条件，证明另外一个成立：①M 在AB 上；②PQ ∥AB ；③|MA |=|MB |．注：若选择不同的组合分别解答，则按第一个解答计分．【答案】(1)x 2-y 23=1(2)见解析:(1)右焦点为F (2,0)，∴c =2,∵渐近线方程为y =±3x ，∴ba=3，∴b =3a ，∴c 2=a 2+b 2=4a 2=4，∴a =1，∴b =3．∴C 的方程为：x 2-y 23=1；(2)由已知得直线PQ 的斜率存在且不为零，直线AB 的斜率不为零，若选由①②推③或选由②③推①：由②成立可知直线AB 的斜率存在且不为零；若选①③推②，则M 为线段AB 的中点，假若直线AB 的斜率不存在，则由双曲线的对称性可知M 在x 轴上，即为焦点F ,此时由对称性可知P 、Q 关于x 轴对称，与从而x 1=x 2，已知不符；总之，直线AB 的斜率存在且不为零．设直线AB 的斜率为k ,直线AB 方程为y =k x -2 ,则条件①M 在AB 上，等价于y 0=k x 0-2 ⇔ky 0=k 2x 0-2 ；两渐近线方程合并为3x 2-y 2=0,联立消去y 并化简整理得：k 2-3 x 2-4k 2x +4k 2=0设A x 3,y 3 ,B x 3,y 4 ,线段中点N x N ,y N ,则x N =x 3+x 42=2k 2k 2-3,y N =k x N -2 =6kk 2-3,设M x 0,y 0 , 则条件③AM =BM 等价于x 0-x 3 2+y 0-y 3 2=x 0-x 4 2+y 0-y 4 2,移项并利用平方差公式整理得：x 3-x 4 2x 0-x 3+x 4 +y 3-y 4 2y 0-y 3+y 4 =0，2x 0-x 3+x 4 +y 3-y 4x 3-x 42y 0-y 3+y 4 =0,即x 0-x N +k y 0-y N =0,即x 0+ky 0=8k 2k 2-3；由题意知直线PM 的斜率为-3, 直线QM 的斜率为3,∴由y 1-y 0=-3x 1-x 0 ,y 2-y 0=3x 2-x 0 ,∴y 1-y 2=-3x 1+x 2-2x 0 ,所以直线PQ 的斜率m =y 1-y 2x 1-x 2=-3x 1+x 2-2x 0 x 1-x 2,直线PM :y =-3x -x 0 +y 0,即y =y 0+3x 0-3x ,代入双曲线的方程3x 2-y 2-3=0,即3x +y 3x -y =3中，得：y 0+3x 0 23x -y 0+3x 0 =3,解得P 的横坐标：x 1=1233y 0+3x 0+y 0+3x 0,。

高考英语五年真题(2019-2023年)专题汇总解析—非谓语动词

高考英语五年真题（2019-2023年）专题汇总解析—非谓语动词一、2023年高考真题1.2023新高考全国Ⅰ卷To eat one, you have to decide whether ____37____ (bite) a small hole in it first, releasing the stream and risking a spill (溢出)...【答案】to bite【解析】考查非谓语动词。

句意：吃小笼包的时候，你必须要决定是先咬一个小口流出汤汁，还是把整个小笼包放进嘴里，让热汤在舌头上爆炸。

decide to do sth.“决定做某事”，用不定式作宾语，空处与后面to put并列作宾语，故填to bite。

2.2023新高考全国Ⅰ卷Shanghai may be the ____39____ (recognize) home of the soup dumplings but food historians will actually point you to the neighboring canal town of Nanxiang as Xiao long hao’s birthplace.【答案】recognized【解析】考查非谓语动词。

句意：上海可能是公认的小笼包之乡，但美食历史学家会告诉你，邻近的运河小镇南翔才是小笼包的发源地。

空格在名词home前面作定语，recognize与home是逻辑上动宾关系，需填过去分词recognized作定语，recognized“被公认的”也可以看作是形容词作定语。

故填recognized。

3.2023新高考全国Ⅰ卷Nanxiang aside, the best Xiao long bao have a fine skin, allowing them ____41____ (lift) out of the steamer basket ...【答案】to be lifted【解析】考查非谓语动词。

通用版五年高考2024_2025高考英语真题分项详解专题17名词性从句含解析

专题17 名词性从句【2024年】1. （2024·江苏卷）It is not a problem __________ we can win the battle; it’s just a matter of time.A. whetherB. whyC. whenD. where【答案】A【解析】考查主语从句。

句意：我们能否打赢这场战斗不是问题；这只是时间问题。

A. whether是否；B. why为什么；C. when什么时候；D. where在哪里。

依据下文it’s justa matter of time可知，此处指”我们能否打赢这场战斗不是问题”，it是形式主语，whether引导的从句是真正的主语。

故选A。

2. （2024·天津卷）The student completed this experiment to make come true__________ Professor Joseph had said.A. thatB. whatC. whenD. where【答案】B【解析】考查名词性从句。

句意：为了使约瑟夫教授所说的成为现实，这个学生完成了这个试验。

_________ Professor Joseph had said作make的宾语从句，该从句中，空处在从句中作said的宾语，表示”……所说的话”，因此应用what引导该从句。

故选B。

3. （2024·浙江卷）Over thousands of years，they began to depend less on 57 could be hunted or gathered from the wild, and more on animals they had raised and crops they had sown.【答案】what【解析】考查名词性从句。

句意：在几千年的时间里，他们起先削减对我们从野外采集的猎物的依靠，而更多地依靠他们饲养的动物和播种的庄稼。

五年高考2016_2020高考数学真题分项详解专题17立体几何综合含解析文

专题17 立体几何综合【2020年】1。

（2020·新课标Ⅰ文）如图，D 为圆锥的顶点,O 是圆锥底面的圆心,ABC 是底面的内接正三角形，P 为DO 上一点，∠APC =90°．（1）证明：平面PAB ⊥平面PAC ；（2）设DO =2，圆锥的侧面积为3π，求三棱锥P −ABC 的体积。

【答案】（1）证明见解析;(26.【解析】 (1)D 为圆锥顶点，O 为底面圆心，OD ∴⊥平面ABC ,P 在DO 上，,OA OB OC PA PB PC ==∴==，ABC 是圆内接正三角形,AC BC ∴=，PAC PBC ≅△△，90APC BPC ∴∠=∠=︒，即,PB PC PA PC ⊥⊥,,PA PB P PC =∴⊥平面,PAB PC ⊂平面PAC ，∴平面PAB ⊥平面PAC ;（2）设圆锥的母线为l ，底面半径为r ,圆锥的侧面积为3,3rl rl ππ==2222OD l r =-=，解得1,3r l ==2sin 603AC r ==在等腰直角三角形APC 中，2622AP AC ==, 在Rt PAO 中，2262142PO AP OA =-=-=,∴三棱锥P ABC -的体积为11236333248P ABCABC VPO S -=⋅=⨯⨯⨯=△。

2。

（2020·新课标Ⅱ文）如图，已知三棱柱ABC –A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ,B 1C 1的中点，P 为AM 上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F ．（1）证明:AA 1//MN ,且平面A 1AMN ⊥平面EB 1C 1F ；（2）设O 为△A 1B 1C 1的中心，若AO =AB =6，AO //平面EB 1C 1F ，且∠MPN =π3，求四棱锥B –EB 1C 1F 的体积．【答案】（1）证明见解析；(2）24。

五年2024_2025高考物理真题专题点拨__专题14热学含解析

6
部大气压相同，温度为 450 K，最终降到 300 K，因皮肤凸起，内部气体体积变为罐容积的 20 。 21
若换用抽气拔罐，抽气后罐内剩余气体体积变为抽气拔罐容积的 20 ，罐内气压与火罐降温 21
后的内部气压相同。罐内气体均可视为志向气体，忽视抽气过程中气体温度的变更。求应抽
出气体的质量与抽气前罐内气体质量的比值。
结合 A 选项可知Wab Wbc 0 ，所以 Qbc Qab 。 b c 过程气体汲取的热量大于 a b 过程汲取的热量，B 错误；气体从 c a ，温度降低，所以 Uca 0 ，气体体积减小，外界对气体做功，所以Wca 0 ，依据热力学第肯定律可知 Qca ，放出热量，C 正确；志向气体的内能只与温度有关，依据Ta Tb 可知从 Tca Tbc ，所以气体从 c a 过程中内能的削减量等于 b c 过程中内能的增加量，D 错误。故选 C。
p1 p0 pgh 0 ， p2 p0 pgh
V1 S 2H l h0 ，V2 SH
联立以上式子并代入题给数据得 h=12.9cm；（ii）密封气体再经等压膨胀过程体积变为 V3，温度变为 T2，由盖一吕萨克定律有
V2 V3 T1 T2
按题设条件有V3 S(2H h) ，代入题给数据得 T2=363K。
则
pV
1 2
p 2V
( p1
p2 ) 3V
则甲乙中气体最终压强
p'
p1
p2
2 3
p
（ii）若调配后将甲气体再等温压缩到气体原来的压强为 p，则 p 'V pV ' ，计算可
得V ' 2V 3
由密度定律可得，质量之比等于 m现 V ' 2 m原 V 3

五年真题新高考1卷古代诗歌阅读-

莫谩拘牵雨花社③，青云依旧是前途。
【注】①江州白司马。雨花社：指佛教讲经的集会。
3．下列对这首诗的理解和赏析，不正确的一项是（）
A．根据内容分析，这首诗的写作时间应该与白居易的《琵琶行》比较接近。
B．第三句使用“一衣带水”的典故，表现出朋友之间“天涯若比邻”之意。
D．词人以议论入词，能够做到情由境出，情至论随，全词并无生硬之感。
2．词人在下阕发表议论，指出如果懂得做人的道理，每天都是人日。词中谈到哪些做人的道理？请结合内容简要分析。
2021
阅读下面这首唐诗，完成下面小题。
寄江州白司马①
杨巨源
江州司马平安否？惠远东林住得无②？
湓浦曾闻似衣带，庐峰见说胜香炉。
题诗岁晏离鸿断，望阙天遥病鹤孤。
【解析】1．本题考查学生对诗歌的综合理解和赏析能力。
A.“因年老体弱，感到此行会比较困难”错。此句意思是处处是春色，人们还要到南山去寻觅。“苦”，形容执著地追求，表达出了人们这种寻觅春色的执着。不是说词人年老体弱，感到此行会比较困难。
故选A。
2．本题考查学生评价诗歌思想内容的能力。
词的末三句“须知此意无今昔，会得为人，日日是人日”，是作者就此情此境所引发的感想，是此词的哲理所在，也正是作者的希望。
把君诗过日①，念此别惊神。
地阔峨眉晚，天高岘首春②。
为于耆旧内③，试觅姓庞人④。
[注]①把：握，执。②岘首山，在襄阳。③耆旧：年高望重的人。④姓庞人：指庞德公，汉末襄阳高士。
5．下列对这首诗的理解和赏析，不正确的一项是（）
A．诗的首联简单交代了兵荒马乱的时代背景和诗人年老多病的艰难境况。
B．虽然日后仍有朋友的诗篇陪伴，但面对离别，诗人还是感到心惊神伤。
C．诗人请郑炼在襄阳寻访庞德公那样的高士，表达了对先贤的仰慕之意。

现代文阅读Ⅰ专题练习一--2020-2024五年高考语文真题分类汇编(参考答案)

现代文阅读Ⅰ专题练习一（五年高考真题）参考答案与解析目录现代文阅读Ⅰ专题练习一（高考真题） (1)参考答案与解析 (1)一、2024全国甲卷（论述类文本） (2)二、2024全国甲卷（实用类文本） (3)三、2024新课标Ⅰ卷（信息类文本） (4)四、2024新课标Ⅱ卷（信息类文本） (6)五、2023全国甲卷（论述类文本） (9)六、2023全国甲卷（实用类文本） (9)七、2023全国乙卷（论述类文本） (11)八、2023全国乙卷（实用类文本） (12)九、2023新高考Ⅰ卷（信息类文本） (13)十、2023新高考Ⅱ卷（信息类文本） (14)十一、2022全国甲卷（论述类文本） (16)十二、2022全国甲卷（实用类文本） (17)十三、2022全国乙卷（论述类文本） (18)十四、2022全国乙卷（实用类文本） (19)十五、2022新高考Ⅰ卷（信息类文本） (19)十六、2022新高考Ⅱ卷（信息类文本） (21)十七、2021全国甲卷（论述类文本） (22)十八、2021全国甲卷（实用类文本） (23)十九、2021全国乙卷（论述类文本） (24)二十、2021全国乙卷（实用类文本） (25)二十一、2021新高考Ⅰ卷（信息类文本） (26)二十二、2021新高考Ⅱ卷（信息类文本） (28)二十三、2020全国Ⅰ卷（论述类文本） (30)二十四、2020全国Ⅰ卷（实用类文本） (31)二十五、2020全国Ⅱ卷（论述类文本） (32)二十六、2020全国Ⅱ卷（实用类文本） (33)二十七、2020全国Ⅲ卷（论述类文本） (35)二十八、2020全国Ⅲ卷（实用类文本） (35)二十九、2020新课标Ⅰ卷（信息类文本） (37)三十、2020新课标Ⅱ卷（信息类文本） (38)一、2024全国甲卷（论述类文本）(一)论述类文本阅读(本题共3小题，9分)1.(3分)C2.(3分)D3.(3分)B【解析】【1题详解】本题考查学生对原文内容的理解和分析能力。

通用版五年高考2024_2025高考数学真题专题归纳专题06三角函数及解三角形含解析理

1 1
tan tan
2 2
1 1
22 22
3， 5
tan( ) tan 1 2 1 1 ， 4 1 tan 1 2 3
11.（2024·江苏卷）已知 sin2 ( ) = 2 ，则 sin 2 的值是____.
4
3
【答案】 1 3
【解析】 sin2 ( ) ( 2 cos 2 sin )2 1 (1 sin 2 )
图1
9
图2
图3
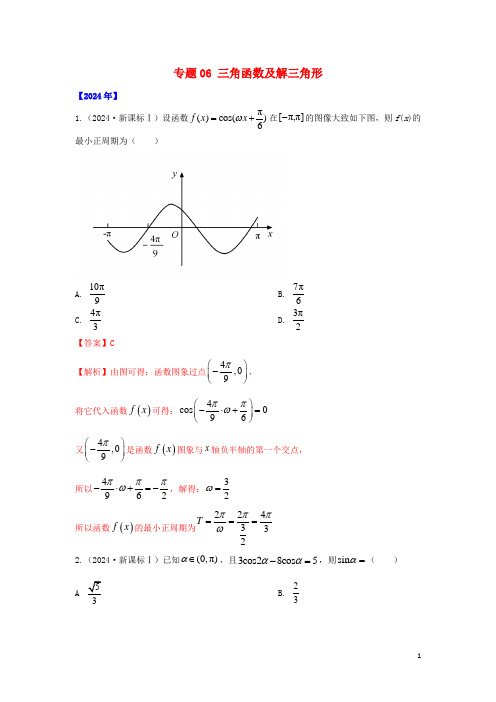
4．【2024·全国Ⅱ卷】已知 α∈(0， )，2sin2α=cos2α+1，则 sinα= 2
A． 1 5
B． 5 5
C． 3 3
【答案】B
D． 2 5 5
【解析】
2sin 2α cos 2α 1，4sin α cos α 2 cos2 α .
α
0,
2
,
cos
α
0
，
sin α 0, 2sin α cos α ，又 sin2 cos2 1，5sin2 α 1,sin2 α 1 ，又 5
f
x
可得：
cos
4 9
6
0
.又
4 9
,
0
是函数
f
x 图象与
x
轴负半轴的第一个交点，
所以 4 ，解得： 3
9
62
2
所以函数
f
x 的最小正周期为T
2
2 3
4 3
2
2.（2024·新课标Ⅰ）已知 (0, π) ，且 3cos2 8cos 5 ，则 sin （
A5 3
B. 2 3
7.（2024·山东卷）下图是函数 y= sin(ωx+φ)的部分图像，则 sin(ωx+φ)= （）

四川省近五年高考历史真题及答案解析

四川省近五年高考历史真题及答案解析2007年:整顿吏治是制度文明建设的重要内容。

回答12—1412．加强对官吏的检察是实现吏治清明的重要措施。

历史上，下列机构或官职具有监察职的是①御史大夫②通判③御史台④军机处A ①②③ B①②④C ①③④D ②③④13．出身“布衣”，重视经济立法并严惩贪污贿赂的古代皇帝是A 隋文帝 B唐玄宗C 明太祖 D乾隆帝14．新中国成立之初。

中国共产党就很重视严惩干部队伍中饿腐化堕落分子。

图4反映的运动的作用不包括A 教育了广大干部和群众 B抵制了资产阶级的腐蚀C 肃清了反革命残余势力D 纠正了官僚主义作风“天下最大事，莫非万民之优乐。

”民生问题是关系社会稳定与发展的基石。

回答15---18题15．宋元时期，话本.杂剧的出现丰富了人们的精神生活。

其流行主要是适应了下列哪一社会阶层的需要A 官僚B 市民C 皇族 D农民16. 在近代中国，系统的出现阐释了民生思想并把它作为纲领的政治派别是A地主阶级洋务派B资产阶级维新派C资产阶级立宪派D资产阶级革命派17．图5所示票证曾百姓购买生活物资的凭证，但现在已经失去了它原本的作用。

这一变化的主要原因不包括A 经济体制改革深化B 农业产量稳步增加C 生活物资日益丰富 D粮棉物资统一管理18．“大萧条”时期，主要资本主义工业国采取了一系列增加就业的措施。

其中美国实行的主要措施是A 兴办公共工程 B发展军事工业 C整农业生产 D加紧殖民掠夺19．小说（最后一课）中，韩麦尔先生对他的学生说：“孩子们。

………柏林来了命令，阿尔萨斯和洛林两省的学校只准教德语……..今天是你们的最后一堂法语课了，”与这一情景密切相关的历史事件是A．普奥战争 B.第一次世界大战 C普法战争 D.第二次世界大战20．下列有关德国影响欧洲局势的表述，符合历史实际的是A.“一战”中德国的盟国包括奥匈帝国，罗马尼亚和保加利亚B.德国在希特勒成为元首后退出可国际联盟C.通过慕尼黑协定德国割占了捷克斯洛伐克D.莫斯科战役后德军在欧洲战场已无力全面进攻21. 图6反映的历史事件对当时德国人意味着A. 欧洲将从此出现和平局面B. 德意志民族即将再度统一C. 东西德经济差距将会迅速缩小D. 影像德国分裂的苏联即将解题22. “好男儿当兵上前线，抗日队伍出四川。

五年2024_2025高考物理真题专题点拨__专题05万有引力定律与航天含解析

专题05 万有引力定律与航天【2024年】1.（2024·新课标Ⅰ）火星的质量约为地球质量的110，半径约为地球半径的12，则同一物体在火星表面与在地球表面受到的引力的比值约为（）A. 0.2B. 0.4C. 2.0D. 2.5【答案】B【解析】设物体质量为m ，则在火星表面有1121M mF GR 在地球表面有2222M mF GR 由题意知有12110M M 1212R R = 故联立以上公式可得21122221140.4101F M R F M R ==⨯=，故选B 。

2.（2024·新课标Ⅱ）若一匀称球形星体的密度为ρ，引力常量为G ，则在该星体表面旁边沿圆轨道绕其运动的卫星的周期是（）D.【答案】A【解析】卫星在星体表面旁边绕其做圆周运动，则2224GMm m R R T， 343V R π= ，M Vρ=知卫星该星体表面旁边沿圆轨道绕其运动的卫星的周期T =3.（2024·新课标Ⅲ）“嫦娥四号”探测器于2024年1月在月球背面胜利着陆，着陆前曾绕月球飞行，某段时间可认为绕月做匀速圆周运动，圆周半径为月球半径的K 倍。

已知地球半径R 是月球半径的P 倍，地球质量是月球质量的Q 倍，地球表面重力加速度大小为g 。

则“嫦娥四号”绕月球做圆周运动的速率为（）A.RKgQPB.RPKgQC.RQgKPD.RPgQK【答案】D【解析】假设在地球表面和月球表面上分别放置质量为m 和m 0的两个物体，则在地球和月球表面处，分别有2Mm Gmg R =，002M m QG m g R P '=⎛⎫⎪⎝⎭解得2P g g Q'= 设嫦娥四号卫星的质量为m 1，依据万有引力供应向心力得1212Mm v QG m R R KK P P =⎛⎫ ⎪⎝⎭解得RPgv QK=，故选D 。

4.（2024·浙江卷）火星探测任务“天问一号”的标识如图所示。

2025届高考专项复习阅读理解应用文五年真题专练(新高考专用) 导学案(原卷版+解析版)

五年2020-2024年高考英语真题阅读理解应用文分类汇编(新高考专用)主题语境考点分布人与自我2022新课标I卷—文科概论课程评分;；2021新课标II 卷—约克郡暑期活动项目；2020新课标卷—诗歌大赛征稿启事；人与社会2024浙江1月卷—名作改编为音乐剧; 2023新课标I卷—广告宣传类(自行车租赁与旅行) 2022新课标II卷—儿童博物馆团体游; 2021新课标I卷—罗马旅游低价旅馆;人与自然2024新课标I卷—栖息地恢复团队招募；2024新课标II 卷—卡洛秋季徒步节2023新课标II卷—广告宣传类(黄石公园护林员项目) 2023浙江1月卷—探险家营地；一、命题取向应用文体裁包括：广告(分商业广告和公益广告)、启事、书影评、传单海报、说明书和备忘录。

其中，广告、启事和书影评出现频率最高。

考查题型除细节题外，主要有：“purpose” 类、“main idea/mainly about ”类、“title”类。

“purpose” 类题目的四个选项常使用“不定式to do” 结构。

“main idea/mainly about ”类题目的选项涉及到短语(名词短语、动名词短语)和句子(陈述句、疑问句)两大类别。

“title”类题目的选项除了包括短语和句子外，还涉及“名词：短语”结构以及混合型(短语、句子、“名词：短语”混合),混合型选项大多是两两对称。

二、技巧点拨1、答案常均匀分布。

每个小标题下面的内容会出一道题，一般不可能就一个小标题的内容连出2至3题。

2、题文不一定同序。

题号在前的题目答案不一定就在前面。

3、选项和文中句子一模一样可以选。

4、主旨题的解法要从各个小标题入手。

一.人与自我1. 2022新课标I卷—文科概论课程评分Grading Policies for Introduction to LiteratureGrading Scale90-100, A; 80-89, B; 70-79, C; 60-69, D; Below 60, E.Essays (60%)Your four major essays will combine to form the main part of the grade for this course: Essay 1 = 10%; Essay 2 = 15%; Essay 3 = 15%; Essay 4 = 20%.Group Assignments (30%)Students will work in groups to complete four assignments(作业) during the course. All the assignments will be submitted by the assigned date through Blackboard our online learning and course management system.Daily Work/In-Class Writings and Tests/Group Work/Homework (10%)Class activities will vary from day to day, but students must be ready to complete short in-class writings or tests drawn directlyfrom assigned readings or notes from the previous class'lecture/discussion, so it is important to take careful notes during class. Additionally, from time to time I will assign group work to be completed in class or short assignments to be completed at home, both of which will be graded.Late WorkAn essay not submitted in class on the due date will lose a letter grade for each class period it is late. If it is not turned in by the 4th day after the due date, it will earn a zero. Daily assignments not completed during class will get a zero. Short writings missed as a result of an excused absence will be accepted.21. Where is this text probably taken fromA. A textbook.B. An exam paper.C. A course plan.D. An academic article.22. How many parts is a student’s final grade made up ofA. Two.B. Three.C. Four.D. Five.23. What will happen if you submit an essay one week after the due dateA. You will receive a zero.B. You will lose a letter grade.C. You will be given a test.D. You will have to rewrite it.2. 2021新课标II卷—约克郡暑期活动项目Things to Do in Yorkshire This SummerHarrogate Music FestivalSince its birth, Harrogate Music Festival has gone from strength to strength. This year, we are celebrating our 50th anniversary. We begin on 1st June with Manchester Camerata and Nicola Benedetti, presenting an amazing programme of Mozart pieces.Dates:1 June-31 JulyTickets: 12- 96Jodie's Fitness Summer ClassesAs the summer months roll in, our Georgian country estate makes the perfect setting for an outdoor fitness session. Come and work out with our qualified personal trainer, Jodie McGregor, on the grounds of the Middleton Lodge estate.We will be holding a free taster session on 23rd May, at 10 am, to demonstrate the variety of effective and active exercises. There are eight spaces available for the taster session. Advance bookings are required(**********************.uk.paris)Dates:23 May-11 JulyTickets: 7.50 per sessionFelt Picture MakingWorking from an inspirational picture, this workshop at Helmsley Arts Centre will teach you the techniques you will need to recreate your picture in wool.We will also discuss the origins of felt what enables wool fibres to become felt and how the processes we use work.Dates: 12 June-12 JulyTickets: 40 including materialsFigure It Out!-Playing with MathA new exhibition in Halifax uses everyday activities to explain the hidden math principles we all use on a regular basis. Pack a bag, cut a cake, guess which juice container holds the most liquid, and much more. Discover how architects, product designers and scientists use similar skills in their work.Dates:7 May-10 JuneTickets: Free21. What should you do if you want to attend the taster session of Jodie's fitness classesA. Join a fitness club.B. Pay a registration fee.C. Make a booking.D. Hire a personal trainer.22. How much is the ticket for Felt Picture MakingA. 7.50.B. 12.C. 40.D. 96.23. Which of the following starts earliestA. Harrogate Music Festival.B. Jodie's Fitness Summer Classes.C. Felt Picture Making.D. Figure It Out!-Playing with Math.3. 2020新课标卷—诗歌大赛征稿启事POETRY CHALLENGEWrite a poem about how courage, determination, and strength have helped you face challenges in your life.Prizes3 Grand Prizes:Trip to Washington, D.C. for each of three winners, a parent and one other person of the winner’s choice. Trip includes round-trip air tickets, hotel stay for two nights, and tours of the National Air and Space Museum and the office of National Geographic World.6 First Prizes:The book Sky Pioneer:A Photobiography of Amelia Earhart signed by author Corinne Szabo and pilot Linda Finch.50 Honorable Mentions:Judges will choose up to 50 honorable mention winners, who will each receive a T-shirt in memory of Earhart’s final flight.RulesFollow all rules carefully to prevent disqualification.■Write a poem using 100 words or fewer. Yo ur poem can be any format, any number of lines.■Write by hand or type on a single sheet of paper. You may use both the front and back of the paper.■On the same sheet of paper, write or type your name, address, telephone number, and birth date.■Mail your entry to us by October 31 this year.21. How many people can each grand prize winner take on the free tripA. Two.B. Three.C. Four.D. Six.22. What will each of the honorable mention winners getA. A plane ticket.B. A book by Corinne Szabo.C. A special T-shirt.D. A photo of Amelia Earhart.23. Which of the following will result in disqualificationA. Typing your poem out.B. Writing a poem of 120 words.C. Using both sides of the paper.D. Mailing your entry on October 30.二.人与社会4. 2024浙江1月卷—名作改编为音乐剧Tom Sawyer Play Is an AdventureA 35-minute hand-clapping, foot-stomping musical version of a Mark Twain favorite returns with this Tall Stacks festival.“Tom Sawyer: A River Adventure” has all the good stuff, including the fence painting, the graveyard, the island and the cave. It is adapted by Joe McDonough, with music by David Kisor. That’s thelocal stage writing team that creates many of the Children’s Theatre of Cincinnati’s original musicals, along with the holiday family musicals at Ensemble Theatre.This year Nathan Turner of Burlington is Tom Sawyer, and Robbie McMath of Fort Mitchell is Huck Finn.Tumer, a 10th-grader at School for Creative and Performing Arts, is a familiar presence on Cincinnati’s stages. He is a star act or of Children’s Theatre, having played leading roles in “The Legend of Sleepy Hollow” and “The Wizard of Oz,” and is fresh from Jersey Production “Ragtime”.McMath is a junior at Beechwood High School. He was in the cast of “Tom Sewyer” when it was first performed and is a Children’s Theatre regular, with five shows to his credit. This summer he attended Kentucky’s Governor’s School for the Arts in Musical Theatre.Note to teachers: Children’s Theatre has a study guide demonstrating how math and science can be taught through “Tom Sawyer.” For downloadable lessons, visit the official website of Children’s Theatre.21. Who wrote the music for “Tom Sawyer: A River Adventure”A. David Kisor.B. Joe McDonough.C. Nathan Turner.D. Robbie McMath.22. What can we learn about the two actorsA. They study in the same school.B. They worked together in “Ragtime”.C. They are experienced on stage.D. They became friends ten years ago.23. What does Children’s Theatre provide for teachersA. Research funding.B. Training opportunities.C. Technical support.D. Educational resources.5. 2023新课标I卷—自行车租赁与旅行Bike Rental & Guided ToursWelcome to Amsterdam, welcome to MacBike. You see much more from the seat of a bike! Cycling is the most economical, sustainable and fun way to explore the city, with its beautiful canals, parks, squares and countless lights. You can also bike along lovely landscapes outside of Amsterdam.Why MacBikeMacBike has been around for almost 30 years and is the biggest bicycle rental company in Amsterdam. With over 2,500 bikes stored in our five rental shops at strategic locations, we make sure there is always a bike available for you. We offer the newest bicycles in a wide variety, including basic bikes with foot brake(刹车), bikes with hand brake and gears(排挡), bikes with c hild seats, and children’sbikes.PricesHand Brake, Three Gears Foot Brake, No Gears1 hour ?7.50 ?5.003 hours ?11.00 ?7.501 day (24 hours) ?14.75 ?9.75Each additional day ?8.00 ?6.00Guided City ToursThe 2.5-hour tour covers the Gooyer Windmill, the Skinny Bridge, the Rijksmuseum, Heineken Brewery and much more. The tour departs from Dam Square every hour on the hour, starting at 1:00 pm every day. You can buy your ticket in a MacBike shop or book online.1. What is an advantage of MacBikeA. It gives children a discount.B. It of offers many types of bikes.C. It organizes free cycle tours.D. It has over 2,500 rental shops.2. How much do you pay for renting a bike with hand brake and three gears for two daysA. ?15.75.B. ?19.50.C. ?22.75.D. ?29.50.3. Where does the guided city tour startA. The Gooyer, Windmill.B. The Skinny Bridge.C. Heineken Brewery.D. Dam Square.6.2022新课标II卷—儿童博物馆团体游Children’s Discovery MuseumGeneral Information about Group PlayPricingGroup Play $7/personScholarshipsWe offer scholarships to low-income schools and youth organizations, subject to availability. Participation in a post-visit survey is required.Scholarships are for Group Play admission fees and/or transportation. Transportation invoices (发票) must be received within 60 days of your visit to guarantee the scholarship.Group SizeWe require one chaperone(监护人) per ten children. Failure to provide enough chaperones will result in an extra charge of $50 per absent adult.Group Play is for groups of 10 or more with a limit of 35 people. For groups of 35 or more, please call to discuss options.HoursThe Museum is open daily from 9:30 am to 4:30 pm.Group Play may be scheduled during any day or time the Museum is open.Registration PolicyRegistration must be made at least two weeks in advance. Register online or fill out a Group Play Registration Form with multiple dates and start time options.Once the registration form is received and processed, we will send a confirmation email within two business days.Guidelines●Teachers and chaperones should model good behavior for the group and remain with students at all times.●Children are not allowed unaccompanied in all areas of the Museum.●Children should play nicely with each other and exhibits.●Use your indoor voic e when at the Museum.21. What does a group need to do if they are offered a scholarshipA. Prepay the admission fees.e the Museum’s transportation.C. Take a survey after the visit.D.Schedule their visit on weekdays.22. How many chaperones are needed for a group of 30 children to visit the MuseumA. One.B. Two.C. Three.D. Four.23. What are children prohibited from doing at the MuseumA. Using the computer.B. Talking with each other.C. Touching the exhibits.D. Exploring the place alone.7.2021新课标I卷—罗马旅游低价旅馆Rome can be pricey for travelers, which is why many choose to stay in a hostel(旅社). The hostels in Rome offer a bed in a dorm room for around $25 a night, and for that, you’ll often get to stay in a central location(位置) with security and comfort.Yellow HostelIf I had to make just one recommendation for where to stay in Rome, it would be Yellow Hostel. It’s one of the best-rated hostels in the city, and for good reason. It’s affordable, and it’s got a fun atmosphere without being too noisy. As an added bonus, it’s close to the main train station.Hostel Alessandro PalaceIf you love social hostels, this is the best hostel for you in Rome. Hostel Alessandro Palace is fun. Staff members hold plenty of bar events for guests like free shots, bar crawls and karaoke. There’s also an area on the rooftop for hanging out with other travelers during the summer.Youth Station HostelIf you’re looking for cleanliness and a modern hostel, look no further than Youth Station. It offers beautiful furnishings and beds. There are plenty of other benefits, too; it doesn’t charge city tax; it has both air conditioning and a heater for the rooms; it also hasfree Wi-Fi in every room.Hotel and Hostel Des ArtistesHotel and Hostel Des Artistes is located just a 10-minute walk from the central city station and it's close to all of the city's main attractions. The staff is friendly and helpful, providing you with a map of the city when you arrive, and offering advice if you require some. However, you need to pay 2 euros a day for Wi-Fi.21. What is probably the major concern of travelers who choose to stay in a hostelA. Comfort.B. Security.C. Price.D. Location.22. Which hotel best suits people who enjoy an active social lifeA. Yellow Hostel.B. Hostel Alessandro Palace.C. Youth Station Hostel.D. Hotel and Hostel Des Artistes.23. What is the disadvantage of Hotel and Hostel Des ArtistesA. It gets noisy at night.B. Its staff is too talkative.C. It charges for Wi-Fi.D. It’s inconveniently located.三.人与自然8.2024新课标I卷—栖息地恢复团队招募HABITAT RESTORATION TEAMHelp restore and protect Marin’s natural areas from the Marin Headlands to Bolinas Ridge. We’ll explore beautiful park sites while conducting invasive(侵入的) plant removal, winter planting, and seed collection. Habitat Restoration Team volunteers play a vital role in restoring sensitive resources and protecting endangered species across the ridges and valleys.GROUPSGroups of five or more require special arrangements and must be confirmed in advance. Please review the List of Available Projects and fill out the Group Project Request Form.AGE, SKILLS, WHAT TO BRINGVolunteers aged 10 and over are welcome. Read our Youth Policy Guidelines for youth under the age of 15.Bring your completed Volunteer Agreement Form. Volunteers under the age of 18 must have the parent/guardian approval section signed.We’ll be working rain or shine. Wear clothes that can get dirty. Bring layers for changing weather and a raincoat if necessary. Bring a personal water bottle, sunscreen, and lunch.No experience necessary. Training and tools will be provided. Fulfills(满足) community service requirements.UPCOMING EVENTSTime Meeting LocationSunday, Jan. 15 10:00am-1:00pm Battery Alexander Trailhead Sunday, Jan. 22 10:00am-2:30pm Stinson Beach Parking Lot Sunday, Jan. 29 9:30am-2:30pm Coyote Ridge Trailhead21. What is the aim of the Habitat Restoration TeamA. To discover mineral resources.B. To develop new wildlife parks.C. To protect the local ecosystem.D. To conduct biological research.22. What is the lower age limit for joining the Habitat Restoration TeamA. 5.B. 10.C. 15.D. 18.23. What are the volunteers expected to doA. Bring their own tools.B. Work even in bad weather.C. Wear a team uniform.D. Do at least three projects.9. 2024新课标II卷—卡洛秋季徒步节Choice of Walks for Beginner and Experienced WalkersThe Carlow Autumn Walking Festival is a great opportunity for the beginner, experienced or advanced walker to enjoy the challenges of Carlow’s mountain hikes or the peace of its woodlan d walks. Walk 1 — The Natural WorldWith environmentalist anna Lamhna as the guide, this walkpromises to be an informative tour. Walkers are sure to learn lots about the habitats and natural world of the Blackstairs.Date and Time: Saturday, 1st October, at 09:00Start Point: Scratoes BridgeWalk Duration: 6 hoursWalk 2 — Introduction to HillwalkingEmmanuel Chappard, an experienced guide, has a passion for making the great outdoors accessible to all. This mountain walk provides an insight into the skills required for hillwalking to ensure you get the most from future walking trips.Date and Time: Sunday, 2nd October, at 09:00Start Point: Deerpark Car ParkWalk Duration: 5 hoursWalk 3 — Moonlight Under the StarsWalking at night-time is a great way to step out of your comfort zone. Breathtaking views of the lowlands of Carlow can be enjoyed in the presence of welcoming guides from local walking clubs. A torch(手电筒) along with suitable clothing is essential for walking in the dark. Those who are dressed inappropriately will be refused permission to participate.Date and Time: Saturday, 1st October, at 18:30Start Point: The Town HallWalk Duration: 3 hoursWalk 4 — Photographic Walk in Kilbrannish ForestThis informative walk led by Richard Smyth introduces you to the basic principles of photography in the wild. Bring along your camera and enjoy the wonderful views along this well-surfaced forest path.Date and Time: Sunday, 2nd October, at 11:45Start Point: Kilbrannish Forest Recreation AreaWalk Duration: 1.5 hours21. Which walk takes the shortest timeA. The Natural World.B. Introduction to Hillwalking.C. Moonlight Under the Stars.D. Photographic Walk in Kilbrannish Forest.22. What are participants in Walk 3 required to doA. Wear proper clothes.B. Join a walking club.C. Get special permits.D. Bring a survival guide.23. What do the four walks have in commonA. They involve difficult climbing.B. They are for experienced walkers.C. They share the same start point.D. They are scheduled for the weekend.10. 2023新课标II卷—黄石公园护林员项目Yellowstone National Park offers a variety of ranger programs throughout the park, and throughout the year. The following are descriptions of the ranger programs this summer. Experiencing Wildlife in Yellowstone (May 26 to September 2) Whether you’re hiking a backcountry trail(小径), camping, or just enjoying the park’s amazing wildlife from the road, this quick workshop is for you and your family. Learn where to look for animals and how to safely enjoy your wildlife watching experience. Meet at the Canyon Village Store.Junior Ranger Wildlife Olympics (June 5 to August 21)Kids can test their skills and compare their abilities to the animals of Yellowstone. Stay for as little or as long as your plans allow. Meet in front of the Visitor Education Center.Canyon Talks at Artist Point (June 9 to September 2)From a classic viewpoint, enjoy Lower Falls, the Yellowstone River, and the breathtaking colors of the canyon(峡谷) while learning about the area’s natural and human history. Disco ver why artists and photographers continue to be drawn to this special place. Meet on the lower platform at Artist Point on the South Rim Drive for this short talk.Photography Workshops (June 19 &July 10)Enhance your photography skills — join Yellowstone’s parkphotographer for a hands-on program to inspire new and creative ways of enjoying the beauty and wonder of Yellowstone.6/19 — Waterfalls &Wide Angles: meet at Artist Point.7/10 — Wildflowers &White Balance: meet at Washburn Trailhead in Chittenden parking area.1. Which of the four programs begins the earliestA. Photography Workshops.B. Junior Ranger Wildlife Olympics.C. Canyon Talks at Artist Point.D. Experiencing Wildlife in Yellowstone.2. What is the short talk at Artist Point aboutA. Works of famous artists.B. Protection of wild animals.C. Basic photography skills.D. History of the canyon area.3. Where will the participants meet for the July 10 photography workshopA. Artist Point.B. Washburn Trailhead.C. Canyon Village Store.D. Visitor Education Center.11. 2023浙江1月卷—探险家营地Explorers CampFull day camp for kids aged 5-13.Monday-Friday, July 8-26, 9am-4pm.Week 1 | July 8-12Week 2 | July 15-19Week 3 | July 22-26Register for a single week or multiple weeks.Fees: $365 per week.The last day to cancel registration and receive a full refund(退款) is June 15.Camp StructureThe day is divided into two thematic sessions per age group. Campers have a three-hour morning class engaging with a morning theme (9am to 12 noon) and a one-hour lunch break, followed by another three-hour class engaging with an afternoon theme (1pm to 4pm). Snack periods are held throughout the day. All campers should bring their own bagged lunch and snacks. Camp ContentExplorers Camp organizes engaging arts, history andscience-related activities in every! class, and focuses on a range of topics that emphasize active learning, exploration and, most of all, fun! All camp sessions are created with age-appropriate activities that are tailored to the multiple ways that kids learn.Camp StaffCampers enjoy a staff-to-child ratio ranging from 1:4 to 1:7 depending on the age group. Instructors are passionate educators who are experts in their fields and have undergone training and abackground check.21. On which of the following dates can you cancel your registration with a full refundA. June 12.B. June 22.C. July 19.D. July 26.22. How are campers divided into different groupsA. By gender.B. By nationality.C. By interest.D. By age.23. How many hours of class will you have altogether if you register for a single weekA. 15.B. 21.C. 30.D. 42.五年2020-2024年高考英语真题阅读理解应用文分类汇编(新高考专用)解析版主题语境考点分布人与自我2022新课标I卷—文科概论课程评分;；2021新课标II 卷—约克郡暑期活动项目；2020新课标卷—诗歌大赛征稿启事；人与社会2024浙江1月卷—名作改编为音乐剧; 2023新课标I卷—广告宣传类(自行车租赁与旅行) 2022新课标II卷—儿童博物馆团体游; 2021新课标I卷—罗马旅游低价旅馆;人与自然2024新课标I卷—栖息地恢复团队招募；2024新课标II 卷—卡洛秋季徒步节2023新课标II卷—广告宣传类(黄石公园护林员项目) 2023浙江1月卷—探险家营地；一、命题趋向应用文体裁包括：广告(分商业广告和公益广告)、启事、书影评、传单海报、说明书和备忘录。