AES算法加解密原理及安全性分析(DOC)
aes加解密算法原理

aes加解密算法原理
AES(Advanced Encryption Standard)是一种对称加密算法,用于数据的加密和解密。
它是美国国家标准与技术研究所(NIST)于2001年发布,并取代了之前的DES(Data Encryption Standard)标准。
AES加解密算法的原理基于分组密码的思想。
它将明文数据按照固定长度的数据块进行分组,并通过多次迭代对每个数据块进行处理。
AES算法规定了三种密钥长度:128位、192位和256位。
在AES加密中,明文数据被分为多个数据块,每个数据块的长度为128位。
这些数据块通过一系列的轮轮函数进行处理,每轮都包括四个步骤:SubBytes(字节替代)、ShiftRows(行移位)、MixColumns(列混淆)和AddRoundKey(轮密钥加)。
这些步骤的组合使得数据块中的每个字节都得到了处理和混淆,从而增强了加密的强度和安全性。
在AES解密中,与加密相反,解密需要对每个数据块进行逆向操作。
这意味着,在每个步骤中应用的操作需要逆向处理,以实现数据的恢复。
解密过程中使用相同的密钥,并按照相反的顺序进行处理,最后可得到明文数据。
AES算法的安全性在于其密钥长度和迭代次数。
由于其更长的密钥长度和复杂的轮函数,它比之前的DES算法更加安全可靠。
当前广泛使用的AES-256算法具有256位的密钥长度,在实际应用中提供了高强度的加密保护。
总结来说,AES加解密算法是一种安全可靠的对称加密算法,广泛应用于数据保护和信息安全领域。
它的原理基于分组密码思想,通过一系列的步骤和操作对数据块进行处理,提供高强度的加密保护。
AES加密算法的安全性分析

AES加密算法的安全性分析随着互联网的快速发展,人们对信息安全的需求越来越高。
对于互联网上的数据传输来说,数据的保密性是最基本的要求。
为了实现数据的保密性,加密技术已经成为了必不可少的一部分。
对于加密技术的研究,人们已经取得了很多的成果,其中AES算法的安全性备受关注。
AES加密算法是一种对称密钥加密算法,是目前广泛应用的加密算法之一。
AES算法是由比利时密码学家Joan Daemen和Vincent Rijmen共同设计的,是DES算法的升级版。
AES算法已被美国政府采用为官方标准,安全性得到了全世界的认可。
但是,AES算法是否真的安全呢?1. AES算法的基本原理在了解AES算法的安全性之前,先来看一下AES算法的基本原理。
AES算法的基本构成是四个部分:密钥扩展、字节替换、行移位和列混淆。
下面对这四个部分做一下详细的介绍。
密钥扩展:在AES算法中,密钥的长度可以是128位、192位或256位。
在进行加密操作之前,需要对密钥进行扩展,得到一组扩展密钥。
这组扩展密钥会被用于加密数据,以保证数据的机密性。
字节替换:对于数据块中的每一个字节,使用一个S盒进行替换。
S盒是一个16x16的矩阵,其中每一个元素都是一个8位的值。
字节替换是AES算法中最重要的一个步骤,可以有效地保护加密数据的机密性。
行移位:将数据块中的每一行进行循环移位。
第一行不移动,第二行向左移动一位,第三行向左移动两位,第四行向左移动三位。
这个步骤用于消除行之间的依赖性,增强AES算法的安全性。
列混淆:对于数据块中的每一列,使用一个固定的矩阵对其进行混淆。
这个固定的矩阵称为MixColumns矩阵,用于消除列之间的依赖性,增强AES算法的安全性。
2. AES算法的安全性分析AES算法的安全性主要是通过密钥长度来保证的。
AES算法支持的密钥长度有128位、192位和256位三种。
其中,128位密钥已经被广泛应用,并得到了全球安全专家的认可。
aes实验报告

aes实验报告AES实验报告引言:AES(Advanced Encryption Standard)是一种对称加密算法,被广泛应用于保护敏感数据的安全传输和存储。
本实验旨在探究AES算法的原理和应用,并通过实验验证其加密和解密的效果。
一、AES算法的原理AES算法是一种分组密码算法,将明文分成固定长度的数据块,并通过一系列的加密和解密操作来保护数据的机密性。
AES算法的核心是轮函数,它通过一系列的轮变换来对数据进行加密和解密。
二、实验准备1. 实验环境搭建:在计算机上安装支持AES算法的编程环境,如Python或Java。
2. 实验材料准备:准备一些测试用的明文和密钥,以及相应的加密和解密结果。
三、AES算法的加密过程1. 密钥扩展:AES算法需要对输入的密钥进行扩展,生成一系列的轮密钥。
这些轮密钥用于后续的加密和解密操作。
2. 初始轮:将明文与第一轮密钥进行异或运算。
3. 轮变换:AES算法中的轮变换包括字节代换、行移位、列混淆和轮密钥加。
这些变换操作按照一定的顺序进行,每一轮都会产生一个新的加密结果。
4. 最终轮:在最后一轮中,省略列混淆操作,并将结果与最后一轮密钥进行异或运算。
四、实验步骤1. 选择一组明文和密钥作为输入数据。
2. 使用AES算法对明文进行加密,得到密文。
3. 使用相同的密钥对密文进行解密,得到还原的明文。
4. 比较还原的明文与原始明文是否一致,验证AES算法的正确性。
五、实验结果与分析在实验中,我们选择了一组明文和密钥进行加密和解密操作。
经过实验,我们成功地得到了相应的密文和还原的明文,并与原始明文进行了比较。
结果显示,还原的明文与原始明文完全一致,证明了AES算法的正确性和可靠性。
六、AES算法的应用AES算法在现代密码学中被广泛应用于数据的加密和解密过程。
它可以用于保护敏感数据的安全传输和存储,如网络通信、文件加密和数据库加密等领域。
AES算法具有高度的安全性和可靠性,被认为是目前最强大的对称加密算法之一。
AES算法文档

2009-03-24AES算法的密码分析与快速实现摘要:高级加密标准(AES) 确定分组密码Rijndael为其算法,取代广泛使用了20多年的数据加密标准(DES),该算法将在各行业各部门获得广泛的应用。
文章以DES为参照对象,阐述了Rijndael算法的设计特色,介绍了AES在密码分析方面国内外已有的一些理论分析成果,描述了AES算法采用软件和硬件的快速实现方案。
关键词:高级加密标准;Rijndael算法;密码分析;快速实现Abstract:Rijndael is defined as the algorithm for the advanced encryption standard (AES). With broad applications in various industries, AES has been superseded the data encryption standard (DES) that has a twenty-year application history. This paper describes the design characteristics of Rijndael, in comparison with that of DES. Then, it introduces the latest academic research achievements in AES cryptanalysis at home and abroad. Finally, primary techniques for various fast implementations of AES on hardware and software platforms are introduced.Key words:AES; Rijndael algorithm; cryptanalysis; fast implementation密码学是保障信息安全的核心技术,应用涉及军事、国防、商贸及人们日常生活的各个方面。
aes解密方法

AES解密方法1. 简介AES(Advanced Encryption Standard)是一种对称加密算法,被广泛应用于保护敏感数据的安全性。
它是美国国家标准与技术研究院(NIST)在2001年发布的一种加密标准,取代了DES(Data Encryption Standard)成为新的标准。
AES使用128位、192位或256位密钥,并且对不同长度的数据块进行加密。
AES算法具有高度的安全性和效率,因此在许多领域得到广泛应用,包括网络通信、数据库存储、文件加密等。
本文将详细介绍AES解密方法,包括解密过程、实现方式和常见应用场景。
2. AES解密过程AES解密过程与加密过程相反,它将密文转换为明文。
下面是AES解密过程的步骤:步骤1:初始化首先,需要获取正确的解密密钥。
解密方必须知道与加密方使用相同的秘钥才能成功解密数据。
步骤2:逆行移位操作将输入数据按列进行逆行移位操作。
逆行移位操作是通过循环右移每个字节来实现的。
步骤3:逆字节替换操作对每个字节进行逆字节替换操作。
逆字节替换操作使用S盒(Substitution Box)来完成,将每个字节映射到另一个字节。
步骤4:轮密钥加操作与加密过程类似,解密过程中也需要进行轮密钥加操作。
解密方需要使用与加密方相同的轮密钥来进行异或运算。
步骤5:逆行列混淆操作对数据进行逆行列混淆操作。
逆行列混淆操作是通过矩阵运算来完成的。
步骤6:重复步骤2-5重复步骤2至步骤5,直到所有轮数都完成。
步骤7:最后一轮解密在最后一轮解密中,省略逆行列混淆操作,只执行逆行移位、逆字节替换和轮密钥加操作。
步骤8:输出明文经过多轮解密后,得到明文数据。
3. AES解密实现方式AES解密可以通过各种编程语言和工具来实现。
下面以Python语言为例,介绍一种常用的AES解密实现方式:from Crypto.Cipher import AESdef aes_decrypt(ciphertext, key):cipher = AES.new(key, AES.MODE_ECB)plaintext = cipher.decrypt(ciphertext)return plaintext以上代码使用了Python的Crypto库来实现AES解密。
常用密码算法的原理及安全性分析

常用密码算法的原理及安全性分析一、对称密码算法对称密码算法也称为共享密钥密码算法,是一种使用相同密钥进行加解密的密码算法。
对称密码算法的加密速度较快,但密钥管理复杂,安全性低。
目前,常见的对称密码算法有DES、3DES、AES等。
1. DES算法DES算法是一种基于置换和替换的对称密码算法,其密钥长度为56位,被认为是不安全的密码算法。
该算法最大的安全性问题是密钥长度太短,易被暴力破解攻击。
因此,该算法已经不再被广泛使用。
2. 3DES算法3DES算法是基于DES算法的加密标准,使用了三个56位的DES密钥进行加密,提高了安全性。
由于密钥长度较长,其安全性较高,目前得到了广泛应用。
3. AES算法AES算法是一种对称密码算法,使用128位、192位或者256位的密钥进行加密。
该算法的加密速度较快,安全性高,被广泛应用于网络通信等领域,是一种比较成熟的对称密码算法。
二、公钥密码算法公钥密码算法也称为非对称密码算法,是一种使用不同密钥进行加解密的密码算法。
该算法的安全性较高,但加密速度较慢。
常见的公钥密码算法有RSA、Diffie-Hellman算法等。
1. RSA算法RSA算法是一种基于大数分解的公钥密码算法,其安全性取决于质因数分解的难度。
该算法使用两个不同的密钥进行加解密,其中一个密钥为公钥,另一个为私钥。
RSA算法广泛应用于数字签名、密钥协商等领域。
2. Diffie-Hellman算法Diffie-Hellman算法是一种密钥协商协议,用于双方之间的密钥协商。
该算法的安全性基于离散对数问题,其加密速度较快,被广泛应用于安全通信等领域。
三、哈希算法哈希算法,也称为摘要算法,是一种将任意长度的输入数据通过哈希函数转换为固定长度输出的算法。
常见的哈希算法有MD5、SHA-1、SHA-2等。
1. MD5算法MD5算法是一种常用的哈希算法,可以将任意长度的输入数据转换为128位长度的输出。
该算法是一种不可逆算法,可以用于校验文件内容、密码等信息的完整性。
区块链应用中AES和RSA混合加密算法分析

222信息技术与安全Information Technology And Security电子技术与软件工程Electronic Technology & Software Engineering消纳的问题分析及建议[J].上海电力学院学报,2019,35(06):539-543+572.[7]王淑云,娄素华,吴耀武,曹侃,周鲲鹏.计及火电机组深度调峰成本的大规模风电并网鲁棒优化调度[J].电力系统自动化,2020,44(01):118-125.[8]陈曈,张伟波,周宇昊,杨帆,李富国,王世朋.分布式能源系统常用储能技术综述[J].能源与环保,2019,41(07):138-142.[9]郭良丹.利用热网储热技术提高供热机组调峰能力研究[D].华北电力大学,2019.[10]赵雅楠,康智强.相变储能技术分析及材料应用[J].科技风,2018(23):123.[11]Javier Menéndez,Jesús M. Fernández-Oro,MónicaGaldo,Jorge Loredo. Efficiency analysis of underground pumped storage hydropower plants[J]. Journal of Energy Storage,2020,28.[12]李广阔,陈来军,谢毓广,高博,郑天文,梅生伟.考虑压缩空气储能变工况特性的风储联合系统运行优化策略[J/OL].高电压技术,2020(02):1-8.[13]董舟,李凯,王永生,王宁,朱青.压缩空气储能技术研究及应用现状[J].河北电力技术,2019,38(05):18-20+33.[14]Preston, R., Kandrac, J.. Report on design, testingand commissioning of 100% Stator Ground Fault Protection at Dominion's Bath County Pumped Storage Station[P]. Protective Relay Engineers, 2009 62nd Annual Conference for,2009.[15]张旭,张鹏,陈昕.海水抽水蓄能电站发展及应用[J].水电站机电技术,2019,42(06):66-70.[16]刘宗浩,张华民,高素军,马相坤,刘玉峰.风场配套用全球最大全钒液流电池储能系统[J].储能科学与技术,2014,3(01): 71-77.[17]谢秋实.电池储能参与含风电力系统调峰与优化调度[D].大连理工大学,2018.[18]李媛媛.模块化超导磁储能系统在电力系统的应用研究[D].华中科技大学,2019.[19]DVORKIN Y,FERNANDEZ-BLANCOR, KIRSCHEND S, et al.Ensuring profitability of energy storage[J]. IEEE Transactions on Power Systems, 2017, 32(1): 611-623.[20]曹昉,张粒子.结合系统调峰容量比确定抽水蓄能机组装机容量的方法[J].电力自动化设备,2007,27(06):47-50.[21]李军徽,张嘉辉,穆钢,葛延峰,严干贵,史松杰.储能辅助火电机组深度调峰的分层优化调度[J/OL].电网技术,2019,1-10.[22]赵书强,刘大正,谢宇琪,刘晋,胡永强.基于相关机会目标规划的风光储联合发电系统储能调度策略[J].电力系统自动化,2015,39(14):30-36+53.[23]马晓迪.调峰约束条件下的电网接纳风电能力研究[D].北京交通大学,2014.作者简介靳一奇(1996-)(通讯作者),男,硕士研究生,研究方向为储能参与含有风力发电电力系统调峰优化调度策略。
AES算法加解密原理及安全性分析

AES算法加解密原理及安全性分析AES(Advanced Encryption Standard,高级加密标准)是一种对称加密算法,用于对数据进行加密和解密。
它是最常用的加密算法之一,被广泛应用于各种信息安全相关领域。
1.密钥扩展:对输入的密钥进行扩展,生成多轮的子密钥用于后续的加密和解密操作。
2.初始轮:将明文与第一轮子密钥进行异或运算。
3.多轮加密:AES算法有128位、192位和256位三种密钥长度,这里以128位密钥为例。
将16字节的明文分为4x4的字节矩阵(称为状态矩阵),与当前轮子密钥进行一系列变换,包括字节替代、行移位、列混淆和轮密钥加等。
这些变换使得密文显示复杂性,增加了破解难度。
4.最后一轮:最后一轮加密与之前的多轮加密略有不同,没有列混淆操作。
5.密文生成:最后一个状态矩阵与最后一轮的子密钥进行异或运算,得到最终的密文。
解密操作与加密操作相似,只是密钥的使用顺序相反,即先使用最后一轮子密钥进行解密,然后逆向进行多轮解密,最后使用第一轮子密钥进行解密,得到原始的明文。
1.密钥长度:AES算法支持三种密钥长度,对于相同的明文和密文,密钥长度越长,破解难度越大。
目前来说,128位密钥足够安全,128位以上的密钥更加安全。
2.穷举攻击:穷举攻击是一种尝试所有可能的密钥组合来破解加密算法的方法。
对于AES算法,由于密钥长度较长,穷举攻击需要耗费巨大的计算资源和时间,对抗穷举攻击具备较高的安全性。
3.差分密码分析:差分密码分析是一种基于统计模型的攻击方法,通过观察明文、密文和密钥对之间的差异性,推断密码的相关信息。
AES算法在设计时考虑了差分密码分析的攻击方法,实现了一系列抵御差分密码分析的特性,提高了算法的安全性。
4.线性密码分析:线性密码分析是一种基于统计特性的攻击方法,通过线性逼近密钥和明文之间的关系,来逐渐推断出密钥。
AES算法在设计时也考虑了线性密码分析的攻击方法,加入了一系列防护机制,提高了算法的安全性。
密码加密算法安全性检测说明

密码加密算法安全性检测说明密码加密算法是保护信息安全的重要手段之一,其安全性直接影响到用户数据的保密性和完整性。
因此,对于密码加密算法的安全性进行检测十分重要。
本文将从密码加密算法的基本原理,安全性评估指标、常见的安全性攻击手段、常用的安全性评估方法等方面进行说明和分析,以提供一定的参考。
一、基本原理密码加密算法是通过将明文转换为密文,通过密码(加密密钥)将密文转换为明文,从而保证信息的安全性。
常见的加密算法包括对称加密算法和非对称加密算法。
对称加密算法使用相同的密钥进行加解密,如DES、AES等。
非对称加密算法使用一对相关的密钥进行加解密,如RSA、ECC等。
二、安全性评估指标对密码加密算法进行安全性评估时,需要考虑以下几个主要指标:1. 密钥空间大小:密钥空间大小越大,破解难度越大。
2. 密文的随机性:密文应该具有很高的随机性,使得攻击者无法根据密文猜测出明文。
3. 抗攻击性:算法应该具备抵御各种已知的攻击手段,如穷举攻击、差分攻击、线性攻击等。
4. 密钥管理:密钥的生成、更新、存储和分发应具备安全性。
5. 高效性:算法的加解密速度较快。
三、常见的安全性攻击手段1. 穷举攻击:通过尝试所有可能的密钥,直到找到正确的密钥破解密文。
2. 字典攻击:使用预先生成的密码字典,逐个尝试将密文破解为明文。
3. 差分攻击:通过分析输入输出对的差异,推导出密钥的一些信息。
4. 线性攻击:通过分析一系列明文-密文对,推导出密钥的一些信息。
5. 暴力攻击:通过不断尝试密钥的组合,直到找到正确的密钥。
6. 中间人攻击:在通信过程中拦截加密数据,窃取密钥或篡改数据。
四、常用的安全性评估方法1. 密钥空间大小分析:通过计算密钥长度和可能的组合数量,确定密钥空间的大小。
2. 线性分析:通过对算法进行线性逼近,推导出密钥的一些信息。
3. 差分分析:通过对算法进行差分逼近,推导出密钥的一些信息。
4. 暴力攻击模拟:通过模拟攻击者的暴力破解行为,评估算法的破解难度和所需时间。
介绍一下AES

介绍一下AES
AES,全称Advanced Encryption Standard,是一种对称加密算法,被广泛用于数据加密。
它属于分组加密,即把明文分成固定长度的块,然后对每个块进行加密。
AES支持三种长度的密钥:128位,192位和256位。
AES加密算法原理包括密钥、填充、轮密钥加变换等步骤。
在AES加密过程中,需要进行一系列复杂的数学运算,如字节代换、行移位变换、列混合变换和轮密钥加变换等。
AES算法属于对称算法,解密过程为加密过程的逆过程。
它有多种工作模式,包括ECB模式、CBC模式、CFB模式、OFB模式和CTR模式等。
在选择工作模式时,应考虑到具体应用场景的安全性需求。
AES算法的优势在于其高度的安全性和可靠性,被广泛用于数据加密和保护。
它已经被多方分析且广为全世界所使用,经过五年的甄选流程,成为有效的标准。
AES算法已成为对称密钥加密中最流行的算法之一。
需要注意的是,虽然AES算法具有很高的安全性,但在某些场景下可能仍然存在潜在的安全威胁。
因此,在实际应用中,应采取额外的安全措施来保护数据的安全性,并定期进行安全评估和测试验证。
AES加密算法原理(图文)

AES加密算法原理(图文)随着对称密码的发展,DES数据加密标准算法由于密钥长度较小(56位),已经不适应当今分布式开放网络对数据加密安全性的要求,因此1997年NIST公开征集新的数据加密标准,即AES[1]。
经过三轮的筛选,比利时Joan Daeman和Vincent Rijmen提交的Rijndael算法被提议为AES的最终算法。
此算法将成为美国新的数据加密标准而被广泛应用在各个领域中。
尽管人们对AES还有不同的看法,但总体来说,AES作为新一代的数据加密标准汇聚了强安全性、高性能、高效率、易用和灵活等优点。
AES设计有三个密钥长度:128,192,256位,相对而言,AES的128密钥比DES的56密钥强1021倍[2]。
AES算法主要包括三个方面:轮变化、圈数和密钥扩展。
AES 是一个新的可以用于保护电子数据的加密算法。
明确地说,AES 是一个迭代的、对称密钥分组的密码,它可以使用128、192 和256 位密钥,并且用128 位(16字节)分组加密和解密数据。
与公共密钥密码使用密钥对不同,对称密钥密码使用相同的密钥加密和解密数据。
通过分组密码返回的加密数据的位数与输入数据相同。
迭代加密使用一个循环结构,在该循环中重复置换(permutations )和替换(substitutions)输入数据。
Figure 1 显示了AES 用192位密钥对一个16位字节数据块进行加密和解密的情形。
Figure 1 部分数据AES算法概述AES 算法是基于置换和代替的。
置换是数据的重新排列,而代替是用一个单元数据替换另一个。
AES 使用了几种不同的技术来实现置换和替换。
为了阐明这些技术,让我们用Figure 1 所示的数据讨论一个具体的AES 加密例子。
下面是你要加密的128位值以及它们对应的索引数组:00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff0 1 2 3 4 5 6 7 8 9 1011 12 13 14 15192位密钥的值是:00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f 10 11 12 13 14 15 16170 1 2 3 4 5 67 8 9 10 1112 13 14 15 16 17 18 19 20 21 22 23Figure 2 S-盒(Sbox )当AES 的构造函数(constructor)被调用时,用于加密方法的两个表被初始化。
安全加密算法之AES分析

0E 0B 0D 09 09 0E 0B 0D 0D 09 0E 0B 0B 0D 09 0E
S0,0 S0,1 S0,2 S0,3 S1,0 S1,1 S1,2 S1,3 S2,0 S2,1 S2,2 S2,3 S3,0 S3,1 S3,2 S3,3
5、密钥扩展
输入密钥直接被复制到扩展密钥数组的前四个字。然后每次用四个字填充扩展密钥数组余下的部分。在扩展密钥数组中,每个新增的字w[i]依赖于w[i-1]和w[i-4]。在四种情形下,三个使用了异或。对w数组中下标为4的倍数的元素采用了更复杂的函数来计算。
g函数:
1、字循环的功能是使一个字中的4个字节循环左移一个字节,即将输入字[B0,B1,B2,B3]变换成[B1,B2,B3,B0]。 2、字代替利用S盒对输入字中的每个字节进行字节代替。 3、将结果与轮常量Rcon[j]相异或。
截至2006年,针对AES唯一的成功攻击是旁道攻击。美国国家安全局审核了所有的参与竞选AES的最终入围者(包括Rijndael),认为他们均能够满足美国政府传递非机密文件的安全需要。2003年6月,美国政府宣布AES可以用于加密机密文件。
Rijndael 被选为AES是经过多个国家的密码专家广泛讨论的结果。Rijndael 算法具有灵活、简便、抗击多种密码分析的优点,它的目标是发展成能够安全用于商业、政治和军事的加密算法。
目录结构
点击此处添加小标题
点击此处添加小标题
貳
壹
1、对称加密算法
1、对称加密算法
对称加密算法[1]是应用较早的加密算法,技术成熟。在对称加密算法中,数据发信方将明文(原始数据)和加密密钥一起经过特殊加密算法处理后,使其变成复杂的加密密文发送出去。收信方收到密文后,若想解读原文,则需要使用加密用过的密钥及相同算法的逆算法对密文进行解密,才能使其恢复成可读明文。在对称加密算法中,使用的密钥只有一个,发收信双方都使用这个密钥对数据进行加密和解密,这就要求解密方事先必须知道加密密钥。
AES算法实验报告

实验报告姓名:XXXXXXX学号:XXXXXXXXXX班级:XXXXXXXXX日期:2013/12/*题目:AES算法实验一、实验环境1.硬件配置:处理器:Inter(R)Core(TM)*******************(4CPUs),~2.4GHz内存:2048MB RAM2.使用软件:(1) 操作系统:win7 旗舰版(2) 软件工具:Microsoft Visual c++ 6.0二、实验涉及的相关概念或基本原理AES 是一个新的可以用于保护电子数据的加密算法。
明确地说,AES 是一个迭代的、对称密钥分组的密码,它可以使用128、192 和 256 位密钥,并且用 128 位(16字节)分组加密和解密数据。
与公共密钥密码使用密钥对不同,对称密钥密码使用相同的密钥加密和解密数据。
通过分组密码返回的加密数据的位数与输入数据相同。
迭代加密使用一个循环结构,在该循环中重复置换(permutations )和替换(substitutions)输入数据。
Figure 1 显示了 AES 用192位密钥对一个16位字节数据块进行加密和解密的情形。
对称密码算法根据对明文消息加密方式的不同可分为两大类 ,即分组密码和流密码。
分组密码将消息分为固定长度的分组 ,输出的密文分组通常与输入的明文分组长度相同。
AES 算法属于分组密码算法 ,它的输入分组、输出分组以及加/ 解密过程中的中间分组都是 128比特。
密钥的长度 K为 128,192或 256 比特。
用 Nk=4,6,8 代表密钥串的字数 ( 1 字 =32 比特) ,在本文编制的程序中由用户选定。
用 Nr 表示对一个数据分组加密的轮数 ( 加密轮数与密钥长度的关系见表 1) 。
每一轮都需要一个和输入分组具有同样长度 ( 128 比特) 的扩展密钥Ke的参与。
由于外部输入的加密密钥 K 长度有限 ,所以在 AES 中要用一个密钥扩展程序 ( KeyExpansion) 把外部密钥 K 扩展成更长的比特串 ,以生成各轮的加密密钥。
AES算法加解密原理及安全性分析

AES算法加解密原理及安全性分析AES(Advanced Encryption Standard),又称Rijndael加密算法,是一种对称加密算法,是目前最常用的对称加密算法之一、它由比利时密码学家Joan Daemen和Vincent Rijmen于1998年发表,并于2001年被美国国家标准与技术研究院(NIST)选为美国政府的加密标准。
AES算法的加密和解密过程都是基于一个固定长度的密钥,并且使用相同的密钥进行加密和解密操作。
它将明文分成128位(16字节)的数据块,并对每个数据块进行加密。
AES算法使用了一系列的加密密钥,称为轮密钥,每个数据块的加密都要经过多轮的加密运算和密钥混合。
AES算法的加密过程主要包括四个步骤:字节替代、行移位、列混合和轮密钥加。
首先,将每个数据块中的每个字节用一个固定的S盒进行替代。
然后,对每一行进行循环左移操作,使得每个字节在一个数据块内的行中发生移位。
接下来,对每一列进行混合,通过有限域上的乘法运算和加法运算,使得每个字节在一个数据块内的列中发生混合。
最后,将每一轮的轮密钥与数据块进行异或运算,并继续进行下一轮的加密运算。
AES算法的解密过程与加密过程相反,主要包括四个步骤:轮密钥解加、逆列混合、逆行移位和逆字节替代。
首先,将每一轮的轮密钥与加密后的数据块进行异或运算,得到解密后的数据块。
然后,对每一列进行逆混合,通过逆有限域上的乘法运算和加法运算,使得每个字节在一个数据块内的列中发生逆混合。
接下来,对每一行进行逆循环左移操作,使得每个字节在一个数据块内的行中发生逆移位。
最后,将每个字节用逆S盒进行替代,得到解密后的明文数据块。
AES算法具有很高的安全性。
首先,AES算法的密钥长度可选为128位、192位和256位,密钥空间非常大,因此暴力破解方法非常困难。
同时,AES算法的设计经过了严格的审查和测试,没有发现明显的弱点和漏洞。
其次,AES算法的加密过程中引入了字节替代、行移位、列混合等多个运算,使得加密后的数据难以与原始数据之间建立简单的数学关系,增加了密码分析的难度。
stm32_RSA、 AES 加密、 解密原理

1.1 RSA 算法原理................................................................................................................. 2 1.2 AES 算法原理................................................................................................................. 2 2. RSA、AES 的应用................................................................................................................. 4 2.1 RSA 加密..........................................................................................................................4 2.2 RSA 解密......................................................................................错误!未定义书签。 2.3 RSA 签名以及认证.........................................................................................................6 2.4 AES 加密..........................................................................................................................7 2.5 AES 解密......................................................................................错误!未定义书签。 3. polarssl 开源库的使用..................................................................................................... 13 3.1 polarssl 开源库介绍.................................................................................................... 13 3.2 polarssl rsa 接口说明.................................................................................................. 13 3.3 polarssl aes 接口说明..................................................................................................14 3.4 移植 polarssl 开源库................................................................................................... 14 3.5 polarss 开源库的使用................................................................................................ 18
加密解密实验报告

加密解密实验报告加密解密实验报告一、引言随着信息技术的飞速发展,数据安全性成为了一个重要的问题。
为了保护敏感数据的安全,加密解密技术应运而生。
本实验旨在探究加密解密的原理与方法,并通过实验验证其可行性和有效性。
二、加密方法1. 对称加密对称加密是一种加密方法,使用相同的密钥进行加密和解密。
在实验中,我们选择了最常用的对称加密算法——AES(Advanced Encryption Standard)。
通过实验我们发现,AES算法能够在保证数据安全的同时,加解密速度较快。
2. 非对称加密非对称加密是一种使用不同密钥进行加密和解密的方法。
在实验中,我们选择了RSA算法进行实验。
RSA算法基于数论的难题,具有较高的安全性。
实验结果表明,RSA算法在加密过程中较为耗时,但加密后的数据安全性较高。
三、实验步骤1. 对称加密实验(1)选择明文:在实验中,我们选择了一段文字作为明文进行加密。
明文内容为:“加密解密实验报告”。
(2)选择密钥:在AES算法中,密钥长度可以选择128位、192位或256位。
我们选择了128位密钥进行实验。
(3)加密过程:将明文和密钥输入AES算法中,得到密文。
(4)解密过程:将密文和密钥输入AES算法中,得到明文。
2. 非对称加密实验(1)选择明文:同样选择了一段文字作为明文,内容为:“加密解密实验报告”。
(2)生成密钥对:使用RSA算法生成一对密钥,包括公钥和私钥。
(3)加密过程:将明文和公钥输入RSA算法中,得到密文。
(4)解密过程:将密文和私钥输入RSA算法中,得到明文。
四、实验结果1. 对称加密实验结果经过AES算法加密和解密后,我们成功地将明文“加密解密实验报告”转化为了密文,并且通过解密过程将密文还原为了明文。
实验结果表明,对称加密算法能够有效地保护数据的安全性。
2. 非对称加密实验结果通过RSA算法的加密和解密过程,我们同样将明文“加密解密实验报告”转化为了密文,并通过解密过程将密文还原为了明文。
AES加密算法
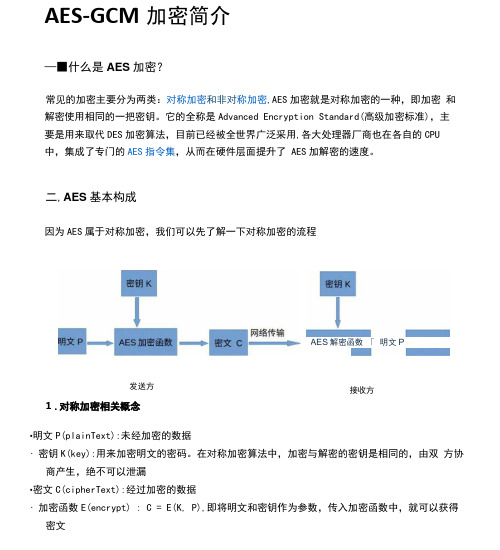
因为AES属于对称加密,我们可以先了解一下对称加密的流程
1
•明文P(plainText):未经加密的数据
・密钥K(key):用来加密明文的密码。在对称加密算法中,加密与解密的密钥是相同的,由双 方协商产生,绝不可以泄漏
•密文C(cipherText):经过加密的数据
・加密函数E(encrypt) : C = E(K, P),即将明文和密钥作为参数,传入加密函数中,就可以获得 密文
14
加密模式:因为分组加密只能加密
定长度的分组,而实际需要加密的明文可能超过分组
长度,此时就要对分组密码算法进行迭代,以完成整个明文加密,迭代的方法就是加密模 式。它有很多种,常见的工作模式如下图:
模式
描述
典型应用
电码本(ECB)
用相同的密钥分别对明文分组独立加密
单个数据的安全传输(如一个加密密钥)
密文分组链接(CBC)
加密算法的输入是上一个密文组和下一个明文组的异或
面向分组的通用传输 认证
密文反馈(CFB)
一次处理s位,上一块密文作为加密算法的输入,产生 的伪随机数输出与明文异或作为下一单元的密文
面向数据流的通用传输 认证
输出反馈(OFB)
与CFB类似,只是加密算法的输入是上一次加密的输 出,且使用整个分组
//第一次XOR
1010A1111 // 0101
//第二次XOR
0101A1111 // 1010
复制代码
XOR的这个特点,使得它可以用于信息的加密
plainText XOR key // cipherText
cipherText XOR key // plainText
了解了上述概念,我们再来看AES的构成
第5章 AES -2014

AES的总体描述
四、AES的基本变换
四、AES的基本变换
四、AES的基本变换
4、S盒变换SubBytes(state)
4、S盒变换SubBytes(state) •字节代换示意图。
•每个字节用十六进制数表示,每个字节按S 盒进行独立代换;
4、S盒变换SubBytes(state)
与 DES 的 S 盒相比, AES 的 S 盒能被代数地定义, 而不像 DES 的 S 盒那样是明显的 “随 机”代换。 AES 的 S 盒(即 SubBytes 操作)是可逆的,它由以下两个可逆变换复合而成: (1)首先,将一个字节变换为有限域 GF(2 )中的乘法逆元素。规定 00 变换为它本身。 (2)其次,对(1)中的结果在 GF(2)上做仿射变换:
一、AES的概况
1、历史时间
1997年,NIST开始了遴选DES替代者—— AES的工 作 。要求AES具有128比特的分组长度,并支持128、 192和256比特的密钥长度,而且能在全世界免费使用 1998年从提交的21个算法中选出15个作为候选 1999年5个算法入围了最后决赛: RC6、Rijndael、 SERPENT、Twofish和MARS 2000年评选出最终结果Rijndael 2001年11月26日接受其作为标准 2001年12月4日正式公布:FIPS-197
三种基本运算:字加法、字乘法、字x乘法
字加法:对应项系数按位模2加 字乘法:多项式乘积再模m(x)=x4+1
AES选定一个固定的可逆多项式做乘法;
字X乘法:相当于字节循环移位;
乘法:多项式乘积再模M ( x) x 1, 记为 。
4Байду номын сангаас
aes密文特征

aes密文特征AES(Advanced Encryption Standard)是一种常用的对称加密算法,它的密文特征是其高度安全性和可靠性。
本文将从AES密文特征的角度,探讨其在数据保护、网络安全和信息传输等领域的应用和重要性。
AES密文特征的高度安全性使其成为数据保护的首选算法。
在现代社会,数据泄露和信息安全问题日益突出,各类机密数据需要得到有效的保护。
AES作为一种对称加密算法,其密钥长度可达到128位、192位和256位,确保了数据的高度加密强度。
这意味着即使黑客获取了密文,也几乎不可能通过破解密文来获取原始数据。
因此,AES密文特征的出色安全性,使其广泛应用于金融、医疗、军事等领域敏感数据的保护。
AES密文特征在网络安全领域具有重要意义。
随着互联网的发展,网络攻击和黑客入侵事件频频发生,网络安全已成为全球关注的焦点。
在传输敏感信息时,使用AES加密将数据转化为密文,可以有效保护数据的安全性。
AES的高度安全性和快速加密速度,使其成为许多网络通信协议的首选加密算法。
例如,HTTPS协议就采用了AES加密算法来保护网站和用户的通信安全,确保敏感信息不被恶意窃取。
AES密文特征的可靠性使其在信息传输领域得到广泛应用。
在现代信息社会,各类数据的传输已成为日常工作和生活的重要组成部分。
使用AES加密算法对数据进行加密,可以有效防止数据在传输过程中被篡改或窃取。
AES加密算法采用的是对称加密方式,发送方和接收方使用相同的密钥进行加解密。
这种简单而可靠的加密方式,使得AES在电子邮件、即时通信、云存储等信息传输场景中得到广泛应用。
AES密文特征的高度安全性和可靠性使其在数据保护、网络安全和信息传输等领域发挥着重要作用。
随着技术的不断发展,AES算法也在不断更新和完善,以应对日益复杂的安全威胁。
然而,我们也应意识到,AES算法并非绝对安全,随着计算能力的提升和密码分析技术的进步,可能会出现破解AES的可能性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AES算法加解密原理及安全性分析刘帅卿一、AES算法简介AES算法是高级加密标准算法的简称,其英文名称为Advanced Encryption Standard。
该加密标准的出现是因为随着对称密码的发展,以前使用的DES(Data Encryption Standard数据加密标准)算法由于密钥长度较小(56位),已经不适应当今数据加密安全性的要求,因此后来由Joan Daeman和Vincent Rijmen提交的Rijndael算法被提议为AES的最终算法。
AES是一个迭代的、对称密钥分组的密码,它可以使用128、192和256位密钥,并且用128位(16字节)分组加密和解密数据。
与公共密钥密码使用密钥对不同,对称密钥密码使用相同的密钥加密和解密数据。
通过分组密码返回的加密数据的位数与输入数据相同。
迭代加密使用一个循环结构,在该循环中重复置换(permutations)和替换(substitutions)输入数据。
加之算法本身复杂的加密过程使得该算法成为数据加密领域的主流。
二、AES算法的基本概念1、有限域(GF)由于AES算法中的所有运算都是在有限域当中进行的,所以在理解和实现该算法之前先得打好有限域这一基石才行。
通常的数学运算都是在实数域中进行,而AES算法则是在有限域中进行,我们可以将有限域看成是有确定边界范围的正整数集合,在该集合当中,任意两个元素之间的运算结果都仍然落在该集合当中,也即满足运算封闭性。
那么如何才能保证这样的“有限性”(也即封闭性)呢?GF(2w)被称之为伽罗华域,是有限域的典型代表。
随着w(=4,8,16,…)的取值不同所形成的有限域范围也不同。
AES算法中引入了GF域当中对数学运算的基本定义:将两数的加减法定义为两者的异或运算;将两数的乘法定义为多项式间的相乘并求余运算,其中被用于求余运算的除数被称为不可约多项式(或者称为求余多项式),它是固定的一个多项式:m(x) =8431x x x x ++++(数值为十六进制的11B ,这里是假定w=8时的情形)。
对于某个有限域而言,可能存在不唯一的不可约多项式,选择合适的多项式是某种算法考虑的主要因素之一。
2、状态矩阵和密钥矩阵状态矩阵是指将要被加密的若干数据所形成的矩阵,我们暂且用state_matrix 来表示;而密钥矩阵则是指密钥数据所形成的矩阵,我们暂且用cipher_matrix 来表示。
随着输入数据个数的不同,这两个矩阵的维数可以为44,4648⨯⨯⨯或者;例如如果输入的被加密数据为24个字符(此处假定是以字符为数据单位进行加密,当然也可以是以一个整数为单位等进行加密),输入的密钥数据为16个字符(假设与上同),那么可以形成一个46⨯维的state_matrix 矩阵和一个44⨯维的cipher_matrix 矩阵。
可见形成的矩阵的行数是固定的,都为4。
因为矩阵的形成是以每4个数据为一列依次构成,所以随着数据的增加只会增加其列数而不会影响其行数。
并且我们用Nb 表示被加密数据矩阵(state_matrix 矩阵)的列数,用Nk 表示密钥数据矩阵(cipher_matrix 矩阵)的列数。
那么有了上述两个矩阵,我们就可以进行AES 的加密过程了。
3、扩展密钥扩展密钥是从密钥矩阵变换而来,之所以称之为“扩展”是因为在AES 的加密过程中,要对数据进行Nr+1轮加密,每次加密的密钥都不一样,我们将着Nr+1轮加密过程中用到的所有的密钥的集合叫做扩展密钥。
那么如何去确定这个轮数Nr 呢?Nr 的取值是根据Nb 和Nk 的值确定的,AES 算法中给出了它们之间如下的对照表:例如:如果Nb=6,Nk=4那么我们的加密过程应该进行Nr+1=13次,那么也就有13个扩展密钥。
由于这些密钥要和state_matirx矩阵做异或运算,所以每个扩展密钥必须转化为一个和state_matirx矩阵同维数的加密矩阵才可以进行每个元素一对一的运算。
由Nb和Nr的值,我们可以计算出扩展密钥的整体“长度”。
如下公式可以给出:Nb*(Nr+1);例如Nb=6,Nr=12则“长度”为78;这78个数字每6个为一个扩展密钥(因为Nb=6,所以要这样分组)。
那么这78个数字是怎么形成的呢?AES算法中将形成扩展密钥的过程定义为:KeyExpansion()。
该过程以cipher_matrix矩阵的值,每一列的4个byte组成一个int数,那么对于Nk=4的cipher_matrix而言必然可以构成4个int数,KeyExpansion()过程(过程的具体实现参照相关文献)就是以这4个整型数为基础,通过它的扩展方式将这4个数字扩展成了78个数字。
这78个数字,每6维的扩展密钥矩阵),个组成一个密钥(再将int化为char型恰好构成一个46总共进行13次加密过程。
为了存储这78个数字,算法中开辟一个W[i]数组。
显然该数组的维数为W[Nb*(Nr+1)]。
4、AES加密过程1# 前面的Nr轮(0 ~ Nr-1)被称之为Round()过程:Round(){ByteSub(); //字节变换过程,该过程参照S_box实现ShiftRow(); //行交换过程,该过程参照既定的交换规则实现MixColumn(); //列变换过程,该过程参照C(x)矩阵实现AddRoundKey(); //扩展密钥加密过程,该过程参照扩展密钥实现}2# 最后一轮加密过程(第Nr轮)被称为FinalRound()过程:FinalRound(){ByteSub();ShiftRow();AddRoundkey();}在上述过程中,ByteSub(), ShiftRow(), MixColumn()三个过程的变换是固定的模式,具体的实现可以参照相关文献。
它们的调用次数分别为:Nr+1次,Nr+1次,Nr次。
而AddRoundkey()过程显然是Nr+1次,它是与扩展密钥相关的。
前Nr轮加密中用去了Nr个扩展密钥,第Nr轮加密中用去最后一个扩展密钥,从而实现Nr+1轮加密过程。
至此AES算法结束。
三、AES算法的实现方案AES加密算法主要分为三大块,即密钥扩展,数据加密和数据解密。
1、密钥扩展(1)使用Rotword()函数对数组中的数字实现循环左移一位的运算,即将数组中左端第一个数字移至数组的末端,而原来在它之后的数字依次前移一位。
要说明的是,由于数组中的4个数字已经合并为一个数字,因此在程序的实际执行过程中并不是做数组的循环左移运算,而是进行数字的循环移位运算,这样一来便大大简化了运算过程,对运算效率有一定程度的提高。
(2)使用SubWord()函数依据S置换表对4个数字进行置换,规则如下。
例如,有一个数字为0x2a,则在表1•1中查找‘2’行‘a’列的数字,得到数字e5,则该数字即是数字0x2a 的置换数字。
此函数的C语言实现相对简单,只是一个查表的问题,但过程比较繁琐细碎,编成时应仔细对待,避免出错。
2、数据加密(1)使用SubByte()函数依据S置换表对状态矩阵State[4][4]中的数字进行置换,查表的方法在前文已经介绍,这里不再赘述。
有一点需要注意的是,虽然SubByte()函数与SubWord()函数原理相同,但在程序中的运算过程却不尽相同。
SubByte()函数是提取状态矩阵State[4][4]中的每一个数组元素进行置换运算,而SubWord()则是提取一unsigned long 整型数字中的某8位数据进行置换运算。
SubByte()函数的C语言实现与SubWord()的C语言实现雷同,这里也不再赘述。
(2)使用ShiftRow()函数对状态矩阵State[4][4] 中的各行数据进行循环移位运算。
该函数所进行的循环移位规则如下。
状态矩阵State[4][4] 中的第一行数据位置不变,第二行数据循环左移一位数字,第三行数据循环左移两位数字,第四行数据循环左移三位数字。
在对ShiftRow()函数进行C语言编程时主要是要注意行数以及所对应的移位个数,保证运算的准确性。
3、数据解密(1)使用InvSubByte()函数依据S置换表的逆表对状态矩阵State[4][4]中的数字进行置换,置换方法与SubByte()函数相同。
该函数的C语言实现与SubByte()函数基本相同,在此不再赘述。
(2)使用InvShiftRow()函数对状态矩阵State[4][4] 中的各行数据进行循环移位运算。
该函数所进行的循环移位规则如下。
状态矩阵State[4][4] 中的第一行数据位置不变,第二行数据循环右移一位数字,第三行数据循环右移两位数字,第四行数据循环右移三位数字。
四、AES实现过程分析AES 算法是基于置换和代替的,置换是数据的重新排列,而代替是用一个单元数据替换另一个,其基本密码算法Rijndael使用的是置换-组合架构,而非Feistel架构。
AES 是一个新的可以用于保护电子数据的加密算法。
AES 使用了几种不同的技术来实现置换和替换。
通过分组密码返回的加密数据的位数与输入数据相同。
迭代加密使用一个循环结构,在该循环中重复置换(permutations )和替换(substitutions)输入数据。
对AES算法按加密处理和密钥调度两个方面进行分析:1、加密处理加密处理过程:加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:(1)、SubBytes —透过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。
(2)、ShiftRows —将矩阵中的每个横列进行循环式移位。
(3)、MixColumns —为了充分混合矩阵中各个直行的操作。
这个步骤使用线性转换来混合每行内的四个字节。
(4)、AddRoundKey —矩阵中的每一个字节都与该次循环的子密钥(round key)做XOR运算;每个子密钥由密钥生成方案产生。
最后一个加密循环中省略MixColumns步骤,而以另一个AddRoundKey取代。
SubBytes 步骤在SubBytes步骤中,矩阵中各字节被固定的8位查找表中对应的特定字节所替换,S; bij = S(aij).如图所示:ShiftRows 步骤在ShiftRows 步骤中,矩阵中每一列的各个字节循环向左方位移。
位移量则随着行数递增而递增。
在ShiftRows 步骤中,矩阵中每一列的各个字节循环向左方位移。
位移量则随着行数递增而递增。
MixColumns 步驟在MixColumns 步骤中,每个直行都在modulo x4 + 1之下,和一个固定多项式c(x)作乘法。
AddRoundKey 步骤AddRoundKey步骤,子密钥将会与原矩阵合并。
在每次的加密循环中,都会由主密钥产生一把子密钥(透过Rijndael密钥生成方案产生),这把子密钥大小会跟原矩阵一样,以与原矩阵中每个对应的字节作异或(⊕)加法。
