强烈推荐---MatLab曲线拟合工具箱的应用
matlab拟合曲线并得到方程和拟合曲线

matlab拟合曲线并得到方程和拟合曲线1. 引言1.1 概述在科学研究和工程实践中,我们通常需要对实验数据或观测数据进行分析和处理。
拟合曲线是一种常用的数学方法,可以通过拟合已有的数据来找到代表这些数据的函数模型。
Matlab作为一款功能强大的数值计算软件,提供了多种拟合曲线的方法和工具,可以帮助用户快速高效地进行数据拟合并得到拟合方程和结果。
1.2 文章结构本文分为五个部分来介绍Matlab拟合曲线方法及其应用。
首先,在引言部分将概述文章的主要内容和结构安排;其次,在第二部分将介绍Matlab拟合曲线的原理,包括什么是拟合曲线、Matlab中常用的拟合曲线方法以及其优缺点;然后,在第三部分将通过一个实例分析来具体讲解使用Matlab进行拟合曲线的步骤,并展示得到方程和拟合曲线的结果;接着,在第四部分将探讨不同领域中对于拟合曲线的应用场景,并给出相应案例研究;最后,在第五部分将总结已有研究成果,发现问题,并对Matlab拟合曲线方法进行评价和展望未来的研究方向。
1.3 目的本文的目的是介绍Matlab拟合曲线的原理、步骤以及应用场景,旨在帮助读者了解和掌握Matlab拟合曲线的方法,并将其应用于自己的科研、工程实践或其他领域中。
通过本文的阅读,读者可以了解到不同拟合曲线方法之间的区别和适用情况,并学习如何使用Matlab进行数据拟合并得到拟合方程和结果。
最终,读者可以根据自己的需求选择合适的拟合曲线方法,提高数据分析和处理的准确性和效率。
2. Matlab拟合曲线的原理2.1 什么是拟合曲线拟合曲线是一种通过数学方法,将已知数据点用一个连续的曲线来近似表示的技术。
它可以通过最小二乘法等统计学方法找到使得拟合曲线与数据点之间误差最小的参数。
2.2 Matlab中的拟合曲线方法在Matlab中,有多种方法可以进行拟合曲线操作。
其中常用的包括多项式拟合、非线性最小二乘法拟合和样条插值等。
- 多项式拟合:利用多项式函数逼近已知数据点,其中最常见的是使用一次、二次或高阶多项式进行拟合。
利用matlab中surface-fitting-tool工具箱进行曲面拟合
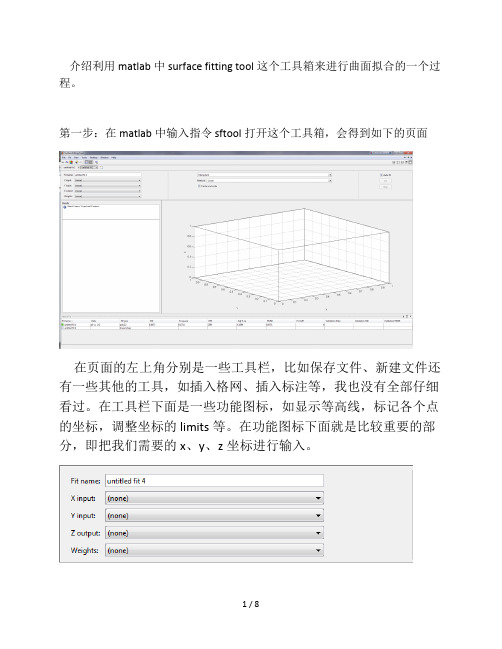
介绍利用matlab中surface fitting tool这个工具箱来进行曲面拟合的一个过程。
第一步:在matlab中输入指令 sftool打开这个工具箱,会得到如下的页面在页面的左上角分别是一些工具栏,比如保存文件、新建文件还有一些其他的工具,如插入格网、插入标注等,我也没有全部仔细看过。
在工具栏下面是一些功能图标,如显示等高线,标记各个点的坐标,调整坐标的limits等。
在功能图标下面就是比较重要的部分,即把我们需要的x、y、z坐标进行输入。
x、y、z的长度必须一致,否则就是会报错,并且x、y、z必须都为向量,否则就无法在下拉菜单中进行选择。
在此,我以一个51*51的二维矩阵为例来说明如何使用sftool进行拟合。
以c5这个矩阵为例x,y是1到51的整数,z是矩阵中的数值,有51*51=2601个数,接下来我们把x 、y、 z都进行向量化。
在matlab中输入下列指令x=[];for i=1:51x=[x;i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i]endx=x’;x=x(:)这样就可以得到一个x为2601行1列的矩阵,首先是51个1然后是51个2…….最后是51个51,总共2601行1列------------------------------------------------ y=[];for i=1:51y=[y;i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i]endy=y(:);注意:y并不需要进行转秩这一步同样得到一个2601行一列的矩阵,矩阵的样子应该是1到51,然后再1到51…….直到最后。
Matlab曲线拟合及其在试验数据处理中的应用

2
采用 8 次,这是根据 xmin >>N- m 的显著性检验得到
的。
利用公式:
N
Σ ρ= xiyi i=1
N
N
姨Σ Σ 2
2
xi * yi
i=1
i=1
(12)
计算拟合结果的相关系数分别为:多项式拟合
0.9917、神经网络和既定样式最小二乘为 1。
3 对实际数据的处理
下面为一组信号传播通路损耗的实测数据:
触的传递效率;yi 是 i 神经元的输出;f 是传递函数,决
定 i 神经元受到输入 x1,x2,…,xn 的共同作用达到阈值
时以何种方式输出。
神经元的输出可以用下面的关系式表达:
n
Σ yi=(f xj*wji- θ)i j=1
(4)
多个神经元进行级联可组成神经网络,神经网络
的学习过程分网络正向传递、误差反向传递、网络调整
39 - 3.05 52.5 - 2.1 66 - 2.45 79 - 1.9
40.5 - 2.9 54 - 2.15 67.5 - 2.3 81 - 1.95
42 - 2.75 55.5 - 2.3 69 - 2.05
对于实测数据通常不知道函数原型,确定拟合函 数样式比较困难,因而通常采用无需先验知识的多项 式拟合和 BP 神经网络拟合比较恰当,图 3 为拟合结 果:
第 17 卷第 2 期
杨云升:Matlab 曲线拟合及其在试验数据处理中的应用
·35·
[a,J]=laqcurvefi(t @fun,a0,X,Y)
(2)
式中:a 为拟合后函数参数,a0 为参数 a 的初值,X,Y
为测试得到的数据矢量,@fun 为设计的函数样式
在Matlab中数值拟合的应用

在Matlab 中数值拟合的应用摘要在科学实验和生产实践中,往往需要从一组实验数据),...2,1)(,(n i y x i i =中,寻找变量x 和y 之间的函数关系)(x f y =的某种近似表达式)(s x 。
而实际去只能通过观测得到一些离散的数据点。
针对这些分散的数据点,运用某种你和方法生成一条连续的曲线,这个过程称为曲线拟合。
插值方法可以构造一个插值函数逼近已知函数你,但是,一般来说,给定的实验数据),...2,1)(,(n i y x i i =的数量较大,且由于观测误差的原因,准确度不一定高,甚至在个别点有很大的误差,形象地成为“噪声”。
如果用插值法来求)(x f y =的近似表达式,要使)(s x 满足插值条件,势必将“噪声”带进近似函数)(s x ,因而不能较好地描绘)(x f y =。
面对着分散的数据点,运用某种你和方法生成一条连续的曲线,这个过程称为曲线拟合。
插值法虽然是函数逼近的一种重要方法,但他还存在以下的缺陷:一是由于测量数据的往往不可避免地带有测试误差,而插值多项式又通过所有的点),(i i y x ,这样就使插值多项式保留了这些误差,从而影响了逼近精度。
此时显然插值效果是不理想的。
二是如果由实验提供的数据较多,则必然得到次数较高的插值多项式,这样近似程度往往既不稳定又明显缺乏实用价值。
因此,怎样从给定的一组实验数据出发,寻求已知函数的一个逼近函数)(s x ,使得逼近函数从总体上来说与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点),(i i y x ,这就需要介绍本论文主要研究的数据拟合。
本文学习目的:(1)熟悉、掌握数据拟合的各种不同准则,重点学习最小二乘准则; (2)提出、分析并掌握Matlab 中各种常见的拟合方法; (3)熟悉掌握拟合工具的使用;(4)能够灵活编程来解决数据拟合的实际问题 。
关键词:Matlab 、数据拟合准则、一元线性拟合、非线性、图像、拟合工具012345678966.577.588.599.510时间t(s)充电电压(V )电容器充电电压与时间t 的曲线1、数据拟合概念数据的拟合主要分为曲线拟合(curve fitting)、曲面拟合(suface fitting)。
使用MATLAB曲线拟合工具箱做曲线拟合

使用MATLAB曲线拟合工具箱做曲线拟合作者:胡庆婉来源:《电脑知识与技术》2010年第21期摘要:介绍了使用MATLAB曲线拟合工具箱(Curve Fitting Toolbox)对数据进行曲线拟合,给出数学建模中的实例用以介绍其具体使用方法,并且给出利用MATLAB曲线拟合工具箱改善拟合结果的方法。
结果显示,用MATLAB曲线拟合工具箱能够很好的对数据进行曲线拟合的处理。
关键词:MATLAB;曲线拟合;曲线拟合工具箱中图分类号:O1-8文献标识码:A文章编号:1009-3044(2010)21-5822-02Curve Fitting by Curve Fitting Toolbox of MatlabHU Qing-wan(Department of Mathematics and Information Science, Qujing Normal University, Qujing 655011, China)Abstract: In this paper,we introduced the use of MATLAB Curve Fitting Toolbox for curve fitting, gave an example of mathematical modeling to introduce the specific use, and gave methods for improving results getting from MATLAB curve fitting toolbox. The results show that MATLAB curve fitting toolbox is excellent in curve fitting.Key words: MATLAB; curve fitting; curve fitting toolboxMATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
Matlab拟合工具箱CFtool使用指南

For personal use only in study and research; not for commercial useFor personal use only in study and research; not for commercial usematlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353; 0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
Matlab拟合工具箱CFtool使用指南
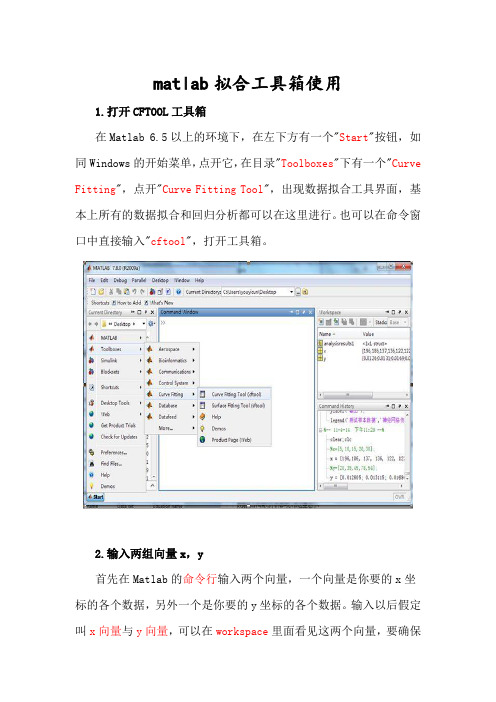
matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。
使用MATLAB曲线拟合工具箱做曲线拟合(2013)

使用 MATLAB 曲线拟合工具箱做曲线拟合在实际的工程应用领域和经济应用领域中,人们往往通过实验或者观测得到一些数据, 为了从这些数据中找到其内在的规律性, 也就是求得自变量和因变量之间的近似函数关系表 达式。
这类问题可以归结曲线拟合。
1.MATLAB 曲线拟合工具箱简介MATLAB 做曲线拟合可以通过内建函数或者拟合工具箱(Curve Fitting Toolbox )。
这个 工具箱集成了用MATLAB 建立的图形用户界面(GUIs )和 M 文件函数。
利用这个工具箱 可以进行参数拟合(当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟 合),或者通过采用平滑样条或者其他各种插值方法进行参数拟合(当回归系数不具有物理 意义并且不在意他们的时候,就采用非参数拟合)。
利用这个界面,可以快速地在简单易用 的环境中实现许多基本的曲线拟合。
2.实际例子应用数学模型书上关于汽车刹车距离模型,建立的模型如下:2 1 d t v kv=+ 其中v 是汽车速度, 1 t 是反应时间,按大多数人平均取 0.75 秒,d 是刹车距离。
交通部 门提供了一组刹车的距离实际数据如表1 所示(刹车距离括号内为最大值)。
表 1车速(英尺 秒)29.3 44 58.7 73.3 88 102.7 1173 刹车距离 (英尺) 42(44) 73.5(78) 116(124) 173(186) 248(268) 343(372) 464(506) 利用表 1 的数据,我们拟合在 MATLAB 的 command window 里输入:>>v=[29.3 44 58.7 73.3 88 102.7 117.3];>>d1=[42 73.5 116 173 248 343 464];>>cftool %cftool 是打开拟合工具箱的命令;则跳出曲线拟合工具箱的界面如图 1 所示, 如果输入数据非常大, 并且每次输入有困难, 可以新建一个 M 文件,依次输入上述命令行,保存之后执行,同样可以进入曲线拟合工具 箱界面。
拟合曲线matlab

拟合曲线matlab拟合曲线是数学中一个非常重要的概念,它可以帮助我们更好地理解数据之间的关系。
在MATLAB中,拟合曲线也是非常实用的工具。
本文将介绍如何使用MATLAB来拟合曲线,以及拟合曲线的优缺点和应用场景。
在MATLAB中,拟合曲线的主要功能是可以通过指定的函数来创建和拟合曲线。
例如,我们可以使用`fit`函数来拟合一个多项式曲线,或者使用`polyfit`函数来拟合一个多项式多项式曲线。
在拟合曲线时,我们需要指定一个函数来描述数据之间的关系,这个函数通常被称为自变量。
在这个函数中,每一项都是关于自变量的多项式,也就是一个多项式曲线。
拟合曲线可以帮助我们更好地理解数据之间的关系。
通过拟合曲线,我们可以了解自变量和因变量之间的相互关系,以及自变量对因变量的影响程度。
在实际应用中,拟合曲线通常是用来进行数据分析和建模的重要工具。
拟合曲线在MATLAB中具有非常丰富的功能和选项。
我们可以使用`fit`函数中的许多选项来调整拟合曲线的形状和参数。
例如,我们可以使用`degree`选项来控制多项式的次数,或者使用`min`和`max`选项来指定多项式的最小和最大值。
此外,我们还可以使用`plot`函数来绘制拟合曲线,或者使用`grid`选项来在图表上添加网格。
拟合曲线虽然是一个非常强大的工具,但也存在一些缺点。
首先,拟合曲线只能在数据点比较多的情况下才能产生较为准确的结果。
如果数据点比较少,那么拟合曲线可能只是一种非常简单的表达方式,并不能很好地反映数据之间的关系。
其次,拟合曲线通常只能描述一个一次多项式曲线,对于复杂的曲线或者非线性关系,拟合曲线可能就无法提供有效的解决方案。
总结起来,拟合曲线是MATLAB中一个非常有用的工具,可以帮助我们更好地理解数据之间的关系。
通过拟合曲线,我们可以了解自变量和因变量之间的相互关系,以及自变量对因变量的影响程度。
拟合曲线具有丰富的功能和选项,可以满足绝大多数数据分析场景的需求。
matalab曲线拟合器横纵坐标

Matalab 曲线拟合器是一个强大的工具,可以帮助用户通过拟合数据点来找出数据之间的关系,并用数学模型描绘出这种关系。
在使用Matalab 曲线拟合器时,用户需要提供数据点的横纵坐标。
这些坐标可以是实验测量得到的结果,也可以是从某种模型或理论中推导出来的。
1. Matalab 曲线拟合器的作用曲线拟合器的主要作用是通过拟合数据点来找出数据之间的规律,并用数学模型描述这种规律。
在实际应用中,曲线拟合器可以用于预测未来的趋势、分析实验数据、优化生产工艺等方面。
在科学研究中,研究人员可以通过拟合实验数据来验证自己的理论模型;在工程领域,工程师可以利用曲线拟合器来优化产品设计和生产工艺。
2. 提供横纵坐标数据点在使用 Matalab 曲线拟合器时,用户需要提供待拟合的数据点的横纵坐标。
这些数据点可以通过实验测量、模拟计算或从其他来源获得。
在提供数据点时,用户需要确保数据的准确性和完整性,以保证曲线拟合的有效性。
3. 选择拟合模型Matalab 曲线拟合器提供了多种拟合模型供用户选择,包括线性拟合、多项式拟合、指数拟合、对数拟合等。
用户在选择拟合模型时需要考虑数据点的分布特点、拟合的目的以及对拟合精度的要求。
不同的拟合模型适用于不同类型的数据规律,选择合适的拟合模型对于得到准确的拟合结果至关重要。
4. 进行曲线拟合一旦选择了拟合模型,用户就可以开始进行曲线拟合。
Matalab 曲线拟合器会根据用户提供的数据点和拟合模型来计算出最优的拟合曲线,并给出拟合的精度评估。
在拟合过程中,用户可以根据需要对拟合参数进行调整,以获得符合实际情况的拟合结果。
5. 分析拟合结果拟合完成后,用户需要对拟合结果进行分析和评估。
首先需要考察拟合曲线与原始数据点的拟合程度,通常可以通过残差分析来进行评估。
其次需要考虑拟合模型的适用性和实际意义,对拟合结果进行科学解释和合理应用。
总结Matalab 曲线拟合器是一个强大的工具,可以帮助用户通过拟合数据点找出数据之间的规律,并用数学模型描述这种规律。
matlab拟合工具箱拟合方法

matlab拟合工具箱拟合方法Matlab拟合工具箱是Matlab软件中的一个重要功能模块,它提供了多种拟合方法,用于拟合数据并得到最佳的拟合曲线。
拟合是一种通过拟合函数来描述数据间关系的方法,可以用于数据分析、模型建立和预测等各个领域。
在Matlab拟合工具箱中,常用的拟合方法包括线性拟合、多项式拟合、非线性拟合、曲线拟合等。
下面将介绍其中几种常用的拟合方法。
线性拟合是一种通过线性函数来拟合数据的方法,其数学表达式为y = a * x + b。
线性拟合方法适用于数据呈现线性关系的情况,通过最小二乘法可以求得最佳拟合直线的参数。
多项式拟合是一种通过多项式函数来拟合数据的方法,其数学表达式为y = a0 + a1 * x + a2 * x^2 + ... + an * x^n。
多项式拟合方法适用于数据呈现非线性关系的情况,通过最小二乘法可以求得最佳拟合曲线的系数。
非线性拟合是一种通过非线性函数来拟合数据的方法,其数学表达式为y = f(x, a1, a2, ..., an),其中f为非线性函数,a1, a2, ..., an为待拟合参数。
非线性拟合方法适用于数据呈现复杂非线性关系的情况,通过最小二乘法或其他优化算法可以求得最佳拟合曲线的参数。
曲线拟合是一种通过拟合曲线来拟合数据的方法,其数学表达式可以是任意复杂的函数形式。
曲线拟合方法适用于数据呈现特殊形状或复杂关系的情况,通过最小二乘法或其他优化算法可以求得最佳拟合曲线的参数。
除了上述介绍的几种常用的拟合方法,Matlab拟合工具箱还提供了其他一些拟合方法,如指数拟合、对数拟合、幂函数拟合等。
这些拟合方法可以根据实际需求选择合适的函数形式进行拟合。
在使用Matlab拟合工具箱进行拟合时,首先需要准备好待拟合的数据。
数据可以通过实验测量、观测记录或其他方式获得。
然后,在Matlab中调用拟合工具箱的相应函数,选择合适的拟合方法,传入待拟合的数据,即可得到最佳拟合曲线的参数。
Matlab拟合工具箱CFtool使用指南

matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。
MatLab曲线拟合工具箱应用资料讲解

.Delete 删去数据组
例:输入数据,采用matlab自带的文件census
census 有两个变量:cdate和pop。 cdate 是一个年向量,包括1790-1990
年,间隔为10年;
pop是对应年份的美国人口。
>> whos -file census
Name
Size
18
20
22
24
26
28
30
>> a=polyfit(x,y,2) a=
-0.2003 8.9782 -72.2150 >> poly2str(a,'x') ans =
-0.20031 x^2 + 8.9782 x 72.215 >> x1=17:0.1:29; >> y1=0.20031*x1.^2+8.9782*x172.215; >> hold on;plot(x1,y1,'b')
.y=polyval(p,x,[],mu)
用x=(x-u1)/u2代替x,其中mu是一个 二维向量[u1,u2], u1=mean(x),u2=std(x),通过这 样处理数据,使数据合理化。
[y,delta]=polyval(p,x,s) [y,delta]=polyval(p,x,s,mu) 产生置信区间y±delta。如果误差结果服从 标准正态分布,则实测数据落在y±delta区 间内的概率至少为50%。
Attributes
Bytes Class
Байду номын сангаас
cdate 21x1
168 double
pop
Matlab拟合工具箱CFtool使用指南

matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。
Matlab拟合工具箱CFtool使用指南

matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353; 0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits上方的横条往下拉就可以看见Fit Editor。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)其他数据预处理方法 其他的预处理方法不便通过曲线拟合工具箱来完成,主要包 括两部分: 响应数据的转换和去除无穷大、缺失值和异常值。 响应数据的转换一般包括对数转换、指数转换,用这些转换 可以使非线性的模型线性化,便于曲线拟合。变量的转换 一般在命令行里实现,然后把转换后的数据输入曲线拟合 工具箱,进行拟合。 无穷大、不定值在曲线拟合中可以忽略,如果想把他们从 数据集中删除,可以用isinf和isnan置换无穷大值和缺 失值。
一、数据预处理 在曲线拟合之前必须对数据进行与处理,去除界外值、不定 值和重复值,以减少认为误差,提高拟合的精度。 数据预处理包括: (1)数据输入与查看 (2)数据的预处理 传输数据通过数据GUI来实现,查看数据点通过曲线拟合工 具的散点图来实现。
1.输入和查看数据集 (1)打开曲线拟合工具界面 通过cftool命令打开曲线拟合工具界面
>> a=polyfit(x,y,2) a = -0.2003 8.9782 -72.2150 >> poly2str(a,'x') ans = -0.20031 x^2 + 8.9782 x - 72.215 >> x1=17:0.1:29; >> y1=-0.20031*x1.^2+8.9782*x1-72.215; >> hold on;plot(x1,y1,'b')
[y,delta]=polyval(p,x,s) [y,delta]=polyval(p,x,s,mu) 产生置信区间y±delta。如果误差结果服从 标准正态分布,则实测数据落在y±delta区 间内的概率至少为50%。 例 >> x=[0 0.0385 0.0963 0.1925 0.2888 0.385]; >> y=[0.042 0.104 0.186 0.338 0.479 0.612]; >> [p,s,mu]=polyfit(x,y,5)
(2)排除法和区间排除法 排除法是对数据中的异常值进行排除。 区间排除法是采用一定的区间去排除那些用于系统误差导致 偏离正常值的异常值。在曲线拟合工具中单击Exclude 按钮,可以打开Exclude对话框
Exclusion rule name指定分离规则的名称 Existing exclusion rules列表产生的文件名,当你选择 一个文件名时,可以进行如下操作: Copy 复制分离规则的文件; Rename重命名;delete 删去一个文件; View以图形的形式展示分离规则的文件。 Select data set 挑选需要操作的数据集; Exclude graphically允许你以图形的形式去除异常值,排 除个别的点用“×”标记。 Check to exclude point 挑选个别的点进行排除,可以通 过在数据表中打勾来选择要排除的数据。 Exclude Sections 选定区域排除数据: Exclude X选择预测数据X要排除的数据范围; Exclude Y选择响应数据Y要排除的数据范围。
二、曲线拟合 Matlab提供两种曲线拟合方法: (1)以函数的形式,使用命令对数据进行拟合。这种方法 比较繁琐,需要对拟合函数有比较好的了解。 (2)用图形窗口进行操作,具有简便、快速,可操作性强 的优点。
1.多项式拟合函数 (1)polyfit函数 P=polyfit(x,y,n) 用最小二乘法对数据进行拟合,返回n次多项式的系数,并 用降序排列的向量表示,长度为n+1.
例:输入数据,采用matlab自带的文件census
census 有两个变量:cdate和pop。 cdate是一个年向量,包括1790-1990年,间隔为10年; pop是对应年份的美国人口。 >> whos -file census Name Size Bytes Class Attributes cdate 21x1 168 double pop 21x1 168 double >> load census >> cftool(cdate,pop)
MATLAB 曲线拟合工具 箱的应用--taotao
曲线拟合定义1 在实际工程应用和科学实践中,经常需要寻求两个(或多个) 变量间的关系,而实际去只能通过观测得到一些离散的数据 点。针对这些分散的数据点,运用某种你和方法生成一条连 续的曲线,这个过程称为曲线拟合。 曲线拟合可分为: (1)参数拟合 ---- 最小二乘法 (2)非参数拟合 ---- 插值法
散点图
单击Data按钮
在X data和Y data两个下拉式列表框中选择变量名,将在 Data对话框中显示散点图的预览效果:
当选择Data sets列表框中的数据集时,单击View按钮, 打开View Data Set对话框
工作表方式
2.数据的预处理 在曲线拟合工具箱中,数据的预处理主要包括平滑法、排除 法和区间排除法等。 (1)平滑数据 打开拟合工具箱,单击Data按钮,打开Data对话框,选择 Smooth选项卡
.Smoothed data sets 对于所有平滑数据集进行列表。 可以增加平滑数据集,通过单击Create smoothed data set按钮,可以创建经过平滑的数据集。 .View按钮 打开查看数据集的GUI,以散点图方式和工作 表方式查看数据,可以选择排除异常值的方法。 .Rename用于重命名。 .Delete可删去数据组。 .Save to workspace保存数据集。
>> x=[1 3 4 5 6 7 8 9 10]; >> y=[10 5 4 2 1 1 2 3 4]; >> [p,s]=polyfit(x,y,4); >> y1=polyval(p,x); >> plot(x,y,'go',x,y1,'b--') >> poly2str(p,'t') ans = -0.0049945 t^4 + 0.11461 t^3 - 0.61143 t^2 - 1.1005 t + 11.5499
p( x ) p1 x p2 x
n
n 1
pn x pn 1
[p,s]=polyfit(x,y,n) 返回多项式系数向量p和矩阵s。s与polyval函数一起用时, 可以得到预测值的误差估计。如数据y的误差服从方差为常数 的独立正态分布,polyval函数将生成一个误 差范围,其中包含至少50%的预测值. [p,s,mu]=polyfit(x,y,n) 返回多项式的系数,mu是一个二维向量 [u1,u2],u1=mean(x),u2=std(x),对数据进行预处理 x=(x-u1)/u2
Smooth选项卡各选项的功能:
.Original data set 用于挑选需要拟合的数据集; .Smoothed data set平滑数据的名称; .Method用于选择平滑数据的方法,每一个相应数据用通过特殊的曲线 平滑方法所计算的结果来取代。平滑数据的方法包括: (ⅰ)Moving average 用移动平均值进行替换; (ⅱ)Lowess局部加权散点图平滑数据,采用线性最小二乘法和一阶 多项式拟合得到的数据进行替换; (ⅲ)Loess局部加权散点图平滑数据,采用线性最小二乘法和二阶多 项式拟合得到的数据进行交换; (ⅳ)Savitzky-Golay 采用未加权的线性最小二乘法过滤数据,利 用指定阶数的多项式得到的数据进行替换; (ⅴ)Span用于进行平滑计算的数据点的数目; (ⅵ)Degree 用于Savitzky-Golay方法拟合多项式的阶数。
>> y=polyval(a,T) %计算多项式在某一点处的值 y = 1.0e+003 * 0.7718 0.8132 0.8754 0.9502 1.0274 >> plot(T,R,'k+',T,y,'r*') >> hold on >> plot(T,y,'b') >> polyval(a,60) ans = 906.0212
s =
自由度为 0 标准偏差为 2.3684e-016
R: [6x6 double] df: 0 normr: 2.3684e-016 mu = 0.1669 0.1499
例:根据表中数据进行4阶多项式拟合 X F(x) 1 10 3 5 4 4 5 2 6 1 7 1 8 2 9 3 10 4
பைடு நூலகம்
(2)Polyval函数 利用该函数进行多项式曲线拟合评价 y=polyval(p,x) 返回n阶多项式在x处的值,x可以是一个矩阵或者是一个向量, 向量p是n+1个以降序排列的多项式的系数。 .y=polyval(p,x,[],mu) 用x=(x-u1)/u2代替x,其中mu是一个二维向量[u1,u2], u1=mean(x),u2=std(x),通过这样处理数据,使数据合理化
.Preview 对所选向量进行图形化预览 .Data set name 设置数据集的名称。工具箱可以随即产 生唯一的文件名,但用户可以重命名。 .Data sets 选项以列表的形式显示所有拟合的数据集。 当选择一个数据集时,可以对它做如下操作: .View 查看数据集,以图标形式和列表形式,可以选 择方法排除异常值; .Rename 重命名 .Delete 删去数据组
例:已知年龄和运动能力的一组数据,试确定二者的关系(根 据图形指定次数) 年龄 17 19 21 23 25 27 29 第一人 20.48 25.13 26.15 30.0 26.1 20.3 19.35 第二人 24.35 28.11 26.3 31.4 26.92 25.7 21.3 >> x1=[17:2:29]; >> x=[x1 x1]; >> y=[20.48 25.13 26.15 30.0 26.1 20.3 19.35 24.35 28.11 26.3 31.4 26.92 25.7 21.3]; >> plot(x,y,'r+')
