南京邮电大学数据结构A第10章
南京邮电大学考研数据结构(811)00-09年真题和答案
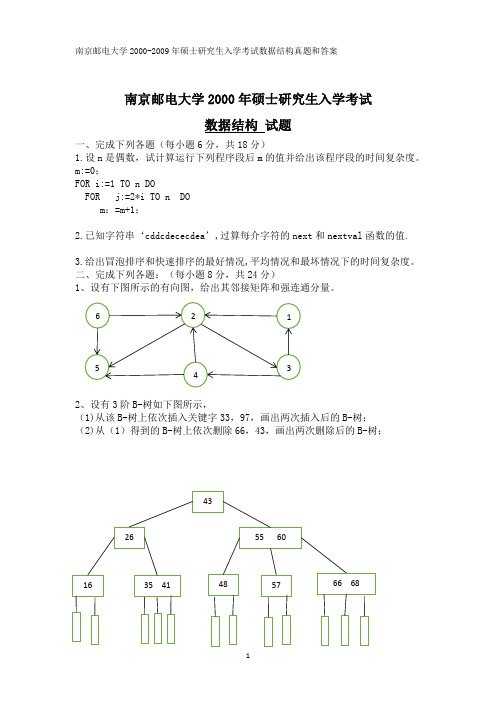
南京邮电大学2000年硕士研究生入学考试数据结构试题一、完成下列各题(每小题6分,共18分)1.设n是偶数,试计算运行下列程序段后m的值并给出该程序段的时间复杂度。
m:=0;FOR i:=1 TO n DOFOR j:=2*i TO n DOm:=m+1;2.已知字符串‘cddcdececd ea’,过算每介字符的next和nextval函数的值.3.给出冒泡排序和快速排序的最好情况,平均情况和最坏情况下的时间复杂度。
二、完成下列各题:(每小题8分,共24分)1、设有下图所示的有向图,给出其邻接矩阵和强连通分量。
2、设有3阶B-树如下图所示,(1)从该B-树上依次插入关键字33,97,画出两次插入后的B-树;(2)从(1)得到的B-树上依次删除66,43,画出两次删除后的B-树;(1)画出据此构造的败选择树(2)画出输出一个记录后的败方树三、阅读下列二叉树算法,每个结点三个域:lchild,element,rchild。
(10分)(1)X(p)对以p为根的二叉树执行什么功能?(2)以下图所示的二叉树调用此算法,则X(p)的执行结果是什么?(3)执行中,栈s中元素个数最多时为多少?给出该时栈中元素的情况。
void X(BinTree *t){struct Stack s;BinTnode *qPush(s,NUL1)While(*p){q=(*p)->lchild(*p)->1child=(*p)->rchild(*p)->rchild=qIf((*p)->lchild)Push(s,(*p)->1child);If((*p)->rchild)Push(s,(*p)->rchild);else(*p)=Pop(s)}}四、阅读下列要求每对顶点之间的最短路径的Floyd算法。
(16分)(1)若对下图所示的有向图执行此算法,写出对k为1到n的各步中,二维数组a和path的值。
南邮_数据结构课后习题答案讲解

?
?
?1 4 7 ?
?
?
?4 4 9 ?
?4 4 9 ?
4.7 求对题图4-1的稀疏矩阵执行矩阵转置时数组
num[]和k[]的值。
col
0
1
2
3
4
num[col] 1
0
2
1
2
k[col]
0
1
1
3
4
2020/2/8
14
第六章 习题讲解
6-2. 对于三个结点 A,B和C,可分别组成多少不同 的无序树、有序树和二叉树?
int i,j,sum=0;
for (i=0;temp[i]<x&&i<n;i++); //找到首个大于等于 x的元素位置 i
if(i>n-1) return; //没有符合条件的元素
ffoorr ((jj==ii;;ljs<tn[j;]<) =y&&j<n;j++); if (lst[j]>y//)找到首个//大大于于yy的的元元素素前位移置 j
?0 0 ???3 0
6 0
0 0
0? 7??
行三元组:???10
2 0
6 ?列三元组:?1
? 3??
??0
0 2
?3?
6
? ?
? 0 0 0 0 0?
?1 4 7 ?
?3 2 ?8?
? ?
0
0 ? 8 10 0??
??3 2 ?8??
??3
3
10
? ?
?? 0 0 0 0 9??
?3 3 10 ?
(2)void Search_Delete(List *lst, T x,T y)
数据结构A第1章(南邮)

程序步数为2n+3。
41
1.5.3 渐近时间复杂度
渐近时间复杂度
使用大 O 记号表示的算法的时间复杂性,称为算法的渐
近时间复杂度,简称时间复杂度。
大O记号 如果存在两个正常数 c 和 n0 ,使得对所有的 n , nn0 ,有 f(n) c g(n) 则有 f(n)=O(g(n))。
42
渐近时间复杂度 使用大 O 记号表示的算法的时间复杂性,称为算法的渐
结点存储块分成两部分,元素本身和该元素后继元素所 在结点的存储地址。
Data
Link
20
小结
逻辑结构 概念
面向 关系
存储结构 数据及其关系在计 算机内的组织方式 面向计算机
数据元素之间逻 辑关系的描述 面向应用问题
存储结构是逻辑结构在计算机内的映像
21
1.2.4 数据结构的运算
• 数据结构最常见的运算 创建运算:创建一个数据结构; 清除运算:删除数据结构中的全部元素; 插入运算:在数据结构的指定位置上插入一 个新元素; 删除运算:将数据结构中的某个元素删除; ……
2.
数据类型 一个数据类型定义了一个值的集合以及作 用于该值集的操作的集合。 即一组值和一组操作。
26
3.抽象数据类型 抽象数据类型( Abstract Data Type, ADT )是一个 数据类型,其主要特征是该类型的对象及其操作的规 范 , 与该类型对象的表示和操作的实现分离,实行封 装和信息隐蔽,即使用和实现分离。 使用和实现分离:使用者通过规范使用该类型的数据,
南邮数据结构答案

第1 章绪论一、基础题1. A2. C3. C4. A5. C二、扩展题1.数据是计算机加工处理的对象;数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理;数据项是组成数据元素的、不可分割的最小单位。
2.数据结构是按某种逻辑关系组织起来的数据元素的集合,使用计算机语言描述并按一定的存储方式存储在计算机中,并在其上定义了一组运算。
3.集合结构、线性结构、树形结构和图形结构。
集合结构中,元素之间没有关系;线性结构中,元素之间存在一对一的关系;树形结构中,元素之间存在一对多的关系,其中最多只有一个元素没有前驱元素,这个元素就是根;图形结构中,元素之间存在多对多的关系。
4.顺序存储、链式存储、索引存储和散列存储。
5.一个算法是对特定问题的求解步骤的一种描述,是指令的有限序列。
其特征包括:➢输入:算法有零个或多个输入➢输出:算法至少产生一个输出➢确定性:算法的每一条指令都有确切的定义,没有二义性。
➢能行性/可行性:可以通过已经实现的基本运算执行有限次来实现➢有穷性:算法必须总能在执行有限步之后终止6.联系:程序是计算机指令的有序集合,是算法用某种程序设计语言的表述,是算法在计算机上的具体实现。
区别:在语言描述上不同,程序必须是用规定的程序设计语言来写,而算法的描述形式包括自然语言、伪代码、流程图和程序语言等;算法所描述的步骤一定是有限的,而程序可以无限地执行下去,比如一个死循环可以称为程序,但不能称为算法。
7.正确性:算法的执行结果应当满足功能需求,无语法错误,无逻辑错误简明性:思路清晰、层次分明、易读易懂,有利于调试维护健壮性:当输入不合法数据时,应能做适当处理,不至于引起严重后果效率:有效使用存储空间和有高的时间效率最优性:解决同一个问题可能有多种算法,应进行比较,选择最佳算法可使用性:用户友好性8(1)执行次数为n-1(n>=2),n=1时执行1次;时间复杂度为O(n)。
(2)执行次数为⌈log3n⌉;时间复杂度为O(logn)(3) 执行次数为n2;时间复杂度为O(n2)(4)执行次数为⌊√n⌋ + 1;时间复杂度为O(√n)第2 章线性表1.A2.D3.B4.C5.B6.D7.D8.C9.A10.D1.编写程序实现对顺序表逆置。
数据结构第10章排序练习及答案

9.1选择题1.从末排序的序列中依次取出一个元素与已排序序列中的元素依次进行比较,然后将其放在排序序列的合适位置,该排序方法称为()排序法。
A)插入B)选择C)希尔D)二路归并【答案】A2.下面各种排序方法中,最好情况下时间复杂度为O(n)的是()A)快速排序B)直接插入排序C)堆排序D)归并排序【答案】B3.用某种排序方法对线性表(25,84,21,47,15,27,68,35,20)进行排序时,无序序列的变化情况如下:25 84 21 47 15 27 68 35 2020 15 21 25 47 27 68 35 8415 20 21 25 35 27 47 68 8415 20 21 25 27 35 47 68 84则所采用的排序方法是()A)选择排序B)希尔排序C)归并排序D)快速排序【答案】D4.下面给出的四种排序法中,()排序是不稳定排序法。
A)插入B)冒泡C)二路归并D)堆【答案】D5.快速排序方法在()情况下最不利于发挥其长处。
A)要排序的数据量太大B)要排序的数据中含有多个相同值C)要排序的数据已基本有序D)要排序的数据个数为奇数【答案】C6.一组记录的关键码为(46,79,56,38,40,84),则利用快速排序的方法,以第一个记录为基准得到的一次划分结果为()A)38,40,46,56,79,84B)40,38,46,79,56,84C)40,38,46,56,79,84D)40,38,46,84,56,79【答案】C7.对记录的关键码{50,26,38,80,70,90,8,30,40,20}进行排序,各趟排序结束时的结果为:50,26,38,80,70,90 ,8,30,40,2050,8,30,40,20,90,26,38,80,7026,8,30,40,20,80,50,38,90,708,20,26,30,38,40,50,70,80,90其使用的排序方法是()A)快速排序B)基数排序C)希尔排序D)归并排序【答案】C8.以下序列不是堆的是()A)100,85,98,77,80,60,82,40,20,10,66B)100,98,85,82,80,77,66,60,40,20,10C)10,20,40,60,66,77,80,82,85,98,100D)100,85,40,77,80,60,66,98,82,10,20【答案】D【解析】根据堆采用完全二叉树的顺序存储形式及堆的特点,因第一个结点即根结点关键字值最大,则应建立一个大根堆,但依据此数据序列建立起堆后关键字值为40的左右孩子结点分别为60、66,不符合大根堆特点。
数据结构第九、十章 作业答案

第九章 查找一、填空题1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 8 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[1..20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ,其下标从小到大依次是1,3,6,8,11,13,16,19______,平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n nn ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m -1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!! 4.折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)8、设一哈希表表长M 为100 ,用除留余数法构造哈希函数,即H (K )=K MOD P (P<=M ), 为使函数具有较好性能,P 应选( 97 )9、在各种查找方法中,平均查找长度与结点个数无关的是哈希查找法 10、对线性表进行二分查找时,要求线性表必须以 顺序 方式存储,且结点按关键字有序排列。
数据结构第九、十章 作业答案

第九章 查找一、填空题1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 8 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[1..20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ,其下标从小到大依次是1,3,6,8,11,13,16,19______,平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n n n ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m -1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!!4.折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)8、设一哈希表表长M 为100 ,用除留余数法构造哈希函数,即H (K )=K MOD P (P<=M ), 为使函数具有较好性能,P 应选( 97 )9、在各种查找方法中,平均查找长度与结点个数无关的是哈希查找法10、对线性表进行二分查找时,要求线性表必须以 顺序 方式存储,且结点按关键字有序排列。
数据结构Ch10习题答案

第十章内部排序一、择题1.用直接插入排序法对下面四个表进行(由小到大)排序,比较次数最少的是(B)。
A.(94,32,40,90,80,46,21,69)插32,比2次插40,比2次插90,比2次插80,比3次插46,比4次插21,比7次插69,比4次B.(21,32,46,40,80,69,90,94)插32,比1次插46,比1次插40,比2次插80,比1次插69,比2次插90,比1次插94,比1次C.(32,40,21,46,69,94,90,80)插40,比1次插21,比3次插46,比1次插69,比1次插94,比1次插90,比2次插80,比3次D.(90,69,80,46,21,32,94,40)插69,比2次插80,比2次插46,比4次插21,比5次插32,比5次插94,比1次插40,比6次2.下列排序方法中,哪一个是稳定的排序方法(BD)。
A.希尔排序B.直接选择排序C.堆排序D.冒泡排序下列3题基于如下代码:for(i=2;i<=n;i++){ x=A[i];j=i-1;while(j>0&&A[j]>x){ A[j+1]=A[j];j--;}A[j+1]=x}3.这一段代码所描述的排序方法称作(A)。
A.插入排序B.冒泡排序C.选择排序D.快速排序4.这一段代码所描述的排序方法的平均执行时间为(D)A.O(log2n) B.O(n) C.O(nlog2n) D.O(n2)5.假设这段代码开始执行时,数组A中的元素已经按值的递增次序排好了序,则这段代码的执行时间为(B)。
A.O(log2n) B.O(n) C.O(nlog2n) D.O(n2)6.在快速排序过程中,每次被划分的表(或了表)分成左、右两个子表,考虑这两个子表,下列结论一定正确是(B)。
A.左、右两个子表都已各自排好序B.左边子表中的元素都不大于右边子表中的元素C.左边子表的长度小于右边子表的长度D.左、右两个子表中元素的平均值相等7.对n个记录进行堆排序,最坏情况下的执行时间为(C)。
数据结构1800试题-第10章 排序 - 答案
第10章排序(参考答案)部分答案解释如下:18. 对于后三种排序方法两趟排序后,序列的首部或尾部的两个元素应是有序的两个极值,而给定的序列并不满足。
20. 本题为步长为3的一趟希尔排序。
24.枢轴是73。
49. 小根堆中,关键字最大的记录只能在叶结点上,故不可能在小于等于n/2的结点上。
64. 因组与组之间已有序,故将n/k个组分别排序即可,基于比较的排序方法每组的时间下界为O(klog2k),全部时间下界为O(nlog2k)。
二、判断题5. 错误。
例如冒泡排序是稳定排序,将4,3,2,1按冒泡排序排成升序序列,第一趟变成3,2,1,4,此时3就朝向最终位置的相反方向移动。
12. 错误。
堆是n个元素的序列,可以看作是完全二叉树,但相对于根并无左小右大的要求,故其既不是二叉排序树,更不会是平衡二叉树。
22. 错误。
待排序序列为正序时,简单插入排序比归并排序快。
三、填空题1. 比较,移动2.生成有序归并段(顺串),归并3.希尔排序、简单选择排序、快速排序、堆排序等4. 冒泡,快速5. (1)简单选择排序 (2)直接插入排序(最小的元素在最后时)6. 免去查找过程中每一步都要检测整个表是否查找完毕,提高了查找效率。
7. n(n-1)/28.题中p指向无序区第一个记录,q指向最小值结点,一趟排序结束,p和q所指结点值交换,同时向后移p指针。
(1)!=null (2)p->next (3)r!=null (4)r->data<q->data(5)r->next (6)p->next9. 题中为操作方便,先增加头结点(最后删除),p指向无序区的前一记录,r指向最小值结点的前驱,一趟排序结束,无序区第一个记录与r所指结点的后继交换指针。
(1)q->link!=NULL (2)r!=p (3)p->link (4)p->link=s (5)p=p->link10.(1)i<n-i+1 (2)j<=n-i+1 (3)r[j].key<r[min].key (4)min!=i (5)max==i(6)r[max]<-->r[n-i+1]11.(1)N (2)0 (3)N-1 (4)1 (5)R[P].KEY<R[I].KEY (6)R[P].LINK(7)(N+2)(N-1)/2(8)N-1 (9)0 (10)O(1)(每个记录增加一个字段) (11)稳定(请注意I的步长为-1)12. 3,(10,7,-9,0,47,23,1,8,98,36) 13.快速14.(4,1,3,2,6,5,7)15.最好每次划分能得到两个长度相等的子文件。
南邮 数据结构A 习题3参考答案

3.4
(1)(a+b)/(c+d)ab+cd+/
(2)b^2-4*a*cb2^4a*c*-
(3)a*c-b/c^2ac*-bc2^/-
(4)(a+b)*c+d/(e+f)ab+c*def+/+
this->Pop();
sq.EnQueue(temp);
}
while (!sq.IsEmpty())
{
sq.Front(temp);
sq.DeQueue();
this->Push(temp);
}
}
3.15
(1)
void max(int a[],int n,int &num)
{
if (n>0)
{
if (a[n-1]>num) num=a[n-1];
(5)(a+b)*(c*d+e)-a*cab+cd*e+*ac*-
3.13
t template <class T>
void SeqStack<T>::Invert(void)
{
SeqQueue<T> sq(maxTop + 1);
T temp;
while (top != -1)
{
this->rn 0;
}
main()
{
int a[10],s,av;
int n=10;
……
2022年南京邮电大学计算机科学与技术专业《数据结构与算法》科目期末试卷A(有答案)

2022年南京邮电大学计算机科学与技术专业《数据结构与算法》科目期末试卷A(有答案)一、选择题1、用有向无环图描述表达式(A+B)*((A+B)//A),至少需要顶点的数目为()。
A.5B.6C.8D.92、将两个各有N个元素的有序表归并成一个有序表,其最少的比较次数是()。
A.NB.2N-1C.2ND.N-13、某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素,则采用()存储方式最节省运算时间。
A.单链表B.仅有头指针的单循环链表C.双链表D.仅有尾指针的单循环链表4、最大容量为n的循环队列,队尾指针是rear,队头:front,则队空的条件是()。
A.(rear+1)MOD n=frontB.rear=frontC.rear+1=frontD.(rear-1)MOD n=front5、在下列表述中,正确的是()A.含有一个或多个空格字符的串称为空格串B.对n(n>0)个顶点的网,求出权最小的n-1条边便可构成其最小生成树C.选择排序算法是不稳定的D.平衡二叉树的左右子树的结点数之差的绝对值不超过l6、若一棵二叉树的前序遍历序列为a,e,b,d,c,后序遍历序列为b, c,d,e,a,则根结点的孩子结点()。
A.只有e B.有e、b C.有e、c D.无法确定7、若元素a,b,c,d,e,f依次进栈,允许进栈、退栈操作交替进行,但不允许连续三次进行退栈操作,则不可能得到的出栈序列是()。
8、已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历结果为()。
A.CBEFDAB.FEDCBAC.CBEDFAD.不定9、有n(n>0)个分支结点的满二叉树的深度是()。
A.n2-1B.log2(n+1)+1C.log2(n+1)D.log2(n-l)10、下列二叉排序树中查找效率最高的是()。
A.平衡二叉树B.二叉查找树C.没有左子树的二叉排序树D.没有右子树的二叉排序树二、填空题11、以下程序的功能是实现带附加头结点的单链表数据结点逆序连接,请填空完善之。
数据结构第九、十章 作业答案

第九章 查找一、填空题1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 8 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[1..20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ,其下标从小到大依次是1,3,6,8,11,13,16,19______,平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n n n ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m -1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!!4.折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)8、设一哈希表表长M 为100 ,用除留余数法构造哈希函数,即H (K )=K MOD P (P<=M ), 为使函数具有较好性能,P 应选( 97 )9、在各种查找方法中,平均查找长度与结点个数无关的是哈希查找法10、对线性表进行二分查找时,要求线性表必须以 顺序 方式存储,且结点按关键字有序排列。
南邮陈慧南版数据结构课后习题答案

}
65
if (p==root) root=root->lchild;
else q->rchild=p->lchild;
37
e=p->element;
25
delete p;
return true;
14
32
}
7.8 以下列序列为输入,从空树开始构造AVL搜索树。 (1)A,Z,B,Y,C,X (2)A,V,L,T,R,E,I,S,O,K
解:1 调用9.4中的函数InDg计算各个顶点的入度; 2 利用拓扑排序算法依次删去入度为0的顶点发出的边,若最后还
有入度不为0顶点,则该有向图存在有向回路,返回真值。
template <class T>
void LinkedGraph<T>::InDg(ENode<T> *a[],int n,int ind[])
int i,j,top=-1; //top为栈顶元素的下标 ENode<T> *p; for(i=0; i<n; i++)
if(!InDegree[i]) {
时间复杂度。
template <class E,class K>
bool BSTree<E,K>::Delete(E&e)
{ BTNode<E> *p=root,*q=p;
if (!p) return flse;
25
37
91
while (p->rchild)
{ q=p;
14
56
p=p->rchild;
if(!visited[i]) DFS1(i,visited,parent); delete []visited, []parent; }
《数据结构A》第01章

南京邮电大学计算机学院 陈慧南 2006年9月 2006年
ADT 1.1 栈ADT ADT Stack { 数据: 数据: 0个或多个元素的线性序列(a0,a1,...,an-1), 其最 个或多个元素的线性序列( 个或多个元素的线性序列 大允许长度为MaxStackSize. 大允许长度为 . 运算: 运算: Create(): 建立一个空栈 : Destroy():撤消一个栈 : Push(x):值为 的新元素进栈,成为栈顶元素 的新元素进栈, :值为x的新元素进栈 Pop():从栈中删除栈顶元素 : Top(x):在x中返回栈顶元素 : 中返回栈顶元素 }
1.1 算法与数据结构
南京邮电大学计算机学院 陈慧南 2006年9月 2006年
程序 = 数据结构+算法 数据结构+
数据结构和算法是计算机学科的基础之一, 数据结构和算法是计算机学科的基础之一, 更是软件技术的基础. 更是软件技术的基础. 数据的组织和表示方法直接影响使用计算机 求解问题的效率. 求解问题的效率. 算法设计通常建立在所处理数据的一定组织 形式之上的,它们之间有着本质的联系. 形式之上的,它们之间有着本质的联系.当 讨论一种算法时, 讨论一种算法时,自然要涉及算法所处理的 数据问题. 数据问题.
1.2.2 数据的逻辑结构
数据的逻辑结构 对数据元素间逻辑关系的描述被称为数据 的逻辑结构(logical structure) ,它可以用 逻辑结构( 一个二元组表示:DS=( 其中, 一个二元组表示:DS=(D,R),其中,D是数 据元素的有限集合, 据元素的有限集合,R是D中元素序偶的集合. 中元素序偶的集合.
南京邮电大学计算机学院 陈慧南 2006年9月 2006年
整型int 整型int的规范 int的规范 的取值范围是: 变量 a 的取值范围是:-32768~32767 执行的操作有: 对变量 a 执行的操作有: 算术运算 +,-,*,/,% 关系运算 <,>,<=,>=,==,!= <=,>=,==, 赋值运算 = 整型int int的实现 整型int的实现 在计算机内存储表示方法. 变量 a 在计算机内存储表示方法. 操作的具体实现方法. 操作的具 in C++
数据结构_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年

数据结构_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年1.向最大堆84,49,82,26,29,46依次插入元素94,99,89,80,94,最终得到的最大堆是____________(提示:堆的元素插入操作需调用AdjustUp方法,请将答案表示成元素序列,并用半角逗号相隔,答案中不要有空格)。
参考答案:99,94,84,89,94,46,82,26,49,29,802.设有5×8的数组A,其每个元素占2个字节,已知A[0][4]在内存中的地址是120,按列优先顺序存储,A[2][6]的地址是_________ 。
参考答案:1443.以下选项_____是下图的深度优先遍历序列。
【图片】参考答案:K,D,A,B,E,C,F,G,J,H,I4.对最大堆序列95,61,66,9,19,27执行1次删除操作(提示:对优先级队列执行删除操作默认删除堆顶元素)后得到最大堆序列_____________(提示:堆元素删除操作需调用AdjustDown方法,请将答案表示成元素序列,并用半角逗号相隔,答案中不要有空格)。
参考答案:66,61,27,9,195.求该方法的渐近时间复杂度为__________.(注意填写答案时不要有空格,用x^y的方式表达x的y次方)void aFunc(int n) { for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) { printf("Hello World\n"); } }}O(n^2)6.已知图的边集合:【图片】若采用邻接表存储,则顶点4对应的边结点链表中共有_________个边结点。
参考答案:27.用克鲁斯卡尔算法构造下图的最小代价生成树,第一条被加入生成树上的边一定是(E,C)。
【图片】参考答案:正确8.假设一棵含有18个结点的完全二叉树中,按层次从上到下、每层结点从左到右的顺序,从0开始编号,则编号为14的结点的左孩子编号为_______(如果孩子不存在,则填写NULL)。
南京邮电大学数据结构A第10章

10.2 简单排序算法
本节介绍三种简单的排序算法: 简单选择排序 冒泡排序 直接插入排序 它们的时间复杂度在最坏情 况下均为O(n2)。 虽然这些算法对数据量较大的情况 不大实用, 但仍然可从中体验排序 课堂提要
第10章 内排序 10.1 排序的基本概念 10.2 简单排序算法 10.2.1 简单选择排序 10.2.2 直接插入排序 10.2.3 冒泡排序 10.3 快速排序 10.4 2路合并排序
48 48 48 48 72 (72 68) 68
02) 48) 48) 48) 48) 68 ) (72) 72)
(02)(36 12 12 12 12 12
12) (68
48) (68
排序结果: (02
图10-1 简单选择排序示意图
10.2 简单排序算法
10.2.1 简单选择排序
程序 10-1 简单选择排序 template <class T> void SelectSort(T A[], int n) { int small; for (int i=0; i<n-1; i++ ) { // n-1趟 small=i; for (int j=i+1; j<n; j++) if (A[j]<A[small]) small=j; Swap(A[i],A[small]); } //endfor } //函数Swap(T &a, T &b)交换两个元素 时间复杂度按比较次数衡量为O(n2)。
…, p(n-1),使得序列按 Kp(0) Kp(1)…Kp(n-1) (非递减) 或 Kp(0)Kp(1)…Kp(n-1) (非递增) 的次序排列为: (Rp(0),Rp(1),…,Rp(n-1))
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.2 简单排序算法
10.2.1 简单选择排序
0 1 2 3 4 5 6
初始序列: (48 第1趟: 第2趟: 第3趟: 第4趟: 第5趟: 第6趟: (02 (02 (02 (02 (02
36
68 68 36) 36 36 36 36
72 72 72 (72 48 48 48
12 12 36 68 48) 48 48
i 48 left 36 68 72 12 48
j 02 ∞ right
找到小于A[left] 接下来会分别把 交换以后, 只要 i 和 j准 尚未相遇,就 的元素 (02), A[left]元素两侧 此时,i和j已经“相遇”过,扫描结束 继续各自的扫描以及交换操作 ; 备和 A[i] 交换 ; 和right“指针”指出了 的序列作为排序对 ,下面要把A[left] 和 A[j]交换,实现 其目的是把较 A[left] 小的元素放到 象递归整个算法过 待排序的元素序列; 了各元素按“左边小右边大”的原则 左边 ,较A[left]大的元素放到右边; 程;(过程略) 分布在A[left]两侧;
为空或只有一个元素时得到有序序列。
(48,36,68,72,12,48,02) (12,36,02,48)48(72,68)
10.3 快速排序
扫描“指针”,向左 扫描“指针”,向右扫 找到大于A[left] 的 扫描寻找 <= A[left] 描寻找 >= A[left] 的 元素 (68), 扫描暂停 ; 36并不大于等 的元素 ; 元素; 准备和 A[j] 交换 ; 于A[left],所 以继续扫描;
10.2 简单排序算法
10.2.2 直接插入排序
temp = 36 68 72 36 12 12
i
i之前是有序区;排序开 始的时候i=1;
48 36 68 72 12 48 02
temp中存放新的欲处 j 理元素; j是扫描 “指针”; 向前寻找插入的位置 ;
10.2 简单排序算法
10.2.2 直接插入排序
12 12 12
12 48 68 12 72
48 48
48 48 48 48
02) 02) 02) 02) 48 02) 72 02) 02) 72 72 72 72 72 72 72
(第1趟) (第2趟) (第3趟) (第4趟) (第5趟) (第6趟)
(36 48 68 12 48 02) (36 48 12 48 02)68 (36 12 48 02)48 68 (12 36 02)48 48 68 (12 02)36 48 48 68 (02)12 36 48 48 68
在最坏情况下需要比较
n( n 1) i i 1 2
n 1
次,移动元素
1 (i 2) (n 4)(n 1) 2 i 1
次。 因此最坏情况时间复杂度为 O(n2),它是稳定的排序方法。
n 1
10.2 简单排序算法
10.2.3 冒泡排序
基本思想:第1趟在序列(A[0]A[n-1])中从前往后进
数据结构A · 第10章
第10章 内排序
内容提要
1、内排序的基本概念; 2、简单排序算法; 3、快速排序算法;
4、两路合并排序;
5、堆排序。
10.1 内排序的基本概念
设有n个数据元素的序列(R0,R1,…,Rn-1),Ki 是Ri 的关 键字。
所谓排序,就是找(0,1, …,n-1)的一种排列p(0), p(1),
10.2 简单排序算法
10.2.3 冒泡排序 A[j+1]<A[j]? Yes(直接后继较小 No(直接后继较大 ), 交换之 ), 无须交换 ; ;
48 36 68 72 12 48
j
02
扫描“指针”;
完成一遍扫描!
10.2 简单排序算法
10.2.3 冒泡排序
冒泡排序最好情况(已有序)下只需进行一趟排序,n-1次 比较,因此最好情况下的时间复杂度是O(n)。 最坏进行n-1趟,第i趟比较(n-i)次,移动元素3(n-i)次, 这样比较次数为:
行两个相邻元素的比较,若后者小,则交换,比较n-1次。
第1趟排序结束,最大元素被交换到A[n-1]中(即沉底)。 下一趟排序只需在子序列(A[0]A[n-2])中进行。如果 在某一趟排序中未交换元素,说明子序列已经有序,则不 再进行下一趟排序。
0 1 2 3 4 5 6
初始序列:(48 第1趟: (36 第2趟: (36
稳定的排序ቤተ መጻሕፍቲ ባይዱ法。
关于稳定性问题:
3,1,3进行简单选择排序: 1,3,3 1,3,3 (似乎是稳定的) 3,3,1进行简单选择排序: 1,3,3 1,3,3
10.2 简单排序算法
10.2.2 直接插入排序
基本思想:将序列中第1个元素作为一个有序序列,然后将 剩下的n-1个元素按关键字大小依次插入该有序序列,经过 n-1趟排序后即成为有序序列。
12
48
48 72) 68 68
02
02 02 02 72) 72)
72) 12 68 48 48
72 ) 48
排序结果: (02
10.2 简单排序算法
10.2.2 直接插入排序
程序 10-2 直接插入排序 template <class T> void InsertSort(T A[], int n){ for(int i=1; i<n; i++ ) { int j=i; T temp=A[i]; while(j>0 && temp<A[j-1]){ A[j]=A[j-1]; j--; } A[j]=temp; } }
…, p(n-1),使得序列按 Kp(0) Kp(1)…Kp(n-1) (非递减) 或 Kp(0)Kp(1)…Kp(n-1) (非递增) 的次序排列为: (Rp(0),Rp(1),…,Rp(n-1))
10.1 内排序的基本概念
序列中两个元素Ri和 Rj (i<j),且 Ki=Kj,排序后,Ri 仍
10.2 简单排序算法
10.2.1 简单选择排序
i指向无序区的 开始位置 small变量用来记录无序 区中最小元素的索引值;
small= 0 14 6
i
48 02
0
36
1
68
2
72
3
12
4
48
5
02 48
6
j
整个无序序列的最小 值02被放到i位置后, 第一遍扫描结束,进 j为扫描“指针” 入第二遍扫描;;
1 ( n i ) n ( n 1) i 1 2
n 1
移动元素次数为3n(n-1)/2。
最坏情况下的时间复杂度为O(n2)。 冒泡排序是稳定的排序方法。
10.3 快速排序
基本思想:对任意给定的序列中元素Rs(关键字为Ks),
经过一趟排序后,将原序列分割成两个子序列,其中,前一
个子序列中的所有元素的关键字均小于等于Ks,后一个子序 列中元素的关键字均大于等于Ks。 称元素Rs 为分割元素。 以后只需对2个子序列分别进行快速排序,直到子序列
10.3 快速排序
0 1 2 3 4 5 6 7
j
算法要求A[n]=+∞,防止i超界。
10.3 快速排序
10.3 快速排序
程序10-4 快速排序 template <class T> void QSort(T A[],int left,int right){ int i,j; if ( left<right ) { i=left; j=right+1; do{ do i++; while (A[i]<A[left]); do j--; while (A[j]>A[left]); if (i<j) Swap(A[i],A[j]); }while (i<j); Swap(A[left],A[j]); QSort(A,left,j-1); QSort(A,j+1,right); }//endif }
48 48 48 48 72 (72 68) 68
02) 48) 48) 48) 48) 68 ) (72) 72)
(02)(36 12 12 12 12 12
12) (68
48) (68
排序结果: (02
图10-1 简单选择排序示意图
10.2 简单排序算法
10.2.1 简单选择排序
程序 10-1 简单选择排序 template <class T> void SelectSort(T A[], int n) { int small; for (int i=0; i<n-1; i++ ) { // n-1趟 small=i; for (int j=i+1; j<n; j++) if (A[j]<A[small]) small=j; Swap(A[i],A[small]); } //endfor } //函数Swap(T &a, T &b)交换两个元素 时间复杂度按比较次数衡量为O(n2)。
0 1 2 3 4 5 6
初始序列: (48) 36 第1趟: (36 48)
68 68
72 72
12 12
48 48
