智能控制及MATLAB实现—水箱液位模糊控制仿真设计
双容水箱液位控制系统设计matlab

双容水箱液位控制系统设计matlab在MATLAB中设计双容水箱液位控制系统,可以使用控制系统工具箱来完成。
以下是一个简单的步骤:1. 创建模型:使用StateSpace函数创建一个双容水箱的状态空间模型。
该模型将包括液位和出流控制的状态变量。
2. 设计控制器:使用控制系统工具箱中的pidtuner函数来设计控制器。
pidtuner函数可以根据指定的性能指标,自动调整PID 控制器的参数。
3. 闭环模拟:使用sim函数对闭环系统进行模拟。
将控制器和系统模型连接起来,并通过输入信号来观察系统的响应。
4. 优化控制器:根据模拟结果,调整控制器的参数以优化系统的性能。
可以使用pidtuner函数的自动调整功能,也可以手动调整参数。
5. 验证性能:通过模拟和实际测试,验证系统的性能是否达到了预期的要求。
如果需要进一步优化,可以返回第4步。
下面是一个简单的示例代码,演示如何在MATLAB中设计和模拟双容水箱液位控制系统:```matlab% 创建模型A = [0 1; 0 -1];B = [0; 1];C = [1 0];D = 0;sys = ss(A, B, C, D);% 设计控制器controller = pidtuner(sys, "pid");% 闭环模拟t = 0:0.01:10;r = 0.5*ones(size(t)); % 设定值[y, t, x] = lsim(controller, r, t);% 绘制结果figureplot(t, y, "b", "LineWidth", 2)hold onplot(t, r, "r--", "LineWidth", 2)xlabel("Time (s)")ylabel("Level")legend("Output", "Reference")% 优化控制器controller = pidtuner(sys, "pid", controller); % 验证性能[y, t, x] = lsim(controller, r, t);% 绘制结果figureplot(t, y, "b", "LineWidth", 2)hold onplot(t, r, "r--", "LineWidth", 2)xlabel("Time (s)")ylabel("Level")legend("Output", "Reference")```这个例子演示了使用PID控制器来控制双容水箱液位。
基于MATLAB的水箱水位模糊控制系统的设计

小相位特性、不稳定性、时滞和负荷干扰等。若采用单一的水位反馈控制难以达到预期的控 制效果,所以采用了仿人的模糊控制方法依据操作人员的现场经验制成模糊控制表,通过判 断水位的偏差及偏差变化率来控制输出,并易于在 PLC 上实现。模糊 PID 控制器的特点是在 大范围内利用模糊推理的方法调整系统的控制量 U,而在小偏差范围内转换成 PID 控制,两 者的转换根据事先给定的偏差范围自动实现[3]。这样做的好处是:既保证动态响应效果,又 能改善稳态控制精度。图 3 为模糊 PID 控制器的系统方框图。
r
+ _
PID 控制器 e
ec 模糊控制器 d/dt
e y
对象 U
变送器
图 3 模糊 PID 控制器系统方框图
其中,模糊控制器和 PID 控制器的切换是通过在 MATLAB 的 M 文件中事先设定误差 e 的 范围来自动实现的[4]。选取水位误差 e 的基本论域为[-10cm,10cm],选取误差变化率 ec 的 基本论域为[-4,4],选取控制量 u 的基本论域为[0,4000]。e、ec、u 的语言变量值分别 为:e={NB,NM,NS,ZE,PS,PM,PB},ec={NB,NM,NS,ZE,PS,PM,PB},u={NB,NM, NS,ZE,PS,PM,PB}。
在现代工业生产及日常生活中,有很多方面都会涉及到水位控制这个问题。而在绝大多 数情况下,我们是很难或是不可能得到被控对象的精确数学模型的,因此采用数学工具或计 算机仿真技术的传统控制理论已经无法解决此类系统的控制问题。[1]智能控制的概念主要是 针对控制对象及其环境、目标和任务的不确定性和复杂性而提出来的,而模糊逻辑控制则作 为一种新颖的智能控制方式越来越受到人们的重视。模糊逻辑控制是智能控制领域的重要发 展方向,模糊控制技术被称为“21 世纪的核心技术”。
基于MATLAB的水箱水位模糊控制

基于MATLAB的水箱水位模糊控制————————————————————————————————作者:————————————————————————————————日期:2目录前言1.模糊控制概述1.1模糊控制的产生及特点 (3)1。
2 模糊控制技术的发展 (4)1。
3 模糊控制理论的研究现状 (5)2.模糊推理原理2。
1模糊控制的基本工作原理 (6)3.基于MATLAB的水箱供水模糊控制3。
1水箱水位模糊控制系统设计 (8)小结 (16)参考文献 (17)第1页前言随着社会经济的迅速发展,水对人们生活与工业生产的影响越来越重要,尤其是近几年,随着居民生活水平的显著提高和城市化进程的加快,居民生活用水和工业用水增长幅度加大,原有的供水系统已经不能满足人们的需求。
为了保证正常的供水,这里应用模糊控制技术,实现对水箱水位的自动控制.第2页3、基于MATLAB的水箱供水模糊控制3。
1水箱水位模糊控制系统设计本系统设计基于MATLAB图形模糊推理系统,设计步骤如下:(1)打开MATLAB,输入指令fuzzy,打开模糊逻辑工具箱的图形用户界面窗口,新建一个Mamdani模糊推理系统。
图3.1 在FIS Editor窗口中新建水位控制模糊推理系统(2)增加一个输入变量,将输入变量命名为水位误差、误差变化,将输出变量命名为阀门开关速度.这样就建立了一个两输入单输出的模糊推理系统,保存为shuixiang.fis。
第3页图3。
2 增加一个输入变量(3)设计模糊化模块:设水位误差的论域为[-1 1],误差变化的论域为[—0.1 0。
1];两个输入量的模糊集都定为5个:其中水位误差定为高、偏高、合适、偏低、低五等;参数分别为[0.3 —1]、[0。
3 —0.5]、[0.3 0]、[0。
3 0.5]、[0.3 1];第4页图3.3 设计水位误差模块误差变化分为大、偏大、合适、偏小、小五等。
参数分别为[0.03 —0。
水箱液位matlab模糊控制例程sltank详解【范本模板】
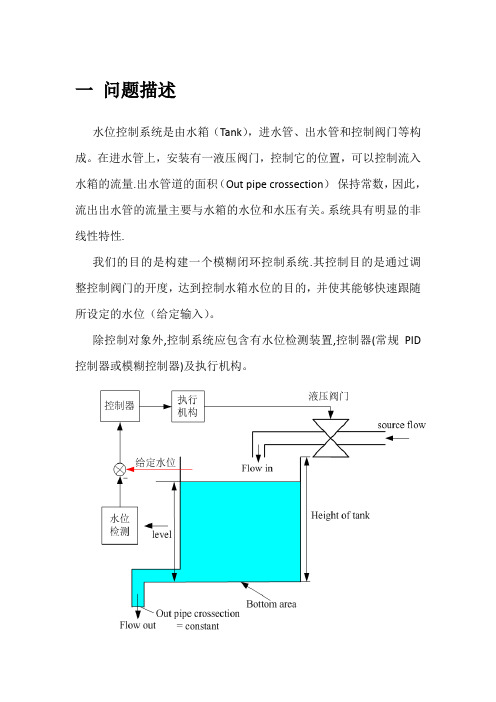
一问题描述水位控制系统是由水箱(Tank),进水管、出水管和控制阀门等构成。
在进水管上,安装有一液压阀门,控制它的位置,可以控制流入水箱的流量.出水管道的面积(Out pipe crossection)保持常数,因此,流出出水管的流量主要与水箱的水位和水压有关。
系统具有明显的非线性特性.我们的目的是构建一个模糊闭环控制系统.其控制目的是通过调整控制阀门的开度,达到控制水箱水位的目的,并使其能够快速跟随所设定的水位(给定输入)。
除控制对象外,控制系统应包含有水位检测装置,控制器(常规PID 控制器或模糊控制器)及执行机构。
二控制系统动态结构图流速计算依据为简化伯努利方程或托里拆利定律,二者结论一致。
其中托里拆利定律内容为:忽略粘滞性,任何液体止点从小孔中流出的速度与它从h高度处自由落下的速度相等。
Level flow out动态模型中主要用到的计算关系式如下:液位=容积/底面积level=tank volume/area流量=流速*出水口面积流速=(2*g*level)^0.5被控对象水箱模型搭建按照上述动态结构图进行,实际设计的水箱模型如下:封装后执行机构:VALVE三水位控制系统模型四模型使用方法启动matlab,命令行输入sltank,既可打开水位模糊控制仿真模型. 设置const大于等于0,系统工作于PID控制模式设置const小于0,系统工作于模糊控制模式模糊控制时液位输入输出关系(双击Comparison示波器)液位动画PID控制时液位的输入输出关系比较两种控制模式下液位曲线可以发现PID控制有超调,这一点在液位动画中也有体现.修改模型参数PID参数的调整可以直接双击PID Controller模块设置,这里着重介绍模糊控制器参数的修改.用到的主要命令如下:例如可通过以下代码以文本形式显示tanka=readfis(’tank’)%读取tank文件showfis(a); %显示在这里通过模糊推理的用户界面来修改水位控制的规则库,查看对控制效果的影响。
模糊控制水箱液位调节

实验二:模糊控制水箱液位调节一实验目的1.掌握模糊控制的原理2.加强模糊控制在实践中的应用二实验器材装有Matlab软件PC电脑一台三实验原理模糊控制的基本原理:它的核心部分为模糊控制器,模糊控制器的控制规律由有计算机程序实现。
详见P32(模糊控制原理)。
四原代码clear allclose allq1=0; %定义第一个水箱的入水量q2=0; %定义第一个水箱的出水量q3=0; %定义第二个水箱的出水量q4=0; %定义第三个水箱的出水量b=1.4; %定义第一个水箱入水量的控制系数a1=8.6; %定义第一个水箱出水量的控制系数a2=8.6; %定义第一个水箱出水量的控制系数h1=100; %定义第一个水箱中水的初始高度h2=100; %定义第二个水箱中水的初始高度h3=100; %定义第三个水箱中水的初始高度v=119; %定义sin函数的系数s=190; %定义水箱底面积k=10; %定义开关控制量e=0; %定义误差e_1=0;ec=0;H=130; %定义第三个水箱的期望高度e=H-h1;a=newfis('fuzz'); %误差函数a=addvar(a,'input','e',[-25,25]);a=addmf(a,'input',1,'NB','zmf',[-25,-10]);a=addmf(a,'input',1,'PS','trimf',[-25,-10,0]);a=addmf(a,'input',1,'Z','trimf',[-10,0,10]);a=addmf(a,'input',1,'PS','trimf',[0,10,25]);a=addmf(a,'input',1,'PB','smf',[10,25]);a=addvar(a,'output','u',[0,100]); %控制量输出函数a=addmf(a,'output',1,'NB','zmf',[0,30]);a=addmf(a,'output',1,'NS','trimf',[0,30,50]);a=addmf(a,'output',1,'Z','trimf',[30,50,70]);a=addmf(a,'output',1,'PS','trimf',[50,70,100]);a=addmf(a,'output',1,'PB','smf',[70,100]);rulelist=[1 1 1 1;2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1];a = addrule(a, rulelist);for i=1:1:8000tt(i)=i; %时间轴q1=b*k; %第一个水箱的进水量q2=a1*sqrt(h1); %第一个水箱的出水量h1=h1+(q1-q2)/s; %第一个水箱中水的高度q3=a2*sqrt(h2); %第二个水箱的进水量h2=h2+(q2-q3)/4; %第二个水箱中水的高度q4=v*abs(sin(2.3*pi*i+0.35)); %第二个谁想的出水量h3=h3+(q3-q4)/s; %第三个水箱中的高度hh(i)=h3;k=evalfis(e,a);e=H-h3;endplot(tt,hh)五、插图。
水箱液位控制PID的MATLAB参数整定及仿真

水箱液位控制PID的MATLAB参数整定及仿真摘要:PID控制器主要针对控制对象来进行参数调节。
PID的归一参数整定法和试凑法费时,费力。
针对这一问题,探讨MATLAB实现PID参数整定及仿真,同时观察控制参数对PID控制规律的影响。
关键词:PID;参数整定;仿真1 引言PID控制器又称为PID调节器,是按偏差的比例P、积分I、微分D进行控制的调节器的简称,它主要针对控制对象来进行参数调节。
因为它算法简单、稳定性好、工作可靠、鲁棒性好,在工程上易于实现,但PID控制器的参数整定方法复杂,通常采用PID归一参数法和试凑法来确定,但较费时、费力。
针对这一问题,文中探讨用MATLAB实现PID参数整定及仿真的方法及控制参数对PID控制规律的影响。
利用MATLAB强大的计算仿真能力,解决了利用试凑法来整定参数浩繁的工作,可以方便、快速地找到使系统达到满意性能指标的参数。
2 PID控制器的原理与算法图1是典型PID控制系统结构图。
在PID调节器作用下,对误差信号分别进行比例、积分、微分控制。
PID控制算法的模拟表达式为μ (t) =Kp [ + +Td de(t) dt ]相应的传递函数为:Gc(s)= Kp(1 +S + TdS)3 水箱水位调节系统:一个典型的水箱水位自动控制系统如下图所示。
这个水位控制系统中,水池的进水量Q1来自手动控制开度的进水阀门,通过调节出水阀门调节出水量Q2,使水箱水位保持设定水位不变。
这个系统是个典型单冲量自动调节系统,在该系统中:系统中各组成单元的模型如下:水箱对象模型:G(s)=液位传感器:量程0~40cm执行阀:对应0~100%开度系统的方框图如图所示:4 PID控制器的MATLAB仿真PID控制器的参数Kp、Ti、Td分别对系统性能产生不同的影响。
在控制过程中如何把Kp、Ti、Td 3参数调节到最佳状态,需要深入了解PID控制中3参数对系统动态性能的影响。
下面讨论水箱水位调节系统中当一个参量发生变化,对应曲线的实时变化。
基于MATLAB水箱液位控制系统的设计课程设计(可编辑)

基于MATLAB水箱液位控制系统的设计课程设计太原理工大学过程控制系统课程设计设计名称水箱液位系统的控制设计目录摘要III任务书IV第1章绪论 41.1过程控制的定义 41.2过程控制的目的 41.3过程控制的特点 51.4过程控制的发展与趋势5第2章水箱液位控制系统的原理 62.1 人工控制与自动控制 6 2.2 水箱液位控制系统的原理框图 7 2.3 水箱液位控制系统的数学模型 8第3章水箱液位控制系统的组成113.1 被控制变量的选择113.2 执行器的选择 113. 3 PID控制器的选择143.4 液位变送器的选择15第4章PID控制规律174.1 比例控制174.2积分控制(I) 194.3微分控制(D) 194.4比例积分控制(PI) 204.5比例积分微分控制(PID) 20第5章利用MATLAB进行仿真设计..205.1MATLAB设计205.2 MATLAB设计任务215.3 MATLAB设计要求215.4 MATLAB设计任务分析215.5 MATLAB设计内容255.5.1主回路的设计255.5.2副回路的设计255.5.3主、副回路的匹配265.5.4 单回路PID控制的设计27 5.5.5串级控制系统的设计32 5.5.6串级控制系统的PID参数整定 34总结36参考文献36摘要在人们生活以及工业生产等诸多领域经常涉及到液位和流量的控制问题,?例如居民生活用水的供应,?饮料、食品加工,?溶液过滤,?化工生产等多种行业的生产加工过程,?通常需要使用蓄液池,?蓄液池中的液位需要维持合适的高度,?既不能太满溢出造成浪费,?也不能过少而无法满足需求。
因此液面高度是工业控制过程中一个重要的参数,特别是在动态的状态下,采用适合的方法对液位进行检测、控制,能收到很好的效果。
?PID控制(比例、积分和微分控制)是目前采用最多的控制方法。
本文主要是对一水箱液位控制系统的设计过程,涉及到液位的动态控制、控制系统的建模、PID算法、传感器和调节阀等一系列的知识。
模糊控制及matlab仿真

模糊控制及matlab仿真1 .实例某个液位控制系统的液体容器中,液体的流出量变化无常,无法建立起数学模型,只能通过控制进液阀门开度调节液位,使容器中的液位保持平衡。
根据积累的操作经验,归纳总结出使液体容器液位保持恒定的下述几条操作规律。
1.如果液位正好,则阀门开度不变;If level is okay then value is no change2.如果液位偏低,则增大阀门开度;If level is low then value is open fast3.如果液位偏高,则减小阀门开度;If level is high then value is close fast4.如果液位正好而进液流速快,则逐渐减小阀门开度;If level is okay and rate is positive then value is close slow5.如果液位正好而进液流速慢,则逐渐增大阀门开度;If level is okay and rate is negation then value is open slow 2. simulink模块及fis文件本系统采用曼达尼模型进行仿真,通过matlab模糊控制编辑器进行控制规则的建立,以及模糊控制器的搭建。
Fis编辑器如下图所示,该控制器为两输入一输出系统。
其中两输入分别为液位高度,及液位变化速率,输出为阀门开度。
“与”算法用求积来表达,“或”算法用代数和来表达,“蕴含”算法用求积来表达,“综合”算法为各条模糊规则结果取并,“清晰化”算法用面积中心法来描述。
隶属函数编辑器液位隶属函数液位变化速率隶属函数阀门开度隶属函数控制规则编写Simulink模块3. 仿真及结果分析液位初始波动与经过阀门调节后系统液位曲线比较。
智能控制及MATLAB实现—水箱液位模糊控制仿真设计

水箱水位模糊控制系统设计一.在MATLAB命令窗口中输入sltank,便可打开如图所示的模型窗口。
图1 sltank仿真图(1)打开MATLAB,输入指令fuzzy,打开模糊逻辑工具箱的图形用户界面窗口,新建一个Mamdani模糊推理系统。
(2)增加一个输入变量,将输入变量命名为水位误差、误差变化,将输出变量命名为阀门开关速度。
这样就建立了一个两输入单输出的模糊推理系统,保存为shuiwei1。
图2 增加一个输入变量(3)设计模糊化模块;设水位误差level的论域为[2、95 3、05],误差变化率rate的论域为[-0、2 0、2];两个输入量的模糊集为level设为为7个,rate设为5个:其中水位误差level定为NB、NM、NS、ZE、PS、PM、PB;参数分别为[0、01 2、95]、[0、01 2、97],[0、01 2、99]、[0、01 3]、[0、01 3、01]、[0、01 3、03]、[0、01 3、05],隶属度均为高斯函数;图3 输入量level的参数设定误差变化率rate分别为负大,负小,不变,正小,正大。
参数分别为,[0、03 -0、2]、[0、03 -0、1]、[0、03 0]、[0、03 0、1]、[0、03 -0、2],隶属度函数均为高斯函数。
图4 误差变化率rate的参数设定阀门的开关速度设为七个等级:快关,中关,慢关,不动,慢开,中开,快开,其论域为[2、95 3、05]。
参数分别为;[2、94 2、95 2、96]、[2、965 2、97 2、975]、[2、99 2、99 2、995]、[2、999 3 3、001]、[3、005 3、01 3、015]、[3、02 3、03 3、035]、[3、04 3、05 3、06],隶属函数为三角形函数。
图5 输出量valve的参数设定(4)设计模糊规则打开Ruel Editor窗口,通过选择添加模糊规则;1)If (level is NB) and (rate is 负大) then (valve is 快关) (1)2)If (level is NB) and (rate is 负小) then (valve is 快关) (1) 3)If (level is NB) and (rate is 不变) then (valve is 快关) (1) 4)If (level is NB) and (rate is 正小) then (valve is 中关) (1)5)If (level is NB) and (rate is 正大) then (valve is 不动) (1) 6)If (level is NM) and (rate is 负大) then (valve is 快关) (1) 7)If (level is NM) and (rate is 负小) then (valve is 快关) (1) 8)If (level is NM) and (rate is 不变) then (valve is 快关) (1) 9)If (level is NM) and (rate is 正小) then (valve is 中关) (1)10)If (level is NM) and (rate is 正大) then (valve is 不动) (1) 11)If (level is NS) and (rate is 负大) then (valve is 中关) (1) 12)If (level is NS) and (rate is 负小) then (valve is 中关) (1) 13)If (level is NS) and (rate is 不变) then (valve is 中关) (1) 14)If (level is NS) and (rate is 正小) then (valve is 不动) (1) 15)If (level is NS) and (rate is 正大) then (valve is 慢开) (1) 16)If (level is ZE) and (rate is 负大) then (valve is 中关) (1) 17)If (level is ZE) and (rate is 负小) then (valve is 慢关) (1) 18)If (level is ZE) and (rate is 不变) then (valve is 不动) (1)19)If (level is ZE) and (rate is 正小) then (valve is 慢开) (1) 20)If (level is ZE) and (rate is 正大) then (valve is 中开) (1) 21)If (level is PS) and (rate is 负大) then (valve is 慢关) (1) 22)If (level is PS) and (rate is 负小) then (valve is 不动) (1) 23)If (level is PS) and (rate is 不变) then (valve is 中开) (1) 24)If (level is PS) and (rate is 正小) then (valve is 中开) (1) 25)If (level is PS) and (rate is 正大) then (valve is 中开) (1) 26)If (level is PM) and (rate is 负大) then (valve is 不动) (1) 27)If (level is PM) and (rate is 负小) then (valve is 中开) (1) 28)If (level is PM) and (rate is 不变) then (valve is 快开) (1) 29)If (level is PM) and (rate is 正小) then (valve is 快开) (1) 30)If (level is PM) and (rate is 正大) then (valve is 快开) (1) 31)If (level is PB) and (rate is 负大) then (valve is 不动) (1) 32)If (level is PB) and (rate is 负小) then (valve is 中开) (1) 33)If (level is PB) and (rate is 不变) then (valve is 快开) (1) 34)If (level is PB) and (rate is 正小) then (valve is 快开) (1) 35)If (level is PB) and (rate is 正大) then (valve is 快开) (1) 这35条模糊控制规则的权重都为1、图6 模糊控制规则的设定(5)利用编辑器的 to Workspace, 将当前的模糊推理系统,以shuiwei1保存到工作空间中。
Matlab 水位控制仿真
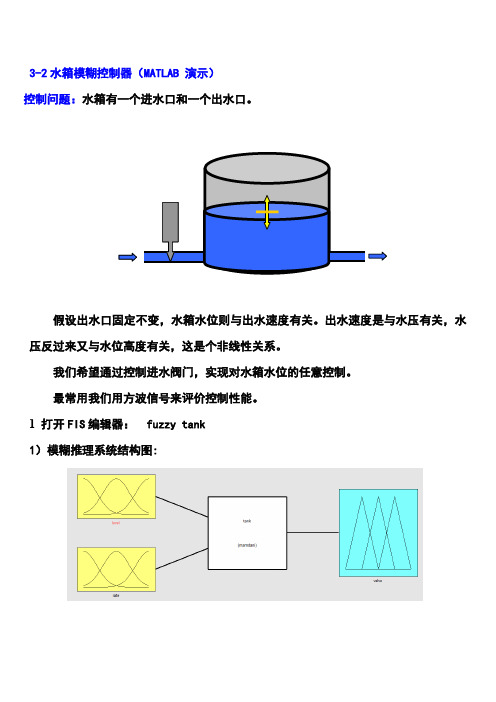
3-2水箱模糊控制器(MATLAB 演示)控制问题:水箱有一个进水口和一个出水口。
假设出水口固定不变,水箱水位则与出水速度有关。
出水速度是与水压有关,水压反过来又与水位高度有关,这是个非线性关系。
我们希望通过控制进水阀门,实现对水箱水位的任意控制。
最常用我们用方波信号来评价控制性能。
1 打开FIS编辑器: fuzzy tank1)模糊推理系统结构图:2)水箱FIS系统结构参数:-----------------------------------a=readfis('tank')---------------------------------a =name: 'tank'type: 'mamdani'andMethod: 'prod'orMethod: 'probor'defuzzMethod: 'centroid'impMethod: 'prod'aggMethod: 'max'input: [1x2 struct]output: [1x1 struct]rule: [1x5 struct]3)水箱FIS详细参数--------------------------------------a=readfis('tank')showfis(a)---------------------------------------1. Name tank2. Type mamdani3. Inputs/Outputs [2 1]4. NumInputMFs [3 3]5. NumOutputMFs 56. NumRules 57. AndMethod prod ;求积运算8. OrMethod probor ;代数和运算9. ImpMethod prod10. AggMethod max11. DefuzzMethod centroid12. InLabels level 输入变量名13. rate14. OutLabels valve 输出变量名15. InRange [-1 1] ;输入论域16. [-0.1 0.1]17. OutRange [-1 1] 输出论域18. InMFLabels high 输入1模糊参考集名称19. okay20. low21. negative 输入2模糊参考集名称22. none23. positive24. OutMFLabels close_fast ;输出模糊参考集名称25. close_slow26. no_change27. open_slow28. open_fast29. InMFTypes gaussmf ;输入模糊参考集形状,高斯型30. gaussmf31. gaussmf32. gaussmf33. gaussmf34. gaussmf35. OutMFTypes trimf ;输出模糊参考集形状,三角形36. trimf37. trimf38. trimf39. trimf40. InMFParams [0.3 -1 0 0] 模糊参考集形状参数41. [0.3 0 0 0]42. [0.3 1 0 0]43. [0.03 -0.1 0 0]44. [0.03 0 0 0]45. [0.03 0.1 0 0]46. OutMFParams [-1 -0.9 -0.8 0]47. [-0.6 -0.5 -0.4 0]48. [-0.1 0 0.1 0]49. [0.2 0.3 0.4 0]50. [0.8 0.9 1 0]51. Rule Antecedent [2 0] 模糊规则前件52. [3 0]53. [1 0]54. [2 3]55. [2 1]51. Rule Consequent 3 模糊规则后件52. 553. 154. 255. 451. Rule Weight 152. 153. 154. 155. 151. Rule Connection 152. 153. 154. 155. 14)列出水箱FIS的模糊规则------------------------------------a=readfis('tank');showrule(a)------------------------------------ans =1. If (level is okay) then (valve is no_change) (1)2. If (level is low) then (valve is open_fast) (1)3. If (level is high) then (valve is close_fast) (1)4. If (level is okay) and (rate is positive) then (valve is close_slow) (1)5. If (level is okay) and (rate is negative) then (valve is open_slow) (1) 5)隶属函数形状6)模糊推理过程图7)模糊推理输入输出关系图sltank,进入Simlink环境观察输入与输出的关系(1)模糊控制器与PID控制器作比较将开关选择“const”, 由-1改为1,表示PID控制器工作观察输出响应情况(4)观察模糊规则变化的影响键入命令:ruleedit tank删除最后两条规则,将结果临时存入工作空间: File /Export / To workspace(退出ruleedit窗口时不要选择保存选择,否则会破坏源程序设置)1. If (level is okay) then (valve is no_change) (1)2. If (level is low) then (valve is open_fast) (1)3. If (level is high) then (valve is close_fast) (1)4. If (level is okay) and (rate is positive) then (valve is close_slow) (1)5. If (level is okay) and (rate is negative) then (valve is open_slow) (1)(c)切换到sltank的Simlink环境,观察结果。
基于MATLAB的双容水箱液位控制系统设计

基于MATLAB的双容水箱液位控制系统设计双容水箱液位控制系统是一种常见的控制系统,用于控制水箱中液位的稳定性。
这个系统的主要目标是保持水箱中的液位在一个提前设定好的范围内。
在这篇文章中,我们将基于MATLAB来设计和实现一个双容水箱液位控制系统。
首先,我们需要定义系统的输入和输出。
在这个系统中,输入是水箱中的水流量,输出是水箱中的液位。
我们假设系统中的水流量是恒定的,并且可以通过控制阀门的开关来改变流量。
接下来,我们需要建立双容水箱液位控制系统的数学模型。
对于这个系统,我们可以使用连续时间的均衡方程来描述液位的变化。
假设水箱中的两个容器分别为C1和C2,它们之间通过阀门进行连接。
液位的变化是由水的流入和流出速度之间的差异决定的。
我们可以用下面的方程来表示两个容器液位变化的速度:C1 * dh1/dt = Qin - q12 - q01C2 * dh2/dt = q12 - q02其中,C1和C2分别表示两个容器的容积,dh1/dt和dh2/dt表示液位的变化速率,Qin表示系统输入的水流量,q12表示C1到C2的流出速度,q01表示C1的流出速度,q02表示C2的流出速度。
我们可以通过求解这个方程组来得到系统的状态空间表示。
为了简化推导,我们假设液位变化的速率很快,即dh1/dt≈0和dh2/dt≈0。
在这种情况下,我们可以得到一个简化的状态空间表示:x=(h1,h2)u = (Qin, q01, q02)其中,x是系统的状态向量,包括两个容器的液位,u是系统的控制输入向量,包括系统的输入流量和阀门的开关。
接下来,我们需要设计一个合适的控制器来控制系统的输出液位。
在这里,我们选择使用PID控制器。
PID控制器通过调整控制输入u来控制输出液位。
PID控制器的输出是根据系统的误差信号计算得到的。
在这里,误差信号是目标液位与实际液位之间的差异。
PID控制器通过比例增益、积分增益和微分增益来调整控制输入,以最小化误差信号。
基于MATLAB水箱液位控制系统的设计

基于MATLAB水箱液位控制系统的设计水箱液位控制系统是水处理领域的一个重要应用,可以实现对水箱液位的监测和控制。
本文将基于MATLAB平台设计一个水箱液位控制系统,并详细介绍其工作原理、设计步骤和实现方法。
1.设计目标和原理设计目标是实现水箱液位的实时监测和自动控制,保持液位在设定值附近波动。
系统原理是通过传感器实时检测水箱液位,将液位信号传输给控制器进行处理,控制器根据设定值和实际液位偏差调整执行机构的动作,使液位保持在设定值范围内。
2.设计步骤(1)确定传感器和执行机构:选择合适的液位传感器和执行机构,如浮球传感器和电动阀门。
(2)建立数学模型:根据系统特性建立数学模型,描述液位与传感器输出和执行机构控制信号之间的关系。
(3)设计控制器:根据液位模型设计控制器,如PID控制器。
(4)编写MATLAB程序:使用MATLAB编写程序,实现液位监测、控制器设计和控制信号输出。
3.系统实现方法(1)建立模拟环境:在MATLAB中建立水箱液位模拟环境,包括液位模型、传感器模型和执行机构模型。
(2)液位监测:读取传感器输出信号,获取实时液位信息。
(3)控制器设计:根据实时液位和设定值计算控制信号,可以使用PID控制器进行设计。
(4)控制信号输出:将控制信号发送给执行机构,实现对阀门的开关控制。
(5)反馈调整:根据执行机构的反馈信号对控制器参数进行调整,以进一步优化系统性能。
4.系统性能指标和优化(1)稳定性:控制系统在干扰的情况下能够保持液位稳定。
(2)响应速度:控制系统对液位变化的响应速度,可以通过调整控制器参数来实现快速响应。
(3)偏差:控制系统的液位偏差大小,可以通过调整控制器参数和设定值来控制偏差范围。
(4)抗干扰性能:控制系统对外界干扰(如水源变化)的抵抗能力。
(5)稳定性分析:通过系统稳定性分析,确定系统参数的合理范围。
(6)优化方法:通过试验和仿真,不断调整控制器参数和设定值,以实现最佳控制效果。
水箱液位控制系统

水箱液位控制及MATLAB仿真实现报告ﻬ目录水箱液位控制及MATLAB仿真实现报告................ 错误!未定义书签。
目录.......................................................................... 错误!未定义书签。
摘要.......................................................................... 错误!未定义书签。
水箱液位控制系统原理ﻩ错误!未定义书签。
水箱液位控制系统的数学模型ﻩ错误!未定义书签。
(一)确定过程的输入变量和输出变量ﻩ错误!未定义书签。
(二)水箱液位控制系统的算法: .............. 错误!未定义书签。
(三)水箱液位控制系统的MATLAB/simulink的仿真:错误!未定义书签。
(四)结果分析:ﻩ错误!未定义书签。
总结ﻩ错误!未定义书签。
摘要在人们生活和工业生产等诸多领域中经常涉及到液位和流量的控制系统问题,因此液面高度是工业控制过程中的一个重要参数,特别是在动态的过程下,采用合适的方法对液位进行检测、控制,能收到很好的效果。
PID控制是目前采用最多的控制方法。
本文介绍了双容水箱中控制液位的控制技术以及使用matlab 仿真软件去进行液位仿真,通过PID控制实现液位的自动控制,用matlab软件建立数学模型,再写出液位控制的PID算法进行数据模拟,最后实现水箱液位通过计算机技术自动控制。
通过matlab软件仿真实现了液位的实时测量和监控。
系统通过matlab仿真对实验所得的参数和仿真数据与曲线进行分析,总结参数变化对系统性能的作用。
关键字:PID控制液位控制matlab仿真算法水箱液位控制系统原理控制系统由四个基本环节组成,即被控对象、侧量传送装置、控制装置和执行装置:水箱液位控制系统的数学模型(一)确定过程的输入变量和输出变量流入水箱的流量Q1是输入变量,流出水箱的流量L2取决于液位L和水箱出水阀门的开度,Q2为输出变量,被控对象是水箱,故系统控制模型图如下:(二)ﻬ水箱液位控制系统的算法:Q1:水箱流入量Q 2:水箱流出量A:水箱截面积u :进水阀开度f:出水阀开度h :水箱液位高度h0:水箱初始液位高度K1:阀体流量比例系数假设f 不变,系统初始态为稳态,H 0=2m,K 1=10,A=10m 2。
双容水箱液位控制系统设计matlab

双容水箱液位控制系统设计matlab
在MATLAB中设计双容水箱液位控制系统,可以遵循以下步骤: 1. 建立系统模型:根据双容水箱液位控制系统的物理特性,建立系统的数学模型。
可以使用差分方程、传递函数或状态空间模型表示系统的动态行为。
2. 设计控制器:选择合适的控制策略,如比例-积分-微分(PID)控制器。
根据系统模型和控制目标,调整控制器的参数以实现所需的控制性能。
3. 进行系统仿真:使用MATLAB提供的仿真工具,如Simulink,搭建双容水箱液位控制系统的仿真模型。
将系统模型和控制器模型连接起来,设置仿真参数,运行仿真并观察系统的响应。
4. 优化控制器:根据仿真结果,对控制器进行调整和优化,以改善系统的稳定性和性能。
可以尝试不同的控制策略和参数组合,比较它们的效果,并选择最佳的控制器配置。
5. 验证控制器:在实际系统中验证优化后的控制器。
将控制器实施到双容水箱液位控制系统中,监测系统的实际响应,并对控制器进行进一步调整和优化。
通过以上步骤,可以设计和优化双容水箱液位控制系统,并在MATLAB环境中进行仿真和验证。
这样可以大大减少实际试错的成本和风险,并提高系统的稳定性和性能。
模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个模糊控制在MATLAB中的简单实例:假设我们要设计一个模糊控制器来控制一个水箱中水位的高低。
我们可以先建立一个模糊推理系统,其中包含输入和输出变量以及规则。
1. 输入变量:水箱中的水位(假设范围为0到100)。
2. 输出变量:水泵的流量(假设范围为0到10)。
我们需要定义一组模糊规则,例如:如果水箱中的水位为低,则水泵的流量为低。
如果水箱中的水位为中等,则水泵的流量为中等。
如果水箱中的水位为高,则水泵的流量为高。
将这些规则转换成模糊集合,如下所示:输入变量:- 低:[0, 30]- 中等:[20, 50]- 高:[40, 100]输出变量:- 低:[0, 3]- 中等:[2, 6]- 高:[4, 10]接下来,我们可以使用MATLAB的Fuzzy Logic Toolbox来建立模糊推理系统。
以下是一个简单的MATLAB脚本:```% 定义输入变量water_level = fisvar("input", "Water Level", [0 100]); water_level.addmf("input", "low", "trapmf", [0 0 30 40]); water_level.addmf("input", "medium", "trimf", [20 50 80]);water_level.addmf("input", "high", "trapmf", [60 70 100 100]);% 定义输出变量pump_flow = fisvar("output", "Pump Flow", [0 10]);pump_flow.addmf("output", "low", "trapmf", [0 0 3 4]); pump_flow.addmf("output", "medium", "trimf", [2 6 8]); pump_flow.addmf("output", "high", "trapmf", [7 8 10 10]); % 建立模糊推理系统rule1 = "If Water Level is low then Pump Flow is low"; rule2 = "If Water Level is medium then Pump Flow is medium"; rule3 = "If Water Level is high then Pump Flow is high"; rules = char(rule1, rule2, rule3);fis = newfis("Water Tank Fuzzy Controller");fis = addvar(fis, water_level);fis = addvar(fis, pump_flow);fis = addrule(fis, rules);% 模糊控制器输入water_level_value = 70;% 运行模糊推理系统pump_flow_value = evalfis([water_level_value], fis);disp(["Water level: " num2str(water_level_value) "%"]); disp(["Pump flow: " num2str(pump_flow_value)]);```在这个简单的例子中,我们使用了Fuzzy Logic Toolbox来定义输入和输出变量以及规则,并运行模糊推理系统来计算输出值。
水箱液位控制器matlab

figure(1); plotfis(a2); figure(2); plotmf(a,'input',1); figure(3); plotmf(a,'output',1);
showrule(a); ruleview('tank');
for i=1:1:7 e(i)=i-4; Ulist(i)=evalfis([e(i)],a2);
end Ulist = round(Ulist);
disp('------------------------------------------------------'); disp('----------模糊控制表:e =[-3,3], u = [-4,4]-----------'); disp('------------------------------------------------------'); fprintf('| a |'); fprintf(' %d |',e); fprintf('\n'); fprintf('| u |'); fprintf(' %d |',Ulist); fprintf('\n');
水箱液面模糊控制及Matlab仿真实现

!"#$
图 " 模糊控制系统结构图
由 图 " 可 知< 要 想 实 现 控 制 目 标< 关 键 在 于 以 下 的三个 步骤 < 即输入 变 量 的 模 糊 化 < 模 糊 关 系 矩 阵 的 获取 < 模糊结果的获 得 以 及 其 输 出 的 去 模 糊 化 D 模 糊 控制系统首先将输入量 M 和 !M 经过模糊化处理< 然 后送到模糊推理环节进行推理 < 推理后得出的输出模 糊量再进行精确化处理 < 最后输出到控制执行环节中 控制被控对象 % 根 据 模 拟 的 实 际 情 况 及 要 求 水 箱 液 面 在 HDICJ "DKC 内波动 < 理想的状态是 "D%C< 易知液面偏差 M 的 基本论域为 PJHDI< HDIQ< 量化为 PJR JS J% J" H " % S RQ T 个 等 级 < 定 义 L 个 模 糊 语 言 变 量 U V 正 大 VNW’XY< V 正 小 V!W’WZ< V 零V!W[MZ< V 负小V!W\WZ< V负大 V!W\XZD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
智能控制及MATLAB实现—水箱液位模糊控制仿真设计智能控制是一种利用先进的智能技术和算法来实现自动控制的方法。
在智能控制中,模糊控制是一种常见且有效的方法之一、模糊控制通过将
模糊逻辑应用于控制系统中的输入和输出,根据模糊规则来进行决策和控制。
水箱液位控制是一个典型的控制问题,常常用于工业和民用领域中的
自动化系统。
在许多控制应用中,水箱液位的控制是一个关键的问题,因
为它需要根据系统的液位情况来实现稳定的控制。
在模糊控制中,首先需要建立一套模糊规则系统,该系统包括模糊化、模糊推理和解模糊化这三个步骤。
模糊化是将实际输入转换为模糊集合的过程。
在水箱液位控制中,可
以将液位分为低、中和高三个模糊集合。
通过将实际液位值映射到这些模
糊集合中的一个,来表示液位状态。
模糊推理是根据一组模糊规则,将模糊输入转换为模糊输出的过程。
通过将输入和规则进行匹配,确定输出的模糊集合。
在水箱液位控制中,
可以使用如下规则:如果液位低且液位变化小,则控制信号为增大水流量;如果液位高且液位变化大,则控制信号为减小水流量;如果液位中等且液
位变化适中,则控制信号为不变。
解模糊化是将模糊输出转换为实际的控制信号的过程。
在水箱液位控
制中,可以使用模糊加权平均值的方法来进行解模糊化。
通过将模糊集合
和其对应的权重进行加权平均计算,得到最终的控制信号。
在MATLAB中,可以使用Fuzzy Logic Toolbox来实现水箱液位模糊
控制仿真设计。
首先需要建立输入和输出的模糊化和解模糊化函数,然后
根据实际的模糊规则,构建模糊系统。
最后通过设定输入的模糊值,使用模糊系统进行推理和解模糊,得到最终的控制信号。
总结起来,智能控制及MATLAB实现水箱液位模糊控制仿真设计包括建立模糊规则系统,进行模糊化、模糊推理和解模糊化三个步骤,通过Fuzzy Logic Toolbox来实现模糊控制系统的构建和仿真。
通过利用模糊控制的方法,可以实现水箱液位的自动稳定控制,并提高了控制系统的鲁棒性和适应性。
