Matlab下多径衰落信道的仿真代码

matlab利用导频信号估计awgn信道衰减的代码

《利用导频信号估计AWGN信道衰减的MATLAB代码实现》在无线通信中，AWGN（Additive White Gaussian Noise）信道衰减是一种常见的干扰形式，对信号的传输质量产生重大影响。

为了在实际通信中更准确地估计AWGN信道的衰减情况，导频信号成为了一种常用的手段。

本文将介绍如何使用MATLAB编写代码，利用导频信号来估计AWGN信道的衰减情况，并给出完整的代码实现。

1. 理论基础在传统的通信系统中，信号经过AWGN信道传输后会受到噪声的影响，导致信号质量下降。

为了准确地估计AWGN信道的衰减情况，通常会使用导频信号。

导频信号是已知的参考信号，通过比较接收到的导频信号和发送端发送的原始导频信号的差异，可以计算出AWGN信道的衰减情况。

2. MATLAB代码实现为了实现对AWGN信道的衰减情况进行估计，我们需要先生成导频信号，然后经过AWGN信道传输，并最终通过接收端获取到传输后的导频信号。

下面是利用MATLAB编写的代码实现：```matlab% 生成导频信号N = 100; % 导频信号长度pre_signal = randn(1, N) + 1i*randn(1, N); % 产生N个随机复数% 将导频信号经过AWGN信道传输SNR = 10; % 信噪比received_signal = awgn(pre_signal, SNR); % 通过awgn函数实现AWGN信道传输% 估计AWGN信道的衰减情况channel_loss = received_signal./pre_signal; % 通过对比接收到的导频信号和发送的原始导频信号，计算出AWGN信道的衰减情况```3. 代码解析以上代码实现了对AWGN信道的衰减情况进行估计的过程。

我们生成了长度为N的随机复数作为导频信号。

利用awgn函数模拟了导频信号经过AWGN信道传输的过程，设置了信噪比SNR为10。

通过对比接收到的导频信号和发送的原始导频信号，计算出了AWGN信道的衰减情况，并存储在channel_loss变量中。

【谷速软件】matlab源码-多径衰落与大尺度衰落

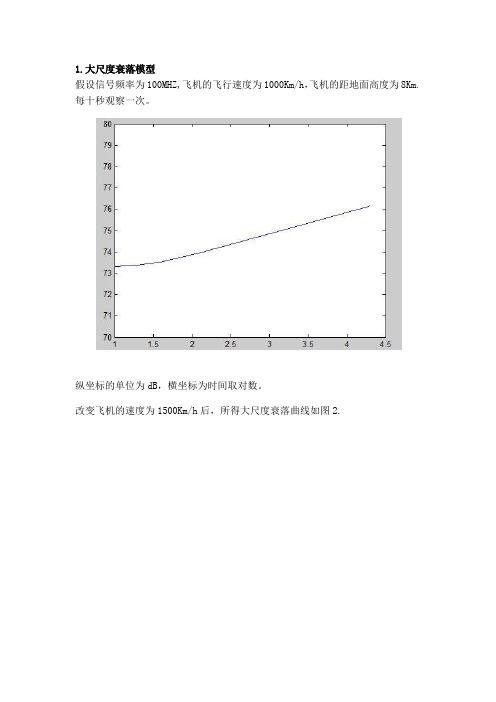
1.大尺度衰落模型
假设信号频率为100MHZ,飞机的飞行速度为1000Km/h，飞机的距地面高度为8Km.每十秒观察一次。

纵坐标的单位为dB，横坐标为时间取对数。

改变飞机的速度为1500Km/h后，所得大尺度衰落曲线如图2.
2.瑞利衰落模型
多径衰落可以用瑞利衰落来近似，使用MATLAB可以绘制出瑞利衰落的曲线。

如图3
3.接收端的初步设计
大尺度衰落是不可避免的，而且它与飞行速度有关，与信号的频率关系不大；而多径效应会导致码间干扰(ISI)，严重影响了接收信号的判决，在接收端应采用均衡措施。

假定传输信号的波形已知为方波，可以设计滤波器，来减小码间干扰。

ISIfilter的设计可以用MATLAB实现，图4
4.眼图
可以通过眼图的观察选择最佳的采样时间点。

眼图的观察效果如图5.。

Rayleigh无线衰落信道的MATLAB仿真

通信原理课程设计汇报书课题名称Rayleigh 无线衰落信道的MATLAB 仿真姓名学号学院专业通信工程指导教师年月日※※※※※※※※※ ※※ ※※ ※※ ※※※※※※※※※通信工程专业通信原理课程设计Rayleigh无线衰落信道的MATLAB仿真1 设计目的〔1〕对瑞利信道的数学分析，得出瑞利信道的数学模型。

〔2〕利用MATLAB对瑞利无线衰落信道进行编程。

〔3〕针对服从瑞利分布的多径信道进行模拟仿真，加深对多径信道特性的了解。

〔4〕对仿真后的结果进行分析，得出瑞利无线衰落信道的特性。

2 设计思路无线衰落信道的MATLAB仿真：〔1〕分析出无线信道符合瑞利概率密度分布函数，写出数学表达式。

〔2〕建立多径衰落信道的根本模型。

〔3〕对符合瑞利信道的路径衰落进行分析，并利用MATLAB进行仿真。

3 设计过程3.1 方案论证3.1.1．瑞利信道环境与数学模型瑞利衰落信道〔Rayleigh fading channel〕是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落〞，并且其包含服从瑞利分布。

瑞利衰落属于小尺寸的衰落效应，它总是叠加于如阴影、衰减等大尺度衰落效应上。

信道衰落的快慢与开展端和接收端的相对运动速度的大小有关，相对运动对导致接受信号的多普勒频移，一固定信号通过单径的瑞利衰落信道后，在1秒内的能量波动，这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz，在GSM1800MHz的载波频率上，其相应的移动速度分别为约6千米每小时和60千米每小时。

特别需要注意的事信号“深衰落〞现象，此时信号能量的衰减到达数千倍，即30到40分贝。

瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。

密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径，而且使得无线信号被衰减、反射、折射、衍射。

在曼哈顿的实验证明，当地的无线信道环境实在接近于瑞利衰落。

matlab通信仿真实例

matlab通信仿真实例在Matlab中进行通信系统的仿真，可以涉及到多种不同的通信技术和协议，包括调制解调、信道编码、多址接入等。

以下以OFDM系统为例，介绍Matlab 中通信仿真的实例。

OFDM（正交频分复用）是一种常用于现代通信系统中的技术，它将高速数据流分割成多个较低速的子流，并将每个子流分配到不同的子载波上。

优点是能够抵抗多径效应和频率选择性衰落，并提供高数据速率。

首先，我们需要创建一个包含OFDM系统参数的结构体。

例如：ofdmParam.M = 16; % 子载波数量ofdmParam.K = 4; % 用于混合多路复用的用户数量ofdmParam.N = ofdmParam.M * ofdmParam.K; % 总子载波数量ofdmParam.CP = 16; % 循环前缀长度接下来，我们可以生成用于OFDM仿真的数据流。

例如，我们可以使用随机整数生成器生成一系列整数，并将其转换为复数形式的调制符号：data = randi([0, ofdmParam.M-1], 1, ofdmParam.N);dataMod = qammod(data, ofdmParam.M);然后，我们可以创建一个包含OFDM信号的函数。

在OFDM系统中，生成的数据符号将分配到不同的子载波上，然后在时域中通过插入循环前缀进行叠加：function[ofdmSignal] = createOFDMSignal(dataMod, ofdmParam) ofdmSignal = [];for k = 0:ofdmParam.K-1% 提取相应的数据符号，并进行IFFTofdmData =ifft(dataMod(k*ofdmParam.M+1:(k+1)*ofdmParam.M));% 添加循环前缀ofdmDataWithCP = [ofdmData(end-ofdmParam.CP+1:end), ofdmData];% 将OFDM符号添加到OFDM信号中ofdmSignal = [ofdmSignal, ofdmDataWithCP];endend将OFDM信号传输到信道中，我们可以使用加性高斯白噪声（AWGN）信道模型来模拟实际通信环境：EbNo = 10; % 信噪比snr =10*log10(ofdmParam.N*ofdmParam.M/(ofdmParam.N*ofdmParam.M+1 )*(10^(EbNo/10)));ofdmSignalNoisy = awgn(ofdmSignal, snr, 'measured');最后，我们可以对接收到的OFDM信号进行解调和信号恢复。

Matlab下多径衰落信道的仿真代码

Matlab下多径衰落信道的仿真代码衰落信道参数包括多径扩展和多普勒扩展。

时不变的多径扩展相当于一个延时抽头滤波器，而多普勒扩展要注意多普勒功率谱密度，通常使用Jakes功率谱、高斯、均匀功率谱。

多径衰落信道由单径信道叠加而成，而单径信道中最重要的就是瑞利(Rayleigh)平坦衰落信道。

下面给出瑞利平坦衰落信道的改进Jakes模型的实现:function [h]=rayleigh(fd,t)%改进的jakes模型来产生单径的平坦型瑞利衰落信道 %Yahong R.Zheng and Chengshan Xiao "Improved Models for%the Generation of Multiple Uncorrelated Rayleigh Fading Waveforms"%IEEE Commu letters, Vol.6, NO.6, JUNE 2002 %输入变量说明:% fd:信道的最大多普勒频移单位Hz % t :信号的抽样时间序列，抽样间隔单位s % h为输出的瑞利信道函数，是一个时间函数复序列%假设的入射波数目N=40;wm=2*pi*fd;射波数目即振荡器数目 %每象限的入N0=N/4;%信道函数的实部Tc=zeros(1,length(t));%信道函数的虚部Ts=zeros(1,length(t));%归一化功率系数P_nor=sqrt(1/N0);%区别个条路径的均匀分布随机相位theta=2*pi*rand(1,1)-pi;for ii=1:N0%第i条入射波的入射角alfa(ii)=(2*pi*ii-pi+theta)/N; %对每个子载波而言在(-pi,pi)之间均匀分布的随机相位fi_tc=2*pi*rand(1,1)-pi;fi_ts=2*pi*rand(1,1)-pi;%计算冲激响应函数Tc=Tc+cos(cos(alfa(ii))*wm*t+fi_tc);Ts=Ts+cos(sin(alfa(ii))*wm*t+fi_ts);end;%乘归一化功率系数得到传输函数h=P_nor*(Tc+j*Ts );改变fd，可以观察到信号功率随着fd的增大而变化加快。

多径信道对信号影响的Matlab仿真

多径信道对信号影响的Matlab仿真多径信道对信号影响的仿真作出Pe～Eb/No曲线。

升余弦滚降系数a＝0.5，取样时间无偏差，但信道是多径信道，C(f)=|1-0.5-j2 ft|,t=T s/21仿真原理及思路仿真原理同最“佳基带系统的Pe~Eb\No曲线”仿真原理，只是信道不同。

2程序流程图最佳基带系统Pe~Eb\No曲线设计流程图3仿真程序及运行结果仿真程序：%多径信道传输的Pe～Eb/No曲线。

升余弦滚降系数a＝0.5，取样时间无偏差。

close allclear allglobal dt t f df N TN=2^14; %采样点数L=32; %每码元的采样点数M=N/L; %码元数Rb=2; %码速率是2Mb/sTs=1/Rb; %码元间隔dt=Ts/L; %时域采样间隔df=1/(N*dt) ; %频域采样间隔T=N*dt ; %截短时间Bs=N*df/2; %系统带宽alpha=0.5; %滚降系数t=linspace(-T/2,T/2,N);%时域横坐标f=linspace(-Bs,Bs,N)+eps; %频域横坐标figure(1)set(1,'Position',[10,50,400,300])%设定窗口位置及大小%升余弦hr1=sin(pi*t/Ts)./(pi*t/Ts);hr2=cos(alpha*pi*t/Ts)./(1-(2*alpha*t/Ts).^2);hr=hr1.*hr2;HR=abs(t2f(hr)); %取模是为了忽略时延GT=sqrt(abs(HR));GR=GT; %发送和接收滤波器模型tao=Ts/2;C=1-0.5*exp(-j*(2*pi*f*tao));%多径信道模型G=C.*HR; %总体特性for loop1=1:20Eb_N0(loop1)=(loop1-1) ;%Eb/N0 in dBeb_n0(loop1)=10^(Eb_N0(loop1)/10);Eb=1;n0=Eb/eb_n0(loop1); %信道的噪声谱密度sita=n0*Bs; %信道中噪声功率n_err=0; %误码计数for loop2=1:5a=sign(randn(1,M));imp=zeros(1,N); %产生冲激序列imp(L/2:L:N)=a/dt;IMP=t2f(imp);n_ch=sqrt(sita)*randn(size(t)); %信道噪声nr=real(f2t(t2f(n_ch).*GR.*C)); %输出噪声sr=real(f2t(IMP.*G))+nr; %接收信号y=sr(L/2:L:N); %取样，取样时刻无偏差aa=sign(y); %判决n_err=n_err+length(find(aa~=a)); %误码个数endPe(loop1)=n_err/(M*loop2); %实际误码率figure(1)semilogy(Eb_N0,Pe,'g'); %实际误码率曲线eb_n0=10.^(Eb_N0/10);hold onsemilogy(Eb_N0,0.5*erfc(sqrt(eb_n0))); % 理论误码率曲线axis([0,9,1e-4,1])xlabel('Eb/N0 in db')ylabel('Pe')end4实验结果：误码率曲线：绿色线(上)为实际曲线，蓝色(下)为理论误码率曲线5实验结果分析从结果可以看出，多径信道对信号影响很大，系统的误码率比经过加性高斯白噪信道高很多。

matlab瑞利衰落信道仿真

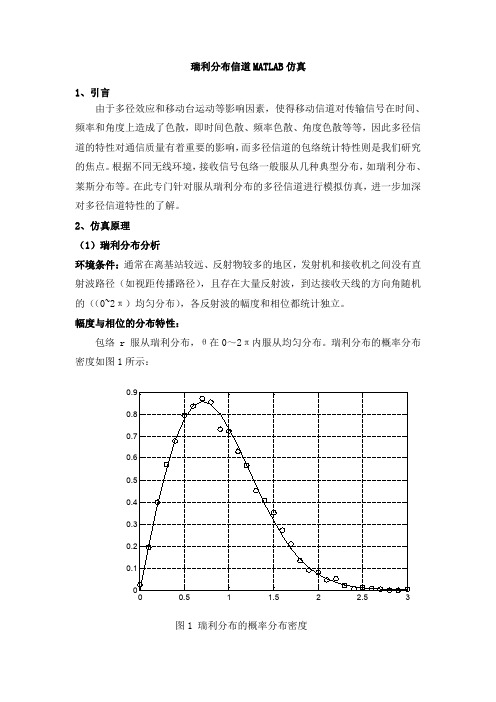
瑞利分布信道MATLAB仿真1、引言由于多径效应和移动台运动等影响因素，使得移动信道对传输信号在时间、频率和角度上造成了色散，即时间色散、频率色散、角度色散等等，因此多径信道的特性对通信质量有着重要的影响，而多径信道的包络统计特性则是我们研究的焦点。

根据不同无线环境，接收信号包络一般服从几种典型分布，如瑞利分布、莱斯分布等。

在此专门针对服从瑞利分布的多径信道进行模拟仿真，进一步加深对多径信道特性的了解。

2、仿真原理（1）瑞利分布分析环境条件：通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路径（如视距传播路径），且存在大量反射波，到达接收天线的方向角随机的（（0~2π）均匀分布），各反射波的幅度和相位都统计独立。

幅度与相位的分布特性：包络r服从瑞利分布，θ在0～2π内服从均匀分布。

瑞利分布的概率分布密度如图1所示：图1瑞利分布的概率分布密度（2）多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k k k yt r t x t τ==-∑ (1)其中,()k r t 复路径衰落，服从瑞利分布;k τ是多径时延。

多径衰落信道模型框图如图2所示：图2多径衰落信道模型框图（3）产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性，其振幅服从瑞利分布，即()r t =（2）上式中()()c s n t n t 、，分别为窄带高斯过程的同相和正交支路的基带信号。

3、仿真框架根据多径衰落信道模型（见图2），利用瑞利分布的路径衰落r(t)和多径延时参数k τ，我们可以得到多径信道的仿真框图，如图3所示；图3多径信道的仿真框图4、仿真结果（1）（1）多普勒滤波器的频响图4多普勒滤波器的频响（2）多普勒滤波器的统计特性图5多普勒滤波器的统计特性（3）信道的时域输入/输出波形图6信道的时域输入/输出波形5、仿真结果（2）（1）当终端移动速度为30km/h时，瑞利分布的包络如下图所示（2）当终端移动速度为100km/h时，瑞利分布的包络如下图所示三、仿真代码%main.mclc;LengthOfSignal=10240;%信号长度(最好大于两倍fc)fm=512;%最大多普勒频移fc=5120;%载波频率t=1:LengthOfSignal;%SignalInput=sin(t/100);SignalInput=sin(t/100)+cos(t/65);%信号输入delay=[03171109173251];power=[0-1-9-10-15-20];%dBy_in=[zeros(1,delay(6))SignalInput];%为时移补零y_out=zeros(1,LengthOfSignal);%用于信号输出for i=1:6Rayl;y_out=y_out+r.*y_in(delay(6)+1-delay(i):delay(6)+LengthOfSignal-delay (i))*10^(power(i)/20);end;figure(1);subplot(2,1,1);plot(SignalInput(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Input');subplot(2,1,2);plot(y_out(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Output');figure(2);subplot(2,1,1);hist(r,256);title('Amplitude Distribution Of Rayleigh Signal')subplot(2,1,2);hist(angle(r0));title('Angle Distribution Of Rayleigh Signal');figure(3);plot(Sf1);title('The Frequency Response of Doppler Filter');%Rayl.mf=1:2*fm-1;%通频带长度y=0.5./((1-((f-fm)/fm).^2).^(1/2))/pi;%多普勒功率谱(基带)Sf=zeros(1,LengthOfSignal);Sf1=y;%多普勒滤波器的频响Sf(fc-fm+1:fc+fm-1)=y;%(把基带映射到载波频率)x1=randn(1,LengthOfSignal);x2=randn(1,LengthOfSignal);nc=ifft(fft(x1+i*x2).*sqrt(Sf));%同相分量x3=randn(1,LengthOfSignal);x4=randn(1,LengthOfSignal);ns=ifft(fft(x3+i*x4).*sqrt(Sf));%正交分量r0=(real(nc)+j*real(ns));%瑞利信号r=abs(r0);%瑞利信号幅值。

多径衰落仿真器

表1ITU-RM.1225Vehicular A
Relative delay（ns）
Average power（dB）
0
0
310
-1.0
710
-9.0
1090
-10.0
1730
-15.0
2510
-20.0
对于频率选择性衰落的仿真需要确定多条信道的延时和功率分布，这就是功率延时分布（PDP），对于功率延时分布有两个常用的模型，分别是ITU-R模型和COST 207模型。在本文中采用的是ITU-R模型中的Vehicular A模型，模型中的延时和平均功率分布如表1中所示。
(一)仿真器的流程图
图9Clarke模型流程图
图10主程序流程图
(二)仿真结果
在仿真中我们设置，，，功率延迟分布按照表1中的模型，仿真的结果如下面两个图所示。
图11Clarke模型的仿真结果
图12多径衰落模型的仿真结果
为了便于观察，图11和图12的时域幅度波形只截取了前0.6s的波形。图11是单条衰落信道的仿真结果，图12是表1中的多径模型的仿真结果。从图11中可以看到，依据图6的建模方法得出来的输出序列，其幅度满足Rayleigh分布，相位满足均匀分布，是一个Rayleigh衰落信道。图7所示的多径模型是一个线性叠加的过程，线性叠加之后结果不改变原序列的统计特性，很明显，图12的结果表明，多径衰落仿真的结果的幅度也是满足Rayleigh分布的，而相位是满足均匀分布的。
图6Smith方法
如图6所示，Smith方法是一种用于实现图5过程的简单的算法。这种方法是采用一个高斯噪声源来产生一个基带线状频谱。利用实信号的性质，负频率分量可以由正频率分量去共轭得到。然后将线状频谱和（20）相乘，得到的频谱取值从到- 。那么为了解决（20）中边缘的值趋于无穷的问题，可以利用靠近边缘的值做多项式拟合，利用拟合出来的多项式求出边缘上的值。

基于matlab ofdm通信系统仿真代码

基于matlab ofdm通信系统仿真代码
基于MATLAB OFDM通信系统仿真代码是一种应用在无线通信领域的高
效的通信技术。

OFDM（正交分频多载波）技术是一种高效的技术，它
能够在有限的信道容量内传输大量的数据，同时也能抵御多径衰减和
多路径效应。

此外，OFDM还可以抵抗非线性干扰和伪噪声，从而提高
系统的可靠性和稳定性。

MATLAB OFDM通信系统仿真代码可以帮助我们快速验证一个OFDM系统的性能，从而帮助我们更好地理解OFDM技术
背后的原理和技术。

MATLAB OFDM通信系统仿真代码由信道模拟、OFDM调制和解调制的子
模块组成，其中每个子模块都可以通过MATLAB编程实现。

首先，我们
需要定义一个简单的信道函数，以模拟实际信道的衰减和多路径效应，然后将信号传输给OFDM调制模块，它将信号转换成OFDM调制的多载
波信号。

接着，多载波信号被发射到信道中，经过信道后，经过OFDM
解调制模块处理，得到恢复后的信号，再经过信道衰减模拟得到最终
信号，完成仿真。

通过使用MATLAB OFDM通信系统仿真代码，我们可以更有效地对OFDM
技术进行仿真评估，同时也可以获得更为准确、直观的仿真结果。

此外，MATLAB OFDM通信系统仿真代码还可以帮助我们了解OFDM技术的
具体实施方法，为实际开发工作提供有效的技术支持。

OFDM技术仿真(MATLAB代码)

第一章绪论1.1简述OFDM是一种特殊的多载波传输方案，它可以被看作是一种调制技术，也可以被当作一种复用技术。

多载波传输把数据流分解成若干子比特流，这样每个子数据流将具有低得多的比特速率，用这样的低比特率形成的低速率多状态符号再去调制相应的子载波，就构成多个低速率符号并行发送的传输系统。

正交频分复用是对多载波调制（MCM，Multi-Carrier Modulation）的一种改进。

它的特点是各子载波相互正交，所以扩频调制后的频谱可以相互重叠，不但减小了子载波间的干扰，还大大提高了频谱利用率。

符号间干扰是多径衰落信道宽带传输的主要问题，多载波调制技术包括正交频分复用(OFDM)是解决这一难题中最具前景的方法和技术。

利用OFDM技术和IFFT方式的数字实现更适宜于多径影响较为显著的环境，如高速WLAN 和数字视频广播DVB等。

OFDM作为一种高效传输技术备受关注，并已成为第4代移动通信的核心技术。

如果进行OFDM系统的研究，建立一个完整的OFDM系统是必要的。

本文在简要介绍了OFDM 基本原理后，基于MATLAB 构建了一个完整的OFDM动态仿真系统。

1.2 OFDM基本原理概述1.2.1 OFDM的产生和发展OFDM的思想早在20世纪60年代就已经提出，由于使用模拟滤波器实现起来的系统复杂度较高，所以一直没有发展起来。

在20世纪70年代，提出用离散傅里叶变换（DFT）实现多载波调制，为OFDM的实用化奠定了理论基础；从此以后，OFDM在移动通信中的应用得到了迅猛的发展。

OFDM系统收发机的典型框图如图1.1所示，发送端将被传输的数字信号转换成子载波幅度和相位的映射，并进行离散傅里叶变换（IDFT）将数据的频谱表达式变换到时域上。

IFFT变换与IDFT变换的作用相同，只是有更高的计算效率，所以适用于所有的应用系统。

其中，上半部分对应于发射机链路，下半部分对应于接收机链路。

由于FFT操作类似于IFFT，因此发射机和接收机可以使用同一硬件设备。

OFDM技术仿真(MATLAB代码)..

第一章绪论1.1简述OFDM是一种特殊的多载波传输方案，它可以被看作是一种调制技术，也可以被当作一种复用技术。

多载波传输把数据流分解成若干子比特流，这样每个子数据流将具有低得多的比特速率，用这样的低比特率形成的低速率多状态符号再去调制相应的子载波，就构成多个低速率符号并行发送的传输系统。

正交频分复用是对多载波调制（MCM，Multi-Carrier Modulation）的一种改进。

它的特点是各子载波相互正交，所以扩频调制后的频谱可以相互重叠，不但减小了子载波间的干扰，还大大提高了频谱利用率。

符号间干扰是多径衰落信道宽带传输的主要问题，多载波调制技术包括正交频分复用(OFDM)是解决这一难题中最具前景的方法和技术。

利用OFDM技术和IFFT方式的数字实现更适宜于多径影响较为显著的环境，如高速WLAN 和数字视频广播DVB等。

OFDM作为一种高效传输技术备受关注，并已成为第4代移动通信的核心技术。

如果进行OFDM系统的研究，建立一个完整的OFDM 系统是必要的。

本文在简要介绍了OFDM 基本原理后，基于MATLAB构建了一个完整的OFDM动态仿真系统。

1.2 OFDM基本原理概述1.2.1 OFDM的产生和发展OFDM的思想早在20世纪60年代就已经提出，由于使用模拟滤波器实现起来的系统复杂度较高，所以一直没有发展起来。

在20世纪70年代，提出用离散傅里叶变换（DFT）实现多载波调制，为OFDM的实用化奠定了理论基础；从此以后，OFDM在移动通信中的应用得到了迅猛的发展。

OFDM系统收发机的典型框图如图1.1所示，发送端将被传输的数字信号转换成子载波幅度和相位的映射，并进行离散傅里叶变换（IDFT）将数据的频谱表达式变换到时域上。

IFFT变换与IDFT变换的作用相同，只是有更高的计算效基于MATLAB实现OFDM的仿真率，所以适用于所有的应用系统。

其中，上半部分对应于发射机链路，下半部分对应于接收机链路。

移动无线信道多径衰落的MATLAB仿真实现

当 N 很大时, hc (t ) 与 hs (t ) 是大量独立随机变量之和。由中心极限定理可知,它们可以近似为正态分布,因此,他们是正态随机过程。令 h(t ) hc (t ) jhs (t ) X (t )e j (t ) ,则 h(t ) 表示信道冲激响应。因为 h(t ) 的两个正交分量为零均值的高斯随机过程,所以其包络 X (t ) 服从瑞利分布,相位服从均匀分布。可以证明 hc (t ) 与 hs (t ) 互不相关,信号受多普勒衰落影响的功率谱密度
(3)
相应的接收端信号为:
S r (t ) A(t ) cos(c (t / ) (t ) 2 π f n t i ) ,i=1～n-1
式中
(4)
f n 为多普勒频移； i 为电波到达相位; Ai 为信号幅度。
令i 2 π ( f n t c / i ) ,则
3
前言
移动通信是当前最主流的通信方式，而无线信道是移动通信中传输信号的媒介，只有深刻掌握和了解移动无线信道的特征，我们才能提出解决各种干扰的措施。移动无线信道传输特性的仿真对移动通信的研究具有重要意义,其中多径衰落仿真又是其中的重点和难点。移动通信的特点是传播的开放性、接收环境的复杂性和通信用户的随机移动性。在无线通信信道中，大气的反射或折射、建筑物和其他物体的反射导致了发送和接收天线之间通常存在多于一条的信号传播路径。由多径引起的信号衰落是影响通信性能的一个主要因素，所以在通信方案可行性研究以及系统设计、优化等过程中，经常要考虑到多径衰落及相关的解决方案。本次设计用 MATLAB 对信号在多径信道中的传输进行了仿真，并与理想条件下的情况进行了对比分析，提出了一些改进措施。

基于Matlab的Mpsk信号在莱斯衰落信道下的性能仿真

课程设计（II）通信系统仿真题目MPSK在莱斯衰落信道下的性能专业学号姓名日期1、课程设计目的多进制绝对相移键控MPSK是2PSK的推广，MPSK利用载波的多种不同相位状态来表征数字信息的调制方式。

本次设计以QPSK为主要设计目标，利用MATLAB 对其进行调制解调及在莱斯信道下的传输性能仿真，以此来熟悉掌握相关的知识和MATLAB的使用方法。

2、课程设计内容本次设计主要是对QPSK在莱斯信道下的性能进行仿真。

为此需要先调制出QPSK信号，QPSK信号原理如下：四进制绝对相移键控（4PSK）直接利用载波的四种不同相位来表四进制信息。

如下图由于一个想为代表两个比特信息，因此每个四进制码元可用两个二进制码元的组合来表示。

两个二进制码元中的前一码元用a表示，后一比特用b表示，则双比特ab与载波相位关系如下表4PSK信号等效为两个正交载波进行双边带调制信号之和，这样就把数字调制和线性调制结合起来，为四相波形的产生提供依据。

4PSK的调制方法有正交调制方式，相位选择法，插入脉冲法等。

正交调制法原理如图4PSK可以看作两个正交的2PSK调制器构成。

图中串并转换将输入的二进制序列分为两个速度减慢的两个并行双极性序列a和b，在分别进行极性变换。

再调制到coswt和sinwt载波上。

两路相乘器输出的信号是相互正交的抑制载波的双边带调制信号，相位与各路码元的极性有关，分别由码元a和码元b决定，经相加电路后输出两路的合波即是4PSK信号，图中两个乘法器，一个用于产生0和180两个相位，另一个用于产生90和270两个相位。

相加后可以得到45，135，225，315四种相位状态。

产生4psk信号同样可以采用相位选择法，在一个码元持续时间内，4psk信号为载波4个相位中的某一个，因此，可以用相位选择的方法来产生4psk信号。

其原理图如下：在图中，四相载波发生器产生4psk信号所需要的4种不同相位的载波，输入的二进制数码经串并变换器输出双比特码元，按照输入的双比特码元的不同，逻辑选相电路输出相应相位的在载波。

移动无线信道多径衰落的仿真

移动无线信道多径衰落的仿真*******************实践教学*******************兰州理工大学计算机与通信学院2011年秋季学期移动通信课程设计题目：移动无线信道多径衰落的仿真专业班级：姓名：学号：指导教师：成绩：摘要在移动通信迅猛发展的今天，人与人的交流越来越多的依赖于无线通信。

而无线信道的好坏直接制约着无线通信质量的提高，因此对无线信道的研究有利于提高通信传输速率。

本次课程设计用simulink对移动无线信道多径衰落特性进行了仿真，并且和理想传输环境下的情况进行比较得出了结论。

关键词：移动通信；无线信道；频率选择性衰落；多径传播前言移动通信是指双方或至少其中一方在运动状态中进行信息传递的通信方式，是实现通信理想目标的重要手段。

移动通信满足了人们在任何时间任何空间上通信的需求，同时，由于集成电路、计算机和软件工程的迅速发展为移动通信的发展提供了技术支持，移动通信的发展速度远远超过了人们的预料。

移动通信追求在任何时间任何地方以任何方式与任何人进行通信，也就是移动通信的理想境界——个人通信。

要实现这个理想，高效率、高质量是前提。

所以，除了研究发射机接收机可以达到目的外，对于无线信道的研究更为重要。

无线信道的好坏直接影响无线通信的质量和效率，对无线信道建立数学模型是一种科学的研究方法，通过建模可以了解影响信号传输质量的因素以及解决的方法。

无线信道中，小尺度衰落占有重要地位，所以，研究小尺度衰落的特性和建模方法对于无线信道的研究具有重大意义。

目录第1章移动通信概述 01.1移动通信的发展史 01.2移动通信的特点 (1)第2章无线信道的概念和特性 (3)2.1 无线信道的定义 (3)2.2 无线信道的类型 (3)传播路径损耗模型(Propagation Path Loss Model) (3)大尺度传播模型(Large Scale Propagation Model) (4)小尺度传播模型(Small Scale Propagation Model) (4)2.3 无线移动信道的概念 (4)2.4 移动信道的特点 (5)移动通信信道的3个主要特点 (5)移动通信信道的电磁波传输 (5)接收信道的3类损耗 (5)三种快衰落（选择性衰落）产生的原因 (6)第3章调制解调 (6)第4章系统仿真及结果分析 (7)4.1 QPSK 调制解调系统的仿真 (8)4.2 利用Matlab研究QPSK信号 (10)总结 (13)参考文献 (14)附录一： (16)附录二： (18)第1章移动通信概述1.1移动通信的发展史移动通信的发展大致经历了以下几个发展阶段：1．20世纪20～30年代：警车无线电调度电话（AM调幅），使用频率为2 MHz。

ofdmmatlab仿真代码

ofdmmatlab仿真代码
OFDM（正交频分复用）是一种广泛应用于无线通信系统中的调制技术。

它通过将数据流分为多个子信道，并在每个子信道上传输正交的子载波来提高频谱效率和抗干扰能力。

MATLAB是一种常用的科学计算软件，可以用来进行OFDM系统的仿真和性能分析。

OFDM技术的原理是将高速数据流分成多个低速数据流，然后将每个低速数据流调制到正交的子载波上进行传输。

这些子载波之间彼此正交，可以避免干扰。

在接收端，通过对接收到的信号进行解调和合并，可以恢复出原始数据流。

在MATLAB中，可以使用通信工具箱中的函数来实现OFDM系统的仿真。

首先，需要设置OFDM系统的参数，如子载波数目、子载波间隔、保护间隔等。

然后，可以生成随机的数据流，并将其调制到各个子载波上。

接下来，可以添加信道模型，如多径衰落等，并对接收到的信号进行解调和合并。

最后，可以评估系统的性能，如误码率、信噪比等。

OFDM技术在无线通信中有许多应用，如Wi-Fi、LTE等。

它具有高频谱效率、抗干扰能力强等优点，能够提供高质量的数据传输和稳定的通信连接。

通过使用MATLAB进行OFDM系统的仿真，可以更好地理解和分析OFDM技术的性能特点，对于无线通信系统的设计和优化具有重要意义。

OFDM是一种重要的调制技术，能够提高无线通信系统的频谱效率和抗干扰能力。

MATLAB提供了丰富的函数和工具箱，可以用来进行OFDM系统的仿真和性能分析。

通过使用MATLAB进行仿真，可以更好地理解和分析OFDM技术的性能特点，对于无线通信系统的设计和优化具有重要意义。

利用MATLAB仿真多径衰落信道

利用MATLAB仿真多径衰落信道利用MATLAB仿真多种多径衰落信道摘要:移动信道的多径传播引起的瑞利衰落，时延扩展以及伴随接收过程的多普勒频移使接受信号受到严重的衰落，阴影效应会是接受的的信号过弱而造成通信的中断:在信道中存在噪声和干扰，也会是接收信号失真而造成误码，所以通过仿真找到衰落的原因并采取一些信号处理技术来改善信号接收质量显得很重要，这里利用MATLAB对多径衰落信道的波形做一比较。

一，多径衰落信道的特点关于多径衰落信道，通过下面一个简单的模拟图来说明多径衰落信道的两个特点:频率选择性衰落和时间衰落。

dr0基站假设在一条笔直的高速公路上一段安装了一个固定的基站，另一端有一面完全反射的电磁波墙面。

当移动台静止时，显然从基站发出的直射信号到达移动台需要时间为r0/c,(c 为光速)，从反射墙反射过来的信号到达移动台需要的时间为(2d-r0)/c。

也就是说，在t时刻，移动台接收分别接受了从时刻t-r0/c基站发出的直射信号和从时刻t-(2d-r0)/c基站发出的反射信号，而且信号在传播过程中要衰减，在自由空间中，直射信号和反射信号相位相反。

1，下面通过MATLAB画出在r0处接收信号会有什么特点:程序代码如下: clear allf=1; %发射信号频率v=1; %移动台速度，静止情况为0c=3e8; %电磁波速度，光速r0=3; %移动台距离基站初始距离d=10; %基站距离反射墙的距离t1=0.1:0.0001:10; %时间E1=cos(2*pi*f*((1-v/c).*t1-r0/c))./(r0+v.*t1); %直射径信号E2=cos(2*pi*f*((1+v/c)*t1+(r0-2*d)/c))./(2*d-r0-v*t1); %反射径信号figureplot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r') %画出直射径、反射径和总的接收信号legend('直射径信号','反射径信号','移动台接收的合成信号')axis([0 10 -0.8 0.8])输出波形如下所示:由上图可以看出，即是移动台是静止的，由于反射径的存在，使得接收到的合成信号最大值要小于直射径信号:2，修改r0=9时，运行程序结果如下:通过上图我们可以看出，当r0=9时，由于靠墙比较近，直射信号要比r0=3处弱一些，反射信号要比r0=3强一些，但是移动台接收到的合成信号更弱了，不仅要小于直射径的信号，而且小于反射径的信号。

多径衰落信道的MATLAB仿真

在无线通信中，发送天线和接收天线之间往往存在多信号ＣＯＳ（２ｎｆｔ）。从基站发出的直射信号到达移动台所需
条传播路径。主要是因为发射机和接收机之间的建筑物等时间为ｒｎ／ｃ（ｃ为光速），从反射墙反射过来的信号到达
物体对电磁波的反射、绕射、散射等引起的。当信号在无移动台所需时间为（２ｄ－ｒ。）／ｃ。在ｔ时刻，移动台接收到
【参考文献】
【１］苏志龙．研究光纤通信系统中光网络性能监测研究与仿真［Ｊ】．电子制作，２０１６（０２）．【２］陈梦迟，赖贵珍，游善红．光纤通信系统中光信噪比的监测－ｆｉｎ［Ｊ】．通信技术，２０１５（１７）．
．
８３
信息记录材料２０１７年９月第１８卷第９期
ＭＡＴＬＡＢ代码［２３如下：
ｃｌｅａｒａｌｌ：ｆ＝１：ｖ＝Ｏ：ｃ＝３ｅ８：ｒ０＝３；ｄ＝ｌＯ：ｔ１＝０．ｉ：０．０００１：１０：
Ｅｌ＝ｃｏｓ（２＊ｐｉ＊ｆ＊（（卜ｖ／ｃ）．＊ｔｌ－ｒ０／ｃ））．／（ｒｏ＋ｖ．＊ｔ１）
的系统扩展性，因此，可以实现与其他仿真软件的衔接。ＯｐｔｉＳｙｓｔｅｍ具备完善的用户界面，可以对各种光软件进行模拟，满足了一般的仿真需求。
光纤通信系统的要求。３．３信号关断法仿真分析信号关断法是对ＯＳＮＲ技术进行的仿真，分为两步，
首先，关断需要进行监测的信道波长，然后通过ＯＳＡ得到噪声功率，随之转换为０．１ｎｍ以内的噪声功率，其次，将信道波长的所有信号功率打开，利用ＯＳＡ得出信道带宽内的信号功率和噪声功率。
ＭＡＴＬＡＢ仿真，很直观，易懂。
ｔ时刻移动台接收到的合成信号为：