2020年SPSS相关性分析Pearson相关与偏相关分析的实现步骤(实用)
SPSS皮尔逊相关分析实例操作步骤精选文档

S P S S皮尔逊相关分析实例操作步骤精选文档 TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-SPSS皮尔逊相关分析实例操作步骤选题:对某地29名13岁男童的身高(cm)、体重(kg),运用相关分析法来分析其身高与体重是否相关。
实验目的:任何事物的存在都不是孤立的,而是相互联系、相互制约的。
相关分析可对变量进行相关关系的分析,计算29名13岁男童的身高(cm)、体重(kg),以判断两个变量之间相互关系的密切程度。
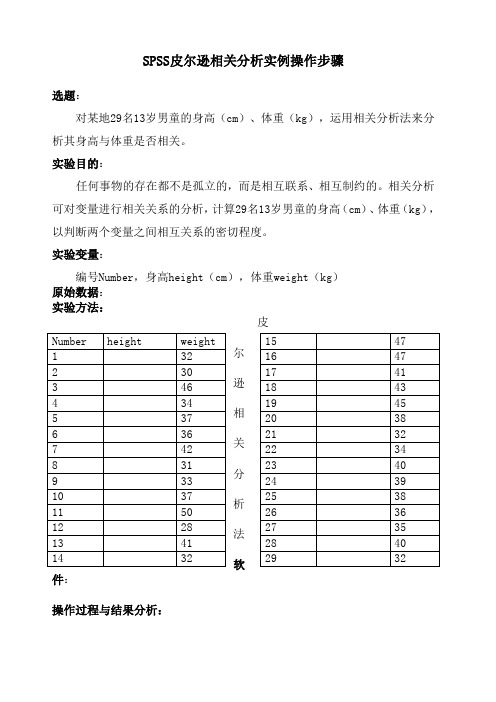
实验变量:编号Number,身高height(cm),体重weight(kg)原始数据:实Array Array验方法:尔逊相关分析法软件:spss19.0操作过程与结果分析: 第一步:导入Excel 数据文件?1.open data document ——open data ——open ;2. Opening excel data source ——OK.第二步:分析身高(cm )与体重(kg )是否具有相关性1. 在最上面菜单里面选中Analyze ——correlate ——bivariate?,首先使用Pearson ,two-tailed ,勾选flag significant correlations 进入如下界面:2. 点击右侧options ,勾选Statistics ,默认Missing Values ,点击Continue 输出结果:图为基本的描述性统计量的输出表格,其中身高的均值(mean )为152.576cm 、标准差(standarddeviation )为8.3622、样本容量(number of cases )为29;体重的均值为37.65kg 、标准差为5.746、样本容量为29。
两者的平均值和标准差值得差距不显着。
Descriptive Statistics Mean Std. Deviation N身高(cm ) 152.576 8.3622 29体重(kg) 37.65 5.746 29Correlations身高(cm )体重(kg)身高(cm )Pearson Correlation 1.719** Sig. (2-tailed).000Sum of Squares and Cross-products 1957.953967.816Covariance 69.92734.565N29 29 体重(kg)Pearson Correlation .719** 1Sig. (2-tailed).000 Sum of Squares and Cross-products967.816924.312析结果表,从表中可以看出体重和身高之间的皮尔逊相关系数为0.719,即|r|=0.719,表示体重与身高呈正相关关系,且两变量是显着相关的。
SPSS皮尔逊相关分析实例操作步骤
SPSS皮尔逊相关分析实例操作步骤选题:对某地29名13岁男童的身高(cm)、体重(kg),运用相关分析法来分析其身高与体重是否相关。
实验目的:任何事物的存在都不是孤立的,而是相互联系、相互制约的。
相关分析可对变量进行相关关系的分析,计算29名13岁男童的身高(cm)、体重(kg),以判断两个变量之间相互关系的密切程度。
实验变量:编号Number,身高height(cm),体重weight(kg)原始数据:实验方法:皮尔逊相关分析法软件:操作过程与结果分析:第一步:导入Excel 数据文件1.open data document ——open data ——open ;2. Opening excel data source ——OK.第二步:分析身高(cm )与体重(kg )是否具有相关性1. 在最上面菜单里面选中Analyze ——correlate ——bivariate ,首先使用Pearson ,two-tailed ,勾选flag significant correlations 进入如下界面:2. 点击右侧options ,勾选Statistics ,默认Missing Values ,点击Continue 输出结果:图为基本的描述性统计量的输出表格,其中身高的均值(mean )为、标准差(standard deviation )为、样本容量(number of cases )为29;体重的均值为、标准差为、样本容量为29。
两者的平均值和标准差值得差距不显着。
图为相关分析结果表,从表中可以看出体重和身高之间的皮尔逊相关系数为,即|r|=,表示体重与身高呈正相关关系,且两变量是显着相关的。
另外,两者之间不相关的双侧检验值为,图中的双星号标记的相关系数是在显着性水平为以下,认为标记的相关系数是显着的,验证了两者显着相关的关系。
所以可以得出结论:学生的体重与身高存在显着的Descriptive StatisticsMean Std. Deviation N身高(cm ) 29体重(kg) 29Correlations身高(cm )体重(kg)身高(cm )Pearson Correlation 1.719** Sig. (2-tailed).000SumofSquaresandCross-productsCovariance N29 29 体重(kg)Pearson Correlation .719** 1Sig. (2-tailed) .000 SumofSquaresandCross-productsCovariance N2929**. Correlation is significant at the level (2-tailed).正相关性,当体重越高时,身高也越高。
SPSS第十四讲偏相关性分析精讲

SPSS第十四讲偏相关性分析精讲SPSS的偏相关性分析是一种探究两个变量之间的关系的统计方法。
它可以消除其他变量的干扰,更准确地评估这两个变量之间的关系。
本文将详细介绍SPSS中偏相关性分析的步骤和解读结果。
偏相关性分析的步骤如下:第一步,打开SPSS软件,并导入数据集。
选择“变量查看器”来查看数据集中的变量。
确保要分析的两个变量已被正确地导入。
第二步,选择“相关性分析”菜单。
在下拉菜单中选择“偏相关”。
在弹出的对话框中,将要分析的两个变量移动到“变量”框中。
同时,将其他可能的干扰变量移动到“控制变量”框中。
单击“确定”按钮。
第三步,在输出窗口中查看分析结果。
输出结果将显示样本的偏相关系数、显著性水平和样本大小。
偏相关性分析的结果解读如下:1.偏相关系数:偏相关系数是表示两个变量关系的统计指标。
它的取值范围从-1到1之间。
当偏相关系数为0时,表示两个变量之间没有任何关系。
当偏相关系数为正时,说明两个变量呈正相关关系,即一个变量的增加会导致另一个变量的增加。
当偏相关系数为负时,说明两个变量呈负相关关系,即一个变量的增加会导致另一个变量的减少。
2.显著性水平:偏相关性分析还会计算一个显著性水平,用于判断偏相关系数的显著性。
显著性水平通常用p值表示,如果p值小于设定的显著性水平(通常设为0.05),则偏相关系数被认为是显著的,即两个变量之间的关系不是由随机性造成的。
3.样本大小:偏相关性分析还会提供样本的大小。
样本的大小对于统计分析的可信度很重要,较小的样本可能导致结果的不稳定性。
偏相关性分析的优势在于可以消除其他变量的干扰,更准确地评估两个变量之间的关系。
它适用于探究变量之间的因果关系,并可以提供结果的显著性。
然而,偏相关性分析也存在一些限制。
首先,偏相关性分析依赖于样本数据。
样本的大小和抽样方法都会对结果产生影响。
其次,偏相关性分析只能确定两个变量之间的关系,不能确定因果关系。
最后,偏相关性分析只适用于连续型变量,无法处理离散型变量。
SPSS皮尔逊相关分析实例操作步骤
SPSS皮尔逊相关分析实例操作步骤选题:对某地29名13岁男童的身高(cm)、体重(kg),运用相关分析法来分析其身高与体重是否相关。
实验目的:任何事物的存在都不是孤立的,而是相互联系、相互制约的。
相关分析可对变量进行相关关系的分析,计算29名13岁男童的身高(cm)、体重(kg),以判断两个变量之间相互关系的密切程度。
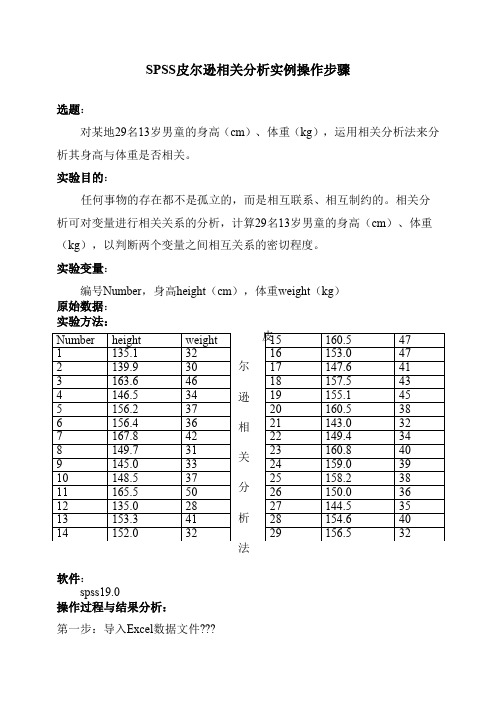
实验变量:编号Number,身高height(cm),体重weight(kg)原始数据:实验方法:逊相关分析法软件:spss19.0操作过程与结果分析:第一步:导入Excel数据文件???1.?open data document ——open data ——open ;2. Opening excel data source ——OK.第二步:分析身高(cm )与体重(kg )是否具有相关性1. 在最上面菜单里面选中Analyze ——correlate ——bivariate?,首先使用Pearson ,two-tailed ,勾选flag significant correlations 进入如下界面:2. 点击右侧options ,勾选Statistics ,默认Missing Values ,点击Continue 输出结果:图为基本的描述性统计量的输出表格,其中身高的均值(mean )为152.576cm 、标准差(standarddeviation )为8.3622、样本容量(number of cases )为29;体重的均值为37.65kg 、标准差为5.746、样本容量为29。
两者的平均值和标准差值得差距不显着。
图为相关分析结果表,从表中可以看出体重和身高之间的皮尔逊相关系数为0.719,即|r|=0.719,表示体重与身高呈正相关关系,且两变量是显着相关的。
另外,两者之间不相关的双侧检验值为0.000,图中的双星号标记的相关系数是在显着性水平为0.01以下,认为标记的相关系数是显着的,验证了两者显着相关的关系。
SPSS相关分析实例操作步骤-SPSS做相关分析

SPSS相关分析实例操作步骤-SPSS做相关分析SPSS(Statistical Product and Service Solutions)是目前在工业、商业、学术研究等领域中广泛应用的统计学软件包之一。
Correlation是SPSS的一个功能模块,可以用于分析两个或多个变量之间的关系。
下面是SPSS进行相关分析的具体步骤:1. 打开SPSS软件,选择“变量视图”(Variable View),输入相关的变量名,包括数字型变量和分类变量。
2. 进入“数据视图”(Data View),输入数据,并保存数据集。
3. 打开菜单栏中的“分析”(Analyze),选择“相关”(Correlate),再选择“双变量”(Bivariate)。
4. 在双变量窗口中,选择包含需要分析的变量的变量名,并将其移至右侧窗口中的变量框(Variables)。
5. 如果需要控制其他变量的影响,可以选择“控制变量”(Options)。
6. 点击“确定”(OK)按钮后,SPSS将输出结果,并将其显示在输出窗口中。
相关系数(Correlation Coefficient)介于-1和1之间,可以用来衡量两个变量之间的线性关系的强度。
7. 如果需要对结果进行图形化展示,可以选择“图”(Plots),并选择适当的图形类型。
需要注意的是,进行相关分析时需要确保变量之间存在线性关系。
如果变量之间存在非线性关系,建议使用其他统计方法进行分析。
同时,SPSS进行相关分析的结果只能描述变量之间的关系,不能用于说明因果关系。
以上是SPSS做相关分析的具体步骤,希望能对大家进行SPSS 数据分析有所帮助。
SPSS相关性分析 Pearson相关与偏相关分析的实现 步骤
SPSS相关性分析Pearson相关与偏相关分析的实现步骤
一、Pearson相关分析
二、偏相关分析
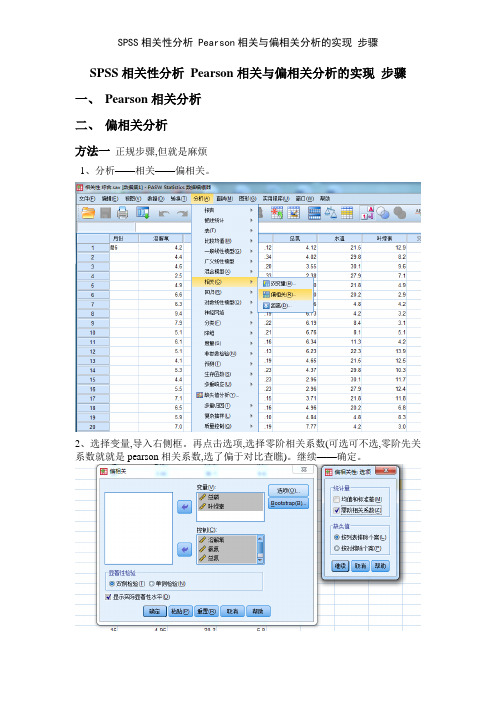
方法一正规步骤,但就是麻烦
1、分析——相关——偏相关。
2、选择变量,导入右侧框。
再点击选项,选择零阶相关系数(可选可不选,零阶先关系数就就是pearson相关系数,选了偏于对比查瞧)。
继续——确定。
3、结果分析:总磷Pearson相关不显著,但偏相关显著。
Pearson相关系数,显著性P值为0、416>0、05,相关性不显著。
偏相关,显著性P值为0、001<o、o1,极显著相关。
(显著性瞧sig、P值,
P<0、05,“*”显著;
P<0、01,“**”极显著)
方法二:简便方法,快捷迅速,不用挨个分析偏相关,可以一下子出来。
1、分析——回归——线性。
2、“溶解氧、氨氮、总磷、总氮、水温”与“叶绿素”的偏相关分析。
如图,先选择变量,再选择“统计量”。
“统计量”一定要选择“部分相关与偏相关性”。
其她的可以不选。
继续—确定。
3、结果分析,分别瞧Sig、显著性,与偏相关系数。
以总磷为例,与之前单独做“偏相关”分析结果就是一样的。
其她变量与叶绿素的偏相关关系也可以在上表瞧出来。
SPSS相关性分析(Pearson,Spearman和卡方检验)

SPSS相关性分析(Pearson,Spearman和卡方检验)一、相关分析方法的选择及指标体系(一)两个连续变量的相关分析1、Pearson相关系数最常用的相关系数,又称积差相关系数,取值-1到1,绝对值越大,说明相关性越强。
该系数的计算和检验为参数方法,适用条件如下:(1)两变量呈直线相关关系,如果是曲线相关可能不准确。
(2)极端值会对结果造成较大的影响(3)两变量符合双变量联合正态分布。
2、Spearman秩相关系数对原始变量的分布不做要求,适用范围较Pearson相关系数广,即使是等级资料,也可适用。
但其属于非参数方法,检验效能较Pearson系数低。
(二)有序分类变量的相关分析有序分类变量的相关性又称为一致性,即行变量等级高的列变量等级也高,如果行变量等级高而列变量等级低,则称为不一致。
常用的统计量有:Gamma、Kendall的tau-b、Kendall的tau-c 等。
(三)无序分类变量的相关分析最常用的为卡方检验,用于评价两个无序分类变量的相关性。
根据卡方值衍生出来的指标还有列联系数、Phi、Cramer的V、Lambda 系数、不确定系数等。
OR、RR也是衡量两变量之间的相关程度的指标。
二、SPSS相关操作SPSS的相关分析散布在交叉表和相关分析两个模块中。
(1)交叉表过程如下图:以上的指标很全面,解释如下:(1)“卡方”复选框:为常用的卡方检验,适用于两个无序分类变量的检验。
(2)“相关性”复选框:适用于两个连续性变量的相关分析,给出两变量的Pearson相关系数和Spearman相关系数。
(3)“有序”复选框组:包含了一组反映有序分类变量一致性的指标,只能用于两变量均为有序分类变量的情况。
(4)“名义”复选框组:包含一组分类变量相关性的指标,有序和无序分类时都可使用,但变量为有序时,检验效能没有“有序”复选框组中的统计量高。
(5)Kappa:为内部一致性系数。
(6)风险:给出OR或RR值。
Spss 的相关分析

3、矩阵散点图
矩阵散点图以方形矩阵的形式分别显示多对变量间的统计关系。矩阵散点图的关键是弄清各矩阵单元中的横纵变量。以3×3的矩阵散点图为例。变量分别 ,矩阵散点图的横纵变量如下表(括号中的前一个变量作为纵轴变量,后一个变量作为横轴变量)
矩阵散点图坐标变量示意
Spss的相关分析
一、相关的概念
相关分析是分析客观事物之间的数量分析方法,明确客观事物之间有怎样的关系对理解和运用相关分析是极为重要的。
客观事物之间的关系大致可归纳为两大类关系,它们是函数关系和统计关系。相关分析是用来分析事物之间统计关系的方法。
所谓函数关系指的是两事物之间的一种一一对应关系,即当一个变量 取一定值时,另一变量 可以依确定的函数取唯一确定的值。
四、计算相关系数
1、相关系数的特点
虽然散点图能够直观地展现变量之间的统计关系,但不准确。
相关系数以数值的方式很精确地反映了两个变量间线性相关的强弱程度。利用相关系数进行变量间线性关系的分析通常需要完成以下两大步骤:
第一、计算样本相关系数 。
利用样本数据计算样本相关系数。样本相关系数反映了两变量间线性相关程度的强弱。对不同类型的变量应采用不同的相关系数指标,但它们的取值范围和含义都是相同的,即
Spss将自动计算Kendall 相关、 检验统计量的观测值和对应的概率P值。
适用条件:
(1)只有两列变量,且具有等级变量性质,具有线性关系的资料,主要用于解决等级和顺序数据的相关问题;
(2)即使是属于等距或等比性质的变量,若按其取值大小,赋以等级或顺序,亦可计算等级相关。
(3)不对数据的整体分布状态做要求,不管数据是不是正态分布,都可以用等级相关计算相关关系。
如何用spss做相关性分析

如何用spss做相关性分析例:学生每天学习时间T与学习综合成绩G之间的相关性原始数据T G1.1 541.5 602.2 623 70.13.4 744 74.54.2 775.5 81.55.9 856 85.56.5 86.28 90G=f(T),其中T为自变量,G为因变量step1:建立数据文件 file——new——data;定义变量选中左下角菜单Variable view,输入变量名T,其他选项不变,令起一行,输入变量名G其他选项不变,切换到data view(在左下角),将数据复制进去。
Step2:进行数据分析:在spss最上面菜单里面选中Analyze——correlate——bivariate(双变量)左边包含G,T的框为源变量框,后面的空白框为分析变量框,我们现在需要分析G和T的关系,因此将源变量框中的G和T选进分析变量框待分析。
(1)correlation coefficients(相关系数)包括三个选项:Pearson:皮尔逊相关,计算连续变量或是等间距测度的变量间的相关分析;Kendall:肯德尔相关,计算等级变量间的秩相关;Spearman:斯皮尔曼相关,计算斯皮尔曼秩相关。
注:Pearson可用来分析①分布不明,非等间距测度的连续变量Kendall可用来分析①分布不明,非等间距测度的连续变量,②完全等级的离散变量,③数据资料不服从双变量正态分布或总体分布型未知。
第②种情况只能用Kendall分析Spearman可用来分析数据资料不服从双变量正态分布或总体分布型未知(2)Test of significance选项Two-tailed:双尾检验,如果事先不知道相关方向(正相关还是负相关)则可以选择此项;One-tailed:单尾检验,如果事先知道相关方向可以选择此项。
(3)Flag significant correlations:表明显著水平,如果选择此项,输出结果中在相关系数值右上方使用*标示显著性水平为5%,用**标示其显著性水平为1%首先使用pearson,two-tailed(下图),点击右侧optionsstatistics为统计量,包括均值和标准差叉积离方差和协方差missing values 选择默认点击continue——ok输出结果(下图)相关系数为0.975,显著性p=0.000<0.01,有统计学意义选用Kendall 肯德尔,结果如下:选用spearman 斯皮尔曼,结果如下:画散点图:选中Graphs——Scatter/dot-----Simple scatter------define。
最快五步用SPSS软件进行相关性分析

第二步:数据视图只能输入数据,要想更改变量的名称就 得在变量:更改后名称后,接下来就到了关键的部分,点击最上方菜 单栏中的“分析”这一栏,在“分析”中的“相关”栏中找到 “双变量”这一栏就行点击。 第四步:在出来的双变量相关中把框内所有的变量点击向右的按钮 过去另一个框,其余的按钮都不要变,再点击确定按钮就行。
采用SPSS进行相关性分析的具体步骤
-
涉及到相关性分析,一般情况下就会用到 SPSS软件,那么怎样采用SPSS软件进行相 关性分析呢?下面我来具体说明一下相关 的步骤: 这一共分为五步
-
第一步:打开SPSS软件,在数据视图中输入变量的数值。 比如我想探究饱和吸附量与阳离子交换量和阴离子交换量 的关系,就将数据粘贴上去。
-
第五步:下图呈现的就是相关性的结果,“双变量”就是 两个变量之间的相关性如何,数值是负值就是没有相关性, 正值就相关,然后自己截图或者做一个结果统计表就行。
-
心理统计SPSS-第六章-相关性研究及其分析过程

9
4 6
10
3 6
3
4 5 6 7
5
1 4 2 7
5
1 3 2 7
5
1 4 3 6
7
2 4 1 5
6
2 3 1 5
6
2 3 1 7
4
2 5 1 6
4
1 6 3 5
5
1 3 2 7
4
2 5 1 7
肯德尔和谐系数分析过程p166 Analyze Nonparametric Test
K Related Sample
第六章
相关性研究及其分析过程
事物是普遍联系的,人的心理和行为也与人的许多内外因素 相联系,表现出复杂性的一面和随机性的一面。对影响人的心理 和行为的内外因素进行分析是揭示心理活动规律和机制的重要途 径,而相关分析是其中初级但很重要的部分。相关分析可发现变 量间的共变关系,一旦发现了共变关系就意味着变量间可能存在 两种关系中的一种: 第一,因果关系(两个变量中一个为因、一个为果); 第二,存在公共因子或中介变量。 心理学的许多研究就是为了寻找这些因果关系,或者是寻找 公共因子。可见,相关研究是许多深入研究的初始阶段。
我们还可以用散点图来直观表达两个变量的变化关系
相关分析包括三大类:二元相关分析、偏相关分析和距离相关分
析。其中二元相关分析( Bivariate Corr.)又可分为连续测量变量 间的简单相关分析和离散变量间的相关分析两类。具体如下图所示:
相关分析 二元变量相关分析 Bivariate Corr. 偏相关分析 Partial Corr. 距离相关分析 Distance Corr.
演示6:分半信度分析过程演示及其结果解释
2.克伦巴赫α系数
SPSS皮尔逊相关分析实例操作步骤

SPSS皮尔逊相关分析实例操作步骤选题:对某地29名13岁男童的身高(cm)、体重(kg),运用相关分析法来分析其身高与体重是否相关。
实验目的:任何事物的存在都不是孤立的,而是相互联系、相互制约的。
相关分析可对变量进行相关关系的分析,计算29名13岁男童的身高(cm)、体重(kg),以判断两个变量之间相互关系的密切程度。
实验变量:编号Number ,身高height (cm ),体重weight (kg )原始数据:实验方法:皮尔逊相关分析法 软件:操作过程与结果分析: 第一步:导入Excel 数据文件 1. open data document ——open data ——open ;28 40 29322. Opening excel data source——OK.第二步:分析身高(cm)与体重(kg)是否具有相关性1.在最上面菜单里面选中Analyze——correlate——bivariate ,首先使用Pearson,two-tailed,勾选flag significant correlations进入如下界面:2.点击右侧options,勾选Statistics,默认Missing Values,点击Continue输出结果:Descriptive StatisticsMean Std. Deviation N身高(cm)29体重(kg)29图为基本的描述性统计量的输出表格,其中身高的均值(mean)为、标准差(standard deviation)为、样本容量(number of cases)为29;体重的均值为、标准差为、样本容量为29。
两者的平均值和标准差值得差距不显著。
Correlations身高(cm)体重(kg)身高(cm)Pearson Correlation1.719**Sig. (2-tailed).000Sum of Squares andCross-productsCovarianceN2929体重(kg)Pearson Correlation.719**1Sig. (2-tailed).000Sum of Squares andCross-productsCovarianceN2929**. Correlation is significant at the level (2-tailed).图为相关分析结果表,从表中可以看出体重和身高之间的皮尔逊相关系数为,即|r|=,表示体重与身高呈正相关关系,且两变量是显著相关的。
最快五步用SPSS软件进行相关性分析

“双变量”就是两个变量之间的相关性如 何,数值是负值就是没有相关性,正值就 相关,然后自己截图或者做一个结果统计
表就行。
采用SPSS进行相关性分析的 具体采用SPSS软件进行相关性分 析呢?下面我来具体说明一下
相关的步骤: 这一共分为五步
第一步:打开SPSS软件,在数据视图中输 入变量的数值。比如我想探究饱和吸附量 与阳离子交换量和阴离子交换量的关系,
就将数据粘贴上去。
第二步:数据视图只能输入数据,要想更 改变量的名称就得在变量视图中就行名称 更改。所以在变量视图中输入变量的名称
。
分,点击最上方菜单栏中的“分析”这一栏,在 “分析”中的“相关”栏中找到 “双变量”这一
栏就行点击。 第四步:在出来的双变量相关中把框内所有的变 量点击向右的按钮过去另一个框,其余的按钮都
【精选】SPSS皮尔逊相关分析实例操作步骤
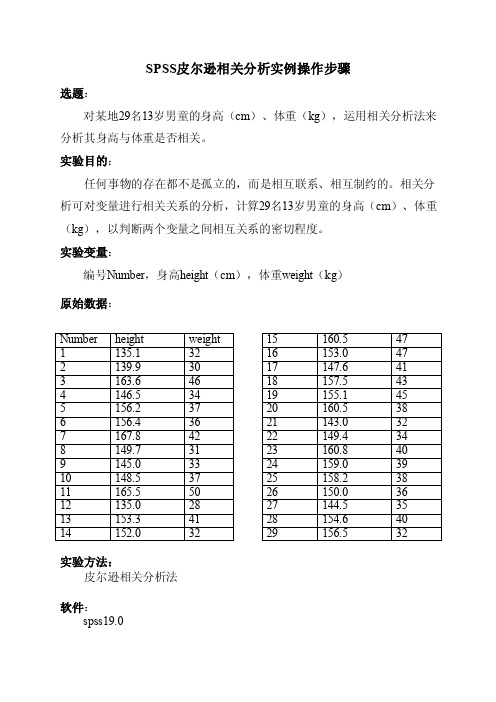
SPSS皮尔逊相关分析实例操作步骤选题:对某地29名13岁男童的身高(cm)、体重(kg),运用相关分析法来分析其身高与体重是否相关。
实验目的:任何事物的存在都不是孤立的,而是相互联系、相互制约的。
相关分析可对变量进行相关关系的分析,计算29名13岁男童的身高(cm)、体重(kg),以判断两个变量之间相互关系的密切程度。
实验变量:编号Number,身高height(cm),体重weight(kg)原始数据:实验方法:皮尔逊相关分析法软件:spss19.0操作过程与结果分析:第一步:导入Excel数据文件1. open data document——open data——open;2. Opening excel data source——OK.第二步:分析身高(cm)与体重(kg)是否具有相关性1.在最上面菜单里面选中Analyze——correlate——bivariate ,首先使用Pearson,two-tailed,勾选flag significant correlations进入如下界面:2.点击右侧options,勾选Statistics,默认图为基本的描述性统计量的输出表格,其中身高的均值(mean)为152.576cm、标准差(standard deviation)为8.3622、样本容量(number of cases)为29;体重的均值为37.65kg、标准差为5.746、样本容量为29。
图为相关分析结果表,从表中可以看出体重和身高之间的皮尔逊相关系数为0.719,即|r|=0.719,表示体重与身高呈正相关关系,且两变量是显著相关的。
另外,两者之间不相关的双侧检验值为0.000,图中的双星号标记的相关系数是在显著性水平为0.01以下,认为标记的相关系数是显著的,验证了两者显著相关的关系。
所以可以得出结论:学生的体重与身高存在显著的正相关性,当体重越高时,身高也越高。
第三步:画散点图:选中Graphs——Legacy Dialogs——Scatter/dot——Simple scatter——define.得到散点图,如下图:测量学试卷 第 6 页(共 7 页)《测量学》模拟试卷1.经纬仪测量水平角时,正倒镜瞄准同一方向所读的水平方向值理论上应相差(A )。
SPSS Pearson相关性分析

SPSS Pearson 相关性分析∙ 1∙ 2∙ 3∙ 4∙ 5∙ 6∙7分步阅读世间万物都是存在相关联系的,我们在医学上以及社会学上都常常需要对两个变量进行相关性分析。
如果两个变量都是分类变量或者有一个是分类变量,则需要用Spearman 相关分析,如果两个变量都是连续性的变量,则Pearson 分析方法更加适合工具/原料∙spss软件∙连续性的两个变量方法/步骤1. 1打开SPSS软件;点击“开始”按钮,双击“SPSS ”软件。
导入数据:点击左上角“文件”-----“打开”-----“数据”,并选择你的数据如果为spss数据可以直接导入,若为excel 格式,需要在“文件类型”框中选择“excel格式”2. 2开始做数据分析:在工具栏处,点击:“分析”----”相关”----“双变量”,如下图所示,则开始进行变量的选择3. 3如图,需要先确定要分析的变量,首先将两个变量放入“变量”框中。
此时,需要注意,要分析哪几个变量就只能选择那几个变量,而不能将所有的变量选入,而且,这里是双变量分析,因此,最多可以选择两个变量4. 4然后,选择在“相关系数”框中选择“Pearson”。
因为,这里的两个变量为连续性的变量,因此采用pearson 相关分析;若为两个分类变量,或者一个分类变量一个连续性的变量,则可以用Spearman 相关分析5. 5选择好变量之后,如果需要对数据进行一定的描述,或者查看,可以打开右上角的按钮,即选择“选项”,如下图所示6. 6大部分分析需要对原始数据进行统计描述,即如果需要进行描述性分析,可以选择均值和标准差,如上图所示的mea n (均值)和 sd (标准差),分别对数据的大小和离散程度作出一定的描述,并点击“确定按钮”7.7如果需要对数据进行模拟分析,则可以选择右上角的“bootsTrap”模拟分析,打开后如下图所示。
其中样本数为需要模拟的总共的次数,可以自己定义;后面的种子数,是开始模拟随机数字的起始种子数,同样可以自行定义。
Pearson相关的超详细SPSS操作方法

Pearson相关的超详细SPSS操作方法Pearson相关的超详细SPSS操作方法作者:张耀文(医咖会)1、问题与数据某研究者拟探讨在45岁至65岁健康男性中胆固醇浓度与观看电视的时间是否有关。
他猜测:看电视时间较长者,血液中的胆固醇浓度要高一些。
研究者收集了研究对象每天看电视时间(变量time_tv)和胆固醇浓度(变量cholesterol)。
部分数据如图1.1。
图1.1 部分数据2、对问题的分析研究者想观察两个连续变量之间的相关性,可以使用Pearson相关分析。
使用Pearson相关分析时,需要考虑5个假设。
假设1:两个变量都是连续变量。
假设2:两个连续变量应当是配对的,即来源于同一个个体。
假设3:两个连续变量之间存在线性关系,通常做散点图检验该假设。
假设4:两个变量均没有明显的异常值。
Pearson相关系数易受异常值影响。
假设5:两个变量符合双变量正态分布。
假设1和假设2与研究设计有关。
经分析,本研究数据符合假设1和2。
如何考虑和处理假设3-5呢?3、SPSS操作3.1 检验假设3:两个连续变量之间存在线性关系Pearson要求两个变量之间存在线性关系。
本例要求观看电视时间(time_tv)和胆固醇浓度(cholesterol)之间存在线性关系。
要确定是否存在线性关系,研究者需要查看两个变量的散点图。
如果散点图大致呈一条直线,说明有线性关系。
但是,如果不是一条直线(如一条曲线)则没有线性关系。
散点图1.2给出了线性和非线性关系的例子:图1.2 两个变量的散点图计算Pearson相关系数时,最好有类似于上述第一个散点图的线性关系。
如果两变量间不存在线性关系,下面还会介绍如何应对这种非线性关系并计算Pearson相关系数。
以下先说明将如何在SPSS中生成散点图,检验线性关系。
在主界面点击Graphs→Chart Builder,在Chart Builder对话框下,选择Gallery→Choose from→Scatter/Dot。
SPSS偏相关性分析

身高 135.1 139.9 163.6 146.5 156.2 156.4 167.8 149.7
体重 32 30.4 46.2 33.5 37.1 35.5 41.5 31
肺活量 1570 2000 2750 2500 2750 2000 2750 1500
编号 9 10 11 12 13 14 15 16
变量1 关系 变量2
控制 变量3
第7页/共43页
• 例:
未知 收入水平
关系? 价格
上升
上升还是 需求量 下降呢?
• 在现实经济生活中,由于收入和价格常 常都有不断提高的趋势,如果不考虑收
入对需求的影响,仅仅利用需求和价格
的时间序列数据去计算简单相关系数,
就有可能得出价格越高需求越大的错误 结论。
第8页/共43页
• 依此类推变量Y与Xi的p-1阶偏相关系数为:
r0ig12L(i
1)(i
1)L p
r0ig12L(i
1)(i1)L( p1) r0 1 r02pg12L( p1)
pg12L( p1)ripg12L(i1)(i1)L( 1 ri2pg12L(i1)(i1)L( p1)
p1)
第10页/共43页
第四部分 偏关分析的SPSS过程
第12页/共43页
• 第三步:选择检验类型。 变量窗口
显著性检验: 双尾检验(默认) 单尾检验(相关方 向明显时)
显示相关系数时,显 示实际的显著性概率
相关变量
控制变量
第13页/共43页
• 第四步:打开OPTION选项框。
均值与标准差,即显示每 个变量的均值、标准差和
非缺失值的例数
显示零阶相关矩阵,即 Pearson相关矩阵 仅剔除当前分析的两个 变量值是缺失值的个案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS相关性分析Pearson 相关与偏相关分析的实现
步骤
SPSS相关性分析Pearso n相关与偏相关分析的实现
步骤
一、Pearson相关分析
二、偏相关分析
方法一正规步骤,但是麻烦
1、分析——相关——偏相关。
2、选择变量,导入右侧框.再点击选项,选择零阶相关系数(可选可不选,零阶先关系数就是pearson相关系数,选了偏于对比查看)。
继续--确定。
3、结果分析:总磷Pearson相关不显著,但偏相关显著.
Pearson相关系数,显著性P值为0。
416〉0.05,相关性不显著。
偏相关,显著性P值为0.001<o.o1,极显
著相关。
(显著性看 sig。
P值,
P<0。
05,“*"显著;
P〈0.01,“**"极显著)
方法二:简便方法,快捷迅速,不用挨个分析偏相关,可以一下子出来.
1、分析——回归——线性.
2、“溶解氧、氨氮、总磷、总氮、水温”与“叶绿素”的偏相关分析。
如图,先选择变量,再选择“统计量”。
“统计量”一定要选择“部分相关和偏相关性”。
其他的可以不选。
继续—确定。
3、结果分析,分别看Sig。
显著性,和偏相关系数。
以总磷为例,与之前单独做“偏相关”分析结果是一样的.其他变量与叶绿素的偏相关关系也可以在上表看出来。
...谢阅...。
