中考相似专题练习
2025届中考数学复习专项(相似三角形-手拉手旋转型综合应用)练习(附答案)

2025届中考数学复习专项(相似三角形-手拉手旋转型综合应用)练习1.如图(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出ΔOB1C1;(2)点B的对应点B1的坐标是,点C的对应点C1的坐标是.2.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)求证:△ABC∽△ADE;(2)判断△ABD与△ACE是否相似?并证明.3.如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC,AC的中点,连接DE.(1)求:的值;(2)将△CDE绕点C逆时针方向旋转一定的角度,的大小有无变化?请仅就图2的情形给出证明.4.如图,在△ABC与△DEC中,已知∠ACB=∠DCE=90°,AC=6,BC=3,CD=5,CE=2.5,连接AD,BE.(1)求证:△ACD∽△BCE;(2)若∠BCE=45°,求△ACD的面积.5.问题背景:如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;尝试应用:如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE =30°,AC与DE相交于点F.点D在BC边上,,求的值.6.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,求证:(1)△ABC∽△ADE(2)若AC:BC=3:4,求BD:CE为多少7.【问题背景】如图1,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,由已知可以得到:①△ ≌△ ;②△ ∽△ .【尝试应用】如图2,在△ABC和△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE =30°,求证:△ACE∽△ABD.【问题解决】如图3,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE =30°,AC与DE相交于点F,点D在BC上,,求的值.8.如图,点B在线段CD上,在CD的同一侧作两个等腰直角△ABC和△BDE,且∠ACB =∠BED=90°,AD与CE,BE分别交于点P,M,连接PB.(1)若AD=k•CE,则k的值是;(2)求证:△BMP∽△DME;(3)若BC=,P A=3,求PM的长.9.如图1,在Rt△ABC中,AC=BC=5,等腰直角△BDE的顶点D,E分别在边BC,AB 上,且BD=,将△BDE绕点B按顺时针方向旋转,记旋转角为α(0°≤α<360°).(1)问题发现当α=0°时,的值为,直线AE,CD相交形成的较小角的度数为;(2)拓展探究试判断:在旋转过程中,(1)中的两个结论有无变化?请仅就图2的情况给出证明:(3)问题解决当△BDE旋转至A,D,E三点在同一条直线上时,请直接写出△ACD的面积.。
中考数学总复习《相似》专项训练题(附有答案)

中考数学总复习《相似》专项训练题(附有答案)学校:___________班级:___________姓名:___________考号:___________ 一、单选题1.已知C 是线段AB 的黄金分割点,AB=2,AC BC >则AC 的长为( ) A .35-B .51-C .23-D .31-2.如图所示,DE 是ABC 的中位线,若2ADE S ∆=,则ABCS等于( )A .2B .4C .6D .83.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm ,光源到屏幕的距离为40cm ,且幻灯片中图形的高度为8cm ,则屏幕图形的高度为( )A .8cmB .12cmC .16cmD .24cm4.已知c 是a 和b 的比例中项2a =,18b =则c =( ) A .6±B .6C .4D .3±5.如图,小明家的客厅有一张高0.8米的圆桌,直径BC 为1米,在距地面2米的A 处有一盏灯,圆桌的影子最外侧两点分别为D 、E ,依据题意建立如图所示的平面直角坐标系,其中点D 的坐标为()2,0,则点E 的坐标是( )A .11,03⎛⎫ ⎪⎝⎭B .()3,0C .()3.6,0D .()4,06.如图,在平面直角坐标系xOy 中,第一象限的点A ,B 分别在反比例函数k y x=,()0nky nk x=≠的图象上,AB x 轴,AD x ⊥轴于点D ,连接OB 交AD 于点C ,交反比例函数ky x=的图象于点E ,若2CE OC =,则n 的值为( )A .9B .8C .4D .37.在四边形ABCD 中()AD BC AD BC <∥,点P 从点B 出发,沿B A D →→运动,点Q 同时以相同的速度从点B 出发,沿B C →运动,结果同时到达点D C BPQ ,,△的面积y 与点P 运动的路程x 满足的函数关系如图所示,其中OM 为抛物线的一部分.根据图象得出下列结论:①90B ;①6ABCD S =四边形;①2CD AD BC =⋅;①当2x =时,四边形CDPQ 是菱形.其中正确的结论有( )A .1个B .2个C .3个D .4个8.如图,在平行四边形ABCD 中,E 是BC 上的3等分点,AE 交BD 于点F ,则BEF △与DAF △的面积比为( )A .12:B .13:C .14:D .19:二、填空题9.如果53x y y +=,那么xy= . 10.如图AD BE CF ∥∥,直线1l ,2l 分别与这三条平行线交于点A ,B ,C 和点D ,E ,F .已知AB=6,AC=15,DE=5,则EF 的长为 .11.阿基米德曾说过:“给我一个支点和一根足够长的杆子,我就能撬起整个地球.”这句话的意思是利用物理学中的杠杆原理,只要有合适的支点和合适的工具,就可以把地球轻松搬动.如图1,这是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图2中,杠杆的D 端被向上翘起的距离7cm BD =,动力臂OA 与阻力臂OB 满足3OA OB =(AB 与CD 相交于点O ),则AC 的长为 cm .12.黄金分割大量应用于艺术、大自然中,例如树叶的叶脉也蕴含着黄金分割.如图,B 为AC 的黄金分割点(AB BC >),如果AB 的长度为10cm ,则BC 的长度为 cm .(结果保留根号)13.如图,在平行四边形ABCD 中,以C 为位似中心,作平行四边形ABCD 的位似平行四边形PECF ,且与原图形的位似比为2:3,连接BP ,DP ,若平行四边形ABCD 的面积为20,则PBE △与PDF △的面积之和为三、解答题14.如图,为了求出海岛上的山峰AB的高度,在D处和F处树立标杆CD和EF,标杆的高都是20米,D,F两处相隔200米,并且AB,CD和EF在同一平面内.从标杆CD后退80米的G处,可以看到顶峰A和标杆顶端C在一条直线上;从标杆EF后退160米的H处,可以看到顶峰A和标杆顶端E在一条直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少米?15.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的ABC和格点O.(1)在所给网格中,以点O 为位似中心,将ABC 放大2倍得到111A B C △(点,,A B C 的对应点分别是111,,A B C ),画出111A B C △;(2)将ABC 进行平移得到格点222A B C △(点,,A B C 的对应点分别是222,,A B C ),使112B C AC ∥,画出222A B C △.16.如图,点F 是四边形ABCD 的边AD 上的一点,直线CF 交线段BA 的延长线于点E .AF=2,DF=4,EF=15,CF=3.(1)求证:D AEF CF ∽△△;(2)若22AB =,2AE =试判断四边形ABCD 的形状并说明理由.17.如图90ABC ∠=︒,AB=2,BC=8,射线CD BC ⊥于点C ,E 是线段BC 上一点,F 是射线CD 上一点,且满足90AEF ∠=︒.(1)若3BE =,求CF 的长; (2)当6CF =时,求BE 的长.18.解答下列各题(1)【基础巩固】如图1,在四边形ABCD 中,对角线BD 平分ABC ADB DCB ∠∠=∠,,求证:2BD BA BC =⋅;(2)【尝试应用】如图2,四边形ABCD 为平行四边形,F 在AD 边上AB AF =,点E 在BA 延长线上,连结EF BF CF ,,,若56EFB DFC BE BF ∠=∠==,,,求AD 的长; (3)【拓展提高】如图3,在ABC 中,D 是BC 上一点,连结AD ,点E ,F 分别在AD ,AC 上,连结BE CE EF ,,.若2410DE DC BEC AEF BE EF =∠=∠==,,,和23CE BC =,求AFFC的值.参考答案:1.B 2.D 3.C 4.A 5.A 6.A 7.C 8.D 9.2310.15211.21 12.555 13.8027/2622714.山峰的高度AB 为70米,它和标杆CD 的水平距离BD 是200米 15.(1)解:如图所示,111A B C △即为所求.(2)解:如图所示,222A B C △即为所求.16.(1)证明:①2AF = 4DF = 1.5EF = 3CF = ①2142AF DF == 1.5132EF CF == ①AF EFDF CF= 又①AFE DFC ∠=∠ ①AEF DCF ∽;(2)解:四边形ABCD 是平行四边形,理由如下: 由(1)知AEF DCF ∽ ①E DCF ∠=∠ 12AE EF CD CF == ①AB CD ∥①22AB = 2AE = ①222CD AE AB === ①四边形ABCD 是平行四边形. 17.(1)152; (2)2或6.18.(1)证明:①BD平分ABC∠①ABD DBC∠=∠①ADB DCB∠=∠①ABD DBC∽①AB BD BD BC=①2BD BA BC=⋅;(2)36 5(3)5 3。
初三相似试题及答案

初三相似试题及答案
一、选择题
1. 在下列选项中,哪两个图形是相似的?
A. 一个正方形和一个矩形
B. 一个正三角形和一个等腰三角形
C. 一个圆形和一个椭圆形
D. 一个菱形和一个正方形
答案:A
2. 如果两个图形相似,那么它们的对应角:
A. 相等
B. 互补
C. 互为余角
D. 互为补角
答案:A
3. 相似图形的对应边成比例,那么下列说法正确的是:
A. 相似比是边长的比值
B. 相似比是面积的比值
C. 相似比是周长的比值
D. 相似比是体积的比值
答案:A
二、填空题
1. 两个相似图形的相似比是2:3,那么它们的面积比是________。
答案:4:9
2. 如果一个图形的长和宽分别是8cm和6cm,那么与它相似的图形的长和宽分别是12cm和________cm。
答案:9
3. 相似三角形的周长比是3:5,那么它们的面积比是________。
答案:9:25
三、解答题
1. 已知三角形ABC与三角形DEF相似,且三角形ABC的边长分别是
3cm、4cm和5cm,三角形DEF的边长分别是6cm、8cm和10cm。
求三角形ABC与三角形DEF的相似比。
答案:三角形ABC与三角形DEF的相似比是3:6,即1:2。
2. 一个矩形的长是10cm,宽是4cm,与它相似的另一个矩形的长是20cm,求这个矩形的宽。
答案:矩形的宽是8cm。
3. 一个正三角形的边长是6cm,与它相似的另一个正三角形的边长是9cm,求这两个三角形的面积比。
答案:这两个三角形的面积比是36:81。
中考数学复习《相似》专题训练--附参考答案
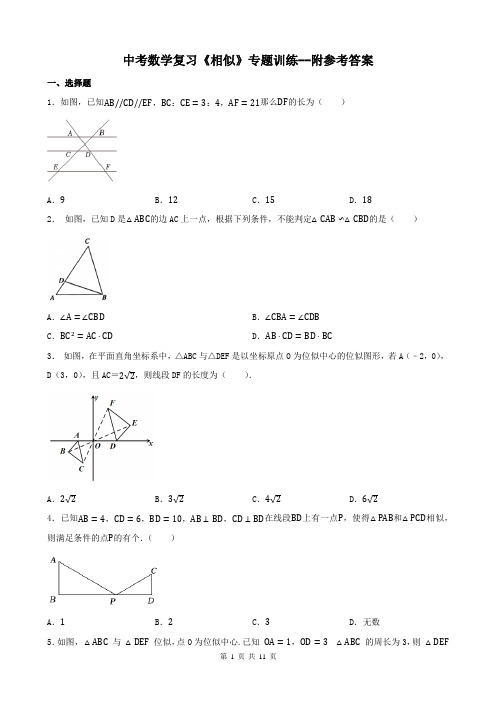
中考数学复习《相似》专题训练--附参考答案一、选择题1.如图,已知AB//CD//EF,BC:CE=3:4,AF=21那么DF的长为()A.9B.12C.15D.182.如图,已知D是△ABC的边AC上一点,根据下列条件,不能判定△CAB∽△CBD的是()A.∠A=∠CBD B.∠CBA=∠CDBC.BC2=AC⋅CD D.AB⋅CD=BD⋅BC3.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC=2√2,则线段DF的长度为().A.2√2B.3√2C.4√2D.6√24.已知AB=4,CD=6,BD=10,AB⊥BD,CD⊥BD在线段BD上有一点P,使得△PAB和△PCD相似,则满足条件的点P的有个.()A.1B.2C.3D.无数5.如图,△ABC与△DEF位似,点O为位似中心.已知OA=1,OD=3△ABC的周长为3,则△DEF的周长是()A.4 B.6 C.9 D.276.如图,为了估计某一条河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS 垂直的直线b的交点为R,如果QS = 60m,ST =120m,QR=80m,则这条河的宽度PQ为()A.40m B.120m C.60m D.180m7.如图,在Rt△ABC中∠ACB=90°,AC=BC,CD⊥AB点E为AC边上的中点,连接BE交CD于点F.若AC=4√2,则BF的长为().A.163B.4 C.2√103D.4√1038.如图,在△OAB中∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=9x(x>0)的图象经过点B和点C,那么点C的坐标是()A.(3,3)B.(3,1.5)C.(4.5,2)D.(9,1)二、填空题9.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为.10.如图,在△ABC中,D为AB上一点,且∠ACD=∠B,若AD=2,BD= 5,则AC=211.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .12.如图,P是平行四边形ABCD边BC上的一点,M、N分别是PA、PD的中点,若△PMN的面积为3cm2,则平行四边形ABCD的面积是cm2.13.如图,四边形ABCD是菱形,E为对角线BD的延长线上一点,且BD=8,DE=2∠BAE=45°则AB 的长为.三、解答题14.如图,AD、BE是的高,连接.(1)求证:∽;(2)若点D是的中点,CE=3,BE=4,求的长.15.已知:如图,在菱形中,点,分别在边,上,的延长线交的延长线于点,的延长线交的延长线于点. (1)求证:; (2)如果,求证:.16.如图,在矩形ABCD 中,点G 在边BC 上(不与点B 、C 重合),连接AG ,作DF ⊥AG 于点F ,BE ⊥AG 于点E.(1)若AG =AD ,求证:AB =DF ;(2)设BG BC =k ,连接BF 、DE ,设∠EDF =α,∠EBF =β,求tana tanβ的值.17.如图1,已知点O 在四边形ABCD 的边AB 上,且OA =OB =OC =OD =2,OC 平分∠BOD ,与BD 交于点G ,AC 分别与BD 、OD 交于点E 、F .(1)求证:OC ∥AD ;(2)如图2,若DE =DF ,求AE AF 的值;(3)当四边形ABCD 的周长取最大值时,求DE DF 的值.18.如图1, ABD 内接于,AD 是直径, BAD 的平分线交BD 于H ,交 于点C ,连接O ODC 并延长,交AB 的延长线于点E.(1)求证: AE=AD ;(2)若 32BEAB = ,求 AHHC 的值(3)如图2,连接CB 并延长,交DA 的延长线于点F ,若 ,6AH HC AF == 求 BEC 的面积.参考答案1.B2.D3.B4.B5.C6.B7.D8.D9.4:910.311.2:112.2413.4√1014.(1)证明:∵、是的高∴∵∴∽;(2)解:∵点D是的中点∴在中∵∴∴∵∽∴∴∴∴.15.(1)证明:∵四边形ABCD是菱形∴∵∴∴∵∴∴∵∴;(2)证明:∵∴ .∵∴∠B=∠EAG,∠BCE=∠G∴△AGE∽△BCE∴∴∵∴∴.16.(1)证明:∵四边形ABCD是矩形∴AD//BC∴∠DAG=∠BGA∵DF⊥AG ∴∠DFA=∠BEG=90°∵∠ABC=90°∴∠DFA=∠ABC在△ADF和△GAB中{∠DAG=∠BGA ∠DFA=∠ABC AD=AG∴△ADF≌△GAB∴AB=DF(2)解:由已知得:∵∠DFA=∠BEG=90°∴在Rt△DEF中tanα=EFDF;在Rt△BEF中∴tanαtanβ=EFDFEFBE=BEDF∵∠DAG=∠BGA∴△DFA∽△BEG∴BEDF =BGAD∵四边形ABCD是矩形∴AD=BC∵BGBC=k∴BEDF =BGAD=BGBC=k∴tanαtanβ=BEDF=k17.(1)证明:∵AO=OD ∴∠OAD=∠ADO∵OC平分∠BOD∴∠DOC=∠COB又∵∠DOC+∠COB∠=∠OAD+∠ADO ∴∠ADO=∠DOC∴CO∥AD;(2)解:∵OA=OB=OC∴∠ADB=90°∴△AOD和△ABD是等腰直角三角形∴AD= √2AO∴ADAO=√2∵DE=DF∴∠DFE=∠AED∵∠DFE=∠AFO∴∠AFO=∠AED∵∠AOF=∠ADE=90°∴△ADE∽△AOF∴AEAF =ADAO= √2;(3)解:如图2∵OD=OB,∠BOC=∠DOC,∴△BOC≌△DOC(SAS),∴BC=CD 设BC=CD=x,CG=m,则OG=2﹣m∵OB2﹣OG2=BC2﹣CG2∴4﹣(2﹣m)2=x2﹣m2,解得:m =14x2,∴OG=2 −14x2∵OD=OB,∠DOG=∠BOG,∴G为BD的中点又∵O为AB的中点,∴AD=2OG=4 −12x2∴四边形ABCD的周长为2BC+AD+AB=2x+4 −12x2+ 4 =−12x2+ 2x+8 =−12(x−2)2+ 10∵−12< 0,∴x=2时,四边形ABCD的周长有最大值为10.∴BC=2∴△BCO为等边三角形,∴∠BOC=60°,∵OC∥AD,∴∠DAC=∠COB=60°∴∠ADF =∠DOC =60°,∠DAE =30°,∴∠AFD =90°,∴DE DA =√33 ,DF =12 DA ∴DE DF =2√33 .18.(1)证明:∵AD 是 的直径90ACD ACE ∴∠=∠=︒∵AC 平分DAC EAC ∴∠=∠在△ACD 和△ACE 中∵∠ACD=∠ACE ,AC=AC ,∠DAC=∠EAC∴△ACD ≌△ACE (ASA )AE AD ∴=(2)解:如图,连接OC 交BD 于G 32BE AB = 设 3,2BE x AB x == 则 5AD AE AB BE x ==+= ,OC= AD= 52x DAC EAC ∠=∠BC CD ∴=∴OC 垂直平分BD又∵O 为AD 的中点∴OG 为△ABD 的中位线 ∴OC ∥AB ,OG= 1AB 2x = ,CG= 53OC OG=22x x x --= ABH CGH ∴~24332AH AB x HC CG x ∴===O BAD ∠12第 11 页 共 11 页 (3)解:如图,连接OC 交BD 于G由(2)可知:OC ∥AB ,OG= AB ∴∠BHA=∠GCH在△BHA 和△GHC 中 ∵∠BHA=∠GCH ,AH=CH ,∠BHA=∠GHC ()BHA GHC ASA ∴≅∴CG AB =设 OG m = ,则 2,3CG AB m OA OC m ==== 又 //OC AB∴FAB FOC ~FA AB FO OC∴= 62633m m m∴=+ 1m ∴= 2,6,4AB AD BE ∴=== ∵AD 是 的直径90ABD EBD ∴∠=∠=︒22226242BD AD AB =--=114428222EBD S EB BD ∴=⋅=⨯⨯= 又 ,ACD ACE ≅ EC CD ∴= 11824222BEC EBD S S ∴==⨯=12O。
中考数学图形的相似专题卷(附答案)

中考数学图形的相似专题卷(附答案)一、选择题1.如图,在ABC ∆中,BC DE //,AD=6,DB=3,AE=4,则EC 的长为( )A 、1B 、2C 、3D 、42.若2a=3b ,则=( )A .B .C .D .3.如图,菱形纸片ABCD 的对角线AC 、BD 相交于点O ,折叠纸片使点A 与点O 重合,折痕为EF ,若AB=5,BD=8,则△OEF 的面积为( )A .12B .6C .3D .234.下列多边形一定相似的为( )A .两个三角形B .两个四边形C .两个正方形D .两个平行四边形5.现给出四个命题:①等边三角形既是轴对称图形,又是中心对称图形;②相似三角形的面积比等于它们的相似比;③菱形的面积等于两条对角线的积;④一组数据2,5,4,3,3的中位数是4,众数是3,其中不正确的命题的个数是( ) A .1个 B. 2个 C. 3个 D .4个6.如图,P 为平行四边形ABCD 边AD 上一点,E 、F 分别是PB 、PC (靠近点P )的三等分点,△PEF 、△PDC 、△PAB 的面积分别为S 1、S 2、S 3,若AD=2,AB=23,∠A=60°,则S 1+S 2+S 3的值为( )7题图A .310B .29C .313D .47.如图,若DC ∥FE ∥AB ,则有( ).A .OD OC OF OE = B .OF OB OE OA = C .OA OD OC OB = D .CD ODEF OE =8.已知△ABC 的面积是1,1A 、1B 、1C 分别是△ABC 三边上的中点,△111A B C 的面积记为1S ;2A 、2B 、2C 分别是△111A B C 三边上的中点,△222A B C 的面积记为2S ;以此类推,则△444A B C 的面积4S 是( ).A .116B .164C .1128D .12569.如图,在平面直角坐标系中,A (2,4)、B (2,0),将△OAB 以O 为中心缩小一半,则A 对应的点的坐标( )A .(1,2)B .(﹣1,﹣2)C .(1,2)或(﹣1,﹣2)D .(2,1)或(﹣2,﹣1)10.如图,在大小为4×4的正方形网格中,是相似三角形的是( )A .①和②B .②和③C .①和③D .②和④11.若53b a =,则b ba +的值为( ) A .85 B .53 C .32 D .85二、填空题12.如图,D 、E 分别是ABC ∆的边AB 、AC 上的中点,则DECB 四边形:S S ADE ∆= .13.现有多个全等直角三角形,先取三个拼成如图1所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,易得BP:QP:QR=3:1:2.(1)若取四个直角三角形拼成如图2所示的形状,S为EF的中点,BS分别交AC,CD,DE 于P,Q,R,则BP:PQ:QR:RS=(2)若取五个直角三角形拼成如图3所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于P,Q,R,S,则BP:PQ:QR:RS:ST= .14.如果地图上A,B两处的图距是4cm,表示这两地实际的距离是20km,那么实际距离500km的两地在地图上的图距是 cm.15.已知两个相似三角形对应高的比为3:10,且这两个三角形的周长之差为56cm,则较小的三角形的周长为______cm.⊥,交16.如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF EC∠=____.AB于点F,则tan ECF17.在△ABC中,已知D、E分别为边AB、AC的中点,若△ADE的周长为3 cm,则△ABC的周长为_____cm.三、解答题18.定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是;当m=5,n=2时,如图2,线段BC与线段OA的距离为;(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,①求出点M随线段BC运动所围成的封闭图形的周长;②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.19.问题背景已知在△ABC中,AB边上的动点D由A向B运动(与A、B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.(1)初步尝试如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.求证:HF=AH+CF.小王同学发现可以由以下两种思路解决问题:思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);(2)类比探究如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是:1,求的值;(3)延伸拓展如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记=m,且点D,E的运动速度相等,试用含m的代数式表示(直接写出结果,不必写解答过程).20.如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.(1)求证:△CDP≌△POB;(2)填空:①若AB=4,则四边形AOPD的最大面积为________;②连接OD,当∠PBA的度数为________时,四边形BPDO是菱形.21.如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?四、计算题22.问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积S1= ,△ADE的面积S2= .探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为h.请证明S2=4S1S2.拓展迁移(3)如图2,▱DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.23.如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B (0,3).(1)求抛物线的解析式;(2)设抛物线顶点为D,求四边形AEDB的面积;(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.答案1.B .2.B3.C4.C5.C6.A .7.D8.D9.C 10.C 11.A .12.1:3 13.(1)4:1:3:2; (2)5:1:4:2:3. 14.100. 15.24cm 16.1217.6 18.(1)2,5;(2)当2≤m ≤4时,d=|n|(-2≤n ≤2)或2812m m -+-;当4≤m ≤6时,d=2;(3)16+4π.19.(1)证明(选择思路一):过点D 作DG ∥BC ,交AC 于点G ,如图1所示: 则∠ADG=∠B ,∠AGD=∠ACB , ∵△ABC 是等边三角形, ∴∠A=∠B=∠ACB=60°, ∴∠ADG=∠AGD=∠A , ∴△ADG 是等边三角形, ∴GD=AD=CE , ∵DH ⊥AC , ∴GH=AH , ∵DG ∥BC ,∴∠GDF=∠CEF ,∠DGF=∠ECF , 在△GDF 和△CEF 中,,∴△GDF ≌△CEF (ASA ), ∴GF=CF ,∴GH+GF=AH+CF , 即HF=AH+CF ;(2)解:过点D 作DG ∥BC ,交AC 于点G ,如图2所示: 则∠ADG=∠B=90°, ∵∠BAC=∠ADH=30°, ∴∠HGD=∠HDG=60°, ∴AH=GH=GD ,AD=GD , 根据题意得:AD=CE , ∴GD=CE , ∵DG ∥BC ,∴∠GDF=∠CEF ,∠DGF=∠ECF , 在△GDF 和△CEF 中,,∴△GDF ≌△CEF (ASA ), ∴GF=CF ,∴GH+GF=AH+CF , 即HF=AH+CF , ∴=2;(3)解:=,理由如下:过点D 作DG ∥BC ,交AC 于点G ,如图3所示: 则∠ADG=∠B ,∠AGD=∠ACB ,AD=EC , ∵AB=AC ,∠BAC=36°,∴∠ACB=∠B=∠ADG=∠AGD=72°,∵∠ADH=∠BAC=36°,∴AH=GH,∠DHG=72°=∠AGD,∴DG=DH=AH,△ADG∽△ABC,△ADG∽△DGH,∴==m,===m,∴△DGH∽△ABC,∴==m,∴=m,∵DG∥BC,∴△DFG∽△EFC,∴==m,∴=m,即=m,∴=,∴==+1=.20.(1)证明:∵PC=PB,D是AC的中点,∴DP∥AB,∴DP=AB,∠CPD=∠PBO,∵BO=AB,∴DP=BO,在△CDP与△POB中,∴△CDP≌△POB(SAS);(2)解:①当四边形AOPD的AO边上的高等于半径时有最大面积,(4÷2)×(4÷2)=2×2=4;②如图:∵DP∥AB,DP=BO,∴四边形BPDO是平行四边形,∵四边形BPDO是菱形,∴PB=BO,∵PO=BO,∴PB=BO=PO,∴△PBO是等边三角形,∴∠PBA的度数为60°.故答案为:4;60°.21.(1)依题意可知,折痕AD是四边形OAED的对称轴,∴在Rt △ABE 中,AE =AO =5,AB =4. BE =222254AE AB -=-=3. ∴CE =2.∴E 点坐标为(2,4).在Rt △DCE 中,DC 2+CE 2=DE 2, 又∵DE =OD .∴(4﹣OD )2+22=OD 2. 解得:OD =2.5.∴D 点坐标为(0,2.5). (2)如图②∵PM ∥ED , ∴△APM ∽△AED . ∴PM APED AE=, 又知AP =t ,ED =2.5,AE =5,PM =0.5t ×2.5=0.5t , 又∵PE =5﹣t .而显然四边形PMNE 为矩形.S 矩形PMNE =PM •PE =0.5t ×(5﹣t )=﹣0.5t 2+2.5t ; ∴S 四边形PMNE =﹣0.5(t ﹣2.5)2+258, 又∵0<2.5<5.∴当t =2.5时,S 矩形PMNE 有最大值258. (3)(i )若以AE 为等腰三角形的底,则ME =MA (如图①)在Rt △AED 中,ME =MA , ∵PM ⊥AE ,∴P 为AE 的中点, ∴t =AP =0.5AE =2.5. 又∵PM ∥ED ,∴M 为AD 的中点.过点M 作MF ⊥OA ,垂足为F ,则MF 是△OAD 的中位线, ∴MF =0.5OD =1.25,OF =0.5OA =2.5,∴当t =2.5时,(0<2.5<5),△AME 为等腰三角形. 此时M 点坐标为(2.5,1.25).(ii )若以AE 为等腰三角形的腰,则AM =AE =5(如图②)在Rt △AOD 中,AD =22OD AO +=22552⎛⎫+ ⎪⎝⎭=552.过点M 作MF ⊥OA ,垂足为F .∵PM ∥ED ,∴△APM ∽△AED .∴AP AMAE AD=. ∴t =AP=AM AE AD ⋅= 55=25 ,∴PM =12t =5.∴MF=MPOF=OA﹣AF=OA﹣AP=5﹣∴当t0<5),此时M点坐标为(5﹣综合(i)(ii)可知,t=2.5或tA,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(2.5,1.25)或(5﹣22.(1)S1=12×6×3=9,过A作AH⊥BC,交DE于G,∵DE∥BC,EF∥AB,∴四边形DEFB是平行四边形,∴DE=BF=2,∵DE∥BC,∴AG⊥DE,△ADE∽△ABC,∴ED AG BC AH=,∴283AGAG=+,解得:AG=1,∴S2=12×DE×AG=1212⨯⨯=1,(2)∵DE∥BC,EF∥AB,∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,∴△ADE∽△EFC,∴22221()S DE mS FC n==,∵S1=12nh,∴S2=22mn×S1=22m hn,∴4S1S2=4×12nh×22m hn=(mh)2,而S=mh,∴S2=4S1S2;(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,∴∠GHC=∠B,BD=HG,DG=BH,∵四边形DEFG为平行四边形,∴DG=EF,∴BH=EF,∴BE=HF,在△DBE和△GHF中DB GHB GHF BE HF=⎧⎪∠=∠⎨⎪=⎩,∴△DBE≌△GHF(SAS),∴△GHC的面积为7+5=12,由(2)得,平行四边形DBHG的面积S,∴△ABC 的面积为3+12+12=27.考点:1.平行四边形的判定与性质;2.三角形的面积;3.全等三角形的判定与性质;4.勾股定理.23.(1)∵抛物线与y 轴交于点(0,3),∴设抛物线解析式为y=ax 2+bx+3(a≠0)根据题意,得30933a b a b -+=⎧⎨++⎩,解得12a b =-⎧⎨=⎩. ∴抛物线的解析式为y=﹣x 2+2x+3;(2)如图,设该抛物线对称轴是DF ,连接DE 、BD .过点B 作BG⊥DF 于点G . 由顶点坐标公式得顶点坐标为D (1,4) 设对称轴与x 轴的交点为F ∴四边形ABDE 的面积=ABO DFEBOFD S S S ++V V 梯形=12AO•BO+12(BO+DF )•OF+12EF•DF =12×1×3+12×(3+4)×1+12×2×4=9;(3)相似,如图, BD=222BG DG +=; ∴BE=2232BO OE +=DE=22DF EF +=25∴BD 2+BE 2=20,DE 2=20即:BD 2+BE 2=DE 2,所以△BDE 是直角三角形∴∠AOB=∠DBE=90°,且22AO BO BD BE==, ∴△AOB∽△DBE.。
中考数学总复习《图形的相似》专项提升训练(带有答案)

中考数学总复习《图形的相似》专项提升训练(带有答案)学校:___________班级:___________姓名:___________考号:___________一、单选题1.两个相似三角形的相似比是1:2,则其对应中线之比是( )A .1:1B .1:2C .1:3D .1:42.如图,在ABC 中2AC =,BC=4,D 为BC 边上的一点,且CAD B ∠=∠.若ADC △的面积为2,则ABD △的面积为( )A .4B .5C .6D .73.若35a b =,则下列各式一定成立的是( )A .53a b =B .35a b =C .65a b a +=D .145a b += 4.如图,在ABC 中DE BC ∥,AD=1,BD=2,AC=6,则CE 的长为( )A .2B .3C .4D .55.如图,在等边ABC 中,点D ,E 分别是BC AC ,上的点72AB CD ==,,60ADE ∠=︒则AE 等于( )A .5B .397C .6D .4176.下列命题正确的是( )A .方程210x x --=没有实数根B .两边成比例及一角对应相等的两个三角形相似C .平分弦的直径垂直于弦D .反比函数的图像不会与坐标轴相交7.已知ABC DEF ∽△△,:1:2AB DE =且ABC 的周长为6,则DEF 的周长为( ) A .3 B .6 C .12 D .248.在平面直角坐标系xOy 中,已知点()()()0,0,1,2,0,3O A B .若OA B ''△与OAB 是原点O 为位似中心的位似图形,且点B 的对应点为()0,9B '-,则点A 的对应点A '坐标为( ) A .()3,6 B .()3,6-- C .()3,6- D .()3,6- 9.如图,D 是ABC 边AB 上一点,添加一个条件后,仍不能使ACD ABC △∽△的是( )A .ACDB ∠=∠ B .ADC ACB ∠=∠ C .AD CD AC BC = D .AC AB AD AC = 10.如图,已知ABC DAC △∽△,37B ∠=︒和116∠=︒D ,则BAD ∠的度数为( )A .37︒B .116︒C .153︒D .143︒二、填空题11.如图,在矩形ABCD 中,8AB =和4BC =,连接AC ,EF AC ⊥于点O ,分别与AB 、CD 交于点E 、F ,连接AF 、CE ,则AF CE +的最小值为 .12.如图,在ABC 中,点D 、E 分别为AB 、AC 的中点,点F 为DE 中点,连接BF 并延长交AC 于点G ,则:AG GE = .13.如图AC ,AD 和CE 是正五边形ABCDE 的对角线,AD 与CE 相交于点F .下列结论:(1)CA 平分BCF ∠;(2)2CF EF =;(3)四边形ABCF 是菱形;(4)2AB AD EF =⋅.其中正确的结论是 .(填写所有正确结论的序号)14.如图AC 、BD 交于点O ,连接AB 和CD ,若要使AOB COD ∽,可以添加条件 .(只需写出一个条件即可)15.如图,在ABC 中4AC AB ==和30C ∠=︒,D 为边BC 上一点,且3CD =,E 为AB 上一点,若30ADE ∠=︒,则BE 的长为 .16.在ABC 中,6810AC BC AB D ===,,,是AB 的中点,P 是CD 上的动点,若点P 到ABC 的一边的距离为2,则CP 的长为 .17.如图,M 是Rt ABC △斜边AB 上的中点,将Rt ABC △绕点B 旋转,使得点C 落在射线CM 上的点D 处,点A 落在点E 处,边ED 的延长线交边AC 于点F .如果3BC =.4AC =那么BE 的长为 ;CF 的长为 .18.如图,在ABC 中,D 是AC 的中点,点F 在BD 上,连接AF 并延长交BC 于点E ,若:3:1BF FD =,8BC =则CE 的长为 .三、解答题19.已知O 为ABCD 两对角线的交点,直线l 过顶点D ,且绕点D 顺时针旋转,过点A ,C 分别作直线l 的垂线,垂足为点E ,F .(1)如图1,若直线l 过点B ,求证:OE OF =;(2)如图2,若EFO FCA ∠=∠,2FC AE =求CFO ∠的度数;(3)如图3,若ABCD 为菱形4AE =,6AO =和8EO =直接写出CF 的长. 20.如图,在ABC 中2BAC C ∠=∠,利用尺规作图法在BC 上求作一点D ,使得ABDCBA .(不写作法,保留作图痕迹)21.如图,在Rt ABC △中90ACB ∠=︒,D 是AB 的中点,连接CD ,过点A 作AE CD ⊥于点E ,过点E 作EF CB ∥交BD 于点F .(1)求证:ACE BAC ∽△△;(2)若5AC =,5AB =求CE 及EF 的长.22.如图,在直角梯形OABC 中BC AO ∥,=90AOC ︒∠点A 、B 的坐标分别为()5,0、()2,6点D 为AB 上一点,且2BD AD =.双曲线()0k y x x=>经过点D ,交BC 于点E .求点E 的坐标.23.如图,点P 是菱形ABCD 的对角线BD 上一点,连结CP 并延长,交AD 于E ,交BA 的延长线点F .求证:APE FPA △∽△.24.如图1,菱形AGBD 边长为3,延长DB 至点C ,使得5BC =.连接AB ,AB AD =点E ,F 分别在线段AD 和AB 上,且满足DE AF =,连接BE ,DF 交于点O ,过点B 作BM BE ⊥,交DF 延长线于点M ,连接CM .图1 图2(1)求OB 与BM 之间的数量关系;(2)当DMB DCM △∽△时,求DO 的长度;(3)如图2,过点M 作MN CD ⊥交CD 于N ,求MN MC的最大值. 1.B2.C3.A4.C5.B6.D7.C8.B9.C10.C11.1012.2:113.①①①14.A C ∠=∠(答案不唯一)15.9416.103或52或3512 17. 59418.16519.(2)60CFO ∠=︒(3)CF 的长为7 21.(2)1CE = 655EF =. 22.4,63⎛⎫ ⎪⎝⎭/11,63⎛⎫ ⎪⎝⎭ 24.(1)3BM OB =(2)1OD =(3)1014101911316206517MN CN ++=。
中考数学《相似形》专题练习含答案

相似形一.选择题(本大题有10个小题,每小题3分,共30分。
请选出每小题中一个符合题意的正确选项,不选、多选、错选均不给分)1. 下列说法中,错误的是( )A.所有的等边三角形都相似B.和同一图形相似的两图形也相似C.所有的等腰直角三角形都相似D.所有的矩形都相似2. 下列图形中,是位似图形的是( )A B C D3. 如图1,小强设计两个直角三角形来测量河宽BC ,他量得AB=2米,BD=3米,CE=9米,则河宽BC 为( )A5米 B.4米 C.6米 D.8米图1 图2 图34.如图2,已知AB∥EF∥CD,则图中相似的三角形有( )A.1对 B.2对 C.3对 D.4对5.如图3,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时,长臂端点升高( )A.11.25米 B.6.6米 C.8米 D.10.5米6.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与ABC 相似的是( )A B C D7.已知,如图4,在ABC 中,P为AB上的一点,在下列四个条件下:①ACP ∠=B ∠;②APC ACB ∠=∠;③2AC AP AB =⋅;④AB CP AP CB ⋅=⋅。
能满足APC 与ACB 相似的条件是( )A.①②④ B.①③④ C.②③④ D.①②③图4 图5 8.如图5所示,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯子上点D距离墙1.4米,BD长0.55米,则梯子的长为( )A.3.85米 B.4.00米 C.4.40米 D4.50米9.如图6,在矩形ABCD中,AE BD ⊥于E,矩形ABCD的面积为40平方厘米,:1:5ABE DBA S S =,则AE的长为( )A4厘米 B.5厘米 C.6厘米 D.7厘米图6 图7 10.如图7,点E是正方形ABCD中边CD的中点,P是BC边上的一点,下列条件中,不能推出ABP 与ECP 相似的是( )A.APB EPC ∠=∠B.90APE ∠=C. P 是BC 的中点D. :2:3BP BC =二.填空题(本大题有10个小题,每小题3分,共30分,将正确答案填在题中的横线上)11.已知线段1,a b c d ====,则这四条线段______比例线段(填“成”或“不成”).12.学校平面图的比例尺是1:500,平面图上校园面积为21300cm ,则学校的实际面积为_______2m .13.如果ABC A B C ''',相似比为3 :2。
中考数学复习《相似》专项综合练习含答案

中考数学复习《相似》专项综合练习含答案一、相似1.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣ x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【答案】(1)解:把A(-2,0),B(4,0)代入抛物线y=ax2+bx-1,得解得∴抛物线解析式为:y= x2−x−1∴抛物线对称轴为直线x=- =1(2)解:存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P 点.设过点C′、O直线解析式为:y=kx∴k=-∴y=- x则P点坐标为(1,- )(3)解:当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,- a-1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,- a−1)∵N为DM中点∴点M坐标为(2a,a−1)把M代入y= x2−x−1,解得a=4则N点坐标为(4,-3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由(2)N(2,-1)∴N点坐标为(4,-3)或(2,-1)【解析】【分析】(1)根据点A、B的坐标,可求出抛物线的解析式,再求出它的对称轴即可解答。
(2)使四边形ACPO的周长最小,只需PC+PO最小,取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P点,利用待定系数法求出直线C′O的解析式,再求出点P的坐标。
中考数学《图形的相似》专项练习题及答案

中考数学《图形的相似》专项练习题及答案一、单选题1.一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是()A.5cm B.6cm C.(6-√3)cm D.(3+√3)cm2.如图,DE△BC,EF△AB,现得到下列结论:AEEC=BFFC,ADBF=ABBC,EFAB=DEBC,CECF=EABF其中正确的比例式的个数有()A.4个B.3个C.2个D.1个3.如图,△ABC与△ADE成位似图形,位似中心为点A,若AD:AB=1:3,则△ADE与△ABC面积之比为()A.1:2B.1:3C.1:9D.1:164.如图,△ABC中,三边互不相等,点P是AB上一点,有过点P的直线将△ABC切出一个小三角形与△ABC相似,这样的直线一共有()A.5条B.4条C.3条D.2条5.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是()A.2B.8C.16D.326.如图,△ADE△△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是()A.1:2B.1:3C.2:3D.3:27.如图,以A为位似中心,将△ADE放大2倍后,得位似图形△ABC,若s1表示△ADE的面积,s2表示四边形DBCE的面积,则s1:s2=()A.1︰2B.1︰3C.1︰4D.2︰38.如图,按如下方法,将△ABC的三边缩小到原来的12,任取一点O,连AO、BO、CO,并取它们的中点D、E、F得△DEF,则下列说法正确的是()①△ABC与△DEF是相似图形;②△ABC与△DEF的周长比为2:1;③△ABC与△DEF的面积比为4:1.A.①、②B.②、③C.①、③D.①、②、③9.如图,已知AB是半圆O的直径,弦AD,CB相交于点P,若∠DPB=45°,则S△CDP:S△ABP 的值()A.25B.23C.13D.1210.如图,AD△BE△CF,直线l1、l2这与三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为()A.4B.5C.6D.811.一个三角形的三边长分别为3,4,5,另一个与它相似的三角形中有一条边长为6.则这个三角形的周长不可能是()A.725B.18C.48D.2412.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与△ABC相似的三角形是()A.B.C.D.二、填空题13.勾股定理是一个基本的几何定理,有数百种证明方法.“青朱出入图”是我国古代数学家证明勾股定理的几何证明法.刘徽描述此图“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,加就其余不动也,合成弦方之幂,开方除之,即弦也”.若图中BF=4,DF=2,则AE=.14.如图,矩形ABCD中,AB=3,BC=4,E是BC上一点,BE=1,AE与BD交于点F.则DF的长为.15.如图,点D在△ABC的边BC的延长线上,AD为△ABC的外角的平分线,AB=2BC,AC=3,CD=4,则AB的长为.16.如图,在△ABC中,△BAC=90°,AD△BC于D,BD=3,CD=12,则AD的长为17.在某一时刻,测得一根高为1m的竹竿的影长为2m,同时测得一栋高楼的影长为40m,这栋高楼的高度是m.18.如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,那么此时小明离电杆AB的距离BD为m.三、综合题19.如图,已知△BAC=90°,AD△BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:(1)△DFB△△AFD;(2)AB:AC=DF:AF.20.一次小组合作探究课上,小明将两个正方形按如图1所示的位置摆放(点E、A、D在同一条直线上).(1)发现BE与DG数量关系是,BE与DG的位置关系是.(2)将正方形AEFG绕点A按逆时针方向旋转(如图2),(1)中的结论还成立吗?若能,请给出证明;若不能,请说明理由.(3)把图1中的正方形分别改写成矩形AEFG和矩形ABCD,且AEAG=ABAD=23,AE=2,AB=4,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请直接写出这个定值.21.如图,已知点D在△ABC的外部,AD△BC,点E在边AB上,AB•AD=BC•AE.(1)求证:△BAC=△AED;(2)在边AC取一点F,如果△AFE=△D,求证:ADBC=AFAC.22.如图,在▱ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF。
专题27 图形的相似(46题)(解析版)--2024年中考数学真题分类汇编

专题27图形的相似(46题)一、单选题1.(2024·重庆·中考真题)若两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是()A .1:3B .1:4C .1:6D .1:9【答案】D【分析】此题考查了相似三角形的性质,根据“相似三角形的面积比等于相似比的平方”解答即可.【详解】解:两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是1:9,故选:D .2.(2024·四川凉山·中考真题)如图,一块面积为260cm 的三角形硬纸板(记为ABC )平行于投影面时,在点光源O 的照射下形成的投影是111A B C △,若123OB BB =::,则111A B C △的面积是()A .290cmB .2135cmC .2150cmD .2375cm 【答案】D【详解】解:∵一块面积为260cm 的三角形硬纸板(记为ABC )平行于投影面时,在点光源O 的照射下形成的投影是111A B C △,123OB BB =::,∴125OB OB =,∴位似图形由三角形硬纸板与其灯光照射下的中心投影组成,相似比为2:5,∵三角形硬纸板的面积为260cm ,∴111224525ABC A B C S S ⎛⎫== ⎪⎝⎭ ,∴111A B C △的面积为2375cm .故选:D .3.(2024·陕西·中考真题)如图,正方形CEFG 的顶点G 在正方形ABCD 的边CD 上,AF 与DC 交于点H ,若6AB =,2CE =,则DH 的长为()A .2B .3C .52D .834.(2024·湖南·中考真题)如图,在ABC 中,点D E ,分别为边AB AC ,的中点.下列结论中,错误的是()A .DE BC ∥B .ADE ABC △△∽C .2BC DE=D .12ADE ABC S S =【答案】D【分析】本题考查了三角形中位线的性质,相似三角形的判定和性质,由三角形中位线性质可判断A C 、;由相似三角形的判定和性质可判断B D 、,掌握三角形中位线的性质及相似三角形的判定和性质是解题的关键.【详解】解:∵点D E ,分别为边AB AC ,的中点,∴DE BC ∥,2BC DE =,故A C 、正确;∵DE BC ∥,∴ADE ABC △△∽,故B 正确;∵ADE ABC △△∽,∴221124ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△,∴14ADE ABC S S =,故D 错误;故选:D .5.(2024·江苏连云港·中考真题)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为()A .甲和乙B .乙和丁C .甲和丙D .甲和丁【答案】D【分析】本题考查相似图形,根据对应角相等,对应边对应成比例的图形是相似图形结合正方形的性质,进行判断即可.【详解】解:由图可知,只有选项甲和丁中的对应角相等,且对应边对应成比例,它们的形状相同,大小不同,是相似形.故选D .6.(2024·浙江·中考真题)如图,在平面直角坐标系中,ABC 与A B C ''' 是位似图形,位似中心为点O .若点(3,1)A -的对应点为(6,2)A '-,则点(2,4)B -的对应点B '的坐标为()A .(4,8)-B .(8,4)-C .(8,4)-D .(4,8)-【答案】A【分析】本题考查了位似变换,根据点'A A 、的坐标可得到位似比,再根据位似比即可求解,掌握位似变换的性质是解题的关键.【详解】解:∵ABC 与A B C ''' 是位似图形,点(3,1)A -的对应点为(6,2)A '-,∴A B C ''' 与ABC 的位似比为2,∴点(2,4)B -的对应点B '的坐标为()22,42-⨯⨯,即()4,8-,故选:A .7.(2024·黑龙江绥化·中考真题)如图,矩形OABC 各顶点的坐标分别为()0,0O ,()3,0A ,()3,2B ,()0,2C ,以原点O 为位似中心,将这个矩形按相似比13缩小,则顶点B 在第一象限对应点的坐标是()A .()9,4B .()4,9C .31,2⎛⎫ ⎪D .21,3⎛⎫ ⎪8.(2024·四川成都·中考真题)如图,在ABCD Y 中,按以下步骤作图:①以点B 为圆心,以适当长为半径作弧,分别交BA ,BC 于点M ,N ;②分别以M ,N 为圆心,以大于12MN 的长为半径作弧,两弧在ABC ∠内交于点O ;③作射线BO ,交AD 于点E ,交CD 延长线于点F .若3CD =,2DE =,下列结论错误的是()A .ABE CBE ∠=∠B .5BC =C .DE DF =D .53BE EF =【答案】D【分析】本题考查角平分线的尺规作图、平行四边形的性质、等腰三角形的判定以及相似性质与判定的综合.先由作图得到BF 为ABC ∠的角平分,利用平行线证明AEB ABE ∠=∠,从而得到3AE AB CD ===,再利用平行四边形的性质得到325BC AD AE ED ==+=+=,再证明AEB DEF △∽△,分别求出32BE EF =,2DF =,则各选项可以判定.【详解】解:由作图可知,BF 为ABC ∠的角平分,∴ABE CBE ∠=∠,故A 正确;∵四边形ABCD 为平行四边形,∴,,AD BC AB CD AD BC == ,∵AD BC∥∴AEB CBE ∠=∠,∴AEB ABE ∠=∠,∴3AE AB CD ===,∴325BC AD AE ED ==+=+=,故B 正确;∵AB CD =,∴ABE F ∠=∠,∵AEB DEF ∠=∠,∴AEB DEF △∽△,∴BE AB AEEF DF ED ==,∴332BE EF DF ==,∴32BE EF =,2DF =,故D 错误;∵2DE =,∴DE DF =,故C 正确,故选:D .9.(2024·山东烟台·中考真题)如图,在正方形ABCD 中,点E ,F 分别为对角线BD AC ,的三等分点,连接AE 并延长交CD 于点G ,连接EF FG ,,若AGF α∠=,则FAG ∠用含α的代数式表示为()A .452α︒-B .902α︒-C .452α︒+D .2α【答案】B【分析】本题考查了正方形的性质,相似三角形的判定和性质,全等三角形的判定和性质,三角形的外角性质.证明EOF DOC ∽△△,求得45OFE ∠=︒,证明ABE GDE ∽,证得12DG CD CG ==,推出()SAS DEG CFG ≌,得到GE GF =,据此求解即可.【详解】解:∵正方形ABCD 中,点E ,F 分别为对角线BD AC ,的三等分点,∴OD OC =,45ODC OCD ∠=∠=︒,DE CF =,∴OE OF =,∵EOF DOC ∠=∠,OE OFOD OC=,∴EOF DOC ∽△△,∴45OFE OCD ∠=∠=︒,∵点E ,F 分别为对角线BD AC ,的三等分点,∴12DE BE =,∵正方形ABCD ,∴AB CD ∥,∴ABE GDE ∽,∴12DG DE AB BE ==,∴12DG CD CG ==,∴()SAS DEG CFG ≌,∴GE GF =,∴()111809022GEF AGF α∠=︒-∠=︒-,∴1190904545222FAG GEF AFE ααα∠=︒-︒--︒=︒-=∠-∠=,故选:B .10.(2024·江苏苏州·中考真题)如图,点A 为反比例函数()0y x x=-<图象上的一点,连接AO ,过点O 作OA 的垂线与反比例()40y x x =>的图象交于点B ,则AOBO的值为()A .12B .14C .33D .13【答案】A【分析】本题考查了反比例函数图象上点的坐标特征,反比例函数系数k 的几何意义,三角形相似的判定和性质,数形结合是解题的关键.过A 作AC x ⊥轴于C ,过B 作BD x ⊥轴于D ,证明AOC OBD △∽△,利用相似三角形的面积比等于相似比的平方求解即可.【详解】解:过A 作AC x ⊥轴于C ,过B 作BD x ⊥轴于D ,∴11122ACO S =⨯-= ,1422BDO S =⨯= ,90ACO ODB ∠=∠=︒,∵OA OB ⊥,∴90AOC OBD BOD ∠=∠=︒-∠,∴AOC OBD △∽△,∴2ACO BDO S OA S OB ⎛⎫= ⎪⎝⎭ ,即2122OA OB ⎛⎫= ⎪⎝⎭,∴12OA OB =(负值舍去),故选:A .11.(2024·山东威海·中考真题)如图,在ABCD Y 中,对角线AC ,BD 交于点O ,点E 在BC 上,点F 在CD 上,连接AE ,AF ,EF ,EF 交AC 于点G .下列结论错误的是()A .若CE ADCF AB=,则EF BD ∥B .若AE BC ⊥,AF CD ⊥,AE AF =,则EF BD ∥C .若EF BD ∥,CE CF =,则EAC FAC ∠=∠D .若AB AD =,AE AF =,则EF BD ∥∴AC BD⊥在Rt ,Rt ACE AFC 中,AE AF AC AC=⎧⎨=⎩∴Rt Rt ACE AFC ≌∴CE CF =又∵AE AF =∴AC EF⊥∴EF BD ∥,故B 选项正确,C.∵CE CF =,∴CFE CEF ∠=∠∵EF BD ∥,∴,CBD CEF CDB CFE ∠=∠∠=∠∴CBD CDB ∠=∠∴CB CD=∴四边形ABCD 是菱形,∴AC BD ⊥,又∵EF BD ∥∴AC EF ⊥,∵CE CF =,∴AC 垂直平分EF ,∴AE AF=∴EAC FAC ∠=∠,故C 选项正确;D.若AB AD =,则四边形ABCD 是菱形,由AE AF =,且BE DF =时,可得AC 垂直平分EF ,∵AC BD⊥∴EF BD ∥,故D 选项不正确故选:D .12.(2024·河南·中考真题)如图,在ABCD 中,对角线AC ,BD 相交于点O ,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为()A .12B .1C .43D .213.(2024·安徽·中考真题)如图,在Rt ABC △中,90ABC ∠=︒,4AB =,2BC =,BD 是边AC 上的高.点E ,F 分别在边AB ,BC 上(不与端点重合),且DE DF ⊥.设AE x =,四边形DEBF 的面积为y ,则y 关于x 的函数图象为()A .B .C.D.【答案】A【分析】本题主要考查了函数图象的识别,相似三角形的判定以及性质,勾股定理的应用,过点E 作EH AC ⊥于点H ,由勾股定理求出AC ,根据等面积法求出BD ,先证明ABC ADB ∽,由相似三角形的性质可得出AB AC AD AB =,即可求出AD ,再证明AED BFD ∽,由相似三角形的性质可得出2AED BFD S AD S BD ⎛⎫= ⎪⎝⎭ ,即可得出4AED BFD S S = ,根据()ABC AED BDC BDF DEBF S S S S S =--- 四边形,代入可得出一次函数的解析式,最后根据自变量的大小求出对应的函数值.【详解】解:过点E 作EH AC ⊥于点H ,如下图:∵90ABC ∠=︒,4AB =,2BC =,∴2225AC AB BC =+=,∵BD 是边AC 上的高.∴1122AB BC AC BD ⋅=⋅,∴455BD =,∵BAC CAB ∠=∠,90ABC ADB ∠=∠=︒,∴ABC ADB ∽△△,∴AB AC AD AB=,解得:855AD =,∴85252555DC AC AD =-=-=,∵90BDF BDE BDE EDA ∠+∠=∠+∠=︒,90CBD DBA DBA A ∠+∠=∠+∠=︒,∴DBC A ∠=∠,BDF EDA ∠=∠,∴AED BFD ∽,14.(2024·山东·中考真题)如图,点E 为ABCD Y 的对角线AC 上一点,5AC =,1CE =,连接DE 并延长至点F ,使得EF DE =,连接BF ,则BF 为()A .52B .3C .72D .4【答案】B【分析】本题考查了平行四边形的性质,平行线分线段成比例定理,平行证明相似等知识点,正确作辅助线是解题关键.作辅助线如图,由平行正相似先证DEC GAE ∽,再证BGF AGE ∽,即可求得结果.【详解】解:延长DF 和AB ,交于G 点,∵四边形ABCD 是平行四边形,∴DC AB ∥,DC AB =即DC AG ∥,∴DEC GAE∽∴CE DE DC AE GE AG==,∵5AC =,1CE =,∴514AE AC CE =-=-=,∴14CE DE DC AE GE AG ===,又∵EF DE =,14DE DE GE EF FG ==+,∴13EF FG =,∵14DC DC AG AB BG ==+,DC AB =,∴13DC BG =,∴13EF DC FG BG ==,∴34BG FG AG EG ==∴AE BF ∥,∴BGF AGE ∽,∴34BF FG AE EG ==∵4AE =,∴3BF =.故选:B .二、填空题15.(2024·江苏盐城·中考真题)两个相似多边形的相似比为12∶,则它们的周长的比为.【答案】12∶/12【分析】本题考查了相似多边形的性质,根据相似多边形周长之比等于相似比即可求解,掌握相似多边形的性质是解题的关键.【详解】解:∵两个相似多边形的相似比为12∶,∴它们的周长的比为12∶,故答案为:12∶.16.(2024·云南·中考真题)如图,AB 与CD 交于点O ,且AC BD ∥.若12OA OC AC OB OD BD ++=++,则AC BD =.17.(2024·江苏扬州·中考真题)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB 经小孔O 在屏幕(竖直放置)上成像A B ''.设36cm AB =,24cm A B ''=.小孔O 到AB 的距离为30cm ,则小孔O 到A B ''的距离为cm .【答案】20【分析】此题主要考查了相似三角形的应用,由题意得AB A B ''∥,AOB A OB ''∽△△,过O 作OC AB ⊥于点C ,CO 交A B ''于点C ',利用已知得出''AOB A OB △∽△,进而利用相似三角形的性质求出即可,熟练掌握相似三角形的性质是解题关键.【详解】由题意得:AB A B ''∥,∴AOB A OB ''∽△△,如图,过O 作OC AB ⊥于点C ,CO 交A B ''于点C ',∴OC A B '''⊥,30cm OC =,∴A B OC AB OC '''=,即243630OC '=,∴20OC '=(cm ),即小孔O 到A B ''的距离为20cm ,故答案为:20.18.(2024·吉林·中考真题)如图,正方形ABCD 的对角线AC BD ,相交于点O ,点E 是OA 的中点,点F 是OD 上一点.连接EF .若45FEO ∠=︒,则EF BC 的值为.【答案】12【分析】本题主要考查了相似三角形的性质与判定,正方形的性质,先由正方形的性质得到45OAD ∠=︒,AD BC =,再证明EF AD ∥,进而可证明OEF OAD △∽△,由相似三角形的性质可得12EF OE AD OA ==,即12EF BC =.【详解】解:∵正方形ABCD 的对角线AC BD ,相交于点O ,∴45OAD ∠=︒,AD BC =,19.(2024·四川眉山·中考真题)如图,ABC 内接于O ,点O 在AB 上,AD 平分BAC ∠交O 于D ,连接BD .若10AB =,BD =BC 的长为.10AB = ,25BD =,()22102545AD ∴=-=,DAC CBD ∠=∠ ,又∵BAD DAE ∠=∠,∴BAD CBD ∠=∠,90ADB BCE ∠=∠=︒ ,ABD BEC ∴ ∽,BE BC AB AD∴=,451045BC ∴=,8BC ∴=,故答案为:8.20.(2024·湖北·中考真题)DEF 为等边三角形,分别延长FD DE EF ,,,到点A B C ,,,使DA EB FC ==,连接AB AC ,,BC ,连接BF 并延长交AC 于点G .若2AD DF ==,则DBF ∠=,FG =.【答案】30︒/30度435/435【分析】本题考查了相似三角形的判定和性质,等边三角形的性质,勾股定理.利用三角形的外角性质结合EB EF =可求得30DBF ∠=︒;作CH BG ⊥交BG 的延长线于点H ,利用直角三角形的性质求得1CH =,3FH =,证明AGF CGH ∽,利用相似三角形的性质列式计算即可求解.【详解】解:∵DEF 为等边三角形,DA EB FC ==,∴112CH CF ==,FH =∵90AFB H ∠=∠=︒,∴AF CH ∥,∴AGF CGH ∽,21.(2024·四川眉山·中考真题)如图,菱形ABCD 的边长为6,120BAD ∠=︒,过点D 作DE BC ⊥,交BC 的延长线于点E ,连结AE 分别交BD ,CD 于点F ,G ,则FG 的长为.【详解】解: 菱形ABCD 的边长为6,120BAD ∠=︒,6AD BC CD ∴===,AD BC ∥,120BCD ∠=︒,60DCE ∴∠=︒,DE BC ⊥ ,90DEC ∴∠=︒,在Rt DCE V 中,9030CDE DCE ∠=-︒∠=︒ ,132CE CD ∴==,2233DE CD CE ∴=-=,9BE BC CE ∴=+=,AD BE ,18090ADE DEC ︒︒∴∠=-∠=,在Rt ADE △中,()222233637AE DE AD =+=+=,AD BE ,AFD EFB ∴ ∽,6293AF AD FE BE ∴===,226737555AF AE ∴==⨯=,AD CE ∥,AGD EGC ∴△∽△,623AG AD EG CE ∴===,22372733AG AE ∴==⨯=,67472755FG AG AF ∴=-=-=.故答案为:475.22.(2024·四川乐山·中考真题)如图,在梯形ABCD 中,AD BC ∥,对角线AC 和BD 交于点O ,若13ABD BCD S S =△△,则AOD BOC S S =△△.【答案】19【分析】本题考查了平行线间的距离,相似三角形的判定与性质等知识.熟练掌握平行线间的距离,相似三角形的判定与性质是解题的关键.设AD BC ,的距离为d ,则112132ABD BCD AD d S S BC d ⋅==⋅△△,即13AD BC =,证明AOD COB ∽,则2AOD BOC S AD S BC ⎛⎫= ⎪⎝⎭△△,计算求解即可.【详解】解:设AD BC ,的距离为d ,∴112132ABD BCD AD d S S BC d ⋅==⋅△△,即13AD BC =,∵AD BC ∥,∴ADO CBO ∠=∠,DAO BCO ∠=∠,∴AOD COB ∽,∴221139AOD BOC S S AD BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V ,故答案为:19.23.(2024·黑龙江绥化·中考真题)如图,已知点()7,0A -,(),10B x ,()17,C y -,在平行四边形ABCO 中,它的对角线OB 与反比例函数()0k y k x =≠的图象相交于点D ,且:1:4OD OB =,则k =.【答案】15-【分析】本题考查了反比例函数与平行四边形综合,相似三角形的性质与判定,分别过点,B D ,作x 轴的垂线,垂足分别为,F E ,根据平行四边形的性质得出()2410B -,,证明ODE OBF △∽△得出6OE =,2.5DE =,进而可得()6,2.5D -,即可求解.【详解】如图所示,分别过点,B D ,作x 轴的垂线,垂足分别为,F E ,∵四边形AOCB 是平行四边形,点()7,0A -,(),10B x ,()17,C y -,∴7OA BC ==,∴24x =-,即()2410B -,,则24OF =,10BF =∵DE x ⊥轴,BF x ⊥轴,∴DE BF∥∴ODE OBF△∽△∴14OE OD DE OF OB BF ===∴6OE =, 2.5DE =∴()6,2.5D -∴6 2.515k =-⨯=-故答案为:15-.24.(2024·四川成都·中考真题)如图,在Rt ABC △中,90C ∠=︒,AD 是ABC 的一条角平分线,E 为AD 中点,连接BE .若BE BC =,2CD =,则BD =.【答案】1712+【分析】连接CE ,过E 作EF CD ⊥于F ,设BD x =,EF m =,根据直角三角形斜边上的中线性质和等腰三角形的性质证得112CF DF CD ===,EAC ECA =∠∠,ECD EDC BEC ∠=∠=∠,进而利用三角形的外角性质和三角形的中位线性质得到2CED CAE ∠=∠,22AC EF m ==,证明CBE CED ∽,利用相似三角形的性质和勾股定理得到232m x =+;根据角平分线的定义和相似三角形的判定与性质证明CAB FBE ∽∵90ACB ∠=︒,E 为AD 中点,∴CE AE DE ==,又2CD =∴112CF DF CD ===,EAC ∠25.(2024·江苏苏州·中考真题)如图,ABC ,90ACB ∠=︒,5CB =,10CA =,点D ,E 分别在AC AB ,边上,5AE =,连接DE ,将ADE V 沿DE 翻折,得到FDE V ,连接CE ,CF .若CEF △的面积是BEC 面积的2倍,则AD =.【答案】103/133【分析】本题考查了相似三角形的判定与性质、折叠性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形的面积公式等知识,是综合性强的填空压轴题,熟练掌握相关知识的联系与运用是解答的关键.设AD x =,5AE x =,根据折叠性质得DF AD x ==,ADE FDE ∠=∠,过E 作EH AC ⊥于H ,设EF 与AC 相交于M ,证明AHE ACB ∽得到EH AH AE BC AC AB==,进而得到EH x =,2AH x =,证明Rt EHD 是等腰直角三角形得到45HDE HED ∠=∠=︒,可得90FDM ∠=︒,证明()AAS FDM EHM ≌得到12DM MH x ==,则3102CM AC AD DM x =--=-,根据三角形的面积公式结合已知可得()31022552x x x ⎛⎫-⋅=- ⎪⎝⎭,然后解一元二次方程求解x 值即可.【详解】解:∵5AE AD =,∴设AD x =,5AE x =,∵ADE V 沿DE 翻折,得到FDE V ,∴DF AD x ==,ADE FDE ∠=∠,过E 作EH AC ⊥于H ,设EF 与AC 相交于M ,则90AHE ACB ︒∠=∠=,又A A ∠=∠,三、解答题26.(2024·四川眉山·中考真题)如图,BE 是O 的直径,点A 在O 上,点C 在BE 的延长线上,EAC ABC ∠=∠,AD 平分BAE ∠交O 于点D ,连结DE .(1)求证:CA 是O 的切线;(2)当8,4AC CE ==时,求DE 的长.【答案】(1)见解析(2)62【分析】本题考查了切线的判定和性质,等腰三角形的性质,勾股定理,圆周角定理,熟练掌握切线的判定是解题的关键.(1)连接OA ,根据圆周角定理得到90BAE ∠=︒,根据等腰三角形的性质得到ABC BAO ∠=∠,求得90OAC ∠=︒,根据切线的判定定理得到结论;(2)根据相似三角形的判定和性质定理得到16BC =,求得12BE BC CE =-=,连接BD ,根据角平分线的定义得到BAD EAD ∠=∠,求得 BDDE =,得到BD DE =,根据等腰直角三角形的性质即可得到结论.【详解】(1)证明:连接OA ,BE 是O 的直径,90BAE ∴∠=︒,90BAO OAE ∴∠+∠=︒,OA OB = ,ABC BAO ∴∠=∠,EAC ABC ∠=∠ ,CAE BAO ∴∠=∠,90CAE OAE ∴∠+∠=︒,90OAC ∴∠=︒,OA 是O 的半径,27.(2024·四川凉山·中考真题)如图,AB 是O 的直径,点C 在O 上,AD 平分BAC ∠交O 于点D ,过点D 的直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F .(1)求证:EF 是O 的切线;(2)连接EO 并延长,分别交O 于,M N 两点,交AD 于点G ,若O 的半径为230F ∠=, ,求GM GN ⋅的值.【答案】(1)见详解(2)7225【分析】(1)连接OD ,根据等腰三角形的性质及角平分线得到OD AC ∥,根据平行线的性质得90ODF ∠=︒即可证明;(2)连接,MD AN ,先解Rt ODF △,求得4OF =,23DF =,则6AF =,3AE =,可证明23AD DF ==,由DGO AGE ∽,得23DG OD AG AE ==,故23,55DG AD AG AD ==,证明MGD AGN △∽△,即可得到7225GM GN GD GA ⋅=⋅=.【详解】(1)解:连接OD ,∵OA OD =,∴23∠=∠,∵AD 平分BAC ∠,∴12∠=∠,∴13∠=∠,∴OD AC ∥,∴ODF AED∠=∠∵DE AC ⊥,∴90AED ∠=︒,∴90ODF ∠=︒,即OD EF ⊥,∵OD 是O 的半径∴EF 是O 的切线;∵30F ∠=︒,∴在Rt ODF △中,24OF OD ==,由勾股定理得:22DF OF OD =-∴246AF =+=,∵在Rt AEF 中,30F ∠=︒,∴132AE AF ==,【点睛】本题考查了圆的切线的判定,相似三角形的判定与性质,勾股定理,30︒的直角三角形的性质,等腰三角形的性质,正确添加辅助线是解题的关键.28.(2024·江苏盐城·中考真题)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l ,过点A 作AD l ⊥,垂足为D ,连接AC BC 、.(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径.【答案】(1)见解析(2)256【分析】题目主要考查切线的性质,相似三角形的判定和性质及勾股定理解三角形,作出辅助线,综合运用这些知识点是解题关键.(1)连接OC ,根据题意得90OCD OCA ACD ∠∠∠=+=︒,90ACB ACO OCB ∠∠∠=+=︒,利用等量代换确定ACD ABC ∠∠=,再由相似三角形的判定即可证明;(2)先由勾股定理确定3AD =,然后利用相似三角形的性质求解即可.【详解】(1)证明:连接OC ,如图所示:∵CD 是O 的切线,点C 在以AB 为直径的O 上,∴90OCD OCA ACD ∠∠∠=+=︒,90ACB ACO OCB ∠∠∠=+=︒,∴ACD OCB ∠∠=,∵OC OB =,∴OBC OCB ∠∠=,∴ACD ABC ∠∠=,∵AD l ⊥,29.(2024·陕西·中考真题)如图,直线l 与O 相切于点A ,AB 是O 的直径,点C ,D 在l 上,且位于点A 两侧,连接BC BD ,,分别与O 交于点E ,F ,连接EF AF ,.(1)求证:BAF CDB ∠=∠;(2)若O 的半径6r =,9AD =,12AC =,求EF 的长.∴90BAF ABD ∠+∠=︒,∴BAF CDB ∠=∠;(2)解:∵6r =,∴212AB r AC ===,222212915BD AB AD =+=+=,∵直线l 与O 相切于点A ,∴90BAC ∠=︒,∴ABC 是等腰直角三角形,∴45ABC ACB ∠=∠=︒,∵AB 是O 的直径,∴90BEA ∠=︒,∴ABE 也是等腰直角三角形,∴cos 4562AE BE AB ==⋅︒=,∵ BFBF =,∴BEF BAF ∠=∠,∵BAF CDB ∠=∠,∴BEF BDC ∠=∠,∴BEF BDC ∽,∴BE EF BD CD =,即6215129EF =+,∴4225EF =.【点睛】本题考查的是等腰三角形的性质和判定,相似三角形的性质和判定,切线的性质,勾股定理等知识点的应用,掌握切线的性质定理、相似三角形的判定定理和性质定理是解题的关键.30.(2024·上海·中考真题)如图所示,在矩形ABCD 中,E 为边CD 上一点,且AE BD ⊥.(1)求证:2AD DE DC =⋅;(2)F 为线段AE 延长线上一点,且满足12EF CF BD ==,求证:CE AD =.∠在矩形ABCD中,ADE ⊥,AE BD∴90∠+∠=︒DAE ADBADB AED∴∠=∠,FEC AED∠=∠,在矩形ABCD 中,12OA OD BD ==, 12EF CF BD ==,OA OD EF CF ∴===,ADO OAD ∴∠=∠,FEC FCE ∠=∠,ADO FEC ∠=∠,FEC E AD F O OAD C ∴∠∠=∠∠==,在ODA V 和FEC 中,ODA FEC OAD FCE OD FE ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ODA FEC ∴ ≌,CE AD ∴=.【点睛】本题考查矩形综合,涉及矩形性质、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质等知识,熟练掌握相关几何性质与判定是解决问题第的关键.31.(2024·内蒙古赤峰·中考真题)如图,ABC 中,90ACB ∠=︒,AC BC =,O 经过B ,C 两点,与斜边AB 交于点E ,连接CO 并延长交AB 于点M ,交O 于点D ,过点E 作EF CD ∥,交AC 于点F .(1)求证:EF 是O 的切线;(2)若42BM =,1tan 2BCD ∠=,求OM 的长.【答案】(1)见解析(2)5OM =【分析】(1)连接OE ,延长EO ,交O 于点P ,连接,,PD BD 根据直径所对的圆周角是直角求出45DBE ∠=︒得45DPE ∠=︒,90DOE ∠=︒,由EF CD ∥可得90FED DOE ∠=∠=︒,从而可证明EF 是O 的切线;(2)由1tan 2BCD ∠=得12DB BC =,即12DB AC =,证明DBM ACM ∽ ,得12BM DM DB AM CM AC ===,由42BM =∵,AB BC ACB =∠∴ABC 是等腰直角三角形,∴45,ABC ∠=︒∵CD 是O 的直径,∴8242122AB AM BM =+=+=,在等腰直角三角形ABC 中,222AC BC AB +=,∴()2222122AC AC AB +==,解得,12AC =,∴12AC BC ==,∴16,2DB BC ==在t R BDC 中,222212665,CD BC DB =+=+=∴35CO DO ==,又12DM CM =,∴2,CM DM =∴265,DM DM CD +==∴25DM =∴35255OM OD DM =-=-=【点睛】本题主要考查平行线的性质,等腰直角三角形的判定与性质,切线的判定,圆周角定理,勾股定理以及相似三角形的判定与性质,正确作出辅助线构造圆周角是解答本题的关键.32.(2024·四川甘孜·中考真题)如图,在四边形ABCD 中,90A ∠=︒,连接BD ,过点C 作CE AB ⊥,垂足为E ,CE 交BD 于点F ,1ABC ∠=∠.(1)求证:23∠∠=;(2)若445∠=︒.①请判断线段BC ,BD 的数量关系,并证明你的结论;②若13BC =,5AD =,求EF 的长.【答案】(1)见解析∴EF BE AD AB =,∴5512EF =,2512EF ∴=.33.(2024·内蒙古赤峰·中考真题)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在ABC 中,AB AC =,点D 是AC 上的一个动点,过点D 作DE BC ⊥于点E ,延长ED 交BA 延长线于点F .请你解决下面各组提出的问题:(1)求证:AD AF =;(2)探究DF DE与AD DC 的关系;某小组探究发现,当13AD DC =时,23DF DE =;当45AD DC =时,85DF DE =.请你继续探究:①当76AD DC =时,直接写出DF DE 的值;②当AD m DC n =时,猜想DF DE的值(用含m ,n 的式子表示),并证明;(3)拓展应用:在图1中,过点F 作FP AC ⊥,垂足为点P ,连接CF ,得到图2,当点D 运动到使ACF ACB ∠=∠时,若AD m DC n =,直接写出AP AD的值(用含m ,n 的式子表示).【答案】(1)见解析(2)①73DF DE =②2DF DE m n =,证明见解析(3)2AP n AD m=【分析】(1)等边对等角,得到B C ∠=∠,等角的余角的相等,结合对顶角相等,得到F ADF ∠=∠,即可得出结论;∵DE BC ⊥,∴AG CE ∥,∴AGD CED ∽△△,∵AD m DC n =,∴GD AD m ==,由(1)知AD AF =,又AG EF ⊥,∴DG FG =,即2DF DG =,∴22GD m DE nDF DE ==;(3)2AP n AD m =,理由如下:过点D 作DG CF ⊥,∵ACF ACB ∠=∠,DE CE ⊥,∴DG DE =,由(2)知,当AD m DC n =时,2DF DE m n=,∴2DE n DF m =,∴2DG n DF m =,∵PF AC ⊥,∴90ACF CFP ∠+∠=︒,∵FE BC ⊥,∴90B AFD ∠+∠=︒,∵AB AC =,∴ACB B =∠∠,∴B ACF ∠=∠,∴AFD CFP ∠=∠,∴AFD PFD CFP PFD ∠-∠=∠-∠,∴AFP DFG ∠=∠,∴sin sin AFP DFG ∠=∠,∴2AP DG n AF DF m==,由(1)知AD AF =,34.(2024·福建·中考真题)如图,在ABC 中,90,BAC AB AC ∠=︒=,以AB 为直径的O 交BC 于点D ,AE OC ⊥,垂足为,E BE 的延长线交 AD 于点F .(1)求OE AE的值;(2)求证:AEB BEC △∽△;(3)求证:AD 与EF 互相平分.∴在Rt AOC 中,tan 2AC AOC AO∠==.AE OC ⊥ ,∴在Rt AOE △中,tan AE AOC OE∠=.2AE OE ∴=,12OE AE ∴=;(2)过点B 作BM AE ∥,交EO 延长线于点M .,90BAE ABM AEO BMO ∴∠=∠∠=∠=︒.AO BO = ,AOE BOM ∴△≌△,,AE BM OE OM ∴==.12OE AE = ,2BM OE EM ∴==,45MEB MBE ∴∠=∠=︒,135AEB AEO MEB ∴∠=∠+∠=︒,180135BEC MEB ∠=︒-∠=︒,AEB BEC ∴∠=∠.,90AB AC BAC =∠=︒ ,45ABC ∴∠=︒,ABM CBE ∴∠=∠,BAE CBE ∴∠=∠,AEB BEC ∴△∽△.(3)如图,连接,DE DF .90ADB AFB ∴∠=∠=,90AB AC BAC ∠== 2,BC BD DAB ∴=∠=由(2)知,AEB △∽△22AE AB AO BE BC BD ∴===35.(2024·北京·中考真题)如图,AB 是O 的直径,点C ,D 在O 上,OD 平分AOC ∠.(1)求证:OD BC ∥;(2)延长DO 交O 于点E ,连接CE 交OB 于点F ,过点B 作O 的切线交DE 的延长线于点P .若56OF BF =,1PE =,求O 半径的长.【答案】(1)见解析(2)32【分析】(1)根据题意,得AOC B C ∠=∠+∠,结合OB OC =,得到B C ∠=∠,继而得到2AOC B ∠=∠,根据OD 平分AOC ∠,得到2AOC AOD ∠=∠,继而得到B AOD ∠=∠,可证OD BC ∥;(2)不妨设5,6OF x BF x ==,则11OB OF BF x OC OE =+===,求得111OP OE PE x =+=+,证明OFE BFC ∽,OBM POB ∠=∠,求得665x BC =,取BC 的中点M ,连接OM ,则335x BM =,求得3cos 5OBM ∠=,3cos 5POB ∠=,结合切线性质,得到3cos 51OB OB OB POB OP OE PE OB ∠====++,解答即可.【详解】(1)根据题意,得AOC B C ∠=∠+∠,∵OB OC =,∴B C ∠=∠,∴2AOC B ∠=∠,∵OD 平分AOC ∠,∴2AOC AOD ∠=∠,∴B AOD ∠=∠,∴OD BC ∥;(2)∵56OF BF =,1PE =,不妨设5,6OF x BF x ==,则11OB OF BF x OC OE =+===,∴111OP OE PE x =+=+,∵OD BC ∥,2【点睛】本题考查了圆的性质,等腰三角形的性质,平行线的判定,三角形相似的判定和性质,切线的性质,解直角三角形的相关计算,等量代换思想,熟练掌握三角形相似的判定和性质,切线的性质,解直角三角形的相关计算是解题的关键36.(2024·四川广元·中考真题)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.在ABC 中,点D 为边AB 上一点,连接CD .(1)初步探究如图2,若ACD B ∠=∠,求证:2AC AD AB =⋅;(2)尝试应用如图3,在(1)的条件下,若点D 为AB 中点,4BC =,求CD 的长;(3)创新提升如图4,点E 为CD 中点,连接BE ,若30CDB CBD ∠=∠=︒,ACD EBD ∠=∠,27AC =BE 的长.【答案】(1)证明见解析(2)22CD =(3)21【分析】(1)根据题意,由ACD B ∠=∠,A A ∠=∠,利用两个三角形相似的判定定理即可得到ACD ABC △△∽,再由相似性质即可得证;(2)设AD BD m ==,由(1)中相似,代值求解得到2AC m =,从而根据ACD 与ABC 的相似比为12AD AC =求解即可得到答案;(3)过点C 作EB 的平行线交AB 的延长线于点H ,如图1所示,设CE DE a ==,过点B 作BF EC ⊥于点F ,如图2所示,利用含30︒的直角三角形性质及勾股定理即可得到相关角度与线段长,再由三角形相似的判定与性质得到21277AD AC CD a AC AH CH a ====,代值求解即可得到答案.【详解】(1)证明:∵ACD B ∠=∠,A A ∠=∠,∴ACD ABC △△∽,∵点E 为CD 中点,∴设CE DE a ==,∵30CDB CBD ∠=∠=︒,∴2CB CD a ==,120DCB ∠=︒,∴60FCB ∠=︒,∴30CBF ∠=︒,∴12CF BC =,∴CF a =,3BF a =,∴2EF a =,∴7BE a =,∵CH BE ∥,点E 为CD 中点,∴227CH BE a ==,243DH DB a ==,EBD H ∠=∠,又∵ACD EBD ∠=∠,∴ACD H ∠=∠,ACD AHC ∽△△,∴21277AD AC CD a AC AH CH a ====,又∵27AC =,∴2AD =,14AH =,∴12DH =,即4312a =,∴3a =,∴721BE a ==.【点睛】本题考查几何综合,涉及相似三角形的判定与性质、含30︒的直角三角形性质、勾股定理等知识,熟练掌握三角形相似的判定与性质是解决问题的关键.37.(2024·安徽·中考真题)如图1,ABCD Y 的对角线AC 与BD 交于点O ,点M ,N 分别在边AD ,BC 上,且AM CN =.点E ,F 分别是BD 与AN ,CM 的交点.(1)求证:OE OF =;(2)连接BM 交AC 于点H ,连接HE ,HF .(ⅰ)如图2,若HE AB ∥,求证:HF AD ∥;(ⅱ)如图3,若ABCD Y 为菱形,且2MD AM =,60EHF ∠=︒,求AC BD 的值.∴OHF OAD ∠=∠,∴HF AD∥(ⅱ)∵ABCD 是菱形,∴AC BD ⊥,又OE OF =,60EHF ∠=︒,∴30EHO FHO ∠=∠=︒,∴3OH OE =,∵AM BC ∥.2MD AM =,∴AHM CHB ∽,∴13AH AM HC BC ==,即3HC AH =,∴()3OA AH OA OH +=-,∴2OA OH =,∵BN AD ∥,2MD AM =,AM CN =,∴BNE DAE ∽,∴23BE BN ED AD ==,即32BE ED =,∴()()32OB OE OB OE -=+∴5OB OE =,故22323555AC OA OH OE BD OB OE OE ⨯====.【点睛】本题主要考查了平行四边形的判定以及性质,全等三角形判定以及性质,相似三角形的判定以及性质,平行线截线段成比例以及菱形的性质,掌握这些判定方法以及性质是解题的关键.38.(2024·内蒙古包头·中考真题)如图,在ABCD Y 中,ABC ∠为锐角,点E 在边AD 上,连接,BE CE ,且ABE DCE S S = .(1)如图1,若F 是边BC 的中点,连接EF ,对角线AC 分别与,BE EF 相交于点,G H .①求证:H 是AC 的中点;②求::AG GH HC ;(2)如图2,BE 的延长线与CD 的延长线相交于点M ,连接,AM CE 的延长线与AM 相交于点N .试探究线段AM 与线段AN 之间的数量关系,并证明你的结论.【答案】(1)①见解析;②::2:1:3AG GH HC =(2)3AM AN =,理由见解析【分析】(1)①根据ABE DCE S S = ,得出E 为AD 的中点,证明出AHE CHF ≌即可;②先证明出AGB HGE ∽得到2AB AG EH GH==,然后再根据平行四边形的性质找到线段的数量关系求解;(2)连接BD 交CN 于点F ,证明()AAS AEB DEM ≌,进一步证明出四边形ABDM 为平行四边形,得出DF 为CMN 的中位线,得到12DF MN =,再证明出AEN DEF ≌得到DF AN =,再通过等量代换即可求解.【详解】(1)解:①ABE DCE S S = ,E ∴为AD 的中点,AE DE ∴=,F 是边BC 的中点,BF CF ∴=,AE CF ∴=,在ABCD Y 中,AD BC∴EAH FCH ∠=∠,又∵AHE CHF ∠=∠,()AAS AHE CHF ∴ ≌,。
初三相似简单练习题

初三相似简单练习题相似是几何学中重要的概念之一,在初三学习中也是必须掌握的内容。
相似的概念和性质是初步了解几何相似的基础,通过练习题的形式可以帮助我们加深对相似的理解和应用。
下面是一些初三相似的简单练习题:1. 已知△ABC和△DEF相似,AB = 4cm,AC = 6cm,DE = 2cm,寻找满足相似的比例因子k。
2. 已知△ABC和△DEF相似,AB = 5cm,AC = 8cm,DE = 6cm,寻找满足相似的比例因子k。
3. 已知△ABC和△DEF相似,AC = 9cm,BC = 12cm,EF = 15cm,寻找满足相似的比例因子k。
4. 已知△ABC和△DEF相似,AC = 10cm,BC = 18cm,EF = 30cm,寻找满足相似的比例因子k。
5. 将一个正方形的边长扩大到原来的2倍,面积变为原来的几倍?6. 将一个正方形的边长缩小到原来的一半,面积变为原来的几倍?7. 将一个矩形的长和宽各乘以2,面积变为原来的几倍?8. 将一个矩形的长和宽都减少到原来的一半,面积变为原来的几倍?9. 已知两个三角形的边长比为3:4,面积比为9:16,求这两个三角形的高的比值。
10. 已知两个三角形的边长比为5:6,面积比为25:36,求这两个三角形的高的比值。
以上是初三相似的简单练习题,通过解题可以加深对相似的理解和运用。
在做题时,需要注意比例因子的计算和面积的计算方法。
相似的概念是初步了解几何相似的基础,掌握了相似的性质和运用方法,才能更好地解决相关问题。
相似的知识在几何学和应用数学中有广泛的应用,对于后续的学习和应用都有重要的作用。
练习题可以帮助我们巩固和拓展对相似的认识,提高解决问题的能力。
总之,相似的概念是初三几何学中的重要内容,通过解答练习题可以加深理解和应用。
练习题中涉及到比例因子和面积的计算,需要运用相关的知识和方法。
掌握相似的性质和运用方法对于几何学和应用数学的学习都具有重要的作用。
中考数学《图形的相似》真题汇编含解析

图形的相似(29题)一、单选题1(2023·重庆·统考中考真题)如图,已知△ABC ∽△EDC ,AC :EC =2:3,若AB 的长度为6,则DE 的长度为()A.4B.9C.12D.13.5【答案】B【分析】根据相似三角形的性质即可求出.【详解】解:∵△ABC ∽△EDC ,∴AC :EC =AB :DE ,∵AC :EC =2:3,AB =6,∴2:3=6:DE ,∴DE =9,故选:B .【点睛】此题考查的是相似三角形的性质,掌握相似三角形的边长比等于相似比是解决此题的关键.2(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC 、△DEF 成位似关系,则位似中心的坐标为()A.-1,0B.0,0C.0,1D.1,0【答案】A【分析】根据题意确定直线AD 的解析式为:y =x +1,由位似图形的性质得出AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,即可求解.【详解】解:由图得:A 1,2 ,D 3,4 ,设直线AD 的解析式为:y =kx +b ,将点代入得:2=k +b 4=3k +b ,解得:k =1b =1 ,∴直线AD 的解析式为:y =x +1,AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,∴当y =0时,x =-1,∴位似中心的坐标为-1,0 ,故选:A .【点睛】题目主要考查位似图形的性质,求一次函数的解析式,理解题意,掌握位似图形的特点是解题关键.3(2023·浙江嘉兴·统考中考真题)如图,在直角坐标系中,△ABC 的三个顶点分别为A 1,2 ,B 2,1 ,C 3,2 ,现以原点O 为位似中心,在第一象限内作与△ABC 的位似比为2的位似图形△A B C ,则顶点C 的坐标是()A.2,4B.4,2C.6,4D.5,4【答案】C【分析】直接根据位似图形的性质即可得.【详解】解:∵△ABC 的位似比为2的位似图形是△A B C ,且C 3,2 ,∴C 2×3,2×2 ,即C 6,4 ,故选:C .【点睛】本题考查了坐标与位似图形,熟练掌握位似图形的性质是解题关键.4(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,则旗杆高度为()A.6.4mB.8mC.9.6mD.12.5m【答案】B【分析】根据镜面反射性质,可求出∠ACB =∠ECD ,再利用垂直求△ABC ∽△EDC ,最后根据三角形相似的性质,即可求出答案.【详解】解:如图所示,由图可知,AB ⊥BD ,CD ⊥DE ,CF ⊥BD∴∠ABC =∠CDE =90°.∵根据镜面的反射性质,∴∠ACF =∠ECF ,∴90°-∠ACF =90°-∠ECF ,∴∠ACB =∠ECD ,∴△ABC ∽△EDC ,∴AB DE =BC CD.∵小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,∴AB =1.6m ,BC =2m ,CD =10m .∴1.6DE =210.∴DE =8m .故选:B .【点睛】本题考查了相似三角形的应用,解题的关键在于熟练掌握镜面反射的基本性质和相似三角形的性质.5(2023·安徽·统考中考真题)如图,点E 在正方形ABCD 的对角线AC 上,EF ⊥AB 于点F ,连接DE 并延长,交边BC 于点M ,交边AB 的延长线于点G .若AF =2,FB =1,则MG =()A.23B.352C.5+1D.10【答案】B 【分析】根据平行线分线段成比例得出DE EM =AF FB =2,根据△ADE ∽△CME ,得出AD CM =DE EM =2,则CM =12AD =32,进而可得MB =32,根据BC ∥AD ,得出△GMB ∽△GDA ,根据相似三角形的性质得出BG =3,进而在Rt △BGM 中,勾股定理即可求解.【详解】解:∵四边形ABCD 是正方形,AF =2,FB =1,∴AD =BC =AB =AF +FG =2+1=3,AD ∥CB ,AD ⊥AB ,CB ⊥AB ,∵EF ⊥AB ,∴AD ∥EF ∥BC∴DE EM =AFFB=2,△ADE∽△CME,∴AD CM =DEEM=2,则CM=12AD=32,∴MB=3-CM=32,∵BC∥AD,∴△GMB∽△GDA,∴BG AG =MBDA=323=12∴BG=AB=3,在Rt△BGM中,MG=MB2+BG2=322+32=352,故选:B.【点睛】本题考查了正方形的性质,平行线分线段成比例,相似三角形的性质与判定,勾股定理,熟练掌握以上知识是解题的关键.6(2023·湖北黄冈·统考中考真题)如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于12EF长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为()A.10B.11C.23D.4【答案】A【分析】由作图可知BP平分∠CBD,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,根据角平分线的性质可知RQ=RC,进而证明Rt△BCR≌Rt△BQR,推出BC=BQ=4,设RQ=RC=x,则DR=CD-CR=3-x,解Rt△DQR求出QR=CR=43.利用三角形面积法求出OC,再证△OCR∽△DCN,根据相似三角形对应边成比例即可求出CN.【详解】解:如图,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,∵矩形ABCD中,AB=3,BC=4,∴CD =AB =3,∴BD =BC 2+CD 2=5.由作图过程可知,BP 平分∠CBD ,∵四边形ABCD 是矩形,∴CD ⊥BC ,又∵RQ ⊥BD ,∴RQ =RC ,在Rt △BCR 和Rt △BQR 中,RQ =RC BR =BR ,∴Rt △BCR ≌Rt △BQR HL ,∴BC =BQ =4,∴QD =BD -BQ =5-4=1,设RQ =RC =x ,则DR =CD -CR =3-x ,在Rt △DQR 中,由勾股定理得DR 2=DQ 2+RQ 2,即3-x 2=12+x 2,解得x =43,∴CR =43.∴BR =BC 2+CR 2=4310.∵S △BCR =12CR ⋅BC =12BR ⋅OC ,∴OC =CR ⋅BC BR =43×44310=2510.∵∠COR =∠CDN =90°,∠OCR =∠DCN ,∴△OCR ∽△DCN ,∴OC DC =CR CN ,即25103=43CN,解得CN =10.故选:A .【点睛】本题考查角平分线的作图方法,矩形的性质,角平分线的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等,涉及知识点较多,有一定难度,解题的关键是根据作图过程判断出BP 平分∠CBD ,通过勾股定理解直角三角形求出CR .7(2023·四川内江·统考中考真题)如图,在△ABC 中,点D 、E 为边AB 的三等分点,点F 、G 在边BC 上,AC ∥DG ∥EF ,点H 为AF 与DG 的交点.若AC =12,则DH 的长为()A.1B.32C.2D.3【答案】C 【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB,解得EF =4,则DH =12EF =2.【详解】解:∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴∠BEF =∠BAC ,∠BFE =∠BCA ,∴△BEF ∽△BAC ,∴EF AC =BE AB,即EF 12=BE 3BE ,解得:EF =4,∴DH =12EF =12×4=2,故选:C .【点睛】本题考查了三等分点的定义、平行线的性质、相似三角形的判定与性质、三角形中位线定理等知识;熟练掌握相似三角形的判定与性质是解题的关键.8(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,O 为原点,OA =OB =35,点C 为平面内一动点,BC =32,连接AC ,点M 是线段AC 上的一点,且满足CM :MA =1:2.当线段OM 取最大值时,点M 的坐标是()A.35,65B.355,655C.65,125D.655,1255 【答案】D【分析】由题意可得点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,先证△OAM ∽△DAC ,得OM CD =OA AD =23,从而当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,然后分别证△BDO ∽△CDF ,△AEM ∽△AFC ,利用相似三角形的性质即可求解.【详解】解:∵点C 为平面内一动点,BC =32,∴点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,∵OA =OB =35,∴AD =OD +OA =952,∴OA AD=23,∵CM :MA =1:2,∴OA AD =23=CM AC,∵∠OAM =∠DAC ,∴△OAM ∽△DAC ,∴OM CD =OA AD=23,∴当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,∵OA =OB =35,OD =352,∴BD =OB 2+OD 2=35 2+352 2=152,∴CD =BC +BD =9,∵OM CD=23,∴OM =6,∵y 轴⊥x 轴,CF ⊥OA ,∴∠DOB =∠DFC =90°,∵∠BDO =∠CDF ,∴△BDO ∽△CDF ,∴OB CF =BD CD 即35CF=1529,解得CF =1855,同理可得,△AEM ∽△AFC ,∴ME CF =AM AC =23即ME 1855=23,解得ME =1255,∴OE =OM 2-ME 2=62-1255 2=655,∴当线段OM 取最大值时,点M 的坐标是655,1255,故选:D .【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.9(2023·山东东营·统考中考真题)如图,正方形ABCD 的边长为4,点E ,F 分别在边DC ,BC 上,且BF =CE ,AE 平分∠CAD ,连接DF ,分别交AE ,AC 于点G ,M ,P 是线段AG 上的一个动点,过点P 作PN ⊥AC 垂足为N ,连接PM ,有下列四个结论:①AE 垂直平分DM ;②PM +PN 的最小值为32;③CF 2=GE ⋅AE ;④S ΔADM =62.其中正确的是()A.①②B.②③④C.①③④D.①③【答案】D【分析】根据正方形的性质和三角形全等即可证明∠DAE =∠FDC ,通过等量转化即可求证AG ⊥DM ,利用角平分线的性质和公共边即可证明△ADG ≌△AMG ASA ,从而推出①的结论;利用①中的部分结果可证明△ADE ∽△DGE 推出DE 2=GE ⋅AE ,通过等量代换可推出③的结论;利用①中的部分结果和勾股定理推出AM 和CM 长度,最后通过面积法即可求证④的结论不对;结合①中的结论和③的结论可求出PM +PN 的最小值,从而证明②不对.【详解】解:∵ABCD 为正方形,∴BC =CD =AD ,∠ADE =∠DCF =90°,∵BF =CE ,∴DE =FC ,∴△ADE ≌△DCF SAS .∴∠DAE =∠FDC ,∵∠ADE =90°,∴∠ADG +∠FDC =90°,∴∠ADG +∠DAE =90°,∴∠AGD =∠AGM =90°.∵AE 平分∠CAD ,∴∠DAG =∠MAG .∵AG =AG ,∴△ADG ≌△AMG ASA .∴DG =GM ,∵∠AGD =∠AGM =90°,∴AE 垂直平分DM ,故①正确.由①可知,∠ADE =∠DGE =90°,∠DAE =∠GDE ,∴△ADE ∽△DGE ,∴DE GE=AE DE ,∴DE 2=GE ⋅AE ,由①可知DE =CF ,∴CF 2=GE ⋅AE .故③正确.∵ABCD 为正方形,且边长为4,∴AB =BC =AD =4,∴在Rt △ABC 中,AC =2AB =4 2.由①可知,△ADG ≌△AMG ASA ,∴AM =AD =4,∴CM =AC -AM =42-4.由图可知,△DMC 和△ADM 等高,设高为h ,∴S △ADM =S △ADC -S △DMC ,∴4×h 2=4×42-42-4 ⋅h 2,∴h =22,∴S △ADM =12⋅AM ⋅h =12×4×22=4 2.故④不正确.由①可知,△ADG ≌△AMG ASA ,∴DG =GM ,∴M 关于线段AG 的对称点为D ,过点D 作DN ⊥AC ,交AC 于N ,交AE 于P ,∴PM +PN 最小即为DN ,如图所示,由④可知△ADM 的高h =22即为图中的DN ,∴DN =2 2.故②不正确.综上所述,正确的是①③.故选:D .【点睛】本题考查的是正方形的综合题,涉及到三角形相似,最短路径,三角形全等,三角形面积法,解题的关键在于是否能正确找出最短路径以及运用相关知识点.10(2023·内蒙古赤峰·统考中考真题)如图,把一个边长为5的菱形ABCD 沿着直线DE 折叠,使点C 与AB 延长线上的点Q 重合.DE 交BC 于点F ,交AB 延长线于点E .DQ 交BC 于点P ,DM ⊥AB于点M ,AM =4,则下列结论,①DQ =EQ ,②BQ =3,③BP =158,④BD ∥FQ .正确的是()A.①②③B.②④C.①③④D.①②③④【答案】A【分析】由折叠性质和平行线的性质可得∠QDF =∠CDF =∠QEF ,根据等角对等边即可判断①正确;根据等腰三角形三线合一的性质求出MQ =AM =4,再求出BQ 即可判断②正确;由△CDP ∽△BQP 得CP BP =CD BQ=53,求出BP 即可判断③正确;根据EF DE ≠QE BE 即可判断④错误.【详解】由折叠性质可知:∠CDF =∠QDF ,CD =DQ =5,∵CD ∥AB ,∴∠CDF =∠QEF .∴∠QDF =∠QEF .∴DQ =EQ =5.故①正确;∵DQ =CD =AD =5,DM ⊥AB ,∴MQ =AM =4.∵MB =AB -AM =5-4=1,∴BQ =MQ -MB =4-1=3.故②正确;∵CD ∥AB ,∴△CDP ∽△BQP .∴CP BP =CD BQ=53.∵CP +BP =BC =5,∴BP =38BC =158.故③正确;∵CD ∥AB ,∴△CDF ∽△BEF .∴DF EF =CD BE =CD BQ +QE=53+5=58.∴EF DE =813.∵QE BE =58,∴EF DE ≠QE BE.∴△EFQ 与△EDB 不相似.∴∠EQF ≠∠EBD .∴BD 与FQ 不平行.故④错误;故选:A .【点睛】本题主要考查了折叠的性质,平行线的性质,等腰三角形的性质,相似三角形的判定和性质,菱形的性质等知识,属于选择压轴题,有一定难度,熟练掌握相关性质是解题的关键.11(2023·黑龙江·统考中考真题)如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF ⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是:①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=22;⑤EP⋅DH=2AG⋅BH.()A.①②③④⑤B.①②③⑤C.①②③D.①②⑤【答案】B【分析】利用正方形的性质和翻折的性质,逐一判断,即可解答.【详解】解:∵四边形ABCD是正方形,∴∠DAE=∠ABF=90°,DA=AB,∵AF⊥DE,∴∠BAF+∠AED=90°,∵∠BAF+∠AFB=90°,∴∠AED=∠BFA,∴△ABF≌△AED AAS,∴AF=DE,故①正确,∵将△ABF沿AF翻折,得到△AMF,∴BM⊥AF,∵AF⊥DE,∴BM∥DE,故②正确,当CM⊥FM时,∠CMF=90°,∵∠AMF=∠ABF=90°,∴∠AMF+∠CMF=180°,即A,M,C在同一直线上,∴∠MCF=45°,∴∠MFC=90°-∠MCF=45°,通过翻折的性质可得∠HBF=∠HMF=45°,BF=MF,∴∠HMF=∠MFC,∠HBC=∠MFC,∴BC∥MH,HB∥MF,∴四边形BHMF是平行四边形,∵BF=MF,∴平行四边形BHMF是菱形,故③正确,当点E运动到AB的中点,如图,设正方形ABCD的边长为2a,则AE=BF=a,在Rt △AED 中,DE =AD 2+AE 2=5a =AF ,∵∠AHD =∠FHB ,∠ADH =∠FBH =45°,∴△AHD ∽△FHB ,∴FH AH =BF AD=a 2a =12,∴AH =23AF =253a ,∵∠AGE =∠ABF =90°,∴△AGF ∽△ABF ,∴AE AF =EG BF =AG AB =a 5a=55,∴EG =55BF =55a ,AG =55AB =255a ,∴DG =ED -EG =455a ,GH =AH -AG =4515a ,∵∠BHF =∠DHA ,在Rt △DGH 中,tan ∠BHF =tan ∠DHA =DG GH=3,故④错误,∵△AHD ∽△FHB ,∴BH DH=12,∴BH =13BD =13×22a =223a ,DH =23BD =23×22a =423a ,∵AF ⊥EP ,根据翻折的性质可得EP =2EG =255a ,∴EP ⋅DH =255a ⋅423a =81015a 2,2AG ⋅BH =2⋅255a ⋅223a =81015a 2,∴EP ⋅DH =2AG ⋅BH =81015a 2,故⑤正确;综上分析可知,正确的是①②③⑤.故选:B .【点睛】本题考查了正方形的性质,翻折的性质,相似三角形的判定和性质,正切的概念,熟练按照要求做出图形,利用寻找相似三角形是解题的关键.二、填空题12(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,△ABC 与△A 1B 1C 1位似,原点O 是位似中心,且AB A 1B 1=3.若A 9,3 ,则A 1点的坐标是.【答案】3,1【分析】直接利用位似图形的性质得出相似比进而得出对应线段的长.【详解】解∶设A1m,n∵△ABC与△A1B1C1位似,原点O是位似中心,且ABA1B1=3.若A9,3,∴位似比为31,∴9 m =31,3n=31,解得m=3,n=1,∴A13,1故答案为:3,1.【点睛】此题主要考查了位似变换,正确得出相似比是解题关键.13(2023·吉林长春·统考中考真题)如图,△ABC和△A B C 是以点O为位似中心的位似图形,点A 在线段OA 上.若OA:AA =1:2,则△ABC和△A B C 的周长之比为.【答案】1:3【分析】根据位似图形的性质即可求出答案.【详解】解:∵OA:AA =1:2,∴OA:OA =1:3,设△ABC周长为l1,设△A B C 周长为l2,∵△ABC和△A B C 是以点O为位似中心的位似图形,∴l1l2=OAOA=13.∴l1:l2=1:3.∴△ABC和△A B C 的周长之比为1:3.故答案为:1:3.【点睛】本题考查了位似图形的性质,解题的关键在于熟练掌握位似图形性质.14(2023·四川乐山·统考中考真题)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE 交于点F .若AE EB =23,则S △ADF S △AEF =.【答案】52【分析】四边形ABCD 是平行四边形,则AB =CD ,AB ∥CD ,可证明△EAF ∽△DCF ,得到DF EF =CD AE =AB AE,由AE EB =23进一步即可得到答案.【详解】解:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴∠AEF =∠CDF ,∠EAF =∠DCF ,∴△EAF ∽△DCF ,∴DF EF =CD AE =AB AE ,∵AE EB =23,∴AB AE =52,∴S △ADF S △AEF =DF EF =AB AE=52.故答案为:52【点睛】此题考查了平行四边形的性质、相似三角形的判定和性质等知识,证明△EAF ∽△DCF 是解题的关键.15(2023·江西·统考中考真题)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC ).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点A ,B ,Q 在同一水平线上,∠ABC 和∠AQP 均为直角,AP 与BC 相交于点D .测得AB =40cm ,BD =20cm ,AQ =12m ,则树高PQ =m .【答案】6【分析】根据题意可得△ABD ∽△AQP ,然后相似三角形的性质,即可求解.【详解】解:∵∠ABC 和∠AQP 均为直角∴BD ∥PQ ,∴△ABD ∽△AQP ,∴BD PQ =AB AQ∵AB =40cm ,BD =20cm ,AQ =12m ,∴PQ =AQ ×BD AB=12×2040=6m ,故答案为:6.【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的性质与判定是解题的关键.16(2023·四川成都·统考中考真题)如图,在△ABC 中,D 是边AB 上一点,按以下步骤作图:①以点A 为圆心,以适当长为半径作弧,分别交AB ,AC 于点M ,N ;②以点D 为圆心,以AM 长为半径作弧,交DB 于点M ;③以点M 为圆心,以MN 长为半径作弧,在∠BAC 内部交前面的弧于点N :④过点N 作射线DN 交BC 于点E .若△BDE 与四边形ACED 的面积比为4:21,则BE CE的值为.【答案】23【分析】根据作图可得∠BDE =∠A ,然后得出DE ∥AC ,可证明△BDE ∽△BAC ,进而根据相似三角形的性质即可求解.【详解】解:根据作图可得∠BDE =∠A ,∴DE ∥AC ,∴△BDE ∽△BAC ,∵△BDE 与四边形ACED 的面积比为4:21,∴S △BDC S △BAC =421+4=BE BC2∴BE BC =25∴BE CE =23,故答案为:23.【点睛】本题考查了作一个角等于已知角,相似三角形的性质与判定,熟练掌握基本作图与相似三角形的性质与判定是解题的关键.17(2023·内蒙古·统考中考真题)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =1,将△ABC 绕点A 逆时针方向旋转90°,得到△AB C .连接BB ,交AC 于点D ,则AD DC的值为.【答案】5【分析】过点D 作DF ⊥AB 于点F ,利用勾股定理求得AB =10,根据旋转的性质可证△ABB 、△DFB是等腰直角三角形,可得DF =BF ,再由S △ADB =12×BC ×AD =12×DF ×AB ,得AD =10DF ,证明△AFD ∼△ACB ,可得DF BC =AF AC ,即AF =3DF ,再由AF =10-DF ,求得DF =104,从而求得AD =52,CD =12,即可求解.【详解】解:过点D 作DF ⊥AB 于点F ,∵∠ACB =90°,AC =3,BC =1,∴AB =32+12=10,∵将△ABC 绕点A 逆时针方向旋转90°得到△AB C ,∴AB =AB =10,∠BAB =90°,∴△ABB 是等腰直角三角形,∴∠ABB =45°,又∵DF ⊥AB ,∴∠FDB =45°,∴△DFB 是等腰直角三角形,∴DF =BF ,∵S △ADB =12×BC ×AD =12×DF ×AB ,即AD =10DF ,∵∠C =∠AFD =90°,∠CAB =∠FAD ,∴△AFD ∼△ACB ,∴DF BC =AF AC,即AF =3DF ,又∵AF =10-DF ,∴DF =104,∴AD =10×104=52,CD =3-52=12,∴AD CD =5212=5,故答案为:5.【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.18(2023·河南·统考中考真题)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为.【答案】2或2+1【分析】分两种情况:当∠MND =90°时和当∠NMD =90°时,分别进行讨论求解即可.【详解】解:当∠MND =90°时,∵四边形ABCD 矩形,∴∠A =90°,则MN ∥AB ,由平行线分线段成比例可得:AN ND =BM MD,又∵M 为对角线BD 的中点,∴BM =MD ,∴AN ND =BM MD=1,即:ND =AN =1,∴AD =AN +ND =2,当∠NMD =90°时,∵M 为对角线BD 的中点,∠NMD =90°∴MN 为BD 的垂直平分线,∴BN =ND ,∵四边形ABCD 矩形,AN =AB =1∴∠A =90°,则BN =AB 2+AN 2=2,∴BN =ND =2∴AD =AN +ND =2+1,综上,AD 的长为2或2+1,故答案为:2或2+1.【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.19(2023·辽宁大连·统考中考真题)如图,在正方形ABCD 中,AB =3,延长BC 至E ,使CE =2,连接AE ,CF 平分∠DCE 交AE 于F ,连接DF ,则DF 的长为.【答案】3104【分析】如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,由CF 平分∠DCE ,可知∠FCM =∠FCN =45°,可得四边形CMFN 是正方形,FM ∥AB ,设FM =CM =NF =CN =a ,则ME =2-a ,证明△EFM ∽△EAB ,则FM AB=ME BE ,即a 3=2-a 3+2,解得a =34,DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2,计算求解即可.【详解】解:如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,则四边形CMFN 是矩形,FM ∥AB ,∵CF 平分∠DCE ,∴∠FCM =∠FCN =45°,∴CM =FM ,∴四边形CMFN 是正方形,设FM =CM =NF =CN =a ,则ME =2-a ,∵FM ∥AB ,∴△EFM ∽△EAB ,∴FM AB =ME BE ,即a 3=2-a 3+2,解得a =34,∴DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2=3104,故答案为:3104.【点睛】本题考查了正方形的判定与性质,勾股定理,相似三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.20(2023·广东·统考中考真题)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为.【答案】15【分析】根据正方形的性质及相似三角形的性质可进行求解.【详解】解:如图,由题意可知AD =DC =10,CG =CE =GF =6,∠CEF =∠EFG =90°,GH =4,∴CH =10=AD ,∵∠D =∠DCH =90°,∠AJD =∠HJC ,∴△ADJ ≌△HCJ AAS ,∴CJ =DJ =5,∴EJ =1,∵GI ∥CJ ,∴△HGI ∽△HCJ ,∴GI CJ =GH CH=25,∴GI =2,∴FI =4,∴S 梯形EJIF =12EJ +FI ⋅EF =15;故答案为:15.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.21(2023·天津·统考中考真题)如图,在边长为3的正方形ABCD 的外侧,作等腰三角形ADE ,EA =ED =52.(1)△ADE 的面积为;(2)若F 为BE 的中点,连接AF 并延长,与CD 相交于点G ,则AG 的长为.【答案】3;13【分析】(1)过点E 作EH ⊥AD ,根据正方形和等腰三角形的性质,得到AH 的长,再利用勾股定理,求出EH 的长,即可得到△ADE 的面积;(2)延长EH 交AG 于点K ,利用正方形和平行线的性质,证明△ABF ≌△KEF ASA ,得到EK 的长,进而得到KH 的长,再证明△AHK ∽△ADG ,得到KH GD =AH AD ,进而求出GD 的长,最后利用勾股定理,即可求出AG的长.【详解】解:(1)过点E作EH⊥AD,∵正方形ABCD的边长为3,∴AD=3,∵△ADE是等腰三角形,EA=ED=52,EH⊥AD,∴AH=DH=12AD=32,在Rt△AHE中,EH=AE2-AH2=522-32 2=2,∴S△ADE=12AD⋅EH=12×3×2=3,故答案为:3;(2)延长EH交AG于点K,∵正方形ABCD的边长为3,∴∠BAD=∠ADC=90°,AB=3,∴AB⊥AD,CD⊥AD,∵EK⊥AD,∴AB∥EK∥CD,∴∠ABF=∠KEF,∵F为BE的中点,∴BF=EF,在△ABF和△KEF中,∠ABF=∠KEF BF=EF∠AFB=∠KFE,∴△ABF≌△KEF ASA,∴EK=AB=3,由(1)可知,AH=12AD,EH=2,∴KH=1,∵KH∥CD,∴△AHK∽△ADG,∴KH GD =AH AD,∴GD=2,在Rt△ADG中,AG=AD2+GD2=32+22=13,故答案为:13.【点睛】本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,作辅助线构造全等三角形和相似三角形是解题关键.22(2023·四川泸州·统考中考真题)如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当PE+PF取得最小值时,APPC的值是.【答案】27【分析】作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,此时PE +PF 取得最小值,过点F 作AD 的垂线段,交AC 于点K ,根据题意可知点F 落在AD 上,设正方形的边长为a ,求得AK 的边长,证明△AEP ∽△KF P ,可得KP AP=2,即可解答.【详解】解:作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,过点F 作AD 的垂线段,交AC 于点K ,由题意得:此时F 落在AD 上,且根据对称的性质,当P 点与P 重合时PE +PF 取得最小值,设正方形ABCD 的边长为a ,则AF =AF =23a ,∵四边形ABCD 是正方形,∴∠F AK =45°,∠P AE =45°,AC =2a∵F K ⊥AF ,∴∠F AK =∠F KA =45°,∴AK =223a ,∵∠F P K =∠EP A ,∴△E KP ∽△EAP ,∴F K AE =KP AP=2,∴AP =13AK =292a ,∴CP =AC -AP =792a , ∴AP CP=27,∴当PE +PF 取得最小值时,AP PC 的值是为27,故答案为:27.【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.23(2023·山西·统考中考真题)如图,在四边形ABCD 中,∠BCD =90°,对角线AC ,BD 相交于点O .若AB =AC =5,BC =6,∠ADB =2∠CBD ,则AD 的长为.【答案】973【分析】过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,根据等腰三角形性质得出BH =HC =12BC =3,根据勾股定理求出AH =AC 2-CH 2=4,证明∠CBD =∠CED ,得出DB =DE ,根据等腰三角形性质得出CE =BC =6,证明CD ∥AH ,得出CD AH=CE HE ,求出CD =83,根据勾股定理求出DE =CE 2+CD 2=62+83 2=2973,根据CD ∥AH ,得出DE AD =CE CH ,即2973AD=63,求出结果即可.【详解】解:过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,如图所示:则∠AHC =∠AHB =90°,∵AB =AC =5,BC =6,∴BH =HC =12BC =3,∴AH =AC 2-CH 2=4,∵∠ADB =∠CBD +∠CED ,∠ADB =2∠CBD ,∴∠CBD =∠CED ,∴DB =DE ,∵∠BCD =90°,∴DC ⊥BE ,∴CE =BC =6,∴EH =CE +CH =9,∵DC ⊥BE ,AH ⊥BC ,∴CD ∥AH ,∴△ECD ~△EHA ,∴CD AH =CE HE ,即CD 4=69,解得:CD =83,∴DE =CE 2+CD 2=62+83 2=2973,∵CD ∥AH ,∴DE AD=CE CH ,即2973AD =63,解得:AD =973.故答案为:973.【点睛】本题主要考查了三角形外角的性质,等腰三角形的判定和性质,勾股定理,平行线分线段成比例,相似三角形的判定与性质,平行线的判定,解题的关键是作出辅助线,熟练掌握平行线分线段成比例定理及相似三角形的判定与性质.三、解答题24(2023·湖南·统考中考真题)在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高.(1)证明:△ABD ∽△CBA ;(2)若AB =6,BC =10,求BD 的长.【答案】(1)见解析(2)BD =185【分析】(1)根据三角形高的定义得出∠ADB =90°,根据等角的余角相等,得出∠BAD =∠C ,结合公共角∠B =∠B ,即可得证;(2)根据(1)的结论,利用相似三角形的性质即可求解.【详解】(1)证明:∵∠BAC =90°,AD 是斜边BC 上的高.∴∠ADB =90°,∠B +∠C =90°∴∠B +∠BAD =90°,∴∠BAD =∠C又∵∠B =∠B∴△ABD ∽△CBA ,(2)∵△ABD ∽△CBA∴AB CB =BD AB,又AB =6,BC =10∴BD =AB 2CB=3610=185.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.25(2023·湖南·统考中考真题)如图,CA ⊥AD ,ED ⊥AD ,点B 是线段AD 上的一点,且CB ⊥BE .已知AB =8,AC =6,DE =4.(1)证明:△ABC∽△DEB.(2)求线段BD的长.【答案】(1)见解析(2)BD=3【分析】(1)根据题意得出∠A=∠D=90°,∠C+∠ABC=90°,∠ABC+∠EBD=90°,则∠C=∠EBD,即可得证;(2)根据(1)的结论,利用相似三角形的性质列出比例式,代入数据即可求解.【详解】(1)证明:∵AC⊥AD,ED⊥AD,∴∠A=∠D=90°,∠C+∠ABC=90°,∵CE⊥BE,∴∠ABC+∠EBD=90°,∴∠C=∠EBD,∴△ABC∽△DEB;(2)∵△ABC∽△DEB,∴AB DE =AC BD,∵AB=8,AC=6,DE=4,∴8 4=6 BD,解得:BD=3.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.26(2023·四川眉山·统考中考真题)如图,▱ABCD中,点E是AD的中点,连接CE并延长交BA的延长线于点F.(1)求证:AF=AB;(2)点G是线段AF上一点,满足∠FCG=∠FCD,CG交AD于点H,若AG=2,FG=6,求GH的长.【答案】(1)见解析(2)65【分析】(1)根据平行四边形的性质可得AB∥CD,AB=CD,证明△AEF≅△DEC ASA,推出AF= CD,即可解答;(2)通过平行四边形的性质证明GC=GF=6,再通过(1)中的结论得到DC=AB=AF=8,最后证明△AGH∽△DCH,利用对应线段比相等,列方程即可解答.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠EAF=∠D,∵E是AD的中点,∴AE=DE,∵∠AEF =∠CED ,∴△AEF ≅△DEC ASA ,∴AF =CD ,∴AF =AB ;(2)解:∵四边形ABCD 是平行四边形,∴DC =AB =AF =FG +GA =8,DC ∥FA ,∴∠DCF =∠F ,∠DCG =∠CGB ,∵∠FCG =∠FCD ,∴∠F =∠FCG ,∴GC =GF =6,∵∠DHC =∠AHG ,∴△AGH ∽△DCH ,∴GH CH =AG DC,设HG =x ,则CH =CG -GH =6-x ,可得方程x 6-x =28,解得x =65,即GH 的长为65.【点睛】本题考查了平行四边形的性质,等腰三角形的判定和性质,相似三角形的判定和性质,熟练运用上述性质证明三角形相似是解题的关键.27(2023·四川凉山·统考中考真题)如图,在▱ABCD 中,对角线AC 与BD 相交于点O ,∠CAB =∠ACB ,过点B 作BE ⊥AB 交AC 于点E .(1)求证:AC ⊥BD ;(2)若AB =10,AC =16,求OE 的长.【答案】(1)见详解(2)92【分析】(1)可证AB =CB ,从而可证四边形ABCD 是菱形,即可得证;(2)可求OB =6,再证△EBO ∽△BAO ,可得EO BO =BO AO,即可求解.【详解】(1)证明:∵∠CAB =∠ACB ,∴AB =CB ,∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形,∴AC ⊥BD .(2)解:∵四边形ABCD 是平行四边形,∴OA =12AC =8,∵AC ⊥BD ,BE ⊥AB ,∴∠AOB =∠BOE =∠ABE =90°,∴OB =AB 2-OB 2=102-82=6,∵∠EBO +∠BEO =90°,∠ABO +∠EBO =90°,∴∠BEO =∠ABO ,∴△EBO ∽△BAO ,∴EO BO =BO AO ,∴EO 6=68解得:OE =92.【点睛】本题考查了平行四边形的性质,菱形的判定及性质,勾股定理,三角形相似的判定及性质,掌握相关的判定方法及性质是解题的关键.28(2023·江苏扬州·统考中考真题)如图,点E 、F 、G 、H 分别是▱ABCD 各边的中点,连接AF 、CE 相交于点M ,连接AG 、CH 相交于点N .(1)求证:四边形AMCN 是平行四边形;(2)若▱AMCN 的面积为4,求▱ABCD 的面积.【答案】(1)见解析(2)12【分析】(1)根据平行四边形的性质,线段的中点平分线段,推出四边形AECG ,四边形AFCH 均为平行四边形,进而得到:AM ∥CN ,AN ∥CM ,即可得证;(2)连接HG ,AC ,EF ,推出S △ANH S △ANC =HN CN=12,S △FMC S △AMC =12,进而得到S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,求出S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,再根据S ▱ABCD =2S ▱AFCH ,即可得解.【详解】(1)证明:∵▱ABCD ,∴AB ∥CD ,AD ∥BC ,AB =CD ,AD =BC ,∵点E 、F 、G 、H 分别是▱ABCD 各边的中点,∴AE =12AB =12CD =CG ,AE ∥CG ,∴四边形AECG 为平行四边形,同理可得:四边形AFCH 为平行四边形,∴AM ∥CN ,AN ∥CM ,∴四边形AMCN 是平行四边形;(2)解:连接HG ,AC ,EF ,∵H ,G 为AD ,CD 的中点,∴HG ∥AC ,HG =12AC ,∴△HNG ∽△CNA ,∴HN CN =HG AC =12,∴S △ANH S △ANC =HN CN=12,同理可得:S △FMC S △AMC =12∴S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,∴S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,∵AH =12AD ,∴S ▱ABCD =2S ▱AFCH =12.【点睛】本题考查平行四边形的判定和性质,三角形的中位线定理,相似三角形的判定和性质,熟练掌握平行四边形的性质,以及三角形的中位线定理,证明三角形相似,是解题的关键.29(2023·上海·统考中考真题)如图,在梯形ABCD 中AD ∥BC ,点F ,E 分别在线段BC ,AC 上,且∠FAC =∠ADE ,AC =AD(1)求证:DE =AF(2)若∠ABC =∠CDE ,求证:AF 2=BF ⋅CE【答案】见解析【分析】(1)先根据平行线的性质可得∠DAE =∠ACF ,再根据三角形的全等的判定可得△DAE ≅△ACF ,然后根据全等的三角形的性质即可得证;(2)先根据全等三角形的性质可得∠AFC =∠DEA ,从而可得∠AFB =∠CED ,再根据相似三角形的判定可得△ABF ∼△CDE ,然后根据相似三角形的性质即可得证.【详解】(1)证明:∵AD ∥BC ,∴∠DAE =∠ACF ,在△DAE和△ACF中,∠DAE=∠ACF AD=CA∠ADE=∠CAF,∴△DAE≅△ACF ASA,∴DE=AF.(2)证明:∵△DAE≅△ACF,∴∠AFC=∠DEA,∴180°-∠AFC=180°-∠DEA,即∠AFB=∠CED,在△ABF和△CDE中,∠AFB=∠CED ∠ABF=∠CDE,∴△ABF∼△CDE,∴AF CE =BF DE,由(1)已证:DE=AF,∴AF CE =BF AF,∴AF2=BF⋅CE.【点睛】本题考查了三角形全等的判定与性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.。
备战中考数学复习《相似》专项综合练习附详细答案

一、相似真题与模拟题分类汇编(难题易错题)1.已知线段a,b,c满足,且a+2b+c=26.(1)判断a,2b,c,b2是否成比例;(2)若实数x为a,b的比例中项,求x的值.【答案】(1)解:设,则a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12;∴2b=8,b2=16∵a=6,2b=8,c=12,b2=16∴2bc=96,ab2=6×16=96∴2bc=ab2a,2b,c,b2是成比例的线段。
(2)解:∵x是a、b的比例中项,∴x2=6ab,∴x2=6×4×6,∴x=12.【解析】【分析】(1)设已知比例式的值为k,可得出a=3k,b=2k,c=6k,再代入a+2b+c=26,建立关于k的方程,求出kl的值,再求出2b、b2,然后利用成比例线段的定义,可判断a,2b,c,b2是否成比例。
(2)根据实数x为a,b的比例中项,可得出x2=ab,建立关于x的方程,求出x的值。
2.已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;(3)延长AD、BO相交于点E,求证:DE=CO.【答案】(1)解:如图1,∵抛物线y=ax2的对称轴是y轴,且AB∥x轴,∴A与B是对称点,O是抛物线的顶点,∴OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∵AB=2,AB⊥OC,∴AC=BC=1,∠BOC=30°,∴OC= ,∴A(-1,),把A(-1,)代入抛物线y=ax2(a>0)中得:a= ;(2)解:如图2,过B作BE⊥x轴于E,过A作AG⊥BE,交BE延长线于点G,交y轴于F,∵CF∥BG,∴,∵AC=4BC,∴ =4,∴AF=4FG,∵A的横坐标为-4,∴B的横坐标为1,∴A(-4,16a),B(1,a),∵∠AOB=90°,∴∠AOD+∠BOE=90°,∵∠AOD+∠DAO=90°,∴∠BOE=∠DAO,∵∠ADO=∠OEB=90°,∴△ADO∽△OEB,∴,∴,∴16a2=4,a=± ,∵a>0,∴a= ;∴B(1,);(3)解:如图3,设AC=nBC,由(2)同理可知:A的横坐标是B的横坐标的n倍,则设B(m,am2),则A(-mn,am2n2),∴AD=am2n2,过B作BF⊥x轴于F,∴DE∥BF,∴△BOF∽△EOD,∴,∴,∴,DE=am2n,∴,∵OC∥AE,∴△BCO∽△BAE,∴,∴,∴CO= =am2n,∴DE=CO.【解析】【分析】(1)抛物线y=ax2关于y轴对称,根据AB∥x轴,得出A与B是对称点,可知AC=BC=1,由∠AOB=60°,可证得△AOB是等边三角形,利用解直角三角形求出OC的长,就可得出点A的坐标,利用待定系数法就可求出a的值。
中考数学总复习《相似》专题训练(附答案)

中考数学总复习《相似》专题训练(附答案)学校:___________班级:___________姓名:___________考号:___________知识点梳理1、相似三角形的判定定义:三个角分别相等,三条边成比例的两个三角形相似。
定理:平行线分线段成比例定理 两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
判定1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
判定2:三边成比例的两个三角形相似。
判定3:两边成比例且夹角相等的两个三角形相似。
判定4:两角分别相等的两个三角形相似。
2、相似三角形的性质相似三角形的对应角相等,对应边成比例;相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比; 相似三角形对应线段的比等于相似比; 相似三角形周长的比等于相似比; 相似三角形面积的比等于相似比的平方。
3、相似三角形模型 模型一:A 、8模型已知:12∠=∠,结论ADE ABC ∆∆∽ 模型二:共边共角型已知:12∠=∠,结论:ACD ABC ∆∆∽ 模型三:一线三角型已知,如图①②③中:∠B=∠ACE=∠D. 结论:△ABC ∽△CDE 模型四:相似与旋转如图①,已知DE ∥BC ,将△ADE 绕点A 旋转一定的角度,连接BD 、CE ,得到如图②,结论:△ABD ∽△ACE 模型五:垂直相似如图,在Rt 三角形ABC 中∠C=90°,CD 为斜边AB 上的高结论:222ACD BCD ABCAC AD AB BC BD AB CD AD BD∆∆∆===∽∽4、位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比。
性质:每一组对应点和位似中心在同一直线上,它们到位似中心的距离之比都等于位似比。
中考数学复习《相似》专题训练-附带有答案

中考数学复习《相似》专题训练-附带有答案一、单选题1.已知△ABC∽△A′B′C′,BCA′C′=23,ABA′B′=34则△ABC与△A′B′C′的面积之比为()A.49B.23C.916D.342.在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是()A.DE∥BC B.∠AED=∠BC.AE:AD=AB:AC D.AE:DE=AC:BC3.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于()A.1 B.2 C.3 D.44.如图,E是矩形ABCD的边CD上的点,BE交AC于O,已知△COE与△BOC的面积分别为2和8,则四边形AOED的面积为()A.16 B.32 C.38 D.405.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为()A.(3,5)B.(3,6)C.(2,6)D.(3,8)6.如图,直线,直线AC分别交,和于点A,B,C,直线DF分别交,和于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为()A.B.2 C.D.7.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的14,那么点B′的坐标是()A.(-2,3)B.(2,-3)C.(3,-2)或(-2,3)D.(-2,3)或(2,-3)8.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足BPAP =APAB,则称点P是AB的黄金分割点,世界上最有名的建筑物中几乎都包含“黄金分割”,若图中AB=8,则BP的长度是()A.12−4√5B.4+4√5C.4√5−4D.2二、填空题9.如图,在Rt△ABC中,∠A=30°,D是斜边AB的中点,G是Rt△ABC的重心,GE⊥AC于点E.若BC=6 cm,则GE= cm.10.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为.的图象11.如图,一次函数y=x+b(b>0)的图象与x轴交于点A,与y轴交于点B,与反比例函数y=8x交于点C,若AB=BC,则b的值为.12.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为.13.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB =7,则AC=.三、解答题14.如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.15.在△ABC中,点D、E、F分别在AC、AB、BC上,且DE=3,BF=4.5,ADAC =AEAB=25求证:EF∥AC.16.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,求BF的长度.17.如图,AB是⊙O的弦,点C是AB⌢的中点,连接BC,过点A作AD∥BC交⊙O于点D.连接CD,延长DA 至E,连接CE,使CD=CE.(1)求证:CE是⊙O的切线;(2)若AB=6,AE=4求AD的长.18.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且ADAC =DFCG.(1)求证:△ADF∽△ACG;(2)若ADAC =12,求AFFG的值.答案1.C2.D3.B4.C5.B6.D7.D8.A9.210.2√5cm11.212.(2.5,5)13.45714.解答:设BE=x∵EF=32,GE=8∴ FG=32-8=24∵平行四边形ABCD∴AD∥BC∴△AFE∽△CBE∴EFEB =AFBC则32x =AD+DFBC=DFBC+1∵DG∥AB∴△DFG∽△CBG∴DFBC =FGBG则DFBC =248+x则32x =248+x+1解得:x=±16(负数舍去)故BE=16.15.证明:∵AD AC=AE AB =25∠DAE =∠CAB ∴△ADE ∽△ACB ∴DE BC =AD AC =25,∠AED =∠B ∴DE ∥BC ∵DE =3 ∴BC =7.5 ∵BF =4.5∴CF =BC −BF =7.5−4.5=3=DE又∵DE ∥CF∴四边形CDEF 是平行四边形 ∴EF ∥CD ,即EF ∥AC .16.解:设BF=x ,则CF=4﹣x ,由翻折的性质得B ′F=BF=x ,当△B ′FC ∽△ABC ,∴B′FAB =CFBC 即x3=4−x 4解得x=127,即BF=127.当△FB ′C ∽△ABC ,∴FB′AB =FCAC 即x3=4−x 4,解得:x=2.∴BF 的长度为:2或127.17.(1)证明:连接OC ,如图所示:∵AB ⌢=AB ⌢,OC 过圆心 ∴OC ⊥AB ∵CD =CE ∴∠E =∠D ∵AD ∥BC ∴∠DAB =∠B ∵∠B =∠D ∴∠B =∠DAB ∴AB ∥EC ∵OC ⊥AB∴OC ⊥EC ∵OC 为半径 ∴CE 是⊙O 的切线(2)解:连接AC ,如图所示:∵AE ∥BC ,AB ∥EC∴四边形AECB 是平行四边形∠ACE =∠CAB ∴EC =AB =6 ∵AC⌢=BC ⌢ ∴∠CAB =∠B ∴∠ACE =∠B ∵∠B =∠D ∴∠D =∠ACE ∵∠E =∠E ∴△CDE ∽△ACE ∴ECAE =ED EC∵EC =6,AE =4 ∴ED =9∴AD =ED −AE =9−4=518.(1)证明:∵∠AED=∠B ,∠DAE=∠DAE ∴∠ADF=∠C ∵AD AC =DFCG ∴△ADF ∽△ACG(2)解:∵△ADF ∽△ACG ∴AD AC = AFAG又∵AD AC =12 ∴AFAG = 12∴AF FG=1。
中考数学总复习《相似》专项提升练习题-附答案

中考数学总复习《相似》专项提升练习题-附答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.如图,在Rt△ABC中,CD是斜边AB上的高,则下列结论正确的是()A.BD= 12AD B.BC2=AB•CD C.AD2=BD•AB D.CD2=AD•BD 2.如图,在△ABC中,∠ACD=∠B,若AD=2,BD=3,则AC长为()A.√5B.√6C.√10D.63.如图,已知AB∥CD∥EF,若AC=6,CE=3,DF=2则BF的长为()A.4 B.4.5 C.5.5 D.64.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AE=3,EC=6,则ADAB的值为()A.12B.13C.14D.165.如图,△ ABC与△ DEF位似,点O是位似中心,若OE=3OB,S△ABC =4,则S△DEF =()A.9 B.12 C.16 D.366.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有()A.0个B.1个C.2个D.3个7.如图,直线y=−x+2与x轴、y轴分别相交于A,B两点,过A,B两点作矩形ABCD,AB=2AD曲在第一象限经过C,D两点,则k的值是()线y=kxA.3 B.6 C.8 D.248.《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF 过点A,且ME=80步,NF=245步,则正方形的边长为()A.140步B.150步C.280步D.300步二、填空题9.已知a=2.4cm,c=5.4cm并且a,b,c,d成比例线段,那么b=cm.10.在△ABC中∠BAC=90°,AD⊥BC垂足为D,AD=3,BD=2则CD的长为.11.如图,在▱ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是.12.如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,点A、B为切点.连接AO并延长交PB 的延长线于点C,过点C作CD⊥PO,交PO的延长线于点D.已知PA=6,AC=8则CD的长为.13.如图,在矩形ABCD中,∠BCD的角平分线CE与边AD交于点E,∠AEC的角平分线与边CB的延长线交于点G,与边AB交于点F,如果AB=3√2,AF=2BF,那么GB= .三、解答题14.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.15.如图,点D为△ABC的边AB的中点,过点D作DE∥BC,交AC于点E,延长DE至点F,使DE=EF,求证:△CFE∽△ABC.16.如图,在梯形ABCD中,DC∥AB,AD=BC,E是DC延长线上的点,连接AE,交BC于点F.(1)求证:△ABF∽△ECF;(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长.17.如图,△ABC和△ADE均为等腰三角形,且∠ABC=∠ADE,AB=BC,AD=DE.(1)求证:△ABC∽△ADE;(2)连接BD、CE,若ABAC =32,△ABD的面积为9,求△ACE的面积.18.在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,利用她所测数据,求旗杆的高.答案1.D2.C3.D4.B5.D6.C7.A8.C9.3.610.9211.2 √312.2√513.2−√214.证明:如图,∵AB∥DE,BC∥EF,CA∥FD,∴四边形AFBC,四边形ABDC,四边形ABCE为平行四边形,∴BF=CA,BD=AC,∴BF=BD;同理可证:AF=AE,CD=CE,∴A,B,C分别是△EFD各边的中点.15.证明:∵点D为△ABC的边AB的中点∴AD=BD∵DE∥BC∴ADBD =AECE,∠ADE=∠B∴AE=CE在△ADE与△CFE中{AE=CE ∠AED=∠CEF DE=EF∴△ADE≌△CFE(SAS)∴∠A=∠ECF,∠ADE=∠F∴∠B=∠F∴△CFE∽△ABC.16.(1)解:∵DC∥AB∴∠B=∠ECF,∠BAF=∠E∴△ABF∽△ECF.(2)解:∵AD=BC,AD=5cm,AB=8cm,CF=2cm ∴BF=3cm.∵由(1)知,△ABF∽△ECF∴BACE =BFCF,即8CE=32.∴CE=163(cm)17.(1)证明:∵AB=BC,AD=DE∴ABAD =BCDE.又∵∠ABC=∠ADE∴△ABC∽△ADE(2)解:∵△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC−∠DAC=∠DAE−∠DAC 即∠BAD=∠CAE∴△BAD∽△CAE,且相似比为ABAC =32∴△ABD与△ACE的面积比为94.∵△ABD的面积为9∴△ACE的面积为4.18.解:设旗杆高AB=x.过F作FG⊥AB于G,交CE于H(如图).因为CE∥AB所以△AGF∽△EHF.因为,FD=1.5,GF=27+3=30,HF=3 所以,EH=3.5-1.5=2,AG=x-1.5. 由△AGF∽△EHF得AGEH =GFHF,即x−1.52=303所以,x-1.5=20解得,x=21.5(米)答:旗杆的高为21.5米。
2023年中考数学一轮专题练习 图形的相似(含解析)

2023年中考数学一轮专题练习 ——图形的相似3一、单选题(本大题共11小题)1. (云南省2022年)如图,在ABC 中,D 、E 分别为线段BC 、BA 的中点,设ABC的面积为S 1,EBD 的面积为S 2.则21S S =( )A .12 B .14 C .34 D .782. (广西百色市2022年)已知△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,则△ABC 与△A 1B 1C 1的面积比( )A .1 :3B .1:6C .1:9D .3:1 3. (广西贺州市2022年)如图,在ABC 中,25DE BC DE BC ==∥,,,则:ADE ABC S S 的值是( )A .325B .425C .25D .35 4. (广西贺州市2022年)某餐厅为了追求时间效率,推出一种液体“沙漏”免单方案(即点单完成后,开始倒转“沙漏”, “沙漏”漏完前,客人所点的菜需全部上桌,否则该桌免费用餐).“沙漏”是由一个圆锥体和一个圆柱体相通连接而成.某次计时前如图(1)所示,已知圆锥体底面半径是6cm ,高是6cm ;圆柱体底面半径是3cm ,液体高是7cm .计时结束后如图(2)所示,求此时“沙漏”中液体的高度为( )A .2cmB .3cmC .4cmD .5cm5. (广西梧州市2022年)如图,以点O 为位似中心,作四边形ABCD 的位似图形''''A B C D ﹐已知'13OAOA ,若四边形ABCD 的面积是2,则四边形''''A B C D 的面积是( )A .4B .6C .16D .186. (贵州省毕节市2022年)矩形纸片ABCD 中,E 为BC 的中点,连接AE ,将ABE △沿AE 折叠得到AFE △,连接CF .若4AB =,6BC =,则CF 的长是( )A .3B .175C .72D .1857. (贵州省贵阳市2022年)如图,在ABC 中,D 是边上的点,,,则与的周长比是()AB B ACD ∠=∠:1:2AC AB =ADC ACB △A .B .C . D.8. (海南省2022年)如图,点(0,3)(1,0)A B 、,将线段AB 平移得到线段DC ,若90,2ABCBC AB ∠=︒=,则点D 的坐标是( )A .(7,2)B .(7,5)C .(5,6)D .(6,5)9. (浙江省金华市2022年)如图是一张矩形纸片ABCD ,点E 为AD 中点,点F 在BC 上,把该纸片沿EF 折叠,点A ,B 的对应点分别为A B A E ''',,与BC 相交于点G ,B A ''的延长线过点C .若23BF GC =,则AD AB的值为( )A .B .C .207D .8310. (黑龙江省哈尔滨市2022年)如图,相交于点E ,,则的长为( )A .32B .4C .D .611. (黑龙江省省龙东地区2022年)如图,正方形ABCD 的对角线AC ,BD 相交于点O ,点F 是CD 上一点,OE OF ⊥交BC 于点E ,连接AE ,BF 交于点P ,连接OP .则下列结论:①AE BF ⊥;②45OPA ∠=︒;③AP BP -=;④若:2:3BE CE =,则4tan 7CAE ∠=;⑤四边形OECF 的面积是正方形ABCD 面积的14.其中正确的结论是( ) 1:21:31:4,,AB CD AC BD ∥1,2,3AE EC DE ===BD 92A .①②④⑤B .①②③⑤C .①②③④D .①③④⑤二、填空题(本大题共11小题)12. (浙江省湖州市2022年)如图,已知在△ABC 中,D ,E 分别是AB ,AC 上的点,DE BC ∥,13AD AB =.若DE =2,则BC 的长是 .13. (浙江省温州市2022年)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M 在旋转中心O 的正下方.某一时刻,太阳光线恰好垂直照射叶片,OA OB ,此时各叶片影子在点M 右侧成线段CD ,测得8.5m,13m MC CD ==,垂直于地面的木棒EF 与影子FG 的比为2∶3,则点O ,M 之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.14. (北京市2022年)如图,在矩形ABCD 中,若13,5,4AF AB AC FC ===,则AE 的长为 .15. (江苏省泰州市2022年)如图上,Δ,90,8,6,ABC C AC BC ∠===中O 为内心,过点O 的直线分别与AC 、AB 相交于D 、E ,若DE=CD+BE ,则线段CD 的长为 .16. (山东省潍坊市2022年)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形A B C D '''',若:2:1A B AB ='',则四边形A B C D ''''的外接圆的周长为 .17. (陕西省2022年)在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做EF 将矩形窗框ABCD 分为上下两部分,其中E 为边AB 的黄金分割点,即2BE AE AB =⋅.已知AB 为2米,则线段BE 的长为 米.18. (浙江省丽水市2022年)一副三角板按图1放置,O 是边()BC DF 的中点,12cm BC =.如图2,将ABC 绕点O 顺时针旋转60︒,AC 与EF 相交于点G ,则FG 的长是 cm .ABCD19. (浙江省杭州市2022年)某项目学习小组为了测量直立在水平地面上的旗杆AB 的高度,把标杆DE 直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC =8.72m ,EF =2.18m .已知B ,C ,E ,F 在同一直线上,AB ⊥BC ,DE ⊥EF ,DE =2.47m ,则AB = m .20. (黑龙江省省龙东地区2022年)在矩形ABCD 中,9AB =,12AD =,点E 在边CD 上,且4CE =,点P 是直线BC 上的一个动点.若APE 是直角三角形,则BP 的长为 .21. (江苏省宿迁市2022年)如图,在矩形ABCD 中,AB =6,BC =8,点M 、N 分别是边AD 、BC 的中点,某一时刻,动点E 从点M 出发,沿MA 方向以每秒2个单位长度的速度向点A 匀速运动;同时,动点F 从点N 出发,沿NC 方向以每秒1个单位长度的速度向点C 匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF ,过点B 作EF 的垂线,垂足为H .在这一运动过程中,点所经过的路径长是 .22. (安徽省2022年)如图,四边形ABCD 是正方形,点E 在边AD 上,△BEF 是以E 为直角顶点的等腰直角三角形,EF ,BF 分别交CD 于点M ,N ,过点F 作AD 的垂线交AD 的延长线于点G .连接DF ,请完成下列问题:H(1)FDG ∠= °;(2)若1DE =,DF =MN = .三、解答题(本大题共8小题)23. (湖南省常德市2022年)在四边形ABCD 中,BAD ∠的平分线AF 交BC 于F ,延长AB 到E 使BE FC =,G 是AF 的中点,GE 交BC 于O ,连接GD .(1)当四边形ABCD 是矩形时,如图,求证:①GE GD =;②BO GD GO FC ⋅=⋅.(2)当四边形ABCD 是平行四边形时,如图,(1)中的结论都成立,请给出结论②的证明.24. (湖北省武汉市2022年)问题提出:如图(1),ABC 中,AB AC =,D 是AC 的中点,延长BC 至点E ,使DE DB =,延长ED 交AB 于点F ,探究AF AB的值.(1)先将问题特殊化.如图(2),当60BAC ∠=︒时,直接写出AF AB的值; (2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.问题拓展:如图(3),在ABC 中,AB AC =,D 是AC 的中点,G 是边BC 上一点,()12CG n BC n=<,延长BC 至点E ,使DE DG =,延长ED 交AB 于点F .直接写出AF AB的值(用含n 的式子表示). 25. (甘肃省金昌市2022年)如图,AB 是O 的直径,AM 和BN 是它的两条切线,过O 上一点E 作直线DC ,分别交AM 、BN 于点D 、C ,且DA =DE .(1)求证:直线CD 是O 的切线;(2)求证:2OA DE CE =⋅26. (湖北省宜昌市2022年)已知菱形ABCD 中,E 是边AB 的中点,F 是边AD 上一点.(1)如图1,连接CE ,CF .CE AB ⊥,CF AD ⊥.①求证:CE CF =;②若2AE =,求CE 的长;(2)如图2,连接CE ,EF .若3AE =,24EF AF ==,求CE 的长.27. (浙江省温州市2022年)如图1,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆于点D ,BE CD ⊥,交CD 延长线于点E ,交半圆于点F ,已知5,3BC BE ==.点P ,Q 分别在线段AB BE ,上(不与端点重合),且满足54AP BQ =.设,BQ x CP y ==.(1)求半圆O 的半径.(2)求y 关于x 的函数表达式.(3)如图2,过点P 作PR CE ⊥于点R ,连结,PQ RQ .①当PQR 为直角三角形时,求x 的值.②作点F 关于QR 的对称点F ',当点F '落在BC 上时,求CF BF ''的值. 28. (江苏省泰州市2022年)已知:△ABC 中,D 为BC 边上的一点.(1)如图①,过点D 作DE ∥AB 交AC 边于点E ,若AB =5,BD =9,DC =6,求DE 的长;(2)在图②,用无刻度的直尺和圆规在AC 边上做点F ,使∠DFA =∠A ;(保留作图痕迹,不要求写作法)(3)如图③,点F 在AC 边上,连接BF 、DF ,若∠DFA =∠A ,△FBC 的面积等于12CD AB •,以FD 为半径作⊙F ,试判断直线BC 与⊙F 的位置关系,并说明理由. 29. (江苏省苏州市2022年)(1)如图1,在△ABC 中,2ACB B ∠=∠,CD 平分ACB ∠,交AB 于点D ,DE //AC ,交BC 于点E .①若1DE =,32BD =,求BC 的长; ②试探究AB BE AD DE-是否为定值.如果是,请求出这个定值;如果不是,请说明理由.(2)如图2,CBG ∠和BCF ∠是△ABC 的2个外角,2BCF CBG ∠=∠,CD 平分BCF ∠,交AB 的延长线于点D ,DE //AC ,交CB 的延长线于点E .记△ACD 的面积为1S ,△CDE 的面积为2S ,△BDE 的面积为3S .若2132916S S S ⋅=,求cos CBD ∠的值.30. (浙江省湖州市2022年)已知在Rt △ABC 中,∠ACB =90°,a ,b 分别表示∠A ,∠B 的对边,a b >.记△ABC 的面积为S .(1)如图1,分别以AC ,CB 为边向形外作正方形ACDE 和正方形BGF C .记正方形ACDE 的面积为1S ,正方形BGFC 的面积为2S .①若19S =,216S =,求S 的值;②延长EA 交GB 的延长线于点N ,连结FN ,交BC 于点M ,交AB 于点H .若FH ⊥AB (如图2所示),求证:212S S S -=.(2)如图3,分别以AC ,CB 为边向形外作等边三角形ACD 和等边三角形CBE ,记等边三角形ACD 的面积为1S ,等边三角形CBE 的面积为2S .以AB 为边向上作等边三角形ABF (点C 在△ABF 内),连结EF ,CF .若EF ⊥CF ,试探索21S S 与S 之间的等量关系,并说明理由.参考答案1. 【答案】B【分析】先判定EBD ABC ,得到相似比为12,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.【详解】解:∵D 、E 分别为线段BC 、BA 的中点, ∴12BE BD AB BC ==, 又∵B B ∠=∠, ∴EBD ABC ,相似比为12, ∴22114S BE S AB ⎛⎫== ⎪⎝⎭, 故选:B .2. 【答案】C【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.【详解】∵△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,∴△ABC 与△A 1B 1C 1的面积比为1:9,故选:C .3. 【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】解:25DE BC DE BC ==∥,,∴ADE ABC , ∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 故选:B .4. 【答案】B【分析】由圆锥的圆锥体底面半径是6cm ,高是6cm ,可得CD =DE ,根据园锥、圆柱体积公式可得液体的体积为63πcm 3,圆锥的体积为72πcm 3,设此时“沙漏”中液体的高度AD =x cm ,则DE =CD =(6-x )cm ,根据题意,列出方程,即可求解.【详解】解:如图,作圆锥的高AC ,在BC 上取点E ,过点E 作DE ⊥AC 于点D ,则AB =6cm ,AC =6cm ,∴△ABC 为等腰直角三角形,∵DE ∥AB ,∴△CDE ∽△CAB ,∴△CDE 为等腰直角三角形,∴CD =DE ,圆柱体内液体的体积为:圆锥的体积为, 设此时“沙漏”中液体的高度AD =x cm ,则DE =CD =(6-x )cm ,∴, ∴,解得:x =3,即此时“沙漏”中液体的高度3cm .故选:B .5. 【答案】D【分析】两图形位似必相似,再由相似的图形面积比等于相似比的平方即可求解.【详解】解:由题意可知,四边形与四边形相似,由两图形相似面积比等于相似比的平方可知:, 又四边形的面积是2,∴四边形的面积为18,故选:D .6. 【答案】D【分析】 连接BF 交AE 于点G ,根据对称的性质,可得AE 垂直平分BF ,BE =FE ,BG =FG =12BF ,根据E 为BC 中点,可证BE =CE =EF ,通过等边对等角可证明∠BFC =90°,利233763cm ππ⨯⨯=2316672cm 3ππ⨯⨯=21(6)(6)72633x x πππ⋅-⋅-=-3(6)27x -=ABCD ''''A B C D ''''22'1139ABCD A B C D S OA S OA ABCD ''''A B C D用勾股定理求出AE,再利用三角函数(或相似)求出BF,则根据FC=算即可.【详解】连接BF,与AE相交于点G,如图,∵将ABE△沿AE折叠得到AFE△∴ABE△与AFE△关于AE对称∴AE垂直平分BF,BE=FE,BG=FG=12 BF∵点E是BC中点∴BE=CE=DF=13 2BC=∴5 AE=∵sinBE BG BAEAE AB ∠==∴341255BE ABBGAE⋅⨯===∴1224 2225 BF BG==⨯=∵BE=CE=DF∴∠EBF=∠EFB,∠EFC=∠ECF∴∠BFC=∠EFB+∠EFC=18090 2︒=︒∴185FC故选 D7. 【答案】B【分析】先证明△ACD∽△ABC,即有,则可得,问题得解.【详解】∵∠B=∠ACD,∠A=∠A,∴△ACD∽△ABC,∴,12AC AD CDAB AC BC===12AC AD CDAB AC BC++=++AC AD CDAB AC BC==∵, ∴, ∴, ∴△ADC 与△ACB 的周长比1:2,故选:B .8. 【答案】D【分析】先过点C 做出轴垂线段CE ,根据相似三角形找出点C 的坐标,再根据平移的性质计算出对应D 点的坐标.【详解】如图过点C 作轴垂线,垂足为点E ,∵∴∵∴在和BCE ∆中,90ABO BCE AOB BEC =⎧⎨==︒⎩∠∠∠∠ , ∴ABO BCE ∆∆∽,∴ , 则 ,22EC OB ==∵点C 是由点B 向右平移6个单位,向上平移2个单位得到,∴点D 同样是由点A 向右平移6个单位,向上平移2个单位得到,∵点A 坐标为(0,3),∴点D 坐标为(6,5),选项D 符合题意,故答案选D9. 【答案】A【分析】12AC AB =12AC AD CD AB AC BC ===12AC AD CD AC AD CD AB AC BC AB AC BC ++====++x x 90ABC ∠=︒90ABO CBE ∠+∠=︒90CBE BCE +=︒∠ABO BCE ABO ∆12AB AO OB BC BE EC ===26BE AO ==令BF =2x ,CG =3x ,FG =y ,易证CGA CFB ''△∽△,得出CG A G CF B F'=',进而得出y =3x ,则AE =4x ,AD =8x ,过点E 作EH ⊥BC 于点H ,根据勾股定理得出EH=,最后求出AD AB的值. 【详解】解:过点E 作EH ⊥BC 于点H ,又四边形ABCD 为矩形,∴∠A =∠B =∠D =∠BCD =90°,AD =BC ,∴四边形ABHE 和四边形CDEH 为矩形,∴AB =EH ,ED =CH , ∵23BF GC =, ∴令BF =2x ,CG =3x ,FG =y ,则CF =3x +y ,2B F x '=,52x y A G -'=, 由题意,得==90CA G CB F ''︒∠∠,又为公共角,∴,∴, 则,整理,得,解得x =-y (舍去),y =3x ,∴AD =BC =5x +y =8x ,EG =3x ,HG =x ,在Rt △EGH 中EH 2+HG 2=EG 2,则EH 2+x 2=(3x )2,解得EH =, EH =-(舍),∴AB =x ,∴.故选:A .GCA '∠CGA CFB ''△∽△CG AG CF B F'='53232x yx x y x-=+()()30x y x y +-=AD AB ==10. 【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长,即可求得BD 的长.【详解】∵∴∴ ∵, ∴∵∴ 故选:C .11. 【答案】B【分析】分别对每个选项进行证明后进行判断:①通过证明得到EC =FD ,再证明得到∠EAC =∠FBD ,从而证明∠BPQ =∠AOQ =90°,即;②通过等弦对等角可证明;③通过正切定义得,利用合比性质变形得到,再通过证明AOP AEC ∽得到OP AE CE AO ⋅=,代入前式得OP AE BP AP BP AO BE⋅⋅-=⋅,最后根据三角形面积公式得到AE BP AB BE ⋅=⋅,整体代入即可证得结论正确;④作EG ⊥AC 于点G 可得EG ∥BO ,根据tan EG EG CAE AG AC CG∠==-,设正方形边长为5a ,分别求出EG 、AC 、CG 的长,可求出3tan 7CAE ∠=,结论错误;⑤将四边形OECF 的面积分割成两个三角形面积,利用()DOF COE ASA ≌,可证明S 四边形OECF =S △COE +S △COF = S △DOF +S △COF =S △COD 即可证明结论正确.【详解】①∵四边形ABCD 是正方形,O 是对角线AC 、BD 的交点,∴OC =OD ,OC ⊥OD ,∠ODF =∠OCE =45°∵OE OF ⊥∴∠DOF +∠FOC =∠FOC +∠EOC =90°∴∠DOF =∠EOC在△DOF 与△COE 中//AB CD ABE CDE ∽AE BE EC DE=1,2,3AE EC DE ===32BE =BD BE ED =+92BD =()DOF COE ASA ≌()EAC FBD SAS ≌AE BF ⊥45OPA OBA ∠=∠=︒tan BE BP BAE AB AP ∠==CE BP AP BP BE ⋅-=ODF OCE OC ODDOF EOC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DOF COE ASA ≌∴EC =FD∵在△EAC 与△FBD 中45EC FD ECA FDB AC BD =⎧⎪∠=∠=︒⎨⎪=⎩∴()EAC FBD SAS ≌∴∠EAC =∠FBD又∵∠BQP =∠AQO∴∠BPQ =∠AOQ =90°∴AE ⊥BF所以①正确;②∵∠AOB =∠APB =90°∴点P 、O 在以AB 为直径的圆上 ∴AO 是该圆的弦∴45OPA OBA ∠=∠=︒所以②正确; ③∵tan BE BP BAE AB AP ∠== ∴AB AP BE BP = ∴AB BE AP BP BE BP --= ∴AP BP CE BP BE-= ∴CE BP AP BP BE⋅-= ∵,45EAC OAP OPA ACE ∠=∠∠=∠=︒ ∴∴ ∴ ∴ ∵1122ABE AE BP AB BE S⋅=⋅= ∴AE BP AB BE ⋅=⋅∴OP AB BE AB AP BP OP AO BE AO⋅⋅-==⋅ 所以③正确;AOP AEC ∽OP AO CE AE =OP AE CE AO⋅=OP AE BP AP BP AO BE ⋅⋅-=⋅④作EG ⊥AC 于点G ,则EG ∥BO , ∴EG CE CG OB BC OC== 设正方形边长为5a ,则BC =5a ,OB =OC, 若:2:3BE CE =,则23BE CE =, ∴233BE CE CE ++= ∴35CE BC =∴35CE EG OB BC =⋅= ∵EG ⊥AC ,∠ACB =45°,∴∠GEC =45°∴CG =EG∴3tan 7EG EG CAE AG AC CG ∠===- 所以④错误;⑤∵()DOF COE ASA ≌,S 四边形OECF =S △COE +S △COF ∴S 四边形OECF = S △DOF +S △COF = S △COD ∵S △COD =∴S 四边形OECF =所以⑤正确;综上,①②③⑤正确,④错误, 故选 B12. 【答案】6【分析】根据相似三角形的性质可得,再根据DE =2,进而得到BC 长. 【详解】 14ABCD S 正方形14ABCD S正方形13DE AD BC AB ==解:根据题意,∵,∴△ADE ∽△ABC ,∴, ∵DE =2, ∴, ∴;故答案为:6.13. 【答案】 10 ;10【分析】过点O 作AC 、BD 的平行线,交CD 于H ,过点O 作水平线OJ 交BD 于点J ,过点B 作BI ⊥OJ ,垂足为I ,延长MO ,使得OK =OB ,求出CH 的长度,根据23EF OM FG MH ==,求出OM 的长度,证明BIO JIB ∽,得出23BI IJ =,49OI IJ =,求出IJ 、BI 、OI 的长度,用勾股定理求出OB 的长,即可算出所求长度.【详解】如图,过点O 作AC 、BD 的平行线,交CD 于H ,过点O 作水平线OJ 交BD 于点J ,过点B 作BI ⊥OJ ,垂足为I ,延长MO ,使得OK =OB ,由题意可知,点O 是AB 的中点,∵OH AC BD ,∴点H 是CD 的中点,∵13m CD =, ∴1 6.5m 2CH HD CD ===, ∴8.5 6.515m MH MC CH =+=+=,又∵由题意可知:23EF OM FG MH ==, ∴2153OM =,解得10m =OM , ∴点O 、M 之间的距离等于10m ,∵BI ⊥OJ ,∴90BIO BIJ ∠=∠=︒,∵由题意可知:90OBJ OBI JBI ∠=∠+∠=︒,又∵90BOI OBI ∠+∠=︒,∴BOI JBI ∠=∠,∴BIO JIB ∽,DE BC ∥13DE AD BC AB ==213BC =6BC =∴23BI OI IJ BI ==, ∴,, ∵, ∴四边形IHDJ 是平行四边形,∴,∵, ∴,,,∵在中,由勾股定理得:,∴,∴,∴,∴叶片外端离地面的最大高度等于,故答案为:10,14. 【答案】1【分析】根据勾股定理求出BC ,以及平行线分线段成比例进行解答即可.【详解】解:在矩形ABCD 中:AD BC ∥,90ABC ∠=︒,∴14AE AF BC FC ==,4BC ==, ∴144AE =, ∴1AE =,故答案为:1.15. 【答案】2或##或2 23BI IJ =49OI IJ =,OJCD OH DJ 6.5m OJ HD ==4 6.5m 9OJ OI IJ IJ IJ =+=+=4.5m IJ =3m BI =2m OI =Rt OBI △222OB OI BI =+OB =OB OK ==(10m MK MO OK =+=(10m 101212【分析】分析判断出符合题意的DE 的情况,并求解即可;【详解】解:①如图,作,,连接OB ,则OD ⊥AC ,∵,∴∵O 为的内心,∴,∴∴,同理,,∴DE=CD+BE ,∵O 为的内心,∴,∴∴∴②如图,作,由①知,,,∵∴ ∴ ∴1061582AB AE AD AC ⋅⨯=== //DE BC OF BC OG AB ⊥⊥,//DE BC OBF BOE ∠=∠ABC ∆OBF OBE ∠=∠BOE OBE ∠=∠BE OE =CD OD=10AB =ABC ∆OF OD OG CD ===BF BG AD AG ==,6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=2CD =DE AB⊥4BE =6AE =ACB AED CAB EAD ∠=∠∠=∠,ABCADE ∆∆AB AD AC AE=∴151822CD AC AD =-=-=∵92DE == ∴19422DE BE CD =+=+= ∴12CD = 故答案为:2或12.16. 【答案】【分析】根据正方形ABCD 的面积为4,求出,根据位似比求出,周长即可得出;【详解】解:正方形ABCD 的面积为4,,,,所求周长;故答案为:.17. 【答案】##【分析】根据点E 是AB 的黄金分割点,可得,代入数值得出答案. 【详解】∵点E 是AB 的黄金分割点,∴. ∵AB=2米,∴米.).18. 【答案】3【分析】BC 交EF 于点N ,由题意得,=90EDF BAC ∠=∠︒,60DEF ∠=︒,30DFE ∠=︒,=45ABC ACB ∠=∠︒,BC =DF =12,根据锐角三角函数即可得DE ,FE ,根据旋转的性质得ONF △是直角三角形,根据直角三角形的性质得3ON =,即3NC =,根据角之间2AB =4A B ''=∴2AB =:2:1A B AB ''=∴4A B ''=∴A C ''==1)15AE BE BE AB ==AE BE BE AB ==1BE =)1的关系得CNG △是等腰直角三角形,即3NG NC ==cm ,根据90FNO FED ∠=∠=︒,30NFO DFE ∠=∠=︒得FON FED △∽△,即ON FN DE DF=,解得FN = 【详解】解:如图所示,BC 交EF 于点N ,由题意得,=90EDF BAC ∠=∠︒,60DEF ∠=︒,30DFE ∠=︒,=45ABC ACB ∠=∠︒,BC =DF =12,在Rt EDF 中,12tan tan 60DF DE EDF ===∠︒12sin sin 60DF EF EDF ===∠︒∵△ABC 绕点O 顺时针旋转60°,∴60BOD NOF ∠=∠=︒,∴90NOF F ∠+∠=︒,∴18090FNO NOF F ∠=︒-∠-∠=︒,∴ONF △是直角三角形, ∴132ON OF ==(cm ), ∴3NC OC ON =-=(cm ),∵90FNO ∠=︒,∴18090GNC FNO ∠=︒-∠=︒,∴NGC 是直角三角形,∴18045NGC GNC ACB ∠=-∠-∠=︒,∴CNG △是等腰直角三角形,∴3NG NC ==cm ,∵90FNO FED ∠=∠=︒,30NFO DFE ∠=∠=︒,∴FON FED △∽△, 即ON FN DE DF=,12FN =,FN =∴3FG FN NG =-=(cm ),故答案为:3.19. 【答案】9.88【分析】根据平行投影得AC ∥DE ,可得∠ACB =∠DFE ,证明Rt △ABC ∽△Rt △DEF ,然后利用相似三角形的性质即可求解.【详解】解:∵同一时刻测得旗杆和标杆在太阳光下的影长分别是BC =8.72m ,EF =2.18m . ∴AC ∥DE ,∴∠ACB =∠DFE ,∵AB ⊥BC ,DE ⊥EF ,∴∠ABC =∠DEF =90°,∴Rt △ABC ∽△Rt △DEF ,∴,即, 解得AB =9.88,∴旗杆的高度为9.88m .故答案为:9.88.20. 【答案】313或154或6 【分析】分三种情况讨论:当∠APE =90°时,当∠AEP =90°时,当∠PAE =90°时,过点P 作PF ⊥DA 交DA 延长线于点F ,即可求解.【详解】解:在矩形ABCD 中,9AB CD ==,12AD BC ==,∠BAD =∠B =∠BCD =∠ADC =90°,如图,当∠APE =90°时,∴∠APB +∠CPE =90°,∵∠BAP +∠APB =90°,∴∠BAP =∠CPE ,∵∠B =∠C =90°,∴△ABP ∽△PCE , ∴AB BP PC CE =,即9124BP BP =-, 解得:BP =6;如图,当∠AEP =90°时,AB BC DE EF =8.722.47 2.18AB=∴∠AED +∠PEC =90°,∵∠DAE +∠AED =90°,∴∠DAE =∠PEC ,∵∠C =∠D =90°,∴△ADE ∽△ECP , ∴AD DE CE PC =,即12944PC-=, 解得:53PC =, ∴313BP BC PC =-=; 如图,当∠PAE =90°时,过点P 作PF ⊥DA 交DA 延长线于点F ,根据题意得∠BAF =∠ABP =∠F =90°,∴四边形ABPF 为矩形,∴PF =AB =9,AF =PB ,∵∠PAF +∠DAE =90°,∠PAF +∠APF =90°,∴∠DAE =∠APF ,∵∠F =∠D =90°,∴△APF ∽△EAD , ∴AF PF DE AD =,即99412AF =-, 解得:154=AF ,即154PB =; 综上所述,BP 的长为313或154或6. 故答案为:313或154或621.【分析】根据题意知EF 在运动中始终与MN 交于点Q ,且 点H 在以BQ 为直径的上运动,运动路径长为的长,求出BQ 及的圆角,运用弧长公式进行计算即可得到结果.【详解】解:∵点、分别是边、的中点,连接MN ,则四边形ABNM 是矩形,∴MN =AB =6,AM =BN =AD ==4,根据题意知EF 在运动中始终与MN 交于点Q ,如图,∵四边形ABCD 是矩形,∴AD //BC ,∴ ∴ ∴ 当点E 与点A 重合时,则NF =, ∴BF =BN +NF =4+2=6,∴AB =BF =6∴是等腰直角三角形,∴∵BP ⊥AF ,∴由题意得,点H 在以BQ 为直径的上运动,运动路径长为长,取BQ 中点O ,连接PO ,NO ,∴∠PON =90°,又∴, AQM FQN ∆∆,:1:2,NQ MQ =PN PN PN M N AD BC 12AQMFQN ∆∆,12NF NQ EM MQ ==123NQ MN ==122AM =ABF ∆45,AFB ∠=︒45PBF ∠=︒PN PN 90,BNQ ∠=︒BQ ===∴, ∴故答案为: 22. 【答案】 45 ;2615【分析】 (1)先证△ABE ≌△GEF ,得FG =AE =DG ,可知△DFG 是等腰直角三角形即可知FDG ∠度数.(2)先作FH ⊥CD 于H ,利用平行线分线段成比例求得MH ;再作MP ⊥DF 于P ,证△MPF ∽△NHF ,即可求得NH 的长度,MN =MH +NH 即可得解.【详解】(1)∵四边形ABCD 是正方形,∴∠A =90°,AB =AD ,∴∠ABE +∠AEB =90°,∵FG ⊥AG ,∴∠G =∠A =90°,∵△BEF 是等腰直角三角形,∴BE =FE ,∠BEF =90°,∴∠AEB +∠FEG =90°,∴∠FEG =∠EBA ,在△ABE 和△GEF 中,A G ABE GEF BE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△GEF (AAS ),∴AE =FG ,AB =GE ,在正方形ABCD 中,AB =ADAD GE ∴=∵AD =AE +DE ,EG =DE +DG ,∴AE =DG =FG ,∴∠FDG =∠DFG =45°.故填:45°.(2)如图,作FH ⊥CD 于H ,12ON OP OQ BQ ===PN∴∠FHD =90°∴四边形DGFH 是正方形,∴DH =FH =DG =2,∴AG FH , ∴=DE DM FH MH, ∴DM =23,MH =43, 作MP ⊥DF 于P ,∵∠MDP =∠DMP =45°,∴DP =MP ,∵DP 2+MP 2=DM 2,∴DP =MP=∴PF∵∠MFP +∠MFH =∠MFH +∠NFH =45°,∴∠MFP =∠NFH ,∵∠MPF =∠NHF =90°,∴△MPF ∽△NHF , ∴=MP PF NH HF,即=NH 332, ∴NH =25, ∴MN =MH +NH =43+25=2615. 故填: 2615. 23. 【答案】(1)证明见详解(2)证明见详解【分析】(1)①证明ADG AEG ≌△即可;②连接BG ,CG ,证明ADG BCG ≌△,BOE GOC ∽△△即可证明;(2)①的结论和(1)中证明一样,证明ADG AEG ≌△即可;②的结论,作DM BC GM ⊥,连接,证明BOE GOM ∽△△即可.(1)证明:①证明过程:四边形ABCD 为矩形,90ABC BAD ∴∠=∠=︒AF 平分BAD ∠45BAF DAF ∴∠=∠=︒ABF ∴为等腰直角三角形AB BF ∴=BE FC =AB BE BF CF AE BC AD ∴+=+==,即AG AG =∴ADG AEG ≌△∴GE GD =②证明:连接BG ,CG ,G 为AF 的中点,四边形ABCD 为矩形,90ABC BAD AD BC ∴∠=∠=︒=,BG AG FG ∴==AF 平分BAD ABF ∠,为等腰直角三角形,45BAF DAF ABG CBG ∴∠=∠=︒=∠=∠∴ADG BCG ≌△∴ADG BCG ∠=∠ADG AEG ≌△E ADG ∴∠=∠E BCG ∴∠=∠BOE GOC ∠=∠BOE GOC ∴∽△△BO GO GO BO BE GC GD CF∴=== ∴BO GD GO FC ⋅=⋅ (2)作DM BC BC M GM GN DM DM N ⊥⊥交于,连接,作交于点,如图所示90DMB GNM GND DMC ∴∠=︒=∠=∠=∠由(1)同理可证:ADG AEG ≌△E ADG ∴∠=∠四边形ABCD 为平行四边形AD BC ∴∥90ADM DMC ∴∠=∠=︒BC GN AD ∴∥∥G 为AF 的中点,由平行线分线段成比例可得DN MN =DG MG ∴=,,GDM GMDADG BMG EBOE GOM ∠=∠BOE GOM ∴∽△△BO GO GO BO BE GM GD CF∴=== ∴BO GD GO FC ⋅=⋅ 24. 【答案】(1)[问题提出](1)14;(2)见解析 (2)[问题拓展]24n - 【分析】[问题探究](1)根据等边三角形的性质结合已知条件,求得30ADF ADB ∠=∠=︒,90AFD ∠=︒,根据含30度角的直角三角形的性质,可得111,222AF AD AD AC AB ===,即可求解; (2)取BC 的中点H ,连接DH .证明DBH DEC △≌△,可得BH EC =,根据DH AB ∥,证明EDH EFB △∽△,根据相似三角形的性质可得32FB EB DH EH ==,进而可得14AF AB =;[问题拓展]方法同(2)证明DBH DEC△≌△,得出,GH EC,证明EDH EFB△∽△,得到2+2FB EB nDH EH==,进而可得AFAB=24n-.(1)[问题探究]:(1)如图,ABC中,AB AC=,D是AC的中点,60BAC∠=︒,ABC∴是等边三角形,12AD AB=30ABD DBE∴∠=∠=︒,60A∠=︒,DB DE∴=,30E DBE∴∠=∠=︒,180120DCE ACB∠=︒-∠=︒,18030ADF CDE E DCE∴∠=∠=︒-∠-∠=︒,60A∠=︒,90AFD∴∠=︒,12AF AD∴=,1124ADAFAB AB∴==.(2)证明:取BC的中点H,连接DH.∵D是AC的中点,∴DH AB∥,12DH AB=.∵AB AC=,∴DH DC=,∴DHC DCH ∠=∠.∵BD DE =,∴DBH DEC ∠=∠.∴BDH EDC ∠=∠.∴DBH DEC △≌△.∴BH EC =. ∴32EB EH =. ∵DH AB ∥,∴EDH EFB △∽△. ∴32FB EB DH EH ==. ∴34FB AB =. ∴14AF AB =. (2)[问题拓展]如图,取BC 的中点H ,连接DH .∵D 是AC 的中点,∴DH AB ∥,12DH AB =. ∵AB AC =,∴DH DC =,∴DHC DCH ∠=∠.∵DE DG =,∴DGH DEC ∠=∠.∴GDH EDC ∠=∠.∴DGH DEC ≌.∴GH EC . HE CG ∴=()12CG nBC n=<BC nCG ∴=()1BG n CG ∴=-,()1111222n CE GH BC BG nCG n CG CG ⎛⎫==-=--=- ⎪⎝⎭∴1221+22nCG EB BC CE n n EH EH n C CG G ⎛⎫-+++==== ⎪⎝⎭. ∵DH AB ∥,∴EDH EFB △∽△. ∴2+2FB EB n DH EH ==. ∴24FB n AB +=. ∴42244AF n n AB ---==. ∴AF AB =24n -. 25. 【答案】(1)见解析;(2)见解析【分析】(1)连接OD ,OE ,证明△OAD ≌△OED ,得∠OAD=∠OED=90°,进而得CD 是切线;(2)连接OC ,得AM ∥BN ,得,DEOOEC ∆∆,再证明2.OE DE CE =•,进而得出结论2.OA DE CE =•.【详解】解(1)如图,连接,OE OD 、 DA 是O 的切线,90OAD ︒∠= 在AOD ∆和EOD ∆中, , ,,OA OE DA DE OD OD ===()AOD EOD SSS ∴∆∆≌90,OAD OED ︒∴∠=∠=,OE CD ∴⊥CD ∴是O 的切线.(2)连接,OC AM BN DC 、、是O 的切线,90OAD OBC DEO OEC ︒∴∠=∠=∠=∠=//,AM BN ∴180ADE BCE ︒∴∠+∠=又AM BN DC 、、是O 的切线,CE CB ∴=,OD 平分,ADE OC ∠平分, .BCE ∠()111809022ODE OCE ADE BCE ︒︒∴∠+∠=∠+∠=⨯=又90ODE DOE ︒∠+∠=,OCE DOE ∴∠=∠又90DEO OEC ︒∠=∠=,,DEO OEC ∴∆∆OE DE CE OE∴= 2.OE DE CE ∴=•又,OA OE =2.OA DE CE ∴=•26. 【答案】(1)①见解析;②CE =(2)6EC =【分析】(1)①根据AAS 可证得:BEC DFC ≌△△,即可得出结论; ②连接AC ,可证得ABC是等边三角形,即可求出CE =(2)延长FE 交的延长线于点,根据可证得,可得出,,,则,即可证得,即可得出的长. (1)(1)①∵,,∴,∵四边形是菱形,∴,,∴()BEC DFC AAS ≌,∴CE CF =.②如图,连接AC .∵E 是边AB 的中点,CE AB ⊥,∴BC AC =,又由菱形ABCD ,得BC AB =,∴ABC 是等边三角形,∴60EAC ∠=︒,CB M AAS AEF BEM ≌4ME =2BM =8MC =MB ME =12ME MC =MEB MCE △∽△EC CE AB ⊥CF AD ⊥90BEC DFC ∠=∠=︒ABCD B D ∠=∠BC CD =在Rt AEC 中,2AE =,∴tan 60EC AE =︒=∴CE =(2)如图,延长FE 交CB 的延长线于点M ,由菱形ABCD ,得AD BC ∥,AB BC =,∴AFE M ∠=∠,A EBM ∠=∠,∵E 是边AB 的中点,∴AE BE =,∴()AEF BEM AAS △≌△,∴=ME EF ,MB AF =,∵3AE =,24EF AF ==,∴4ME =,2BM =,3BE =,∴26BC AB AE ===,∴8MC =, ∴2142MB ME ==,4182ME MC ==, ∴MB ME ME MC=,而M ∠为公共角. ∴MEB MCE △∽△, ∴24BE MB EC ME ==, 又∵3BE =,∴6EC =.27. 【答案】(1)(2) (3)①或;② 【分析】 (1)连接OD ,设半径为r ,利用,得,代入计算即可; (2)根据CP =AP 十AC ,用含x 的代数式表示 AP 的长,再由(1)计算求AC 的长即可;(3)①显然,所以分两种情形,当 时,则四边形RPQE 是矩形,当 ∠PQR =90°时,过点P 作PH ⊥BE 于点H , 则四边形PHER 是矩形,分别根据图形可得答案;②连接,由对称可知,利用三角函数表示出和BF 的长度,从而解决问题.(1)解:如图1,连结.设半圆O 的半径为r .∵切半圆O 于点D ,∴.∵,∴,∴,∴, 即, ∴,即半圆O 的半径是. (2) 由(1)得:. 1585544y x =+972111199△∽△COD CBE OD CO BE CB =90PRQ ∠<︒90RPQ ∠=︒,AF QF ',45QF QF F QR EQR ∠∠'=='=︒BF 'OD CD OD CD ⊥BE CD ⊥OD BE ∥△∽△COD CBE OD CO BE CB =535r r -=158r =1581555284CA CB AB =-=-⨯=∵, ∴. ∵,∴. (3)①显然,所以分两种情况. ⅰ)当时,如图2.∵,∴.∵,∴四边形为矩形,∴.∵, ∴, ∴. ⅱ)当时,过点P 作于点H ,如图3,则四边形是矩形,∴.∵,∴.5,4AP BQ x BQ ==54AP x =CP AP AC =+5544y x =+90PRQ ∠<︒90RPQ ∠=︒PR CE ⊥90ERP ∠=︒90E ∠=︒RPQE PR QE =333sin 544PR PC C y x =⋅==+33344x x +=-97x =90PQR ∠=︒PH BE⊥PHER ,PH RE EH PR ==5,3CB BE ==4CE ==∵, ∴3PH RE x EQ ==-=, ∴45EQR ERQ ∠=∠=︒, ∴45PQH QPH ∠=︒=∠, ∴3HQ HP x ==-, 由EH PR =得:33(3)(3)44x x x -+-=+, ∴2111x =. 综上所述,x 的值是97或2111. ②如图4,连结,AF QF ',由对称可知QF QF =',F QR EQR ∠=∠' ∵BE ⊥CE ,PR ⊥CE , ∴PR ∥BE , ∴∠EQR =∠PRQ , ∵BQ x =,5544CP x =+, ∴EQ =3-x , ∵PR ∥BE , ∴CPR CBE △∽△, ∴CP CB CR CE=, 即:x CR +=555444, 解得:CR =x +1, ∴ER =EC -CR =3-x , 即:EQ = ER∴∠EQR =∠ERQ =45°, ∴45F QR EQR ∠=∠='︒ ∴90BQF ∠='︒, 4cos 15CR CP C y x =⋅==+∴4tan 3QF QF BQ B x ==⋅='. ∵AB 是半圆O 的直径,∴90AFB ∠=︒, ∴9cos 4BF AB B =⋅=, ∴4934x x +=, ∴2728x =, ∴319119CF BC BF BC BF BF BF x -==''''=-='-. 28. 【答案】(1)2(2)图见详解(3)直线BC 与⊙F 相切,理由见详解【分析】(1)由题意易得23CD BD =,则有,然后根据相似三角形的性质与判定可进行求解;(2)作DT ∥AC 交AB 于点T ,作∠TDF =∠ATD ,射线DF 交AC 于点F ,则点F 即为所求;(3)作BR ∥CF 交FD 的延长线于点R ,连接CR ,证明四边形ABRF 是等腰梯形,推出AB =FR ,由CF ∥BR ,推出,推出CD ⊥DF ,然后问题可求解.(1)解:∵DE ∥AB ,∴,∴, ∵AB =5,BD =9,DC =6,∴, ∴;(2)解:作DT ∥AC 交AB 于点T ,作∠TDF =∠ATD ,射线DF 交AC 于点F ,则点F 即为所求;如图所示:点F 即为所求,25CD CB =1122CFB CFR SS AB CD FR CD ==⋅=⋅CDE CBA ∽DECD AB CB 6569DE =+2DE =(3)解:直线BC 与⊙F 相切,理由如下:作BR ∥CF 交FD 的延长线于点R ,连接CR ,如图,∵∠DFA =∠A ,∴四边形ABRF 是等腰梯形,∴,∵△FBC 的面积等于, ∴, ∴CD ⊥DF ,∵FD 是⊙F 的半径,∴直线BC 与⊙F 相切.29. 【答案】(1)①94BC =;②AB BE AD DE -是定值,定值为1;(2)3cos 8CBD ∠= 【分析】(1)①证明CED CDB ∽,根据相似三角形的性质求解即可;②由DE AC ∥,可得AB BC AD DE =,由①同理可得CE DE =,计算AB BE AD DE-1=; (2)根据平行线的性质、相似三角形的性质可得12S AC BC S DE BE==,又32S BE S CE =,则1322S S BC S CE ⋅=,可得916BC CE =,设9BC x =,则16CE x =.证明CDB CED ∽△△,可得12CD x =,过点D 作DH BC ⊥于H .分别求得BD BH ,,进而根据余弦的定义即可求解.【详解】(1)①∵CD 平分ACB ∠,AB FR =12CD AB •1122CFB CFR S S AB CD FR CD ==⋅=⋅2∵2ACB B ∠=∠,∴ACD DCB B ∠=∠=∠. ∴32CD BD ==. ∵DE AC ∥,∴ACD EDC ∠=∠.∴EDC DCB B ∠=∠=∠.∴1CE DE ==.∴CED CDB ∽. ∴CE CD =CD CB. ∴94BC =. ②∵DE AC ∥, ∴AB BC AD CE=. 由①可得CE DE =, ∴AB BC AD DE=. ∴1AB BE BC BE CE AD DE DE DE DE-=-==. ∴AB BE AD DE -是定值,定值为1. (2)∵DE AC ∥,BDE BAC ∴∽△△BC AB AC BE BD DE ∴== ∴12S AC BC S DE BE==. ∵32S BE S CE=, ∴1322S S BC S CE⋅=. 又∵2132916S S S ⋅=, ∴916BC CE =. 设9BC x =,则16CE x =.∵CD 平分BCF ∠,2∵2BCF CBG ∠=∠,∴ECD FCD CBD ∠=∠=∠.∴BD CD =.∵DE AC ∥,∴EDC FCD ∠=∠.∴EDC CBD ECD ∠=∠=∠.∴CE DE =.∵DCB ECD ∠=∠,∴CDB CED ∽△△. ∴CD CB CE CD=. ∴22144CD CB CE x =⋅=.∴12CD x =.如图,过点D 作DH BC ⊥于H .∵12BD CD x ==, ∴1922BH BC x ==. ∴932cos 128x BH CBD BD x ∠===. 30. 【答案】(1)①6;②见解析 (2)2114S S S -=,理由见解析 【分析】(1)①将面积用a ,b 的代数式表示出来,计算,即可②利用AN 公共边,发现△FAN ∽△AN B ,利用FA AN AN NB=,得到a ,b 的关系式,化简,变形,即可得结论(2)等边ABF 与等边CBE △共顶点B ,形成手拉手模型,△ABC ≌△FBE ,利用全等的对应边,对应角,得到:AC =FE =b ,∠FEB =∠ACB =90°,从而得到∠FEC =30°,再利用Rt CFE △,cos30FE b CE a ︒===,得到a 与b 的关系,从而得到结论 (1)∵19S =,216S =∴b =3,a =4∵∠ACB =90° ∴11S ab 34622==⨯⨯= ②由题意得:∠FAN =∠ANB =90°,∵FH ⊥AB∴∠AFN =90°-∠FAH =∠NAB∴△FAN ∽△AN B ∴FA AN AN NB = ∴a b a a b+=, 得:22ab b a +=∴122S S S +=.即212S S S -= (2)2114S S S -=,理由如下: ∵△ABF 和△BEC 都是等边三角形∴AB =FB ,∠ABC =60°-∠FBC =∠FBE ,CB =EB∴△ABC ≌△FBE (S A S )∴AC =FE =b∠FEB =∠ACB =90°∴∠FEC =30°∵EF ⊥CF ,CE =BC =a∴cos30b FE a CE ==︒=∴b =∴212S ab ==由题意得:21S ,22S =∴22221S S -== ∴2114S S S -=。
中考数学专题训练:相似三角形(附参考答案)

中考数学专题训练:相似三角形(附参考答案)1.若a3=b2,则a+bb的值为( )A.32B.53C.52D.232.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )A.3 B.4C.5 D.63.如图,AD∥BE∥FC,直线l1,l2分别与三条平行线交于点A,B,C和点D,E,F.若AB=3,BC=5,DF=12,则EF的长为( )A.4.5 B.6C.7.5 D.84.如图,小雅同学在利用标杆BE测量建筑物的高度时,测得标杆BE高1.2 m,又知AB∶BC=1∶8,则建筑物CD的高是( )A.9.6 m B.10.8 mC.12 m D.14 m5.如图,在平面直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3,2).现以原点O为位似中心,在第一象限内作与△ABC的相似比为2的位似图形△A′B′C′,则顶点C′的坐标是( )A.(2,4) B.(4,2)C.(6,4) D.(5,4)6.如图(单位:mm),小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字高度为72.7 mm,当测试距离为3 m时,最大的“E”字高度为( )A.121.17 mm B.43.62 mmC.29.08 mm D.4.36 mm7.如图,AC是□ABCD的对角线,点E在CD的延长线上,连接BE分别交AC,AD 于点F,G,则下列式子一定正确的是( )A.AFCF =AGDGB.ABCE=CFAFC.BFFG =EFBFD.ADDG=ABDE8.如图,在△ABC中,D,E分别为边AB,AC上的点,试添加一个条件:________________________,使得△ADE与△ABC相似.(任意写出一个满足的条件即可)9.如图,已知在梯形ABCD中,AD∥BC,S△ABDS△BCD =12,则S△BOCS△BCD=______.10.如图,在矩形ABCD中,若AB=3,AC=5,AFFC =14,则AE的长为_____.11.如图,为了测量山坡的护坡石坝高,把一根长为4.5 m 的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为________m.12.已知在平面直12角坐标系中,△AOB的顶点分别为A(2,1),B(2,0),O(0,0).若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为__________________________.13.如图,在△ABC中,点D,E分别是AB,AC的中点.若S△ADE=2,则S△ABC=_____.14.如图,在平面直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是____________.15.如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.(1)求证:△ABC∽△DEC;(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.16.如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE =2AE,BE交AD于点F,则△AFE面积的最大值是______.17.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布前形成倒立的实像CD(点A,B的对应点分别是C,D).若物体AB的高为6 cm,小孔O到物体和实像的水平距离BE,CE分别为8 cm,6 cm,则实像CD的高度为________cm.18.如图,在正方形ABCD中,点E是边CD上一点,连接BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连接AF,有以下五个结论:①∠ABF=∠DBE;②△ABF∽△DBE;③AF⊥BD;④2BG2=BH·BD;⑤若CE∶DE=1∶3,则BH∶DH=17∶16.你认为其中正确的是____________.(填写序号)19.已知,如图1,若AD是△ABC中∠BAC的内角平分线,通过证明可得ABAC =BDCD,同理,若AE是△ABC中∠BAC的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在△ABC中,BD=2,CD=3,AD是△ABC的内角平分线,则△ABC的BC边上的中线长l的取值范围是_____________.20.如图,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB 上,且CF=BE,AE2=AQ·AB.求证:(1)∠CAE=∠BAF;(2)CF·FQ=AF·BQ.21.在等腰三角形ABC中,AB=AC,点D是边BC上一点(不与点B,C重合),连接AD.(1)如图1,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE=________.(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.①在图2中补全图形;②探究CD与BE的数量关系,并证明.(3)如图3,若ABBC =ADDE=k,且∠ADE=∠C,试探究BE,BD,AC之间满足的数量关系,并证明.参考答案1.C 2.B 3.C 4.B 5.C 6.B 7.C8.ADAB =AEAC(答案不唯一) 9.2310.1 11.2.712.(4,2)或(-4,-2)13.8 14.(4,2) 15.(1)证明略(2)EC=916.43 17.4.5 18.①②③④ 19.12<l<25220.(1)证明略(2)证明略21.(1)30°(2)①图略②CD与BE的数量关系为CD=BE,证明略(3)AC=k(BD+BE),证明略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点名称:相似三角形得性质
•相似三角形性质定理:
(1)相似三角形得对应角相等。
(2)相似三角形得对应边成比例。
(3)相似三角形得对应高线得比,对应中线得比与对应角平分线得比都等于相似比。
(4)相似三角形得周长比等于相似比。
(5)相似三角形得面积比等于相似比得平方。
(6)相似三角形内切圆、外接圆直径比与周长比都与相似比相同,内切圆、外接圆面积比就是
相似比得平方
(7)若a/b =b/c,即b2=ac,b叫做a,c得比例中项
(8)c/d=a/b 等同于ad=bc、
(9)不必就是在同一平面内得三角形里
①相似三角形对应角相等,对应边成比例、
②相似三角形对应高得比,对应中线得比与对应角平分线得比都等于相似比、
③相似三角形周长得比等于相似比
定理推论:
推论一:顶角或底角相等得两个等腰三角形相似。
推论二:腰与底对应成比例得两个等腰三角形相似。
推论三:有一个锐角相等得两个直角三角形相似。
推论四:直角三角形被斜边上得高分成得两个直角三角形与原三角形都相似。
推论五:如果一个三角形得两边与其中一边上得中线与另一个三角形得对应部分成比例,那么
C A
B D O E F 第1题图 E A F
图5 这两个三角形相似。
推论六:如果一个三角形得两边与第三边上得中线与另一个三角形得对应部分成比例,那么这两个三角形相似。
一、选择题
1、(青海)如图,DEF △就是由ABC △经过位似变换得到得,点O 就是位似中
心,D E F ,,分别就是OA OB OC ,,得中点,则DEF △与ABC △得面积比就是
( ) A.1:6 B.1:5 C.1:4 D.1:2
2、(山东烟台)如图,在Rt △ABC 内有边
长分别为,,a b c 得三个正方形,则,,a b c 满足得关系式就是( )
A 、b a c =+
B 、b ac =
C 、222b a c =+
D 、22b a c ==
3、(广东茂名市)如图,△ABC 就是等边三角形,被一平行于BC 得矩形所截,
AB 被截成三等分,则图中阴影部分得面积就是△ABC 得面积得 ( ) A.
91 B.92 C.31 D.94 4、(江西南昌)下列四个三角形,与左图中得三角形相似得就是( )
二、填空题
5、 (上海市)如图5,平行四边形ABCD 中,E 就是边BC 上得点,AE 交BD 于点F ,如果
23BE BC =, 那么BF FD = . 6、(浙江温州)如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且(第4题) A. B. C. D. E H
F
G C B
A
((第3题图) (第6题图)
O A 1 A 2 A 3 A 4 A
B
1 B
2 B
3 1
4
图8 A B C
D A C B (B ) D 1(D 2) A C
E
F B 2 1D 1 D 2 112233A B A B A B ∥∥,213243A B A B A B ∥∥.若212A B B △,323A B B △得面积分别为1,4,则图中三个阴影三角形面积之与
为 .
7、(南宁市)如图4,已知AB ⊥BD,ED ⊥BD,C 就是线段BD 得中点,且AC ⊥CE,ED=1,BD=4,
那么AB=
8、(年广东梅州市) 如图8,要测量A 、B 两点间距离,在O 点打桩,取OA 得中点 C ,OB
得中点D ,测得CD =30米,则AB =______米.
9、(新疆建设兵团)如图,一束光线从y 轴上点A (0,1)发出,经过x 轴上点C 反射后,经过点B (6,2),则光线从A 点到B 点经过得路线得长度为 .(精确到0、01)
三、证明题
10、(遵义)(14分)如图(1)所示,一张平行四边形纸片ABCD,AB=10,AD=6,BD=8,沿对角线BD 把这张纸片剪成△AB 1D 1与△CB 2D 2两个三角形(如图(2)所示),将△AB 1D 1沿直线AB 1方向移动(点B 2始终在AB 1上,AB 1与CD 2始终保持平行),当点A 与B 2重合时停止平移,在平移过程中,AD 1与B 2D 2交于点E,B 2C 与B 1D 1交于点F,
(1)当△AB 1D 1平移到图(3)得位置时,试判断四边形B 2FD 1E 就是什么四边形?并证明您得结论;
(2)设平移距离B 2B 1为x,四边形B 2FD 1E 得面积为y,求y 与x 得函数关系式;并求出四边形B 2FD 1E 得面积得最大值; (3)连结B 1C(请在图(3)中画出)。
当平移距离B 2B 1得值就是多少时,△ B 1B 2F 与△ B 1CF 相似?
一.1、C,2、A,3、C,4、B 二.5、 2/3, 6、 10、5, 7、 4, 8、 60, 9、 6、71 三.10、解:(1) 四边形B 2FD 1E 就是矩形。
因为△AB 1D 1平移到图(3)得,所以四边形B 2FD 1E 就是一个平行四边形,又因为在平行四边形ABCD 中,AB=10,AD=6,BD=8,则有∠ADB 就是直角。
所以四边形B 2FD 1E 就是矩形。
(2)因为三角形B 1B 2F 与三角形AB 1D 1相似,则有B 2F=
2153B B =0、6X,B 1F=2154B B =0、8x 所以s B 2FD 1E =B 2F ×D 1
F=0、6X × (8-0、8x)=4、8x-0、48x 2 即y=4、8x-0、48x 2
=12-0、48(x-5)
当x=5时,y=12就是最大得值。
(3)要使△ B 1B 2F 与△ B 1CF 相似,则有FC F B F B F B 112= 即0.6X)-(60.6X 0.8X 0.6X = 解之得:x=3、6。
