有限元划分网格的基本原则
有限元网格划分

1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
采用疏密不同的网格划分,既可以保持相当的计算精度,又可使网格数量减小。
因此,网格数量应增加到结构的关键部位,在次要部位增加网格是不必要的,也是不经济的。
划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采用较均匀的钢格形式。
这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
第07讲-有限元网格划分的基本原则及技巧

7-6
网格疏密
• • 网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分 布特点。 在计算数据变化梯度较大的部位(如应力集中处、几何形状、材料、厚度变化的 位置),为了较好地反映数据变化规律,需要采用比较密集的网格。而在计算数 据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。这样,整 个结构便表现出疏密不同的网格划分形式。—— 网格数量应增加在结构的关键 部位,在次要部位增加网格是不必要的,也是不经济的。 边界上最好要在8个单元以上,至少不少于4个; 分析结果完成后,需要检查以下各项,误差较大的位置要进行细分: 单元应力的连续性,比较相邻单元应力值的差值; 应力偏差:结点上的单元结点应力和结点平均应力的差值的较大值; 当以上差值与其中的最大应力的比值较大时,该位置的网格需要细分。
精度 计算时间 精确解 1 2 O
7-4
•
•
P
网格数量
网格数量(续)
在决定网格数量时应考虑分析数据的类型。 实体单元:
• •
1、在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。如 果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。 2、在响应计算中,计算应力响应所取的网格数应比计算位移响应多。 3、在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较 少的网格,如果计算的模态阶次较高,则应选择较多的网格。
左图中(a)、(b)改 变了结构质量的对称分 布,应避免。 (c)是 比较理想的结果。
(a)
7-8
(b)
(c)
单元的形状及评价
• 形状比(长边与短边距离之比) 一般实体单元的长宽比越大,分析误差也越大。 对于板壳单元,评价应力为主时不宜超过1:3,评价位移为主时不宜超过1:5; 对于块体单元,评价应力为主时不宜超过1:2,评价位移为主时不宜超过1:3; 在应力分布几乎没有变化的区域里使用的单元,适当放大也没问题。 倾角(表示单元偏离直角四边形的程度(Angular Deviation)) 四边形的内倾角最好是在45度~135度之间,不要超过15度~165度。 锥度(限于四边形) 用几何偏离(Geometric Deviation)表示四边形单元的变形程度。
Deform网格划分原则及方法

[原]Deform网格划分原则及方法2009-04-04 23:48引言:划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍网格划分时的一些基本原则及方法。
关键词:Deform 网格局部细化一、网格划分的原则1 网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线,曲线2代表计算时间随网格数量的变化。
可以看出,网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1 位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2 网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
小圆孔附近存在应力集中,采用了比较密的网格。
板的四周应力梯度较小,网格分得较稀。
有限元网格划分的基本原则与通用方法

有限元网格划分的基本原则与通用方法本文首先研究和分析有限元网格划分的基本原则,再对当前典型网格划分方法进行科学地分类,结合实例系统地分析各种网格划分方法的机理、特点及其适用范围,如映射法、基于栅格法、节点连元法、拓扑分解法、几何分解法和扫描法等。
最后阐述当前网格划分的研究热点,综述六面体网格和曲面网格划分技术,展望有限元网格划分的发展趋势。
引言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素,在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯 (Gauss) 积分,而壳、板、梁单元的厚度方向采用辛普生 (Simpson) 积分。
有限元网格划分基本原则有限元方法的基本思想是将结构离散化,即对连续体进行离散化,利用简化几何单元来近似逼近连续体,然后根据变形协调条件综合求解。
所以有限元网格的划分一方面要考虑对各物体几何形状的准确描述,另一方面也要考虑变形梯度的准确描述。
为正确、合理地建立有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1. 网格数量网格数量直接影响计算精度和计算时耗,网格数量增加会提高计算精度,但同时计算时耗也会增加。
当网格数量较少时增加网格,计算精度可明显提高,但计算时耗不会有明显增加;当网格数量增加到一定程度后,再继续增加网格时精度提高就很小,而计算时耗却大幅度增加。
所以在确定网格数量时应权衡这两个因素综合考虑。
2. 网格密度为了适应应力等计算数据的分布特点,在结构不同部位需要采用大小不同的网格。
在孔的附近有集中应力,因此网格需要加密;周边应力梯度相对较小,网格划分较稀。
由此反映了疏密不同的网格划分原则:在计算数据变化梯度较大的部位,为了较好地反映数据变化规律,需要采用比较密集的网格;而在计算数据变化梯度较小的部位,为减小模型规模,网格则应相对稀疏。
有限元网格划分和收敛性
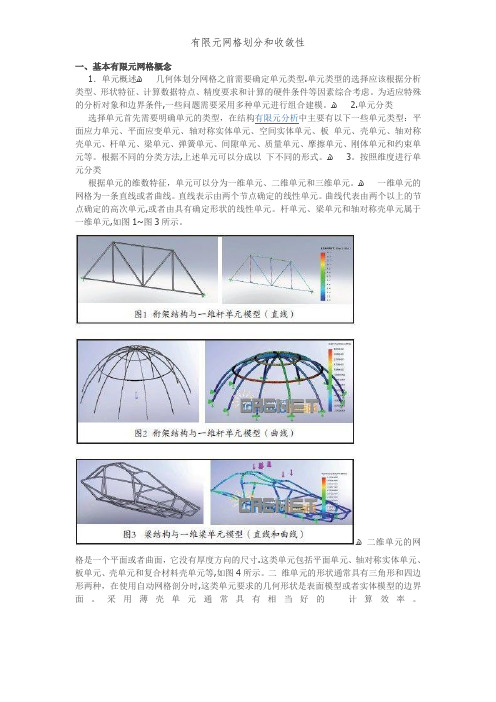
一、基本有限元网格概念1.单元概述ﻫ几何体划分网格之前需要确定单元类型.单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
ﻫ 2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
ﻫ3。
按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
ﻫ一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
ﻫ二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸.这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
ﻫﻫ三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示.在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
ﻫ4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面.这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模.但是由于单元位移函数是线性的,单元内的位移呈线性变化,而应力是常数,因此会造成单元间的应力不连续,单元边界上存在着应力突变,如图6所示。
有限元分析网格单元的选用原则

收稿日期:2020-05-13 作者简介:杨俊生(1987—),男,硕士,研究方向:机械设计及结构有限元分析与应用。
Copyright©博看网 . All Rights Reserved.
·36·
有限元分析网格单元的选用原则
总 715 期第十七期 2020 年 6 月
河南科技 Journal of Henan Science and Technology
信息技术
有限元分析网格单元的选用原则
杨俊生
(法雷奥汽车空调湖北有限公司,湖北 荆州 434000)
摘 要:有限元分析可以对企业产品设计做出快速响应,有效节省昂贵的现场试验费用,缩短产品开发周期,
三结点二次空间梁 单元 B32
杂交单元 B32H、 开口截面 B32OS
注:在连续体单元类型中,楔形单元并未列出,当实体划分六面体单元时,采用平滑过渡,允许少量使用楔形体单元,在实际运用中不推荐将实体划分为 楔形体单元,各单元的几何描述请参见 Abaqus 帮助文件。
Abstract: Finite element analysis can quickly respond to enterprise product design, effectively save expensive field test costs, shorten product development cycles, and advance time to market. This paper summarized the grid cell types, qualified evaluation indicators and selection principles, and selected the best grid cell type for different analy⁃ sis types to avoid repeated redundant cycles. Practical cases show that a reasonable choice of grid type can effectively shorten the solution cycle. Keywords: grid cell type;gridding;conformity assessment;selection principle;solution period
ANSYS网格划分原则

ANSYS有限元网格划分的基本原则默认分类 2009-05-20 13:56:46 阅读508 评论0 字号:大中小订阅1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则。
在选用单元时要注意剪力自锁、沙漏和网格扭曲、不可压缩材料的体积自锁等问题ANSYS软件平台提供了网格映射划分和自由适应划分的策略。
有限元复习题及答案.pdf

有限元课程习题1、试简要阐述有限元分析的基本步骤主要有哪些。
有限元分析的主要步骤主要有:1、结构的离散化2、单元分析。
选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力与位移的关系、根据虚功原理建立节点力与节点位移的关系(单元刚度方程)3、等效节点载荷计算4、整体分析,建立整体刚度方程2、有限元网格划分的基本原则是什么?提出图示网格划分中不合理的地方。
有限元划分网格的基本原则是:1、拓朴正确性原则。
即单元间是靠单元顶点、或单元边、或单元面连接2、几何保形原则。
即网格划分后,单元的集合为原结构近似3、特性一致原则。
即材料相同,厚度相同4、单元形状优良原则。
单元边、角相差尽可能小5、密度可控原则。
即在保证一定精度的前提下,网格尽可能稀疏一些(a)单元间没有考虑节点相联(b)网格形状太差,单元边长相差太大(c)没有考虑对称性,单元边长相差太大3、分别指出图示平面结构划分为什么单元?有多少个节点?多少个自由度?(a)桁架结构模型• 划分为杆单元, 8个节点,12个自由度出师表两汉:诸葛亮先帝创业未半而中道崩殂,今天下三分,益州疲弊,此诚危急存亡之秋也。
然侍卫之臣不懈于内,忠志之士忘身于外者,盖追先帝之殊遇,欲报之于陛下也。
诚宜开张圣听,以光先帝遗德,恢弘志士之气,不宜妄自菲薄,引喻失义,以塞忠谏之路也。
宫中府中,俱为一体;陟罚臧否,不宜异同。
若有作奸犯科及为忠善者,宜付有司论其刑赏,以昭陛下平明之理;不宜偏私,使内外异法也。
侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下:愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰“能”,是以众议举宠为督:愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
亲贤臣,远小人,此先汉所以兴隆也;亲小人,远贤臣,此后汉所以倾颓也。
先帝在时,每与臣论此事,未尝不叹息痛恨于桓、灵也。
有限元网格划分

本文讨论了有限元网格的重要概念,包括单元的分类、有限元误差的分类与影响因素;并讨论分析结果的收敛性控制方法,并由实例说明了网格质量及收敛性对取得准确分析结果的重要性。
同时讨论了一些重要网格控制的建议及其他网格设定的说明。
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
3.按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
《2024年有限元网格剖分与网格质量判定指标》范文

《有限元网格剖分与网格质量判定指标》篇一一、引言有限元法是一种广泛应用于工程和科学计算中的数值分析方法。
其核心步骤之一是进行网格剖分,即将求解域划分为一系列小的、相互连接的子域或元素。
网格的质量直接影响到有限元分析的准确性和效率。
因此,本文将重点讨论有限元网格剖分的方法以及网格质量的判定指标。
二、有限元网格剖分1. 网格剖分的基本原则有限元网格剖分应遵循以下基本原则:一是尽可能保持单元的规则性,如六面体单元;二是确保网格的连续性和兼容性;三是考虑网格的适应性,以适应求解域的几何形状和边界条件;四是尽可能减少单元的数量,以节省计算资源。
2. 常见的网格剖分方法(1)自动剖分法:利用计算机程序自动进行网格剖分,如基于Delaunay三角化的剖分方法。
(2)映射法:将求解域映射到参数空间进行剖分,再映射回原空间得到网格。
(3)手动剖分法:根据求解域的几何形状和边界条件,手动进行网格剖分。
三、网格质量判定指标1. 单元形态指标(1)扭曲度(Skewness):用于衡量单元的形状与理想形状的偏差程度,扭曲度越大,单元的形状越不规则,影响计算的精度和效率。
(2)内角分布:单元的内角应尽可能接近标准值(如四边形单元为90度),内角分布的均匀性可以反映单元的规则性。
(3)面积/体积变化率:用于衡量单元尺寸变化对整体网格的影响,变化率越小,网格质量越好。
2. 连接性指标(1)节点连接数:每个节点的连接单元数应适中,过多或过少的连接都可能导致计算误差。
(2)相邻单元的协调性:相邻单元在公共边界上应具有良好的协调性,避免出现不连续或重复的单元边界。
3. 整体性指标(1)网格均匀性:整体网格的尺寸和密度应保持均匀,避免出现过大或过小的单元。
(2)边界拟合度:网格应尽可能贴合求解域的边界,提高边界条件的准确性。
四、结论有限元网格剖分是有限元法的重要步骤之一,而网格质量直接影响到有限元分析的准确性和效率。
本文介绍了有限元网格剖分的基本原则和常见方法,以及网格质量的判定指标。
ANSYS有限元网格划分浅析

ANSYS有限元网格划分浅析有限元分析作为现代工程设计领域中不行或缺的工具,旨在通过对复杂结构进行数值模拟,猜测其力学行为和性能。
而有限元网格划分作为有限元分析的前提条件,直接影响着分析结果的准确性和计算效率。
本文将对ANSYS有限元网格划分的原理和技巧进行浅析,并探讨其在工程设计中的应用。
一、有限元网格划分的基本原理有限元网格划分是将连续物体离散化成有限个离散单元,构建有限元模型的过程。
其原理主要涉及两个方面:几何划分和节点生成。
1.1 几何划分几何划分是将实际结构划分为有限单元的过程,主要包括自动划分和手动划分两种方式。
自动几何划分是ANSYS通过对实际结构进行自动网格划分的功能,依据用户指定的几何参数进行自适应划分,最大程度地保持结构的准确外形。
这种划分方法具有快速、高效的优点,特殊适用于复杂结构的网格划分。
手动几何划分是由用户通过手动操作构建网格划分,使用ANSYS提供的几何划分工具进行几何实体的划分和组合,依据结构外形和特点进行网格划分的方式。
这种划分方法需要用户具备一定的几何划分技巧和阅历,能够对结构进行合理的划分。
1.2 节点生成节点生成是指依据坐标系和几何划分,自动生成有限元网格中的节点坐标。
在划分完成后,节点将依据有限元单元的外形和尺寸进行生成。
节点生成过程中主要包括节点编号、坐标值和自由度的定义。
节点编号是为每个节点赐予唯一的标识,便利在后续分析中进行节点相关的计算;坐标值是节点在几何坐标系中的坐标值,用于描述节点在空间中的详尽位置;自由度的定义是为节点定义相应的位移或位移的导数,用于后续求解分析中的节点位移计算。
二、ANSYS有限元网格划分的技巧2.1 网格密度的控制网格密度是指网格单元数目与结构体积之比,其决定了有限元模型对结构细部行为的描述能力。
合理控制网格密度能够提高分析结果的准确性和计算效率。
一般来说,细节丰富的区域应接受较小的网格单元,而结构较简易的区域可以接受较大的网格单元。
2+有限元法的基本概念与求解方法

a11x1+ a12x2 +…+ a1nxn =b1 a21x1+ a22x2 +…+ a2nxn =b2 …………
an1x1+ an2x2 +…+ annxn =bn 当其系数行列式 A 不等于零时
A
上述的方程组有唯一解:
x j
j
A
(a11 ann系数) (j=1,2…n)
其中 A 是将A中第j列元素替换为右端项而得到的行列式 j
综上所述,三角形常应变单元属于协调元
位移函数与形函数
面积坐标
面积坐标是利用三角形的面积关系表示三角形单元任一点位置 的一种方法。优点:简明,方便。
位移函数与形函数
面积坐标
对于图中三角形单元任一点P(x , y)可用下三个比值来确定:
l i ,l j ,l m
i
j
m
Li , Lj , Lm 称为P点的面积坐标,显然面积坐标具有以下性质: 性质1. Li + Lj + Lm =1 ( i+ j + m = )
性质2. 平行于三角形jm边的直线上所有点其Li相同 AB变化时, hi’不变, 故i不变, Li 不变
位移函数与形函数
面积坐标
性质3. Li =1 Lj =0 Lm =0 (i) Li =0 Lj =1 Lm =0 (j) Li =0 Lj =0 Lm =1 (m)
性质4. Li = Lj = Lm=1/3 在三角形形心处 面积坐标与形函数的关系:
结构离散化: 1)网格划分 将结构划分为有限个单元; 2)载荷移置 将作用在结构上的非节点载荷等效地移置为节点载荷; 3)简化约束 把结构边界上的约束,用适当的节点约束代替。
有限元网格划分方法与基本原理

结构有限元分析中的网格划分技术及其应用实例结构有限元分析中的网格划分是否直接关系到解算的效果。
本文简述了网格划分应用的基本理论,并以空间自由曲面覆盖件和大型整体网络钢筋壳体产品的有限元分析中的网格划分为实例对象,详细讲述了空间自由和三维实体的网格划分基本理论及其在工程中的实际应用,非常具有现实意义和借鉴价值。
一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法。
Pro/E和S oildWorks是特征参数化造型的代表,而 CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。
现有CAD软件对表面形态的表示法已经大大超过了CAE软件,因此,在将CAD实体模型导入CAE软件的过程中,必须将CAD模型中其他表示法的表面形态转换到CAE软件的表示法上,转换精度的高低取决于接口程序的好坏。
在转换过程中,程序需要解决好几何图形(曲线与曲面的空间位置)和拓扑关系(各图形数据的逻辑关系)两个关键问题。
其中几何图形的传递相对容易实现,而图形间的拓扑关系容易出现传递失败的情况。
数据传递面临的一个重大挑战是,将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。
有限元网格划分原理

有限元网格划分原理
有限元网格划分原理是一种用于计算领域离散化的数值方法。
它将连续的领域划分为有限数量的小单元,每个小单元称为有限元。
这些有限元可被视为数学模型中的局部区域,其内部的物理过程可以被近似为线性或非线性的形式。
有限元网格划分原理的目标是将整个领域划分为足够多的有限元,以便能够准确地描述所研究的问题。
划分时需要考虑几何形状、边界条件、计算资源等因素,以获取一个高效且准确的离散模型。
通常,将整个领域划分为小单元可以更好地逼近真实物理过程,并提供对系统行为的详细理解。
在有限元网格划分过程中,首先确定领域的几何形状和边界条件。
然后,选择适当的离散化方法,将领域划分为小单元,如三角形、四边形、六边形或四面体。
每个小单元内的变量以形函数的形式进行逼近,形函数可根据问题的特点进行选择。
一旦完成网格划分,就可以在每个有限元中设置数学方程,在整个领域上建立一个代数系统。
该系统由一系列线性或非线性方程组组成,其中每个方程对应于一个小单元。
通过求解这些方程,可以获得在整个领域中变量的近似解。
有限元网格划分原理的核心思想是将复杂问题转化为简单的局部问题,并通过将领域划分为小单元来近似描述整个系统。
通过调整网格大小和形状,可以调整计算精度和效率。
因此,有限元网格划分原理是计算力学、结构力学、流体力学等领域中常用的数值方法之一。
网格划分方法

Total number of elements:197
电子科技大第7学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
电子科技大第8学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
有限元分析与建模 Finite Element Analysis and Modeling
第16章 网 格 划 分 方 法
第一节 网格划分原则
划分什么样的网格?
第二节 网格划分方法
怎样划分网格?
电子科技大第1学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
二、网格疏密 ( relative density)
(a) 一阶振型
(b) 二阶振型
电子科(c) 三技阶振第型大1学5页机/共械48电页(d)子四阶工振型程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
电子科技大第3学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling 在相同网格数量下,位移计算精度高于应力计算精度
电子科技大第4学页机/共械48电页 子工程学院
2013,10
有限元分析与建模
ANSYS网格划分总结大全

有限元分析中的网格划分好坏直接关系到模型计算的准确性.本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素.从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的.同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分.辛普生积分点的间隔是一定的,沿厚度分成奇数积分点.由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则.在选用单元时要注意剪力自锁、沙漏和网格扭曲、不可压缩材料的体积自锁等问题ANSYS软件平台提供了网格映射划分和自由适应划分的策略。
有限元计算单元网格划分

有限元语言及编译器(Finite Element Language And it’s Compiler,以下简称FELAC) 是中国科学院数学与系统科学研究院梁国平研究院于1983年开始研发的通用有限元软件平 台,是具有国际独创性的有限元计算软件,是PFEPG系列软件三十年成果(1983年—2013 年)的总结与提升,有限元语言语法比PFEPG更加简练,更加灵活,功能更加强大。目前 已发展到2.0版本。其核心采用元件化思想来实现有限元计算的基本工序,采用有限元语 言来书写程序的代码,为各领域,各类型的有限元问题求解提供了一个极其有力的工具。 FELAC可以在数天甚至数小时内完成通常需要一个月甚至数月才能完成的编程面或体单元过渡
1)从小单元到大单元过渡时,应使同一节点所连接的单元不致相差太大,避免突然过渡现象。 通常用计算结果调整,保证同一节点所连接的单元精度值至少在0.1以下。单元精度值根据单元内节 点应力与节点平均应力的误差计算。
2)难于过度处最好使用过渡单元,过渡单元的使用要比用同一单元勉强过渡的计算结果要好。 例如:对于复杂体结构间的过渡,最好使用“金子塔”单元过渡。 (5)面或体转接部位的单元 几何模型圆角过渡处的单元划分,根据弧长对应的圆心角和半径确定,对于半径为3mm左右、 圆心角大于90度的转接弧长,通常至少要划分3~4个单元。 (6)高应力区的单元 对高应力区,要进行网格细分应力稳定性计算。即采用多次局部网格细分并进行计算,当前、 后两次计算结果满足所需的精度要求时(通常要求小于0.03)确定网格。 总之,几何模型网格划分时,要在单元类型、单元形态、单元大小、单元过渡和局部应力稳定 等方面下功夫,才能满足工程上的精度要求,达到预期的结果。
有限元网格划分的基本原则

有限元网格划分的基本原则划分网格是建立有限元模型的一个重要环节,它要求考虑的题目较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、公道的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1网格数目。
网格数目的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数目增加,计算精度会有所进步,但同时计算规模也会增加,所以在确定网格数目时应权衡两个因数综合考虑。
2网格疏密。
网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
3单元阶次很多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可进步计算精度,由于高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构外形不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数目相同的情况下由高阶单元组成的模型规模要大得多,因此在使用时应权衡考虑计算精度和时间。
4网格质量网格质量是指网格几何外形的公道性。
质量好坏将影响计算精度。
质量太差的网格甚至会中止计算。
直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等份点四周的网格质量较好。
网格质量可用细长比、锥度比、内角、翘曲量、拉伸值、边节点位置偏差等指标度量。
划分网格时一般要求网格质量能达到某些指标要求。
在重点研究的结构关键部位,应保证划分高质量网格,即使是个别质量很差的网格也会引起很大的局部误差。
而在结构次要部位,网格质量可适当降低。
5网格分界面和分界点结构中的一些特殊界面和特殊点应分为网格边界或节点以便定义材料特性、物理特性、载荷和位移约束条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元网格划分的基本原则
划分网格是建立有限元模型的一个重要环节,它要求考虑的题目较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、公道的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1网格数目
网格数目的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数目增加,计算精度会有所进步,但同时计算规模也会增加,所以在确定网格数目时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数目收敛的一般曲线,曲线2代表计算时间随网格数目的变化。
可以看出,网格较少时增加网格数目可以使计算精度明显进步,而计算时间不会有大的增加。
当网格数目增加到一定程度后,再继续增加网格时精度进步甚微,而计算时间却有大幅度增加。
所以应留意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,假如两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1位移精度和计算时间随网格数目的变化
在决定网格数目时应考虑分析数据的类型。
在静力分析时,假如仅仅是计算结构的变形,网格数目可以少一些。
假如需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,假如计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2网格疏密
网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
小圆孔四周存在应力集中,采用了比较密的网格。
板的四周应力梯度较小,网格分得较稀。
其中图b中网格疏密相差更大,它比图a中的网格少48个,但计算出的孔缘最大应力相差1%,而计算时间却减小了36%。
由此可见,采用疏密不同的网格划分,既可以保持相当的计算精度,又可使网格数目减小。
因此,网格数目应增加到结构的关键部位,在次要部位增加网格是不必要的,也是不经济的。
图2带孔方板的四分之一模型
划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采
用较均匀的钢格形式。
这是由于固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
3单元阶次
很多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可进步计算精度,由于高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构外形不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数目相同的情况下由高阶单元组成的模型规模要大得多,因此在使用时应权衡考虑计算精度和时间。
图3是一悬臂梁分别用线性和二次三角形单元离散时,其顶端位移随网格数目的收敛情况。
可以看出,但网格数目较少时,两种单元的计算精度相差很大,这时采用低阶单元是分歧适的。
当网格数目较多时,两种单元的精度相差并不很大,这时采用高阶单元并不经济。
例如在离散细节时,由于细节尺寸限制,要求细节四周的网格划分很密,这时采用线性单元更合适。
图3不同阶次单元的收敛情况
增加网格数目和单元阶次都可以进步计算精度。
因此在精度一定的情况下,用高阶单元离散结构时应选择适当的网格数目,太多的网格并不能明显进步计算精度,反而会使计算时间大大增加。
为了兼顾计算精度和计算量,同一结构可以采用不同阶次的单元,即精度要求高的重要部位用高阶单元,精度要求低的次要部位用低阶单元。
不同阶次单元之间或采用特殊的过渡单元连接,或采用多点约束等式连接。
4网格质量
网格质量是指网格几何外形的公道性。
质量好坏将影响计算精度。
质量太差的网格甚至会中止计算。
直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等份点四周的网格质量较好。
网格质量可用细长比、锥度比、内角、翘曲量、拉伸值、边节点位置偏差等指标度量。
划分网格时一般要求网格质量能达到某些指标要求。
在重点研究的结构关键部位,应保证划分高质量网格,即使是个别质量很差的网格也会引起很大的局部误差。
而在结构次要部位,网格质量可适当降低。
当模型中存在质量很差的网格(称为畸形网格)时,计算过程将无法进行。
图4是三种常见的畸形网格,其中a单元的节点交叉编号,b单元的内角大于180°,c单元的两对节点重合,网格面积为零。
图4几种常见的畸形网格
5网格分界面和分界点
结构中的一些特殊界面和特殊点应分为网格边界或节点以便定义材料特性、物理特性、载荷和位移约束条件。
即应使网格形式满足边界条件特点,而不应让边界条件来适应网格。
常见的特殊界面和特殊点有材料分界面、几何尺寸突变面、分布载荷分界线(点)、集中载荷作用点和位移约束作用点等。
图5是具有上述几种界面的结构及其网格划分形式。
图5特殊界面和特殊点网格划分
6位移协调性
位移协调是指单元上的力和力矩能够通过节点传递相邻单元。
为保证位移协调,一个单元的节点必须同时也是相邻单元的节点,而不应是内点或边界点。
相邻单元的共有节点具有相同的自由度性质。
否则,单元之间须用多点约束等式或约束单元进行约束处理。
图6是两种位移不协调的网格划分,图a中的节点1仅属于一个单元,变形后会产生材料裂缝或重叠。
图b中的平面单元和梁单元节点的自由度性质不同,粱单元的力矩无法传递到平面单元。
图6位移不协调的网格划分
7网格布局
当结构外形对称时,其网格也应划分对称网格,以使模型表现出相应的对称特性(如集中质矩阵对称)。
不对称布局会引起一定误差,如在图7中,悬臂粱截面相对y轴对称,在对称载荷作用下,自由端两对称节点1、2的挠度值本应相等。
但若分图b所示的不对称网格,计算出的y1=0.0346,y2=0.0350。
若改用图c所示的网格,则y1和y2完全相同。
图7网格布局对计算结果的影响
8节点和单元编号
节点和单元的编号影响结构总刚矩阵的带宽和波前数,因而影响计算时间和存储容量的大小,因此公道的编号有利于进步计算速度。
但对复杂模型和自动分网而言,人为确定公道的编号很困难,目前很多有限元分析软件自带有优化器,网格划分后可进行带宽和波前优化,从而减轻人的劳动强度。
