流速流量习题
流体力学习题解答4

习 题 四1. 油(μ=3⨯103-kg/m*s )和水(μ=1.14⨯103-kg/m*s )在管径d=100mm 的圆管中流动,如果压力降相同,流态都是层流,试求这两种流动中管轴线上的流速之比。
2. 动力粘度μ=0.072kg/m*s 的油在管径d=0.1m 的圆管中作层流运动,流量Q=3⨯103-m 3/s ,试计算管壁切应力τ0。
3. 水(运动粘度υ=106-m2/s )在直径d=200mm ,长l=20m 的圆管流动,流量Q=24⨯103-m 3/s ,如果管壁粗糙度∆=0.2mm ,求沿程水头损失。
4. 圆管直径d=80mm ,当流量很大时,测得沿程损失系数是一个常数,其值为λ=0.025,试计算管壁的粗糙度∆。
5. 一条管道,新使用时,相当粗糙度∆/d=104-,使用多年后,发现在水头损失相同的情况下,流量减少了35%,试估算此旧管的相对粗糙度。
6. 如图,串联管道由两段管组成,其长度和直径分别为l 1=500m ,d 1=300mm ,l 2=400m ,d 2=250mm ,壁面粗糙度都是∆=0.6mm ,水位H=10m ,如果沿程损失系数按阻力平方区计算,求流量Q 。
11题图7. 一段水管,长l=150m ,流量Q=0.12 m 3/s ,该管段内总的局部损失系数为ζ=5,沿程损失系数那λ=3.002.0d计算,如果要求水头损失h=3.96m ,求管径d 。
8. 为了测量截面突然扩大的局部损失系数ζ和管道沿程损失系数λ,在管道三个截面上装有测压管,其中测压管1在扩大前端,其余两个测压管等距离地安装在下游,已知三支测压管液面读数为h 1=156.5mm, h 2=163mm, h 3=113mm ,管径d=15mm ,D=20mm ,长度l=100mm ,测得流量Q=2.65⨯104-m 3/s ,求ζ和λ的值。
15题图9. 一条输油管道,直径d=250mm ,长l=6.5km ,壁面粗糙度∆=0.8mm ,流量Q=0.06 m 3/s ,油的运动粘度υ=2.4⨯106-m 2/s ,求沿程损失。
第一章 流体流动 习题

第一二章习题一、选择题1.如图示,某直管管路,阀门A、B全开时,截面1和截面2的测压管液面高为h1和h2,液体先后流经A、B阀,若关小A阀,h1___↓____; h2____↓____, h1-h2____↓____;若A阀不变,关小B阀,h1__↑_____; h2____↑____, h1-h2____↓____.2.管路上装一阀门,减小开度,则流量流速___↓___;液体流经总阻力损失_____不变__;直管阻力___↓__,局部阻力___↑____。
3.水由敞口恒液位的高位槽通过一管道流向压力恒定的反应器,当管道上的阀门开度减小后,水流量将___↓____;管道总阻力损失__不变______;摩擦系数______不变___(如在阻力平方区)。
4.有一并联管路,如图所示,两段管路的流量、流速、管径、管长、流动阻力损失分别为V1 V2 u1 u2 d1 d2 L1 L2 hf1 hf2 ,及d1=2d2, L1=2L2,则(1)hf1/ hf2=_____1___(2)当两段管路中流动均为滞流时,V1/ V2=____8___; u1/ u2=___2____(3)当两段管路中流动均为湍流时,并取相同的摩擦系数,V1/V2=_4____; u1/ u2=___1___5. 水在下图管道中流动,流量为42.4m3/h,A B两截面的内径分别为dA=50mm, dB=100mm,AB两截面的压强计读数为pA=53.5 kPa, pB=60kPa,那么水流动的方向是由___A___流向__B_______.6. 敞口容器底部有一(出)进水管,如图,容器内水面保持恒定,管内水流动速度头为0.5m水柱,(1)对a,水由容器流入管内,则2点的表压p2=__0.75_ m水柱____(2)对b,水由水管流入容器,则2点的表压p2=__1 m水柱______7. 在下面两种情况下,假如流体流量不变,而圆形直管如果直径减少1/2,则因直管阻力而引起的压强降为原来的________A 如两种情况都为层流 16倍B 两种情况均在阻力平方区,且认为摩擦系数为常数. 32倍8. 某流体在直管中作层流流动,在流速不变的情况下,管长管径同时增加一倍,其阻力损失为原来的 ___1/2______.9. 流体在一圆形直管中流动,平均流速0.5m/s,压降强为10Pa,Re为1000, 则管中心处点速度为____1m/s____;若流速增到1 m/s,则压强降为___20______Pa.10. 因次分析法的基础为是__因次一致性原则和π定理11.流体流动的直管阻力hf,当层流流动时,hf=d a u b L c,则a=__-2__, b=__1__,c=__1___.当完全湍流时,a=_-1_, b=__2__,c=_1.12.图中高位槽液面保持恒定,液体以一定的流量流经等径管路,ab与cd两段长度相等,管径与管壁粗糙度相同(1)U型压差计读数___B____A R1>R2BR1=R2CR1<R2D不确定(2) 液体通过ab与cd段能量损失B_A h ab> h cd B h ab = h cd C h ab < hcd D 不确定(3)ab与cd段的压差CA△Pab>△Pcd B △Pab= △Pcd C△Pab< △Pcd D不确定(4)R1值表示CAab段的压差值Bab段的位能变化Cab段的流动能量损失Dab段压差与流动能量损失之和.13 如图所示垂直管中,水自下而上流动,测压点ab间有一阀门,ab间垂直距离为h,指示液为汞,则压强差Pa-Pb的计算式为:A(ρHg-ρ水)gR B(ρHg -ρ水)gR+ρ水gh C(ρHg -ρ水)gR-ρ水ghD(ρHg -ρ水)gR+ρHg gh14. 如图所示,若水槽液位不变,123点的流体的总机械能的关系为________(认为水槽内流动速度为0)当阀门打开时,B当阀门关闭时,CA 1>2>3 B 1=2>3 C 1=2=3 D 1>2=315 离心泵的调节阀开大时,则___B_____A 吸入管路的阻力损失不变B泵出口的压力变小C泵入口处的真空度减少D泵工作点的扬程升高16.离心泵在一定的管路系统工作,如被输送的液体密度发生变化(其余性质不变),则___D___A任何情况下扬程与密度无关B只有当Z1=Z2时,扬程与密度无关C只有当阻力损失为0时扬程与密度无关D只有当P1-P2=0是扬程与密度无关17. 如在测定离习泵的性能曲线时,错误地将压力表安装在调节阀后,则操作时,压力表读数(表压P2)将_____D____A随真空表读数的增大而减小B随流量的增大而减小C 随泵实际的扬程的增大而增大D 随流量的增大而增大18.往复泵在操作中____A____A 不开旁路阀,流量与出口阀开度无关 B允许安装高度与流量无关C 流量与转速无关D 开启旁路阀后,输入设备中的液体流量与出口阀开度无关。
流体流动习题课

2 1
2 2
实际流体流动过程中的柏努利方程
2 m u12 m p1 m u2 m p2 m gz m Qe m We m gz2 m Wf 1 2 2
2 u12 p1 u 2 p2 或 : gz1 Qe We gz2 Wf 2 2
实验证明,流体在管内稳定流动时,当Re≤______时, 流动类型为滞流,滞流时的摩 擦系数λ与______成反比, 而与管壁的_______无关;湍流时,当Re一定,则λ随 ε/d的增加而_________。
2000;Re;粗糙度;增大
P/(ρg)的物理意义是表示流动系统某截面处单 位____流体所具有的静压能,称为__________。
5.离心泵吸入口压强为30 KPa,当地大气 压强为100 KPa,则泵吸入口真空表的读数 为 。 A.130 KPa B.70 KPa C.65 KPa B D.30 KPa 6.可压缩流体在等径水平直管中流动时,下 列说法正确的是 。 A.流体的平均流速为定值; B B.流体的质量流量为定值; C.流体的体积流量为定值; D.流体的体积流量、质量流量均为定值。
qv , m / h
3
例:水在一倾斜管中流动,如附图所示, 已知压差计读数为200mm,试问测量段 的阻力为多少? 解:在两测压孔之间列柏努利方程式:
u P u P2 1 z1 z2 Hf 2 g g 2 g g
2 u12 u2 P P2 H f ( z1 z2 ) ( ) ( 1 ) 2g 2g g g
连通的、同一液体、同一水平面。
某液体在套管环隙内流动,大管规格为φ56×3mm,小 管规格为φ30 ×2.5mm,液体粘度为1mN· 2,密度为 s/m 1000kg/m3,流速为1m/s则该液体在套管环隙内流动 的Re=_________。
热工基础题

热工基础复习题一、名词解释压缩性、膨胀性、粘性、静压强、流速、流量、流态、压头、煤的低热值、空气过剩系数黑体、温度场、辐射能力、灰体、温度梯度、黑度、角系数、绝对湿度湿含量、露点、二、填空:1、()称为液体的粘性。
2、平衡流体中某点静压强的方向()其作用面,其大小与()无关。
3、流体运动的两种状态是()和(),其判别式是(),判别标准是()。
4、流体在管路中流动时阻力损失有()和()。
5、流体最基本的特性是()。
6、服从()定律的流体称为牛顿型流体。
7、按流速和压强等物理参数是否随时间变化可把流体的运动分为()和()两类。
8、流体在外力作用下改变自身容积的特性,称为(),通常用()来表示流体这种性能。
9、()称为流体的密度。
气体的密度与温度和压力的关系式为()。
10、牛顿粘性定律的数学表达式为(),公式中的负号表示()。
11、静压强的国际单位为(),绝对压强与表压强的关系为()。
一封闭容器内盛有空气,测得容器内的绝对压强为5000Pa,则容器内的真空度为( )。
12、流体在管内作层流流动时,流速在管道截面上按()分布,最大流速与平均速度的关系为()。
13、有一变截面的自来水管,已知直径d1=100毫米处的断面平均流速为w1=1米/秒,则直径d2=200毫米处的断面平均流速为(w2=)。
14、气体垂直流动的原则是()。
15、风机采用联合工作方式来增加流量时,若( )应采用串联,若( )应用并联。
16、叶轮是风机的主要工作部件,起着()的作用。
17、离心风机按叶片的安装角度的大小范围可分为()、()、()三种型式。
18、离心风机应当()闸门启动,因为()。
19、通风管道特性是指()。
20、H-Q曲线上相应于效率最高之点,称为风机或泵的()。
21、离心风机主要由()和()组成。
22、任何一系列几何相似的通风机的比转数都是一个(),并且其大小又综合地反映出该系列的通风机在最高效率点运行时的()、()、及()三者之间的关系。
流体流动练习题

流体流动练习题在学习流体力学的过程中,进行练习题是巩固理论知识的重要途径。
本文将为大家提供一些流体流动的练习题,通过解答这些问题,帮助读者更好地掌握流体力学的基本概念和计算方法。
题目一:水管中的流量计算在水管中,水的流速为2 m/s,管道的截面积为0.2 m²,求水管中的流量。
解析:流量的计算公式为Q=A×V,其中Q表示流量,A表示管道的截面积,V表示水的流速。
根据给定条件,代入公式可得:Q=0.2 m²× 2 m/s = 0.4 m³/s。
因此,水管中的流量为0.4立方米/秒。
题目二:狭缝中的流速计算一个狭缝的宽度为0.1 mm,狭缝中的液体通过速度为0.5 m/s,求液体通过狭缝时的流速。
解析:狭缝中的流速计算可以使用泊松公式:V=Q/A,其中V表示流速,Q表示流量,A表示狭缝的横截面积。
根据给定条件,流量Q=0.1 mm × 0.5 m/s = 0.05 mm²/s。
由于1 mm²=10⁻⁶ m²,所以流量Q=0.05 × 10⁻⁶ m²/s。
代入公式可得:V = (0.05 × 10⁻⁶ m²/s) / (0.1 ×10⁻³ m²) = 0.5 m/s。
因此,液体通过狭缝时的流速为0.5 m/s。
题目三:贯流管中的压力计算贯流管的入口直径为10 cm,出口直径为5 cm,入口处的压力为1 MPa,求出口处的压力。
解析:贯流管中的压力计算可以使用伯努利方程:P₁ + (1/2)ρV₁²+ ρgh₁ = P₂ + (1/2)ρV₂² + ρgh₂,其中P₁和P₂分别表示入口和出口处的压力,V₁和V₂分别表示入口和出口处的速度,ρ表示液体的密度,g表示重力加速度,h₁和h₂分别表示入口和出口处的高度。
根据问题的描述,入口处的压力P₁为1 MPa,入口和出口处的高度相同,速度V₁和V₂与流体的密度无关,因此可以将伯努利方程简化为:P₁+ (1/2)ρV₁² = P₂ + (1/2)ρV₂²。
流速计算

请教:已知管道直径D,管道内压力P,能否求管道中流体的流速和流量?怎么求已知管道直径D,管道内压力P,还不能求管道中流体的流速和流量。
你设想管道末端有一阀门,并关闭的管内有压力P,可管内流量为零。
管内流量不是由管内压力决定,而是由管内沿途压力下降坡度决定的。
所以一定要说明管道的长度和管道两端的压力差是多少才能求管道的流速和流量。
对于有压管流,计算步骤如下:1、计算管道的比阻S,如果是旧铸铁管或旧钢管,可用舍维列夫公式计算管道比阻s=0.001736/d^5.3 或用s=10.3n2/d^5.33计算,或查有关表格;2、确定管道两端的作用水头差H=P/(ρg),),H 以m为单位;P为管道两端的压强差(不是某一断面的压强),P以Pa为单位;3、计算流量Q:Q = (H/sL)^(1/2)4、流速V=4Q/(3.1416d^2)式中:Q―― 流量,以m^3/s为单位;H――管道起端与末端的水头差,以m^为单位;L――管道起端至末端的长度,以m为单位。
管道中流量与压力的关系管道中流速、流量与压力的关系流速:V=C√(RJ)=C√[PR/(ρgL)]流量:Q=CA√(RJ)=√[P/(ρgSL)]式中:C――管道的谢才系数;L――管道长度;P――管道两端的压力差;R――管道的水力半径;ρ――液体密度;g――重力加速度;S――管道的摩阻。
管道的内径和压力流量的关系似呼题目表达的意思是:压力损失与管道内径、流量之间的关系,如果是这个问题,则正确的答案应该是:压力损失与流量的平方成正比,与内径5.33方成反比,即流量越大压力损失越大,管径越大压力损失越小,其定量关系可用下式表示:压力损失(水头损失)公式(阻力平方区)h=10.3*n^2 * L* Q^2/d^5.33上式严格说是水头损失公式,水头损失乘以流体重度后才是压力损失。
式中n――管内壁粗糙度;L――管长;Q――流量;d――管内径在已知水管:管道压力0.3Mp、管道长度330、管道口径200、怎么算出流速与每小时流量?管道压力0.3Mp、如把阀门关了,水流速与流量均为零。
化工原理(少学时)课件和辅导教程、考试重点例题复习题及课后答案1.6流速及流量的测量

p1
2 p0 u 0 u12 z1 g z0 g 2 2
p1 p 0 ( z 0 z1 ) g
2018/8/11
2
2 (u 0 u12 )
15
( p1 p 0 ) A f A f ( z 0 z1 ) g A f
CR相同,同刻度时
qv 2 qv1
1 ( f 2 ) 2 ( f 1 )
式中:1——标定流体;
2——被测流体。
气体转子流量计
qv 2 qv1
1 2
18
2018/8/11
三、安装及优缺点 (1)永远垂直安装,且下进、上出, 安装支路,以便于检修。 ( 2 )读数方便,流动阻力很小,测量 范围宽,测量精度较高; ( 3 )玻璃管不能经受高温和高压,在 安装使用过程中玻璃容易破碎。
小结
2 u2 A2 (稳定流动) g z 1 z 2
2 u1 d 12 u 2 d 2 (圆管内) 2 u12 p1 u2 p2 he gz 2 hf 机械能衡算方程: gz1 2 2
u1 A1 u 2 A2 (不可压缩流体)
64 层流: l u h Re f 要求能够进行 阻力计算式: 直管 d 2 管路计算及分 湍流: f Re, d 2 析: 2 入 0 .5 u le u 简单管路 局部 h f 或hf 2 出 1 d 2
质量流量
qv u0 A0 C0 A0
qm C0 A0 2Rg ( 0 )
C0——流量系数(孔流系数) A0——孔面积。
2018/8/11 8
流体流动习题(计算题)解答

习题解答1-41一敞口贮槽中装有油(密度为917kg/m 3)和水,液体总深度为3.66m ,其中油深为3m 。
试计算油水分界处及贮槽底面的压力,分别用绝压和表压表示。
(当地大气压为101.3kPa )解:油水分界处:表压:kPa gh p 0.27381.9917111=⨯⨯==ρ 绝压:kPa p 12810013.1107.2541=⨯+⨯= 贮槽底面的压力:表压:kPa gh p p 5.3366.081.91000107.242212=⨯⨯+⨯=+=ρ 绝压:kPa p 13510013.110347.3542=⨯+⨯=1-42用U 形压力计测量容器内液面上方的压力,指示液为水银。
已知该液体密度为900kg/m 3,h 1=0.3m ,h 2=0.4m ,R=0.4m 。
试求: (1)容器内的表压;(2)若容器内的表压增大一倍,压力计的读数R ‘。
解:(1)如图,1-2为等压面。
)(211h h g p p ++=ρ gR p p a 02ρ+= gR p h h g p a 021)(ρρ+=++ 则容器内表压:kPa h h g gR p p a 2.4781.97.090081.94.013600)(210=⨯⨯-⨯⨯=+-=-ρρ(2)当容器内的表压增大一倍时,此时2'2'2RR h h -+= )2()('21'02'1'0'RR h h g gR h h g gR p -++-=+-=ρρρρ表整理得 2/)2/(021'g g R h h g p R ρρρ--++=‘表m 77.02/81.990081.913600)2/4.07.0(81.9900102.4723=⨯-⨯-⨯⨯+⨯⨯=1-43如图所示,用复式压差计测量某蒸汽锅炉液面上方的压力,指示液为水银,两U 形压差计间充满水。
相对于某一基准面,各指示液界面高度分别为z 0=2.0m, z 2=0.7m, z 4=1.8m, z 6=0.6m, z 7=2.4m 。
流体的运动详细答案解析

习题2-1.一水平圆管,粗处的直径为8cm ,流速为1m•s –1,粗处的直径为细处的2倍,求细处的流速和水在管中的体积流量.2-2.将半径为2cm 的引水管连接到草坪的洒水器上,洒水器装一个有20个小孔的莲蓬头,每个小孔直径为0.5cm .如果水在引水管中的流速为1m•s –1,试求由各小孔喷出的水流速度是多少?2-3.一粗细不均匀的水平管,粗处的截面积为30cm 2,细处的截面积为10cm 2.用此水平管排水,其流量为3×10–3m 3•s –1.求:(1)粗细两处的流速;(2)粗细两处的压强差.2-4.水在粗细不均匀的管中做定常流动,出口处的截面积为10cm 2,流速为2m•s –1,另一细处的截面积为2cm 2,细处比出口处高0.1m .设大气压强P 0≈105Pa ,若不考虑水的黏性,(1)求细处的压强;(2)若在细处开一小孔,水会流出来吗?2-5.一种测流速(或流量)的装置如2-5图所示.密度为ρ的理想液体在水平管中做定常流动,已知水平管中A 、B 两处的横截面积分别为S A 和S B ,B 处与大气相通,压强为P 0.若A 处用一竖直细管与注有密度为ρ'(ρ<ρ')的液体的容器C 相通,竖直管中液柱上升的高度为h ,求液体在B 处的流速和液体在管中的体积流量.2-6.用如图2-6图所示的装置采集气体.设U 形管中水柱的高度差为3cm ,水平管的横截面积S 为12cm 2,气体的密度为2kg•m –3.求2min 采集的气体的体积.2-7.一开口大容器底侧开有一小孔A ,小孔的直径为2cm ,若每秒向容器内注入0.8L 的水,问达到平衡时,容器中水深是多少?2-8.设37℃时血液的黏度η=3.4×10–3Pa•s ,密度ρ=1.05×103kg•m –3,若血液以72cm•s –1的平均流速通过主动脉产生了湍流,设此时的雷诺数为1000,求该主动脉的横截面积.2-9.体积为20cm 3的液体在均匀水平管内从压强为 1.2×105Pa 的截面流到压强为1.0×105Pa 的截面,求克服黏性力所作的功.2-10.某段微血管的直径受神经控制而缩小了一半,如果其他条件不变,问通过它的血流量将变为原来的多少?2-11.假设排尿时,尿从计示压强为5.33×103 Pa 的膀胱经过尿道后由尿道口排出,已知尿道长4cm ,体积流量为21cm 3•s –1,尿的黏度为6.9×10–4 Pa•s ,求尿道的有效直径.2-12.某条犬的一根大动脉,内直径为8mm ,长度为10cm ,流过这段血管的血流流量为1cm 3•s –1,设血液的黏度为2.0×10–3Pa•s .求:(1)血液的平均速度;(2)这段动脉管的流阻;(3)这段血管的血压降落.2-13.设某人的心输出量为8.2×10–5 m 3•s –1,体循环的总压强差为1.2×104Pa ,试求此人体循环的总流阻(也称总外周阻力).2-14.液体中有一空气泡,其直径为lmm ,密度为1.29 kg•m –3,液体的密度为0.9×103 kg•m –3,黏度为0.15Pa•s .求该空气泡在液体中上升的收尾速度.2-15.一个红细胞可近似看为一个直径为5.0×10–6m 、密度为1.09×103kg•m –3的小球.设习题2-5 习题2-6血液的黏度为1.2×10–3Pa•s ,密度为1.03×103kg•m –3.试计算该红细胞在37℃的血液中沉淀2cm 所需的时间.如果用一台加速度为106g 的超速离心机,问沉淀同样距离所需时间又是多少?2-1.一水平圆管,粗处的直径为8cm ,流速为1m•s -1,粗处的直径为细处的2倍,求细处的流速和水在管中的体积流量.解:(1)已知:d 1=8cm ,v 1=1m•s -1,d 1= 2d 2.求:v 2=?,Q =?根据连续性方程1122S S =v v ,有22112244d d ππ=v v ,代入已知条件得()12144m s -==⋅v v(2)水的体积流量为()()2223311122118101 5.02410m s 44Q S S d ππ---====⋅⨯⨯=⨯⋅v v v2-2.将半径为2cm 的引水管连接到草坪的洒水器上,洒水器装一个有20个小孔的莲蓬头,每个小孔直径为0.5cm .如果水在引水管中的流速为1m•s -1,试求由各小孔喷出的水流速度是多少?解:已知:总管的半径r 1=2cm ,水的流速v 1=1m•s -1;支管的半径为r 2=0.25cm ,支管数目为20.求:v 2=?根据连续性方程1122S nS =v v ,有221122r n r ππ=v v ,代入数据,得()()222222101200.2510--⨯⨯=⨯⨯v 从而,解得小孔喷出的水流速度()12 3.2m s -=⋅v .2-3.一粗细不均匀的水平管,粗处的截面积为30cm 2,细处的截面积为10cm 2.用此水平管排水,其流量为3×10-3 m 3•s -1.求:(1)粗细两处的流速;(2)粗细两处的压强差.解:已知:S 1=30cm 2,S 2=10cm 2,Q =3×10-3 m 3•s -1.求:(1) v 1=?,v 2=?;(2) P 1-P 2=?(1)根据连续性方程1122Q S S ==v v ,得()()33111244123103101m s , 3m s 30101010Q Q S S ------⨯⨯===⋅===⋅⨯⨯v v (2)根据水平管的伯努利方程22112211++22P P ρρ=v v ,得粗细两处的压强差 ()()22322312211111031410Pa 222P P ρρ-=-=⨯⨯-=⨯v v 2-4.水在粗细不均匀的管中做定常流动,出口处的截面积为10cm 2,流速为2m•s -1,另一细处的截面积为2cm 2,细处比出口处高0.1m .设大气压强P 0≈105Pa ,若不考虑水的黏性,(1)求细处的压强;(2)若在细处开一小孔,水会流出来吗?解:(1) 已知:S 1=10cm 2,v 1=2m•s -1,S 2=2cm 2,P 1= P 0≈105Pa ,h 2-h 1=0.1m .求:P 2=? 根据连续性方程S 1v 1=S 2v 2,得第二点的流速()111212 510m s S S -===⋅v v v 又根据伯努利方程2211122211+g +g 22P h P h ρρρρ+=+v v ,得第二点的压强 ()()()()()222112125322341-g 211010210109.80.12=5.10210Pa P P h h ρρ=++-=+⨯⨯-+⨯⨯-⨯v v (2) 因为()4205.10210Pa P P =⨯<,所以在细处开一小孔,水不会流出来.2-5.一种测流速(或流量)的装置如右图所示.密度为ρ的理想液体在水平管中做定常流动,已知水平管中A 、B 两处的横截面积分别为S A 和S B ,B 处与大气相通,压强为P 0.若A 处用一竖直细管与注有密度为ρ'(ρ<ρ')的液体的容器C 相通,竖直管中液柱上升的高度为h ,求液体在B 处的流速和液体在管中的体积流量. 解:根据水平管的伯努利方程22A A B B 1122P P ρρ+=+v v 和连续性方程A A B B S S =v v ,解得B 处的流速B S =v 又由竖直管中液柱的高度差,可知B A P P gh ρ'-=,因而B 处的流速为B S =v 进而得水平管中液体的体积流量为B B A Q S S S ==v 习题2-52-6.用如下图所示的装置采集气体.设U 形管中水柱的高度差为3cm ,水平管的横截面积S 为12cm 2,气体的密度为2kg•m -3.求2min 采集的气体的体积. 解:根据水平管的伯努利方程2211221122P P ρρ+=+v v , 因弯管处流速v 2=0,因此上式可化为211212P P ρ+=v , 又由U 形管中水柱的高度差知1、2两处的压强差为21P P gh ρ-=水,联立上面两式,解得气体的流速()1117.15m s -===⋅v 2min 采集的气体的体积为()4311121017.32260 2.5m V S t -=∆=⨯⨯⨯⨯=v2-7.一开口大容器底侧开有一小孔A ,小孔的直径为2cm ,若每秒向容器内注入0.8L 的水,问达到平衡时,容器中水深是多少?解:已知: Q =0.8L ,r 2=1cm .根据连续性方程Q =S 1v 1=S 2v 2,可得小孔处的流速()()312222220.810 2.55m s 3.14110Q Q S r π---⨯====⋅⨯⨯v 又因容器的截面积S 1远大于小孔的截面积S 2,所以v 1≈0.根据伯努利方程 2211122211+g +g 22P h P h ρρρρ+=+v v 因容器上部和底部小孔均通大气,故P 1=P 2=P 0≈1.0×105Pa ,将已知条件代入上式,得 21221g g 2h h ρρρ=+v解得 ()22212 2.550.332m 2g 29.8h h -===⨯v 2-8.设37℃时血液的黏度η=3.4×10-3Pa•s ,密度ρ=1.05×103kg•m -3,若血液以72cm•s -1的平均流速通过主动脉产生了湍流,设此时的雷诺数为1000,求该主动脉的横截面积. 解:根据雷诺数的定义e r R ρη=v ,可知主动脉的半径e R r ηρ=v , 习题2-6代入已知条件,得33323.4101000 4.510m 1.05107210e R r ηρ---⨯⨯===⨯⨯⨯⨯v , 进一步得到主动脉的横截面积()223523.14 4.510=6.3610m S r π--==⨯⨯⨯2-9.体积为20cm 3的液体在均匀水平管内从压强为 1.2×105Pa 的截面流到压强为1.0×105Pa 的截面,求克服黏性力所作的功. 解:根据黏性流体的伯努利方程221112221122P gh P gh ρρρρ++=+++v v w 又因为在均匀水平管中,即v 1=v 2,h 1=h 2,因此单位体积液体克服黏性力做的功12P P =-w那么体积为20cm 3的液体克服黏性力所作的功()()55612 1.210 1.01020100.4J W P P V -=-=⨯-⨯⨯⨯= 2-10.某段微血管的直径受神经控制而缩小了一半,如果其他条件不变,问通过它的血流量将变为原来的多少?解:根据泊肃叶定律知,其他条件不变时,体积流量与半径的四次方成正比.因此,其他条件不变,直径缩小了一半,则通过它的血流量将变为原来的1/16.2-11.假设排尿时,尿从计示压强为5.33×103 Pa 的膀胱经过尿道后由尿道口排出,已知尿道长4cm ,体积流量为21cm 3•s -1,尿的黏度为6.9×10-4 Pa•s ,求尿道的有效直径.解:根据泊肃叶定律,体积流量4π8r P Q Lη∆= 得尿道的有效半径11426444388 6.91041021107.2610m π 3.14 5.3310LQ r P η----⎛⎫⨯⨯⨯⨯⨯⨯⎛⎫===⨯ ⎪ ⎪∆⨯⨯⎝⎭⎝⎭故尿道的有效直径为3=1.4510m d -⨯.2-12.某条狗的一根大动脉,内直径为8mm ,长度为10cm ,流过这段血管的血流流量为1cm 3•s -1,设血液的黏度为2.0×10-3Pa•s .求:(1)血液的平均速度;(2)这段动脉管的流阻;(3)这段血管的血压降落.解:(1)根据体积流量的定义,得血液的平均速度()()61231100.02m s 3.14410Q S ---⨯===⋅⨯⨯v (2) 根据流阻的定义:R =8ηL/πr 4,可得该段动脉管的流阻()()326544388 2.010*******N s m 3.14410L R r ηπ----⨯⨯⨯⨯===⨯⋅⋅⨯⨯ (3) 根据泊肃叶定律:P Q R∆=,得这段血管的血压降落 ()661102102Pa P QR -∆==⨯⨯⨯=2-13.设某人的心输出量为8.2×10-5 m 3•s -1,体循环的总压强差为1.2×104Pa ,试求此人体循环的总流阻(也称总外周阻力).解:根据泊肃叶定律,得此人体循环的总流阻()48551.210 1.4610N s m 8.210P R Q --∆⨯===⨯⋅⋅⨯ 2-14.液体中有一空气泡,其直径为lmm ,密度为1.29 kg•m -3,液体的密度为0.9×103 kg•m -3,黏度为0.15Pa•s .求该空气泡在液体中上升的收尾速度.解:当空气泡在液体所受的重力、黏性阻力与浮力达到平衡时,小球速率达到最大,此后它将匀速上升,即33m 44633r g r r g πρπηπρ'+=v 从而得空气泡在液体中上升的收尾速度()()()()232331m 20.51029.80.910 1.29 3.2610m s 990.15r g ρρη---⨯⨯'=-=⨯⨯⨯-=⨯⋅⨯v 2-15.一个红细胞可近似看为一个直径为5.0×10-6m 、密度为1.09×103kg•m -3的小球.设血液的黏度为1.2×10-3Pa•s ,密度为1.03×103kg•m -3.试计算该红细胞在37℃的血液中沉淀2cm 所需的时间.如果用一台加速度为106g 的超速离心机,问沉淀同样距离所需时间又是多少?解:(1)红细胞在液体所受的重力与黏性阻力和浮力达到平衡,速率达到最大,此后它将匀速下降,即33m 44633r g r g r πρπρπη'=+v 从而得红细胞的收尾速度()()()()262371m 32 2.5109.82 1.09 1.0310 6.810m s 99 1.210r g ρρη----⨯⨯⨯'=-=⨯-⨯=⨯⋅⨯⨯v所以该红细胞在37℃的血液中沉淀2cm 所需的时间()247210 2.9410s 6.810t --⨯==⨯⨯ (2)如果用一台加速度为106g 的超速离心机,则红细胞的收尾速度为()61m m100.68m s -''==⋅v v 所以该红细胞在37℃的血液中沉淀同样距离所需时间()6210 2.9410s t t --'==⨯。
一道工程流体力学练习题

一道工程流体力学练习题一、流体性质及流体静力学1. 水的密度为1000 kg/m³,求水在标准大气压下的绝对压力。
2. 某容器内气体压力为0.1 MPa,气体密度为1.2 kg/m³,求该气体的重力加速度。
4. 某点在液体中的深度为3m,液体密度为800 kg/m³,求该点的静压力。
5. 一根直径为100mm的管道,内充满水,求管道内水柱的压头。
二、流体运动学及动力学1. 某液体在管道内流动,流速为2 m/s,管道直径为150mm,求该液体的体积流量。
2. 水在直径为200mm的管道内流动,流速为1.5 m/s,求水流的雷诺数。
3. 某气体在管道内流动,管道直径为100mm,气体密度为1.5 kg/m³,流速为10 m/s,求气体的动能因子。
4. 求解直径为50mm的管道内,水流动时的摩擦系数。
5. 一根水平放置的管道,直径为200mm,水在管道内流动,流速为3 m/s,求管道内的沿程损失。
三、泵与风机1. 某离心泵的流量为100 m³/h,扬程为50m,求该泵的轴功率。
2. 一台轴流风机的风量为5000 m³/h,全压为200 Pa,求风机的轴功率。
3. 某泵的进口直径为150mm,出口直径为100mm,求泵的进出口流速比。
4. 一台离心泵的转速为1450 r/min,求泵的理论扬程。
5. 某风机的全压为300 Pa,风量为6000 m³/h,求风机的效率。
四、管路系统及管网计算1. 一根长100m的管道,直径为200mm,输送水,求管道的水头损失。
2. 某管网由直径为150mm和100mm的管道组成,求管网的最小阻力系数。
3. 一根直径为100mm的管道,输送水,流量为50 m³/h,求管道的流速。
4. 某管网由三根管道组成,求管网的总阻力系数。
5. 一根直径为200mm的管道,输送水,求管道的临界流速。
五、开放渠道流动1. 一条矩形渠道,底宽为3m,水深为1.5m,粗糙系数为0.035,求渠道的流量。
流体流量与流速的关系练习题

流体流量与流速的关系练习题
流体的流量和流速是流体力学中的基本概念,它们之间存在一定的关系。
下面是一些关于流体流量和流速的练习题,以帮助加深对这些概念的理解和运用。
1.问题:如果一条管道的截面积为A,流体在该管道内的平均流速为v,求流体通过管道的流量。
答案:流量 = 流速 ×截面积
Q = v × A
2.问题:如果流体通过一个流量计的时间为t,流量计截面积为A,求流体通过流量计的流速。
答案:流速 = 流量 / 截面积
v = Q / A
注意:这里的流速为平均流速。
3.问题:一辆汽车在公路上行驶,车头前方有一个水平方向的喷水口,喷水口对车辆喷出的水流量为Q,车前方的截面积为A,求车头前方的水流速度。
答案:流速 = 流量 / 截面积
v = Q / A
4.问题:如果一个圆柱形容器中的流速为v,容器的底面半径为r,求通过容器底部的流量。
答案:流量 = 流速 ×截面积
Q = v × π × r²
5.问题:如果一段管道中的流量为Q,管道的长度为L,管道内流体的流速为v,求管道中的平均流速。
答案:流速 = 流量 / 长度
v = Q / L
注意:这里的流速为平均流速。
这些练习题可以帮助巩固流体流量与流速之间的关系。
通过这些练习,您可以更加熟悉流体力学中的基本概念,并且能够运用这些概念解决实际问题。
管径流速流量计算

25.4
壁厚(mm)
1.2
重力加速度g
管内直径(mm)
23
压降Hf(m)
流量T/h
0.2
阻力系数ζ
横截面积m2
0.0004
流速u(m/S)
流速m/s
0.13
流量(m³/h)
管外径(mm)
横截面积m2 管内径(mm)
0.00038340 壁厚(mm)
横截面积m2
管道中水的质量(Kg) 最低流速m/s
1 3 15.02 45.06 10 25.02
用水点数量(个) 18
管道中的水量 100L水中含的硝酸溶质
硝酸溶质
65%的硝酸溶液 1%的NaOH溶液
管道长度(m) 63
压缩空气 0.958504625
8.695 8.334197714
300 8.695 26.085
12.82184264 40.13076923 L 3.03030303 Kg
95.85
最大流速m/s 最低流量T/h
压力降与流速
最大流量T/h
实际用水量T/h
9.8
管中实际的流量 T/h
1
1
横截面积m2
4.427188724 长度
6.618443492 体积
25.4 23 1.2 0.00041527 1 3 1.49 4.48 10 11.49
38.1
50.8
63.5
34.8
黄色区为 填写区
计算流量
管外直径(mm)
25.4
管内直径(mm) 壁厚(mm)
流速m/s
1.2
22.10
1.65
流量T/h
1.6563
实际用水量T/h
工程流体力学第4、第6章 习题解答

第四章 习题解答4-1 用直径为100mm 的管道输送流量为10kg/s 的水,如水温为5℃,试确定管内水的流态。
如用这管道输送同样质量流量的石油,已知石油密度为3/850m kg =ρ运动粘滞系数为s cm /14.12,试确定石油的流态。
解:水温为5℃时,其密度为3/1000m kg =ρ,运动粘滞系数为s m /10519.126−×=γ因此,水在管道中流动的体积流量为: s m mkg skg Q /01.0/1000/1033== 流速为:s m mm sm A Q /27.11000100(14.341/01.023=××==υ雷诺数为:83863/10519.11000100/27.1Re 26=××=−sm mms m 为紊流 当输送石油时: s m mkg s kg Q /012.0/850/1033== 流速为:s m mm sm A Q /5.1)1000100(14.341/012.023=××==υ雷诺数为:1316/1014.11000100/5.1Re 24=××=−sm mms m 为层流 4-2 一圆形风道,管径为300mm ,输送的空气温度为20℃,求气流保持层流时的最大流量。
若输送的空气量为200kg/h ,气流是层流还是紊流?解:空气温度为20℃时,运动粘滞系数s m /107.1526-×=γ,根据题意有:6107.1510003002000−××=mm υ 解方程得:s m /105.0=υ气体流量为: s m s m mm Q /0074.0/105.01000300(14.34132=×××=质量流量为:h kg s kg m kg s m Q /29/0081.0/093.1/0074.033==×= 若输送的空气量为200kg/h ,因此,空气在管道中流动的体积流量为:s m m kg hkg Q /051.03600/093.1/20033=×= 流速为:s m mm sm A Q /72.0)1000300(14.341/051.023=××==υ雷诺数为:13758/107.151000300/72.0Re 26=××=−sm mms m 为紊流 4-3 断面为矩形的排水沟,沟底宽为20cm ,水深为15cm ,流速为0.15m/s ,水温为15℃。
流体流量及流速分析与计算

本节概要本节讨论喷管内流量、流速的计算。
工程上通常依据已知工质初态参数和背压,即喷管出口截面处的工作压力,并在给定的流量等条件下进行喷管设计计算,以选择喷管的外形及确定其几何尺寸;有时也需就已有的喷管进行校核计算,此时喷管的外形和尺寸已定,须计算在不同条件下喷管的出口流速及流量。
在喷管的计算中要注意到背压对确定喷管出口截面上压力的作用。
本节内容4.8.1 流速计算及其分析4.8.2 临界压力比4.8.3 流量计算及分析4.8.4 例题本节习题4-24、4-25、4-26、4-27、4-29下一节流速计算及其分析1.喷管出口截面的流速计算2.压力比对流速的影响喷管出口截面的流速计算据能量方程,气体在喷管中绝热流动时任一截面上的流速可由下式计算:(4-28)因此,出口截面上流速:(4-28a)或(4-28b)在入口速度较小时,上式中可忽略不计,于是:(4-28c)(4-28)各式表明,气流的出口流速取决于气流在喷管中的绝热焓降。
值得注意的是,上述各式中焓的单位是J/kg。
如果理想气体可逆绝热流经喷管,可据初态参数(p1,T1)及速度求取滞止参数,然后结合出口截面参数如p2 按可逆绝热过程方程式求出T2 从而计算h2 再求得;对水蒸汽可逆绝热流经喷管,可以利用h-s 图,根据进口蒸汽的状态查得初态点1,通过点 1 作垂线与喷管出口截面上压力p2 相交,得出状态点2,从点1 和2 可查出h1 和h2,代入式(4-28)即可求出出口流速。
☆式子对理想气体和实际气体均适用;与过程是否可逆无关,但不可逆绝热流动,若用可逆的关系求出h2 在求得的需修正,若h2 是不可逆过程终态的焓,则求出的不需修正。
式的适用范围是什么?是否与过程的可逆与否有关?与工质的性质有关?返回压力比对流速的影响为了分析截面上压力对流速的影响,假定喷管的几何形状满足流速变化的几何条件,气体为理想气体,并取定值比热容。
分析得出的结论可定性地应用于水蒸汽等实际气体。
化工原理例题[1]
![化工原理例题[1]](https://img.taocdn.com/s3/m/e8a0e06b01f69e31433294c4.png)
第一章1、有密度为的液体,在内径为60mm 的管中输送到某处。
若其流速为,试求该液体的体积流量、质量流量与质量流速。
解 (1) 体积流量(2) 质量流量(3) 质量流速2、如习题附图所示,有一高位槽输水系统,管径为。
已知水在管路中流动的机械能损失为 (u 为管内流速)。
试求水的流量为多少。
欲使水的流量增加20%,应将高位槽水面升高多少米?解 管径, 机械能损失(1) 以流出口截面处水平线为基准面,水的流量(2)高位槽应升高3、25℃的水在内径为50mm 的直管中流动,流速为2m/s 。
试求雷诺数,并判断其流动类型。
解 25℃,水的黏度,密度,管内径,流速/31800kg m /0.8m s ()3/m h ()/kg s ()/2⎡⎤⋅⎣⎦kg m s ./.223330.060.822610814 /44ππ-==⨯⨯=⨯=V q d u m s m h ../m V q q kg s ρ-==⨯⨯=3226101800407 ./().22407===1440 0064m q kg m s A ωπ⋅⨯.mm mm φ⨯57352452∑=⨯f u h /3m h .005=d m 2452∑=⨯f u h ,,,1212500?Z m Z u u ====222214522=+⨯u u Zg ./u m s ==2146 ().../.V q d u m s m h ππ-==⨯⨯=⨯=22333200514628710103 /44()'..10212=+=V V V q q q '..../221212146175 ==⨯=u u m s '(')21223=Z g u (.)'..Z m ⨯==2123175781 981..m -=7185218 .30893710μ-=⨯⋅Pa s /3997ρ=kg m .005=d m /2=u m s .Re ..530052997112104000 为湍流0893710du ρμ-⨯⨯===⨯>⨯4、水的温度为10℃,流量为,在直径、长为100m 的直管中流动。
管径、压力、流速、流量计算

标况流量Q0 Nm³/h 115.89 备注:黄底为手动输入数据,灰底为不可修改数据,红底为计算结果。
已知流量Q0、压力O、管径D,求流速V
名称 管道内径D 管道半径R 工况压力P 流速V 工况流量Q 工况温度t 标况压力P0 标况温度t0 单位 mm mm MPa m/s m³/h ℃ MPa ℃ 数值 19.00 9.50 1.4 4.41 4.50 20 0.1 0 备注 计算公式
已知流速V、压力P、管径D,求流量Q0
名称 管道内径D 管道半径R 工况压力P 流速V 工况流量Q 工况温度t 标况压力P0 标况温度t0 单位 m m MPa m/s m³/h ℃ MPa ℃ 数值 19 9.5 0.8 4.41 4.50 20 0.1 0 备注 计算公式
绝对压力 绝对压力=表压+0.1 Q=π ×R2×V×3600=π ×D2×V×3600/4=V×(D/18.8) 2
标况流量Q0 Nm³/h 33.57 Q0=Q(P/P0)×(T0/T)=Q(P/P0)×(273/(273+t)) 备注:黄底为手动输入数据,灰底为不可修改数据,红底为计算结果。
已知流量Q0、压力P、流速V,求管径D
名称 管道内径D 管道半径R 工况压力P 流速V 工况流量Q 工况温度t 标况压力P0 标况温度t0 单位 mm mm MPa m/s m³/h ℃ MPa ℃ 数值 12.61 6.31 0.9 10 4.50 20 0.1 0 备注 计算公式 R=sqrt(Q/3600Vπ )=9.4aqrt(Q/V) 绝对压力 绝对压力=表压+0.1 Q=Q0(P0/P)×(T/T0)=Q(P0/P)×((243;0.1 V=Q/(D/18.8)2 Q=Q0(P0/P)×(T/T0)=Q(P0/P)×((273+t)/273)
流量、流速计算
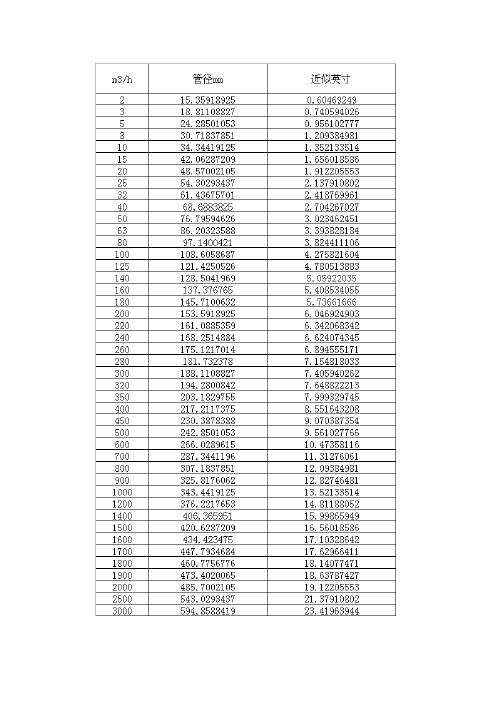
源压力4公斤,用25管径接出,不同管长流量是不等的呀!分别用1米、100米、1000米、10000米长的管接出,流量悬殊很大很大!举例说明:200mm管道,水管起端与未端的压力差为0.8Mpa,当管道长度不同时,流量是不等的:假设管道长度L=100m,水管起端与未端的压力差是0.8Mpa,即管道两端的水头差H=80m,则流量可计算如下:200mm管道的摩阻S=9.029流量Q=[H/(SL)]^(1/2)=[80/(9.029*100)]^(1/2)=0.298 m^3/s=1072.8 m^3/h流速V=4Q/3.1416D^2=9.49 m/s假设管道长度L=1000m,水管起端与未端的压力差是0.8Mpa,即管道两端的水头差H=80m,则流量可计算如下:200mm管道的摩阻S=9.029流量Q=[H/(SL)]^(1/2)=[80/(9.029*1000)]^(1/2)=0.094m^3/s=338.4 m^3/h流速V=4Q/3.1416D^2= 2.99m/s由以上计算知,管道长度不同,其他条件一样,流量是不等的。
水头差与管道长度的比值(H/L)称为水力坡度,有水头(或有压力)不一定有流量,流量大小取决与水力坡度(或压力坡度),而不是取决于水头(或压力)!安的梦|六级DN15、DN25、DN50管径的截面积分别为:DN15:15²*3.14/4=176.625平方毫米,合0.0177平方分米。
DN25:25²*3.14/4=490.625平方毫米,合0.0491平方分米。
DN50:50²*3.14/4=1962.5平方毫米,合0.1963平方分米。
设管道流速为V=4米/秒,即V=40分米/秒,且1升=1立方分米,则管道的流量分别为(截面积乘以流速):DN15管道:流量Q=0.0177*40=0.708升/秒,合2.55立方米/小时。
DN25管道:流量Q=0.0491*40=1.964升/秒,合7.07立方米/小时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、按流量所使用的单位不同,它可分为哪几种?为何在流量计中提出“标准体积流量”的概念?
2、试分析毕托管和均速管在流量测量中的应用及其自身特点。
3、已知管径为120mm ,管道内水流动的平均速度为1.8m /s ,这时水的密度为990kg /m 3 ,确定该状态下水的容积流量和质量流量。
4、转子流量计的测量准确度受哪些影响?
5、涡轮流量计输出___________ 信号()
A .模拟
B .数字
C .电流
D .电压
6、下列原理中不能用于速度测量的是()。
A .散热率法
B .动压法
C .霍尔效应
D .激光多普勒效应
7、不需要借助压力计测量流速的仪表是()。
A .热电风速仪
B .毕托管
C .圆柱型三孔测速仪
D .三管型测速仪
8、试比较机械式风速仪里翼式和杯式两种仪器的异同。
9、为何热线风速仪要分为恒流式与恒温式两种?
10、简述动力测压法测量流速的原理。
11、流动方向如何测量,平面流场和空间流场分别使用什么仪器进行测量?。
