数学建模物流配送中心选址模型
数学建模--物流配送中心选址模型
物流配送中心选址模型姓名：学号：班级：摘要：在现代物流网络中，配送中心不仅执行一般的物流职能，而且越来越多地执行指挥调度、信息处理、作业优化等神经中枢的职能，是整个物流网络的灵魂所在。
因此，发展现代化配送中心是现代物流业的发展方向。
文章首先使用重心法计算出较为合适的备选地，再考虑到各项配送中心选址的固定成本和可变成本，从而使配送中心选址更加优化和符合实际。
关键词：物流选址；选址；重心法；优化模型；1．背景介绍1．1 研究主题如下表中，有四个零售点的坐标和物资需求量，计算并确定物流节点的位置。
1.2 前人研究进展1.2.1国内外的研究现状：国外对物流配送选址问题的研究已有60余年的历史，对各种类型物流配送中心的选址问题在理论和实践方面都取得了令人注目的成就，形成了多种可行的模型和方法。
归纳起来，这些配送中心选址方法可分为三类：（1）应用连续型模型选择地点；（2）应用离散型模型选择地点；（3）应用德尔菲（Delphi）专家咨询法选择地点。
第一类是以重心法为代表，认为物流中心的地点可以在平面取任意点，物流配送中心设置在重心点时，货物运送到个需求点的距离将最短。
这种方法通常只是考虑运输成本对配送中心选址的影响，而运输成本一般是运输需求量、距离以及时间的函数，所以解析方法根据距离、需求量、时间或三者的结合，通过坐标上显示，以配送中心位置为因变量，用代数方法来求解配送中心的坐标。
解析方法考虑影响因素较少，模型简单，主要适用于单个配送中心选址问题。
解析方法的优点在于计算简单，数据容易搜集，易于理解。
由于通常不需要对物流系统进行整体评估，所以在单一设施定位时应用解析方法简便易行。
第二类方法认为物流中心的各个选址地点是有限的几个场所，最适合的地址只能按照预定的目标从有限个可行点中选取。
第二类方法的中心思想则是将专家凭经验、专业知识做出的判断用数值形式表示，从而经过分析后对选址进行决策。
国内在物流中心选址方面的研究起步较晚，只有10余年历史，但也有许多学者对其进行了较深入的研究，在理论和实践上都取得了较大的成果。
数学建模论文-物流配送中心的合理选择
故此处有两种情况，应分选 4、7、 12、13、 20、23、 26、28 、 45 这九个个城市和选取 4、7、11、20、23、26、28、45 这八个城市 作为配送中心的情行进行讨论： 一、在选取 4、7、12、13、20、23、26、28、45 九个城市的情 况下，根据各个城市间的距离可确定各个供应点城市所供应的城市。 具体如下： 4——1、2、3、5、15、16、27、46、47、 7——6、8、39、40、41、42 12——9、10、14、38、43 13——11、32、36、37 20——19、21、25、24、33、35、34、48、49 23——22 26——无 28——29、30、31 45——17、18、44
利用 matlab 软件，使用公式 1 对选取的供应点和供应城市进行 计算得： （matlab 计算程序附于论文后程序 1 中） Y = 9618177（元）
二、选取 4、7、11、20、23、26、28、45 这八个城市作为配送 中心的情况下， 根据各个城市间的距离可确定各个供应点城市所供应 的城市。具体如下：
Y40 2341203.0 Y43 1343567.0 Y44 1223214.0 Y45 21204380 表1 对以上表格中的 Y 值排序，取其前五个值 Y4、Y30、Y5、Y28、 Y7 结合 49 各城市的坐标图进行分析: 从图中和看出，4 城市作为配送中心非常合适，由于 4 和 5、 30 相邻，故不选 5 和 30 作为配送中心，城市 28 和 7 也非常符合作 为配送中心。又因为城市 26 的基本建设费用非常小，而且距离其周 边城市非常远，以 28 号城市也可作为配送中心。现在确定下了 4、7、 26、28 这四个城市作为配送中心。 将上述配送中心相邻的城市都排除掉，只剩下 1、2、9、10、
matlab配送中心选址问题的建模
【matlab配送中心选址问题的建模】1. 引言在现代物流管理中，配送中心的选址问题是一个至关重要的决策。
合理的配送中心选址可以有效减少物流成本、提高配送效率，对于企业而言具有重要意义。
本文将以matlab为工具，探讨配送中心选址问题的建模及解决方案。
2. 配送中心选址问题的背景配送中心选址问题是指在满足用户需求的前提下，寻找最佳的位置建立配送中心，以实现物流配送的最优化。
这其中涉及到多个因素，如客户位置分布、物流成本、运输距离等。
通过合理选址，可以降低物流成本、提高配送效率，从而提升企业竞争力。
3. matlab在配送中心选址问题中的应用matlab作为一种强大的数学建模和仿真工具，可以很好地应用于配送中心选址问题的建模和求解。
通过matlab，可以将配送中心选址问题转化为数学模型，并利用优化算法求解最优位置。
4. 配送中心选址问题的数学建模在进行配送中心选址问题的数学建模时，需要考虑多个因素。
需要确定客户位置分布情况，可以利用统计学方法进行数据分析和处理。
需要考虑物流成本和运输距离等因素，这些因素可以通过数学模型进行量化和分析。
需要建立一个评价指标函数，以评估不同选址方案的优劣。
5. matlab在配送中心选址问题中的应用案例以某电商公司为例，通过matlab对配送中心选址问题进行了建模和求解。
利用matlab对客户位置数据进行了处理和分析，得到了客户位置分布图。
建立了数学模型，考虑了物流成本、运输距离等因素，最终利用matlab的优化算法求解出了最佳的配送中心选址方案。
6. 个人观点和理解在配送中心选址问题中，利用matlab进行数学建模和求解是一种高效且可行的方法。
通过matlab，可以快速准确地分析和求解配送中心选址问题，为企业的物流配送提供科学依据。
未来，我认为随着数据的不断积累和算法的不断优化，matlab在配送中心选址问题中的应用将会更加广泛和深入。
7. 结语通过本文对matlab配送中心选址问题的建模和求解的探讨，希望能够对读者有所启发。
带道路容量限制的多配送中心选址问题的数学模型与算法
表6 生 产基地 1 2
从生产基地到配送中心备选点的道路容量 （吨） 备选点 1 80 40 4 72 58 5 60 67 9 254 200 10 54 72 13 146 134 15 49 57 16 110 114
决策参考
表7 备选点 1 4 5 9 10 13 15 16 需求点 备选点 1 4 5 9 10 13 15 16 从配送中心备选点到需求点的道路容量 （吨） 需求点 1
Zi =
分别列出了从生产基地到配送中心备选点、 从配送中心备 选点到需求点的道路容量限制。问如何从 8 个配送中心备 选点中选择最多 3 个建立配送中心， 使得总费用最低？
表1 序号 1 2 3 4 5 6 7 8 9 10 表2 需求点 灌云县 连云港 徐州市 宿迁市 淮安市 盐城市 镇江市 扬州市 宝应县 高邮市 需求点对应序号及年需求量 （吨） 年需求量 （吨） 32 40 48 34 36 38 40 40 30 32 序号 11 12 13 14 15 16 17 18 19 20 需求点 东台市 泰州市 南通市 南京市 高淳县 溧水县 常熟市 常州市 无锡市 苏州市 年需求量 （吨） 32 36 58 80 28 30 32 40 56 60
与需求点的供需关系？
， 但现有研究成果中均未考虑道路容量限制。在实际的
图 1 物流配送系统网络图
配送过程中， 由于受客观条件限制， 生产基地到配送中心、 配送中心到需求点的配送量往往有一定的限制， 如： 由于 道路的拥挤导致一定时间内的配送量有限， 另外由于配送 中心的车辆数量有限， 也会导致不同配送道路上的最大配 送容量不同。 带道路容量限制的配送中心选址问题可以描述为： 已 知各个需求点之间的距离及需求点的需求量， 各生产基地 到备选配求点的需求， 如何选择配送中心的位置， 才 能使总成本 （包括运输费用、 配送中心的年固定费用和周 转费用） 达到最小？ 1 带道路容量限制的多配送中心选址问题及数学模型 1.1 带道路容量限制的多配送中心选址问题描述 假设有 a 个生产基地生产某种货物满足 n 个需求点的 需求， 现欲从 m 个备选点中选择若干个建立配送中心， 形 成如图 1 所示的物流配送系统网络结构。生产基地和需 求点的数量和位置是固定的， 为了使总费用最小， 如何选
物流配送中心选址建模
上海海事大学交通运输学院院系交通运输学院专业年级物流管理133 学生姓名刘笑颜学号 2二○一六年六月物流配送中心选址问题建模摘要：在现代物流网络中，配送中心不仅执行一般的物流职能，而且越来越多地执行指挥调度、信息处理、作业优化等神经中枢的职能，是整个物流网络的灵魂所在。
因此，物流中心选址、发展现代化配送中心是现代物流业的发展方向。
（我的创新：本文建立了关于中心仓库选址问题的数学模型，但并未给出具体案例。
我的创新在于将这个模型运用到一个实例中，并给出了这个模型不足和可改进的地方。
）关键字：物流网络、配送中心、最优路径、最低成本、营运费用1背景介绍工厂和中心仓库位置的选择，将显著影响其实际营运的效率与成本，以及日后仓储规模的扩充与发展。
因此在决定中心仓库设置的位置方案时，必须谨慎参考相关因素，按适当步骤进行。
在选择过程中，如果已经有预定地点或区域方案，应于规划前先行提出，并成为规划过程中的限制因素;如果没有预定的地点，则可于可行性研究时提出几个备选方案,并对比各备选方案的优劣,以供决策者选择。
2.问题介绍：在现实当中，一个企业通常不会只考虑建设一个中心仓库，而是考虑建设多个中心仓库。
因此，多中心仓库选址模型在实际当中更加受欢迎。
不同产品从不同的工厂运到中心仓库，再由中心仓库转运给不同的顾客，为使企业成本最低应考虑仓库的建造费用、运输费用、仓库营运费用等。
下面需要建立模型来解决这些问题。
3.建模：3.1.模型的假设本文建立的选址模型是在给定某一地区所有被选点的地址集合中选出一定数目的地址作为中心仓库，使选出点建立的中心仓库在满足城市的需求前提下，在考虑工厂和城市重要度的情况下使得总费用最小。
为了便于模型求解，同时使模型具有使用价值，作如下的假设：（1）仅在一定的备选范围内考虑设置新的中心仓库；（2）模型包括从工厂到中心仓库之间的运输以及从中心仓库到城市之间的运输；（3）一个中心仓库可由多个工厂供货，一个城市的需求也可由多个中心仓库提供；（4）中心仓库的容量能够满足城市的需求；（5）各城市的需求量一定且为已知。
城市物流配送方案优化模型_数学建模
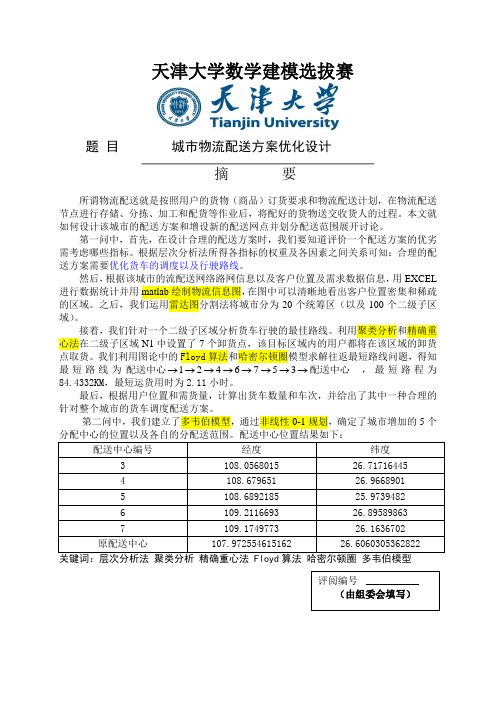
天津大学数学建模选拔赛题目城市物流配送方案优化设计摘要所谓物流配送就是按照用户的货物（商品）订货要求和物流配送计划，在物流配送节点进行存储、分拣、加工和配货等作业后，将配好的货物送交收货人的过程。
本文就如何设计该城市的配送方案和增设新的配送网点并划分配送范围展开讨论。
第一问中，首先，在设计合理的配送方案时，我们要知道评价一个配送方案的优劣需考虑哪些指标。
根据层次分析法所得各指标的权重及各因素之间关系可知：合理的配送方案需要优化货车的调度以及行驶路线。
然后，根据该城市的流配送网络路网信息以及客户位置及需求数据信息，用EXCEL 进行数据统计并用matlab绘制物流信息图，在图中可以清晰地看出客户位置密集和稀疏的区域。
之后，我们运用雷达图分割法将城市分为20个统筹区（以及100个二级子区域）。
接着，我们针对一个二级子区域分析货车行驶的最佳路线。
利用聚类分析和精确重心法在二级子区域N1中设置了7个卸货点，该目标区域内的用户都将在该区域的卸货点取货。
我们利用图论中的Floyd算法和哈密尔顿圈模型求解往返最短路线问题，得知最短路线为1246753配送中心配送中心，最短路程为→→→→→→→→84.4332KM，最短运货用时为2.11小时。
最后，根据用户位置和需货量，计算出货车数量和车次，并给出了其中一种合理的针对整个城市的货车调度配送方案。
第二问中，我们建立了多韦伯模型，通过非线性0-1规划，确定了城市增加的5个配送中心编号经度纬度3 108.0568015 26.717164454 108.679651 26.96689015 108.6892185 25.97394826 109.2116693 26.895898637 109.1749773 26.1636702原配送中心107.972554615162 26.6060305362822评阅编号（由组委会填写）一．问题重述配送是指在经济合理区域范围内，根据客户要求，对物品进行拣选、加工、包装、分割、组配等作业，并按时送达指定地点的物流活动，即按用户定货要求，在配送中心或其它物流结点进行货物配备，并以最合理方式送交用户。
物流配送中心选址数学模型的研究和优化
物流配送中心选址数学模型的研究和优化【摘要】本文研究物流配送中心选址数学模型的研究和优化问题。
在介绍了研究背景、研究意义和研究内容。
在包括模型建立、数据采集与分析、参数优化、模型评价和优化策略的讨论。
通过建立数学模型，利用实际数据进行分析，对配送中心选址进行参数优化，并评价模型效果。
在结论中总结了研究成果，展望未来研究方向，并对本文进行了总结。
本文旨在为物流行业提供选址决策的方法和策略，提高配送效率，优化物流网络布局，降低成本和提高服务质量。
通过本文的研究，为物流行业的发展和进步提供了一定的参考和指导。
【关键词】物流配送中心、选址、数学模型、研究、优化、背景、意义、内容、模型建立、数据采集、分析、参数优化、评价、策略、成果、展望未来、总结。
1. 引言1.1 研究背景物流配送中心选址是物流配送系统中的重要环节，选址的合理与否直接影响到物流效率和成本控制。
随着电子商务的快速发展，物流需求不断增加，物流配送中心也面临着更多的挑战。
对物流配送中心选址进行数学模型研究和优化具有重要的意义和价值。
在过去的研究中，物流配送中心选址主要依靠经验和专家判断，缺乏科学的分析和决策支持。
随着数学建模和优化算法的发展，可以通过建立数学模型来辅助决策者进行选址决策。
通过对物流需求、市场结构、交通网络等多方面因素进行综合分析，可以预测不同选址方案的效果，并进行优化选择。
本研究旨在通过建立数学模型，采集和分析相关数据，优化模型参数，评价优化效果，并提出相应的优化策略，以提高物流配送中心选址的效率和准确性。
通过本研究的开展，将为物流配送中心选址提供更科学的决策支持，促进物流行业的发展和进步。
1.2 研究意义物流配送中心选址数学模型的研究和优化具有重要的意义。
物流配送中心的选址决定着整个物流系统的效率和成本。
一个合理的选址能够减少货物的运输距离和时间，降低运输成本，提高配送效率。
选址还关系着配送中心对周边地区的服务覆盖范围，直接影响着客户的满意度和品牌形象。
数学建模论文--物流及选址问题
物流预选址问题2摘要错误!未定义书签。
一、问题重述3二、问题的分析32.1 问题一：分析确定合理的模型确定工厂选址和建造规模42.2 问题二：建立合理的仓库选址和建造规模模型42.3 问题三：工厂向中心仓库供货的最正确方案问题42.4 问题四：根据一组数据对自己的模型进展评价4三、模型假设与符号说明53.1条件假设53．2模型的符号说明5四、模型的建立与求解64.1 问题一：分析确定合理的模型为两个工厂合理选址并确定建造规模64.1.1模型的建立64.2 问题二：建立合理模型确定中心仓库的位置及建造规模84.2.1 基于重心法选址模型94.2.2 基于多元线性回归法确定中心仓库的建造规模104.3 问题三：工厂向中心仓库供货方案114.4 问题四：选用一组数据进展计算12五、模型评价175.1模型的优缺点175.1.1 模型的优点175.1.2 模型的缺点17六参考文献17物流预选址问题摘要在物流网络中，工厂对中心仓库和城市进展供货，起到生产者的作用，而中心仓库连接着工厂和城市，是两者之间的桥梁，在物流系统中有着举足轻重的作用，因此搞好工厂和中心仓库的选址将对物流系统作用的发挥乃至物流经济效益的提高产生重要的影响。
本论文在综述工厂和中心仓库选址问题研究现状的根底上，对二者选址的模型和算法进展了研究。
对于问题一二，通过合理的分析，我们采用了重心法选址模型找到了工厂和中心仓库的大致位置并给出了确定工厂和中心仓库建造规模的参数和公式，通过用数据进展实例化分析，我们确定了工厂和中心仓库位置和建造规模。
对于问题三我们运用LINGO软件简单的解决了工厂对中心仓库的供货情况。
问题四我们选用了一组数据通过求解多元线性规划对问题进展了实例化分析。
为中心仓库的选址问题做了合理说明。
最后我们对模型进展了评价和分析。
关键词：物流网络重心法选址模型多元线性规划一、问题重述某公司是生产某种商品的省知名厂家。
该公司根据需要,方案在本省建立两个生产工厂和假设干个中心仓库向全省所有城市供货。
物流配送中心选址建模
(三)物流配送中心选址的主要方法与类型1.选址方法类型近年来，随着选址理论迅速发展，各种各样的选址越来越多，层出不穷。
特别是计算机技术的发展与应用，促进了物流系统选址的理论发展，对不同方案的可行性分析提供了强有力的工具。
但是现阶段选址的理论方法大体上有以下几类：(1)运筹法运筹法是通过数学模型进行物流网点布局的方法。
采用这种方法首先根据问题的特征、己知条件以及内在的联系建立数学模型或者是图论模型。
然后对模型求解获得最佳布局方案。
采用这种方法的优点是能够获得较为精确的最优解缺乏是对一些复杂问题建立适当的模型比较困难，因而在实际应用中受到很大的限制。
解析法中最常用的有重心法和线性规划法。
(2)专家意见法专家意见法是以专家为索取信息的对象，运用专家的知识和经验考虑选址对象的社会环境和客观背景，直观地对选址对象进行综合分析研究寻求其特点和发展规律并进行选择的一类选址方法是专家选择法，其中最常用的有因素评分法和德尔菲法。
(3)仿真法仿真法是将实际问题用数学方法和逻辑关系表示出来然后通过模拟计算及逻辑推理确定最佳布局方案。
这种方法的优化是比较简单，缺点是选用这种方法进行选址，分析者必须提供预定的各种网点组合力案以供分析评价，从中找出最佳组合。
因此，决策的效果依赖于分析者预定的组合方案是否接近最佳方案该法是针对模型的求解而言的，是种逐次逼近的方法。
对这种方法进行反复判断实践修正直到满意为止。
该方法的优点是模型简单，需要进行方案组合的个数少，因而，容易寻求最佳的答案。
缺点是这种方法得出的答案很难保证是最优化的一般情况下只能得到满意的近似解用启发式进行选址，一般包括以下步骤：①定义一个计算总费用的方法；②制定评判准则；③规定方案改进的途径；④给出初始方案；⑤迭代求解。
2.典型物流中心选址决策方法(1)单点物流中心选址方法所谓单点网点选址，就是指在规划区域内设置网点的数目惟一的物流设施的选点问题，其中主要包含以下几种方法：1交叉中值法选址在城市内建立物流设施，不可能不受限制任意选址，可能的情况是只能沿着相互交叉的街道选择某一处地点。
鲍摩-瓦尔夫(Baumol-Wolfe)模型
3.鲍摩－瓦尔夫(Baumol －Wolfe)模型（1）问题鲍摩－瓦尔夫(Baumol －Wolfe)模型是一个非线性整数规划模型，由运输费用和仓储费用构成的总费用最小。
从几个工厂经过几个配送中心，向用户输送货物。
对此问题，一般只考虑运费为最小时配送中心的选址问题。
这里所要考虑的问题是：各个工厂向哪些配送中心运输多少商品?各个配送中心向哪些用户发送多少商品？图6-5 鲍摩－瓦尔夫模型选址示意图（2） 建立模型（6.19）1111111111min ().10q q q q n m ik ik kj kj k k k K k i k j k k n m k ik kj i j q ik i k q kj j k k F c x c y v w G w x y x a s t y b w θδ===========+++⎧==⎪⎪⎪=⎪⎪⎨⎪=⎪⎪≠⎧⎪∑∑∑∑∑∑∑∑∑∑式中c ik —从工厂到配送中心，每单位运量的运输费：X ik —从工厂到配送中心运送的运量；c kj —通过配送中心向用户发送单位运量的运费；Y ki —从配送中心到用户运送的运量；W k —通过配送中心的运量；V k —配送中心的单位运量的可变费用；G k —配送中心的固定费用（与其规模无关的固定费用）；θ—规模指数系数（0<θ<1）；δk—为备选网点k 是否选中的决策变量（0--1 变量）。
总费用函数F(x)的第一项是工厂到节点的运输费用，第二项是节点到需求点的运输费用，第三项是配送中心的可变费用，第四项是配送中心的固定费用。
（3）模型的求解启发式算法是在可接受的费用内寻找最好的解的技术，但不一定能保证所得解的可行性和最优性。
鲍摩－瓦尔夫(Baumol －Wolfe)模型求解思想，通过求解边际成本，对规模仓储进行分段线性化。
边际成本表示网点在一定规模下的单位货物储存费用 ，即存储费用率，用边际成本成本代替可变费用率，从而把非线性函数转化为线性。
多个配送中心的选址问题
(二)多个配送中心的选址1．奎汉 - 哈姆勃兹( Kuehn-Hamburger )模型奎汉 -哈姆勃兹模型是多个配送中心地址选定的典型方法。
本方法是一种启发式的算法。
所谓的“启发式的算法”就是逐次求近似解得的方法，即简单地先求出初次解，然后经过反复计算修改这个解，使之逐步达到近似最佳解的方法。
奎汉 - 哈姆勃兹模型是按式(5-9 )〜式(5-11 )确定它的目标函数和约束条件的。
f(X)=(A hij +B hjk )X hijk + Z F j Z j+ X S hj( X X hijk )+ 匸D hk(T hk)(5-9)E X hijk =Q hk(5-10)D(hijk W Y hi (5-11)I j( E X hijk) W W j(5-12)式中h——产品(1，…，p);i —工厂(1，…，P)；j —仓库(1，…，P)；k—顾客( 1 ，…，p )；A hij —从工厂(j)到仓库(j)运输产品(h)的单位运输费；B hjk —从仓库( j) 到顾客(k) 之间配送产品(h) 时的单位运输费；X hijk —从工厂(i)经过仓库(j)向顾客运输产品(h) 的数量；F i—在仓库( j )期间的平均固定管理费；Z j—当E X hik>0时取1，否则取o；S hj (Y X hijk ) 在仓库(i)中，为保管产品(h) 而产生的部分可变费用(管理费，保管费，税金以及投资的利息等) ；D hk(T hk )—向顾客(k) 配送产品(h) 时，因为延误时间(T) 而支付的损失费；Q hk—顾客(k) 配送产品(h) 时，因为延误时间(T) 而支付的损失费；W j —仓库(j)的能力；I j L X hijk —各工厂经由仓库(j) 向所有顾客配送产品的最大库存定额。
这是用上述各项条件，按图的流程求解算术解的方法。
2 ．鲍摩－瓦尔夫 (Baumol －Wolfe) 模型(1)鲍摩－瓦尔夫模型的建立如图 5-4 所示的是从几个工厂经过几个配送中心，向用户输送货物。
数学建模配送中心选址
配送中心选址摘要本文针对配送中心的选址问题进行了研究。
在设计配送中心选址问题方案时，所追求的目标应该是总费用最小，因此应该建立优化模型来解决。
遵循从简单到复杂、从特殊到一般，循序渐进，逐步贴近实际情况的策略进行建模。
针对问题（1），先对92个城市的位置进行绘图分析,进而在92个城市之间建立最短路模型,将最短路和该省标号前20位的城市的产品销售量结合,求解出配送中心建立在各个城市中对前20位城市的运输成本,得到成本由高到低的排序,最终可得建立在35号城市,运输成本最低。
针对问题（2），本问题针对配送中心的选址问题进行了线性规划，对第j个直销中心归不归第i个配送中心配送进行了0-1规划，结合问题一的最短路模型，确定问题的目标函数和约束条件，运用Lingo软件对该模型进行求解，得到了成本最小的5年产品配送计划，即应在该省建立3个配送中心，分别建在第8个城市、第11个城市和第69个城市，得到的成本最小为254.033万元。
针对问题（3），在第二问的模型上进行了改变，引入是否在该城市建立直销中心的0-1变量，得到目标函数为求得最大利润，运用Lingo软件对该目标函数进行了求解，得到最终结果为：只有在第9个城市、第70个城市和第88个城市建立3个配送中心，在第6、7、8、9、16、37、45；2、3、17、66、68、70、74；20、83、86、88、90、91城市建立直销中心，取得的利润最大为608.6152万元。
针对问题（4），依据图1划分为两个区域，以62-4-39-38的公路为边界，左边的为一个地区，右边的为一个地区。
对不同的地区分别求解最低成本，最终得到最佳的5年产品销售、配送计划。
结果为：第一个地区在21、25城市建设2个配送中心，在12、13、21、22、23、23、25城市设立直销中心；第二个地区在16、53、57城市建设配送中心，在5、6、16、49、50、51、52、53、56、57、58、59、61城市设立直销中心。
冷链物流配送中心选址的多目标优化模型 物流专业数学建模。
冷链物流配送中心选址的多目标优化模型 2012 年 3月 30日冷链物流配送中心选址的多目标优化模型【摘要】针对冷链物流所配送物品易腐坏的特性，综合考虑了物流总成本和物流服务可靠度，建立了冷链物流配送中心选址多目标规划模型。
通过主要目标法将此模型转化为单目标优化模型，并运用运筹学软件lingo 对优化模型进行验证，最后通过实例计算，证明了该模型在冷链物流配送中心选址问题中的可行性和通用性。
【关键词】冷链物流；效益背反；优化模型；服务可靠度1背景介绍由于冷链中所配送物品易腐坏的特性，使得冷链物流配送中心选址与其他一般配送中心选址方法有所不同。
我国的物流发展本身就比较迟缓，而冷链物流又是物流中比较棘手的难题，所以我国关于冷链物流配送中心选址方面的文献比较少。
2003年姜大立、杨西龙建立了一种求解易腐坏物品配送中心连续选址问题的算法，注重的是模型求解算法的提出；2008年翟庆对冷链配送中心选址进行了研究，建立了一个双层成本模型；还有一些关于冷链配送中心选址的研究都是片面的考虑物流成本最小，但是很少考虑到服务可靠性的影响。
针对以上情况，建立冷链物流配送中心选址的多目标规划模型，在考虑了服务可靠性的情况下，使得物流总成本最小。
本文先是提出服务可靠性的不可忽略性，进而忽略其他次要的影响因素来筹划模型，构建出优化数学模型，并对模型进行分析，最后再举例对模型进行检验，从而得出结论。
2 冷链配送中心服务可靠性及计算方法冷链配送中心服务可靠性是物流服务水平的一个度量。
在冷链物流中，物流系统服务可靠性显得尤为重要。
配送中心系统的可靠性是配送中心内部所有有关联的物流作业可靠性的逻辑组合。
在这里，假设其他物流作业的可靠性均为1，服务可靠性只由配送过程决定。
在一定的条件下在客户规定的时间内将产品送到客户手中的概率为P ij 表示，则：()()()()j ij ij j ij ij j ij ij j ij t s FV s V p t V s p t T P -=≥=≤=≤=1p ij （1） T ij ——货物从配送中心i 送到客户j 所需要的时间；T j ——客户要求的送货时间；S ij ——配送中心i 与客户j 之间的距离；V ij ——车辆从配送中心i 到客户j 的速度分布函数，车辆的行驶速度因车辆性能和交通状况的不同而不同，具有一定的统计规律，呈现正态分布的特征。
数学建模--物流配送中心选址模型
物流配送中心选址模型姓名：学号：班级：摘要：在现代物流网络中，配送中心不仅执行一般的物流职能，而且越来越多地执行指挥调度、信息处理、作业优化等神经中枢的职能，是整个物流网络的灵魂所在。
因此，发展现代化配送中心是现代物流业的发展方向。
文章首先使用重心法计算出较为合适的备选地，再考虑到各项配送中心选址的固定成本和可变成本，从而使配送中心选址更加优化和符合实际。
关键词：物流选址；选址；重心法；优化模型；1．背景介绍1．1 研究主题如下表中，有四个零售点的坐标和物资需求量，计算并确定物流节点的位置。
1.2 前人研究进展1.2.1国内外的研究现状：国外对物流配送选址问题的研究已有60余年的历史，对各种类型物流配送中心的选址问题在理论和实践方面都取得了令人注目的成就，形成了多种可行的模型和方法。
归纳起来，这些配送中心选址方法可分为三类：（1）应用连续型模型选择地点；（2）应用离散型模型选择地点；（3）应用德尔菲（Delphi）专家咨询法选择地点。
第一类是以重心法为代表，认为物流中心的地点可以在平面取任意点，物流配送中心设置在重心点时，货物运送到个需求点的距离将最短。
这种方法通常只是考虑运输成本对配送中心选址的影响，而运输成本一般是运输需求量、距离以及时间的函数，所以解析方法根据距离、需求量、时间或三者的结合，通过坐标上显示，以配送中心位置为因变量，用代数方法来求解配送中心的坐标。
解析方法考虑影响因素较少，模型简单，主要适用于单个配送中心选址问题。
解析方法的优点在于计算简单，数据容易搜集，易于理解。
由于通常不需要对物流系统进行整体评估，所以在单一设施定位时应用解析方法简便易行。
第二类方法认为物流中心的各个选址地点是有限的几个场所，最适合的地址只能按照预定的目标从有限个可行点中选取。
第二类方法的中心思想则是将专家凭经验、专业知识做出的判断用数值形式表示，从而经过分析后对选址进行决策。
国内在物流中心选址方面的研究起步较晚，只有10余年历史，但也有许多学者对其进行了较深入的研究，在理论和实践上都取得了较大的成果。
多配送中心选址问题的数学模型及算法
基本上都只考虑 固定建设 费用 和运 输费用 ， 考虑存储费用 。 不
１ 引言
从物流发展 的趋势来看 ，配送 中心不仅 执行一般 的物流
在实际 的选址过程 中，存储 费用是 影响配送 中心运行效 益的
一
个重要因素。存储费用是物资在库存过程中发生的费用 ， 一
般与存储数量和存储 时间成正 比关 系 ，存储费用包括仓 库保
２ Ｓｈｏ ｆｎ ｒ ｉｎ Ｂ ｉｎ ｚ Ｕ ｉ ｒｉ， ｅｉｇ１ １４ ， ｈｎ） ． ｃ ｏｌ ｆ ｍａｔ ， ｅ ｉｇＷｕｉ ｎｖ ｓ ｙ Ｂ ｉｎ ０ ９ Ｃ ｉａ ｏ Ｉｏ ｏ ｊ ｅ ｔ ｊ １
Ａｂ ｔ ａ ｔ ｎ ｃ ｍｐ ｅ ｅ ｓｖ ｏ ｓｄ ｒ ｔ ｎ ｏ ｈ ｏ ｔ ｏ ｔｒ ｇ ，ｔ ｎ ｐ ｒａｉ ｎ ａ ｄ ｃ ｎ ｔ ｃ ｉｎ，ｈｅ ｐ ｐ ｒｅ ｔ ｂ ｉｈ ｓａ ｓ ｒ ｃ ：Ｉ ｏ ｒ ｈ ｎ ｉｅ ｃ ｎ ｉ ｅ ａｉ ｆｔ ｅ ｃ ｓｓｆ ｓｏ ａ ｅ ｒ ｓ ｏ ｔｔｏ ｏ ｓｒ ｔ ｏ ａ ｎ ｕ ｏ ｔ ａ ｅ ｓａ ｌ ｅ ｓ ｍａｈ ｍａ ｉａ ｄｅ ｉ ｄ ａ ｈ ｎ ｍｕ ｔ ｔ ｏ ｔｆ ｒａ ｍｕ ｔ ｌ ｉｔｉ ｕ ｉｎ ｃ ｎ ｅ ｃ ｉｎ ｐ ｏ ｌ ｍ，ｐ ｅ ｅ ｔ ｈ ｘ ｃ ｇ ｒ ｈ ａ ｄ ｔ ｅ ｔ ｌ ｍｏ ｌａｍｅ ｔ ｅ ｍｉ ｉ ｍ ｏａ ｃ ｓ ｏ ｌ ｐ ｅ ｄ ｓ ｒ ｔｏ ｅ ｔ ｒｌ ａ ｏ ｒ ｂ ｅ ｃ ｔ ｌ ｉ ｂ ｏｔ ｒ ｓ ｎ ｓ ｔ ｅ ｅ ａ ｔ ｏ ｉ ｍ ｎ ｌ ａ ｔ ａ ｐ ｏ ｉ ｔ ｎ ａ ｇ ｒｔ ｍ ｅ ｐ ｃｉ ｅｙ ａ ｄ ｏ ｔｉ ｓｓ ｌ ｔ ｎ ｔ ｅ ｍｏ ｅ ｓｎ ｐ ｃ ｆ ａ ｅ ａ ａ ｉ． ｐ ｒ ｘ ｍａｉ ｏ ｈ ｒ ｓ ｅ ｔ ｌ ｎ ｂ ａ ｎ ｏ ｕ ｉ ｏ ｔ ｄ ｌｕ ｉ ｇ ｓ ｅ ｉ ｃ ｅ ｓ ｎ ｓｓ ｏ ｌ ｉ ｖ ｏ ｈ ｉ Ｋ ｅ ｗｏ ｄ ：ｍｕ ｉ ｌ ｉ ｔ ｂ ｔ ｎ ｃ ｎ ｅ ； ｏ ａ ｉｎ； ｔ ｒ ｇ ｏ ｔ ｉ ｅ ｏ ｓ ｒ ｃ ｉｎ Ｃ Ｓ ｙ ｒｓ ｔ ｅ ｄ ｓｒ ｕ ｉ ｅ ｔｒ ｌ ｃ ｔ ｐ ｉ ｏ ｏ ｓｏ ａ ｅ ｃ ｓ；ｆ ｄ ｃ ｎ ｔ ｔｏ Ｏ ｘ ｕ
数学建模题目解答 物流中心位置选择
物流中心位置选择摘要本题为物流运输问题，属于有约束的线性规划模型。
本文通过对运输费用、需求量、供应量、运输方式、建设费用等因素之间关系的综合分析，建立了待建仓储选址的一般数学模型。
然后我们通过对模型进行编程求解，得出物流公司的新仓储位置选择和向销售中心供货的具体方案。
接着我们进行了灵敏度分析，并求解出了在需求量增大5%和仓储容量增大5%的情况下，新的仓储选址方案。
通过对供需有小幅改变的前后数据及图表的分析，我们得出了供需小幅改变不改变选址方案，配送方案也只有小幅改变的结论，作为对物流公司的一点建设性的意见。
然后我们分析了模型与实际的联系，并对模型的实际意义进行了建设性的分析，提出了有益的改进方案。
最后我们对基于“供求平衡”、“供求失衡”时方案关系及模型进行了几点分析、总结，得出了一切“供需”模型均可以转化为“供求平衡”模型，我们还进行了进一步探究，提出了“供需平衡”问题的求解思路，作为对“运输问题”的一种有益的探索和有价值的总结。
关键词数学模型 物流 供需 线性规划 选址1. 模型的分析本题属于物流公司运输的模型，通常该模型中包含了不同运输路径的单价，运输量，需求量，存储量以及运输成本。
由它们之间的关系可知，设第一个销售中心至第n 个销售中心的需求量分别为-，第一个仓库到第m 个仓库的存储量分别为-，而从第i 个仓库向第j 个销售中心运输的货物量为ij x ，运输成本为ij c ，总费用为f ，则有；i=1,2,3,…,nj=1,2,3,…,ms.t.j=1,2,3,…,m （*）i=1,2,3,…,ni=1,2,3,…,12 j=1,2,3,…,12 而对于当仓库存储的货物总量正好等于销售中心需求量时，*式则变为了：j=1,2,3,…,m通过求解如上的数学模型，我们就可以得出具体问题的最优化方案，我们就能在生活、工作中做出正确的选择！2. 本次大赛问题的分析分析本次题目中给出的物流公司建设新仓储的过程可知，需要考虑的因素包括：（1）销售中心货物的需求量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
物流配送中心选址模型
姓名：学号：班级：
摘要：在现代络中，配送中心不仅执行一般的职能，而且越来越多地执行指挥调度、信息处理、作业优化等神经中枢的职能，是整个络的灵魂所在。
因此，发展现代化配送中心是现代业的发展方向。
文章首先使用重心法计算出较为合适的备选地，再考虑到各项配送中心选址的固定成本和可变成本，从而使配送中心选址更加优化和符合实际。
关键词：物流选址；选址；重心法；优化模型；
1．背景介绍
1．1 研究主题
如下表中，有四个零售点的坐标和物资需求量，计算并确定物流节点的位置。
前人研究进展
1.2.1国内外的研究现状：
国外对物流配送选址问题的研究已有60余年的历史，对各种类型物流配送中心的选址问题在理论和实践方面都取得了令人注目的成就，形成了多种可行的模型和方法。
归纳起来，这些配送中心选址方法可分为三类：（1）应用连续型模型选择地点；
（2）应用离散型模型选择地点；
（3）应用德尔菲（Delphi）专家咨询法选择地点。
第一类是以重心法为代表，认为物流中心的地点可以在平面取任意点，物流配送中心设置在重心点时，货物运送到个需求点的距离将最短。
这种方法通常只是考虑运输成本对配送中心选址的影响，而运输成本一般是运输需求量、距离以及时间的函数，所以解析方法根据距离、需求量、时间或三者的结合，通过坐标上显示，以配送中心位置为因变量，用代数方法来求解配送中心的坐标。
解析方法考虑影响因素较少，模型简单，主要适用于单个配送中心选址问题。
解析方法的优点在于计算简单，数据容易搜集，易于理解。
由于通常不需要对进行整体评估，所以在单一设施定位时应用解析方法简便易行。
第二类方法认为物流中心的各个选址地点是有限的几个场所，最适合的地址只能按照预定的目标从有限个可行点中选取。
第二类方法的中心思想则是将专家凭经验、专业知识做出的判断用数值形式表示，从而经过分析后对选址进行决策。
国内在物流中心选址方面的研究起步较晚，只有10余年历史，但也有许多学者对其进行了较深入的研究，在理论和实践上都取得了较大的成果。
北方交通大学鲁晓春等对配送中心的重心法地址做出了深入的研究，认为原有的重心法存在着问题，并把原有的计算公式用流通费用偏微分方程来取代。
中国矿业
大学周梅华也用重心法和微分法相结合的方法在徐州矿业集团自用型配送中心的选址中进行应用，取得了很好地效果。
对于第三类物流中心选址方法，国内进行的研究相对较少，主要在物流园区的布局规划中有所应用[1]。
2.建模
假设
(1) 假设需求量集中以某一点
(2) 模型没有区分在不同地点建设仓库所需的资本成本，以及与在不同地点经营有关的其他成本差别，而只计算运输成本。
(3) 不考虑需求点的库存策略。
(4) 分销渠道内只有一种产品或者有多种产品，但假设其分拨储运方式及其费用率均相同。
(5) 备选物流中心有容量限制，且限制容量已知。
[2]
概念模型
假设有n个客户P1，P2，P3，…,P n分布在同一个平面上，其坐标分别为（x i,y i）,客户需求量为wi,费用函数为配送中心与客户间距离和相应的运费、需求量的乘积，确定P0(x0,y0),使总运用最小。
数据模型
设总运费Z为：
w i---与第i个点对应的权重，例如需求；
x i,y i---第i个需求点的坐标；
n---需求点的总数目
x s,y s---服务设施的坐标；
精确重心法目标函数为双变量系统，分别对x s和y s求偏导，并令导数为零，求得隐含最优解的等式[2]：
软件求解
用Excel求解[3]：
①在Excel中输入数据，并且假设原点坐标为（1，1），在G3中输
入“=SQRT(($D$9-D3)^2+($E$9-E3)^2)”,并将右下角的十字光标下拉复
制公式。
权重为：距离×运输费率×物资需求量
②规划求解
③第一次迭代求得重心坐标为（,）此时总费用为。
④第二次迭代求得重心坐标（,），此时总费用为。
⑤第100次迭代求得重心坐标为（,），此时总费用为。
模型分析
1)敏感性报告
2）运算结果报告
2)极限值报告
关于重心法，尽管理论上能够求得比较精确的最优化结果，但是在现实的作中，却不一定容易实现。
首先，在精确的最优化解的位置上由于其
他因素的影响，决策者考虑其他因素后，又是不得不放弃这一最优化解的
结果，转而选择现实中满意的其他方案。
其次，在该模型中将距离刚坐标
来表示，这样就把运输费用看成是两点间直线距离的函数，这一点与实际
是不相符的，虽然可通过在距离计算公式中增加一个调整系数来加以修
正，但系数的合理选取还是有一定的难度。
最后，当供给点和需求点同在
一个系统中时，求得的“重心”的最优性是在供给点必须通过该“重心”再到达需求点的前提下取得的，而事实上，这个前提并不是真正必须的，在很多情况下，由于明显的不合理性而会对结果进行调整，调整的结果也难以保证其最优性。
[4]
下面对重心法模型进行改进，根据重心法选择的地点有可能在江流之上或者在街道中间，此时就需要根据客观条件，放弃最有位置而另外选择一比较满意的位置,还需要对重心法求得的坐标点进行分析，当考虑可变成本、固定成本和决策权值时，最佳选址地点是什么。
3.模型改进
假设
设有n个零售点，它们的坐标是（x i,y j）(i,j=1,2,3,……,n),配送中心的坐标是（x0,y0）,假设：
（1）运输费用只与配送中心和配送点的直线距离有关，不考虑城市交通情况；
（2）选择配送中心时，不考虑配送中心所在地理位置，不考虑城市交通情况；
（3）选择配送中心时，不考虑配送中心所处地理位置的地产价格；
（4）各需求点的需求量已知；
（5）可以估计各个备选配送中心的固定费用(包括基本建设费和固定经营费)；
（6）可以估计经营管理产生的可变费用，并在总费用中加以考虑。
数学模型
H = h j w j d j(j=1,2,3, ……,n)
Min F(x)=ρ1H1+ρ1νIi(W j)θ+ρ2F Ii
其中：h j---从配送中心到零售店i的发送费率；
w j---从配送中心向零售店i的发送量；
d j---从配送中心到零售店i的距离；
I i一由重心法得到的各个备选地址；
W j---各个零售店的需求量之和；
H Ii---指备选地址I．总的运输费用；
νIi---指各备选配送中心考虑经营管理的单位可变费用；
νIi(W j)θ---指各备选地址I．总的可变费用；
F Ii---指各备选地址I 的固定费用；
θ---经验值，且θ∈(0，1)；
ρ1，ρ2---权系数 (可以根据决策者的需求来定)且ρ1+ρ2=l，其中ρ1，ρ2∈(0，1)。
假设ρ1=，ρ2=。
根据上面的例题，可知有三个方案（,），（,）和（,）。
设方案1的可变费用为350，固定费用为400；方案2的可变费用为400，固定费用为350；第三个方案的可变费用为500，固定费用为340。
根据公式软件求解的：
有结果可知此时方案一的总费用最低，为，是最佳方案。
4．结论
配送中心是提高流通企业组织化程度、实现集约化经营、优化社会资源配置、创造规模效益、推动流通科技进步、实现流通现代化的有效形式。
重心法模型是连续型模型，相对于离散模型来说，其物流配送中心地点的选择是不加特定限制的，有自由选择的长处，而且由于改进模型不仅考虑了运输成本，而且还考虑了配送中心的可变运营成本、固定成本和决策权系数，比传统重心法又有了明显的优越性，因此有较好的实用性。
还可以推广到其它的选址问题上，如投资问题，不足之处在于只能解决单配送中心的选址问题，如果要用于多配送中心的选址还需改进。
参考文献
[1].物流设施选址模型间就现状及新思考［EB/OL］.
[2] 基于重心法的配送中心选址研究及应用［EB/OL］.
[3]李孟涛，徐建.物流常用数学工具实验教程[M].北京：中国人民大学出版社，2011-4：25-28.
[4] 蒋长兵，王姗姗. 精确重心算法在物流节点选址中的应用[J]. 物流技术，2005(9):32-36.。