现代控制工程第一章答案
现代控制理论第版课后习题答案

习题答案Document number : WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:令0(s) = y,则,=册所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压"⑴为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻R?上的电压作为输出量的输出方程。
解:由图,令ii =x}J2 =x2,u c =x3l输出量y = R2X2• & 1 1Rg + L, Xj + x y = u有电路原理可知:L2XI+R2X2=X3= x2 +C x3写成矢量矩阵形式为:14两输入也,两输出比,比的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令x, = y,吃=,,兀3 =,,则有相应的模拟结构图如下:并画岀相应的模拟结构图10 £初・ 117/ \ 6(5 + 1) -4 V 3 a解:VV (5)= ------ ---------- = --------- +— + ------------+ 丄s(s + 2)(s + 3y (s + 3y 5 + 3 s + 2 s1- 7给定下列状态空间表达式y = [0 0 1 x 2_V 3_(1) 画出其模拟结构图 (2) 求系统的传递函数解:-1 0(2) W(s) = (s/ — A)= 25 + 31 — 1 5 + 31-8求下列矩阵的特征矢量_0 1 0 _ (3)32-12 -7 -6-1 0解:A 的特征方程 |刀—A|= —3 2-2 =23+6/l 2 + lU + 6 = 0 1272 + 6解之得:入=—1,/?2 = —2,/?3 = —31-6 (2)已知系统传递函数W(s)=6(5 + 1)5(5 +2)(5+ 3)2,试求岀系统的约旦标准型的实现,■ 010 '/AiP113 0 2 P11 =— P21 -12 -7 -6_ ■皿■叽当人=一1时,令內=1Ai-1 (或令Pll =一1,得片=P21 =1 )1■ 0 1 0 ■P\2Pn 3 02 Pll =-2 P22-12 -7 _6. L/^2.解得:”22=一2卩2丿32 =>12'P22 =P\2(或令从2 T,得4 = "22“320 1当人=一3时, 3 0 -12 -71 -2£ 2解得:〃23=-3/心〃33=3门3令戸3 = 1得1・9将下列状态空间表达式化成约旦标准型(并联分解)~4 1 -2■3 fX 2 = 1 0 2X 2 + 2 7⑵-.1-1 d_5 3_得解得:P 2] =^31 =-P\\当人=一2时,令门2 = 2 得P 2 = 2 -41'4 1 -2'当人=3时, 1 02=3 "211 -13 .解之得 Pl2 = P12 + 1,P22 = “32 令 Pl2 =1并联联结(第3版教材)已知如图1・22所示的系统,其中子系统1、2的传递函数阵分别求系统的闭环传递函数_4 1 -2 P11PwT 1 0 2 "21 =3 P21 + 11 -1 3 -■叽丄 当An =3时,解:A 的特征方程2-4 -1 |27 - A| = -12 -1 1 2-2 =(2-1)(2-3)2 =02- 3解之得 P2! =Pj] =P11令/“iPw■fP21 = 1■叽丄当人=1时, 解之得 P13 = °,“23 = 2^33 令 “33 = 1约旦标准型1- 10已知两系统的传递函数分别为W|(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解: (D 串联联结MlR = 得10 -1得1-H (第2版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:M2已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数I】的系数b(即控制列阵)为⑴b=;解法1 :解法2 :求T,使得厂,;得宀鳥所以T=所以,状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数屛‘。
现代控制理论第3版课后答案

现代控制理论第3版刘豹唐万生机械工业出版社课后全部 答案第一章答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-3取输入双输由系统模拟结构图系统的状态方程如下:图1-2添统方块结构图KnS(s)解:系统的模拟结构图如x 1 x 2令(s ) y ,则 y X 1所以,系统的状态空间表达式及输出方程表达式为X i X 2 X 3y i 0 0 0 0 0X 4 X 5 X 6i-28所示。
以电压u(t)为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻R 2上的电压作为输出量的输出方程。
X 2K bJ2X 3? KP KnX 3— X 3 X 4J 1 J 1 ?X 4X 3?X 5 K 1X 3 K 1X 6 1K p X 5 —— X J iJ iX 6K i K P X i K iK PX 6 K iu K PX i ? X 2 ? X 3 ? X 4 ? X 5?X 60 i 0 0 0 0 00 0K i-00 K b J2K J i i K i 0 0 0 0K n i J i J 0 0 0 0 00 0 K p J i 0 K i K i K?X i X 2 X 3 X 4 X 5 X 60 0 0 0 u0 K i K pi-2有电路如图x 4解:由图,令 i 1 x 1,i 2 x 2,u c x 3 ,输出量 y R 2x 2图i-30双输入--双输出系统模拟结构图x 2 x 3有电路原理可知: Ri x 1 L 1 x 1 x 3uL 2 x 2 R 2x 2 x 3 既得x i x 2 Cx 3 x i?x 2?x 3R i i i x i x 3 u L i L i L i R 2 i-- x 2 --- x3L 2L 2i i —x 1 — x 2 C Cy R 2x 2写成矢量矩阵形式为: R i o _____ x i L io x 20 o x 3 1 C i iLi x i i 匚x 2 0 u L2 x3 00 R 2 L 2 1 C x i0 R 2 0 x 2x 3i-4两输入小,U2,两输出yi ,i-30所示,试求其状态空间表达式和传递函数阵。
现代控制理论习题解答(第一章)

Ra
La
i f = 常数
ua
f ia D J
ω
ML
【解】: 设状态变量为:
题 1-2 图
⎡ x1
⎢ ⎣
x
2
⎤ ⎥ ⎦
=
⎡ia ⎢⎣ω
⎤ ⎥ ⎦
其中 ia 为流过电感上的电流, ω 电动机轴上的角速度。 电动机电枢回路的电压方程为:
eb 为电动机反电势。 电动机力矩平衡方程为
•
ua = La ia + Ra ⋅ ia + eb
(4) y (4) + 3y + 2y = −3u + u
【解】:
5
在零初始条件下,方程两边拉氏变换,得到传递函数,再根据传递函数求状态空间 表达式。 此题多解,一般写成能控标准型、能观标准型或对角标准型,以下解法供参考。 (1)传递函数为:
状态空间表达式为:
G(s) =
2
s3 + 2s2 + 4s + 6
1⎤
R 2 C1 −1
R2C2
⎥ ⎥ ⎥
⎡ ⎢ ⎣
x1 x2
⎥⎦
⎤ ⎥ ⎦
+
⎡ ⎢ ⎢ ⎣
1
R1C1 0
⎤ ⎥⎥u i ⎦
y = u0 = [0
1]⎢⎡
⎣
x1 x2
⎤ ⎥ ⎦
(2)
设状态变量: x1 = iL 、 x2 = uc 而
1
根据基尔霍夫定律得: 整理得
•
iL = C uc
•
ui = R ⋅ iL + LiL + uc
•
M D = J ω + fω + M L
《现代控制理论》课后习题答案(完整版)
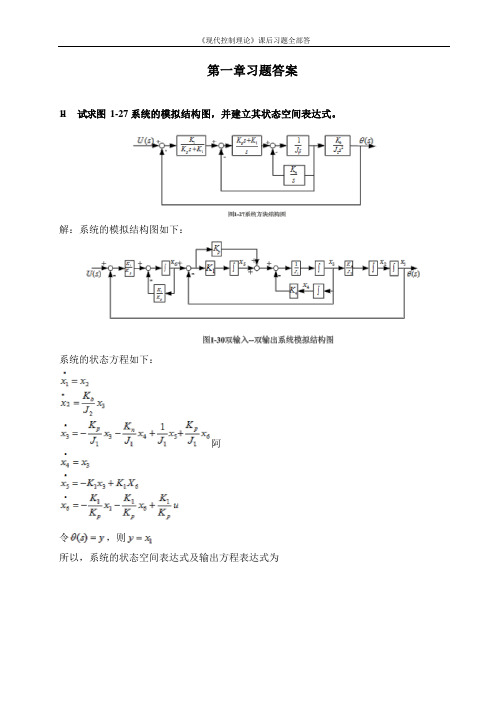
1-1
解:系统的模拟结构图如下:
系统的状态方程如下:
阿
令 ,则
所以,系统的状态空间表达式及输出方程表达式为
1-2
解:由图,令 ,输出量
有电路原理可知:既得
写成矢量矩阵形式为:
1-3
1-4 两输入 , ,两输出 , 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
当时,
解之得 令 得
当时,
解之得 令 得
当 时,
解之得令得
约旦标准型
1-10
试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:(1)串联联结
(2)并联联结
1-11
求系统的闭环传递函数解:
求系统的闭环传递函数解:
1-12已知差分方程为
试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为
(1)
解法1:
解法2:
求T,使得得所以
解:系统的状态空间表达式如下所示:
1-5
列写其相应的状态空间表达式,并画出相应的模拟结构图。解:令 ,则有
相应的模拟结构图如下:
1-6
解:
1-7
‘
(1)画出其模拟结构图
(2) 求系统的传递函数解:
(2)
1-8
(3)(3)
解:A的特征方程
解得: 令得
(或-9
(2)
解:A的特征方程
(完整word版)现代控制原理习题答案

第一章自动控制的一般概念一.是非题1.开环控制是一种反馈控制(×)2.开环控制的稳定性比闭环控制的稳定性要好(×)3.线形系统的主要特点是具有齐次性和叠加性(√)4.线性定常系统的各项系数是与时间有关的 (×)5.闭环控制的控制精度在很大程度上由形成反馈的测量元件的精度决定的(√)6.自动控制就是采用控制装置使被控对象自动的按给定的规律运行,使被控对象的一个或数个物理量能够在一定的精度范围内按给定的规律变化(√)7.自动控制系统有两种最基本的控制形式即开环控制,闭环控制(√)二.选择题1.下述(D)不属于对闭环控制系统的基本要求。
(A)稳定性(B)准确性(C)快速性 (D)节能性2.自动控制系统一般由(D)组成(A)输入和输出(B)偏差和反馈 (C)控制量和扰动(D)控制器和被控对象3.在组成系统的元件中,(A),即为非线形系统(A)只要有一个元、器件的特性是非线形的(B)有且只有一个元、器件的特性是非线形的(C)两个及两个以上的元、器件的特性是非线形的(D)所有的元器件的特性都是非线形的4.古典控制理论形成于(D)(A)2000年前 (B)1000年前(C)100年前(D)20 世纪20—40年代 5.对于一个自动控制、系统的性能要求可以该概括为三个方面:(A)快速性和准确性(A)稳定性(B)定常性(C)振荡性(D)抗干扰性6.传递函数的概念除了适用于定常系统之外,还可以描述(A)系统(A)线形时变(B)非线性定常(C)非线形时变( D )以上都不是 7.在控制系统中被控制的物理量是被控量,直接改变被变量的元件称为(A)(A)执行元件 (B)控制元件(C)调节器(D)测量元件8.在通常的闭环控制系统结构中,系统的控制器和控制对象共同构成了(B)(A)开环传递函数(B)前向通道(C)反馈通道(D)闭环传递函数 9.下面数学模型中(D)是线形定常系统的外部描述(A)传递函数(B)微分方程 (C)频率特性(D)前面三种都是三.填空题1.自动控制系统的两种最基本形式即开环控制 ,闭环控制。
《现代控制理论》课后习题答案1.pdf

《现代控制理论》第一章习题解答1.1 线性定常系统和线性时变系统的区别何在? 答:线性系统的状态空间模型为:xAx Bu y Cx Du=+=+线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和中的各分量均为常数,而对线性时变系统,其系数矩阵D A ,B ,C 和中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
D 1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别? 答: 传递函数模型与状态空间模型的主要区别如下:传递函数模型(经典控制理论)状态空间模型(现代控制理论) 仅适用于线性定常系统 适用于线性、非线性和时变系统用于系统的外部描述 用于系统的内部描述基于频域分析基于时域分析1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于阶传递函数n 1212101110()n n n n n n n b s b s b s b G s d s a s a s a −−−−−−++++=+++++"",分别有[]012101210100000100000101n n n xx ua a a a yb b b b x du−−−⎧⎡⎤⎪⎢⎥⎪⎢⎥⎪⎢⎥=+⎪⎢⎥⎨⎢⎥⎪⎢⎥⎪−−−−⎣⎦⎪=+⎪⎩"" ###%##"""⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⑴ 能控标准型:[]0011221100010********001n n n b a b a xa x ub a b y xdu −−−⎧−⎡⎤⎡⎤⎪⎢⎥⎢⎥−⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=−+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪−⎣⎦⎣⎦⎪=+⎪⎩"" "######""⑵ 能观标准型:[]1212001001001n n p p x x up y c c c x du⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎪=+⎩"" ##%##""⑶ 对角线标准型: 式中的和可由下式给出,12,,,n p p p "12,,,n c c c "12121012111012()n n n n n n n n nb s b s b s bc c c G sd d s a s a s a s p s p s p −−−−−−++++=+=++++++−−−"""++能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1外,其余全为0。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论习题解答(第一章)

g
题 1-3 图 2
Y2 (s)
3
U (s)
K1
x6
x6
T1 1
T1
K2
x4
x4
T2 1
K3 x2
x2 1 T4
T2
x3
x3
x5
x5
K5
T5
1 T5
写成矩阵的形式得:
题 1-3 图 3
x 1
=− 1 T4
x1
+
1 T4
x2
x2 = K 3 (x4 − x3 )
x3 = x2
x 4
1⎤
R 2 C1 −1
R2C2
⎥ ⎥ ⎥
⎡ ⎢ ⎣
x1 x2
⎥⎦
⎤ ⎥ ⎦
+
⎡ ⎢ ⎢ ⎣
1
R1C1 0
⎤ ⎥⎥u i ⎦
y = u0 = [0
1]⎢⎡
⎣
x1 x2
⎤ ⎥ ⎦
(2)
设状态变量: x1 = iL 、 x2 = uc 而
1
根据基尔霍夫定律得: 整理得
•
iL = C uc
•
ui = R ⋅ iL + LiL + uc
(4) G(s)
=
s3
s2 + 2s + 3 + 3s 2 + 3s + 1
【解】: 此题多解,一般可以写成能控标准型、能观标准型或对角标准型,以下解法供参考。 (1)
⎡0 1
x
=
⎢ ⎢
0
0
⎢⎣− 6 −11
y = [1 1 1]x
0 ⎤ ⎡0⎤
1
⎥ ⎥
x
现代控制理论第一章答案
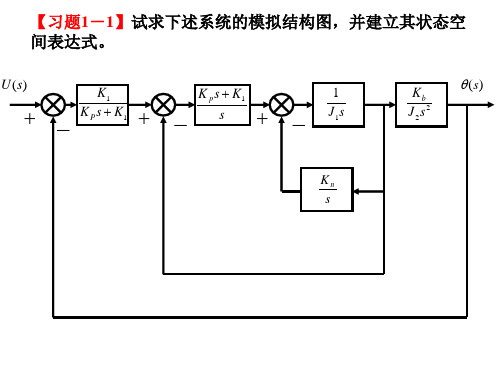
a0 3 a1 7 a2 5 b0 2 b1 1 b2 0 b3 0
标准型实现
1 0 0 0 x 0 u 0 x 0 1 3 7 5 1
y (b0 a 0 b3 ) (b1 a1b3 ) (b2 a 2 b3 )x 2 1 0x
1 0 0 0 x 0 0 1 x 0 u 3 7 5 1
y (b0 a 0 b3 ) (b1 a1b3 ) (b2 a 2 b3 )x 2 3 1x
【习题1-6】已知系统传递函数
10( s 1) (1) W ( s ) s ( s 1)(s 3) 6( s 1) (2) W ( s ) s ( s 2)(s 3) 2
x1
0 0 0 x 0 K1 Kp 0
1
0 Kb 0 J2 Kp 0 J1 0 K1 0 0 0 Kn
0 0 1 J1 0 0 0
0 0 Kp J1 K1 K1 Kp 0
0 0 0 0 1 0 J1 x 0 0 K1 Kp 0 0 0
y 0 0 1x
【解】(1)画模拟结构图的步骤 第一步:画出三个积分器 第二步:画出各增益系数和信号综合点 第三步:根据各变量的相互关系用信号线连接起来 (2)求系统的传递函数矩阵
Y ( s) 2s 2 7 s 3 1 W ( s) c( sI A) b U ( s) ( s 1)(s 2)(s 3) 2s 1 ( s 1)(s 2)
1 0
4 3
【习题1-10】已知两个子系统的传递函数分别为:
《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得2221332222213*********1x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有 相应的模拟结构图如下:1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P (或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=14222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ) 当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23132313311201214p p p p p p解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为 (1)⎥⎦⎤⎢⎣⎡=11b 解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
《现代控制理论》课后习题全部答案(最完整打印版)
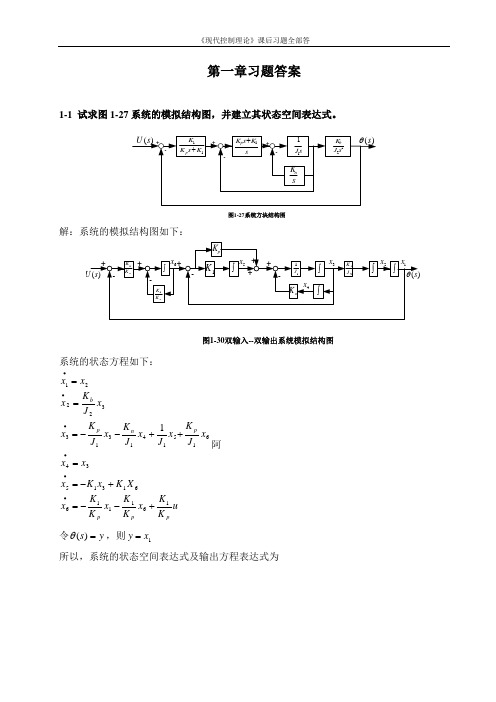
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
《现代控制理论》课后习题答案1

G ( s) =
每一个环节的状态空间模型分别为:
1 2s + 5 ⋅ s+3 s+5
2 = −5 x 2 + u1 ⎧x ⎩ y = −5 x 2 + 2u1
1 = −3x1 + u ⎧x ⎨ ⎩ y1 = x1
又因为 y1 = u1 , 所以
和 ⎨
1 = −3 x1 + u ⎧x ⎨ 2 = x1 − 5 x 2 ⎩x y = 2 x1 − 5 x 2
由此得到的 d 就是状态空间实现中的直接转移项 D 。 1.6 在例 1.2.2 处理一般传递函数的状态空间实现过程中,采用了如图 1.12 的串联分解, 试问:若将图 1.12 中的两个环节前后调换,则对结果有何影响? 答: 将图 1.12 中的两个环节调换后 y a(s)
5
1.10
已知单输入单输出时不变系统的微分方程为:
(t ) + 3 y (t ) = u ( t ) + 6u ( t ) + 8u ( t ) y (t ) + 4 y
试求:(1)建立此系统状态空间模型的对角线标准形; (2)根据所建立的对角线标准形求系统的传递函数。 答: (1)由微分方程可得:
s 2 + 6s + 8 2s + 5 G(s) = 2 = 1+ 2 s + 4s + 3 s + 4s + 3
记
G 1 (s) =
其中,
c c 2s + 5 2s + 5 = = 1 + 2 , s + 4 s + 3 ( s + 1)( s + 3) s + 1 s + 3
王金城现代控制理论第一章_习题答案

王金城化工出版社第1章习题参考答案:1-1(a )选123123,,,,,y y y v v v 为状态变量,根据牛顿定律,对1M ,有()11112121dv M g K y K y y M dt---= 对2M ,有()()222123232dv M g K y y K y y M dt+---= 对3M ,有()33323433dv M g K y y K y M dt+--= 令312112233415263,,,,,dy dy dyx y x y x y x v x v x v dt dt dt=========,整理得 ()()()122214253641112334233251262322233,,,,,K K K x x x x x x x x xg M M K K K K K x K K xx x g x x x g M M M M M +====-++++=-++=-+()()()1221123222223433300010000001000000010000001100010000K K K M M x x g K K K K M M M K K K M M ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥+-⎢⎥⎢⎥⎣⎦100000010000001000y x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(b )选12,12,,y y v v 为状态变量,根据牛顿定律,对1M ,有()11121111dv M g B v v K y M dt+--= 对2M ,有()22221212dv f M g B v B v v M dt+---= 令1211223142,,,dy dyx y x y x v x v dt dt ======,整理得 11113243134111,,K B Bxx x x x x x x g M M M ===--++ ,112434222B B B f x x x g M M M +=-++所以状态空间描述为1111111122220010000001000011100K B B xx g f M M M B B B M M M ⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎢⎥-⎢⎥⎣⎦⎣⎦10000100y x ⎡⎤=⎢⎥⎣⎦1-2(a )取电感电流i 和电容电压u 为状态变量,列回路方程122c rc c c u u R (i )u u R di L u u dt u du C dt R ⎧=+++⎪⎪⎪=+⎨⎪⎪=⎪⎩令12c x i,x u,y u ===()1212121212112121211r R R R R L(R R )L(R R )L(R R )xx u R C R RC(R R )C(R R )-⎡⎤⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥=+⎢⎥⎢⎥--⎢⎥⎢⎥+++⎣⎦⎣⎦1222121212r R RR R y x u R R R R R R ⎡⎤=--+⎢⎥+++⎣⎦ (b )选择回路电流a i 和电枢角速度ω为状态变量,有aa a a ae di u R i L K dt ω=++ 力矩平衡方程:a a d J B K i ,dtωω+= 其中a K 为转矩常数 1a a e a a a a adi R K i u dt L L L ω=--+a a K d B i dt J J ωω=-- 令12a x i ,x ,ω==有10a e a aa a R K L L L xx u K B JJ -⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦ , []01y x ω==1-3 (1)传递函数为3221375Y(s )U(s )s s s =+++将传递函数中的公因子提出,于是有3123211375Y(s )s U(s )s s s----=+++ 按梅逊公式构建系统的状态变量图能控标准形:0100001057131x x ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦u []200y x =能观标准形:0052107001130x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y =x(2)传递函数为:2332132223123Y(s )s s s U(s )s s s s----++==++++ 按梅逊公式构建系统的状态变量图能控标准形:010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦[]210y x =能观标准形:003210010120x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =(3)传递函数为:3212332123324515471547Y(s )s s s s s s U(s )s s s s s s------+++---==+++++++ 按梅逊公式构建系统的状态变量图状态空间描述为:010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]514y x u =---+(4)①12121221212121b s b b s b s Y(s )U(s )s a s a a s a s ----++==++++ 状态空间描述为:1322140101xx u x a a x ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦ ,[]21y b b x =②22121201200111s c Z(s )c c Y(s )c s c s c s s c c ---==++++ 状态空间描述为:332144000101x x y c c x x c c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦ ,301z x c = 两系统串联,得112122332121440001000001000100x x a a x x u x x c c b b x x c c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦(5)由G(z)有,y(k+3)+4y(k+2)+5y(k+1)+2y(k)=u(k)令12312x (k )y(k )x (k )y(k )x (k )y(k )=⎧⎪=+⎨⎪=+⎩ 1230100100102541x (k )x(k )x (k )u(k )x (k )⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦[]123100x (k )y(k )x (k )x (k )⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(6)由G(z)有,y(k+3)+6y(k+2)+11y(k+1)+6y(k)=2u(k+2)+u(k+1)+2u(k)01001001061161x(k )x(k )u(k )⎡⎤⎡⎤⎢⎥⎢⎥+=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]123212x (k )y(k )x (k )x (k )⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1-4 (a )化简系统结构图得系统状态空间描述:1234010000010024220025025x x x u x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ []0100y x =(b) 化简系统结构图得系统状态空间描述:1112221323255223735353xx u ///x x u ////--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ []110y x = []201y x =1-5 (1) 传递函数为21233212332322461246s s s s s G(s )s s s s s s ------++++==++++++ 能控标准形:010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]231y x =能观标准形:006210430121x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =(2)传递函数为24422431332132s s s G(s )s s s s -----+-+==++++ 能控标准形:01000001000001020301xx u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦[]1300y x =-能观标准形:00021100030103000100x x u -⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=+⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦[]0010y x = 1-6(1) 24512122123123(s )(s )G(s )(s )(s )(s )s s s ++-==++++++++状态空间描述:100102010031x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]12122y x =- (2)223533313313(s )G(s )(s )(s )s s (s )+--==+++++++ 状态空间描述:310003010011x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]333y x =-- 1-7(1)∵31I A ()()λλλ-=++ 1213,λλ=-=-∴1003A -⎡⎤=⎢⎥-⎣⎦11111111,p Ap ,p λλ⎡⎤=-==⎢⎥⎣⎦,22222131,p Ap ,p λλ⎡⎤=-==⎢⎥-⎣⎦∴1111P ⎡⎤=⎢⎥-⎣⎦1111112P ---⎡⎤=-⎢⎥-⎣⎦ 11112B P B -⎡⎤==⎢⎥-⎣⎦∴11020312x x u ⎡⎤⎢⎥-⎡⎤=+⎢⎥⎢⎥-⎣⎦⎢⎥-⎢⎥⎣⎦(2)1230123I A ,,,λλλλ-==-=-=-∴100020003A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦111111111,p Ap ,p λλ⎡⎤⎢⎥=-==-⎢⎥⎢⎥-⎣⎦,2222212212,p Ap ,p λλ⎡⎤⎢⎥⎢⎥=-==-⎢⎥⎢⎥⎢⎥⎣⎦333331333,p Ap ,p λλ⎡⎤⎢⎥=-==-⎢⎥⎢⎥⎣⎦∴1111231132P ⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥-⎢⎥⎣⎦137272304027162B P B -⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎣⎦∴37271002020304000327162x x u ⎡⎤⎢⎥-⎡⎤⎢⎥⎢⎥=-+--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦(3)519400433030114003433114j x j x j j ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥-+⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦+⎢⎥⎢⎥⎣⎦1-8 (1)∵A 为友矩阵123012I A ,,λλλλ-====∴ 110010002A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 101112124P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 1111B P B --⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦ ∴100101010021x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(2)212331031I A ()(),,λλλλλλ-=--====310030001A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 120112111P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 11335234B P B --⎡⎤⎢⎥==-⎢⎥⎢⎥-⎣⎦ ∴3101330305200134x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦1-9(1)110061031002P -⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦111000062300100111000152020233302100313000222AP AP -⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦1106203502BP B -⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦203640C CP ⎡⎤==⎢⎥⎣⎦ 11000621102203333502022xx u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦203640y x ⎡⎤=⎢⎥⎣⎦ (2)①1111I A I P AP P P P AP P (I A)P λλλλ-----=-=-=-11I A P I A P P P I A I A λλλλ---=-=-=-∴特征值不变②1111G(s )C(sI A)B CP(sI P AP )P B ----=-=- 111C P(sI P AP )P B ---⎡⎤=-⎣⎦11111C P(sI )P PP APP B C(sI A )B -----⎡⎤=-=-⎣⎦∴传递函数不变1-10证明:11G (s )c(sI A)b -=- 12G (s )c(sI A)b -=- ∵T T TA A ,b c ,c b ===∴12T T T T T T TG (s )b (sI A )c b (sI )A c -⎡⎤=-=-⎣⎦ [11T T T T T Tb (sI A )c b (sI A)c --⎤⎡⎤=-=-⎦⎣⎦11TTc(sI A )b G (s )-⎡⎤=-=⎣⎦ ∵系统为单输入单输出,11T G (s )G (S )= ∴两者传递函数相同。
现代控制工程第一章答案

《现代控制理论》第1章习题解答1.1 线性定常系统和线性时变系统的区别何在? 答:线性系统的状态空间模型为:x Ax Buy Cx Du=+=+线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和D 中的各分量均为常数,而对线性时变系统,其系数矩阵A ,B ,C 和D 中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别? 答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于n 阶传递函数1212101110()n n n n n n n b s b s b s b G s d s a s a s a ------++++=+++++, 分别有⑴ 能控标准型: []012101210100000100000101n n n x x u a a a a y b b b b x du---⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪----⎣⎦⎣⎦⎪=+⎪⎩ ⑵ 能观标准型: []00112211000100010001001n n n b a b a x a x u b a b y x du ---⎧-⎡⎤⎡⎤⎪⎢⎥⎢⎥-⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=-+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪-⎣⎦⎣⎦⎪=+⎪⎩⑶ 对角线标准型: []1212001001001n n p px x u p y c c c x du⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎪=+⎩ 式中的12,,,n p p p 和12,,,n c c c 可由下式给出,12121012111012()n n n n nn n n nb s b s b s bc c c G sd d s a s a s a s p s p s p ------++++=+=++++++++--- 能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1外,其余全为0。
现代控制系统第十二版课后习题1章答案中文版吐血整理

第1章控制系统导论基础练习题下面的系统都可以用框图来表示它们的因果关系和反馈回路(有反馈时)。
试辨识每个方框的功能,指出其中的输入变量、输出变量和待测变量。
必要时请参考图1.3。
E1.1描述能测量下列物理量的典型传感器:(a)线性位置(b)速度(或转速)(c)非重力加速度(d)旋转位置(或角度)(e)旋转速度(f)温度(g)压力(h)液体(或气体)流速(i)扭矩(j)力【解析】(a)位置传感器:用来测量机器人自身位置的传感器。
(b)转速传感器:是将旋转物体的转速转换为电量输出的传感器。
(c)重力加速度传感器:能够感知到加速力的变化的传感器。
(d)角度传感器:用来检测角度的传感器。
(e)转速传感器:是将旋转物体的转速转换为电量输出的传感器。
(f)温度传感器:指能感受温度并转换成可用输出信号的传感器。
(g)压力传感器:是能感受压力信号,并能按照一定的规律将压力信号转换成可用的输出的电信号的传感器。
(h)流量传感器:测定吸入发动机的空气流量的传感器。
液体流量计传感器:用来测量各种导电液体介质的体积流量的传感器。
(i)扭矩传感器:将扭力的物理变化转换成精确的电信号的传感器。
(j)测力传感器:在受到外力作用后,粘贴在弹性体的应变片随之产生形变引起电阻变化,电阻变化使组成的惠斯登电桥失去平衡输出一个与外力成线性正比变化的电量电信号的传感器。
E1.2描述能实现下列转化的典型执行机构:(a)流体能到机械能(b)电能到机械能(c)机械形变到电能(d)化学能到运动能【解析】(a)液压马达、液压缸(b)电动机(c)形变发电装置(d)内燃机E1.3精密的光信号源可以将功率的输出精度控制在1%之内。
激光器由输入电流控制,产生所需要的输出功率。
作用在激光器上的输入电流由一个微处理器控制,微处理器将预期的功率值,与由传感器测量得到的,并与激光器的实际输出功率成比例的信号进行比较。
试辨识指明输出变量、输入变量、待测变量和控制装置,从而完成这个闭环控制系统的如图E1.3所示的框图。
现代控制理论答案 刘豹
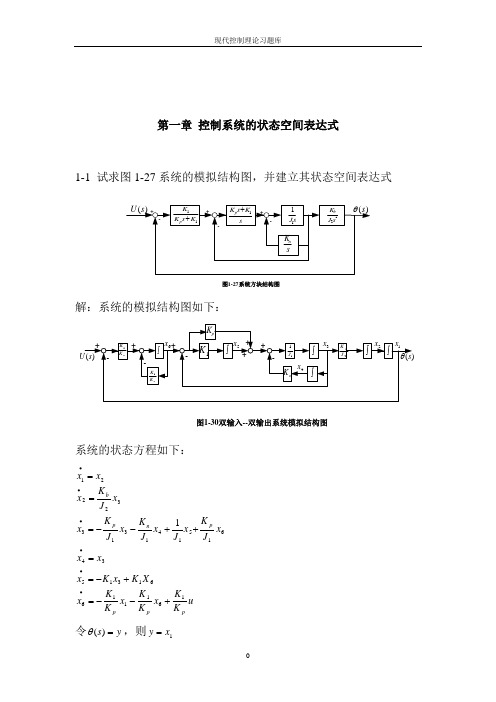
第一章 控制系统的状态空间表达式1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
控制工程第一章习题解答
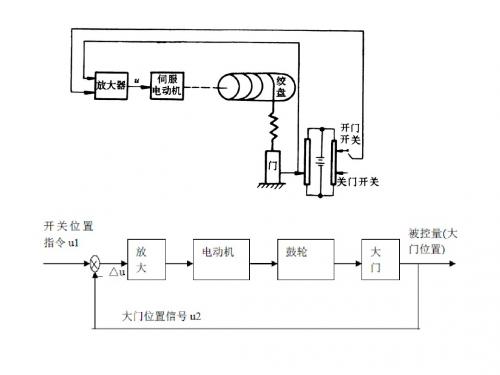
工作原理:电压U2——大门实际位置;电压U1——开门(关门)开关的指令状 态确定的电压大小。 △u=U1-U2 当大门在打开位置时,电压U2 =U上: 若合上开门开关,U1=U上,△u=0,大门不动作;如合上关门开关, U1=U下,△u<关闭位置,U2=U下:
5
6
若合上开门开关,U1=U上,△u>0,大门执行开门指令,直至完全打开,
使△u=0;如合上关门开关,U1=U下,△u=0,大门不动作。
2
工作原理: a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆 的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。当有 扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮 球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小), 进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降 低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。此为连续 3 控制系统。
4
B)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后, 在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进 水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。 随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。此 系统是离散控制系统。
《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得2221332222213*********1x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有 相应的模拟结构图如下:1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P (或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=14222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ) 当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23132313311201214p p p p p p解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为 (1)⎥⎦⎤⎢⎣⎡=11b 解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
