小学奥数四年级1-4讲
小学数学四年级奥数基础教程目录

小学奥数基础教程(四年级)第1讲速算与巧算(一)第2讲速算与巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法(一)第15讲盈亏问题与比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算与巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
小学四年级奥数教材

第二讲除法(简算)……………………………………………………(6)
第三讲角(巧数图形的个数)…………………………………………(9)
第四讲角(等差数列求和)(一)……………………………………(13)
第五讲混合运算(等差数列求和)(二)……………………………(17)
3.1+3+5+7+…+49 4.2+4+6+8+…+2006+2008
7.在□里填入合适的数字。
8.在□里填入合适的数字。
第二讲除法(简算)
例题精讲
例1.计算下列各题。
⑴5380÷5⑵6475÷25⑶52500÷125
例2.简便计算。
⑴8200÷25÷4⑵7272720÷9÷8⑶510÷15÷17
例3.简便运算。
⑴525÷(25×7)⑵660000÷121×11
例4.计算:
拓展提高
1.在下面的竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字。且WHAT是一个大于5000的四位数,那么WHAT为多少?
2.在下面的方框中填上合适的数字,使竖式成立。
3.在下面的方框中填上合适的数字,使竖式成立。
4.在□里填入合适的数字。
5.在□里填入合适的数字。
6.在□里填入合适的数字。
例2.选择合适的数字填在□里,使下面的算式成立。
例3.已知除法竖式:
那么除数是▁▁▁▁▁,商是▁▁▁▁▁。
例4.在□里上适当的数字使除法算式成立。
同步练习
1.下面是一个乘法算式,问:当乘积最大时,所填的四位数字的和是多少?
2.在下面乘法竖式的空格内各填入一个合适的数字,是竖式成立。
小学数学奥数辅导讲座(四年级)

- 1 -小学四年级奥数辅导讲座第1讲速算与巧算(一)第2讲速算与巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法(一)第15讲盈亏问题与比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算与巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
四年级奥数讲义

第一讲和倍问题知识点:已知两个量的和与这两个量的倍数关系,要我们求这两个量分别是几。
和÷(倍数+1)= 较小数;较小数×倍数= 较大数;和-较小数= 较大数例1:甲、乙两个仓库共存货物960吨,已知甲仓库所存货物是乙仓库的2倍,问甲、乙两个仓库各存货物多少吨?例2:果园里有梨树,苹果树和桃树共1800棵,其中梨树的棵数是苹果树的2倍,桃树的棵数是苹果树的2倍,问三种树各多少棵?例3:学校里的足球只数是排球的3倍,篮球的只数是排球的5倍,足球和篮球共72只,问三种球各多少只?例4:三块钢板共重207千克,第一块的重量是第二块的3倍,第二块的重量是第三块的2倍,第三块钢板重多少千克?例5:某小学购进红粉笔和白粉笔共244盒,购进的白粉笔比红粉笔的7倍少12盒,问购进红粉笔、白粉笔各多少盒?例6:两箱茶叶共重88千克,如果从甲箱取15千克放入乙箱,那么乙箱的重量是甲箱的3倍,问两箱原有茶叶各多少千克?例7:甲水池有水1500升,乙水池有水1200升,每分钟从甲水池流入乙水池25升水,问多少分钟后乙水池的水是甲水池的2倍?自我检测:填空。
小红和妈妈的年龄加在一起是40岁,妈妈的年龄是小红年龄的4倍。
妈妈岁,小红岁。
生产队养公鸡、母鸡共404只,其中公鸡是母鸡的3倍。
公鸡有只,母鸡有只。
小明买语文本和数学本共25本,其中语文本比数学本的2倍多4本,语文练习本买了本,数学练习本买了本。
师傅和徒弟一共生产零件190个,师傅生产的个数比徒弟的3倍少10个。
徒弟生产零件个,师傅生产零件个。
A、B两人同时从学校出发相背而行,2小时共行48千米,A的速度是B的2倍,求A的速度是,B的速度是。
一块长方形木板,长是宽的2倍,周长是54厘米。
这块长方形木板的长是厘米,宽是厘米,面积是平方厘米。
甲、乙两个冷藏库原来共存肉92吨,从甲库运出28吨后,乙库存肉比甲库的4倍少6吨。
原来甲库存肉吨,乙库存肉吨。
两个仓库共存粮2200千克,由乙库运出210千克,甲库存粮是乙库的2倍少380千克。
《小学奥数》小学四年级奥数讲义之精讲精练第4讲 应用题(一)

第4讲应用题(一)一、知识要点解答应用题时,必须认真审题,理解题意,深入细致地分析题目中数量间的关系,通过对条件进行比较、转化、重新组合等多种手段,找到解题的突破口,从而使问题得以顺利解决。
二、精讲精练【例题1】某玩具厂把630件玩具分别装在5个塑料箱和6个纸箱里,1个塑料箱与3个纸箱装的玩具同样多。
每个塑料箱和纸箱各装多少件玩具?练习1:(1)百货商店运来300双球鞋分别装在2个木箱和6个纸箱里。
如果两个纸箱同一个木箱装的球鞋同样多,每个木箱和每个纸箱各装多少双球鞋?(2)新华小学买了2张桌子和5把椅子,共付款195元。
已知每张桌子的价钱是每把椅子的4倍,每张桌子多少元?【例题2】一桶油,连桶重180千克,用去一半油后,连桶还有100千克。
问:油和桶各重多少千克?练习2:(1)一筐梨,连筐重38千克,吃去一半后,连筐还有20千克。
问:梨和筐各重多少千克?(2)一筐苹果,连筐共重35千克,先拿一半送给幼儿园小朋友,再拿剩下的一半送给一年级小朋友,余下的苹果连筐重11千克。
这筐苹果重多少千克?【例题3】有5盒茶叶,如果从每盒中取出200克,那么5盒剩下的茶叶正好和原来4盒茶叶的重量相等。
原来每盒茶叶有多少克?练习3:(1)有6筐梨子,每筐梨子个数相等,如果从每筐中拿出40个,6筐梨子剩下的个数总和正好和原来两筐的个数相等。
原来每筐有多少个?(2)在5个木箱中放着同样多的橘子。
如果从每个木箱中拿出60个橘子,那么5个木箱中剩下的橘子的个数的总和等于原来两个木箱里橘子个数的和。
原来每个木箱中有多少个橘子?【例题4】一个木器厂要生产一批课桌。
原计划每天生产60张,实际每天比原计划多生产4张,结果提前一天完成任务。
原计划要生产多少张课桌?练习4:(1)电视机厂接到一批生产任务,计划每天生产90台,可以按期完成。
实际每天多生产5台,结果提前1天完成任务。
这批电视机共有多少台?(2)小明看一本故事书,计划每天看12页,实际每天多看8页,结果提前2天看完。
小学四年级下册奥数讲义确定稿

第一讲速算巧算(简便计算)内容简析一、什么叫做简便计算?就是利用加法运算定律、减法的性质、乘法的意义及定律、除法中商不变的性质及性质,把能够凑成整十、整百、整千……的数通过变形重新整合在一起,从而达到提高计算速度和准确性的计算过程,叫做简便计算。
二、简便计算中应注意的问题:1、注意把原题中的运算顺序进行改变.2、注意有减法和除法的简便计算中运算符号的改变。
3、注意口算时的准确性。
三、教学指导:第一类:加法的运算定律例1、简便计算375+1087+125 89+368+111 362+678+322+138小结:加法交换律a+b=b+a加法结合律(a+b)+b=a+(b+c)第二类:减法的性质例2、1078—147—53 289—(123+89)685—(485—399)小结:减法的性质a—(b+c)=a—b-c a—(b—c)=a-b+c第三类:乘法的意义及定律例三、325+325+323+327+325 125×87×8 125×32×2567×23+67×77 134×87—86×134—134小结;乘法的意义a+a+a+a+×…+a+a+a(b个a)=a×b乘法交换律a×b=b×a乘法结合律(a×b)×c=a×(b×c)乘法分配律(a±b)×c=a×c±b×c第四类:除法的性质例四、12300÷25 8700÷25÷4 8÷7+11÷7+20÷7小结:商不变的性质a÷b(b≠0)=(a÷c)÷(b÷c)=(a×c)÷(b×c)(c≠0)连除 a÷b÷c= a÷(b×c)几个数同时除以一个相同的数 a÷e+b÷e+c÷e=(a+b+c)÷e学生作业:1、625÷252、58500÷9003、75×164、25×64×1255、(350+165)÷56、(702—213—414)÷37、1248÷96×248、1000÷(125÷4)9、999+999×999 10、6237÷63 11、90000÷125÷2÷5÷8 12、176-98—22 13、60×25×4 14、175+99+101+125 15、14×42 16、53×99×25能力提高题:1、7272720÷9÷82、125×312×4×8×253、1111×99994、9999×9999+99995、8÷7+9÷7+11÷76、871×364÷1827、(10000-1000—100—10)÷108、864×37×279、146×31÷73×75 10、454500÷(25×45) 11、9600÷2512、125×792 13、5498—1928—387—1072—161314、5723—(723—189)+576—(276-211)15、99999×88888÷1111116、9999×2222+3333×3334第二讲平均数问题内容简析一、应用范围比较班级之间、同学之间成绩的高低,就是要求出各科成绩的平均分,还有平常生活和工作中,求平均身高、平均气温等。
高斯小学奥数四年级下册含答案第04讲_格点图形面积计算
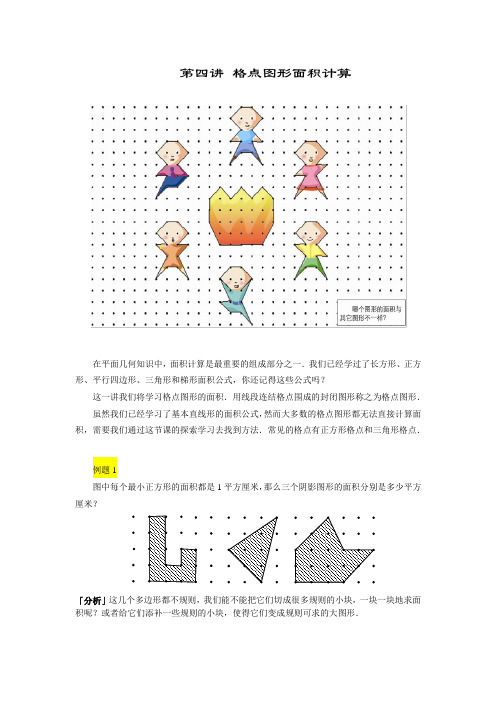
第四讲格点图形面积计算在平面几何知识中,面积计算是最重要的组成部分之一.我们已经学过了长方形、正方形、平行四边形、三角形和梯形面积公式,你还记得这些公式吗?这一讲我们将学习格点图形的面积.用线段连结格点围成的封闭图形称之为格点图形.虽然我们已经学习了基本直线形的面积公式,然而大多数的格点图形都无法直接计算面积,需要我们通过这节课的探索学习去找到方法.常见的格点有正方形格点和三角形格点.例题1图中每个最小正方形的面积都是1平方厘米,那么三个阴影图形的面积分别是多少平方厘米?「分析」这几个多边形都不规则,我们能不能把它们切成很多规则的小块,一块一块地求面积呢?或者给它们添补一些规则的小块,使得它们变成规则可求的大图形.练习1图中相邻两格点间的距离均为1厘米,那么阴影图形的面积分别是多少平方厘米?通过例1中的第1小题我们学会了将大块不规则图形“分割”成许多规则的图形,这种方法称为“分割法”;但是不一定每个图形都很容易分割,第2小题我们学会了把不好算的图形“添补”成规则的大图形,计算时用大图形的面积减去空白部分的面积,这种方法称为“添补法”.分割法,正所谓“大事化小”,把不规则的大图形化为规则的小图形.添补法则正好相反,是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.使用割、补法的时候,一般应该从图形的顶点出发,尽量沿着格线划分,以便与小方格的面积找到联系或者利用垂直等性质.接下来我们用分割、添补的方法计算一下三角形格点图形的面积.例题2下图是一个三角形点阵,其中能连出的最小等边三角形的面积为1平方厘米.那么这五个图形的面积分别为多少平方厘米?「分析」前三个图是可以直接计算的,④、⑤是无法直接计算的,试着用分割、添补的方法解决吧!我们发现:如果一个三角形的两边都沿三角形格线方向,并且分别是最短线段的m 倍和n 倍,那么这个三角形的面积就是最小等边三角形面积的m n 倍.练习2下图是一个三角形点阵,其中能连出的最小等边三角形的面积为1平方厘米.那么这四个图形的面积分别为多少平方厘米?要计算格点图形的面积,我们只需要应用合适的方法,数一下要求的图形占了几个单位面积即可.当单位面积不为1时,我们就要格外小心了,千万不能在数完后再乘单位面积!对于复杂的格点图形,使用割补法一定能计算面积.但是割补法有时显得有些繁琐,有没有更简单明了的方法呢?那么我们接下来看一个简单快捷的方法.例如,我们要计算如下图的格点多边形的面积(假设最小的正方形面积是1).我们可以用割补的方法求出图形的面积,现在还有另一种方法,从格点数入手.围成阴影部分的边线,经过了一些格点.这些边界上的格点叫做边界格点,一共有12个;格点图形还完全盖住了一些格点,这些图形内部的格点叫做内部格点,一共有1个. 一般的,在最小正方形面积为1的正方形网格中,我们有:这样,按公式计算:122116÷+-=,我们就得出图中阴影部分的面积了.例题3 如图,相邻两格点间的距离均为1厘米,求阴影部分的面积?「分析」尝试着用格点图形面积公式计算一下把!先数数边界格点、内部格点分别有多少个呢?练习3如图,每一个最小正方形的面积都是2,阴影部分的面积是多少?类似地,在最小正三角形面积为1的三角形网格中,三角形格点图形也有面积计算公式:仔细比较这两个公式,可以发现:三角形格点的公式正好是正方形格点公式的2倍.大家想一下,为什么是这样呢?例题4如图,每个最小等边三角形的面积都是1平方厘米.阴影部分的面积是多少平方厘米?「分析」尝试着用格点图形面积公式计算一下把!先数数边界格点、内部格点分别有多少个呢?练习4如图,每个最小等边三角形的面积都是1平方厘米,阴影部分的面积是多少平方厘米?例题5如图,每一个最小正方形的面积都是3平方厘米.阴影部分的面积是多少平方厘米?「分析」试着比较分割法、添补法、公式法,这三个方法哪个更合适呢?例题6(1)左图中每个最小正三角形的面积是2平方厘米.阴影部分面积是多少平方厘米?(2)右图中每个最小正三角形的面积是4平方厘米.阴影部分面积是多少平方厘米?「分析」试着比较分割法、添补法、公式法,这三个方法哪个更合适呢?对于大部分格点图形而言,分割法和添补法都可以用来求面积.对于特殊的格点图形,如果不易分割,可以试试添补;如果不易添补,可以试试分割.如果用分割法和添补法都不易解决,那么格点公式就派上用场了!在使用格点公式时,有以下几点需要注意:(1)注意是正方形格点还是三角形格点;(2)按照顺序来数边界格点和内部格点;(3)用格点公式计算出来的不是面积,而是最小的正方形或正三角形的面积的倍数.看似这一讲的题目不是很难,怎么保证计算的准确性呢?如果你用分割法计算面积,不妨再用添补法验算一下.如果你用割补法计算面积,不妨再用格点公式算一算.用不同方法得到的都是同样的结果,基本上就不会出错了.课堂内外几何的起源古埃及人聚居在尼罗河附近,以在河边的农田耕作为生.可是尼罗河每隔一段时间会泛滥,河水涌上岸,把河边的农田淹没,冲毁农田的边界.所以,每次河水泛滥后,埃及人都要重新划分农田的范围和界限.埃及人在划分土地时,发现很多不同形状的农田,都可以分割为几块较细小的三角形农田,例:1块长方形农田2块大小相同的三角形农田1块梯形农田3块三角形农田这些不同形状的农田,其实就是不同的几何图形;把农田分割为几块较细小的农田,即是把几何图形分割.原来古埃及人是研究几何图形的先锋呢!作业1. 如图,每相邻两个格点的距离都是1,那么两个阴影图形的面积分别是________、________.2. 下图中三角形点阵所能连出的最小正三角形面积为1,图中两个图形的面积分别是________、________.3. 如图,最小正三角形的面积是4平方厘米,那么阴影部分的面积是________平方厘米.4. 右图中,每个最小正方形面积为2,则图中阴影部分的面积是________.5. 下图三角形点阵所能连出的最小正三角形面积为2,图形的面积是_________.第四讲 格点图形面积计算1. 例题1答案:7平方厘米;5平方厘米;11平方厘米详解:如图所示,用分割法、添补法.三个图形的面积分别是:4111127⨯+⨯+⨯=平方厘米; 4⨯⨯÷32⨯⨯÷2. 例题2答案:6;12;4;7;9详解:①:326⨯=平方厘米;②:4312⨯=平方厘米;③:224⨯=平方厘米;3. 例题3答案:6.5平方厘米 详解:内部格点:3个,边界格点:9个.面积=3921 6.5+÷-=平方厘米.4. 例题4答案:34平方厘米详解:内部格点:7个;边界格点:22个.面积:7222234⨯+-=平方厘米.5.例题5答案:19.5平方厘米;31.5平方厘米④: ⑤: 121212+17⨯+⨯+⨯= 或:441313137⨯-⨯-⨯-⨯= 2339⨯+= 或:441212139⨯-⨯-⨯-⨯=详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:7个.面积:()7241319.5÷+-⨯=平方厘米;(2)内部格点:8个;边界格点:7个.面积:()7281331.5÷+-⨯=平方厘米.6. 例题6答案:28平方厘米;56平方厘米详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:8个.面积:()4282228⨯+-⨯=平方厘米;(2)内部格点:3个;边界格点:10个.面积:()32102456⨯+-⨯=平方厘米.7. 练习1答案:3平方厘米;10平方厘米详解:如图,分别用分割法、添补法.8. 练习2答案:12;20;5;18 详解:①:3412⨯=平方厘米; ②:直接数,每层4个,共5层,4520⨯=9. 练习3答案:13 简答:内部格点:1个,边界格点:13个.面积=()11321213+÷-⨯=.10. 练习4答案:17平方厘米简答:内部格点:1个;边界格点:17个.面积:1217217⨯+-=平方厘米. ③: ④:1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案:6;6.5简答:可用分割或添补法完成.12.作业2答案:7;12简答:使用割补法分别计算.13.作业3答案:56简答:大正三角形的面积是254100⨯=平方厘米,利用添补法可得.14.作业4答案:29简答:综合利用分割法与添补法.也可以用正方形格点图形面积公式计算.注意每个最小正方形面积是2.15.作业5答案:44简答:综合利用分割法与添补法.也可以用三角形格点图形面积公式计算.注意每个最小正三角形面积是2.。
(完整版)小学四年级奥数教程第4讲:竖式数字谜

四年级奥数教程第4讲:竖式数字谜竖式数字谜是一种猜数的游戏。
解竖式数字型,就得根据有关的运算法则、数的性质(和差积商的为数,数的乘除性、奇偶性、尾数规律等)来进行正确地推理、判断。
解答竖式数字谜时应注意以下几点:(1)空格中只能填写0,1,2,3,4,5,6,7,8,9,而且最高位不能为0;(2)进位要留意,不能漏掉了;(3)答案有时不唯一;(4)两数字相加,最大进位为1,三个数字相加最大进位为2;(5)两个数字相乘,最大进位为8;(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字。
例1:下面的算式中,只有5个数字已写出,请补上其他的数字。
6□7+□2 □□□1 5例2:在下面算式的□内各填入一个合适的数字,使算式成立。
□0 0 □- 5 0 □91 □9 3补充:本题还可以根据加减法是互逆运算的关系,将减法算式转化成下面的加法算式:1 □9 3+ 5 0 □9□0 0 □随堂练习1:在下面竖式的空格内,各填入一个合适的数字,使竖式成立。
(1) 3 (2) 5 8 □□ 5 -2 □7+□ 2 □□9 4□□0 6例3:下面是一个六位数乘以一个一位数的算式,不同的汉字表示不同的数,相同的汉字表示相同的数,其中的六位数是。
小学希望杯赛×赛9 9 9 9 9 9例4:请在下面算式的□里填上合适的数字,使算式成立:□ 4 □×□ 61 □□0□□ 58 □□□随堂练习2:下面是一道题的乘法算式,请问:式子中,A B C D E分别代表什么数字?1 A B C D E× 3A B C D E 1例5:在下面竖式□里填入合适的数字,使竖式成立。
9 □□5 5 □□3 7□□□随堂练习3:在下面竖式的□里,填入合适的数字,使竖式成立。
(1)(2)□7 6□ 1 ×□□□□ 1 8 □□□□□□□□□□ 3 1 □□06提高练习1 要使右边竖式成立,四个□中的数字之和为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例5:明明做两位数乘两位数的题时,把乘数的个位数4错当成1,乘得的结果是525,实际应为600,这两个两位数各是多少?
练习:
1.小明在计算除法时,把除数540末尾的“0”漏写了,结果得到商是60,正确的商应该是多少?
(1)3、8、18、33、53、78、()。
(2)0、1、3、8、21、()。
(3)
例5:根据前面两个圈里三个数的关系,想一想,在第三个圈里的()应填什么数?
5 4 9
15 12 12 9(27)(24)20 18 ຫໍສະໝຸດ 510 20 8 16()()
12 8 20
10 20 8 16()()
9 12 15
学习应用题的关键在于掌握数量关系,了解应用题的条件和问题之间的联系,找出解答方法
例1:一桶水,连桶重250千克,用去一半水后,连桶还有145千克,问桶里原有多少千克水?水桶重多少千克?
例2:百货商店运来300双球鞋,分别装在2个木箱和6个纸箱里,如果2个纸箱同1个木箱装的球鞋一样多,每个木箱和每个纸箱各装多少双球鞋?
第四讲错中求解
例1:小虎在计算除法时,把除数65写成56,结果得到商是13,还余52,正确的商是多少?
例2:小明在计算有余数的除法时,把被除数137错写成173.这样商比原来多了3,而余数正好相同。请你算出这道题的除数和余数各是多少?
例3:甲乙两学生同算两数之和,甲得685,计算正确;乙得460,计算错误,乙之所以算错的原因是将其中一个加数末尾的0漏掉了。两个加数各是多少?
例1: 9 13 7=100
14 2 5=
把“ ”分别填在适当的圆圈中(运算符号只能用一次)并在方框中填上适当的整数,可以使上面的两个等式成立,这时,方框中的数是几?
例2:下式中“数学俱乐部”分别代表那些数字
1数学俱乐部
X3
数学俱乐部1
例3:在象棋算式里,不同的棋子代表不同的数,请你想一想,这些棋子各代表那些数字?
例5:小敏考的4门功课,平均成绩是92分。如果数学成绩不算在内,平均成绩是90分。小敏的数学成绩是多少分?
例6:一个木器厂要生产一批桌子。原计划每天生产48张。实际每天比原计划多生产两张,结果提前一天完成。原计划要生产多少张桌子?
例7:甲乙两个仓库存粮若干吨。如果甲库运5吨到乙库,那么甲、乙两库的存粮吨数就一样多;如果乙库运5吨到甲库,那么乙库的吨数就只有甲库的一半。甲、乙两仓库原来各存粮多少吨?
第一讲规律填数
按照一定规律排列成的一列数叫做数列,根据数列规律填上适当的数,必须先找出已知数列的各个数之间的规律
例1:找出下列各数列的排列规律,并填上合适的数
(1)7、11、15、19、()、……
(2)1、4、3、6、5、()、()、……
(3)1、4、16、64、()、……
分析:如何从数列中找出规律?一般有两种情况,一种是根据前后两个数之间的关系,找出规律,推断出索要填的数;另一种是根据相隔两个数之间的关系,找出规律,推断出所要填的数。
练习
1.玻璃瓶里装着一些水,把水加到原来的2倍,称得重5千克;把水加到原来的4倍,再称一称重9千克。问原来水重多少千克?
2.一筐鲜鱼,连筐重56千克,先卖出鲜鱼的一半,再卖出剩下鲜鱼的一半,这时连筐还重17千克。原来这筐鲜鱼中多少千克?
3.买4张办公桌9把椅子共用252元,1张桌子和3把椅子的价钱正好想等,桌、椅单价各多少元?
5在下面数列里,写出后面各数
(1)1、6、7、12、13、18、19、__、__、__
(2)2、3、5、8、12、__、__
(3)1、3、6、8、16、18、__、__
6将整数1、2、3、4……按下图的顺序排列在正方形格子中“?”应填什么数
16
11
17
7
12
?
4
8
13
2
5
9
14
1
3
6
10
15
?
应用题
兵炮马卒
+兵炮马卒
车卒马兵卒
例4:如果将6放在一个两位数的右端,所得到的三位数比原来的两位数多294,问原来的两位数是多少?
例5:下列各题中的每一个汉字都代表一个数字,不同的汉字代表不同的数字,当他们各代表什么数字时,以下各算式都成立
(1)优优优优优优 学+学习再学习
(2)红花映绿叶
X春
叶绿映花红
例6:一个六位数的末位数字是2,如果把2移到头一位数,而其他五位数字不动,原数就是这个新数的3倍,求原6位数
例3:在5个木箱里放着同样多的桔子。如果从每个木箱里拿出60个桔子,则五个箱子里剩下的桔子的个数的总和等于原来两个箱子的桔子个数的和。原来每个箱子里多少个桔子?
例4:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。又问:“谁做完数学作业?请举手!”有42人举手。最后问:“谁语文、数学作业没有做完?”没有人举手。求这个班语文、数学作业都完成的人数。
4.在100位游客中,有75人懂法语,83人懂英语,另有10人这两种语言都不懂。既懂法语,又懂英语的游客是多少人?
5.王强今年8岁,他父亲已经40岁了。问再过几年,父亲的年龄是王强的2倍
第三讲算式谜题
“算式谜”是一种有趣的数学问题。特点是给出算术运算式子,但式中某些数字或运算符号未确定,要求我们依据运算法则,进行适当的判断推理,从而把算式补充完整。
2.一个数乘以4,小华把乘号误当成加号,得到的结果是20,正确的积应该是多少?
3.小红在计算有余数的除法时,把被除数171错写成117,结果商比原来少3,但余数恰好相同,这题的除数和余数各是多少?
例2:先找出规律,然后在括号内填上适当的数
(1)11、3、8、3、5、3、()、()。
(2)15、6、13、7、11、8、()、()。
例3:下面数列1、1、2、3、5、8、13、()、34、55……中。()中应填什么数?
分析:上面数列是斐波那契(中世纪意大利著名数学家)数列。
例4:按照下面数列的规律,在括号中填上合适的数。
5 20()
6()12
3填出所缺的数
(1)
8
17
5
12
16
10
11
9
(2)
7
16
9
5
21
16
9
4
(3)
7
14
12
4
12
9
6
24
4下面括号内两个数按一定规律组合,在( )里填上适当的数
(1)(8、7)、(6、9)、(10、5)、(、13);
(2)(2、3)、(5、9)、(7、13)、(9、);
(3)(18、10)(10、6)、(20、11)(、4)
45 15 60 20()()
练习
1:找规律,在()内填数
(1)160、145、130、()、100、()。
(2)2、6、18、54、()、()、1458。
(3)15、4、13、4、11、4、()、()。
(4)8、15、10、13、12、11、()、()。
2:空格中应填什么数?
3 12 6
4 16 8
