大学物理第8章 稳恒磁场 课后习题及答案
大学物理稳恒磁场习题及答案 (1)

衡水学院 理工科专业 《大学物理B 》 稳恒磁场 习题解答一、填空题(每空1分)1、电流密度矢量的定义式为:dI j n dS ⊥=v v,单位是:安培每平方米(A/m 2) 。
2、真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量? = 0 .若通过S 面上某面元d Sv的元磁通为d ?,而线圈中的电流增加为2I 时,通过同一面元的元磁通为d ?',则d ?∶d ?'= 1:2 。
3、一弯曲的载流导线在同一平面内,形状如图1(O 点是半径为R 1和R 2的两个半圆弧的共同圆心,电流自无穷远来到无穷远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。
4、一磁场的磁感强度为k c j b i a B ϖϖϖϖ++= (SI),则通过一半径为R ,开口向z 轴正方向的半球壳表面的磁通量的大小为πR 2c Wb 。
5、如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情况下,等于:对环路a :d B l ⋅⎰v v Ñ=____μ0I __;对环路b :d B l ⋅⎰vv Ñ=___0____; 对环路c :d B l ⋅⎰v v Ñ =__2μ0I __。
6、两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,运动轨迹半径之比是_____1∶2_____。
二、单项选择题(每小题2分)( B )1、均匀磁场的磁感强度B v垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为A. 2?r 2BB.??r 2BC. 0D. 无法确定的量( C )2、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B 1 / B 2为A. B. C. D.( D )3、如图3所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C .方向在环形分路所在平面内,且指向aD .为零( D )4、在真空中有一根半径为R 的半圆形细导线,流过的电流为I ,则圆心处的磁感强度为A.R 140πμ B. R120πμ C .0 D .R140μ ( C )5、如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度??绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B 1;此正方形同样以角速度??绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B 2,则B 1与B 2间的关系为A. B 1 = B 2B. B 1 = 2B 2 C .B 1 =21B 2 D .B 1 = B 2 /4 ( B )6、有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4. (D) 2倍和1/2. 三、判断题(每小题1分,请在括号里打上√或×)( × )1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时,非静电力作的功。
重庆理工大学-大学物理-习题册-稳恒磁场答案

A:
B:
2、如图所示,同轴电缆由两个同轴导体薄圆筒组成,其间充满磁导率为的磁介质,如图所示。使用时内外圆筒分别沿轴向流过大小相等、方向相反的电流。设电缆长度为l内外圆筒半径分别为R1和R2,求(1)电缆的自感系数(2)磁场能量
解:
3、有一段10号铜线,直径为2.54mm,单位长度的电阻为3.28*10(-3),在铜线上载有10A的电流,试计算(1)磁能密度(2)电能密度
解:
在CD杆上取微元 ,微元距右边导线 ,则微元处磁感强度大小为
方向垂直纸面向外
微元上的感生电动势为
CD杆中的感应电动势为
D点电势较高
2、如图所示,有有一半径为r的半圆环导线在匀磁场B中以角速度绕与磁场垂直地轴ab旋转,当它转到如图位置时,求圆环上的动生电动势
解:
此题用积分来计算颇为麻烦,可考虑作一回路来帮助我们分析。设想连接ab,形成一个半圆回路,由于转轴不运动,所以ab段上没有动生电动势,若求出回路上的电动势,就应该等于半圆环上的电动势。回路上的电动势正好是一个交变电动势。如图设回路l的绕行为正方向,则此时回路面积S的法向n向外,与磁场B的夹角 ,故回路电动势为
解:
将半圆柱面分成许多宽为dl的细长条,并将其视为长直电流,电流强度为 ,它在轴线上产生的磁场为 。
,代入得
由对称性可知,
3如图所示,两根无限长载流直导线互相垂直地放置,已知,I1=4A,I2=6A(I2电流的流向为垂直于纸面朝外),d=2cm,求P处的磁感应强度
解:
4、设在无限大导体薄板中有均匀电流沿板平面流动,在垂直于电流的单位长度上流过的电流为j(称电流线密度)。求此平面电流产生的磁场的磁感应强度的大小。(1)积分法(2)安培环路
解:(1)
河北科技大学大学物理答案稳恒磁场
习 题12-1 若电子以速度()()616120103010.m s .m s --=醋+醋v i j 通过磁场()0030.T =-B i ()015.T j 。
(1)求作用在电子上的力;(2)对以同样速度运动的质子重复上述计算。
解:(1)()()kj i j i B v F 136610624.015.003.0100.3100.2-⨯=-⨯⨯+⨯-=⨯-=e e (2)k F 1310624.0-⨯-=12-2 一束质子射线和一束电子射线同时通过电容器两极板之间,如习题12-2图所示。
问偏离的方向及程度有何不同?质子射线向下偏移,偏移量较小;电子射线向上偏移,偏移量较大。
12-3 如习题12-3图所示,两带电粒子同时射入均匀磁场,速度方向皆与磁场垂直。
(1)如果两粒子质量相同,速率分别是v 和2v ;(2)如果两粒子速率相同,质量分别是m 和2m ;那么,哪个粒子先回到原出发点? 解:qBmT π2=(1)同时回到原出发点;(2) 质量是m 先回到原出发点。
12-4 习题12-4 图是一个磁流体发电机的示意图。
将气体加热到很高温度使之电离而成为等离子体,并让它通过平行板电极1、2之间,在这习题12-2图习题12-3图习题12-4图里有一垂直于纸面向里的磁场B 。
试说明这两极之间会产生一个大小为vBd 的电压(v 为气体流速,d 为电极间距)。
问哪个电极是正极? 解:qE qvB =,vB E =,vBd Ed U ==,电极1是正极。
12-5 一电子以713010.m s v -=醋的速率射入匀强磁场内,其速度方向与B 垂直,10T B =。
已知电子电荷191610.C e --=-?。
质量319110.kg m -=?,求这些电子所受到的洛仑兹力,并与其在地面上所受重力进行比较。
解:11719108.410100.3106.1--⨯=⨯⨯⨯⨯==evB F N ,3031109.88.9101.9--⨯=⨯⨯==g m G e N18104.5⨯=GF12-6 已知磁场B 的大小为04.T ,方向在xy 平面内,并与y 轴成3p 角。
大学物理第8章 稳恒磁场 课后习题及答案

第8章 稳恒磁场 习题及答案6. 如图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R 。
若通以电流I ,求O 点的磁感应强度。
解:O 点磁场由AB 、C B、CD 三部分电流产生,应用磁场叠加原理。
AB 在O 点产生的磁感应强度为01=BC B在O 点产生的磁感应强度大小为θπμR I B 402=RIR I 123400μππμ=⨯=,方向垂直纸面向里CD 在O 点产生的磁感应强度大小为)cos (cos 421003θθπμ-=r IB)180cos 150(cos 60cos 400︒︒-=R Iπμ)231(20-=R I πμ,方向垂直纸面向里 故 )6231(203210ππμ+-=++=R I B B B B ,方向垂直纸面向里 7. 如图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连。
已知圆环的粗细均匀,求环中心O 的磁感应强度。
解:圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
且θπθ-==21221R R I I 电阻电阻 1I 产生的磁感应强度大小为)(θππμ-=24101RI B ,方向垂直纸面向外 2I 产生的磁感应强度大小为θπμRIB 4202=,方向垂直纸面向里 所以, 1)2(2121=-=θθπI I B B 环中心O 的磁感应强度为0210=+=B B B8. 如图所示,一无限长载流平板宽度为a ,沿长度方向通过均匀电流I ,求与平板共面且距平板一边为b 的任意点P 的磁感应强度。
解:将载流平板看成许多无限长的载流直导线,应用叠加原理求解。
以P 点为坐标原点,垂直载流平板向左为x 轴正方向建立坐标系。
在载流平板上取dx aIdI =,dI 在P 点产生的磁感应强度大小为x dI dB πμ20=dx axIπμ20=,方向垂直纸面向里 P 点的磁感应强度大小为⎰⎰+==a b b x dx a I dB B πμ20bab a I +=ln 20πμ 方向垂直纸面向里。
大学物理 第08章 恒定磁场习题
第八章 电磁感应与电磁场
5
物理学
第五版
第八章 习题
(2)如 dB 0.010 T s1,求距螺线管中心 dt
轴 r 5.0 cm 处感生电场的大小和方向.
第八章 电磁感应与电磁场
6
物理学
第五版
第八章 习题
6 在半径为 R 的圆柱形空间中存在
着均匀磁场 B 的方向与柱的轴线平行. 如
图所示,有一长为 l 的
电动势E 大小. 哪一端电
势较高?
第八章 电磁感应与电磁场
2
物理学
第五版
第八章 习题
3 如图所示,长为 L 的导体棒 OP, 处于均匀磁场中, 并绕 OO’ 轴以角速
度 旋转,棒与转
轴间夹角恒为 ,
磁感强度 B 与转轴 平行. 求 OP 棒在图 示位置处的电动势.
第八章 电磁感应与电磁场
3
物理学
第八章 电磁感应与电磁场
11
物理学
第五版
10 如图所示,一 面积为 4.0cm2 共 50 匝 的小圆形线圈 A ,放 在半径为 20cm共 100 匝的大圆形线圈 B 的 正中央,此两线圈同 心且同平面.
第八章 习题
第八章 电磁感应与电磁场
12
物理学
第五版
第八章 习题
设线圈 A 内该各点的磁 感强度可看作是相同的. 求:(1)两线圈的互感; (2)当线圈 B 中电流的 变化率为 50A s1 时,线圈 A 中感应电动 势的大小和方向.
第五版
第八章 习题
4 如图所示,金属杆
AB 以匀速率 v = 2.0 m s1
平行于一长直导线移动,
v
此导线通有电流 I = 40 A .
大学物理第8章答案

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为212022322()x Lx R nIdxB dB R x μ==+⎰⎰0212212221221[]2()()nIx x R x R x μ=-++ 由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得 021(cos cos )2nIB μββ=-式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有nI B 0μ=上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
习题解答---大学物理第八章习题 2

专业班级_____ 姓名________学号________第八章稳恒电流的磁场一、选择题:1、在磁感应强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量n与B的夹角为α,则通过半球面S的磁通量为:[ D ](A)Br2π(B)Br22π(C)απsin2Br-(D)απcos2Br-。
2、无限长直导线在P处弯成半径为R的圆,当通以电流I时,则在圆心O点的磁感应强度大小等于:[ D ](A)RIπμ20(B)RI4μ(C)0(D))11(2πμ-RI(E))11(4πμ+RI3、电流由长直导线1沿切向经a点流入一个电阻均匀分布的圆环,再由点沿切向从圆环流出,经长直导线2返回电源(如图)。
已知直导线上的电流强度为I,圆环的半径为R,且a、b和圆心O在同一直线上。
设长直载流导线1、2和分别在O点产生的磁感应强度为1B、2B、3B,则圆心处磁感应强度的大小[ C ](A)0=B,因为0321===BBB。
(B)0=B, 因为虽然01≠B,02≠B,但021=+BB,03=B。
(C)0≠B,因为01≠B,02≠B,03≠B。
(D)0≠B,因为虽然03=B,但021≠+BB。
4、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,x坐标轴垂直圆筒轴线,原点在中心轴线上,图(A )——(E )哪一条表示x B -的关系?[ D ] 5、无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(R r <)的磁感应强度为i B ,圆柱体外(r> R )的磁感应强度为e B 。
则有:[ B ] (A)i B 、e B 均与r 成正比。
(B) i B 、e B 均与r 成反比。
(C)i B 与r 成反比,e B 与r 成正比。
(D) i B 与r 成正比,e B 与r 成反比。
6、如右图所示,在磁感应强度为B的均匀磁场中,有一圆形载流导线,a 、b 、c 是其上三个长度相等的电流元,则它们所受安培力大小的关系为[ B ](A )c b a F F F >>。
稳恒磁场及答案
第七章稳恒电流1、在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B的夹角为 ,则通过半球面S 的磁通量(取弯面向外为正)为 (A) r 2B . . (B) 2r 2B . (C) -r 2B sin . (D) -r 2B cos .2、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B -x 的关系[ ]3、如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分 LlB d 等于(A) I 0 . (B) I 031. (C) 4/0I . (D) 3/20I .4、如图,在一固定的载流大平板附近有一载流小线框能自由转动或平动.线框平面与大平板垂直.大平板的电流与线框中电流方向如图所示,则通电线框的运动情况对着从大平板看是: (A) 靠近大平板. (B) 顺时针转动. (C) 逆时针转动. (D) 离开大平板向外运动.5、在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图所示.在此情形中,线框内的磁通量 =______________.n B SOB x O R (A) BxO R (B)Bx O R (D) Bx O R (C)BxO R (E)x电流 圆筒II ab c d120°I 1I 2b baI6、如图所示,在真空中有一半圆形闭合线圈,半径为a ,流过稳恒电流I ,则圆心O 处的电流元l I d 所受的安培力Fd 的大小为____,方向________.7、有一根质量为m ,长为l 的直导线,放在磁感强度为 B的均匀磁场中B 的方向在水平面内,导线中电流方向如图所示,当导线所受磁力与重力平衡时,导线中电流I =___________________.8、如图所示,一无限长载流平板宽度为a ,线电流密度(即沿x 方向单位长度上的电流)为,求与平板共面且距平板一边为b的任意点P 的磁感强度.9、一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成.中间充满磁导率为的各向同性均匀非铁磁绝缘材料,如图.传导电流I 沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.答案:一 选择题1、D2、A3、D4、B5、2ln 20Ia6、a l I 4/d 20 垂直电流元背向半圆弧(即向左)7、)/(lB mgIlI dIBI8、解:利用无限长载流直导线的公式求解. (1) 取离P 点为x 宽度为d x 的无限长载流细条,它的电流x i d d(2) 这载流长条在P 点产生的磁感应强度x i B 2d d 0 xx2d 0 方向垂直纸面向里.(3) 所有载流长条在P 点产生的磁感强度的方向都相同,所以载流平板在P 点产生的磁感强度B B dba bxdx x20b b a x ln 20 方向垂直纸面向里.9、解:由安培环路定理: i I l Hd 0< r <R 1区域: 212/2R Ir rH 212R Ir H, 2102R Ir BR 1< r <R 2区域: I rH 2r I H 2, rIB 2R 2< r <R 3区域: )()(22223222R R R r I I rH )1(22223222R R R r r IH )1(2222322200R R R r r IH B r >R 3区域: H = 0,B = 0x d x PO x。
大学物理稳恒磁场习题及答案
衡水学院理工科专业《大学物理B 》稳恒磁场习题解答 【1 】一.填空题(每空1分)1.电流密度矢量的界说式为:dIj n dS ⊥=,单位是:安培每平方米(A/m2). 2.真空中有一载有稳恒电流I 的细线圈,则经由过程包抄该线圈的关闭曲面S 的磁通量=0 .若经由过程S 面上某面元d S 的元磁通为d,而线圈中的电流增长为2I 时,经由过程统一面元的元磁通为d ',则d ∶d '=1:2 .3.一曲折的载流导线在统一平面内,外形如图1(O 点是半径为R1和R2的两个半圆弧的配合圆心,电流自无限远来到无限远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=.4.一磁场的磁感强度为k c j b i a B++= (SI),则经由过程一半径为R,启齿向z 轴正偏向的半球壳概况的磁通量的大小为πR2cWb. 5.如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情形下,等于: 对环路a :d B ⋅⎰=____μ0I__;对环路b :d B ⋅⎰=___0____; 对环路c :d B ⋅⎰=__2μ0I__.6.两个带电粒子,以雷同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,活动轨迹半径之比是_____1∶2_____. 二.单项选择题(每小题2分)( B )1.平均磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S,则经由过程S 面的磁通量的大小为( C )2.有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中间产生的磁感强度的大小之比B1 / B2为(D )3.如图3所示,电流从a 点分两路经由过程对称的圆环形分路,会合于b 点.若ca.bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 偏向垂直环形分路地点平面且指向纸内B. 偏向垂直环形分路地点平面且指向纸外C .偏向在环形分路地点平面内,且指向aD .为零( D )4.在真空中有一根半径为R 的半圆形细导线流过的电流为I,则圆心处的磁感强度为 A.R 140πμ B. R120πμ C .0D .R 140μ ( C )5.如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度绕AC 轴扭转时,在中间O 点产生的磁感强度大小为B1;此正方形同样以角速度绕过O 点垂直于正方形平面的轴扭转时,在O 点产生的磁感强度的大小为B2,则B1与B2间的关系为A. B1= B2B. B1= 2B2C .B1=21B2D .B1= B2 /4O IR 1 R 2图1b⊗ ⊙ cI I c a图2c I db a图3A CqqqqO图4(B )6.有一半径为R 的单匝圆线圈,通以电流I,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中间的磁感强度和线圈的磁矩分离是本来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4.(D) 2倍和1/2. 三.断定题(每小题1分,请在括号里打上√或×)( × )1.电源的电动势是将负电荷从电源的负极经由过程电源内部移到电源正极时,非静电力作的功. ( √ )2.磁通量m SB dS φ=⋅⎰的单位为韦伯.( × )3.电流产生的磁场和磁铁产生的磁场性质是有区此外. ( × )4.电动势用正.负来暗示偏向,它是矢量.( √ )5.磁场是一种特别形态的物资,具有能量.动量和电磁质量等物资的根本属性. ( × )6.知足0m SB dS φ=⋅=⎰的面积上的磁感应强度都为零.四.简答题(每小题5分)1.在统一磁感应线上,各点B 的数值是否都相等?为何不把感化于活动电荷的磁力偏向界说为磁感应强度B的偏向?答:在统一磁感应线上,各点B 数值一般不相等.(2分)因为磁场感化于活动电荷的磁力偏向不但与磁感应强度B 的偏向有关,并且与电荷速度偏向有关,即磁力偏向其实不是独一由磁场决议的,所以不把磁力偏向界说为B 的偏向.(3分)2.写出法拉第电磁感应定律的数学表达式,解释该表达式的物理意义. 答:法拉第电磁感应定律的数学表达式r lS BE dl dS t∂⋅=-⋅∂⎰⎰(2分) 物理意义:(1)感生电场是由变更的磁场激发的;(1分)(2)感生电场r E 与Bt∂∂组成左手螺旋关系;(1分)(3)右侧的积分面积S 为左侧积分路径L 包抄的面积.(1分)五.盘算题(每题10分,写出公式.代入数值.盘算成果.)1.如图5所示,AB.CD 为长直导线,BC 为圆心在O 点的一段圆弧形导线,其半径为R.若通以电流I,求O 点的磁感应强度. 解:如图所示,O 点磁场由AB .C B.CD 三部分电流产生.个中AB 产生01=B(1分)CD 产生RIB 1202μ=,(2分)偏向垂直向里(1分)CD 段产生)231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,(2分)偏向⊥向里(1分)∴)6231(203210ππμ+-=++=R I B B B B ,(2分)偏向⊥向里.(1分) 2.如图6所示.半径为R 的平均带电圆盘,面电荷密度为σ.当盘以角速度ω绕个中间轴OO '扭转时,求盘心O 点的B 值.解法一:当带电盘绕O 轴迁移转变时,电荷在活动,因而产生磁场.可将圆盘算作很多齐心圆环的组合,而每一个带电圆环迁移转变时相当图5于一圆电流.以O 为圆心,r 为半径,宽为dr 的圆环,此环上电量rdr ds dq πσσ2⋅==(2分)此环迁移转变时,其等效电流rdr dq dI ωσπω=⋅=2(3分) 此电流在环心O 处产生的磁感应强度大小2200drrdIdB ωσμμ==(2分)其偏向沿轴线,是以全部圆盘在盘心O 处产生的磁感应强度大小是R dr dBB Rωσμωσμ0002121==⎰⎰(3分) 解法二:依据活动电荷的磁场公式304r rv q B ⨯=πμ,(2分)求解,在圆盘上取一半径为r,宽为dr 的圆环,电量rdr dq πσ2=,ωr v =(2分)dr rdr r r dq r dB 22440020σωμπσπωμπωμ=⋅==(3分)偏向垂直于盘面向上,同样RqRdr dB B Rπωμωσμσωμ2220000====⎰⎰(3分) 3.图7所示,在一长直载流导线旁有一长为L 导线ab,其上载电流分离为I1和I2,a 端到直导线距离为d 求当导线ab 与长直导线垂直,求ab 受力.解:取如图8所示坐标系直导线在距其为x 处,产生的磁场xI B πμ210=(2分) 其偏向垂直低面向里,电流之I2dx 受安培力大小为dx xI I Bdx I df πμ22102==(3分) df 偏向垂直向上,且各电流之受力偏向雷同,(2分)故,ab 受力为012012ln22d L LdI I I I d Lf df dx x dμμππ++===⎰⎰(3分) 4.一长直导线通有电流120A I =,旁边放一导线ab,个中通有电流210A I =,且两者共面,如图8所示.求导线ab 所受感化力对O 点的力矩.解:如图9所示,在ab 上取r d ,它受力ab F ⊥d 向上,(2分)大小为rI rI F πμ2d d 102=(2分) F d 对O 点力矩F r M⨯=d (2分)图6I 1I2dL图7Md 偏向垂直纸面向外,大小为r I I F r M d 2d d 210πμ==(2分) ⎰⎰-⨯===ba bar II M M 6210106.3d 2d πμm N ⋅(2分)5.两平行长直导线相距d=40cm,每根导线载有I1=I2=20A 如图10所示.求: ⑴两导线地点平面内与该两导线等距的一点A 处的磁感应强度; ⑵经由过程图中斜线所示面积的磁通量.(r1=r3=10cm,l=25cm)解: (1)图中的A 点的磁场122222O O A I I B d d μμππ=+⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭()512124010O O OI I I I T d d dμμμπππ-=+=+=⨯(4分) (2)在正方形中距中间x 处,取一窄条ds ldx =,则经由过程ds 的磁通量m d B ldx φ=()1222O O I I ldxx d z μμππ⎛⎫=+ ⎪ ⎪-⎝⎭ 122O l I I dx x d x μπ⎛⎫=+ ⎪-⎝⎭(3分)31122d r O m m r l I I d dx x d x μφφπ-⎛⎫==+ ⎪-⎝⎭⎰⎰311213ln ln 2O l d r d r I I r r μπ⎛⎫--=+ ⎪⎝⎭ ()121ln 2O l d n I I r μπ⎛⎫-=+ ⎪⎝⎭6111ln 2.210O l d r I wb r μπ--==⨯(3分) 6.已知磁感应强度B=2.0Wb ·m -2的平均磁场, 偏向沿X 轴正偏向,如图11所示,试求:(1) 经由过程abcd 面的磁通量; (2) 经由过程图中befc 面的磁通量; (3)经由过程图中aefd 面的磁通量. 解:(1)经由过程abcd 面的磁通量mabcd abcd B S φ= 2.00.40.3=⨯⨯ 0.24wb =(4分)(2)经由过程ebfc 面的磁通量,因为B 线擦过此面 故0mbdfc φ=(3分)(3)经由过程aefd 面的磁通量图110.24 maefd mabcd wbφφ==(3分)。
大学物理第8章 磁场题库2(含答案)

第八章 磁场 填空题 (简单)1、将通有电流为I 的无限长直导线折成1/4圆环形状,已知半圆环的半径为R ,则圆心O 点的磁感应强度大小为08I Rμ 。
2、磁场的高斯定理表明磁场是 无源场 。
3、只要有运动电荷,其周围就有 磁场 产生;4、(如图)无限长直导线载有电流I 1,矩形回路载有电流I 2,I 2回路的AB 边与长直导线平行。
电 流I 1产生的磁场作用在I 2回路上的合力F 的大小为01201222()I I L I I La ab μμππ-+,F 的方向 水平向左 。
(综合)5、有一圆形线圈,通有电流I ,放在均匀磁场B 中,线圈平面与B 垂直,则线圈上P 点将受到 安培 力的作用,其方向为 指向圆心 ,线圈所受合力大小为 0 。
(综合)6、∑⎰==⋅n i i lI l d B 00μ是 磁场中的安培环路定理 ,它所反映的物理意义是 在真空的稳恒磁场中,磁感强度B 沿任一闭合路径的积分等于0μ乘以该闭合路径所包围的各电流的代数和。
7、磁场的高斯定理表明通过任意闭合曲面的磁通量必等于 0 。
8、电荷在磁场中 不一定 (填一定或不一定)受磁场力的作用。
9、磁场最基本的性质是对 运动电荷、载流导线 有力的作用。
10、如图所示,在磁感强度为B 的均匀磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为α。
求通过该半球面的磁通量为2cos B R πα-。
(综合) 12、一电荷以速度v 运动,它既 产生 电场,又 产生 磁场。
(填“产生”或“不产生”)13、一电荷为+q ,质量为m ,初速度为0υ的粒子垂直进入磁感应强度为B 的均匀磁场中,粒子将作 匀速圆周 运动,其回旋半径R=0m Bqυ,回旋周期T=2mBq π 。
14、把长直导线与半径为R 的半圆形铁环与圆形铁环相连接(如图a 、b 所示),若通以电流为I ,则 a 圆心O4题图 5题图的磁感应强度为___0__________; 图b 圆心O 的磁感应强度为04IRμ。
浙江工业大学大学物理稳恒磁场习题答案

稳恒磁场习题答案7-1解:令1B 、2B 、acb B 和ab B分别代表长直导线1、2和三角形框ac 、cb 边和ab 边中的电流在O 点产生的磁感强度.则 ab acb B B B B B+++=211B :由于O 点在导线1的延长线上,所以1B= 0. 2B :由毕奥-萨伐尔定律,有 )60sin 90(sin 402︒-︒π=dIB μ式中 6/330tan 21l l Oe d =︒⋅==)231(34602-⋅π=lI B μ)332(40-π=l I μ 方向:垂直纸面向里.acb B 和ab B:由于ab 和acb 并联,有 a c ba cb ab ab R I R I ⋅=⋅ 又由于电阻在三角框上均匀分布,有21=+=cb ac ab R R acb ab ∴ acb ab I I 2= 由毕奥-萨伐尔定律,有ab acb B B =且方向相反. ∴ )332(402-π==lIB B μ,B的方向垂直纸面向里.7—2. 解:两折线在P 点产生的磁感应强度分别为:⎪⎪⎭⎫ ⎝⎛+=22141a I B o πμ 方向为⊗, ⎪⎪⎭⎫⎝⎛-=22142a I B o πμ 方向为⊙ 所以:aIB B B o πμ4221=-= 方向为⊗7-3. 解:O 点处的磁场由三部分构成,即:cd bc ab B B B B++=, 方向垂直纸面向里。
其中:()R Ia I B o o ab πμπμ4/90cos 0cos 4=-=(半无限长载流导线), RIB o bc 4μ=(半圆环), 0=cd B (其延长线过O 点)。
()T RIR I B B B B o o cd bc ab 5101.244-⨯=+=++=μπμ7-4解:设L 1中电流在O 点产生的磁感强度为B 1,由于L 1与O 点在一条直线上,由毕奥-萨伐定律可求出 01=B 设L 2中电流在O 点产生的磁感强度为B 2,L 2为半无限长直电流,它在O 处产生的场是无限长直电流的一半,由安培环路定律和叠加原理有RIR I B π=⋅π=4212002μμ 方向垂直图面向外.以下求圆环中电流在O 点产生的磁感强度.电流由L 1经a 点分两路流入圆环,一路由a 点经1/4圆弧流至b ,称此回路为L 3.另一路由a 点经3/4圆弧流至b ,称此段回路为L 4.由于圆环为均匀导体,若L 2的电路电阻为R ,则L 4的电阻必为3R .因此电流在L 3、L 4上的分配情况为L 3中电流为3 I /4,L 4中电流为I / 4.L 3、L 4中电流在O 点产生的磁感强度的大小相等,方向相反,总值为0.即043=+B B故O 点的磁感强度: =+++=43210B B B B B RIπ40μ方向垂直图面向外.7-57-6. 解:取一个窄长条dx ,它在P 点产生磁场()x b a a dx a I dB p -+=πμ20 所以,P 点磁场bba a I xb a dx o a a I B p +=-+=⎰ln2200πμπμ 方向向外。
大学物理学-稳恒磁场习题课

⑶电子进入均匀磁场B中,如图所示,当电子位于 A点的时刻,具有与磁场方向成 角的速度v,它绕螺旋 线一周后到达B点,求AB的长度,并画出电子的螺旋轨 道,顺着磁场方向看去,它是顺时针旋进还是逆时针旋 进?如果是正离子(如质子),结果有何不同?
1、均匀磁场的磁感应强度B垂直于半径为r的圆面,今以该圆面
其中 直电流 ab和cd的延长线
o dc
fI
R1 R2
eI
过o
b
电流bc是以o为圆心、以 R2为半径的1/4圆弧
I
电流de也是以o为圆心、
但,是以R1为半径的1/4 圆弧
a
直电流ef与圆弧电流de在
e点相切
求:场点o处的磁感强度 B
解:
场点o处的磁感强度是由五段
特殊形状电流产生的场的叠加,f I
o dc
磁场力的大小相等方向相反; (3)质量为m,电量为q的带电粒子,受洛仑兹力作用,
其动能和动量都不变; (4)洛仑兹力总与速度方向垂直,所以带电粒子运动的
轨迹必定是圆。
习题课 1 一电子束以速度v沿X轴方向射出,在Y轴上 有电场强度为E的电场,为了使电子束不发生偏 转,假设只能提供磁感应强度大小为B=2E/v的
df
2ds
n
2 0
2 0
i dl 单位面积受力
da
df Idl B其余
da dl 0i
B总 0i
2 其余 0i
2
df
0i 2
n
dadl 2
表三 作用力
4.应用
静电场
稳恒磁场
类比总结
电偶极子 pe
fi 0
i M pE
三
磁偶极子 pm
fi 0
稳恒磁场习题答案

稳恒磁场习题答案稳恒磁场习题答案磁场是物理学中一个重要的概念,它在我们日常生活中扮演着重要的角色。
稳恒磁场习题是物理学中常见的练习题,通过解答这些习题,我们可以更好地理解磁场的性质和应用。
下面是一些常见的稳恒磁场习题及其答案,希望对大家的学习有所帮助。
1. 一根长直导线产生的磁场强度与距离的关系是怎样的?答:根据安培定律,长直导线产生的磁场强度与距离成反比关系。
即磁场强度随着距离的增加而减小。
2. 一根长直导线中心点的磁场强度为B,如果将导线弯成一个半径为r的圆环,中心点的磁场强度会发生怎样的变化?答:当将导线弯成一个半径为r的圆环后,中心点的磁场强度会变为零。
这是因为在圆环的中心点,由于对称性的原因,导线上的每一段磁场强度都会相互抵消,最终导致中心点的磁场强度为零。
3. 一个平面线圈中心的磁场强度与电流的关系是怎样的?答:根据比奥-萨伐尔定律,平面线圈中心的磁场强度与电流成正比关系。
即磁场强度随着电流的增加而增加。
4. 一个平面线圈中心的磁场强度与线圈的面积的关系是怎样的?答:一个平面线圈中心的磁场强度与线圈的面积成正比关系。
即磁场强度随着线圈的面积的增加而增加。
5. 一个平面线圈中心的磁场强度与距离的关系是怎样的?答:一个平面线圈中心的磁场强度与距离成反比关系。
即磁场强度随着距离的增加而减小。
6. 一个匀强磁场中,一个带电粒子的运动轨迹是怎样的?答:在一个匀强磁场中,一个带电粒子的运动轨迹是一个半径为r的圆。
这是因为带电粒子在匀强磁场中受到洛伦兹力的作用,该力垂直于带电粒子的速度和磁场方向,导致粒子做圆周运动。
7. 在一个匀强磁场中,一个带电粒子的运动速度对轨道半径的影响是怎样的?答:在一个匀强磁场中,一个带电粒子的运动速度对轨道半径没有影响。
这是因为带电粒子的运动速度只会影响圆周运动的周期,而不会影响圆周运动的半径。
8. 一个匀强磁场中,一个带电粒子的运动轨迹会受到哪些因素的影响?答:一个匀强磁场中,一个带电粒子的运动轨迹受到带电粒子的电荷量、质量、速度以及磁场的强度和方向的影响。
大连理工大学大学物理作业8(稳恒磁场二)及答案详解

⼤连理⼯⼤学⼤学物理作业8(稳恒磁场⼆)及答案详解S 当⾯S 向长直导线靠近的过程中,穿过⾯S 的磁通量Φ及⾯上任⼀点P 的磁感应强度B ⼤⼩的变化为[ ]。
A. Φ增⼤,B 不变B. Φ不变, B 增⼤C. Φ增⼤,B 增⼤D. Φ不变, B 不变答案:【B 】解:由磁场的⾼斯定理0=S S d B ,即穿过闭合曲⾯的磁通量为零,或者说,磁感应线为闭合曲线,所以Φ不变;由于长直载流导线的磁场aI B πµ20=,与距离成反⽐,所以,当闭合曲⾯靠近载流直导线时,闭合曲⾯上各点的磁感应强度增⼤。
2.⼀电⼦以速度ν→垂直地进⼊磁感应强度为B →的均匀磁场中,此电⼦在磁场中运动的轨迹所围的⾯积内的磁通量将是[ ]。
A.反⽐于B ,正⽐于2νB. 反⽐于B ,正⽐于νC. 正⽐于B ,反⽐于2νD. 正⽐于B ,反⽐于ν答案:【A 】解:电⼦垂直于磁场进⼊磁场,将在洛伦兹⼒的作⽤下,在垂直于磁场的平⾯内作圆周运动。
电⼦在磁场中运动的轨迹半径qBmv R = 由于磁场与⾯积S 垂直,所围的⾯积内的磁通量Bq v m B R S B 2222ππ==?=Φ3. 如图9-2所⽰,⼀⽆限长密绕真实螺线管,通电流强度为I 。
对套在螺线管轴线外的环路L (螺线管穿过环路)作积分=??L l B d 。
答案:I l B 0d µ=?? 解:①根据安培环路定理;②真实螺线管。
4.两平⾏长直导线相距0.4m ,每条导线载有电流10A (如图9-3所⽰),则通过图中矩形⾯积abcd 的磁通量m Φ= 。
答案:Wb 101.16-?解:电流1I 和2I ⼤⼩相等,⽅向相反,由毕萨定律可以判知,它们在矩形⾯积内产⽣的电磁感应强度⽅向均垂直于纸⾯向外。
由对称性可知,电流1I 和2I 产⽣的电磁感应强度穿过矩形⾯积的磁通量⼤⼩相等,因此只须计算⼀个电流产⽣磁场的磁通量。
x I B πµ2101=3ln 203.01.0111πµI ab dx B ab S d B d a ==?=Φ?? 76012ln 31010ln 3 1.110(W b)ab I µπ--Φ=Φ==?≈? 5.有⼀很长的载流导体直圆管,内半径为a ,外半径为b ,电流强度为I ,电流沿轴线⽅向流动,并且均匀地分布在管壁的横截⾯上,如图9-4所⽰。
大学物理3第08章习题分析与解答

习题8-6图IOR 第八章 恒定磁场8-1 均匀磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为[ ]。
(A) B r 22π (B) B r 2π (C) 0 (D) 无法确定 分析与解 根据高斯定理,磁感线是闭合曲线,穿过圆平面的磁通量与穿过半球面的磁通量相等。
正确答案为(B )。
8-2 下列说法正确的是[ ]。
(A) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过(B) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D) 磁感强度沿闭合回路的积分不为零时,回路上任意点的磁感强度必定为零分析与解 由磁场中的安培环路定理,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和一定为零。
正确答案为(B )。
8-3 磁场中的安培环路定理∑⎰=μ=⋅nLI1i i0d l B 说明稳恒电流的磁场是[ ]。
(A) 无源场 (B) 有旋场 (C) 无旋场 (D) 有源场分析与解 磁场的高斯定理与安培环路定理是磁场性质的重要表述,在恒定磁场中B 的环流一般不为零,所以磁场是涡旋场;而在恒定磁场中,通过任意闭合曲面的磁通量必为零,所以磁场是无源场;静电场中E 的环流等于零,故静电场为保守场;而静电场中,通过任意闭合面的电通量可以不为零,故静电场为有源场。
正确答案为(B )。
8-4 一半圆形闭合平面线圈,半径为R ,通有电流I ,放在磁感强度为B 的均匀磁场中,磁场方向与线圈平面平行,则线圈所受磁力矩大小为[ ]。
(A) B R I 2π (B)B R I 221π (C) B R I 241π (D) 0 分析与解 对一匝通电平面线圈,在磁场中所受的磁力矩可表示为B e M ⨯=n IS ,而且对任意形状的平面线圈都是适用的。
第章稳恒磁场习题包含答案
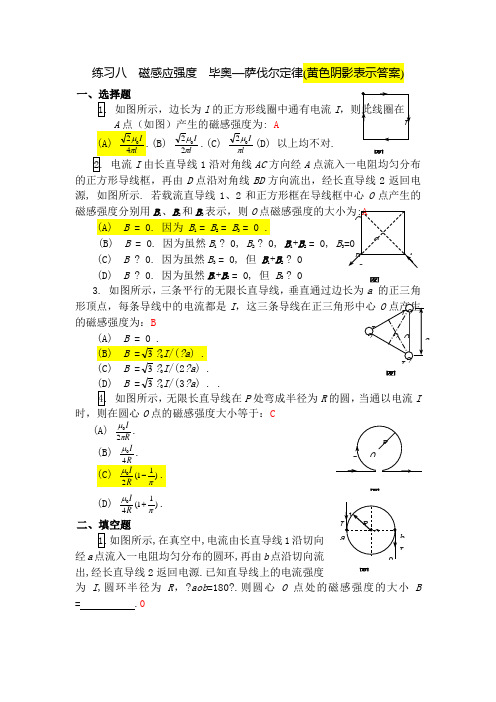
练习八 磁感应强度 毕奥—萨伐尔定律(黄色阴影表示答案)一、选择题如图所示,边长为l 的正方形线圈中通有电流I: AlI πμ220.(C)lI πμ02(D) 以上均不对.1沿对角线AC 方向经A 点流入一电阻均匀分布的正方形导线框,再由D 点沿对角线BD 方向流出,经长直导线2返回电源, 如图所示. 若载流直导线1、2和正方形框在导线框中心O 点产生的磁感强度分别用B 1、B 2和B 3表示,则O(A) B = 0. 因为 B 1 = B 2 = B 3 = 0 .(B) B = 0. 因为虽然B 1 ? 0, B 2 ? 0, B 1+B 2 = 0, B 3(C) B ? 0. 因为虽然B 3 = 0, 但 B 1+B 2 ? 0(D) B ? 0. 因为虽然B 1+B 2 = 0, 但 B 3 ? 03. 如图所示,三条平行的无限长直导线,垂直通过边长为a 的正三角形顶点,每条导线中的电流都是I 的磁感强度为:B(D) B =3?0I /(3?a ) . . 如图所示,无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于:C(A)R Iπμ20. (B) I 0μ.(D))11(40πμ+RI .二、填空题 如图所示,在真空中,电流由长直导线1沿切向经a 点流入一电阻均匀分布的圆环,再由b 点沿切向流出,经长直导线2返回电源.已知直导线上的电流强度为I ,圆环半径为R ,?aob =180?.则圆心O 点处的磁感强度的大小B = .0图图图图图练习九 毕奥—萨伐尔定律(续)一、选择题1. 在磁感强度为B 的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B 的夹角为?,如图所示. 则通过半球面S 的磁通量为:(A) ?r 2B . (B) 2?r 2B . (C) ??r 2B sin ?. (D) ??r 2B cos ?.如图,载流圆线圈(半径为R )与正方形线圈(边长为a )通有相同电流I ,若两线圈中心O 1与O 2R : a 为(A) 1:1.(B) π2:1. π2 三、计算题1.在无限长直载流导线的右侧有面积为S 1和S2的两个矩形回路, 回路旋转方向如图所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S 1回路的磁通量与通过S 2回路的磁通量之比. (此题作为悬赏题)练习十 安培环路定理图图 图图一、选择题2. 无限长直圆柱体,半径为R ,沿轴向均匀流有电流. 设圆柱体内(r < R )的磁感强度为B 1,圆柱体外(r >R )的磁感强度为B 2,则有:(A) B 1、B 2均与r 成正比. (B) B 1、B 2均与r 成反比.(C) B 1与r 成正比, B 2与r 成反比. (D) B 1与r 成反比, B 2与r 成正比.在图(a )和(b )中各有一半径相同的圆形回路L 1和L 2,圆周内有电流I 2和I 2,其分布相同,且均在真空中,但在图(b )中,L 2回路外有电流I 3,P 1、P 2为两圆形回路上的对应点,则:(A) ⎰⋅1d L l B =⎰⋅2d Ll B , 21P P B B =.(B) ⎰⋅d L l B ?⎰⋅ d L l B , 21P P B B =.(D) ⎰⋅1d L l B ⎰⋅2d L l B , 21P P B B ≠.如图所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a 端流入而从d 端流出,则磁感强度B 沿图中闭合路径的积分⎰⋅Ll B d 等于:(A) ?0I . (B) ?0I/3. 0I /4. 2?0I /3 .如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,(B) 0 d =⋅⎰Ll B ,且环路上任意点B =0.(C) 0 d ≠⋅⎰Ll B ,且环路上任意点B ?0.(D) 0 d ≠⋅⎰Ll B ,且环路上任意点B =0.二、填空题两根长直导线通有电流I ,图所示有三种环路对于环路a , =⋅⎰aL l B d ;图图P 1 (aI 2P 2 (b图对于环路b , =⋅⎰bL l B d ;对于环路c , =⋅⎰cL l B d . ?0I , 0, 2?0I .练习十一 安培力 洛仑兹力一、选择题如图所示. 匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是:B(A) ab 边转入纸内,cd 边转出纸外. (B) ab 边转出纸外,cd 边转入纸内. (C) ad 边转入纸内,bc 边转出纸外. (D) ad 边转出纸外,cd 边转入纸内.5. 一电子以速度v 垂直地进入磁感强度为B 的均匀磁场中,此电子在磁场中运动的轨道所围的面积内的磁通量是(A) 正比于B ,反比于v 2. (B) 反比于B ,正比于v 2. (C) 正比于B ,反比于v. (D) 反比于B ,反比于v练习十三 静磁场习题课一、选择题1. 一质量为m 、电量为q 的粒子,以与均匀磁场B 垂直的速度v 射入磁场中,则粒子运动轨道所包围范围内的磁通量F m 与磁场磁感强度B 的大小的关系曲线是图中的哪一条 D图(AB OBO(DB O(CB O(B)B O(E图边长为l 的正方形线圈,分别用图所示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为:(A) B 1 = 0 . B 2 = 0.(B) B 1 = 0 . l I B πμ0222=l π1l I π02.如图, 质量均匀分布的导线框abcd 置于均匀磁场中(B 的方向竖直向上),线框可绕AA ?轴转动,导线通电转过? 角后达到稳定平衡.如果导线改用密度为原来1/2的材料做,欲保持原来的稳定平衡位置(即? 角不变),可以采用哪一种办法(A) 将磁场B 减为原来的1/2或线框中电流减为原来的1/2. (B) 将导线的bc 部分长度减小为原来的1/2. (C) 将导线ab 和cd 部分长度减小为原来的1/2. (D) 将磁场B 减少1/4,线框中电流强度减少1/4.图图l (d (。
稳恒磁场习题答案

方向:与电流满足右手螺旋定则。
单位:安培· 2 米 4.平面载流线圈在均匀磁场中受到的力矩M
定义: M p m B
单位:牛顿· 米
5.洛仑兹力
F m qv B
6.电荷垂直于磁场作圆周运动
R mv qB
T
2 m qB
0 dI
2r
dI ndq
2
O
dq
r
a dI
dq dr
dB B
0
a b
2r 2 4
dr b
dr
ω
0 dr
r
0
4
ln
ab a
a
B dS 0
B dl 0 I
H dl
I
5
c
B H
0r
(常数) 顺磁质: r 1 (常数) 抗磁质: r 1 铁磁质: r 1
(10 ~ 10 )
2
通常不是常数
四.几个典型载流导体的磁场 1.载流直导线
0I
2 x
b
I 1 dx
0 II 1
2
ln
a b b
9-13 一根很长的铜导线,均匀载有强度为I的电流。在导线内 部,通过中心线作一平面S。试计算通过导线单位长度的S平面 内的磁感通量。 解:
B 2 r 0 j r
B
2
0 Ir
2 R
2
R
d m B d S B ld r
I 2 R a
a
Ia 2 R
大学物理稳恒磁场作业题参考答案

8.3.7 设题8.3.7图中两导线中的电流均为8A,对图示的三条闭合曲线 a , b , c ,
分别写出安培环路定理等式右边电流的代数和.并讨论:
(1)在各条闭合曲线上,各点 的磁感应强度 B 的大小是否相等?
(2)在闭合曲线 c 上各点的 B 是否为 零?为什么?
解:
B a
dl
8
0
b
B
dl
80
cB dl 0
∴
Fab
b
Idl
B
I
(
b
dl
)
2 B
I ab B
a
a
方向⊥ ab 向上,大小 Fab BI ab
题 8.3.11 图
8.3.11 如题8.3.11图所示,在长直导线 AB 内通以电流 I1 =20A,在矩形线圈 CDEF 中通有电流 I 2 =10 A, AB 与线圈共面,且 CD , EF 都与 AB 平行.已知 a =9.0cm, b =20.0cm, d =1.0 cm,求:
(C)内外部磁感应强度 B 都与 r 成反比;
(D)内部磁感应强度 B 与 r 成反比,外部磁感应强度 B 与 r 成正比。
[答案:B]
(5)在匀强磁场中,有两个平面线圈,其面积 A1 = 2 A2,通有电流 I1 = 2 I2,它
们所受的最大磁力矩之比 M1 / M2 等于 [
]
(A) 1;
(B) 2;
(1)导线 AB 的磁场对矩形线圈每边所作用的力;
(2)矩形线圈所受合力和合力矩. 解:(1) FCD 方向垂直 CD 向左,大小
FCD
I2b
0 I1 2d
8.0 104
N
同理 FFE 方向垂直 FE 向右,大小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章 稳恒磁场 习题及答案6. 如图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R 。
若通以电流I ,求O 点的磁感应强度。
解:O 点磁场由AB 、C B、CD 三部分电流产生,应用磁场叠加原理。
AB 在O 点产生的磁感应强度为01 BC B在O 点产生的磁感应强度大小为R I B 402 RIR I 123400 ,方向垂直纸面向里CD 在O 点产生的磁感应强度大小为)cos (cos 421003 r IB)180cos 150(cos 60cos 400R I)231(20 R I ,方向垂直纸面向里 故 )6231(203210R I B B B B ,方向垂直纸面向里 7. 如图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连。
已知圆环的粗细均匀,求环中心O 的磁感应强度。
解:圆心O 点磁场由直电流 A 和 B 及两段圆弧上电流1I 与2I 所产生,但 A 和 B 在O 点产生的磁场为零。
且21221R R I I 电阻电阻 1I 产生的磁感应强度大小为)(24101RI B ,方向垂直纸面向外 2I 产生的磁感应强度大小为RIB 4202 ,方向垂直纸面向里 所以, 1)2(2121I I B B 环中心O 的磁感应强度为0210 B B B8. 如图所示,一无限长载流平板宽度为a ,沿长度方向通过均匀电流I ,求与平板共面且距平板一边为b 的任意点P 的磁感应强度。
解:将载流平板看成许多无限长的载流直导线,应用叠加原理求解。
以P 点为坐标原点,垂直载流平板向左为x 轴正方向建立坐标系。
在载流平板上取dx aIdI ,dI 在P 点产生的磁感应强度大小为x dI dB 20dx axI20 ,方向垂直纸面向里 P 点的磁感应强度大小为a b b x dx a I dB B 20bab a I ln 20 方向垂直纸面向里。
9. 如图所示,真空中有两个点电荷A ,B ,分别带有电量q 和q ,相距为d 。
它们都以角速度 绕轴'OO 转动,轴'OO 与AB 连线相互垂直,其交点为C ,距A 点为3d。
求C 点的磁感应强度。
解:q 电荷运动形成电流大小为21q T q I1I 在C 点产生的磁感应强度大小为3/2210101d I R I B dq 430方向沿O O 方向同理,q 电荷运动形成电流的电流2I 在C 点产生的磁感应强度大小为3/22202d I Bdq830方向沿O O 的反方向所以,C 点的磁感应强度大小为21B B B dq830方向沿O O 方向10. 已知磁感应强度大小0.2 B Wb ·m -2的均匀磁场,方向沿x 轴正方向,如图所示。
试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量。
解:(1)通过abcd 面积1S 的磁通量为24.0cos 4.03.00.211 S BWb(2)通过befc 面积2S 的磁通量为022 S B(3)通过aefd 面积3S 的磁通量为cos 5.03.0233 S B24.0545.03.02 Wb11.如图所示,真空中一半径为r 的金属小圆环,在初始时刻与一半径为R (r R )的金属大圆环共面且同心,在大圆环中通以恒定的电流I ,如果小圆环以匀角速度 绕其直径转动,求任一时刻t 通过小圆环的磁通量m 。
解:载流大圆环在圆心处产生的磁感应强度大小为RIB 20,方向垂直纸面向外任一时刻t 通过小圆环的磁通量为t r B S B m cos 212. 如图所示,电流I I I 21,求沿回路1L 、2L 以及3L 的磁感应强度的环流。
解:由安培环路定理得I I l d B L 0101I I l d B L 02020)(2103I I l d B L13. 一根很长的同轴电缆,由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成,横截面如图所示。
使用时,电流I 从一导体流去,从另一导体流回,设电流都是均匀地分布在导体的横截面上。
求:(1)导体圆柱内(r <a );(2)两导体之间(a <r <b );(3)导体圆筒内(b <r <c )以及(4)电缆外(r >c )各点处磁感应强度的大小。
解:磁场分布具有轴对称性,在横截面内取同心圆为回路,应用安培环路定理,有iI r B l d B 02(1)当a r 时,22r aI I i,所以 202aIrB(2)当b r a 时,I I i ,所以rI B 20(3)当c r b 时,)()(2222b r b c I I I i,所以 )(2)(22220b c r r c I B (4)当c r 时,0 i I ,所以0 B14. 有一长直导体圆管,内外半径分别为R 1和R 2,如图所示,它所载的电流1I 均匀分布在其横截面上。
导体旁边有一绝缘“无限长”直导线,载有电流2I ,且在中部绕了一个半径为R 的圆圈。
设导体管的轴线与长直导线平行,相距为d ,而且它们与导体圆圈共面,求圆心O 点处的磁感应强度。
解:应用磁场叠加原理求解。
长直载流导体圆管产生的磁场分布具有轴对称性,在横截面内取圆心在轴线上、过O 点的圆周为回路,应用安培环路定理,有iI d R B l d B 01)(210I所以,长直载流导体圆管在O 点产生的磁感强度大小为dR I B 112 ,方向垂直纸面向里电流2I 的长直导线在O 点产生的磁感强度大小为RIB 2022 ,方向垂直纸面向外电流2I 的圆线圈在O 点产生的磁感强度大小为dR O I 1 I 2I 2RI B 2203,方向垂直纸面向外所以,O 点的磁感强度大小为])1([2120132dR I RI B B B B方向垂直纸面向外。
15. 在半径为R 的长直圆柱形导体内部,与轴线平行地挖成一半径为r 的长直圆柱形空腔,两轴间距离为a ,且a >r ,横截面如图所示。
现在电流I 沿导体管流动,电流均匀分布在管的横截面上,而电流方向与管的轴线平行。
求:(1)圆柱轴线上的磁感应强度的大小; (2)空心部分轴线上的磁感应强度的大小。
解:在空腔处补上沿导体管流动、在横截面均匀分布的电流2I 和2I ,应用补偿法求解。
电流2I 和2I 在空间产生的磁场相互抵消,因此空间各点磁场可看作半径为R 、电流21I I I 均匀分布在横截面上的圆柱导体和半径为r 、电流2I 均匀分布在横截面上的圆柱导体产生的磁场的叠加。
2I 和1I 的大小为2222)(r r R II 222rR Ir 21I I I 222r R IR1I 和2I 产生的磁场分布具有轴对称性,应用安培环路定理求磁感应强度。
(1)电流1I 在O 点产生的01 B ,电流2I 在O 点产生的磁感应强度满足iI a B l d B 02220I222020222r R Ir a a I B圆柱轴线上的O 点B 的大小为)(22220210r R a Ir B B B(2) 电流2I 在O 点产生的02B ,电流1I 在O 点产生的磁感应强度满足 i I a B l d B 012 2210a RI 221012R a I a B )(2220r R Ia空心部分轴线上O 点磁感应强度的大小为)(2220210r R IaB B B16. 通以电流I 的导线abcd 形状如图所示,l cd ab ,bc 弧是半径为R 的半圆周,置于磁感应强度为B的均匀磁场中,B的方向垂直纸面向里。
求此导线受到安培力的大小和方向。
解:应用安培定律求解。
ab 边受力大小为BIl F ab ,方向:向左cd 边受力大小为y xl dF dBIl F cd ,方向:向右对于bc 边,建立图示坐标系。
在bc 边上取电流元l Id, BIRd BIdl dF 根据对称性有0 x Fd BIR dF dF y sin sinsin d BIR dF F y y BIR 2此导线受到安培力的大小为BIR F 2 ,方向沿y 轴正向。
17. 在长直导线AB 内通以电流1I ,在矩形线圈CDEF 中通有电流2I ,AB 与线圈共面,且CD ,EF 都与AB 平行,线圈的尺寸及位置均如图所示。
求:导线AB 的磁场对矩形线圈每边所作用的力及矩形线圈所受合力。
解:CD F方向垂直CD 向左,大小dIb I F CD 2102同理,FE F方向垂直FE 向右,大小)(2102a d I b I F FECF F方向垂直CF 向上,大小为ad dCF dad I I r r I I F ln 2d 2210210 ED F方向垂直ED 向下,大小为CF ED F F线圈所受合力ED CF FE CD F F F F F方向向左,大小为)(2210a d d aI bI F F F FE CD18. 有圆线圈直径8cm ,共12匝,通电流5A ,将此线圈置于磁感应强度为 0.6T 的匀强磁场中。
试求:(1)作用在线圈上的最大磁力矩;(2)线圈法线方向与磁场方向夹角多大时,力矩是线圈上最大力矩的一半?(取最小角度)解:(1)NI R NIS P m 2m N NIB R B P M m 18.090sin 2(2) B P B P M m m 21sin,所以 619. 一线圈由半径为R 的1/4圆弧和相互垂直的二直线组成,通以电流I ,把它放在磁感应强度大小为B 的均匀磁场中(磁感应强度B 的方向如图所示)。
求:(1)线圈平面与磁场垂直时,圆弧 ⌒AB 所受的磁力; (2)线圈平面与磁场成60°角时,线圈所受的磁力矩大小。
解:(1)建立图示坐标系。
在圆弧上取电流元l IdBIRd BIdl dF根据对称性有0 x Fyxl dF dd BIR dF dF y cos cos44cosd BIRdF F y y IRB 2圆弧 ⌒ AB 所受的磁力的大小为BIR F 2 ,方向与直线AB 垂直,且与OB 的夹角为045;(2)线圈的磁矩大小为I R IS P m 241线圈所受的磁力矩大小为030sin B P M m IB R 28120. 电子在T B 3100.7 的匀强磁场中作圆周运动,圆周半径cm r 0.3 。
已知B 垂直于纸面向外,某时刻电子在A 点,速度向上,如图所示。
(1)试画出这电子运动的轨道;(2)求这电子速度的大小; (3)求这电子的动能k E 。
解:(1)轨迹如图(2)由牛顿第二定律得, rm B e 2故 7107.3m eBr1s m (3) 162K 102.621 m E J21. 如图所示的三条线表示三种不同磁介质的H B 关系曲线,虚线是B =H 0 关系的曲线,试指出哪一条是表示顺磁质?哪一条是表示抗磁质?哪一条是表示铁磁质?解:曲线Ⅱ是顺磁质,曲线Ⅲ是抗磁质,曲线Ⅰ是铁磁质。
