libSVM核函数实现【matlab】

合集下载

SVM分类核函数及参数选择比较_奉国和

摘要：支持向量机（SVM）被证实在分类领域性能良好，但其分类性能受到核函数及参数影响。讨论核函数及参数对 SVM 分类性能的影响，并运用交叉验证与网格搜索法进行参数优化选择，为 SVM 分类核函数及参数选择提供借鉴。关键词：支持向量机；核函数；分类 DOI：10.3778/j.issn.1002-8331.2011.03.037 文章编号：1002-8331（2011）03-0123-02 文献标识码：A 中图分类号：TP316
coef ) 。
2 参数选取方法
SVM 的参数选择问题，其实质就是一个优化问题。目前 SVM 参数选取方法主要有：经验选择法、实验试凑法、梯度下降法、交叉验证法、Bayesian 法等。同时随着遗传算法、粒子群优化、人工免疫等智能优化方法的成功，陆续有学者采用这些方法来优化选择 SVM 参数。近几年，进化计算领域兴起了一类新型优化算法，即分布估计算法，并迅速成为进化计算领域
（1）Polynomial 核函数：K(xxi) =[γ*(x·xi) + coef ]d ，其中 d 为多项式的阶，coef 为偏置系数。
（2）RBF 核函数：K(xxi) = exp(-γ* x - xi 2) ，其中 γ 为核
函数的宽度。（3）Sigmoid核函数（两层神经网络）：K(xxi) = tanh(γ(x·xi) +
1 支持向量机原理
支持向量机是基于结构风险最小化原理（Structural Risk
Mininization，SRM），为了控制泛化能力，需要控制两个因素，即经验风险和置信范围值。传统的神经网络是基于经验风险最小化原则，以训练误差最小化为优化目标，而支持向量机以训练误差作为优化问题的约束条件，以置信范围最小化为优化目标。它最终化为解决一个线性约束的凸二次规划（QP）求解问题，所以支持向量机的解具有唯一性，也是全局最优的。 [3-4] 应用核函数技术，将输入空间中的非线性问题，通过函数映射到高维特征空间中，在高维空间中构造线性判别函数，常用的核函数有如下三种。

matlab调用高斯核函数

matlab调用高斯核函数如何在MATLAB中调用高斯核函数。

第一步：了解高斯核函数的概念和数学表达式。

高斯核函数是一种常用的核函数，用于非线性支持向量机（SVM）和高斯过程回归。

它被广泛应用于模式识别、数据挖掘和机器学习等领域。

高斯核函数的数学表达式为：K(x, y) = exp(- x-y ^2 / (2*sigma^2))其中，x和y是向量或矩阵，x-y 表示欧氏距离的平方，sigma是高斯核函数的参数，控制函数的平滑度。

第二步：在MATLAB中编写高斯核函数的代码。

可以使用MATLAB内置的函数来实现高斯核函数的计算。

首先，定义一个函数来计算高斯核函数的数值：matlabfunction result = gaussian_kernel(x, y, sigma)result = exp(-norm(x-y)^2 / (2*sigma^2));end在这个函数中，norm函数用于计算向量x和y的欧式距离的平方。

参数x和y可以是向量或矩阵，sigma是高斯核函数的参数。

第三步：在MATLAB中调用高斯核函数。

在MATLAB中，可以使用上述定义的高斯核函数来计算两个向量或矩阵之间的高斯核函数值。

以下是一个示例：matlabx1 = [1 2 3];x2 = [4 5 6];sigma = 1;result = gaussian_kernel(x1, x2, sigma);disp(result);在这个示例中，我们定义了两个向量x1和x2，并将sigma设置为1。

然后，使用gaussian_kernel函数计算x1和x2之间的高斯核函数值，并将结果显示在命令窗口中。

第四步：调整高斯核函数的参数。

高斯核函数的性能受到参数sigma的影响。

根据具体的应用场景，可以调整sigma的值来达到最佳结果。

一般情况下，sigma的取值范围为0.01到10之间。

可以使用交叉验证或网格搜索等方法来确定最佳的sigma值。

支持向量机(SVM)、支持向量机回归(SVR)：原理简述及其MATLAB实例

支持向量机（SVM）、支持向量机回归（SVR）：原理简述及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1）关于拉格朗日乘子法2）关于KKT条件2、范数1）向量的范数2）矩阵的范数3）L0、L1与L2范数、核范数二、SVM概述1、简介2、SVM算法原理1）线性支持向量机2）非线性支持向量机二、SVR：SVM的改进、解决回归拟合问题三、多分类的SVM1. one-against-all2. one-against-one四、QP（二次规划）求解五、SVM的MATLAB实现：Libsvm1、Libsvm工具箱使用说明2、重要函数：3、示例支持向量机（SVM）：原理及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1）关于拉格朗日乘子法首先来了解拉格朗日乘子法，为什么需要拉格朗日乘子法呢？记住，有需要拉格朗日乘子法的地方，必然是一个组合优化问题。

那么带约束的优化问题很好说，就比如说下面这个：这是一个带等式约束的优化问题，有目标值，有约束条件。

那么你可以想想，假设没有约束条件这个问题是怎么求解的呢？是不是直接 f 对各个 x 求导等于 0，解 x 就可以了，可以看到没有约束的话，求导为0，那么各个x均为0吧，这样f=0了，最小。

但是x都为0不满足约束条件呀，那么问题就来了。

有了约束不能直接求导，那么如果把约束去掉不就可以了吗？怎么去掉呢？这才需要拉格朗日方法。

既然是等式约束，那么我们把这个约束乘一个系数加到目标函数中去，这样就相当于既考虑了原目标函数，也考虑了约束条件。

现在这个优化目标函数就没有约束条件了吧，既然如此，求法就简单了，分别对x求导等于0，如下：把它在带到约束条件中去，可以看到，2个变量两个等式，可以求解，最终可以得到,这样再带回去求x就可以了。

那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。

更高一层的，带有不等式的约束问题怎么办？那么就需要用更一般化的拉格朗日乘子法，即KKT条件，来解决这种问题了。

libsvmread函数

libsvmread函数libsvmread函数是Matlab中一个用于读取LIBSVM格式数据的函数。

LIBSVM 是一个开源的支持向量机（Support Vector Machine，SVM）实现库，其数据格式通常为文本文件。

libsvmread函数可以将LIBSVM格式的文本文件转换为Matlab中的矩阵格式，方便后续的数据处理和模型训练。

libsvmread函数的语法如下：[x, y] = libsvmread(filename)其中，filename为LIBSVM格式的文件名，x和y分别为Matlab中的数据矩阵和标签向量。

具体来说，x是一个n×m的矩阵，其中每一行代表一个样本，每一列代表一个特征，n为样本数，m为特征数。

y是一个n×1的向量，记录每个样本的分类标签。

注意，LIBSVM格式的文件中标签是放在第一列的，因此读入后需将其从x中去除，并将其赋值给y。

值得注意的是，libsvmread函数读入的数据必须符合LIBSVM格式的要求。

LIBSVM格式要求每行代表一个样本，以一个标签开头，后跟一系列的特征值及其索引，特征值与索引之间用冒号分隔。

例如：-1 1:0.1 3:0.2 5:0.31 2:0.4 4:0.5 6:0.6-1 1:0.2 2:0.3 4:0.8其中，第一列为标签，后面的数字代表特征的索引，冒号后面的数字代表该特征的值。

在使用libsvmread函数时，需要注意几个问题。

首先，libsvmread函数只能读取LIBSVM格式的文本文件，对于其他格式的数据需要先进行转换。

其次，由于Matlab中读取的文件大小受到内存限制，因此对于较大的数据文件需要采取适当的措施，如分批读取等。

最后，读入的数据需要进行预处理，包括特征缩放、异常值处理等，以保证训练的效果。

动态场景下的基于SIFT和CBWH的目标跟踪

动态场景下的基于SIFT和CBWH的目标跟踪王芬芬;陈华华【摘要】针对动态背景下的目标跟踪，提出了基于SIFT特征和CBWH特征的卡尔曼跟踪算法。

算法利用卡尔曼滤波器预测目标的大概位置；在所在位置区域内提取SIFT特征，与第一帧和前一帧进行特征匹配，并投票获得候选目标位置；利用CBWH特征获得目标可能位置；将二者位置加权对卡尔曼滤波器预测值进行修正，得到目标位置。

实验表明，所提算法取得了较好的实验结果。

%An object tracking algorithm based on Kalman filter using scale invariant feature transform (SIFT) and CBWH is proposed to solve the problem that trackers always drift or even lose target in dynamic scenes . Kalman filter predictsan area ,each matched keypoint casts a vote for the object center ,then the voting results are evaluated by the nearest neighbor clustering , the weighted result is a candidate position of the object's center.Another possible position is calculated by mean shift tracking using CBWH .The positions above are weighted into the object's center.This center is then sent to Kalman filter to get the final position and velocity . Experimental results demonstrate that the proposed method obtains good tracking results .【期刊名称】《杭州电子科技大学学报》【年(卷),期】2015(000)004【总页数】4页(P46-49)【关键词】动态场景;目标跟踪;卡尔曼滤波;尺度不变特征变换【作者】王芬芬;陈华华【作者单位】杭州电子科技大学通信工程学院，浙江杭州310018;杭州电子科技大学通信工程学院，浙江杭州310018【正文语种】中文【中图分类】TP391运动目标跟踪是计算机视觉的重要研究方向，其中对先验未知的物体进行跟踪越来越引起人们的关注。

matlab核函数

matlab核函数在MATLAB中，核函数主要用于支持向量机（SVM）和其他机器学习算法。

这些函数用于计算两个向量之间的相似性或距离。

以下是一些常见的核函数：1. **线性核函数（Linear Kernel）**:```matlabK = x * y';```2. **多项式核函数（Polynomial Kernel）**:```matlabK = (gamma * x * y' + coef0)^degree;```3. **高斯径向基函数（Gaussian RBF Kernel）**:```matlabK = exp(-gamma * (x - y)' * (x - y));```4. **Sigmoid核函数（Sigmoid Kernel）**:```matlabK = tanh(gamma * x * y' + coef0);```其中，`x` 和`y` 是输入向量，`gamma` 和`coef0` 是核函数的参数，`degree` 是多项式核函数的度数。

在MATLAB的机器学习工具箱中，你可以使用`fitcknn` 函数来训练一个基于核的k近邻（KNN）分类器，其中你可以选择不同的核函数类型。

例如：```matlab% 创建一些数据X = [randn(100, 2) randn(100, 2)]; % 创建两个类别Y = [ones(100, 1) -1*ones(100, 1)]; % 对应的标签% 使用'rbf' 核函数训练一个基于核的KNN分类器SVMModel = fitcknn(X, Y, 'KernelFunction', 'rbf');```请注意，选择哪种核函数通常取决于你的具体应用和数据特性。

不同的核函数可能会产生不同的结果，因此需要根据你的问题进行适当的调整和实验。

matlab调用高斯核函数 -回复

matlab调用高斯核函数-回复Matlab是一种高效、强大的科学计算软件工具，具有广泛的应用领域。

在机器学习领域中，常常需要使用高斯核函数进行模型的训练和预测。

本文将逐步介绍如何在Matlab中调用高斯核函数，并解释其原理和应用。

第一步：了解高斯核函数高斯核函数，也被称为径向基函数（Radial Basis Function，RBF），是一种常用的核函数。

核函数是一种在机器学习中广泛应用的数学工具，用于将输入数据从原始空间映射到一个更高维度的特征空间。

高斯核函数的表达式为：K(x, y) = exp(- x-y ^2 / (2 * sigma^2))其中，x和y是输入样本，x-y ^2表示欧几里得距离的平方，sigma^2为高斯核函数的参数。

高斯核函数的核心思想是通过计算输入样本与训练样本之间的相似度，来评估它们之间的相关性。

相似度越高，相关性就越强。

高斯核函数的输出结果在0到1之间，可以表示样本之间的相似度或相关性。

第二步：在Matlab中定义高斯核函数在Matlab中，可以通过定义一个函数来实现高斯核函数的计算。

下面是一个例子：matlabfunction K = gaussian_kernel(x, y, sigma)K = exp(-norm(x-y)^2 / (2 * sigma^2));end上述代码中，我们定义了一个名为gaussian_kernel的函数，它接受两个输入样本x和y，以及高斯核函数的参数sigma。

函数的输出结果是它们之间的相似度。

在函数体内，我们使用了Matlab内置函数norm来计算输入样本之间的欧几里得距离。

第三步：使用高斯核函数进行模型训练在机器学习中，高斯核函数常被用于支持向量机（Support Vector Machine，SVM）的训练过程。

SVM是一种二分类模型，通过寻找一个最优超平面来分割不同类别的样本。

高斯核函数可以用于在非线性可分的情况下，将样本映射到一个更高维度的特征空间，从而增加了模型的表达能力。

LIBSVM使用方法

LIBSVM1 LIBSVM简介LIBSVM是台湾大学林智仁(Lin Chih-Jen)副教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包，他不但提供了编译好的可在Windows 系列系统的执行文件，还提供了源代码，方便改进、修改以及在其它操作系统上应用；该软件还有一个特点，就是对SVM所涉及的参数调节相对比较少，提供了很多的默认参数，利用这些默认参数就可以解决很多问题；并且提供了交互检验(Cross -SVM回归等问题，包括基于一对一算法的多类模式识别问题。

SVM用于模式识别或回归时，SVM方法及其参数、核函数及其参数的选择，目前国际上还没有形成一个统一的模式，也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。

ν-SVM回归和ε-SVM分类、νValidation)的功能。

该软件包可以在.tw/~cjlin/免费获得。

该软件可以解决C-SVM分类、-SVM回归等问题，包括基于一对一算法的多类模式识别问题。

2 LIBSVM使用方法LibSVM是以源代码和可执行文件两种方式给出的。

如果是Windows系列操作系统，可以直接使用软件包提供的程序，也可以进行修改编译；如果是Unix类系统，必须自己编译，软件包中提供了编译格式文件，我们在SGI工作站(操作系统IRIX6.5)上，使用免费编译器GNU C++3.3编译通过。

2.1 LIBSVM 使用的一般步骤：1) 按照LIBSVM软件包所要求的格式准备数据集；2) 对数据进行简单的缩放操作；3) 考虑选用RBF 核函数；4) 采用交叉验证选择最佳参数C与g；5) 采用最佳参数C与g 对整个训练集进行训练获取支持向量机模型；6) 利用获取的模型进行测试与预测。

libsvm参数说明

libsvm参数说明摘要：一、libsvm 简介- 什么是libsvm- libsvm 的作用二、libsvm 参数说明- 参数分类- 参数详细说明- 核函数参数- 松弛参数- 惩罚参数- 迭代次数参数- 其他参数三、libsvm 参数调整- 参数调整的重要性- 参数调整的方法正文：【libsvm 简介】libsvm 是一款广泛应用于机器学习领域的开源软件，全称是“LIBSVM”，它提供了支持向量机（SVM）的完整实现，可以用于分类和回归等多种任务。

libsvm 不仅支持常见的数据集格式，还提供了丰富的API 接口，方便用户进行二次开发和应用。

libsvm 的主要作用是帮助用户解决高维数据分类和回归问题。

在面对高维数据时，传统的分类算法可能会遇到“维数灾难”，导致分类效果不佳。

而libsvm 通过使用核函数技术，将高维数据映射到低维空间，从而有效地解决了这个问题。

【libsvm 参数说明】libsvm 提供了丰富的参数供用户调整，以达到最佳分类效果。

这些参数主要分为以下几类：1.核函数参数：包括核函数类型（如线性核、多项式核、径向基函数核等）和核函数参数（如径向基函数核的核径宽）。

2.松弛参数：用于控制分类间隔的大小，对最终分类结果有一定影响。

3.惩罚参数：控制模型对误分类的惩罚力度，对分类效果有重要影响。

4.迭代次数参数：控制支持向量机算法的迭代次数，影响模型的收敛速度。

5.其他参数：如学习率、最小化目标函数的迭代次数等。

【libsvm 参数调整】参数调整是libsvm 使用过程中非常重要的一环，合适的参数设置可以使模型达到更好的分类效果。

参数调整的方法主要有以下几种：1.网格搜索法：通过遍历参数空间的各个点，找到最佳参数组合。

这种方法适用于参数空间较小的情况。

2.随机搜索法：在参数空间中随机选取一定数量的点进行遍历，找到最佳参数组合。

这种方法适用于参数空间较大，且网格搜索法效果不佳的情况。

3.贝叶斯优化法：利用贝叶斯理论，对参数进行加权调整，以提高搜索效率。

libsvm安装教程matlab中使用(详细版)

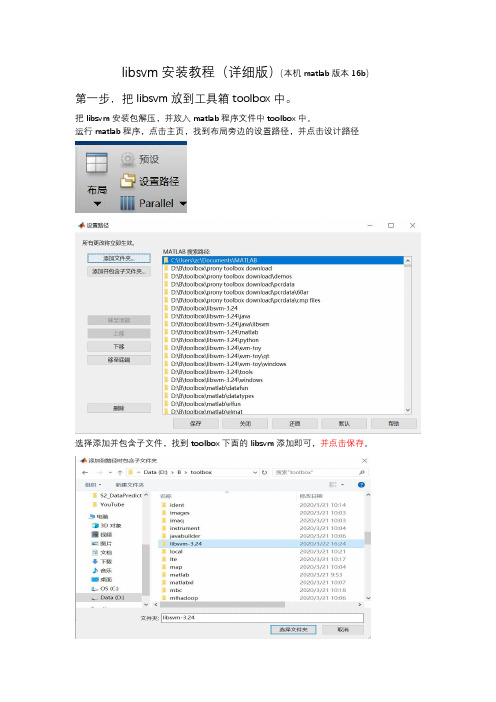
libsvm安装教程（详细版）（本机matlab版本16b）第一步，把libsvm放到工具箱toolbox中。

把libsvm安装包解压，并放入matlab程序文件中toolbox中。

运行matlab程序，点击主页，找到布局旁边的设置路径，并点击设计路径选择添加并包含子文件，找到toolbox下面的libsvm添加即可，并点击保存。

第二步更新工具箱找到布局旁边的预测按钮，并点击预设按钮。

找到常规，选择更新工具箱路径缓存，并点击应用，最后点击确定。

第三步，更改libsvm文件在matlab文件行，打开如下地址：D:\B\toolbox\libsvm-3.24\matlab打开make.m文件，将make.m中的CFLAGS改为COMPFLAGS。

注：因为matlab中有自带的svm，为了防止libsvm和自带的svm发生冲突，所以将D:\B\toolbox\libsvm-3.24\matlab中将svmtrian.c和svmpredic.c前面加入lib，相应的make.m文件中也做修改第四步，安装编译器编译器采用最新版tdm64-gcc-9.2.0，安装教程很简单选择Creat，保存路径直接选择C盘即可，C:\TDM-GCC-64。

第五步，使用matlab读取C语言程序。

Matlab文件行调整到此目录下D:\B\toolbox\libsvm-3.24\matlab 并在命令行窗口输入：setenv('MW_MINGW64_LOC','C:\TDM-GCC-64')make点击回车，当命令行窗口出现：使用'MinGW64 Compiler (C)' 编译。

MEX 已成功完成。

使用'MinGW64 Compiler (C)' 编译。

MEX 已成功完成。

使用'MinGW64 Compiler (C)' 编译。

MEX 已成功完成。

libsvm的matlab代码

尊敬的读者，今天我将向大家介绍libsvm在Matlab中的代码实现。

libsvm是一个非常流行的用于支持向量机（SVM）的软件包，它具有训练和预测的功能，并且支持多种核函数。

而Matlab作为一种强大的科学计算环境，也提供了丰富的工具和函数库来支持机器学习和模式识别的应用。

将libsvm与Matlab结合起来，可以实现更加高效和便捷的SVM模型训练和预测。

1. 安装libsvm我们需要在Matlab中安装libsvm。

你可以在libsvm的官方全球信息湾上下载最新版本的libsvm，并按照官方指引进行安装。

安装完成后，你需要将libsvm的路径添加到Matlab的搜索路径中，这样Matlab才能够找到libsvm的函数和工具。

2. 数据准备在使用libsvm进行SVM模型训练之前，我们首先需要准备好训练数据。

通常情况下，训练数据是一个包含特征和标签的数据集，特征用来描述样本的属性，标签用来表示样本的类别。

在Matlab中，我们可以使用矩阵来表示数据集，其中每一行代表一个样本，每一列代表一个特征。

假设我们的训练数据保存在一个名为"train_data.mat"的文件中，可以使用以下代码加载数据：```matlabload train_data.mat;```3. 数据预处理在加载数据之后，我们可能需要对数据进行一些预处理操作，例如特征缩放、特征选择、数据平衡等。

这些步骤可以帮助我们提高SVM模型的性能和泛化能力。

4. 模型训练接下来，我们可以使用libsvm在Matlab中进行SVM模型的训练。

我们需要将训练数据转换成libsvm所需的格式，即稀疏矩阵和标签向量。

我们可以使用libsvm提供的函数来进行模型训练。

下面是一个简单的示例：```matlabmodel = svmtrain(label, sparse(train_data), '-s 0 -t 2 -c 1 -g0.07');```上面的代码中，label是训练数据的标签向量，train_data是训练数据的稀疏矩阵，'-s 0 -t 2 -c 1 -g 0.07'是SVM训练的参数设置，具体含义可以参考libsvm的官方文档。

一种新的基于脑电信号相似性分析的癫痫性发作自动检测方法

一种新的基于脑电信号相似性分析的癫痫性发作自动检测方法李斯卉;吕可嘉;潘敏;张瑞【摘要】癫痫是最常见的神经系统疾病之一.脑电图是大脑电活动的记录,已成为检测癫痫发作的一种有效工具.如何通过数据分析以挖掘癫痫脑电的本质特征,是实现癫痫性发作自动检测的关键.提出了一种新的脑电信号相似性的分析方法,进而在这一方法的基础上定义了待测脑电与模版脑电之间的最大余弦相似度为癫痫脑电特征,并将其应用于癫痫性发作的自动检测.采用BONN和CHB-MIT两个公开数据库来验证该文所提方法的性能.和已有方法相比,该文所提自动检测方法将检测准确率从97.53％提高至99.85％.该文所提出的脑电信号相似性分析方法可以成功应用于癫痫性发作的自动检测.【期刊名称】《西北大学学报（自然科学版）》【年(卷),期】2019(049)002【总页数】9页(P309-317)【关键词】癫痫;癫痫性发作;脑电图;最大余弦相似度;支持向量机;极限学习机【作者】李斯卉;吕可嘉;潘敏;张瑞【作者单位】西北大学医学大数据研究中心,陕西西安710127;西安交通大学医学部,陕西西安710061;西北大学医学大数据研究中心,陕西西安710127;西北大学医学大数据研究中心,陕西西安710127【正文语种】中文【中图分类】O29癫痫是最常见的神经功能障碍之一,世界范围内的患病率接近0.9%。

其最主要的临床症状表现为癫痫性发作,通常是由大脑内大量神经细胞群异常超同步放电所引起。

脑电图(Electroencephalogram,EEG)通过追踪和记录脑电波来呈现大脑的放电活动,是目前用于检测癫痫性发作等神经功能障碍异常脑电模式的有效手段。

然而,传统的癫痫诊断往往需要专业医师依据经验对长时程脑电图通过视觉上的检查来完成,这一过程不仅耗时、主观性强,而且大量噪声的存在也使得这一工作极具挑战。

因此,近几十年来,越来越多的研究者开始致力于开展癫痫性发作自动检测的研究。

支持向量机用于电离层 foF2的短期区域预报

支持向量机用于电离层 foF2的短期区域预报李美玲;胡耀垓;周晨;赵正予;张援农;刘静;邓忠新【摘要】为了提高电离层短期区域预报效果，提出了基于支持向量机方法考虑太阳活动、地磁活动、中高层大气、地理位置等因素对电离层的影响．对中国地区电离层F2层临界频率（foF2）提前1 h的区域预报模型，将支持向量机的预报模型与输入同样参数的反向传播神经网络和国际参考电离层模型从多方面进行对比分析，结果显示，支持向量机模型的年平均预报相对误差相对神经网络和国际参考电离层模型在太阳活动高年分别降低了2.5％和9.6％，在太阳活动低年分别降低了1.9％和7.5％．在低纬度地区，支持向量机模型的预报优势更加显著，在高年和低年相对反向传播神经网络分别降低了3.2％和2.7％．对暴时，支持向量机模型也表现出一定的预报能力．这表明支持向量机模型应用在中国区域电离层foF2短期预报上，相对反向传播神经网络和国际参考电离层模型更有优势．%Ionospheric short‐term forecasting is very important to radio communication , navigation and radar systems . In this paper , in order to improve the regional prediction accuracy of ionosphere , a model of regional prediction of the ionospheric F2 layer critical frequency in China area 1 hour in advance is set up based on the support vector machine (Support Vector Machine , referred to as SVM for short) method . In this model , the influence of solar activity , geomagnetic activity , the upper atmosphere , geographical location and other factors on the ionosphere is taken into consideration . Results of this model is compared to Back‐Propagation referred to as BP for short the neural network of the same input parameters and the IRI model ( International Reference Ionosphere ,referred to as IRI for short) . The results show that the average relativeerror of annual prediction of SVM in high solar activity years decreases by 2.5% and 9.6% , respectively , compared with the neural network and the IRI models and in low solar activity decreases by 1.8% and 7.5% , respectively . In the low latitude area , the prediction of SVM has more significant advantages over the BP neural network . In the high and low solar activity years it decreases by 3.2% and 2.7% , respectively . During the storm time SVM also shows a relatively good prediction ability . This proves that the developed model based on SVM in the paper has more advantages over the BP neural network and IRI model .【期刊名称】《西安电子科技大学学报（自然科学版）》【年(卷),期】2015(000)005【总页数】8页(P147-153,206)【关键词】支持向量机;电离层f o F2;区域预报;对比分析【作者】李美玲;胡耀垓;周晨;赵正予;张援农;刘静;邓忠新【作者单位】武汉大学电子信息学院，湖北武汉430072;武汉大学电子信息学院，湖北武汉 430072;武汉大学电子信息学院，湖北武汉 430072;武汉大学电子信息学院，湖北武汉 430072;武汉大学电子信息学院，湖北武汉 430072;中国地震局地震预测所，北京 100036;中国电波传播研究所，山东青岛 266107【正文语种】中文【中图分类】P352电离层受太阳活动、地磁活动等多方面因素的影响,不但存在日变化、年变化等规则变化,而且存在季节异常、赤道异常、电离层暴时变化等不规则变化.电离层这种高度变化的特性,对利用电离层作为传输媒质的短波通信和微波通信等使用固定频率工作的系统产生重大的影响.F2层的临界频率foF2是电离层重要的特征参数之一,它的高度变化特性可对无线电系统产生不利影响,严重时甚至导致通信中断.为了保证这些系统的正常工作,减少由于电离层异常变化带来的损失,对foF2进行以小时和天为时间尺度的短期预报具有重要的意义.foF2的短期预报已经被很多国内外学者所研究,取得了很多的研究成果,主要有多元线性回归方法[1]、同化技术[2]、自相关函数法[3]、神经网络法[4]、暴时电离层修正模型[5]等.但这些方法在区域预报上的应用与单站相比并不多,并且预报效果不理想,例如使用比较广泛的国际参考电离层模型(International Reference Ionosphere,IRI)对中国地区尤其是低纬度地区的预报误差很大,这与该模型在建立时缺乏中国区域数据有关.为了提高中国区域电离层foF2预报效果,同时避免不断对新增单站建立预报模型,国内的学者尝试建立中国区域的电离层预报模型,主要有中国及周边地区的参考电离层模型[6]、采用人工神经网络对中国地区的区域预报[7]、利用改进克里格方法对区域电离层重构[8]等.在这些方法中,中国参考电离层模型与国际参考电离层模型类似,描述的是电离层平均特性,更适于长期预报;改进的克里格方法依赖于参考背景场,背景场偏差较大时预报的误差将扩大;反向传播(Back-Propagation,BP)神经网络容易陷入局部极值,且可重复性差.笔者提出采用支持向量机(Support Vector Machine,SVM)方法对中国地区电离层foF2进行短期区域预报.该方法在空间天气预报领域已经得到了部分应用,国内学者利用支持向量机建立了中国地区电离层foF2的预报模型[9].采用该方法对电离层foF2短期预报效果主要受两大因素影响:一是支持向量机算法本身的惩罚因子和核函数的选取;二是训练数据是否充分考虑各影响因素.文献[9]忽视了热层风对电离层的影响,也未考虑地理位置的变化,因此不能预报训练数据集范围外的地区.为了提高预报效果,笔者在支持向量机模型的输入样本数据中充分考虑地磁活动、太阳活动、中高层大气以及地理位置的变化对电离层的影响,并对该方法预报误差进行定量估计,最后将支持向量机方法的预报性能同反向传播神经网络和国际参考电离层模型从多方面进行了比较.1.1 支持向量机算法简介支持向量机[10]是建立在结构风险最小化原理基础上的一种机器学习方法,它有着严格的数学理论基础,不依赖于经验知识和先验知识,有很好的函数逼近能力与泛化性能,在回归领域有很好的应用前景.其本质是对二次规划问题的求解,是二次型在约束条件下的极小化问题,理论上得到的将是全局最优解,因而保证了对于未知样本的良好泛化性能,解决了神经网络中容易陷入局部极小值的问题.由于支持向量机是专门针对有限样本情况的,神经网络是基于样本数据趋于无穷大时的统计性质的,而实际的样本数据是有限的,因此在样本数据有限的情况下,支持向量机相比神经网络算法更容易取得理想的结果,且克服了神经网络可重复性差的缺点.具体算法如下.假设数据样本为(xi,yi),i=1,2,…,n;xi∈Rm,为输入参数;yi∈R,为输出参数;n为样本数.对于线性回归,设回归函数f(x)=〈w,x〉+b,w和b分别为权重向量和偏置.若所有训练数据在精度ε下用线性函数拟合,则其中,ξi和是松弛因子.基于结构风险最小化原理,该问题将转化为带有约束条件式(1)求式(2)最小值的凸二次优化问题:其中,C为惩罚因子.根据线性规划对偶性理论,建立拉格朗日方程,将最小值问题转化为对偶问题的最大值问题,对其进行求解,得到的回归函数为其中,xi为支持向量;ai和b为回归得到的参数.对于非线性回归估计,其基本思想是通过事先确定的非线性映射Φ(x)将输入空间映射到一个高维特征空间,再在这个高维特征空间中进行线性回归,从而得到原空间非线性回归的效果,对函数进行逼近.由于寻找非线性映射Φ(x)是一个比较复杂的过程,因此引入一个满足Mercer的核函数K(xi,xj)代替映射函数的内积Φ(xi)Φ(xj),可不必知道Φ(x)的具体形式,从而避免了复杂的计算.最终得到的非线性回归函数为在使用中,常用的核函数类型有3种:线性核K(xi,xj)=〈xi,xj〉,多项式核K(xi,xj)=(〈xi, xj〉+1)d,高斯径向基核文中的支持向量机是基于Matlab平台Libsvm工具箱实现的,选用的是RBF核函数.核函数参数g和支持向量机惩罚因子C的选取:首先对少数少部分的数据采用基于粒子群寻优算法的支持向量机确定C和g的粗略值,再使用全部的训练数据在粗略范围多次试验,最后确定C=1,g=0.2.1.2 支持向量机的输入与输出电离层是一个复杂的非线性系统,受多种因素控制.在前人电离层研究的基础上,输入样本中充分考虑地磁活动、太阳活动、中高层大气以及地理位置等因素对电离层的影响,确定了支持向量机模型的单个输入样本向量.(1)日变化及季节变化.日变化和季节变化是电离层较为显著的变化,可由地方时和天数分别表示.由于地方时和天数都会在一个周期结束时发生跳变,为了保证变量的连续性,将两个变量分别正交化,形成4个输入分量[11].(2)空间地理位置相关的输入.电离层foF2具有很强的区域特点[12],在低纬地区有明显的赤道异常;在中高纬地区,纬度相同、经度不同的两地区的foF2也有明显差异.因此将经纬度作为与空间相关的输入,这使得训练之后的模型能够反映foF2的空间特征,不仅可对参加过网络训练的区域进行预报,也可对其范围之外的区域进行预报.为统一变量归一化方式,类似当地时间,将与角度相关的经纬度正交化[11]. (3)与中高层大气相关的输入.很多的研究者已经证实中高层大气对电离层有着重要的影响[13-14].文献[13]证实,热层风和磁偏角导致了电离层TEC的经度效应.但在电离层foF2预报中,大多数的研究者都未意识到中高层大气对F层的影响.电离层和热层几乎处于相同的空间区域,热层环流也引起F层的抬升或下降,对F层的影响不可忽视.笔者充分考虑其对F层的影响,根据公式W=U cos(θ-D)cos I sin I知道,垂直离子漂移速度W与地磁偏角D和地磁倾角I有关;U为热层风在纬度θ下的水平风速,与地方时T和纬度θ有关.因此,将θ、T、D和I作为与中高层大气有关的输入,即可充分体现中高层大气对电离层的影响,增强模型在中高层大气对电离层影响较大时的预报能力.由于W的相位与D和θ的正余弦有关,因此将D正交化,即由于W的幅度和cos I sin I成正比,因此将I转换为(4)过去相关的值.研究结果[15]表明,foF2待预报值f(t+1)与当前时刻值f(t)、预报时刻的前24小时的值f(t-23)有很好的相关性,因此在输入参数中加入当前时刻的值f(t)和预报时刻的前24小时的值f(t-23).(5)其他的输入参数.另外,还有前两个月太阳等效黑子数滑动均值、ap指数、太阳天顶角(正交化后为2个输入分量)等参数.以上的输入变量形成单个样本的输入分量,共17个,输出为下一小时的foF2的值f(t+1),所有的输入输出样本数据均归一化到了(-1,1).1.3 国际参考电离层模型和神经网络模型笔者采用的国际参考电离层模型版本是IRI2012.神经网络模型采用的是单隐层反向传播神经网络,由Matlab2008自带的神经网络工具箱实现,输入输出与节1.2中支持向量机的输入输出相同.经过多次试验,确定隐含层神经元20个,其隐含层使用双曲正切传递函数,输出层使用log-sigmoid传递函数.网络的训练函数是trainbr,学习速率lr为0.05,训练目标最小误差为0.000 1.1.4 样本数据样本数据是由中国电波传播研究所提供的1990年到2004年期间中国海口、广州、重庆、拉萨、兰州、北京、长春、乌鲁木齐、满洲里、武汉这10个电离层垂测站的数据,站点的经纬度如表1.训练样本集为除去武汉站的其他9个站1990～2004年间(除去1996年和2000年)每个站随机选取7000个样本数据,其他未参与训练的1996年(太阳活动低年)和2000年(太阳活动高年)的数据作为校验集.为了验证模型对于训练集地区之外的预报能力,对完全未参与过训练的武汉站在1996年和2000年进行预报.利用均方根误差(RMSE)和相对误差(PD)这两个指标来评估模型的预报性能[11],指标的具体定义为其中,fobsi为某个时刻的观测值,fprei为该时刻的预报值,N为每个站全年的样本总数.将支持向量机的预报结果与反向传播神经网络、IRI2012的预报结果分别进行对比,如表2所示.由于1996年拉萨站数据缺失严重,故未参与检验,仅给出了2000年的结果.表2给出了太阳活动高年和太阳活动低年除去武汉站的其他站点支持向量机、反向传播神经网络和国际参考电离层模型各自的预报结果、这些站预报的整体统计结果以及低纬地区预报的统计结果.这些站点整体统计的结果由overall表示,低纬地区结果统计的是海口和广州两站,由low_lat表示.从整体统计结果overall的相对误差来看,支持向量机的预报误差相对反向传播神经网络和国际参考电离层模型在太阳活动高年分别降低了2.5%和9.6%,在太阳活动低年分别降低了1.9%和7.5%.显然,支持向量机和神经网络的预报结果都远优于国际参考电离层模型,后面将着重比较支持向量机和神经网络的预报效果.从表中可以看到,在中纬地区,支持向量机的均方根误差和相对误差都要略小于神经网络,个别地区(如长春站)两者的预报误差则相当.在低纬地区,通常foF2变化比较大,预报难度大.由表中low_lat的相对误差来看,支持向量机的预报效果较好,在高年和低年预报误差相对反向传播神经网络分别降低了3.2%和2.7%,降低的幅度大于整体水平,这表明了支持向量机泛化性能要优于神经网络,在低纬地区支持向量机的预报能力优势更加显著.下面将从预报值与观测值的误差绝对值的累积分布对支持向量机、反向传播神经网络和国际参考电离层模型进行比较分析.以广州、乌鲁木齐、海口、满洲里这4个站为例,如图1所示,实线、点划线、虚线分别表示支持向量机、反向传播神经网络、国际参考电离层模型的预报值和观测值之差的绝对值累积分布.该图表示了3种模型的误差绝对值在某一范围所占的比例.支持向量机和反向传播神经网络模型在中纬地区(乌鲁木齐、满洲里)误差累积分布比较接近,无论是太阳活动高年还是低年,误差绝对值在1 MHz以内占90%以上,曲线上升较快.在低纬地区(广州、海口),反向传播神经网络和国际参考电离层模型的误差都很大,累积分布曲线上升比较平缓,而支持向量机曲线较陡,绝对误差在2 MHz以内占90%以上,优势更加明显.累积分布图再次直观地表明,无论是太阳活动高年还是低年,支持向量机预报效果较反向传播神经网络和国际参考电离层模型的好,累积分布曲线更陡.为了检验模型对于训练集外的地区的预报能力,对未参与网络训练的武汉地区进行了预报.预报结果如表3所示,图2给出了武汉站的预报值和观测值之间绝对误差直方统计图.从表3及图2可以看到,支持向量的误差比神经网络和国际参考电离层模型的要小,具有相对较好的区域预报性能.图3为在2000年的4月7～9日发生磁暴事件中,地磁指数Dst最小值达-280 nT时海口站和广州站用支持向量机、反向传播、国际参考电离层模型对foF2的预报值,其中使用这3种方法统计的海口站均方根误差分别为1.270 MHz、1.978 MHz、1.975 MHz,广州站的分别为1.544 MHz、2.242 2 MHz、2.585 MHz.从图3可以看出,支持向量机相比国际参考电离层模型和反向传播神经网络,在磁暴时的预报值与观测值较为接近,均方根误差最小,能够显示出电离层foF2逐日的一些细微变化,对暴时电离层扰动变化有更好的预报能力.笔者基于支持向量机方法开展了中国地区电离层foF2短期区域预报.通过与神经网络模型、国际参考电离层模型预报结果进行对比,显示该模型相对神经网络和国际参考电离层模型有很大的优势,初步结论如下:(1)从均方根误差和相对误差上衡量,该模型的预报误差相对神经网络和国际参考电离层模型整体上降低很多,在低纬度地区的优势更加显著,相对中纬地区预报误差降低幅度更大,反映了该模型良好的预报精度和泛化性能.(2)支持向量机的预报值与观测值的绝对误差绝对值累积分布曲线比神经网络和国际参考电离层模型更陡,对训练集之外的地区有较好的预报.(3)在磁暴时对电离层能较好地预报,反映了支持向量机良好的抗干扰能力,可能还缺少其他与电离层磁暴相关的输入,对磁暴时的预报效果相对单站磁暴时模型还是有差距的.(4)为了提高模型的预报效果,在模型的输入参数中还加入了foF2的过去相关值,这也导致模型对于过去值的依赖,而不能对缺乏历史数据的地区进行预报.综上所述,基于支持向量机方法建立的中国地区区域预报模型是有效可行的.今后工作的重点是如何选择有效的输入变量,减少对过去值的依赖,挖掘更多与电离层相关的输入,提高对电离层扰动时期的预报效果.【相关文献】[1]Akam A,Alberca L.Multi Regression Method for foF2 Short-termPrediction[R].Poland:Space Research Center, 1999:140-142.[2]Mc Namara L F,Angling M J,Elvidge S,et al.Assimilation Procedures for Updating Ionospheric Profiles below the F2 Peak[J].Radio Science,2013,48(2),143-157.[3]Liu R Y,Liu S L,Xu Z H,et al.Application of Autocorrelation Method on Ionospheric Short Term Forecasting in China[J].Chinese Science Bulletin,2006,51(3):352-357.[4]Zhao X K,Ning B Q,Liu L B.A Prediction Model of Short-term Ionospheric foF2 Based on AdaBoost[J].Advance in Space Research,2013,53(3):387-394.[5]Sun S J,Ban P P,Chen C.An Empirical Correction Model for Low-latitude Storm-time Ionospheric foF2 Considering E ×B Drift[J].Advance in Space Research,2012,49(9):1356-1362.[6]刘瑞源,权坤海,戴开良,等.国际参考电离层用于中国地区时的修正计算方法[J].地球物理学报,1994,37(4): 422-432. Liu Ruiyuan,Quan Kunhai,Dai Kailiang,et al.Application of of the International Reference Ionosphere to the Revise Calculation[J].Chinese Journal of Geophysics,1994,37(4):422-432.[7]Wang R P,Zhou C.Predicting foF2 in the China Region Using the Neural Networks Improved By the Genetic Algorithm [J].Journal of Atmospheric and Solar Terrestrial Physics,2013,92:7-17.[8]刘瑞源,王建平,武业文,等.用于中国地区电离层总电子含量短期预报方法[J].电波科学学报,2011,26(1):18-24. Liu Ruiyuan,Wang Jianping,Wu Yewen,et al.The Short-term Ionospheric Prediction Method for Total Electron Content in China Area[J].Chinese Journal of Radio Science,2011,26(1):18-24.[9]Chen C,Wu Z S,Ban P P,et al.Diurnal Specification of the Ionospheric foF2 Parameter Using a Support Vector Machine[J].Radio Science,2010,45(5):2629-2642.[10]邓乃扬,田英杰.数据挖掘中的新方法[M].北京:科学出版社,2004.[11]Zhou C,Wang R P,Lou W,et al.Preliminary Investigation of Real Time Mapping of foF2 in Northern China Based on Oblique Ionosonde Data[J].Journal Geophysics Research:Space Physics,2013,118(5):2536-2544.[12]Cander L R.Spatial Correlation of foF2 and v TEC under Quiet and Disturbed Ionospheric Conditions:a Case Study[J]. Acta Geophysica,2007,55(3),410-423.[13]徐继生,李雪璟,刘裔文,等.磁偏角和热层风对中纬电离层TEC经度分布的影响[J].地球物理学报,2013,56(5): 1425-1434. Xu Jisheng,Li Xuejing,Liu Yiwen,el at.Effects of Declination and Thermospheric Wind on TEC Longitude in the Mid Latitude Ionospher[J].Chinese Journal of Geophysics,2013,56(5):1425-1434.[14]Oyeyemi E O,Poole A W V,Mckinnell L A.On the Global Model for foF2 Using Neural Networks[J].Radio Science, 2005,40(6):5347-5356.[15]孔庆颜,柳文,凡俊梅,等.利用人工神经网络预测电离层foF2参数[J].地球物理学报,2009,52(6):1438-1443. Kong Qingyan,Liu Wen,Fan Junmei,et al.On the Prediction of foF2 Using Artificial Neural Networks[J].Chinese Journal of Geophysics,2009,52(6):1438-1443.。

libsvm的原理及使用方法介绍

LibSVM学习目录LibSVM学习 (1)初识LibSVM (1)第一次体验libSvm (3)LibSVM使用规范 (5)1. libSVM的数据格式 (5)2. svmscale的用法 (5)3. svmtrain的用法 (6)4. svmpredict 的用法 (7)逐步深入LibSVM (7)分界线的输出 (11)easy.py和grid.py的使用 (13)1. grid.py使用方法 (13)2. easy.py使用方法 (14)参考 (16)LibSVM学习初识LibSVMLibSVM是台湾林智仁(Chih-Jen Lin's) 教授2001年开发的一套支持向量机的库，这套库运算速度还是挺快的，可以很方便的对数据做分类或回归。

由于libSVM程序小，运用灵活，输入参数少，并且是开源的，易于扩展，因此成为目前国内应用最多的SVM的库。

这套库可以从林智仁的home page上免费获得，目前已经发展到3.0版。

下载.zip格式的版本，解压后可以看到，主要有5个文件夹和一些c++源码文件。

Java ——主要是应用于java平台的源码和libsvm.jar包；Python ——是用来参数优选的工具，稍后介绍；svm-toy ——一个可视化的工具，用来展示训练数据和分类界面，里面是源码，其编译后的程序在windows文件夹下；tools ——主要包含四个python文件，用来数据集抽样(subset.py)，参数优选（grid.py），集成测试(easy.py), 数据检查(checkdata.py)；windows ——包含libSVM四个exe程序包，我们所用的库和程序就是它们。

其他.h和.cpp文件都是程序的源码，可以编译出相应的.exe文件。

其中，最重要的是svm.h 和svm.cpp文件，svm-predict.c、svm-scale.c和svm-train.c（还有一个svm-toy.cpp在svm-toy\qt 文件夹中）都是调用的这个文件中的接口函数，编译后就是windows下相应的四个exe程序。

libsvm参数说明

libsvm参数说明摘要：1.LIBSVM 简介2.LIBSVM 参数说明3.LIBSVM 的使用方法4.LIBSVM 的应用场景5.总结正文：1.LIBSVM 简介LIBSVM 是一个开源的支持向量机（Support Vector Machine，简称SVM）算法库，它可以在各种平台上运行，包括Windows、Linux 和MacOS 等。

LIBSVM 提供了一系列的机器学习算法，如线性SVM、多项式SVM、径向基函数SVM 等，这些算法可以广泛应用于各种数据挖掘和机器学习任务中，如分类、回归和排序等。

2.LIBSVM 参数说明在使用LIBSVM 时，需要对数据进行预处理，主要包括数据格式转换、特征选择和样本划分等。

此外，还需要对SVM 算法的参数进行设置，以优化模型的性能。

LIBSVM 中常用的参数包括：（1）核函数（Kernel）：LIBSVM 支持多种核函数，如线性核、多项式核、径向基函数核和Sigmoid 核等。

核函数的选择会影响到模型的复杂度和分类性能。

（2）惩罚参数（C）：惩罚参数用于控制模型对训练数据的拟合程度。

较小的C 值会导致模型过于复杂，容易出现过拟合现象；较大的C 值则会使模型过于简单，容易出现欠拟合现象。

（3）度量函数（Metric）：LIBSVM 支持多种度量函数，如欧氏距离、汉明距离和马氏距离等。

度量函数的选择会影响到模型的性能。

（4）迭代次数（Max_iter）：迭代次数用于控制模型的训练过程，较小的迭代次数会导致模型训练不充分，较大的迭代次数则会使模型训练时间过长。

（5）终止条件（Epsilon）：终止条件用于控制模型的训练过程，当模型的误差小于指定的Epsilon 时，训练过程将终止。

3.LIBSVM 的使用方法使用LIBSVM 时，需要先下载并安装LIBSVM 库，然后按照以下步骤进行操作：（1）准备数据集：将数据集转换为LIBSVM 所支持的格式，通常为文本格式或ARFF 格式。

matlab调用高斯核函数 -回复

matlab调用高斯核函数-回复Matlab是一种常用的科学计算和数据分析工具，提供了丰富的函数库和工具箱，可以用于实现各种算法和模型。

其中，高斯核函数是机器学习和模式识别领域常用的一种核函数，用于非线性分类和回归任务。

本文将介绍如何在Matlab中调用高斯核函数，并详细解释其原理和应用。

首先，我们需要知道什么是高斯核函数。

高斯核函数也被称为径向基函数（Radial Basis Function，简称RBF），它是一种基于距离度量的非线性变换。

其定义如下：K(x, y) = exp(- x-y ^2 / (2 * sigma^2))其中，x和y是样本点的特征向量，x-y 表示欧式距离（即样本点之间的直线距离），sigma是高斯核函数的带宽参数，控制了函数的变化速度。

在Matlab中，我们可以使用内置函数pdist2来计算两个样本点之间的欧式距离，使用exp函数来计算指数函数。

以下是一个示例的Matlab代码，实现了高斯核函数的计算：matlabfunction [kernel] = gaussian_kernel(X1, X2, sigma)X1和X2分别是两个样本点的特征向量矩阵，大小分别为N1 x d和N2 x d，sigma是带宽参数返回一个N1 x N2大小的高斯核矩阵使用pdist2函数计算欧式距离矩阵distance_matrix = pdist2(X1, X2);计算高斯核矩阵kernel = exp(-distance_matrix.^2 / (2 * sigma^2));end在这段代码中，我们定义了一个函数`gaussian_kernel`，该函数接受两个特征向量矩阵`X1`和`X2`，以及带宽参数`sigma`作为输入。

函数中首先使用`pdist2`函数计算两个特征向量矩阵之间的欧式距离矩阵`distance_matrix`，然后根据高斯核函数的定义，计算每个距离的高斯核值，并返回一个高斯核矩阵`kernel`。

matlab中最简单的svm例子

在MATLAB中，最简单的SVM（支持向量机）例子可以通过以下步骤实现：1. 导入数据：首先，我们需要导入一些用于训练和测试的数据集。

这里我们使用MATLAB 内置的鸢尾花数据集。

```matlabload fisheriris; % 加载鸢尾花数据集X = meas; % 提取特征矩阵Y = species; % 提取标签向量```2. 划分训练集和测试集：我们将数据集划分为训练集和测试集，以便评估模型的性能。

```matlabcv = cvpartition(size(X,1),'HoldOut',0.5); % 划分训练集和测试集idx = cv.test; % 获取测试集的索引XTrain = X(~idx,:); % 提取训练集的特征矩阵YTrain = Y(~idx,:); % 提取训练集的标签向量XTest = X(idx,:); % 提取测试集的特征矩阵YTest = Y(idx,:); % 提取测试集的标签向量```3. 创建SVM模型：接下来，我们创建一个SVM模型，并设置相应的参数。

```matlabSVMModel = fitcsvm(XTrain,YTrain,'KernelFunction','linear'); % 创建线性核函数的SVM 模型```4. 预测和评估：最后，我们使用训练好的模型对测试集进行预测，并评估模型的性能。

```matlabYPred = predict(SVMModel,XTest); % 对测试集进行预测accuracy = sum(YPred == YTest)/length(YTest) * 100; % 计算准确率fprintf('Accuracy: %.2f%%', accuracy); % 输出准确率```这个例子展示了如何在MATLAB中使用最简单的SVM方法进行分类。

SVM算法原理及其Matlab应用

SVM算法原理及其Matlab应用支持向量机（Support Vector Machine，SVM）是一种常用的机器学习算法，它在分类和回归问题中都有广泛的应用。

本文将介绍SVM算法的原理，并探讨其在Matlab中的应用。

一、SVM算法原理SVM算法的核心思想是通过在特征空间中找到一个最优的超平面，将不同类别的样本分开。

其基本原理可以归结为以下几个关键步骤：1. 数据预处理：首先，需要对数据进行预处理，包括数据清洗、特征选择和特征缩放等。

这一步骤的目的是将原始数据转化为适合SVM算法处理的形式。

2. 特征映射：在某些情况下，数据在原始特征空间中无法线性可分。

为了解决这个问题，可以将数据映射到高维特征空间中，使得数据在新的特征空间中线性可分。

3. 构建超平面：在特征空间中，SVM算法通过构建一个超平面来将不同类别的样本分开。

这个超平面被定义为使得两个类别的间隔最大化的平面。

4. 支持向量：在构建超平面的过程中，SVM算法会选择一些样本点作为支持向量。

这些支持向量是距离超平面最近的样本点，它们对于分类结果的决策起到关键作用。

5. 分类决策：当新的样本点浮现时，SVM算法会根据其在特征空间中的位置，通过计算与超平面的距离来进行分类决策。

距离超平面较近的样本点很可能属于一个类别，而距离较远的样本点则很可能属于另一个类别。

二、SVM在Matlab中的应用Matlab作为一种强大的科学计算软件，提供了丰富的工具箱和函数来支持SVM算法的应用。

下面以一个简单的二分类问题为例，介绍SVM在Matlab中的应用过程。

首先，我们需要准备训练数据和测试数据。

在Matlab中，可以使用内置的数据集，或者自己准备数据。

然后，将数据进行预处理，包括特征选择和特征缩放等。

接下来，使用svmtrain函数来训练SVM模型。

该函数需要输入训练数据和相应的标签，以及一些参数，如核函数类型和惩罚参数等。

训练完成后，可以得到一个训练好的SVM模型。

混合核函数svrmatlab

混合核函数支持向量回归（SVR）是一种广泛应用于非线性回归分析中的机器学习算法。

该算法在预测问题中具有良好的鲁棒性和泛化能力，因此在实际应用中得到了广泛的应用。

在机器学习领域，SVR 通过寻找最优超平面来逼近真实数据的复杂性，以此来实现对未知数据的预测。

混合核函数SVR在处理非线性数据时具有比较好的性能，而且可以通过选择不同的核函数类型和参数来适应不同的数据特征。

1. 算法原理混合核函数SVR的基本原理是在支持向量机（SVM）的基础上，引入核函数来实现对非线性数据的拟合。

所谓核函数，就是将原始的输入空间映射到一个更高维的空间中，使得原本线性不可分的数据在新的空间中变得线性可分。

在SVR中，常用的核函数包括线性核函数、多项式核函数和径向基核函数等。

2. Matlab实现在Matlab中，可以利用libsvm库来实现混合核函数SVR。

该库提供了一组函数，可以方便地调用SVR算法，并且支持多种核函数类型的选择。

通过设置不同的参数和核函数类型，可以灵活地对不同的数据集进行回归分析，从而实现对非线性数据的拟合和预测。

3. 应用案例混合核函数SVR在实际应用中具有较好的效果。

例如在金融领域，可以利用SVR来预测股票价格的走势；在医疗领域，可以利用SVR来预测疾病的发展趋势；在工程领域，可以利用SVR来预测材料的性能等。

由于混合核函数SVR具有较好的泛化能力，因此在处理非线性数据时往往能够取得比较好的效果。

4. 总结混合核函数SVR是一种在非线性回归分析中具有较好性能的机器学习算法。

通过引入核函数，并通过选择不同的参数和核函数类型，可以灵活地适应不同的数据特征，从而实现对非线性数据的拟合和预测。

在实际应用中，SVR在多个领域都得到了广泛的应用，并取得了较好的效果。

混合核函数SVR具有较大的应用前景和发展空间。

由于混合核函数SVR在处理非线性数据时具有较好的性能，因此在实际应用中得到了广泛的应用。

作为一种强大的机器学习算法，混合核函数SVR能够有效地应对现实生活中的各种复杂数据，为决策提供有力支持。