一元线性回归方程的建立
1一元线性回归方程
i =1 n
i =1 n
2
Lxy = ∑( Xi − X ) (Yi −Y )
i=1
ˆ ˆ β0 = Y − β1 X ˆ Lxy β1 = Lxx
二、OLS回归直线的性质 回归直线的性质
ˆ (1)估计的回归直线 Yi )
(2) )
ˆ ˆ = β 0 + β 1X i
前三个条件称为G-M条件 条件 前三个条件称为
§1.2 一元线性回归模型的参数估计
普通最小二乘法( Squares) 普通最小二乘法(Ordinary Least Squares) OLS回归直线的性质 OLS回归直线的性质 OLSE的性质 OLSE的性质
一、普通最小二乘法
对于所研究的问题, 对于所研究的问题,通常真实的回归直线 E(Yi|Xi) = β0 + β1Xi 是观 测不到的。可以通过收集样本来对真实的回归直线做出估计。 测不到的。可以通过收集样本来对真实的回归直线做出估计。
Y
55 80 100 120140 160
X
二、随机误差项εi的假定条件 随机误差项
为了估计总体回归模型中的参数,需对随机误差项作出如下假定: 为了估计总体回归模型中的参数,需对随机误差项作出如下假定: 假定1: 假定 :零期望假定:E(εi) = 0。 。 假定2: 假定 :同方差性假定:Var(εi) = σ 2。 假定3: 假定 :无序列相关假定:Cov(εi, εj) = 0, (i ≠ j )。 。 假定4: 假定 : εi 服从正态分布,即εi ∼ N (0, σ 2 )。 。
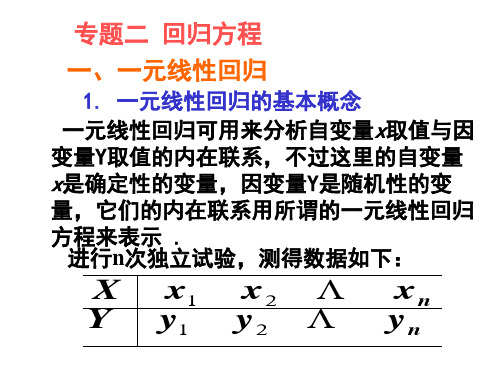
以下设 x 为自变量(普通变量 Y 为因变量(随机变 普通变量) 普通变量 随机变 量) .现给定 x 的 n 个值 x1,…, xn, 观察 Y 得到相应的 n 个 值 y1,…,yn, (xi ,yi) i=1,2,…, n 称为样本点 样本点. 样本点 以 (xi ,yi) 为坐标在平面直角坐标系中描点,所得到 的这张图便称之为散点图 散点图. 散点图
9.3一元线性回归模型构建

0
正规方程组
n
n
n
n
( Xi X )(Yi Y ) n XiYi Xi Yi
ˆ1
i 1
n
(Xi X )2
i 1
i1 n
i1 i1 n
n
X
2 i
(
Xi )2
i 1
i 1
n
n
n
n
ˆ0
i 1
一元线性回归模型构建
1.最小二乘法 2.正规方程组 3.一元线性回归模型构建实例
最小二乘法(Method of Least Squares )
一元线性回归模型 Yi 0 1Xi i (i 1, 2,...)
样本回归方程
Yˆi ˆ0 ˆ1Xi (i 1, 2,..., n)
一元线性回归模型构建实例
销售周期
1 2 3 4 5 … 26 27 28 29 30
表 牙膏销售量与广告费用的数据
销售量/百万支
广告费用/百万元
7.38 8.51 9.52 7.50 9.33
… 9.21 8.27 7.67 7.93 9.26
5.50 6.75 7.25 5.50 7.00
… 6.80 6.50 5.75 5.80 6.80
最小二乘法(Method of Least Squares )
Y
Yˆi ˆ0 ˆ1 X i
.( X n ,Yn ) ..
. . . ..
. ( X1,Y1)
.ei Yi Yˆi
( X i ,Yi )
.
( X 2 ,Y2 )
一元线性回归方程的建立

第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这(i=1,2,3,…,n)。
这样,我们就可以用残差平种偏差称为残差,记为e i方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为: (2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
一元线性回归方程的应用

第四节一元线性回归方程的应用回归方程最主的应用就是用它进行估计或预测。
只要r2≠1,估计误差就不可避免。
因而在应用回归方程时,需要对估计的误差以及与之相联系的一些问题有所了解。
一、回归方程的建立与预测(或估计)对于一组X、Y的数据,我们可以建立回归方程,有了y对X的回归方程,也就找到了X与y之间变化的数量关系,对于任意一个X值都可估计出与之对应的y值。
一)回归方程的建立例下面是20名工作人员的智商和某一次技术考试成绩,根据这个结果求出考试成绩对智商的回归方程。
如果另有一名工作人员智商为120,则估计一下若让他也参加技术考试,将会得多少分?解:经检验两者具有线性关系计算得:X与Y的均值:107 71标准差:13.69 11.63 r=0.86代入公式则回归方程为:NO 智商X成绩Y估计Y'NO智商X成绩Y估计Y'1 89 55 57.86 11 84 53 54.212 97 74 63.7 12 121 82 81.223 126 87 84.87 13 97 58 63.74 87 60 56.4 14 101 60 66.625 119 71 79.76 15 92 67 60.056 101 54 66.62 16 110 80 73.197 130 90 87.79 17 128 85 86.338 115 73 76.84 18 111 73 73.929 108 67 71.73 19 99 71 65.1610 105 70 69.54 20 120 90 80.49二)回归方程的检验1.方差分析法SSR=1997.48 SST=2705.14 SSE=707.66F=MSR/MSE=(SSR/dfR)/(SSE/dfE)= 1997.48 /(707.66/18)=50.81查表F(1,18)=8.28(0.01) 或 4.41(0.05) 结果显著2.回归系数法SX=13.69 SY=11.63 b=0.73 r=0.86三)用回归方程进行预测若X=120,代入回归方程得=80.5就是说,这位工作人员虽没参加技术考试,但根据他的智商,估计其技术考试的分数应该为80.5。
一元线性回归
i
x )Yi
l xx
,
3
一元回归方程检验
⑴ F检验法:
当H0为真时,
SSE
SSE
2
2
~ 2 ( n 2),
2
~ (1);
且SSR与SSE相互独立;因此,当H0为真时,
SSR F ~ F (1, n 2), SSE ( n 2)
当F≥F1-α(1,n-2)时应该放弃原假设H0。
Y0的观测值y0的点预测是无偏的。
⑵ 当x=x0时,用适合不等式P{Y0∈(G,H)}≥ 1-α的统计量G和H所确定的随机区间(G,H) 预测Y0的取值范围称为区间预测,而(G,H)称 为Y0的1-α预测区间。 若Y与样本中的各Y相互独立,则根据 Z=Y0-(a+bx0)服从正态分布,E(Z)=0, 2 1 ( x0 x ) 2 D( Z ) (1 ), n l xx SSE 及 2 ~ 2 ( n 2), Z与SSE相互独立,
Q 2 ˆ 是 的无偏估计。 n2
2
2. 总体中未知参数的估计 根据最小二乘法的要求由
Q Q 0, 0, 得 a b
n
2 [ y i (a bx i )] 0, i 1 n 2 [ y i (a bx i )] x i 0, i 1
(2)t检验法:
b ~ N ( ,
2
l xx
),
SSE
2
~ 2 (n 2),
当H0为真时,
l xx t b ~ T (n 2), SSE (n 2)
当|t|≥t1-0.5α(n-2)时应该放弃原假设H0。
根据x与Y的观测值的相关系数 (3)r检验法:
一元线性回归方程的建立
第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)我们称(2-1-1)式为回归方程,a与b是待定常数,称为回归系数。
从理论上讲,(2-1-1)式有无穷多组解,回归分析的任务是求出其最佳的线性拟合。
二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这种偏差称为残差,记为e i(i=1,2,3,…,n)。
这样,我们就可以用残差平方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为:(2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
三、正规方程组根据微分中求极值的方法可知,Q(a,b)取得最小值应满足(2-1-3)由(2-1-2)式,并考虑上述条件,则(2-1-4)(2-1-4)式称为正规方程组。
一元线性回归方程

一元线性回归方程
一元线性回归方程:当直线方程Y'=a+bx的a和b确定时,即为一元回归线性方程。
一元线性回归方程反映一个因变量与一个自变量之间的线性关系
一元线性回归方程反映一个因变量与一个自变量之间的线性关系,当直线方程Y'=a+bx的a和b确定时,即为一元回归线性方程。
经过相关分析后,在直角坐标系中将大量数据绘制成散点图,这些点不在一条直线上,但可以从中找到一条合适的直线,使各散点到这条直线的纵向距离之和最小,这条直线就是回归直线,这条直线的方程叫作直线回归方程。
注意:一元线性回归方程与函数的直线方程有区别,一元线性回归方程中的自变量X对应的是因变量Y的一个取值范围。
1. 根据提供的n对数据在直角坐标系中作散点图,从直观上看有无成直线分布的趋势。
即两变量具有直线关系时,才能建立一元线性回归方程。
2. 依据两个变量之间的数据关系构建直线回归方程:Y=a+bx。
简单线性回归(Simple linear regression)也称为一元线性回归,是分析一个自变量(x)与因变量(y)之间线性关系的方法,它的目的是拟合出一个线性函数或公式来描述x与y之间的关系。
第十三章 一元线性回归

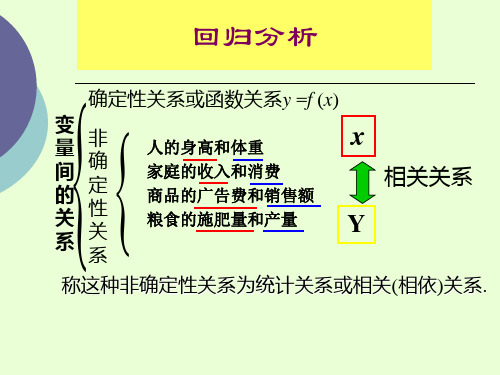
变量之间存在关系的两种类型: 确定性关系(函数关系) 不确定性关系(相关关系)
函数关系
1.
2.
3.
是一一对应的确定关系:一 个(或多个)确定的自变量 的值对应一个确定的因变量 的值。 y 设有两个变量 x 和 y ,变量 y 随变量 x 一起变化,并完 全依赖于 x ,当变量 x 取某 个数值时, y 依确定的关系 取相应的值,则称 y 是 x 的 函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量 x 各观测点落在一条线上
l xy = ( x x)( y y ) = xy N x y
则:a = y b x
b = l xy / l xx
步骤:1、由变量x求 x来自l xx (自方差) 2、由变量y求 y,l yy 3、由x、y求l xy (协方差) 4、求a、b ˆ 5、写出方程:y = a + bx
【例】有15个学生,数学和物理成绩列于表内, 现想求一个物理成绩对数学成绩的一元回归方 程。
23 8 40 19 60 69 21 66 15 46 26 32 30 58 28 22 23 33 41 57 7 57 37 68 27 41 20 30
数学(x) 31 物理(y) 32
解:
1.
2.
3.
相关分析中,变量 x 变量 y 处于平等的地位;回 归分析中,变量 y 称为因变量,处在被解释的地 位,x 称为自变量,用于预测因变量的变化 相关分析中所涉及的变量 x 和 y 都是随机变量; 回归分析中,因变量 y 是随机变量,自变量 x 可 以是随机变量,也可以是非随机的确定变量 相关分析主要是描述两个变量之间线性关系的密 切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控制
建立一元线性回归模型

建立一元线性回归模型
建立一元线性回归模型的步骤如下:
1.选择自变量和因变量:确定自变量和因变量之间的关系,并准备
好数据。
2.计算自变量的平均值和标准差,因变量的平均值和标准差:使用
公式计算自变量和因变量的平均值和标准差。
3.计算自变量和因变量的相关系数:使用公式计算自变量和因变量
的相关系数。
4.计算回归系数:使用公式计算回归系数。
5.建立回归方程:使用计算得到的回归系数和自变量的平均值,建
立回归方程。
6.对回归方程进行检验:使用残差平方和、残差平均值、残差标准
差和相关系数等指标对回归方程进行检验。
7.进行预测:使用建立的回归方程进行预测,得出因变量的预测值。
8.对预测结果进行评估:使用预测误差、预测精度、预测准确率等
指标对预测结果进行评估。
总的来说,建立一元线性回归模型的过程包括选择自变量和因变量、计算自变量和因变量的平均值和标准差、计算自变量和因变量的相关系数、计算回归系数、建立回归方程、对回归方程进行检验、进行预测和对预测结果进行评估。
一元线性回归

2020/2/1
中山学院经济与管理系
4
2.1 模型的建立及其假定条件
2 回归分析的概念 回归分析研究一个变量关于另一个(些)变量的
具体依赖关系的计算方法和理论。
其用意:在于通过后者的已知或设定值,去估计 (或)预测前者的(总体)均值。
2020/2/1
中山学院经济与管理系
5
2.1 模型的建立及其假定条件
一般来说,回归模型的随机误差项中可能包 括如下几项内容。
(1)未在模型中列出的影响y变化的非重要
解释变量。如消费模型中家庭人口数、消 费习惯、物价水平差异等因素的影响都包 括在随机误差项中。
(2)人的随机行为。经济活动都是人参与 的。人的经济行为的变化也会对随机误差 项产生影响。
2020/2/1
中山学院经济与管理系
squares estimators)。
2020/2/1
中山学院经济与管理系
24
2.2 一元线性回归模型的参数估计
3 最小二乘直线的性质
(1)残n 差ei的均值等于0
因为 ei 0 ,所以 e
n
ei
i1
0
i 1
n
(2)残差ei与解释变量xi不相关
n
即
ei xi 0
(3)i1样本回归直线经过点( x, y )
y=33.73+0.516 x 这一方程表明:父母平均身高每增减一个单位时,其年 子女的身高仅平增减0.516个单位
2020/2/1
中山学院经济与管理系
6
这项研究结果表明,虽然高个子父辈有生高个子儿子
的趋势,矮个子的父辈有生矮个子儿子的趋势,但父辈
身高增减一个单位,儿子身高仅增减半个单位左右。通
一元线性回归

回归方程有效性的r检验法 回归方程有效性的 检验法
回忆相关系数
ρ XY =
离散型随机变量
Cov( X , Y ) D ( X ) D(Y )
∑∑ ( x − E ( X ))( y
i i j i j
j
− E (Y )) Pij
ρ XY =
样本 ( xi , Yi )
( xi − E ( X )) 2 Pi. ∑ ( y j − E (Y )) 2 P. j ∑
Y = β0 + β1 x + ε , 2 ε ~ N(0,σ )
其中 β 0、β 1、σ 2 是与 而
(β1 ≠ 0)
(9.1) )
无关的未知常数 未知常数。 x 无关的未知常数。
称为回归函数或回归方程。 Y = β0 + β1x 称为回归函数或回归方程。
称为回归系数。 β0、β1 称为回归系数。
回归方程反映了因变量 Y 随自变量 的平均变化情况. 的平均变化情况. 对的回归关系的数学模型为: 对的回归关系的数学模型为: Y = g ( x) + ε ε 为随机误差,对任意的x, ε N (0,σ 2 )且相互独立
x 的变化而变化
一元线性回归模型
一般地, 一般地,称如下数学模型为一元线性模型
ˆ L = r2L SSR = β1 xy yy
回归方程有效性的r检验法 回归方程有效性的 检验法
记 R=
Lxy Lxx Lyy
——样本的相关系数 ——样本的相关系数
因为 SS = Q = 1 − r 2 L E yy (1 ) r ≤ 1
(
)
SSR = r 2 Lyy
SST = Lyy
(2) r = 1 时, E = 0, SST = SS R SS 有线性相关关系; y 与 x 有线性相关关系; (3) r = 0 时, = 0, SS = SS SSR T E 无线性相关关系; y 与 x 无线性相关关系; 越大, 之间的线性相关程度越强。 r 越大,变量 y 与 x 之间的线性相关程度越强。
一元线性回归方程

n
n
避免其偏离差(有正误差、负误差)相互抵消,采用偏离差平方和 Q(a ,b) ( yi yi )2
i 1
i 1
( yi a bxi )2(也称残差平方和)来刻画观测值(xi ,yi )与直线 y a bx 的偏离程度 . 一般
所说的回归直线就是使 Q(a ,b) 最小的直线,求所需回归直线的截距和斜率,就转化成了求使
Lxx (4)写出回归(估计)方程 y a bx .
一元线性回归方程
1.2 线性相关关系的显著性检验
从以上建立回归直线方程的过程不难看出,用最小二乘法所建立的回归直线方程,只是通 过一组样本观察值 (xi ,yi ) (i 1,2 , ,n) 来建立的 . 变量 x 与 y 之间是否存在线性关系,或者 其线性关系是否显著,还需进行检验.常用的线性相关关系的显著性检验有两种方法,即 F 检 验法和相关系数检验法 . 在此仅介绍相关系数检验法 .
0, 0.
即nan b a i1 xi
n
n
xi yi ,
i 1
i 1
n
n
b xi2 xi
i 1
i 1
yi
,取
x
y
1 n 1 n
n
i 1 n
i 1
xi , yi .
一元线性回归方程
n
n
n
n xi yi xi yi
n
xi yi nx y
b
解之得
i 1
,
即Q(a ,b) Lyy (1 R2 ) .
一元线性回归方程
n
n
因为Q(a ,b) ( yi yi )2 0 ,Lyy ( yi y)2 0 ,
i 1
一元线性回归

· · ·· ·· · · ·· ·
2 4 6 8 10
o线附 近, 这告诉我们变量x和y之间大致可看作线 性关系. 从图中还看到, 这些点又不完全在 一条直线上, 这表明x和y的关系并没有确切 到给定x就可以唯一确定y的程度.
其原因在于人有较大的个体差异, 因而身高 和体重的关系, 是既密切但又不能完全确定 的函数关系.
类似的变量间的关系在大自然和社会中 屡见不鲜.
例如 , 小麦的穗长与穗重的关系 ; 某班学生最 后一次考试分数与第一次考试分数的关系;温 度、降雨量与农作物产量间的关系;人的年龄 与血压的关系;最大积雪深度与灌溉面积间的 关系;家庭收入与支出的关系等等.
这种大量存在的变量间既互相联系但又不 是完全确定的关系,称为相关关系. 从数量的角度去研究这种关系,是数 理统计的一个任务. 这包括通过观察和试 验数据去判断变量之间有无关系,对其关 系大小作出数量上的估计 , 对互有关系的 变量通过其一去推断和预测其它,等等. 回归分析就是研究相关关系的一种重 要的数理统计方法.
V=I. R
以上两例的共同点在于,三个量中任意 两个已知,其余一个就可以完全确定. 也就 是说,变量之间存在着确定性的关系,并且 可以用数学表达式来表示这种关系. 然而,在大量的实际问题中,变量之 间虽有某种关系,但这种关系很难找到一 种精确的表示方法来描述.
例如,人的身高与体重之间有一定的关系, 知道一个人的身高可以大致估计出他的体重, 但并不能算出体重的精确值.
y=a+bx+ε, ε ~N(0, )
2
(1)
现对模型(1)中的变量x , y进行了n次独 立观察, 得样本 (x1,y1),…,(xn,yn) (3)
建立y对x的一元线性回归方程由表可知根据公式

试用指数曲线预测1998年的肥皂销量。
解:设 y aebx令 y ln y 为了计算方便,再定
义 x x 1993 ,列表计算如下:
x y y ln y x2 xy
1
-3 95 4.5539 9 -13.6616
2
-2 104 4.6444 4 -9.2888
设相关关系的两个变量为 x 和 y , y 的值由两
部分构成:一部分由 x 的影响确定, 用 x 的
函数 f ( x)表示,称为回归函数;另一部分则由众多
不确定性因素影响产生,可看成 y 取值的随机波
动,记为 ,并且假定其平均值为零,即
。
于是E得( 到) 数0 学模型:
y f (x)
b 7 3.3976 0.1213,a 34.0321 4.8617
7 28
7
所以 ln y 4.8617 0.1213x
y 129.2437e0.1213 x
已知1996年的序号是 x 3 ,那么1998年应 为 x 5
所以预计1998年的销量为
(11.2)
x 上式称为回归模型,它表明当 取某个数值时,y
并不必然表现为一个确定的值,而是在 f ( x)附近波
动,但其平均数在大量观察下趋向于确定的值 。
f (x)
图11-1 企业产量与生产费用散点图
x 我点们图容大易致看呈出直企 线业 关产 系量 。但y图i和形生中产的费各用点并不i 之都间在的—散
y 129.2437e0.12135 237( 箱)
回归模型的拟合优度和显著性
一 、 回归模型的拟合优度
y
{}} (Yˆi Yi)=总离差
一元线性回归的基本步骤
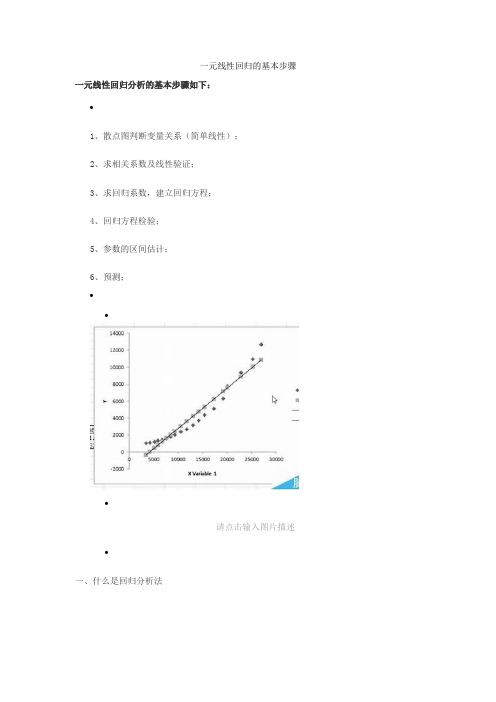
一元线性回归的基本步骤一元线性回归分析的基本步骤如下:•1、散点图判断变量关系(简单线性);2、求相关系数及线性验证;3、求回归系数,建立回归方程;4、回归方程检验;5、参数的区间估计;6、预测;•••请点击输入图片描述•一、什么是回归分析法“回归分析”是解析“注目变量”和“因于变量”并明确两者关系的统计方法。
此时,我们把因子变量称为“说明变量”,把注目变量称为“目标变量址(被说明变量)”。
清楚了回归分析的目的后,下面我们以回归分析预测法的步骤来说明什么是回归分析法:回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。
只有当变量与因变量确实存在某种关系时,建立的回归方程才有意义。
因此,作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。
进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关的程度。
二、回归分析的目的回归分析的目的大致可分为两种:第一,“预测”。
预测目标变量,求解目标变量y和说明变量(x1,x2,…)的方程。
y=a0+b1x1+b2x2+…+bkxk+误差(方程A)把方程A叫做(多元)回归方程或者(多元)回归模型。
a0是y截距,b1,b2,…,bk是回归系数。
当k=l时,只有1个说明变量,叫做一元回归方程。
根据最小平方法求解最小误差平方和,非求出y截距和回归系数。
若求解回归方程.分别代入x1,x2,…xk的数值,预测y的值。
第二,“因子分析”。
因子分析是根据回归分析结果,得出各个自变量对目标变量产生的影响,因此,需要求出各个自变量的影响程度。
希望初学者在阅读接下来的文章之前,首先学习一元回归分析、相关分析、多元回归分析、数量化理论I等知识。
根据最小平方法,使用Excel求解y=a+bx中的a和b。
EXCEL一元线性回归

EXCEL一元线性回归一、概述在数据分析中,对于成对成组数据的二、一元线性回归基本概念➢一元线性回归方程的建立回归系数ˆˆˆiiy x αβ=+αβˆi yˆi i i e y y=-[]222111ˆ(,)()()nnniii ii i i i Q eyyyx αβαβ=====-=-+∑∑∑(,)Q αβ,αβ,αβ1111222111()()()()ˆ()()n n i i n ni i i i i i xy i i nnxxii ni i ii x y x x y y x y L n L xx x xnβ=======---===--∑∑∑∑∑∑∑ˆˆy xαβ=-根据最小二乘法,可以得到一组正规方程组,对方程组求解,即可得到回归系数, 的计算式:ˆαˆβ三、软件(EXCEL)实现过程本功能需要使用Excel扩展功能,如果Excel尚未安装数据分析,需加载“分析数据库”。
加载成功后,可以在“数据”菜单中看到“数据分析”选项汽车马力(HP)每加仑汽油行驶里程(MPG)4965.455565555.970495346.57046.25545.46259.26253.38043.47341.49240.99240.97340.46639.67339.37838.99238.87838.29042.29240.97440.79540散点图直线拟合分析结果SUMMARY OUTPUT回归统计Multiple R 0.789925583R Square 0.623982426Adjusted R Square0.619282206标准误差6.174780275观测值82方差分析df SS MS F Significance F 回归分析15061.709525061.709523132.75601341.13931E-18残差803050.2329238.12791145总计818111.94244Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0%Intercept 50.07566277 1.5696920531.90158406 2.94532E-4746.951876153.199449446.951876153.19944943X Variable 1-0.1390738520.01207031-11.521979581.13931E-18-0.163094531-0.1150532-0.163094531-0.115053172Y=-0.1391+50.075和前面散点图直线拟合的结果一致“回归”工具为我们提供残差图、线性拟合图:线性拟合图谢谢!请批评指正!。
第一节 回归方程的建立

x)
2
(x
i 1
n
x)
2
b
ˆ x ) Ey xE ( b ˆ) ˆ ) E( y b E(a a bx bx a
ˆ 的方差 ˆ、b 2、关于a
ˆ 由b Lxy Lxx
n
(x
i 1
n
i
x ) yi y (x i x )
i 1 2 ( x x ) i i 1 n n
(x
i 1 n
n
i
x )( yi y )
2 ( x x ) i i 1
记
Lxx (x i - x) x i nx
2 2
n
n
2
L yy (y i - y) y i ny
2 2 i 1 i 1 n n
i 1 n
i 1 n
2
Lxy (x i - x)(y i - y) x i yi nx y
n
i 1
i 1
由于yi 相互独立,且D(yi )=2
(x i x ) 2 2 ˆ 所以D( b ) (n ) 2 i 1 ( x x ) i
n i 1
n i 1
2
2 ( x x ) i
2 ˆ 回归系数b的波动不仅与随机误差 的方差 有关,
还与观测数据 xi的波动有关,如果 xi 取值较分散, ˆ 的波动就小,即估计量 ˆ 就较稳定。 则b b
第九章
§9.1
一元线性回归
回归方程的建立
一、变量间的关系 1、函数关系:确定性关系,它反映客观现 象的严格依存关系。
如:圆的半径 r 与周长 L 可以看成两个变 量,它们之间关系式 :L = 2r
试验设计与数据处理第4章回归分析

a' ln a
y' ln y
yˆ abx ln yˆ ln a xln b
yˆ a bx
a' ln a
b' ln b
对数函数 (logarithmic function)
x' lg x
yˆ a blg x
yˆ a bx'
x' ln x
yˆ a bln x
yˆ a bx'
幂函数 (power function)
(2)回归系数的确定 根据最小二乘法原理 :求偏差平方和最小时的回归系数
偏差平方和:
n
n
Q ( yi $yi )2 ( yi a b1x1 b2x2 ... bmxm )2
i 1
i 1
根据:
Q 0
Q 0
a
bj
得到正规方程组,正规方程组的解即为回归系数。
应用条件:
注意:虽然模型要求因变量是连续数值变量,但对自变量的类型不限。若 自变量是分类变量,特别是无序分类变量,要转化为亚变量才能分析。对 于自变量是分类变量的情形,需要用广义线性回归模型分析。
-1≤r≤1 r=±1:x与y有精确的线性关系
y
y
r=1 x
r=-1
x
r<0:x与y负线性相关(negative linear correlation) r>0:x与y正线性相关(positive linear correlation)
y y
0<r<1 x
-1<r<0 x
r=0
r=0
y y
b0 11.9259 0.1424 5.8126 0.3515 2.8407 0.2706 6.1467 0.6382 9.1185
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)我们称(2-1-1)式为回归方程,a与b是待定常数,称为回归系数。
从理论上讲,(2-1-1)式有无穷多组解,回归分析的任务是求出其最佳的线性拟合。
二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这种偏差称为残差,记为e i(i=1,2,3,…,n)。
这样,我们就可以用残差平方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为:(2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
三、正规方程组根据微分中求极值的方法可知,Q(a,b)取得最小值应满足(2-1-3)由(2-1-2)式,并考虑上述条件,则(2-1-4)(2-1-4)式称为正规方程组。
解这一方程组可得(2-1-5)其中(2-1-6)(2-1-7) 式中,L xy称为xy的协方差之和,L xx称为x的平方差之和。
如果改写(2-1-1)式,可得(2-1-8)或(2-1-9)由此可见,回归直线是通过点的,即通过由所有实验测量值的平均值组成的点。
从力学观点看,即是N个散点的重心位置。
现在我们来建立关于例1的回归关系式。
将表2-1-1的结果代入(2-1-5)式至(2-1-7)式,得出a=1231.65b=-2236.63因此,在例1中灰铸铁初生奥氏体析出温度(y)与氮含量(x)的回归关系式为y=1231.65-2236.63x四、一元线性回归的统计学原理如果X和Y都是相关的随机变量,在确定x的条件下,对应的y 值并不确定,而是形成一个分布。
当X取确定的值时,Y的数学期望值也就确定了,因此Y的数学期望是x的函数,即E(Y|X=x)=f(x) (2-1-10) 这里方程f(x)称为Y对X的回归方程。
如果回归方程是线性的,则E(Y|X=x)=α+βx (2-1-11) 或Y=α+βx+ε (2-1-12) 其中ε―随机误差从样本中我们只能得到关于特征数的估计,并不能精确地求出特征数。
因此只能用f(x)的估计式来取代(2-1-11)式,用参数a和b分别作为α和β的估计量。
那么,这两个估计量是否能够满足要求呢?1. 无偏性把(x,y)的n组观测值作为一个样本,由样本只能得到总体参数α和β的估计值。
可以证明,当满足下列条件:(1)(x i,y i)是n个相互独立的观测值(2)εi是服从分布的随机变量则由最小二乘法得到的a与b分别是总体参数α和β的无偏估计,即E(a)= αE(b)=β由此可推知E( )=E(y)即y是回归值在某点的数学期望值。
2. a和b的方差可以证明,当n组观测值(x i,y i)相互独立,并且D(y i)=σ2,时,a 和b的方差为(2-1-13)(2-1-14)以上两式表明,a和b的方差均与x i的变动有关,x i分布越宽,则a和b的方差越小。
另外a的方差还与观测点的数量有关,数据越多,a 的方差越小。
因此,为提高估计量的准确性,x i的分布应尽量宽,观测点数量应尽量多。
第三节回归方程的显著性检验一、相关系数的显著性检验在上面的分析中,为了求得回归方程,我们曾假定x与y之间存在着线性关系。
在求得回归方程后,我们必须对这一假定进行检验,以确定x与y是否的确存在线性关系。
设(X,Y)为二维随机变量,如果E[X-EX][Y-EY]存在,则称它为X与Y之间的协方差,记为Cov(X,Y)。
即Cov(X,Y)=E[X-E(x)][Y-E(y)] (2-1-15) 如果D(X)>0,D(Y)>0,则称(2-1-16)为X与Y之间的相关系数。
对于一个具有n组观测值的样本,其相关系数γ定义为(2-1-17)其中L yy称为观测值的离差平方和,记为(2-1-18)见式(2-1-7)。
相关系数是绝对值小于1,大于0的无量纲统计量。
接近于1,表明x与y之间线性关系密切。
当确定性的线性函数关系。
当=0时,表示两个变量间无线性关系。
这时有两种可能情况,一种是二者没有关系(如图2-1-2(c)),另一种可能是二者有非线性关系(如图2-1-2(d))。
相关系数的正负号由决定,即与b同号。
当>0时,y随x的增加而增加,当<0时,y 随的x增加而减少。
相关系数的直观意义参见图2-1-2。
见方开泰《实用回归分析》P32图2.2相关性检验一般利用相关系数检验表(见附录)进行。
该表中给出的值为相关系数的起码值。
只有当求出的相关系数大于表上相应的数值时,才能考虑用直线来描述x和y之间的相关关系。
查表时要遇到三个参数:变量总数、自由度和置信水平。
对于一元回归分析,变量只有两个(x,y)。
自由度等于数据组数与变量个数之差。
大于表上相置信水平(5%和1%)表示线性相关的程度。
通常当应的值,但小于表上如果如果小于表上相应的值时,称为x与y没有明显的线性关系,即回归方程没有实际意义。
对于本章例1,变量有2个,共5组数据,故自由度数为5-2=3,相应的值为0.878,相应的值为0.959。
由式(2-1-17)表中计算得到的相关系数。
可见<0.9590.878<二、方差分析与F检验n个观测值之间存在着差异,我们用观测值y i与其平均值的偏差平方和来表示这种差异程度,称其为总离差平方和,记为(2-1-19) 由于(2-1-20) 所以(2-1-21)式中称为回归平方和,记为S回。
称为残差平方和,记为。
不难证明,最后一项。
因此S总=S回+S残(2-1-22) 上式表明,y的偏差是由两个因素造成的,一是x变化所引起,二是各种偶然因素干扰所致。
事实上,S回和S残可用下面更简单的关系式来计算。
(2-1-23)(2-1-24)见方开泰《实用回归分析》P34表2.2这里要注意S回的自由度为1,S残的自由度为n-2,S总的自由度为n-1。
如果x与y有线性关系,则(2-1-25) 其中,F(1,n-2)表示第一自由度为1,第二自由度为n-2的分布。
在F表中显著性水平用表示,一般取0.10,0.05,0.01,1-表示检验的可靠程度。
在进行检验时,表2-1-2中的F值应大于F表中的临界值Fα。
若F<0.05(1,n-2),则称x与y没有明显的线性关系,若F0.05(1,n-2)<F<F0.01(1,n-2),则称x与y有显著的线性关系;若F>F0.01(1,n-2),则称x与y有十分显著的线性关系。
当x与y有显著的线性关系时,在表2-1-2的显著性栏中标以〝*〞;当x与y有十分显著的线性关系时,标以〝**〞。
下面对例1中x与y的线性关系进行F检验。
由式(2-1-6)、式(2-1-7)、式(2-1-18)、式(2-1-23)及式(2-1-24),可得计算结果如表2-1-3。
由F表查得F0.05(1,3)=10.1,F0.01(1,3)=34.1,而计算值F=16.37,可见F0.05<F<F0.01,因此x与y之间有显著的线性相关关系,在表2-1-3中标以〝*〞。
表2-1-3 例1方差分析表第四节残差分析、预报和控制一、残差分析前面我们介绍了线性回归方程的建立和检验。
在实际问题中,由于观察人员的粗心或偶然因素的干扰。
常会使我们所得到的数据不完全可靠, 即出现异常数据。
有时即使通过相关系数或F检验证实回归方程可靠,也不能排除数据存在上述问题。
残差分析的目的就在于解决这一问题。
所谓残差是指实际观察值与回归估计值的差,即(2-1-26) 显然,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。
首先介绍如何检查异常数据。
异常数据是指与其它数据产生的条件有明显不同的数据,因此异常数据的残差会特别的大。
一旦发现异常数据应及时剔除,用剩余数据重新建立回归方程,以提高回归方程的质量。
发现异常数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方法。
由数理统计方法可以证明(2-1-27) 或记为(2-1-28)这说明残差的方差D(e)是x的函数,且二者呈曲线关系。
以回及方程和作图。
归方程考虑到较小,当n较大时(2-1-29) 此时图中的两条曲线可近似于两条平行直线。
从而有(2-1-30) 或近似地(2-1-31) 这表明,当n较大时y i落在图2-1-3的长条形带子中的概率约为95%,只要知道,就可以得到残差的置信区域。
来估计。
可用下式一般是未知的,通常用残差标准差求得(2-1-32) 由此可得残差置信带(2-1-33)对残差在置信带以外的数据都要进行检查,以区别是否是异常数据,如果是异常数据就要剔除掉。
现在我们对例1做残差检查。
由式(2-1-32)残差置信带为(-5.712,5.712)。
计算5个实验点的预报值与残差值(见表2-1-4),并作出残差检查图(见图2-1-4)表2-1-4 例1的残差值图2-1-4 例1的残差图由图2-1-4可见,例1中全部数据的残差都在置信带内,没有异常数据。
除此以外,残差图还可以为我们提供许多有用信息。
比如,在研究铁水质量时我们看到1号高炉的残差偏于2处,而2号高炉的残差偏于-2处(见图2-1-5)。
在图2-1-5所示的这种情况下,建立统一的回归方程是不合适的,应该分别按1号和2号高炉建立回归方程。
图2-1-5数据有周期性变化的残差图图2-1-6数据有倾向性变化的残差图有时我们还会发现数据有倾向性变化。
