进位计数制转换综合练习题
进位制之间的转换

“十进制转k进制”的算法步骤:
• 给定十进制正整 数a,确定转化后 的进位k;
第 2步
• 求出a除以k所得 的余数、商,并 分别赋值给r、a;
• 若a≠0,则重复 第2步, 直到a=0;
第 4步
• 将依次得到的余 数从右往左排列 起来,则得到k进 位数.
第 1步
第 3步
5.“十进制转k进制”的程序框图:
到底什么是进位计数制??
进位计数制:把数码按照先后顺序排列成
数位,由低到高位计数,且满进位。是
人们利用符号进行计数的科学方法。
在计算机中常用的数制有:十进制,二进制和十六进制。
思考一下为什么计算机内部采用二进制?
1.易于用器件实现
• 二进制只有0和1两个状态,电子元件就可以用对立的两个状态来表示,可用自然界存在的两 种对立的物理状态表示。
开始 输入n,k b=“
”
mod(a,k)->r:int(a/k)->a b=string(r)&b a=0 Y 输出b 结束 N
小数部分的转换
乘基取整法:小数乘以目标数制的基数,第一次相乘结果的整数部分为目的数的最高位,将其小 数部分再乘基数依次记下整数部分,反复进行下去,直到小数部分为“0”,或满足要求的精度为 止。
2.二进制数运算简便
• 二进制数的运算法则比其他进制简单 • 例如:加法 0+0=0 0+1=1+0=1 1+1=10 • 乘法 0*0=0 0*1=1*0=0 1*1=1
3.易于实现逻辑运算
• 采用二进制可以进行逻辑运算,使逻辑代数和逻辑电路成为计算机电路设计的数学基础。
进位计数制的三个基本要素
例如:把(1001.01)2转换为十进制数。 解:(1001.01)2 =1×23+0×22+0×21+1×20+0×2-1+1×2-2 =8+0+0+1+0.5+0.25 =9.75
进制转换

-1
问题:将时钟由两点拨到六点有几种方式 问题:
有两种:时针前进(顺时针)4个格 有两种:时针前进(顺时针) 个格 时针倒退(逆时针) 个格 时针倒退(逆时针)8个格 显然,倒退8个格(减8) 个格( 显然,倒退 个格 ) 和前进4个格 个格( 和前进 个格(加4)是等价的, )是等价的, 的补数。 即4是(-8)对12的补数。 是 ) 的补数 在数学上常表示为: 在数学上常表示为: -8≡+4 (mod 12) ≡ ) mod 12表示是以 为模。 表示是以12为模 表示是以 为模。
↓001 ↓ ↓ ↓ 5
八进制数 :将二进制数 1011010100 转换为八进制数 八进制数 二进制数 例 二进制数 0 1 2 3
②
100 101 110 111
1 010 3
2
64
∴ (1011010100)2=(1324)8 011 7
八进制数 → 二进制数:一位变三位
例:(12345)8
=(001,010,011,100,101)2
即
+127(27-1) 0111,1111 用8个二进位表 +127 127 个二进位表 注意: 注意:数0的 的 示时取值范围是 1000,0000 -0 128 反码 7-128~ +127(2 +0=00000000 1000,00011) 129 -1 . . -0=11111111 注意: 注意:数0的补 . 的补 . . . 码 1111,1110+0=-0=00000000 -126 254
补码
整数X的补码指:正数的补码与其原码相同, 整数X的补码指:正数的补码与其原码相同,负数的补码是原 码除符号位外的各位取反,然后最低位加1 码除符号位外的各位取反,然后最低位加1。 例: [+4]补=00000100 [-4]原=10000100 [-4]反=11111011 [-4]补=11111100 [+43]补=00101011 [-43]原=10101011 [-43]反=11010100 [-43]补=11010101
《计算机基础-1.4.1 数制》练习题

§1.4.1《数制》练习题相关知识点:①常用进制的表示方法;②各种进制之间的转换方法。
一、单选题1. 十六进制数的1个位能够表示的不同状态有(D)。
A. 10种B. 9种C. 15种D. 16种2. 有关二进制的叙述,下面(C)是错误的。
A. 二进制数只有0和l两个数码B. 二进制的计数规则是逢二进一C. 二进制数只有二位数组成D. 二进制数各位上的权是2n3. 二进制数11000000对应的十进制数是(D)。
A. 96B. 384C. 320D. 1924. 二进制数1110111转换成十进制数是(D)。
A. 219B. 117C. 319D. 1195. 二进制数1111.1对应的十进制数是(A)。
A. 15.5B. 14.5C. 16.1D. 17.16. 与二进制数1011011对应的十进制数是(D)。
A. 133B. 107C. 87D. 917. 与十进制数254等值的二进制数是(C)。
A. 11111011B. 11101110C. 11111110D. 111011118. 十进制数125对应的二进制数是(D)。
A. 1011111B. 1111010C. 1110111D. 11111019. 下列四种不同数制表示的数中,数值最大的一个是(D)。
A. 十六进制数A6B. 二进制数10101000C. 八进制数247D. 十进制数16910. 在下列十进制整数中,能用8位二进制表示的是(B)。
A. 317B. 255C. 289D. 25611. 十进制数“255”转换为八进制数是(C)。
A、357B、367C、377D、40712. 与十六进制数AB等值的十进制数为(B)。
A. 170B. 171C. 168D. 16613. 下列各种进制的数中,数值最小的是(A)。
A. (101000)2B. (2F)16C. (53)8D. (43)1014. 下列二进制运算中,结果正确的是(D)。
进制转换(简介)

1
0
1
1
+
1
1
1
进位 1 1
1
1
结果 1 0
0
1
0
二进制运算法则—举例
求: 1101B+101B=10010B
1
1
0
1
+
1
0
1
进位 1 1
1
结果 1 0
0
1
0
1.3.4 数制间的转换
1.其它进制转换为十进制 将其R进制按权位展开,然后各项相加,就得到
相应的十进制数。 可表示为:对于任意R进制数:
D)前者各字节的最高位二进制值各为0、1,而后者 为1、0
国标码
1、一个汉字的国标码需用2字节存储,其每个字节 的最高二进制位的值分别为( )。 A) 0,0 B) 1,0 C) 0,1 D) 1,1
位权 27 26 25 24 23 22 21 20 位权 128 64 32 16 8 4 2 1
01000000
2.二进制转换成八进制
二进制转换为八进制时,将二进制以小数点为中心, 分别向左右两边分组,每3位为一组,整数部分向左 分组,不足位数向左补0,小数部分向右分组,不足 位数向右边补0,然后将每组二制数转换成八进制数。
第1章 计算机基础知识
内存
用来存储当前正在运行的应用程序及相应数据的存储器是 ________。 A) ROM B) 硬盘 C) RAM D) CD-ROM 参考答案:C 【解析】存储计算机当前正在执行的应用程序和相应数据的 存储器是RAM,ROM为只读存储器。
特别注意的题目
综合练习:23,26,25,60,115-109,115,112 (PPT) 单项训练_电子表格:51,77,78,79 系列产生在列:即数据区的首列内容做为图表横坐 标。 系列产生在行:即数据区的首行内容做为图表横坐 标
四年级数论进位制
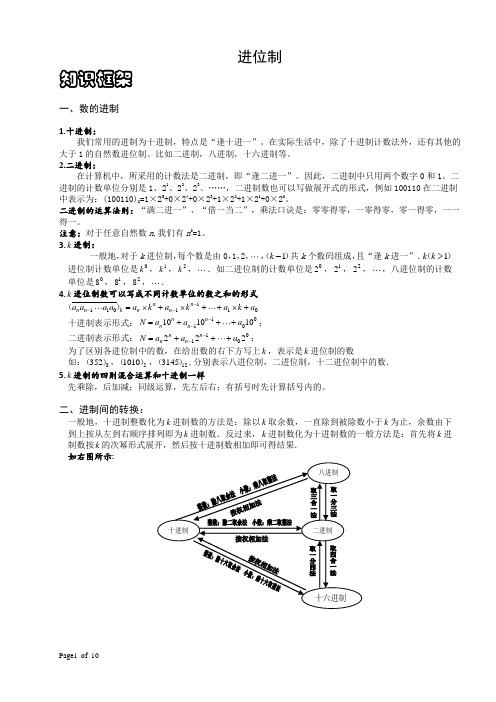
进位制知识框架一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:例题精讲【例 1】 把9865转化成二进制、五进制、八进制,看看谁是最细心的。
数字逻辑随堂练习答案

*数字逻辑o第一章进位计数制o第二章、布尔代数▪第一节、“与”“或”“非”逻辑运算的基本定义▪第二节、布尔代数的基本公式及规则▪第三节、逻辑函数的代数化简法▪第四节、逻辑函数的图解化简法▪第五节、逻辑函数的列表化简法o第三章组合逻辑电路的设计▪第一节、常用门电路▪第二节、半加器和全加器的分析▪第三节译码器的分析▪第四节、其它常用电路分析o第四章组合逻辑函数的设计▪第一节、采用门电路实现组合逻辑电路的设计▪第二节、转化成“与非”“或非”“与或非”形式▪第三节、组合电路设计中几个问题的考虑▪第四节、组合逻辑电路设计举例o第五章大规模集成电路▪第一节、由中规模器件构成的组合逻辑电路▪第二节、由中规模器件构成的组合逻辑电路设计▪第三节、采用只读存贮器实现组合逻辑电路设计▪第四节、组合逻辑电路中的竞争与险象*o第六章时序电路的分析▪第一节、同步时序电路▪第二节、触发器的逻辑符号及外部特性▪第三节、时序电路的状态表和状态图▪第四节、同步时序电路的分析方法o第七章同步时序电路的设计▪第一节、概述▪第二节、形成原始状态表的方法▪第三节、状态化简▪第四节、同步时序电路设计举例▪第五节、状态编码*o第八章异步时序电路的分析和设计▪第一节、脉冲异步电路的分析和设计▪第二节、电平异步电路概述▪第三节、电平异步电路分析▪第四节、电平异步电路的设计▪第五节、时序电路中的竞争与险象*o第九章数字逻辑计算机辅助设计方法▪3 / 205 / 207 / 209 / 2011 / 20A. B. C. D. 参考答案:D13 / 2015 / 2017 / 20。
进制之间的转换

计算机中常用的数制一、几种常用的进位计数制1.十进制 (10个基本数码:0、1、2、3、4、5、6、7、8、9)2.二进制(2个基本数码:0、1)3.八进制(8个基本数码:0、1、2、3、4、5、6、7)4.十六进制(16个基本数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F)二、计算机常用的各种进制数的特点三、不同进位计数制间数据的转化1.二进制数转换成十进制数方法:把二进制各数位的权和该位上的数码相乘,乘积逐项相加。
注意:整数部分权由0,1,2依次展开,小数部分权由-1,-2依次展开。
遇0时可以省略,因为0乘以任何数都为0。
例题:把二进制111010和101.101转换成十进制数。
(111010)2=1ⅹ25+1ⅹ24+1ⅹ23+1ⅹ21=(58)10(101.101)2=1ⅹ22+1ⅹ20+1ⅹ2-1+1ⅹ2-3=(5.625)102.十进制数转换成二进制数方法:整数部分“除2取余法”,小数部分“乘2取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.8125转换成二进制数。
整数部分205转换过程如下:小数部分0.8125转换过程如下:(205.8125)10=(11001101.1101)23.十进制数转换成八进制数方法:整数部分“除8取余法”,小数部分“乘8取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制1645.6875转换成八进制数。
(1645.6875)10=(3155.54)84.十进制数转换成十六进制数方法:整数部分“除16取余法”,小数部分“乘16取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.21875转换成十六进制数。
(205.21875)10=(CD.38)165.十六进制数和八进制数转换成二进制数方法:十六进制和八进制到二进制分别为24和23,因此,把十六进制和八进制数的每一个数码转成3位和4位的二进制即可.注意:整数前的高位O和小数后的低位O可以去掉。
进位计数制练习

进位计数制练习1.与十六进制数37.A等值的二进制数是()2.二进制数1101111.11B转换成十六进制数是_____3.11.01B转成十进制是 ________4. 217.5Q转成十进制是__ _______5. ABCH转成十进制是____6.(11.01)8转成二进制是_____7. 32.6转成二进制是_ _____(保留4位)8. 320.2转成十六进制是_ _______9.98.12转成二进制是___ (保留4位)10.二进制数"1110"所对应的十进制数为()A.12 B.16 C.14 D.1011. 二进制数"1010.11"所对应的十进制数为()A.20.3 B.22.6 C.14.125 D.10.7512. 八进制数"1060"所对应的十进制数是()。
A.1024 B.560 C.256 D.51213. 十六进制数"10E9"所对应的十进制数是()A.4096 B.1024 C.4329 D.819214. 十六进制数"FF.1"所对应的十进制数是()A.255.0625 B.255.125 C.127.0625 D.127.12515. 十进制数"15"所对应的二进制数是()A.1111 B.1110 C.1010 D.110016. 十进制数"215.6875"所对应的二进制数是()A. 11010111.1011 B.1110101.10011C.10110101.1101 D.110010011.0100117. 十进制数"269"所对应的十六进制数是()A.10E B.10D C.10C D.10B18. 十进制数"0.7109375"所对应的二进制数是()A.0.1011001 B.0.0100111 C.0.1011011 D.0.1010011 19. 二进制数"101110"所对应的八进制数是()A.45 B.56 C.67 D.78 20. 二进制数是"1100100"所对应的十六进制数是()A.64 B.63 C.100 D.14421. 八进制数"712.521"所对应的二进制数是()A.110010110.01010001B.111001010.101010001C.101011001.111001011 D.111001100.11010001122. 二进制数"101.01011"所对应的十六进制数是()A.A.B B.A5.51 C.A.51 D.5.5823.下列一组数中最小的是()A. (11011001)B B. (37)O C.(2A7)H D.(35)D24. 下列一组数中,最大的是()A. (227)O B.(1FF)H C.(10100001)B D.(1789)D25.与十六进制数(BC)等值的二进制数是()A. 10111011 B. 10111100 C. 11001100 D. 1100101126.与十进制数100等值的二进制数是()A.0010011 B.1100010 C.1100100 D.110011027.某汉字的区位码为3135,其国标码为 ( )A.2F44 B.3F33 C.3343 D.3F4328.某汉字的机内码为BFC3,则其区位码为 ( )A.3141 B.3145 C.3135 D. 3F4329.存储一个32×32点阵汉字字型信息的字节数是()A. 64B B. 128B C. 256B D. 512B30.将十进制数215转换为八进制数是( )A.327B.268.75C.352D.32631.十六进制数7A对应的八进制数为( )A.144B.172C.136D.37232.二进制数101110转换为八进制数是( )A.45B.56C.67D.7833.将二进制数1101001.0100111转换成八进制数是( )A. 151.234B.151.236C.152.234D.151.23734..将十六进制数1A6.2D转换成二进制数是( )A.111010101.10101010B.1111010101.000011010C.110100110.00101101D.1110010001.10001110135. 二进制数11011+1101等于( )A.100101B.10101C.101000D.1001136. 将二进制数0.0100111转换成八进制小数是( )A. 0.235B.0.234C.37D. 0.23637.十六进制数1000转换成十进制数是( )A. 4096B.1024C. 2048D. 819238.十进制数180对应的八进制数是( )A.270B.462C.113D.26439.八进制数127对应的十进制数是( )A.117B.771C.87D.7740.将十六进制数163.5B转换成二进制数是( )A.1101010101.1111001B.110101010.11001011C.1110101011.1101011D. 101100011.0101101141. 将十进制数35转换成二进制数是( )A. 100011B.100111C.111001D. 11000142. 将二进制数11001.1001转换成十进制数是( )A. 25.5625B.26.5625C.25.6D.2643. 将二进制数101101101.111101转换成十六进制数是( )A.16A.F2B.16D.F4C.16E.F2D. 16B.F244.二进制数101.01011等值的十六进制数为( )A.A.BB.5.51C.A.51D.5.5845.十进制纯小数0.5转换成二进制数应为( )A. 0.2B.0.1C.0.00D. 0.1146.八进制数126对应的十进制数是_ ______47. 将二进制数01100101转换成八进制数是___ ____________48. 将二进制数01100101转换成十六进制数是__ ____________49. 将二进制数1101000转换成八进制数是__ _____________50. 将十进制数34转换成二进制数是___ ____________51. 将八进制数150转换成二进制数是__ ____________52.十六进制数7B对应的十进制数为_______________ 53. 十进制数10转换成八进制数是______________54. 十六进制数7B对应的八进制数为________________55. 十进制数852写成二进制编码是_ ______________56. 十进制数10转换成二进制数是___ _____________57.二进制数1101000转换成八进制数是__ _____________58.十六进制数163.5B转换成二进制数是_ ____________59.八进制数126对应的十进制数是__ ___________60.二进制数01100110转换成十进制数是__ _____________61.二进制数01100101转换成八进制数是___ _____________62.二进制数01100101转换成十六进制数___ ____________63.八进制数150转换成二进制数是___ _____________64.二进制数101101100.111101转换成十六进制数是_______________65.把十六进制数A301(H)转换成二进制数是( )A、10100011 00000001B、10010010 00000010C、10100111 10001000D、 10101100 0000100066.与十六进制数D8H等值的十进制数是()A.218B.216C.138D.9867.与二进制数101101等值的十六进制数是()A.1DB.2CC.2DD.2E68.汉字点阵32*32,那么100个汉字的字形信息所占用的字节数是()A.3200B.128KC.12800D.32*320069.下列数中最小的一个是()A.100BB.8C.12HD.15Q70.小写字母d的ASCII码是二进制数()A.1100100B.1000100C.1000111D.1110111。
汉字数字与进位制的计算

汉字数字与进位制的计算一、汉字数字1.汉字数字的分类:阿拉伯数字、罗马数字、汉字数字。
2.汉字数字的读法:万以内、万以上、亿以内、亿以上。
3.汉字数字的写法:零、一、二、三、四、五、六、七、八、九、十、百、千、万、亿。
4.汉字数字的换算:万以内、万以上、亿以内、亿以上的换算方法。
5.汉字数字的运用:整数、小数、分数、四则运算。
6.进位制的概念:进位制是一种计数方法,每满一定数就向前一位进一。
7.常见进位制:十进制、二进制、八进制、十六进制。
8.进位制的转换:不同进位制之间的转换方法。
9.进位制的运用:计算机科学、数学计算、编码等领域。
三、计算方法1.加法:同位数相加,满十进一。
2.减法:同位数相减,借一当十。
3.乘法:按位相乘,进位相加。
4.除法:长除法、短除法。
5.混合运算:四则运算的顺序、运算法则。
四、综合应用1.数字与生活的联系:时间、日期、货币、计数器等。
2.数字与科技的发展:计算机、手机、互联网等。
3.数字与文化:数字成语、数字诗词、数字故事等。
4.数字与数学:数字谜语、数字游戏、数字魔方等。
5.数字与艺术:数字绘画、数字音乐、数字影视等。
五、学习方法与技巧1.记忆数字:编故事、唱数数歌、做数字游戏等。
2.理解进位制:生活实例、趣味故事、动手操作等。
3.计算练习:多做题、多思考、多总结。
4.学以致用:生活中的计算、解决实际问题。
六、注意事项1.培养良好的计算习惯:细心、认真、快速、准确。
2.提高计算速度:速算技巧、练习、比赛。
3.培养逻辑思维:分析问题、解决问题、创新思维。
4.注重数学素养:知识运用、学科交叉、综合素质。
知识点:__________习题及方法:一、汉字数字读写练习1.习题:将数字123456789写作汉字数字。
答案:一十二亿三千四百五十六万七千八百九十。
解题思路:根据汉字数字的写法,从高位到低位依次为一、二、三、四、五、六、七、八、九。
2.习题:将汉字数字“九亿八千六百五十四万三千二”写作数字。
数制间的转换

计算机中的数制与编码一、数制1、什么是进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的原则进行计数的方法,称为进位计数制。
比如,在十进位计数制中,是按照“逢十进一”的原则进行计数的。
常用进位计数制:a、十位制(Decimal notation);b、二进制(Binary notation);c、八进制(Octal notation);d、十六进制数(Hexdecimal notation)2、进位计数制的基数与位权"基数"和"位权"是进位计数制的两个要素。
(1)基数:所谓基数,就是进位计数制的每位数上可能有的数码的个数。
例如,十进制数每位上的数码,有"0"、"1"、"3",…,"9"十个数码,所以基数为10。
(2)位权:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为100、101、102、103。
因为:4567=4x103+5x 102+6x 101 +7x100(3)数的位权表示:任何一种数制的数都可以表示成按位权展开的多项式之和。
比如:十进制数的435.05可表示为:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2位权表示法的特点是:每一项=某位上的数字X基数的若干幂次;而幂次的大小由该数字所在的位置决定。
3、二进制数计算机中为何采用二进制:二进制运算简单、电路简单可靠、逻辑性强(1)定义:按“逢二进一”的原则进行计数,称为二进制数,即每位上计满2 时向高位进一。
(2)特点:每个数的数位上只能是0,1两个数字;二进制数中最大数字是1,最小数字是0;基数为2;比如:10011010与00101011是两个二进制数。
(3)二进制数的位权表示:(1101.101)2=1x23+1x 22+0x 21+1x 20+1x2-1 +0x 2-2+1x2-3 (4)二进制数的运算规则1 加法运算① 0+0=0 ③ 1+1=10② 0+1=1+0=12 乘法运算① 0×0=0 ③ 1×1=1② 0×1=1×0=04、八进制数(1)定义:按“逢八进一”的原则进行计数,称为八进制数,即每位上计满8时向高位进一。
计算机专业基础综合计算机组成原理(数据的表示和运算)历年真题试卷汇编2

计算机专业基础综合计算机组成原理(数据的表示和运算)历年真题试卷汇编2(总分:102.00,做题时间:90分钟)一、单项选择题(总题数:37,分数:86.00)1.下列数中最大的是____。
【中南大学1998年】A.(1100lOl0)2B.(102)8C.(E9)16 √D.(121)3考查进位计数制及其相互转换。
本题将B、C选项改写为二进制表示,可更快找到最大数。
2.下列数中最小的是____。
【北京邮电大学2002年】A.(101001)2B.(52)8C.(101001)BcD √D.(233)16考查进位计数制及其相互转换。
C选项补齐为00101001,即为十进制数29,为最小数。
3.把十进制数172转换为八进制数和十六进制数分别是____。
【中南大学1998年】A.(543),(AC)B.(543),(AB)C.(254),(AC) √D.(253),(AC)考查不同进位计数制之间的转换。
十进制数172表示成二进制为10101100。
转换为八进制时,从最低位每3位对应一位八进制,则得(254)。
转换为十六进制时,从最低位每4位对应一位十六进制,则得(AC)。
4.下列____种说法有误差。
【华中师范大学1997年】A.任何二进制整数都可用十进制表示B.任何二进制小数都可用十进制表示C.任何十进制整数都可用二进制表示D.任何十进制小数都可用二进制表示√考查二进制与十进制的转换。
计算机中,小数的表示是离散的,并不是所有十进制小数都可用二进制表示。
5.下列____是不合法的BCD码。
【哈尔滨工程大学2003年】A.1111001B.11010110 √C.100D.10000101考查BCD码。
BCD码中,1010~1111为冗余编码,故B选项为不合法的BcD码。
6.余3编码是____。
【华中科技大学2002年】A.字符编码B.有权编码C.无权编码√D.汉字编码考查余3码。
余3码是一种无权码,是在8421码的基础上加上(0011) 2形成的,因每个数都多余“3”,故称余3码。
计算机专业基础综合计算机组成原理(数据的表示和运算)历年真题试卷汇编2

计算机专业基础综合计算机组成原理(数据的表示和运算)历年真题试卷汇编2(总分:102.00,做题时间:90分钟)一、单项选择题(总题数:37,分数:86.00)1.下列数中最大的是____。
【中南大学1998年】(分数:2.00)A.(1100lOl0)2B.(102)8C.(E9)16 √D.(121)3解析:解析:考查进位计数制及其相互转换。
本题将B、C选项改写为二进制表示,可更快找到最大数。
2.下列数中最小的是____。
【北京邮电大学2002年】(分数:2.00)A.(101001)2B.(52)8C.(101001)BcD √D.(233)16解析:解析:考查进位计数制及其相互转换。
C选项补齐为00101001,即为十进制数29,为最小数。
3.把十进制数172转换为八进制数和十六进制数分别是____。
【中南大学1998年】(分数:2.00)A.(543),(AC)B.(543),(AB)C.(254),(AC) √D.(253),(AC)解析:解析:考查不同进位计数制之间的转换。
十进制数172表示成二进制为10101100。
转换为八进制时,从最低位每3位对应一位八进制,则得(254)。
转换为十六进制时,从最低位每4位对应一位十六进制,则得(AC)。
4.下列____种说法有误差。
【华中师范大学1997年】(分数:2.00)A.任何二进制整数都可用十进制表示B.任何二进制小数都可用十进制表示C.任何十进制整数都可用二进制表示D.任何十进制小数都可用二进制表示√解析:解析:考查二进制与十进制的转换。
计算机中,小数的表示是离散的,并不是所有十进制小数都可用二进制表示。
5.下列____是不合法的BCD码。
【哈尔滨工程大学2003年】(分数:2.00)A.1111001B.11010110 √C.100D.10000101解析:解析:考查BCD码。
BCD码中,1010~1111为冗余编码,故B选项为不合法的BcD码。
计算机应用基础进位计数制

计算机应用基础进位计数制在计算机科学和应用中,进位计数制是一种数值表示法,它使用不同的符号来表示不同的数值。
这种表示法通常用于计算机内部数据存储和计算,因为它可以有效地表示大范围的数值,并且可以进行简单的算术运算。
在进位计数制中,每个数字的权值等于它所在位置的次方。
例如,在十进制中,个位的权值为1,十位的权值为10,百位的权值为100,以此类推。
因此,数字918可以表示为9×100+1×10+8。
在计算机中,最常用的进位计数制是二进制、八进制和十六进制。
这些进位计数制的符号和权值如下:二进制:符号为0和1,权值分别为2的次方。
例如,数字1101可以表示为1×23+1×22+0×21+1。
八进制:符号为0到7,权值分别为8的次方。
例如,数字17可以表示为1×8+7。
十六进制:符号为0到9和A到F,权值分别为16的次方。
例如,数字255可以表示为2×162+5×161+5×160。
这些进位计数制在计算机科学和应用中有许多优点。
它们可以有效地表示大范围的数值,因为它们的权值通常比十进制大得多。
它们可以进行简单的算术运算,例如加法、减法、乘法和除法。
它们也适用于计算机内部的存储和传输,因为它们可以减少数据的大小并提高效率。
进位计数制是计算机科学和应用中非常重要的概念之一。
它不仅可以有效地表示大范围的数值,还可以进行简单的算术运算,并且适用于计算机内部的存储和传输。
随着信息技术的不断发展,计算机已经成为我们生活中不可或缺的一部分。
在农业领域,计算机的应用也日益广泛,为农业生产带来了巨大的改变。
本文将介绍农大计算机计算机应用基础的相关知识,包括计算机在农业生产中的应用、农业信息化技术、农业物联网技术、农业大数据技术等。
计算机在农业生产中有着广泛的应用,包括农业专家系统、农业遥感监测、农业智能机器人等。
这些技术的应用,使农业生产更加智能化、高效化,提高了农产品的产量和质量。
进位计数制及其相互转换

进位计数制及其相互转换
1.1 进位基数和位的权
“基数”是指计数制中所用到的数码的个数。 对于进位计数制,同一数码在不同的数位时,它所代表的
数值大小是不同的。每一数位上有一个所谓的“权”,“权” 是一个以基数为底的指数,得 积才是该位数值的大小。
进位计数制及其相互转换
1.4 二进制与十进制间的相互转换
二级制转换为十进制 二进制各位的权为2i ,将二进制数按权展开,相加即得十 进制数。
十进制转换为二进制 二进制各位的权为2i ,将十进制数按权对应展开,即得二 进制数。
2.3 计算机中数值的表示
2.3.1 机器数的编码表示
1. 原码表示法 整数的最高位用于符号位,规定0表示“+”号,1表示“-”
一个数的数值就等于各位数码乘以该位的“位权”所得积 之和。如 12345.876=l×104+2×103+3×102+4×101+5×100+8×10-1+7×
10-2+6×10-3
进位计数制及其相互转换
1.2 二进制数制
二进制数制的基数是2,只有2个不同的数码0和1,它是“逢二进 位”的 。 (1)移位性质:小数点右移一位(数值位左移),数值增大一倍,小数 点左移一位(数值位右移),数值减小为原来的一半。 (2)奇偶性质:最低位为0是偶数,最低位为1是奇数。 (3)二进制数与十进制数的等位性:经计算,一位十进制数需用3.32位 二进制数码来表示。这对计算精度的估计十分有用。若要表示一 个十万分之一的精度,十进制数就要用到小数点后五位,而二进 制数则要:n=3.32×5=16.6位,即采用16位字长的数就可满足 要求。
复杂进制之间的转换

十进制转成十六进制
数值由十进制转换成十六 进制,要将整数部分和小 数部分分别进行转换。
例:把(958.6484)10转换 成十六进制数 (958.6484)10=
(3BE.A5FD)16
0.6484*16=10.374 0.374*16=5.9904 0.9904*16=15.8464 0.8464*16=13.5424
用按权展开式 展开
二进制
八进制
十六进制
整数部分:除基取余,倒序排列
小数部分:乘基取整,顺序排列
三位合一位
四位合一位
分组转换
逐位 一位拆三位
以二进制为桥
转换 一位拆四位 以二进制为桥
*八进制数与十六进制数间的转换
以二进制数为中介,先将要转换的进制数化为二进制 数,再转换成目的进制数。
如: ( 7 3 ) 8 =(111 011) 2 =( 00 11 1011) 2 =( 3 B ) 16
163=4096 164=65536 16-1=0.0625
16-2=0.00390625
16-3=0.00024414
16-4=0.00001526
R进制转换为十进制的形式
1. R(R=2、8、16)进制数转换为十进制 转换规则:将R进制数转换为十进制数一般使用按权展开多
项式的形式,然后计算求和得到对应的十进制数据。可简述为 口诀:“利用按权展开式展开”。 例1.8 把(1100101.101)2转换成十进制数。 解:(1100101.101)2=1×26+1×25+0×24+0×23+1×22+0×21+
温故上节课所讲得内容:
作业: 1、 十进制数7转换成二进制数是( )。 (A)111;(B)011;(C)100;(D)110。
