进位计数制
进位计数制概念

进位计数制概念
嘿,朋友们!今天咱来聊聊进位计数制这个有意思的玩意儿。
你说这进位计数制啊,就好像是我们生活中的一套特别规则。
咱平时用的十进制,不就像是走路一样自然嘛。
你看啊,从 0 到 9,满了 10 就得进一位,这多顺溜呀!
想象一下,这数字就像一群小兵,按照特定的规则排兵布阵。
十进制就是那个最常见的阵形,大家都习惯了。
可还有其他的进位计数制呢!好比二进制,那就是个特别的存在。
它就只有 0 和 1 这两个数字,就像个简单却又充满神秘的小世界。
咱平时电脑里的那些程序、数据啥的,可都跟二进制有关系呢!这二进制就像是电脑世界的秘密语言,虽然咱看着有点头疼,但电脑可喜欢它啦!
还有八进制、十六进制啥的,它们就像是数字世界里的各种奇妙门派。
每个都有自己的特点和用处。
你说这进位计数制是不是很神奇?就好像数字们在玩不同的游戏,有着不同的玩法。
十进制是我们最熟悉的游戏,可其他的进制也都有着独特的魅力呀!
咱平时生活中很多地方也能看到进位计数制的影子呢。
比如时间,一天24 个小时,这不也是一种进位嘛!再比如货币,元角分之间也是有进位关系的呀。
进位计数制就像是数字世界的基石,没有它,那数字世界不就乱套啦?它让数字变得有序,让我们能更好地理解和处理数字。
所以啊,可别小瞧了这进位计数制,它可是有着大用处呢!它让我们的数字生活变得丰富多彩,让那些看不见摸不着的数字变得有意义起来。
怎么样,是不是觉得进位计数制很有趣呀?是不是对数字又多了一份好奇和喜爱呢?反正我是这么觉得的!。
数制及其转换

阶码的位数决定了表示数的范围; 尾数的位数决定了所表示数的精度;
3、机器数的表示
在计算机中对带符号数的表示方法有原码、补码和反码三种形式。 1)原码 规定符号位用数码0表示正号,用数码1表示负号, 数值部分按一般二进制形式表示数的绝对值。 +7: 00000111 +0: 00000000 零有两种表示方法
例 3:将 ( 237 . 625 ) 10 转化成二进制
整数: 除2取余 2 |2 3 7 2 |1 1 8 2 |5 9 2 |2 9 2 |1 4 2 |7 2 |3 2 |1 0
1 0 1 1 0 1 1 1
取 值 方 向
小数: 乘2取整 0. 6 2 5 × 2 1 1. 2 5 0 0. 2 5 × 2 0 0. 5 0 × 2 1 1. 0
M
k
Di N
i
i m 1
其中D i为数制采用的基本数符; Ni为权;N为基数
M
k
Di N
i
i m 1
例:十进制数,3058.72 可表示为: 3×103+0×102+5×101+8×100+ 7×10-1+2×10-2 例: 二进制数10111.01 可表示为: 1×24+0×23+1×22+1×21+1×20+0×2-1+1×2-2
-7: 10000111
-0:10000000
3、机器数的表示
在计算机中对带符号数的表示方法有原码、补码和反码三种形式。
2)反码
规定正数的反码和原码相同, 负数反码是对该数的原码除符号位外各位求反
+7: 00000111 -7: 11111000
进位计数制

常用的计数制
• • • • 十进制:D (Decimal) 二进制:B (Binary) 八进制:O (Octal) 十六进制:H (Hexadecimal)
各种进位计数制的表示方法
•方法一:
(dn-1dn-2……d2d1d0.d-1d-2……d-m)r r为计数制
例如 (365.2)10,(11011.01)2,(3460.36)8, (596.12)16 •方法二:利用后缀表示各种进位计数制
高位
低位
要掌握不同进位计数制之间转换规律
• 10进制 • r进制 • 2/8/16进制
例如
r 进制 10 进制 8/16/2 进制
(7 5 3 . 3 7)8 =( 111 101 011 . 011 111 )2
再如 ( 0 11, 101 ,011 . 011, 11 0 )2 =( 3 5 3 . 3 6 )8
后缀B表示二进制数;后缀O表示八进制数; 后缀H表示十六进制数,后缀D表示十进制数。
例如 365.2D, 11011.01B, 3460.36O, 596.12H
计算机中数值信息是如何处理的?
进位计数制:r进制的四个特例
• 10进制数码(D):0,1,2,3,4,5,6,7,8,9 • 2进制数码(B): 0 和 1 • 8进制数码(O): 0,1,2,3,4,5,6,7 • 16进制数码(H):0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
1.r进制换成十进制 2.十进制换成r进制 3.二进制、八进制和十六进制 之间的转换
进位计数制:不同进制之间的转换
• 1. r进制 十 进制(已知di , 求十进制的N)
(dn-1dn-2……d2d1d0.d-1d-2……d-m)r
常用的进位计数制
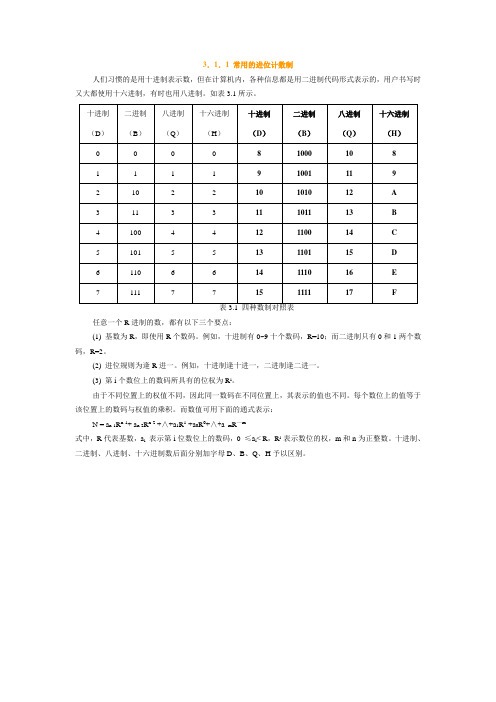
3.1.1 常用的进位计数制
人们习惯的是用十进制表示数,但在计算机内,各种信息都是用二进制代码形式表示的,用户书写时又大都使用十六进制,有时也用八进制。
如表3.1所示。
任意一个R进制的数,都有以下三个要点:
(1) 基数为R,即使用R个数码。
例如,十进制有0~9十个数码,R=10;而二进制只有0和1两个数码,R=2。
(2) 进位规则为逢R进一。
例如,十进制逢十进一,二进制逢二进一。
(3) 第i个数位上的数码所具有的位权为R i。
由于不同位置上的权值不同,因此同一数码在不同位置上,其表示的值也不同。
每个数位上的值等于该位置上的数码与权值的乘积。
而数值可用下面的通式表示:
N = a n-1R n-1+ a n-2R n-2 +∧+a1R1 +a0R0+∧+a--m R—m
式中,R代表基数,a i表示第i位数位上的数码,0 ≤a i< R,R i 表示数位的权,m和n为正整数。
十进制、二进制、八进制、十六进制数后面分别加字母D、B、Q、H予以区别。
进位计数制ppt课件

键盘
❖ 键盘区的划分 ❖ 键盘上的基本指法
金山打字程序
❖ 功能键
Ctrl Alt Shift
Caps Lock
Num Lock
Enter
Back Space
……
27
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
1.1.3 计算机的分类
❖ 按照处理数据分类
数字计算机、模拟计算机
❖ 按照使用范围分类
专用计算机、通用计算机
❖ 按照性能分类
巨型机、大型机、小型机、工作站、微 型机(PC)
7 7
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
1、硬件系统
运算器
输入设备
存储器
数据流 控制流 输出设备
控制器
❖ 控制器担负着对程序的每一条指令进行分析、判断,发出 各种控制信号,使计算机的有关设备实现协调工作的任务, 它是整个计算机的指挥中心 。
❖ 运算器负责计算机中的各类运算,如加、减、乘、除四则
运算;与、或、非、比较等逻辑运算;还能进行代码的传
单击选择提示框中的“安全删除USB Mass Storage Device –驱动器(F:,G:)”,将U盘关 闭,并拔下U盘。
或者 右击布告栏区的U盘图标,弹出一个 “安全删除硬件”对话框。
26
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
2、计算机的工作原理
输入设备
进位计数制

(1)进位计数制我们习惯使用的是十进制,另外还有八进制、十二进制、十六进制、六十进制等等。
而计算机使用的是二进制,由于二进制中只有两个数字0和1,所以很容易用电子元件的两种状态来表示(如电平的高或低,晶体管的导通或截止),所以二进制具有硬件上容易实现、运算规则简单、便于机器执行等优点。
但同时也存在着位数长、书写和阅读都不方便且容易出错等缺点。
有时八进制和十六进制能方便地与二进制实现转换,所以常用八进制十六进制进行输入或输出。
进位计数制①进位计数制的基本特点:逢N进一。
N是指进位计数制表示一位数所需要的符号数目。
②采用位权表示法:处于不同位置上的数字代表的数字代表不同的数值。
位权和基数是进位计数制中的两个要素。
进位计数制的基本的表示方法几种数制的表示法:二进制。
由数字0,1组成,基数为2,逢二进一。
(1011.101)2=1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3八进制。
由数字0~7组成,基数为8,逢八进一。
一个八进制数可按权展开成一个多项式,列如:(274)8=2×82+7×81+4×80十六进制。
由数字0~9和英文字母A至F组成,用A表示10,B表示11……用F表示15,逢十六进一。
一个十六进制数可按权展开成一个多项式,列如:(2EA6)16=2×163+14×162+10×161+6×160表1.2给出了这几种数制间0-16数值的对照表。
表1.2为了表达方便起见,常在数字后加一缩写字母作为不同进制数的标识。
B -→二进制Q -→八进制D -→十进制(可省略)H -→十六进制(2)不同进位计数制之间的转换①十进制与二进制之间的转换一个十进制数一般可分为整数部和小数两个部分。
通常把整数部分和小数部分分别进行转换,然后再组合起来。
进位计数制

p9
3、计算机中数的表示
· 计算机中所有的信息都是以二进制形式存放的。
2.3.1、正、负数
· 方法: 二进制数的最高位(最左边的)称为符号位,符号位为“0”表示该
数为正数,符号位为“1”表示该数为负数。
· 例子: 用八位二进制数表示十进制的+50和-50: 总目录
(+50)10 = (00110010)2 (-50)10 = (10110010)2
– 数值表示 – 字符表示 – 图像表示 – 声音表示 – 视频表示 – 数据压缩
p7
23. 数值表示
1/2
• 计算机内部表达的数值我们称为“机器数”, 而日常表达的数值为“真值” • 符号位也用 0(正数)和 1(负数)表示 • 受限于计算机的字长和数据类型,机器数能 够表达的数据范围有限
– 定点数:小数点位置固定,表达纯小数或整数
1、进位计数制
· 计算机中常用的计数制
十进制 基数 位权 数字符号
总目录
二进制 2 21 0, 1
八进制 8 81 0~7
十六进制 16 161 0~9,A~F
10 101 0~9
章目录
节目录 退出
2.1.1、十进制数(D)
· 特点: (1)、有0、1、2、…、9十个数字 (2)、逢十进一,进位基数为10,位的权数是十的幂。 · 举例: 十进制数569.28可以表示为: 569.28=5×102 + 6×101 + 9×100 + 2×10-1 + 8×10-2 换一个角度: 102 5 101 6 100 9 10-1 2 8 10-2
2.2.4、十六进制数转换成二进制数
总目录 【方法】将每一位十六进制数用对应的4位二进制数来表示,其最左 侧和最右侧的0可以省去。 十六进制数: 1 6 B . 6 二进制数:0001 0110 1011 . 0110 8 1000
进位计数制及其转换方法过程详解

进位计数制及其转换方法过程详解数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的原则进行计数的方法,称为进位计数制。
比如,在十进位计数制中,是按照“逢十进一”的原则进行计数的。
常用进位计数制:1、十进制(Decimal notation),有10个基数:0 ~~ 9 ,逢十进一;2、二进制(Binary notation),有2 个基数:0 ~~ 1 ,逢二进一;3、八进制(Octal notation),有8个基数:0 ~~ 7 ,逢八进一;4、十六进制数(Hexdecimal notation),有16个基数:0 ~~ 9,A,B,C,D,E,F (A=10,B=11,C=12,D=13,E=14,F=15) ,逢十六进一。
二、进位计数制的基数与位权"基数"和"位权"是进位计数制的两个要素。
1、基数:所谓基数,就是进位计数制的每位数上可能有的数码的个数。
例如,十进制数每位上的数码,有"0"、"1"、"3",…,"9"十个数码,所以基数为10。
2、位权:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为100、101、102、103。
因为:?4567=4x103+5x 102+6x 101 +7x100?3、数的位权表示:任何一种数制的数都可以表示成按位权展开的多项式之和。
比如:十进制数的435.05可表示为:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2位权表示法的特点是:每一项=某位上的数字X基数的若干幂次;而幂次的大小由该数字所在的位置决定。
?三、二进制数计算机中为何采用二进制:二进制运算简单、电路简单可靠、逻辑性强。
1、定义:按“逢二进一”的原则进行计数,称为二进制数,即每位上计满2 时向高位进一。
数的进位知识点

数的进位知识点进位是数学中非常基础的概念,它涉及到整数的表示和运算。
在日常生活和各个学科都会涉及到进位的概念,尤其在计算机科学和金融领域中更为重要。
本文将介绍数的进位的相关知识点,包括进位制、进位运算和进位的应用。
一、进位制进位制是一种计数的方法,根据不同的进位基数,可以分为十进制、二进制、八进制和十六进制等。
具体如下:1. 十进制:十进制是我们常用的计数方式,以0-9的十个数字为基础。
每当个位到达9时,就需要进位到十位,十位到达9时就需要进位到百位,以此类推。
2. 二进制:二进制是计算机中最常用的进位制,只包含0和1两个数字。
每当个位到达1时,就需要进位到十位,十位到达1时就需要进位到百位,以此类推。
3. 八进制:八进制以0-7的八个数字为基础。
每当个位到达7时,就需要进位到十位,十位到达7时就需要进位到百位,以此类推。
4. 十六进制:十六进制以0-9和A-F的共十六个数字表示。
其中A代表10,B代表11,依此类推。
每当个位到达F时,就需要进位到十位,十位到达F时就需要进位到百位,以此类推。
进位制的转换非常常见,可以通过多种方法进行计算和转换。
例如,将十进制转换为二进制可以使用除以2取余法,将十进制转换为八进制可以使用除以8取余法,将十进制转换为十六进制可以使用除以16取余法。
二、进位运算进位运算是指在进行数学运算中,当某一位的结果超过了进位制的基数时,需要把多余的进位向高位进行传递的过程。
进位运算的常见形式包括加法进位和乘法进位。
1. 加法进位:在两个数相加的过程中,当某一位的结果超过了进位制的基数时,就会产生进位。
例如,对于十进制数相加时,当个位相加的结果大于10时,就会产生进位,将个位的进位加到十位上。
2. 乘法进位:在两个数相乘的过程中,当某一位的结果超过了进位制的基数时,也会产生进位。
例如,对于十进制数相乘时,当个位相乘的结果大于10时,就会产生进位,将个位的进位加到十位上。
进位运算在数学计算过程中非常常见,可以通过列竖式的方法进行演算和解决。
数学进位制的计算方法

数学进位制的计算方法数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的方法进行计数,称为进位计数制。
在日常生活和计算机中采用的是进位计数制。
在日常生活中,人们最常用的是十进位计数制,即按照逢十进一的原则进行计数的。
二进制二进制是计算技术中广泛采用的一种数制。
二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前的计算机系统使用的基本上是二进制系统。
计算机内部采用二进制的原因:(1)技术实现简单,计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示。
(2)简化运算规则:两个二进制数和、积运算组合各有三种,运算规则简单,有利于简化计算机内部结构,提高运算速度。
(3)适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
(4)易于进行转换,二进制与十进制数易于互相转换。
(5)用二进制表示数据具有抗干扰能力强,可靠性高等优点。
因为每位数据只有高低两个状态,当受到一定程度的干扰时,仍能可靠地分辨出它是高还是低。
三进制三进制是“逢三进一,退一还三”的进制。
三进制数码包括“0,1和2。
”三进制数位小数点前从右往左依次是1位,3位,9位,27位,81位,243位……三进制数位小数点后从左往右依次是3分位,9分位,27分位,81分位……整数的三进制表示法不如二进制那样冗长,但仍然比十进制要长。
例如,365在二进制中的写法是101101101(9个数字),在三进制中的写法是111112(6个数字)。
在三进制中表示三分之一是很方便的,不像在十进制中,需要用无限小数来表示。
但是,二分之一、四分之一之类的分数在三进制中都是无穷小数,这是因为2不是3的因子。
七进制七进制是以7为底数的记数系统。
使用数字0-6。
进位计数制

进位计数制:是人们利用符号来计数的方法。
一种进位计数制包含一组数码符号和两个基本因素。
(1)数码:用不同的数字符号来表示一种数制的数值,这些数字符号称为"数码"。
(2)基:数制所使用的数码个数称为"基"。
(3)权:某数制每一位所具有的值称为"权"。
1、常用进位计数制(1)十进制(D)数码:0、1、…… 8、9基数:10位权:10i (i=……-2,-1,0,1,2,……)逢10进1(2)二进制 (B)数码:0、1基数:2位权:2i (i=……-2,-1,0,1,2,……)逢2 进1(3)八进制 (O)数码:0、1、…… 6、7基数:8位权:8i (i=……-2,-1,0,1,2,……)逢8进1(4)十六进制 (H)数码:0、1、…… 8、9、A、B、C、D、E、F基数:16位权:16i (i=……-2,-1,0,1,2,……)逢16进1--------上面是他们的基本构成,下面是他们间的转换关系---------1 为什么需要八进制和十六进制?编程中,我们常用的还是10进制……必竟VB是高级语言。
比如:a = 99;不过,由于数据在计算机中的表示,最终以二进制的形式存在,所以有时候使用二进制,可以更直观地解决问题。
但,二进制数太长了。
比如int 类型占用4个字节,32位。
比如100,用int类型的二进制数表达将是:0000 0000 0000 0000 0110 0100面对这么长的数进行思考或操作,没有人会喜欢。
因此,C,C++ 没有提供在代码直接写二进制数的方法。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
不过,为什么偏偏是16或8进制,而不其它的,诸如9或20进制呢?2、8、16,分别是2的1次方,3次方,4次方。
这一点使得三种进制之间可以非常直接地互相转换。
8进制或16进制缩短了二进制数,但保持了二进制数的表达特点。
进位计数制教学ppt课件

十六进制数中,A-F表示十进制的10-15,例如:A表示十进 制的10,F表示十进制的15。
十六进制数的运算规则
加法运算
逢16进1,例如:2A+3F=5F。
减法运算
借位时从16借1,例如:5F-2A=36。
乘法运算
除法运算
按位相乘后相加,例如:(2A)x(3F)=7EF。
从被除数中连续去掉大于除数的位数,直 到被除数小于除数为止,例如: 7EF/3F=2A余1E。
在其他领域的应用
数学和物理
在数学和物理中,进位计数制被 广泛应用于数论、组合数学、图 论等领域,以及物理量的测量和
计算。
金融和商业
在金融和商业中,使用进位计数 制来表示货币、股票价格பைடு நூலகம்信息
,以及进行财务计算和分析。
语言学和社会科学
在语言学和社会科学中,使用进 位计数制来表示音节、单词、句 子等信息,以及进行语言分析和
在电子工程中的应用
数字电路设计
在数字电路设计中,使用进位计 数制来表示信号的状态和变化, 实现逻辑运算和组合电路的设计
。
通信系统
在通信系统中,使用进位计数制来 表示信号的幅度、频率和相位等信 息,实现信号的传输和调制解调。
自动控制系统
在自动控制系统中,使用进位计数 制来表示控制信号的状态和变化, 实现自动化控制和调节。
进位计数制教学ppt 课件
目录
CONTENTS
• 进位计数制简介 • 二进制数制 • 八进制数制 • 十六进制数制 • 进位计数制的应用
01 进位计数制简介
进位计数制的定义
总结词
进位计数制是一种数字表示方法,它根据进位规则将数值表示为不同的符号或 数字的组合。
计算机应用基础进位计数制

计算机应用基础进位计数制在计算机科学和应用中,进位计数制是一种数值表示法,它使用不同的符号来表示不同的数值。
这种表示法通常用于计算机内部数据存储和计算,因为它可以有效地表示大范围的数值,并且可以进行简单的算术运算。
在进位计数制中,每个数字的权值等于它所在位置的次方。
例如,在十进制中,个位的权值为1,十位的权值为10,百位的权值为100,以此类推。
因此,数字918可以表示为9×100+1×10+8。
在计算机中,最常用的进位计数制是二进制、八进制和十六进制。
这些进位计数制的符号和权值如下:二进制:符号为0和1,权值分别为2的次方。
例如,数字1101可以表示为1×23+1×22+0×21+1。
八进制:符号为0到7,权值分别为8的次方。
例如,数字17可以表示为1×8+7。
十六进制:符号为0到9和A到F,权值分别为16的次方。
例如,数字255可以表示为2×162+5×161+5×160。
这些进位计数制在计算机科学和应用中有许多优点。
它们可以有效地表示大范围的数值,因为它们的权值通常比十进制大得多。
它们可以进行简单的算术运算,例如加法、减法、乘法和除法。
它们也适用于计算机内部的存储和传输,因为它们可以减少数据的大小并提高效率。
进位计数制是计算机科学和应用中非常重要的概念之一。
它不仅可以有效地表示大范围的数值,还可以进行简单的算术运算,并且适用于计算机内部的存储和传输。
随着信息技术的不断发展,计算机已经成为我们生活中不可或缺的一部分。
在农业领域,计算机的应用也日益广泛,为农业生产带来了巨大的改变。
本文将介绍农大计算机计算机应用基础的相关知识,包括计算机在农业生产中的应用、农业信息化技术、农业物联网技术、农业大数据技术等。
计算机在农业生产中有着广泛的应用,包括农业专家系统、农业遥感监测、农业智能机器人等。
这些技术的应用,使农业生产更加智能化、高效化,提高了农产品的产量和质量。
进位计数制ppt课件

进位计数制的种类
总结词
进位计数制可以分为二进制、八进制、 十进制和十六进制等几种。
VS
详细描述
二进制是基数为2的进位计数制,它只有 0和1两种符号。八进制是基数为8的进位 计数制,它有0、1、2、3、4、5、6、7 共8种符号。十进制是人们日常生活中最 常用的进位计数制,它有0、1、2、3、4 、5、6、7、8、9共10种符号。十六进制 是基数为16的进位计数制,它有0、1、2 、3、4、5、6、7、8、9、A、B、C、D 、E、F共16种符号。
进位计数制ppt课件
目 录
• 引言 • 二进制数制 • 八进制数制 • 十六进制数制 • 进位计数制的转换
01
引言
进位计数制的定义
总结词
进位计数制是一种数字表示方法,它 按照某种规则将数值转换为符号序列 。
详细描述
进位计数制是一种数字系统,它使用 不同的符号来表示不同的数值。在进 位计数制中,数值的大小取决于符号 的位值和进位规则。
字表示。
减法运算规则
在八进制数制中,减法运算按 照借位规则进行,即每逢8则借 位,借位后用7至0的数字表示 。
乘法运算规则
在八进制数制中,乘法运算按 照乘法表进行,即每一位的乘 积都是8的幂次方。
除法运算规则
在八进制数制中,除法运算按 照除法表进行,即每一位的商
都是8的幂次方。
04
十六进制数制
十六进制数的定义
八进制数的基数
八进制数的进位规则
逢八进一,即每逢8则进位,进位后 用0至7的数字表示。
在八进制数制中,基数为8,即有8个 不同的数码。
八进制数的表示方法
1 2
八进制数的基数表示
在八进制数制中,用数字前加0表示该数为八进 制。例如,8在十进制中表示为010,在八进制 中表示为0o10。
第二章 进位计数制

第二章第一部分数制转换及运算1 进位计数制1.1现实生活中存在的进位计数制1.2分析十进制数1.3进位计数制三要素基数:逢N进一,N为基数数码:基数为N,共有N个数码,0—N-1位权:数位上固定大小的值。
对于基数为N的进位计数制,由小数点分割,分别是[…N4,N3,N2,N1,N0,N-1,N-2,N-3,N-4…]1.4分析二进制数、八进制数和十六进制数1.5数按位权展开任何一种数制表示的数,都可以写成按位权展开的多项式之和的形式。
此多项式之和是该数所对应的十进制数值大小(结果为十进制数,提供了由其它进制数向十进制数转换的方法)。
2不同进位计数制间的转换2.1 R进制数转换成十进制数按位权展开求和。
2.2 十进制数转换成R进制数对于整数部分采用“除R取余法”;对于小数部分采用“乘R取整法”。
下面以十进数转换为二进数为例进行分析。
1)十进制整数转换为二进制整数除2取余法:将十进制整数反复除以2,若余数为1则对应于二进制数相应位为1,余数为0则对应于二进制数相应位为0。
第一次相除得到的余数是二进制数的最低位,最后一次余数是二进制数的最高位。
从低位到高位逐次进行,直到商为0为止。
例:(215)10=( )22)十进位纯小数转换为二进制纯小数乘2取整法:将十进制纯小数反复乘以2,所得新数的整数部分为1,则二进制数相应位为1,整数部分为0,则二进制数相应位为0。
第一次得到的整数是二进制数的最高位,最后一次得到的整数是二进制数的最低位。
从高位到低位逐次进行,直到满足精度要求或小数部分为0为止。
例:(0.6531)10=( )2(0.125)10=( )23)十进制数转换为二进制数例:(215.6531)10=( )22.3二进制数与八进制数之间的转换1)二进制数转换成八进制数由于八进制数的最大数码为7,需要用三位二进制数来表示,因此:方法:由小数点作为分隔,对于整数部分,由低位到高位将二进制数每三位分为一组,不够三位时在高位左边用0被足(或不补),对于小数部分,由高位到低位,每三位一组,不足三位时在低位右边填0补足。
进位计数制的三要素

进位计数制的三要素
首先,基数是决定计数制度的最基本要素之一、它代表了计数系统中
每个数字的取值范围。
例如,十进制系统中的基数为10,即从0到9共
有10个数字。
而二进制系统的基数为2,只有0和1两个数字。
其次,数码是组成数字的符号或字符。
在十进制系统中,数码是从0
到9共10个数字。
在二进制系统中,数码是只有0和1两个数字。
数码
的取值范围取决于所使用的基数。
最后,进位是一种规则,用于处理在一些位置上计数超过基数的情况。
当一些位置上的数达到基数时,将会发生进位。
在十进制系统中,进入十
位的进位是常见的例子。
例如,在计算12+9时,个位上的数相加为2,
超过了基数10,所以要进位到十位。
这就意味着在十位上的数加上进位1,最终得到的结果为20。
进位计数制的三要素相互关联,共同构成了计数系统。
基数决定了每
个数码的取值范围,数码则表示数的具体值,而进位规则则用于处理当数
码超过基数时的情况。
这种计数制不仅在数学中有重要的应用,也广泛用
于计算机科学中,特别是在二进制系统中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
打印机
液晶(LED)显示器
CRT显示器
15
2、计算机的工作原理
运算器 输入设备 存储器 输出设备
控制器
16
3、微机的硬件组成
输入设备 CPU
内存储器 两个组成部分 两个技术指标
微 机
主机
外存储器 主板
输出设备
输入输出接口电路、电源系统
17
CPU
AMD公司的CPU 还有Cyrix公司
Intel公司的CPU
13
1、硬件系统
输入设备
用来向计算机输入人们编写的程序和数据,可分
为字符输入设备、图形输入设备和声音输入设备 等。有键盘、鼠标、扫描仪等。
14
1、硬件系统
输出设备
向用户报告计算机的运算结果或工作状态,它
把存储在计算机中的二进制数据转换成人们需 要的各种形式的信号 。
常用的输出设备有显示器、打印机、音箱等。
多媒体应用:CAI
计算机网络
9 9
1.2 计算机系统的组成
硬件 系统 软件 系统
计算机系统 = 硬件系统 + 软件系统
硬件:是计算机中“看得见”、“摸的着”的所有物 理设备 软件:是用来指挥计算机运算的各种程序的总和 10 两者协同工作,缺一不可
1、硬件系统
运算器 输入设备 存储器
1.1.1 计算机的发展
第一代
19世纪四五十年代
第二代
19世纪五六十年代
第三代
19世纪六七十年代
第四代
19世纪六七十年代以来
电子管
晶体管
集成电路
大规模集成电路
存 磁鼓、纸带、卡 储 片 器 性 能 应 用
磁盘、磁带
半导体存储器
高集成度半导体 存储器
几千次~几万次/ 几十万次/秒 秒 存储几十万字节 存储几千个字节 使用机器语言和 高级语言: 汇编语言 FORTRAN、 COBOL等
数据流 控制流
输出设备
控制器
控制器担负着对程序的每一条指令进行分析、判断,发出 各种控制信号,使计算机的有关设备实现协调工作的任务, 它是整个计算机的指挥中心 。 运算器负责计算机中的各类运算,如加、减、乘、除四则 运算;与、或、非、比较等逻辑运算;还能进行代码的传 送、移位等操作。 11 控制器 + 运算器 = CPU
3
1.1.1 计算机的发展
ENIAC (Electronic Numerical Integrator And Calculator)即“埃尼阿克” ,电 子数值积分计算机 美国宾夕法尼亚大学的技术人员于 1946年2月14日研发成功 运算速度达到每秒钟5000次加法 占地160平方米 标志信息时代的到来 重达30吨 缺点: 使用近18,000个电子管 无法存储程序 电子管太多 4 经常出现故障
20
内存
高速缓冲存储器Cache
Cache是介于CPU和内存之间的一种可高速存取信
息的芯片,用于解决CPU速度快而内存速度慢的 矛盾问题。
CPU
Cache
RAM
CMOS
安装在主板上,存放计算机当前配置信息
21
外存
磁表面存储器
磁盘(硬盘) 磁带 移动硬盘
光介质存储器{CD、DVD等}
半导体存储器{优盘}
第1章 计算机基础知识
北京科技大学天津学院 计算机教研室
1
本章内容
1.1 计算机概述 1.2 计算机系统的组成 1.3 计算机中的数据 1.4 计算机安全
2
什么是计算机
计算机是一种能快速、高效地按照指令对各种 信息进行存储和处理的电子设备。 具有以下几个特征: ⑴ 运算速度快 ⑵ 计算精度高 ⑶ 可靠性高 ⑷ 具有记忆能力和逻辑判断能力 ⑸ 程序运行自动化等
1、硬件系统
存储器是电子计算机的“记忆”装置,用来存放原 始数据、中间结果、最终计算结果和程序等。 存储器是由若干个单元组成的,每个单元依次给予一个编号,这就是地址 每个单元只可以存储一个二进制信息(即0或1),这 样的单元就叫做位,也叫比特位
8位(bit)=1字节(Byte)
1KB=1024B 1MB=1024KB
字节是存储器的基本单位
一个英文字母存储占多少 字节?一个汉字?
1GB=1024MB
什么叫字长?
12
存储器分为内存储器和外存储器
简称为内存与外存。
两者主要区别
ROM、RAM、Cache和CMOS 内存 外存 磁表面存储器{磁盘(计算机中的硬盘)、磁带、移动 硬盘}; 光介质存储器{CD、DVD等}; 半导体存储器{优盘}
几十万~几百万次/ 几百万次~上亿次 秒 /秒 存储达到“兆字节 大容量存储 ” 软件技术大发展 操作系统走向成熟 面向用户的应用软 件出现 数据库技术 分布式系统技术 应用软件成为产 6 业
1.1.2 计算机的特点
计算机是一种可以进行自动控制、具有记忆功能的 现代化计算工具和信息处理工具。 具有以下几个特征: ⑴ 运算速度快 ⑵ 计算精度高 ⑶ 记忆能力强(存储容量大) ⑷ 可靠性高 ⑸ 工作全自动(存储程序控制)、通用性强
18
内存
随机读写存储器RAM
存放运算器正在处理和待处理的数据、程序和
运算结果。 程序和数据信息必须调入内存后才能被CPU处 理。 特点:断电后信息会消失
19
内存
只读存储器ROM
特点:断电信息不丢失
掩膜ROM:存放由厂家预先写入的程序和数据,
用于启动计算机与控制计算机的工作方式,如 BIOS信息等。用户只能读取这些信息,而不能修 改这些信息,ROM一般固化在主板上。 PROM EPROM EEPROM
第一台现代意义的通用计算机 -EDVAC 离散变量自动电子计算机
冯· 诺依曼在长达101页的 “关于EDVAC的报告草案” 的总结报告,提出:
(1)5个组成部分:运算器;
控制器;存储器;输入装置; 输出装置 (2)采用二进制 (3)“存储程序”和“程序控 计算机之父--冯· 诺伊曼 制”结合的原理 5
22
外存——磁介质存储器
磁盘分为:硬磁盘和软磁盘,简称硬盘和软盘。 存取数据都是通过磁盘驱动器对盘片进行读写来实 现的。 存数据叫做写磁盘,取数据叫做读磁盘。 软驱的盘符命名为A。
7 7
1.1.3 计算机的分类
按照处理数据分类
数字计算机、模拟计算机
按照使用范围分类
专用计算机、通用计算机
按照性能分类
巨型机、大型机、小型机、工作站、微
型机(PC)
8 8
1.1.4 计算机的应用
科学计算 数据处理(信息处理):MIS,OA等
自动控制
计算机辅助系统:CAD,CAM等 人工智能
