常用的进位计数制
进位计数制

常用的计数制
• • • • 十进制:D (Decimal) 二进制:B (Binary) 八进制:O (Octal) 十六进制:H (Hexadecimal)
各种进位计数制的表示方法
•方法一:
(dn-1dn-2……d2d1d0.d-1d-2……d-m)r r为计数制
例如 (365.2)10,(11011.01)2,(3460.36)8, (596.12)16 •方法二:利用后缀表示各种进位计数制
高位
低位
要掌握不同进位计数制之间转换规律
• 10进制 • r进制 • 2/8/16进制
例如
r 进制 10 进制 8/16/2 进制
(7 5 3 . 3 7)8 =( 111 101 011 . 011 111 )2
再如 ( 0 11, 101 ,011 . 011, 11 0 )2 =( 3 5 3 . 3 6 )8
后缀B表示二进制数;后缀O表示八进制数; 后缀H表示十六进制数,后缀D表示十进制数。
例如 365.2D, 11011.01B, 3460.36O, 596.12H
计算机中数值信息是如何处理的?
进位计数制:r进制的四个特例
• 10进制数码(D):0,1,2,3,4,5,6,7,8,9 • 2进制数码(B): 0 和 1 • 8进制数码(O): 0,1,2,3,4,5,6,7 • 16进制数码(H):0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
1.r进制换成十进制 2.十进制换成r进制 3.二进制、八进制和十六进制 之间的转换
进位计数制:不同进制之间的转换
• 1. r进制 十 进制(已知di , 求十进制的N)
(dn-1dn-2……d2d1d0.d-1d-2……d-m)r
数制 进位计数制

数制进位计数制数制是表示数值的一套符号和规则。
进位计数制是一种常用的数制,用于表示和计算数值。
在进位计数制中,每个数位上的数值是通过逐位相加,达到一定值后进位到更高的位的。
常见的进位计数制有十进位(十进制)、二进位(二进制)、八进位(八进制)和十六进位(十六进制)等。
每种进位计数制都有其特定的表示方式和各位数值的范围。
下面将分别介绍几种常见的进位计数制。
十进位是我们平常生活中使用的进位计数制。
它包含了从0到9的十个数值。
每个数位上的数值是通过相加达到9后进位到更高的位的。
例如,十进位数100表示一百,其中百位上的数值是1,十位和个位上的数值都是0。
二进位是计算机中最常用的进位计数制。
它只包含了0和1这两个数值。
每个数位上的数值是通过相加达到1后进位到更高的位的。
例如,二进位数101表示五,其中十位上的数值是1,个位上的数值是0,一位上的数值是1。
八进位是一种少见但仍然被使用的进位计数制。
它包含了0到7这八个数值。
每个数位上的数值是通过相加达到7后进位到更高的位的。
例如,八进位数777表示五百五十五,其中百位上的数值是5,十位上的数值是5,个位上的数值是5。
十六进位是一种常用于计算机中的进位计数制。
它包含了0到9这十个数值以及A到F这六个字母,字母A表示十,字母F表示十五。
每个数位上的数值是通过相加达到F后进位到更高的位的。
例如,十六进位数1FF表示五百十五,其中百位上的数值是5,十位和个位上的数值都是15。
在进位计数制中,数值不仅可以表示正整数,还可以表示小数和负数。
小数的表示方式是在整数部分的数值后面加上小数点,然后逐位表示小数部分的数值。
负数的表示方式是在数值前面加上负号。
例如,十进位数-3.14表示负三点一四。
总结起来,进位计数制是一种用于表示和计算数值的数制。
它包含了一组数值,并且根据进位规则,每个数位上的数值逐位相加,达到一定值后进位到更高的位的。
不同的进位计数制有不同的表示方式和数值范围,常见的进位计数制有十进位、二进位、八进位和十六进位。
进位制

一、进位制的概念
1、定义:“满几进一”就是几进制,几进制的基数就是几 定义: 满几进一”就是几进制, 进位制是人们为了计数和运算方便而约定的计数系统。 比如: 满二进一,就是二进制; 满十进一,就是十进制; 满二进一,就是二进制; 满十进一,就是十进制; 满十二进一,就是十二进制; 满六十进一, 满十二进一,就是十二进制; 满六十进一,就是六十进制 常见的进位制: 2、常见的进位制: 十进制、二进制、七进制、十二进制、六十进制…… 十进制、二进制、七进制、十二进制、六十进制 十进制数用0 十进制数用0-9十个数字来表示 二进制只有0 二进制只有0和1两个数字,七进制用0~6七个数字 两个数字,七进制用0~6七个数字 0~6 十六进制有0~9十个数字及ABCDEF六个字母. 十六进制有0~9十个数字及ABCDEF六个字母. 0~9十个数字及ABCDEF六个字母
an an −1 ⋅ ⋅ ⋅ a1a0 ( k ) (0 < an < k ,0 ≤ an −1 ,⋅ ⋅ ⋅a1 , a0 < k )
3721=3×103+7 ×102+2 ×101+1 ×100 × 110011(2)=1×25+1 ×24+ 0×23+0 ×22 + × × 1×21+1 ×20 × 7342(8)=7×83+3 ×82+4 ×81+2×80 × ×
INPUT i=1 b=0
a, k, n
t=a MOD 10 WHILE i<=n
b=b+t*k^(i-1) a=a\10 t=a i=i+1 WEND PRINT END b MOD 10
① 开始 输入a,k 输入 求a除以 的商q 除以k的商 除以 的商 求a除以 的余数r 除以k的余数 除以 的余数 输出r 输出 a=q 否 q=0? 是 ① 将依次输出的r从右到左排列 将依次输出的 从右到左排列
进位计数制及其相互转换

进位计数制及其相互转换整理人:星辰·樱1.常用的进位计数制进位计数制,简称数制,是人们利用符号来计算的方法。
在计算机中常用到的数制是十进制、二进制、八进制和十六进制。
数制中的三个基本名词术语:·数码--用不同的数字符号来表示一种数制的数值,这些数字符号称为“数码。
·基--数制所使用的数码个数称为“基。
·位权--某数制各位所具有的值称为“位权”。
1.十进制数,数的基为10,有10个数码0-9。
逢十进一,借一当十。
2.二进制数,数的基为2,只有两个数码0和1。
逢二进一,借一当二。
3.八进制数,数的基为8,有8个数码0-7,逢八进一,借一当八。
4.十六进制数,数的基为16,有16个数码0-9和A,B,C,D,E,F,逢十六进一,借一当十六。
其中A-F相当于十进制中的10—15。
2.常用进位计数制间的相互转1.各种进位计数制可统一表示为:i nmiiRK⨯∑-=(这个公式是在word中的插入-公式中可以制作,上标快捷键Ctrl+shift+=和下标快捷键Ctrl+=。
注意:有些输入法可能会与这些快捷键相冲突,最好切换到英文输入法。
)各参说明:R--某种进位计数制的基数。
i--位序号。
K i--第i位上的一个数码为0~R-1中的任一个。
R i--则表示第i位上的权。
m,n--最低位和最高位的位序号。
例题1:把二进制数(1011.0101)2转换为十进制数。
解:(1011.0101)2=1×23+0×22+1×21+1×20+0×2-1+0×2-2+0×2-3+1×2-4=8+0+2+1+0+1/4+0+1/16=(11.3125)10解:(75.21)8=7×81+5×80+2×8-1+1×8-2=56+5+2/8+1/64=(61.265625)10例题3:把十六进制数(175.F B)16转换为十进制数。
大学计算机基础知识点整理

大学计算机基础知识点整理1.CAD是计算机辅助设计的缩写,指利用计算机软件辅助进行设计制图的过程。
2.CAM是计算机辅助制造的缩写,指利用计算机软件辅助进行制造加工的过程。
3.在计算机工作时,内存用来存储当前正在使用的程序和数据,是计算机操作的关键部分。
4.机器语言和汇编语言是低级语言,是计算机硬件能够理解和执行的指令。
5.CAI是计算机辅助教学的缩写,指利用计算机技术提高教学效果的过程。
6.关闭电源后,RAM的存储内容会丢失,需要重新加载。
7.ROM是只读存储器的缩写,指存储在计算机中的只读数据。
8.8位二进制数所表示的最大无符号十进制整数为255,是计算机二进制表示中的重要概念。
9.电子元件的发展经过了电子管、晶体管、集成电路和大规模集成电路四个阶段,是计算机技术不断发展的历程。
10.计算机病毒一般具有破坏性、传染性、隐蔽性、潜伏性等特点,需要注意计算机安全。
11.根据规模大小和功能强弱,计算机可分为巨型机、大型机、中型机、小型机和微型机,是计算机分类的基本方式。
12.bit的意思是位,是计算机中最小的数据单位。
13.计算机可分为主机和外设两部分,主机是计算机的核心部分,外设是主机的配件。
14.内存储器也称为随机存储器,是计算机中存储数据的重要部分。
15.计算机主要是运算速度快、存储容量大、精度高,是现代社会不可或缺的工具。
16.存储器分为内存储器和外存储器两类,内存储器用于存储当前使用的数据和程序,外存储器用于长期存储数据和程序。
17.运算器和控制器合称为中央处理器,是计算机中最重要的部件。
18.在微型计算机中常用的总线有地址总线、数据总线和控制总线,是计算机内部信息传输的重要通道。
19.计算机的存储容量通常使用KB、MB或GB等单位来表示,是计算机性能的重要指标。
20.在计算机内部,一切信息均表示为二进制数,是计算机运行的基础。
21.根据软件的用途,计算机软件一般分为系统软件和应用软件,是计算机功能实现的基础。
数字进位制

数字进位制一、十进制(Decimal System)十进制是我们日常生活中最常用的进位制。
它由0-9这10个数字组成。
每一位的权值都是10的幂次方,从右往左依次为10^0、10^1、10^2...以此类推。
在十进制中,数字的数值大小由高位到低位依次递增,方便人们理解和计算。
二、二进制(Binary System)二进制是计算机系统中最基础的进位制。
它只由0和1这两个数字组成。
每一位的权值都是2的幂次方,从右往左依次为2^0、2^1、2^2...以此类推。
二进制中的数值大小由高位到低位递增,与十进制不同的是,每一位只能是0或1,所以运算更加简单高效。
三、八进制(Octal System)八进制是一种较为少见的进位制,它由0-7这8个数字组成。
每一位的权值都是8的幂次方,从右往左依次为8^0、8^1、8^2...以此类推。
八进制在计算机领域中用得较少,但在Unix系统中经常使用,例如文件权限的表示就是用八进制。
四、十六进制(Hexadecimal System)十六进制是计算机系统中常见的进位制之一。
它由0-9和A-F这16个数字组成,其中A-F分别表示10-15。
每一位的权值都是16的幂次方,从右往左依次为16^0、16^1、16^2...以此类推。
十六进制在计算机领域中广泛应用,例如表示颜色、内存地址等。
五、三进制(Ternary System)三进制是一种基于3的进位制。
它由0-2这3个数字组成。
每一位的权值都是3的幂次方,从右往左依次为3^0、3^1、3^2...以此类推。
三进制在现实生活中较少使用,但在某些领域如电子工程中有一定应用,例如存储器中的三值逻辑。
六、五进制(Quinary System)五进制是一种基于5的进位制。
它由0-4这5个数字组成。
每一位的权值都是5的幂次方,从右往左依次为5^0、5^1、5^2...以此类推。
五进制在现实生活中较少使用,但在某些领域如音乐理论中有一定应用,例如五线谱的音符表示就是用五进制。
进位制

进位制1、十进制计数法我们已经学习过,十进制计数法有以下特点:(1)数字(数码):0、1、2、3、4、5、6、7、8、9;(2)满十进一;(3)位置值原则:用不同数位上的数表示不同单位的数;(4)计数单位和数位顺序。
如:693528.47=6×105+9×104+3×103+5×102+2×105+8×100+4×10-1+7×10-22、二进制计数法前面已经初步学习过二进制,二进制计数法的特点是:(1)2个数字:0、1;(2)满二进一;(3)位置值原则:用不同数位上的数表示不同单位的数;(4)计数单位:由低到高有:…1/23、1/22、1/2、1、2、22、23、24、25、26…如:1011001.01=1×26+0×25+1×24+1×23+0×22+0×2+1×20+0×1/22+1×1/22=89.253、和十进制、二进制一样,任意进制数有类似的特点,K 进制计数法(K=2、3、4、5…10、11、12…)的特点是:(1)K个数字:0、1、2、3、…、K-1;(2)满K进一;(3)位置值原则;(4)计数单位由低到高有:…1/K3、1/K2、1/ K、1、K、K 2、K 3、K 4…如:K=4312133=3×45+1×44+2×43+1×42+3×41+3×40=3×1024+1×256+2×64+1×16+3×4+3×1=3487用20, 21, 22, 23,…,2n作单位,可以表示1到2n+1-1的所有自然数(n=1,2,3,…)。
用天平称物体,要使用到的砝码个数最少,能称同最多的不同的重量,选用砝码的方法如下:(1)砝码和被物体各放在天平的一边,砝码的重量应该是二进制的单位:1,2,4,8,16,32,……。
四年级数论进位制
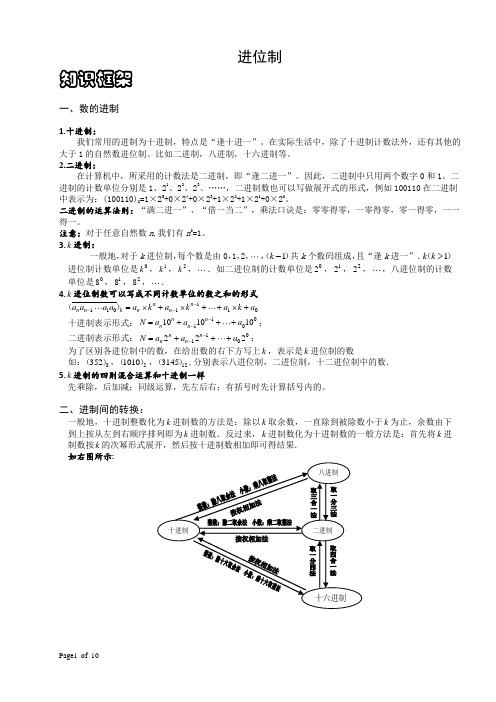
进位制知识框架一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:例题精讲【例 1】 把9865转化成二进制、五进制、八进制,看看谁是最细心的。
数制间的转换

计算机中的数制与编码一、数制1、什么是进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的原则进行计数的方法,称为进位计数制。
比如,在十进位计数制中,是按照“逢十进一”的原则进行计数的。
常用进位计数制:a、十位制(Decimal notation);b、二进制(Binary notation);c、八进制(Octal notation);d、十六进制数(Hexdecimal notation)2、进位计数制的基数与位权"基数"和"位权"是进位计数制的两个要素。
(1)基数:所谓基数,就是进位计数制的每位数上可能有的数码的个数。
例如,十进制数每位上的数码,有"0"、"1"、"3",…,"9"十个数码,所以基数为10。
(2)位权:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为100、101、102、103。
因为:4567=4x103+5x 102+6x 101 +7x100(3)数的位权表示:任何一种数制的数都可以表示成按位权展开的多项式之和。
比如:十进制数的435.05可表示为:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2位权表示法的特点是:每一项=某位上的数字X基数的若干幂次;而幂次的大小由该数字所在的位置决定。
3、二进制数计算机中为何采用二进制:二进制运算简单、电路简单可靠、逻辑性强(1)定义:按“逢二进一”的原则进行计数,称为二进制数,即每位上计满2 时向高位进一。
(2)特点:每个数的数位上只能是0,1两个数字;二进制数中最大数字是1,最小数字是0;基数为2;比如:10011010与00101011是两个二进制数。
(3)二进制数的位权表示:(1101.101)2=1x23+1x 22+0x 21+1x 20+1x2-1 +0x 2-2+1x2-3 (4)二进制数的运算规则1 加法运算① 0+0=0 ③ 1+1=10② 0+1=1+0=12 乘法运算① 0×0=0 ③ 1×1=1② 0×1=1×0=04、八进制数(1)定义:按“逢八进一”的原则进行计数,称为八进制数,即每位上计满8时向高位进一。
浅析“进位计数制及数制转换”

浅析“进位计数制及数制转换”姓名:唐章琪学号:1007021003班级:数学(1)班摘要:我们时刻都在和数打交道。
然而人类对数的认识和发展经历了一个极为漫长的过程。
进位制是数学发展史上的一个转折点,是古代文明最了不起的成就之一,标志着人类对数的认识进入一个崭新的时代。
在日常生活中,我们用的最多的、最习惯的是十进制。
除了十进制外,还有其他的进位制。
例如,角度和时间的单位都是60进制。
随着计算技术的迅速发展,我们需要掌握R进位制,目前,多数电子计算机都是对二进制数进行运算的,与二进制数密切关联的还有八进制数、十六进制数等等。
首先,本文对“进位计数制”作了简单介绍;其次,本文着重对在进位计数制的前提下定义的各种数制进行了转换。
关键词:进位计数制R进位制数制转换正文:日常生活中我们的计数方式有很多,如一年有12个月,则它是12的进制;一周有7天,则它是7的进制,等等。
实际这些计数方式都是我们人为规定的,而平常我们用的最多的、最习惯的是十进制(由于古人的10根手指便于帮助计数,便采用这种计数法(十进制),我们则遗留了古人留下来的财富)。
需要强调的是,任何一个值都可以用任何一种进制描述,但它的值是不变的,正如我们今天在一周中可以描述为星期几,在一个月中描述为多少号一样。
随着计算技术的迅速发展,我们需要掌握R进位制,目前,多数电子计算机都是对二进制数进行运算的,与二进制数密切关联的还有八进制数、十六进制数等等。
虽然计算机能极快地进行运算,但其内部并不像人类在实际生活中使用的十进制,而是使用只包含0和1两个数值的二进制。
当然,人们输入计算机的十进制被转换成二进制进行计算,计算后的结果又由二进制转换成十进制,这都由操作系统自动完成,并不需要人们手工去做。
接下来,我们对“进位计数制”作简单介绍;同时,着重对在进位计数制的前提下定义的各种数制进行了转换。
<一>进位计数制(数制)1.进位计数制的概念:数制也称计数制,是用一组固定的符号和统一的规则来表示数值的方法。
常用的进位计数制2007

常用的进位计数制2007-06-19 10:54不管是人类还是计算机都可以进行计算,这种计算包括1+2=3这样的算术运算,也包括1>2这样的逻辑运算。
在人类发展的过程中,通过"逢十进一"的计算方法已经得到了广泛的运用,由于计算机所采用的物理材料的特点,计算机从一开始就设计成采用"逢二进一"的计算方法。
那么,计算机是如何进行计算的,又是采用何中规则与人类惯用的"十进制"进行转换的呢?进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的方法进行计数,称为进位计数制。
在日常生活中,人们最常用的是十进位计数制,即按照逢十进一的原则进行计数;在计算机中采用的是二进位计数制,即按照逢二进一的原则进行计数。
在进位计数制中有数位、基数和位权三个要素。
数位是指数码在一个数中所处的位置;基数是指在某种进位计数制中,每个数位上所能使用的数码的个数;位权是指在某种进位计数制中,每个数位上的数码所代表的数值的大小,等于在这个数位上的数码乘上一个固定的数值,这个固定的数值就是这种进位计数制中该数位上的位权。
数码所处的位置不同,代表数的大小也不同。
例如数1011,在不同进位数制中所表示的数的大小不同。
见图3.1图 3.1 不同进位制中数的表示其中任何一个数的运算通式为:knkn-1。
k1k0 k-1。
k-m = ki R i几种常用的进位计数制进位计数制很多,这里主要介绍与计算机技术有关的四种常用进位计数制。
1.十进制十进位计数制简称十进制.十进制数具有下列特点:(1)有十个不同的数码符号0、1、2、3、4、5、6、7、8、9。
(2)每一个数码符号根据它在这个数中所处的位置(数位),按"逢十进一"来决定其实际数值,即各数位的位权是以10为底的幂次方。
例如:数(123.456) 10(123.456)10=1×102+2×101+3×100+4×10-1+5×10-2+6×10-3 (1)由上述分析可归纳出,任意一个十进制数K,可表示成如下形式:(K)10=Kn-1×10n-1+Kn-2×10n-2+…+K1×101+K0×100+K-1×10-1+K-2×10-2+…+K-m+1×10-m+1+K-m×10-m (2)式(2)中K为数位上的数码,其取值范围为0~9;N为整数位个数,M为小数位个数,10为基数,10n-1,10n-2…,101,100,10-1,…,10-m是十进制数的位权。
单片机数制基本知识

(3)非运算
规则为“按位取反”,即运算结果为参与运算的操作数取反后的值。具体规则如下:
(4)异或运算
0 =1, 1 =0
原则为“相异为1,相同为0”,即当两个操作不同时,结果为1;当两个操作数相同时,结
果为0。具体规则如下:
0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0
8
实际应用中存在正负数的问题,由于计算机只能识别0和1代码,因此,若要在计算机中表示正 负数,需要指定一位二进制位为符号位。通常指定二进制数据的最高位为符号位,最高位为0表示正 数,最高位为1表示负数。
其中:0的原码不唯一,即[+0]原=00000000B,[−0]原=10000000B。
9
(4)反码 正数的反码与该数的原码相同;负数的反码等于该数的原码保留符号位,其余位按位取反。
反码通常用[X]反表示。例如: X=+101,则[X]反=[X]原=01100101B X= - 101,则[X]原=11100101B,[X]反=10011010B
十六进制数 0 1 2 3 4 5 6 7
十进制数 8 9 10 11 12 13 14 15
4位二进制数 1000 1001 1010 1011 1100 1101 1110 1111
十六进制数 8 9 A B C D E F
6
1.算术运算
(1)二进制加法运算 根据“逢二进一”的原则,二进制加法法则为: 0+0=0,0+1=1,1+0=1,1+1=10(为2时向高位进一位)
1010
1010
0111
1101
8
1000
1011
1011
1110
1110
进位计数制

进位计数制:是人们利用符号来计数的方法。
一种进位计数制包含一组数码符号和两个基本因素。
(1)数码:用不同的数字符号来表示一种数制的数值,这些数字符号称为"数码"。
(2)基:数制所使用的数码个数称为"基"。
(3)权:某数制每一位所具有的值称为"权"。
1、常用进位计数制(1)十进制(D)数码:0、1、…… 8、9基数:10位权:10i (i=……-2,-1,0,1,2,……)逢10进1(2)二进制 (B)数码:0、1基数:2位权:2i (i=……-2,-1,0,1,2,……)逢2 进1(3)八进制 (O)数码:0、1、…… 6、7基数:8位权:8i (i=……-2,-1,0,1,2,……)逢8进1(4)十六进制 (H)数码:0、1、…… 8、9、A、B、C、D、E、F基数:16位权:16i (i=……-2,-1,0,1,2,……)逢16进1--------上面是他们的基本构成,下面是他们间的转换关系---------1 为什么需要八进制和十六进制?编程中,我们常用的还是10进制……必竟VB是高级语言。
比如:a = 99;不过,由于数据在计算机中的表示,最终以二进制的形式存在,所以有时候使用二进制,可以更直观地解决问题。
但,二进制数太长了。
比如int 类型占用4个字节,32位。
比如100,用int类型的二进制数表达将是:0000 0000 0000 0000 0110 0100面对这么长的数进行思考或操作,没有人会喜欢。
因此,C,C++ 没有提供在代码直接写二进制数的方法。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
不过,为什么偏偏是16或8进制,而不其它的,诸如9或20进制呢?2、8、16,分别是2的1次方,3次方,4次方。
这一点使得三种进制之间可以非常直接地互相转换。
8进制或16进制缩短了二进制数,但保持了二进制数的表达特点。
进位计数制教学ppt课件

十六进制数中,A-F表示十进制的10-15,例如:A表示十进 制的10,F表示十进制的15。
十六进制数的运算规则
加法运算
逢16进1,例如:2A+3F=5F。
减法运算
借位时从16借1,例如:5F-2A=36。
乘法运算
除法运算
按位相乘后相加,例如:(2A)x(3F)=7EF。
从被除数中连续去掉大于除数的位数,直 到被除数小于除数为止,例如: 7EF/3F=2A余1E。
在其他领域的应用
数学和物理
在数学和物理中,进位计数制被 广泛应用于数论、组合数学、图 论等领域,以及物理量的测量和
计算。
金融和商业
在金融和商业中,使用进位计数 制来表示货币、股票价格பைடு நூலகம்信息
,以及进行财务计算和分析。
语言学和社会科学
在语言学和社会科学中,使用进 位计数制来表示音节、单词、句 子等信息,以及进行语言分析和
在电子工程中的应用
数字电路设计
在数字电路设计中,使用进位计 数制来表示信号的状态和变化, 实现逻辑运算和组合电路的设计
。
通信系统
在通信系统中,使用进位计数制来 表示信号的幅度、频率和相位等信 息,实现信号的传输和调制解调。
自动控制系统
在自动控制系统中,使用进位计数 制来表示控制信号的状态和变化, 实现自动化控制和调节。
进位计数制教学ppt 课件
目录
CONTENTS
• 进位计数制简介 • 二进制数制 • 八进制数制 • 十六进制数制 • 进位计数制的应用
01 进位计数制简介
进位计数制的定义
总结词
进位计数制是一种数字表示方法,它根据进位规则将数值表示为不同的符号或 数字的组合。
计算机应用基础进位计数制

计算机应用基础进位计数制在计算机科学和应用中,进位计数制是一种数值表示法,它使用不同的符号来表示不同的数值。
这种表示法通常用于计算机内部数据存储和计算,因为它可以有效地表示大范围的数值,并且可以进行简单的算术运算。
在进位计数制中,每个数字的权值等于它所在位置的次方。
例如,在十进制中,个位的权值为1,十位的权值为10,百位的权值为100,以此类推。
因此,数字918可以表示为9×100+1×10+8。
在计算机中,最常用的进位计数制是二进制、八进制和十六进制。
这些进位计数制的符号和权值如下:二进制:符号为0和1,权值分别为2的次方。
例如,数字1101可以表示为1×23+1×22+0×21+1。
八进制:符号为0到7,权值分别为8的次方。
例如,数字17可以表示为1×8+7。
十六进制:符号为0到9和A到F,权值分别为16的次方。
例如,数字255可以表示为2×162+5×161+5×160。
这些进位计数制在计算机科学和应用中有许多优点。
它们可以有效地表示大范围的数值,因为它们的权值通常比十进制大得多。
它们可以进行简单的算术运算,例如加法、减法、乘法和除法。
它们也适用于计算机内部的存储和传输,因为它们可以减少数据的大小并提高效率。
进位计数制是计算机科学和应用中非常重要的概念之一。
它不仅可以有效地表示大范围的数值,还可以进行简单的算术运算,并且适用于计算机内部的存储和传输。
随着信息技术的不断发展,计算机已经成为我们生活中不可或缺的一部分。
在农业领域,计算机的应用也日益广泛,为农业生产带来了巨大的改变。
本文将介绍农大计算机计算机应用基础的相关知识,包括计算机在农业生产中的应用、农业信息化技术、农业物联网技术、农业大数据技术等。
计算机在农业生产中有着广泛的应用,包括农业专家系统、农业遥感监测、农业智能机器人等。
这些技术的应用,使农业生产更加智能化、高效化,提高了农产品的产量和质量。
进位计数制名词解释

进位计数制名词解释
进位计数制是一种数学计数系统,它使用不同的进位基数来表
示数字的不同位数。
在进位计数制中,每个位上的数值都是基于进
位基数的倍数。
常见的进位计数制包括十进制、二进制、八进制和
十六进制。
十进制是我们最常用的计数制,它使用基数10,即每个位上的
数值可以是0到9之间的数字。
例如,数字123表示1个百位数、2
个十位数和3个个位数。
二进制是一种使用基数2的进位计数制,只有两个数字0和1。
它在计算机科学和电子工程中得到广泛应用。
例如,数字1011表示
1个八位数、0个四位数、1个二位数和1个个位数,相当于十进制
的11。
八进制使用基数8,每个位上的数值可以是0到7之间的数字。
它在计算机编程和控制系统中常用。
例如,数字567表示5个百位数、6个十位数和7个个位数,相当于十进制的375。
十六进制使用基数16,它除了0到9的数字外,还使用A到F
的字母表示10到15。
它在计算机科学、网络和颜色表示中经常使用。
例如,数字3A7表示3个256位数、10个16位数和7个个位数,相当于十进制的935。
进位计数制的优点是可以用较少的位数表示较大的数值,同时在某些领域中更易于处理和转换。
不同进位计数制之间可以通过进位和借位的方式进行转换。
了解和掌握不同进位计数制有助于我们更好地理解数字表示和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.1 常用的进位计数制
人们习惯的是用十进制表示数,但在计算机内,各种信息都是用二进制代码形式表示的,用户书写时又大都使用十六进制,有时也用八进制。
如表3.1所示。
任意一个R进制的数,都有以下三个要点:
(1) 基数为R,即使用R个数码。
例如,十进制有0~9十个数码,R=10;而二进制只有0和1两个数码,R=2。
(2) 进位规则为逢R进一。
例如,十进制逢十进一,二进制逢二进一。
(3) 第i个数位上的数码所具有的位权为R i。
由于不同位置上的权值不同,因此同一数码在不同位置上,其表示的值也不同。
每个数位上的值等于该位置上的数码与权值的乘积。
而数值可用下面的通式表示:
N = a n-1R n-1+ a n-2R n-2 +∧+a1R1 +a0R0+∧+a--m R—m
式中,R代表基数,a i表示第i位数位上的数码,0 ≤a i< R,R i 表示数位的权,m和n为正整数。
十进制、二进制、八进制、十六进制数后面分别加字母D、B、Q、H予以区别。
